страница 1
1 Переходные процессы в линейных цепях с сосредоточенными
параметрами
Переходные процессы (ПП) возникают в цепях при всех изменениях режима электрической цепи: включение и выключение цепи или её отдельных участков, короткое замыкание, обрыв и т. п. Эти процессы не могут протекать мгновенно, так как не возможны мгновенные изменения энергии, запасённой в электрическом и магнитном полях цепи.
В цепях с сосредоточенными параметрами энергия запасается в ёмкостях в виде энергии электрического поля 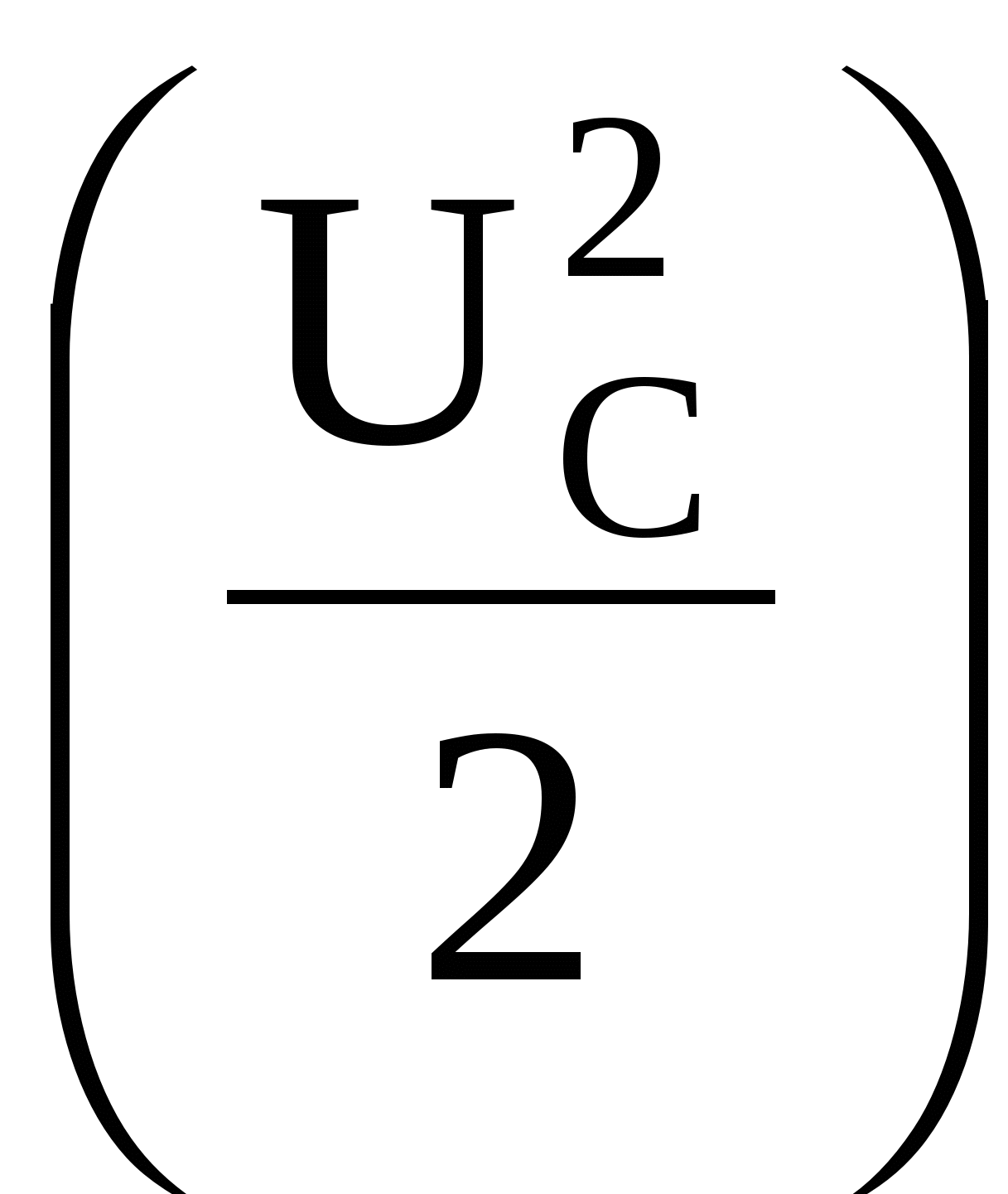 и в индуктивностях в виде энергии магнитного поля и в индуктивностях в виде энергии магнитного поля 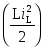 . Из-за невозможности мгновенных изменений энергии на конечную величину вытекает невозможность скачков напряжения UC на ёмкостях и токов iL в индуктивностях L. Отсюда вытекают законы коммутаций. . Из-за невозможности мгновенных изменений энергии на конечную величину вытекает невозможность скачков напряжения UC на ёмкостях и токов iL в индуктивностях L. Отсюда вытекают законы коммутаций.
Первый закон коммутации: в ветви с индуктивностью ток (магнитный поток) после коммутации при t = + 0 сохраняет то значение, которое он имел непосредственно перед коммутацией, то есть при t = 0, далее в переходном процессе ток индуктивности (магнитный поток) начинает изменяться именно с этого значения:
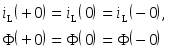 (1.1) (1.1)
Второй закон коммутации: на конденсаторе напряжение (заряд) в момент коммутации (t = + 0) сохраняет то значение, которое оно имело непосредственно перед коммутацией (t = 0), и далее в переходном процессе напряжение (заряд) начинает изменяться именно с этого значения:
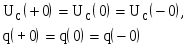 (1.2) (1.2)
Коммутацией называется любое изменение в цепи. На схемах коммутации изображаются в виде ключей, которые показывают исходные (докоммутационные) состояния цепи (рисунок 1.1, а, б). На рисунке 1.1, а ключ замыкается, на рисунке 4.1, б ключ размыкается при t = 0. Так как принято считать, что коммутации происходят мгновенно.
   
а б
Рисунок 1.1
К независимым начальным условиям (ННУ) относятся iL(0), Ф(0) - ток и магнитный поток в индуктивности в момент коммутации при t = 0, UC(0), q(0) - напряжение и заряд на конденсаторе в момент коммутации.
К зависимым начальным условиям относятся ток в ёмкости, напряжение на индуктивности, ток и напряжение на резисторе в момент коммутации iC(0), UL(0), ir(0),Ur(0).
Для расчёта переходных процессов в цепях составляется система дифференциальных уравнений по законам Ома и Кирхгофа для мгновенных значений токов и напряжений. Решение линейных дифференциальных уравнений с постоянными коэффициентами представляет сумму двух решений
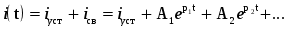 , ,
где i(t) - ток переходного процесса, искомая величина;
iуст – частное решение неоднородного дифференциального уравнения;
iсв – общее решение однородного дифференциального уравнения, выраженное через постоянные интегрирования А1, А2, ... и р1, р2, ... - корни характеристического уравнения для случая, когда все корни различны.
Ток установившегося режима iуст. При постоянных и периодических источниках рассчитывается любым из методов расчёта линейных цепей.
Общее решение iсв однородного уравнения описывает процесс, происходящий без воздействия внешних источников. Ток iсв имеет одинаковый вид для любого переходного процесса в заданной цепи. Это решение называют свободной составляющей переходного процесса.
Постоянные интегрирования А1, А2, ... определяются из начальных условий. Переходный ток i(t) переходит в установившийся iуст при затухании свободного тока iсв. Теоретически переходный процесс длится бесконечно, но практически время переходных процессов в большинстве электрических цепей исчисляется долями секунды.
1.1 Классический метод расчета переходных процессов
Классический метод расчёта переходных процессов состоит в составлении дифференциальных уравнений цепи в переходном процессе, их решении и определении постоянных интегрирования из начальных условий. Рассмотрим методику расчета ПП классическим методом на примере расчета переходного тока i2(t) в разветвленной цепи с источником постоянной ЭДС (рисунок 1.2).
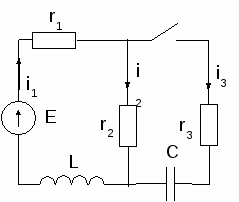
Рисунок 1.2
1 Определение ННУ производится из анализа докоммутационной цепи расчетом значений тока в индуктивности iL(0) и напряжения uC(0) на емкости при t = 0
iL(0)=i1(0)=iL(0)=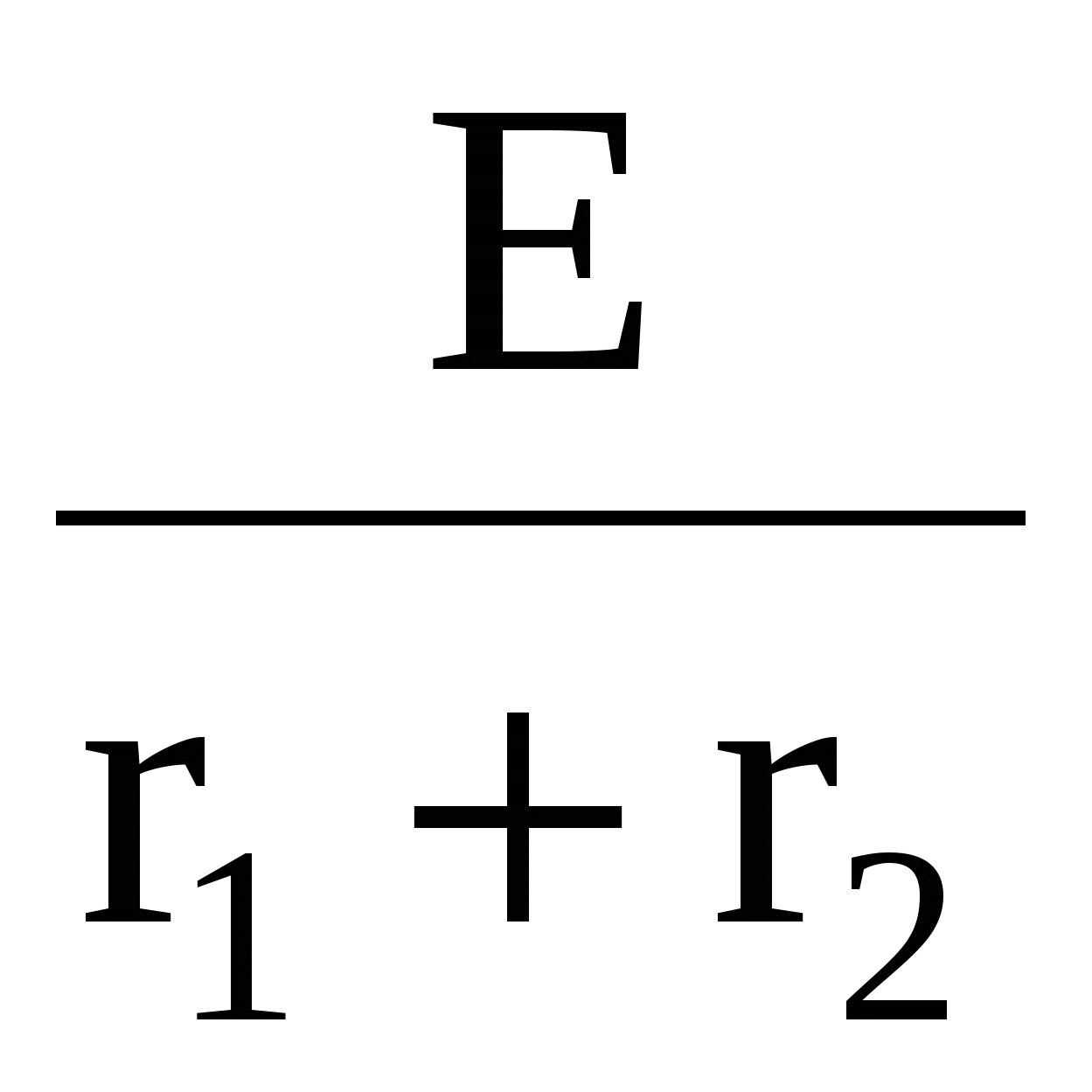 (1.3) (1.3)
uC(0) = uC(0) =0.
-
Определение корней характеристического уравнения
-
характеристическое уравнение составляется по дифференциальному уравнению для свободной составляющей;
- составляется выражение для комплексного входного сопротивления послекоммутационной схемы с последующей заменой j на р, полученное выражение приравнивается к нулю.
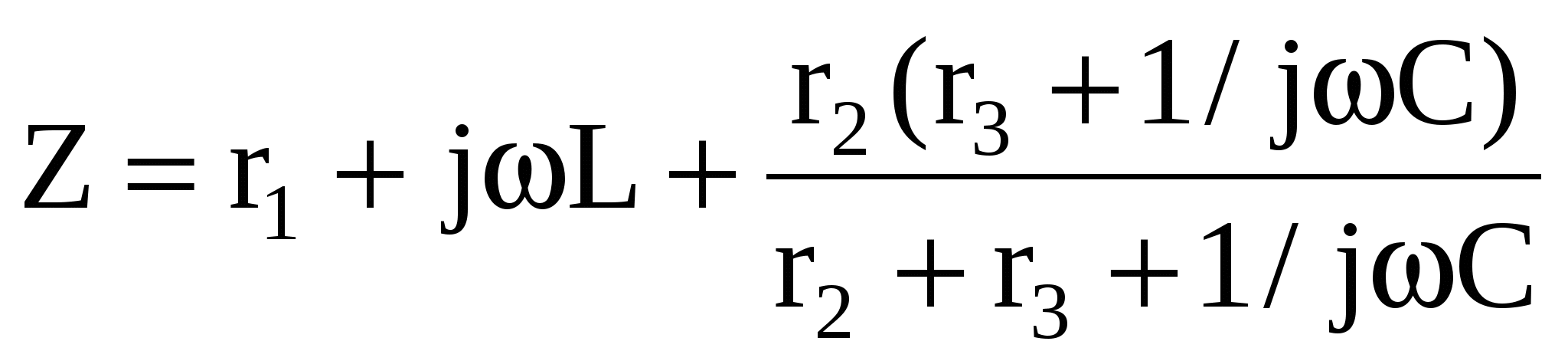 , ,
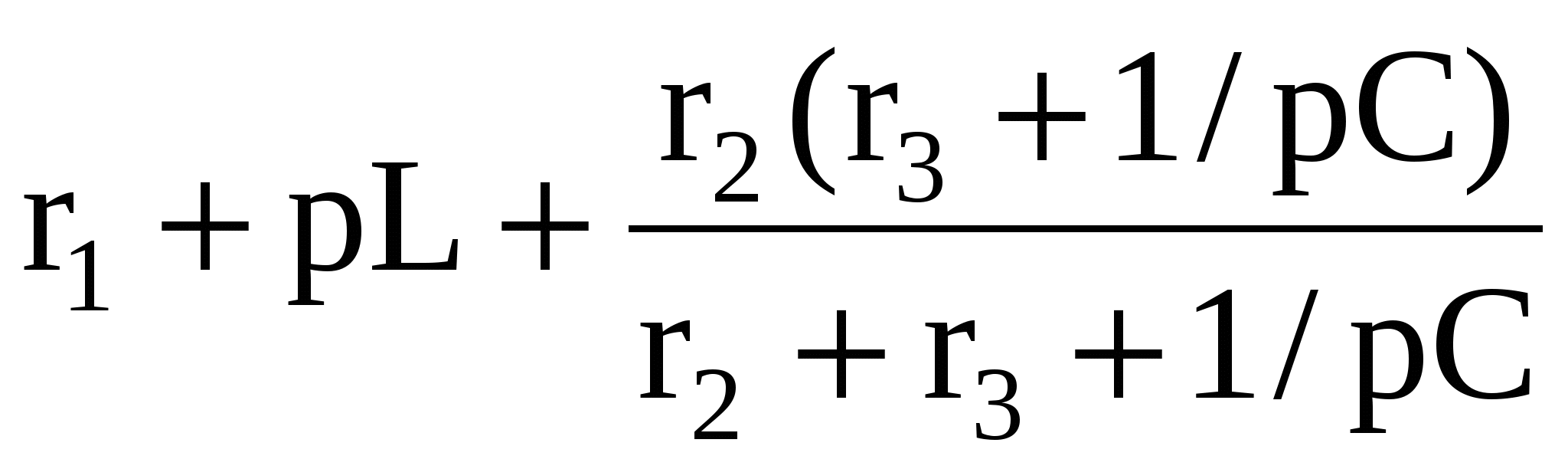 = 0 = 0
После преобразований получим характеристическое уравнение
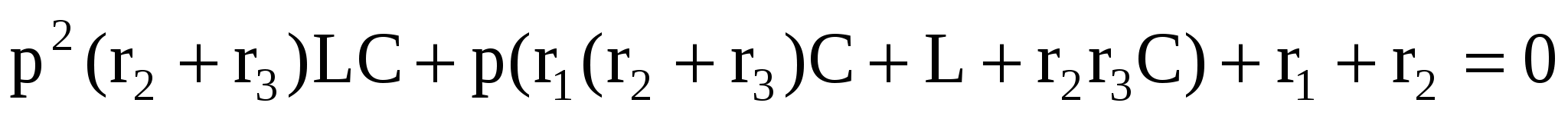 (1.4) (1.4)
Решением характеристического уравнения (1.4) относительно р находят его корни.
По виду корней характеристического уравнения записывается выражение свободной составляющей искомой величины. При этом возможны три варианта (нижеследующие записи даны для тока, но такие же записи используются и для напряжения).
а) корни действительные (всегда отрицательные), неравные: р1р2. В этом случае
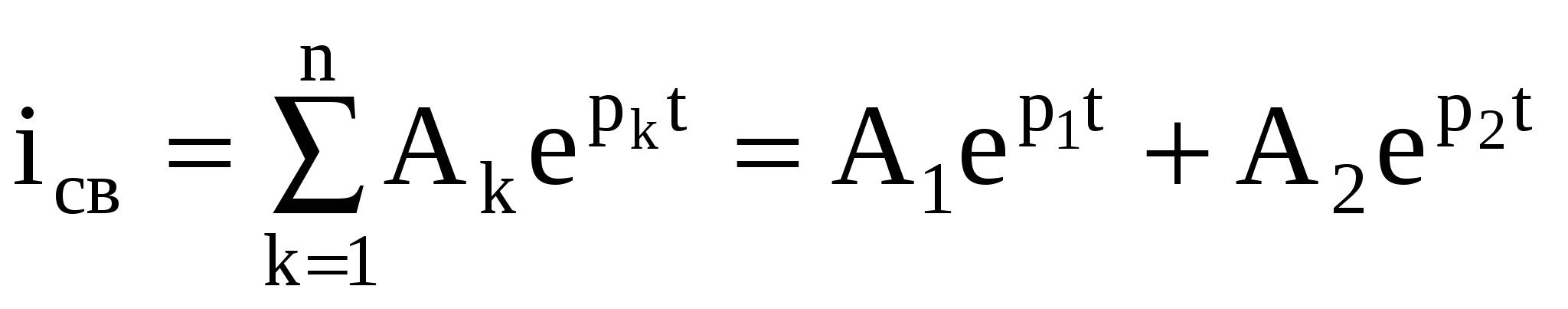 , ,
где рк – к-тый корень уравнения (1.4); Ак – неизвестные константы, представляющие собой постоянные интегрирования, получаемые при решении однородного дифференциального уравнения; к=1 при n=1 и к=1,2 при n=2;
б) корни комплексно-сопряженные р1= - + j0, р2= - - j0.
В этом случае свободная составляющая тока в ПП определяется так
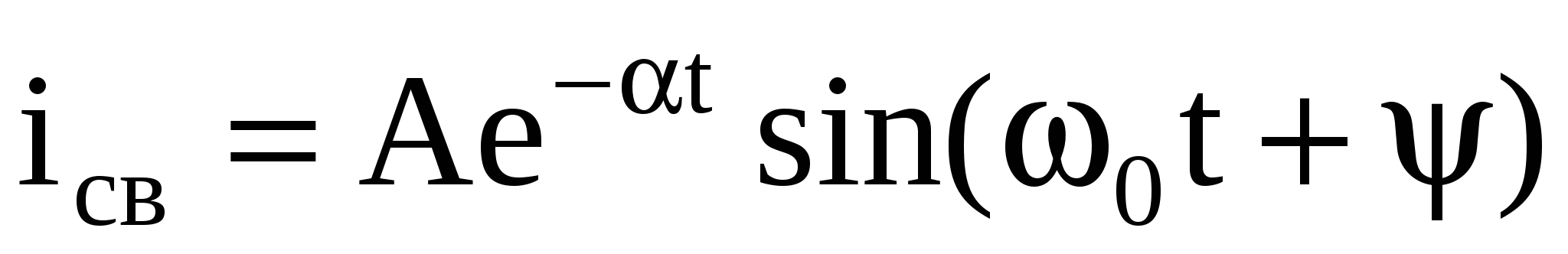 , ,
где , 0 – положительные действительные числа, - коэффициент затухания, 0 – частота собственных колебаний контура, А и - неизвестные константы, подлежащие определению на последующих этапах решения задачи.
в) корни равные (действительные, отрицательные) р1 = р2 = - а.
Тогда iсв = (А1 + А2t)е-at,
где А1 и А2 – неизвестные постоянные интегрирования.
3 Определение выражения искомого тока i2(t) в переходном процессе
i2(t) = i2уст + i2св
Ток установившегося режима i2уст определяем из анализа и расчёта схемы после окончания ПП. Переходный процесс в цепи возникает из-за того, что конденсатор заряжается. Свободный ток i2св определяется видом корней характеристического уравнения. В нашем случае при вещественных и неравных корнях имеем
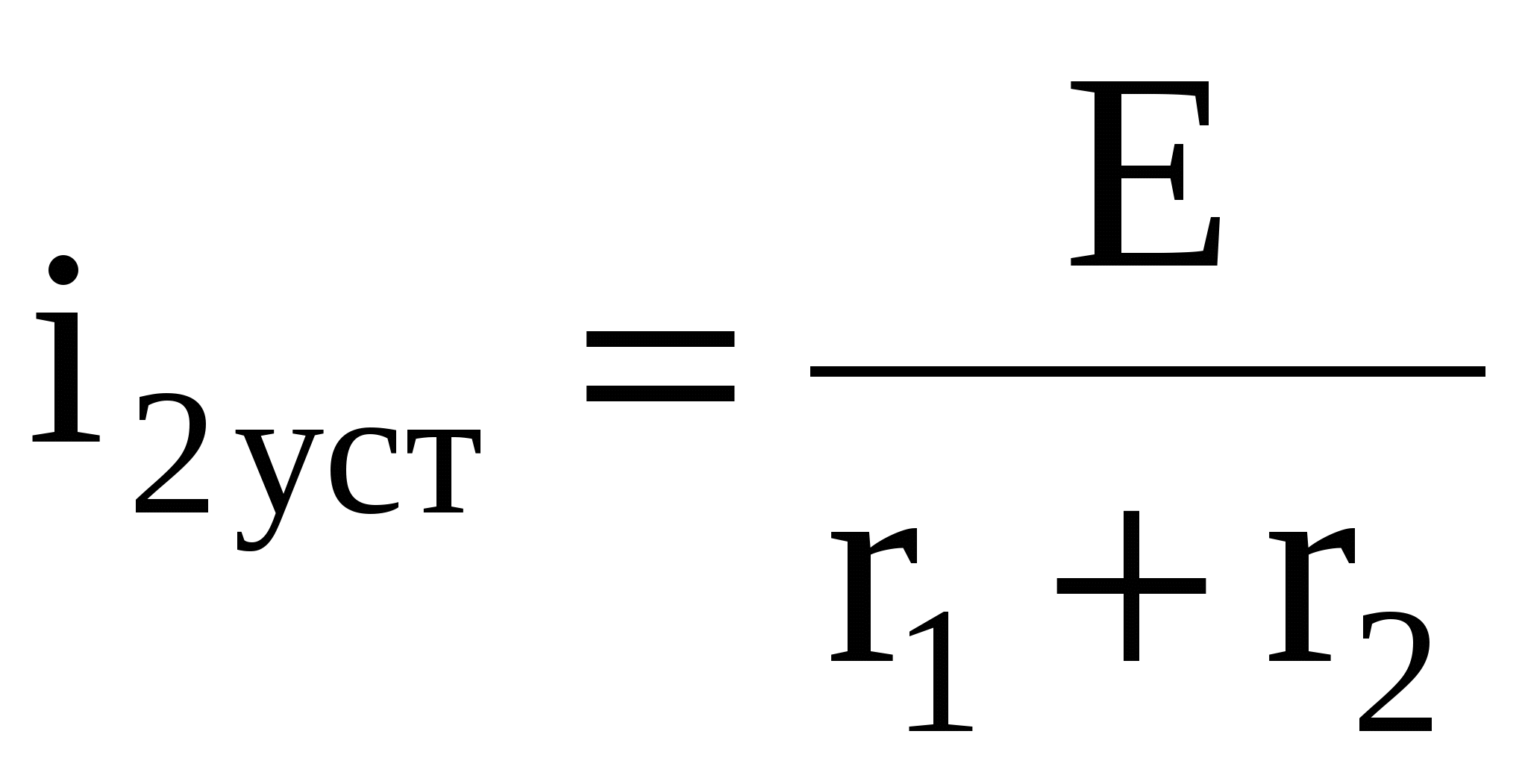 , , 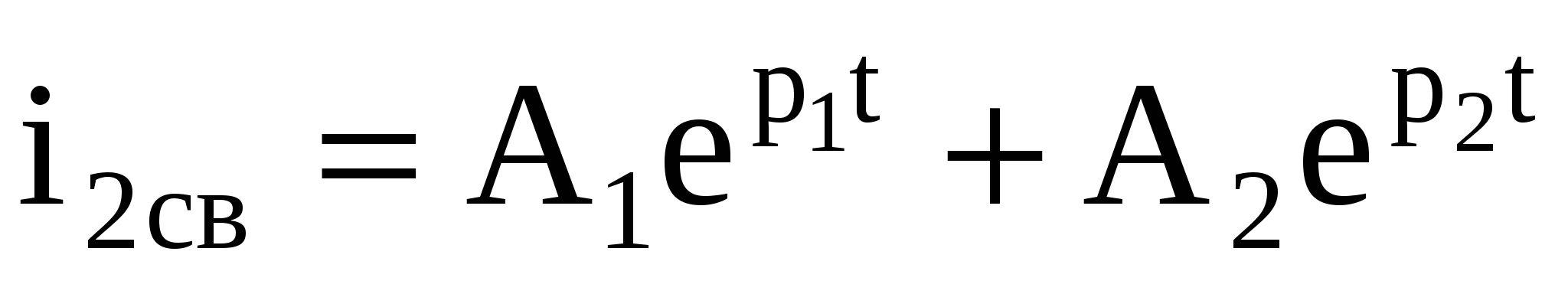 (1.5) (1.5)
Ток переходного процесса
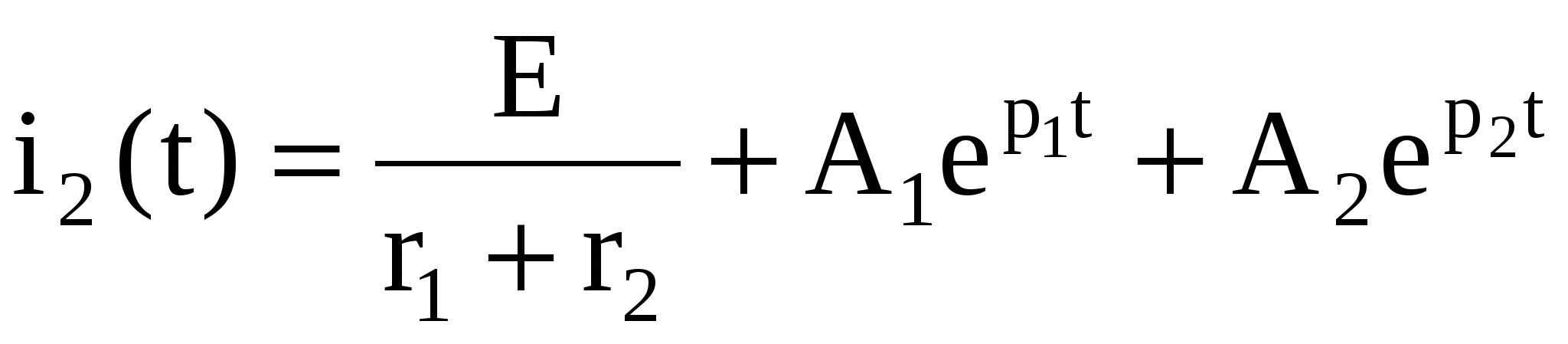 (1.6) (1.6)
Для определения двух неизвестных А1 и А2 составляем второе уравнение, дифференцируя полученное выражение переходного тока i2(t)
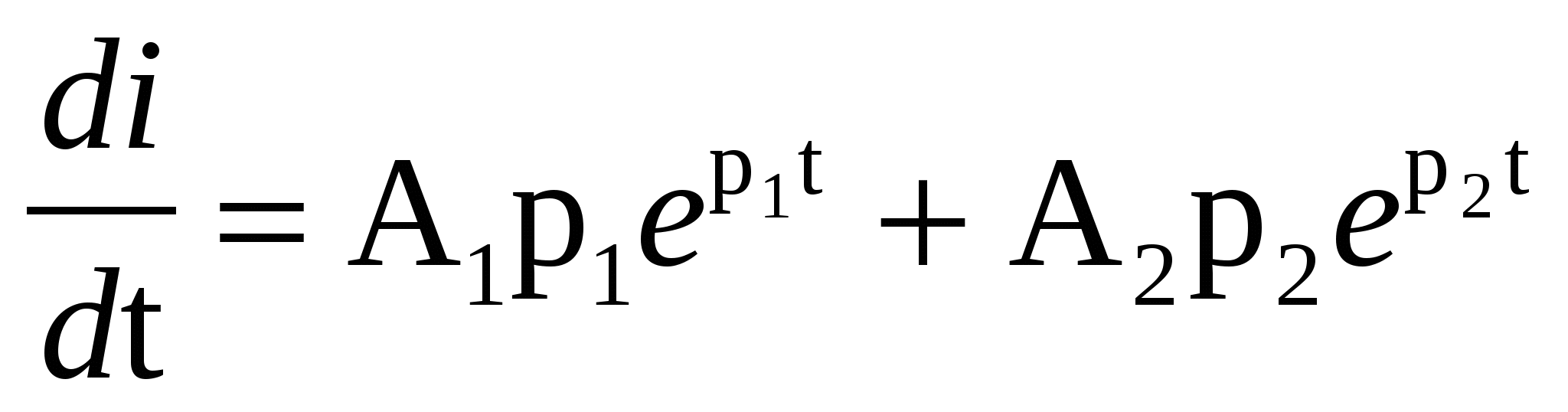 (1.7) (1.7)
4 Определение постоянных интегрирования А1 и А2 из начальных условий при t = 0 из следующей системы уравнений, получаемой при рассмотрении уравнений (1.6) и (1.7) в момент коммутации
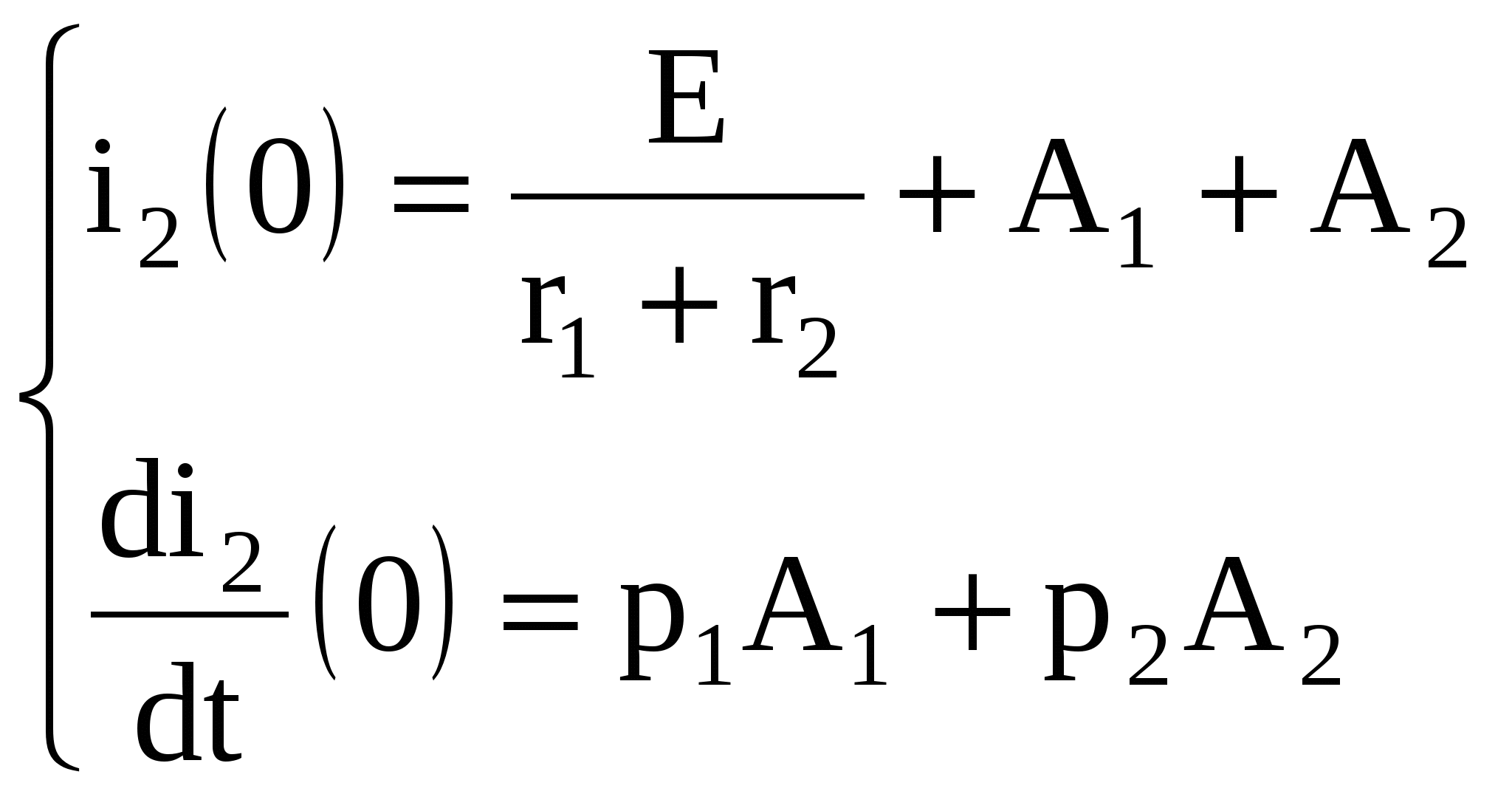 (1.8) Для решения системы (1.8) необходимо знать значение тока i2 и его производной на момент коммутации (t = 0). (1.8) Для решения системы (1.8) необходимо знать значение тока i2 и его производной на момент коммутации (t = 0).
5 Для определения i2(0) и di2(0)/dt составляется система уравнений по первому и второму законам Кирхгофа для любого момента времени после коммутации
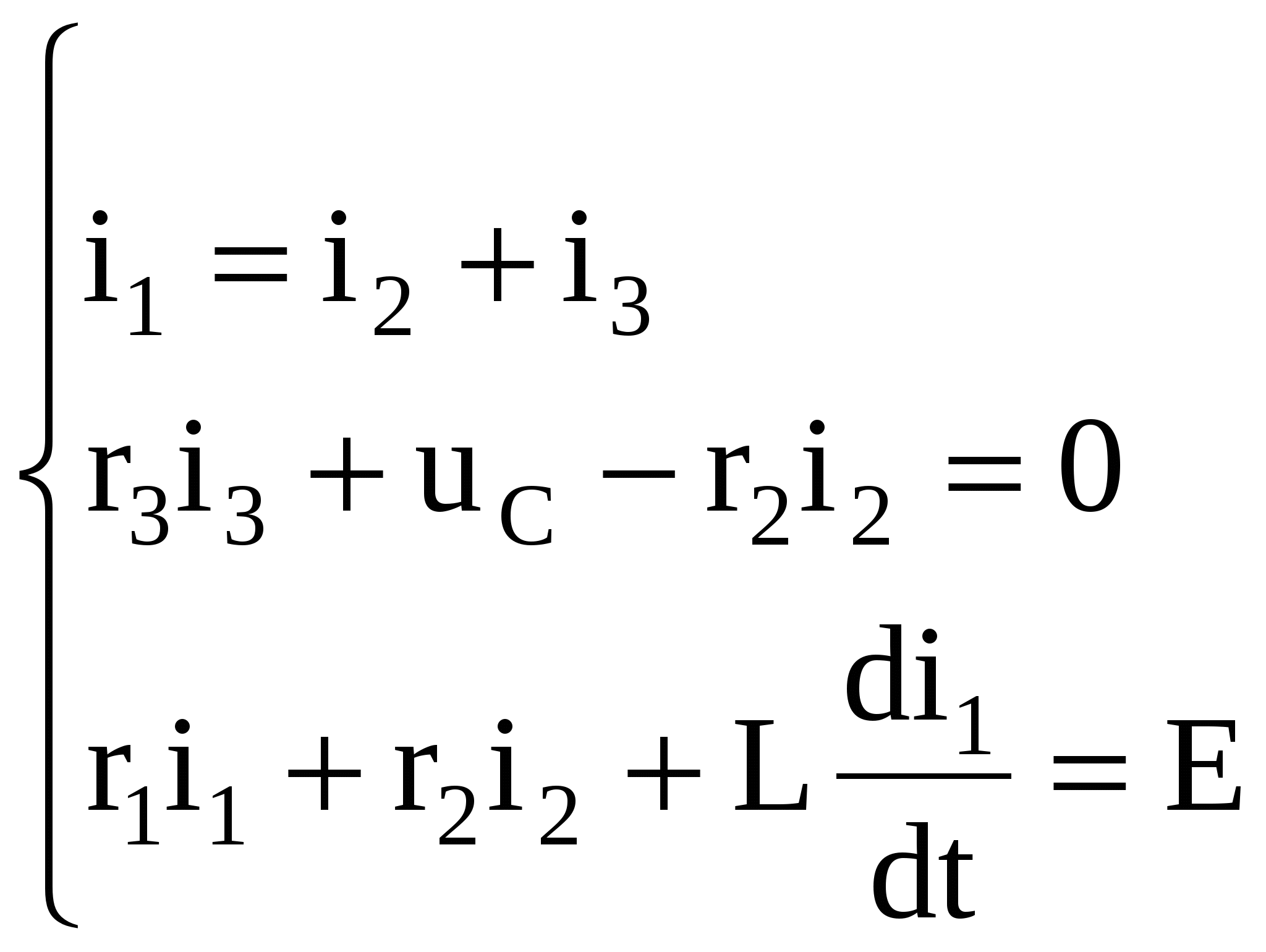 (1.9) (1.9)
Записываем первые два уравнения системы (1.9) на момент коммутации (t = 0)
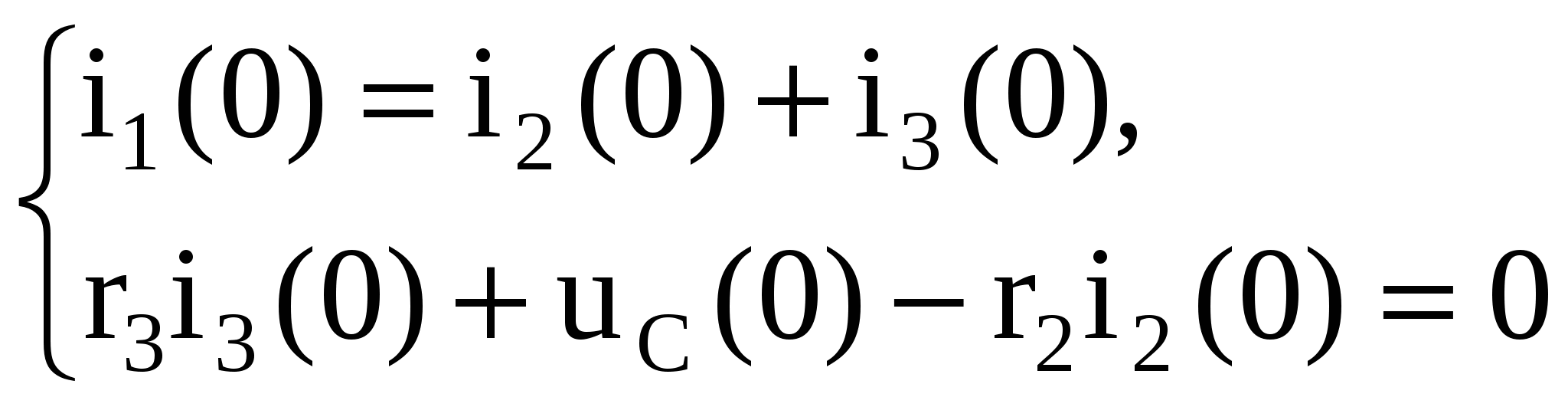 (1.10) (1.10)
Из системы (1.10) с учетом ННУ (1.3) определяются значения i3(0), i2(0).
Первое и второе уравнения системы (1.9) дифференцируются, получившаяся система уравнений записывается при t = 0
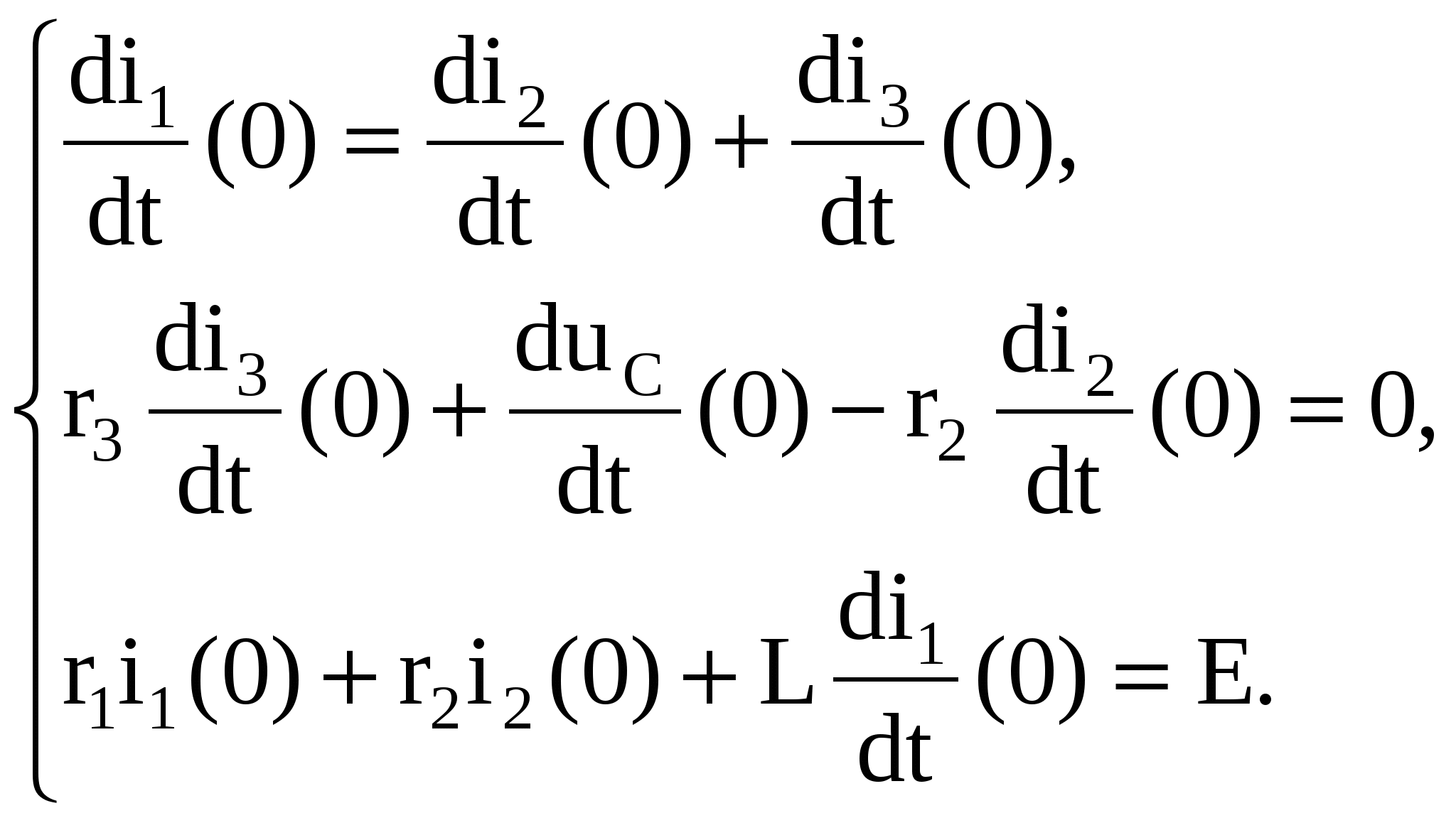 (1.11) (1.11)
Из системы (1.11) находится значение 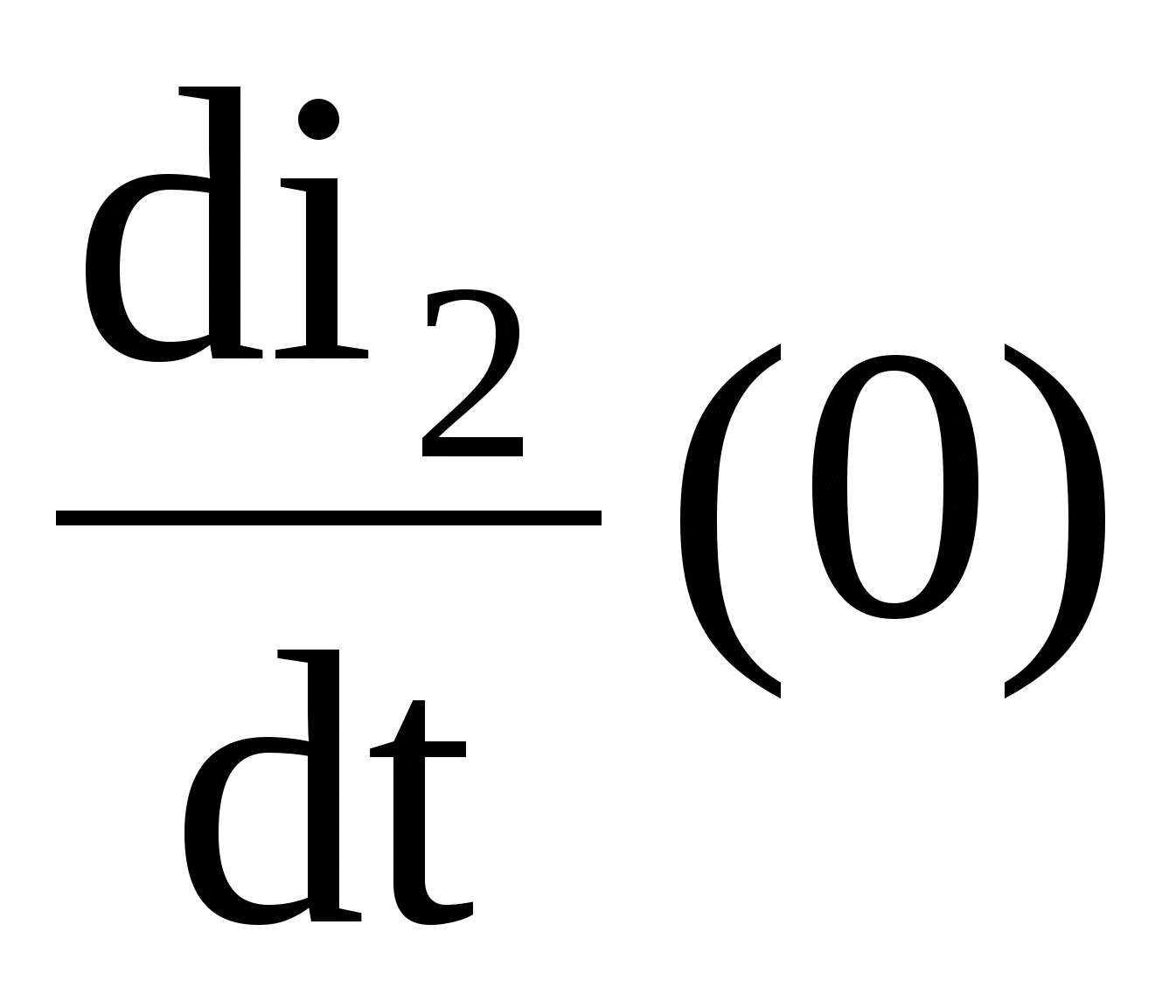 . При этом учитывается, что . При этом учитывается, что 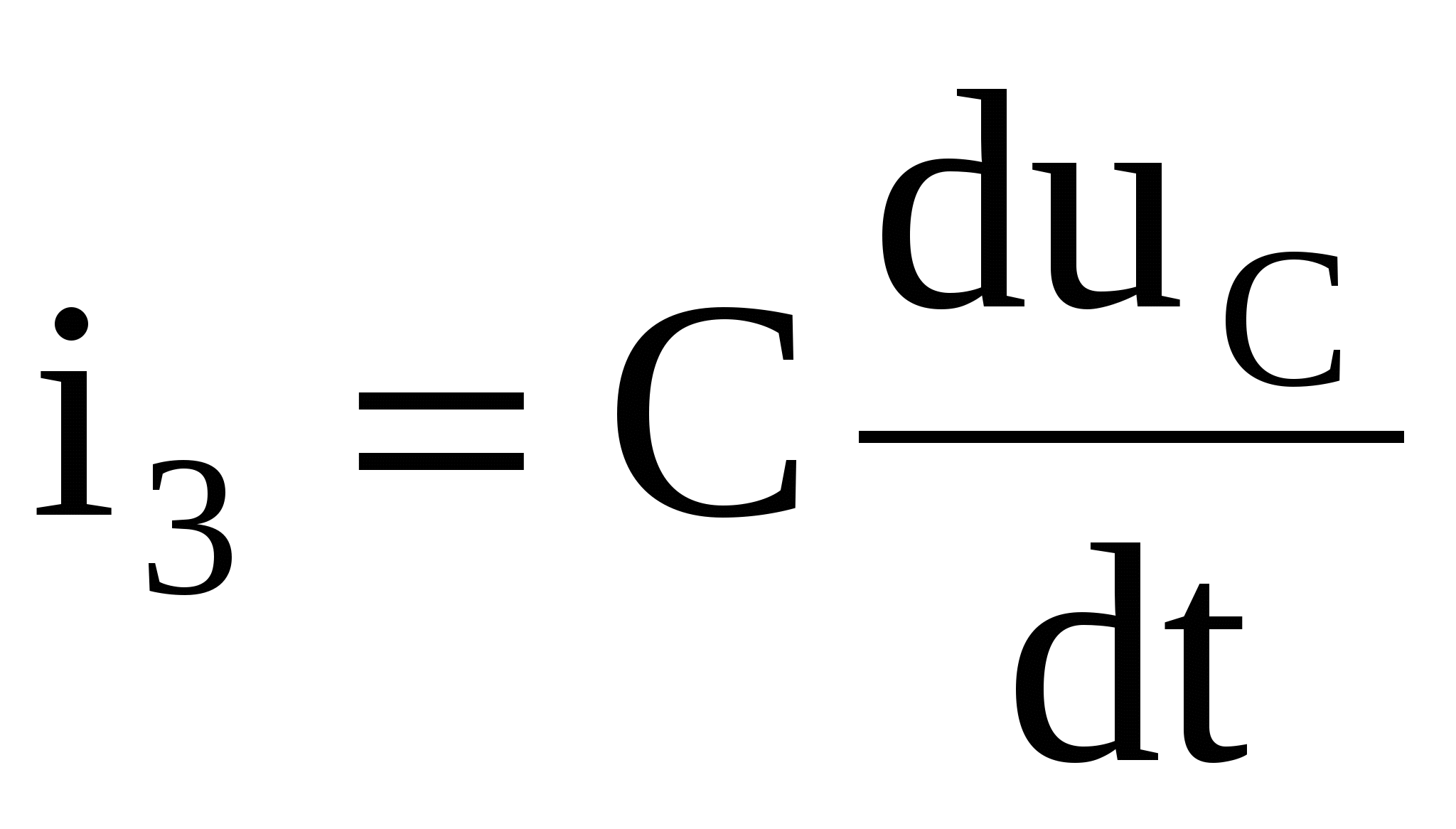 , то есть , то есть 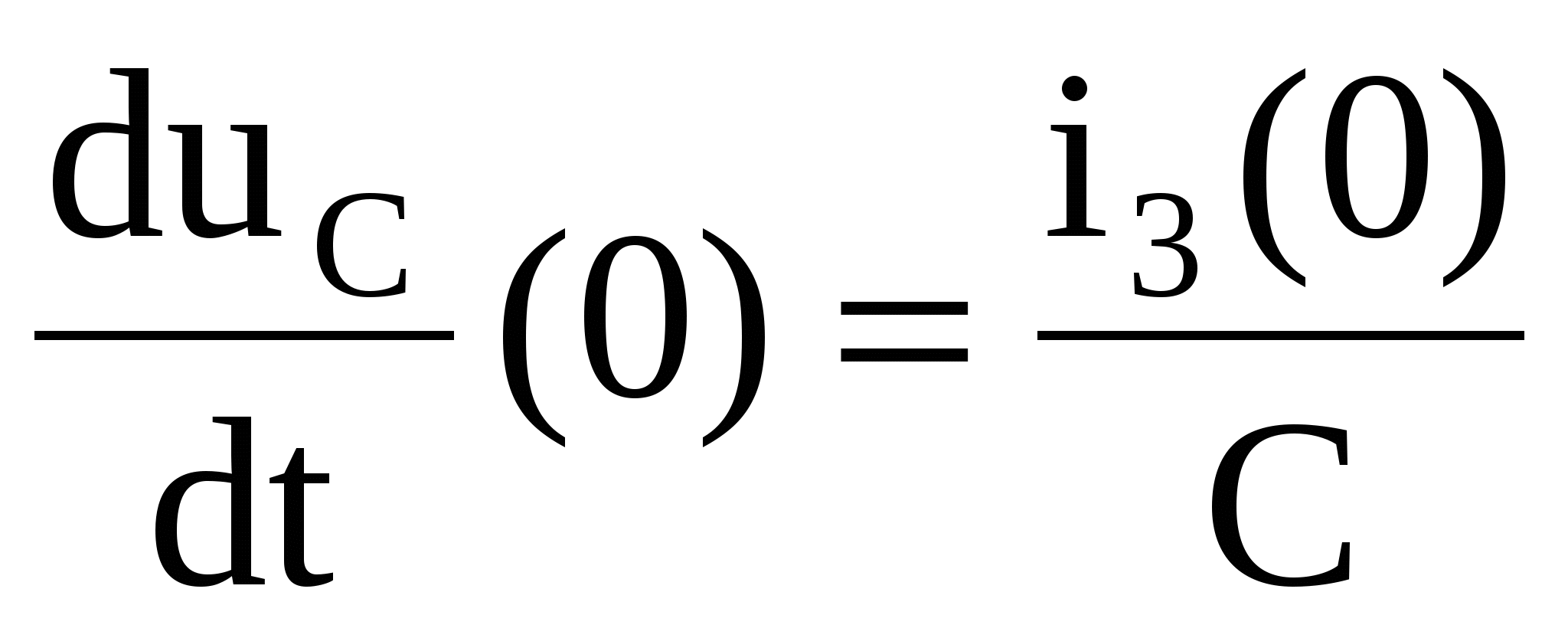 . Значение i3(0) найдено из системы (1.10). . Значение i3(0) найдено из системы (1.10).
Найденные значения i2(0), di2(0)/dt подставляются в систему (1.8), из которой определяются постоянные интегрирования А1 и А2. После подстановки значений А1, А2 в уравнение (1.6) находится искомое выражение тока i2(t) в режиме переходного процесса.
1.2 Операторный метод расчета переходных процессов
При расчете переходных процессов классическим методом требуется в общем случае многократное решение систем алгебраических уравнений для определения постоянных интегрирования по начальным условиям, что и представляет основную трудность расчета этим методом.
Дифференциальные уравнения, описывающие ПП в линейных цепях с сосредоточенными параметрами, являются линейными с постоянными коэффициентами. Решение этих уравнений, то есть их интегрирование можно проводить и операторным методом, основанным на преобразовании Лапласа. Преобразование Лапласа позволяет осуществить переход от действительного переменного времени t – к комплексной переменной р, при этом происходит замена дифференциальных уравнений алгебраическими относительно изображений.
При решении системы алгебраических уравнений определяется изображение искомой величины, по которому при использовании теоремы разложения находится оригинал искомой величины (функция времени t).
Вследствие того, что ПП описываются дифференциальными уравнениями с постоянными коэффициентами, то необходимо показать изображения:
-
производной от оригинала f(t)
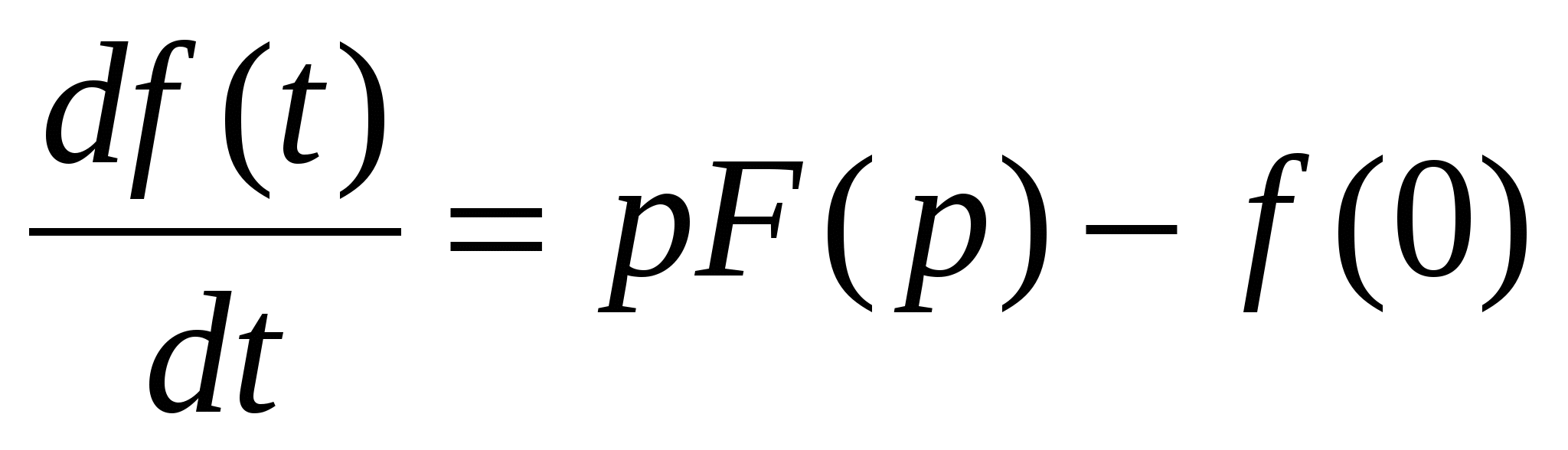 , (1.11) где F(p) – изображение оригинала (функции f(t)), , (1.11) где F(p) – изображение оригинала (функции f(t)),
f(0) – значение функции f(t) при t = 0;
-
интеграла от оригинала f(t)
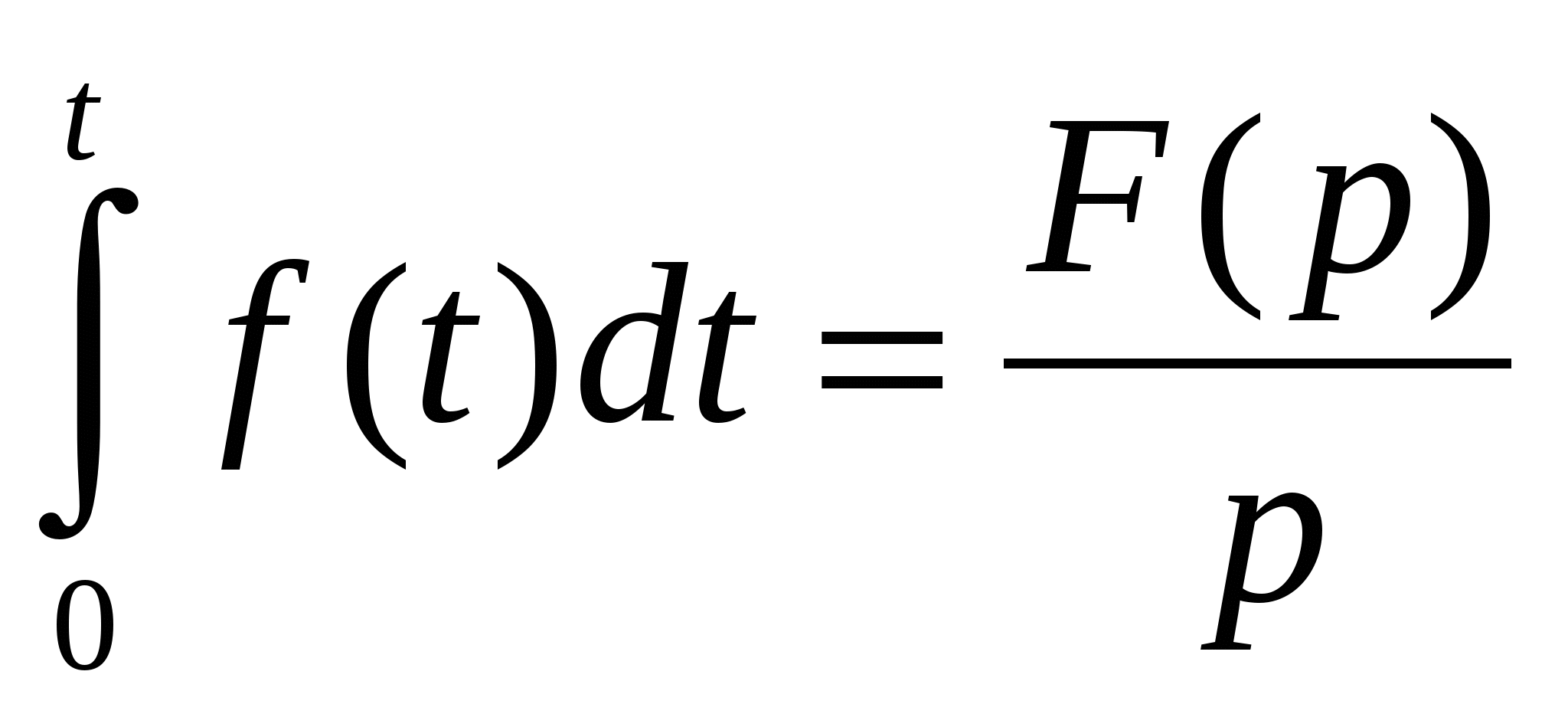 (1.13) (1.13)
Например, изображение напряжения на индуктивности определяется следующим выражением
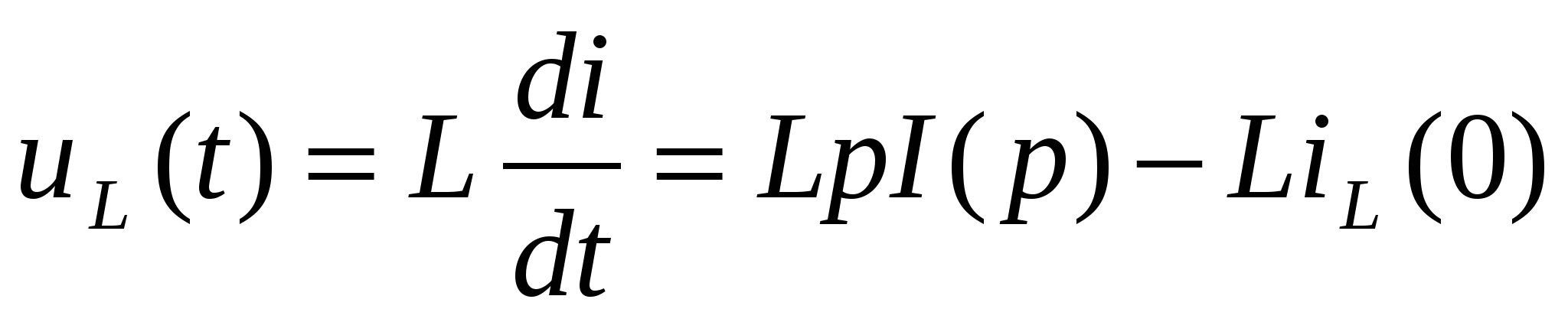 , (1.14) , (1.14)
где I(p) – изображение тока i(t); iL(0) – значение тока в ветви с индуктивностью при t = 0 (ННУ). Если iL(0) = 0, то
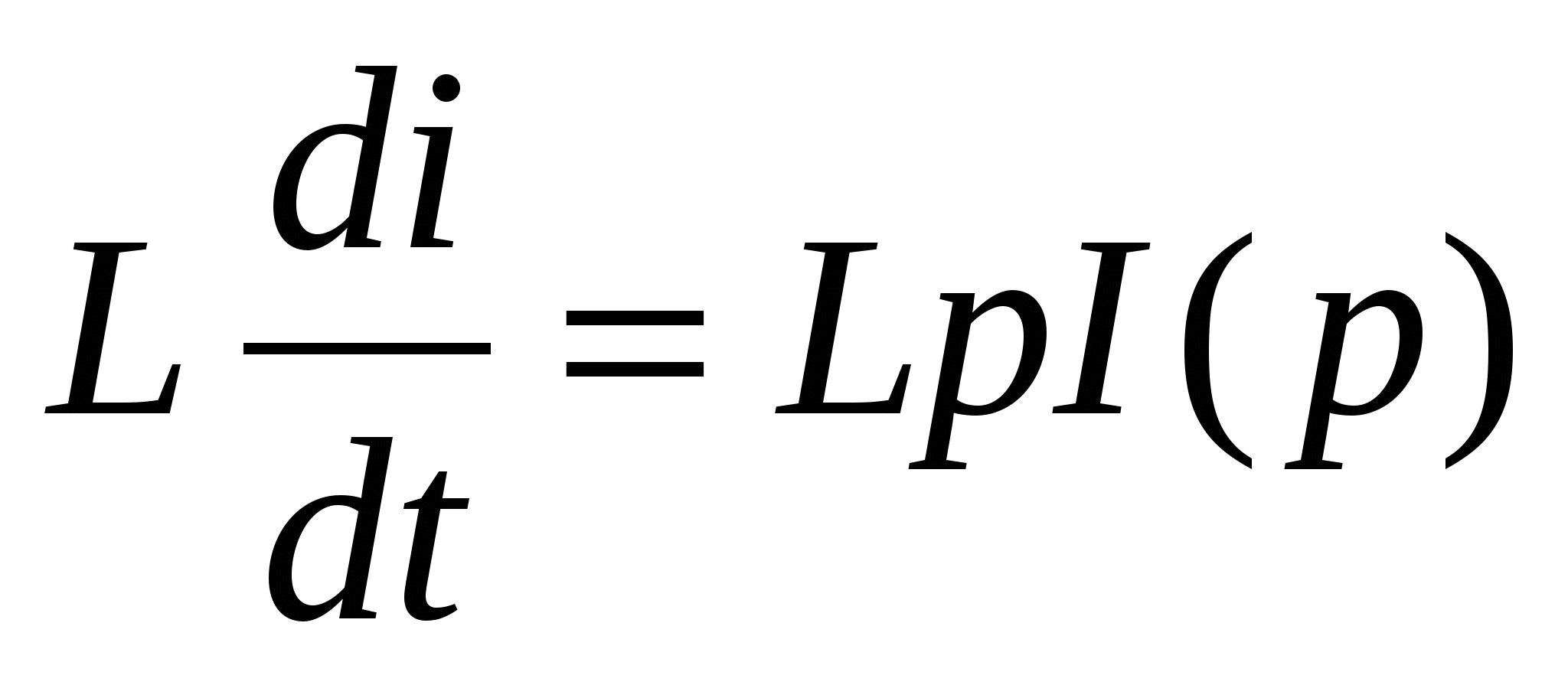
Изображение напряжения на конденсаторе
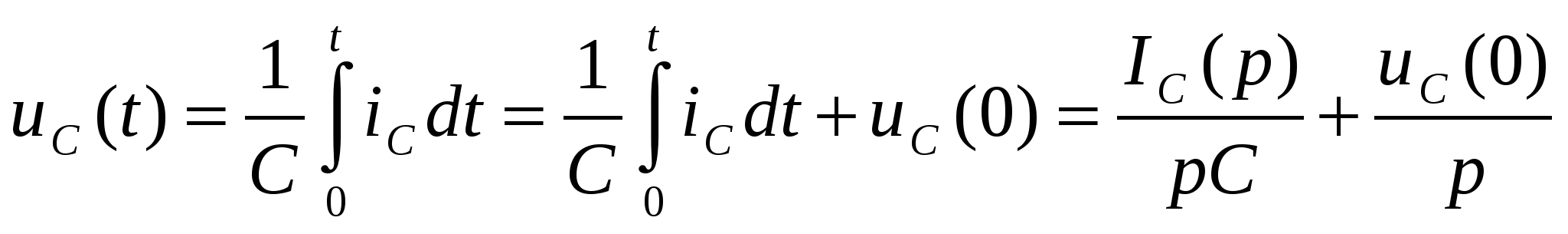 , (1.15) где uC(0) – значение напряжения на конденсаторе при t = 0 (ННУ). Если uC(0) = 0, то , (1.15) где uC(0) – значение напряжения на конденсаторе при t = 0 (ННУ). Если uC(0) = 0, то
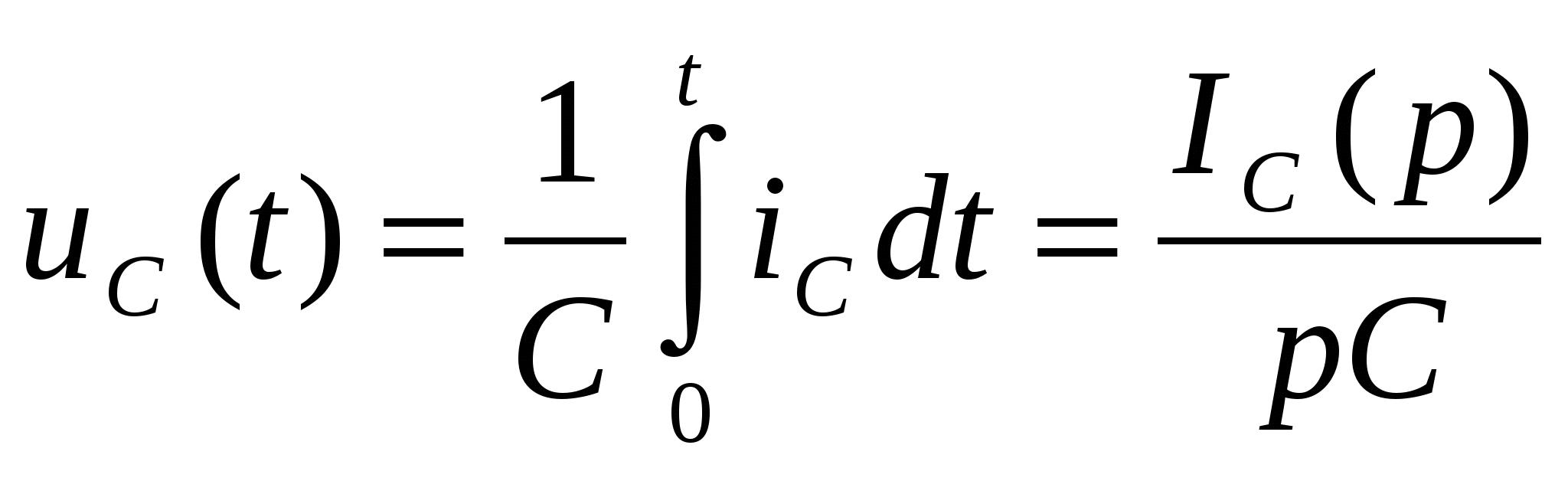
Изображение постоянной К представляется следующим образом
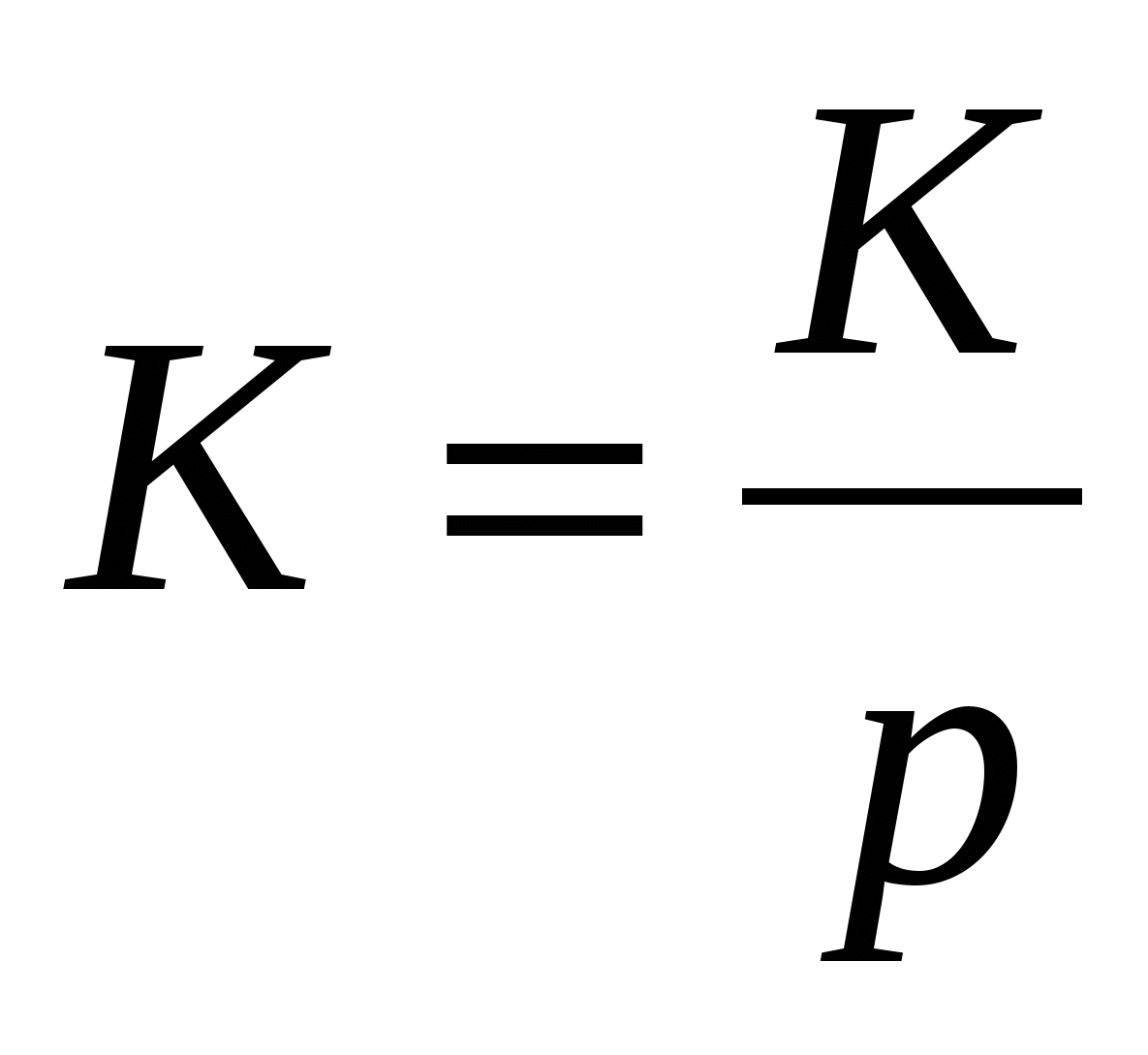 (1.16) Источник постоянной ЭДС Е представляется как (1.16) Источник постоянной ЭДС Е представляется как 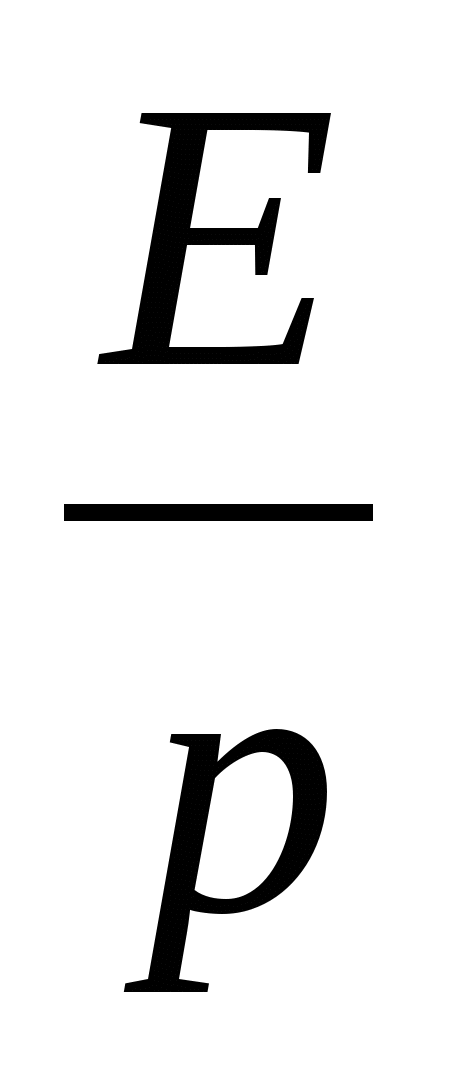 . .
Изображение синусоидальной функции
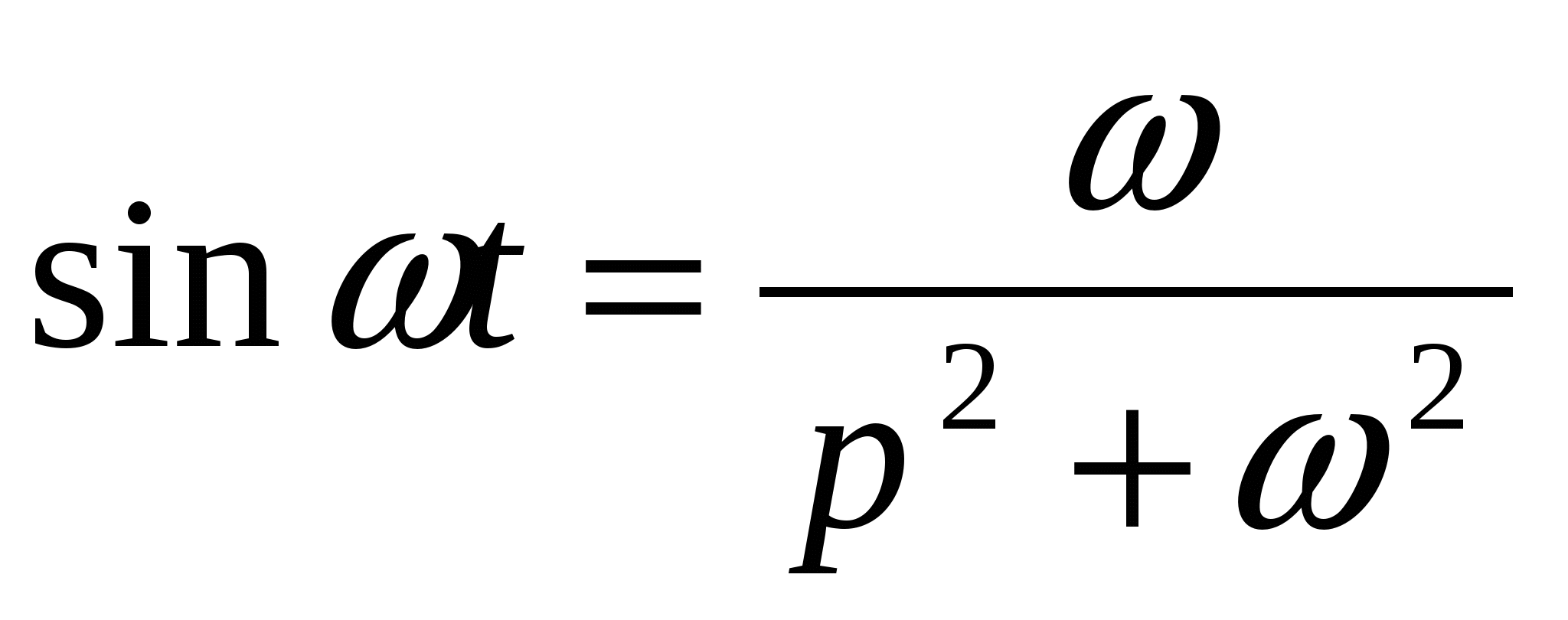 , ,
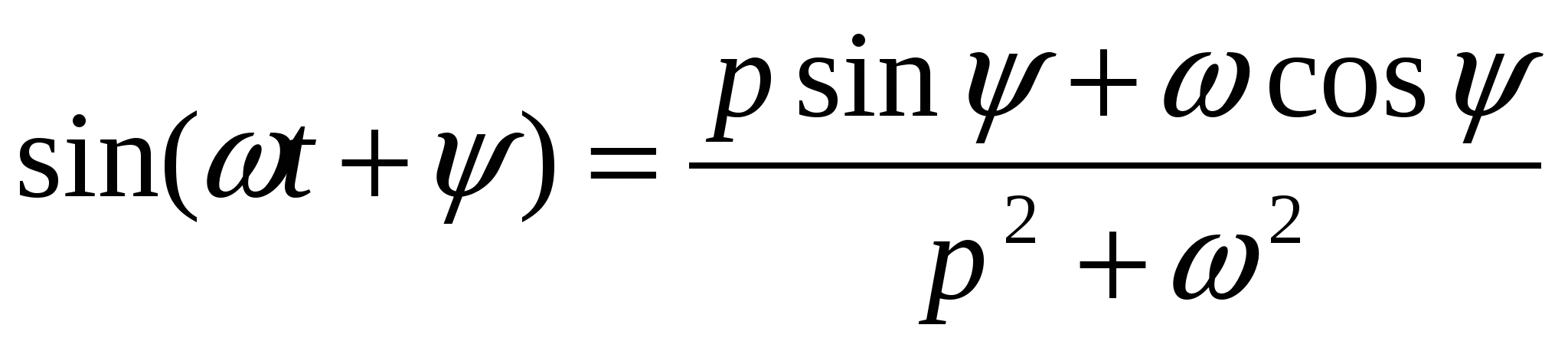 . .
В изображения напряжений на индуктивности и конденсаторе (1.14, 1.15) входят независимые начальные условия iL(0) и uC(0), которые обуславливают запасы энергии магнитного поля в индуктивности и электрического поля в конденсаторе. Эти запасы энергии при операторном методе расчета ПП учитываются при помощи внутренних ЭДС (L iL(0)); (uC(0)/p). При этом направление внутренней ЭДС (L iL(0)) совпадает с направлением тока iL(0), а направление внутренней ЭДС на емкости (uC(0)/p) противоположно направлению тока в ветви с конденсатором.
Операторные расчетные схемы составляются для режима после коммутации в соответствии с выражениями (1.14, 1.15), включающими внутренние ЭДС.
Методику расчёта переходных процессов операторным методом рассмотрим на примере (рисунок 1.3). Требуется найти ток i1(t) в ПП.
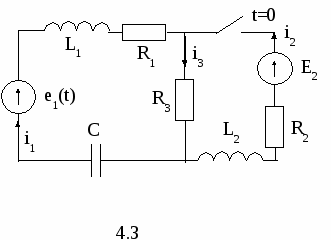
Рисунок 1.3
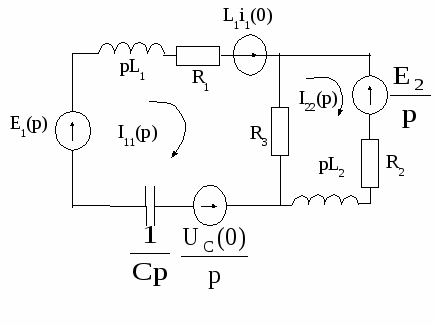
Рисунок 1.4
1 Определение ННУ производится из расчета схемы в докоммутационном режиме
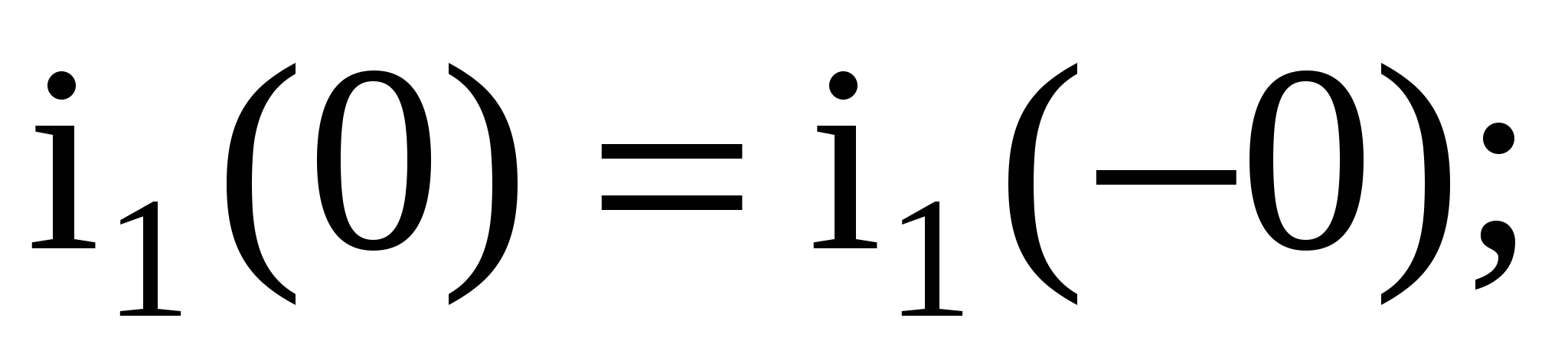 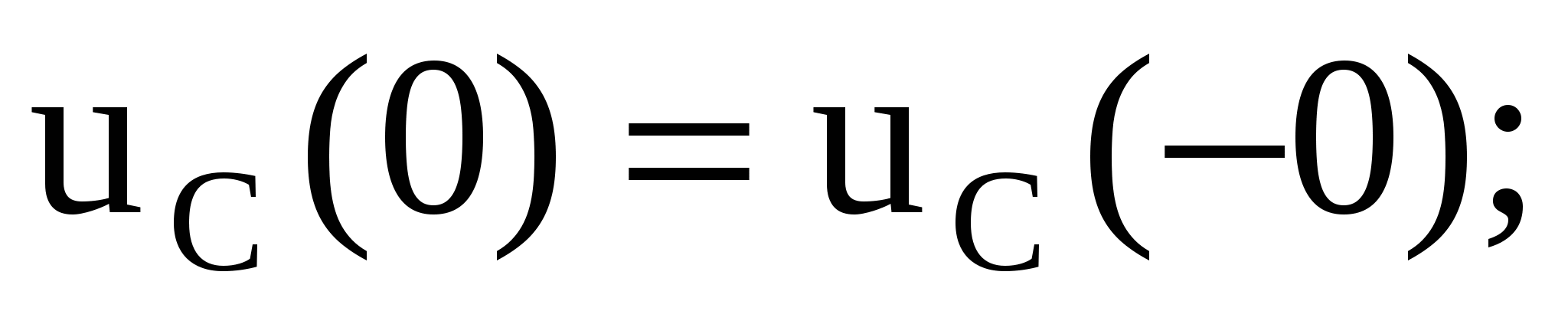 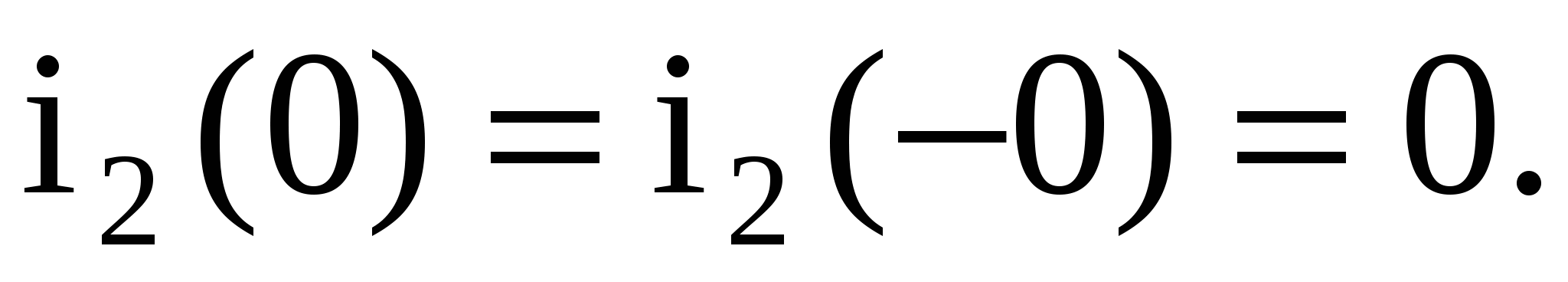
2 Составление операторной схемы для режима после коммутации с учетом ННУ (рисунок 1.4). Из рассмотрения схемы рисунка 1.4 следует, что рL – операторное индуктивное сопротивление, 1/рС – операторное емкостное сопротивление, т.е. операторные сопротивления можно получить из комплексных сопротивлений при замене j на оператор р.
3 Определение изображения 1(р) искомого тока i1(t) производится любым методом расчета линейных цепей (методом контурных токов, узловых потенциалов, двух узлов и т.д.).
По методу контурных токов для схемы рисунка 1.4
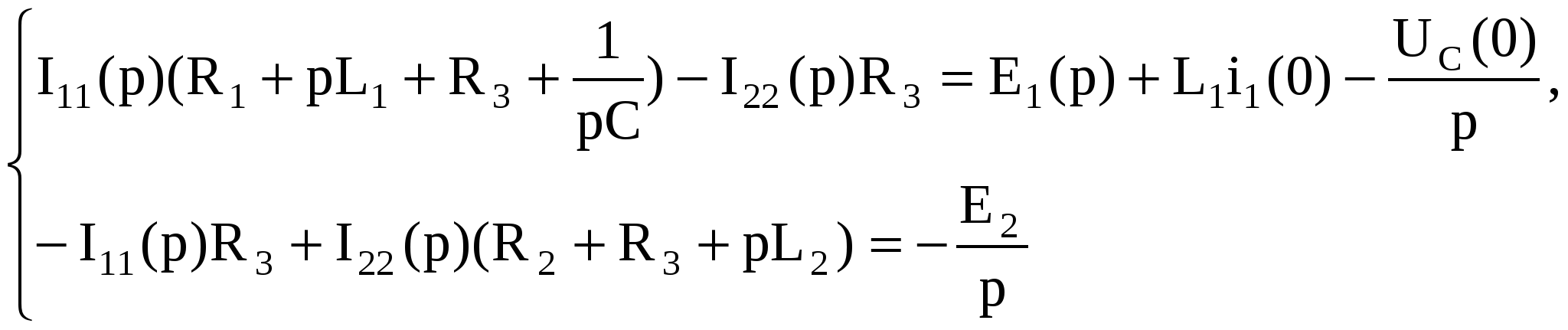 (1.17) (1.17)
В результате решения системы уравнений (1.17) получаем выражение для изображения тока 1(р) искомой функции i1(t)
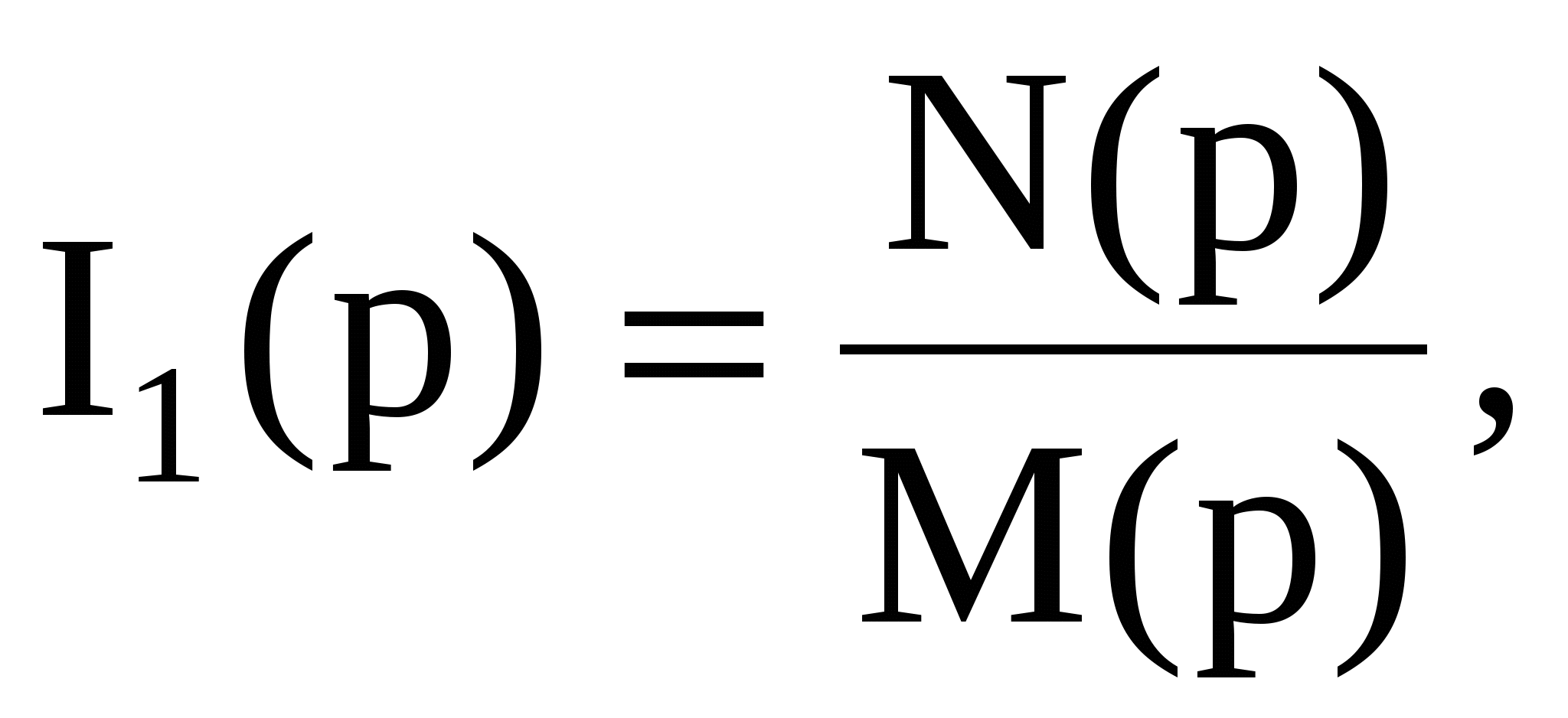
где (р) – многочлен с высшей степенью n оператора р, М(р) – многочлен с высшей степенью m оператора р, при этом n
4 Переход от изображения 1(р) к оригиналу i1(t) производится по теореме (формуле) разложения.
Формула разложения в случае разных вещественных корней рк уравнения М(р) = 0 имеет вид
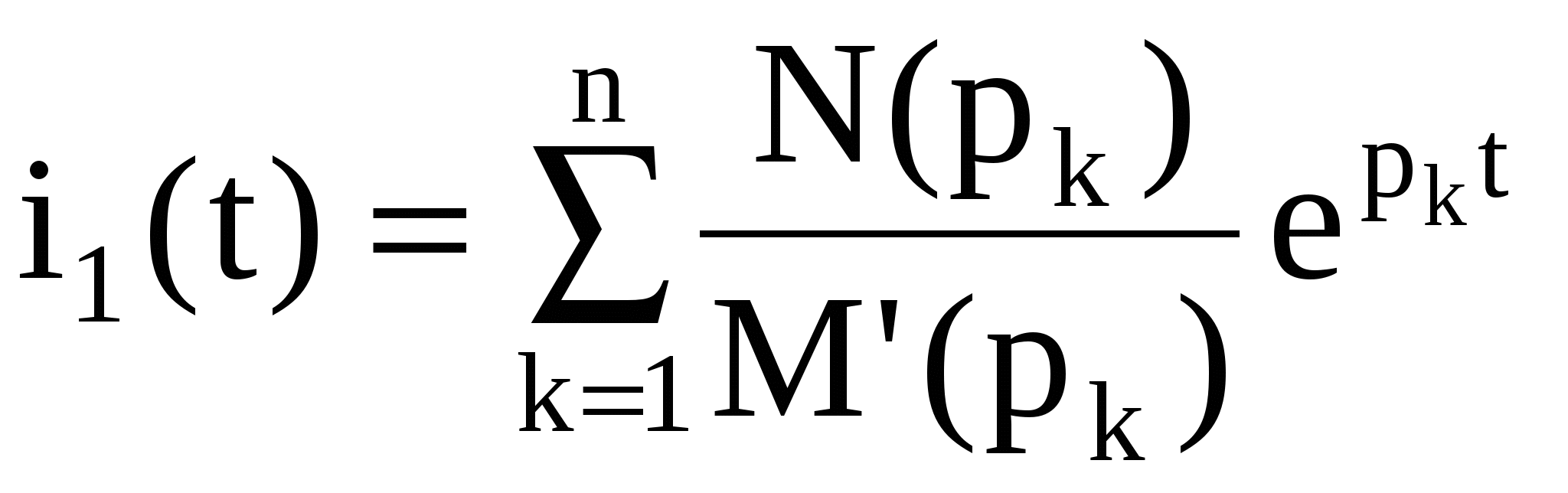 , ,
где (рк) – значение полинома (р) при величине корня рк; М(рк) – значение производной полинома М(р) при значении корня рк.
Формула разложения в случае двух комплексно-сопряженных корней р1,2 = - j0 представляется следующим образом
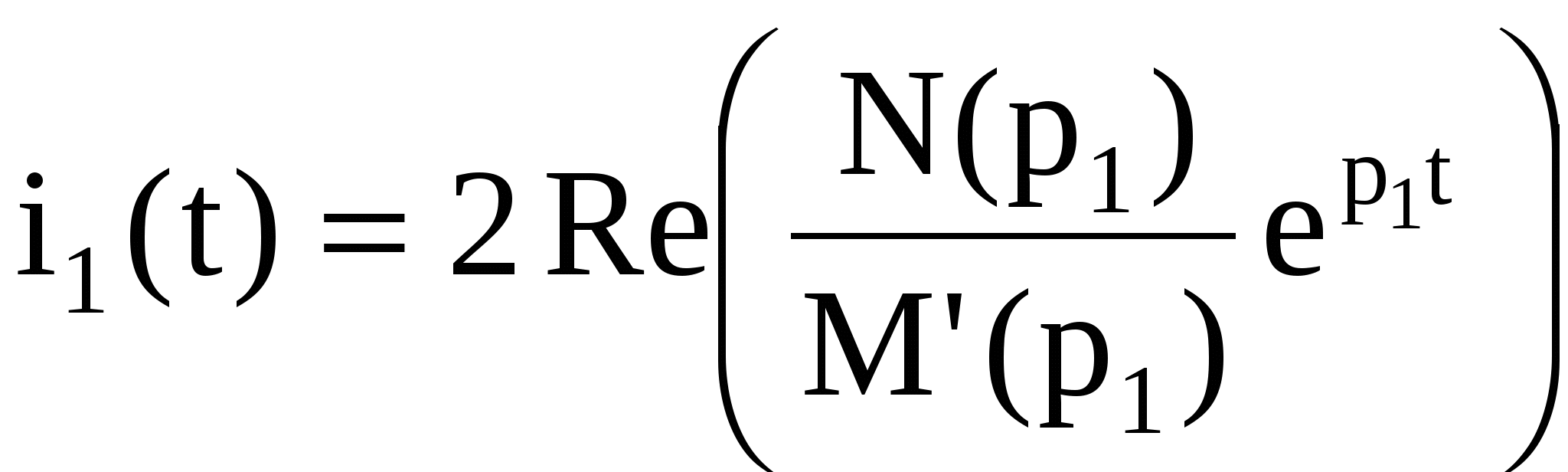 . .
В случае двух кратных корней уравнения М(р) = 0 рациональная дробь 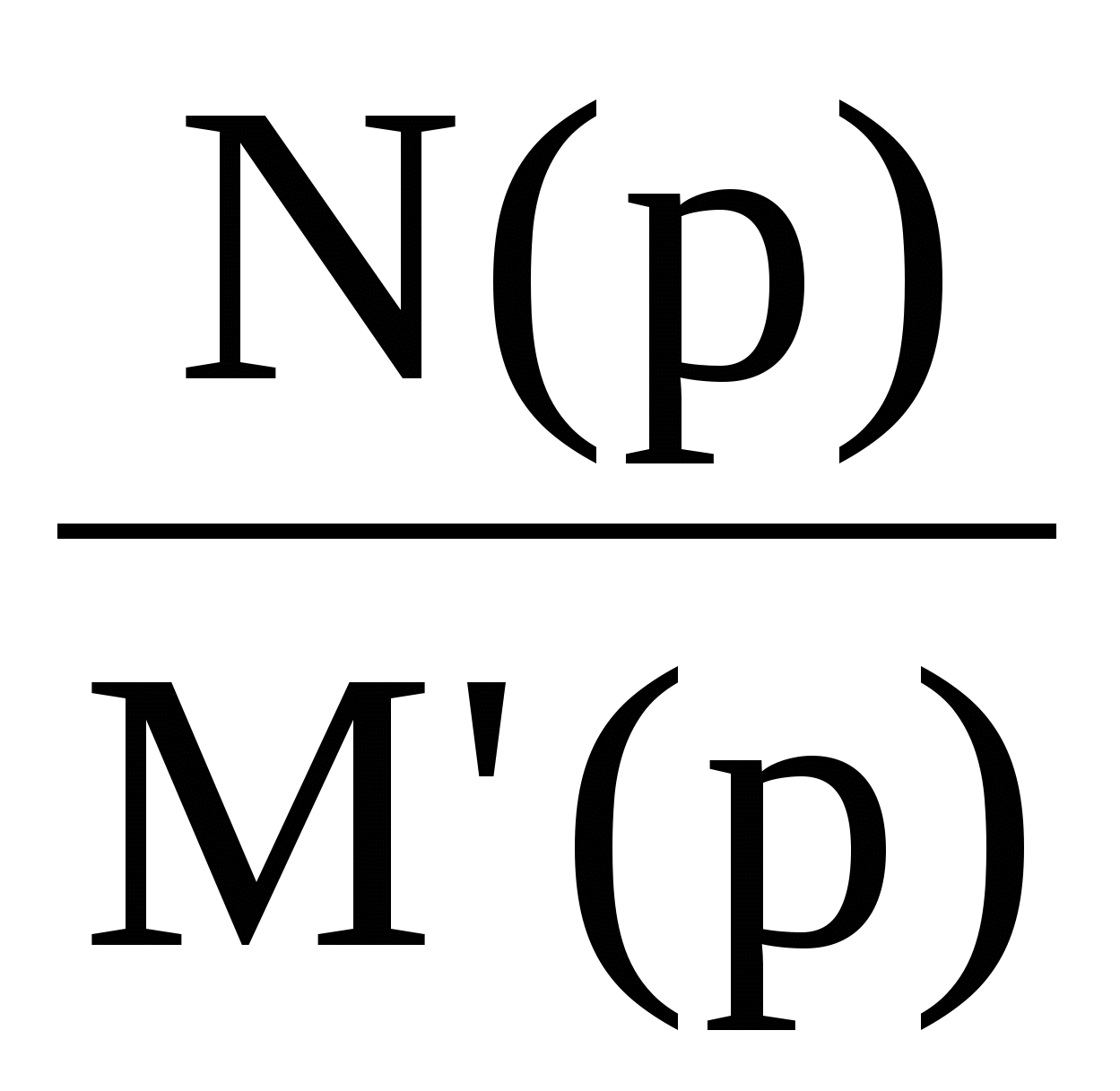 представляется в виде суммы простейших дробей, при этом неизвестные коэффициенты определяются методом неопределенных коэффициентов. представляется в виде суммы простейших дробей, при этом неизвестные коэффициенты определяются методом неопределенных коэффициентов.
Вследствие того, что изображение синусоидальной функции определяется сложной формулой, при решении задач на ПП операторным методом удобнее установившуюся составляющую тока определять символическим (комплексным) методом, рассчитав установившийся режим после коммутации. Свободную составляющую тока определять операторным методом из расчета операторной схемы, составленной для этой составляющей.
страница 1
|