страница 1 страница 2
3.5 Контрольные вопросы
3.5.1 Физический смысл уравнения Бернулли.
3.5.2 Уравнение Бернулли для несжимаемой жидкости.
3.5.3 Что такое гидравлический уклон?
3.5.4 Что такое пьезометрический уклон?
3.5.5 Как строятся линии полного и пьезометрического напоров?
Лабораторная работа № 4 Определение коэффициента теплопроводности материала по методу цилиндрического слоя.
Цель работы: ознакомление с методикой экспериментального определение коэффициента теплопроводности материала цилиндрической формы и углубление знаний по теплопроводности.
4.1 Введение
Источником тепловой энергии является кинетическая энергия микрочастиц тела, которая вместе с потенциальной энергией микрочастиц в термодинамике определяется как внутренняя энергия тела.
При столкновении двух молекул кинетическая энергия передается от более быстрой молекулы к менее быстрой, т.е. кинетическая энергия быстрой молекулы уменьшается, а медленной увеличивается. Обратный процесс невозможен, т.к. медленная молекула попросту не догонит быструю молекулу. При этом изменение кинетической энергии молекул равно работе, совершаемой силами инерции при изменении скорости молекул. Макроскопическим параметром, характеризующим среднюю кинетическую энергию молекул, является температура.
Самопроизвольный необратимый процесс передачи кинетической энергии быстрых молекул медленным молекулам называется теплообменном или теплопереносом.
Обмен кинетической энергии между молекулами может происходить не только при их столкновении, но и путем испускания и поглощения различных частиц (гравитонов, фотонов, электронов и т.п.), несущих определенный запас кинетической энергии. В соответствии с этим различают три способа переноса энергии (передачи кинетической энергии): тепловое излучение, теплопроводность и конвекцию.
Если носителями кинетической энергии являются только фотоны, то в этом случае процесс теплообмена называется тепловым излучением. Тепловое излучение в чистом виде имеет место только в космосе или вакууме.
В случае теплопроводности носителями кинетической энергии могут быть как различные частицы, испускаемые молекулами, так и сами молекулы, если результирующий поток молекул во всех направлениях равен нулю, т.е. нет макроскопического перемещения среды в пространстве. Так, в металлах носителями кинетической энергии в основном являются свободные электроны; в жидкостях и твердых телах-диэлектриках фонолы (частицы упругих волн подобно фотонам частицам электромагнитных волн); в газах молекулы и атомы.
Теплопроводность в чистом виде большей частью имеет место в твердых телах. В жидкостях и газах чистая теплопроводность может быть реализована лишь при условии отсутствия макроскопического перемещения среды в пространстве. Конвекция (от латинского convection - перенос, доставка) возможна только в текучей среде. В случае конвекции носителями кинетической энергии являются молекулы, которые наряду с хаотическим движением внутри некоторого элементарного объема (макрочастицы), совершают направленное движение в пространстве вместе с самой макрочастицей.
Количество кинетической энергии, переданное молекулам системы через всю ее поверхность в процессе теплообмена за время t, называется теплотой Q, Дж (чтобы не путать обозначение времени с температурой Цельсия, для обозначения последней можно ввести символ Тс. Все величины имеют одинаковую единицу температуры - Кельвин (К) подобно тому, как все виды давления имеют одинаковую единицу давления - Паскаль (Па); Т - температура (абсолютная), К; Т0 = 273,15 К - температура таяния льда; Тс - температура Цельсия.
В термодинамике под теплотой понимается та часть изменения кинетической энергии молекул системы, в произвольном процессе, которую пока не удается рассчитать как произведения силы на перемещение, т.е. как работу микроперемещения. Согласно 1-му закону термодинамики теплоту можно определить как разность изменения кинетической энергии молекул и работы макроперемещения внешних сил или как сумму внутренней энергии и работы изменения объема внутренних сил
dQ = dEK - dLвнеш - dEK - (- PмолdV - pdV) = dU + pdV (4.1.1)
Поскольку теплота в общем случае не характеризует полное изменение кинетической энергии молекул, то она не может рассматриваться как функция состояния, изменение которой характеризует полное изменение кинетической энергии микрочастиц системы.
Количество теплоты, проходящее в единицу времени через изотермическую поверхность, называется тепловым потоком Ф, Вт,
Ф = dQ/dt; Q = ∫Фdt (4.1.2)
Тепловой поток проходящий через единицу площади поверхности теплообмена, называется плотностью теплового потока φ, Вт/м2,
φ = dФ/dА= d2Q/dA*dt; Q = ∫∫ φdA*dt (4.1.3)
Согласно закону Фурье вектор плотности теплового потока ф пропорционален и противоположен по направлению градиенту температуры
gradT=n0dT/dn (4.1.4)
φ =-λgradT =-λ(dT/dn) n0 (4.1.5)
где λ – теплопроводность – физическая величина, характеризующая теплопроводящие свойства вещества, Вт/(мК). Зависит от агрегатного состояния вещества (таблица 4.2.1), его атомно-молекулярного строения, температуры и давления, состава (в случае смеси или раствора) и т.д.;
n0 - единичный вектор, нормальный к изотермической поверхности и направленный в сторону возрастания температуры;
dT/dn - производная от температуры по направлению нормали n.
Градиент температуры - это вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной от температуры в направлении нормали. Градиент температуры характеризует наибольшее изменение температуры на единицу длины в данной точке пространства.
На основании закона Фурье выводятся зависимости для расчета теплопроводности плоской стенки
Ф = λ/δ(Т,-Т2)А (4.1.6)
и цилиндрической стенки
Ф =2πl/ln(d2/d1)*(T1 -Т2) (4.1.7)
где Т1 и Т2 - температура горячей и холодной поверхностей стенки, К;
δ - толщина стенки, м; А - площадь поверхности стенки, м2;
d1 и d2 - внутренний и наружный диаметры стенки цилиндрической, м;
λ - теплопроводность материала стенки, Вт/(м К).
4.2 Методика экспериментального определения теплопроводности материала
В данной работе определяется теплопроводность сыпучего материала методом цилиндрического слоя (трубы). Сущность метода состоит в том, что испытуемому материалу придают форму цилиндрической трубы. В центре трубы равномерно по длине расположен электронагреватель, причем длина трубы должна быть больше в 30 раз для создания одномерного теплового потока через слой исследуемого материала. Для уменьшения тепловых потерь через торцы трубы, они дополнительно теплоизолируются. Если пренебречь тепловыми потерями через торцы трубы, то тепловой поток Ф, Вт, проходящий через слой исследуемого материала, может быть найден непосредственно путем измерения мощности Р, потребляемой электронагревателям, или по величине силы тока I и падению электронного напряжения в нагревателе U.
Ф = Р = IU (4.2.1)
Теплопроводность исследуемого материала находится из уравнения 1.7
λ=(Фℓnd2/d1)/2nℓ(Ť1-Ť2) (4.2.2)
где ℓ - длина цилиндрического слоя из исследуемого материала, м;
d2 и d1 - внутренний и наружный диаметры цилиндрического слоя, м;
Ť1 и Ť2 средние арифметические температуры внутренней и наружной поверхностей цилиндрического слоя, К.
Таблица 4.2.1.
Вещество
|
Тс, К
|
λ, Вт/(м К)
|
Вещество
|
Тс, К
|
λ, Вт/(м К)
|
Газы.
Водород
Гелий
Кислород
Азот
Воздух
Металлы.
Серебро
Медь
Золото
Алюминий
Железо
Олово
Свинец
|
0
0
-3
4
0
0
0
0
0
0
0
0
|
0.1655
0.1411
0.0237
0.0266
429
403
311
202
86.5
68.2
35.6
|
Жидкости.
Ртуть
Вода
Ацетон
Этиловый
спирт
Бензол Минералы
и
материалы.
Хлорид
натрия
Турмалин Стекло
Дерево
Асбест
Песок
Текстолит
|
0
20
16
20
22.5
0
0
18
18
18
0+160
20
|
7.82
0.599
0.190
0.167
0.158
6.9
4.9
0.4/ 1
0.16/0.25 0.12
0.30/0.38
1.23/0.34
|
Теплопроводность исследуемого материала находится из уравнения 4.1.7
λ=(Фℓnd2/d1)/2nℓ(Ť1-Ť2) (4.2.2)
где ℓ - длина цилиндрического слоя из исследуемого материала, м;
d2 и d1 - внутренний и наружный диаметры цилиндрического слоя, м;
Ť1 и Ť2 средние арифметические температуры внутренней и наружной поверхностей цилиндрического слоя, К.
-
Описание лабораторной установки
Опытная установка состоит из внешней металлической трубы, диаметром d2, внутри которой концентрично установлена металлическая труба, диаметром d1, промежуток между этими трубами заполнен исследуемым сыпучим материалом. В стенки труб заделаны горячие спаи термопар (по три термопары на трубу). Внутрь трубы вставлена керамическая трубка, в которой установлен электронагреватель. Мощность электронагревателя замеряется ваттметром и может регулироваться с помощью лабораторного автотрансформатора ЛАТРа. Значения температур определяется с помощью милливольтметра 8, который поочередно подключается к каждой термопаре с помощью переключателя. Торцы трубы теплоизолированы специальными крышками.
-
Порядок выполнения работы
-
Ознакомиться с приборами и устройством лабораторной установки.
-
Под руководством, преподавателя включить электропитание установки и установить заданную мощность нагревателя.
4.4.3 Подключить милливольтметр к одной из термопар с помощью переключателя 9 и дождаться наступления стационарного теплового режима, о чем будет свидетельствовать неизменность показаний милливольтметра во времени.
-
Произвести замеры следующих величин:
а) температуры на внутренней трубе Т4, Т5 иТ6;
б) температуры на внешней трубе Т1, Т2 и Т3;
в) мощность электронагревателя Р, Вт или силы тока I, А и падения напряжения U, В;
г) записать геометрические размеры d1, d2 и ℓ, м, которые указаны на установке.
4.4.5 При обработке результатов измерений вычислить:
а) средние значения температур на внутренней трубе
Ť1 = (Т4 + Т5 + Т6) / 3 (4.1)
и на внешней трубе
Ť 2 = (Т1 + Т2 +Т3) / 2 (4.2)
б) среднюю температуру исследуемого материала
Tмат = (Ť1 - Ť 2) / 2 (4.3)
в) теплопроводность материала λ по формуле (2.2).
4.4.6 Повторить опыт 3 раза, меняя мощность нагрева с помощью ЛАТНа по показаниям ваттметра или вольтметра (например, U = 100, 150 и 200 В).
-
Данные измерений и расчетов занести в таблицу 4.1.
-
Построить зависимость теплопроводности материала от температуры λ = ƒ(Тмат).
-
Определить предельную относительную ошибку измерений теплопроводности материала εn(λ) по формуле (1.2).
Отчет о работе должен содержать наименование и цель работы, краткое описание методики экспериментального определения, схему лабораторной установки, график зависимости λ = ƒ(Тмат), таблицу и необходимые расчеты.
Таблица 4.4.1-Результаты измерений
Ф=Р,
Вт
|
Т1, К
|
Т2, К
|
Т3, К
|
Т4, К
|
Т5, К
|
Т6, К
|
Ť1, К
|
Ť2, К
|
Тмат, К
|
Λ,
Вт/мК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.5 Контрольные вопросы
4.5.1 Сущность метода цилиндрического слоя.
4.5.2 Способы переноса теплоты.
4.5.3 Закон Фурье.
4.5.4 Зависимости для расчета теплового потока через плоскую цилиндрическую стенку.
Лабораторная работа №5 Исследование теплоотдачи при свободной конвекции в неограниченном объёме
Цель работы
Ознакомление с методикой экспериментального определения коэффициента теплоотдачи и коэффициентов критериального уравнения при свободной конвекции в неограниченном объёме и изучение сложного теплообмена.
5.1 Вводная часть
Сложный теплообмен. Различают три элементарных способа переноса теплоты в пространство: теплопроводность, конвекцию и тепловое излучение.
Теплопроводность представляет собой способ переноса теплоты в телах (или между ними) путем энергообмена между микрочастицами вещества. Теплопроводность в чистом виде имеет место лишь в твердых телах.
Конвекция представляет собой способ переноса тепла путем перемещения вещества из области с одной температурой в область с другой температурой. Конвекция возможна только в текучей среде. При этом перенос теплоты неразрывно связан с переносом самой среды.
Тепловым излучением называется способ переноса тепла с помощью электромагнитных волн.
Разделение общего процесса переноса теплоты на элементарные явления – теплопроводность, конвекцию и излучение – производится в основном из методологических соображений. В действительности же эти явления протекают одновременно и влияют друг на друга.
Совместный перенос теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Совместный перенос тепла теплопроводностью и излучением называется радиационно-кондуктивным теплообменом. Совместный перенос тепла излучением, конвекцией и теплопроводностью называется радиационно-конвективным или сложным теплообменом. Примером сложного теплообмена является теплообмен между газом и стенкой. В данной работе исследуется радиационно-конвективный теплообмен между нагретым горизонтальным цилиндром и окружающей средой (воздухом), где в качестве основного явления рассматривается конвективный теплообмен.
Теплоотдача при свободной конвекции в неограниченном пространстве. Процесс теплообмена при свободной конвекции (при свободном движении) происходит в следствии разности нагретых и холодных частиц жидкости в гравитационном поле. Возникновение и интенсивность конвективного теплообмена определяется тепловыми условиями процесса и зависит от рода жидкости, разности температур, напряженности гравитационного поля и объёма пространства, в котором происходит процесс. При теплообмене температура жидкости переменна, поэтому возникает разность плотностей и как следствие разность гравитационных сил, представляющих собой архимедову или подъёмную (опускную) силу. Например, при соприкосновении воздуха с нагретым телом воздух нагревается, становится легче и поднимается вверх, т.е. воздух у поверхности тела движется снизу вверх, на его место поступают новые холодные частицы, которые также нагреваются и поднимаются вверх. При свободной конвекции движение жидкости (воздуха) возникает без внешнего возбуждения в результате самого процесса теплообмена.
Интенсивность конвективного теплообмена характеризуется коэффициентом теплоотдачи α, который определяется по формуле Ньютона-Рихмана
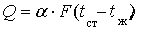 (5.1.1) (5.1.1)
Согласно этому закону тепловой поток Q пропорционален поверхности теплообмена F и разности температур стенки и жидкости (под жидкостью может пониматься и газ).
Коэффициент теплоотдачи можно определить как количество теплоты, отдаваемое в единицу времени единице поверхности при разности температур между поверхностью и жидкостью, равной одному градусу, Вт/(м2/К)
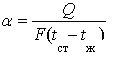 (5.1.2) (5.1.2)
В общем случае коэффициент теплоотдачи является сложной функцией формы Ф, размеров 1, температуры стенки и жидкости, скорости жидкости и её физических свойств – коэффициента теплопроводности 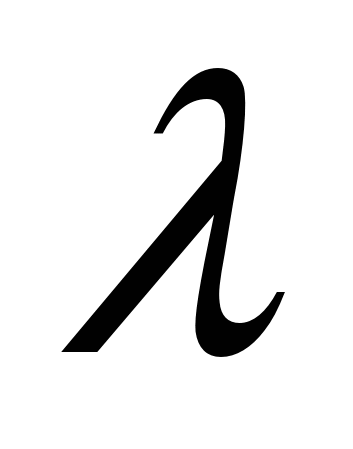 , теплоемкости , теплоемкости 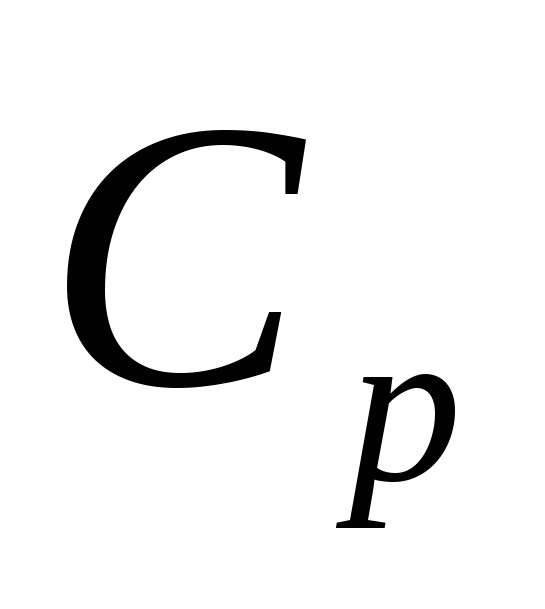 , плотности , плотности 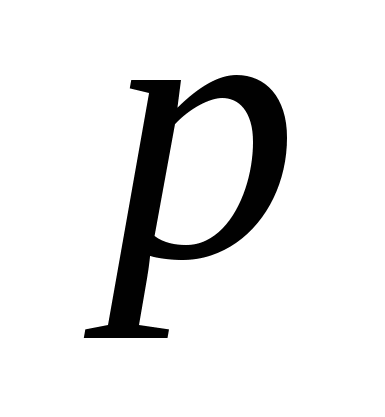 , коэффициента вязкости , коэффициента вязкости  и других факторов: и других факторов:
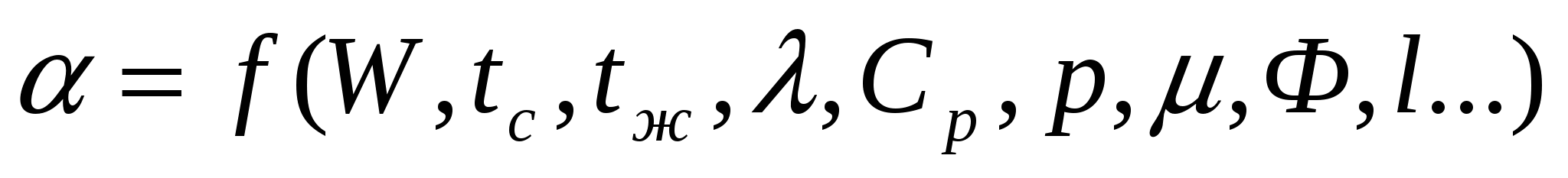 (5.1.3) (5.1.3)
Число Прандтля является теплофизической характеристикой теплоносителя
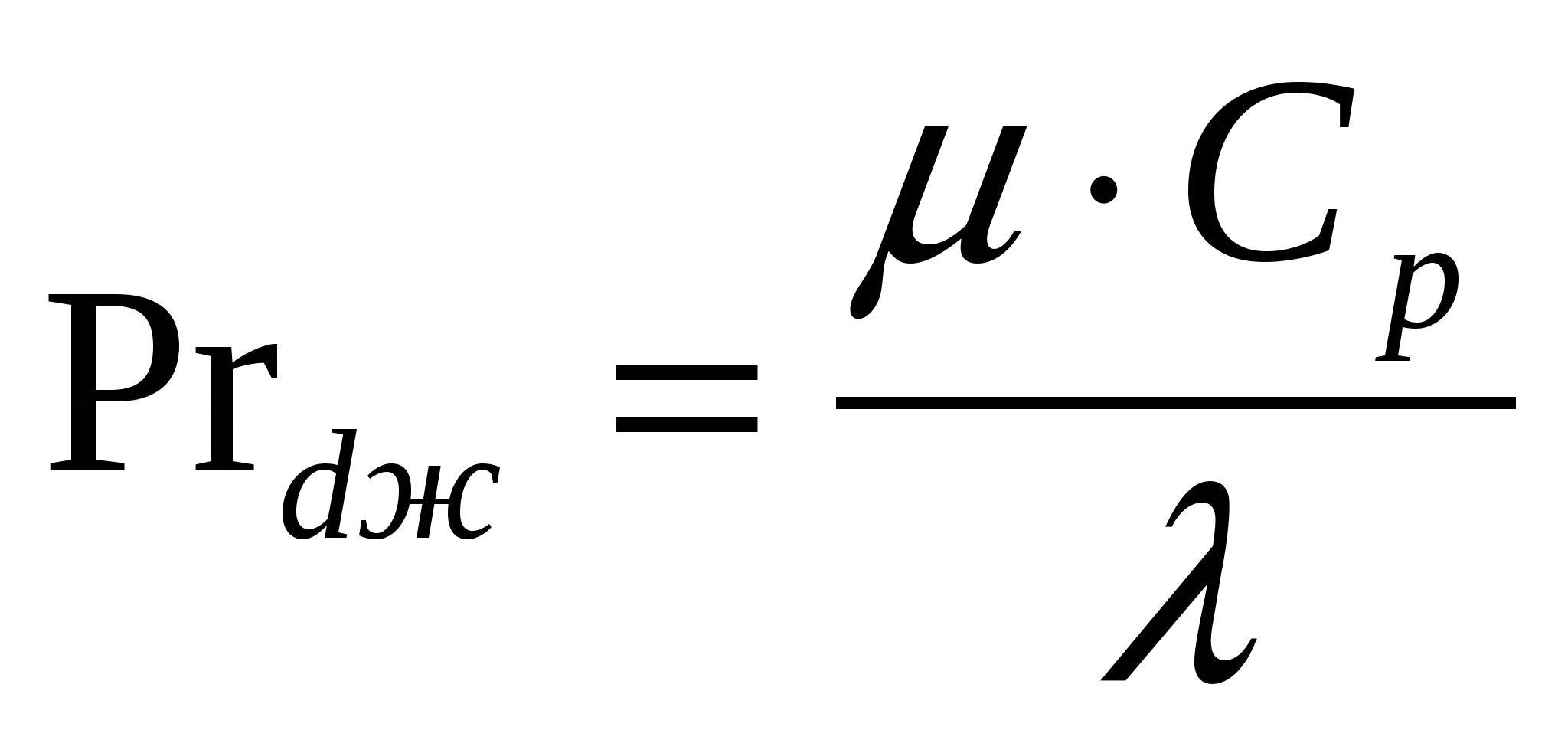 (5.1.4) (5.1.4)
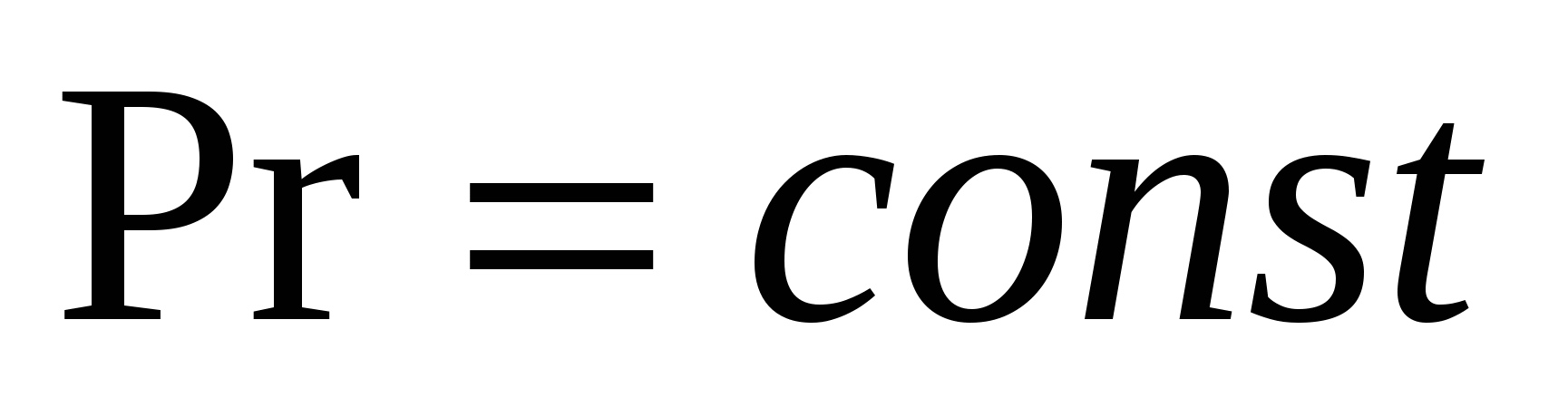 и, тогда зависимость (1.1) можно представить в виде и, тогда зависимость (1.1) можно представить в виде 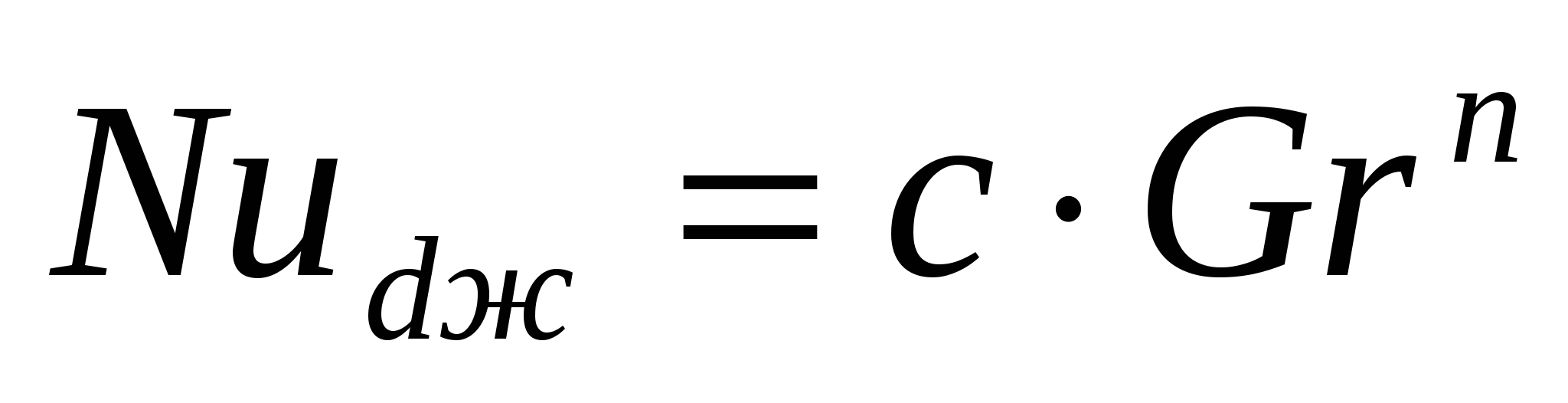 Постоянные с и n являются искомыми величинами в этом уравнении. Методики экспериментального определения коэффициента теплоотдачи и коэффициентов критериального уравнения. В условиях опыта тепло рассеиваемое нагревателем передается боковой поверхностью горизонтального цилиндра в окружающее пространство путем теплового излучения, конвенцией и теплопроводностью и может быть определено по эквивалентной мощности электронагревателя Постоянные с и n являются искомыми величинами в этом уравнении. Методики экспериментального определения коэффициента теплоотдачи и коэффициентов критериального уравнения. В условиях опыта тепло рассеиваемое нагревателем передается боковой поверхностью горизонтального цилиндра в окружающее пространство путем теплового излучения, конвенцией и теплопроводностью и может быть определено по эквивалентной мощности электронагревателя
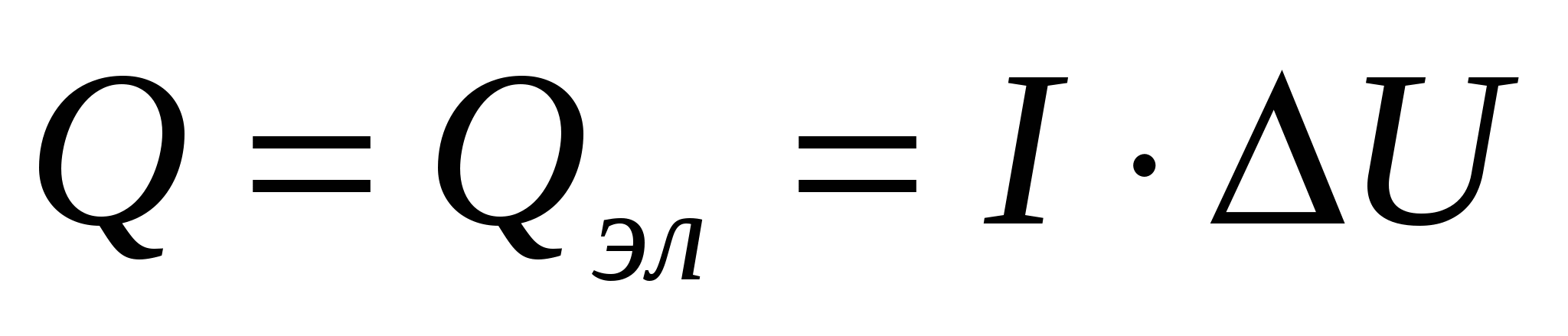 (5.1.5) (5.1.5)
где 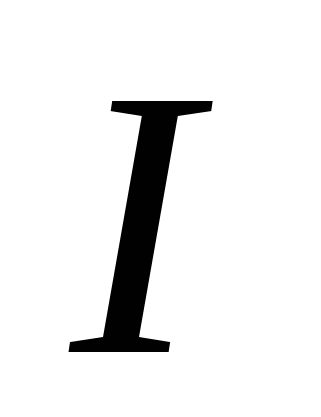 - величина тока, А; - величина тока, А;
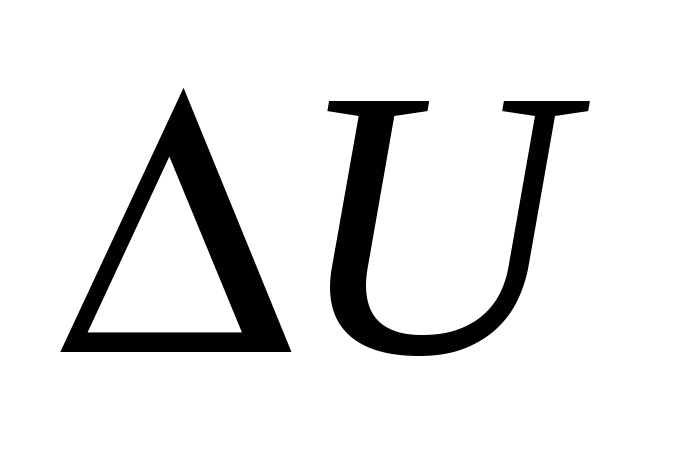 - падение напряжения в нагревателе, Вт. - падение напряжения в нагревателе, Вт.
Суммарный тепловой поток 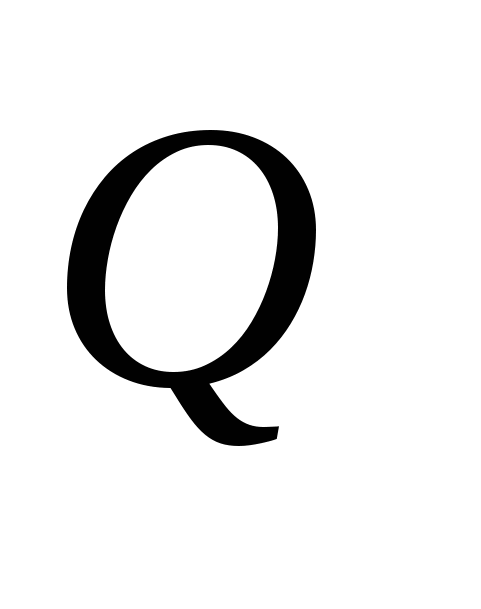 складывается из тепловых потоков путем конвективного теплообмена складывается из тепловых потоков путем конвективного теплообмена 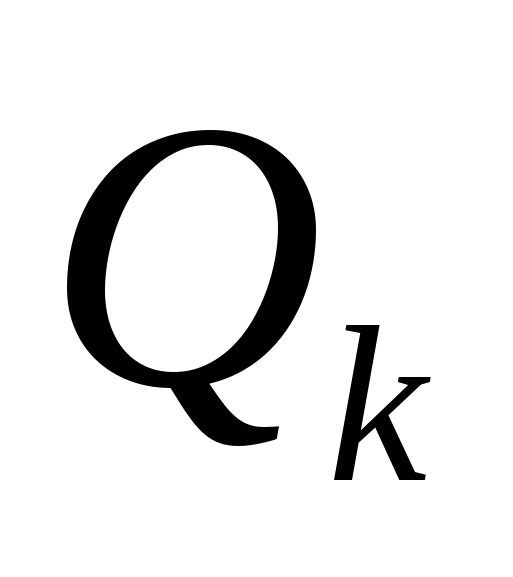 и излучения и излучения 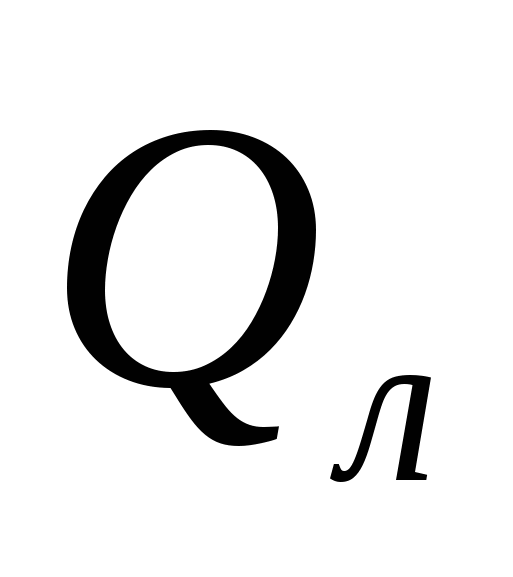 , определяемого по формуле лучистого теплообмена , определяемого по формуле лучистого теплообмена
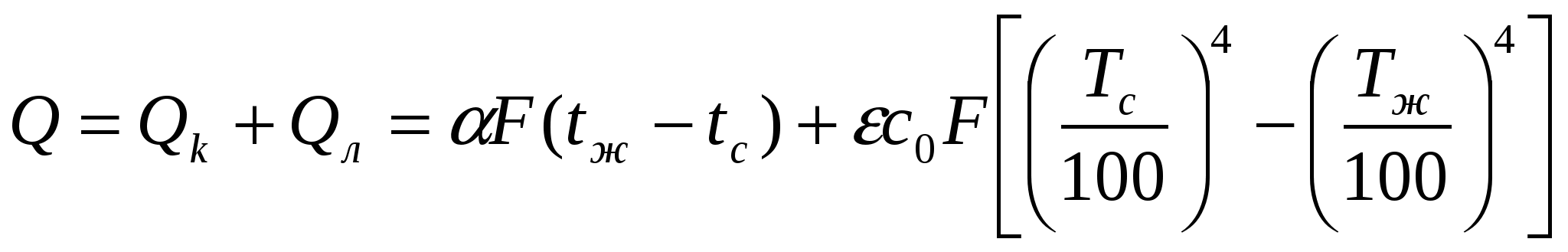 (5.1.6) (5.1.6)
Откуда находится коэффициент теплоотдачи 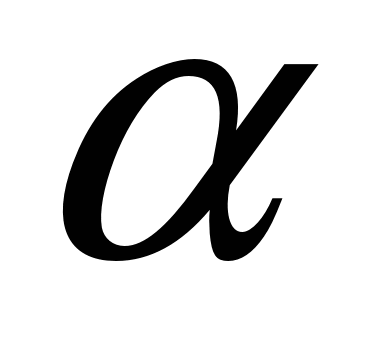
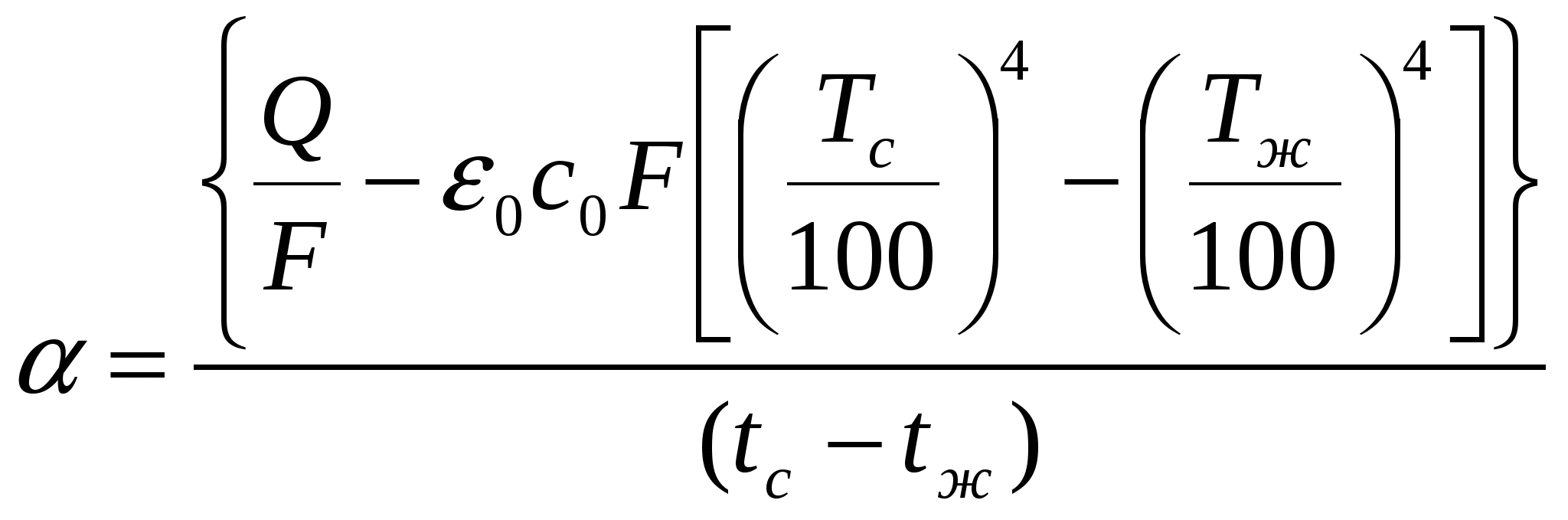 (5.1.7) (5.1.7)
где 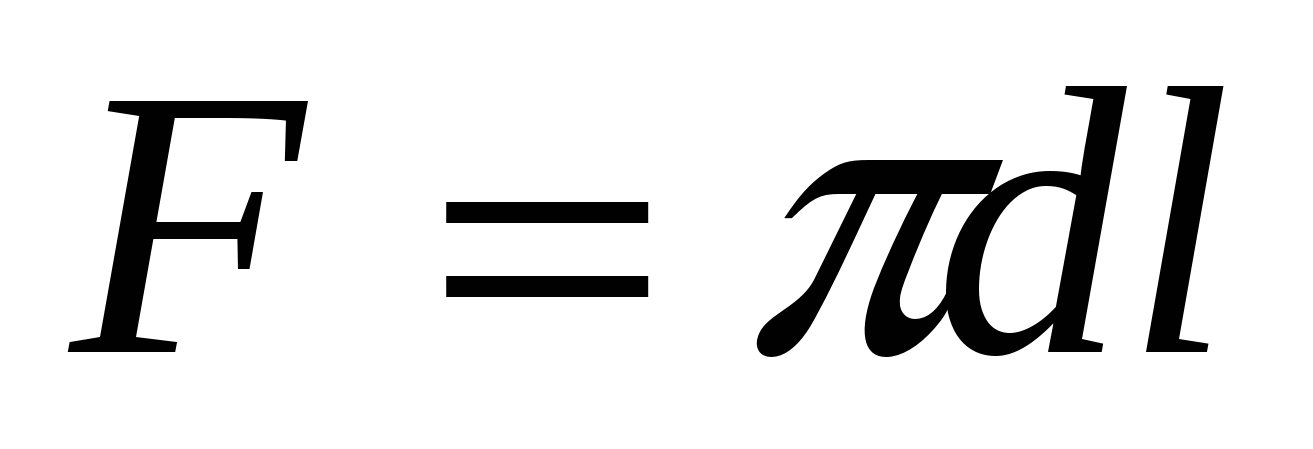 - боковая поверхность цилиндра диаметром d и длиной l; - боковая поверхность цилиндра диаметром d и длиной l;
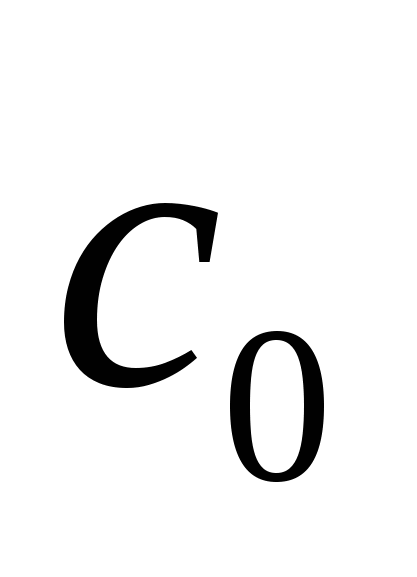 =5,67 Вт/(м2К2) - коэффициент абсолютно чёрного тела; =5,67 Вт/(м2К2) - коэффициент абсолютно чёрного тела;
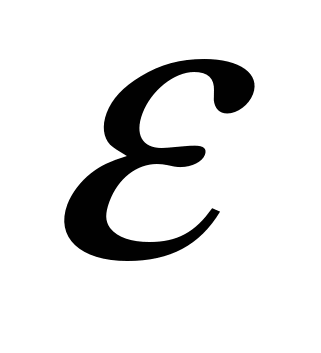 - степень черноты поверхности цилиндра (для поверхности цилиндра из окисленной стали можно принять - степень черноты поверхности цилиндра (для поверхности цилиндра из окисленной стали можно принять 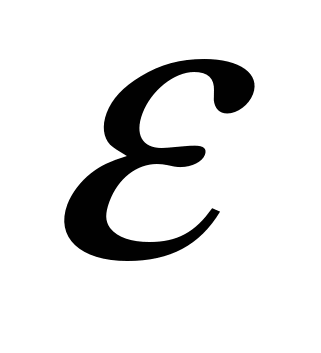 =0,79, а для фарфоровой трубы =0,79, а для фарфоровой трубы 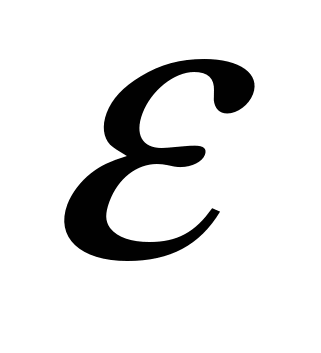 =0,92); =0,92);
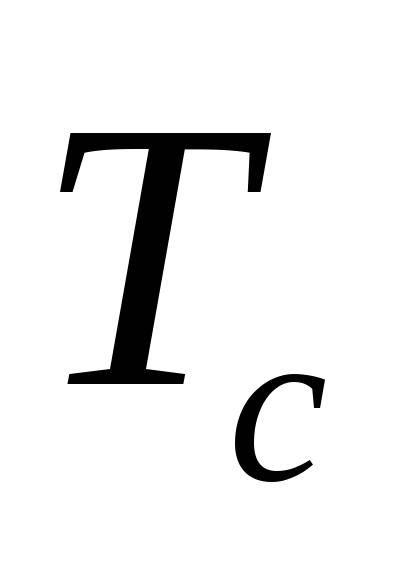 и и 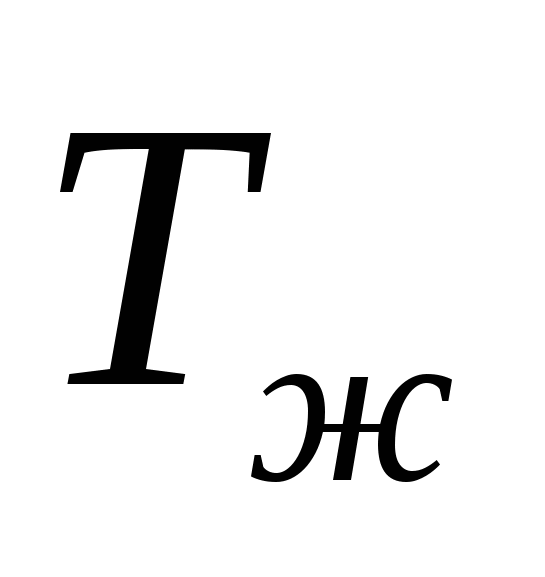 - температура стенки трубы и окружающей среды (воздуха вдали от поверхности цилиндра), К. - температура стенки трубы и окружающей среды (воздуха вдали от поверхности цилиндра), К.
Для определения постоянных с и n вычисляются численные значения критериев Нуссельта и Грасгофа. Затем по найденным значениям этих критериев строится график в логарифметических координатах.
Эту зависимость можно значительно упростить, если представить её в виде критериального уравнения, которое для естественной конвекции имеет вид
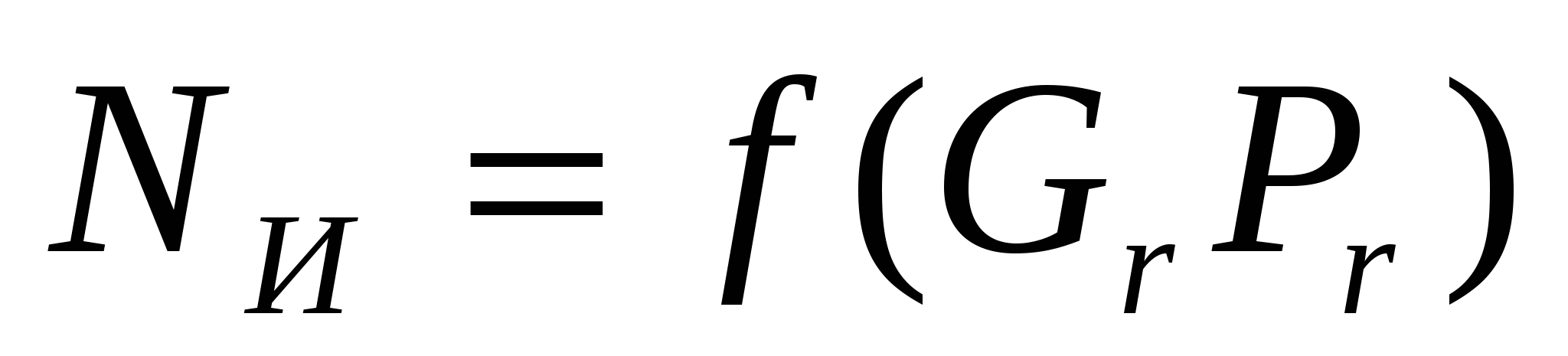 (1.8) (1.8)
Число Грасгофа характеризует относительную эффективность подъемной силы, вызывающей свободно-конвективное движение среды
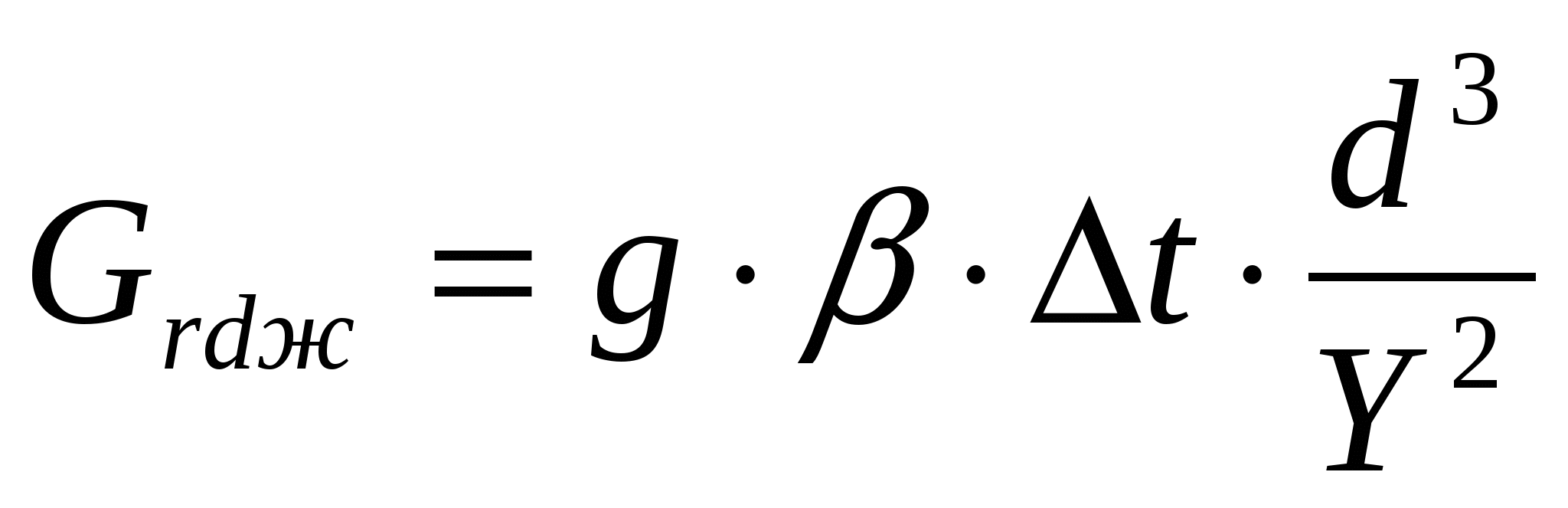 (1.9) (1.9)
где g-ускорение свободного падения, м/с2;
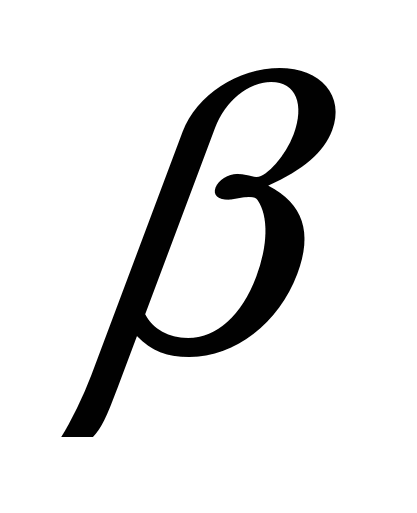 - температурный коэффициент объёмного расширения среды (для газа - температурный коэффициент объёмного расширения среды (для газа 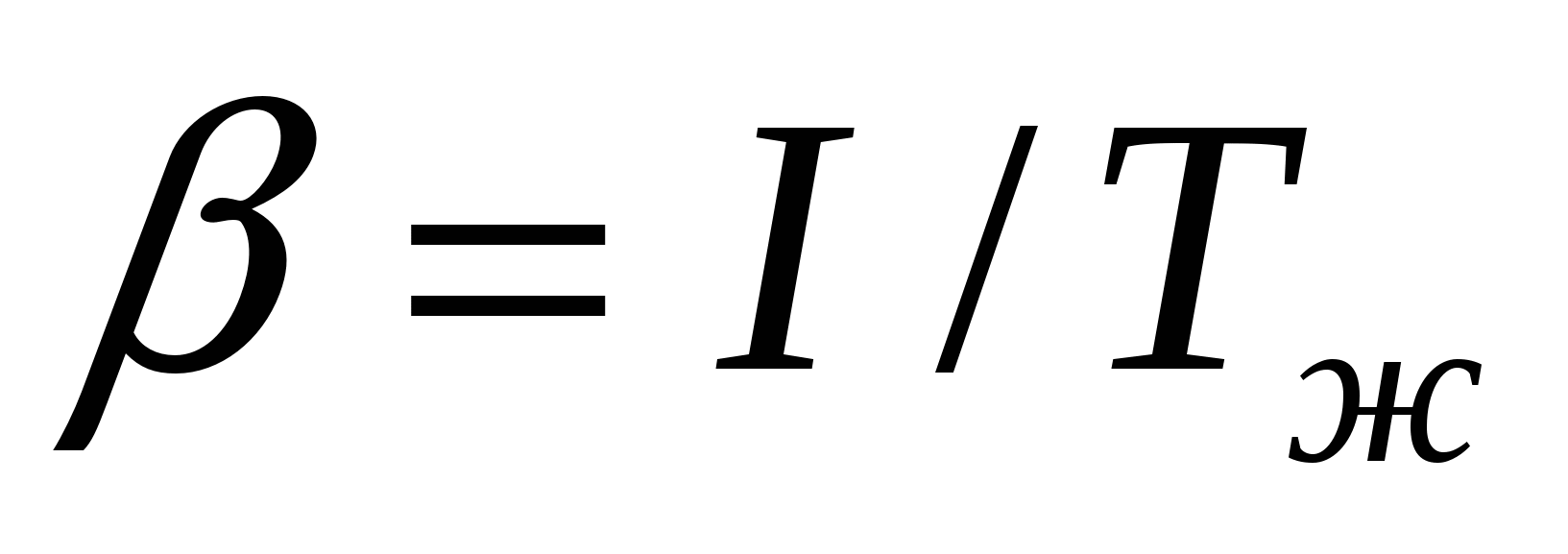 , , 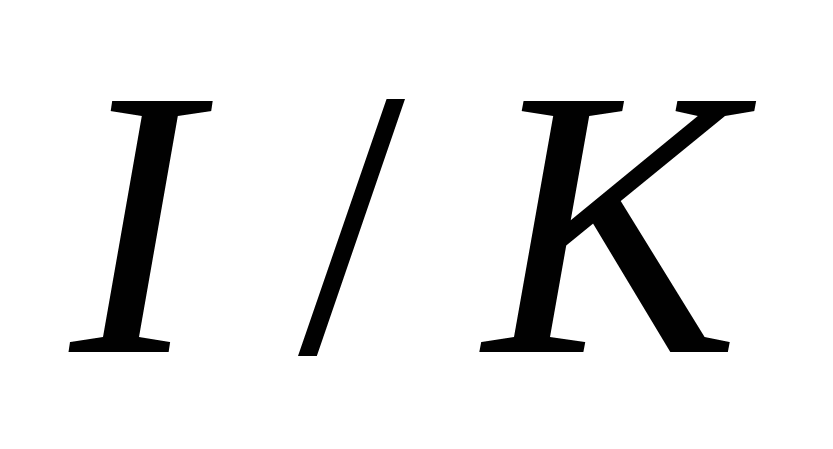 ); );
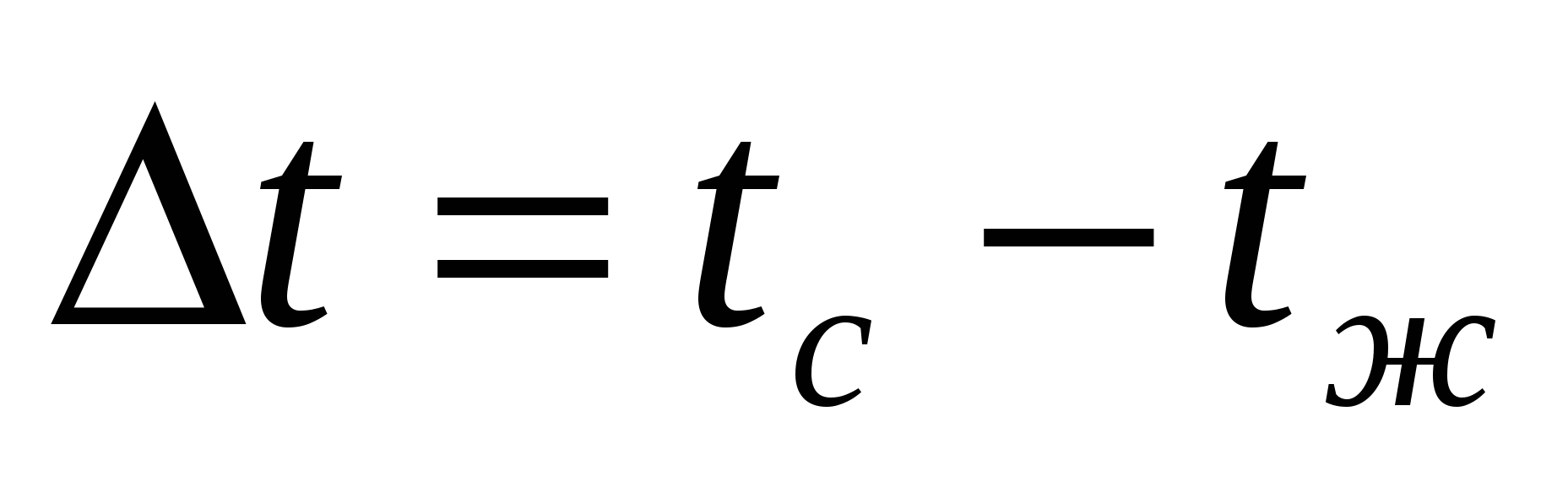 - характерный температурный напор; - характерный температурный напор;
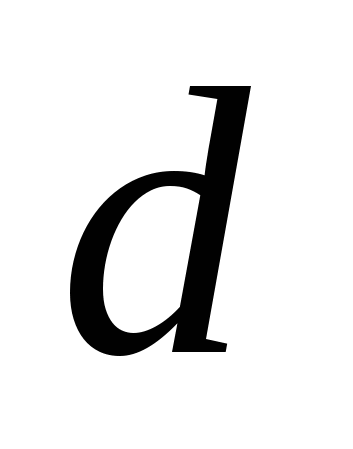 - диаметр трубы, м; - диаметр трубы, м;
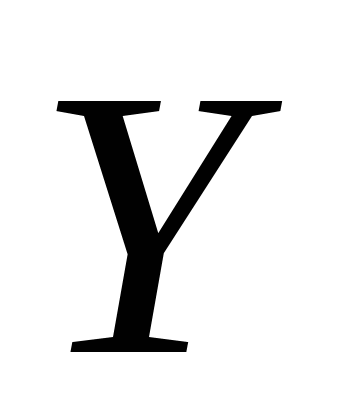 - кинематический коэффициент вязкости (выбирается в зависимости от температуры жидкости по соответствующим таблицам, например, для воздуха по таблице 5.1.1) - кинематический коэффициент вязкости (выбирается в зависимости от температуры жидкости по соответствующим таблицам, например, для воздуха по таблице 5.1.1)
Число Нуссельта характеризует интенсивность процесса конвективного теплообмена и из него определяется коэффициент теплоотдачи 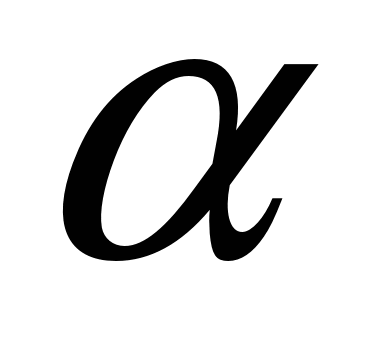
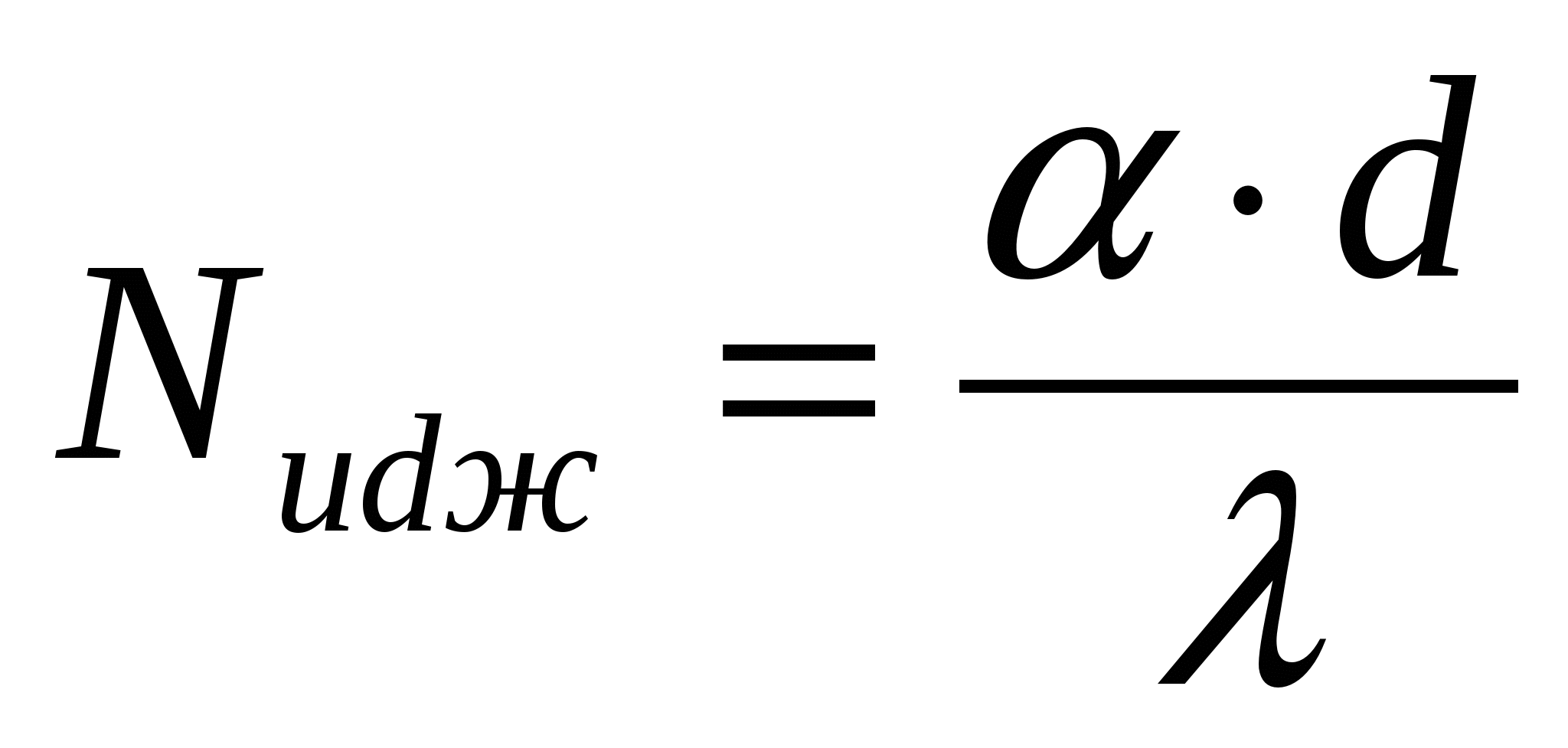 (5.1.10) (5.1.10)
где 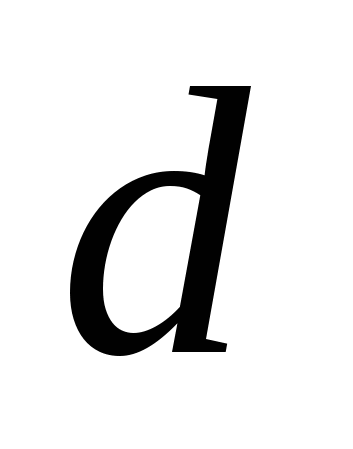 - диаметр трубы, м; - диаметр трубы, м;
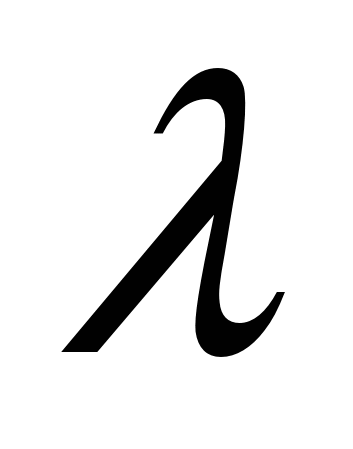 - коэффициент теплопроводности теплоносителя, выбирается в зависимости от его температуры, - коэффициент теплопроводности теплоносителя, выбирается в зависимости от его температуры,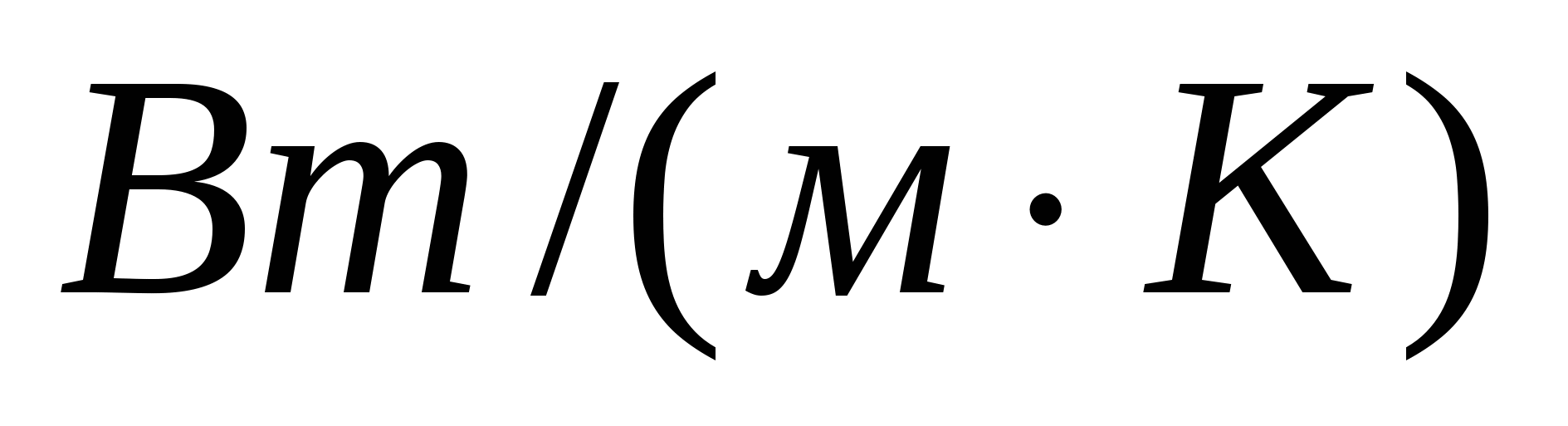 . .
Таблица 5.1.1 - Физические параметры воздуха при Р=760 мм. ст.
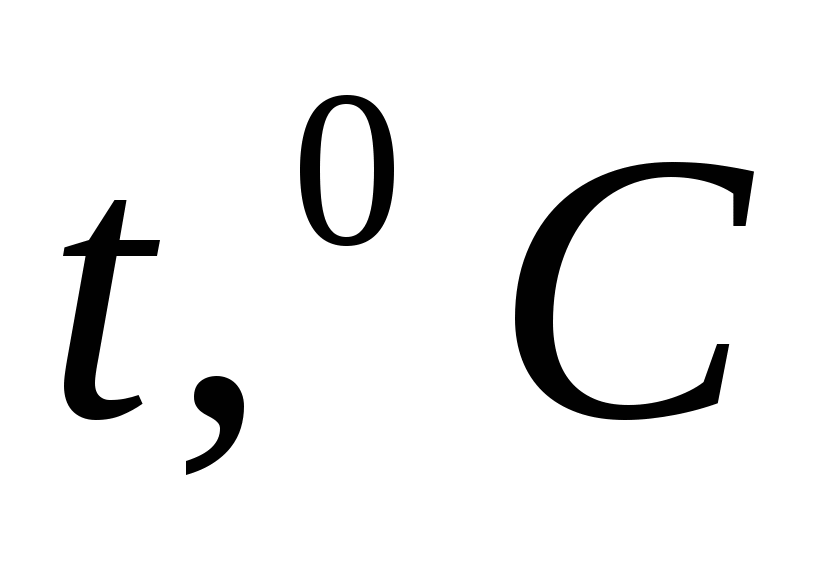
|
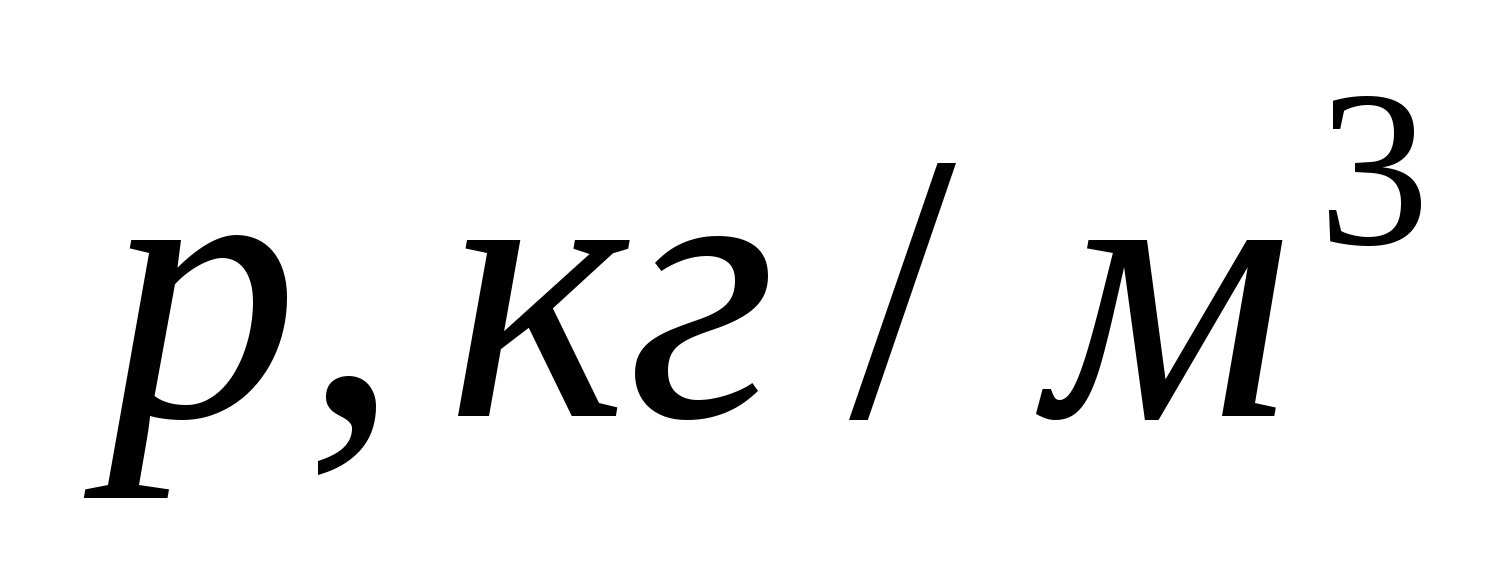
|
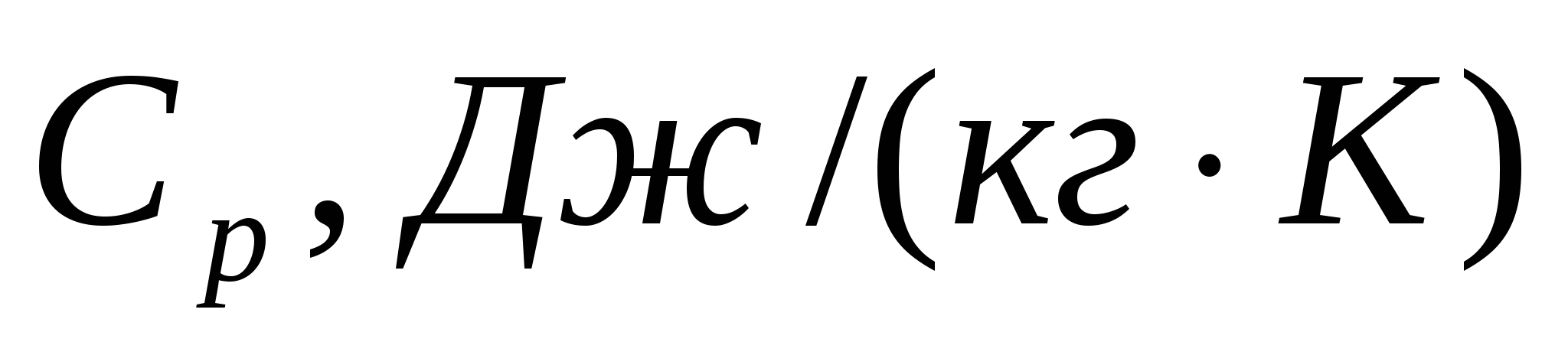
|
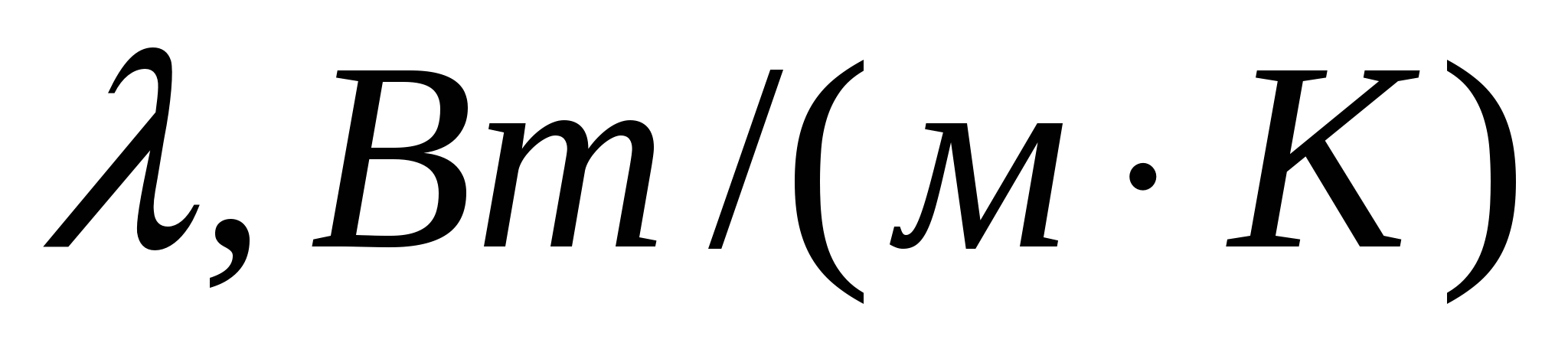
|
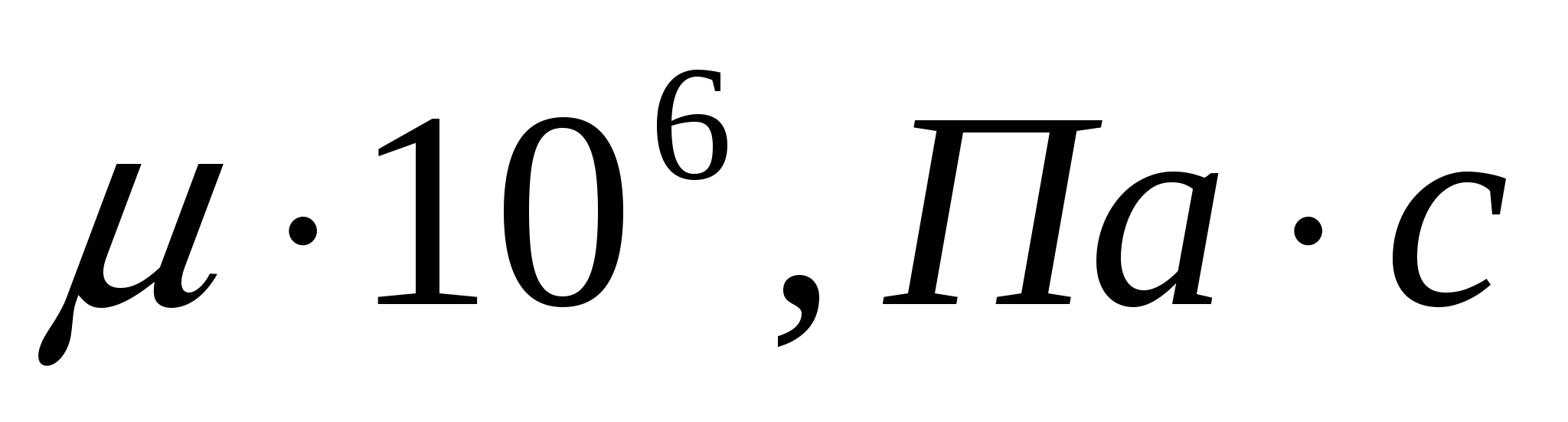
|
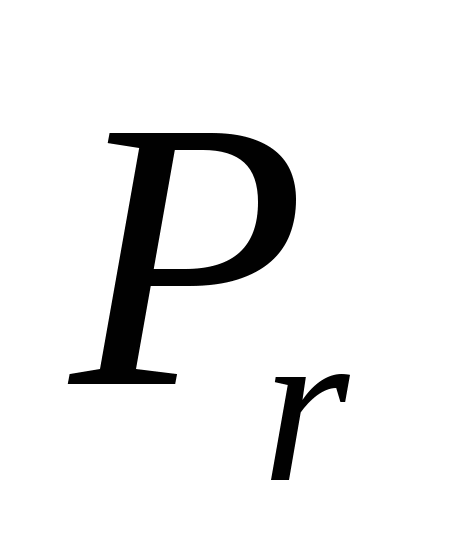
|
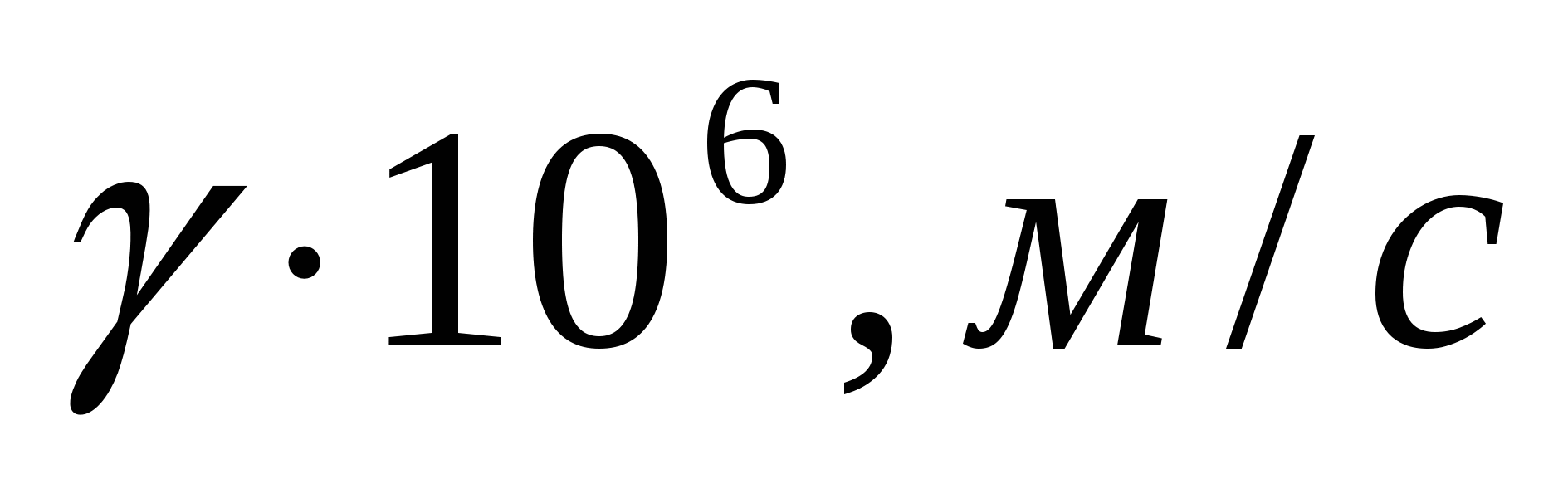
|
0
|
1,294
|
1005
|
0,0244
|
17,2
|
0,707
|
13,82
|
10
|
1,247
|
1005
|
0,0259
|
17,6
|
0,705
|
14,16
|
20
|
1,205
|
1005
|
0,0261
|
18,1
|
0,703
|
15,06
|
30
|
1,165
|
1005
|
0,0267
|
18,6
|
0,701
|
16,00
|
40
|
1,128
|
1005
|
0,0276
|
19,1
|
0,699
|
16,96
|
50
|
1,093
|
1005
|
0,0283
|
19,6
|
0,698
|
17,95
|
Индексы "d " и "ж" у критериев подобия указывают на то, что в качестве определяющего размера (для горизонтальной трубы) берется диаметр трубы, а за определяющую температуру берется температура жидкости или газа 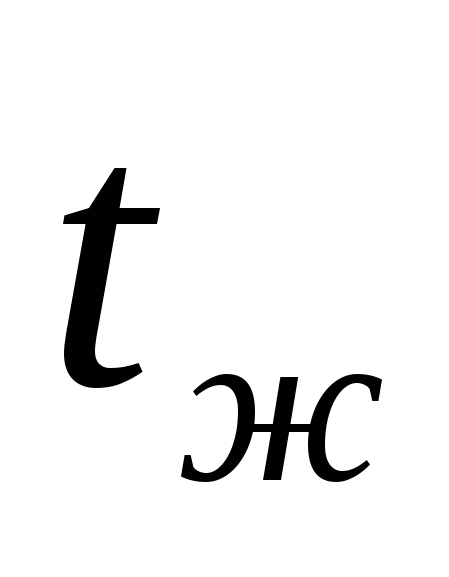 . .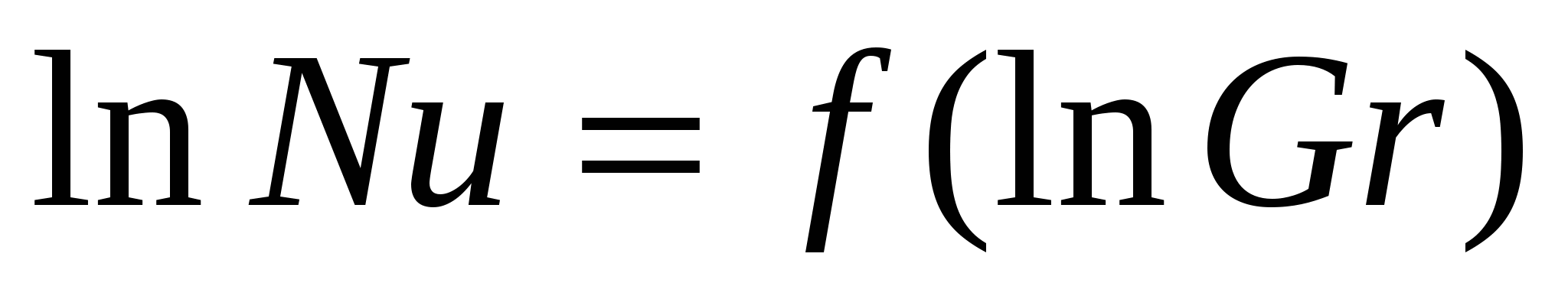 . В указанных координатах опытные данные описываются прямолинейно зависимостью вида . В указанных координатах опытные данные описываются прямолинейно зависимостью вида
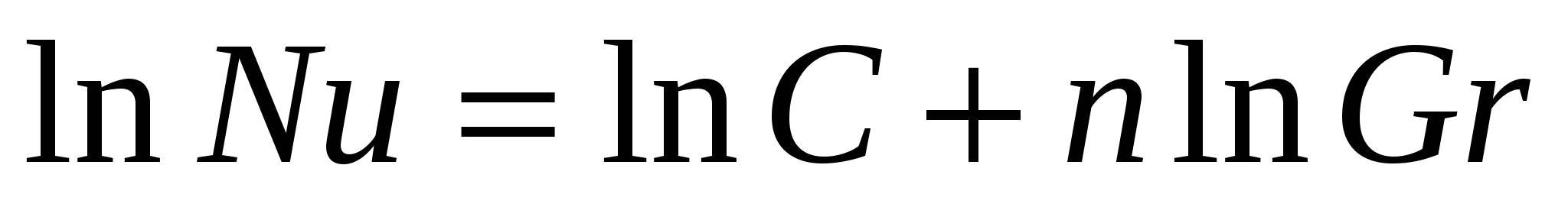 (5.1.11) (5.1.11)
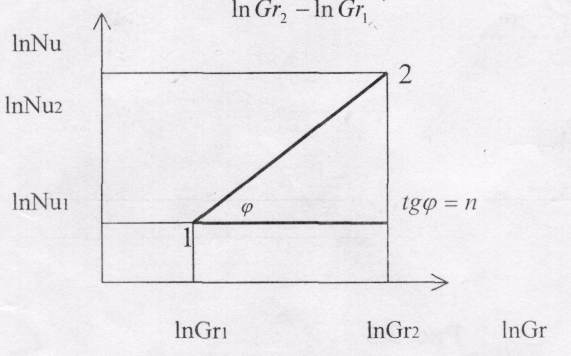
Рисунок 5.1.1 - Определение углового коэффициента
Значение n в этом уравнении характеризует угловой коэффициент (тангенс наклона) прямой на графике. Взяв на этой прямой две какие-либо произвольные точки с координатами 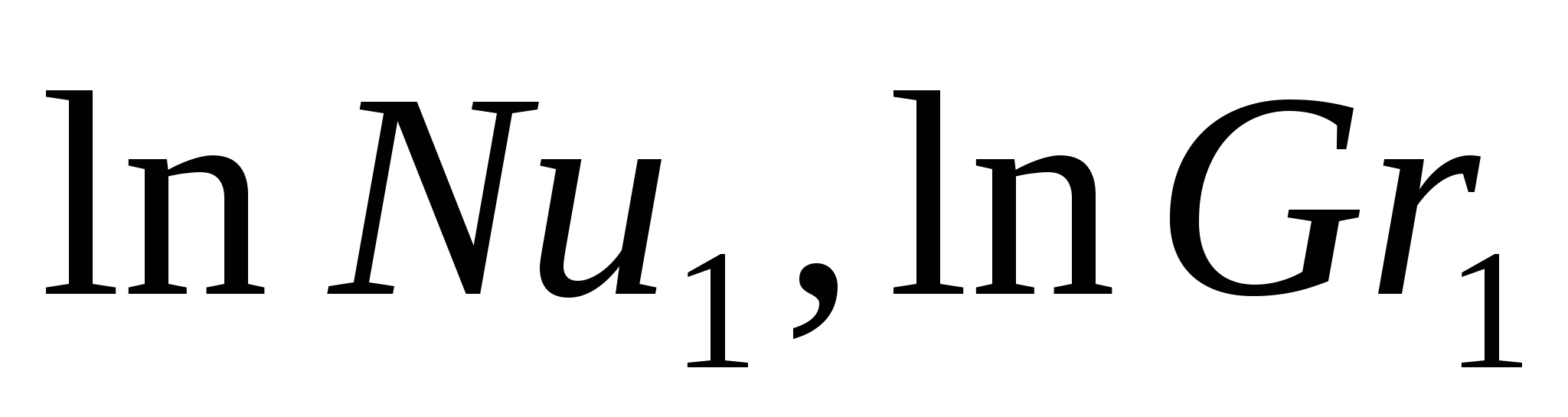 и и 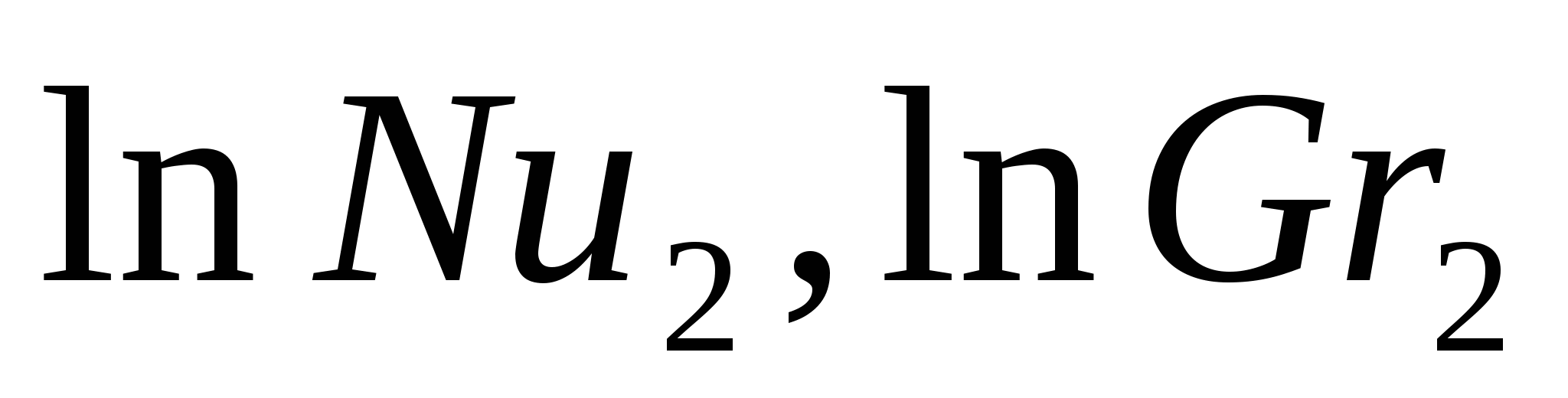 , можно вычислить угловой коэффициент (рисунок 5.1.1) , можно вычислить угловой коэффициент (рисунок 5.1.1)
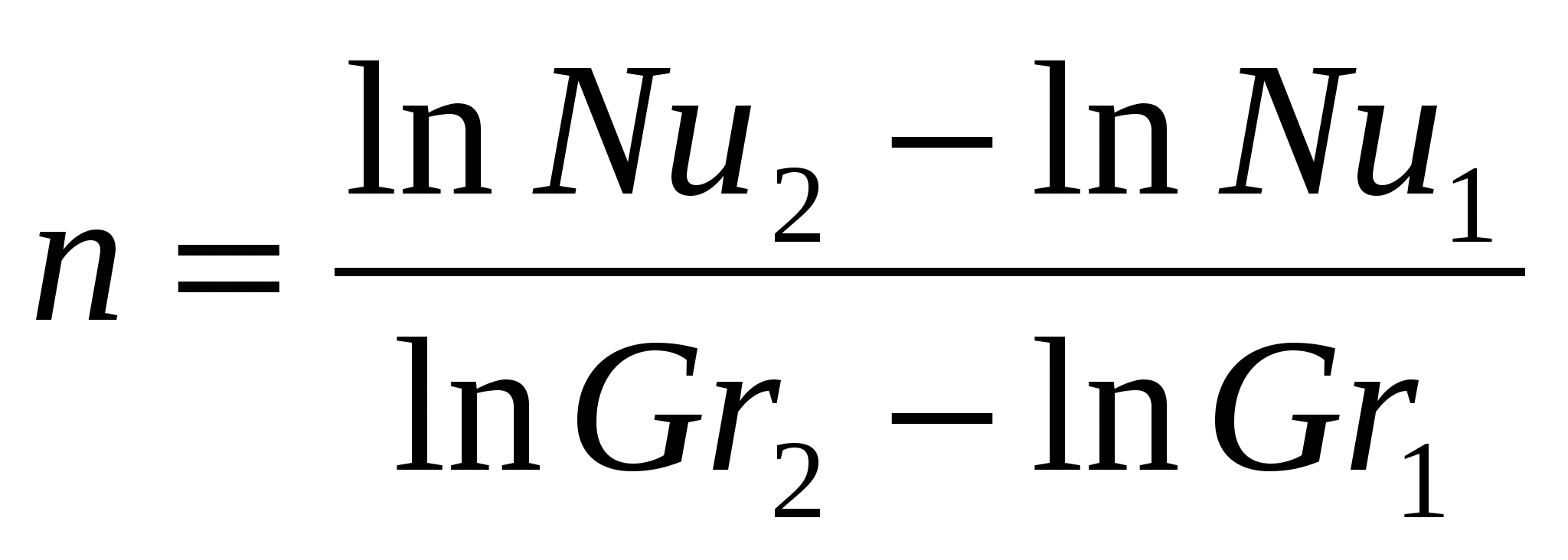 (5.1.12) (5.1.12)
Используя уравнение (5.1.11), можно найти постоянную с
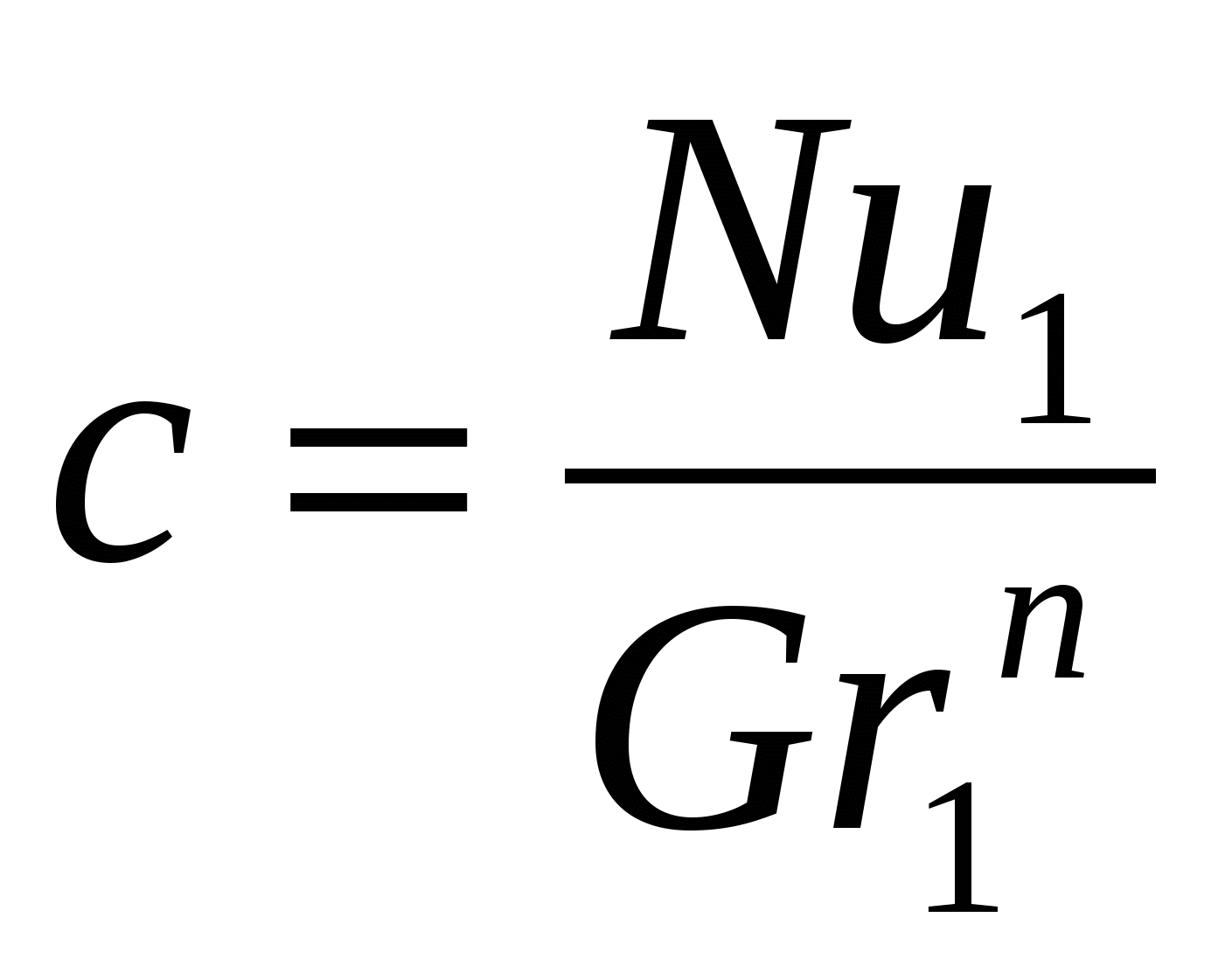 (5.1.13) (5.1.13)
Подставляя найденные значения с и n в уравнение (5.1.11), получим конкретный вид критериального уравнения для горизонтальных труб при свободной конвекции в неограниченном объёме.
5.2 Описание лабораторной установки
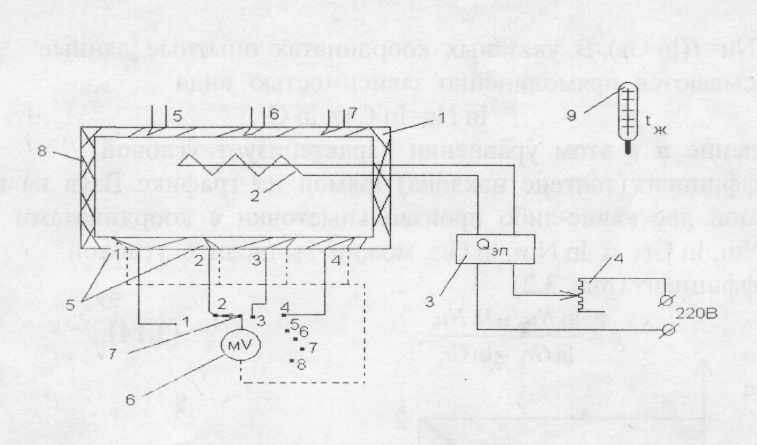
Рисунок 5.2.1 - Схема лабораторной установки
Установка состоит из горизонтального цилиндра 1 (из стали или фарфора) с вмонтированным в него нагревателем 2 (рисунок 5.2.2). Мощность нагревателя замеряется ваттметром 3 и может регулироваться с помощью лабораторного автотрансформатора 4. Для измерения средней температуры стенки трубы на её поверхности установлены горячие спаи термопар 5, причём в нижней части трубы, где температура измеряется наиболее значительно, термопары установлены чаще. Значения температур измеряются с помощью милливольтметра 6, который поочерёдно подключается к каждой термопаре с помощью переключателя 7. Для уменьшения тепловых потерь через торцы трубы они изолируются крышками 8. Температура окружающей среды (воздуха) 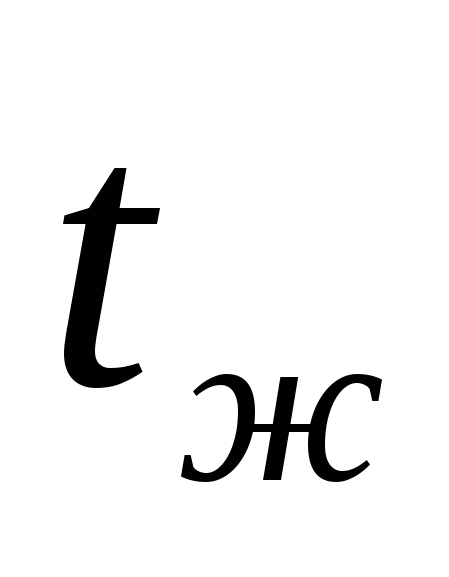 замеряется термометром 9, который должен быть расположен не ближе одного метра от трубы. замеряется термометром 9, который должен быть расположен не ближе одного метра от трубы.
5.3 Порядок выполнения работы
5.3.1 Ознакомится с приборами и устройством лабораторной установки.
5.3.2 С разрешения преподавателя включить электропитание установки и установить заданную мощность нагревателя.
5.3.3 Подключить милливольтметр к одной из термопар с помощью переключателя 7 и дождаться наступления стационарного теплового режима,о чём свидетельствует неизменность показаний милливольтметра во времени.
5.3.4 Произвести замеры следующих величин:
а) температур на поверхности трубы 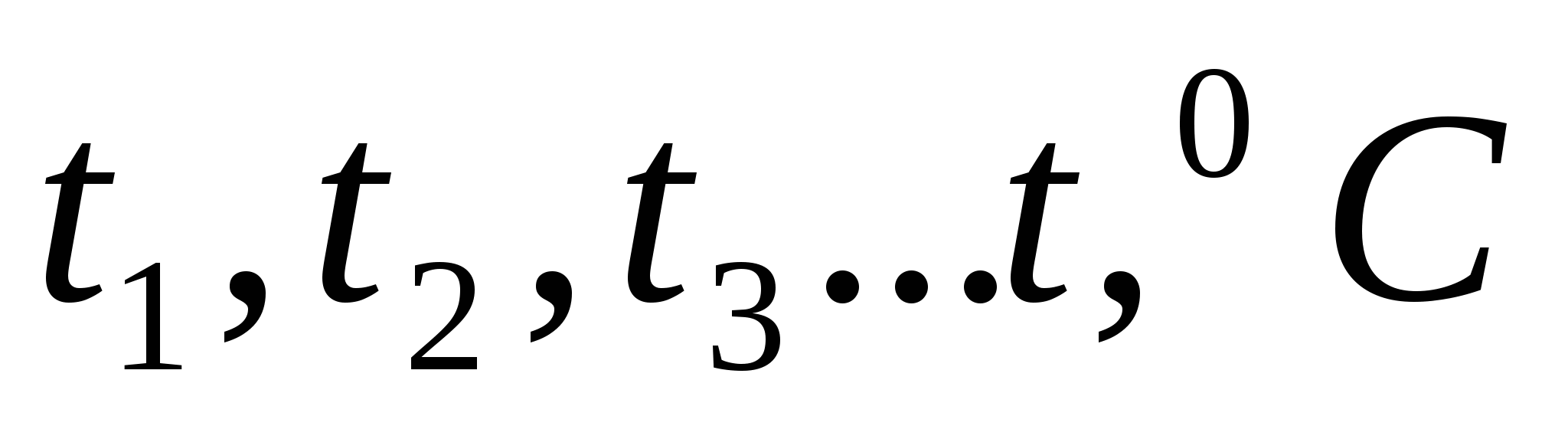 ; ;
б) температуру воздуха 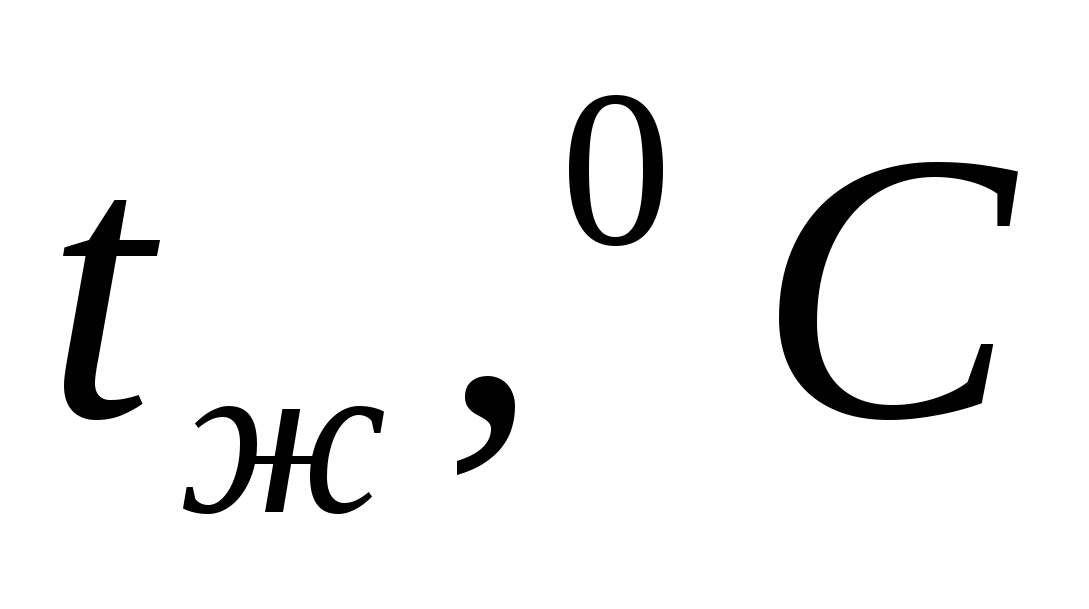 ; ;
в) мощности электронагревателя или тока и падения напряжения, если в схеме установки нет ваттметра;
г) записать геометрические размеры трубы d и l, которые указаны на установке (d1=0,020 м; d2=0,036 м; l=0,72 м).
5.3.5 При обработке результатов измерений вычислить:
а) Среднюю температуру стенки трубы 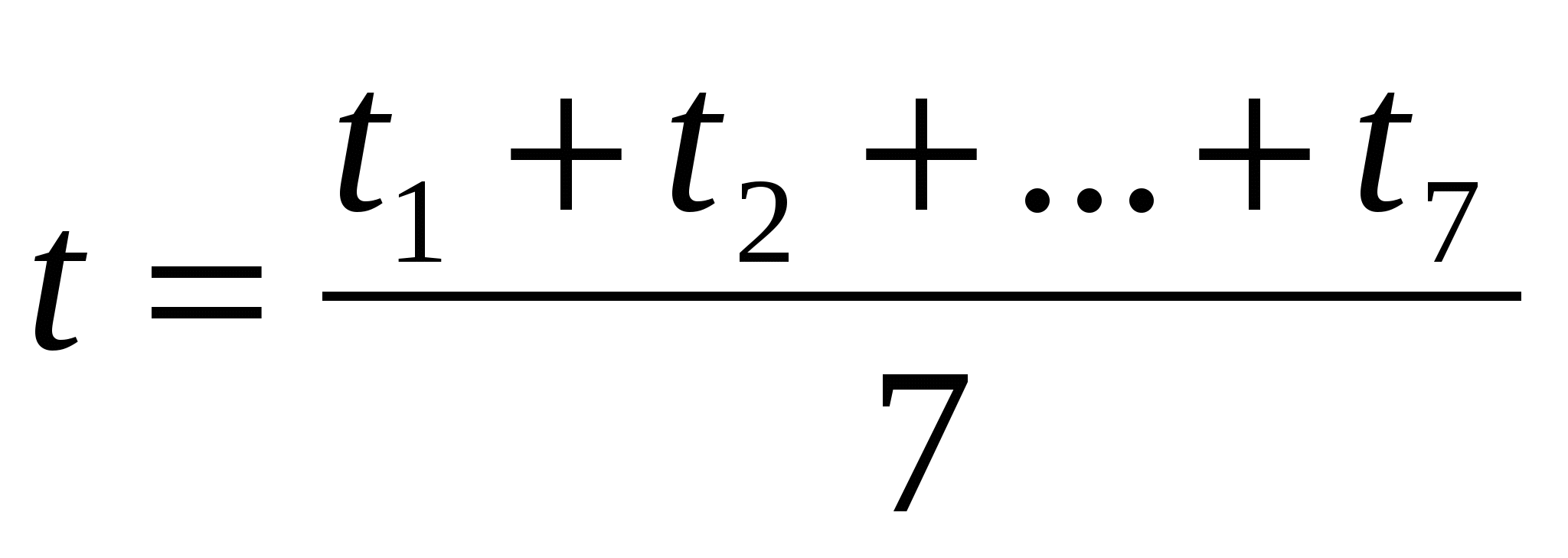
б) Коэффициент теплоотдачи 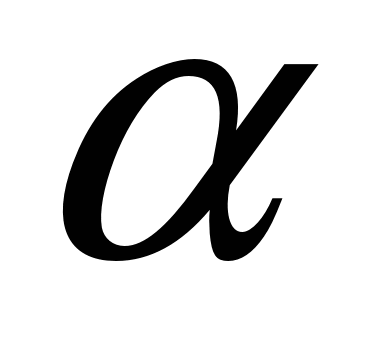 по формуле (5.1.7); по формуле (5.1.7);
в) Критерии Нуссельта и Грасгофа по формулам (5.1.8) и (5.1.9) и их натуральные логарифмы.
5.3.6 Повторить опыт три раза, меняя мощность нагрева с помощью ЛАТРа, ориентируясь по показаниям вольтметра (например, U=100, 150, 200В).
5.3.7 Данные измерений и расчётов занести в таблицу 5.3.1.
5.3.8 Построить прямолинейную зависимость 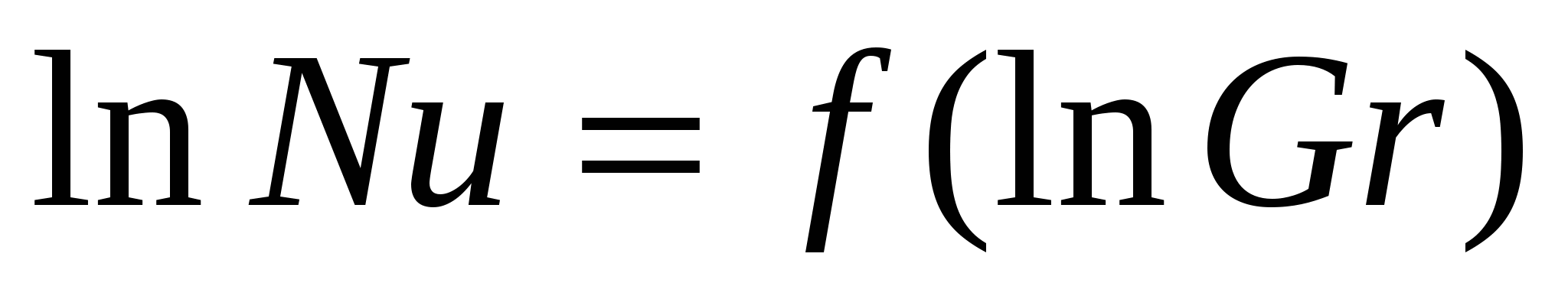 . .
5.3.9 Определить постоянные критериального уравнения с и n по формулам (5.1.12) и (5.1.13).
Таблица 5.3.1 - Результаты измерений
Отчет по работе должен содержать наименование и цель работы, краткое описание методики экспериментального определения коэффициента теплоотдачи 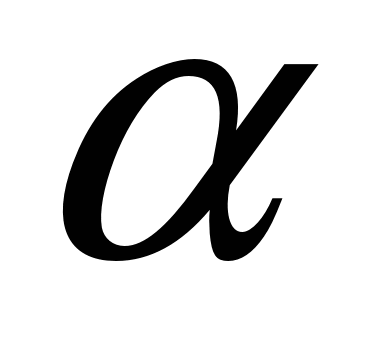 , схему лабораторной установки, график зависимости , схему лабораторной установки, график зависимости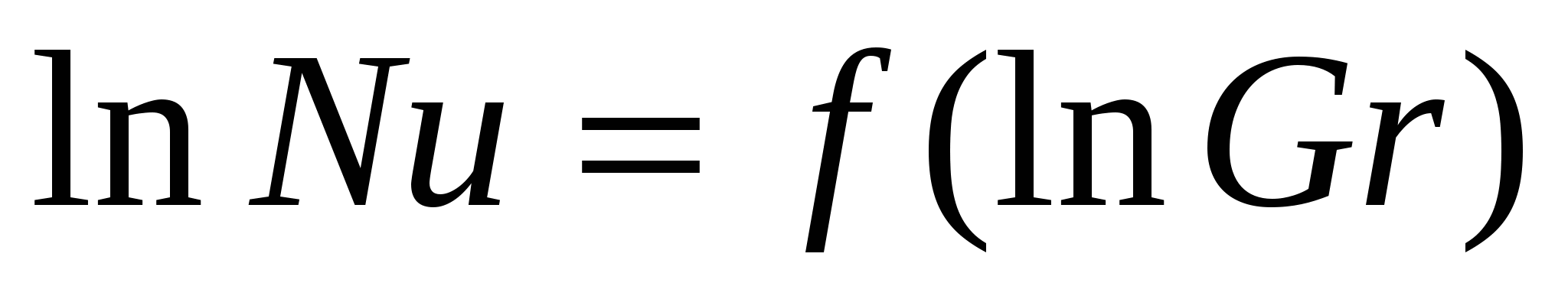 , таблицу и необходимые расчеты. , таблицу и необходимые расчеты.
5.5 Контрольные вопросы
5.5.1 Способы переноса тепла в пространстве.
5.5.2 Сложный теплообмен.
5.5.3 Уравнение Ньютона-Рихмана.
5.5.4 Что такое коэффициент теплоотдачи а и от каких факторов
он зависит?
5.5.5 Критериальное уравнение для свободной конвекции в
неограниченном пространстве.
5.5.6 Как определялись в работе постоянные критериального
уравнения с и n?
Лабораторная работа №6 Исследование теплоотдачи при вынужденном поперечном обтекании цилиндра
Цель работы
Ознакомление с методикой экспериментального определения среднего коэффициента теплоотдачи и постоянной С в критериальном уравнении при поперечном обтекании цилиндра (трубы).
6.1 Вводная часть
Конвективный теплообмен. Конвективным теплообменом или теплоотдачей называется процесс переноса теплоты между поверхностью твердого тела и жидкой средой путем теплопроводности и конвекции. Конвекция возможна лишь в жидкостях и газах, частицы которых могут легко перемещаться. По природе возникновения различают два вида движения - свободное и вынужденное. Свободное движение (естественная конвекция) происходит вследствие разности плотностей нагретых и холодных слоев жидкости. Вынужденное движение (вынужденная конвекция) возникает под действием посторонних возбудителей, например, насоса, вентилятора и пр. В общем случае наряду с вынужденным движением одновременно может развиваться и свободное. Относительное влияние последнего тем больше, чем больше разность температур в отдельных точках жидкости и чем меньше скорость вынужденного движения.
Интенсивность конвективного теплообмена характеризуется коэффициентом теплоотдачи 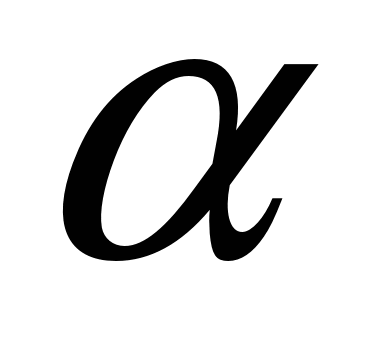 , который определяется по формуле Ньютона – Рихмана. В общем случае коэффициент теплоотдачи может изменяться вдоль поверхности теплообмена, и поэтому различают средний по поверхности коэффициент теплоотдачи и местный (локальный) коэффициент теплоотдачи, соответствующий единичному элементу поверхности. , который определяется по формуле Ньютона – Рихмана. В общем случае коэффициент теплоотдачи может изменяться вдоль поверхности теплообмена, и поэтому различают средний по поверхности коэффициент теплоотдачи и местный (локальный) коэффициент теплоотдачи, соответствующий единичному элементу поверхности.
Процесс теплоотдачи неразрывно связан с условиями движения жидкости. Различают два режима течения жидкости - ламинарный и турбулентный. При ламинарном режиме течение имеет спокойный, струйчатый характер. При турбулентном режиме движение неупорядоченное, вихревое (рисунок 6.1.1). Режим течения зависит от числа Рейнольдса
Re = ω*d/v (6.1.1)
которое учитывает основные факторы, определяющие это течение ω - среднюю скорость движения жидкости, м/с.
При этом характер и условия омывания передней (фронтовой) и задней (кормовой) половины цилиндра совершенно различны. В лобовой точке набегающий поток разделяется на две части и плавно обтекает переднюю часть периметра трубы. На поверхности трубы образуется пограничный слой, который имеет наименьшую толщину в лобовой точке и далее постепенно нарастает в размерах. Скорость слоев жидкости, примыкающих к внешней границе пограничного слоя, увеличивается вдоль периметра трубы, а давление в соответствии с уравнением Бернулли уменьшается. При достижении точки периметра, отвечающей углу φ=90° (угол отсчитывается от лобовой точки), скорость достигает наибольших значений и далее начинает уменьшаться, что сопровождается соответствующим увеличением давления и отрывом потока с образованием вихревой зоны, охватывающей кормовую часть трубы.

Рисунок 6.1.1 - Режимы течения
Такая своеобразная картина обтекания трубы в сильной мере отражается и на теплоотдаче. Интенсивность теплоотдачи по окружности трубы неодинакова. Максимальное значение коэффициента теплоотдачи наблюдается на лобовой образующей цилиндра (φ=0), где толщина пограничного слоя наименьшая. По поверхности цилиндра в направлении движения жидкости интенсивность теплообмена резко падает и при φ=90 – 100° достигает минимума. Это изменение связано с нарастанием толщины пограничного слоя, который как бы изолирует поверхность трубы от основного потока. В кормовой части трубы коэффициент теплоотдачи снова возрастает за счет улучшения отвода теплоты вследствие вихревого движения и перемещения жидкости.
В условиях опыта тепло, рассеиваемое боковой поверхностью цилиндра F в окружающее пространство путем теплового излучения, конвекцией и теплопроводностью, может быть определено по эквивалентной мощности электронагревателя. Суммарный тепловой поток Q складывается из тепловых потоков путем конвективного теплообмена QK и излучения
QЛ – Q = QК + QЛ = αφ * F (tсφ- tЖ) + εC0 * F[(ТСφ / 100)4 - (Тж / 100)4] (6.1.2)
где d - диаметр трубы, м;
v - кинематический коэффициент вязкости (для воздуха таблица 1.1).
Переход турбулентного режима в ламинарный происходит при критическом числе Рейнольдса
Reкр=2300
Если Rе > 2300, то режим турбулентный, если Rе< 2300, то режим ламинарный.
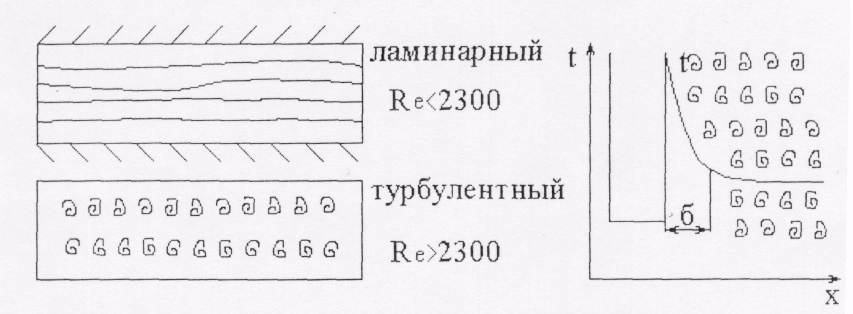
Рисунок 6.1.2 - Пограничный слой при различных режимах течения
При турбулентном движении весь поток насыщен беспорядочно движущимися вихрями, которые непрерывно возникают и исчезают. Однако при любом виде турбулентности в тонком слое у поверхности из-за наличия вязкости трения течения жидкости затормаживается, и скорость падает до нуля.
Для процессов теплоотдачи режим движения жидкости имеет очень большое значение, т.к. им определяется механизм переноса теплоты. При ламинарном режиме перенос теплоты в направлении нормали к стенке в основном осуществляется путем теплопроводности. При турбулентном режиме перенос теплоты путем теплопроводности происходит лишь в вязком подслое, а внутри турбулентного ядра перенос осуществляется путем интенсивного перемещения (конвекции) частиц жидкости. В этих условиях интенсивность теплоотдачи в основном определяется термическим сопротивлением пристенного подслоя толщиной б, где происходит наибольшее изменение температуры жидкости (рисунок 6.1.2).
Теплоотдача при вынужденном поперечном обтекании цилиндра. Процесс теплоотдачи при поперечном обтекании цилиндра (трубы) имеет ряд особенностей, которые объясняются гидродинамической картиной движения жидкости вблизи поверхности цилиндра. Опыт показывает, что плавный, безотказный характер обтекания цилиндра имеет место только при очень малых числах Re < 5. При значительно больших числах Рейнольдса, характерных для практики, обтекание трубы всегда сопровождается образованием в кормовой части вихревой зоны.
Откуда находится локальный (соответствующий углу φ) коэффициент теплоотдачи 
α4= (Q / F – εС0[(ТСφ / 100)4 - (Тж / 100)4]} / (tСφ – tж) (6.1.3)
где F = Пd1 - боковая поверхность цилиндра диаметром d и длиной 1, м2;
С0 = 5,67 Вт /(м4*К4) — коэффициент излучения абсолютно черного тела;
ε- степень черноты поверхности цилиндра (для фарфоровой трубы ε - 0.92);
tCφ - температура стенки трубы в точке, соответствующей углу φ, °С, ТCφ = tCφ + 273, К;
tж - температура омывающей жидкости (газа), °С и Тж = tж + 273, К.
После расчета локальных коэффициентов теплоотдачи определяется средний по периметру трубы коэффициент теплоотдачи ά как среднее арифметическое значение
ά = Σαφ / N, Вт / (м2*К) (6.1.4)
где N - число значений локальных коэффициентов теплоотдачи.
Критерий Нуссельта вычисляется для среднего коэффициента теплоотдачи
Ńudж = ά*d/λ (6.1.5)
Критериальное уравнение для конвективного теплообмена при вынужденном обтекании цилиндра воздухом имеет вид
Ńudж= C*Rеn (6.1.6)
Поскольку в работе скорость постоянна и влияние числа Re на теплоотдачу не исследуется, то значение коэффициента n принять равным при Re< 103n = 0,5 и при Re> 103n = 0,6.
Постоянная определяется по формуле
C= Ńudж/Ren (6.1.7)
6.2 Описание лабораторной установки
Исследуемый цилиндр (фарфоровая трубка) 1 с вмонтированным в него нагревателем помещен в трубу 2, через которую просасывается воздух вентилятором 3. Для определения средней по длине трубы температуры три термопары 4 на одной образующей цилиндра. Цилиндр может поворачиваться вокруг своей оси, что позволяет замерять температуру по окружности цилиндра одними и теми же термопарами. Термопары с помощью переключателя 5 подключаются к милливольтметру 6. Для определения мощности нагревателя служат амперметр 7 и вольтметр 8. Скорость потока определяется с помощью чашечного анемометра, который устанавливается в трубу 2. Измерение скорости сводится к определению числа оборотов по счетчику анемометра за соответствующий отрезок времени, измеренный секундомером. По найденному числу оборотов в минуту определяется скорость потока с помощью градуированного графика, прилагаемого к анемометру.
5 6
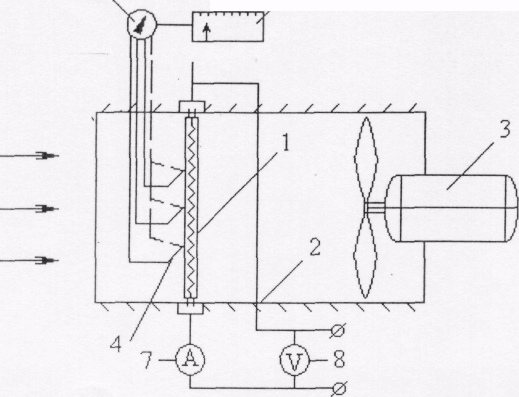
Рисунок 6.2.1- Опытная установка
6.3 Порядок выполнения работы
6.3.1 Ознакомление с приборами и устройством лабораторной
установки.
6.3.2 Включить электронагреватель цилиндра и вентилятор.
6.3.3 После наступления установившегося режима (о чем свидетельствует постоянство показаний милливольтметра) произвести следующие замеры:
а) температуры воздуха в трубе с помощью термометра tж, 0С;
б) скорости воздуха в трубе с помощью анемометра ω, м / с;
в) показаний амперметра I, А и вольтметра ΔU, В;
г) температуры стенки цилиндра при положении термопар в лобовой точке цилиндра (φ = 0°) с помощью трех термопар t1, t2 и t3, °С;
6.3.4 Поворачивая цилиндр вокруг своей оси, произвести замеры температур с помощью термопар t1, t2 и t3 через каждые 30° поворота цилиндра.
6.3.5 При обработке результатов опыта вычислить:
а) тепловой поток по формуле Q = Qэл, Вт;
б) среднее значение температуры по образующей цилиндра для данного угла φ
tСр = t1 + t2 + t3/3, °С
в) локальный коэффициент теплоотдачи α1 по формуле (1.3);
г) средний коэффициент теплоотдачи ά по формуле (1.4);
д) критерий Рейнольдса по формуле (1.1);
е) по найденному значению числа Rе выбрать показатель степени n;
ж) критерий Нуссельта по формуле (1.5);
з) постоянную С по формуле (1.7) и записать критериальное уравнение в окончательном виде применительно к условиям опыта.
6.3.6 Результаты опытов и расчетов занести в таблицу 4.1.
6.3.7 Построить график изменения относительного коэффициента теплоотдачи αφ / ά по окружности αφ / ά = ƒ(φ).
Таблица 6.3.1- Результаты измерений
-
φ
|
tж
|
t1
|
t2
|
t3
|
tcφ
|
I
|
ΔU
|
Q
|
αφ
|
ά
|
ω
|
Re
|
Nu
|
αφ/ά
|
град
|
°С
|
А
|
В
|
Вт
|
Вт/(м2,К)
|
м/с
|
|
|
|
0
30
60
---
180
|
Отчет о работе должен содержать наименование и цель работы, схему установки, основные расчетные формулы, краткую методику экспериментального определения среднего коэффициента теплоотдачи цилиндра при вынужденной конвекции, таблицу опытных и расчетных данных, график зависимости относительного коэффициента теплоотдачи от угла.
6.4 Контрольные вопросы
6.4.1 Чем объясняется неодинаковость коэффициента теплоотдачи по окружности цилиндра?
6.4.2 Где больше значения коэффициента теплоотдачи: в боковой или лобовой точке цилиндра и почему?
6.4.3 Как в работе определяется средний коэффициент теплоотдачи по окружности цилиндра?
6.4.4 Как влияет режим течения жидкости на теплоотдачу?
6.4.5 Что называется конвективным теплообменом?
6.4.6 Ламинарный и турбулентный режим течения жидкости.
6.4.7 Что характеризует критерии Нуссельта и Рейнольдса?
Литература
Основная литература
1.Альтшуль А.Д. Гидравлика и аэродинамика: учебник для вузов – М. : Стройиздат, 1987.- 210 с.
2. Альтшуль А.Д., и др. Примеры расчетов по гидравлике: Учеб.пособие для вузов – М. : Стройиздат, 1976. – 175 с.
3. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. Учебник для вузов. – М. : Энергия, 1975 г.- 320 с.
Дополнительная литература
4. Нащокин В.В. Техническая термодинамика и теплопередача. – М. : Высшая школа, 1975. – 250 с.
5.Рындин В.В. Методические указания к лабораторным работам. Часть 1.- Алма-Ата: НМК, 1992. – 67 с.
6. Юдаева Б.Н. Сборник задач по технической термодинамике.- М.: Высшая школа, 1981. – 150 с.
Содержание
-
Введение......................................................................................
|
3
|
Лабораторная работа №1. Изучение способов измерения гидростатического давления.....................................................
|
4
|
Лабораторная работа №2. Ламинарный и турбулентный режимы течения жидкости........................................................
|
12
|
Лабораторная работа № 3 Применение уравнения Бернулли к анализу потока жидкости......................................
|
18
|
Лабораторная работа № 4 Определение коэффициента теплопроводности материала по методу цилиндрического слоя.........................................................
|
24
|
Лабораторная работа №5 Исследование теплоотдачи при свободной конвекции в неограниченном объёме...................
|
31
|
Лабораторная работа №6 Исследование теплоотдачи при вынужденном поперечном обтекании цилиндра.....................
|
39
|
Литература..................................................................................
|
46
|
|
|
|
|
|
|
|
|

УТВЕРЖДАЮ
Проректор по УР
______Пфейфер Н.Э.
«__»_________2009г.
Составитель: ст.преподаватель________ Мергалимова А.К.
Кафедра теплоэнергетики
Методические указания к лабораторным работам по дисциплине «Гидрогазодинамика и тепломассообмен» для студентов специальности 050731 «Безопасность жизнедеятельности и охрана окружающей среды»
Рекомендована на заседании кафедры, от «__»______2009г., протокол №__
Заведующий кафедрой___________ Глазырин С.А.
Одобрена методическим советом энергетического факультета
«__»_________2009г., протокол №__
Председатель МС __________ Кабдуалиева М.М.
Декан ЭФ _________________Кислов А.П., «__»______2009г.
Нормоконтроль ОМК ________Баяхметова Г.С., «__»______2009г.
Одобрено ОП и МОУП
Начальник ОП и МОУП _______________Варакута А.А.
Министерство образования и науки Республики Казахстан
Павлодарский государственный университет
им. С. Торайгырова
ГИДРОГАЗОДИНАМИКА И ТЕПЛОМАССООБМЕН
Методические указания к лабораторным работам
для студентов специальности 050731 "Безопасность жизнедеятельности и охрана окружающей среды"
Павлодар
2009
страница 1 страница 2
|