страница 1 страница 2
Министерство образования и науки Республики Казахстан
Павлодарский государственный университет
им. С. Торайгырова
Энергетический факультет
Кафедра теплоэнергетики
ГИДРОГАЗОДИНАМИКА И ТЕПЛОМАССООБМЕН
Методические указания к лабораторным работам
для студентов специальности 050731 "Безопасность жизнедеятельности и охрана окружающей среды"
Павлодар
Кереку
2009
УДК 621.1.016(07)
ББК 31.31я7
Г46
Рекомендовано к изданию заседанием кафедры теплоэнергетики энергетического факультета Павлодарского государственного университета им. С. Торайгырова
Рецензент:
кандидат технических наук, доцент С.А.Глазырин
Составитель А.К.Мергалимова
Г46 Гидрогазодинамика и тепломассообмен : методические указания
к лабораторным работам для студентов специальностей 050731
"Безопасность жизнедеятельности и охрана окружающей
среды", / сост. А.К.Мергалимова – Павлодар: Кереку,2009. –
46 с.
В методическом указании приводятся материалы для подготовки к лабораторным работам и методика их выполнения по дисциплине "Гидрогазодинамика и тепломассообмен", показаны цели работ.
Методические указания разработаны в соответствии с рабочим учебным планом специальности 050731 "Безопасность жизнедеятельности и охрана окружающей среды" и рабочей программой.
УДК 621.1.016(07)
ББК 31.31я7
© Мергалимова А.К., 2009
© ПГУ им. С. Торайгырова, 2009
За достоверность материалов, грамматические и орфографические ошибки ответственность несут авторы и составители
Введение
Данные методические указания по дисциплине «Гидрогазодинамика и тепломассообмен» разработаны для студентов специальности 050731 «Безопасность жизнедеятельности и охрана окружающей среды».
Здесь рассмотрены вопросы: понятие технической термодинамики и тепломассообмена, различные способы применения тепловой энергии, законы идеальных и реальных газов в основных теплотехнических расчетах, газовые смеси, единицы измерения, законы теплопередачи.
Лабораторная работа № 1 Изучение способов измерения гидростатического давления
Цель работы: ознакомление с конструкцией приборов для измерения давления и правилами пользования ими.
-
.1 Введение
Покоящаяся под действием внешних массовых и поверхностных си жидкость находится в напряженном состоянии, которое в каждой точке характеризуется давлением Р, равным
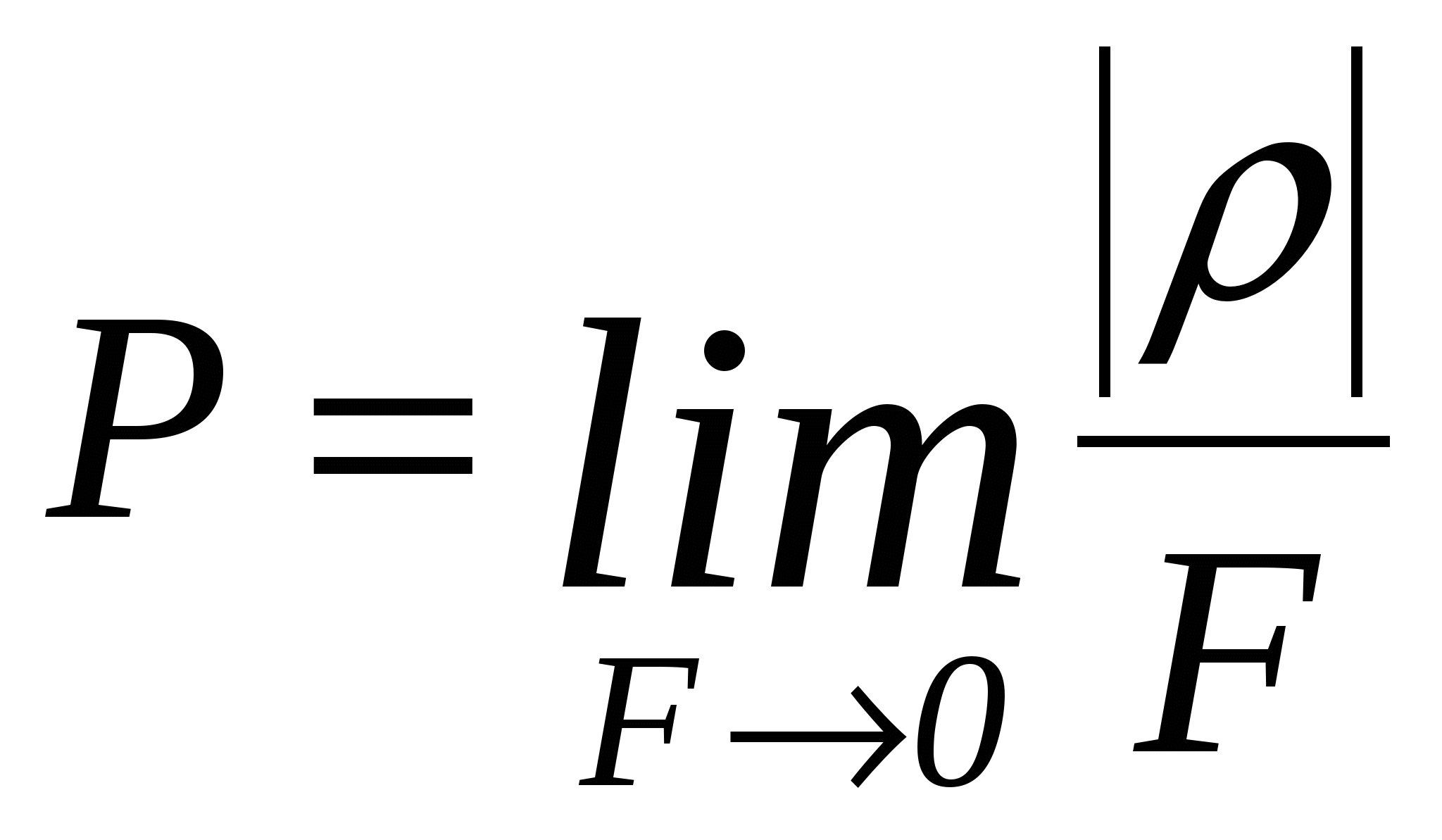 (1.1.1) (1.1.1)
где p- модуль силы, действующей на некоторую площадку, имеющую площадь, равную F.
Это давление называется гидростатическим давлением.
Давление измеряется в единицах силы, отнесенных к единице площади. В системе СИ единицей давления служит Н/м2 = Па (паскаль), а в технической системе – кгс/см2 = атм (техническая атмосфера). Наряду с этим давление можно измерять в единицах длины столба данной жидкости. При выражении давления высотой столба жидкости чаще всего применяют метры и милливольтметры водяного столба (1 атм = 10 м вод. ст., 1 мм вод ст. = 9,81 Па), миллиметры ртутного столба ( 1 атм = 760 мм рт. ст., 1 мм рт. ст. = 133,3 Па).
Ели жидкость находится в ненапряженном состоянии, т.е. в ней отсутствуют напряжения сжатия, то Р = 0. Значения Р, отсчитанные от этого нуля, называют абсолютным давлением Рат. Давление может отсчитываться и от атмосферного давления (рисунок 1.1.1)
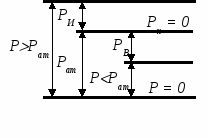
Рисунок 1.1.1 – Схема давлений
Избыток абсолютного давления над атмосферным называется избыточным давлением РИ = Р – Рат Недостаток абсолютного давления до атмосферного называется вакуумом или разрежением РВ = Рат – Р, максимально возможный в технической жидкости вакуум ограничен величиной, соответствующей при данной температуре давлению насыщенного пара жидкости РВ = Рат – РНП
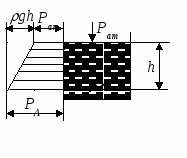
Рисунок 1.1.2 - Распределение давления в объеме
Распределение давления в объеме покоящейся жидкости выражается основным законом гидростатики (рисунок 1.1.2)
Р = РА = Рат + g h (1.1.2)
где РА – абсолютное давление в точке А, расположенной на глубине h, отсчитанной от свободной поверхности жидкости;
- плотность жидкости;
g – ускорение свободного падения.
Если все члены выражения (1.1.2) разделить на g, то они приобретут линейную размерность
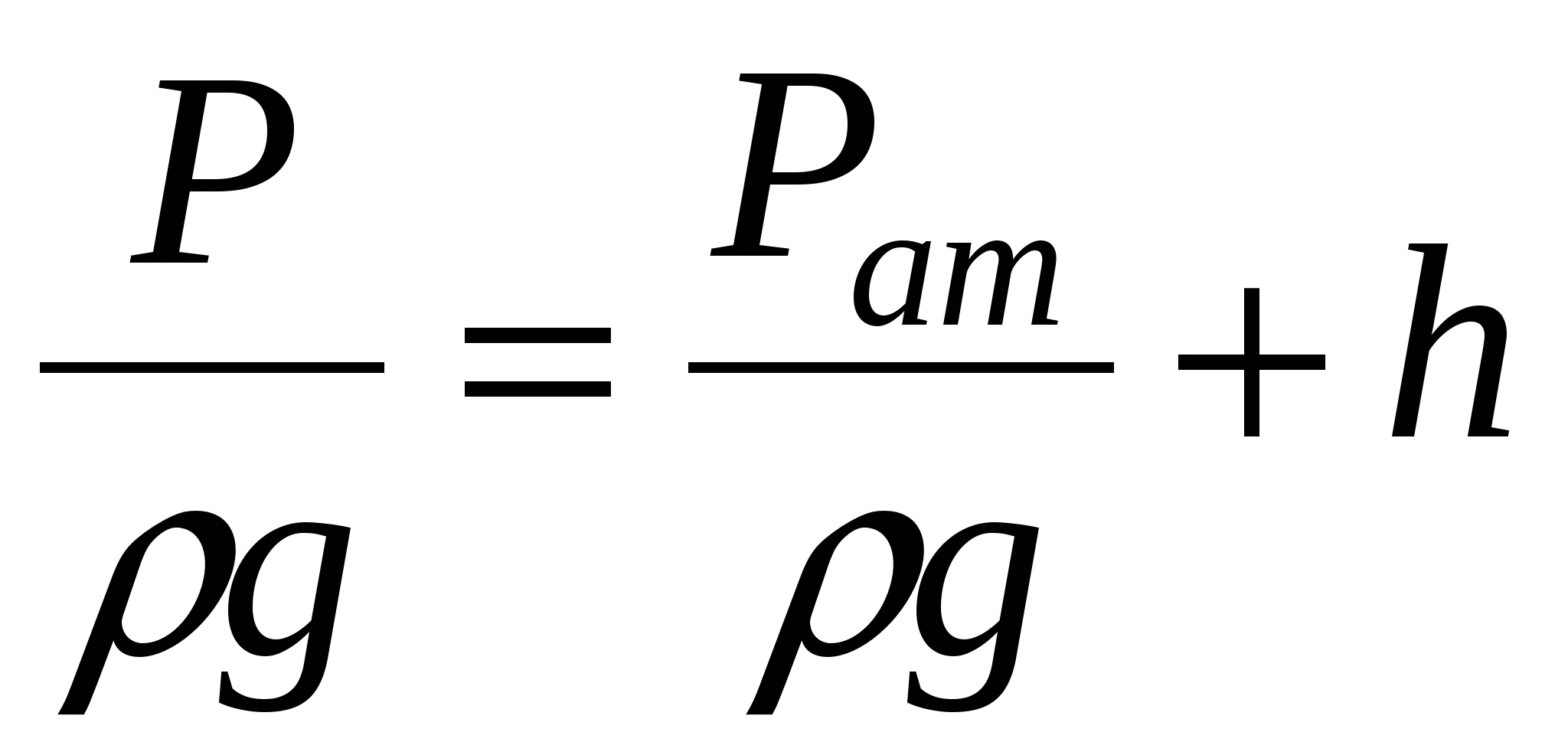 (1.1.3) (1.1.3)
Отсюда следует, что каждому давлению Р можно поставить в соответствие линейную величину Р/g, которая представляет собой величину столба жидкости, создающего в своем основании данное давление.
Для измерения давления применяются самые разнообразные приборы. Условно все приборы для измерения давления можно классифицировать по следующим признакам:
1) по роду измеряемой величины;
2) по принципу действия;
3) по классу точности.
По роду измеряемой величины в зависимости от необходимости измерения атмосферного, абсолютного, избыточного давления или вакуума существует несколько видов приборов.
Приборы, предназначенные для измерения атмосферного давления, называются барометрами, для измерения избыточного давления – манометрами, для измерения вакуума – вакуумметрами. Приборы, позволяющие измерять и избыточное давление и вакуум, называются мановакуумметрами. Для измерения абсолютного давления необходимо наличие двух приборов – барометра и манометра, если абсолютное давление больше атмосферного; и барометра и вакуумметра, если абсолютное давление меньше атмосферного. Приборы, предназначенные для измерения разности давлений, называются дифференциальными манометрами. Для измерения малых давлений применяют микроманометры.
По принципу действия все приборы можно разделить на жидкостные, механические, грузопоршневые, электрические и комбинированные.
К жидкостным относятся приборы, в которых измеряемое давление уравновешивается давлением, создаваемым весом столба жидкости, высота которого служит мерой давления.
Пьезометр применяется для измерения избыточного давления и разрежения и представляет собой стеклянную трубку с открытым в атмосферу верхним концом. Нижний конец пьезометра соединяется с местом измерения давления. На рис. 1.1.3 изображен пьезометр для измерения избыточного давления. Под действием избыточного давления в сосуде жидкость в пьезометре поднимается на высоту h, измеряемую по линейной шкале, установленной строго вертикально.
Избыточное давление РИ в точке А жидкости
РИ = g h (1.1.4)
а абсолютное давление в этой точке
Р = РА = РИ + Рат. (1.1.5)
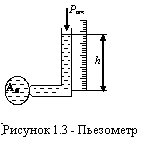
Давление, выраженное высотой столба жидкости h = Pи/ g, носит название пьезометрической высоты.
Точность измерения определяется погрешностью в определении плотности, неточностями установки и градуировки шкалы прибора, погрешностями при отсчетах показаний и дополнительной высотой подъема жидкости в стеклянной трубке, обусловленной действием сил поверхностного натяжения (явление капиллярности).
Дополнительная высота подъема жидкости h,мм, в стеклянной трубке диаметром d определяется по формуле
h = К / d (1.1.6)
где величина К имеет следующие значения: для воды – 30 мм2, для ртути – 14 мм2, для спирта – 12 мм2.
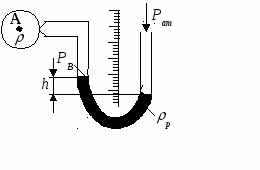
Рисунок 1.1.4 - U – образный манометр
U – образный манометр (рисунок 1.1.4) представляет собой U- образную стеклянную трубку, заполненную до некоторого уровня рабочей жидкостью (спирт, ртуть и др.). конец одной ветви манометра соединяется с местом измерения, конец другой ветви открыт в атмосферу. Разность высот уровней рабочей жидкости в ветвях является показанием прибора. Разрежение РВ на уровне рабочей жидкости в левой ветви
РВ = р g h (1.1.7)
где р – плотность рабочей жидкости. Точность измерений зависит от тех же факторов, что и в пьезометре. Поправкой на капиллярность для U – образного манометра обычно пренебрегают.
Чашечный манометр (рисунок 1.1.5) представляет собой модификацию U – образного манометра, одна из ветвей которого заменена чашкой. Под действием давления РИ рабочая жидкость в стеклянной трубке прибора поднимается на высоту h. Нуль шкалы прибора помещен на уровне мениска рабочей жидкости в трубке при атмосферном давлении на поверхности рабочей жидкости в чашке; такой способ установки нуля дает возможность сразу учесть поправку на капиллярность.
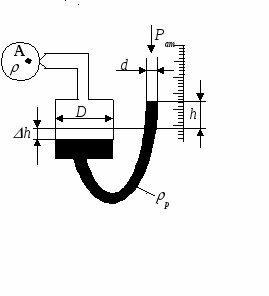
Рисунок 1.1.5 – Чашечный манометр
Избыточное давление на уровне рабочей жидкости в чашке прибора
РИ = р g (h + h) (1.1.8)
где h – показания прибора;
h = h d2/D2 – поправка на положение уровня рабочей жидкости в чашке прибора при подъеме жидкости в трубке на высоту h;
d – диаметр прибора (трубки);
D – диаметр чашки.
Обычно D » d и поправкой h на положение уровня в чашке можно пренебречь. Преимущество чашечного манометра перед U – образным, что первый имеет постоянный нуль и не требует измерения нескольких высот для определения давления.
В пружинных манометрах деформация упругого элемента (полая трубка, мембрана и т.п.), вызванная давлением, по закону Гука пропорциональна давлению и служит его мерой. В манометре с одновитковой трубчатой пружиной (манометр Бурдона) основной деталью является согнутая по дуге окружности полая трубка, имеющая на конце овальную форму. Большая ось овала перпендикулярна плоскости оси трубки. Один из концов трубки запаян. Измеренное давление передается внутрь трубки через второй открытый ее конец. Под действием давления овальное сечение трубки деформируется: большая ось овала уменьшается, малая увеличивается. При такой деформации каждого сечения трубки появляется момент М, разгибающий эту трубку. Стрелка прибора, связанная со свободным концом трубки через передаточный механизм, поворачивается на некоторый угол, пропорциональный измеренному давлению.
Важным преимуществом пружинных приборов по сравнению с жидкостными являются портативность, универсальность, огромный диапазон измеряемых давлений. Недостатком является нестабильность их показаний, вызываемая рядом причин: изменением упругости деформируемого элемента, износ передаточного механизма. В связи с чем возникает необходимость периодически определять поправку, компенсирующую систематическую погрешность прибора.
-
Описание лабораторной установки
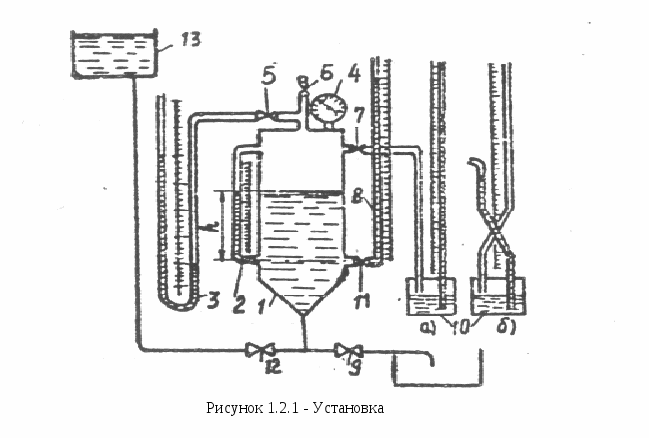
Экспериментальная установка (рисунок 1.2.1) состоит из герметичного сосуда 1, к которому присоединены водомерное стекло 2, пьезометр 8, чашечный манометр 10, пружинный мановакуумметр 4 и U - образный манометр 3, заполненный водой. Уровень жидкости в сосуде 1 и давление над ее свободной поверхностью можно менять, регулируя доступ воды из напорного бака 13 при помощи вентилей 5, 6, 7, 9, 11 и 12. Вентиль 6 служит для сообщения сосуда с атмосферой.
-
Порядок выполнения работы
-
Порядок выполнения работы
-
Ознакомиться с устройством лабораторной установки.
-
Закрыть вентиль 9 и открыть вентили 6 и 12. Заполнить сосуд водой до половины его объема, ориентируясь по уровню воды в водомерном стекле. Закрыть вентиль 6 (разобщить сосуд с атмосферой). Вода, продолжая поступать в сосуд через вентиль 12, повысит давление воздуха над свободной поверхностью воды в сосуде.
-
Записать показания мановакуумметра, U – образного манометра и чашечного манометра, показывающих избыточное давление воздуха в сосуде, и показания пьезометра, показывающего избыточное давление в жидкости в сосуде на глубине h, которая определяется по уровню жидкости в водомерном стекле.
-
Закрыть вентиль 12 и открыть вентиль 9. Часть воды вытечет из сосуда, в результате чего давление в сосуде станет меньше атмосферного. Закрыть вентиль 7 и поменять местами соединительные трубки чашечного манометра как показано на рис. 1.7,б. Открыть вентиль 7.
-
Записать показания приборов, показывающих величину вакуума в сосуде.
-
Привести установку в исходное состояние: поменять местами соединительные трубки на чашечном манометре, вентиль 12 закрыть, 6 и 9 открыть.
-
Результаты замеров занести в таблицу 1.3.1
Таблица 1.3.1-Результаты измерений
Приборы
|
Показания приборов
|
Перевод показаний в кПа
|
Абсолютное давление
|
Погрешность измерения
|
h, мм
|
hВ, мм
|
РИ, ат
|
РВ, ат
|
РИ
|
РВ
|
Р = Рат + РИ, кПа
|
Р = Рат – РВ, кПа
|
абсолютная
|
относительная
|
Мановакуумметр
|
-
|
-
|
|
|
|
|
|
|
|
|
Пьезометр
|
|
-
|
-
|
-
|
|
|
|
|
|
|
Чашечный манометр
|
|
|
-
|
-
|
|
|
|
|
|
|
U – образный манометр
|
|
|
-
|
-
|
|
|
|
|
|
|
Барометр
|
-
|
-
|
|
-
|
|
|
|
|
|
|
Водомерное стекло
|
|
|
-
|
-
|
|
|
|
|
|
|
-
Обработка результатов опыта
-
Перевести показания всех приборов в кПа. Определить абсолютное давление воздуха в сосуде по показаниям каждого прибора (атмосферное давление Рат определить по показаниям барометра), а также абсолютное давление жидкости на глубине h.
-
Определить предельную и абсолютную погрешности измерения давления каждым прибором по формулам:
Предельная абсолютная погрешность измерения давления
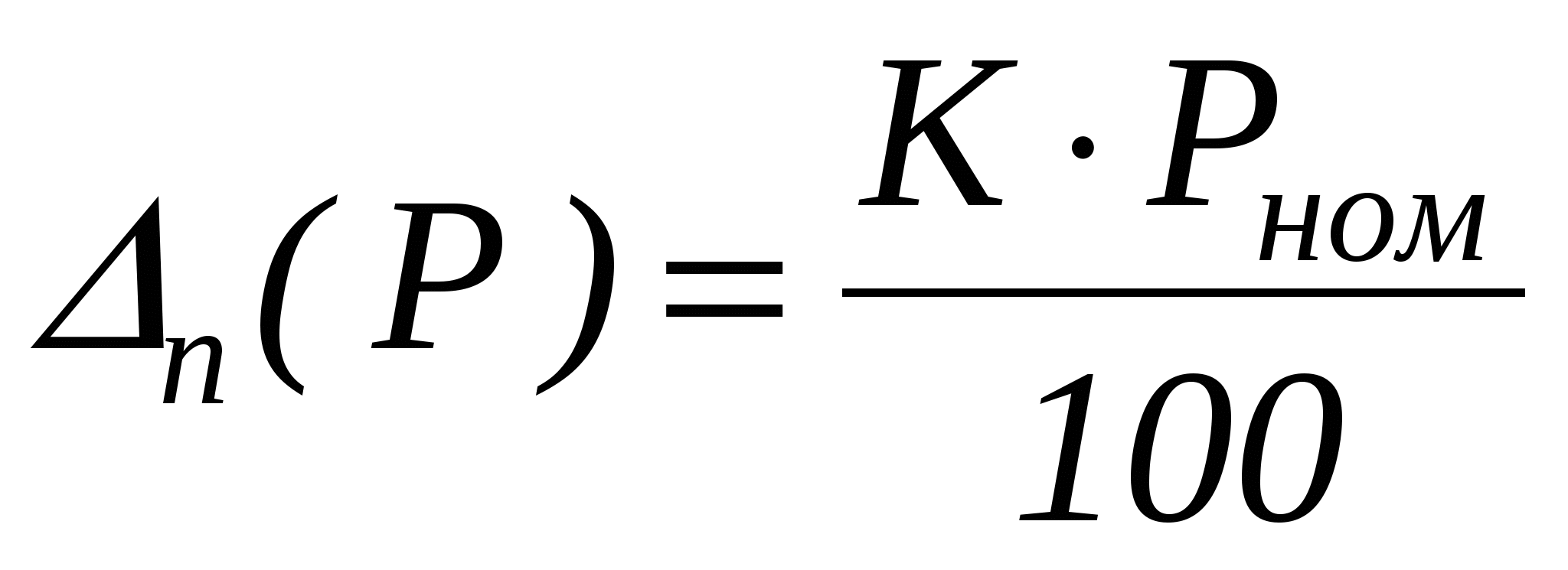 (1.4.1) (1.4.1)
где К – класс точности прибора;
Рном – номинальное значение давления (за него принимается верхний предел прибора).
Предельная относительная погрешность
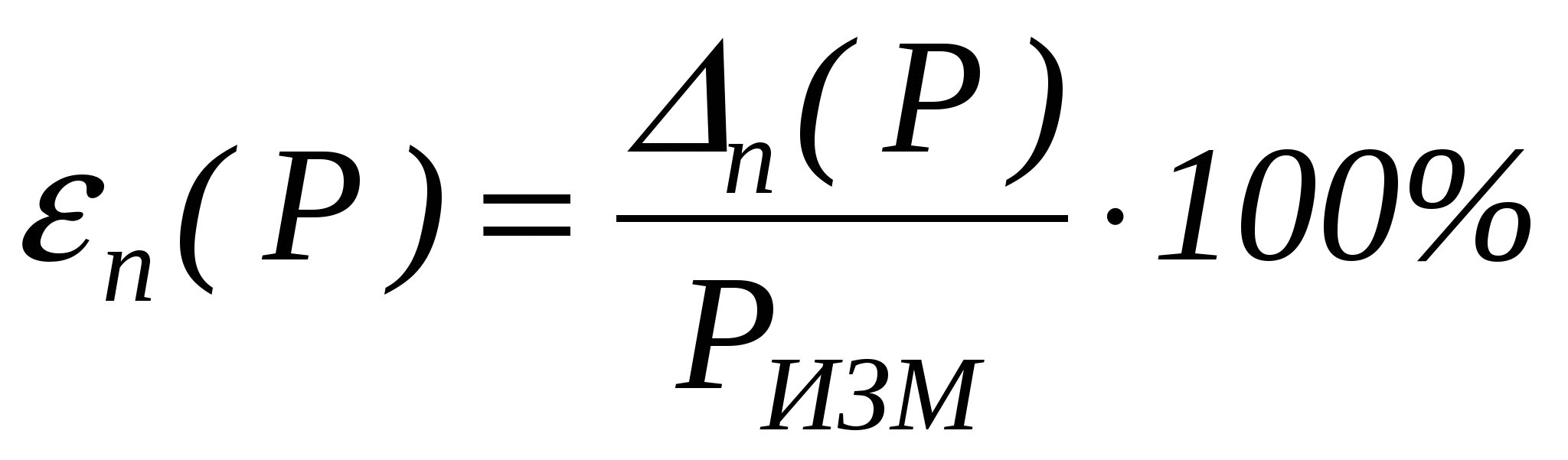 , (1.4.2) , (1.4.2)
где РИЗМ – измеренное значение давления.
-
Результаты расчетов занести в таблицу 1.3.1.
-
Контрольные вопросы
1.5.1 Что называется давлением?
1.5.2 Что такое абсолютное, избыточное и вакуумметрическое давление?
1.5.3 Основной закон гидростатики?
1.5.4 Приборы для измерения давления?
1.5.5 Связь между различными единицами измерения давления.
Лабораторная работа № 2 Ламинарный и турбулентный режимы течения жидкости
Цель работы: ознакомление с методикой визуального определения критического числа Рейнольдса для потока, движущегося в стеклянной трубе, на приборе Рейнольдса и исследование режимов движения жидкости.
2.1 Введение
Наблюдения показывают, что в природе существует два различных режима движения жидкости. В первом случае отдельные струйки движутся параллельно, не смешиваясь между собой. Этот вид упорядоченного движения жидкости, при котором жидкость перемещается как бы слоями, параллельными направлению течения, называется ламинарным течением (от латинского lamina – пластина).
Во втором случае поток характеризуется беспорядочным, хаотичным движением жидкости. Наряду с основным поступательным перемещением жидкости вдоль трубы наблюдается незакономерное поперечное перемещение и вращательное движение частиц. Этот вид беспорядочного движения жидкости называется турбулентным течением (от латинского turbulentus – буйный, беспорядочный).
Кинематические и динамические характеристики потока в трубе существенно зависят от режима движения жидкости. Так, при ламинарном движении распределение скоростей по сечению имеет параболический характер: непосредственно у стенок скорости равны нулю, а при удалении от них непрерывно и плавно возрастают, достигая максимума на оси трубы (рисунок 2.1.1,а). Средняя скорость при этом равняется половине максимальной.
При турбулентном течении скорость в каждой точке потока изменяется по величине и направлению около некоторого среднего значения. Следовательно, турбулентный поток является по своей природе неустановившимся. При гидравлических расчетах турбулентных поток обычно пользуются их осредненными во времени характеристиками. Замена действительного неустановившегося движения более простой схемой осредненного установившегося потока чрезвычайно облегчает изучение турбулентного потока, сохраняя вместе с тем его главные закономерности.
Измерения скоростей показывают, что при переходе к турбулентному режиму у стенок сохраняется тонкий слой жидкости, в котором частицы жидкости, подторможенные и направленные стенками, сохраняют, в основном, слоистый характер движения (так называемый ламинарный или вязкий подслой). Поэтому профиль осредненных скоростей имеет два значительно различных участка (рисунок 2.1.1,б). В турбулентном ядре благодаря интенсивному перемешиванию, приводящему к выравниванию скоростей частиц, осредненные скорости отличаются незначительно и их распределение по основной части сечения оказывается более равномерным, чем при ламинарном режиме. В пределах вязкого подслоя происходит весьма резкое падение скорости до нулевого значения на стенке. Толщина вязкого подслоя чрезвычайно мала (сотые и тысячные доли диаметра трубопровода).
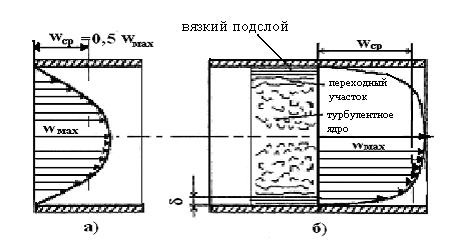
Рисунок 2.1.1- а) Ламинарный режим течения жидкости,
б)турбулентный режим течения жидкости
Измерения скоростей показывают, что при переходе к турбулентному режиму у стенок сохраняется тонкий слой жидкости, в котором частицы жидкости, подторможенные и направленные стенками, сохраняют, в основном, слоистый характер движения (так называемый ламинарный или вязкий подслой). Поэтому профиль осредненных скоростей имеет два значительно различных участка (рисунок 1.1). В турбулентном ядре благодаря интенсивному перемешиванию, приводящему к выравниванию скоростей частиц, осредненные скорости отличаются незначительно и их распределение по основной части сечения оказывается более равномерным, чем при ламинарном режиме. В пределах вязкого подслоя происходит весьма резкое падение скорости до нулевого значения на стенке. Толщина вязкого подслоя чрезвычайно мала (сотые и тысячные доли диаметра трубопровода).
Между турбулентным ядром и вязким подслоем имеется тонкий переходной участок, в котором по мере приближения к подслою резко уменьшаются турбулентные пульсации и интенсивно уменьшаются осредненные скорости. Так как характеристики потока изменяются по радиусу непрерывно, установить границы между этими участками можно только условно. Ясность в вопрос о том, как именно будет происходить движение жидкости в тех или иных условиях, была внесена в 1883 г. в результате опытов английского физика Рейнольдса. Основываясь на некоторых теоретических соображениях, а также на результатах этих опытов, Рейнольдс установил общие условия, при которых возможны существование ламинарного и турбулентного режимов движения жидкости и переход от одного режима к другому. Оказалось, что режим потока жидкости в трубе зависит от величины безразмерного числа, которое учитывает основные факторы, определяющие это движение: среднюю скорость , диаметр трубы d, плотность жидкости и ее абсолютную (динамическую) вязкость . Это число (позже ему было присвоено название числа Рейнольдса) имеет вид
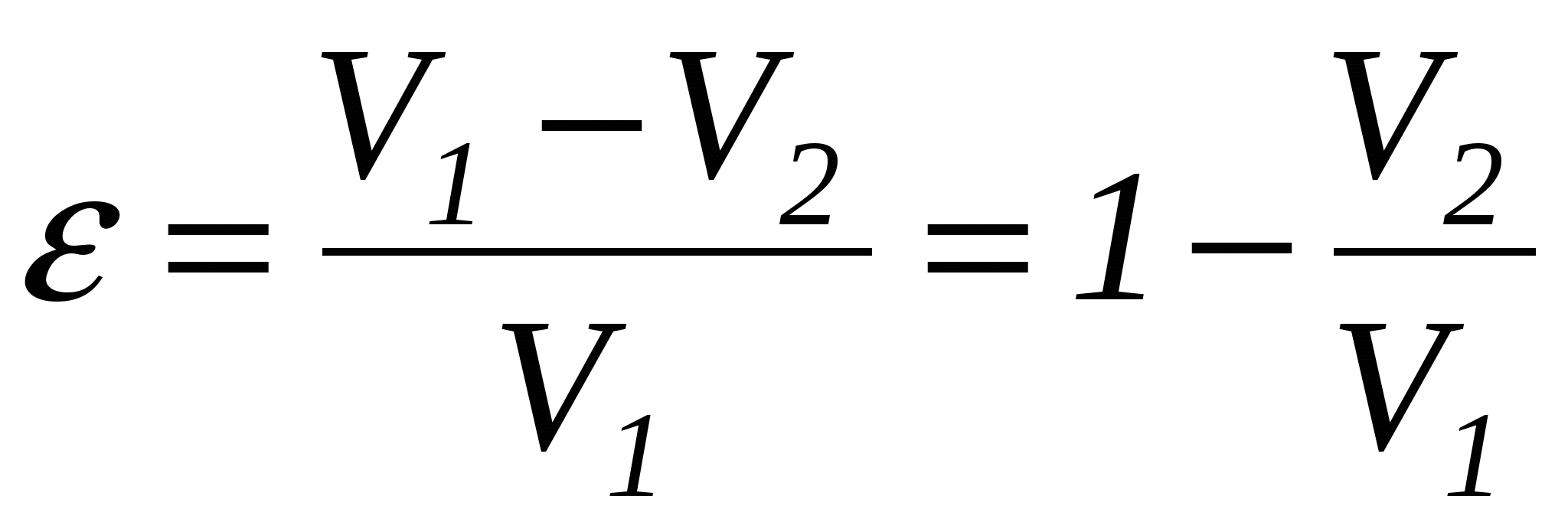 (2.1.1) (2.1.1)
Если ввести понятие кинематической вязкости = /, то для сечений любой формы число Рейнольдса определяется из выражения
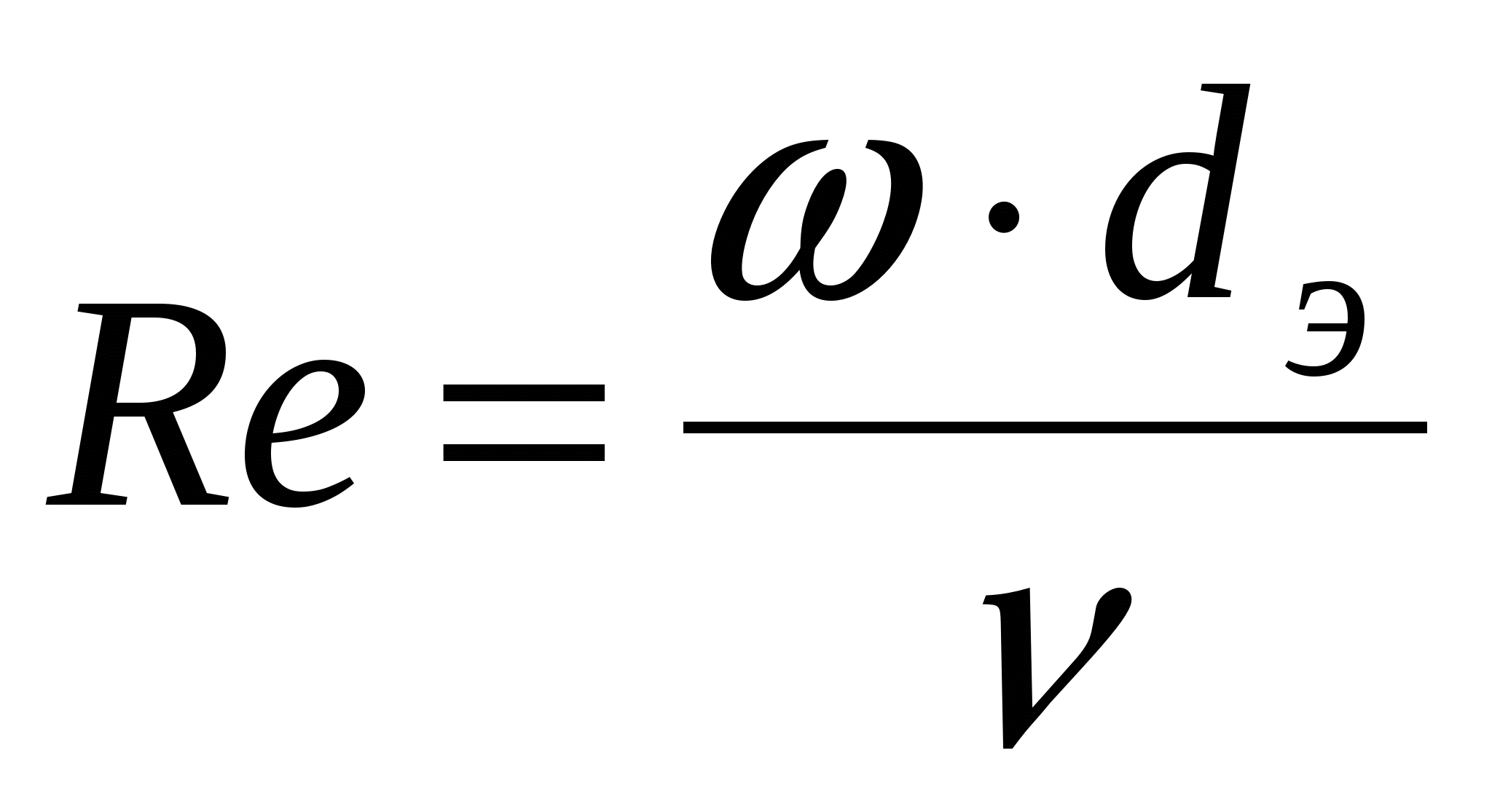 (2.1.2) (2.1.2)
где 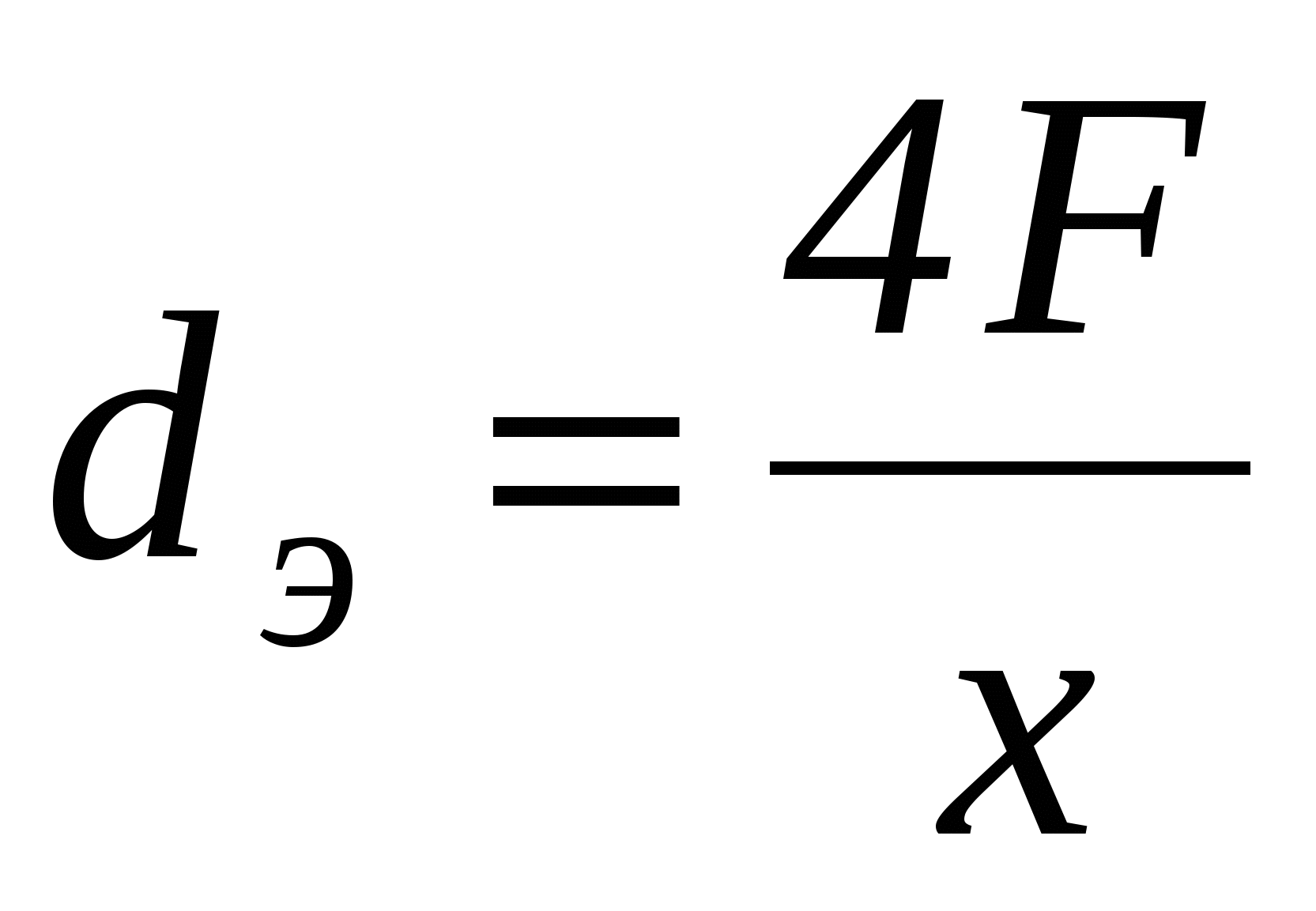 - эквивалентный диаметр, равный отношению учетверенной площади проходного сечения канала к его смачиваемому периметру (для трубы круглого поперечного сечения dэ= d. - эквивалентный диаметр, равный отношению учетверенной площади проходного сечения канала к его смачиваемому периметру (для трубы круглого поперечного сечения dэ= d.
Значение числа Рейнольдса, при котором происходит переход от ламинарного движения к турбулентному, называют верхним критическим числом Рейнольдса и обозначают (Reкр)в. Величина (Reкр)в зависит от условий входа в трубу, отсутствия или наличия первоначальных возмущений в жидкости, конвективных токов и др.
Число Рейнольдса, при котором турбулентный режим сменяется ламинарным, называется нижним критическим числом (Reкр)н.
Вопрос о неустойчивости ламинарного движение и его переходе в турбулентное, а также о величине критического числа Рейнольдса подвергся тщательному теоретическому и экспериментальному изучению, но до сих пор не получил еще достаточного решения. Наиболее часто в расчетах труб круглого сечения принимают для критического числа Рейнольдса значение (Reкр)н = 2300, отвечающее переходу жидкости из турбулентного в ламинарное. При переходе движения из ламинарного в турбулентное критическое число (Reкр)в имеет большую величину (для плавного входа оно может быть доведено до 20000).
В настоящее время в практике принято исходить только из одного критического значения числа Рейнольдса, считая, что: при Re 2300 режим ламинарный, при Re 2300 режим турбулентный.
-
Описание лабораторной установки
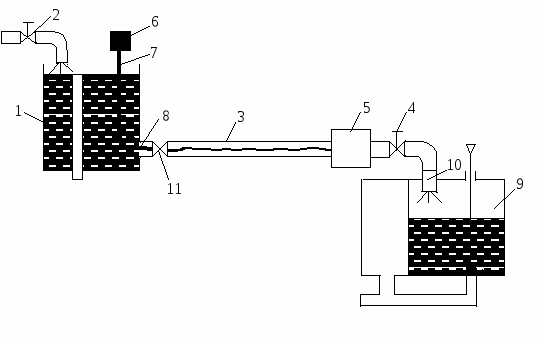
Рисунок 2.2.1- Опытная установка
Опытная установка для исследования режимов движения жидкости (рисунок 2.2.1) состоит из бака постоянного напора 1, в который поступает жидкость из трубопровода через вентиль 2. К напорному баку присоединена прозрачная труба 3 для наблюдения характера движения жидкости.
Расход жидкости, а значит и ее скорость регулируется вентилями 4 и 11. Для уменьшения возмущений, создаваемых вентилем 4 предусмотрен дополнительный объем 5. Вытекающая из трубопровода вода направляется либо в мерную емкость 9, либо на слив в канализацию с помощью шланга 10. Подкрашенная жидкость поступает из бачка 6 через кран 7, служащий для регулирования подачи подкрашенной жидкости, в трубку 8 и в виде тонкой струйки вводится в основной поток.
-
Порядок выполнения работы
-
Ознакомиться с приборами и устройством лабораторной установки.
-
Залить подкрашенную жидкость в бачок 6 и заполнить водой бак 9.
-
Несколько приоткрыв, начиная от положенного полного закрытия, вентиль 4, установить ламинарный режим течения в стеклянной трубе (струйка краски должна четко выделяться в потоке и не перемешиваться с основным потоком).
-
Направить шланг 10 в мерную емкость 9 и одновременно включить секундомер. Остановить секундомер после заполнения мерной емкости объемом V и записать время .
-
Увеличивая постепенно открытие вентиля 4, установить момент перехода ламинарного режима в турбулентный (момент полного перемешивания окрашенной струйки с водой основного потока). Для этого случая определяется верхнее критическое число Рейнольдса. Повторить пункт 4.
-
Установить турбулентный режим течения в трубе, полностью открыв вентиль 4. Повторить пункт 4.
-
Уменьшая открытие вентиля 4, зафиксировать момент перехода турбулентного режима в ламинарный. Для этого случая вычисляется нижнее критическое число Рейнольдса. Повторить пункт 4.
2.3.8 Результаты опытных данных занести в таблицу 2.3.1.
Таблица 2.3.1-Результаты измерений
-
Номер опыта
|
Объем жидкости V, м3
|
Время замера , с
|
Расход Vсек, м3/с
|
Скорость , м/с
|
Число Рейнольдса Re
|
Режим движения жидкости
|
1
|
|
|
|
|
|
|
2
|
|
|
|
|
(Reкр)в
|
|
3
|
|
|
|
|
|
|
4
|
|
|
|
|
(Reкр)н
|
|
2.4 Обработка результатов опыта
2.4.1 Найти объемный расход, м3/с, по формуле
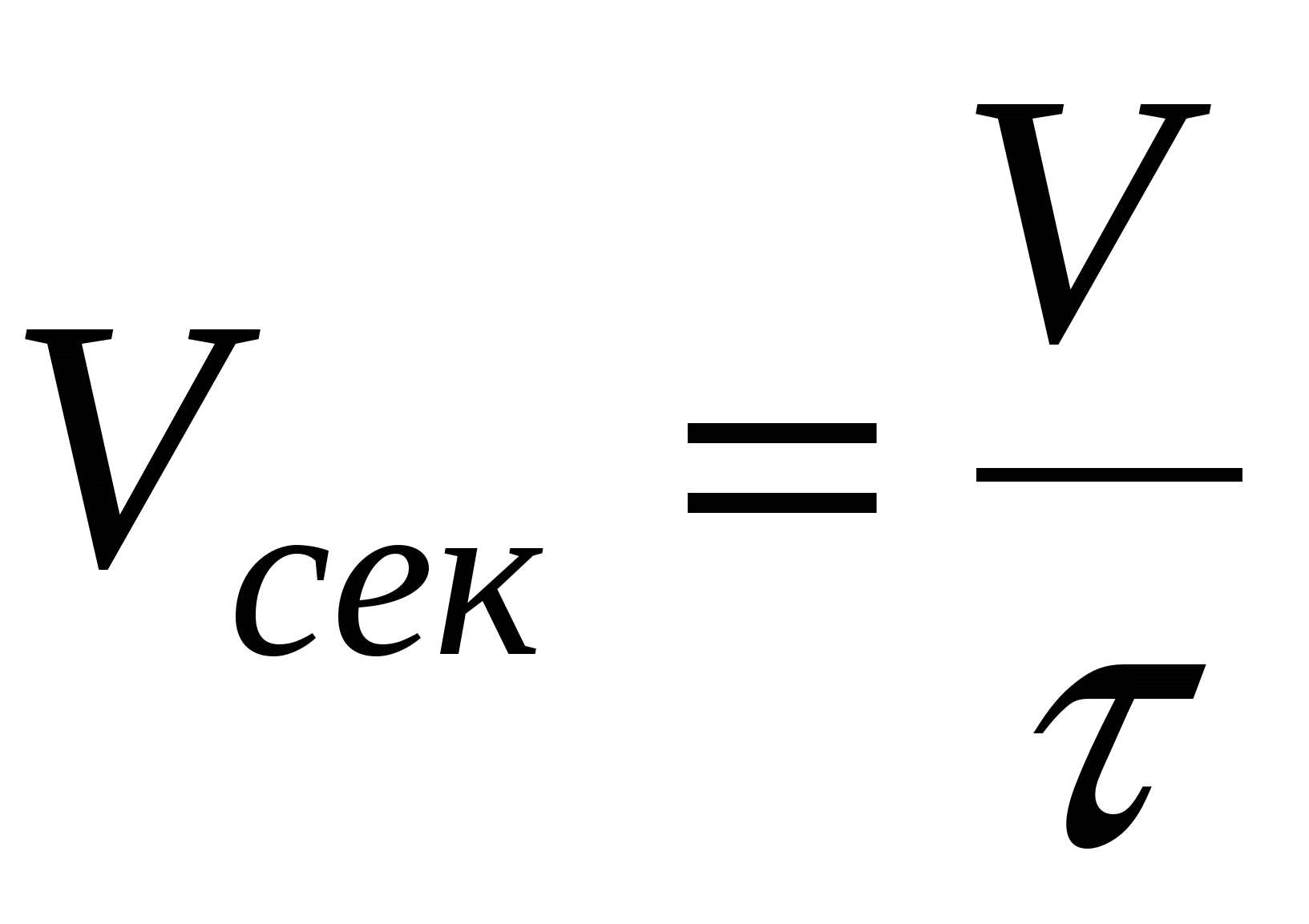 (2.4.1) (2.4.1)
где V – объем воды в мерной емкости, м3;
- время заполнения мерной емкости, с.
2.4.2 Вычислить среднюю скорость потока, м/с, в стеклянной трубе
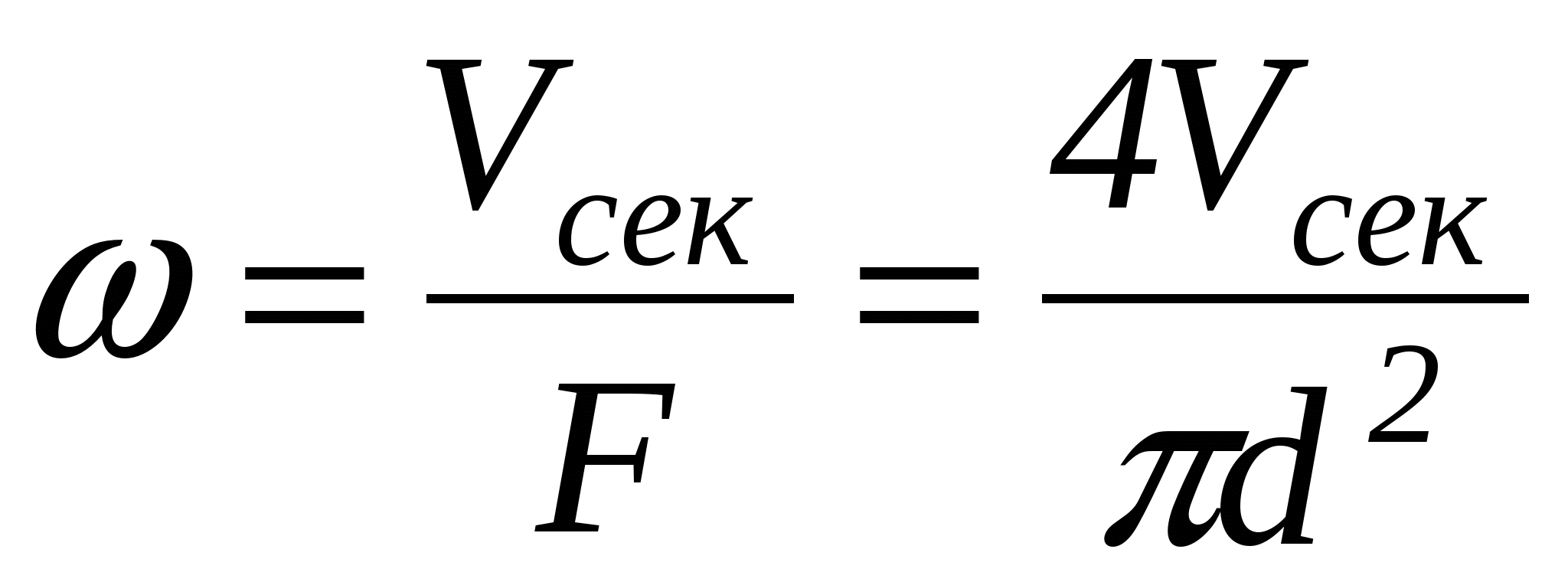 (2.4.2) (2.4.2)
где d – внутренний диаметр трубы, м.
2.4.3 Числа Рейнольдса определить по формуле (1.2).
2.4.4 Результаты расчетов занести в таблицу 3.1.
2.4.5 Зарисовать характерные режимы течения жидкости.
2.4.6 Произвести сопоставление критических чисел Рейнольдса, найденных по опыту, с указанными в начале работы.
2.5 Контрольные вопросы
2.5.1 Особенности ламинарного и турбулентного режимов движения жидкости. Распределение скоростей при различных видах движения.
-
От каких величин зависит режим движения жидкости?
-
Что называется верхним и нижним критическим числом Рейнольдса?
-
Методика визуального определения критического числа Рейнольдса.
Лабораторная работа № 3 Применение уравнения Бернулли к анализу потока жидкости
Цель работы: ознакомиться с методикой экспериментального построения линий полного и пьезометрического напоров и определение пьезометрического и гидравлического уклонов для произвольного трубопровода.
3.1 Введение
Уравнение Бернулли является выражением закона сохранения энергии применительно к потоку жидкости, связывающим его потенциальную и кинетическую энергии жидкой частицы, массой М в двух ее положениях с работой внешних сил давления и работой сил сопротивления. В совокупности с законом сохранения массы, который применительно к потоку принимает вид уравнения неразрывности
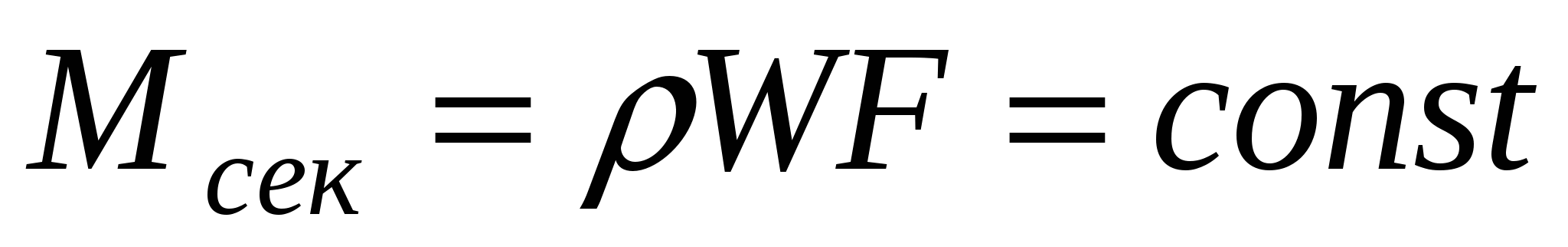 (3.1.1) (3.1.1)
Уравнение Бернулли является одним из основных уравнений гидромеханики.
Для установившегося потока несжимаемой жидкости в поле сил тяжести уравнение Бернулли имеет вид
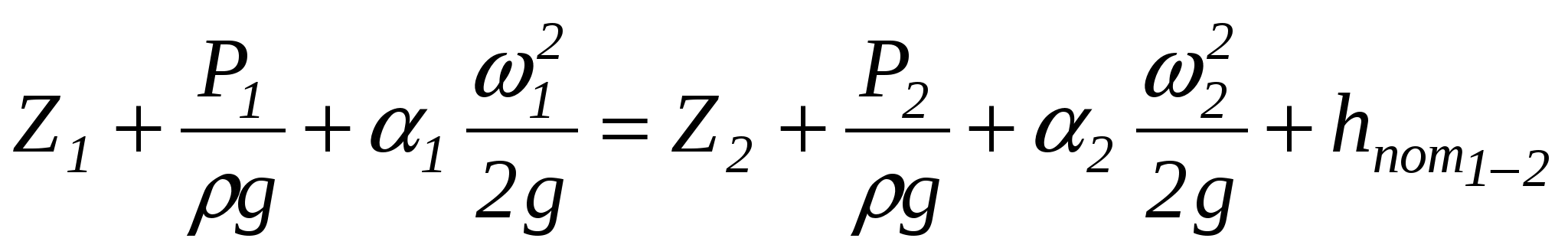 (3.1.2) (3.1.2)
где Z1 и Z2 – высоты положения центров тяжести сечений 1 и 2 относительно произвольной плоскости сравнения О-О (рисунок 3.1.1);
Р1 и Р2 – избыточные статические давления в сечениях 1 и 2;
- плотность жидкости;
g – ускорение свободного падения;
1 и 2 – средние скорости потока в сечениях 1 и 2;
1 и 2 – коэффициенты кинетической энергии для сечений 1 и 2.
Коэффициенты кинетической энергии представляют собой отношение действительной кинетической энергии потока, вычисленной по местным скоростям, к кинетической энергии, вычисленной по средней скорости. При турбулентном режиме течения 1,1 и во многих случаях (например, при расчете трубопроводов) практически можно полагать = 1.
Трехчлен 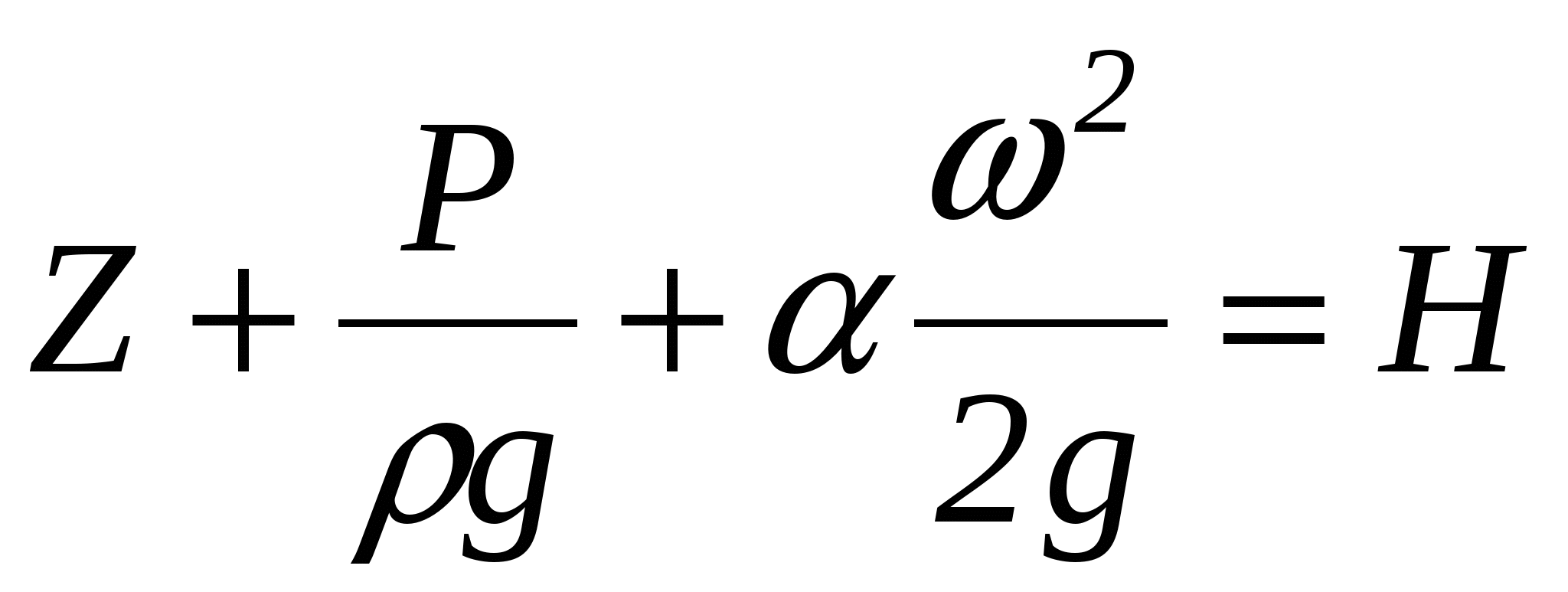 называется полным напором потока в соответствующем сечении и представляет собой удельную, отнесенную к единице веса, механическую энергию, проносимую потоком через это сечение. называется полным напором потока в соответствующем сечении и представляет собой удельную, отнесенную к единице веса, механическую энергию, проносимую потоком через это сечение.
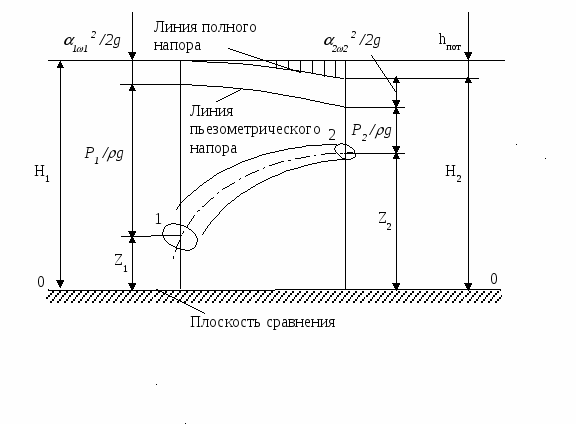
Рисунок 3.1.1- Пьезометрический график
Двучлен 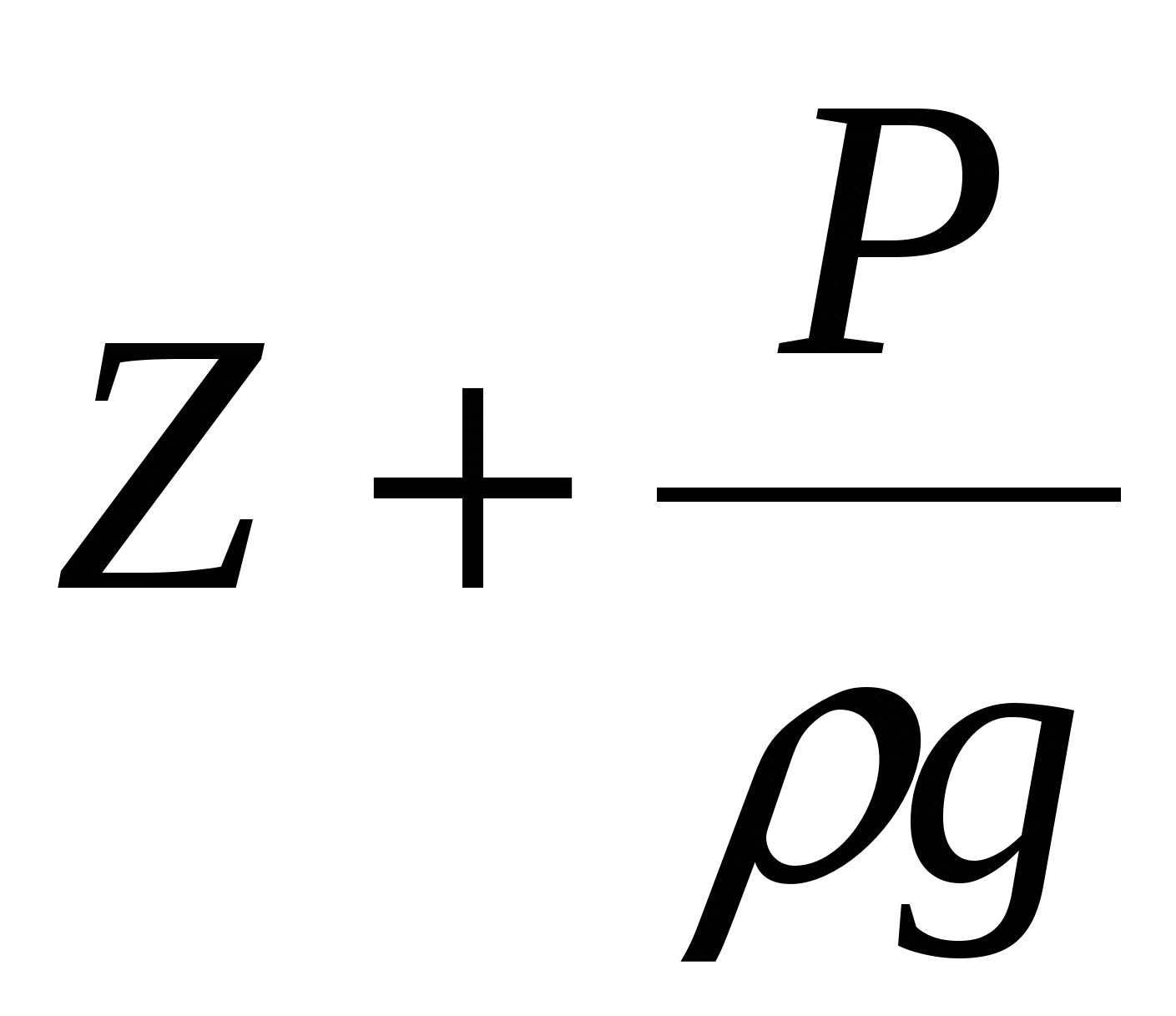 называется пьезометрическим или потенциальным напором и представляет собой полную удельную потенциальную энергию. называется пьезометрическим или потенциальным напором и представляет собой полную удельную потенциальную энергию.
Слагаемые напора:
Z – геометрический напор;
P/g – пьезометрическая высота;
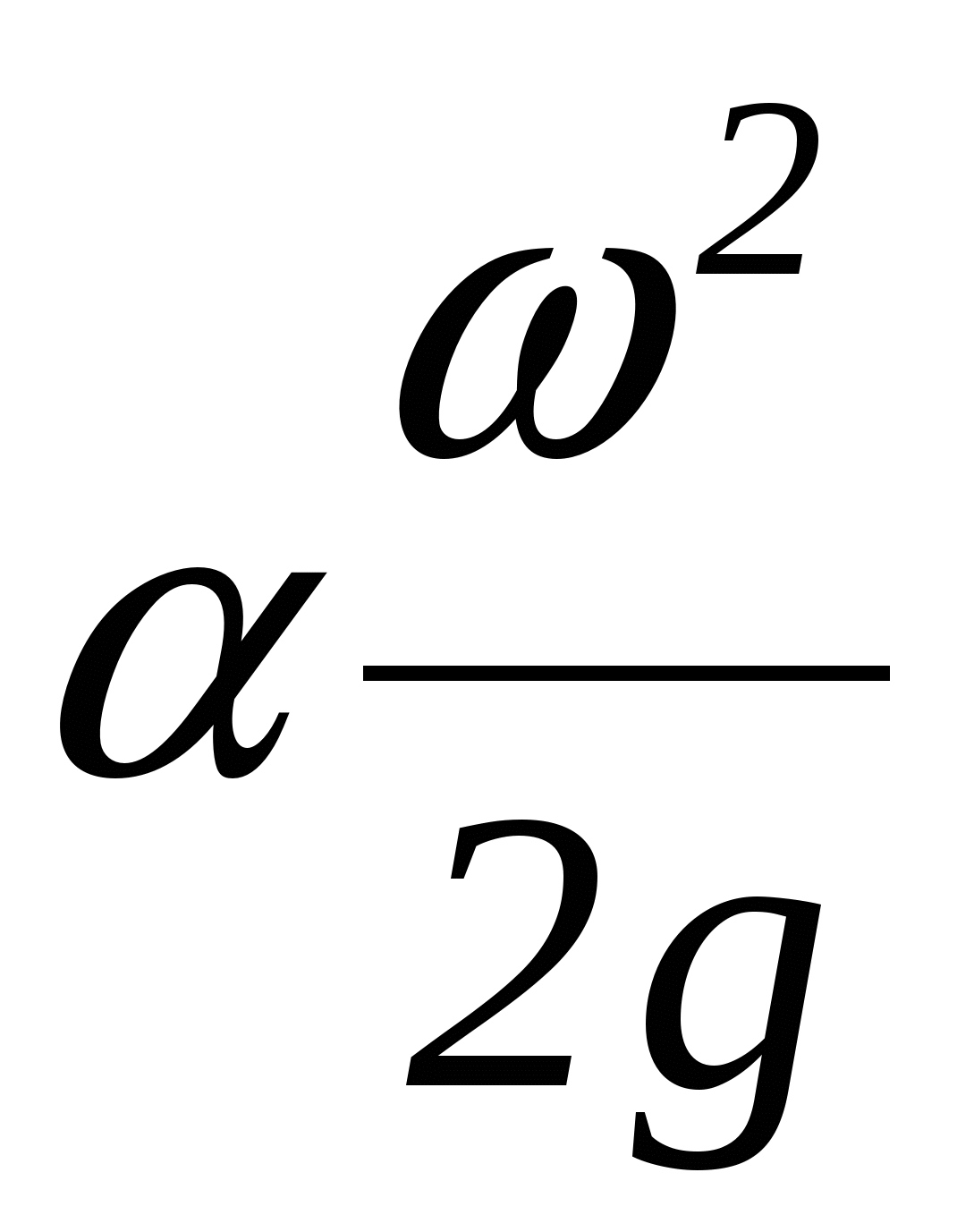 - скоростной напор представляет собой соответственно удельную (отнесенную к единице веса) потенциальную энергию положения, удельную потенциальную энергию давления (возможную работу сил) и удельную кинетическую энергию потока в данном сечении. - скоростной напор представляет собой соответственно удельную (отнесенную к единице веса) потенциальную энергию положения, удельную потенциальную энергию давления (возможную работу сил) и удельную кинетическую энергию потока в данном сечении.
Слагаемое hпот (потери напора) представляет собой уменьшение удельной механической энергии потока на участке между сечениями 1 и 2, происходящие в результате работы сил внутреннего трения, сопровождающейся переходом механической энергии потока в тепловую энергию. Таким образом, уравнение Бернулли свидетельствует о том, что по длине потока реальной жидкости полный напор (удельная механическая энергия) уменьшается. Из этого уравнения вытекает также, что по длине потока с ростом давления скорость потока уменьшается и, наоборот – с увеличением скорости потока уменьшается давление.
Для характеристики относительного изменения полного напора на единицу длины трубопровода вводится понятие о так называемом гидравлическом уклоне. Среднее значение гидравлического уклона на участке между сечениями 1 и 2 определяется как величина потери полного напора на единицу длины участка
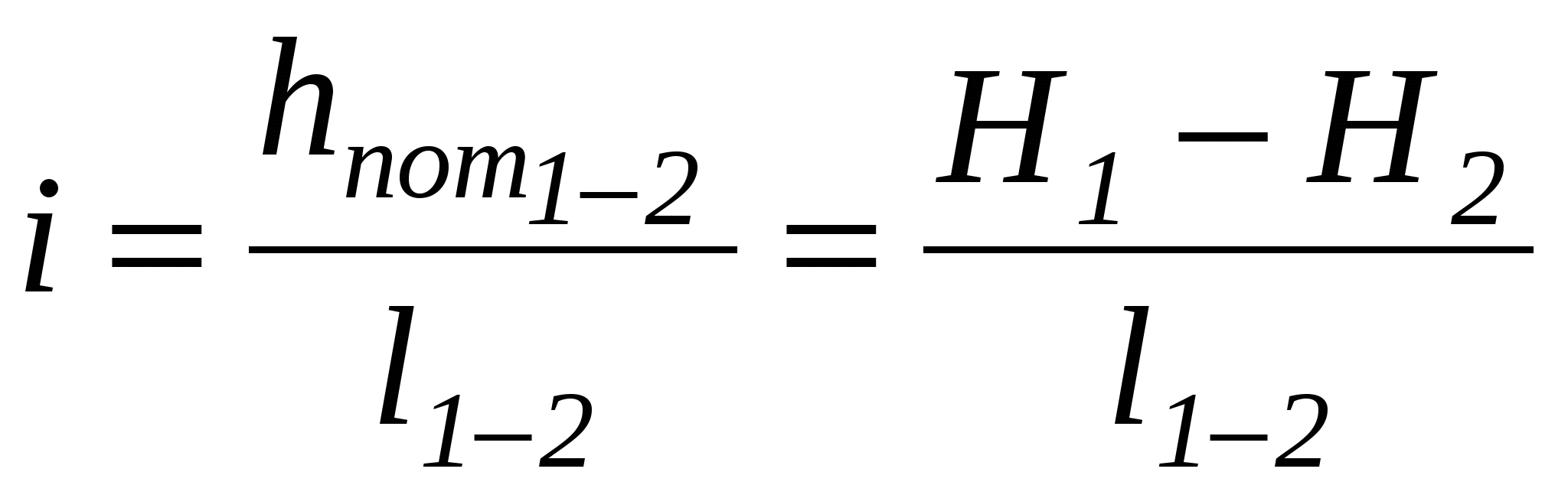 (3.1.3) (3.1.3)
Гидравлический уклон – величина безразмерная и в общем случае переменная. Понятие об уклоне можно ввести и для пьезометрической длины. Средний пьезометрический уклон тогда определится по формуле
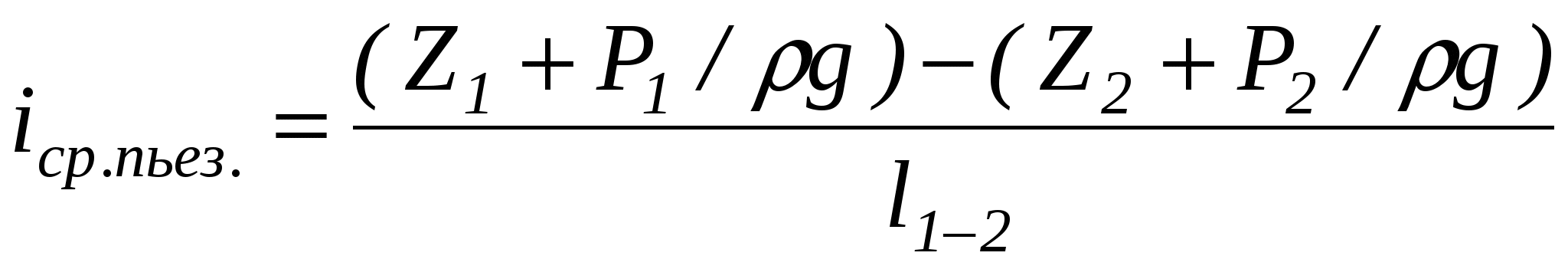 (3.1.4) (3.1.4)
Пьезометрический уклон может быть положительным, равным нулю и отрицательным.
3.2 Описание лабораторной установки
Установка (рисунок 3.2.1) для анализа потока с помощью уравнения Бернулли состоит из бака 1 со сливной трубой 2, трубопровода 3 с участками различного поперечного сечения. Расход воды регулируется двумя вентилями 4 и 5. Вытекающая из трубопровода вода направляется либо в мерную емкость 6, либо на слив в канализацию с помощью шланга 7. В напорный бак вода поступает через вентиль 8. Для замера пьезометрического напора установлены пьезометры.
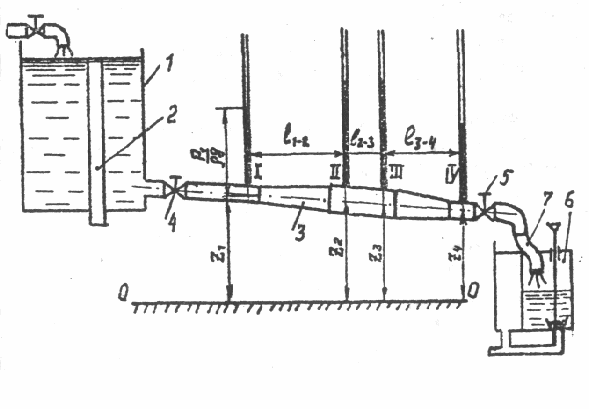
Рисунок 3.2.1- Опытная установка
3.3 Порядок выполнения работы
3.3.1 Ознакомиться с приборами и устройством лабораторной установки.
3.3.2 Открыть вентиль 4 (вентиль 8 открывается лаборантом) и при закрытом вентиле 5 убедиться в равенстве показаний каждой пары пьезометров на соответствующем участке трубопровода, при необходимости ввести поправку.
3.3.3 Направить шланг 7 на слив в канализацию и открыть вентиль 5 (вентиль 4 должен быть полностью открыт). После того, как уровень воды в пьезометрах перестанет изменяться, можно приступать к замерам.
-
Направить шланг в мерную емкость 6 и одновременно включить секундомер. Остановить секундомер после заполнения мерной емкости объемом V и записать время .
-
Замерить температуру воды t в емкости с помощью термометра и пьезометрической высоты Pi/g в каждом мерном сечении с помощью пьезометров.
-
Записать координаты Zi положения центров сечений трубы, диаметр di и длину участков трубы ln.
3.4 Обработка результатов измерений
3.4.1 Найти объемный расход Vсек, м3/с, по формуле
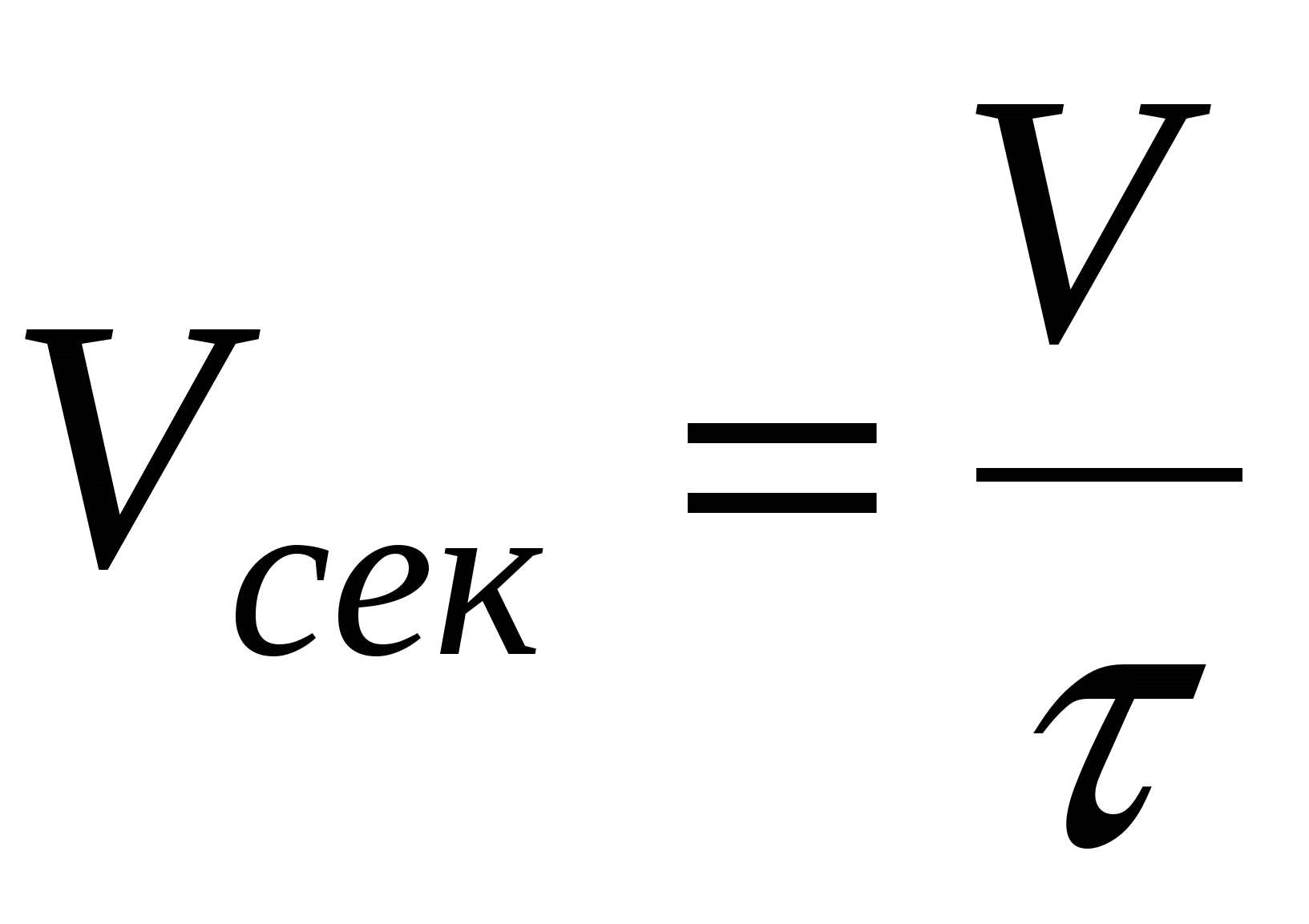 (3.4.1) (3.4.1)
где V – объем воды в мерной емкости, м3;
- время заполнения мерной емкости, с.
3.4.2 Найти среднюю скорость потока, м/с, в соответствующем сечении трубопровода
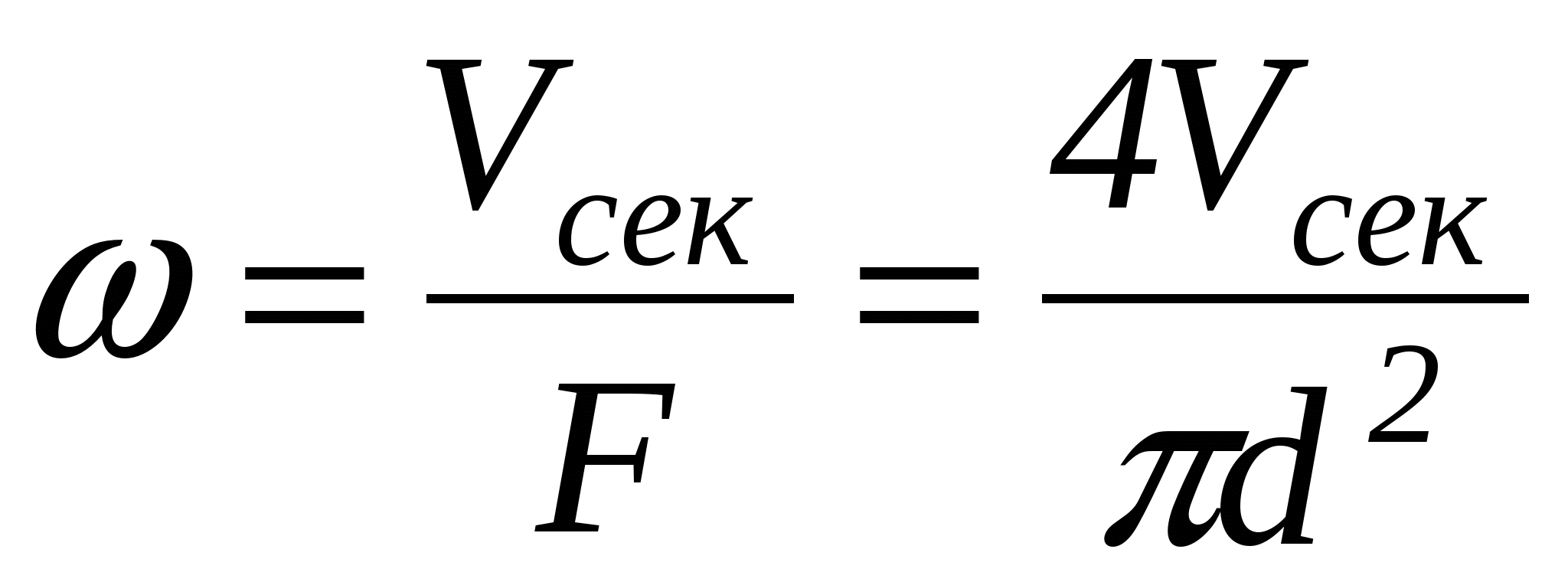 (3.4.2) (3.4.2)
где d - внутренний диаметр трубы (dI = 40 мм, dII = 80 мм, dIII = 80 мм, dIY = 45 мм).
-
Найти динамический напор в каждом сечении, м.
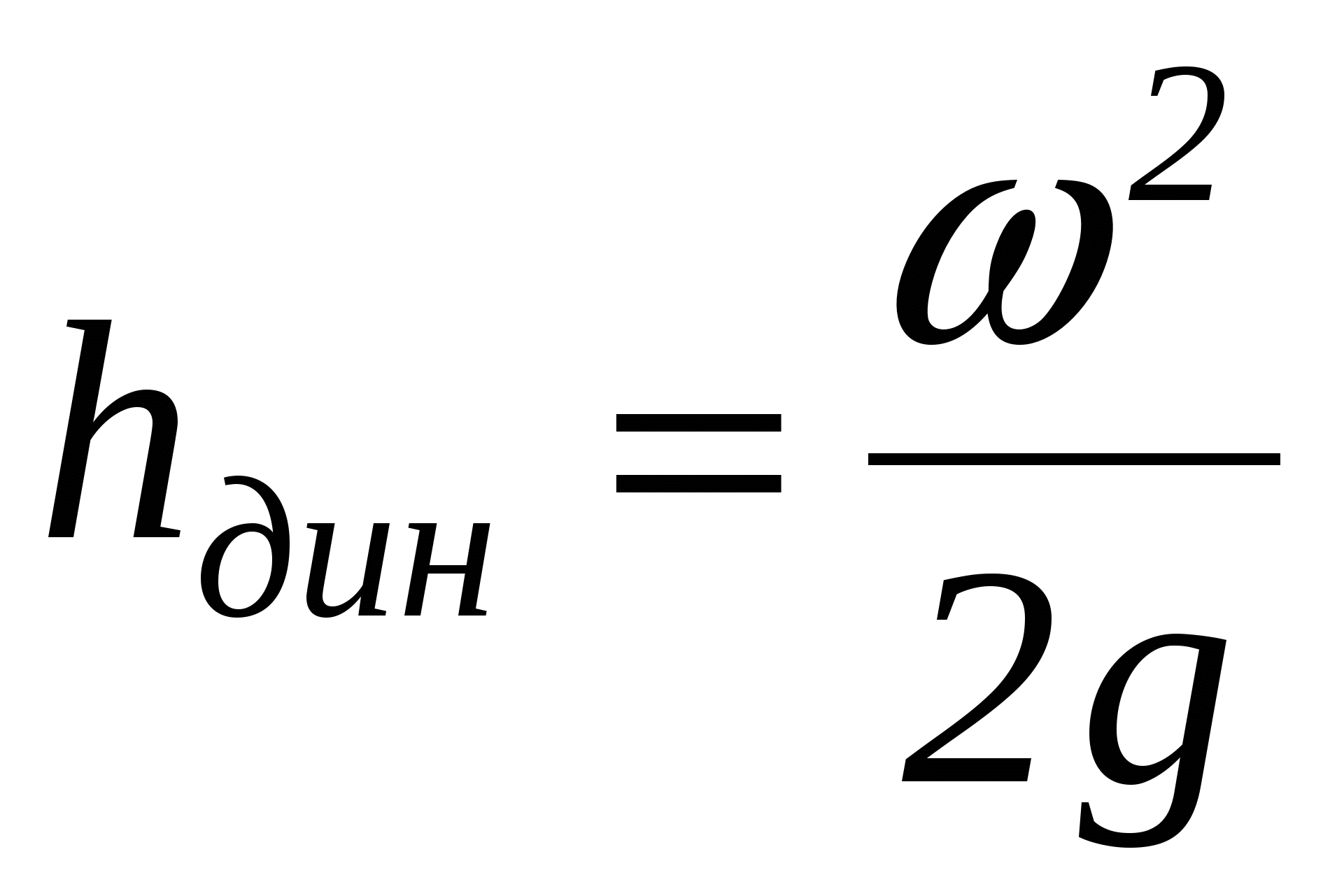 (3.4.3) (3.4.3)
-
Полный напор в каждом сечении, м.
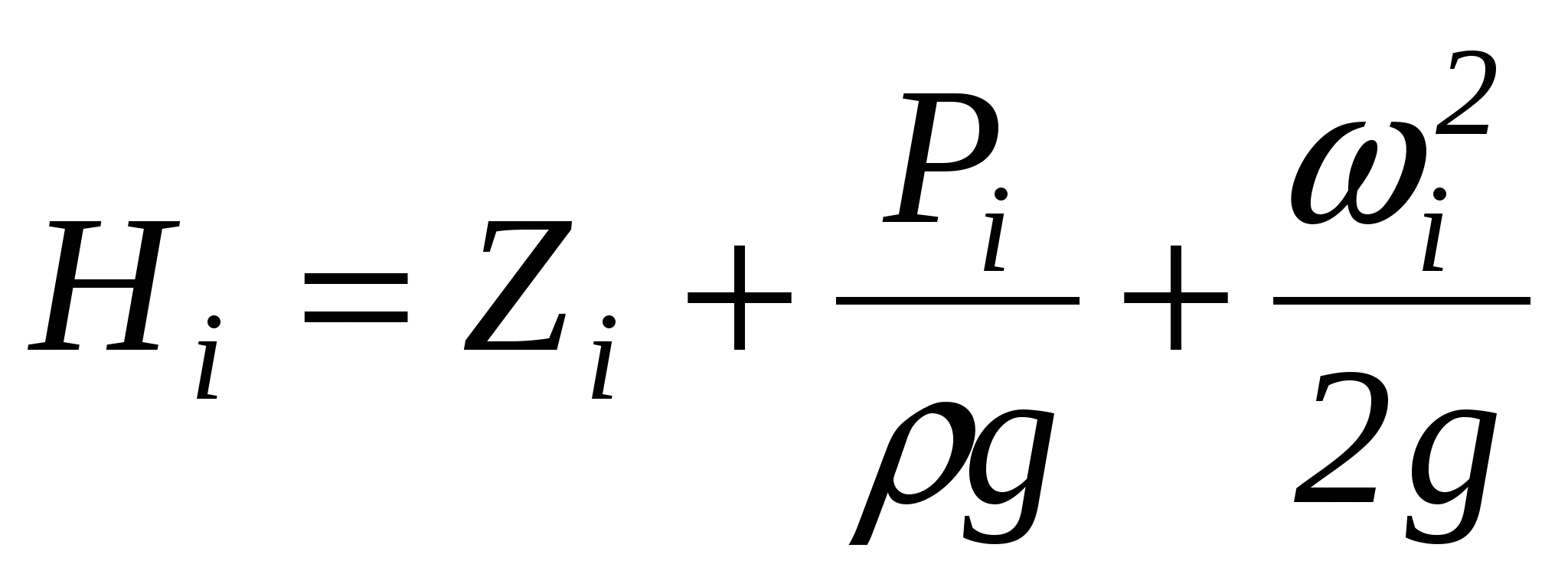 (3.4.4) (3.4.4)
-
Потерю напора на каждом участке трубопровода как разность полных напоров в двух смежных сечениях, м.
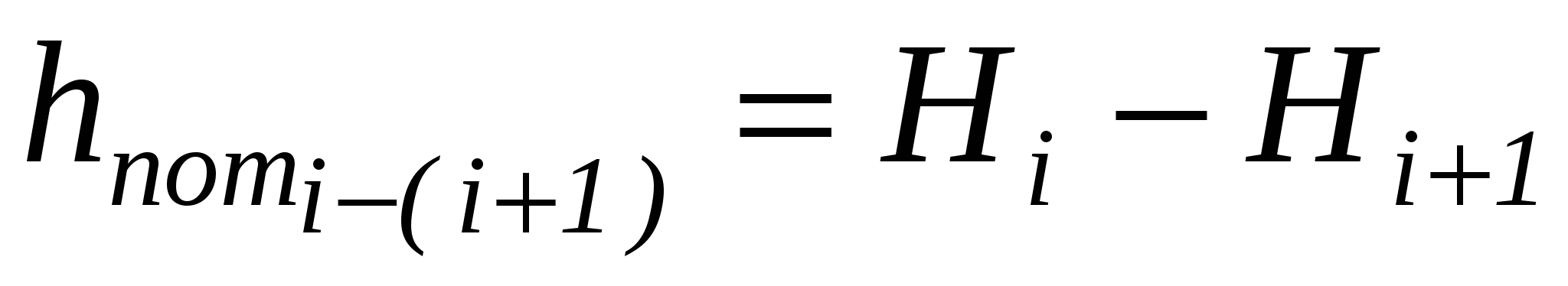 (3.4.5) (3.4.5)
-
Полную потерю напора на участке I-IY.
-
Пьезометрический уклон для каждого участка по формуле (1.4).
-
Гидравлический уклон для каждого участка по формуле (1.3).
-
Построить непосредственно на схеме установки в соответствующем масштабе линии пьезометрического и полного напоров.
-
Результаты измерений и вычислений занести в таблицу 3.4.1
Таблица 3.4.1-Результаты измерений
-
Номер мерного сечения
|
I
|
II
|
III
|
IY
|
Пьезометрическая высота Рi /g, м
|
|
|
|
|
Координата центра сечения трубы Zi, м
|
|
|
|
|
Диаметр трубы di, м
|
|
|
|
|
Средняя скорость потока i, м/с
|
|
|
|
|
Номер мерного сечения
|
I
|
II
|
III
|
IY
|
Динамический напор hдин, м
|
|
|
|
|
Полный напор Нi, м
|
|
|
|
|
Номер участка трубы п
|
I-II
|
II-III
|
III-IY
|
Длина участка трубы ln, м
|
|
|
|
Потери полного напора hпот = Hi – Hi+1, м
|
|
|
|
Гидравлический уклон i = hпот /ln
|
|
|
|
Пьезометрический уклон iпьез
|
|
|
|
страница 1 страница 2
|