.
Результаты работы Pascal-программы
Как тебя зовут ? Тимур
Привет, Тимур !
|
Пример 5 . Определить объём и площадь боковой поверхности цилиндра с заданными радиусом основания R и высотой H.
Тест
Данные
|
Результат
|
R = 1 | H = 1 | V = 3.14 | S = 6.28 |
|
|
|
|
Псевдокод
алг Цилиндр (арг вещ R, H, рез вещ V, S)
нач вещ Pi
Pi := 3.14
V := Pi * R**2 * H
S := 2 * Pi * R * H
кон
Turbo Pascal
Program Cylinder;
Uses Crt; {Подключение библиотеки Crt}
Var
R, {радиус основания цилиндра}
H, {высота цилиндра }
V, {объем цилиндра }
S: Real; {площадь боковой поверхности цилиндра}
BEGIN
ClrScr; {Вызов из библиотеки Crt процедуры очистки экрана}
Write('Введите высоту цилиндра : '); ReadLn(H);
Write('Введите радиус основания : '); ReadLn(R);
V := Pi * R * R * H;
S := 2 * Pi * R * H; WriteLn;
WriteLn('Объем цилиндра = ', V : 5 : 2); {Здесь 5 – общее количество позиций, занимаемых переменной V при выводе, а 2 - количество позиций в дробной части значения V}
WriteLn('Площадь боковой поверхности = ', S : 5 : 2);
ReadLn
END.
Пример 6. Даны три точки на плоскости. Определить, какая из них ближе к началу координат.
Система тестов
Номер теста
|
Данные
|
Результат
|
xA
|
yA
|
xB
|
yB
|
xC
|
yC
|
Otvet
|
1
|
2
|
1
|
2
|
2
|
-1
|
3
|
"Это точка A"
|
2
|
2
|
2
|
2
|
1
|
-1
|
3
|
"Это точка B"
|
3
|
2
|
2
|
-1
|
3
|
2
|
1
|
"Это точка C"
|
Псевдокод
алг Точки(арг вещ xA,yA,xB,yB,xC,yC, рез лит Otvet)
н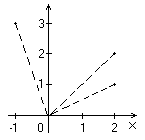
ач вещ DistA,DistB,DistC
ввод xA,yA,xB,yB,xC,yC
DistA := sqrt(xA**2 + yA**2)
DistB := sqrt(xB**2 + yB**2)
DistC := sqrt(xC**2 + yC**2)
если (DistA < DistB) и (DistA < DistC)
то Otvet := "Это точка А"
иначе если DistB < DistC
то Otvet := "Это точка B"
иначе Otvet := "Это точка C"
все
все
вывод Otvet
кон
Turbo Pascal
Program Points;
Uses Crt;
Var xA, yA, xB, yB, xC, yC, DistA, DistB, DistC : Real;
BEGIN ClrScr;
WriteLn('Введите координаты точки А:');
Write('x = '); ReadLn(xA); Write('y = '); ReadLn(yA);
WriteLn('Введите координаты точки B:');
Write('x = '); ReadLn(xB); Write('y = '); ReadLn(yB);
WriteLn('Введите координаты точки C:');
Write('x = '); ReadLn(xC); Write('y = '); ReadLn(yC);
DistA := sqrt(sqr(xA) + sqr(yA)); {расстояние до точки А}
DistB := sqrt(sqr(xB) + sqr(yB)); {расстояние до точки B}
DistC := sqrt(sqr(xC) + sqr(yC)); {расстояние до точки C}
WriteLn; Write('Ответ : ');
If (DistA < DistB) and (DistA < DistC) {сравнение расстояний}
then WriteLn( 'Это точка А.')
else If (DistB < DistC) {сравнение расстояний}
then WriteLn('Это точка B.')
else WriteLn('Это точка C.');
ReadLn
END.
Пример 7 Найти произведение цифр заданного целого четырехзначного числа.
Система тестов
Номер теста
|
Проверяемый
случай
|
Число
|
Результат
|
1
|
Число положительное
|
2314
|
P = 24
|
2
|
Число отрицательное
|
-1245
|
P = 40
|
Псевдокод
алг Произведение цифр (арг цел Num, рез цел P)
нач цел i, j, k, l
Num := abs(Num) | abs - абсолютная величина
i := div(Num, 1000) | i - первая цифра
| div - частное от деления с остатком
j := mod(div(Num, 100), 10) | j - вторая цифра
| mod - остаток от деления с остатком
k := mod(div(Num, 10), 10) | k - третья цифра
l := mod(Num, 10) | l - четвертая цифра
P := i * j * k * l;
кон
Turbo Pascal
Program DigitsProduct;
Uses Crt;
Var Number, {заданное число}
i, j, k, l, {цифры числа}
P : Integer; {произведение цифр}
BEGIN ClrScr;
Write( 'Введите четырехзначное число : ' ); ReadLn(Number);
Number:=Abs(Number);
Write( 'Цифры числа ' , Number , ' : ' );
i := Number div 1000; Write(i:3); { выделение первой цифры}
j := Number div 100 mod 10; Write(j:3); { выделение второй цифры}
k := Number div 10 mod 10; Write(k:3); { выделение третьей цифры}
l := Number mod 10; WriteLn(l:3); { выделение четвертой цифры}
P := i * j * k * l ;
WriteLn( 'О т в е т : произведение цифр равно ' , P );
ReadLn
END.
Пример 8. Решить квадратное уравнение ax2 + bx + c = 0.
Таблица Система тестов
Номер теста
|
Проверяемый случай
|
Коэффициенты
|
Результаты
|
a
|
b
|
c
|
1
|
d >0
|
1
|
1
|
-2
|
x1 = 1, x2 = - 2
|
2
|
d=0
|
1
|
2
|
1
|
Корни равны: x1 = - 1, x2 = - 1
|
3
|
d<0
|
2
|
1
|
2
|
Действительных корней нет
|
4
|
a=0, b=0, c=0
|
0
|
0
|
0
|
Все коэффициенты равны нулю. х -любое число.
|
5
|
a=0, b=0, c<>0
|
0
|
0
|
2
|
Неправильное уравнение
|
6
|
a=0, b<>0
|
0
|
2
|
1
|
Линейное уравнение. Один корень: x = - 0,5
|
Псевдокод (упрощенный алгоритм)
алг Квур (арг вещ а, b, c, рез вещ x1, x2, рез лит t)
дано a <> 0
нач вещ d
d := b**2-4*a*c | d - дискриминант квадратного уравнения
если d<0
то t := "Действительных корней нет"
иначе если d=0
то t := "Корни равны"; x1 := -b/(2*a); x2 := x1
иначе t := "Два корня"
x1 := (-b + sqrt(d)) / (2*a)
x2 := (-b - sqrt(d)) / (2*a)
все
все
кон
Turbo Pascal
Program QuadraticEquation;
Uses Crt; { подключение библиотеки Crt }
Var a, b, c : Real; {a, b, c - коэффициенты уравнения}
Discr : Real;
x1, x2 : Real; {x1, x2 - корни }
Test, NTest : Integer; {Ntest - количество тестов }
BEGIN
ClrScr;
Write('Введите количество тестов : ');
ReadLn(NTest);
For Test := 1 to NTest do {цикл по всем тестам задачи }
begin
Write('Тест ', Test, '. Введите коэффициенты a, b, c : ');
ReadLn(a, b, c);
If (a=0) and (b=0) and (c=0) {проверка 4-го случая}
then begin Write('Все коэффициенты равны нулю.');
WriteLn('x - любое число ')
end
else
If (a=0) and (b<>0) {проверка 6-го случая}
then WriteLn('Линейное уравнение. Oдин корень: x =', (-c/b):6:2)
else
If (a=0) and (b=0) and (c<>0) {проверка 5-го случая}
then WriteLn('Неправильное уравнение.')
else
begin
Discr := b*b - 4*a*c; {вычисление дискриминанта}
If Discr > 0 {проверка 1-го случая}
then begin {вычисление корней}
x1:=(-b + Sqrt(Discr)) / (2*a);
x2:=(-b - Sqrt(Discr)) / (2*a);
WriteLn('x1=' , x1:6:2 , '; x2=' , x2:6:2)
end
else
If Discr = 0 {проверка 2-го случая}
then begin
x1 := -b/(2*a);
WriteLn('Корни равны: x1=', x1:6:2, ' x2=', x1:6:2)
end
else WriteLn('Действительных корней нет.'); {проверка 3-го случая}
end;
WriteLn
end;
ReadLn
END.
Пример 9 Контроль корректности данных. Составить программу расчета площади треугольника S по трем сторонам a, b,c, значения которых запрашиваются с клавиатуры, по формуле Герона
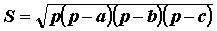, где 
.
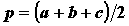Var a, b, c, p,S: real;
Begin
Write(‘Ввести сторону а=’); ReadLn(a);
Write(‘Ввести сторону b=’); ReadLn(b);
Write(‘Ввести сторону c=’); ReadLn(c);
IF (a>0) and (b>0) and (c>0) {проверка положительности}
and (a+b>c) and (a+c>b) and (c+b>a) {каждая сторона должна быть меньше суммы двух других сторон}
THEN begin p:=(a+b+c)/2;
S:=sqrt(p*(p-a)*(p-b)*(p-c));
WriteLn(‘Площадь:’, S:15:5) end
ELSE Writeln(“Неверные входные данные!’);
ReadLn
END.
Пример 10 Программа случайного предсказания одного из десяти вариантов ближайшего будущего с вероятностью 1/20, в остальных случаях – Вы «неудачник».
Var N:word;
Begin
WriteLn(‘Предсказание будущего!’);
Randomize; N:=Random(20)+1; {N-случайное число от 1 до 20}
WriteLn; Write(‘Вас ожидает_’);
Case N of
1: WriteLn(‘счастье’); 6: WriteLn(‘здоровье’);
2: WriteLn(‘пятерка’); 7: WriteLn(‘деньги’);
3: WriteLn(‘дорога’); 8: WriteLn(‘любовь’);
4: WriteLn(‘двойка’); 9: WriteLn(‘встреча’);
5: WriteLn(‘болезнь’); 10: WriteLn(‘мама’)
Else WriteLn(‘неудача’) end;
WriteLn(‘Нажми клавишу Enter’);
ReadLn
END.
Здесь функция Random(x) генерирует случайное число, с равномерной плотностью распределения на заданном интервале. Для инициализации распределения в начале программы необходимо вызвать процедуру Randomize.
6 Задачи для самостоятельного решения
6.1. Вычислить длину окружности, площадь круга и объём шара одного и того же заданного радиуса.
6.2. Вычислить периметр и площадь прямоугольного треугольника по длинам двух его катетов.
6.3. По координатам трёх вершин некоторого треугольника найти его площадь и периметр.
6.4. Вычислить дробную часть среднего геометрического трёх заданных вещественных чисел.
6.5. Определить, является ли заданное целое число А нечётным двузначным числом.
6.6. Определить, имеется ли среди заданных целых чисел A, B, C хотя бы одно чётное.
6.7. Даны три числа. Выбрать те из них, которые принадлежат заданному отрезку [ e, f ].
6.8. Определить число, полученное выписыванием в обратном порядке цифр заданного целого трёхзначного числа.
6.9 Вычислить площадь кольца, ширина которого равна Н, а отношение радиуса большей окружности к радиусу меньшей окружности равно D.
6.10 Определить, есть ли среди цифр заданного целого трёхзначного числа одинаковые.
6.11 Заданы площади круга и квадрата. Определить, поместится ли квадрат в круге.
6.12 Для задачи 6.12 определить, поместится ли круг в квадрате.
6.13 Заданы координаты двух точек. Определить, лежат ли они на одной окружности с центром в начале координат.
6.14 Определить, лежит ли заданная точка на одной из сторон треугольника, заданного координатами своих вершин.
6.15 Проверить, можно ли построить треугольник из отрезков с длинами x, y, z и, если можно, то какой – остроугольный, прямоугольный или тупоугольный.
6.16 Проверить, можно ли построить параллелограмм из отрезков с длинами x, y, v, w.
6.17 Даны координаты (как целые от 1 до 8) двух полей шахматной доски. Определить, может ли конь за один ход перейти с одного из этих полей на другое.
6.18 Треугольник задан величинами своих углов (град.) и радиусом описанной окружности. Вычислить стороны треугольника.
6.19 Смешали v1 литров воды с температурой t1 градусов Цельсия с v2 литрами воды с температурой t2 градусов Цельсия. Вычислить объём и температуру образовавшейся смеси.
6.20 Выбрать наибольшее из трёх заданных чисел.
6.21 Два прямоугольника заданы длинами сторон. Определить, можно ли первый прямоугольник целиком разместить во втором.
6.22 Значения заданных переменных a, b и c перераспределить таким образом, что a, b, c станут, соответственно, наименьшим, средним и наибольшим значениями.
6.24 Решить линейное уравнение ax = b.
6.24 Решить биквадратное уравнение ax4 + bx2 + c = 0.
6.25 Определить номер квадранта, в котором находится точка с заданными координатами (x, y).
6.26 Записать заданное смешанное число в виде неправильной дроби.
6.27 Определить, пройдет ли кирпич с рёбрами a, b, c в прямоугольное отверстие со сторонами x и y. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его рёбер было параллельно или перпендикулярно каждой из сторон отверстия.
6.28 Идет k-ая секунда суток. Определить, сколько полных часов и полных минут прошло к этому моменту.
6.29 Найти центр и радиус окружности, проходящей через три заданные точки на плоскости.
6.30 Даны четыре точки на плоскости. Определить, можно ли построить треугольник с вершинами в этих точках такой, что оставшаяся точка окажется внутри треугольника.
6.31 Составить программу случайного выбора трех дисциплин, по которым придется сдавать экзамены, из предлагаемых на выбор четырех (всего возможно 4 варианта выбора);
6.32 Составить программу случайного выбора летнего отдыха из семи предлагаемых туристическим агенством курортов, причем с вероятностью 3/10 придется отдыхать в деревне.
6.33 Составить программу выбора дежурного в группе из списка 10 студентов с вероятностью 1/15, в остальных случаях дежурит староста.
6.34 Вывести на экран сообщение в зависимости от полученного значения оценки (по десятибальной системе), например: 1..2: плохо; 3..5: удовлетворительно и т.д., иначе – неправильный ввод данных.
6.35 Вывести на экран сообщение в зависимости от значения температуры воздуха на улице (от –50 до +50оС), например: -50..-20: очень холодно; -19..-10 : холодно и т.д., иначе – неправильный ввод данных.
Библиография
1. Вальвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для персональных ЭВМ: Справочное пособие.-Минск: Вышейш. шк., 1989.-223с.
2. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: Нолидж, 2000. – 576с.
ПРИЛОЖЕНИЕ А
Основные функциональные элементы блок-схем алгоритмов в соответствии с ГОСТ 19002-89 ЕСПД (Единая система программной документации)
Название символа
|
Обозначение и пример заполнения
|
Пояснение
|
Процесс
|
|
Вычислительное действие или последовательность действий
|
Решение
|
|
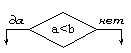
Проверка условий
|
Модификация
|
|
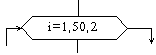
Начало цикла
|
Предопределенный процесс
|
|
Вычисления по подпрограмме, стандартной подпрограмме
|
Ввод-вывод
|
|
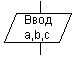
Ввод-вывод в общем виде
|
Пуск-останов
|
|
Начало, конец алгоритма, вход и выход в подпрограмму
|
Документ
|
|
Вывод результатов на печать
|
Блок процесс применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок решение используется для обозначения переходов управления по условию. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок модификация используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок предопределенный процесс используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам
ПРИЛОЖЕНИЕ Б
Название "алгоритм" произошло от латинской формы имени среднеазиатского математика аль-Хорезми — Algorithmi. Алгоритм — одно из основных понятий информатики и математики.
Основные свойства алгоритмов следующие:
Понятность для исполнителя — т.е. исполнитель алгоритма должен знать, как его выполнять.
Дискpетность (прерывность, раздельность) — т.е. алгоpитм должен пpедставлять пpоцесс pешения задачи как последовательное выполнение пpостых (или pанее опpеделенных) шагов (этапов).
Опpеделенность — т.е. каждое пpавило алгоpитма должно быть четким, однозначным и не оставлять места для пpоизвола. Благодаpя этому свойству выполнение алгоpитма носит механический хаpактеp и не тpебует никаких дополнительных указаний или сведений о pешаемой задаче.
Pезультативность (или конечность). Это свойство состоит в том, что алгоpитм должен пpиводить к pешению задачи за конечное число шагов.
Массовость. Это означает, что алгоpитм pешения задачи pазpабатывается в общем виде, т.е. он должен быть пpименим для некотоpого класса задач, pазличающихся лишь исходными данными. Пpи этом исходные данные могут выбиpаться из некотоpой области, котоpая называется областью пpименимости алгоpитма.
Приложение В
Типы ошибок
Вид ошибки
|
Пример
|
Неправильная постановка задачи
|
Правильное решение неверно сформулированной задачи
|
Неверный алгоритм
|
Выбор алгоритма, приводящего к неточному или эффективному решению задачи
|
Ошибка анализа
|
Неполный учет ситуаций, которые могут возникнуть; логические ошибки
|
Семантические ошибки
|
Непонимание порядка выполнения оператора
|
Синтаксические ошибки
|
Нарушение правил, определяемых языком программирования
|
Ошибки при выполнении операций
|
Слишком большое число, деление на ноль, извлечение квадратного корня из отрицательного числа и т. п.
|
Ошибки в данных
|
Неудачное определение возможного диапазона изменения данных
|
Опечатки
|
Перепутаны близкие по написанию символы, например, цифра 1 и буквы I, l
|
Ошибки ввода-вывода
|
Неверное считывание входных данных, неверное задание форматов данных
|
Методические указания
к ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО КУРСУ «ИНФОРМАТИКА»
АЛГОРИТМЫ ЦИКЛИЧЕСКОЙ СТРУКТУРЫ
1 Цель занятия
Изучение основ построения алгоритмов и программ циклической структуры
2 Задачи занятия
Освоение основных приемов и приобретение навыков в составлении алгоритмов и программ циклической структуры
3 Содержание занятия
3.1 Ознакомиться с основными элементами блок-схем алгоритмов и программ циклической структуры .
3.2 Освоить приемы построения блок-схем алгоритмов циклической структуры.
3.3 Разобрать приведенные в методических указаниях примеры.
3.4 Выполнить индивидуальные задания (по указанию преподавателя).
4 Требования к отчету
Отчет должен содержать название занятия, результаты выполнения индивидуальных заданий, а также основные теоретические положения по теме занятия.
5 Основные положения
Командой повторения или циклом называется такая форма организации действий, при которой одна и та же последовательность действий повторяется до тех пор, пока сохраняется значение некоторого логического выражения. При изменении значения логического выражения на противоположное повторения прекращаются (цикл завершается).
Для организации цикла необходимо выполнить следующие действия:
· перед началом цикла задать начальное значение параметра;
· внутри цикла изменять параметр цикла с помощью оператора присваивания;
· проверять условие повторения или окончания цикла;
· управлять циклом, т.е. переходить к его началу, если он не закончен, или выходить из цикла в противном случае.
Различают циклы с известным числом повторений (цикл с параметром) и итерационные (с пред- и постусловием).
В цикле с известным числом повторений параметр изменяется в заданном диапазоне.
Если в цикле изменяется простая переменная, то она является параметром цикла; если в цикле изменяется переменная с индексом, то индекс этой переменной является параметром цикла.
Ниже приведены графические обозначения (обозначения на блок-схемах) алгоритмов циклических структур (рисунок 1).
На схемах СЕРИЯ обозначает один или несколько любых операторов; УСЛОВИЕ есть логическое выражение (ЛВ) (если его значение ИСТИНА, переход происходит по ветви ДА, иначе — по НЕТ). На схеме цикла с параметром использованы обозначения: ПЦ — параметр цикла, НЗ — начальное значение параметра цикла, КЗ — конечное значение параметра цикла, Ш — шаг изменения параметра цикла.
Рисунок 1
а-цикл с предусловием (цикл ПОКА), б-цикл с постусловием (цикл ДО), в-цикл с параметром
Начало и конец алгоритма на блок-схемах обозначают овалом, вводимые и выводимые переменные записываются в параллелограмме.
В примерах мы будем использовать запись алгоритмов с помощью блок-схем и словесное описание.
Пример 1. Подсчитать количество нечетных цифр в записи натурального числа n.
Идея решения. Из заданного числа выбирать из младшего разряда цифру за цифрой до тех пор, пока оно не исчерпается, т.е. станет равным нулю. Каждую нечётную цифру учитывать.
|
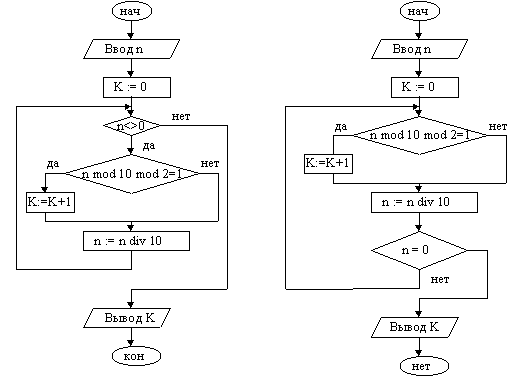
1. Ввести число n
2. K := 0 {подготавливаем счётчик}
3. Если n = 0, переход к п. 7
4. Если n mod 10 mod 2 = 1, то K := K +1
5. n := n div 10
6. Переход к п. 3
7. Вывод K
8. Конец
|
Задача решена двумя способами. Слева решение оформлено с использованием цикла с предусловием, справа — с постусловием.
Пример 2. Дана последовательность, общий член которой определяется формулой
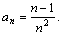
Вычислить при n>2 сумму тех ее членов, которые больше заданного числа e.
При решении задачи находится очередной член последовательно и, если он больше e, добавляется к сумме.
|
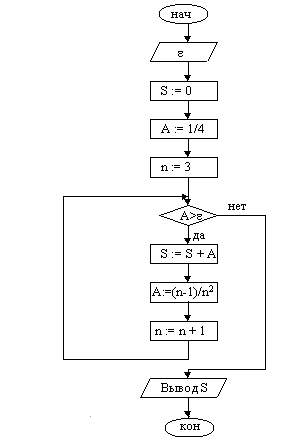
1. Ввести e
2. S := 0
3. A := 1/4
4. n := 3
5. Сравнить А с e. Если A>=e, переход к п. 10
6. S := S + A
7. A := (n-1)/(n*n)
8. n := n + 1
9. Переход к п. 5
10. Вывод S
11. Конец
|
В рассмотренных выше примерах количество повторений заранее неизвестно. В первом оно зависит от количества цифр в записи натурального числа, во втором — от числа e.
В тех же случая, когда количество шагов известно из условия задачи, проще и предпочтительней использовать цикл с параметром.
Пример 3. Найти произведение первых k натуральных чисел, кратных трём.
При составлении алгоритма учтем, что первое натуральное число, кратное 3, есть тройка, а все последующие больше предыдущего на 3.
|
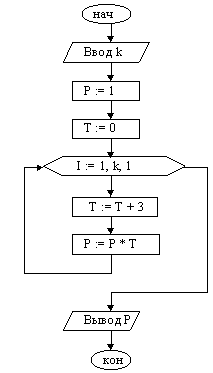
1. Ввод k
2. P := 1 {здесь накапливаем произведение}
3. T := 0 {здесь будут числа, кратные 3}
4. I := 1
5. Если I > k, переход к п. 10
6. T := T + 3
7. P := P * T
8. I := I + 1
9. Перейти к п. 5
10. Вывод P
11. Конец
|
Для проверки работоспособности алгоритма необходимо задать значения входных переменных, вычислить конечный результат по алгоритму и сравнить с результатом ручного счета.
Пример 4. Для заданного x и n вычислить
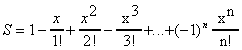
Здесь n! = 1. 2. 3 .... n (читается как "n-факториал").
Тест
Данные
|
Результат
|
X=1
|
n=3
|
|
|
|
|
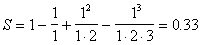
Псевдокод
алг Сумма Ряда (арг вещ х, арг цел n, рез вещ S)
нач цел i, вещ P | P - очередное слагаемое
S := 1; P := 1
нц для i от 1 до n
P := - P*x /i | получение очередного слагаемого
S := S + P
кц
кон
Turbo Pascal
Program SumUp;
Uses Crt;
Var x, S, P : Real;
{P - очередное слагаемое}
i, n : Integer;
BEGIN ClrScr;
Write('Введите n = '); ReadLn(n);
Write('Введите x = '); ReadLn(x); WriteLn;
S := 1; P := 1;
For i := 1 to n do
begin
P := - P*x /i; {получение очередного слагаемого}
S := S + P
end;
WriteLn('О т в е т : S = ', S : 7 : 3 ); ReadLn
END.
|
Блок-схема
|
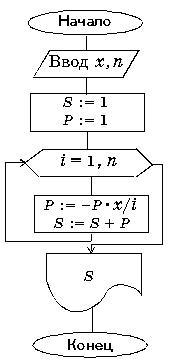
Пример 5 Фрагмент программы простой парольной защиты
For I:=1 to 3 do begin {дается три попытки ввести пароль}
Write (‘Введите ПАРОЛЬ’);
ReadLn(S); {переменные S и Parol – одного типа}
IF S=Parol
THEN BREAK {прерывание цикла защиты}
ELSE IF I<3 THEN CONTINUE; {даем еще попытки}
WriteLn(‘Не знаете Пароль!’); {сработает при I=3}
ReadLn;
HALT {прерывание программы}
End;
{ Защищаемый участок программы }
Пример 7. Числа Фибоначчи ( Fi ) определяются по формулам F0 = F1 = 1; Fi = Fi –1 + Fi –2 при i = 2, 3, ... (каждое очередное число равно сумме двух предыдущих). Вычислить сумму всех чисел Фибоначчи, которые не превосходят заданного натурального числа М.
Тест
Номер теста
|
Данные
|
Результат
|
1
|
M=10
|
S=1+1+2+3+5+8=20
|
2
|
M=1
|
S=1+1=2
|
Псевдокод
алг Фибоначчи (арг цел М, рез цел S)
дано | M>0
нач цел F0, F1, F2
F0:=1; F1:=1; F2:=2
S:=4 | 4 – сумма первых трех чисел Фибоначчи
нц пока F2<=M
F0:=F1; F1:=F2; F2:=F0+F1 | серия переприсваиваний
S:=S+F2;
кц
S:=S–F2 | из S вычитается последнее значение F2, превосходящее M
Кон
Исполнение алгоритма
F0
|
F1
|
F2
|
S
|
F2 |
1
1
2
3
5
|
1
2
3
5
8
|
2
3
5
8
13
|
4
4+3=7
7+5=12
12+8=20
20+13=33
|
+
+
+
+
-(кц)
|
|
|
|
33-13=20
|
|
|
Блок-схема
|
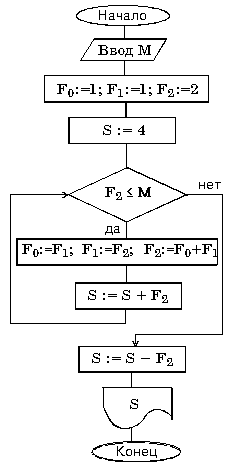
Turbo Pascal
Program SummaFib;
Uses Crt;
Var M, {заданное число }
F0, F1, F2, {три последовательных числа Фибоначчи}
S : Integer; {сумма чисел Фибоначчи}
BEGIN
ClrScr;
Write(’Введите натуральное М : ’);
ReadLn(M);
F0:=1; F1:=1; F2:=2;
S:=4; {4 – сумма первых трех чисел Фибоначчи}
Write(’Числа Фибоначчи, не превосходящие ’, M, ’ :’, F0:4, F1:4);
While F2<=M do
begin
F0:=F1; F1:=F2; Write(F1 : 4);
F2:=F0+F1; S:=S+F2;
end;
S:=S–F2; {вычитание из суммы последнего числа, которое превосходит М}
WriteLn; WriteLn;
WriteLn(’О т в е т : Сумма этих чисел равна ’, S); ReadLn
END.
Результаты работы Pascal-программы
Введите натуральное M>0 : 10
Числа Фибоначчи, не превосходящие 10 : 1 1 2 3 5 8
О т в е т : Сумма этих чисел равна 20
|
Пример 8 Определим сумму ряда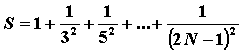 
, пока очередной член ряда не станет меньше 10-8.
Var S,a,eps : real;
N : word;
Begin
Eps:=1e-8; {точность вычислений}
S:=0; N:=0; {начальные значения параметров}
REPEAT
a:=1/(2*N+1)/(2*N+1); {текущий член ряда}
inc(N); {счетчик членов ряда}
S:=S+a;{частичная сумма ряда}
UNTIL a
WriteLn(‘S=’,S:10:8);
ReadLn
END.
Пример 10 Предотвращение неверного ввода данных. Модернизируем программу определения площади треугольника по трем сторонам (из предыдущего практического занятия) так, чтобы при неверном вводе данных происходило не просто прерывание программы, а возникал запрос на их корректировку (с повтором до выполнения нужных условий).
Var a,b,c,p,S: real;
Begin
REPEAT {проверка корректности ввода данных}
REPEAT
Write(‘Ввести сторону а=’); ReadLn(a);
IF a<=0 THEN WriteLn(‘должно быть a>0!’) Until a>0;
REPEAT
Write(‘Ввести сторону b=’); ReadLn(b);
IF b<=0 THEN WriteLn(‘должно быть b>0!’) Until b>0;
REPEAT
Write(‘Ввести сторону c=’); ReadLn(c);
IF с<=0 THEN WriteLn(‘должно быть с>0!’) Until с>0;
IF (a+b<=c) and (a+c<=b) and (c+b<=a)
THEN WriteLn(‘сумма двух сторон должна больше третьей!’)
UNTIL (a+b>c) and (a+c>b) and (c+b>a);
{Расчет по проверенным данным}
p:=(a+b+c)/2;
S:=sqrt(p*(p-a)*(p-b)*(p-c));
WriteLn(‘Площадь:’, S:15:5);
ReadLn
END.
Цикл с предусловием в подобных случаях использовать менее удобно, в частности потому, что он может ни разу не выполниться, если переменные, которым задаются значения с клавиатуры, уже имели удовлетворяющие условиям «защиты» значения.
Пример 11 Рассчитать период (в месяцах) роста банковского вклада в m раз при известной ежемесячной процентной ставке pr (1% cсоответствует pr=1).
Var pr,m,s,s0: double;
N: word;
Begin
Repeat
Write (‘Введи проценты по вкладу:’); redLn(pr);
Write (‘Введи коэффициент роста вклада:’); redLn(m)
Until (m>1) and (pr>0);
N:=0: {счетчик месяцев}
s0:=1000; {начальная сумма вклада – произвольно}
s:=s0; {текущая сумма вклада}
Repeat {перебор по месяцам}
s:=s*(1+pr/100);
inc(N)
Until s/s0>=m;
WriteLn (‘количество месяцев вклада:’,N);
ReadLn
End.
6 Задачи для самостоятельного решения
6.1 Даны действительные числа х, а, натуральное число n. Вычислить
((… ((х+а)2+…а)2+а)2+а
n cкобок
6.2 Дано действительное число х. Вычислить:
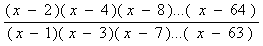
6.3 Даны натуральное n, действительное х. Вычислить:
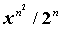
6.4 Даны натуральное n, действительное х. Вычислить:
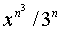
6.5 Даны натуральное n, действительное х. Вычислить:
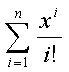
6.6 Вычислить: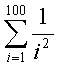 
6.7 Вычислить: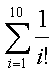 
6.8 Вычислить: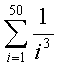 
6.9 Вычислить: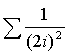 
6.10 Дано натуральное n. Вычислить: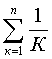 
6.11Дано натуральное n. Вычислить:
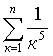
6.12 Дано натуральное n. Вычислить:
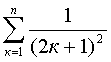
6.13 Дано натуральное n. Вычислить:
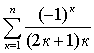
6.14 Дано натуральное n. Вычислить:
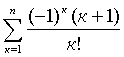
6.15 Дано натуральное n. Вычислить:
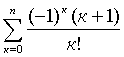
6.16 Дано натуральное n. Вычислить:
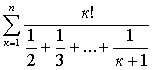
6.17 Дано натуральное n, действительное число х. Вычислить:
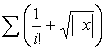
6.18 Дано натуральное n, действительное число х. Вычислить:
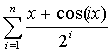
6.19 Дано натуральное n, действительное число х. Вычислить:
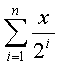
6.20 Дано натуральное n, действительное число х. Вычислить:
sin x+sin2 x+…+sin xn
6.21 Дано натуральное n, действительное число х. Вычислить:
sin x+sin x2+…+sin xn
6.22 Вычислить сумму Z = 1 + 2 + 3 + ... . Вычисления прекратить, когда значение Z превысит заданное значение A.
6.23. Известен начальный вклад клиента в банк и процент годового дохода. Определить, через сколько лет вклад превысит заданный размер и каков при этом будет размер вклада.
6.24. Торговая фирма в первый день работы реализовала товаров на P тыс. руб., а затем ежедневно увеличивала выручку на 3%. Какой будет выручка фирмы в тот день, когда она впервые превысит заданное значение Q? Сколько дней придется торговать фирме для достижения этого результата?
6.25. Малое предприятие в первый день работы выпустило P единиц товарной продукции. Каждый последующий день оно выпускало продукции на Q единиц больше, чем в предыдущий. Сколько дней потребуется предприятию, чтобы общее количество выпущенной продукции за все время работы впервые превысило запланированный объем?
6.26 Рассчитать сумму бесконечного ряда. Суммирование проводить, пока очередной член ряда по модулю не станет меньше заданной точности e. Результат сравнить с точным значением ST, а погрешность сопоставить с величиной e.
Таблица
№
|
Вид суммы
|
N
|
Вид ряда
|
ST
|
e
|
|
6.26.1
|
|
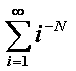
2
|
|
|
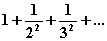
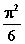
10-4
|
|
6.26.2
|
4
|
|
|
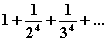
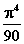
10-6
|
|
6.26.3
|
|
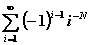
2
|
|
|
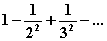
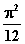
10-5
|
|
|
6.26.4
|
4
|
|
|
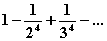
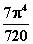
10-7
|
|
6.26.5
|
|
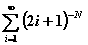
2
|
|
|
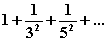
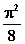
10-4
|
|
6.26.6
|
4
|
|
|
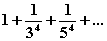
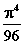
10-5
|
|
6.26.7
|
|
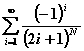
2
|
|
|
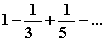
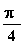
10-4
|
|
6.26.8
|
4
|
|
|
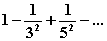
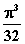
10-5
|
|
Библиография
1. Вальвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для персональных ЭВМ: Справочное пособие.-Минск: Вышейш. шк., 1989.-223с.
2. Фаронов В.В. Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: Нолидж, 2000. – 576с.
