страница 1
Пищенко Людмила Григорьевна – учитель математики Краснооктябрьской средней школы Камыстинского района, Костанайской области.
Формы контроля знаний учащихся по математике
(геометрия -7 класс)
Предмет математики настолько серьезен, что не надо упускать возможность сделать его занимательным.
Блез Паскаль
Контроль знаний, умений и навыков учащихся –составная часть учебного процесса. Необходимость контроля объясняется потребностью в получении информации об эффективности функционирования системы преподавания предмета математики. Контроль является неотъемлемой частью учебного процесса, благодаря которому реализуется обратная связь в обучении. Позволяет своевременно устранять пробелы в знаниях, конкретизировать задачи на новый урок, выполняет воспитывающую, развивающую, образовательную функции в современной школе.
Обучающая функция: учащиеся привлекаются к анализу ответов одноклассников. Развивающая функция: формируются навыки самоконтроля, устойчивого внимания, расширение объемов памяти. Воспитывающая функция: формирование чувства ответственности, дисциплинированности, трудолюбия.
Я думаю, что учитель математики в своей работе наряду с использованием общепринятых форм контроля (контрольная работа, самостоятельная работа, устный опрос у доски) должен изобретать и внедрять свои средства контроля. Именно в результате использования нетрадиционных форм контроля знаний, умений и навыков раскрываются индивидуальные особенности детей, повышается интерес и уровень подготовки к уроку, что позволяет своевременно устранять пробелы в знаниях.
На уроках я часто применяю тестовый контроль. В работе собраны различные тесты: тест дополнение, тест напоминания, альтернативный тест, выборочный тест, тест сличения, тест ранжирования, открытый тест.
Собранный дидактический материал предназначен для учителей, преподающих геометрию в 7 классе.
Простейшие геометрические фигуры и их основные свойства. Точка, прямая, отрезок, полуплоскость, луч.
Тема№1. Тест дополнение.
1 вариант
1. Какова бы ни была _______, существуют _____, ________ этой прямой, и _____, __ ___________ ей
2. Через любые __ ______ можно провести _______, и _____ ______
3. Из _____ точек на ______, ______ и только _____ лежит _____ двумя _______
4. ______ разбивает _______ на ____ ________
5. Каждый угол имеет _______ ____, определяемый ________ ______
6. Развернутый ____ равен ___
7. Градусная _____ угла _____ _____ градусных ___ углов на которые он разбивается _____ _____, исходящим из его _____ и проходящим ______ ___
2 вариант
1. Через ____ , не лежащую на данной ____, можно провести ___ _______ не более ____ _____, ________ данной
2. Каждый отрезок имеет ______, выражаемую _______ числом. ______ отрезка _____ _____ длин ___ _____, на которые _____ его _____ _____
3. На любом ____ от его ______ точки, можно _____ _____ заданной ___, и только ____
4. От ______ луча в заданной _______ можно отложить ___, градусная ___ которого ____ ___ и только ____
5. Каков бы ни был _______, существует _____ ему ______ в заданной полуплоскости
Тест-напоминание.
1 вариант
1. Как называются разделы геометрии, изучаемые
2. Как называется раздел геометрии, в котором изучаются свойства фигур на плоскости?
3. Жители кокой страны считаются первыми, кто занимался геометрией?
4. Как называют геометрию основы, которой изложены в труде ученого жившего в III веке до н.э.?
5. Как называются основные геометрические фигуры на плоскости?
6. Как обозначаются прямые на плоскости?
7. Как называются не пересекающиеся прямые?
8. Как называется длина отрезка, концами которого являются две точки на прямой?
9. Как называются части плоскости, на которые разбивает плоскость каждая прямая?
10. Как называется фигура, состоящая из точки и двух лучей, исходящих из этой точки?
11. Как называется угол, стороны которого образуют прямую линию?
12. Чему равна величина развернутого угла?
13. Как называется луч, делящий угол пополам?
14. Как называется фигура, состоящая из трех точек одной прямой и трех точек соединяемым эти отрезки?
15. Как называется утверждение, которое принимается без доказательства?
2 вариант
1. Что означает в переводе с греческого слово геометрия?
2. Как называется раздел геометрии, в котором изучаются свойства фигур в пространстве?
3. Имя древнегреческого ученого, который систематизировал весь накопленный материал по геометрии?
4. Назвать имя ученого, выходца из Отрара, внесшего весомый вклад в развитие геометрии?
5. Как обозначаются точки на плоскости?
6. Как называются прямые, имеющие общую точку пересечения?
7. Как называется часть прямой, ограниченная двумя точками?
8. Как называются отрезки, имеющие длину
9. Как называется часть прямой, ограниченная только с одной стороны?
10. Как называется общее начало двух лучей, выходящих из 1 точки?
11. На какие части угол делит плоскость?
12. Сколько углов заданной градусной меры, можно отложить в заданную полуплоскость?
13. Как называются углы, имеющие одинаковые градусные меры?
14. Как называется утверждение о свойствах геометрических фигур, которое надо доказать?
15. Назвать части, из которых состоит теорема?
Тест выборочный.
-
Точки обозначаются прописными буквами греческого алфавита.
-
Точки обозначаются прописными буквами
-
Точки обозначаются прописными буквами латинского алфавита
-
Прямая бесконечна
-
Через две точки можно провести множество прямых
-
Чрез две точки можно провести только одну прямую
-
Прямые имеют общую точку
-
Пересекающиеся прямые параллельны
-
Часть прямой называется лучом
-
Часть прямой, ограниченная с двух сторон, называется отрезком
-
Развернутый угол равен 180º
-
Луч, выходящий из вершины, называется биссектрисой
-
Градусная мера угла – это положительное число
-
Фигура, состоящая из трех точек, называется треугольником
-
Треугольники равны, если у них равны соответствующие стороны и углы
-
Утверждения называются аксиомами
-
Транспортир служит для измерений
-
Углы, имеющие одинаковые градусные меры, равны
-
Если стороны угла образуют прямую, то он называется развернутым
-
Фигура, состоящая из двух лучей, называется лучом
Альтернативный тест.
Верно ли, что:
-
Основными фигурами на плоскости являются точки, прямые, отрезки, лучи?
-
На плоскости можно изобразить всю прямую?
-
Прямые обозначаются буквами латинского алфавита?
-
Точки обозначаются прописными буквами латинского алфавита?
-
Какова бы ни была прямая, существуют точки?
-
Через две точки можно провести прямые?
-
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую?
-
Через две точки можно провести единственную прямую?
-
Если две прямые имеют общую точку, то они совпадают?
-
Непересекающиеся прямые, называются параллельными?
Открытый тест.
В-1
-
Определить расположение точки В на прямой АС, если АС=15 см, ВС=9 см, АВ=6 см.
-
Слева от А
-
Справа от С
-
Между А и С
-
Слева от С и А
-
Справа от А и С
-
Точка С лежит между А и В, определите половину длины отрезка ВС, если АВ=17 см, АС=9 см.
-
8 см
-
5 см
-
6 см
-
4 см
-
3 см
-
На прямой отмечены 6 точек A, B, C, D, E, F. Сколько различных отрезков с концами в этих точках можно составить?
-
10
-
5
-
15
-
12
-
6
-
Точки А, В, С лежат на одной прямой, длина отрезка ВС больше длины отрезка АС в 3 раза, длина АВ меньше длины ВС на 3,6 см. Найти длину отрезка АС.
-
2,4 см
-
1,2 см
-
3,6 см
-
10,8 см
-
4,8 см
-
На сколько частей могут разбить плоскость 3 различные прямые?
-
4, 5, 6 частей
-
4, 6, 7 частей
-
4, 5, 6, 7 частей
-
3, 4, 5, 6 частей
-
3, 4, 7 частей
В-2
1. Определить расположение точки В на прямой, если АС=14 см, ВС=8 см, АВ=6 см.
-
Слева от А
-
Слева от С
-
Справа от С
-
Слева от А и С
-
Справа от А и С
2. Точка С лежит между точками А и В. Определите треть отрезка ВС, если: АВ=18 см, АС=9 см.
-
9 см
-
6 см
-
3 см
-
27 см
-
4,5 см
3. Проведите различные прямые, каждая из которых проходит через две из указанных шести точек. Сколько таких прямых можно провести?
-
15
-
12
-
6
-
30
-
36
4. Точки С, D, E лежат на одной прямой. Длина отрезка DЕ в 2 раза меньше длины отрезка СD, а длина СD больше длины СЕ на 4,8 см. Найдите длину отрезка DЕ.
-
2,4 см
-
4,8 см
-
9,6 см
-
3,2 см
-
3,6 см
5. На какое наибольшее число частей могут разбить плоскость 4 прямые?
-
9 частей
-
10 частей
-
11 частей
-
12 частей
-
16 частей
Определения и термины
Л
|
О
|
Т
|
К
|
П
|
Т
|
Р
|
Е
|
У
|
К
|
С
|
У
|
О
|
П
|
Р
|
О
|
О
|
Л
|
У
|
П
|
Г
|
И
|
М
|
М
|
Г
|
Р
|
Е
|
З
|
Л
|
И
|
Н
|
Л
|
О
|
Н
|
А
|
С
|
У
|
Я
|
М
|
А
|
Л
|
У
|
И
|
О
|
Л
|
Ь
|
В
|
У
|
П
|
Р
|
Г
|
Я
|
Г
|
Ч
|
Я
|
С
|
Ш
|
Р
|
Е
|
В
|
Ф
|
И
|
М
|
О
|
Е
|
Я
|
О
|
К
|
И
|
Г
|
Р
|
А
|
И
|
Н
|
Е
|
Т
|
Р
|
И
|
С
|
Т
|
Н
|
М
|
А
|
Я
|
Г
|
А
|
П
|
Е
|
Ч
|
П
|
О
|
Ь
|
А
|
Я
|
Р
|
И
|
У
|
Д
|
Е
|
С
|
Е
|
Е
|
Л
|
Ц
|
П
|
Р
|
Т
|
С
|
Р
|
Л
|
Р
|
Е
|
Н
|
И
|
И
|
С
|
С
|
Е
|
К
|
С
|
А
|
Е
|
Ж
|
И
|
П
|
А
|
Л
|
Л
|
Ь
|
Я
|
Н
|
У
|
К
|
У
|
Б
|
Т
|
А
|
Р
|
Л
|
Е
|
Н
|
А
|
А
|
Л
|
Полуплоскость. Полупрямая (луч). Отрезок. Угол. Измерение углов.
1 вариант
1. Что такое луч?
2. Как можно назвать части, на которые разбивается плоскость любой прямой?
3. Какие лучи называются дополнительными?
4. Как называется фигура, состоящая из точки и двух лучей, исходящих из этой точки?
5. Сколько способов обозначения угла существует?
6. Как называется угол, равный половине развернутого угла?
7. Какую часть развернутого угла составляет 1 градус?
8. На какие части (области) делит угол всю плоскость?
9. Как называется луч, выходящий из вершины угла и делящий угол пополам?
10. Каким инструментом измеряют углы?
11. Как называется точка, из которой проводят лучи при построении угла?
12. Как называются точки, ограничивающие отрезок?
13. Сколько точек из трех заданных может лежать между двумя другими?
2 вариант
1. Что такое отрезок?
2. Сформулировать свойство расположения точек относительно прямой на плоскости?
3. Какие отрезки называются равными?
4. Как называются лучи исходящие из одной точки при построении угла?
5. Какой угол называется развернутым?
6. Как называется угол меньший прямого угла?
7. Какую часть прямого угла составляет 1 градус?
8. Как называется область, которой принадлежит отрезок с концами на сторонах заданного на плоскости угла?
9. Сколько углов заданной градусной меры можно отложить от заданной прямой в заданную полуплоскость?
10. Какие углы называются равными?
11. В записи названия угла, где должна быть записана точка, обозначающая вершину угла?
12. Сколько точек необходимо для проведения отрезка?
13. Каким числом всегда выражается длина отрезка?
Альтернативный тест.
Верно ли, что:
1.На любом луче, от его начальной точки, можно отложить два отрезка заданной длины?
2.Любая прямая разбивает плоскость на две полуплоскости?
3.Часть прямой, называется отрезком?
4.Из трех точек, только одна может лежать с левой стороны?
5.Сумма длин частей отрезка равна его длине?
6.Часть прямой, ограниченная с одной стороны, называется лучом?
7.Два луча, лежащие на одной прямой, называются дополнительными друг другу лучами?
8.Отрезок обозначают одной заглавной буквой латинского алфавита?
9.Каждый отрезок имеет определенную положительную величину?
10.Точка, лежащая между концами отрезка, называется его серединой?
11.Отрезок, оба конца которого лежат в одной полуплоскости, пересекают границу полуплоскости?
Альтернативный тест.
Верно ли, что:
1.Угол обозначают заглавной буквой?
2.Угол обозначают строчными буквами – обозначающими лучи, которые являются сторонами угла?
3.Фигура, состоящая из двух лучей, называется углом?
4.Любой угол разделяет плоскость на две части
5.Буква, обозначающая вершину угла, всегда в обозначении угла пишется первой?
6.Угол, стороны которого образуют прямую, называется развернутым?
7.Часть плоскости, лежащая между сторонами угла, градусная мера которого меньше развернутого, называется внутренней областью угла?
8.Каждый угол может иметь градусную меру, выраженную любым числом?
9.Развернутый угол равен 180º?
10.Луч, делящий угол, называется биссектрисой?
Смежные, вертикальные углы.
Перпендикулярные прямые.
Тест дополнение.
1 вариант
1. ____ смежных ____ равна ___
2. Если два ___ равны, то ______ с ними углы ____
3. Если смежные углы ____, то градусная ___ каждого из них ____ ___
4. ____, смежный с _____ углом, прямой
5. ____, смежный с _____ углом, тупой
6. Угол, _______ с тупым углом, ______
2 вариант
1. Два ___ называются вертикальными, если ____ ____ угла, являются ________ _____ другого ___
2. Угол ____ 90º, называется _____
3. ____ меньший __, называется ____
4. Угол _____ 90º, называется ____
5. Внутренние углы ______
6. Две _______ прямые называются _______, если они образуют ____ прямых ___
Тест –напоминание.
1 вариант.
1. Как называются углы, у которых одна сторона общая, а две другие являются продолжениями одна другой?
2. Каким свойством обладают смежные углы?
3. Как называется угол, градусная мера которого >90º
4. Как называется угол, величина которого <90º
5. Как называется угол, смежный с тупым углом?
6. Как называются прямые, при пересечении которых образуются 4 прямых угла?
7. Чему равен угол между биссектрисами смежных углов?
8. Как называется длина перпендикуляра, проведенного из точки к прямой?
2 вариант.
1. Какой угол называется прямым?
2. Как называются углы, если стороны одного являются продолжениями сторон другого?
3. Каким углом является угол смежный с острым углом?
4. Свойство вертикальных углов?
5. Как называется угол, смежный с углом = 90º
6. Чему равна градусная мера каждого из двух смежных углов?
7. Как называется прямая, образующая с другой прямой при пересечении угол 90º?
Тест выборочный.
-
Два угла, у которых одна сторона общая, называются смежными
-
Сумма смежных углов равна 180º
-
смежные углы равны
-
Если два угла равны, то смежные с ним углы равны
-
Угол равный 90º, называется тупым углом
-
Угол, больший 90º, называется тупым углом
-
Вертикальные углы равны
-
Угол, смежный с острым углом, прямой
-
Угол, смежный с тупым углом, острый
-
Угол равный 90º - прямой угол
-
Биссектрисы смежных углов перпендикулярны
-
Две пересекающиеся прямые, называются перпендикулярными
-
Через каждую точку прямой можно провести только одну, перпендикулярную ей прямую
-
Угол, меньший 90º называется острым углом
-
Если стороны одного угла являются продолжениями сторон другого угла, то они называются вертикальными
-
Угол, смежный с прямым углом, прямой
-
Биссектрисы смежных углов параллельны
-
При пересечении двух прямых, образуются четыре пары углов
-
Угол, смежный с углом 45º равен 145º
20.Расстояние от точки до прямой – это длина
перпендикуляра проведенного из точки к прямой
Альтернативный тест.
Верно ли, что:
1.Два угла, у которых одна сторона общая, называются смежными?
2.Сумма вертикальных углов равна 180º?
3.Угол больше прямого – тупой?
4.Угол, смежный с тупым, острый?
5.Угол, смежный с острым, прямой?
6.Сумма смежных углов равна 180º?
7.Если один из смежных углов прямой, то второй тоже прямой?
8.Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными?
9.Пересекающиеся прямые, которые образуют 4 прямых угла, называются перпендикулярными?
10.Если вертикальные углы равны, то прямые перпендикулярны?
Открытый тест.
В-1
1. Один из смежных углов на 24º меньше другого. Найдите меньший угол.
-
66º
-
68º
-
72º
-
78º
-
76º
2. При пересечении двух прямых, один из образовавшихся углов, больше другого на 38º. Найдите больший угол.
-
119º
-
99º
-
112º
-
142º
-
109º
3. В одном из смежных углов проведена биссектриса, она образует с прямой лишний угол 32º, определите величину другого угла из смежных.
-
158º
-
118º
-
98º
-
116º
-
96º
4. При пересечении двух прямых, два из образовавшихся углов пропорциональны числам 3:7. Найдите больший из углов.
-
133º
-
147º
-
140º
-
126º
-
136º
5. Углы АОВ и ВОС смежные. Найти угол АОВ, если угол ВОС в 1,5 раза меньше угла АОВ.
-
80º
-
72º
-
120º
-
108º
-
130º
В-2
1. Один из смежных углов на 42º меньше другого. Найдите больший угол.
-
69º
-
111º
-
89º
-
101º
-
132º
2. При пересечении двух прямых, один из образовавшихся углов на 82º больше другого. Найти меньший угол.
-
49º
-
82º
-
131º
-
98º
-
72º
3. В одном из смежных углов проведена биссектриса. Она образует с прямой линией угол 46º. Найдите другой из смежных углов.
-
92º
-
136º
-
88º
-
44º
-
134º
4. При пересечении двух прямых два из образовавшихся углов пропорциональны числам 8:7. Найти меньший из углов.
-
12º
-
84º
-
165º
-
65º
-
96º
5. Углы COD и DOK смежные. Найти угол DOK, если угол COD в 3,5 раза меньше угла DOK.
-
128º
-
132º
-
40º
-
140º
-
80º
Термины, названия, определения
П
|
Р
|
В
|
Е
|
Р
|
Д
|
О
|
О
|
В
|
О
|
К
|
Т
|
|
Я
|
М
|
О
|
Т
|
О
|
С
|
Н
|
А
|
И
|
Е
|
Р
|
О
|
С
|
Т
|
Й
|
И
|
К
|
А
|
З
|
Н
|
С
|
С
|
У
|
Й
|
Ы
|
Р
|
У
|
К
|
А
|
Л
|
А
|
И
|
Е
|
А
|
С
|
Т
|
У
|
П
|
Г
|
О
|
Л
|
Ь
|
Т
|
Е
|
Л
|
С
|
Т
|
Р
|
А
|
З
|
О
|
Й
|
С
|
Н
|
Ы
|
Й
|
Ь
|
Р
|
О
|
П
|
А
|
Р
|
В
|
Е
|
М
|
Е
|
Ж
|
Н
|
С
|
О
|
Н
|
Л
|
Л
|
А
|
П
|
Р
|
Р
|
А
|
Й
|
Ы
|
Т
|
С
|
А
|
Е
|
Л
|
Ь
|
Р
|
Н
|
Л
|
С
|
С
|
Т
|
В
|
В
|
О
|
Я
|
А
|
Н
|
Я
|
Ц
|
Т
|
Ы
|
Р
|
О
|
О
|
С
|
Й
|
Р
|
Е
|
П
|
М
|
А
|
Я
|
Й
|
Я
|
Я
|
|
Т
|
В
|
П
|
Е
|
Н
|
Д
|
И
|
К
|
У
|
Л
|
Н
|
И
|
Е
|
О
|
Виды треугольников.
Тест-дополнение.
1 вариант
1. Треугольник, у которого все __ _____ равны, называется ________
2. ___________, у которого __ ______ равны, называется ________
3. Равные ______ равнобедренного __________, называются _______ сторонами
4. Сторона _________ треугольника, не являющаяся _______, называется ________
5. __________, у которого нет ______ сторон, называется ___________
6. Сумма ____ всех _____ треугольника называется _________
7. Перпендикуляр, проведенный из _______ треугольника к _____, содержащей ___________ сторону, называется ______
2 вариант
1. Треугольник, у которого _____ угол прямой, называется ________ треугольником
2. ________, которые образуют прямой ____ __________ треугольника, называются ______
3. Сторона ____________ треугольника, лежащая напротив ______ угла, называется ________ треугольника
4. Треугольник, у которого _____ угол ____, называется тупоугольным треугольником
5. Треугольник, у которого ____ углы острые, называется _________ треугольником
6. Против каждого ____ треугольника лежит _____ сторона, против каждой ______ лежит _____ угол
7. Отрезок, соединяющий _____ треугольника с серединой __________ стороны, называется _______ треугольника
Тест-напоминание.
1 вариант
1. Как называется фигура, состоящая из трех точек соединенных отрезками?
2. Как называется луч, выходящий из вершины треугольника и делящий противоположную сторону на две равные части?
3. Как называется треугольник, у которого две стороны равны?
4. Как называется треугольник, у которого один угол прямой?
5. Чему равны углы равностороннего треугольника?
6. Как называется сторона прямоугольного треугольника, лежащая напротив прямого угла?
7. Сколько тупых углов может быть в треугольнике?
8. Свойство медианы равнобедренного треугольника?
9. Чему равна сумма острых углов прямоугольного треугольника?
10. Как называются меньшие стороны прямоугольного треугольника?
11. Как называется треугольник, у которого все углы острые?
12. Чему равна сумма внутренних углов любого треугольника?
2 вариант
1. Как называется треугольник с одним прямым углом?
2. Как называется треугольник, у которого все углы острые?
3. Как называется сторона треугольника, лежащая напротив угла 90º?
4. Как обозначаются вершины треугольника?
5. Как называется треугольник, у которого две стороны равны?
6. Как называется третья сторона треугольника, у которого две стороны равны?
7. Как называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны?
8. Сколько сторон лежит против каждого угла треугольника?
9. Чему равна величина углов в равностороннем треугольнике?
10. Чему равна медиана, проведенная из вершины прямого угла?
3 вариант
1. Как называется треугольник, у которого один угол тупой?
2. Как называются стороны треугольника, образующие прямой угол?
3. Как называется сумма сторон треугольника?
4. Как называется треугольник, у которого все стороны равны?
5. Как называются равные стороны у треугольника?
6. Как называется перпендикуляр, проведенный из вершины треугольника и прямой, соединяющей противолежащую сторону?
7. Как называется точка пересечения биссектрис, медиан и высот?
8. Как называется треугольник, у которого не равных сторон?
9. Сколько медиан можно провести в каждом треугольнике?
10. Сколько замечательных точек содержит каждый треугольник?
Тест выборочный
-
Треугольник – это фигура, состоящая из трех точек
-
Треугольник, у которого все углы острые, называется равносторонним
-
Треугольник, у которого 2 угла равны, называется равнобедренным
-
Треугольник, у которого 2 стороны равны, называется равнобедренным
-
Треугольник с тупым углом называется равноугольным
-
Треугольник, у которого нет равных сторон, называется равноугольным
-
Треугольник, у которого все стороны равны, называется равносторонним
-
Сумма длин всех сторон, называется площадью треугольника
-
Треугольник, у которого есть угол равный 90º, называется прямоугольным
-
Против каждого угла в треугольнике лежит одна сторона
-
Стороны треугольника, образующие острый угол, называются катетами
-
Сторона в треугольнике, лежащая напротив угла 90º, называется гипотенузой
-
Две стороны треугольника, образующие прямой угол, называются катетами
-
В равнобедренном треугольнике может быть один прямой угол
-
Отрезок, соединяющий вершину с противоположной стороной треугольника, называется медианой
-
Любой треугольник имеет три биссектрисы
-
Периметр – это сумма всех сторон треугольника
-
В любом треугольнике есть равные углы
-
Высоты, биссектрисы, медианы треугольника пресекаются в одной точке
-
Самая большая сторона в треугольнике – это основание
Выборочный тест.
Прямоугольный треугольник.
-
Два прямоугольных треугольника могут быть равны по двум катетам
-
Прямоугольные треугольники могут быть равны по двум углам
-
Если в двух прямоугольных треугольниках равны катет и гипотенуза, то треугольники равны
-
Существует признак равенства прямоугольных треугольников по трем сторонам
-
Если сумма острых углов прямоугольного треугольника равна 90º, то он равнобедренный
-
Если катеты прямоугольного треугольника раны, то треугольник равнобедренный
-
Если прямоугольный треугольник равнобедренный, то его острые углы по 45º
-
Если один из углов прямоугольного треугольника 45º, то треугольник равнобедренный
-
Если один из углов прямоугольного треугольника 45º, то треугольник равносторонний
-
Если катет прямоугольного треугольника равен половине гипотенузы, то у треугольника есть угол равный 30º
-
Если в прямоугольном треугольнике, гипотенуза в 2 раза больше одного из катетов, то в треугольнике есть угол 60º
-
Напротив гипотенузы лежит острый угол
-
Напротив гипотенузы лежит один из больших углов
-
Напротив гипотенузы лежит самый большой угол прямоугольного треугольника
-
Самый большой угол прямоугольного треугольника равен 90º
-
Если в прямоугольном треугольнике острый угол равен 30º, то катет, лежащий напротив этого угла равен половине гипотенузы
-
Прямоугольные треугольники могут быть равны по гипотенузе и острому углу
-
Если катеты равны, то все углы в прямоугольном треугольнике равны
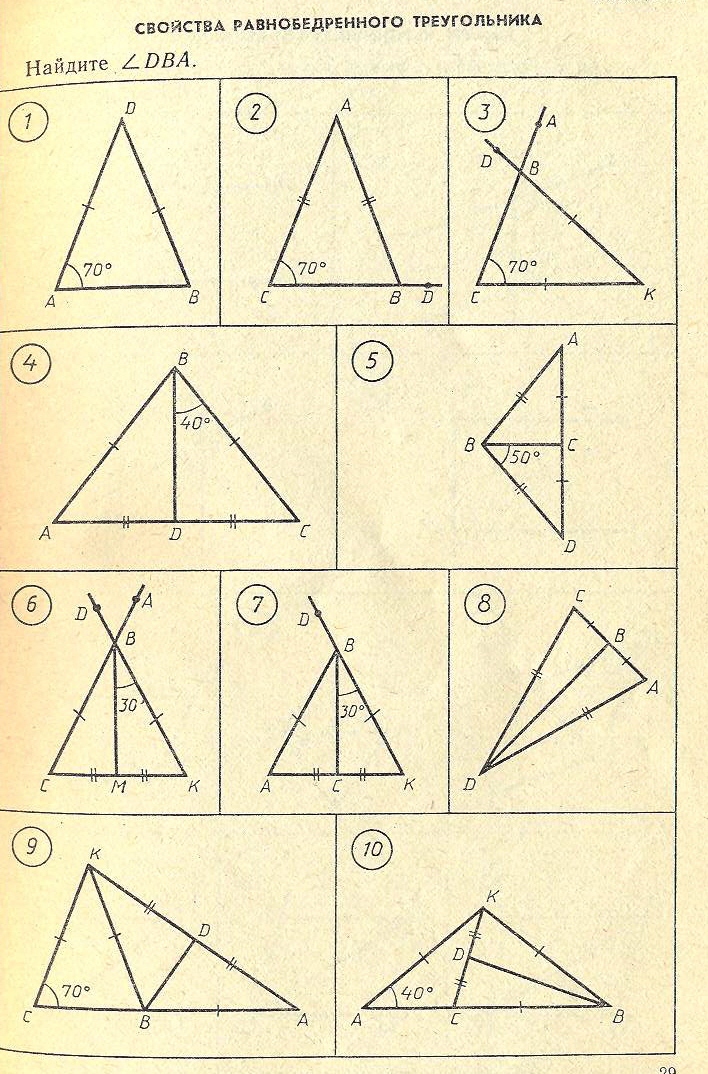
Выборочный тест.
Равнобедренный треугольник.
В равнобедренном треугольнике:
1. Углы при основании по 60º
2. Углы при основании равны
3. Боковые стороны меньше основания в два раза
4. Боковые стороны равны
5. Самая большая сторона – это основание
6. Углы равны
7. Медиана равна высоте
8. Медиана равна биссектрисе
9. Медиана, проведенная к основанию равна высоте
10. Все медианы пересекаются с высотами
11. Если один угол тупой, то все острые
12. Биссектриса является медианой
13. Периметр равен сумме боковых сторон
14. Биссектриса, проведенная из вершины угла противоположного основанию, является высотой
Альтернативный тест.
Вариант 1.
Верно ли, что:
1.Треугольник, у которого один острый угол, называется остроугольным?
2.У равностороннего треугольника все углы равны?
3.Медиана делит сторону пополам?
4.Биссектриса перпендикулярна стороне?
5.Высота делит тупой угол треугольника на две равные части?
6.Против каждого угла в треугольнике, лежит одна сторона?
7.Стороны треугольника можно обозначать любой строчной буквой латинского алфавита?
8.Сумма всех углов треугольника, называется периметром?
9.Углы А и В, называются прилежащими к стороне АВ треугольника?
10.Треугольник, у которого две стороны равны, называется равнобедренным?
Вариант 2.
Верно ли, что:
1.Треугольник, у которого все 3 стороны равны, называется равносторонним?
2.По величине углов треугольники бывают трех видов?
3.Стороны прямоугольного треугольника, называются катетами?
4.Сторона, лежащая напротив прямого угла в треугольнике, называется гипотенузой?
5.Сумма всех сторон треугольника, называется периметром?
6.Треугольник, у которого все углы острые, называется остроугольным?
7.Две стороны треугольника, образующие прямой угол, называются катетами?
8.Треугольник, у которого нет равных сторон, называется разносторонним?
9.Биссектриса в равнобедренном треугольнике, является высотой и медианой?
10.Треугольник, с равными медианами, называется равнобедренным?
Вариант 3.
Верно ли, что:
1.Точка пересечения серединных перпендикуляров к сторонам треугольника, называется замечательной?
2.Все медианы, биссектрисы, высоты, пересекаются в одной точке?
3.Любой треугольник имеет три высоты?
4.Высота перпендикулярна стороне треугольника?
5.Высоты, биссектрисы, медианы в равностороннем треугольнике пересекаются в одной точке?
6.У треугольника существуют четыре замечательные точки?
7.В равнобедренном треугольнике, сторона не равная двум другим, называется основанием?
8.В равнобедренном треугольнике, биссектриса делит любой угол пополам?
9.Серединные перпендикуляры пересекаются в двух точках?
10.Гипотенуза в треугольнике самая маленькая из сторон?
Названия, термины
Р
|
А
|
В
|
Н
|
О
|
Т
|
Р
|
Н
|
О
|
У
|
Г
|
Н
|
В
|
А
|
Р
|
Б
|
Р
|
А
|
В
|
Ь
|
Л
|
О
|
О
|
Е
|
Р
|
Д
|
Е
|
Е
|
Й
|
|
Н
|
Г
|
И
|
С
|
Н
|
Н
|
Ы
|
Й
|
У
|
|
Й
|
Н
|
Е
|
П
|
Т
|
О
|
Р
|
О
|
Н
|
Г
|
О
|
Ы
|
У
|
Т
|
О
|
У
|
О
|
М
|
Я
|
Н
|
И
|
Л
|
Н
|
З
|
Ь
|
Н
|
Г
|
Р
|
А
|
Р
|
П
|
Й
|
Ь
|
Ь
|
А
|
Л
|
Ы
|
О
|
Н
|
З
|
О
|
Н
|
И
|
Н
|
Л
|
Г
|
О
|
Й
|
Л
|
О
|
О
|
Р
|
И
|
К
|
Г
|
О
|
У
|
Ы
|
В
|
Ь
|
С
|
Т
|
О
|
Й
|
О
|
У
|
П
|
О
|
С
|
О
|
Н
|
Ы
|
Й
|
С
|
Т
|
Р
|
Т
|
У
|
|
А
|
Т
|
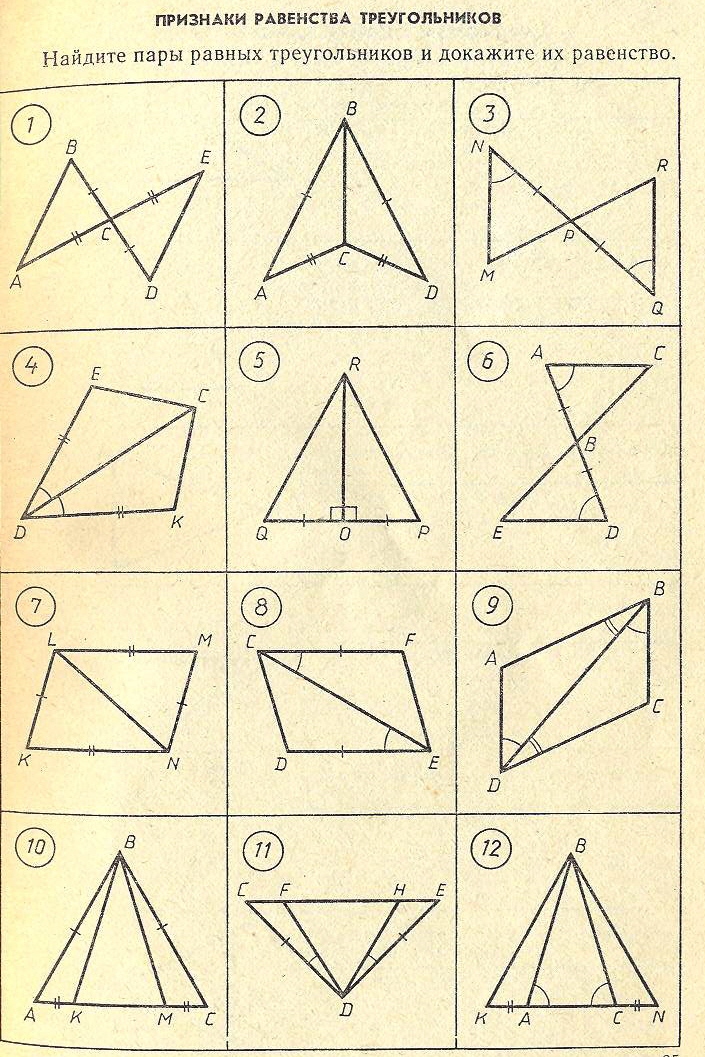
Признаки равенства треугольников. Параллельные прямые.
Тест-дополнение.
1. Если две ______ и угол _____ ____ одного треугольника соответственно равны _____ сторонам и _____ между ними ______ ________, то такие треугольники _____
2. Если сторона __ ___ прилежащих __ ___ угла ____ треугольника соответственно _____ стороне __ _____ прилежащим к ней ____ другого ____________, то такие треугольники ______
3. Если ____ стороны одного треугольника ___________ равны _____ сторонам ______ треугольника, то такие треугольники ______
4. В равнобедренном треугольнике ______ проведенная к основанию является _________ и высотой
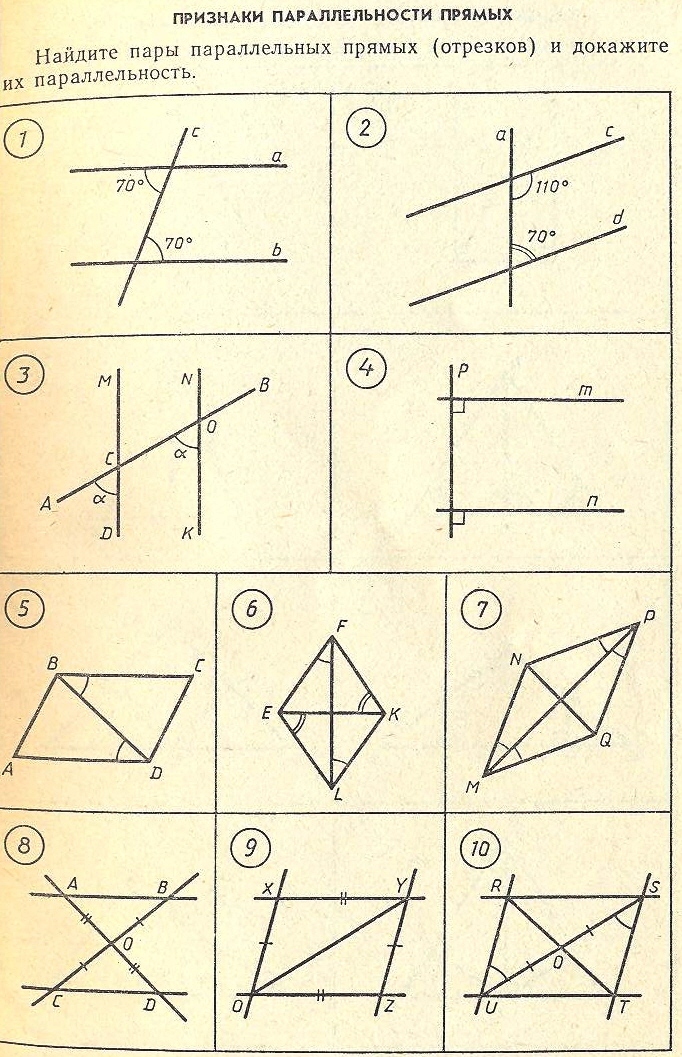
Тест-дополнение.
-
____ прямые, параллельные _____ прямой _______
-
Если при _________ двух _____ секущей, ______ лежащие углы __, то прямые ________
-
Две ______, перпендикулярные _______ прямой, __________
-
Если при _________ двух прямых ______, сумма ___________ углов равна ___, то ______ параллельны
-
Если при пересечении _____ прямых секущей, __________ углы ___, то прямые ___________
Тест-дополнение.
-
Если ______ одного прямоугольного __________ соответственно равны _________ другого ____________ треугольника, то такие _________ ____
-
Если _____ и прилежащий к нему ____ угол ____ прямоугольного ____________, ___________ равны _______ и прилежащему ____ другого ___________ треугольника, то такие треугольники _____
-
Если _______ и острый _____ одного прямоугольного треугольника ___________ равны _________ и ______ углу другого ___________ треугольника, то такие _________ равны
-
Если _______ и один ______ прямоугольного треугольника __________ равны _________ и ______ другого _________ треугольника, то такие ___________ ______
Тест-напоминание.
1 вариант.
1. Сколько элементов треугольника надо знать, чтобы можно было сравнить их?
2. Какие элементы треугольника сравниваются при применении 3 признака равных треугольников?
3. Как называется треугольник, у которого углы при основании равны?
4. Как делит треугольник медиана, проведенная из вершины, лежащей напротив основания равнобедренного угла?
5. Сколько прямых углов может быть у равнобедренного треугольника?
6. Чем является биссектриса, проведенная к основанию равнобедренного треугольника?
7.Каким свойством обладают две прямые каждая, из которых параллельна третьей прямой?
8. Каким свойством обладают внутренние накрест лежащие углы при пересечении двух параллельных прямых третьей?
9. Как называются две прямые, пересеченные третьей при условии, что получившиеся соответственные углы, равны?
10. Сколько видов углов получается при пересечении двух прямых третьей?
2 вариант.
1. Какие элементы треугольника сравниваются при применении 1 признака равных треугольников?
2. Каким свойством обладают углы при основании равнобедренного треугольника?
3. Каким свойством обладает медиана равнобедренного треугольника?
4. Сколько тупых углов может быть у равнобедренного треугольника?
5. Сколько острых углов может быть у равнобедренного треугольника?
6. В сравнении двух углов 1 треугольника равного двум углам другого треугольника, каике элементы треугольника сравниваются при применении 2-го признака равенства треугольников?
7. Сколько углов образуется при пересечении двух прямых третьей?
8. При каком условии сумма внутренних односторонних углов равна 180º?
9. Как называется прямая, пересекающая любые две прямые?
10. Чему равна сумма углов, получившихся при пересечении двух прямых?
Открытый тест.
В-1
1. В треугольнике АВС проведена медиана BD, на ее продолжении взята точка Е, DЕ=ВD, АВ=5,8 см, ВС=7,4 см, АС=9 см. Найти СЕ.
-
3,7 см
-
5,8 см
-
7,4 см
-
4,5 см
-
2,9 см
2. Треугольник АВС равен треугольнику DEF, периметр АВС =39 см. Сторона DЕ в 1,5 раза меньше стороны ЕF, DF на 3 см меньше DE. Найти большую сторону треугольника АВС.
-
15 см
-
16 см
-
18 см
-
19 см
-
12 см
3. Основание равнобедренного треугольника =5 см, боковая сторона = 6см. Найти периметр.
-
11 см
-
16 см
-
17 см
-
30º
-
8 см
4. Сумма двух боковых сторон равнобедренного треугольника =18 см, основание =5 см. Найти сумму основания и боковые стороны.
-
23 см
-
14 см
-
13 см
-
19 см
-
4 см
5. Треугольник АВС равен треугольнику DEF. АВ=12см, СВ=8 см, <Е=73º. Какое из высказываний верное:
-
DE=8 см, EF=12 см
-
<А= 73º, EF=12 см
-
DE=12 см, <В=73º
-
EF=12 см, <В=73º
-
АС=8 см, DE=12 см.
В-2
1. В треугольнике АВС проведена медиана АО. На ее продолжении взята точка К, ОК=ОА, АВ=6,3 см, ВС=6,5 см, АС=6,7 см. Найти СК.
-
6,4 см
-
6,7 см
-
6,5 см
-
6,3 см
-
6,6 см
2. Треугольник CDE равен треугольнику C1D1E1. Периметр треугольника CDE равен 76 см. Сторона C1D1 в 2,5 раза меньше D1E1 , а C1E1 на 8 см меньше стороны D1E1. Найти большую сторону треугольника CDE.
-
30 см
-
28 см
-
35 см
-
18 см
-
14 см
3. Основание равнобедренного треугольника равно 5 см. Сумма основания и боковой стороны 13 см. Найти периметр треугольника.
-
18 см
-
23 см
-
21 см
-
24 см
-
31 см
4. Разность боковой стороны и основания равнобедренного треугольника равно 3 см. Основание равно 6 см. Найти периметр треугольника.
-
24 см
-
15 см
-
18 см
-
12 см
-
30 см
5. Треугольник АВС равен треугольнику DEF. Угол В равен 73º, ВС=6,9 см, DF=7,6 см. Какое из высказываний верное?
-
DE=6,9 см, АС=7,6 см
-
<Е=73º, АС=7,6 см
-
DF=6,9 см, <Е=73º
-
АС=7,6 см,
Термины, названия углов, прямых.
В
|
Н
|
У
|
С
|
М
|
Н
|
Ы
|
Н
|
Ы
|
Р
|
Н
|
Ы
|
В
|
Н
|
Т
|
Р
|
Е
|
Ж
|
Е
|
Ь
|
Е
|
А
|
В
|
Е
|
С
|
Е
|
Ш
|
Е
|
Н
|
И
|
В
|
Л
|
А
|
К
|
А
|
Л
|
О
|
И
|
Н
|
Т
|
В
|
Е
|
Е
|
Р
|
Т
|
И
|
М
|
У
|
О
|
Е
|
Т
|
С
|
Е
|
О
|
Н
|
А
|
С
|
У
|
М
|
Ч
|
Т
|
В
|
Е
|
Н
|
Н
|
Д
|
Н
|
К
|
Р
|
Е
|
С
|
Т
|
П
|
Л
|
Е
|
Ы
|
Я
|
Е
|
О
|
С
|
Т
|
О
|
Р
|
Л
|
А
|
Л
|
Л
|
Е
|
Я
|
К
|
У
|
Е
|
И
|
Н
|
О
|
Е
|
Р
|
А
|
Ь
|
Н
|
А
|
А
|
Ш
|
П
|
Е
|
Р
|
П
|
Ж
|
П
|
Е
|
Ч
|
Г
|
Р
|
Я
|
Л
|
У
|
К
|
И
|
Е
|
А
|
Е
|
С
|
Е
|
Н
|
А
|
С
|
Я
|
А
|
К
|
Д
|
Н
|
Щ
|
Р
|
Е
|
Е
|
И
|
Д
|
У
|
Р
|
Т
|
Е
|
Т
|
Е
|
И
|
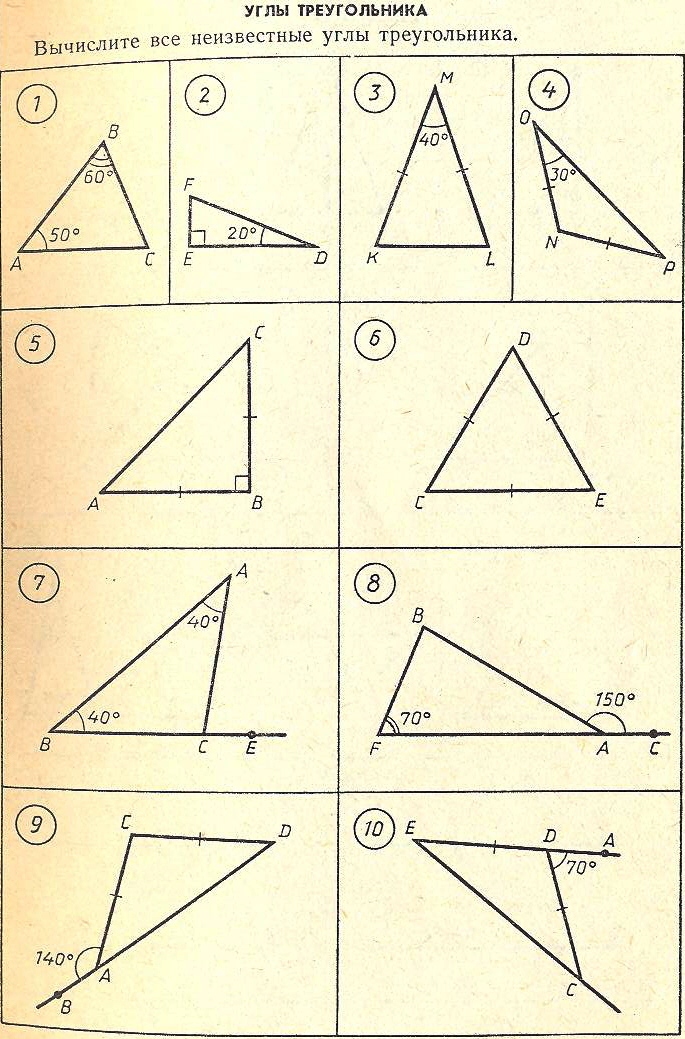
Сумма внутренних углов треугольника.
Тест-дополнение.
-
Сумма __________ углов ____________ равна ____
-
______ угол ___________ треугольника _____ 60º
-
Внешним _____ треугольника при _____ вершине, называется ____, смежный _ _____ треугольника при этой _______
-
________ угол треугольника равен сумме _____ внутренних углов, не ________ с ним
-
При ______ вершине _________ можно _________ только один _____ угол
-
В прямоугольном _________ может быть только два _____ угла
-
В тупоугольном _________ может ______ два _____ угла
Тест-напоминание.
1 вариант
1.Чему равна сумма внутренних углов треугольника?
2. Чему равна сумма углов равностороннего треугольника?
3. Как называется угол треугольника, смежный с каждым его внешним углом?
4. Сколько острых углов в прямоугольном треугольнике?
5. Если внутренний угол треугольника – тупой, то каков внешний угол?
6. Сколько элементов прямоугольного треугольника надо сравнить, чтобы доказать равенство прямоугольных треугольников?
7. Сколько перпендикуляров можно провести из точки, не принадлежащей данной прямой, на эту прямую?
8. Какая сторона в треугольнике лежит напротив большего угла?
9. Какая сторона в прямоугольном треугольнике самая большая?
10. Каким свойством обладает каждая сторона треугольника?
11. Чему равен катет, лежащий против угла в 30º в прямоугольном треугольнике?
2 вариант
1. Чему равна сумма внешних углов треугольника?
2. Градусная мера углов равностороннего треугольника?
3. Сколько внешних углов при каждой вершине треугольника?
4. Как называется угол треугольника, равный сумме двух внутренних углов треугольника, не смежных с ним?
5. Каким свойством обладает любой внешний угол треугольника, в сравнении с каждым внутренним углом треугольника?
6. Сколько признаков равенства прямоугольных треугольников существует?
7. Как называют длину перпендикуляра, опущенного из данной точки на прямую?
8. К какой стороне в разностороннем треугольнике, проведена самая большая высота?
9. Какими могут быть стороны треугольника, лежащие напротив углов, имеющих одинаковую градусную меру?
10. Какая сторона лежит напротив меньшего угла?
11. Какими могут быть катеты прямоугольного треугольника, если один из углов его равен 45º
Выборочный тест.
-
Две прямые параллельны третьей
-
При пересечении двух прямых третьей, образуются 8 углов
-
Две прямые параллельные третьей, параллельны
-
При пересечении двух прямых третьей, образуются 4 пары односторонних углов
-
При пересечении двух параллельных прямых третьей, внутренние углы равны
-
Если внутренние накрест лежащие углы равны, то прямые параллельны
-
Две прямые, перпендикулярные третьей, перпендикулярны
-
Две прямые, перпендикулярные третьей, параллельны
-
При пересечении двух прямых секущей, соответственные углы равны
-
При пересечении двух параллельных прямых третьей, сумма односторонних углов равна 180º
-
Сумма внутренних углов треугольника равна 180º
-
Сумма внутренних углов равностороннего треугольника равна 180º
-
Каждый угол равностороннего треугольника прямой
-
Каждый угол равностороннего треугольника равен 60º
-
У каждого внутреннего угла треугольника есть тупой смежный угол
-
В тупоугольном треугольнике только острый угол
-
Внешний угол треугольника равен сумме двух других углов не смежных с ним
-
Внешний угол треугольника меньше любого внутреннего угла не смежного с ним
-
При каждой величине треугольника есть два внешних угла
Открытый тест.
В-1
1. В треугольнике АВС угол В в 1,5 раза больше угла А, а угол С на 12º больше угла треугольника. Найти угол В.
-
52º
-
63º
-
42º
-
78º
-
85º
2. В равнобедренном треугольнике АВС угол С=104º. Найти углы А и В.
-
76º, 104º
-
104º, 104º
-
76º, 76º
-
80º, 100º
-
74º, 106º
3. Внешний угол при вершине основания равнобедренного треугольника равен 100º. Найти внутренний угол треугольника не смежный с ним.
-
80º
-
100º
-
50º
-
20º
-
40º
4. Величины внутренних углов треугольника пропорциональны числам 8:6:4. Найти величину большего угла.
-
60º
-
80º
-
40º
-
10º
-
52º
5. Один из углов прямоугольного треугольника равен 70º. Найти второй острый угол.
-
90º
-
160º
-
20º
-
70º
-
40º
В-2
1. В треугольнике CDB угол D в 2,5 раза больше угла С, а угол Е на 24º меньше угла D. Найдите угол Е.
-
73º
-
74º
-
61º
-
68º
-
82º
2. Внешний угол при вершине равнобедренного треугольника равен 130º. Найти углы при основании треугольника.
-
25º, 25º
-
130º, 130º
-
65º, 65º
-
50º, 50º
-
60º, 60º
3. В равнобедренном треугольнике угол при основании равен 35º. Найти угол при вершине треугольника.
-
70º
-
110º
-
105º
-
140º
-
17,5º
4. Величины внутренних углов треугольника пропорциональны числам 12:6:2. Найти величину среднего из углов.
-
108º
-
36º
-
54º
-
18º
-
20º
5. Найти углы равнобедренного прямоугольного треугольника.
-
90º, 60º, 80º
-
90º, 90º, 45º
-
90º, 45º, 45º
-
90º, 30º, 30º
-
60º, 60º, 60º
Соотношение между сторонами и углами треугольника
-
В треугольнике:
-
против ______ стороны лежит ______ угол
-
против ______ угла лежит _______ сторона
-
В прямоугольном треугольнике ________ больше ______ катета
-
Если два ______ треугольника равны, то _______ треугольника, лежащие против этих ______, также _____
-
_______, лежащий ______ угла 30º, ______ половине _______
-
_______ сторона треугольника ______ суммы двух других _______
Окружность и ее элементы.
Тест-дополнение.
1. _____________ называется ____________ фигура, которая состоит из ______ точек ________, равноудаленных __ _____ _____, которая называется _______ ___________
2. Любой ______ соединяющий точку ___________ с ее центром, называется _________
3. Отрезок, соединяющий ___ точки окружности, называется ______
4. ______, проходящая через центр __________, называется __________
5. Любые ____ точки окружности, делят ее на ___ части, каждая из этих _______, называется _____ окружности
6. Угол, с _______ в ______ окружности, называется __________ углом
7. _________, проходящая через точки ____________ перпендикулярно ________, проведенному в эту точку, называется _____________
8. Отрезки ____________ к окружности, проведенные из ____ точки, _____ и составляют ______ углы с ______, проходящей через эту точку и ______ окружности
Выборочный тест.
-
Окружностью называется геометрическая фигура, состоящая из точек плоскости
-
Чтобы провести окружность, используют транспортир
-
Любой отрезок, соединяющий две точки окружности, называется радиусом
-
Любой отрезок соединяющий центр окружности с точкой окружности, называется радиусом
-
Хорда – это отрезок
-
Самая большая хорда – это радиус
-
Хорда, проходящая через центр – это диаметр
-
Отрезок, соединяющий две точки окружности, называется хордой
-
Диаметр в 2 раза больше радиуса
-
Радиус в 2 раза меньше самой большой хорды окружности
-
Часть окружности, заключенная между двумя точками на окружности, называется хордой
-
Две точки, лежащие на окружности, делят ее на две дуги
-
Если дуга меньше полуокружности, то ее можно обозначать двумя заглавными буквами
-
Угол с вершиной на окружности, называется центральным углом
-
Угол с вершиной в центре окружности, называется центральным углом
-
Прямая и окружность могут не иметь общих точек
-
Часть плоскости называется кругом
-
Прямая имеющая хотя бы одну общую точку с окружностью, называется касательной
-
Прямая проходящая через точку окружности перпендикулярно радиусу, называется касательной
-
Окружности, имеющие общий центр называются равными
Открытый тест.
В-1
1. Длина радиуса окружности 8 см. Найти длину диаметра.
-
16 см
-
4 см
-
16π см
-
4π см
-
32π см
2. Длина радиуса окружности на 20 см меньше длины диаметра. Найти произведение длин диаметра и радиуса.
-
80 см
-
800 см
-
8 см
-
60 см
-
600 см
3. Радиусы концентрических окружностей 8 см и 4 см. Между ними проведена окружность, касающаяся обеих окружностей. Найти ее радиус.
-
6 см
-
4 см
-
2 см
-
32 см
-
1 см
4. Длина диаметра на 5 см больше радиуса. Найти радиус окружности.
-
10 см
-
10π см
-
2,5 см
-
2,5π см
-
5 см
5. Радиус первой окружности 26 см, радиус второй окружности 13 см. Окружности касаются внутренним образом. Найти расстояние между их центрами.
-
39 см
-
13 см
-
52 см
-
26 см
-
65 см
В-2
1. Длина радиуса окружности 10 см. найти длину диаметра.
-
5 см
-
20 см
-
15 см
-
5π см
-
20π см
2. Длина радиуса окружности на 10 см меньше диаметра. Найти произведение диаметра и радиуса.
-
100 см
-
200 см
-
300 см
-
400 см
-
500 см
3. Радиусы концентрических окружностей 16 см и 8 см. Между ними проведена другая окружность касающаяся обеих. Найдите радиус окружности.
-
4 см
-
8 см
-
24 см
-
32º
-
12 см
4. Длина диаметра на 6 см больше радиуса. Найдите сумму длин диаметра и радиуса.
-
12 см
-
18 см
-
6 см
-
24 см
-
8 см
5. Радиус одной окружности 25 см, радиус другой 14 см. Окружности касаются внешним образом. Найти расстояние между центрами.
-
11 см
-
32 см
-
26,5 см
-
39 см
-
25 см
Литература:
-
Алтынов П.И. «Тесты, 7-9 класс, геометрия», Москва: Дрофа -2001 г.
-
Бевз Г.П. «Геометрия 7-11 класс», Москва: Просвещение -1992 г.
-
Букубаева К.О. «Геометрия, 7 класс», Алматы: Атамура -2003 г.
-
Вульф С.И. «ЕНТ. Геометрия без проблем», г.Рудный, 2006 г.
-
Журнал «Математика в казахстанской школе»,
2004 г.
Содержание:
Введение 1
Простейшие геометрические фигуры и их основные свойства 2
Полуплоскость, луч, отрезок, измерение углов 9
Смежные и вертикальные углы. Перпендикулярные прямые 11
Виды треугольников 16
Признаки равенства треугольников 24
Внутренние и внешние углы треугольника 29
Соотношение между сторонами и углами треугольника 34
Окружность 34
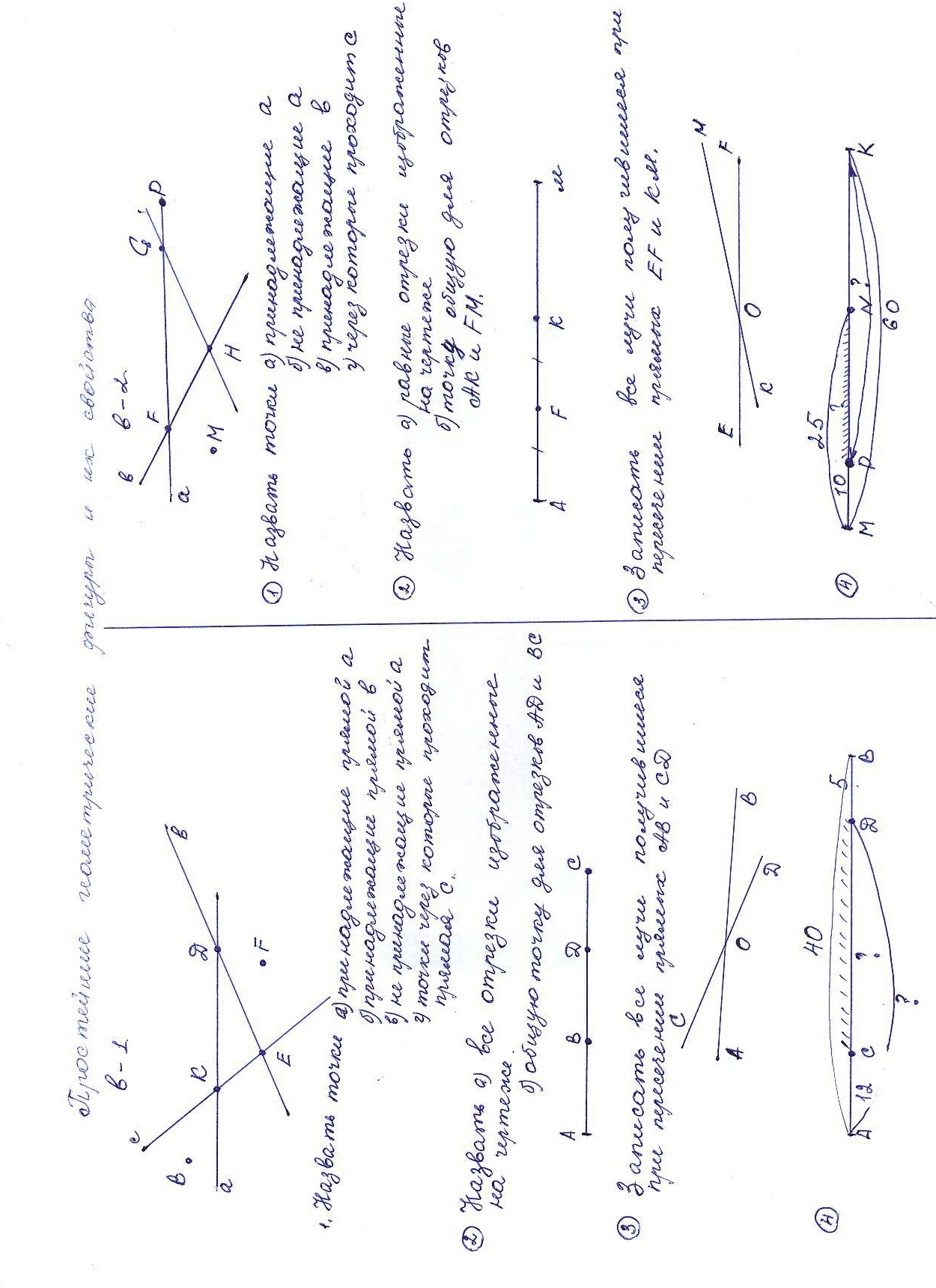
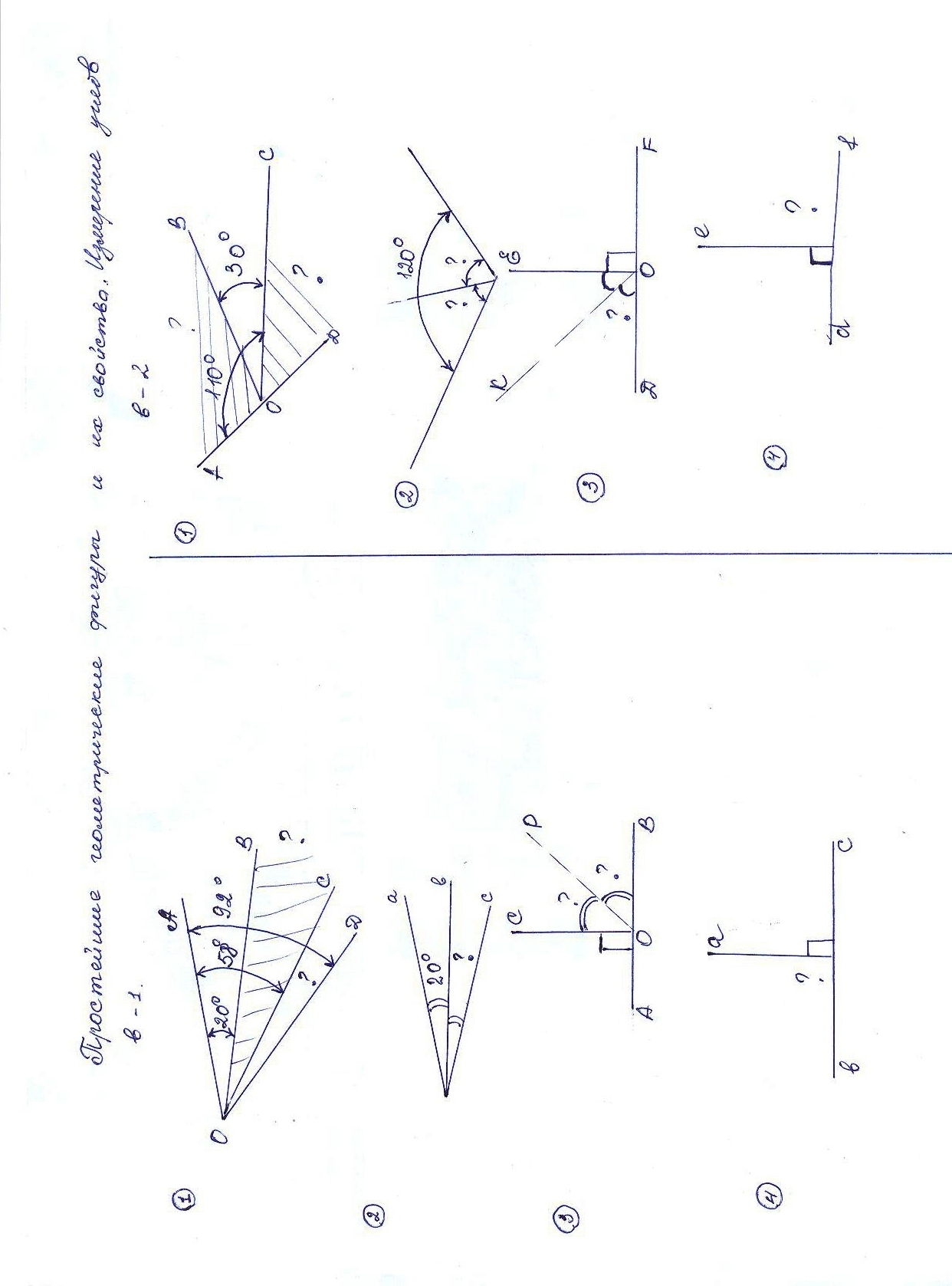
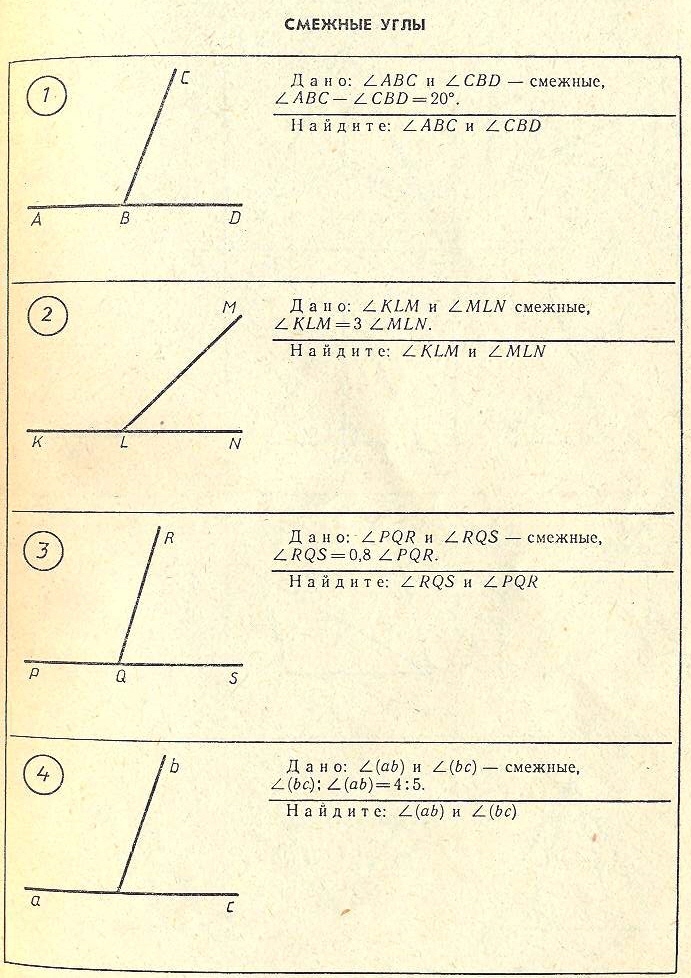
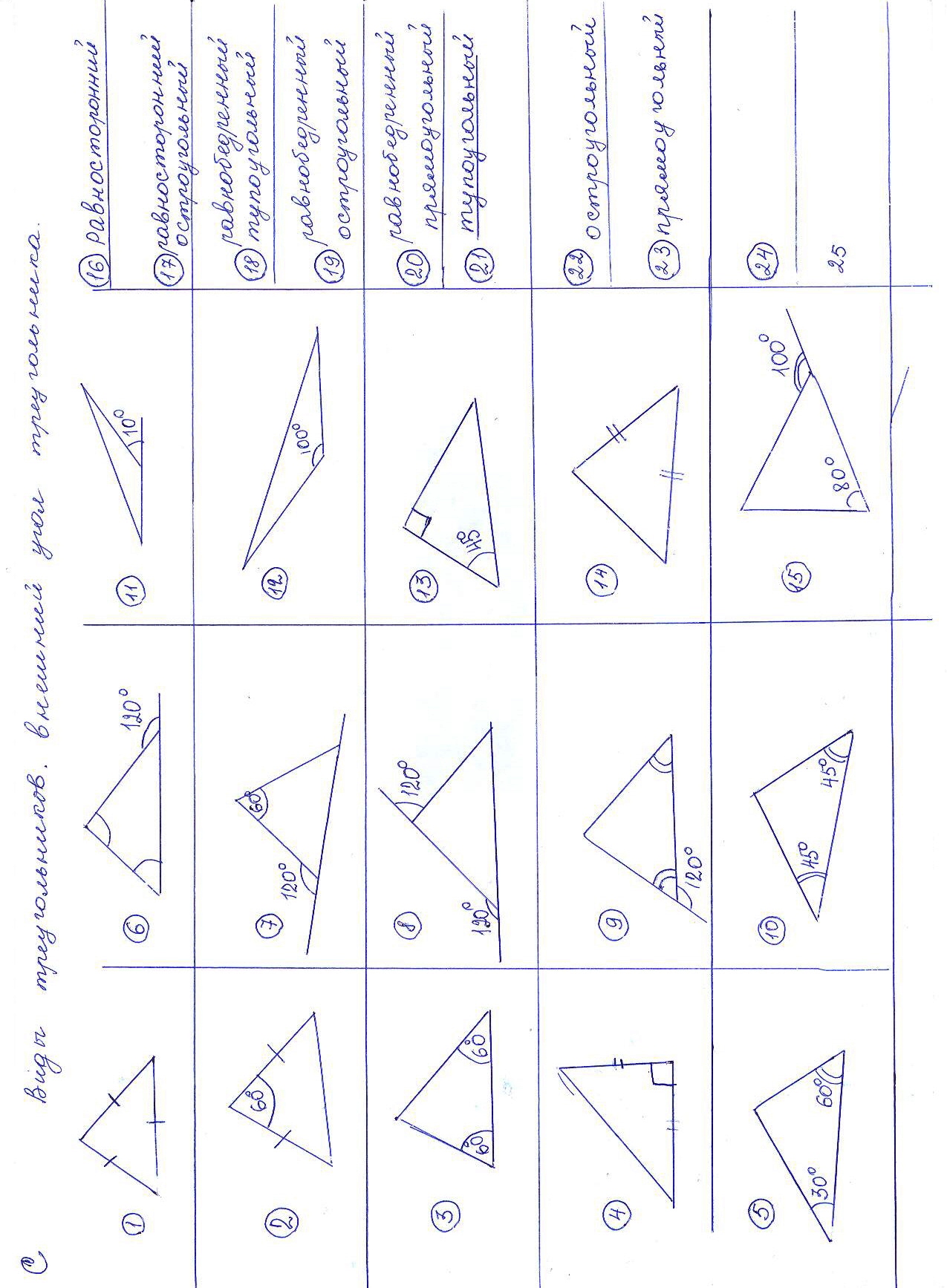
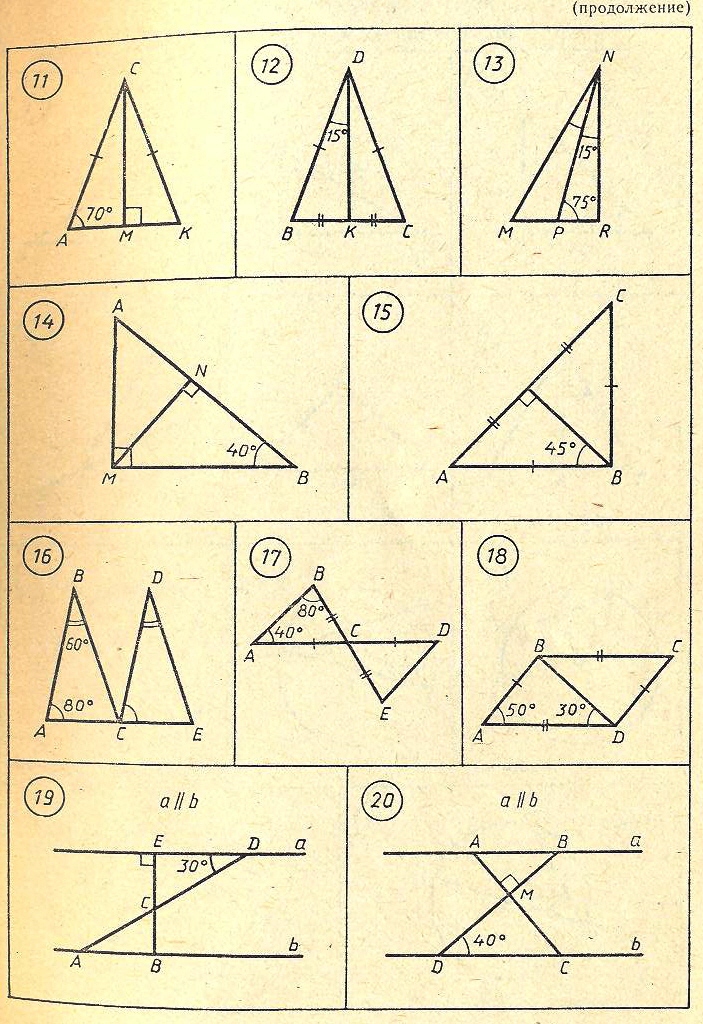
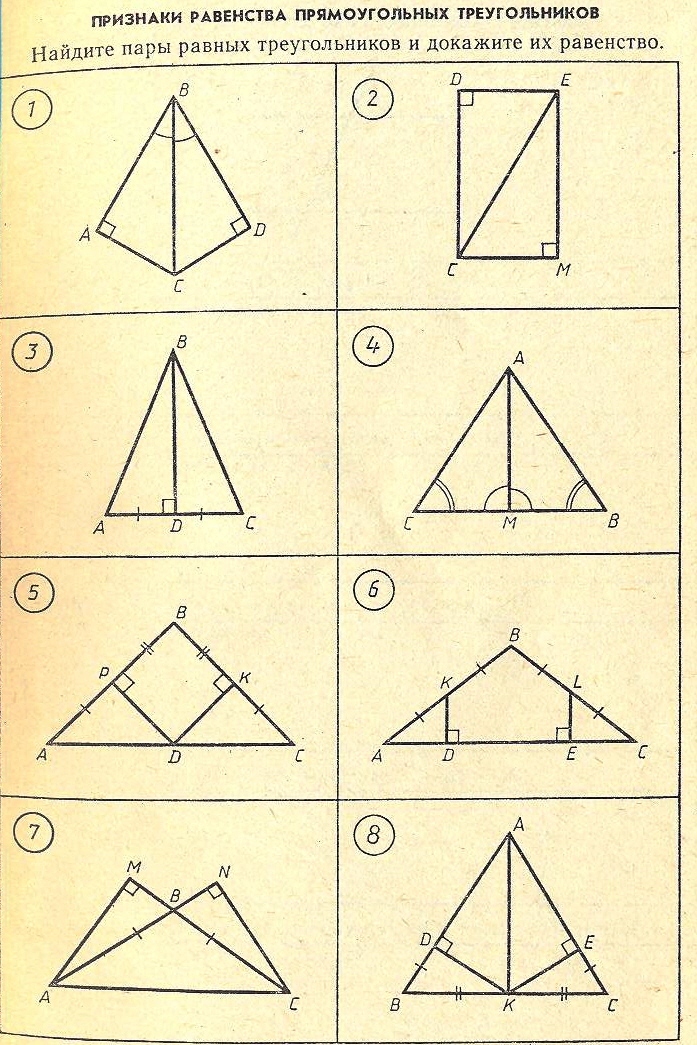
Задачи по готовым чертежам 39
Литература 49
страница 1
|