страница 1
Вариант 6
1. Зная закон распределения случайной величины имеет вид:
Чему равно математическое ожидание данной величины?
-
2,3;
-
3,5;
-
3,9;
-
6,4;
-
8,3.
2. Зная закон распределения случайной величины имеет вид:
Чему равна мода данной величины?
-
3;
-
5;
-
6;
-
2;
-
0,6.
3. Зная закон распределения случайной величины имеет вид:
Чему равна мода данной величины?
-
3;
-
5;
-
6;
-
2;
-
10.
4. Известны дисперсии двух независимых случайных величин: D(X) = 4, D(Y) = 3.Чему будет равна дисперсия произведения этих величин?
-
4
-
3
-
12
-
7
-
1
5. Каков геометрический смысл производной первого порядка?
-
скорость точки в данный момент времени 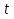 ; ;
-
ускорение точки в данный момент времени 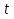 ; ;
-
угловой коэффициент касательной к графику функции в соответствующей точке;
-
свободной коэффициент касательной к графику функции в соответствующей точке;
-
совокупность кривых, каждая из которых получается путем сдвига.
6. Произведение данной функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной. О чем идет речь?
-
дифференциал функции;
-
геометрический смысл первой производной;
-
физический смысл дифференциала;
-
производная сложной функции;
-
производная финкции.
7. Чему равно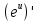 ? ?
-
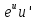 ; ;
-
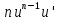 ; ;
-
 ; ;
-
 ; ;
-
 . .
8. Чему равно 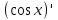 ? ?
-
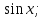
-
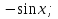
-
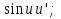
-
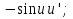
-
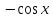 . .
9. Чему равна производная данной функции:  ? ?
-
 ; ;
-
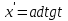 ; ;
-
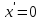 ; ;
-
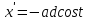 ; ;
-
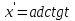 . .
10. Чему равна производная данной функции: 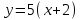 ? ?
-
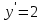 ; ;
-
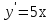 ; ;
-
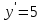 ; ;
-
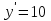 ; ;
-
 . .
11. Как называется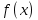 в выражении: в выражении:  ? ?
-
подынтегральная функция;
-
подынтегральное выражение;
-
переменная интегрирования;
-
знак интеграла;
-
произвольная функция оту.
12. Чему равно  ? ?
-
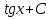 ; ;
-
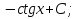
-
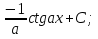
-
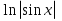 ; ;
-
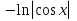
13. В чем заключается метод интегрирования по частям для нахождения неопределенного интеграла?
-
подынтегральная функция раскладывается на сумму функций, от каждой из которых можно найти первообразную;
-
подынтегральная функция раскладывается на произведение функций, от каждой из которых можно найти первообразную;
-
осуществляется переход от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения;
-
интеграл преобразуют с помощью формулы 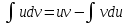 ; ;
-
интеграл преобразуют с помощью формулы 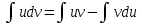 . .
14. Вычислите:  . .
-
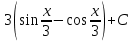 ; ;
-
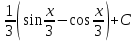 ; ;
-
 ; ;
-
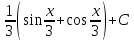 ; ;
-
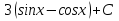 . .
15. Как изменится определенный интеграл, если пределы интегрирования будут одинаковыми?
-
не изменится;
-
меняет знак на противоположный;
-
увеличится в два раза;
-
уменьшится в два раза;
-
станет равным нулю.
16. Наиболее важными методами интегрирования определенных интегралов являются: 1) метод разложения; 2) метод почленного деления; 3) метод непосредственного интегрирования; 4) метод замены переменной; 5) метод представления; 6) метод интегрирования по частям. Какие методы существуют?
-
1,3,4,6;
-
1,2,4,6;
-
2,5,6;
-
2, 5;
-
1,3,4.
17. Вычислить: 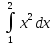 . .
-
1;
-
0;
-
 ; ;
-
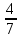 ; ;
-
 . .
18. Как записывается общий вид дифференциального уравнения?
-
 ; ;
-
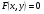 ; ;
-
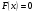 ; ;
-
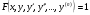 ; ;
-
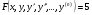 . .
19. К какому виду дифференциального уравнению относиться уравнение 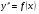 ? ?
-
однородное дифференциальное уравнение;
-
линейные дифференциальные уравнение:
-
дифференциальные уравнения, допускающие понижения порядка;
-
дифференциальные уравнения с разделяющимися переменными;
-
дифференциальные уравнения второго порядка.
20. Чему равен порядок дифференциального уравнения 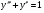 ? ?
-
2;
-
3;
-
4;
-
5;
-
1.
21. Чему равен порядок дифференциального уравнения 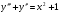 ? ?
-
1;
-
2;
-
3;
-
4;
-
5.
22. Чему равен порядок дифференциального уравнения  ? ?
-
1;
-
2;
-
3;
-
4;
-
5.
23. Какой вид имеет общее решение дифференциального уравнения:  ? ?
-
 ; ;
-
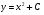 ; ;
-
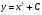 ; ;
-
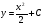 ; ;
-
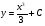 . .
24. Какой вид имеет общее решение дифференциального уравнения: 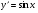 ? ?
-
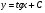 ; ;
-
 ; ;
-
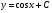 ; ;
-
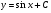 ; ;
-
 . .
25. Какой вид имеет общее решение дифференциального уравнения: 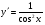 ? ?
-
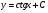 ; ;
-
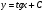 ; ;
-
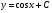 ; ;
-
 ; ;
-
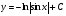 . .
26. Какую замену применяют при решении дифференциальных уравнений с разделяющимися переменными?
-
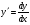 ; ;
-
 ; ;
-
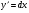 ; ;
-
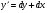 ; ;
-
 . .
27. Как называются комбинацией, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов?
-
размещение;
-
сочетание;
-
перстановка;
-
вероятность;
-
закон распределения.
28. По какой формуле вычисляется размещение?
-
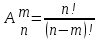 ; ;
-
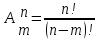 ; ;
-
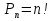 ; ;
-
C ; ;
-
C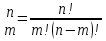 . .
29. По какой формуле вычисляется вероятность?
-
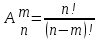 ; ;
-
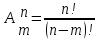 ; ;
-
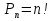 ; ;
-
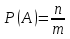 ; ;
-
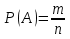 . .
30. Чему равна вероятность невозможного события?
-
2;
-
1;
-
0;
-
[0;1];
-
3.
31. Соответствие между средними значениями случайной величины и их вероятностями. О чем идет речь?
-
закон распредиления дискретной величины;
-
математическое ожидание случайной величины;
-
мода случайной величины;
-
дисперсия случайной величины;
-
среднее квадратическое отклонение случайной величины.
32. Математическое ожидание квадрата отклонения случайной велечины от ее математического ожидания.О чем идет речь?
-
закон распредиления дискретной величины;
-
математическое ожидание случайной величины;
-
мода случайной величины;
-
дисперсия случайной величины;
-
среднее квадратическое отклонение случайной величины.
33. При благоприятных условиях увеличение количества бактерий с течением времени происходит по экспоненциальному закону, математическая модель данного закона имеет вид: 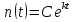 , где t - время, k - коэффициент пропорциональности. Чему равна скорость увеличения количества бактерий с течением времени? , где t - время, k - коэффициент пропорциональности. Чему равна скорость увеличения количества бактерий с течением времени?
-
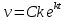 ; ;
-
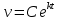 ; ;
-
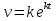 ; ;
-
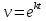 ; ;
-
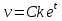 . .
34. Чему равно общее решение линейного однородного дифференциального уравнения второго порядка:  ? ?
-
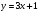 ; ;
-
 ; ;
-
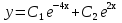 ; ;
-
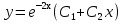 ; ;
-
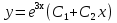 . .
35. Чему равно общее решение линейного однородного дифференциального уравнения второго порядка: 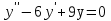 ? ?
-
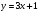 ; ;
-
 ; ;
-
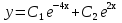 ; ;
-
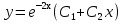 ; ;
-
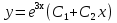 . .
36. Чему равно общее решение линейного однородного дифференциального уравнения второго порядка: 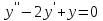 ? ?
-
 ; ;
-
 ; ;
-
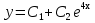 ; ;
-
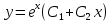 ; ;
-
 . .
37. В партии ампул с липокаином вероятность того, что ампулы будут без дефекта, равна 0,85. Сколько ампул без дефектов в партии из 10000 ампул?
-
150;
-
8500;
-
850;
-
1500;
-
10000.
38. Студент отвечает два раза. Какова вероятность правильного ответа хотя бы один раз?
-
0,25;
-
0,5;
-
0,75;
-
0,85;
-
0,875.
39. В результате проведенного анализа было установлено, что из 200 поступивших студентов оканчивают университет 190. Какова вероятность того, что студент не получит высшее образование?
-
0,95;
-
0,75;
-
0,55;
-
0,25;
-
0,05.
40. Зная закон распределения случайной величины имеет вид:
Чему равно математическое ожидание данной величины?
-
2,3;
-
3,5;
-
3,9;
-
6,4;
-
8,3.
41. Как называются а и b в выражении 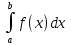 ? ?
-
а – нижний, b – верхний пределы;
-
а – верхний, b – нижний пределы;
-
а – средний, b – верхний пределы;
-
а – нижний, b – средний пределы;
-
а – средний, b – нижний пределы.
42. Как называется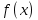 в выражении: в выражении: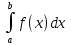 ? ?
-
подынтегральная функция;
-
подынтегральное выражение;
-
переменная интегрирования;
-
знак интеграла;
-
произвольная функция оту.
43. Каков геометрический смысл определенного интеграла?
-
скорость точки в данный момент времени 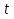 ; ;
-
площадь криволинейной трапеции численно равна интегралу от функции;
-
угловой коэффициент касательной к графику функции в соответствующей точке;
-
площадь криволинейной трапеции численно равна интегралу от функции, взятому по основанию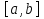 ; ;
-
совокупность кривых, каждая из которых получается путем сдвига.
44. Как изменится определенный интеграл, если пределы интегрирования будут одинаковыми?
-
не изменится;
-
меняет знак на противоположный;
-
увеличится в два раза;
-
уменьшится в два раза;
-
станет равным нулю.
45. По какой формуле осуществляется связь между определенным и неопределенным интегралами?
-
асимптотическая формула;
-
формула Муавра-Лапласа;
-
формула Байеса;
-
формула Бернулли;
-
формула Ньютона-Лейбница.
46. Наиболее важными методами интегрирования определенных интегралов являются: 1) метод разложения; 2) метод почленного деления; 3) метод непосредственного интегрирования; 4) метод замены переменной; 5) метод представления; 6) метод интегрирования по частям. Какие методы существуют?
-
1,3,4,6;
-
1,2,4,6;
-
2,5,6;
-
2, 5;
-
1,3,4.
47. В чем заключается метод интегрирования по частям для нахождения определенного интеграла?
-
подынтегральная функция раскладывается на сумму функций, от каждой из которых можно найти первообразную;
-
подынтегральная функция раскладывается на произведение функций, от каждой из которых можно найти первообразную;
-
осуществляется переход от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения;
-
интеграл преобразуют с помощью формулы 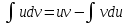 ; ;
-
интеграл преобразуют с помощью формулы  . .
48. Вычислить: 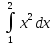 . .
-
1;
-
0;
-
 ; ;
-
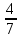 ; ;
-
 . .
49. Вычислить: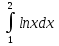 . .
-
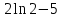 ; ;
-
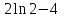 ; ;
-
 ; ;
-
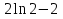 ; ;
-
 . .
50. Вычислить: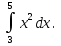
-

-

-
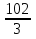
-

-
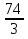
51. Вычислить: . .
-
 ; ;
-
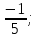
-
0;
-
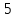 ; ;
-
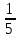 . .
52. Вычислите: 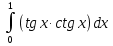 . .
-
1;
-
2;
-
0;
-
-1;
-
-2.
53. Вычислите:  . .
-
1;
-
2;
-
0;
-
-1;
-
-2.
54. Вычислите: 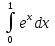 . .
-
 ; ;
-
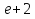 ; ;
-
 ; ;
-
 ; ;
-
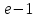 . .
55. Вычислите:  .. ..
-
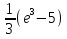 ; ;
-
 ; ;
-
 ; ;
-
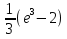 ; ;
-
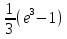 . .
56. Как записывается общий вид дифференциального уравнения?
-
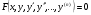 ; ;
-
 ; ;
-
 ; ;
-
 ; ;
-
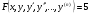 . .
57. Что описывается формулой 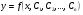 ? ?
-
дифференциальное уравнение;
-
частное решение дифференциального уравнения;
-
порядок дифференциального уравнения;
-
общее решение дифференциального уравнения;
-
вид дифференциального уравнения.
58. Чему равен порядок дифференциального уравнения  ? ?
-
1;
-
2;
-
3;
-
4;
-
5.
59. К какому виду дифференциального уравнению относиться уравнение 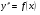 ? ?
-
однородное дифференциальное уравнение;
-
линейные дифференциальные уравнение:
-
дифференциальные уравнения, допускающие понижения порядка;
-
дифференциальные уравнения с разделяющимися переменными;
-
дифференциальные уравнения второго порядка.
60. Если 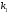 и и 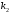 различные действительные корни характеристического уравнения, как записывается общее решение данного уравнения? различные действительные корни характеристического уравнения, как записывается общее решение данного уравнения?
-
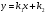 ; ;
-
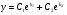 ; ;
-
 ; ;
-
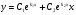 ; ;
-
 . .
61. Что называется первообразной функции для данной функции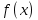 ? ?
-
предел отношения приращения функции к приращению аргумента;
-
произведение производной на приращение независимой переменной;
-
такая функция 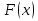 , производная которой равна , производная которой равна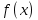 или дифференциал которой равен или дифференциал которой равен 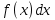 ; ;
-
такая функция 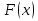 , производная которой равна , производная которой равна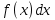 или дифференциал которой равен или дифференциал которой равен 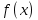 ; ;
-
предел отношения приращения аргумента к приращению функции.
62. Как обозначается неопределенный интеграл?
-
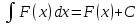 ; ;
-
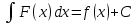 ; ;
-
 ; ;
-
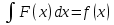 ; ;
-
 . .
63. Как называется 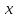 в выражении: в выражении:  ? ?
-
подынтегральная функция;
-
подынтегральное выражение;
-
переменная интегрирования;
-
знак интеграла;
-
произвольная функция оту.
64. Чему равно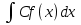 ? ?
-
произвольному выражению;
-
не имеет решение;
-
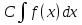 ; ;
-
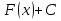 ; ;
-
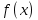 . .
65. Чему равно 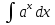 ? ?
-
 ; ;
-
 ; ;
-
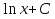 ; ;
-
 ; ;
-
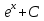 . .
66. Какая формула верно указана?
-
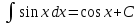 ; ;
-
 ; ;
-
 ; ;
-
 ; ;
-
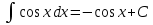 . .
67. Какая формула верно указана?
-
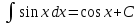 ; ;
-
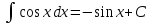 ; ;
-
 ; ;
-
 ; ;
-
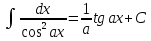 ; ;
68. Чему равно 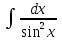 ? ?
-
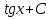 ; ;
-
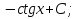
-
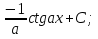
-
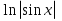 ; ;
-
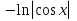
69. Наиболее важными методами интегрирования неопределенных интегралов являются: 1) метод разложения; 2) метод почленного деления; 3) метод непосредственного интегрирования; 4) метод замены переменной; 5) метод представления; 6) метод интегрирования по частям. Какие методы не существуют?
-
1,3,4,6;
-
1,2,4,6;
-
2,5,6;
-
2, 5;
-
1,3,4.
70. В чем заключается метод замены переменой для нахождения неопределенного интеграла?
-
подынтегральная функция раскладывается на сумму функций, от каждой из которых можно найти первообразную;
-
подынтегральная функция раскладывается на произведение функций, от каждой из которых можно найти первообразную;
-
осуществляется переход от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения;
-
интеграл преобразуют с помощью формулы 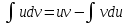 ; ;
-
интеграл преобразуют с помощью формулы 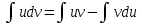 . .
71. Какая формула используется при интегрирования по частям для неопределенного интеграла?
-
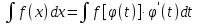 ; ;
-
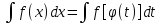 ; ;
-
 ; ;
-
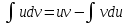 ; ;
-
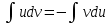
72. Вычислите: . .
-
 ; ;
-
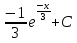 ; ;
-
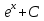 ; ;
-
 ; ;
-
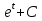 . .
73. Вычислите:  . .
-
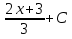 ; ;
-
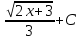 ; ;
-
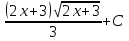 ; ;
-
 ; ;
-
 . .
74. Вычислите: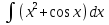 . .
-
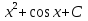 ; ;
-
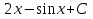 ; ;
-
 ; ;
-
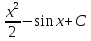 ; ;
-
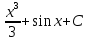 . .
75. Вычислите: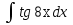 . .
-
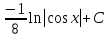 ; ;
-
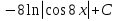 ; ;
-
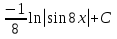 ; ;
-
 ; ;
-
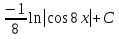 . .
76. Вычислите: 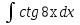 . .
-
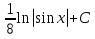 ; ;
-
 ; ;
-
 ; ;
-
 ; ;
-
 . .
77. Вычислите: 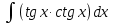 . .
-
1+C;
-
2+C;
-
x+C;
-
3x+C;
-
2x+C.
78. Вычислите: 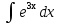 . .
-
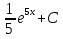 ; ;
-
 ; ;
-
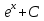 ; ;
-
 ; ;
-
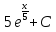 . .
79. Вычислите: 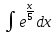 . .
-
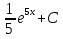 ; ;
-
 ; ;
-
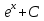 ; ;
-
 ; ;
-
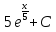 . .
80. Вычислите:  . .
-
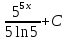 ; ;
-
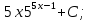
-
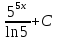 ; ;
-
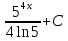 ; ;
-
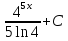 . .
81. Что выражает данная формула 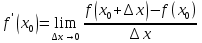 ? ?
-
дифференциал;
-
определенный интеграл;
-
производную;
-
неопределенный интеграл;
-
первообразную.
82. Чему равно 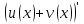 ? ?
-
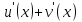 ; ;
-
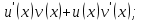
-
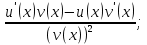
-

-
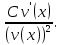
83. Чему равно ? ?
-
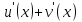 ; ;
-
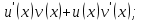
-
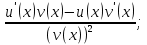
-

-
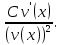
84. Как обозначается сложная функция?
-
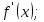
-
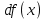 ; ;
-
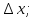
-
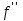 ; ;
-
 . .
85. Как обозначается дифференциал функции?
-
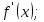
-
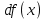 ; ;
-
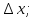
-
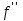 ; ;
-
 . .
86. Чему равно 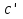 ? ?
-
0;
-
2;
-
1;
-
С;
-
e.
87. Чему равно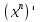 ? ?
-
0;
-
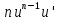 ; ;
-
1;
-
 ; ;
-
 . .
88. Чему равно ? ?
-
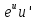 ; ;
-
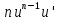 ; ;
-
 ; ;
-
 ; ;
-
 . .
89. Чему равно  ? ?
-
 ; ;
-
 ; ;
-
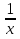 ; ;
-
 ; ;
-
 . .
90. Чему равно 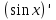 ? ?
-
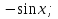
-
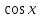 ; ;
-
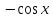 ; ;
-

-
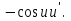
91. Чему равно  ? ?
-
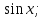
-
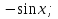
-
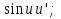
-
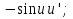
-
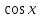 . .
92. Чему равно 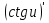 ? ?
-
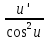 ; ;
-
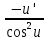 ; ;
-
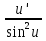 ; ;
-
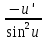 ; ;
-
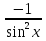 . .
93. Что такое дифференциал функции?
-
предел отношения приращения аргумента к приращению функции;
-
предел отношения приращения функции к приращению аргумента;
-
отношение приращения функции к приращению аргумента;
-
отношения приращения аргумента к приращению функции;
-
произведение производной на приращение независимой переменной.
94. Чему равна производная данной функции:  ? ?
-
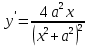 ; ;
-
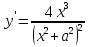 ; ;
-
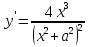 ; ;
-
 ; ;
-
 / /
95. Чему равна производная данной функции: 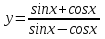 ? ?
-
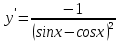 ; ;
-
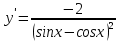 ; ;
-
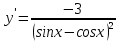 ; ;
-
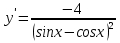 ; ;
-
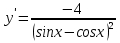 . .
96. Чему равна производная данной функции: 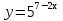 ? ?
-
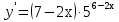 ; ;
-
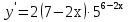 ; ;
-
 ; ;
-
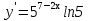 ; ;
-
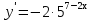 . .
97. Чему равна производная данной функции: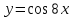 ? ?
-
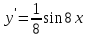 ; ;
-
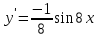 ; ;
-
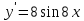 ; ;
-
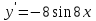 ; ;
-
 . .
98. Чему равна производная данной функции: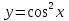 ? ?
-
 ; ;
-
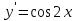 ; ;
-
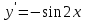 ; ;
-
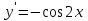 ; ;
-
 . .
99. Чему равна производная данной функции: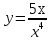 ? ?
-
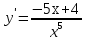 . .
-
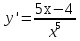 . .
-
 . .
-
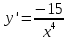 . .
-
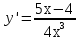 . .
100. Чему равна производная данной функции: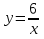 ? ?
-
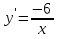 ; ;
-
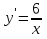 ; ;
-
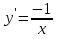 ; ;
-
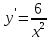 ; ;
-
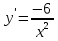 . .
страница 1
|