страница 1
8.1. Метод ломаных Эйлера
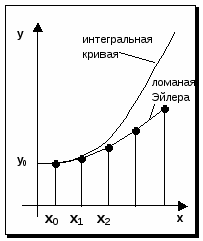
В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения. Этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.
И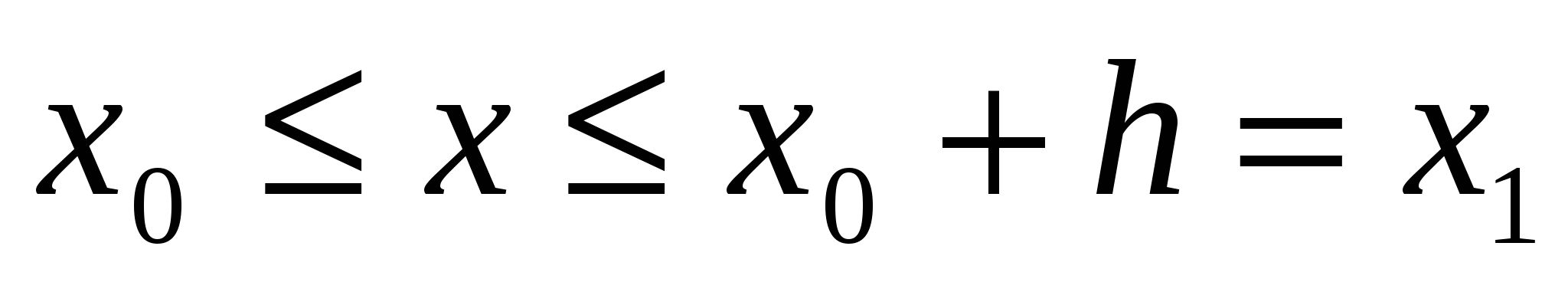 дея метода заключается в том, что на малом промежутке изменения независимой переменной дея метода заключается в том, что на малом промежутке изменения независимой переменной
и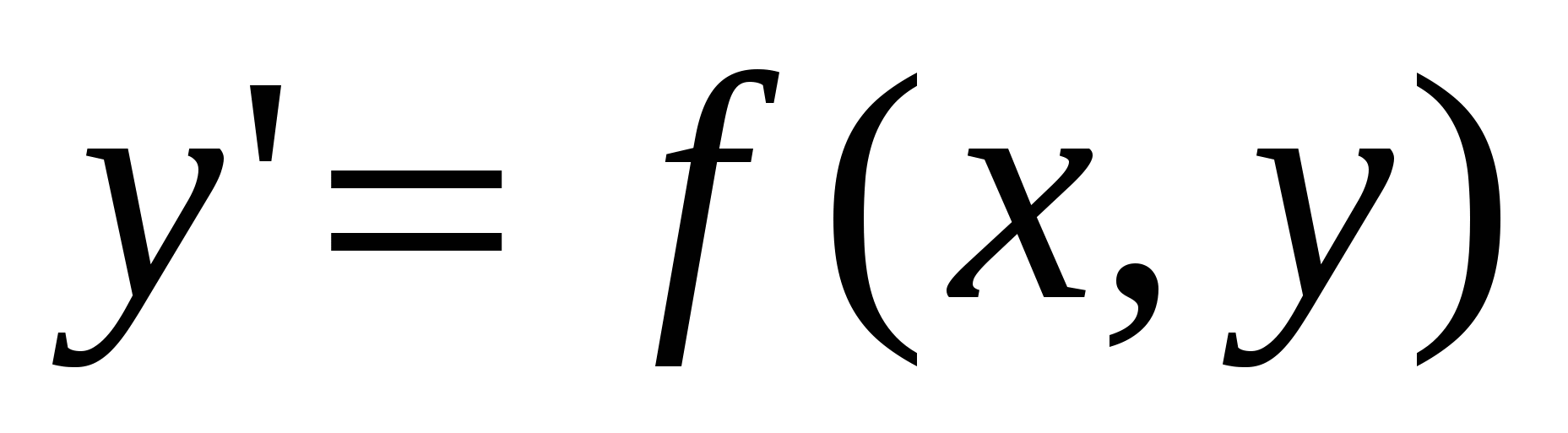 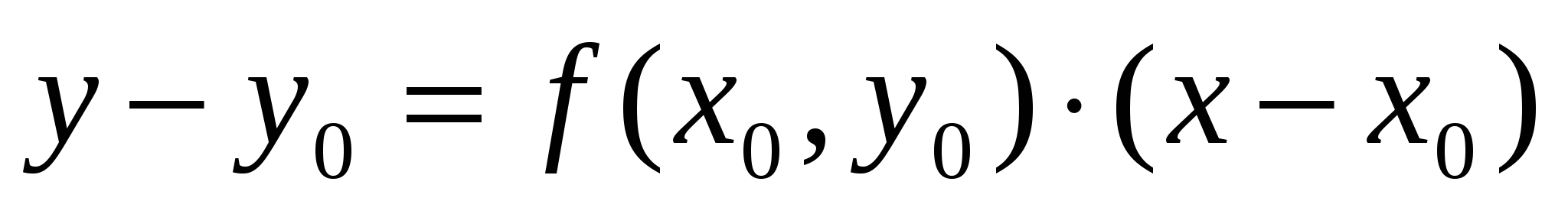 нтегральная кривая дифференциального уравнения нтегральная кривая дифференциального уравнения
з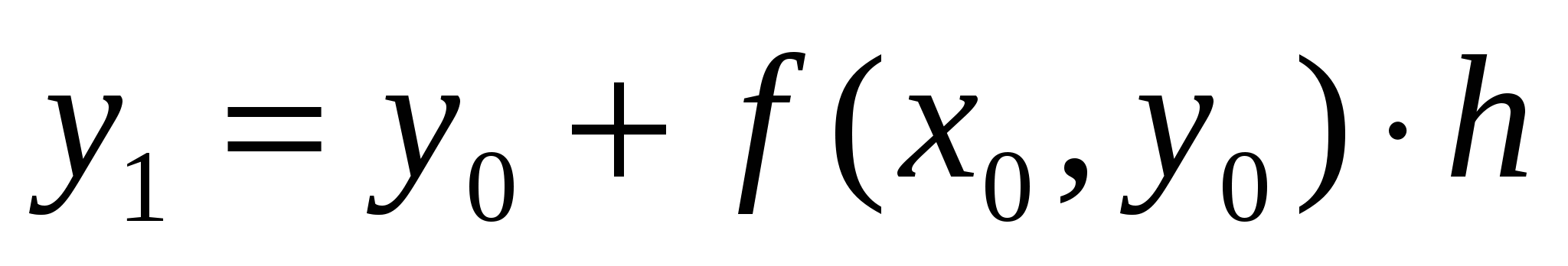 аменяется отрезком прямой (касательной) (8) аменяется отрезком прямой (касательной) (8)
О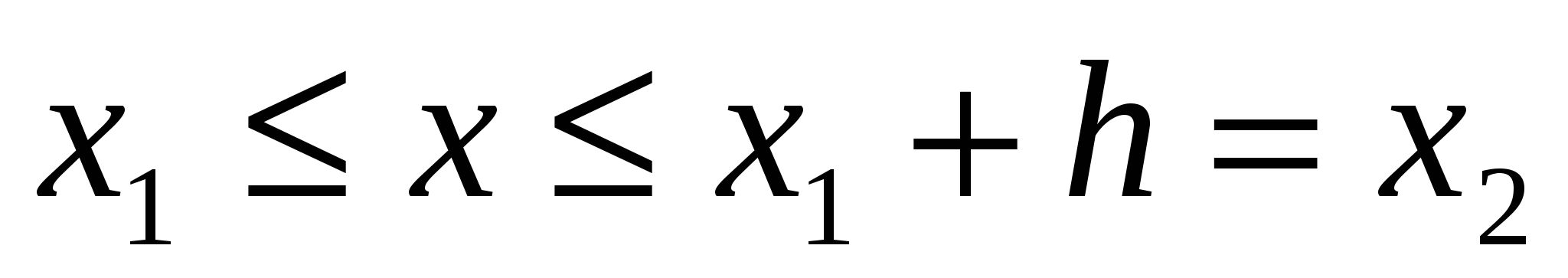 тсюда тсюда
и процесс можно повторить для промежутка и т.д.
Таким образом, интегральная кривая заменяется при этом ломаной, называемой ломаной Эйлера (рис.).
Рассмотрим задачу (1), где 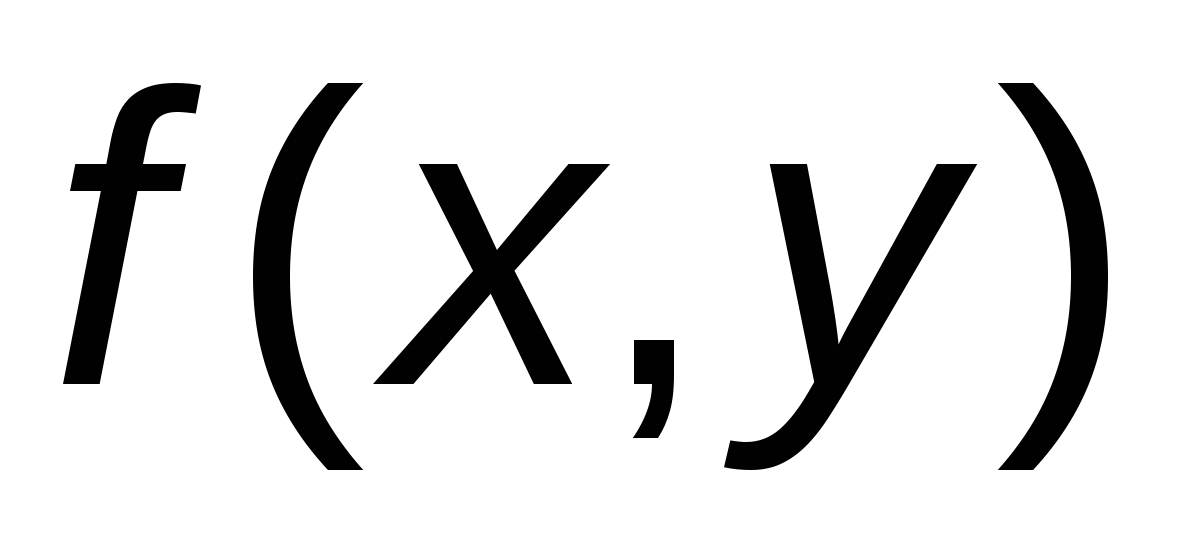 — непрерывно дифференцируемая функция в прямоугольнике — непрерывно дифференцируемая функция в прямоугольнике 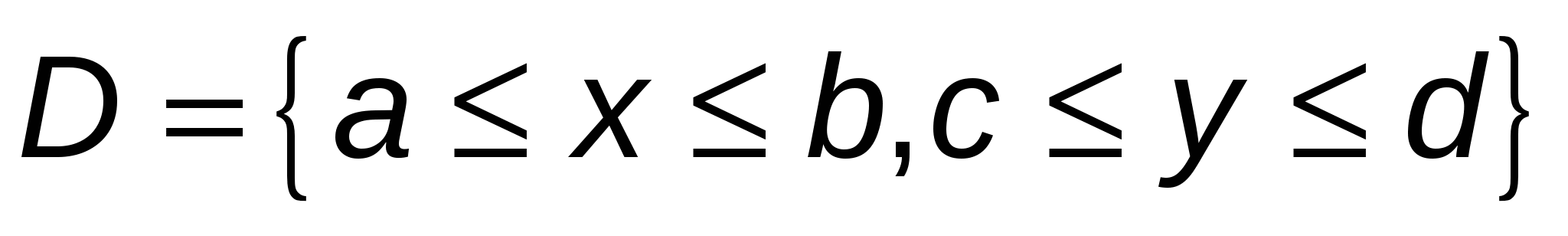 , ,  . .
Построим систему равноотстоящих узлов x , x , x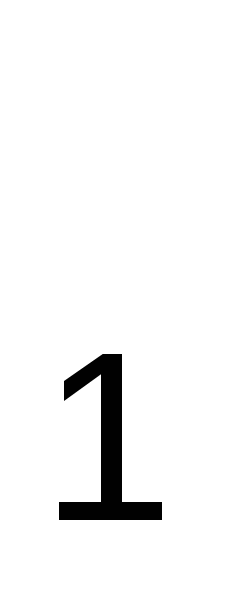 , … ,x , … ,x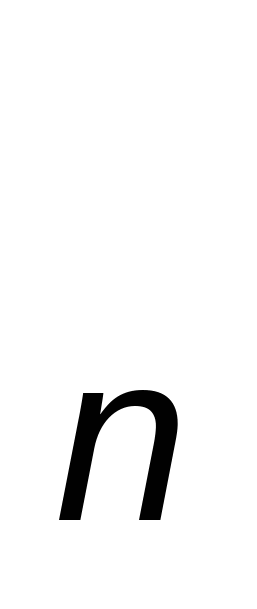 , ,
где x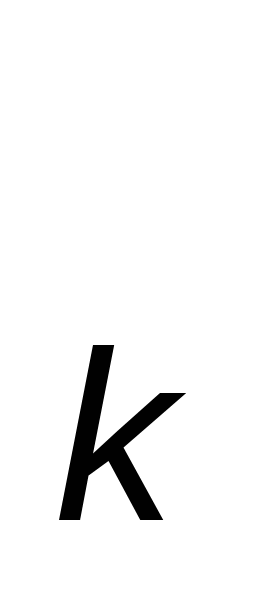 = x = x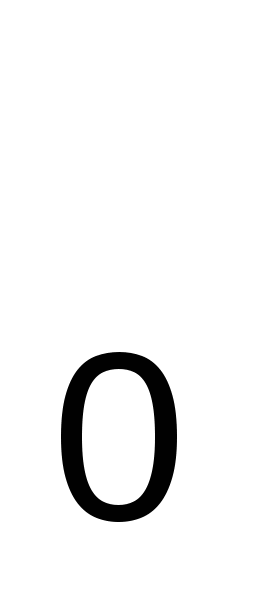 + kh, k = 0,1,2, … , h — достаточно малый шаг интегрирования. + kh, k = 0,1,2, … , h — достаточно малый шаг интегрирования.
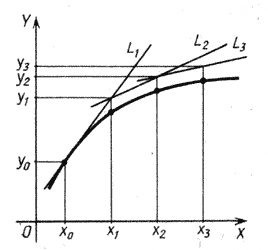
Проведем касательную в точке 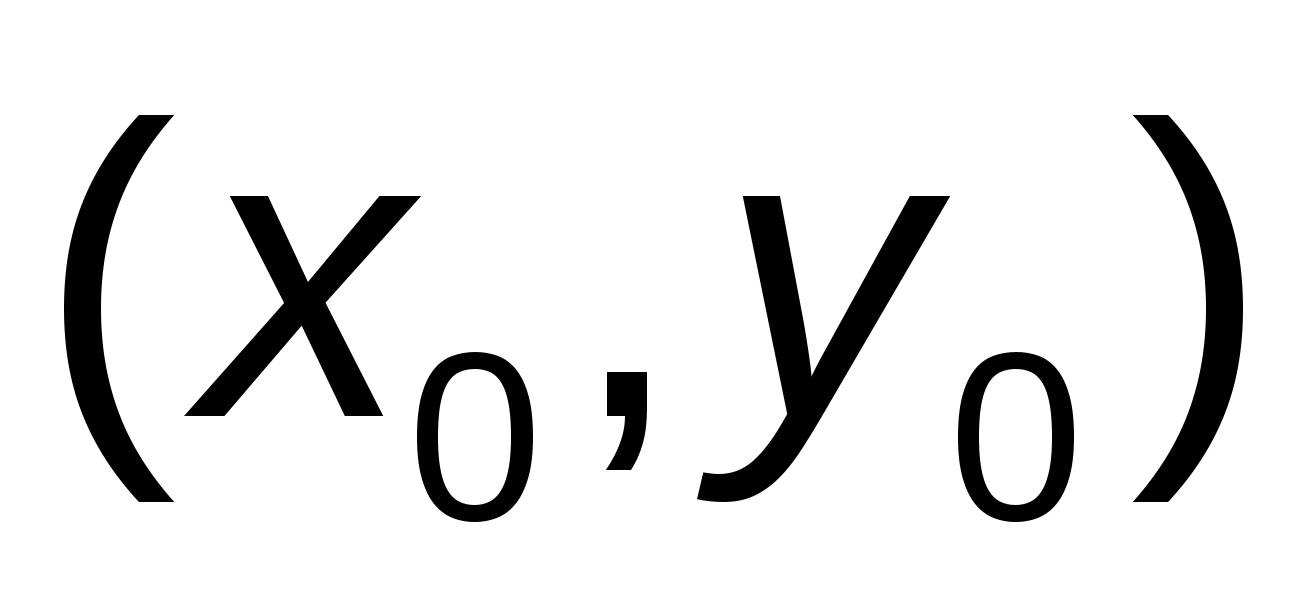 к графику решения y = y(x) дифференциального уравнения (1) с угло-вым коэффициентом к графику решения y = y(x) дифференциального уравнения (1) с угло-вым коэффициентом 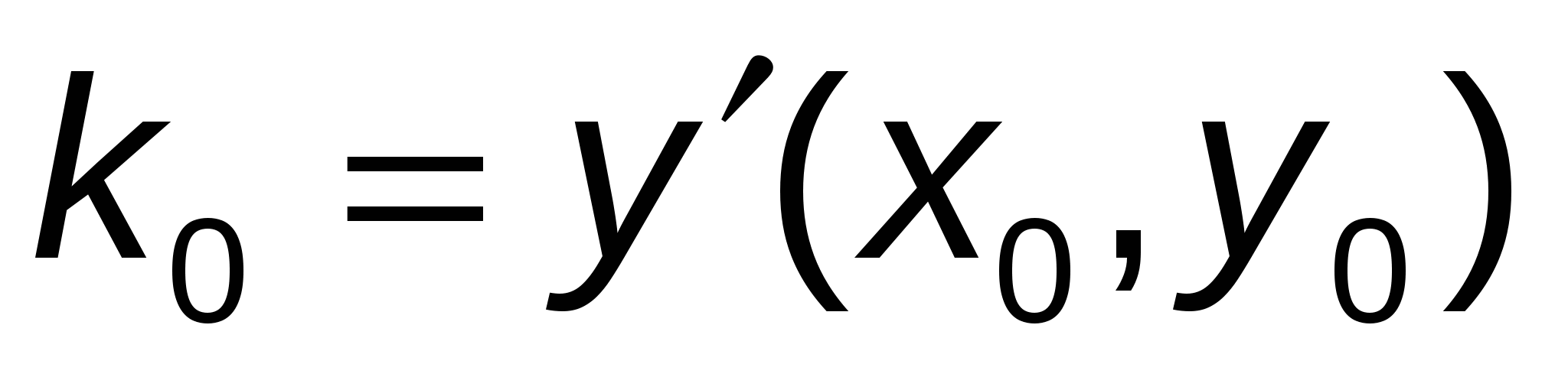 . .
Уравнение этой касательной имеет вид: 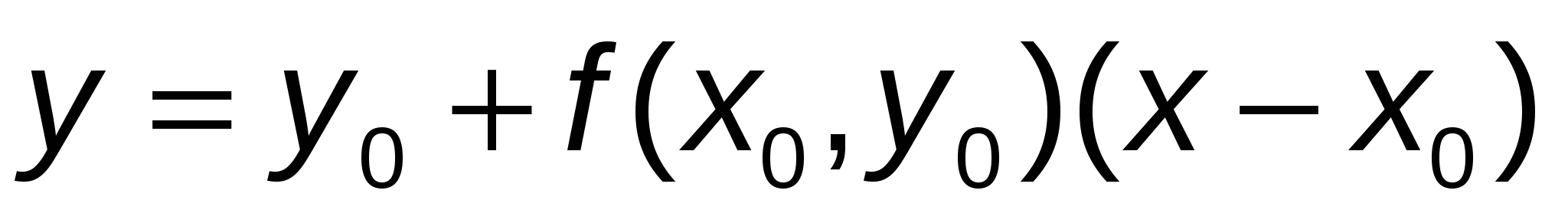 . .
За приближенное решение уравнения 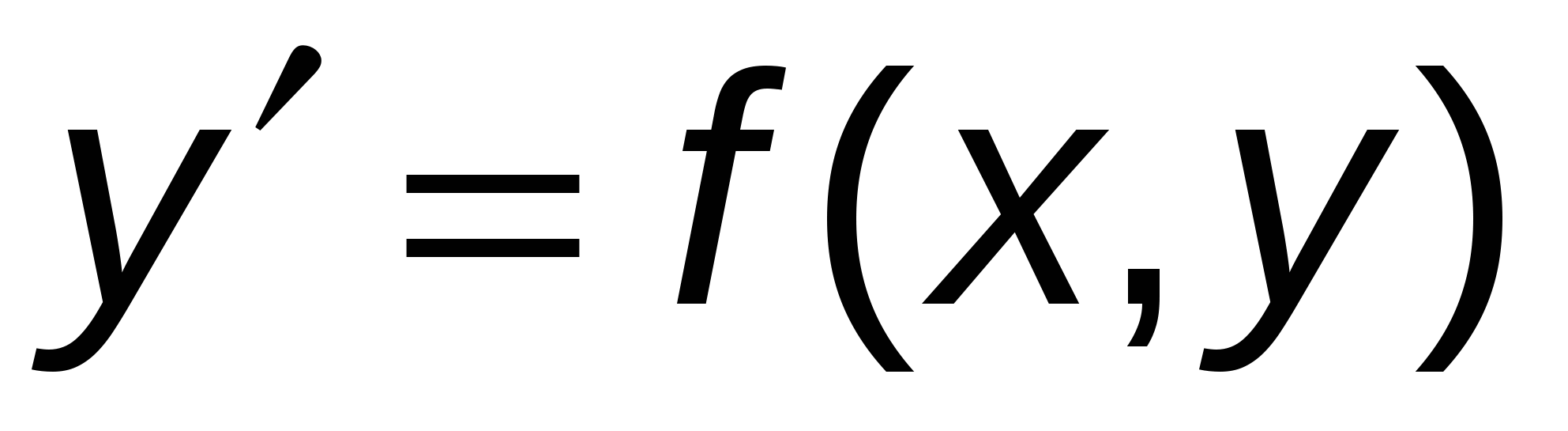 в точке в точке 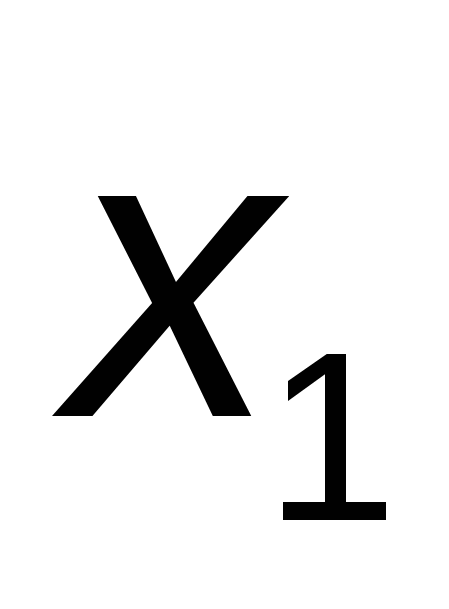 возьмем ординату возьмем ординату 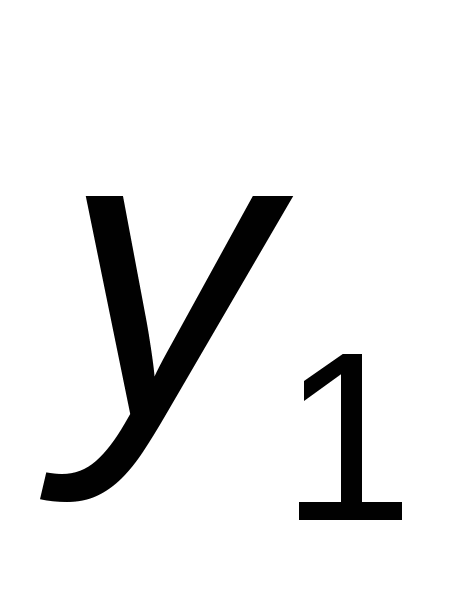 точки пересечения касательной с прямой точки пересечения касательной с прямой 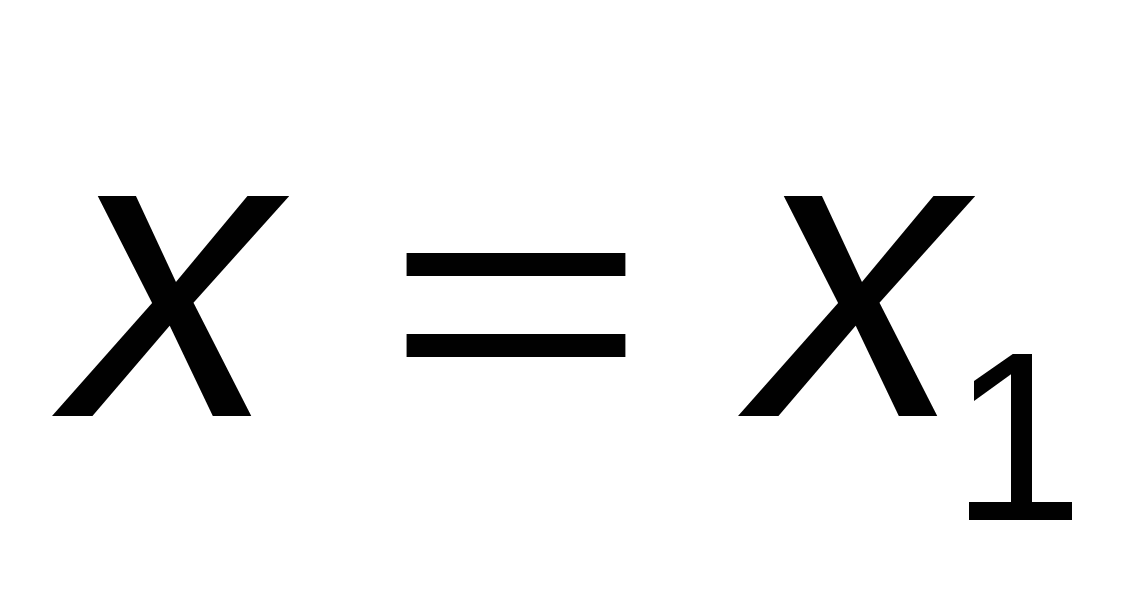 , т. е. , т. е.
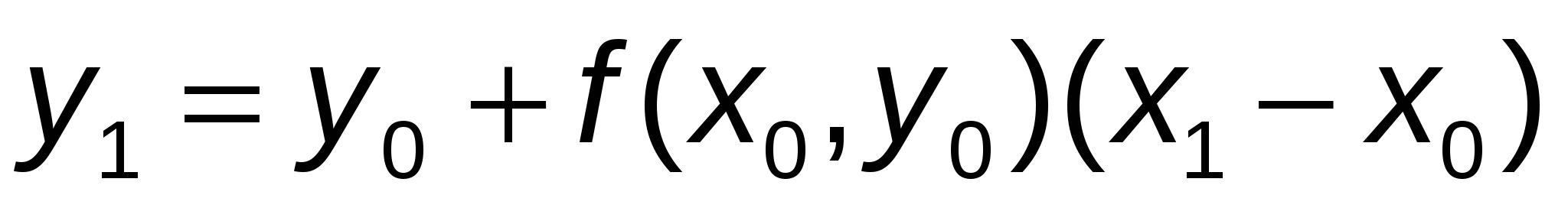
или  . .
Через точку 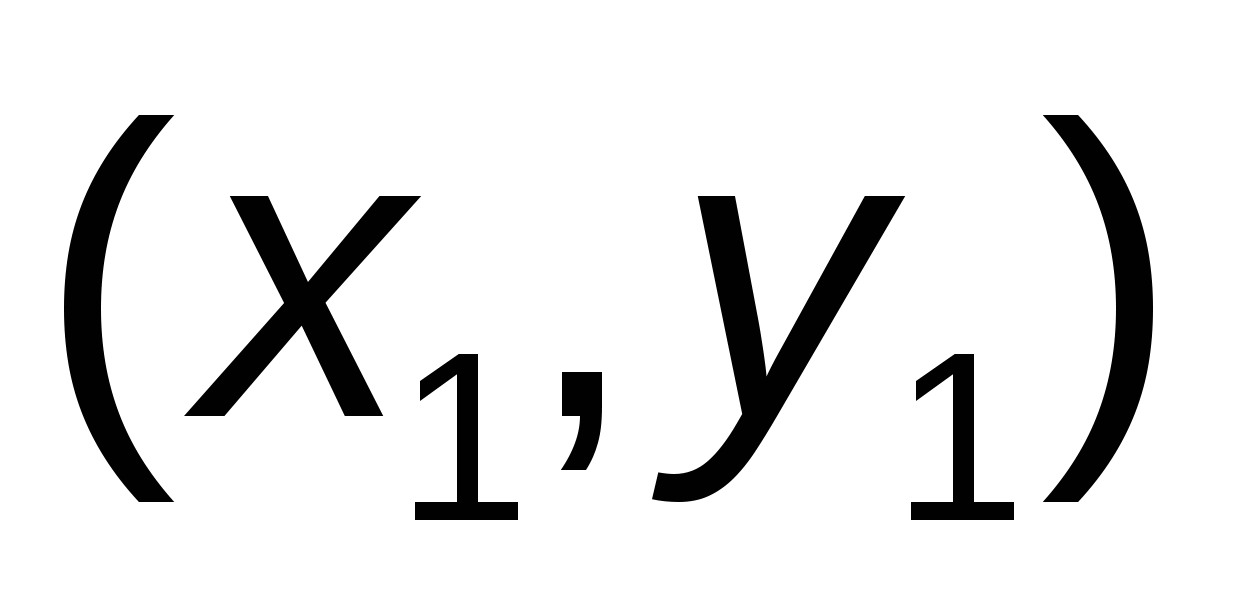 проведем прямую с угловым коэффициентом проведем прямую с угловым коэффициентом 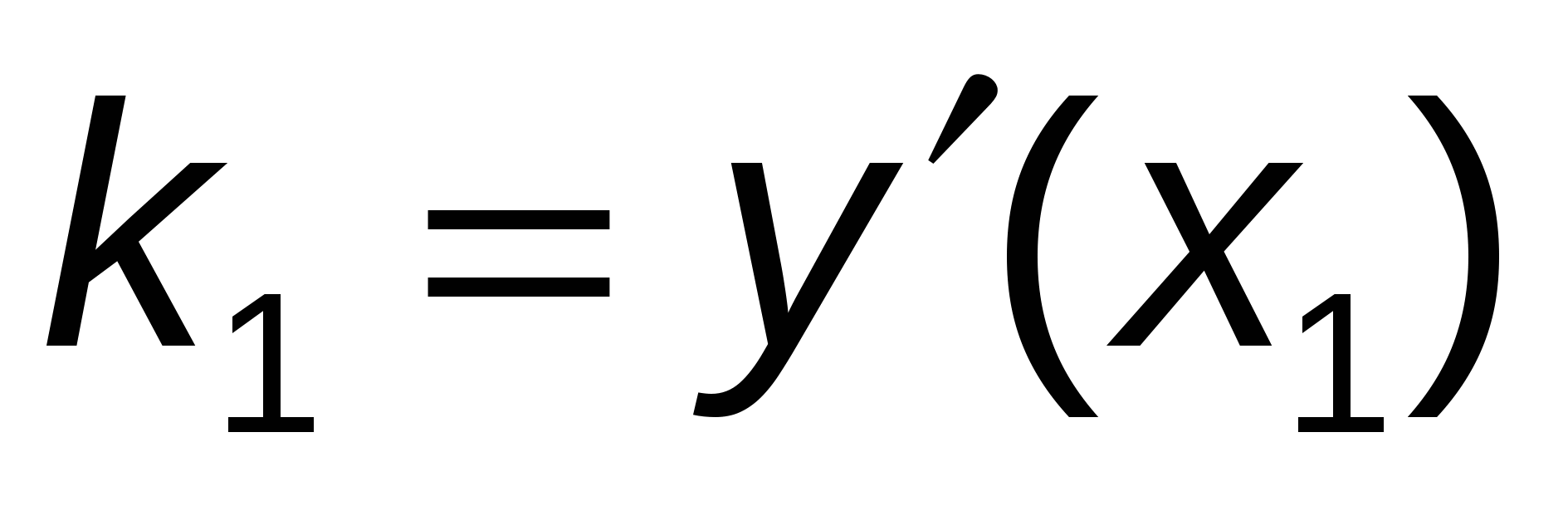 , где , где 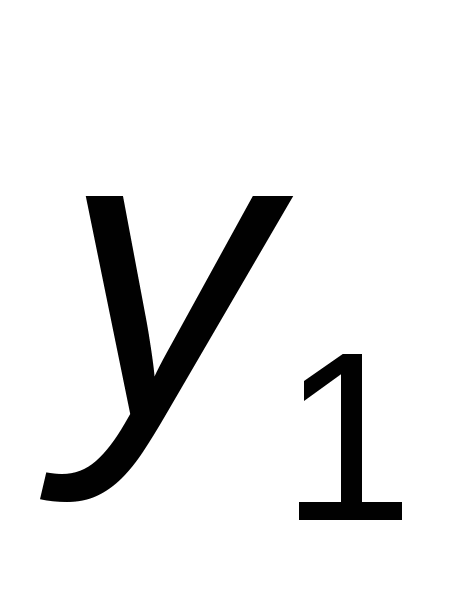 определен только что выше: определен только что выше: 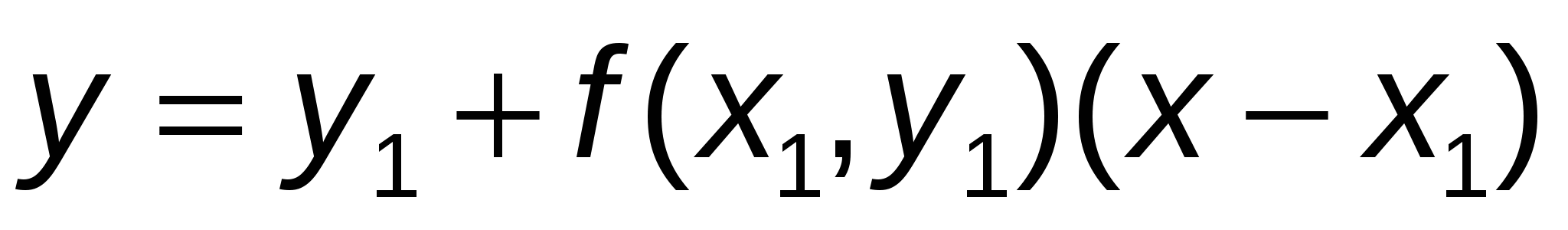 . .
Находим точку пересечения полученной прямой с прямой 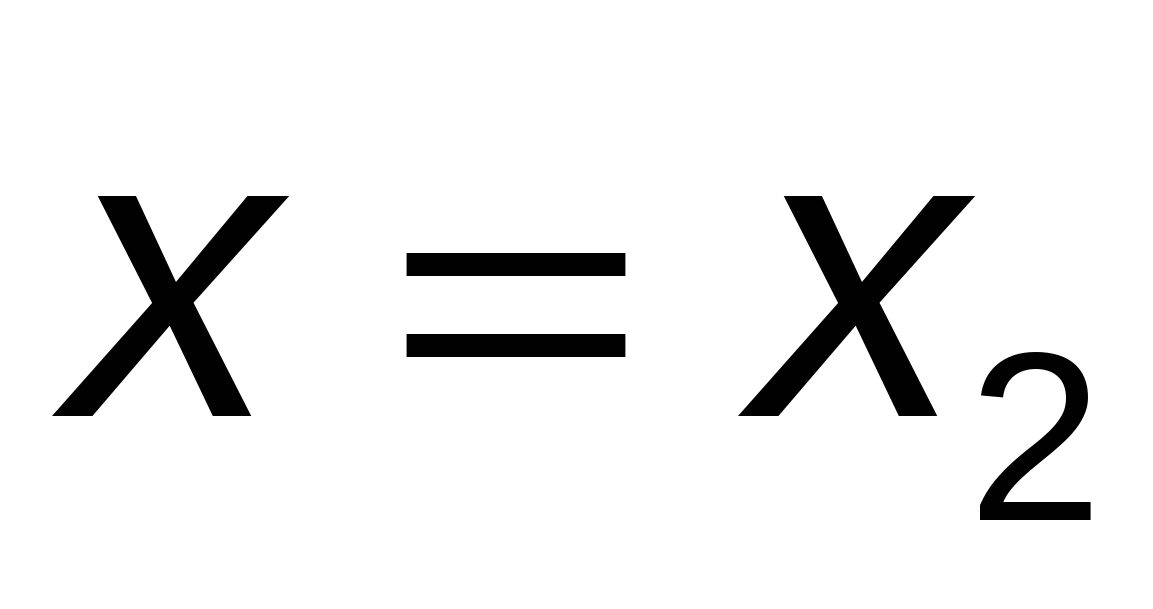 , ,
ордината этой точки: 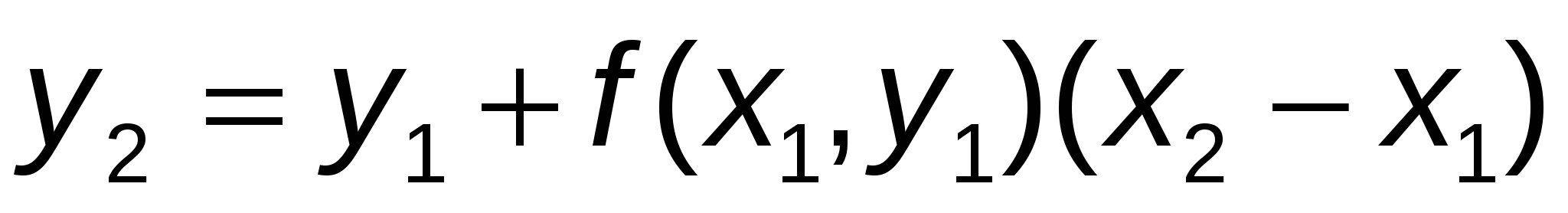 , ,
или 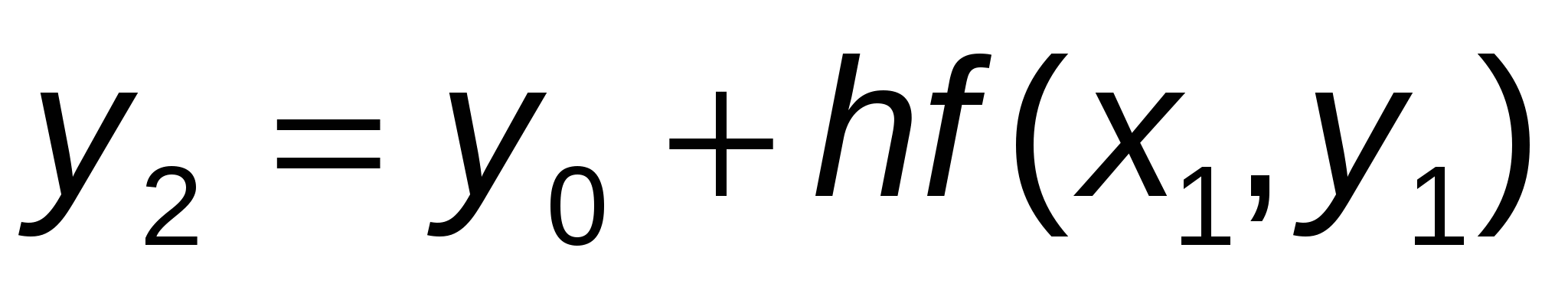 . .
Продолжая этот процесс, получаем семейство отрезков прямых:
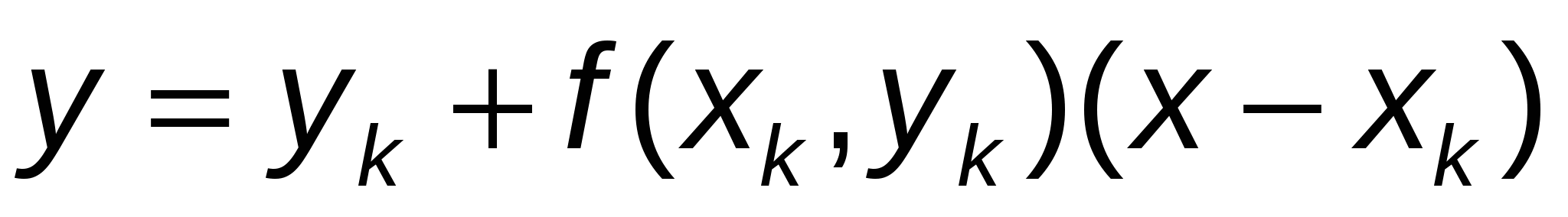 , ,
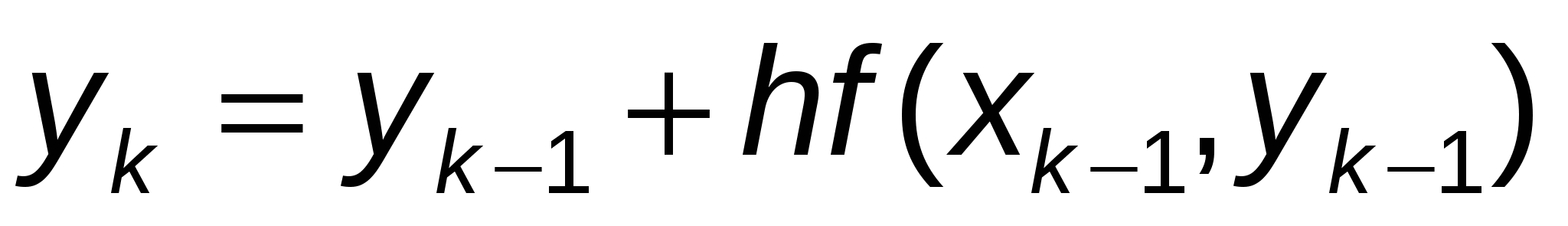 , (9) , (9)
где 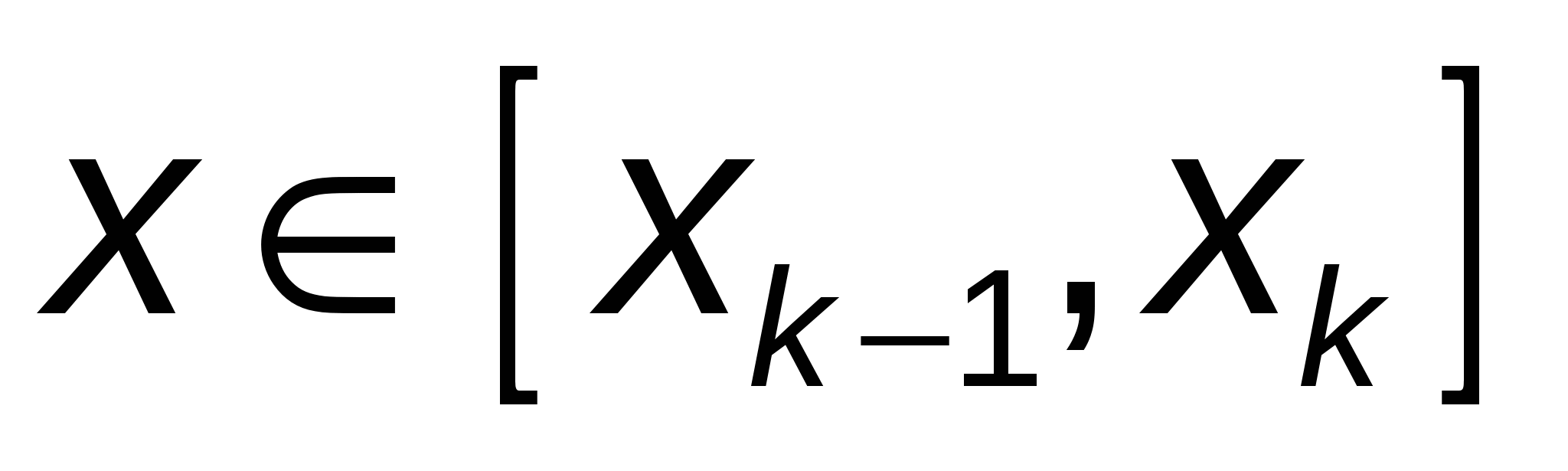 , , 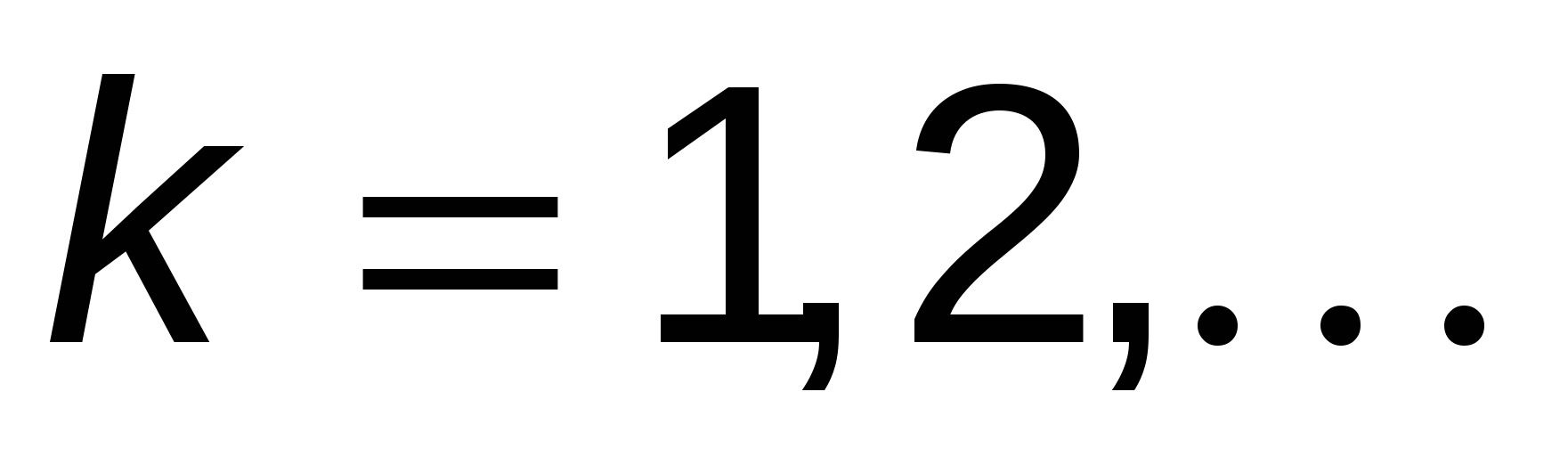
Эти отрезки образуют ломаную, называемую ломаной Эйлера. Она является приближенным решением исходной задачи (1) методом ломаных Эйлера.
Метод Эйлера обладает удовлетворительной точностью лишь при достаточно малых 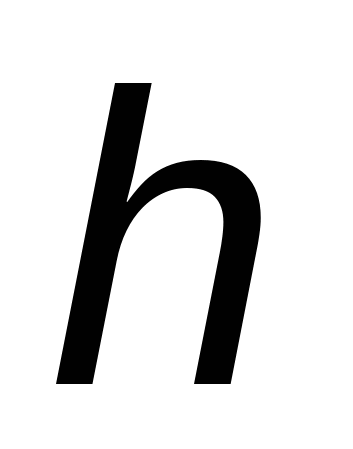 . Действительно, разложим точное решение уравнения (1) в ряд Тейлора в окрестности узла . Действительно, разложим точное решение уравнения (1) в ряд Тейлора в окрестности узла 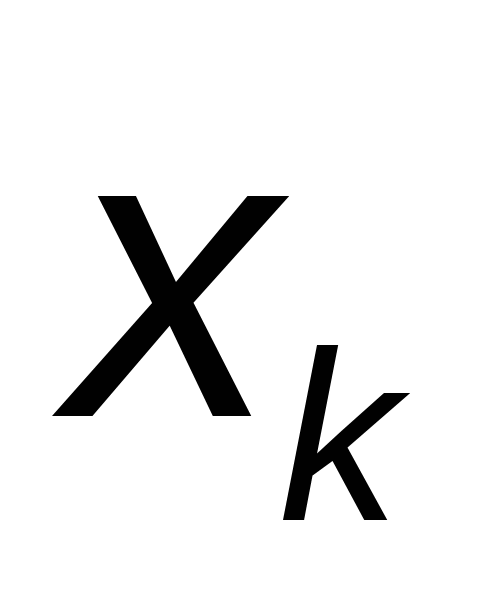 : :
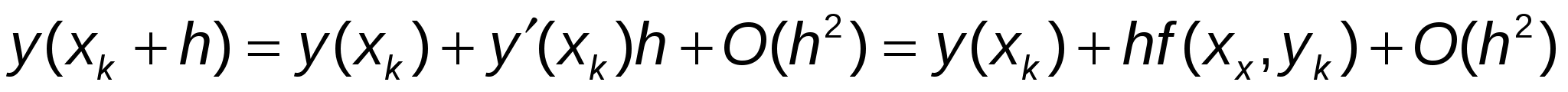 . .
Сравнив полученное выражение с формулой (9), приходим к выводу, что погрешность приближенного метода Эйлера 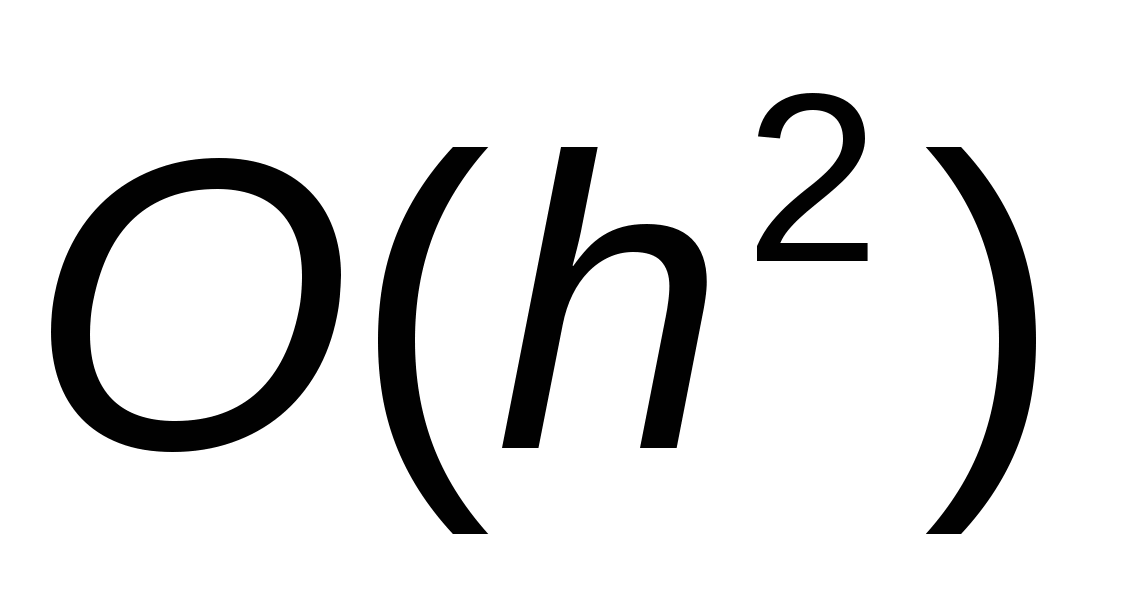 . .
Отметим, что особенностью метода Эйлера является то, что на каждом шаге интегрирования приближенное значение 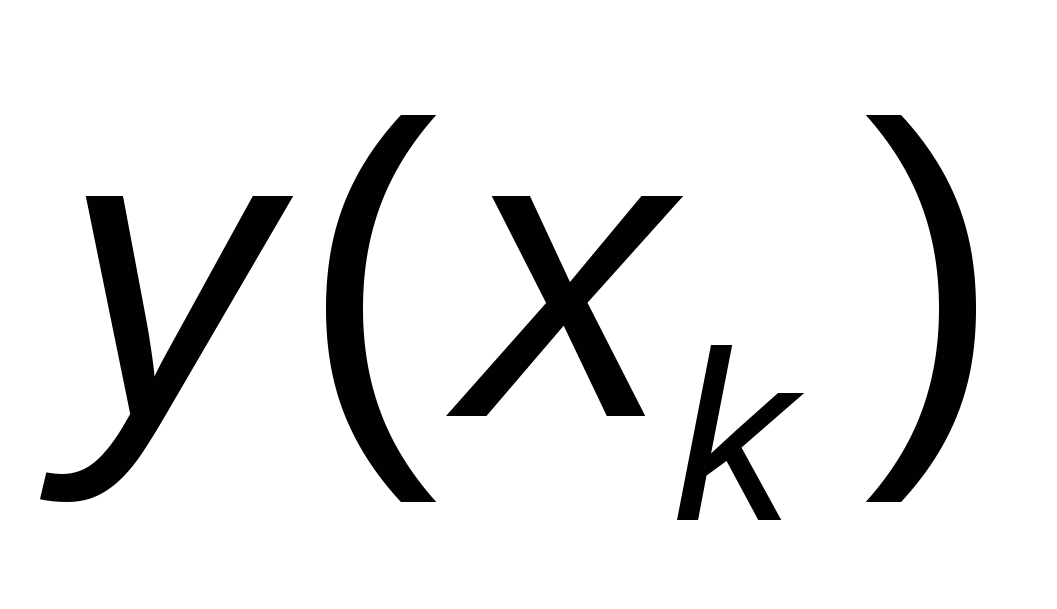 определяется через определяется через 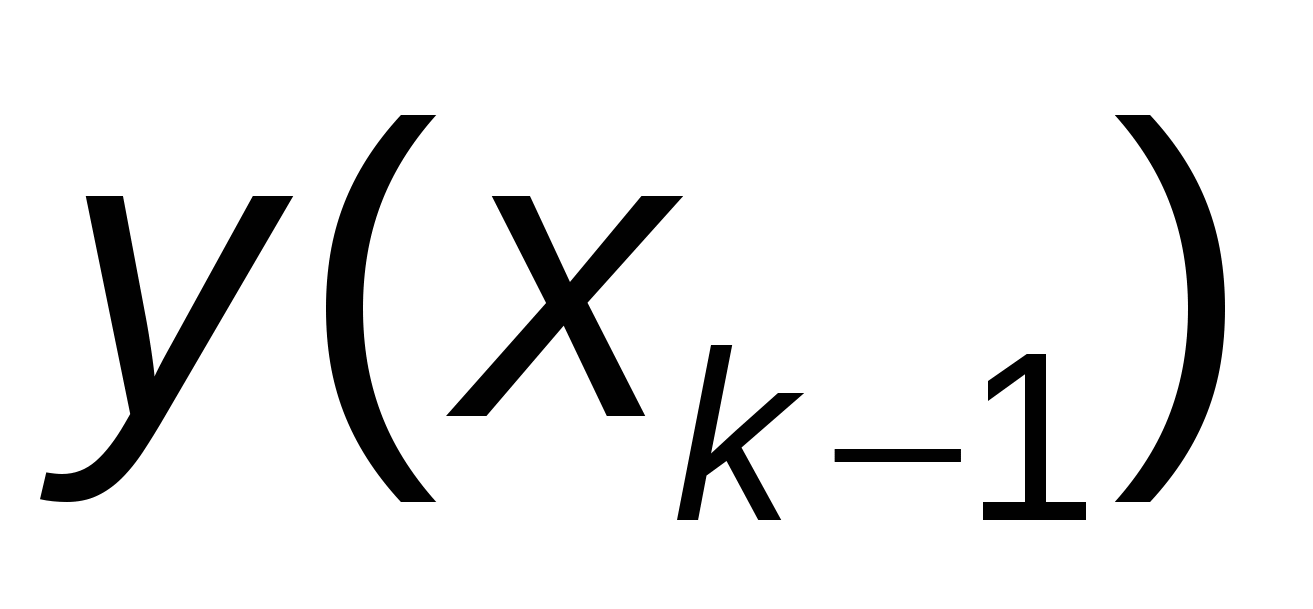 . Таким образом, на каждом отрезке . Таким образом, на каждом отрезке 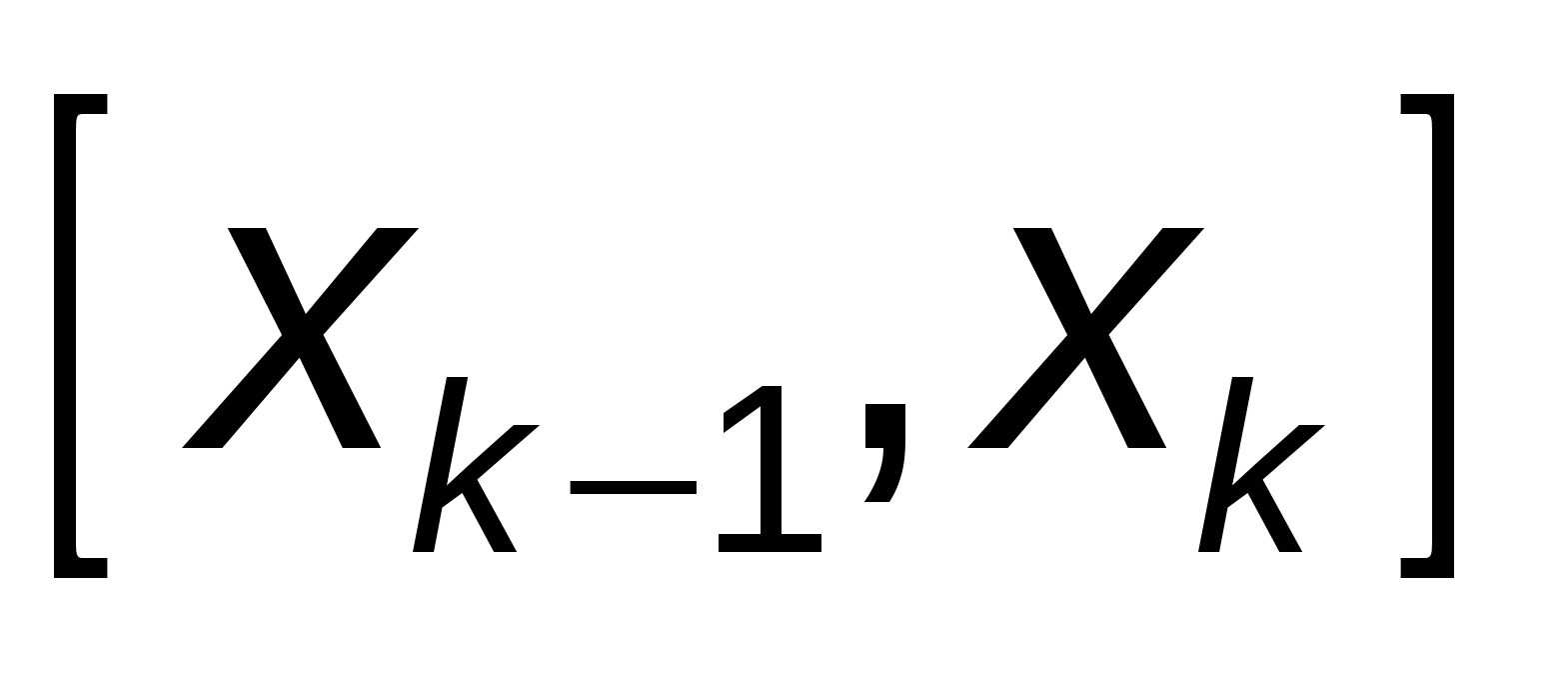 решается задача Коши: решается задача Коши:
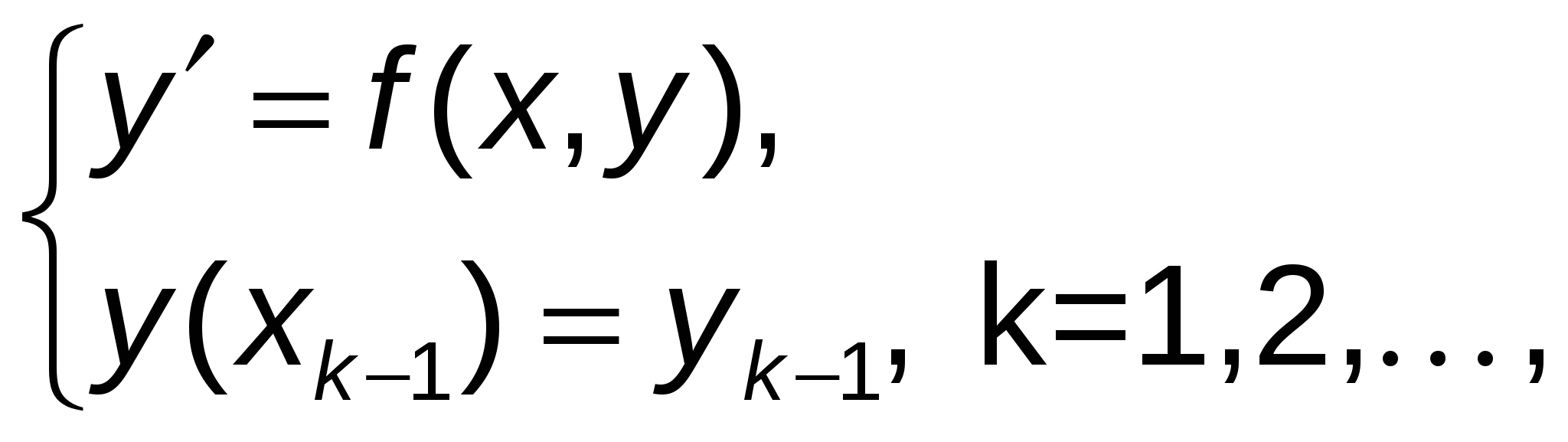
что удобно с точки зрения вычислений.
Метод Эйлера является
простейшим численным методом
интегрирования дифференциального уравнения.
Его недостатки:
-
малая точность;
-
систематическое накопление ошибок:
погрешность каждого нового шага
систематически возрастает.
Существуют различные уточнения метода Эйлера, повышающие его точность
8.2. Модификации метода Эйлера
Более точным является усовершенствованный метод Эйлера, при котором сначала вычисляют промежуточные значения:
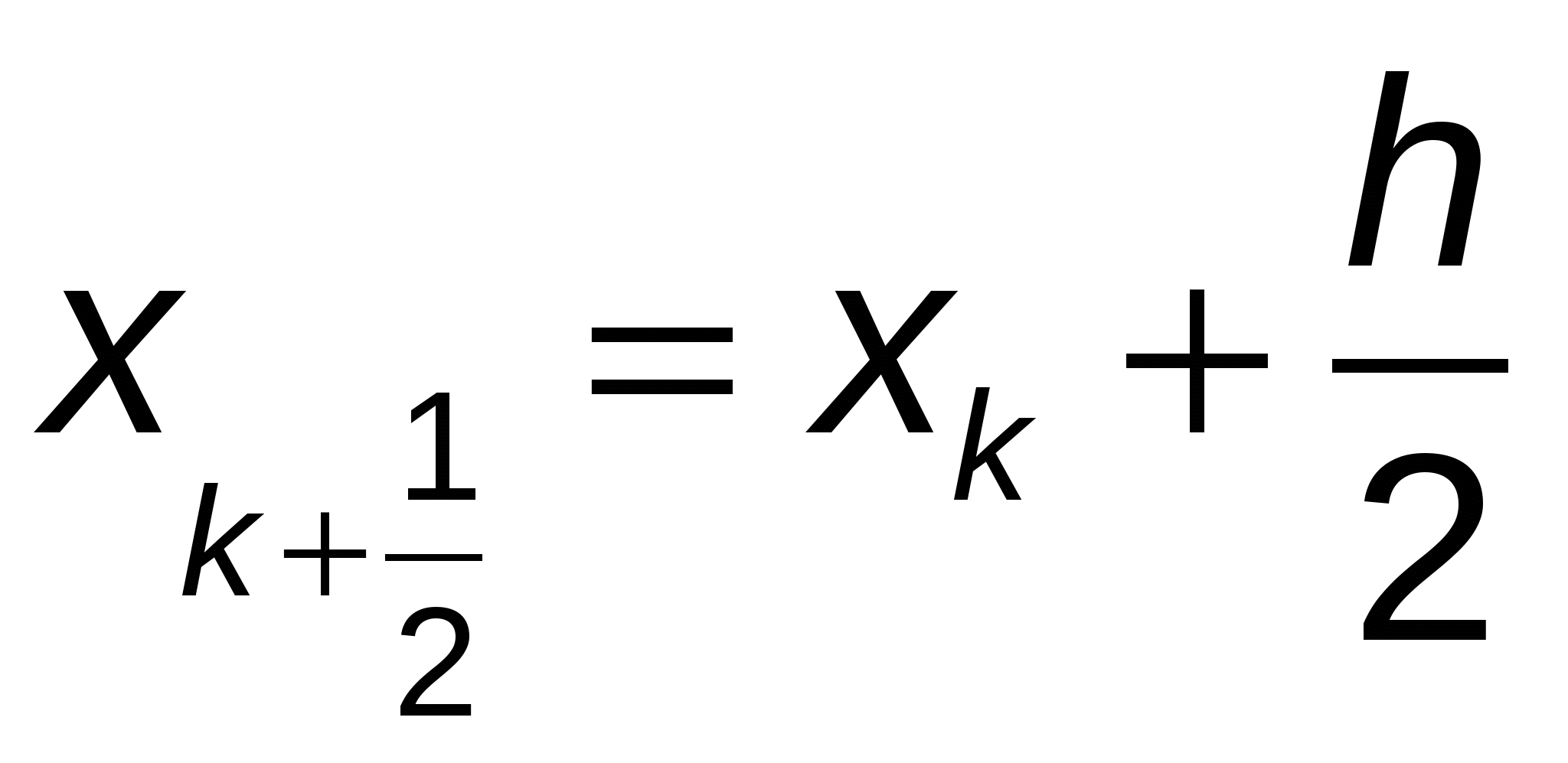 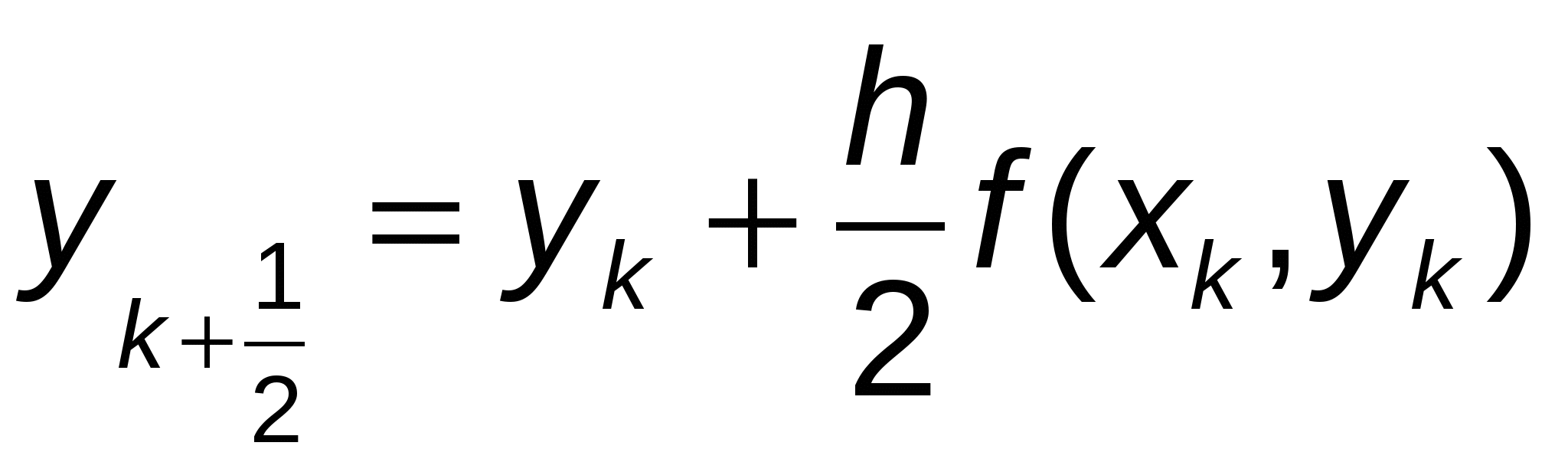 , ,
а затем полагают 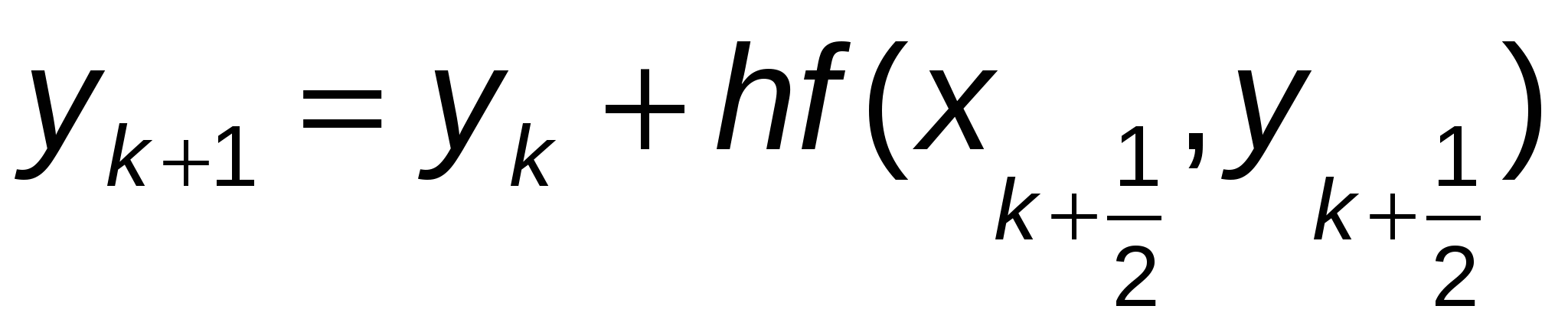 . (10) . (10)
Получим оценку точности построенного метода. Для этого разложим точное решение (1) в ряд Тейлора в окрестности точки 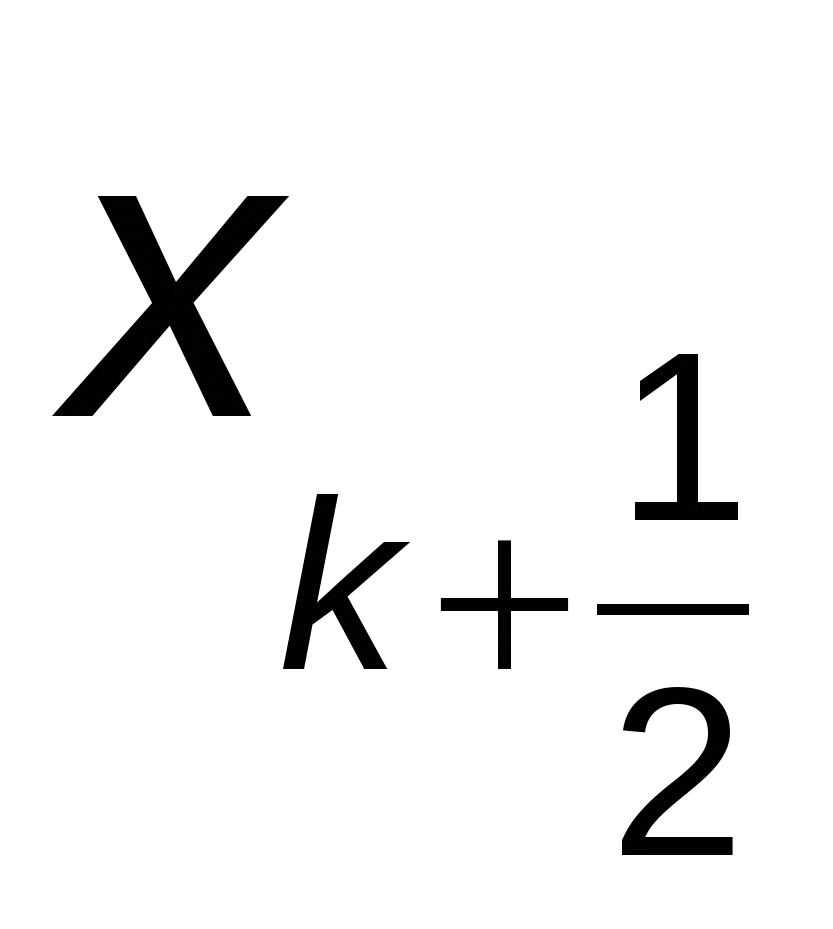 , получим: , получим:
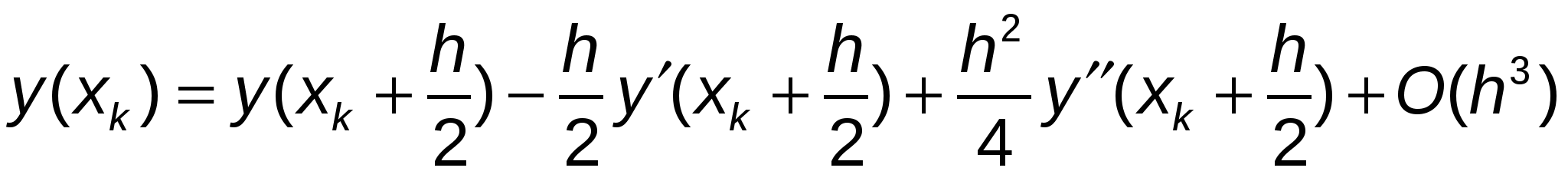 , ,
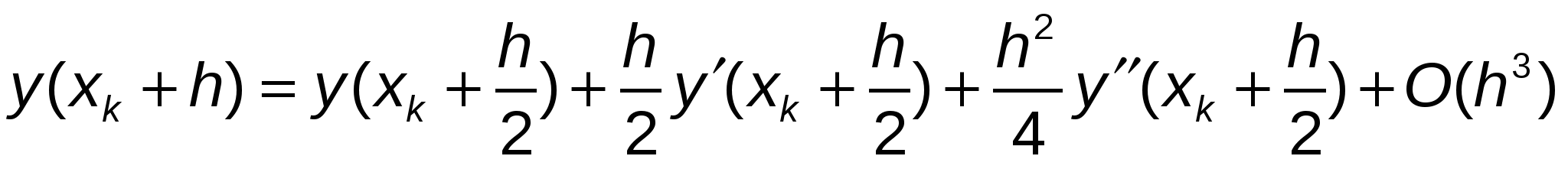 , ,
отсюда 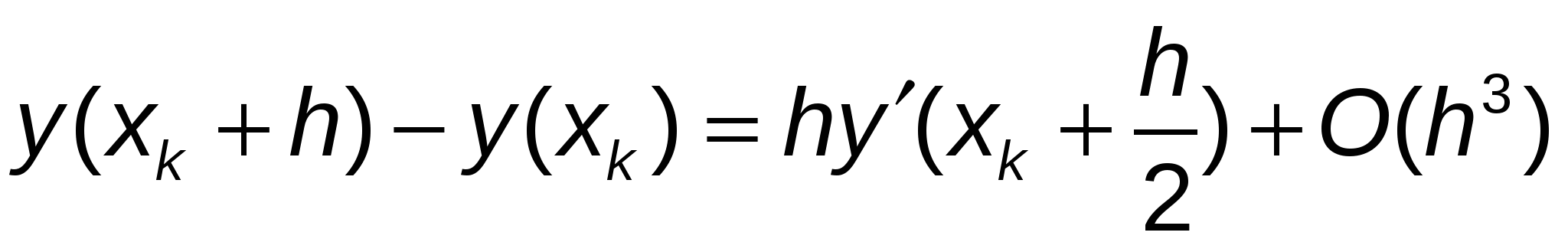
или 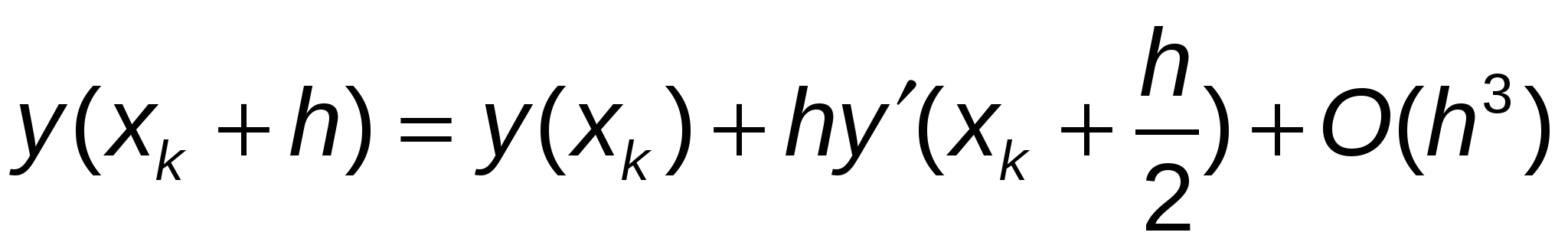 , ,
а это значит 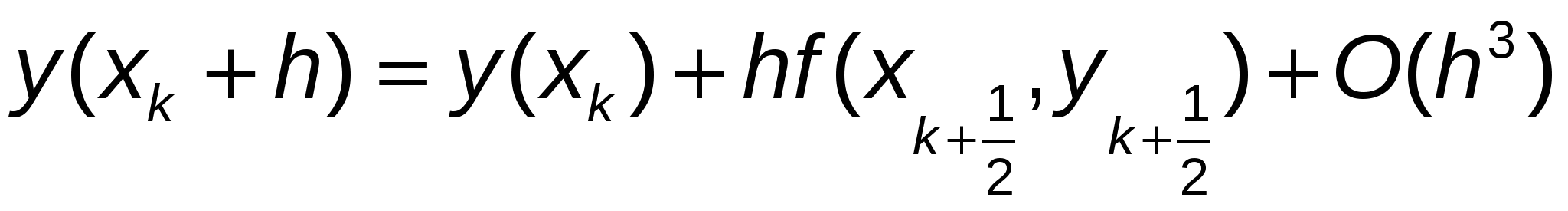 . .
Сравнив полученную формулу с (10), получим погрешность 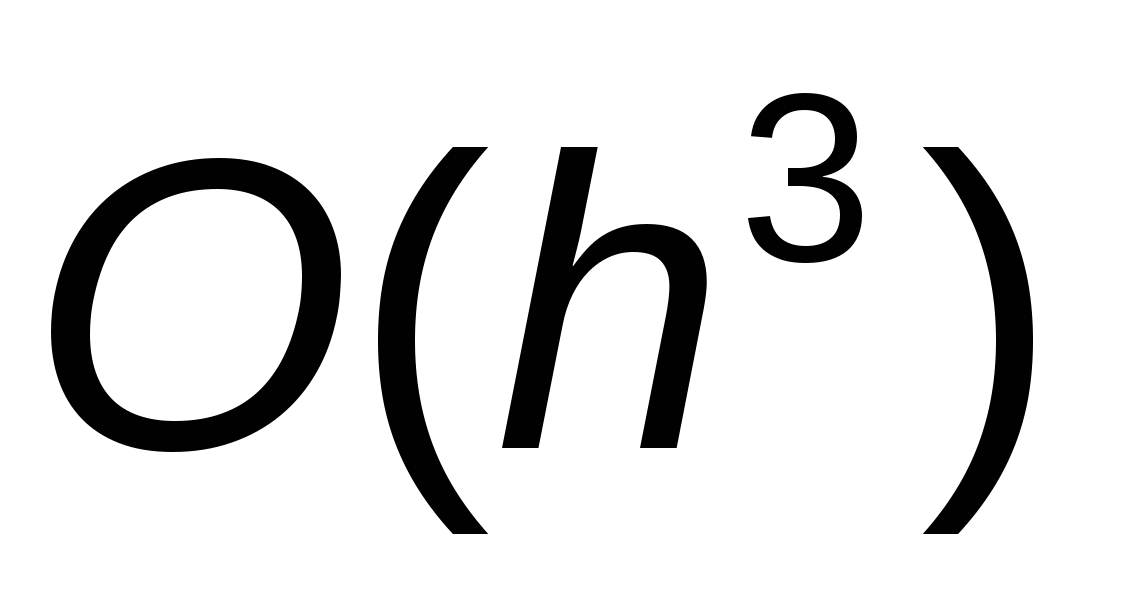 . .
Другой модификацией метода Эйлера является усовершенствованный метод Эйлера — Коши, при котором сначала определяется «грубое» приближение решения: 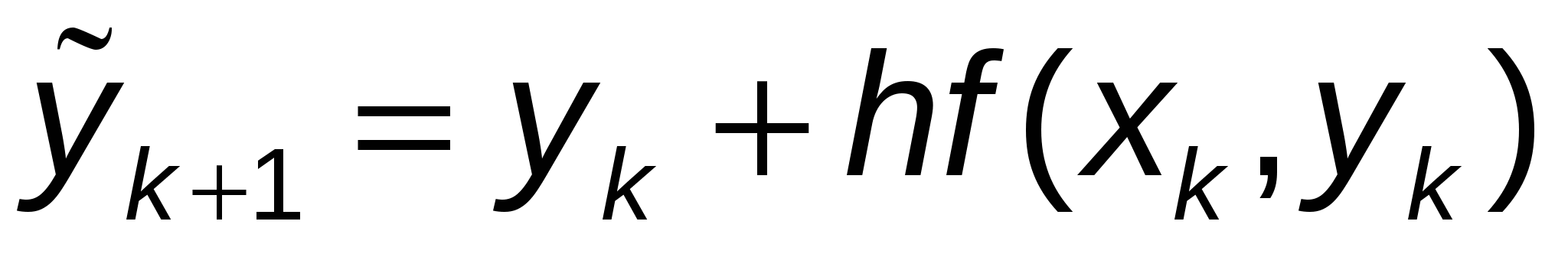 . .
Исходя из данного выражения, вычисляют: 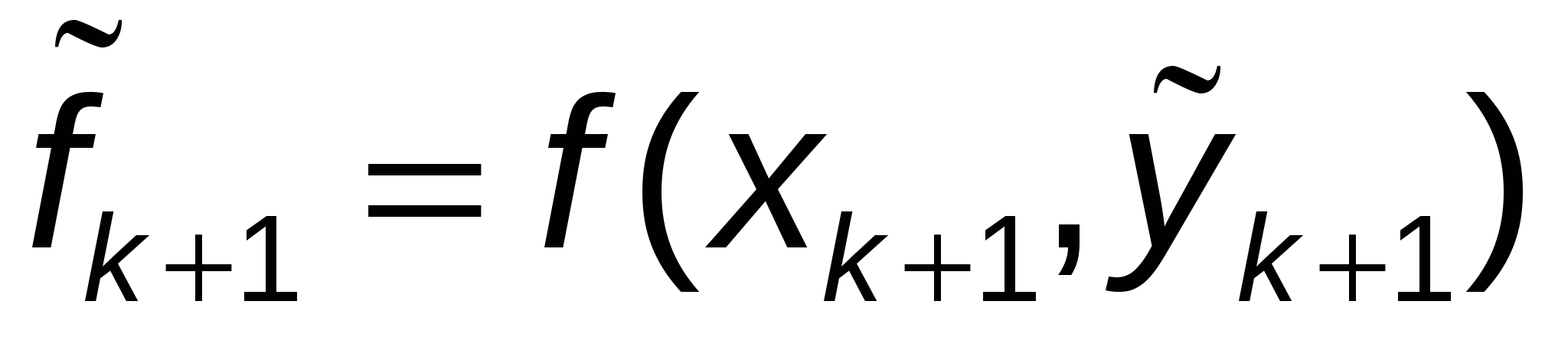 . .
Затем приближенно полагают 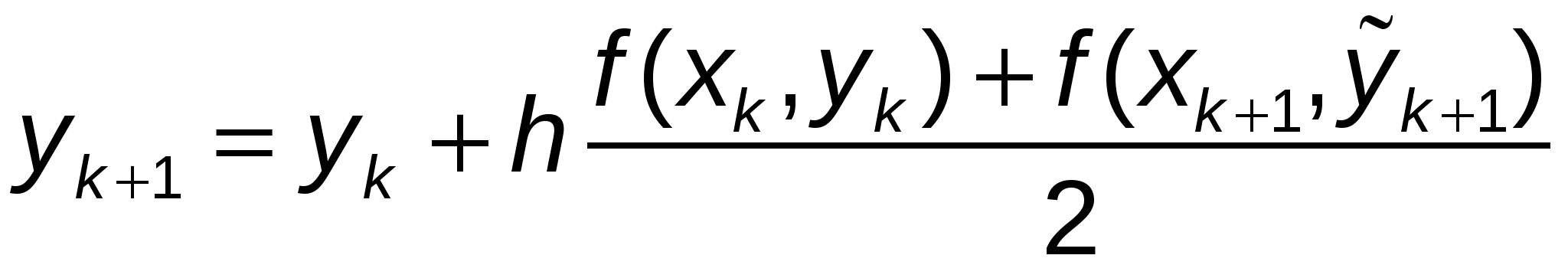 . (11) . (11)
Усовершенствованный метод Эйлера — Коши можно еще более уточнить, применяя итерационную обработку каждого значения 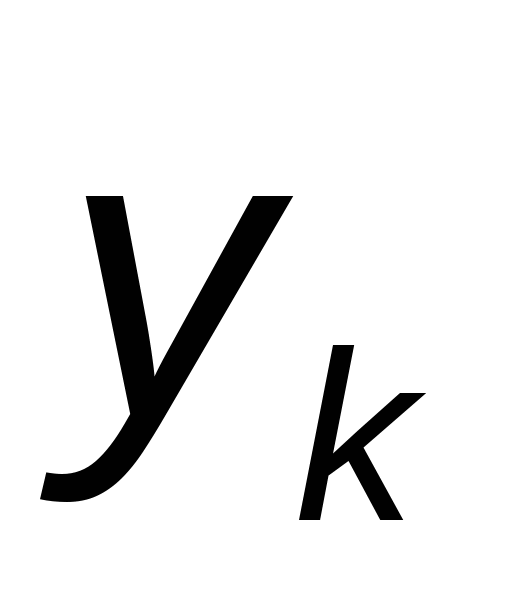 . А именно, исходя из грубого приближения . А именно, исходя из грубого приближения 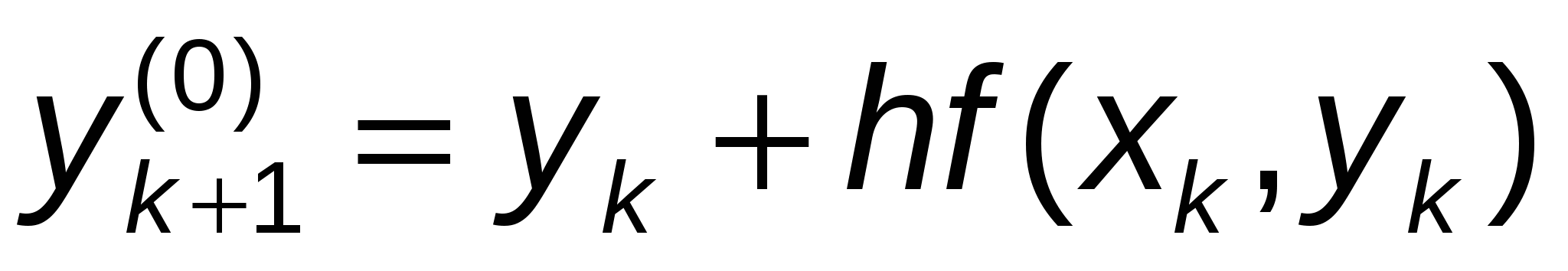 , ,
строится итерационный процесс 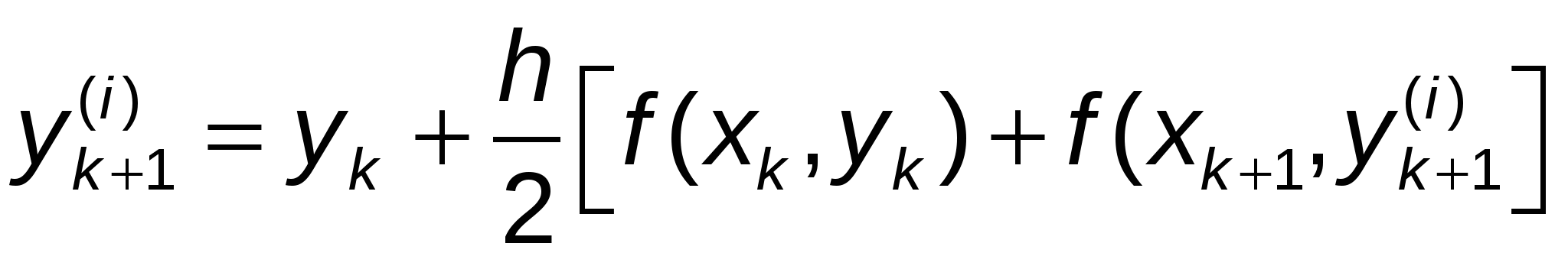 , (12) , (12)
Итерирации продолжаются до тех пор, пока некоторые два последовательных приближения 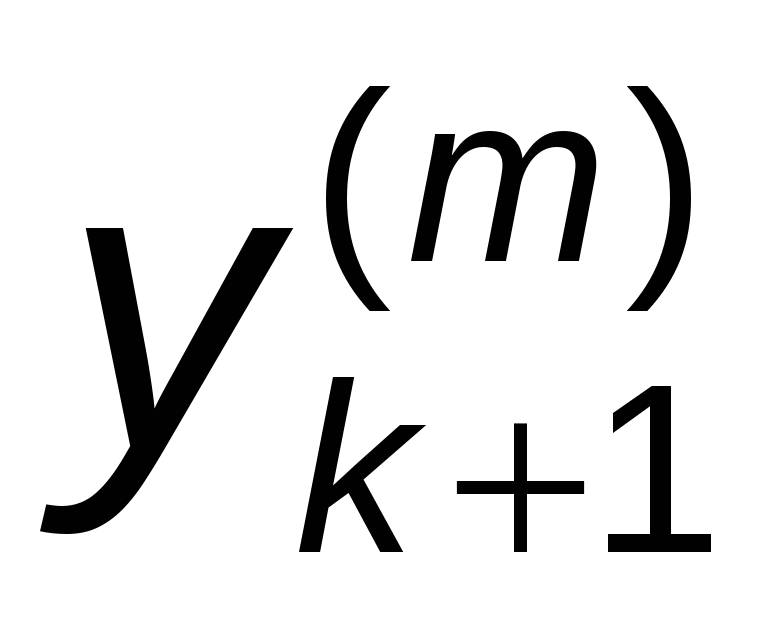 и и 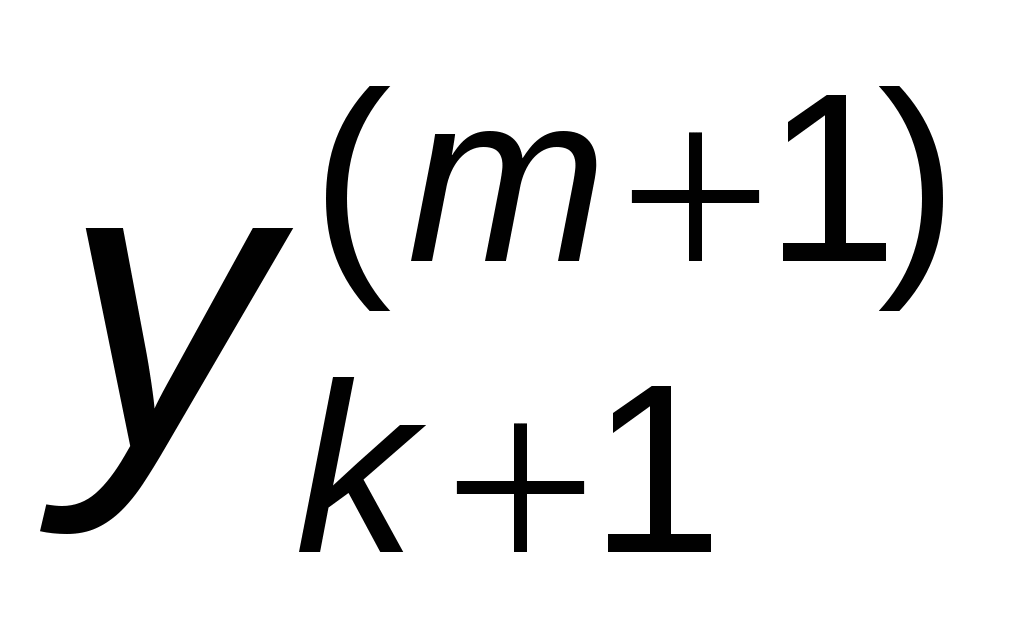 станут меньше заданной погрешности. станут меньше заданной погрешности.
После этого принимается 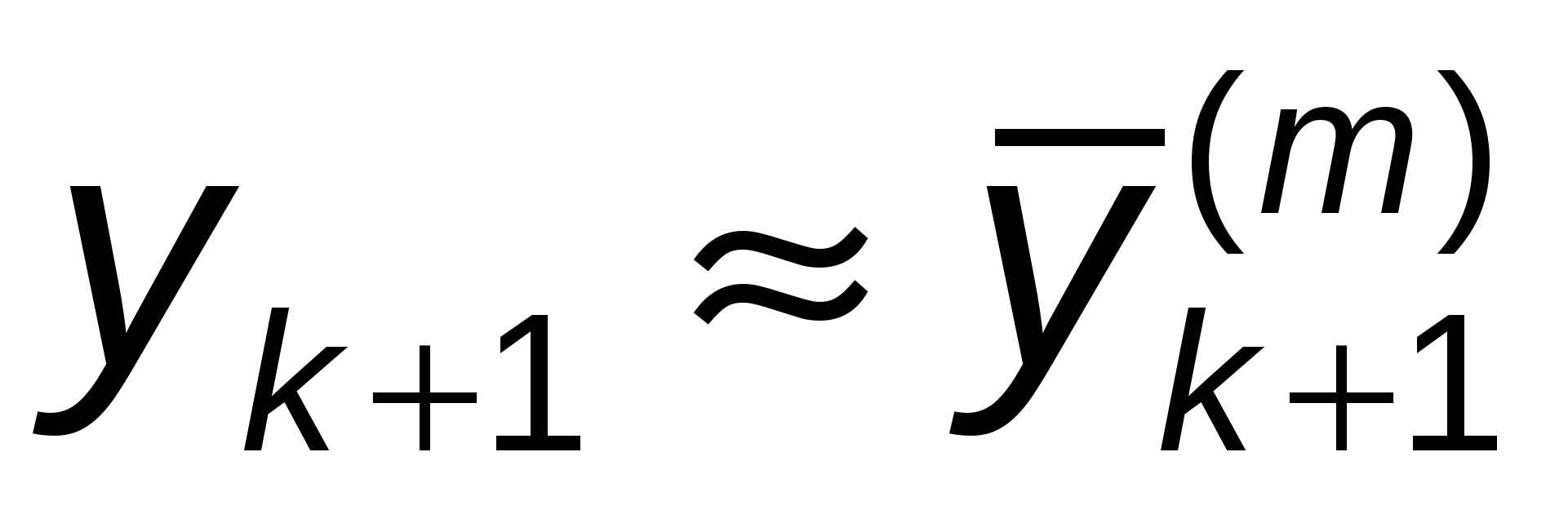 , ,
где 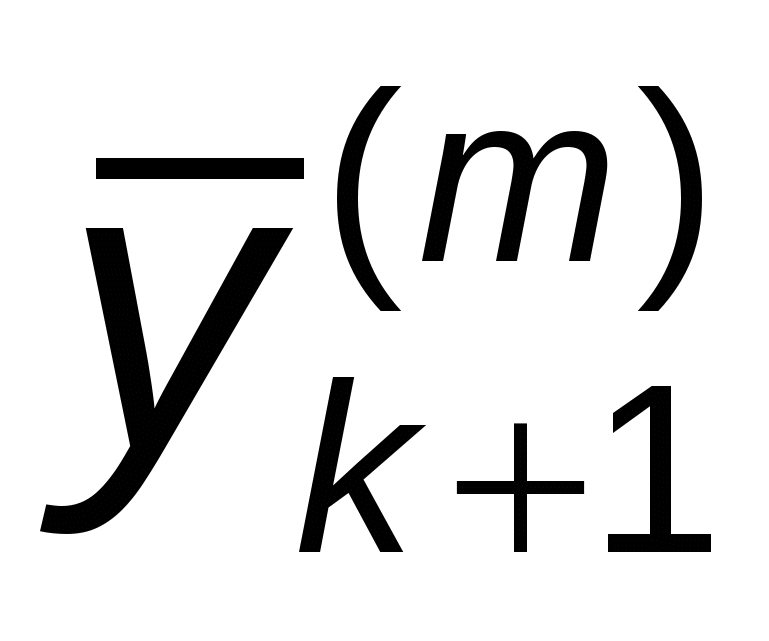 — общая часть приближений — общая часть приближений 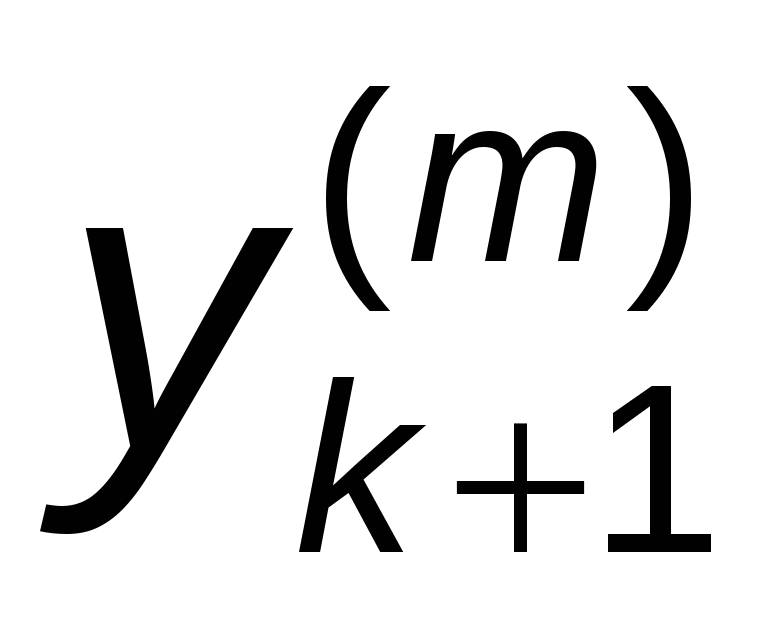 и и 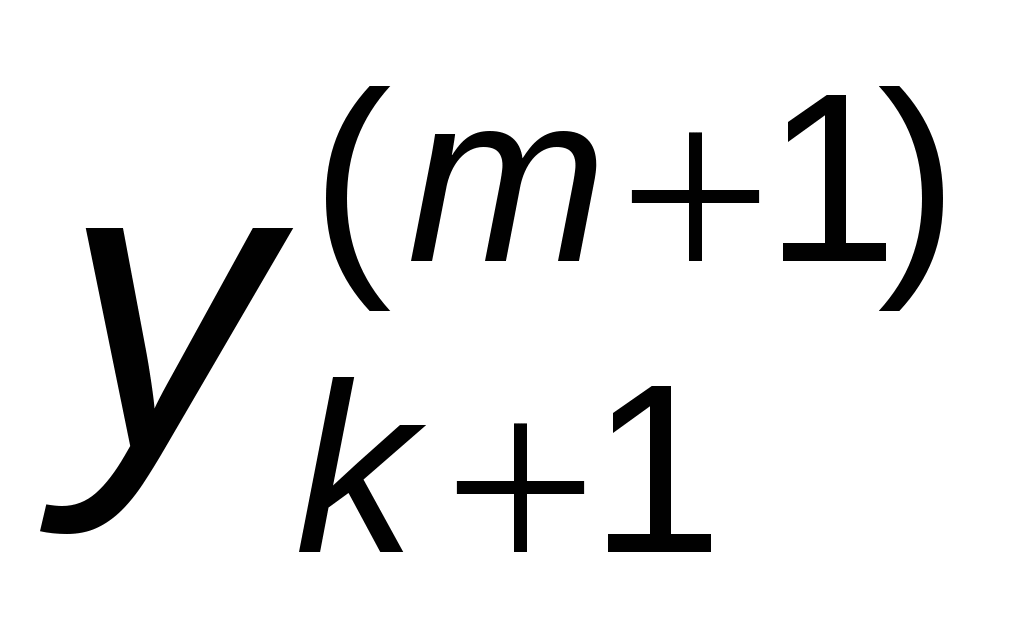 . .
Отметим, что метод Эйлера с итерационной обработкой дает на каждом шаге погрешность порядка 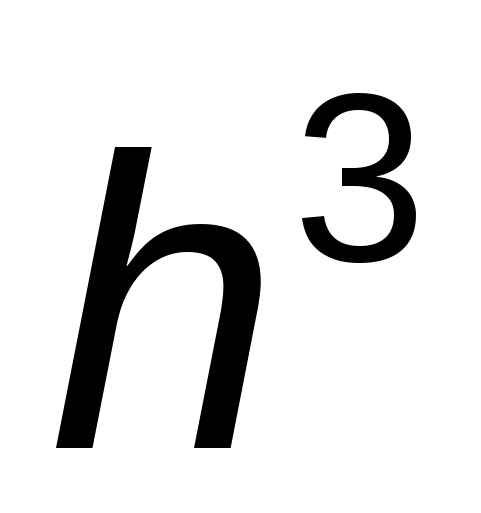 и нередко применяется в вычислительной практике. и нередко применяется в вычислительной практике.
8.3. Метод Рунге — Кутта
Этот метод является одним из методов повышенной точности и относится к одношаговым методам численного интегрирования задачи Коши (1), т. е. к таким методам, которые позволяют найти приближенное значение решения заданной задачи в узле 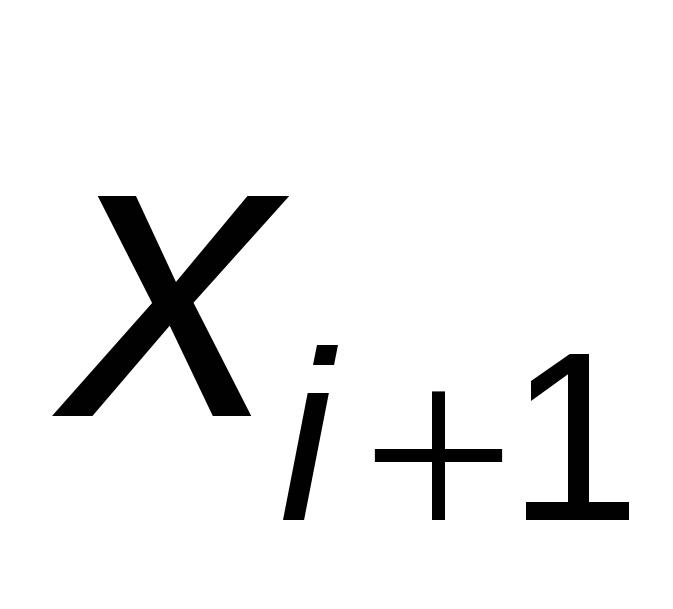 по информации об этом решении лишь в одной предыдущей узловой точке по информации об этом решении лишь в одной предыдущей узловой точке 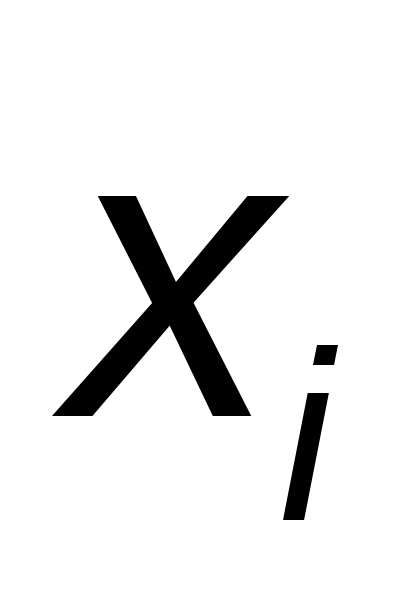 . .
Метод Рунге — Кутта является одним из самых распространенных методов решения задач с начальными условиями для обыкновенных дифференциальных уравнений.
Метод описывается следующими шестью соотношениями:
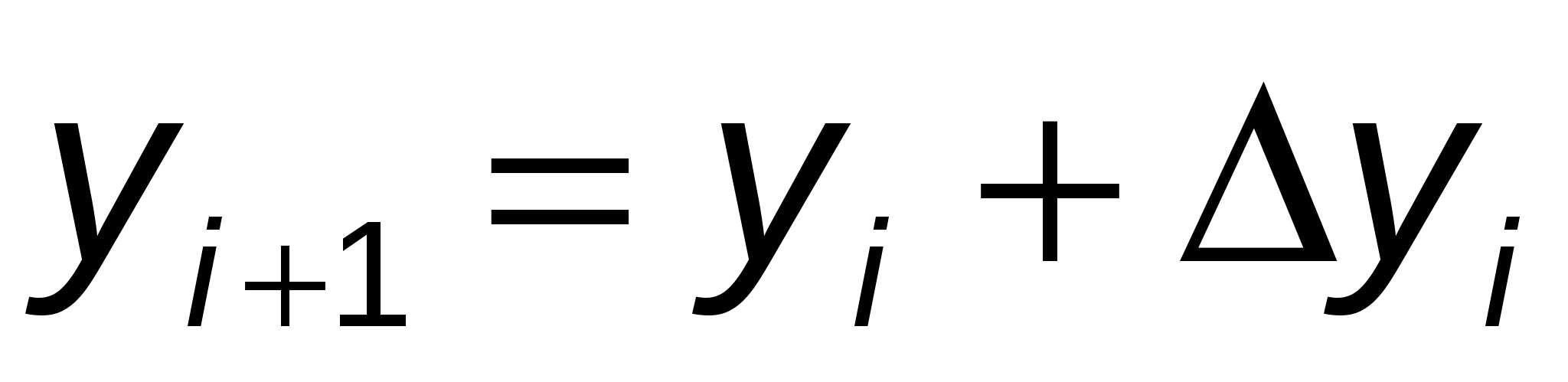 , , 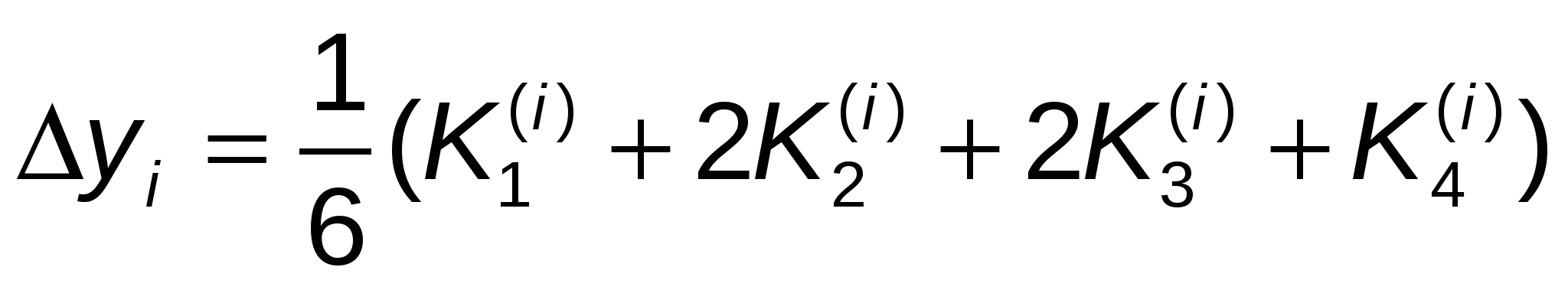 , ,
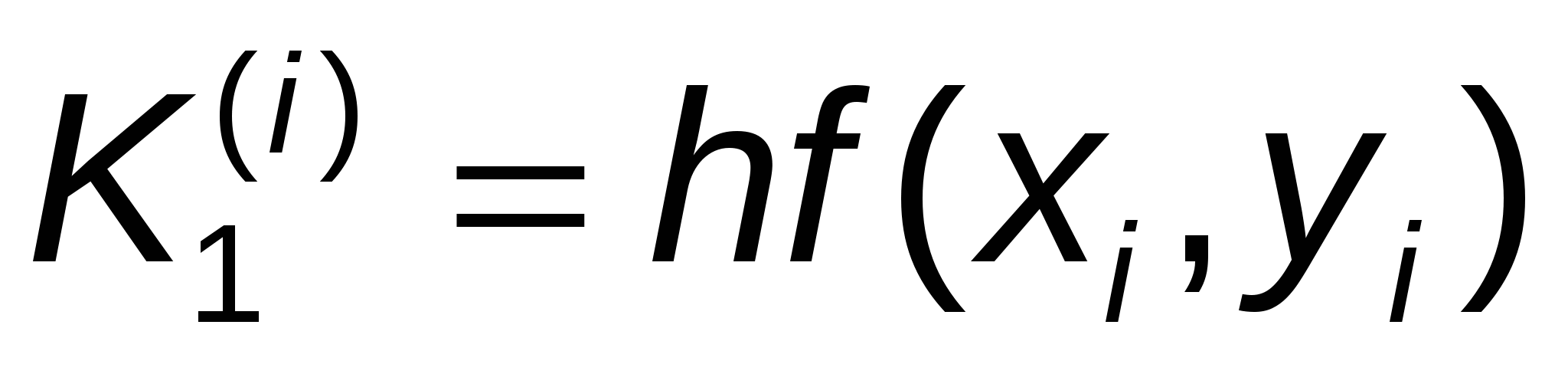 , , 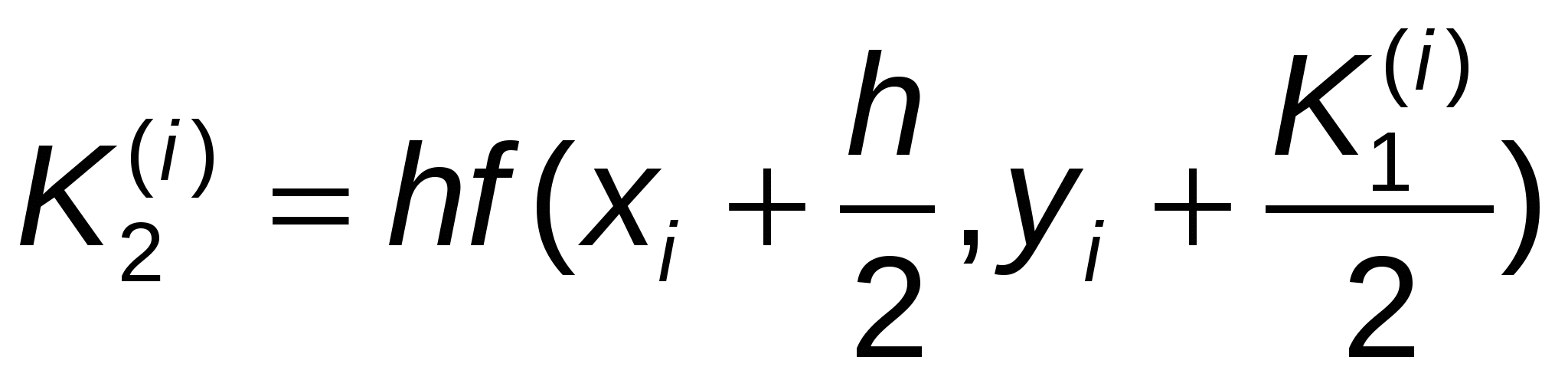 , ,
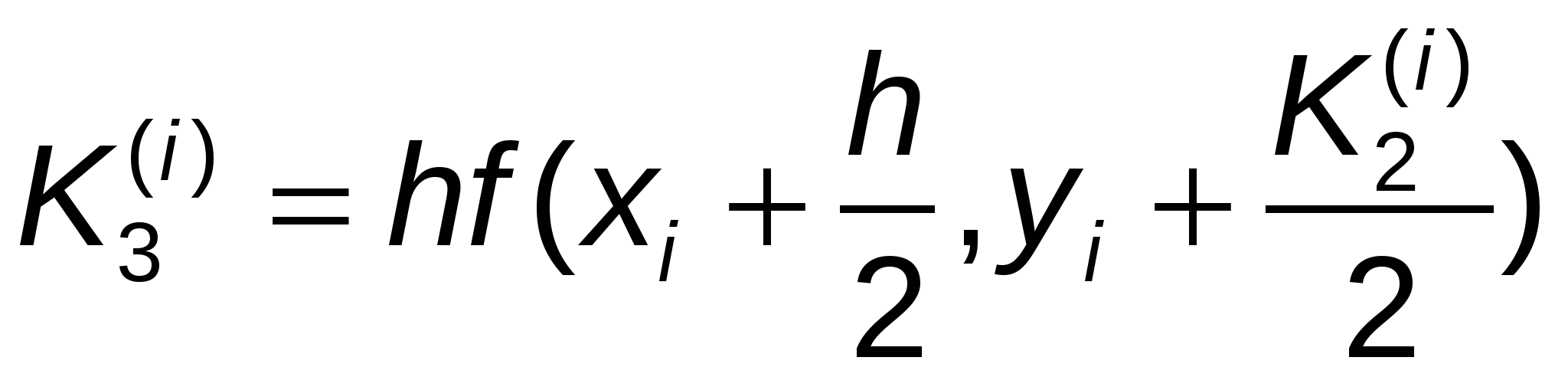 , , 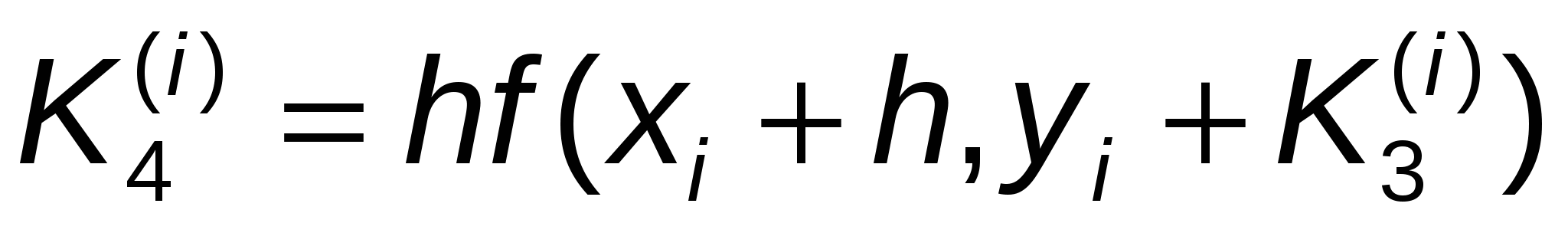 . .
Как видно, с алгоритмической точки зрения метод Рунге — Кутта не имеет принципиальных различий от метода Эйлера. Разница лишь в объеме вычислений: для получения нового значения 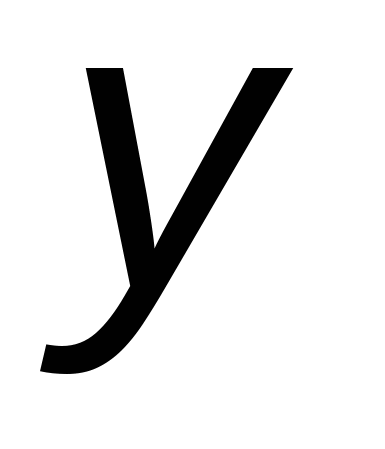 на каждом шаге необходимо проделать все действия, предусмотренные формулами выше. на каждом шаге необходимо проделать все действия, предусмотренные формулами выше.
Метод Рунге — Кутта является методом повышенной точности (он имеет четвертый порядок точности), несмотря на свою трудоемкость широко используется при численном решении уравнений с помощью компьютера.
На практике применяется следующий способ контроля точности — двойной счет. Если 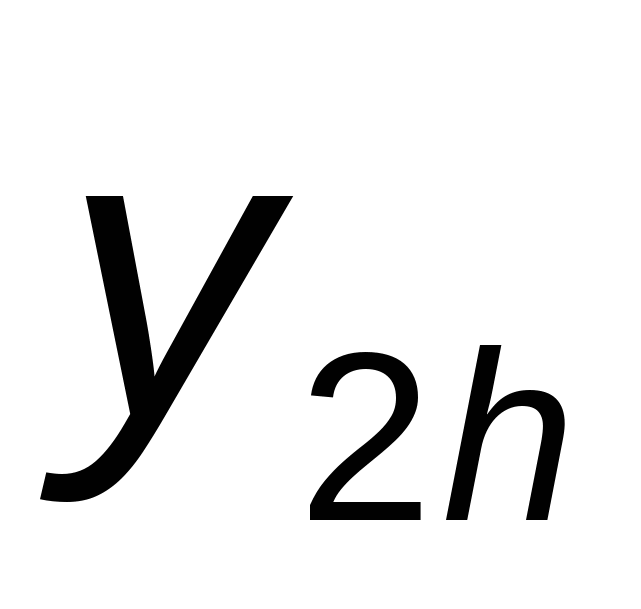 — вычисленное значение — вычисленное значение 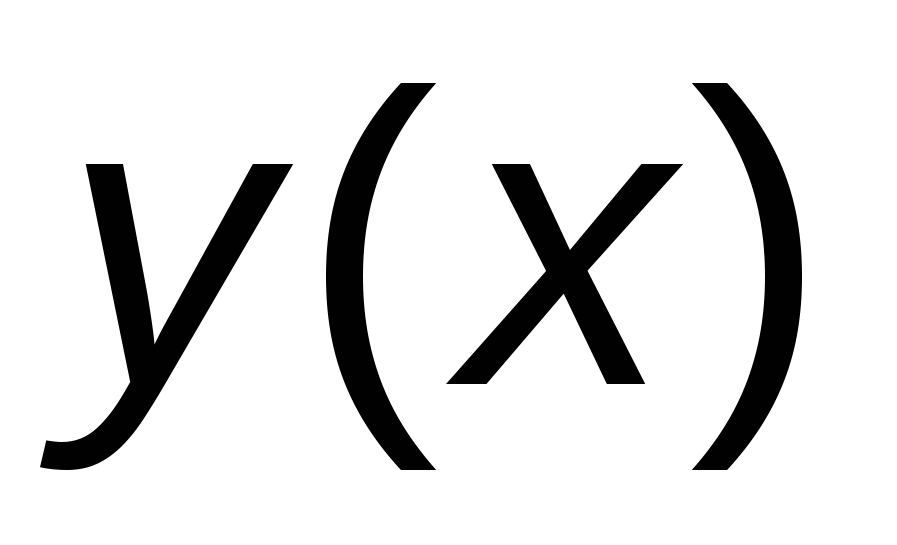 с шагом с шагом 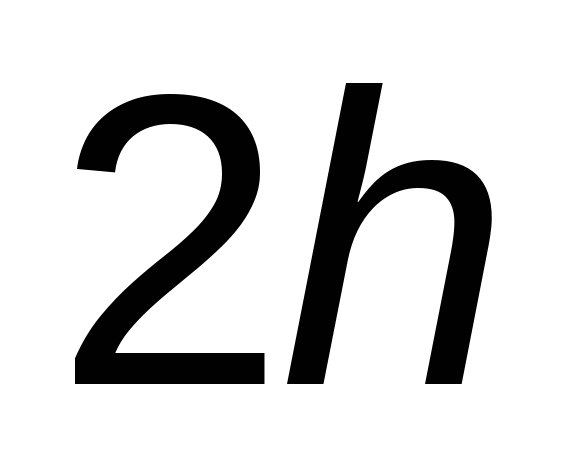 , а , а 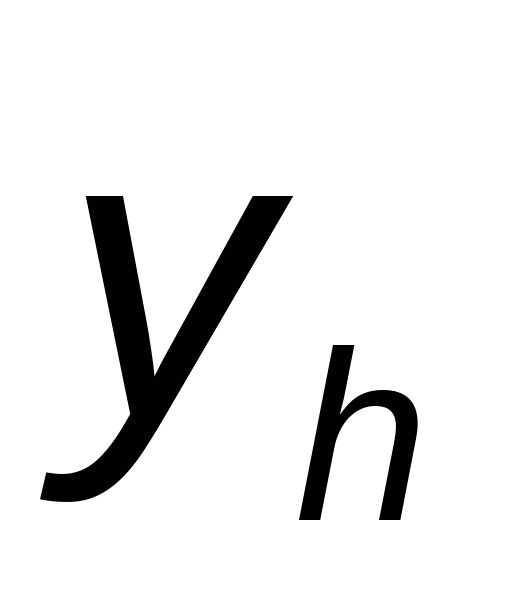 — соответствующее узловое значение, полученное с шагом — соответствующее узловое значение, полученное с шагом 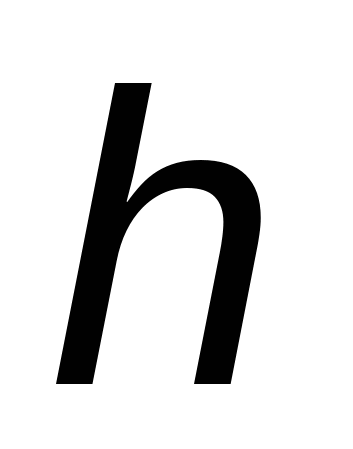 , то для ориентировочной оценки погрешности , то для ориентировочной оценки погрешности 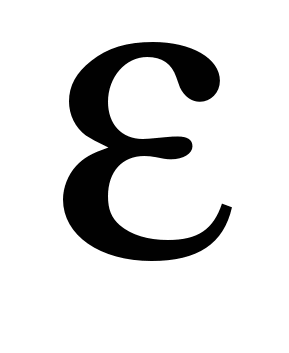 последнего значения последнего значения 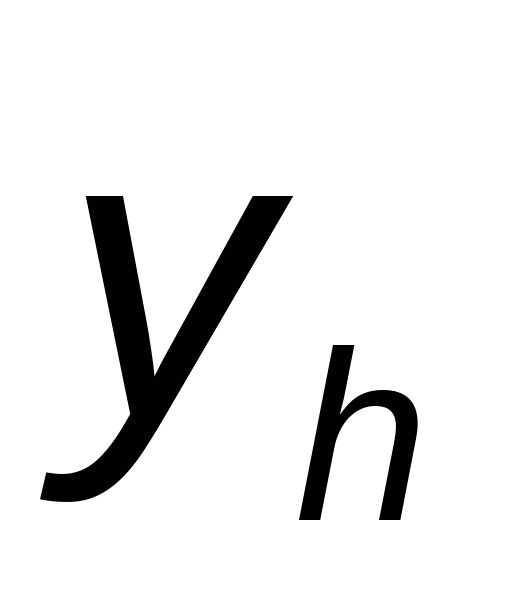 можно использовать формулу: можно использовать формулу:
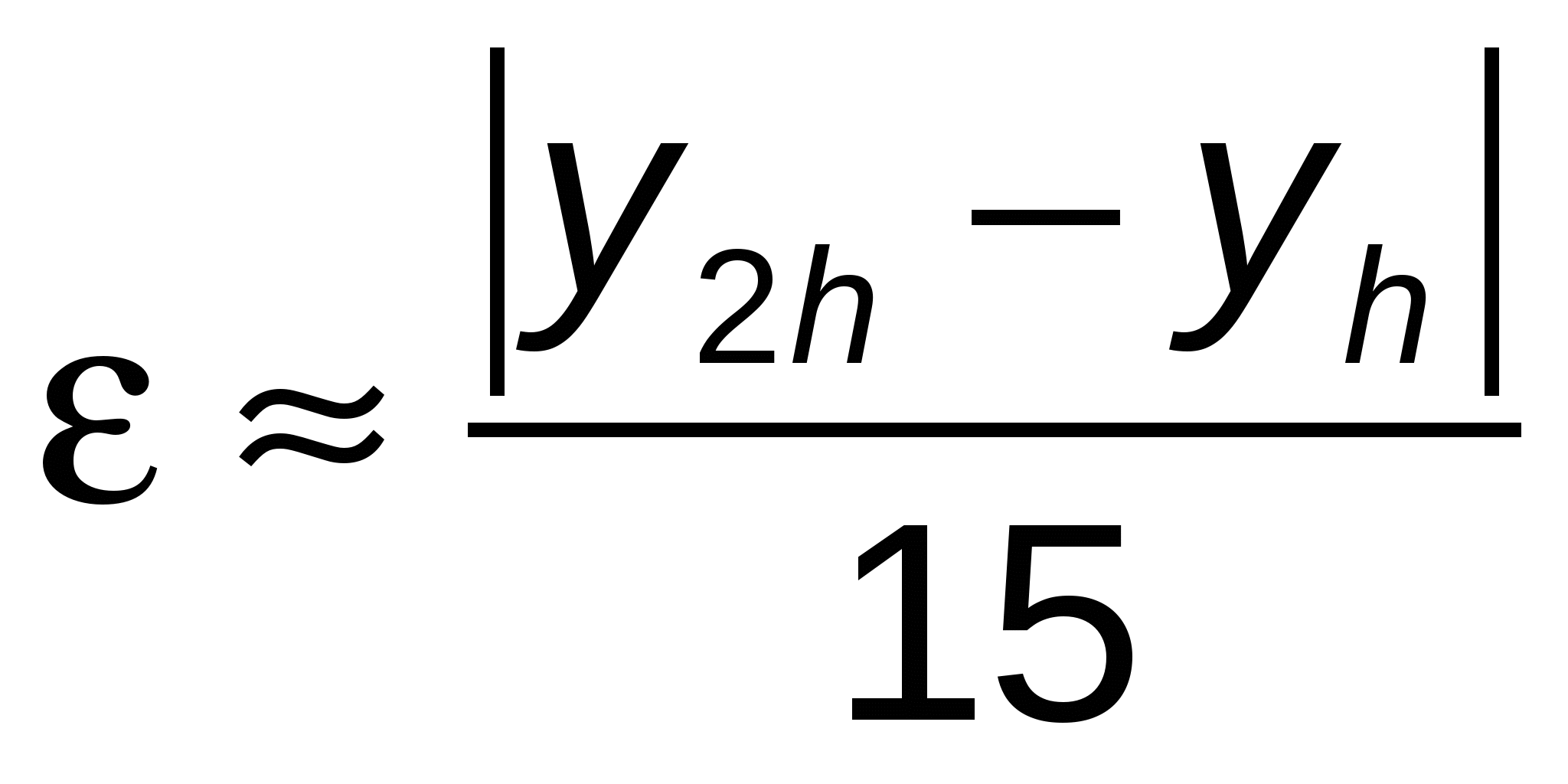 . .
страница 1
|