страница 1
Алгебры логики.
Гумаров Р.Н.
8б, школа №23, г. Караганда
рук. Бухарицына Л.В
Введение
В данной работе рассматриваются булевы функции и функции к-значной логики как их обобщение. Рассматриваются их определения, вопрос о их количестве, примеры решения элементарных функций и их свойства.
 §1 Булевы функции §1 Булевы функции
В данной работе рассматриваются функции к-значной логики.
Пусть E2 = {0,1}
Определение 1. Отображение f:E2n → E2 называется n-местной булевой функцией.
В дальнейшем множество всех булевых функций будем обозначать P2. Произвольная n-местная булева функция f(х1,х2,…,хn) может быть задана с помощью таблиц следующего вида:
х1,х2,…,хn
|
f(х1,х2,…,хn)
|
0 0 ….0
0 0 ….1
………..
1 1…..1
|
f(0 0 ….0)
f(0 0 ….1)
………..
f(1 1…..1)
|
Теорема 1. Число p2 (n) всех функций из P2 зависящих от n переменных х1, х2, .... , хn равно 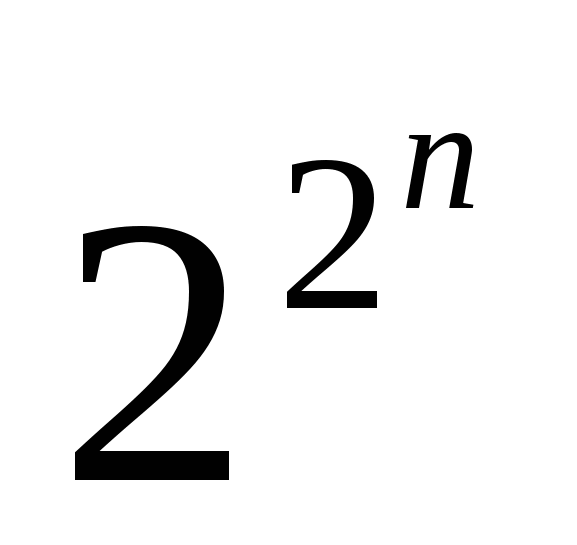
Например, P2(2)=16. P2(3)=256. P2(4) =65536....
Далее рассмотрим примеры булевых функций.
1)одноместные
х
|
f1(x)
|
f2(x)
|
f3(x)
|
f4(x)
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
f1(x) =0-константа 0
f2(x)=x тождественная функция
f3(х)= 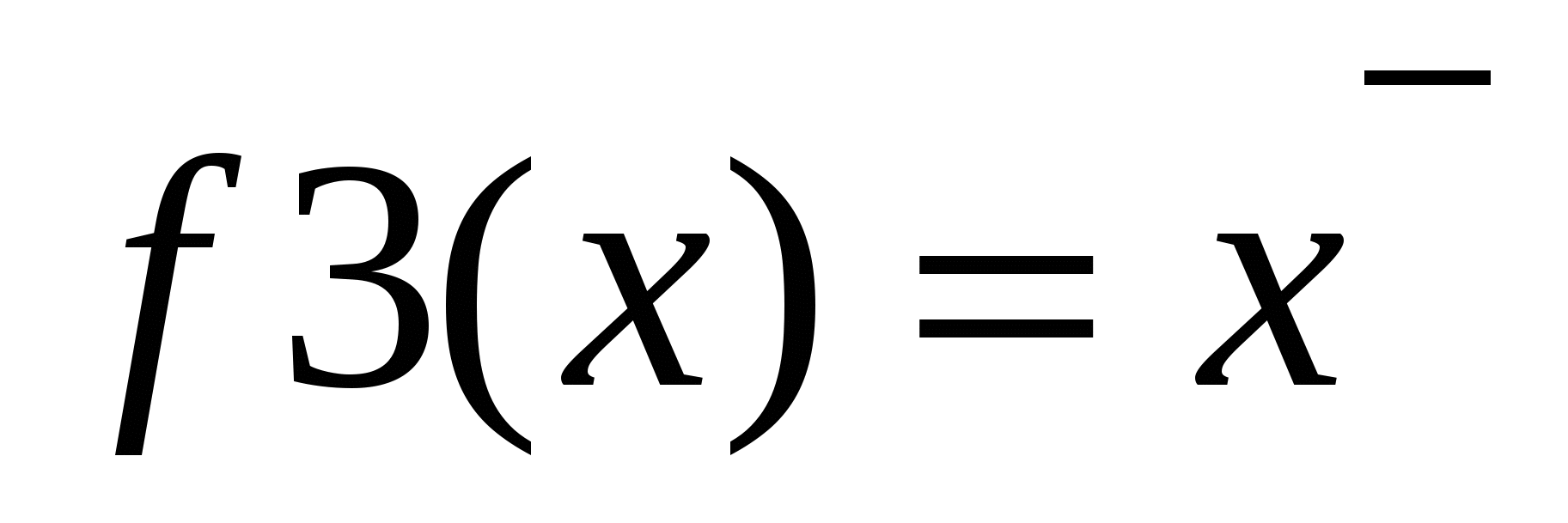
f4(x)=1- константа 1
2) двух местные
х1
|
х2
|
f5
|
F6
|
F7
|
F8
|
F9
|
F10
|
f11
|
f12
|
f13
|
f14
|
f15
|
f16
|
f17
|
f18
|
f19
|
f20
|
0
0
1
1
|
0
1
0
1
|
0
0
0
0
|
0
0
0
1
|
0
0
1
0
|
0
0
1
1
|
0
1
0
0
|
0
1
0
1
|
0
1
1
0
|
0
1
1
1
|
1
0
0
0
|
1
0
0
1
|
1
0
1
0
|
1
0
1
1
|
1
1
0
0
|
1
1
0
1
|
1
1
1
0
|
1
1
1
1
|
f5(х1,х2)=0 константа 0
f6(х1,х2)= х1&х2 конъюнкция
f11(х1,х2)= х1+х2 mod 2
f12(х1,х2)= х1х2 дизъюнкция
f13(х1,х2)= х1 ↓ х2 стрелка Пирса(анти дизъюнкция)
f14(х1,х2)= х1 ~ х2 эквиваленция
f18(х1,х2)= х1 → х2 импликация
f19(х1,х2)= х1|х2 штрих Шеффера(анти конъюнкция)
f20(х1,х2)=1 константа 1
Свойства элементарных булевых функций.
1.Коммутитавность
х1&х2=х2&х1
х1х2=х2х1
х1+х2=х2+х1
х1|х2=х2|х1
х1↓х2=х2↓х1
х1~х2=х2~х1
2.Ассоцитиативность
(х1&х2) &х3 = х1&(х2&х3)
(х1х2) х3 = х1 (х2х3)
сейчас выполним проверку
-
х1
|
х2
|
х3
|
х1х2
|
(х1х2) х3
|
0
0
0
0
1
1
1
1
|
0
0
1
1
0
0
1
1
|
0
1
0
1
0
1
0
1
|
0
1
1
1
1
1
1
1
|
0
1
1
1
1
1
1
1
|
х1
|
х2
|
х3
|
х2х3
|
х1 (х2х3)
|
0
0
0
0
1
1
1
1
|
0
0
1
1
0
0
1
1
|
0
1
0
1
0
1
0
1
|
0
1
1
1
0
1
1
1
|
0
1
1
1
1
1
1
1
|
3.Дистрибутивность
(х1&х2) &х3= (х1х3)& (х2х3)
(х1х2) &х3= (х1&х3) (х2&х3)
4.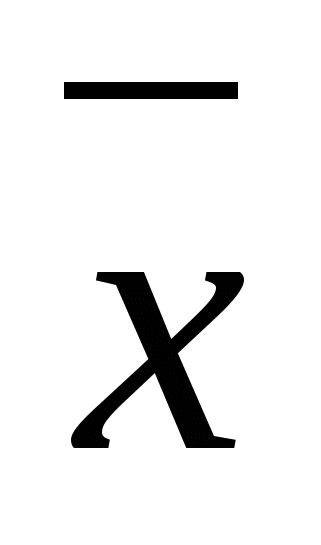 =х =х
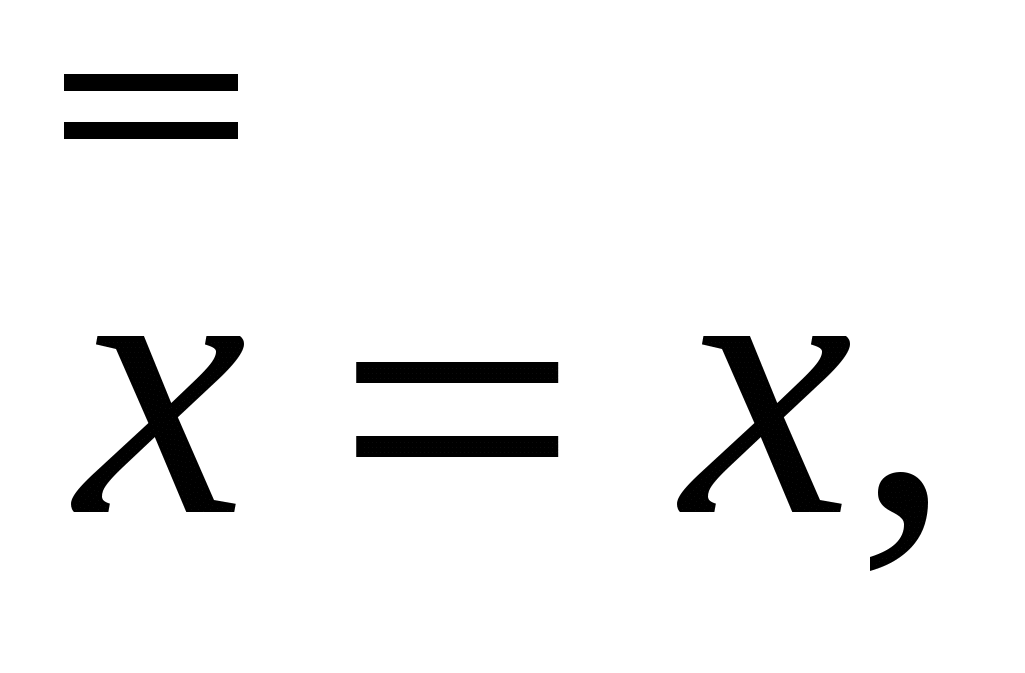 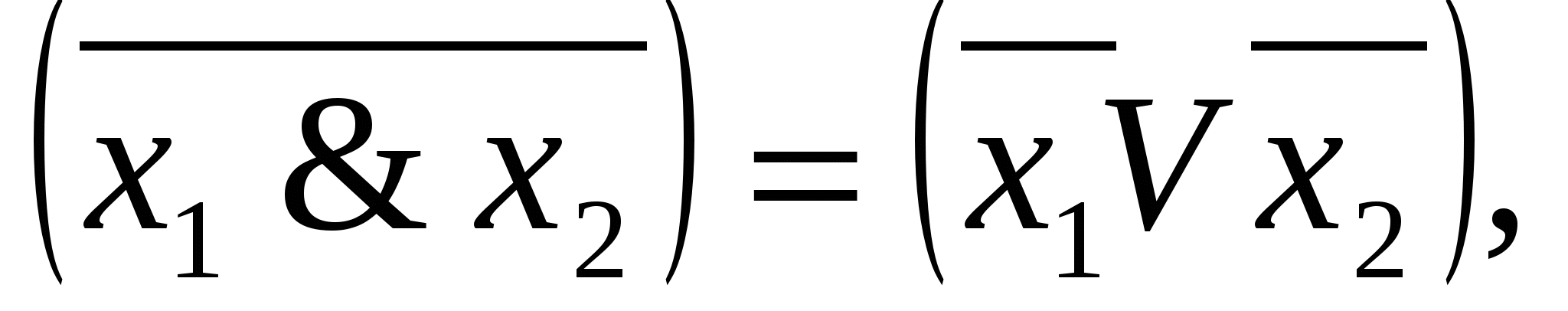 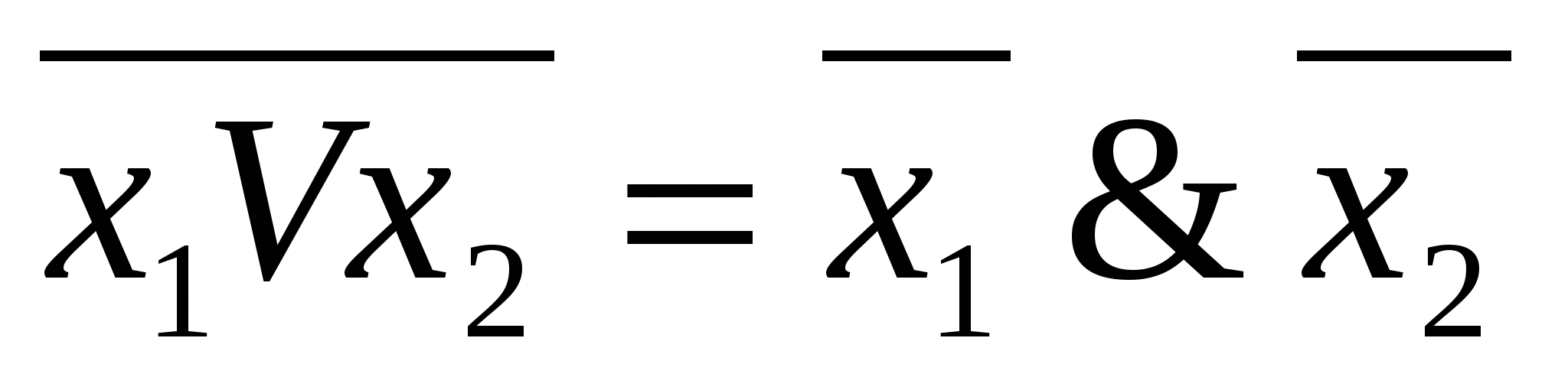
5. (х&x) =х
(х&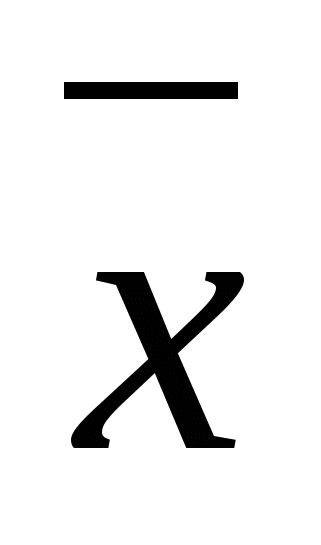 ) =0 ) =0
(х&0) =0
(х&1) =х
(хvx) =х
(хv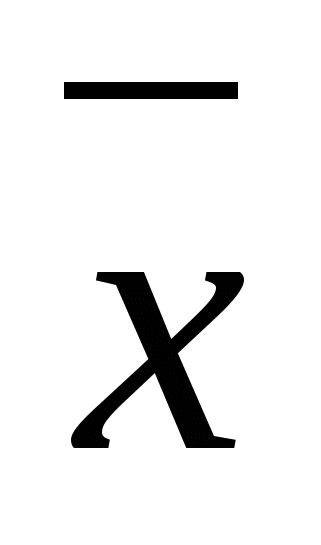 ) =1 ) =1
(хv0) =х
(хv1) =1
§2 функции к-значной логики.
Определение2. Отображение f:Ekn называется n-местной функцией к-значной логики.
В дальнейшем множество всех функций к-значной логики будем обозначать Pk
Замечание. При к=2, мы получаем множество P2 всех булевых функций.
Произвольная n-местная функция к-значной логики может быть задана с помощью таблицы следующей.
-
х1…хn-1 хn
|
f (х1…хn-1, хn)
|
0 …. 0 0
0 …….. 0 1
…………………….
0 ……. 0 к-1
0 …… 1 0
……………….
К-1 ….к-1 к-1
|
F(0 …. 0 0)
F(0 …….. 0 1)
…………………….
F(0 ……. 0 к-1)
F(0 …… 1 0)
……………….
F(К-1 ….к-1 к-1)
|
Теорема. Число всех функций из Pk , зависящих от n переменных х1,…., хn равно 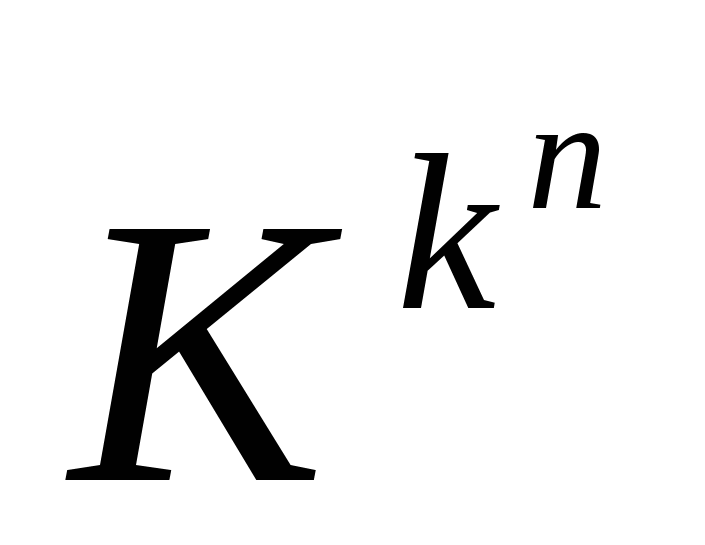 . .
Например, Уже в P3 число функций от двух переменных равно 39 = 19683, т.е. это множество практически необозримо.
Далее рассмотрим некоторые примеры функций к-значной логики, учитывая, что в Pk при к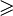 3 в значительной степени возрастают трудности по сравнению с P2 как в возможности эффективного использования табличного задания функций, так и в возможности просмотра всех функций от n переменных. 3 в значительной степени возрастают трудности по сравнению с P2 как в возможности эффективного использования табличного задания функций, так и в возможности просмотра всех функций от n переменных.
1)
к=3
х
|
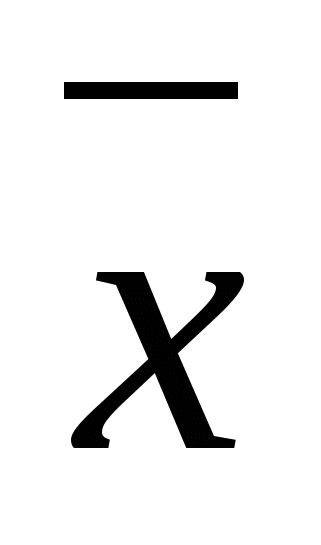
|
0
1
2
|
1
2
0
|
К=4
х
|
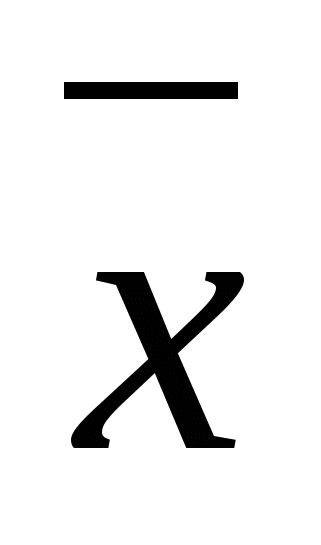
|
0
1
2
3
|
1
2
3
0
|
2)
к=2
Nx=2-1-х=1-х
К=3
Nx=3-1-x=2-x
К=4
Nx=4-1-х=3-х
3)
k=3
х1+х2 (mod 3)
х1
|
х2
|
х1+х2(mod 3)
|
0
0
0
1
1
1
2
2
2
|
0
1
2
0
1
2
0
1
2
|
0
1
2
1
2
0
2
0
1
|
K=4
х1
|
х2
|
х1+х2(mod 4)
|
0
0
0
0
1
1
1
1
2
2
2
2
3
3
3
3
|
0
1
2
3
0
1
2
3
0
1
2
3
0
1
2
3
|
0
1
2
3
1
2
3
0
2
3
0
1
3
0
1
2
|
Свойства элементарных функций к-значной логики.
-
Коммутативность
Min(x1,х2)= Min(x2,х1)
x1,х2 mod k= x2,х1 mod k
max(x1,х2)= Max(x2,х1)
x1+х2 mod k= x2+х1 mod k
-
Ассоциативность
Min (Min(x2,х1), х3)= Min (х1,Min(x2,х3))
(x1,х2 mod k) х3 mod k= x1(x2,х3 mod k) mod k
Max (Max(x2,х1), х3)= Max (х1,Max(x2,х3))
((x1+х2 mod k)+ х3) mod k= (x1+(x2+х3 mod k)) mod k
-
Дистрибутивность
(х1х2)х3= (х1х3) (х2х3)
(х1х2) х3=(х1х3) (х2х3)
-
х=1*I1(x) 2* I2(x) …(к-1) Iк-1(x)
-
х1= х1(I0(x2) … Iк-1(x2))
-
I0(x) Ij(x)= 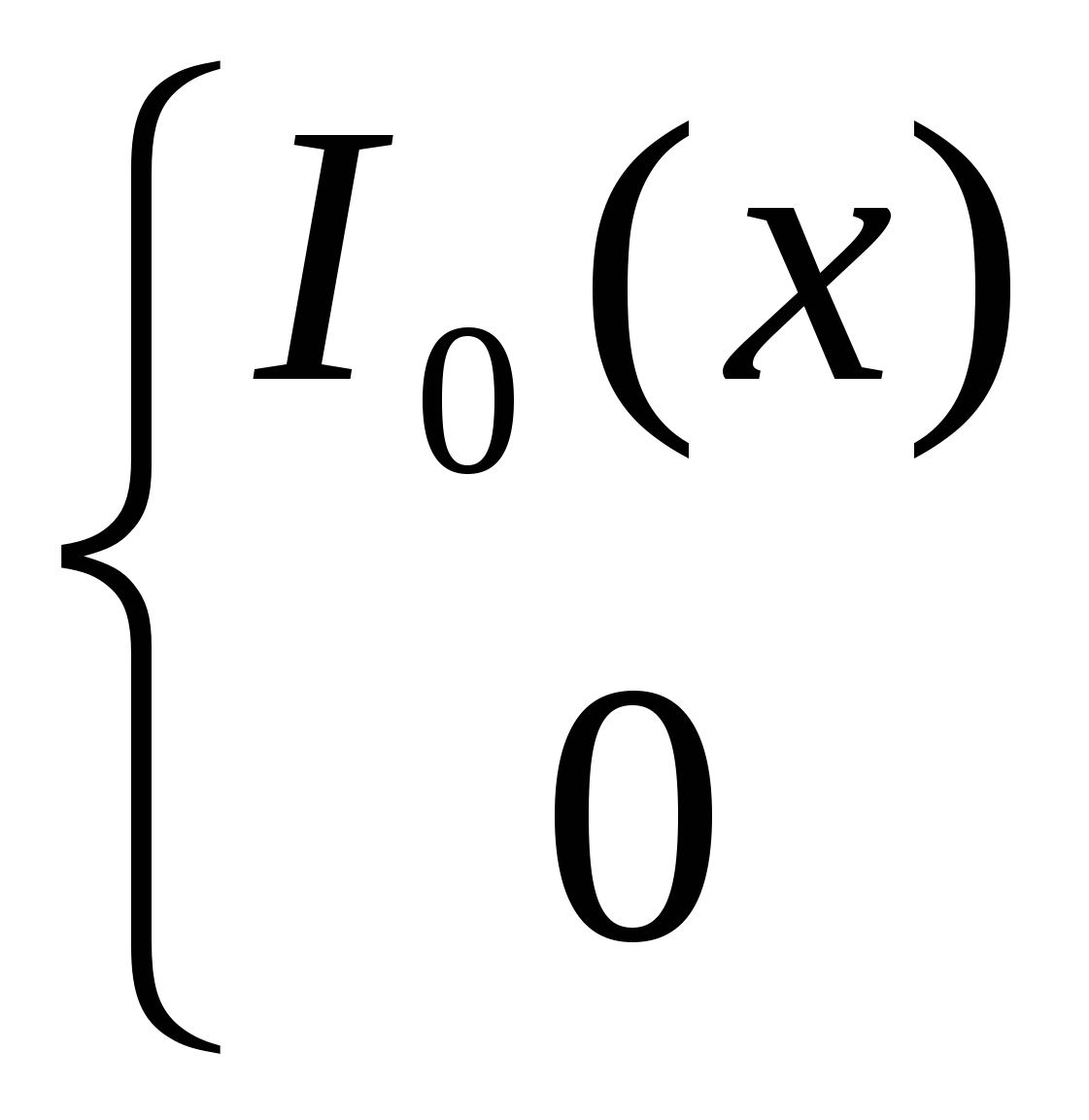 при j=0, при j при j=0, при j 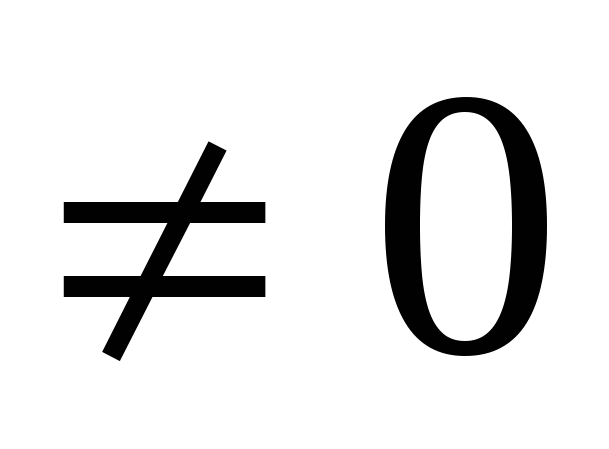
0j=min(0.j); 0j=max(0.j);
(к-1)х=х; 0*х=0;
(к-1) х=к-1; 0х=х
страница 1
|