страница 1
Министерство образования науки Республики Казахстан
Отдел образования г. Караганды
Школа-лицей № 101
Согласована Утверждена
На научно-методическом совете Директор ШЛ № 101
Протокол № ___ _____ Жумабекова А.А.
«___» ____________ 2009 г. «____» _________2009 г.
Программа курса по выбору
«Практикум по подготовке к ЕНТ»
для учеников 11 класса
Караганды, 2009
Составитель: Ревякина Т.М., учитель математики
Программа обсуждена на заседании кафедры, протокол № ___ от «___» ________2009 г.
Руководитель: Телиман В.Я. ____________________
Одобрена методическим советом школы, протокол № ___ от «___» __________ 2009 г.
Председатель научно-методического совета: заместитель директора по инновациям
__________________Привалова Е.Н.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Последние годы выпускники школ Казахстана сдают единое национальное тестирование, обеспечивающее совмещение итоговой государственной аттестации учеников 11 класса средних общеобразовательных школ и приёмных экзаменов в средние профессиональные и высшие учебные заведения. В связи с этим перед школой ставится задача качественно подготовить учащихся к внешнему контролю знаний. Для решения поставленной задачи необходима целенаправленная системная работа педагогического коллектива, направленная на повышение мотивации учащихся, корректировку учебных программ в сторону перераспределения часов для углубленное и дополнительного изучения отдельных тем, изменение педагогических технологий обучения.
Анализ тестовых заданий, входящих в сборники ЕНТ по математике, показывает, что некоторые нетиповые задачи нельзя решить по заученному раз и навсегда алгоритму. Этот факт усложняет подготовку педагога и учеников к тестированию. Учитывая, что математика является обязательным предметом при сдаче ЕНТ всеми выпускниками независимо от интересов и способностей и не все учащиеся имеют аналитический склад мышления (например, те, кто поступает на гуманитарные специальности) возникла необходимость создания программы курса «Практикум по подготовке к ЕНТ», в котором рассматривается решение нестандартных задач, предлагаемых в рамках государственного тестирования.
Курс рассчитан на 34 часа.
Цель курса: создать условия для организации обобщения и систематизации программного материала по математике.
Курс призван развивать логическую культуру, навыки перехода от аналитической постановки задачи к её наглядной интерпретации и наоборот, учит умениям отыскивать примеры и контрпримеры для подтверждения или опровержения некоего предположения, учит обобщать полученные результаты, делать выводы, активизирует мыслительную деятельность.
Введение данного курса позволяет повысить психологический комфорт учащихся на уроках, уверенность во время проведения единого национального тестирования.
Задачи курса:
-
проанализировать программный материал и найти противоречия с тестовыми заданиями НЦГЦ;
-
организовать деятельность учащихся по усвоению нестандартного материала;
-
создать условия для развития и саморазвития учащихся и педагога;
-
способствовать развитию практических навыков в решении нестандартных задач и упражнений;
-
организовать тренинг навыков умственного труда,
самостоятельной работы при подготовке к ЕНТ.
Программа опирается на базовый курс математики 5-11, предусмотренный государственным стандартом курса математики Республики Казахстан.
В данном курсе рассмотрены темы:
- «Классификация чисел»;
- «Делимость, НОД и НОК»;
- «Рациональные числа»;
- «Степень числа»;
- «Числа с радикалами»;
- «Разложение на множители, тождественные преобразования»;
- «Уравнения и неравенства»;
- «Тестовые задачи»;
- «Основы тригонометрии»;
- «Логарифмы»;
- «Последовательность»;
- «Функции и графики»;
- «Основы дифференциального исчисления».
Теория и практика заданий по выше перечисленным темам имеет важное значение для школьного математического образования, в развитии интеллектуальных и других качеств учащихся через овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности. Выше перечисленные темы позволяют объединить и обобщить знания, полученные в курсе средней школы и подготовиться к ЕНТ.
Теоретико-практический курс «Практикум по подготовке к ЕНТ» развивает математическую грамотность.
Основными методами проведения занятий являются лекции, семинары, практикумы.
Формы организации учебной деятельности - коллективная, групповая, индивидуальная, использование мозговых атак, блицтурниры, деловые игры.
Формы контроля: тестирование.
Требования к уровню подготовки учащихся
В результате изучения курса учащиеся должны знать:
-
обобщённые приёмы решения;
-
рациональные приёмы устного счёта, тождественные преобразования.
Должны овладеть следующими умениями:
-
решать нестандартные математические задания;
-
анализировать ответы до решения математической задачи;
-
разумно распределять время;
Ожидаемый результат
-
достаточный уровень математической грамотности;
-
психологическая готовность к сдаче ЕНТ.
Диагностический инструментарий
-
анкеты изучения затруднений учащихся при решении нестандартных задач;
-
тесты по математике;
-
тесты по таксономии Блума;
-
текущий контроль знаний учащихся.
Учебно – тематический план
№
|
Разделы
|
Колич. часов
|
Формы
и методы обучения
|
Образова -тельный продукт
|
Приме
чание
|
1
|
Тема №1.
Классификация чисел
|
1
|
Мини-лекция
|
Опорный конспект,
решённые задания
|
|
2
|
Тема №2
Делимость.НОД и НОК
|
1
|
Минил-екция
|
опорный конспект,
решённые задания
|
|
3
|
Тема №3.
Рациональные числа
|
1
|
Мини-лекция
|
опорный конспект,
решённые задания
|
|
4
|
Тема№4
Степень числа
|
1
|
семинар
|
конспект
|
|
5
|
Тема №5
Числа с радикалами. Корни с натуральными показателями
|
2
|
семинар
|
конспект,
решённые задания
|
|
6
|
Тема№6
Разложение на множители и тождественные преобразования
|
2
|
семинар, практикум,
тестирования
|
конспект,
решённые задания
|
|
7
|
Тема№7
Уравнения
|
4
|
Мини-лекция,
практикум
|
конспект,
решённые задания
|
|
8
|
Тема№8
Текстовые задачи
|
3
|
семинар, тестирова -
ние
|
алгоритмы решений
|
|
9
|
Тема №9
Неравенства
|
3
|
Мини-лекция
|
опорный конспект
|
|
1о
|
Тема№10.Тригонометрические функции
|
4
|
Мини-лекция, практикум
|
решённые задания
|
|
1
|
Тема №11
Логарифмы
|
3
|
Мини-лекция, практикум
|
решённые задания
|
|
1
|
Тема №12
Арифметическая и геометрическая профессии
|
2
|
Мини-лекция, практикум
|
решённые задания
|
|
1
|
Тема №13
Производная и ее применение
|
3
|
Мини-лекция, практикум
|
решённые задания
|
|
1
|
Тема №14
Интеграл и его применение
|
2
|
Мини-лекция, практикум
|
решённые задания
|
|
1
|
Тема №15.
Практикум по решению итоговых тестов
|
2
|
практикум
|
решённые задания
|
|
Содержание курса
( 1 час в неделю, всего 34 часа)
Тема №1. Классификация чисел- 1 час.
Натуральные, целые, рациональные, иррациональные, действительные числа. Числовые последовательности и их суммы числа. Простые числа.. Модуль числа и его свойства. Решение упражнений. Техника счёта.
Тема № 2. Делимость . НОД и НОК.- 1 час.
Делимость на 2,3,4,5, 6,9,11,13. Нахождение НОД и НОК." Решение упражнений. Психологический тренинг.
Тема № 3. Рациональные числа - 1 час
Дроби. Действия с дробями обыкновенными и десятичными, периодические десятичные числа и их перевод в рациональные числа. Сравнение рациональных чисел.
Тема № 4. Степень числа - 1 час.
Степень числа. Действия со степенями. Степень действительного числа. Преобразование выражений, содержащих степени.
Тема №5. Числа с радикалами. Корни с натуральными показателями --2часа.
Выражения с радикалами. Степень с рациональным показателем, рационализация знаменателя и числителя дроби. Корень из радикала, бесконечные корни, сравнение чисел с радикалами. Психологический тренинг.
Тема №6. Разложение на множители и тождественные [преобразования.-2 часа.
Алгоритмы разложения на множители. Тождественные преобразования алгебраических выражений.
Тема №7. Уравнения-4 часа.
Уравнения, корни уравнений, свойства уравнений. Решение линейных уравнений. Линейное уравнение с двумя переменными. Системы линейных уравнений. Способы решения. Квадратные уравнения и уравнения сводимые к ним. Иррациональные уравнения Показательные уравнения. Способы решения. Уравнения с модулем. Психологический тренинг
.
Тема №8. Текстовые задачи-3 часа
Числовые задачи, задачи с дробями, производственные задачи, задачи на скорость и движение, задачи на проценты.
Тема №9. Неравенства -3 часа
Неравенства, Свойства. Линейные неравенства, квадратные неравенства и неравенства высших порядков Метод интервалов при решении неравенств. Неравенства, содержащие модуль. Системы неравенств. Показательные неравенства. Иррациональные неравенства, алгоритмы их решений.
Тема№10.Тригонометрические функции.-4 часа
Единичная окружность, измерения углов и дуг. Тригонометрические соотношения в прямоугольном треугольнике. Тригонометрические функции. Тригонометрические значения специальных углов. Формулы приведения. Таблица формул курса тригонометрии и ее применение при преобразовании тригонометрических выражений. Обратные тригонометрические функции. Тригонометрические уравнения, способы их решения. Алгоритмы решения тригонометрических неравеств. Системы неравенств. Психологический тренинг.
Тема №11. Логарифмы-3 часа
Показательная и логарифмическая функции, их свойства и графики.
Свойства логарифмов. Классификация логарифмов. Вычисление и преобразования логарифмов. Логарифмические уравнения, неравенства
системы. Психологический тренинг.
Тема №12. Арифметическая и геометрическая прогрессии-2 часа
Арифметическая прогрессия, ее свойства, сумма u арифметической прогрессии. Геометрическая прогрессия, ее свойства. сумма членов геометрической прогрессии, бесконечно убывающая геометрическая прогрессия. Психологический тренинг.
Тема №13 Производная и ее применение -3 часа
Производная, теоремы, таблица. Производная высших пор; Производная сложной функции. Геометрический и физический смысл : первой и второй производной. Уравнение касательной. Критические точки, точки экстремума .
Проблемы максимума и минимума. Применение производной при исследовании функций. Психологический тренинг.
Тема №14. Интеграл и его применение - 2 часа.
Неопределенный интеграл, свойства. Таблица. Опреде.лённый интеграл Свойства. Вычисление. Криволинейные фигуры и их площадь. Применение интеграла при решении задач. Психологический тренинг.
Тема №15. Практикум по решению итоговых тестов - 2часа
Психологический тренинг.
Список литературы:
-
Абылкасымова А.Е. Алгебра и начала анализа (естественно-математическое направление). – Алматы: Мектеп, 2006 г.
-
Галицкий М.Л. Сборник задач по алгебре для 8 – 9 классов. - М: Просвещение,1992г.
-
Звавич Л.И. Алгебра и начало анализа: 3600 задач для школьников и поступающих в вузы. - М.: Дрофа, 1999г.
-
Кудрявцев Л.Д. Краткий курс математического анализа. - Москва Физматит - 2006 г.
-
Рустюмова И.П. Пособие для подготовки к единому национальному тестированию (ЕНТ) по математике. – Алматы: Галым, 2005 г.
-
Математика. Учебно-методическое пособие (2003 – 2009 года). – Астана: Национальный центр государственных стандартов образования и тестирования, 2003-2009 г.
-
Шыныбеков А.Н. Алгебра и начала анализа. - Алматы: Атамура, 2006 год.
Приложение 1
Методические рекомендации
При повторении темы «Классификация чисел» целесообразно повторить технику счёта:
-
возведение в квадрат чисел, оканчивающихся на 5;
-
приёмы умножения чисел на 11;
-
деление на 25; 125.
При повторении темы «Рациональные числа»:
-
рекомендуется превращать периодическую дробь в обыкновенную с помощью «0» и «9», рассмотреть ряд уравнений, встречающихся в тестах.
-
Необходимо твёрдо владеть формулами сокращённого умножения и формулой квадрата трёхчлена. (Облегчает решение задач на нахождение абсолютной величины вектора  а+в+с). а+в+с).
При преобразовании двойных радикалов рекомендуется представить подкоренное выражение в виде квадрата.
При рассмотрении темы «Тождественные преобразования алгебраических выражений»:
-
для упрощения дробных рациональных выражений нецелесообразно приведение слагаемых к общему знаменателю без предварительного сокращения дроби;
-
перед приведением дробей к общему знаменателю следует проанализировать можно ли эти дроби предварительно сократить;
-
иногда бывает более рациональным не выполнять действия в скобках, а воспользоваться распределительным свойством умножения;
-
кроме традиционных способов разложения на множители можно использовать правило деления многочлена на многочлен «уголком», теорему Безу, схему Горнера
Уравнения. Системы уравнений:
-
при решении квадратных уравнений целесообразно использовать свойства коэффициентов квадратного уравнения.
Метод введения новой переменной:
-
в сложных случаях замена видна после некоторых преобразований;
-
интересная замена неизвестного применяется при решении симметрических уравнений ( если равноудалённые от концов коэффициенты попарно равны);
-
Общих формул нахождения корней алгебраических уравнений высоких степеней нет, и поэтому ученик должен догадаться что-то прибавить и отнять, выделить полный квадрат, на что –то разделить, умножить…
-
В симметрических системах полезно ввести замену х+у=а, ху=в
Данная система решается с помощью свойств корней квадратного уравнения;
Неравенства
-
При решении иррациональных неравенств надо помнить, что при возведении обеих частей неравенства в нечётную степень всегда получается эквивалентное неравенство. Если же обе части неравенства возводим в чётную степень, то будет получаться неравенство эквивалентное исходному и имеющее тот же знак неравенства лишь тогда, когда обе части данного неравенства были неотрицательны. Кроме того нужно помнить, что мы работаем с арифметическими корнями.
Иногда при решении иррациональных неравенств бывает достаточно проанализировать ОДЗ и учесть, что значение арифметического корня всегда неотрицательно.
Показательные уравнения
-
Если даны два сопряжённых числа, то удобно одно заменить через другое
-
Если функция f(х) монотонно возрастает, а д(х) монотонно убывает или константа , тогда уравнение f(х)= д(х) имеет единственное решение которое можно подобрать.
Логарифмические уравнения
-
При решении любых задач. содержащих логарифмы по различным основаниям следует запомнить одну рекомендацию: необходимо перейти во всех логарифмах к одному основанию.
Тригонометрия
-
Вычисление значений тригонометрических функций от аркфункций.
-
В тех случаях, когда аргумент выражен через обратные тригонометрические функции, надо преобразовывать данное выражение т.о, чтобы можно было воспользоваться определением обратных тригонометрических функций.
-
Если в аргументе тригонометрических функций стоит арифметическая. прогрессия, то преобразуем умножением и делением на 2 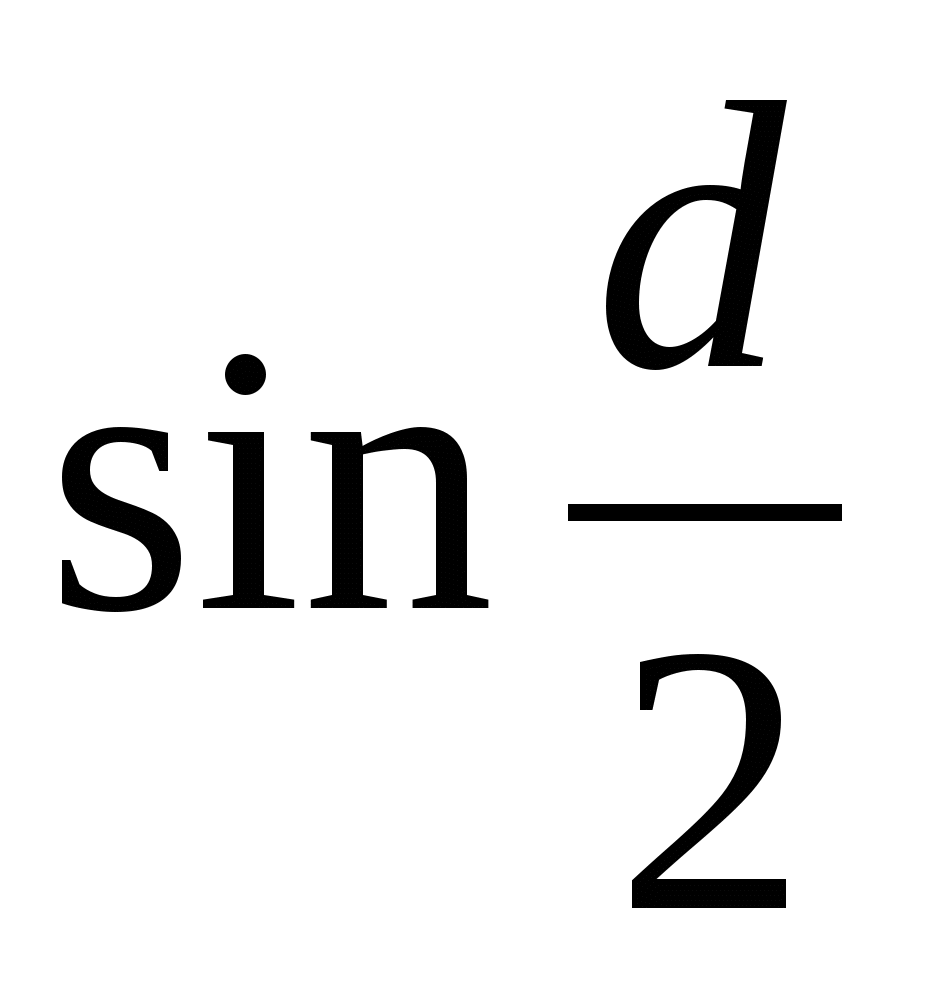 с последующим применением к слагаемым формул преобразования произведения тригонометрических функций в сумму или разность. с последующим применением к слагаемым формул преобразования произведения тригонометрических функций в сумму или разность.
-
Научить учащихся отличать множество решений от подмножества, для принятия правильного ответа
Прогрессии
-
При решении задач на арифметическую и геометрическую прогрессию рекомендуется использование свойств среднего члена арифметической и геометрической прогрессии.
Текстовые задачи
-
Решение текстовых задач у многих учащихся вызывает затруднение. Однако можно использовать следующие рекомендации
-
При решении задач на концентрацию пользоваться формулой
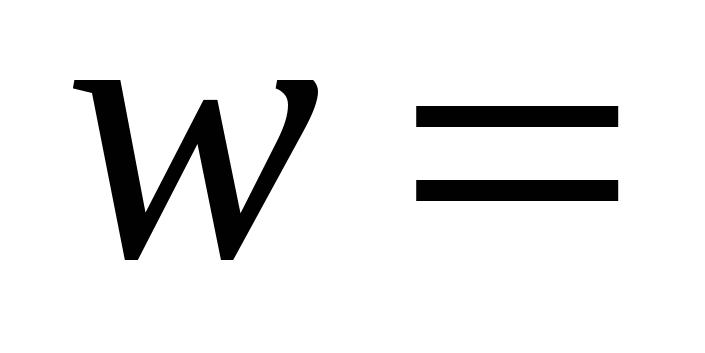  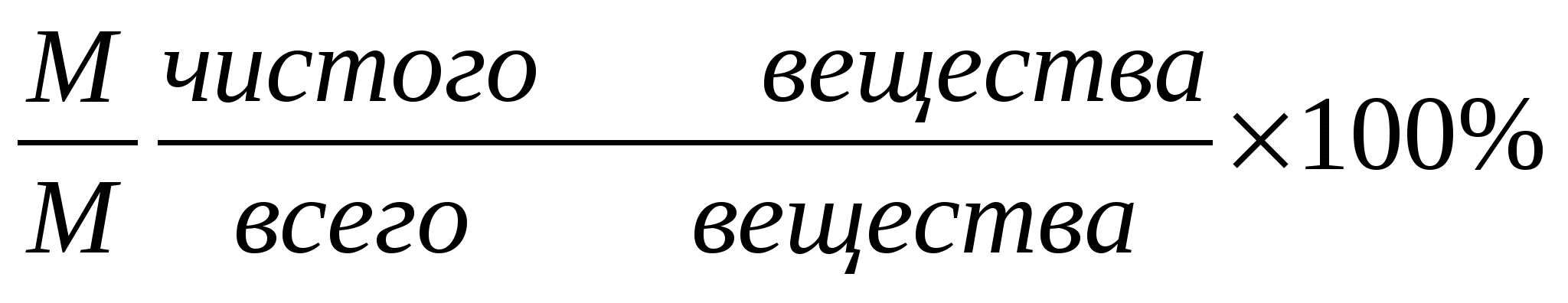
-
Задачи на выпаривание и высушивание решать через обратную пропорциональность, выделяя чистое вещество
-
задачи на производительность решать по схеме
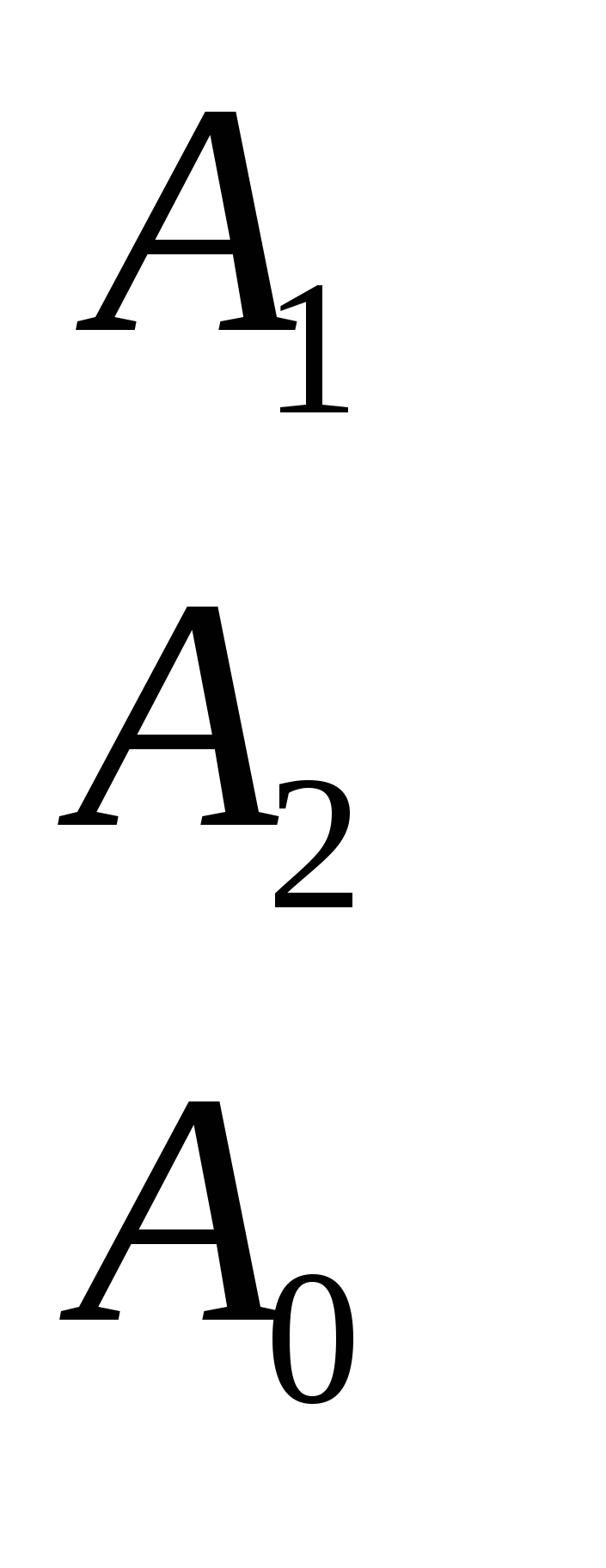   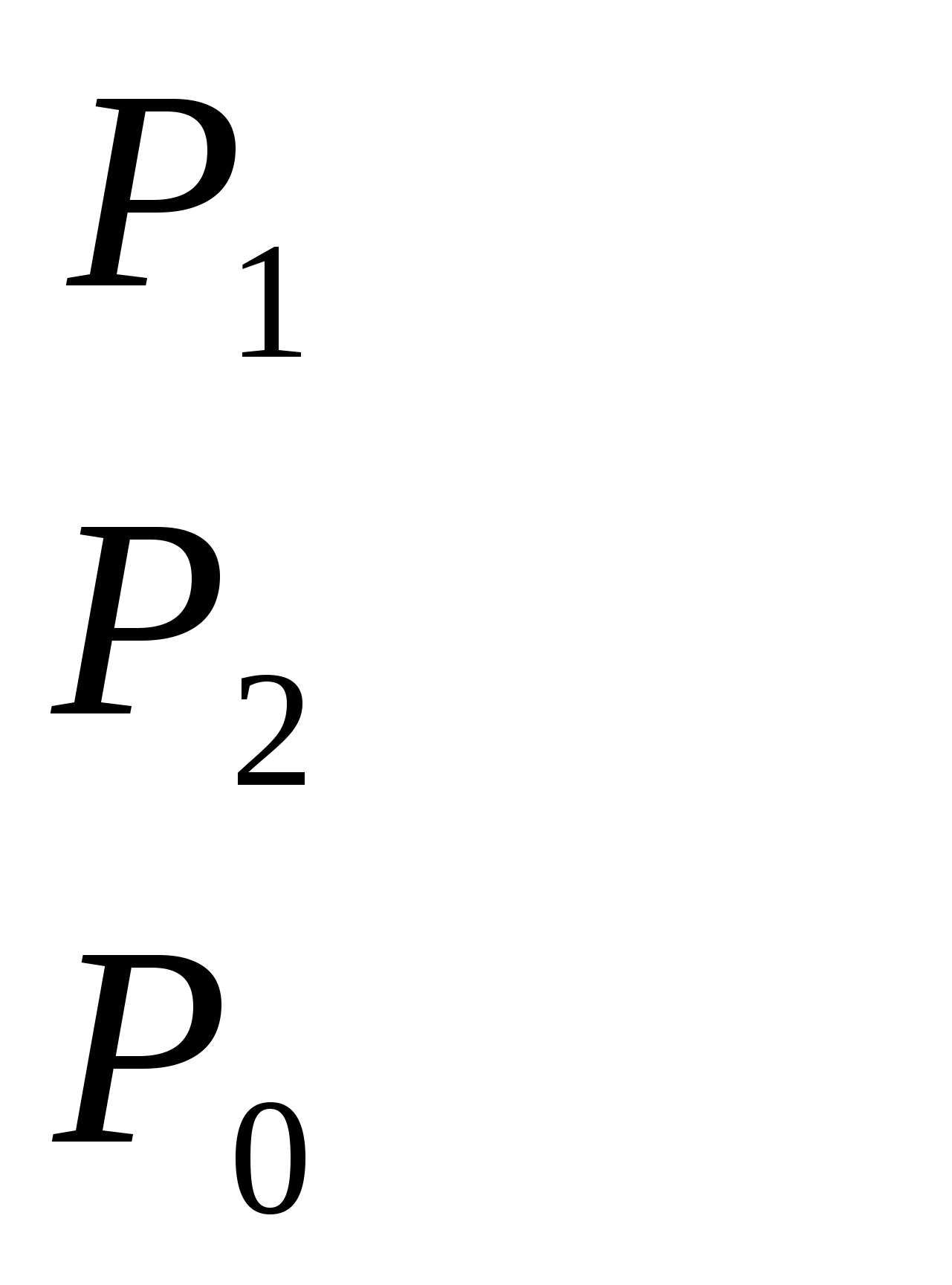 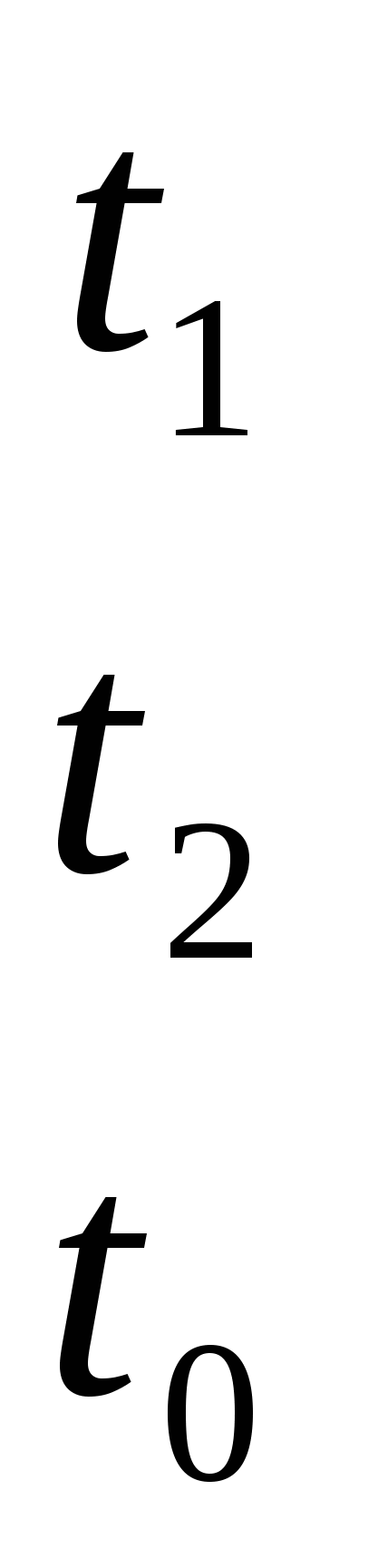  
И составлять уравнение
P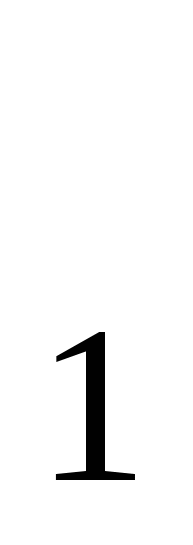 + P + P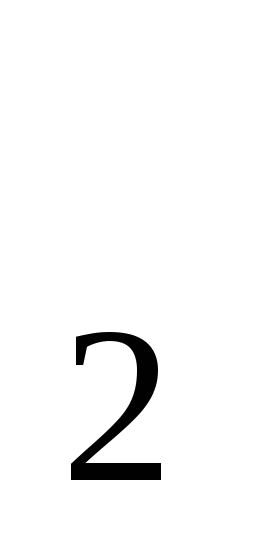 = P = P
-
задачи на движение по стандартной схеме
Приложение 2
Технологическое обеспечение курса
Описание приемов и средств организации УВП
Мини-лекция. Как правило, это занятия, на которых излагается значительная часть теоретического материала изучаемой темы. Лекционная форма проведения занятия целесообразна при:
-
изучении нового материала, мало связанного с ранее изученным;
-
рассмотрении сложного для самостоятельного изучения материала;
-
подаче информации крупными блоками;
-
выполнении определенных видов заданий по одной или нескольким
темам, разделам и т.д.;
-
применении изучаемого материала для решении практических задач.
Структура лекции определяется выбором темы и цели занятия.
Семинар. Семинары характеризуются, прежде всего, двумя взаимосвязанными признаками: самостоятельным изучением учащимися программного материала и обсуждением на занятии результатов их познавательной деятельности. На них ребята учатся выступать с самостоятельными сообщениями, дискутировать, отстаивать свои суждения. Семинары способствуют развитию познавательных и исследовательских умений учащихся, повышению культуры общения.
Практикум. Практикумы, помимо решения своей специальной задачи
- усиления практической направленности обучения, должны быть
тесным образом связаны с изученным материалом, а также
способствовать прочному, неформальному его усвоению. Основной
формой их проведения являются практические и лабораторные
работы, на которых учащиеся самостоятельно упражняются в
практическом применении усвоенных теоретических знаний и умений.
Атака мыслей. В школе применяется при опросе, изучении нового учебного материала, повторенной.., обобщении пройденного, при решении проблем, при составлении планов класса и т.д. Может применяться на всех предметах. Цель данной работы - решение проблемы посредством объединения творческих мыслей учащихся, созданию «коллективного мозга».
Деловая игра «Снежный ком»
Первый вариант. Класс разбивается на 5 групп по б человек (4группы по 4 человека).
Столы имеют указатели: А,В,С,Д,Е.
Каждая группа садится за одним из этих столов.
Каждый участник игры имеет свой индивидуальный номер(бейджик): учащиеся стола А:А1, А2, A3, А4, А5; за столом В: В1.В2, ВЗ, В4,В5ит.д.
-
этап игры- групповая форма работы: каждой группе дается
задание, которое они выполняют вместе(пятером) за определенное
заранее время.
-
этап - коллективная форма работы. Со столов убираются
указатели А,В, С,Д,Е.
Вместо них ставятся номера 1,2,3,4,5 соответственно.
Учащиеся пересаживаются так: за первым столом садятся все первые номера:А1,В1,С1,Д1,Е1.
За вторым столом все вторые номера, за третьим -все третьи и т.д.
После такой пересадки за каждым столом снова по 5 человек, но у каждого свой изученный вопрос т.е. 5 разных тем. Начинается взаимообучение, каждый ученик будет один раз учителем, а 4 раза -учеником. Дается определенное время для коллективной работы(время заранее обговаривается).
Зэтап фронтальная форма работы. Восстанавливаются номера А,В,С,Д,Е. Учащиеся возвращаются на свои первоначальные места. Учитель начинает опрос. При опросе первой темы могут отвечать учащиеся любой группы, кроме стола А. Они выступают экспертами по данной теме, т.е. оценивают правильность ответа. Аналогично с другими темами.
4 этап. Подведение итогов и рефлексия.
Второй вариант. Изменение на втором этапе: участники за столами 1,2,3,4 работают аналогично первому варианту, а участники стола5(А 1,В1,С1,Д1,Е1) в это время работают у доски. Вместо доски можно использовать кодопленку, ватман, компьютер и т.п.
-
этап. Учащиеся возвращаются на свои первоначальные места. Игроки под номерами 5 у доски один за другим начинают «защищать»
свою тему. Учитель и учащиеся наблюдают за правильностью
усвоения учебного материала, умением кратко, конкретно, грамотно излагать суть материала.
-
этап. Подведение итогов и рефлексия.
Игру «Снежный ком» можно использовать при самостоятельном изучении материала (если входящие в одну тему разделы относительно самостоятельны), при закреплении полученной информации (выполнение практической работы) при разработке проекта и тому подобное.
Приложение 3
Диагностический инструментарий
Анкета на входе
Фамилия, имя, класс
В каких темах вы испытываете большее затруднение?
Имеете ли вы навыки решения нестандартных задач?
Как вы оцениваете свой учебный уровень готовности к изучению курса:
а) низкий; б) средний; в) высокий?
Анкета на выходе
Фамилия, имя, класс.
Что нового Вы узнали на занятиях курса?
Чему новому научились на занятиях курса?
Принимали ли Вы участие в исследовательской или проектной
работе?
Можете ли Вы применить знания, полученные на курсах, в других областях? ,
Каков Ваш уровень знаний после окончания курса:
а) низкий; б) средний; в) высокий?
Пригодится ли Вам знания, полученные на курсах в Вашей
дальнейшей жизнедеятельности?
Определение уровня творческих способностей по таксономии Б. Блума
Тест на «выходе»
-
Среди заданных формулой последовательностей укажите являющуюся арифметической прогрессией:
А. аn=a1+d
B. an=a1+d(n-1)
C. an=a1+d(n-1)
D. an=a1+dn
-
x, y, z – разные положительные числа. Чему равно выражение loga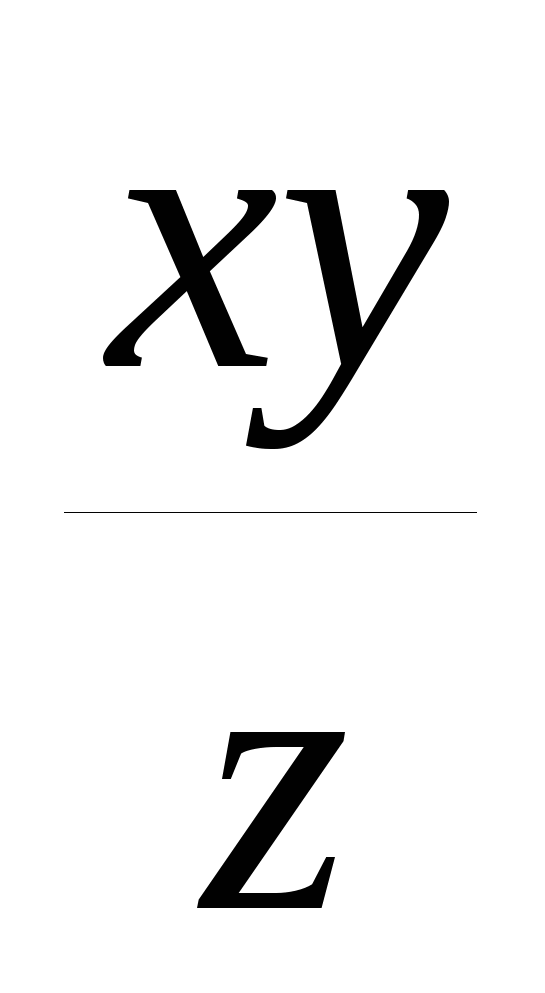 ? ?
А. 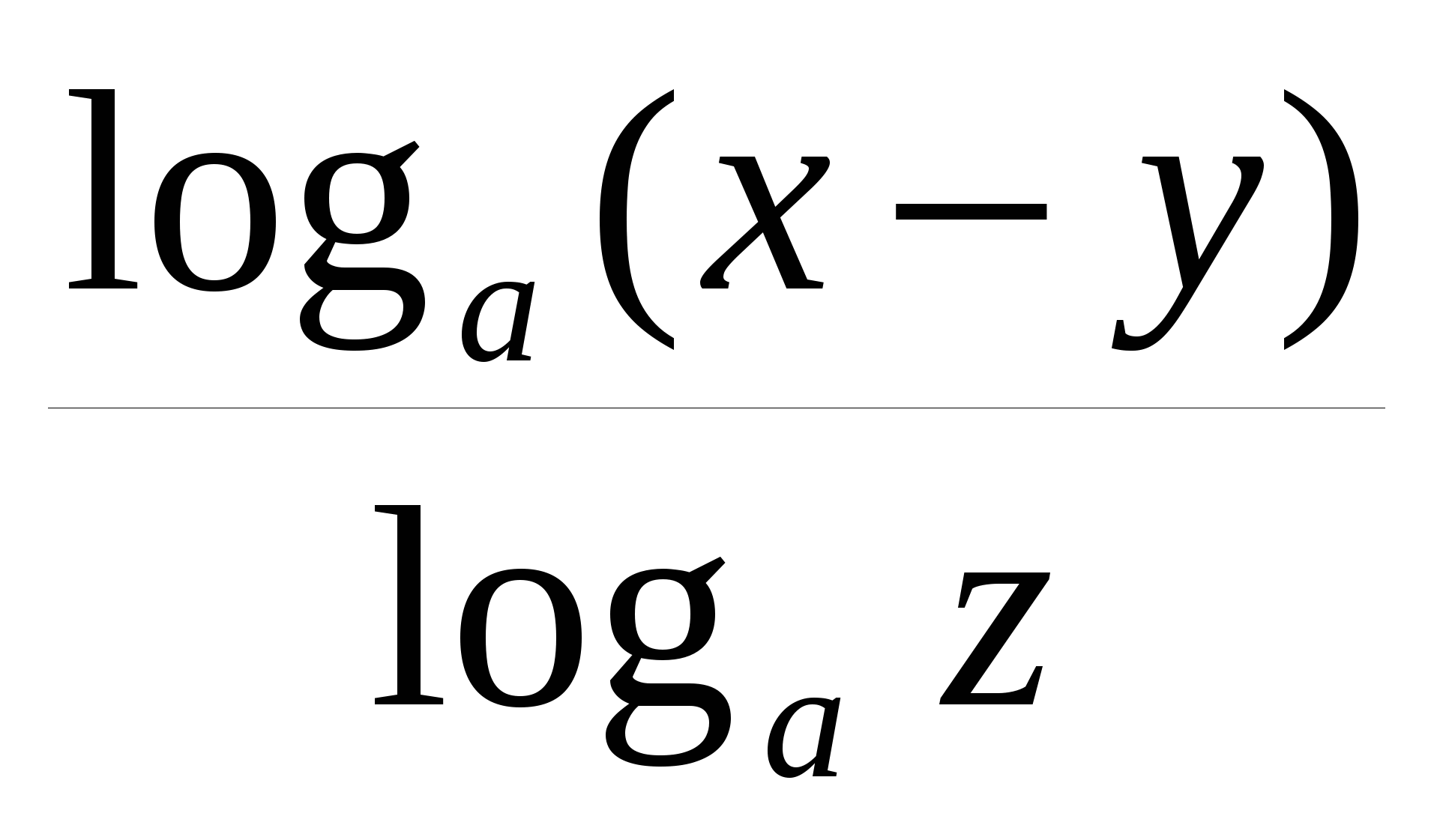
B. 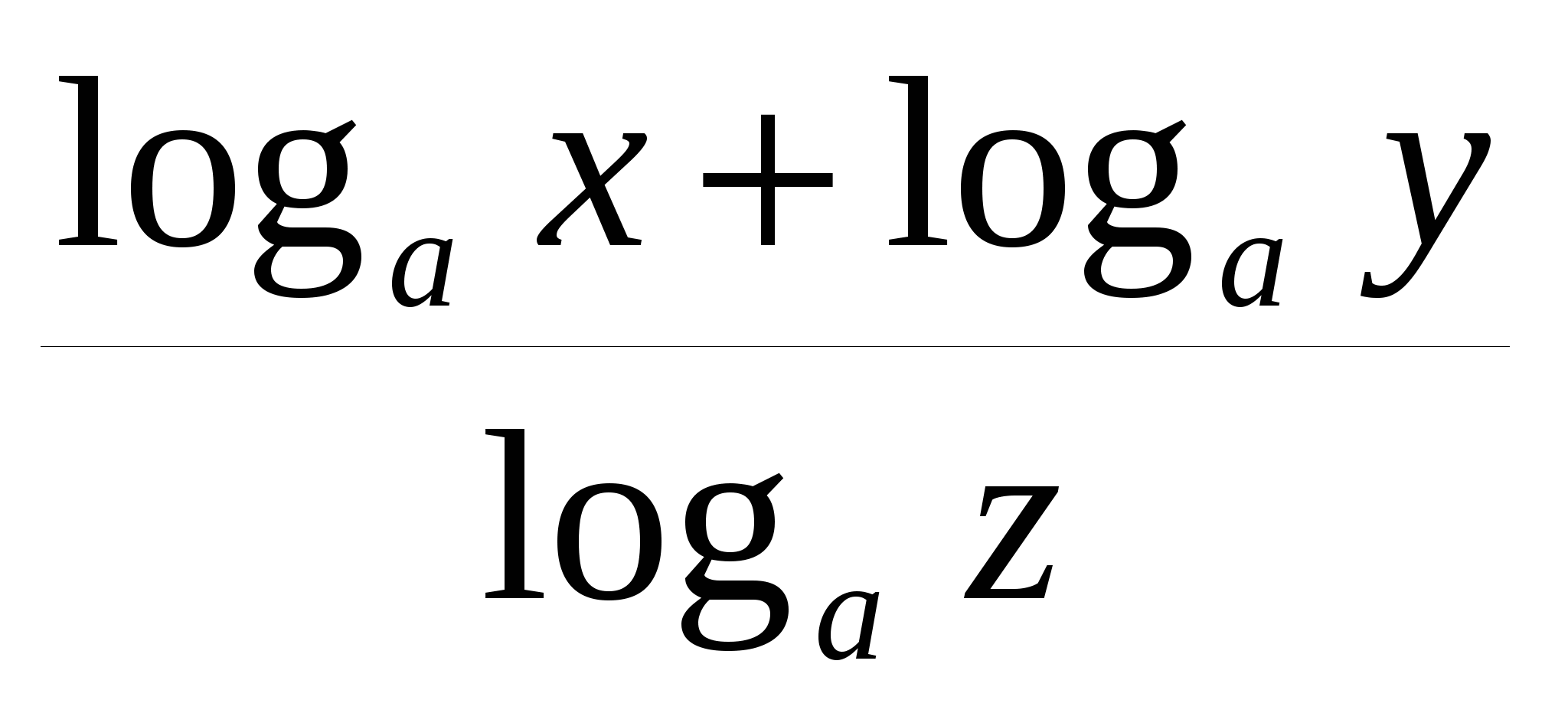
C. 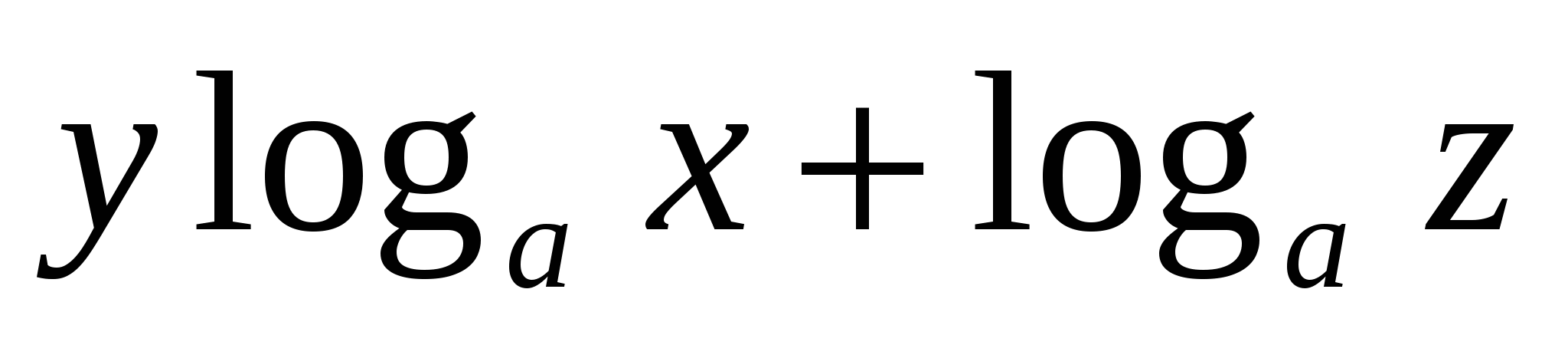
D. 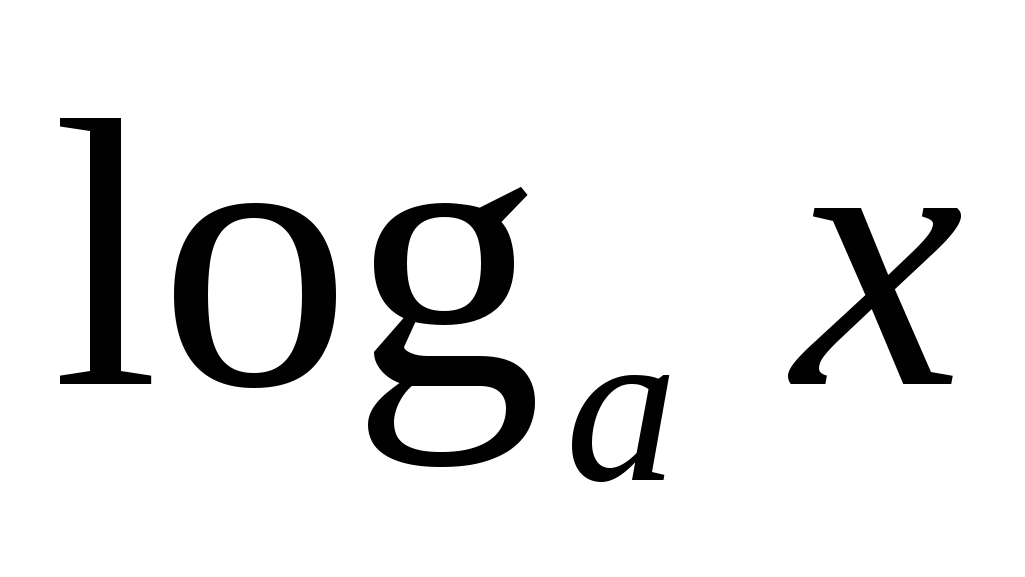 + +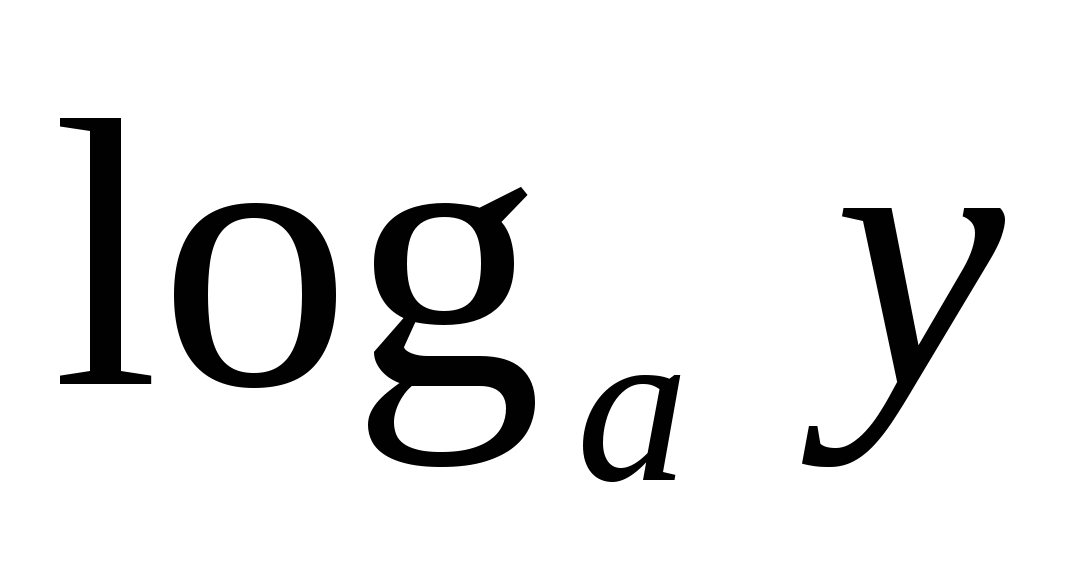 - -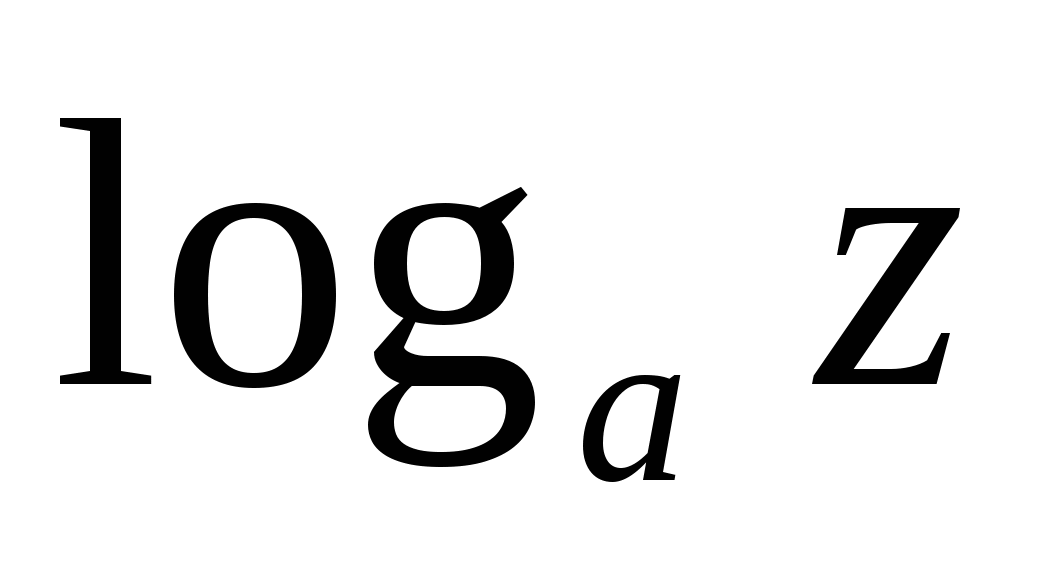
E. 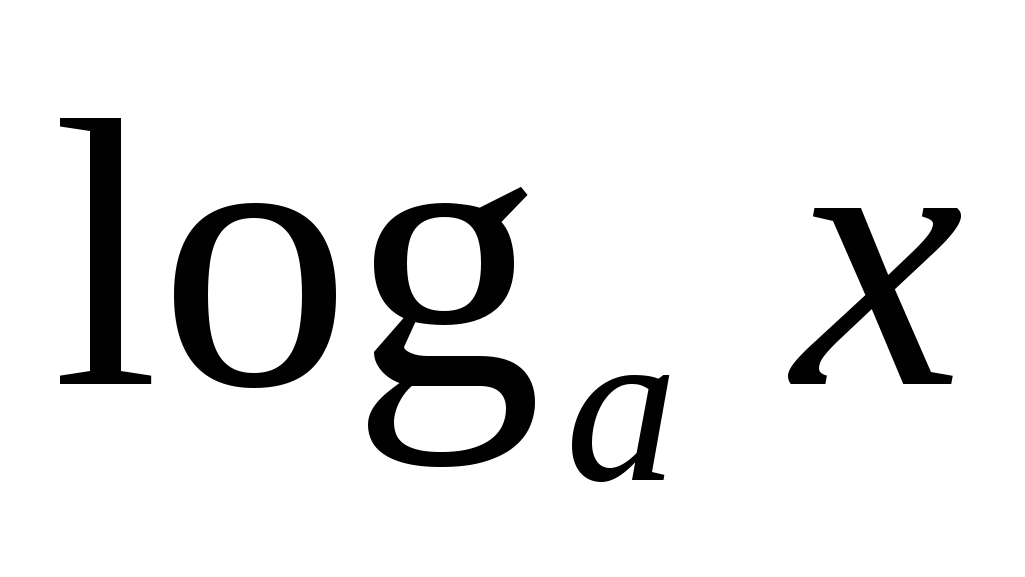 - -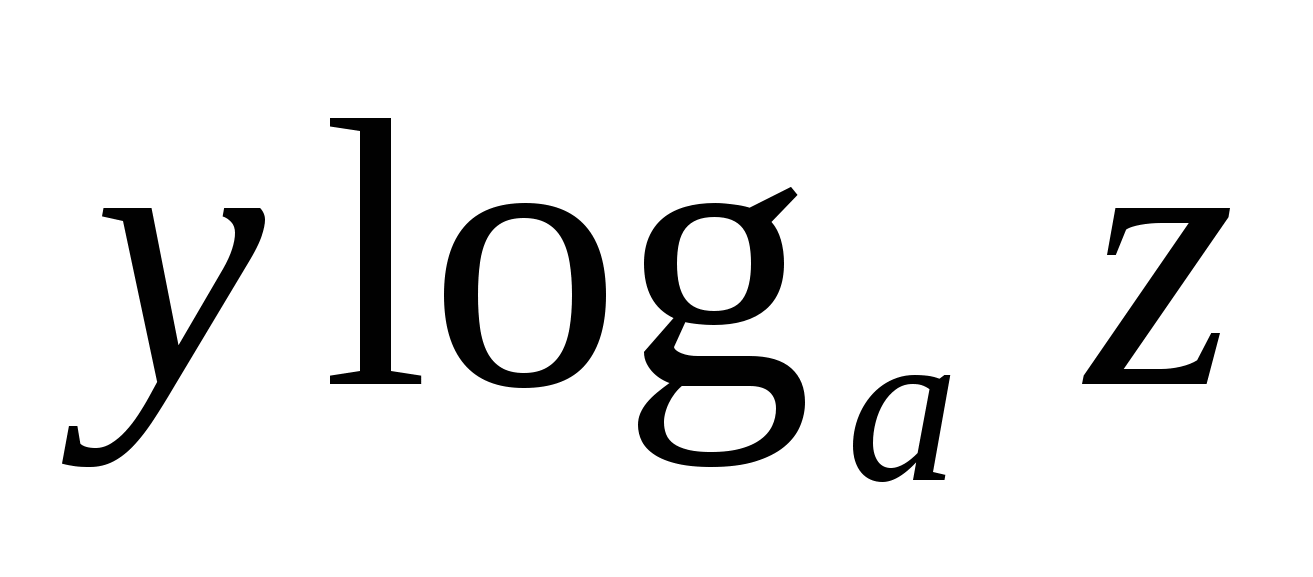
-
Целые числа –
А. числа, употребляемые при счете предметов
B. числа, которые делятся на 1 и на само себя
C. натуральные, им противоположные и 0
D. числа от 0 до 10
E. числа, которые имеют более двух делителей
-
Модуль –
А. расстояние
B. наибольшее из чисел a и –a
C. нет правильного ответа
D. расстояние от начала отсчета до данной точки
-
Какая из данных формул является верной
А. 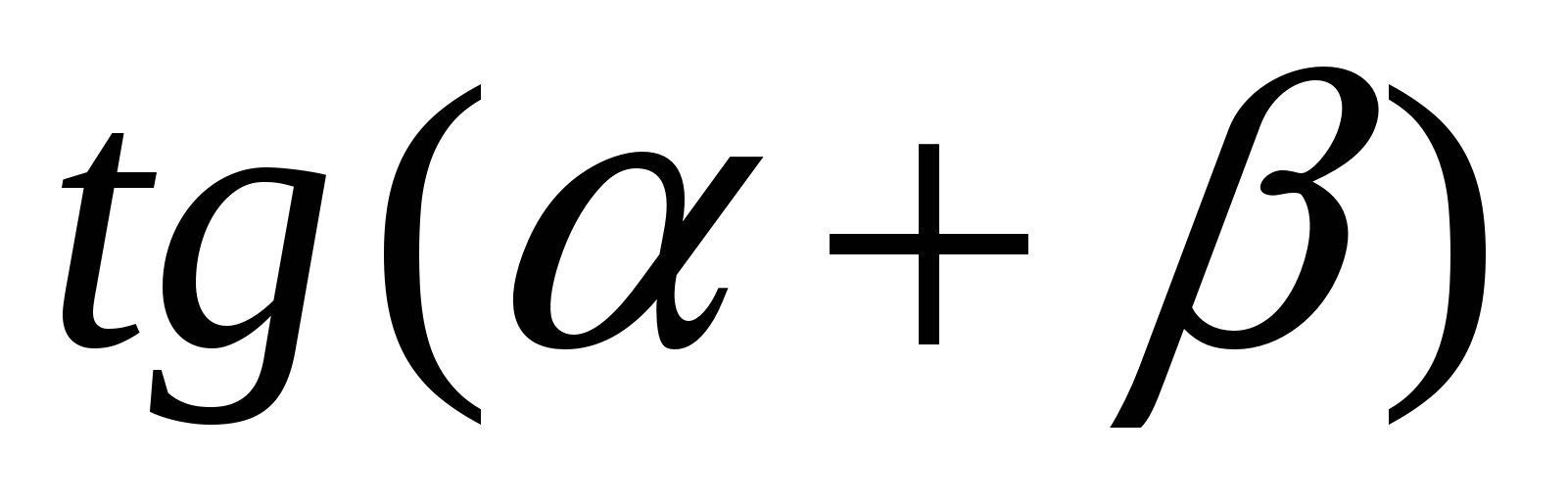 = =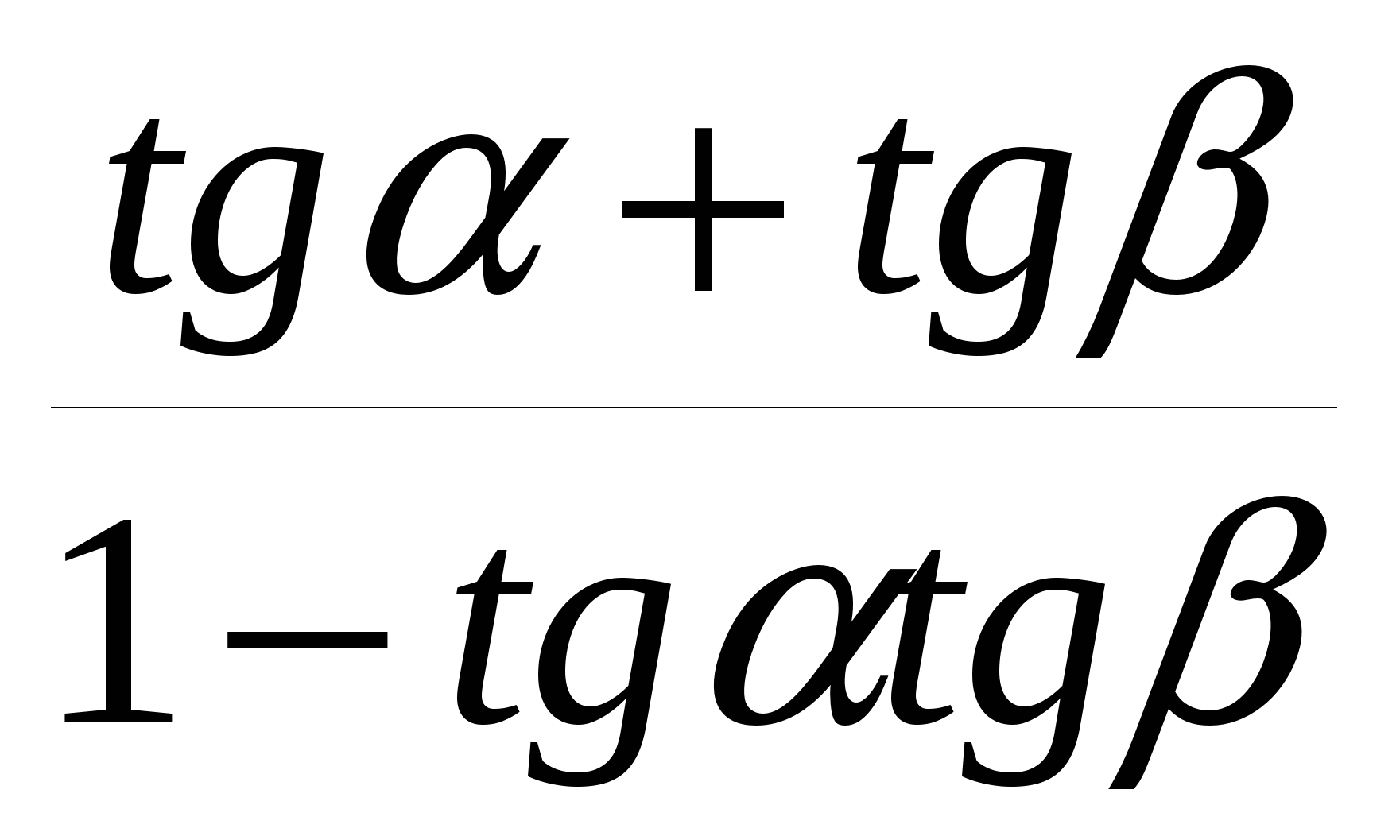
B. 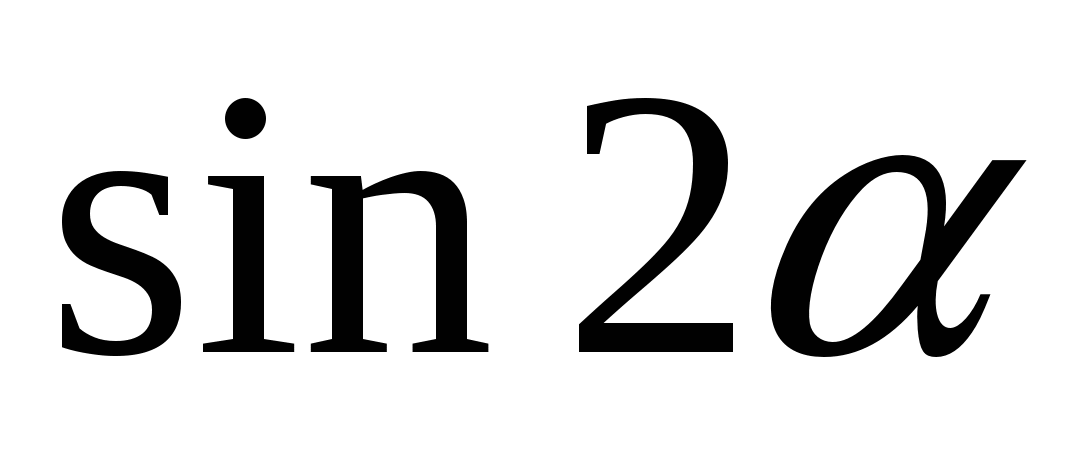 = =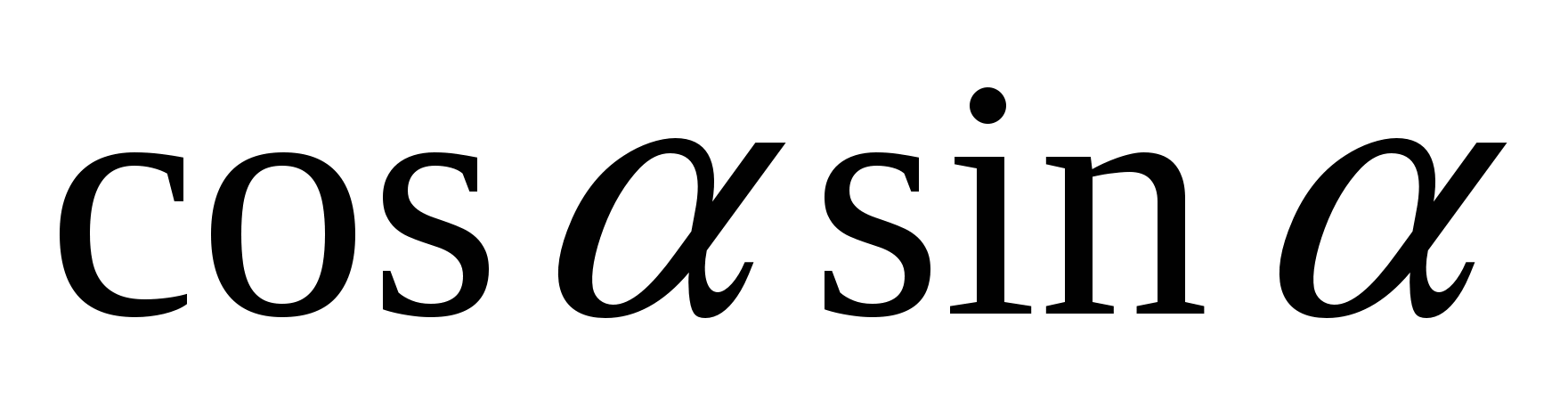
C. 1+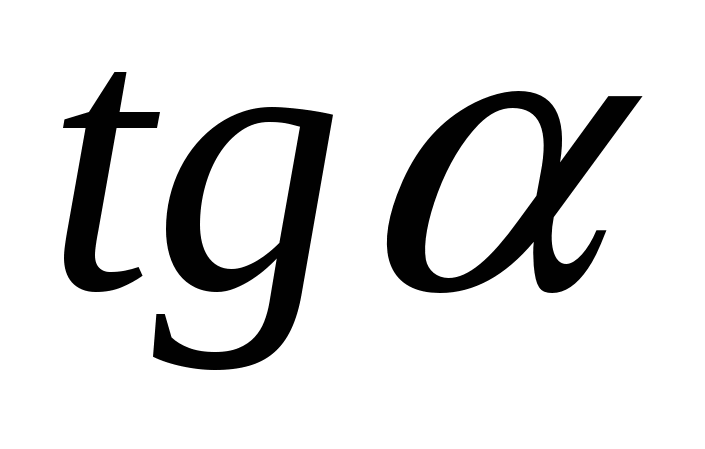 = =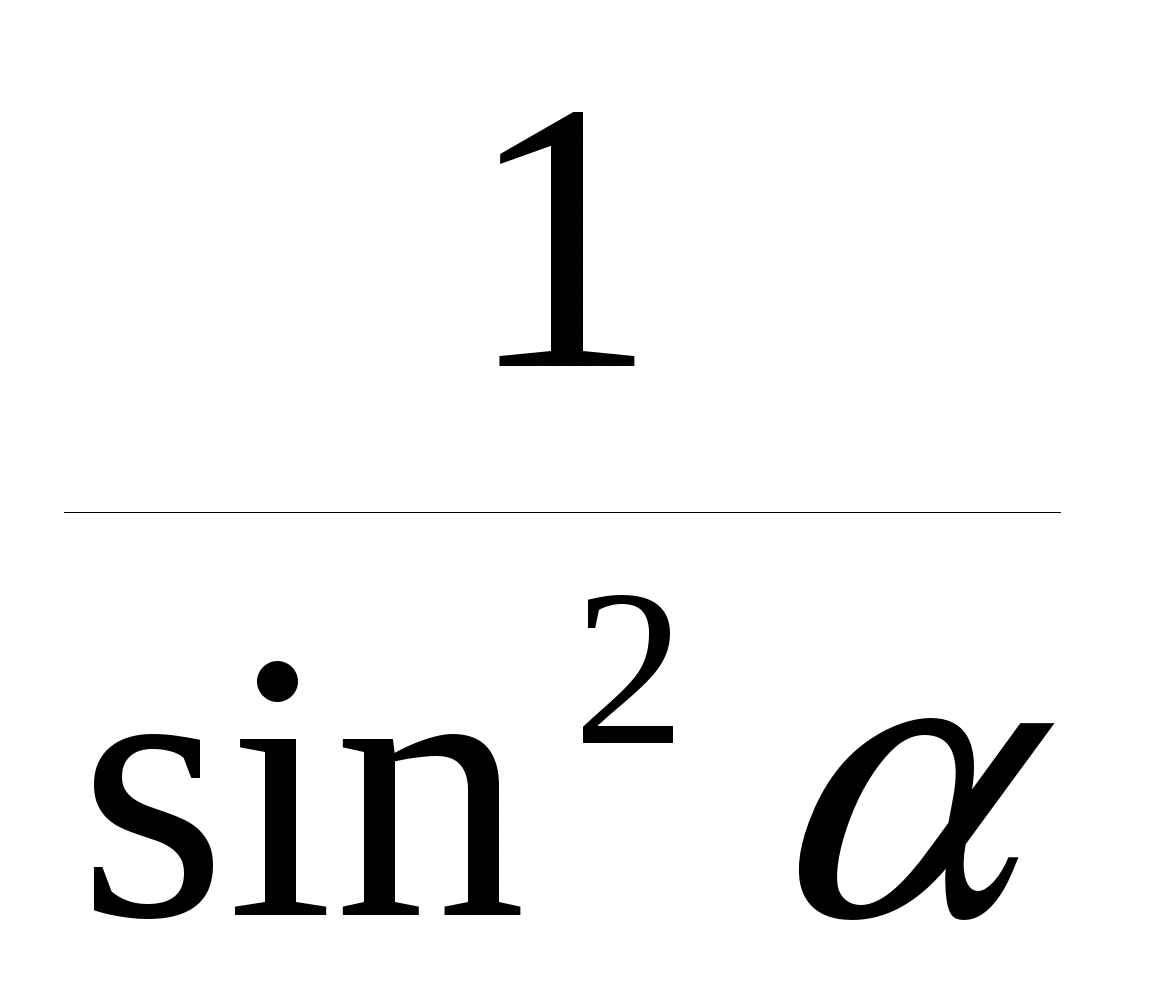
D. 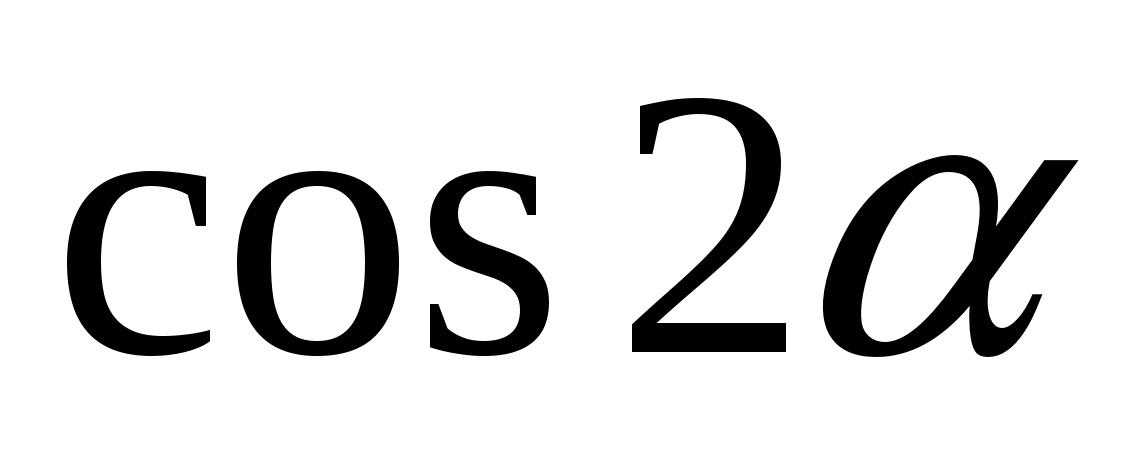 = =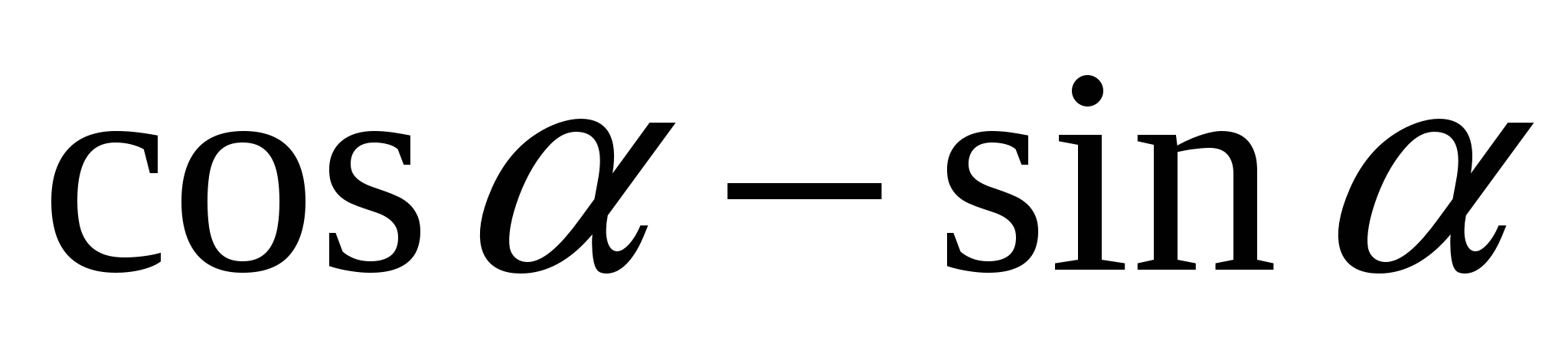
E. 1+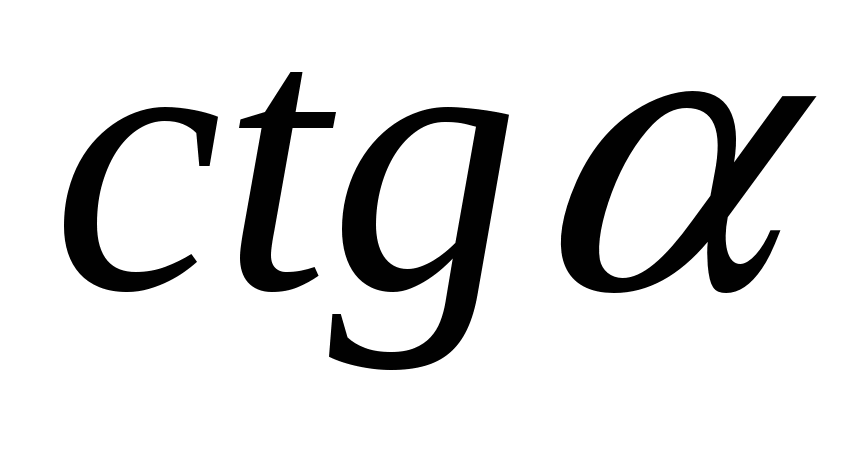 = =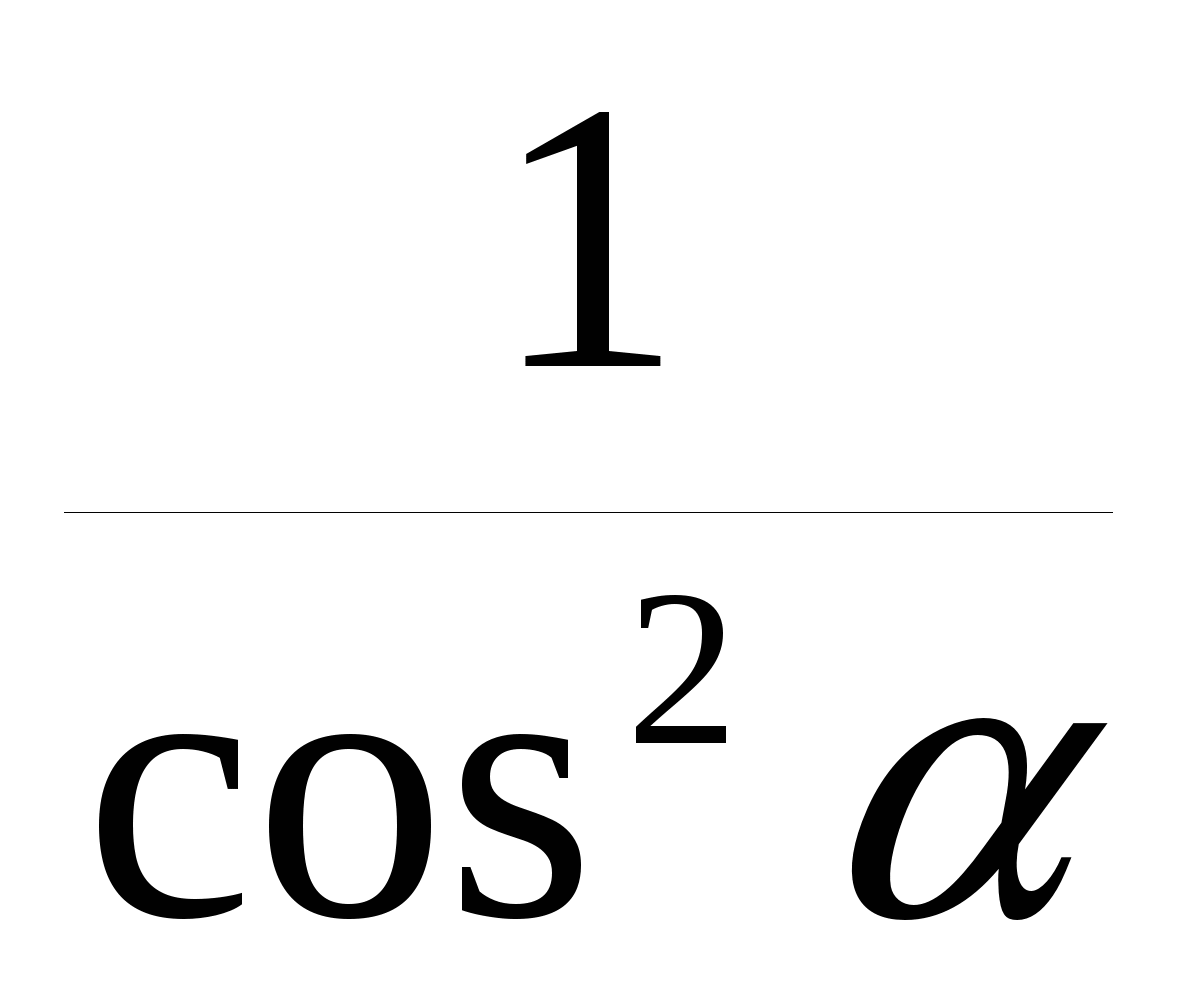
-
Радиус шара 3 см. Найдите объем шара
А. 48 см3 см3
B. 72 см3 см3
С. 18 см3 см3
D. 36 см3 см3
E. 16 см3 см3
-
Расстояние между пунктами на карте равно 4,5 см, а на местности 27 км. Найдите масштаб карты
А. 1:60000
B. 1:600
С. 1:600000
D. 1:6000000
E. 1:6000
-
Сумма корней уравнения 6х2+х-7=0 равна:
А. 6
B. 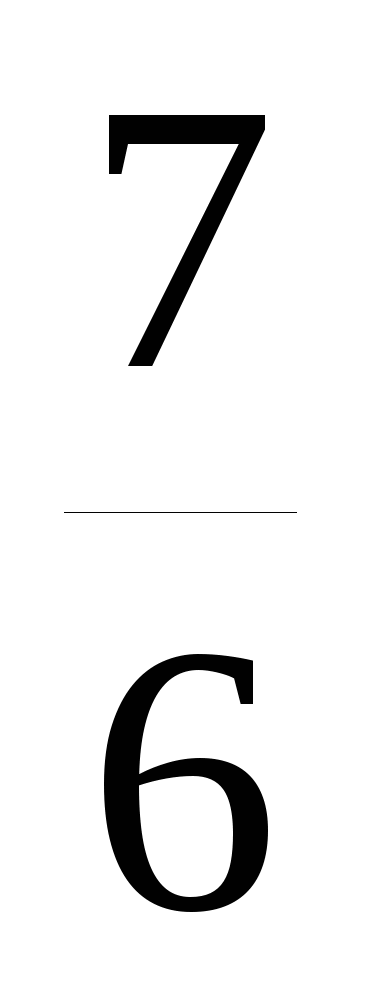
С. 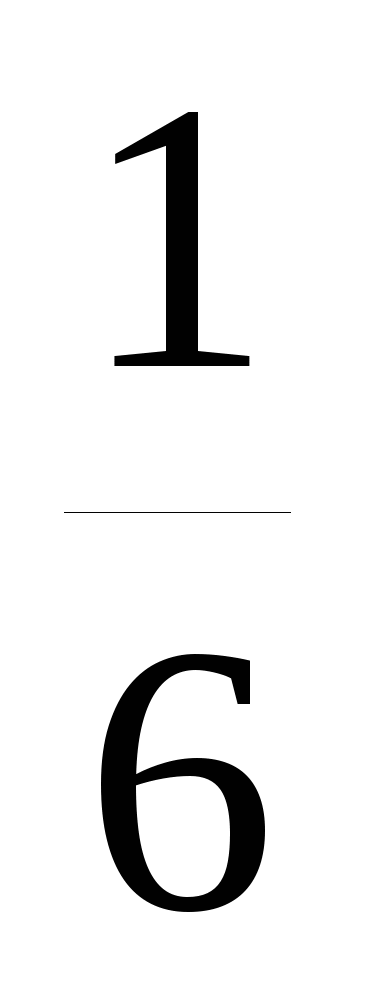
D. -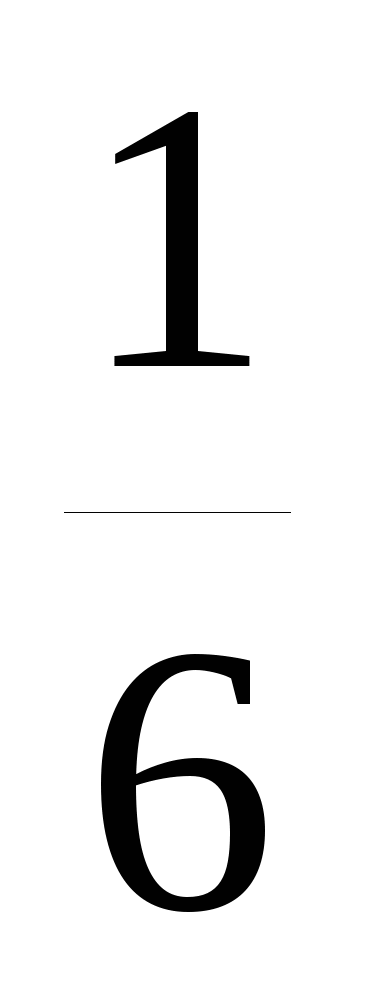
E. -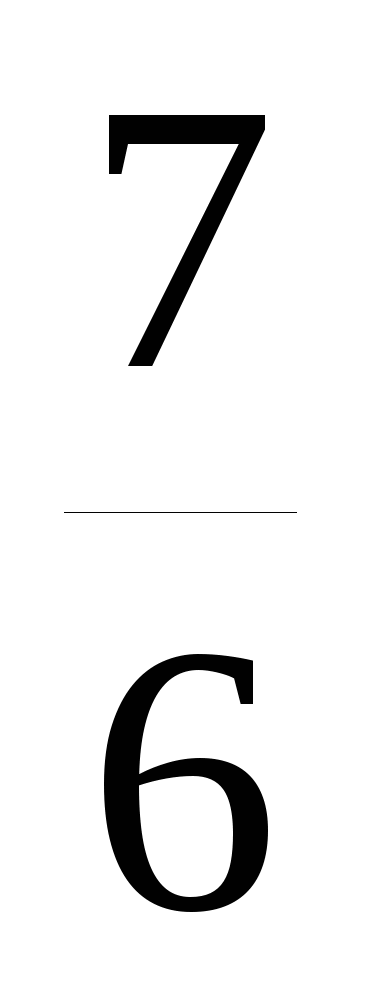
-
Найдите значение выражения (3,1(6)-2,4(6)):1,4
А. 0,5
B. 1
С. 1,5
D. 2
E. 7
10.Найдите область определения функции y=arcsin(2x-5)
А. -1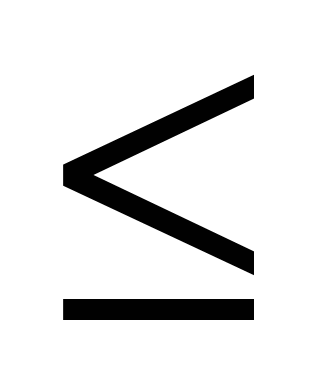 x x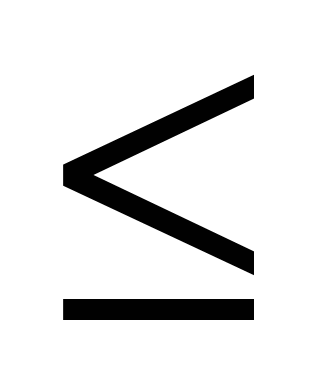 1 1
B. x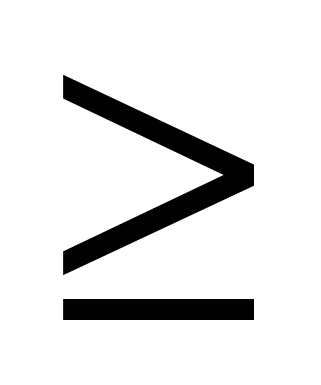 2 2
С. x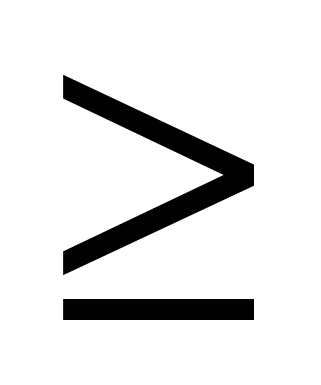 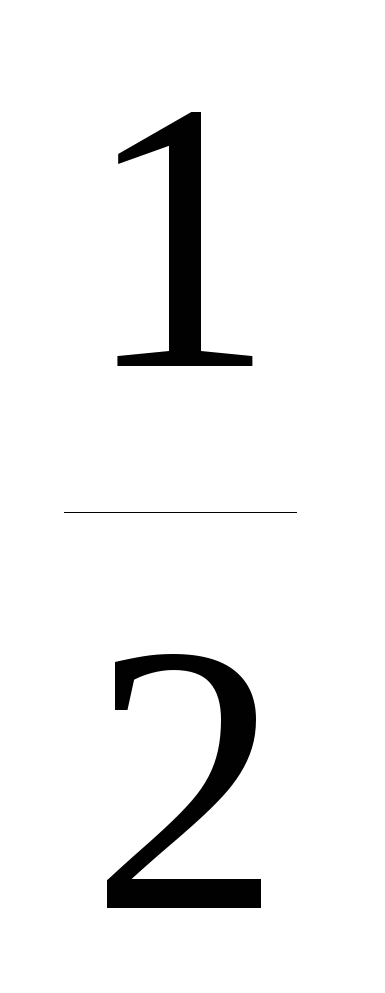
D. x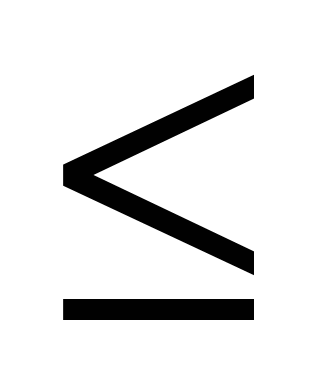 3 3
E. 2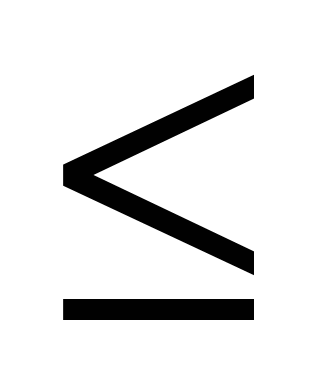 x x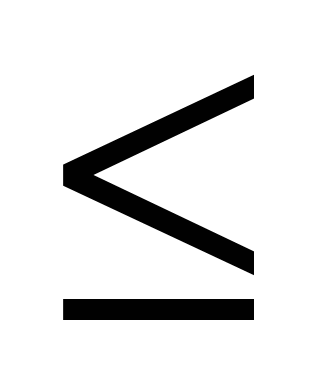 3 3
11.Упростить выражение: (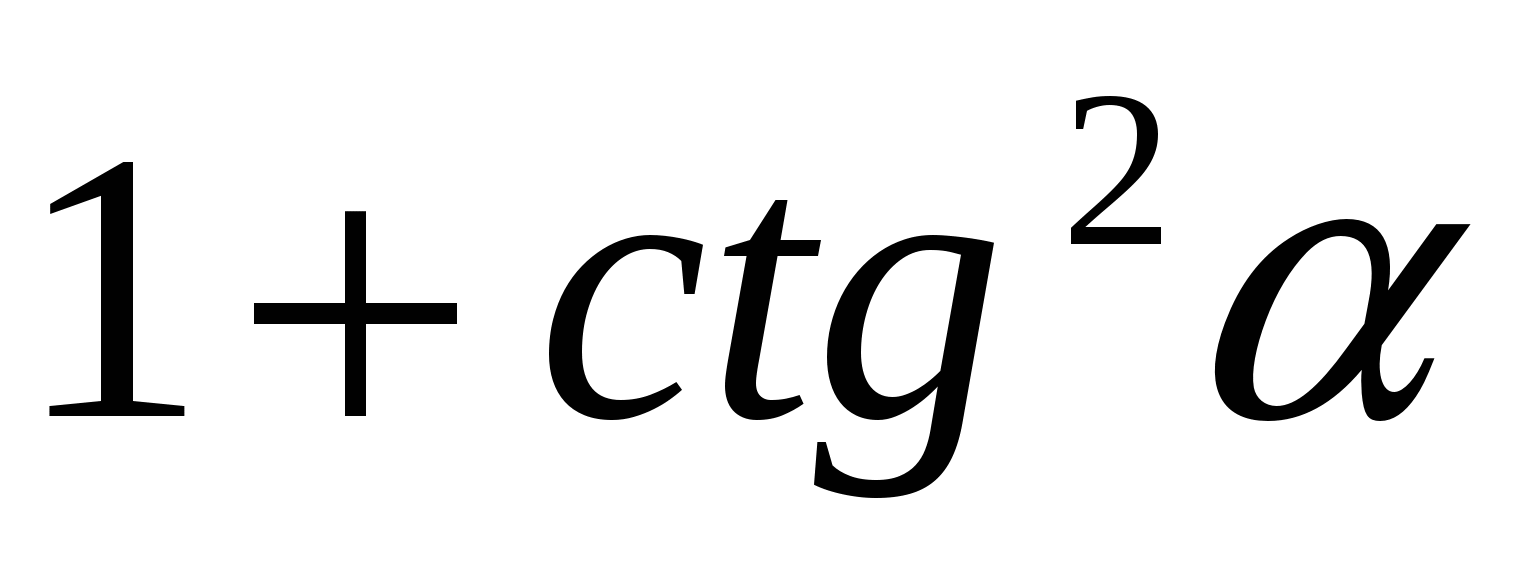 )( )(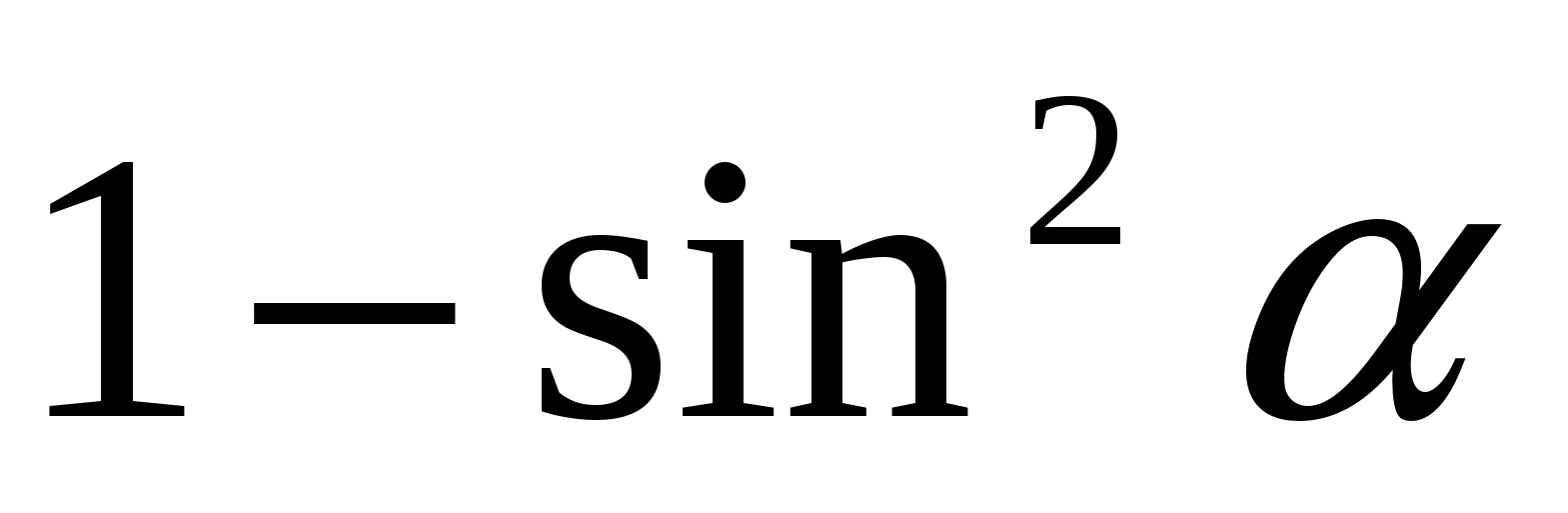 ) )
А. 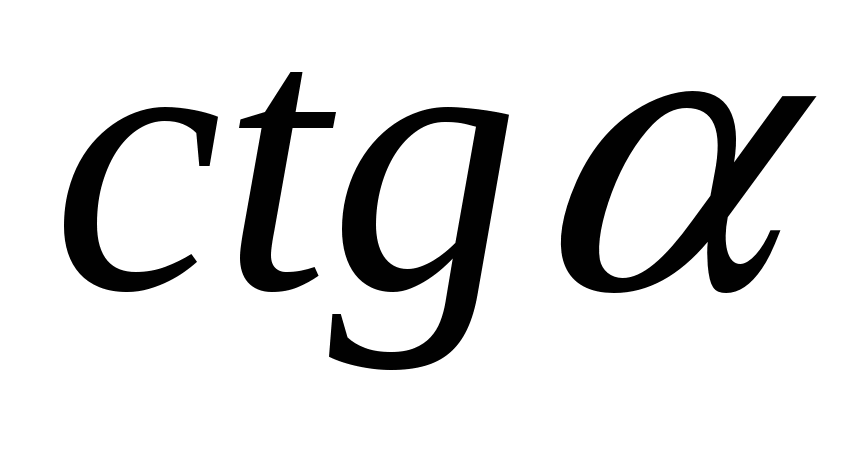
B. 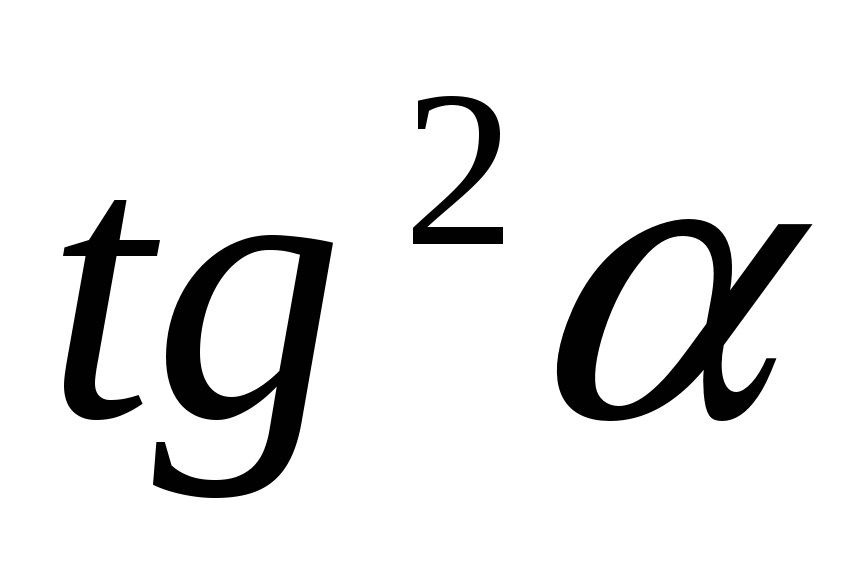
С. 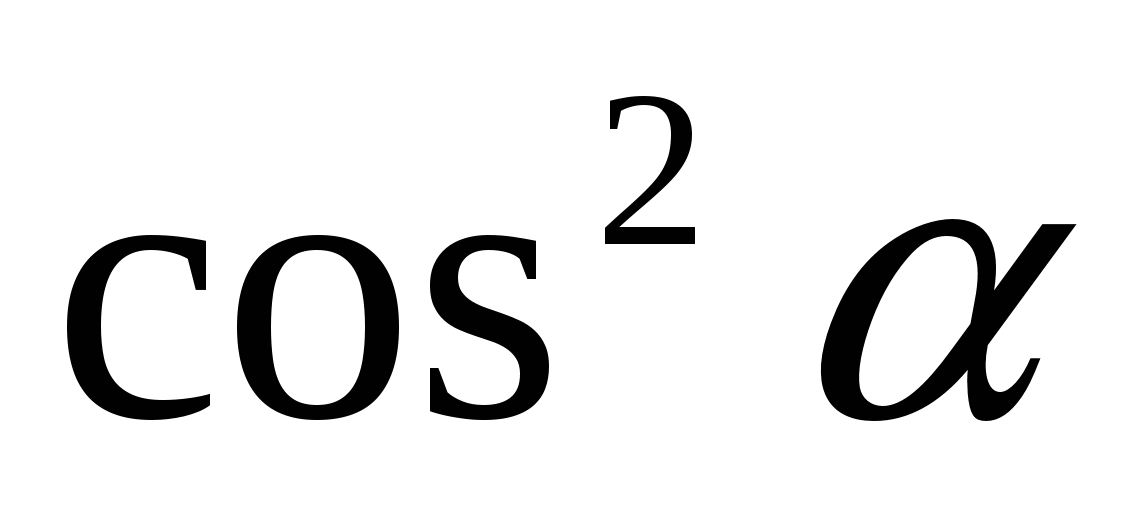
D. 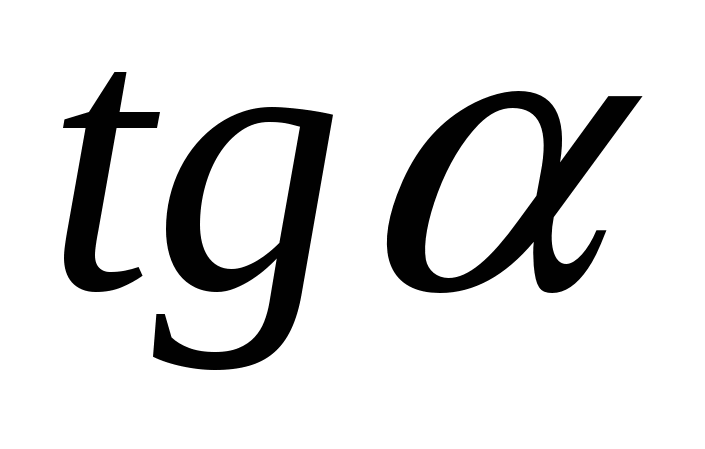
E. 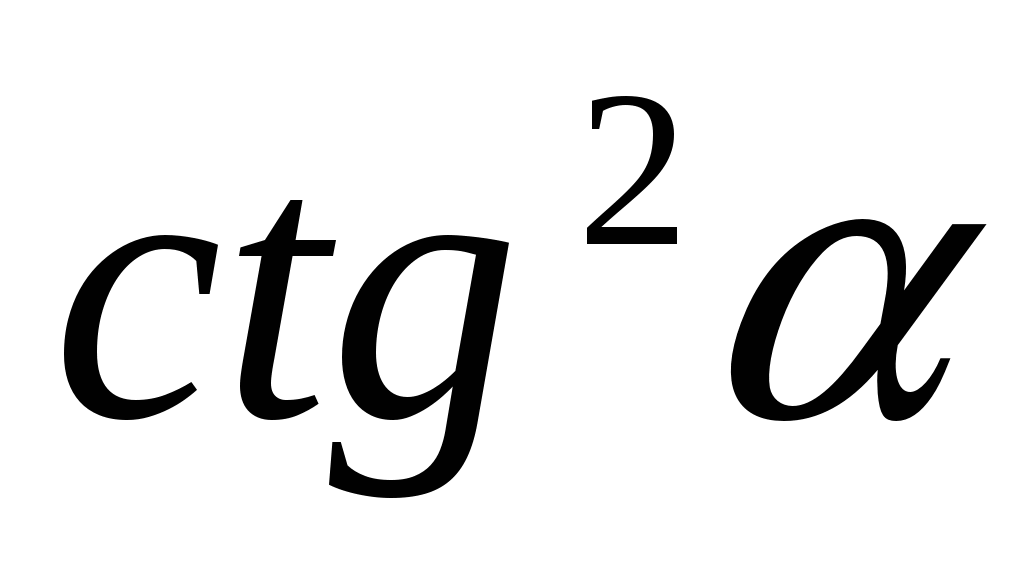
12. Исследуйте функцию f(x)=x2+2x-3 на экстремум
А. х=-4, точка минимума
B. х=1, точка максимума
С. х=-1, точка максимума
D. х=4, точка минимума
E. х=-1, точка минимума
13. Решите уравнение (х-5)(х+2)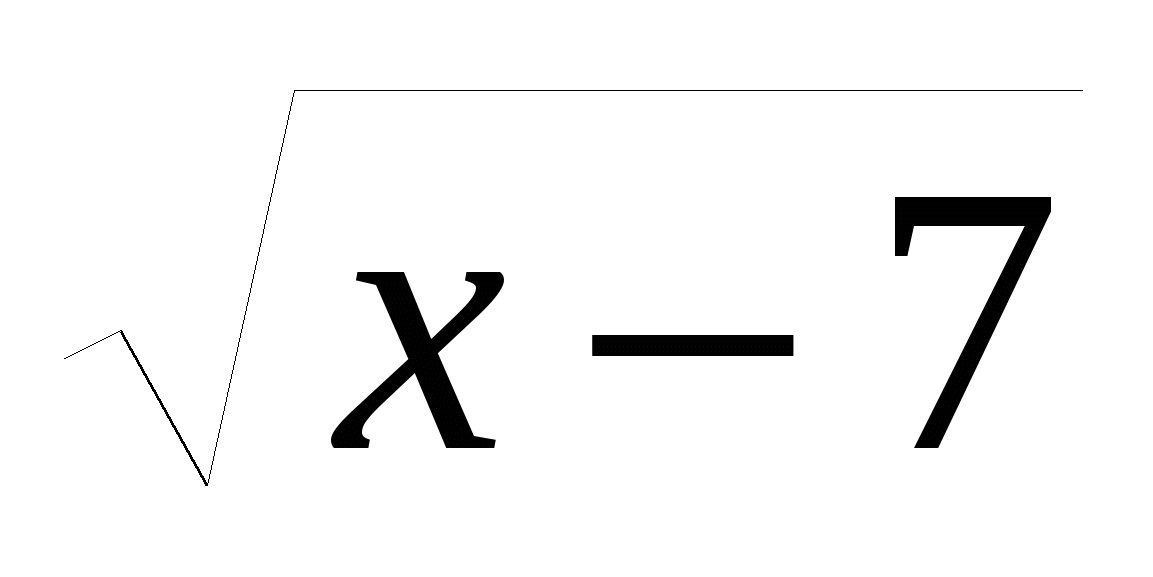 =0 =0
А. х=3
B. х1=5, х2=-2, х3=7
С. х=5
D. х1=7, х2=-2
E. х=7
14. Две трубы вместе наполняют бассейн за 7,5 часов. Первая труба в отдельности наполняет бассейн на 8 часов быстрее, чем вторая. Определите за сколько часов наполнит бассейн первая труба?
А. 15ч.
B. 12ч.
С. 11ч.
D. 14ч.
E. 10ч.
15. В каких точках касательная к графику функции y=f(x) образует с осью ОХ угол 450, если f(x)= 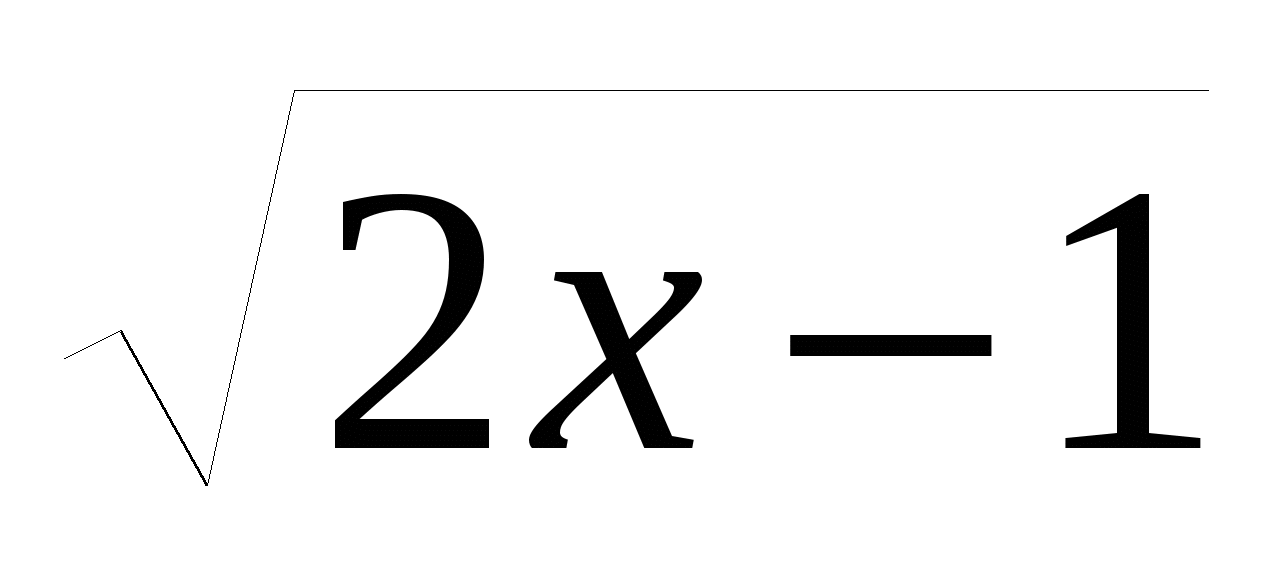
А. (0;1)
B. (-1;0)
С. (-1;1)
D. (1;1)
E. (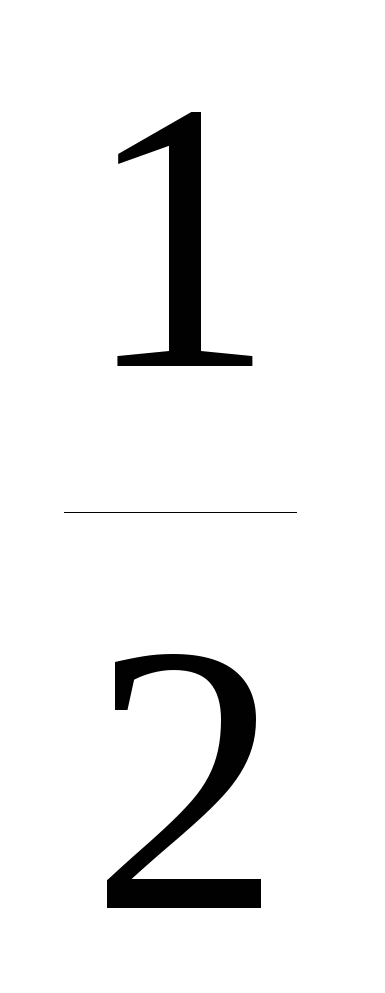 ;0) ;0)
16. Сухие фрукты содержат 20% воды, а свежие 72% воды. Найдите массу свежих фруктов, чтобы получить 7 кг. сухих
А. 23,8 кг.
B. 35 кг.
С. 25,2 кг.
D. 19,4 кг.
E. 20 кг.
17. Найдите общий вид первообразной для функции 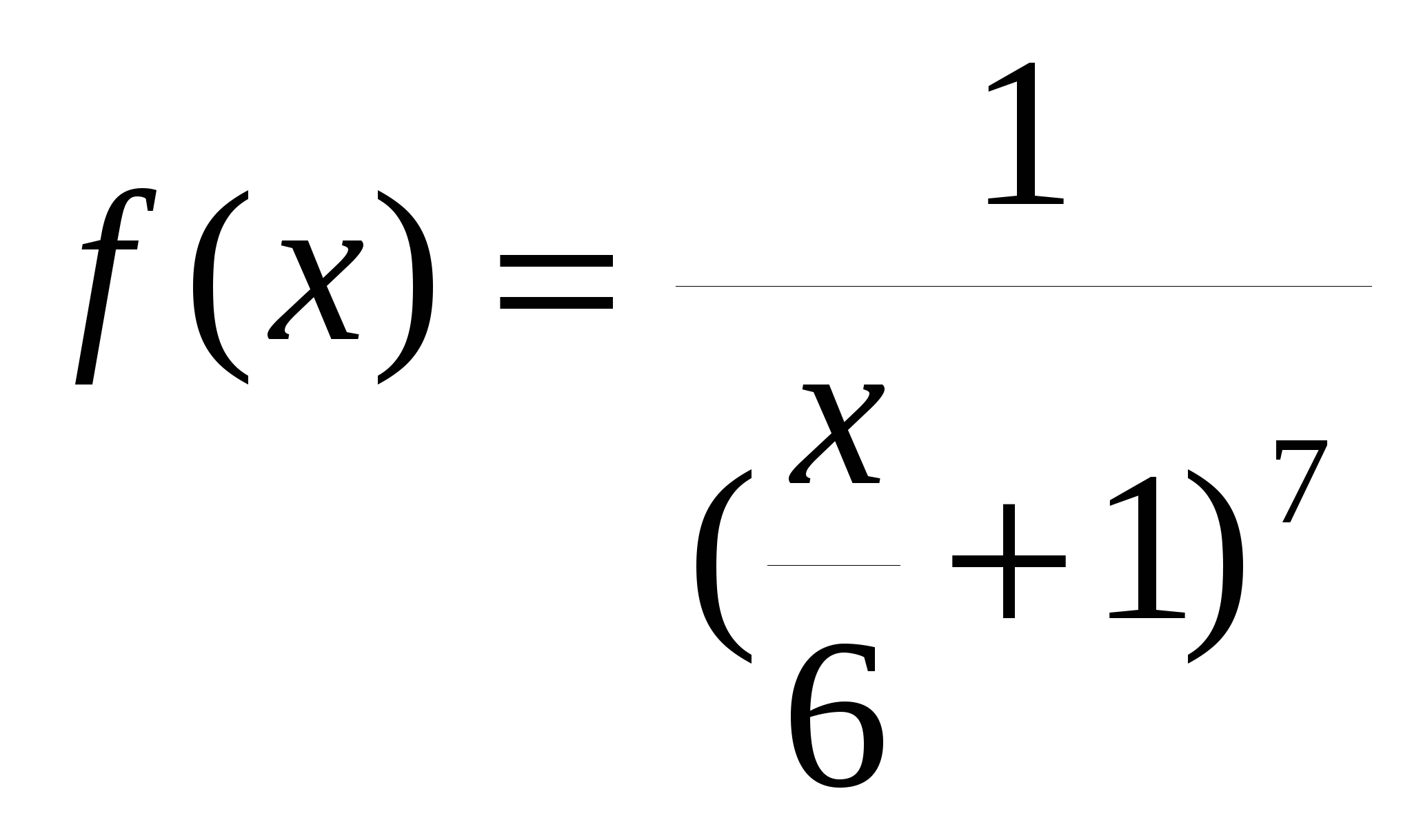
А. 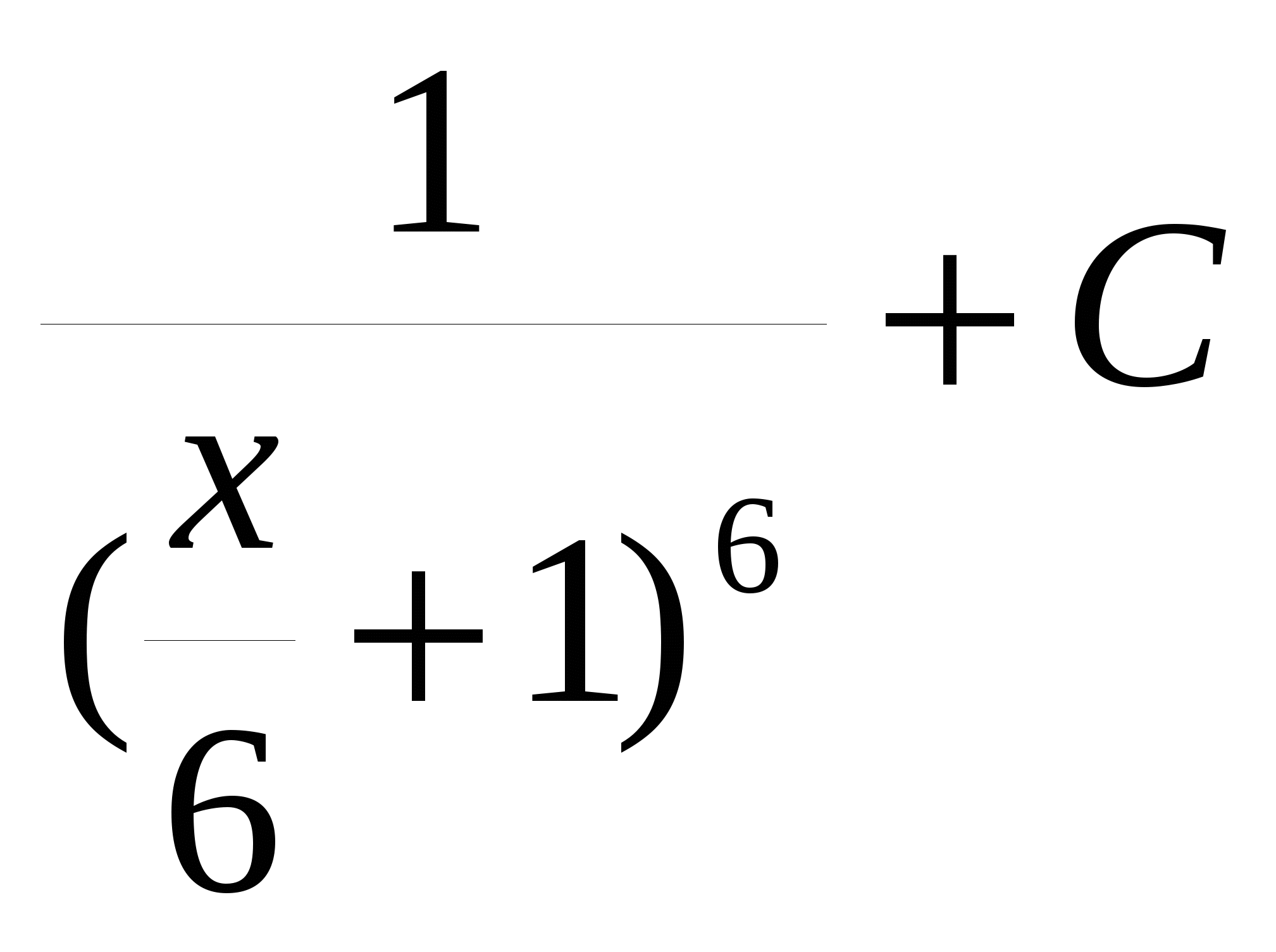
B. 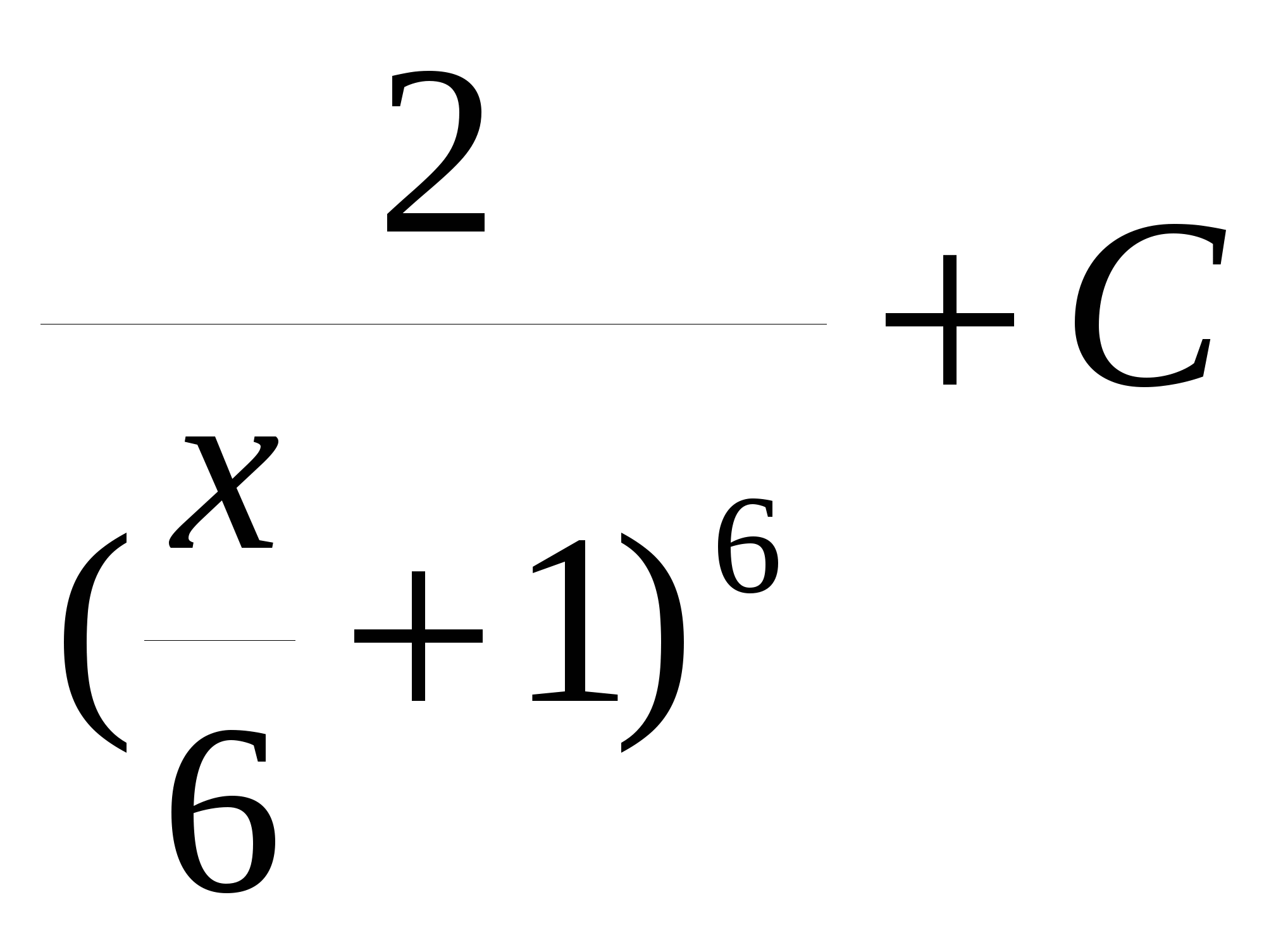
С. 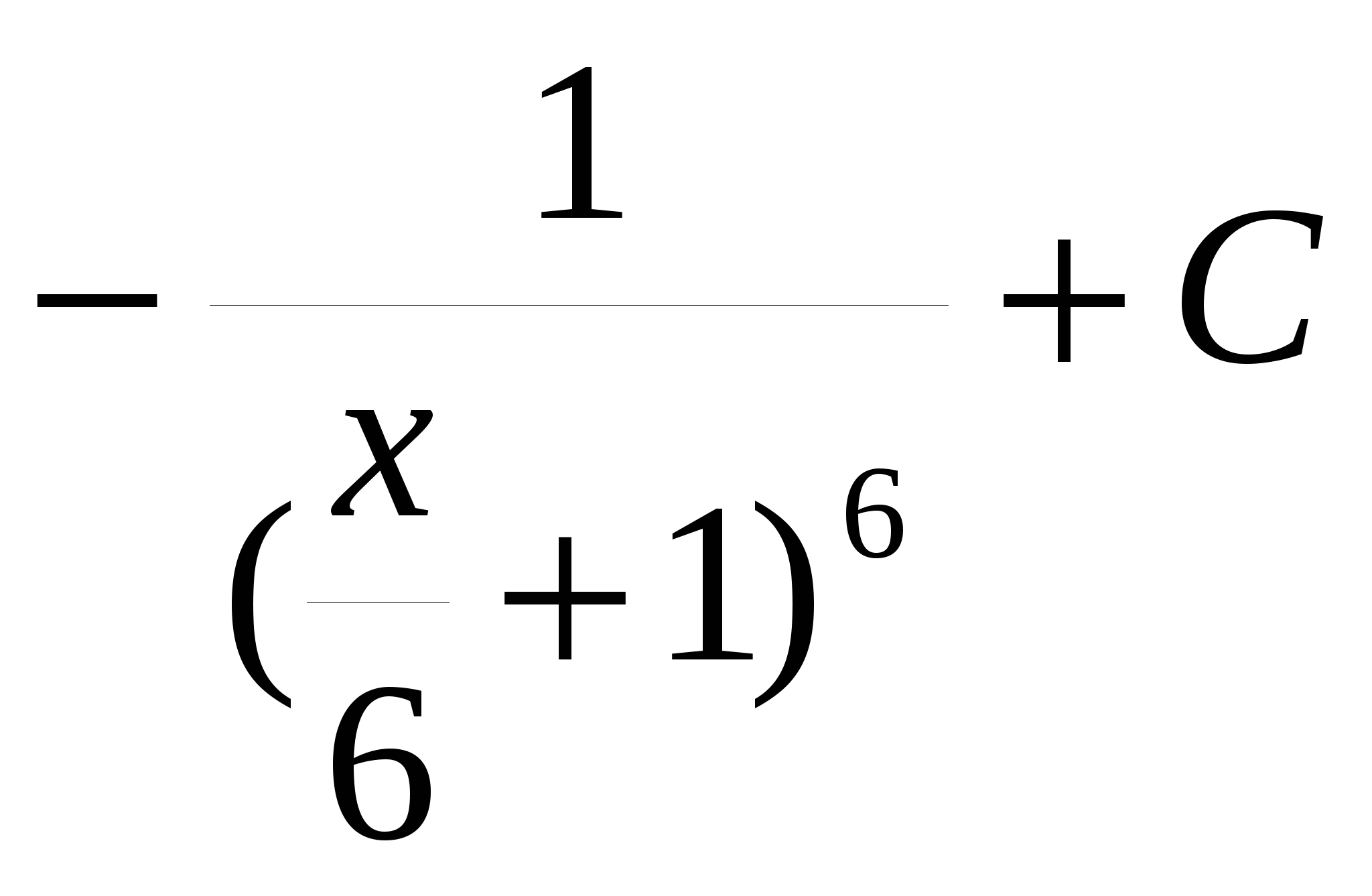
D. 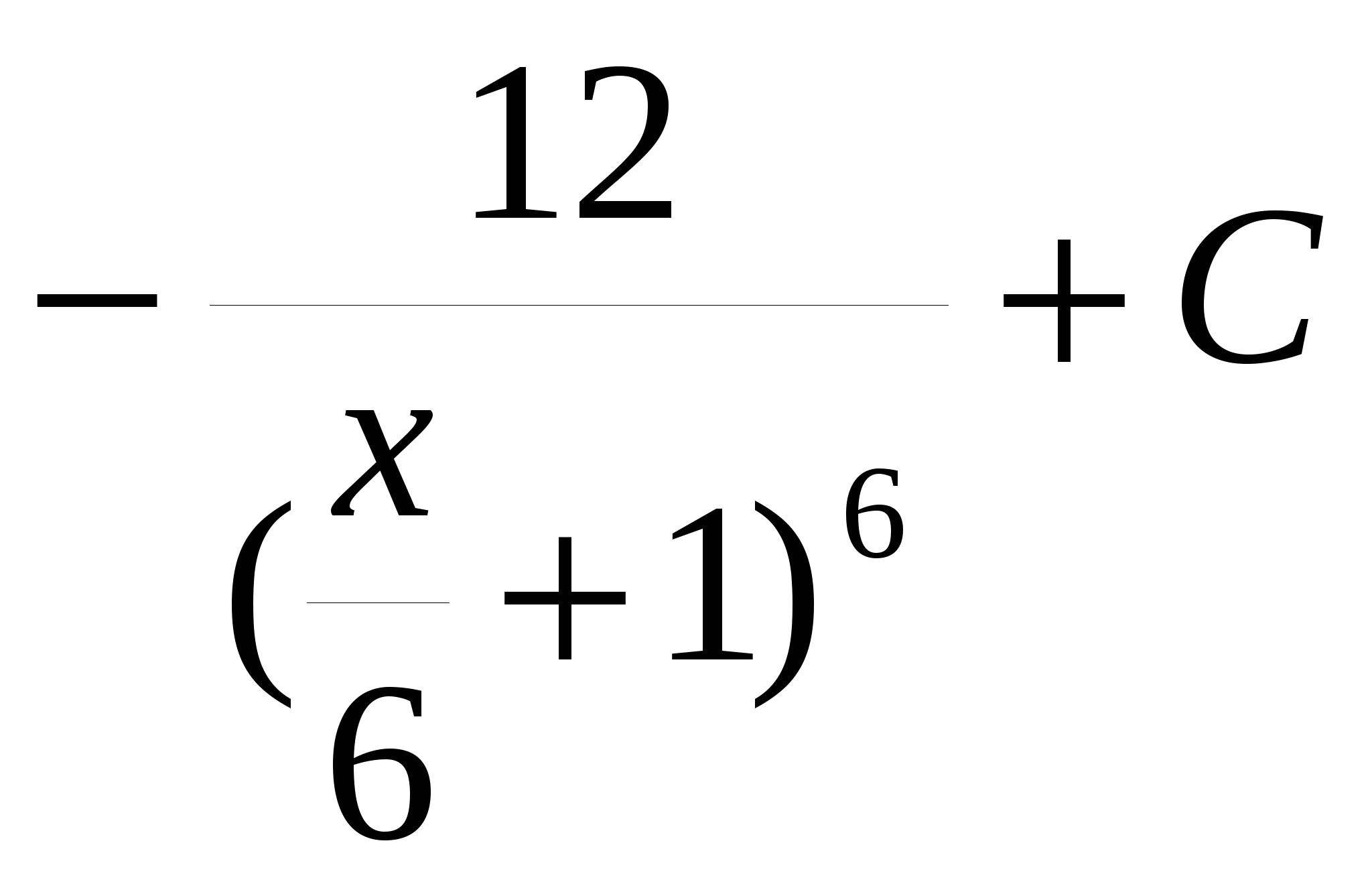
E. 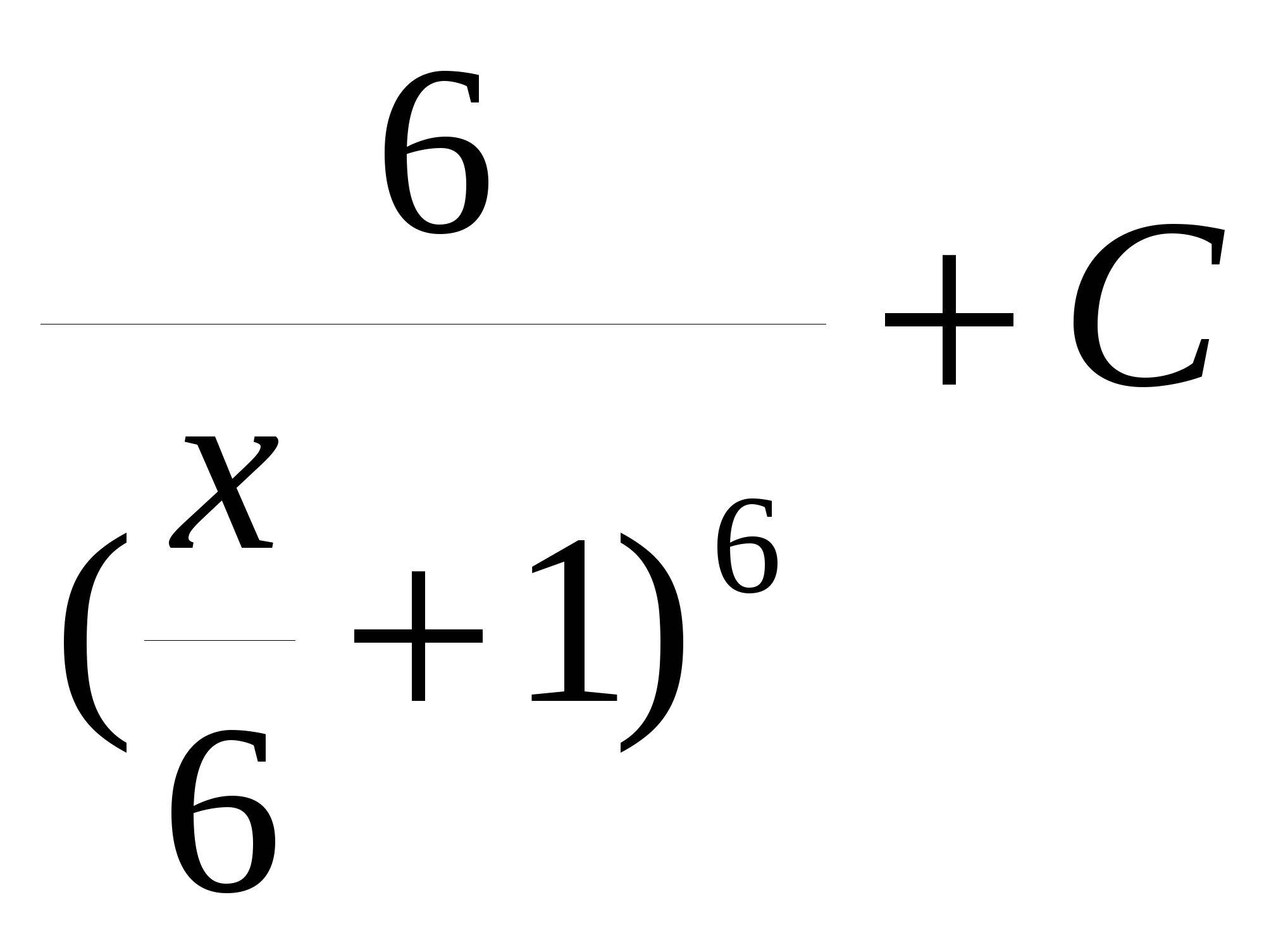
18. 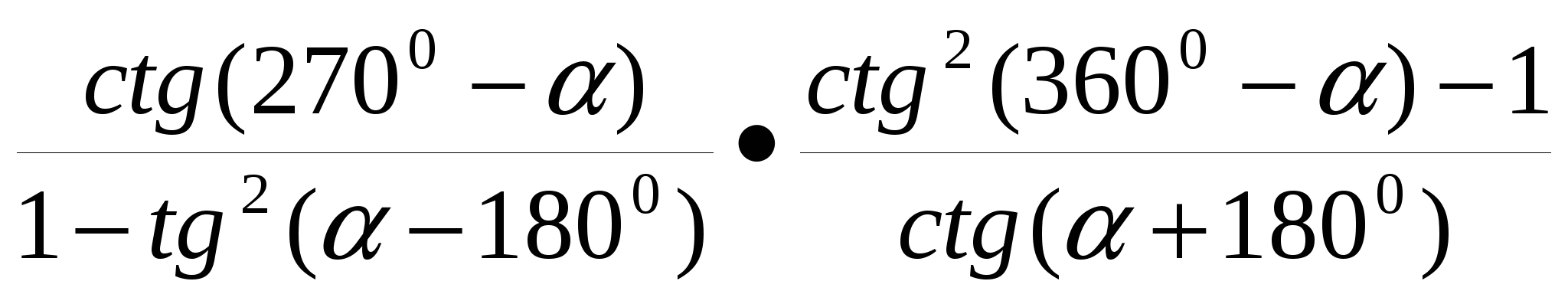
А. 1
B. -1
С. -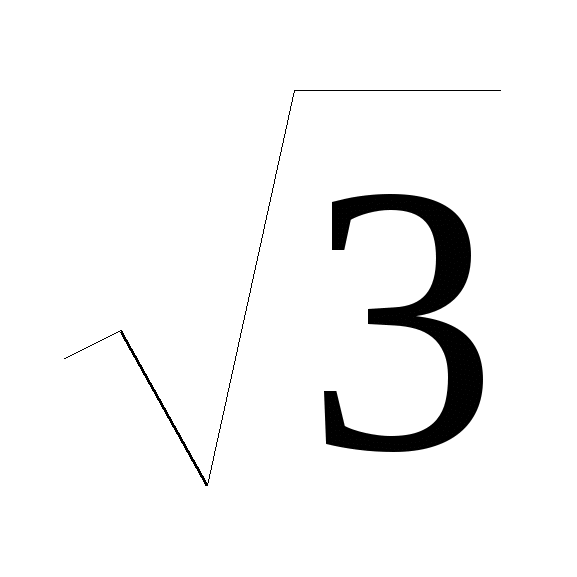
D. 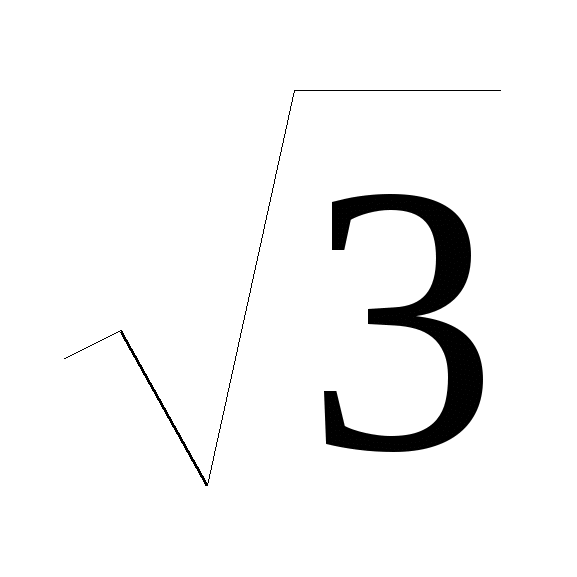
E. 0
19. Составьте уравнение касательной к графику функции у=3х2+6х+1 в точке пересечения этого графика с осью ординат
А. у=-6х+1
B. у=х+6
С. у=6х+1
D. у=6х
E. у=6х-1
20. Упростите 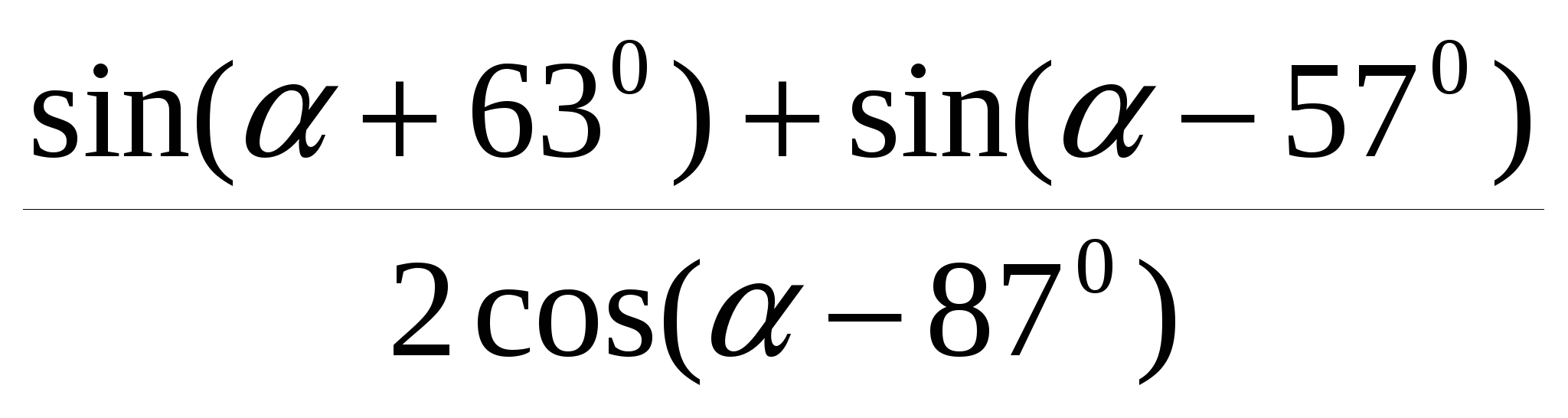
А. 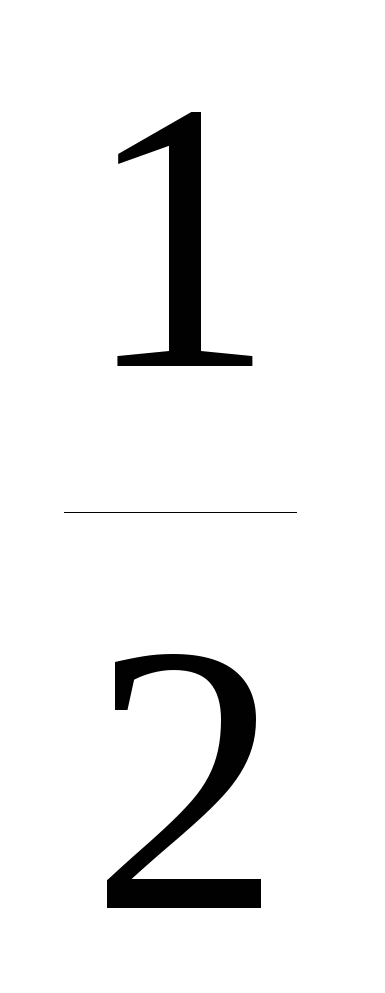
B. -1
С. 1
D. -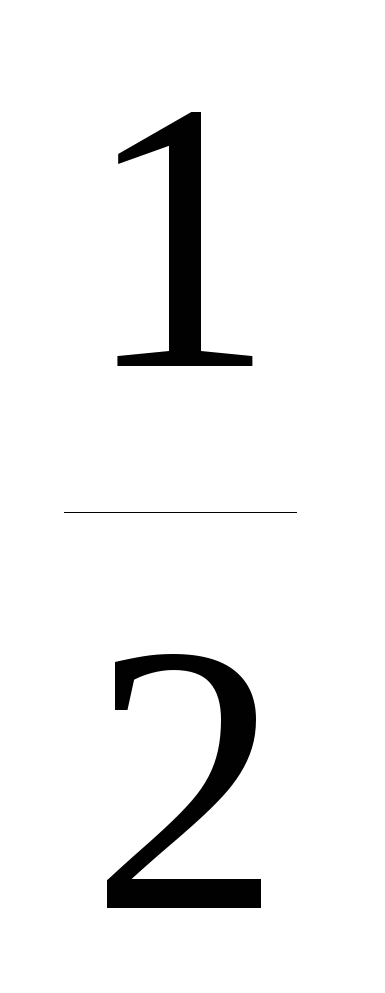
E. 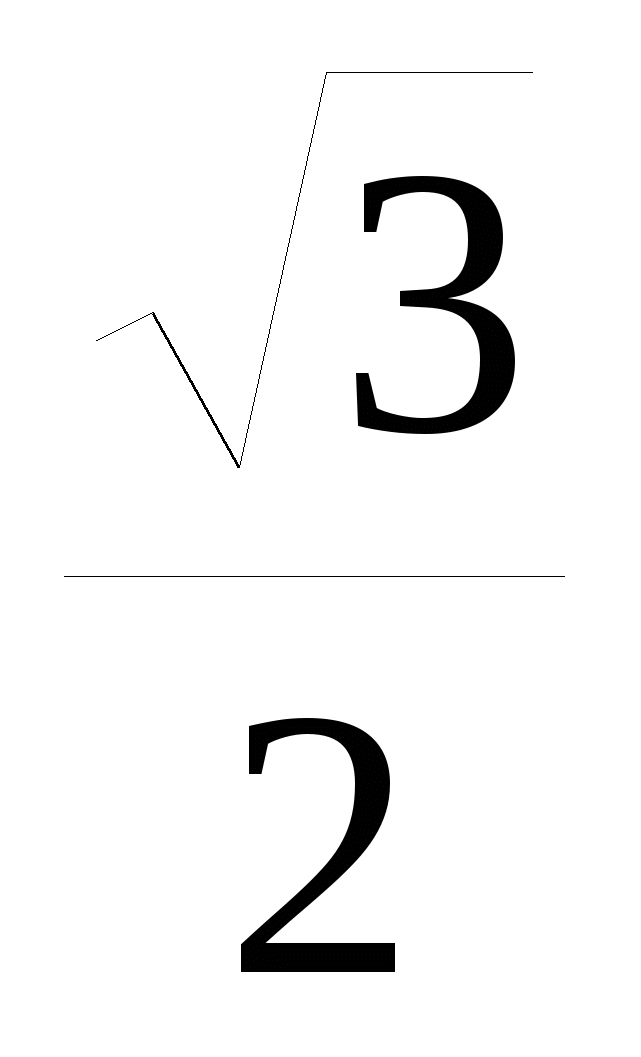
21. Вычислить sin100sin500sin700
А. 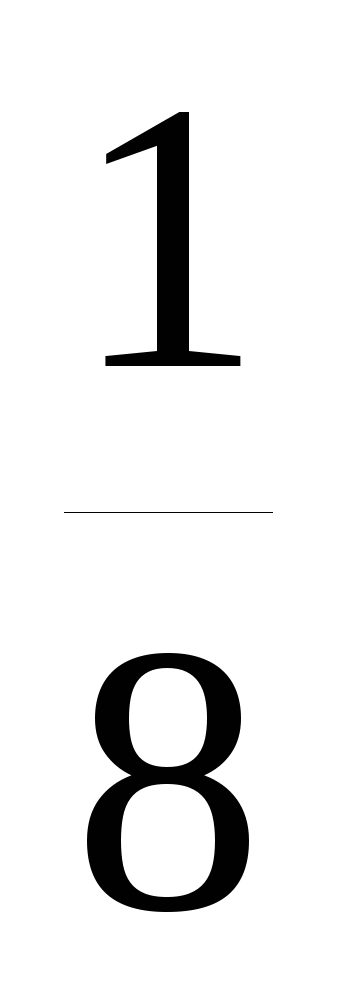
B. -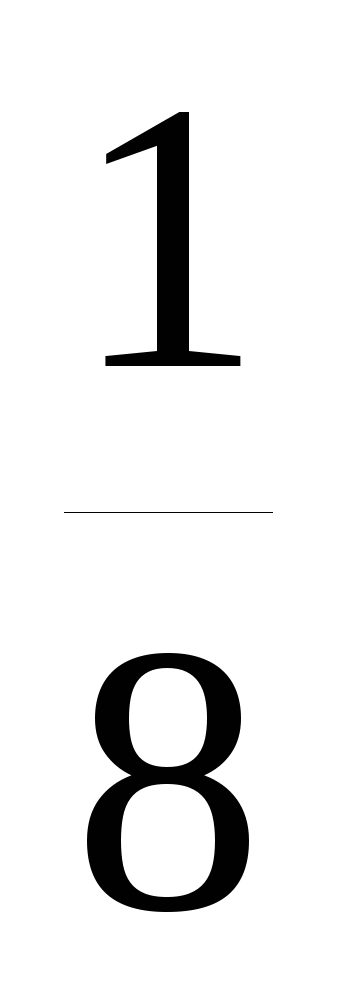
С. 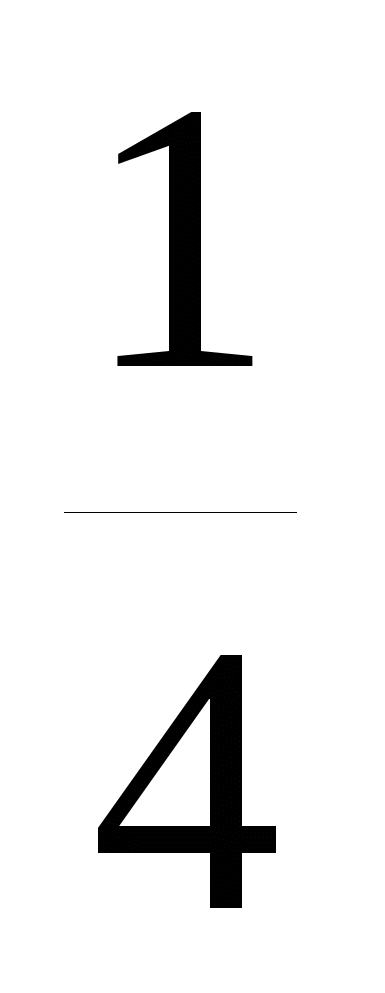
D. -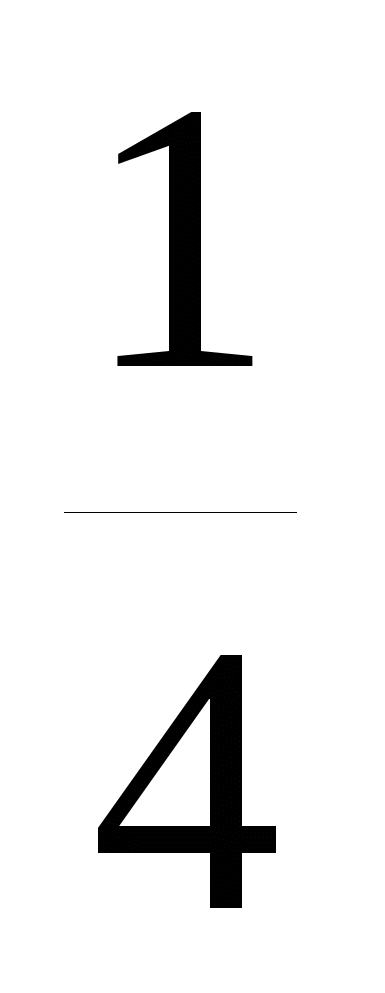
E. 1
22. Упростите выражение 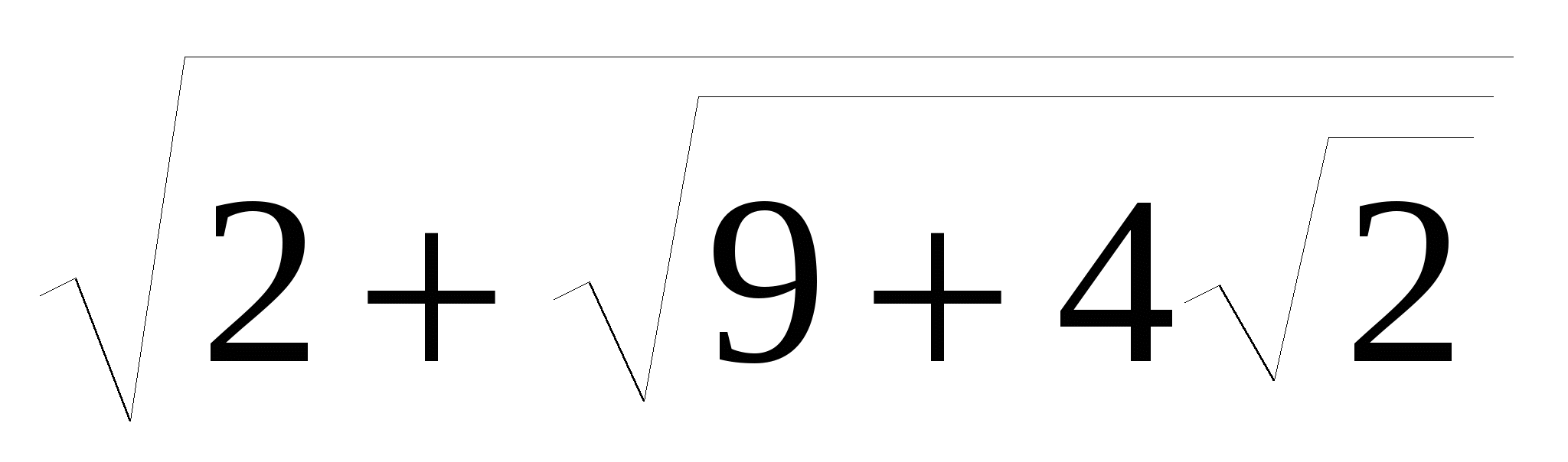
А. 5
B. 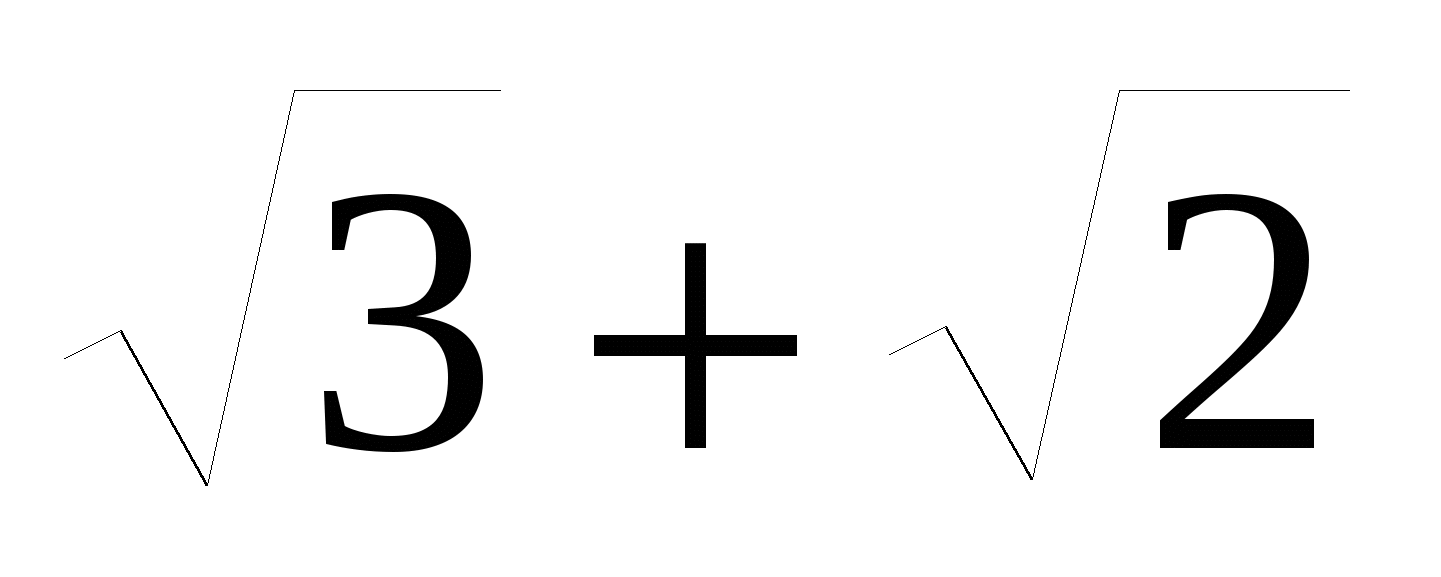
С. 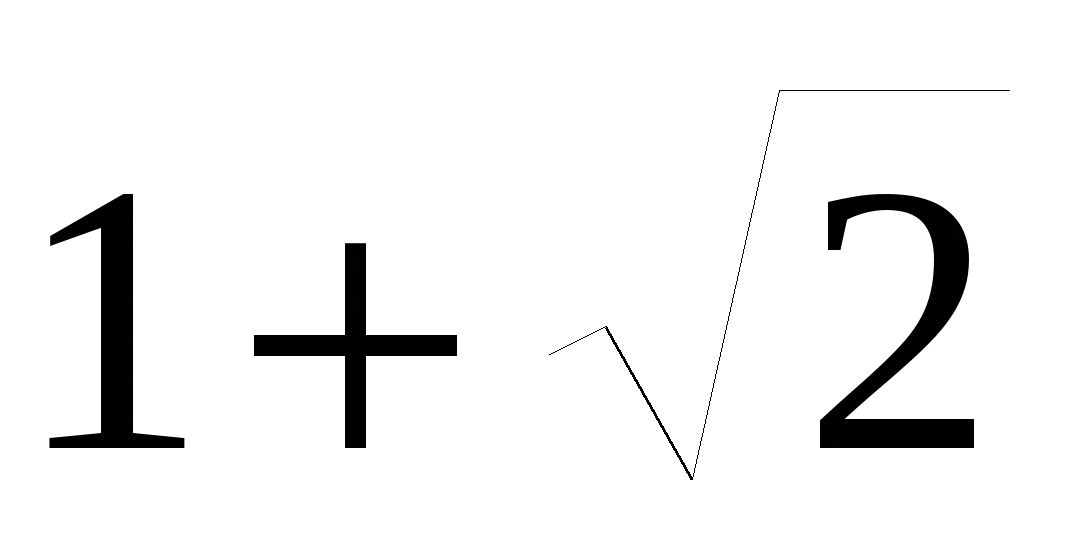
D. 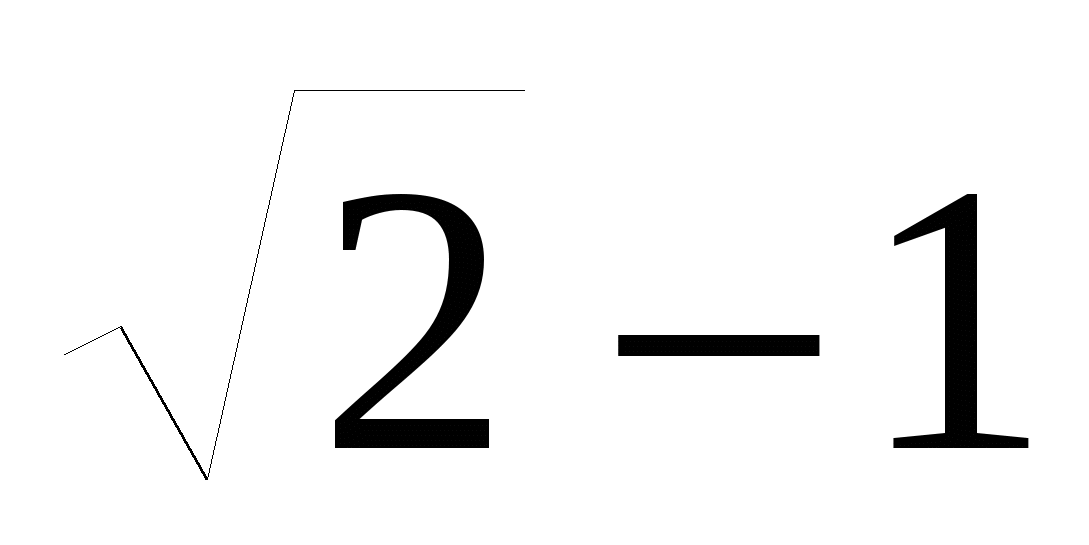
E. 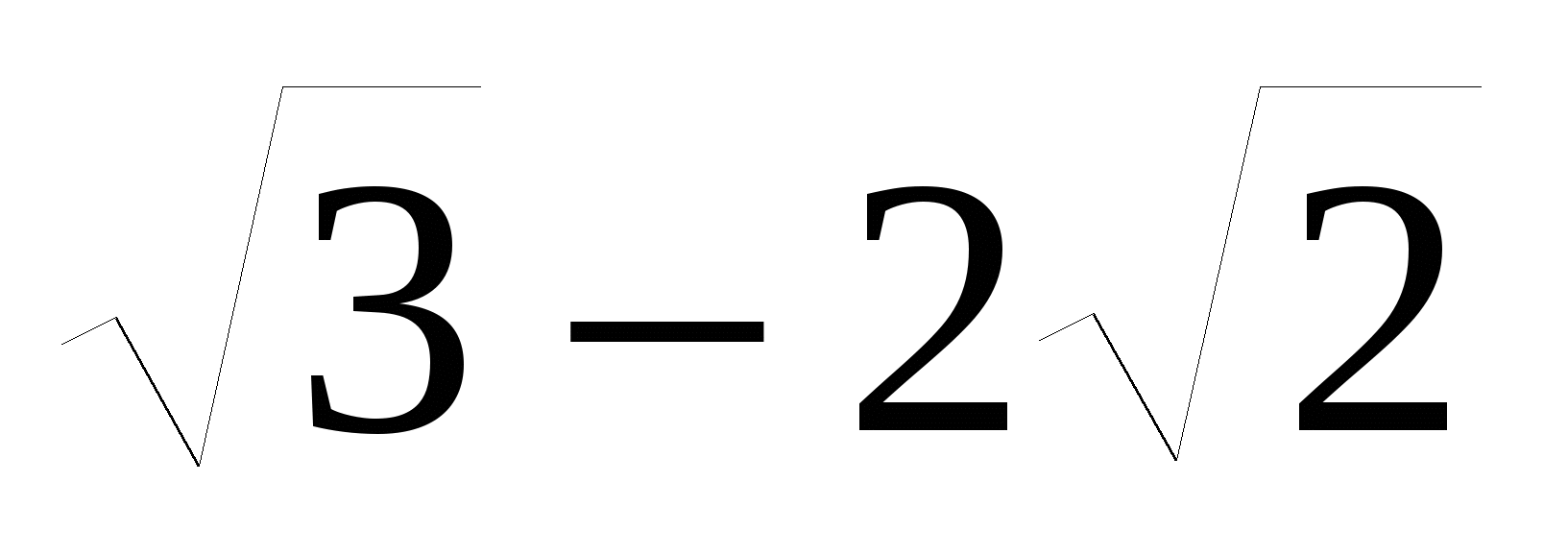
23. Найти производную 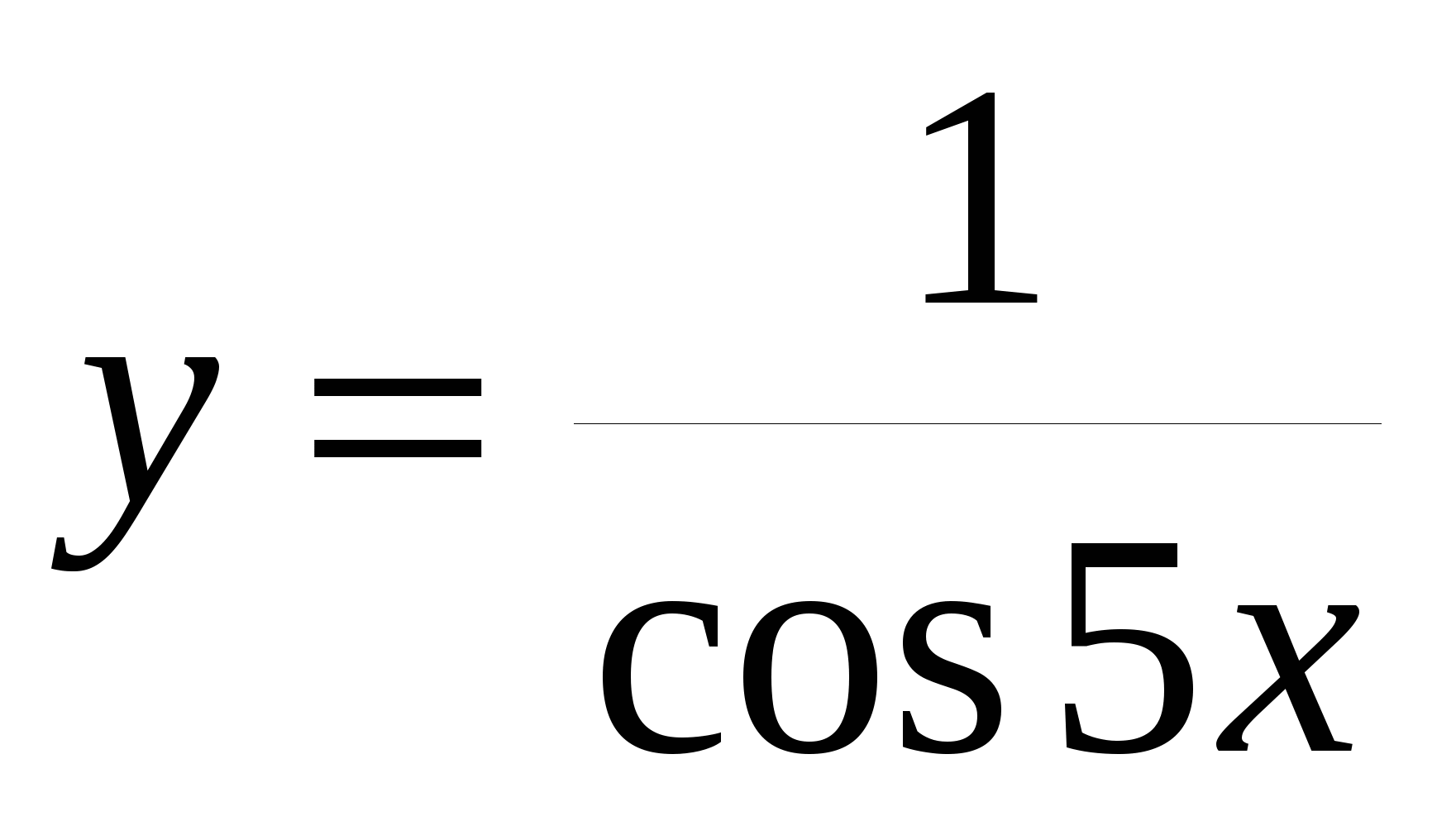
А. 5tg5xsin5x
B. 5tg5xcos5x
С. 5sin5x
D. 5tg5x
E. -5sin5x
24. Решите уравнение 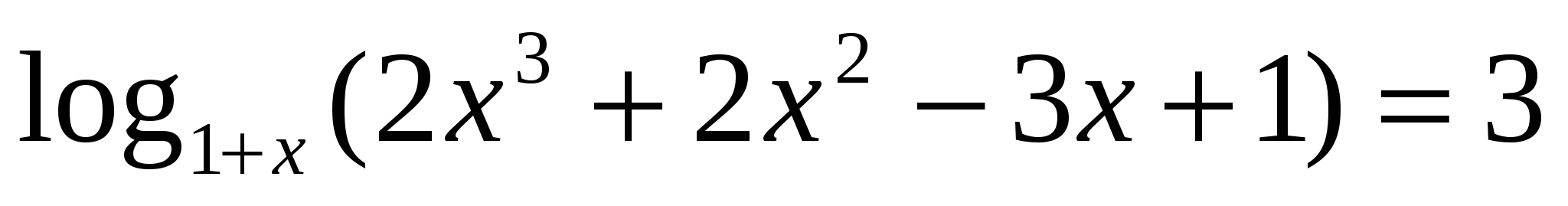
А. -2;0;3
B. -3;0;2
С. -2;3
D. 0;3
E. 3
25. Найти область значений функции 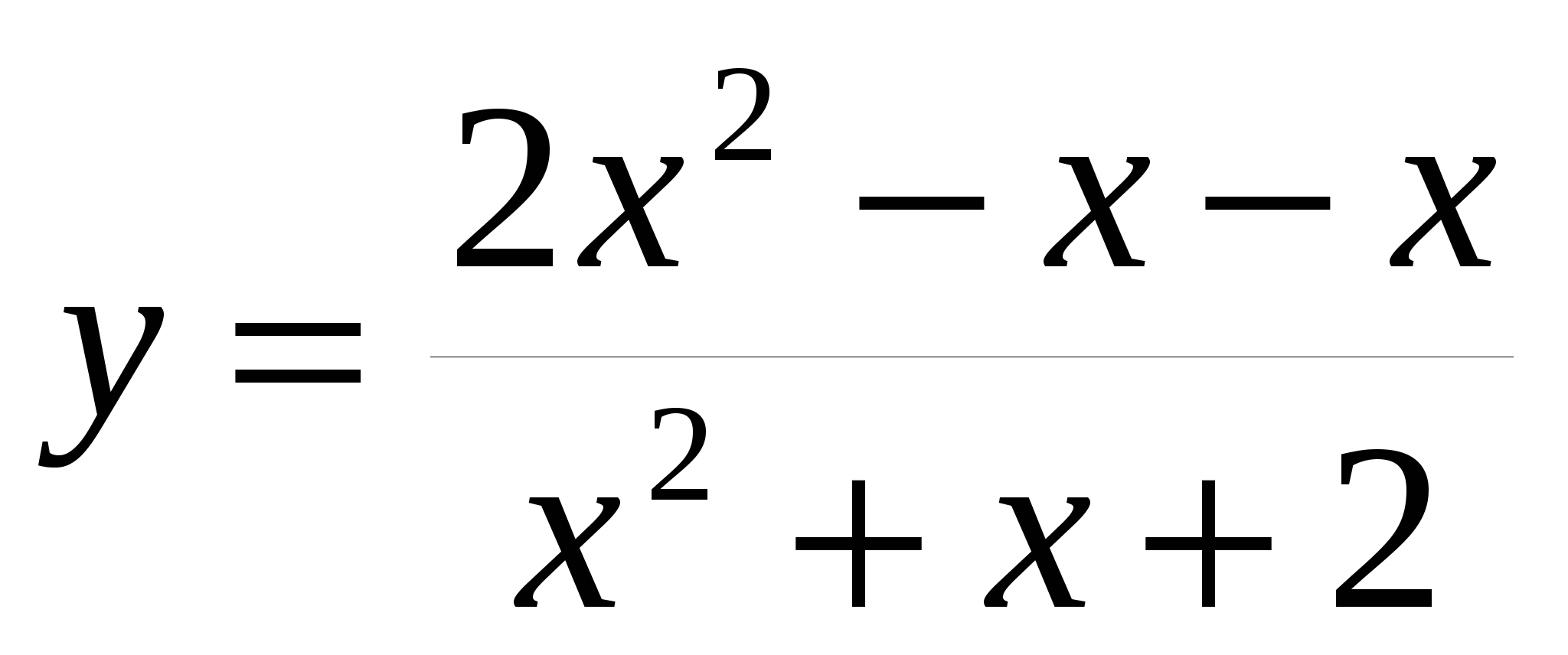
А.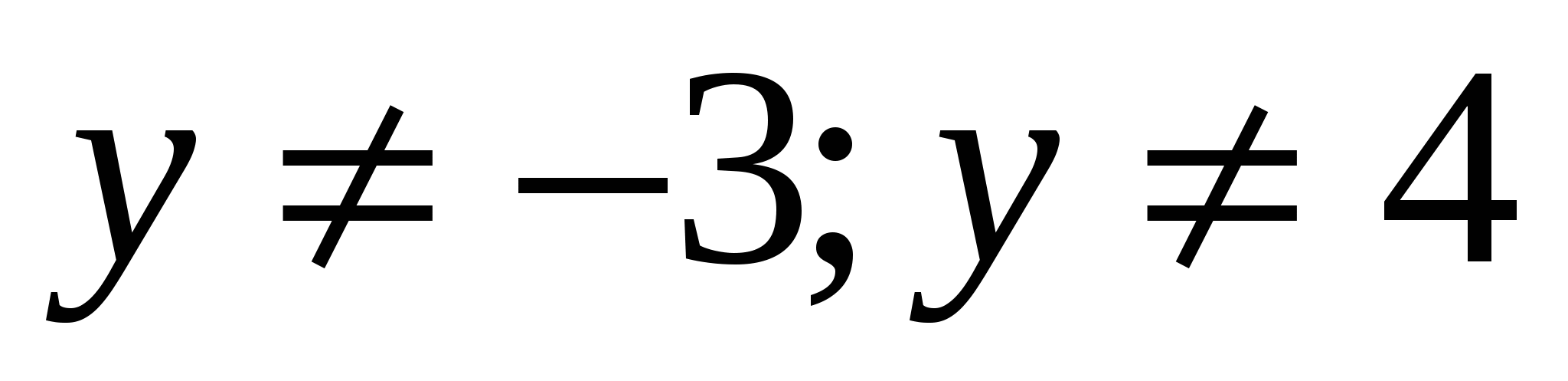
B. 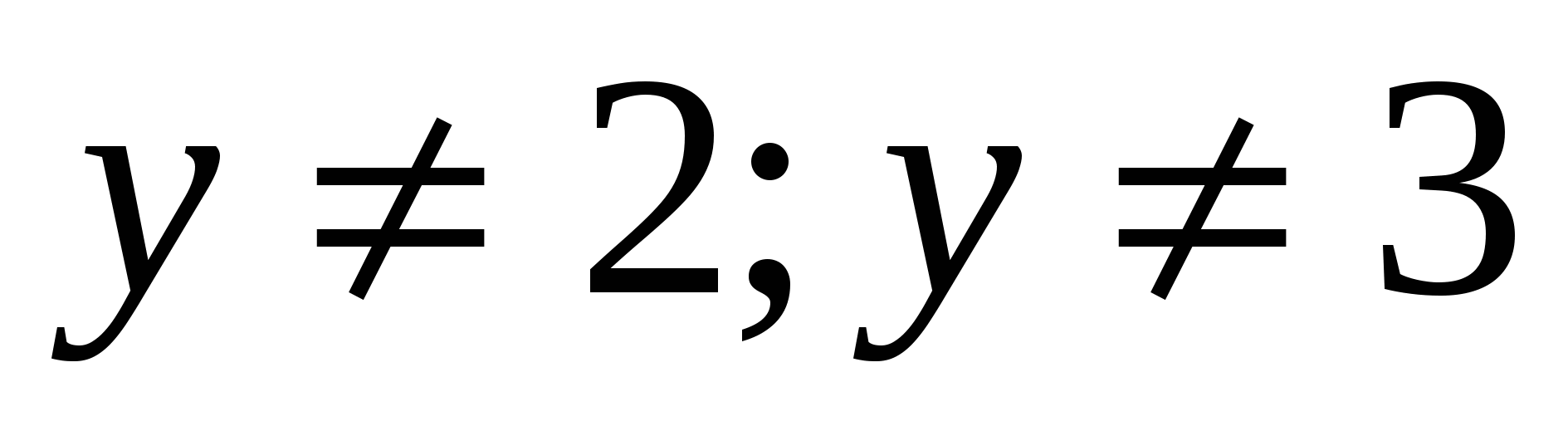
С. 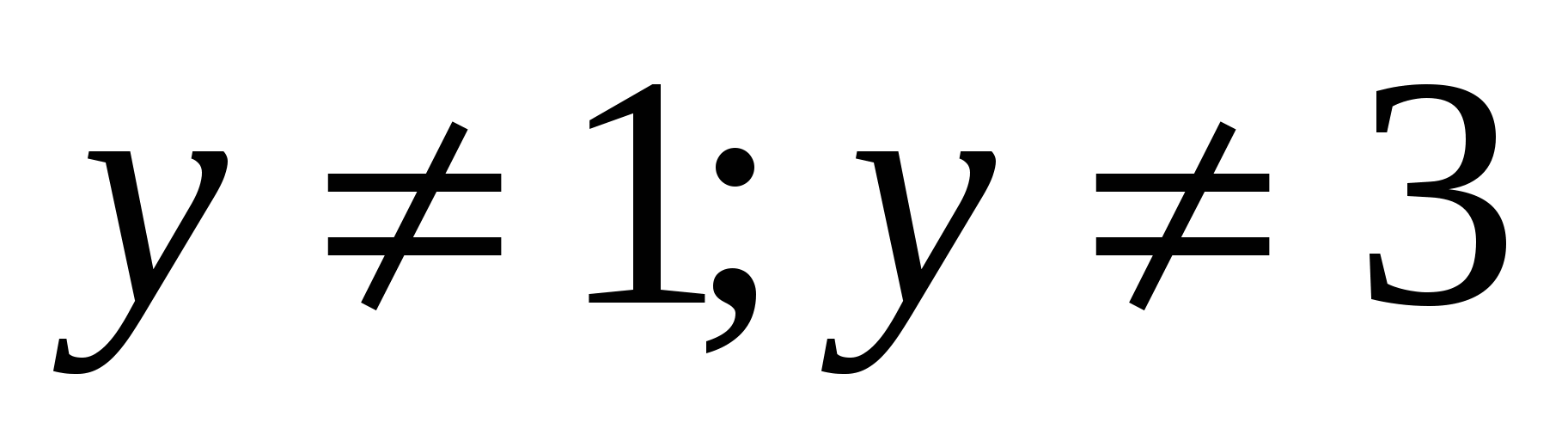
D. 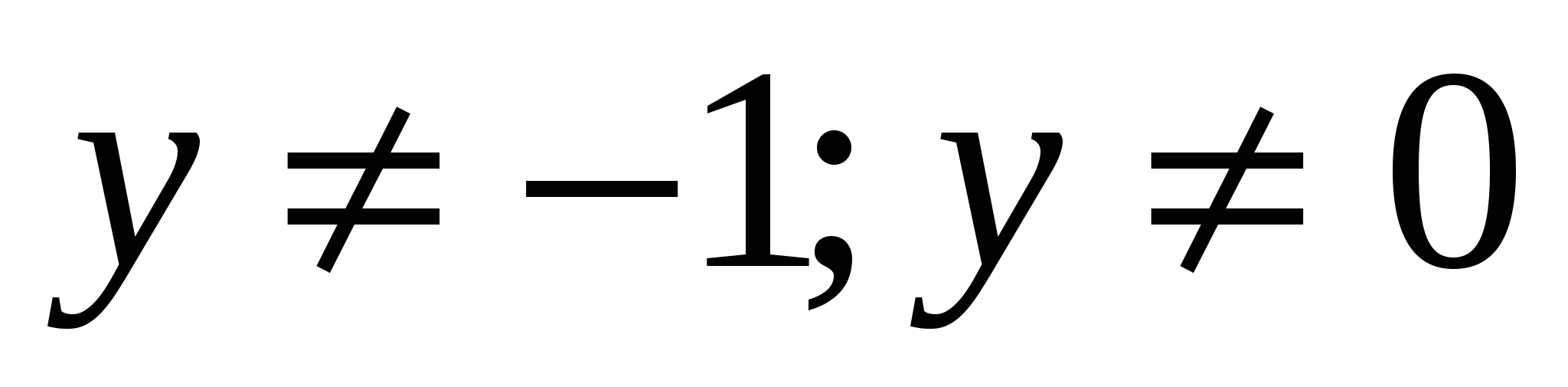
E. 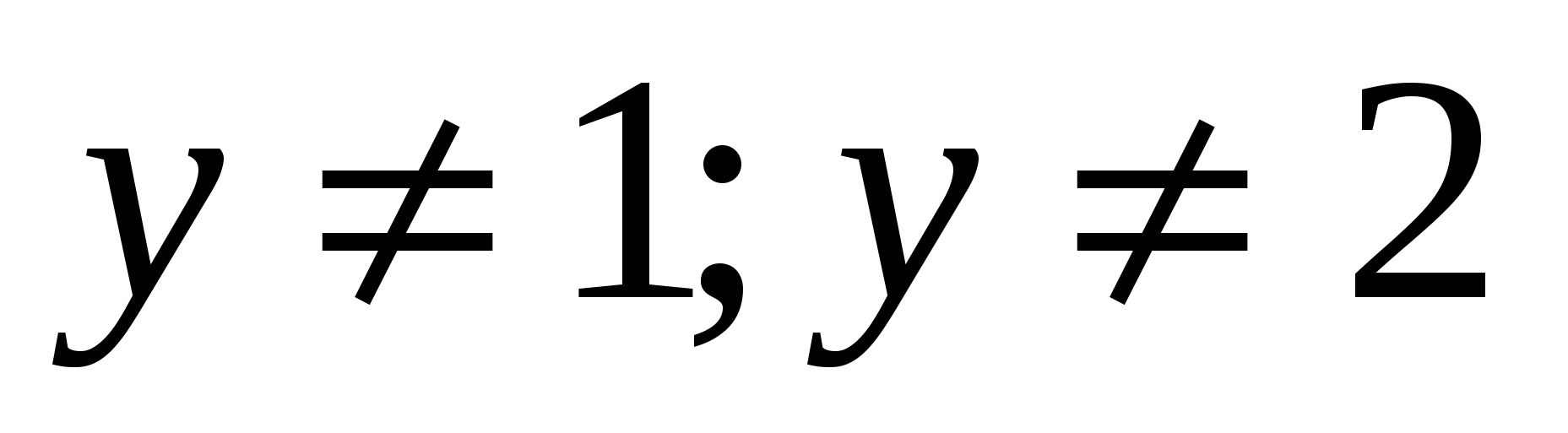
страница 1
|