страница 1
МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ
РЕСПУБЛИКИ КАЗАХСТАН
ГЕОМЕТРИЧЕСКИЕ
ПОСТРОЕНИЯ
Направление: математическое моделирование
экономических и социальных процессов
Секция: математика
Выполнил
ученик 9 класса А
Гимназии № 38
г. Караганды
Душехватов Клим
Научный руководитель
Сыропятова Н.М., учитель математики
Караганда – 2010
Оглавление
-
Абстракт.
-
Введение.
-
Примеры задач на построение одним циркулем.
-
Условия и решения своих задач. Вневписанная окружность. Примеры задач.
-
Построение правильных многоугольников. Исследование. Построение правильных вписанных многогранников.
-
Заключение.
-
Список литературы.
1. Абстракт
1. Цели исследования
a) Изучить методы решения задач на построение с помощью одного циркуля. Дополнить список задач в геометрии циркуля условием своей задачи.
b) Изучить, проверить и дополнить своими исследованиями информацию о вневписанных окружностях.
c) Дополнить своими исследованиями информацию о построении правильных многоугольников и правильных многогранников, вписанных один в другой.
2. Гипотеза
a) Все задачи на построение, разрешимые циркулем и линейкой, могут быть точно решены и одним только циркулем.
b) С помощью циркуля и линейки можно построить развертки правильных многогранников, вписанных один в другой.
3. Этапы исследования
a) Диагностический: Выявление проблемы и обоснование актуальности.
b) Прогностический: Разработка программы исследования.
c) Организационный: Сбор информации, анализ, консультации.
4. Методика эксперимента
a) Аналитический обзор литературы.
b) Изучение литературы.
c) Консультации учителей гимназии.
d) Составление плана работы.
e) Выполнение работы.
5. Новизна исследования
a) Изучение теоретического материала, выходящего за рамки школьной программы.
b) Приминение теорем о свойствах внепвисанных окружностях в решении задач на построение.
c) Создание моделей правильных многогранников, вписанных один в другой.
6. Степень самостоятельности
Самостоятельное изучение литературы, составление плана, исследования по теме. Построение моделей правильных многогранников, вписанных один в другой.
7. Выводы
В данной работе:
a) Изучено, что с помощью каждого из инструментов циркуля и линейки можно точно решать одни и те же геометрические задачи на построение, дополнен список задач в геометрии циркуля условием своей задачи.
b) Изучено и дополнено своими исследованиями информация о вневписанных окружностях и построении правильных многоугольников.
c) Рассчитаны и fccxbnfys b построены модели правильных многогранников: куба, икосаэдра и додекаэдра, вписанных один в другой.
2. Введение
Геометрические построения являются существенным фактором математического образования; они представляют собой мощное орудие геометрических исследований.
Раздел геометрии, изучающий геометрические построения одним циркулем, называют геометрией циркуля.
Знаменитая геометрия Евклида (III век до нашей эры) была основана на геометрических построениях, выполняемых циркулем и линейкой; при этом циркуль и линейка рассматривались как равноправные инструменты.
Уже давно было замечено, что циркуль является более точным, более совершенным инструментом, чем линейка, что некоторые построения можно выполнить одним циркулем, например, разделить окружность на шесть равных частей, построить точку, симметричную данной точке относительно данной прямой.
В геометрии циркуля прямая считается построенной, если даны две её любые точки. Таким образом с помощью одного циркуля можно построить прямую.
В 1833 году швейцарский геометр Якоб Штейнер опубликовал работу «Геометрические построения, производимые с помощью прямой линии и неподвижного круга», в которой наиболее полно исследовал построения одной линейкой. Основной вывод этой работы: «Каждая задача на построение, разрешимая циркулем и линейкой, может быть решена и одной линейкой, если в плоскости чертежа дана постоянная окружность и её центр».
Таким образом, чтобы линейку сделать равносильной циркулю, достаточно однократное употребление циркуля.
Геометрия играет важную роль в архитектуре. Только неотступно следуя законам геометрии, архитекторы древности могли создавать свои шедевры. Не случайно говорят; что пирамида Хеопса — немой трактат по геометрии, а греческая архитектура — внешнее выражение геометрии Евклида.
Геометрия по-прежнему остается «грамматикой архитектора». Только сегодня, с появлением новых строительных материалов (бетон, металл, стекло, пластик) и новой технологии строительства, архитектор может опираться на более широкий круг геометрических законов. Это расширяет творческие возможности архитектора и порождает новые конструкции, новые архитектурные формы, новую эстетику.
Совершенствование конструкций сопровождается не только усложнением их геометрического построения, но и общим расширением применяемого в архитектуре математического аппарата, включением в него современных математических методов.
3. Примеры задач
Задача 1. Построить точку, симметричную данной точке относительно данной прямой. (рисунок 1)
Дано: (AB) и точка С.
Построить: точку C1, симметричную точке C относительно прямой AB.
Анализ: Если C AB, то делаем данное построение. Если C AB, то делаем данное построение. Если C AB, то C симметрична сама себе. AB, то C симметрична сама себе.
Построение: Проводим окружности (A, |AC|) и (B, |BC|), которые пересекутся в точке C1. Точка C1 – искомая.
Доказательство:  ACB = ACB =  AC1B, следовательно AC1B, следовательно  1 = 1 =  2 и 2 и  3 = 3 =  4, следовательно BO и AO – биссектрисы 4, следовательно BO и AO – биссектрисы  BO и AO – медианы и высоты, BO и AO – медианы и высоты,  AOC = = AOC = = AOC1 = 90 AOC1 = 90 и CO = C1O, следовательно С1 симметрична C относительно AB. и CO = C1O, следовательно С1 симметрична C относительно AB.
Исследование: Чтобы определить лежит или не лежит данная точка (обозначим её X) на прямой AB, выполним построение пары точек C (произвольная) и С1. Если CX = C1X, то X лежит на прямой AB, т. к. AB – серединный перпендикуляр к СС1, а каждая точка равноудалённая от его концов, лежит на серединном перпендикуляре к нему.
Задача 2. Построить отрезок, в 2, 3, 4, … и вообще в n раз больший данного отрезка (n – любое натуральное число). (рисунок 2)
Дано: |AA1|.
Построить: |AAn|, |AAn| = n|AA1|, где n N. N.
Построение: (Первый способ) Построение осуществляется постоянным раствором ножек циркуля, равным r = |AA1|. Проводим окружность (А1, r) и определяем на ней точку А2, диаметрально противоположную точке А (для чего последовательно проводим окружности (А, r), (B, r), (C, r); в пересечении этих окружностей с окружностью (А1, r) последовательно получим точки B, C и A2). Отрезок |AA2| = 2r.
Проводим затем окружность (A2, r), которая пересечёт окружность (С, r) в точке D. В пересечении окружности (А2, r) с (D, r) получим точку А3. Отрезок |AA | = 3r и т. д.
Проделав приведенное построение n раз, построим отрезок |AAn| = nr.
Исследование: Справедливость построения следует из того, что циркуль с раствором, равным радиусу окружности, делит её на шесть равных частей.
Построение: (Второй способ) Берём вне прямой АА1 произвольную точку B и проводим окружности (А1, |AB|) и (B, r), в пересечении которых получим точку C.
Если теперь описать окружности (А1, r) и (С, |A1B|), то они пересекутся в искомой точке А2. Отрезок |AA2| = 2r. Проводим окружности (А2, r) и (С, |A1B|) и обозначаем точку А3 их пересечения. Здесь |AA3| = 3r и т. д.
Анализ: Справедливость построения немедленно следует из того, что фигуры ABCА1, A1BCA2, A2BCA3, … являются параллелограммами.
Задача 3. Разделить дугу AB окружности (O, r) пополам, если центр О известен. (рисунок 3)
Дано: дуга AB окружности (О, r) и центр окружности (О, r).
Построение: Полагая a = |AB|, проводим окружности (О, а), (A, r) и (B, r); в пересечении получим точки C и D. Проводим окружности (C, |CB|) и (D, |AD|); в пересечении получим точку E. Проводим окружности (C, |OE|) и (D, |OE|); в пересечении получим точки X и X1. Точка Х делит пополам дугу AB, точка Х1 делит пополам дугу, дополняющую первой до полной окружности.
Доказательство: Фигуры ABOC и ABDO являются параллелограммами, поэтому точки C, O и D лежат на одной прямой ([CO] || [AB], [OD] || [AB]). Из равнобедренных треугольников CED и CXD следует, что 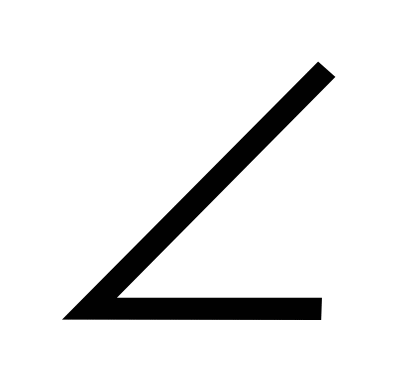 COE = COE = 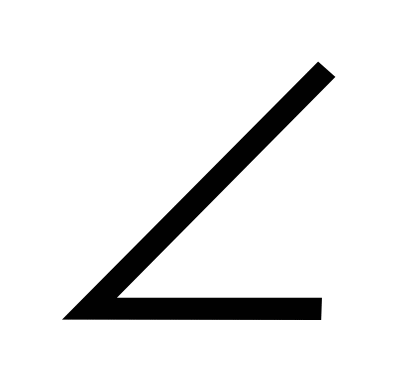 COX = 90 COX = 90 . Итак, отрезок OX перпендикулярен к хорде AB; следовательно, для доказательства того, что точка Х делит дугу AB пополам, достаточно показать, что |OX| = r. . Итак, отрезок OX перпендикулярен к хорде AB; следовательно, для доказательства того, что точка Х делит дугу AB пополам, достаточно показать, что |OX| = r.
Докажем, что |OX| = r.



 (по теореме Пифагора) (по теореме Пифагора) 


Из прямоугольного треугольника COX получим
 , т.к. , т.к. 
ОХ = r.  X лежит на окружности (O, r) и делит дугу AB пополам. X лежит на окружности (O, r) и делит дугу AB пополам.
Исследование: Приведённое построение остаётся справедливым и в случае, когда заданная дуга AB является полуокружностью. В этом случае точки A и B будут лежать на отрезке CD, а окружности (A, r) и (B, r) будут касаться окружности (O, a) соответственно в точках C и D. Из-за несовершенства чертёжных инструментов (циркуля) установить точное расположение этих двух точек C и D достаточно трудно. В этом случае следует делить пополам дугу A1B1 (A1B1 180 180 ) такую, что дуга AA1 равна BB1 и больше нуля и AA1 + A1B1 + B2B = AB. Очевидно, что точка , делящая пополам дугу A1B1, будет делить пополам и дугу AB. ) такую, что дуга AA1 равна BB1 и больше нуля и AA1 + A1B1 + B2B = AB. Очевидно, что точка , делящая пополам дугу A1B1, будет делить пополам и дугу AB.
4. Условия и решения своих задач
Задача 1. Построить равнобедренный треугольник по основанию и радиусу описанной окружности, если известен центр окружности. (рисунок 5)
Дано: отрезок AB (основание треугольника), радиус описанной окружности r и её центр O.
Построить: Равнобедренный треугольник AXB.
Построение: Построим окружность с центром О и радиусом r. Произвольно расположим отрезок AB как хорду на окружности. Теперь нужно найти середину дуги AB. Полагая что a – расстояние между точками A и B, проводим окружности (О, а), (A, r) и (B, r); в пересечении получим точки C и D. Проводим окружности (C, |CB|) и (D, |AD|); в пересечении получим точку E. Проводим окружности (C, |OE|) и (D, |OE|); в пересечении получим точки X и X1. Точка Х делит пополам дугу AB, точка Х1 делит пополам дугу, дополняющую первой до полной окружности.
Доказательство: Фигуры ABOC и ABDO являются параллелограммами, поэтому точки C, O и D лежат на одной прямой ([CO] || [AB], [OD] || [AB]). Из равнобедренных треугольников CED и CXD следует, что 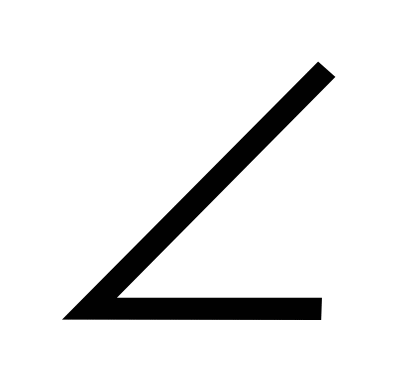 COE = COE = 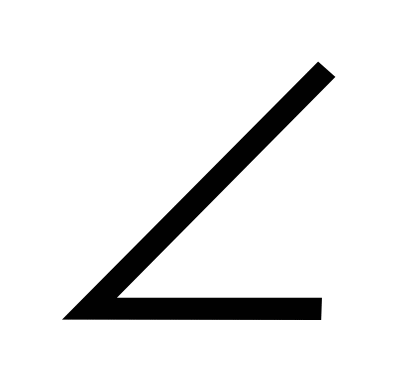 COX = 90 COX = 90 . Итак, отрезок OX перпендикулярен к хорде AB; следовательно, для доказательства того, что точка Х делит дугу AB пополам, достаточно показать, что |OX| = r. . Итак, отрезок OX перпендикулярен к хорде AB; следовательно, для доказательства того, что точка Х делит дугу AB пополам, достаточно показать, что |OX| = r.
Докажем, что |OX| = r.



 (по теореме Пифагора) (по теореме Пифагора) 


Из прямоугольного треугольника COX получим
 , т.к. , т.к. 
ОХ = r.  X лежит на окружности (O, r) и делит дугу AB пополам. X лежит на окружности (O, r) и делит дугу AB пополам.
Исследование: Приведённое построение остаётся справедливым и в случае, когда заданная дуга AB является полуокружностью. В этом случае точки A и B будут лежать на отрезке CD, а окружности (A, r) и (B, r) будут касаться окружности (O, a) соответственно в точках C и D. Из-за несовершенства чертёжных инструментов (циркуля) установить точное расположение этих двух точек C и D достаточно трудно. В этом случае следует делить пополам дугу A1B1 (A1B1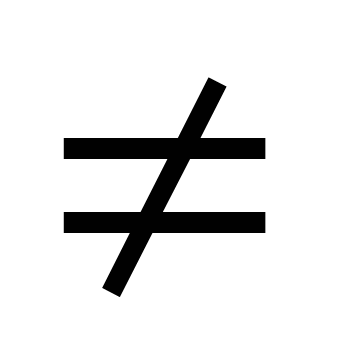 180 180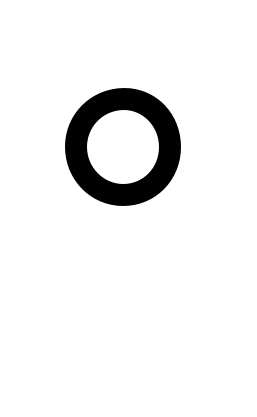 ) такую, что дуга AA1 равна BB1 и больше нуля и AA1 + A1B1 + B2B = AB. Очевидно, что точка , делящая пополам дугу A1B1, будет делить пополам и дугу AB. ) такую, что дуга AA1 равна BB1 и больше нуля и AA1 + A1B1 + B2B = AB. Очевидно, что точка , делящая пополам дугу A1B1, будет делить пополам и дугу AB.
Вневписанная окружность
Определение. Вневписанная окружность – окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон.
Теорема I. Биссектриса внутреннего угла BAC треугольника ABC и биссектрисы двух внешних углов при вершинах B и C пересекаются в одной точке.
Теорема II. Пусть T1 – точка касания вневписанной окружности с продолжением стороны AC треугольника ABC. Тогда длина отрезка AT1 равна полупериметру треугольника ABC.
Теорема III. Радиус вписанной окружности равен 1/3 среднего гармонического радиусов его вневписанных окружностей.
Теорема IV. SABC = ra(p – a)
Задача 2. Построить равносторонний треугольник по радиусу вневписанной окружности.
Свойство вневписанной окружности. (Мое исследование)
Высота любого равностороннего треугольника равна радиусу вневписанной окружности.
Пусть:
а – сторона равностороннего треугольника
h – высота равностороннего треугольника
r – радиус вневписанной окружности
 
Примеры задач на вневписанную окружность.
Задача 1. Постройте треугольник ABC, зная положение трех точек A1, B1 и C1, являющихся центрами вневписанных окружностей треугольника ABC.
Решение: Пусть искомый треугольник АВС построен. Центр каждой его вневписанной окружности лежит на пересечении соответствующих биссектрис внутреннего и внешнего углов. Проведя их, получим точки А1, В1 и С1.
Т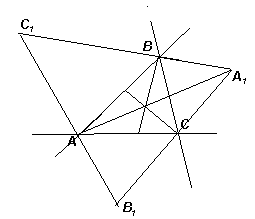 ак как биссектрисы вертикальных углов лежат на одной прямой, то вершины А, В и С искомого треугольника лежат на сторонах треугольника А1В1С1. Кроме того, так как биссектриса внешнего угла треугольника перпендикулярна биссектрисе внутреннего угла, проведенной из той же вершины, то А1А В1С1, В1В А1С1, С1С А1В1. ак как биссектрисы вертикальных углов лежат на одной прямой, то вершины А, В и С искомого треугольника лежат на сторонах треугольника А1В1С1. Кроме того, так как биссектриса внешнего угла треугольника перпендикулярна биссектрисе внутреннего угла, проведенной из той же вершины, то А1А В1С1, В1В А1С1, С1С А1В1.
Таким образом, решение задачи сводится к построению треугольника A1B1C1 и его высот.
Задача имеет единственное решение тогда и только тогда, когда треугольник А1В1С1 – остроугольный.
Вершины остроугольного треугольника являются центрами вневписанных окружностей для его ортотреугольника (треугольника, образованного основаниями высот).
Задача 4. Постройте прямую, проходящую через данную точку и отсекающую от данного угла треугольник с заданным периметром.
Решение: Пусть на плоскости даны угол О и точка М. Предположим, что искомая прямая АВ построена, то есть треугольник АОВ имеет заданный периметр Р. Проведем окружность, касающуюся сторон данного угла и отрезка АВ (см. рис. 5). Пусть K и L – точки касания этой окружности со сторонами угла, тогда OK = OL = p.
Т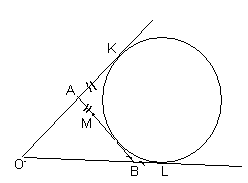 аким образом, решение задачи сводится к построению вспомогательного равнобедренного треугольника KOL (сторону KL которого можно не проводить) и окружности, касающейся сторон данного угла в точках K и L. После этого через точку М проводится касательная АВ к этой окружности. аким образом, решение задачи сводится к построению вспомогательного равнобедренного треугольника KOL (сторону KL которого можно не проводить) и окружности, касающейся сторон данного угла в точках K и L. После этого через точку М проводится касательная АВ к этой окружности.
Отметим, что, зависимости от расположения точки М, задача может иметь два решения, одно решение или не иметь решений.
5. Построение правильных многоугольников
Правильный пятиугольник может быть построен с помощью циркуля и линейки, или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Первый метод.
1. Построить окружность, в которую будет вписан пятиугольник и обозначить её центр как O.
2. Выбрать на окружности точку A, которая будет одной из вершин пятиугольника. Построить прямую через O и A.
3. Построить прямую перпендикулярно прямой OA, проходящую через точку O. Обозначить одно её пересечение с окружностью как точку B.
4. Построить точку C посередине между O и B.
5. Провести окружность с центром в C через точку A. Обозначить её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
6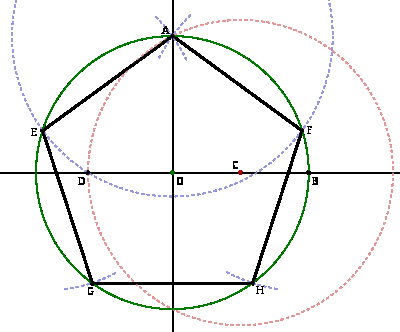 . Провести окружность с центром в A через точку D. Обозначить её пересечения с оригинальной окружностью как точки E и F. . Провести окружность с центром в A через точку D. Обозначить её пересечения с оригинальной окружностью как точки E и F.
7. Провести окружность с центром в E через точку A. Обозначить её другое пересечение с первоначальной окружностью как точку G.
8. Провести окружность с центром в F через точку A. Обозначить её другое пересечение с первоначальной окружностью как точку H.
9. Построить правильный пятиугольник AEGHF.
Второй метод. (рисунок 9)
1. Построить окружность, в которую будет вписан пятиугольник и обозначить её центр как O.
2. Выбрать на окружности точку A, которая будет одной из вершин пятиугольника. Построить прямую через O и A.
3. Построить прямую перпендикулярно прямой OA, проходящую через точку O. Обозначить одно её пересечение с окружностью как точку B.
4. Построить точку C посередине между O и B.
5. Соединить точки C и A.
6. Построить биссектрису угла ACO. Точка D – точка пересечения биссектрисы угла ACO и прямой AO.
7. Построить прямую, проходящую через точку D, параллельную промой BO. E – точка пересечения прямой DE и окружности, в которую вписан пятиугольник; Вторая вершина пятиугольника.
(Аналогично проделать тоже самое относительно второй вершины пятиугольника)
Задачи на построение находят большое применение в технике, архитектуре, дизайне, черчении и д.т. Рассмотрим задачу на модели правильного и большого додекаэдра. Правильный додекаэдр состоит из 12 правильных пятиугольников. Построение правильного пятиугольника рассматривается в курсе черчения. Можно ли найти решение отличное от решения Евклида? Если вписать правильный пятиугольник в окружность, то центральный угол (образованный радиусами, проведенными из центра окружности к двум его соседним вершинам) равен 72 . .
Возникают вопросы:
1. Можно ли построить угол 72 градуса с помощью циркуля и линейки?
2. Разрешима ли эта задача?
Для ответа на второй вопрос воспользуемся следующей теоремой:
Если аналитическое решение задачи на построение не выражается рациональными действиями и извлечением квадратного корня, то эта задача неразрешима с помощью циркуля и линейки. И наоборот, если аналитическое решение задачи на построение выражается рациональными действиями и извлечением квадратного корня, то эта задача разрешима с помощью циркуля и линейки (1).
Следовательно, если построить угол 72 ,то построение правильного пятиугольника не доставит особых проблем. Для начала построим правильный 10-угольник. В нем центральный угол, соединяющий центр описанной окружности с двумя соседними вершинами, равен 36 ,то построение правильного пятиугольника не доставит особых проблем. Для начала построим правильный 10-угольник. В нем центральный угол, соединяющий центр описанной окружности с двумя соседними вершинами, равен 36 . Тогда в равнобедренном треугольнике AOB; OA=OB=R и . Тогда в равнобедренном треугольнике AOB; OA=OB=R и 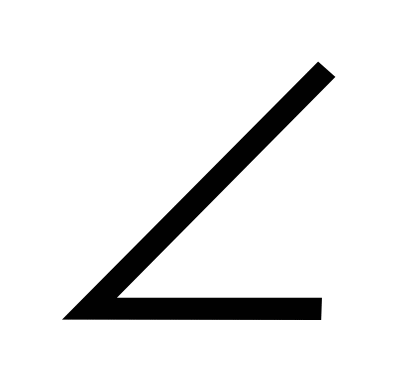 AOB=36 AOB=36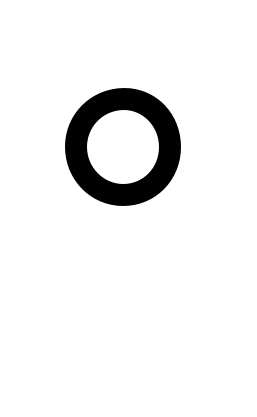 (Рисунок 11). (Рисунок 11).
Биссектриса угла А делит этот треугольник на два равнобедренных: AOC и ABC. Обозначим: AO=OB=R, AB=x, следовательно, AB=AC=OC=x. Так как, биссектриса, проведенная из вершины угла треугольника, делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, то 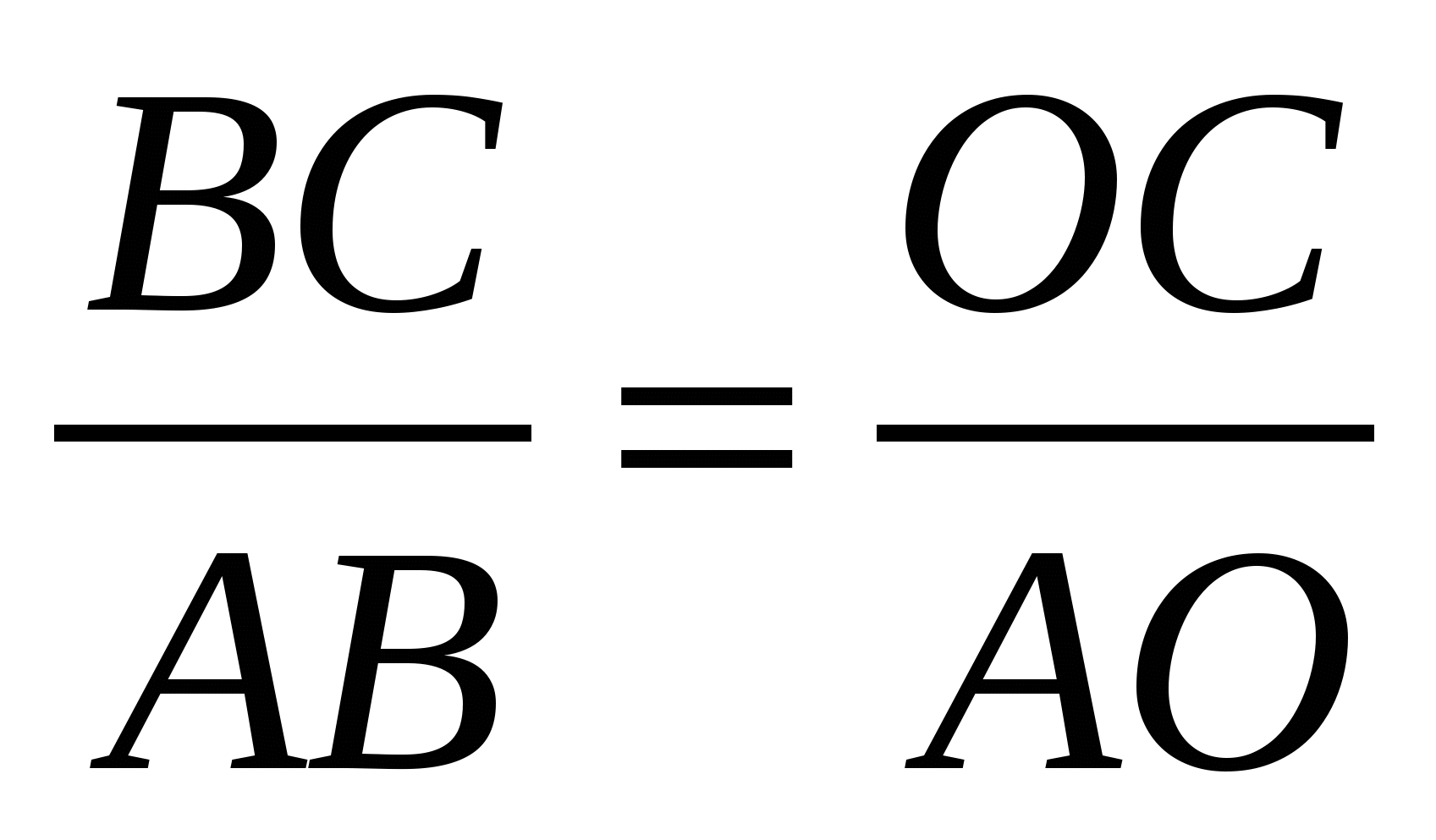 , то есть , то есть
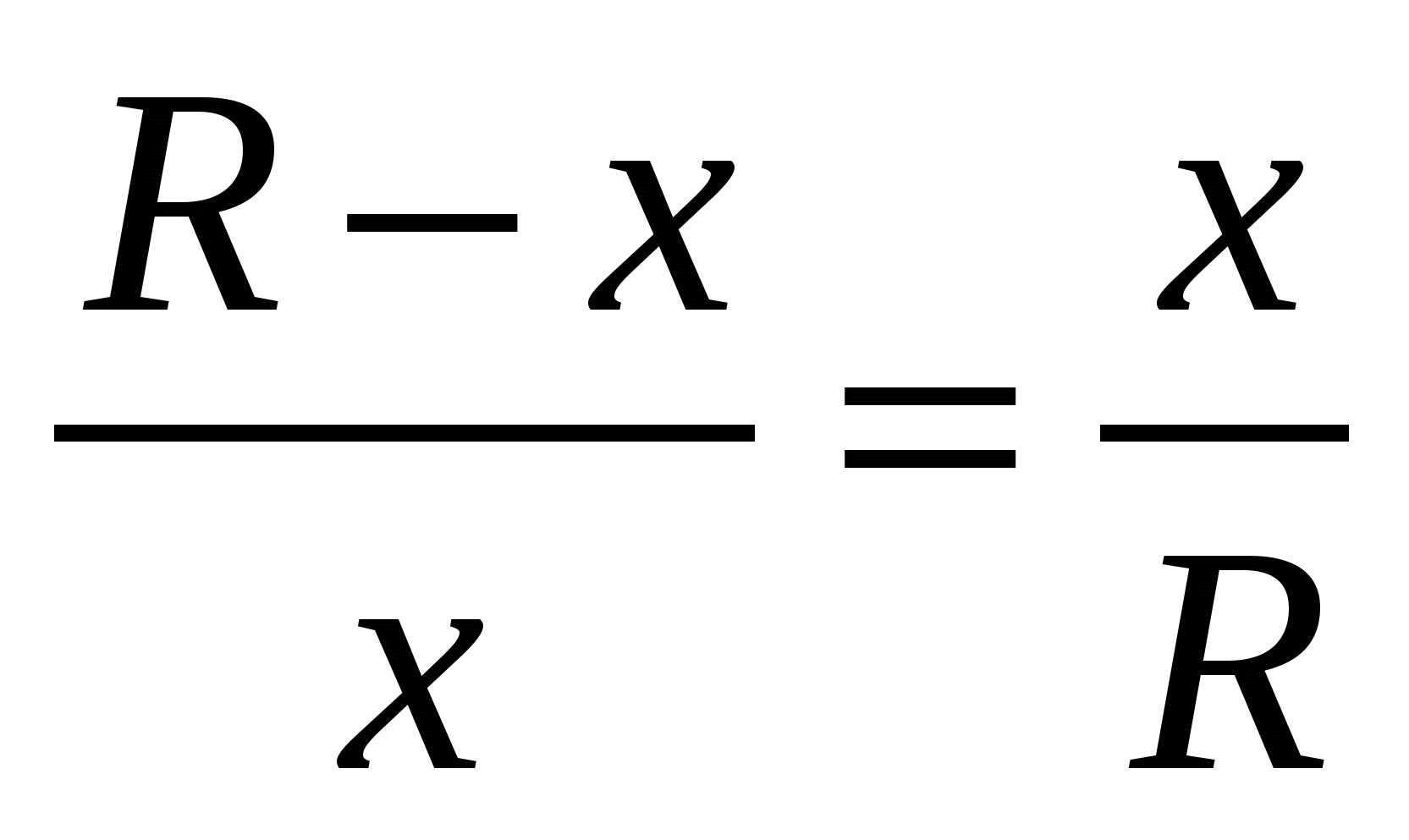 . .
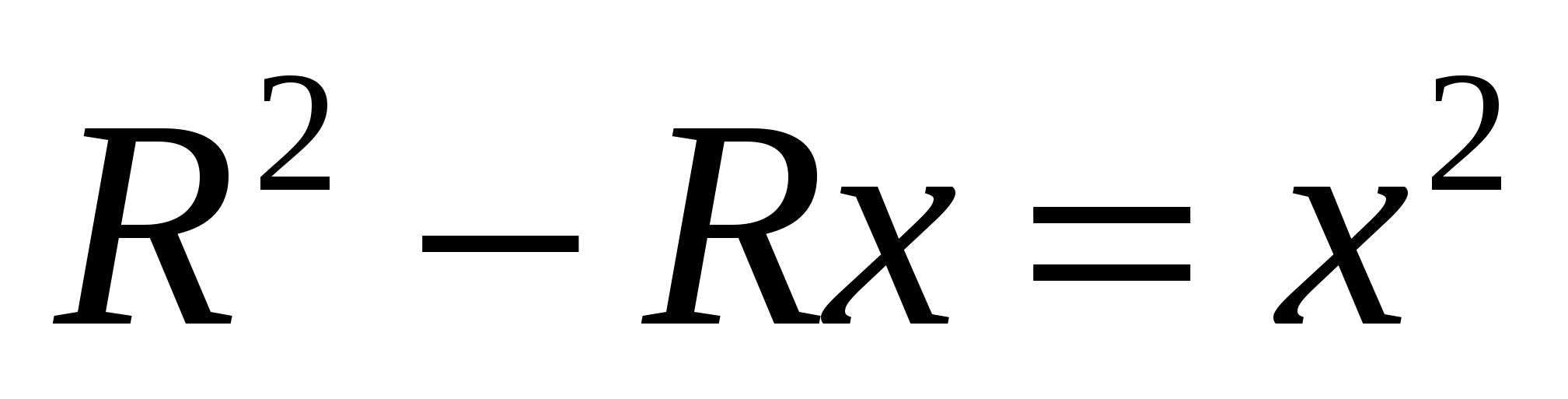
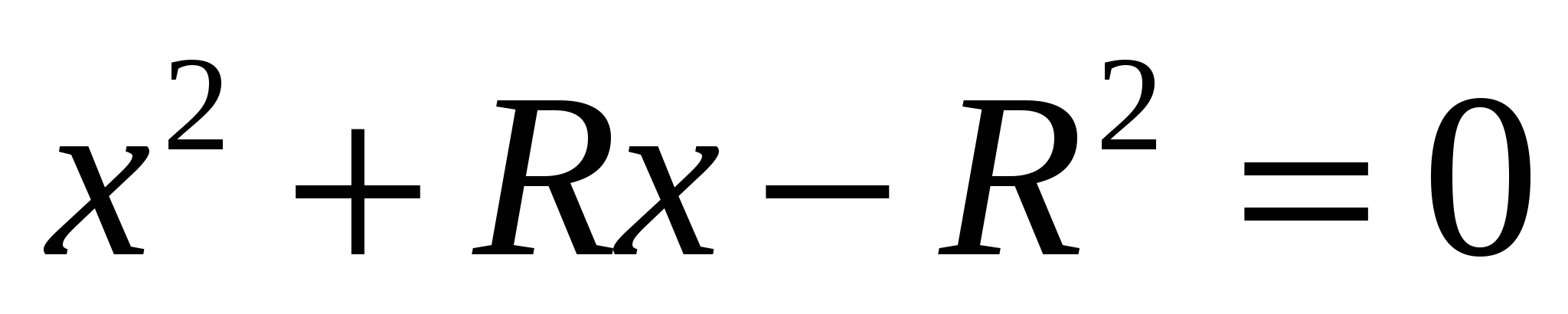
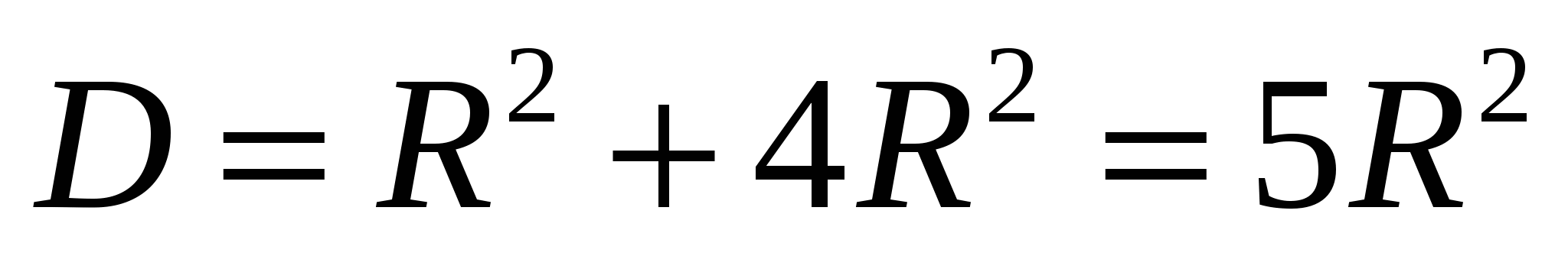
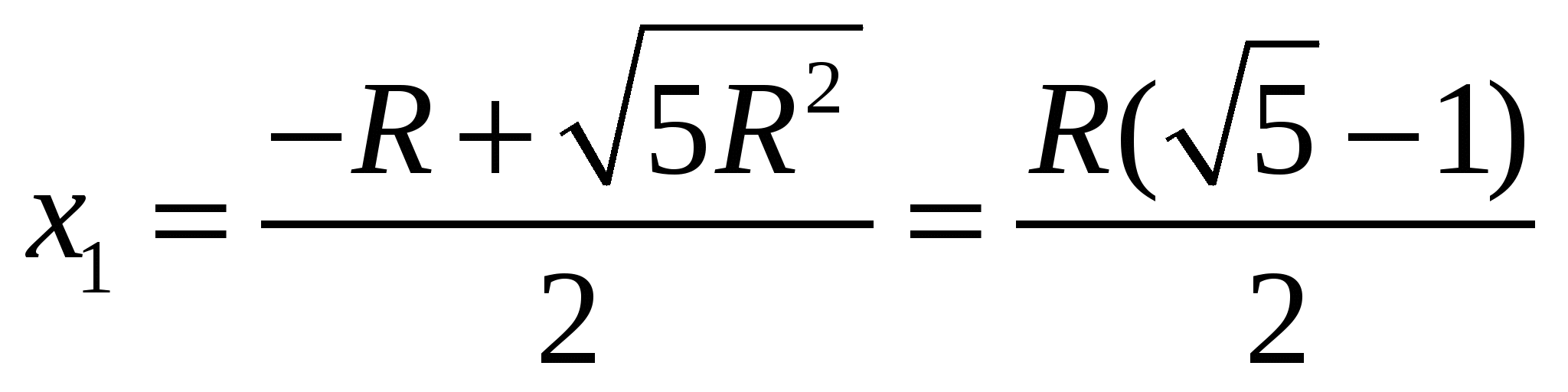
 (не удовлетворяет условию задачи) (не удовлетворяет условию задачи)
Следуя теореме 1, если аналитическое решение задачи на построение выражается рациональными действиями и извлечением квадратного корня, то эта задача разрешима с помощью циркуля и линейки. Знаю R, мы всегда сможем найти x, следовательно можем и построить угол 36  . .
Трафарет для построения (звездчатого платонова тела) большого додекаэдра – равнобедренный треугольник с углами 36 , 36 , 36 , 108 , 108 (Рисунок 12). По внешнему виду он похож на додекаэдр, над каждой пятиугольной гранью которого выступает пятиугольная звезда. Трафареты для моделей додекаэдра и большого додекаэдра (Рисунок 13). (Рисунок 12). По внешнему виду он похож на додекаэдр, над каждой пятиугольной гранью которого выступает пятиугольная звезда. Трафареты для моделей додекаэдра и большого додекаэдра (Рисунок 13).
Построение правильных вписанных многогранников
Возьмём куб (гексаэдр) и впишем в него правильный икосаэдр, а в икосаэдр впишем правильный додекаэдр так, чтобы вершины икосаэдра лежали на гранях куба, а вершины додекаэдра – в центрах граней икосаэдра.
Для построения икосаэдра необходимо найти длину его ребра. Расположим икосаэдр так, чтобы две его соседние вершины лежали на одной грани, а ребро с концами в этих точках – на основной симметрии грани.
Обозначив длину ребра AB=d, а расстояния концов отрезка AB до перпендикулярных ему рёбер грани за x, получим:
AF+AB+BE=1
x+d+x=1
2x+d=1 (1)
Т реугольник BCD – равносторонний, так как его стороны являются ребрами икосаэдра, следовательно его высота реугольник BCD – равносторонний, так как его стороны являются ребрами икосаэдра, следовательно его высота
Треугольник BEH – прямоугольный.

BE=x, , EH=1/2, следовательно по теореме Пифагора

BE2+EH2=BH2, то есть (2)
Н айдём d из полученной системы уравнений. айдём d из полученной системы уравнений.
2 x+d=1 x+d=1
 

1 – 2d + d2 + 1 = 3d2
2d2 + 2d – 2 = 0
d2 + d – 1 = 0
D = 1 + 4 = 5
 
, так как d > 0, то .
Для построения ребра данной длины рассмотрим прямоугольный треугольник с

катетами 1 и 2, тогда его гипотенуза равна .
С помощью циркуля отсечем от гипотенузы отрезок длиной, равной 1. Оставшуюся часть разделим пополам. Длина полученного отрезка равна длине ребра икосаэдра.
Для построения отрезка, длина которого равна длине ребра вписанного додекаэдра, рассмотрим правильную пятиугольную пирамиду, являющуюся частью икосаэдра. О1 и О2 – центры граней икосаэдра, следовательно ребро додекаэдра равно длине отрезка О1О2.
В равных равносторонних треугольниках ASB и CSB проведём высоты AH и CH и рассмотрим треугольник ACH. О1 и О2 лежат соответственно на сторонах AH и

CH, и по свойству медианы треугольника , так
как треугольники AHC и О1HО2 подобны.
AC является диагональю правильного пятиугольника ABCDE со стороной, равной ребру икосаэдра. Примем длину ребра икосаэдра за b = 1 (единица).
Построим правильный пятиугольник с ребром b, затем построим новый пятиугольник с ребром m = 1/3AC. Это и будет грань искомого додекаэдра. Построенные таким образом, многогранники будут вписаны друг в друга.
Длину ребра додекаэдра можно непосредственно измерить с помощью циркуля на готовой модели икосаэдра.
6. Заключение
В данной работе:
a) Изучено, что с помощью каждого из инструментов циркуля и линейки можно точно решать одни и те же геометрические задачи на построение, дополнен список задач в геометрии циркуля условием своей задачи.
b) Изучено и дополнено своими исследованиями информация о вневписанных окружностях и построении правильных многоугольников.
Построены грани правильных многогранников: куба , икос и додек, вписанных один в другой. Построении модели
Область применения
Архитектура, черчение, дополнительный материал в программе углубленного курса геометрии, начертательная и проективная геометрия.
8. Список литературы
1. Адлер А. Теория геометрических построений. 1940 г.
2. Александров И.И. Сборник геометрических задач на построение. 1950 г.
3. Аргунов Б.И., Бланк М.Б. Геометрические построения на плоскости. 1957 г.
4. Костовский А.Н. О возможности решения задач на построение одним циркулем с ограниченным раствором ножек. 1954 г.
5. Воронец А.М. Геометрия циркуля. 1934 г.
6. Шыныбеков А.Н. Геометрия 9 класс. 2005 г.
7. Ботвинников А.Д., Виноградов В.Н., Вышнепольский И.С. Черчение (Учебник для 6 – 7 классов средней общеобразовательной школы) 1988 г.
8. Веннинджер М. Модели многогранников. 1974 г.
Отзыв о работе
Душехватова Клима «Геометрические построения».
В работе представлены результаты исследований, связанные с реализацией и развитием идей, заложенных в теории геометрических построений циркулем и линейкой, а также одним только циркулем.
Геометрические построения являются существенным фактором математического образования, они представляют собой мощное оружие геометрических исследований. Геометрические построения широко применяются как в самой геометрии, так и в черчении, начертательной и проективной геометрии, дизайне, архитектуре. В работе исследуется возможность решения задачи на построение, решение некоторых задач на построение одним циркулем, предлагаются авторские решения задач. Изучается, проверяется, дополняется авторскими исследованиями информация о вневписанных окружностях.
Автор, несомненно, проделал большую исследовательскую работу. Он почерпнул обширные сведения из теории и практики геометрических построений и получил ряд самостоятельных результатов.
Несмотря на то, что построения одним циркулем являются в большинстве случаев долее громоздкими, чем построения циркулем и линейкой, они являются более точными. Данная работа может быть адресована любителям математики, в частности, старшеклассникам для подготовки к олимпиадам различного уровня, так как исследуемый материал далеко выходит за рамки школьной программы.
Заведующий кафедрой естественно-математического цикла______Абляева Ф.М.
страница 1
|