4. Исследование работы алгоритма вейвлет-анализа.

4.1. Исследование поведения алгоритма в различных конфигурациях.

• 
  длины вейвлетов: 32–4096;
  
• 
  размерность вейвлет-вектора: 256;
  
• 
  тип базового вейвлета: Морле
  
• 
  тип внутреннего представления данных: вещественные;
  
• 
  разрешение: 800х600 (число вейвлет-векторов – 512);
  
• 
  «моментальное» отображение данных включено.
  

В результате процедура вейвлет-преобразования заняла 27412 мс, что, в принципе, является достаточно большим временем. Будем исследовать влияние различных настроек на время работы алгоритма.

Зависимость отображена на следующем графике.

Рис.5.1 График зависимости времени работы от размерности вектора.

При включении временного прореживания используемых данных (то есть, фактически, уменьшении числа подсчитываемых векторов в два раза) общее время работы при расчёте 256-мерных вейвлет-векторов составило 13759 мс, то есть примерно вдвое меньше исходного времени.

Таким образом, при уменьшении размерности вектора либо при уменьшении числа подсчитываемых векторов мы наблюдаем линейную зависимость увеличения скорости от объёма оставшихся данных. Однако этот метод ускорения работы алгоритма не является оптимальным, так как, уменьшая размерность вейвлет-векторов, мы сильно огрубляем общую вейвлет-картину, и уменьшение числа подсчитываемых векторов также приводит к огрублению вейвлет-картины.
3. Зависимость от максимальной длины вейвлета.

Иногда отпадает необходимость исследовать достаточно низкочастотные области сигнала, и в этом случае мы можем уменьшить максимальный масштаб используемых вейвлетов.

График зависимости представлен на рисунке 5.2

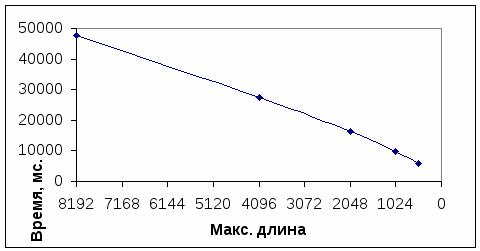
Рис. 5.2. Зависимость времени работы от максимальной длины вейвлета.

Как видно из графика, зависимость времени работы от максимальной длины вейвлета тоже близка к линейной. Таким образом, уменьшая максимальную длину, мы добиваемся более быстрой работы алгоритма, однако, при этом мы теряем часть информации, относящейся к низкочастотной области сигнала (однако плюсом этого является то, что при сохранении размерности вектора мы получаем больше информации о высокочастотной области, что иногда является полезным).

4. Использование целочисленной арифметики.

На многих процессорах на вычисления с плавающей точкой затрачивается больше времени, нежели на целочисленные вычисления. Исходя из этого логично предположить, что если заменить большинство данных, используемых в вычислениях, на целочисленные, то алгоритм может начать работать быстрее.

Действительно, при проверке данной гипотезы на процессоре Celeron 1700 получились следующие результаты (конфигурации программы различались лишь использованием различного представления данных):

• 
  Время выполнения алгоритма при использовании арифметики с плавающей точкой – 27540 мс.
  
• 
  Время выполнения алгоритма при использовании целочисленной арифметики с фиксированной точкой (10.6) – 10967 мс.
  

Также тестирование использования целочисленной арифметики с такими же файлом и конфигурацией было проведено на компьютере на базе процессора Duron 750. В этом случае:

• 
  Время выполнения алгоритма при использовании арифметики с плавающей точкой – 21487 мс.
  
• 
  Время выполнения алгоритма при использовании целочисленной арифметики с фиксированной точкой (10.6) – 27653 мс.
  

Наиболее интересным в плане оптимизации является использование разработанного алгоритма октавного вейвлет-преобразования. Построим зависимость времени работы алгоритма от максимального номера октавы, в которой этот алгоритм ещё используется (0 соответствует работе обычного алгоритма).

Для большей точности при исследовании поведения алгоритма отключим «моментальное» отображение результатов на экран (так как это при малых временах работы алгоритма может оказывать существенное влияние).

Результаты представлены в таблице:

График зависимости времени работы от максимальной октавы приведён на следующем рисунке:

Р
ис. 5.3. Зависимость времени работы от максимального номера октавы, использующейся для октавного алгоритма.
Можно заметить, что, во-первых, на участке для октав 0-5 (особенно это заметно на участке 1-5) зависимость экспоненциальная (ось времени на графике – логарифмическая). Это легко объясняется, т.к. при увеличении числа используемых в октавном алгоритме октав экспоненциально (по степеням двойки) снижается объём данных, используемых при вычислении (так как всё меньше октав вычисляется по «обычному» алгоритму, и всё больше – по октавному). Однако, вместе с тем, и на графике, и в таблице видно, что при увеличении числа используемых октав до 6 идёт очень резкое (почти на порядок) снижение времени работы. Этому есть логическое объяснение, связанное с тем, что, вероятнее всего, в этом случае все используемые массивы вейвлетов попадают во внутренний кэш процессора (который намного быстрее внешней памяти), что и приводит к резкому увеличению быстродействия программы. Это косвенно подтверждается и тем, что объём данных как раз по порядку приближается к размеру внутреннего кэша процессора.

Как видно, данный метод оптимизации наиболее действенен. Однако здесь есть одно «но»: при вычислениях с помощью октавного метода на вейвлет-картине могут возникать артефакты, связанные с отсутствием НЧ-фильтрации сигнала при его временном сжатии. Как уже было сказано, для большинства типов сигнала эти искажения общей картины незначительны (однако их число возрастает по мере увеличения используемых в октавном алгоритме октав). Это видно на следующем рисунке:

а) б)

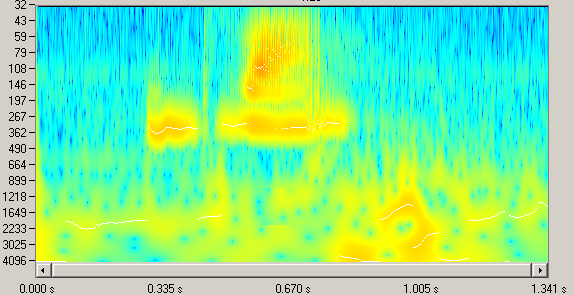
в) г)

Однако не следует забывать, что для некоторых специальных типов сигналов быстрый октавный алгоритм неприменим (по крайней мере, в той реализации, в которой он используется в программе Wavelet). Пример такого сигнала – синусоида с плавно изменяющейся частотой, причём начальная частота лежит практически у самого «потолка» частот, возможных при данной дискретизации. Это наглядно иллюстрирует рис. 5.5:

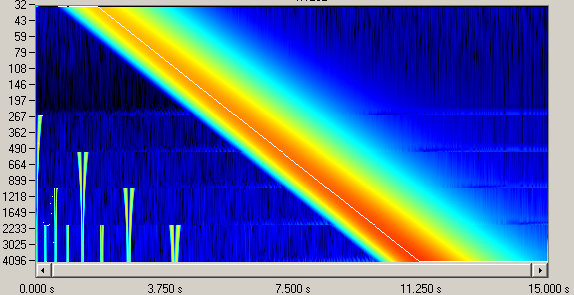
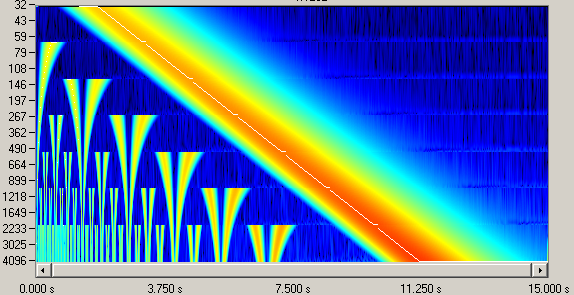
Рис. 5.5. Вверху – обычный алгоритм, посередине – октавный с MaxOctave=4, внизу – октавный с MaxOctave=6.

Возможно, при дальнейшем развитии октавного алгоритма данная проблема будет решена с помощью какого-либо достаточно быстрого алгоритма НЧ-фильтрации при временном сжатии.