страница 1
Лекция 1 Введение. Цели
и задачи дисциплины
С точки зрения выбора методов и технических средств обработки случайных сигналов важно выделить два основных направления развития радиофизики.
Первое направление. Изучение физических явлений, существенных для радиосвязи (в широком ее понимании), т. е. для всех основных этапов всякой радиосвязи – генерации электромагнитных сигналов, изучения и распространения электромагнитных волн и, наконец, приема радиосигналов. Это направление можно назвать «физикой для радио».
Второе направление. Изучение методами и средствами радиотехники самых разнообразных физических (и не только физических) объектов – атомных ядер, молекул, живых организмов, земной атмосферы, небесных тел и т. д. Можно считать, что это – «радио для физики».
Область распространения статистических методов исследования и обработки сигналов-носителей полезной информации практически безгранична. Связь, навигация, управление (процессами, движением и т. п.), диагностика (как техническая, так и медицинская), исследование среды и многие другие области немыслимы без знания и использования свойств сигналов и помех, описываемых их вероятностными характеристиками.
Случайные явления, с которыми приходится иметь дело в указанных направлениях радиофизики, – это процессы, протекающие во времени, или еще шире – поля, зависящие и от времени, и от точки пространства. Адекватным математическим аппаратом для трактовки таких явлений служит теория случайных функций, которая за последние десятилетия приобрела большое значение во многих областях физики и техники. Эта теория представляет собой непосредственное обобщение классической теории вероятностей, рассматривающей случайные события и величины.
При детектировании исследуемых случайных процессов, при кодировании, передаче и приеме происходит искажение сигнала за счет прибавления к нему шума. Необходимость обработки сигналов возникает каждый раз, когда нужно отделить передаваемое сообщение от искажающего шума. Целью обработки может быть восстановление первоначального сигнала на фоне шумов или определение факта
наличия сигнала. В более сложных случаях для экспериментатора представляет интерес статистическая природа сигнала, т. е. его вероятностные характеристики.
Потребность в изучении свойств случайных процессов привела к развитию соответствующих методов и средств. Объектами измерений являются реализации случайных процессов или их последовательностей. Появление анализаторов функций распределения вероятностей, коррелометров, анализаторов спектральной плотности мощности, измерителей математического ожидания, дисперсиометров и других видов измерительных средств повлекло за собой интенсивное накопление информации и углубление знаний о свойствах реальных процессов. С другой стороны, возникла острая потребность в обеспечении необходимого метрологического уровня измерений вероятностных характеристик. Параллельно формировались основы теории измерения вероятностных характеристик случайных процессов, что было обусловлено как широким использованием измерительных методов и средств в практических исследованиях свойств случайных процессов, так и солидным багажом разработанных алгоритмов, устройств и подходов к описанию и изучению их возможностей.
К сказанному следует добавить, что средства статистических измерений в связи с развитием вычислительной техники все в большей степени превращаются в измерительно-вычислительные устройства, характеризующиеся сквозным нормированием метрологических характеристик. Учитывая накопленный опыт и исходя из того, что экспериментальное определение числовых значений характеристик физических объектов есть измерение, можно сформулировать две проблемы, без решения которых нельзя эффективно развивать методологию и технику измерений вероятностных характеристик случайных процессов. При этом учитывается, что формальный аппарат и методология описания и изучения свойств случайных процессов разрабатываются в рамках теории вероятностей, теории случайных функций и математической статистики.
Первая проблема сводится к выбору такого пути развития теории измерений вероятностных характеристик случайных процессов, который учитывал бы положения теории классической метрологии
(детерминистской) и обеспечивал использование того огромного опыта, который накоплен последней. Вторая же обусловлена необходимостью установления связи между сформированными в рамках перечисленных выше математических дисциплин определениями вероятностных характеристик с результатами измерений.
В процессе изложения материала лекций мы будем часто использовать в качестве эквивалентных следующие выражения: «статистические методы обработки информации», «измерения вероятностных характеристик случайных процессов», «статистические измерения», понимая недостаточную корректность такой замены. Однако компактность и широкое распространение такой терминологии вполне оправдывают ее использование.
Лекционный материал включает рассмотрение методов и результатов измерений функций распределения вероятностей, корреляционных и спектральных функций. Анализируются методические погрешности, приводятся базовые алгоритмы и типовые структуры устройств. Особое внимание уделяется устройствам, обеспечивающим параллельно-конвейерные принципы измерения и обработки сигналов.
В спецкурсе практически отсутствует материал по основам теории измерений вероятностных характеристик случайных процессов. Они хорошо представлены в монографии Э. И. Цветкова «Основы теории статистических измерений» (Л., Энергия, 1979 г.). Нами затрагиваются только вопросы оптимальной оценки параметров случайных сигналов. Опущены вопросы, относящиеся к формированию реализаций или последовательностей, представляющих исследуемый случайный процесс. Масштабы проблем, относящихся к оптимизации измерительных процедур, методологии аттестации и поверки средств измерения вероятностных характеристик, настолько значительны, что мы не в состоянии провести их детальный анализ в рамках данного спецкурса.
Как уже отмечалось, при использовании случайных процессов различной природы конечная цель состоит в определении тех или иных вероятностных характеристик. Для определения вероятностных характеристик случайных процессов используются:
-
теоретические исследования;
-
натурные испытания;
-
комбинированные методы исследования.
В обобщенном виде упомянутые виды исследований представлены на рис. 1.
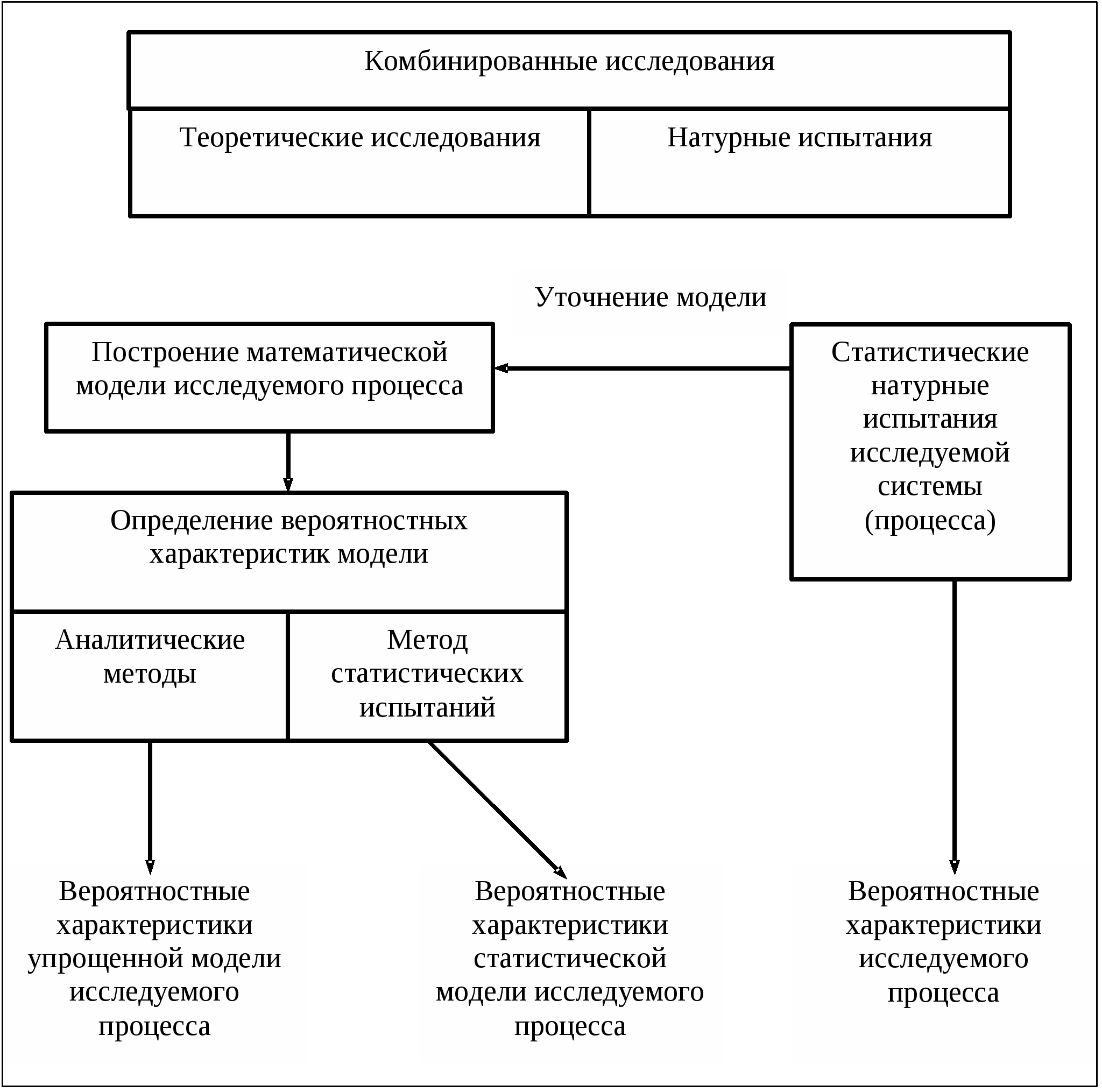
Рис.1. Основные виды исследования случайных процессов
В настоящее время все в большей степени появляется необходимость в разработке комбинированных методов исследования вероятностных характеристик случайных процессов, одновременно использующих аналитические методы, метод статистических испытаний и метод натурных испытаний.
При этом решаются две основные задачи:
-
по возможности более полное использование всей информации о вероятностных характеристиках анализируемых процессов, полученных при различных видах исследований;
-
получение по возможности более точных оценок этих характеристик или получение заданной точности за минимально возможное время измерений.
Необходимость в комбинированных методах исследования случайных процессов (в том числе в сложных системах управления) возникла в первую очередь при исследовании процессов, для которых статистическое моделирование и натурные испытания весьма трудоемки, а требуемая точность обеспечивается проведением большого числа экспериментов.
1. ОСОБЕННОСТИ ИЗМЕРЕНИЯ
ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК
СЛУЧАЙНЫХ ПРОЦЕССОВ
Случайной величиной называется такая переменная величина, которая в результате опыта может принимать то или иное заранее неизвестное значение. Различают два основных типа случайных величин: дискретные и непрерывные. Дискретная случайная величина может принимать конечное или бесконечное счетное множество значений 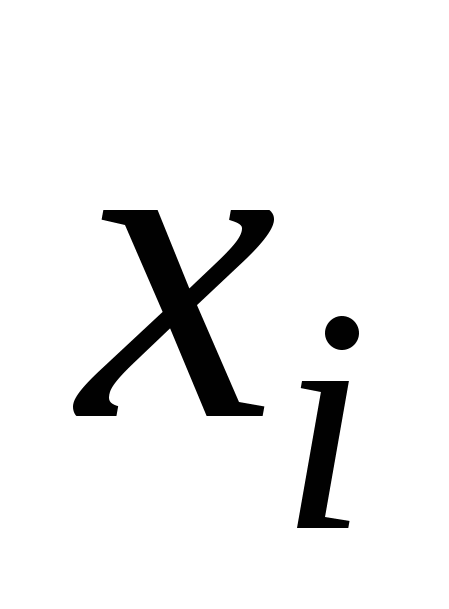 (их можно пронумеровать). Возможные значения непрерывных случайных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток или даже всю ось. Часто встречаются случайные величины смешанного типа, которые могут и непрерывно заполнять некоторый промежуток и принимать отдельные дискретные значения. (их можно пронумеровать). Возможные значения непрерывных случайных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток или даже всю ось. Часто встречаются случайные величины смешанного типа, которые могут и непрерывно заполнять некоторый промежуток и принимать отдельные дискретные значения.
2. ОСНОВНЫЕ ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ
СЛУЧАЙНЫХ ПРОЦЕССОВ
Наиболее фундаментальные исследования случайного процесса выполняются путем анализа основных вероятностных характеристик:
-
функций распределения вероятностей,
-
корреляционных функций,
-
спектральной плотности мощности.
Основные задачи статистической обработки информации сводятся к формированию и измерению оценок математических ожиданий, корреляционных и структурных функций, спектральных плотностей, интервалов корреляции и др. (рис. 2). Применительно к обработке нестационарных случайных процессов возникают дополнительные задачи по их классификации и формированию количественно оцениваемых параметров нестационарности.
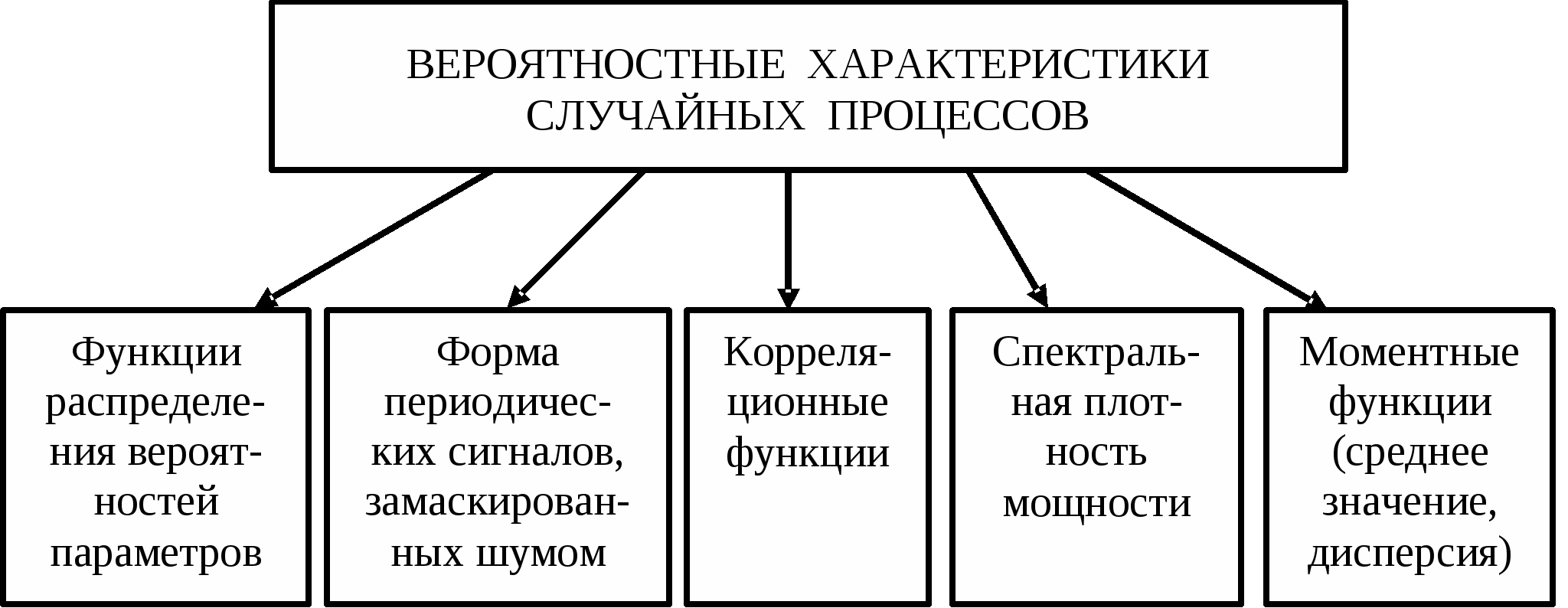
Рис. 2. Основные задачи статистической обработки
измерительной информации
Закон распределения дискретной случайной величины можно задать в различных формах: табличной (ряд распределения), графической (многоугольник распределения), аналитической (в виде формулы).
Универсальной характеристикой, одинаково пригодной как для дискретных, так и для непрерывных одномерных случайных величин, является функция распределения вероятностей 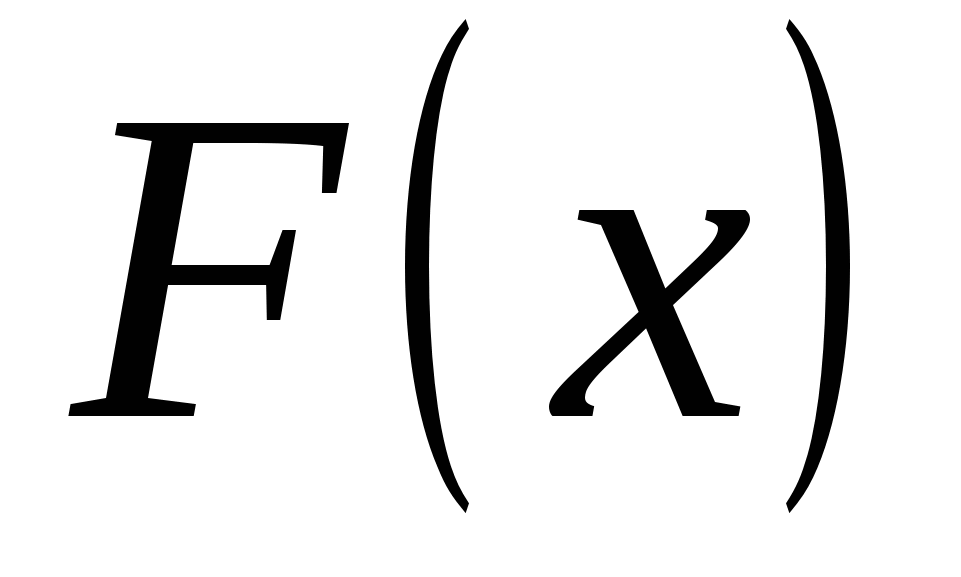 , определяющая вероятность , определяющая вероятность 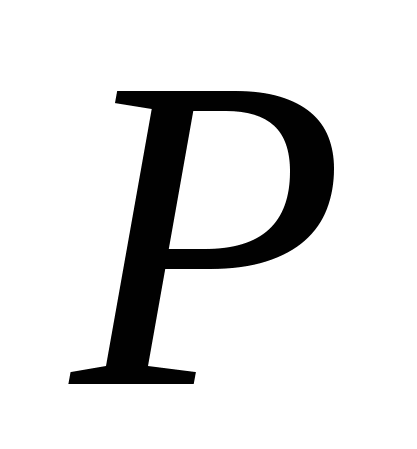 того, что случайная величина того, что случайная величина 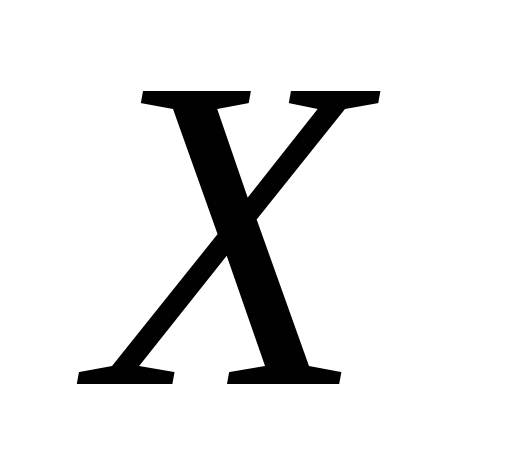 примет значение меньше некоторого числа примет значение меньше некоторого числа 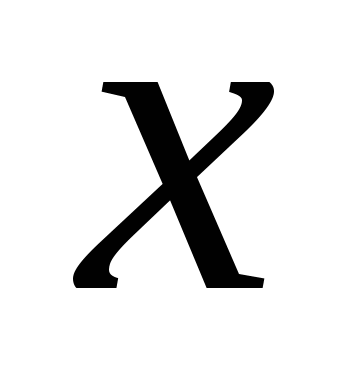 : :
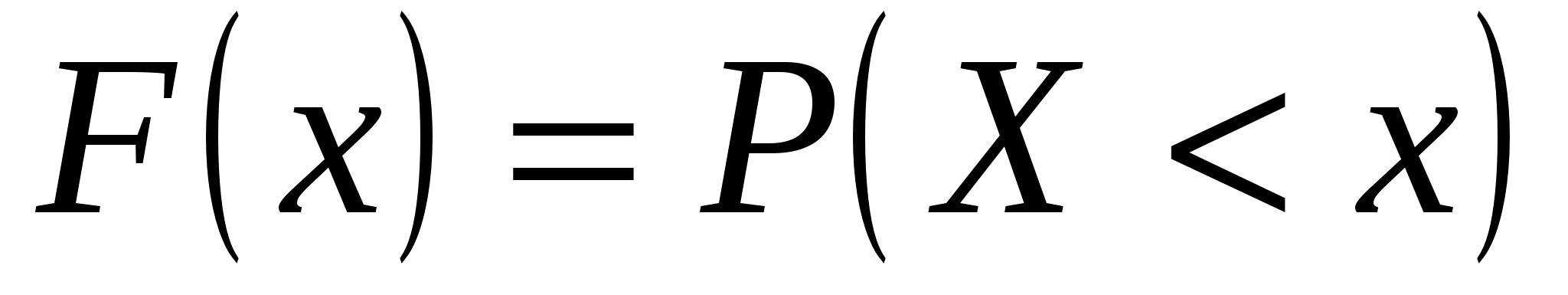 . .
Во многих практических задачах трудно или даже невозможно полностью определить функцию распределения случайной величины. Иногда в этом и нет необходимости. В таких случаях полное описание случайной величины при помощи закона распределения может быть заменено указанием отдельных параметров (числовых характеристик) этого распределения.
Наиболее важными числовыми характеристиками случайной величины 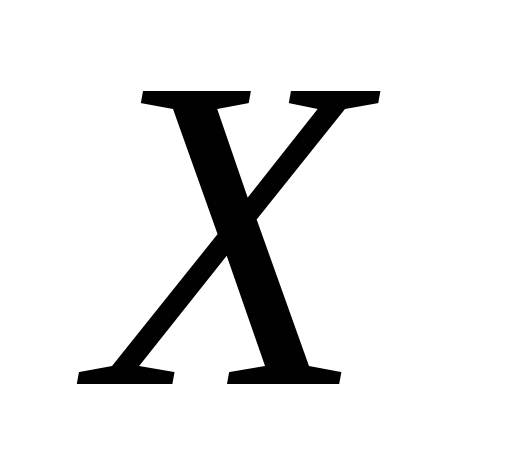 являются математическое ожидание являются математическое ожидание 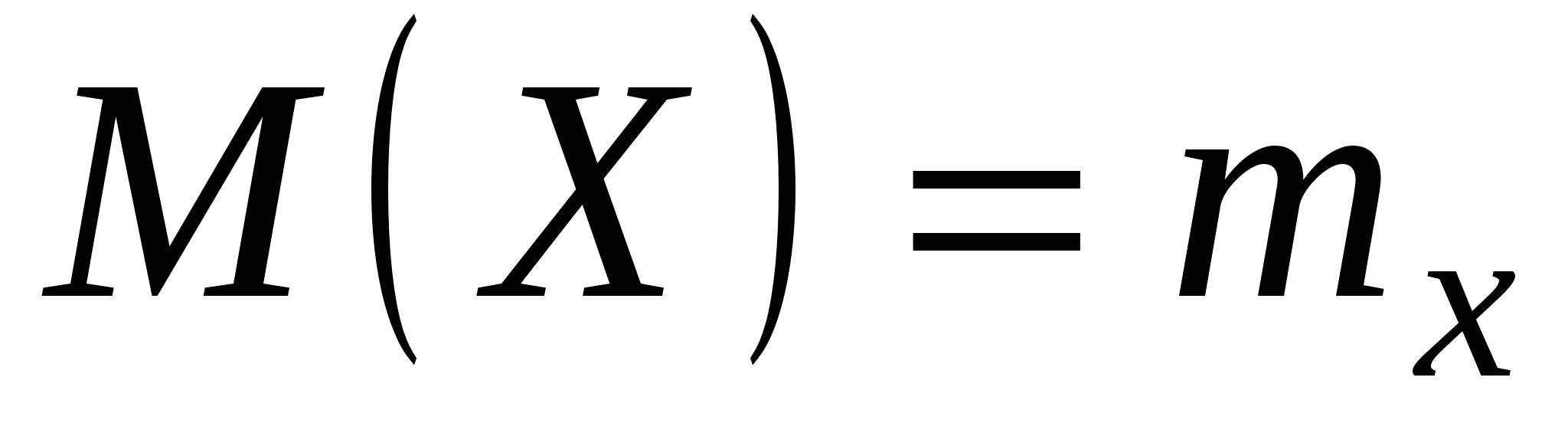 и дисперсия и дисперсия 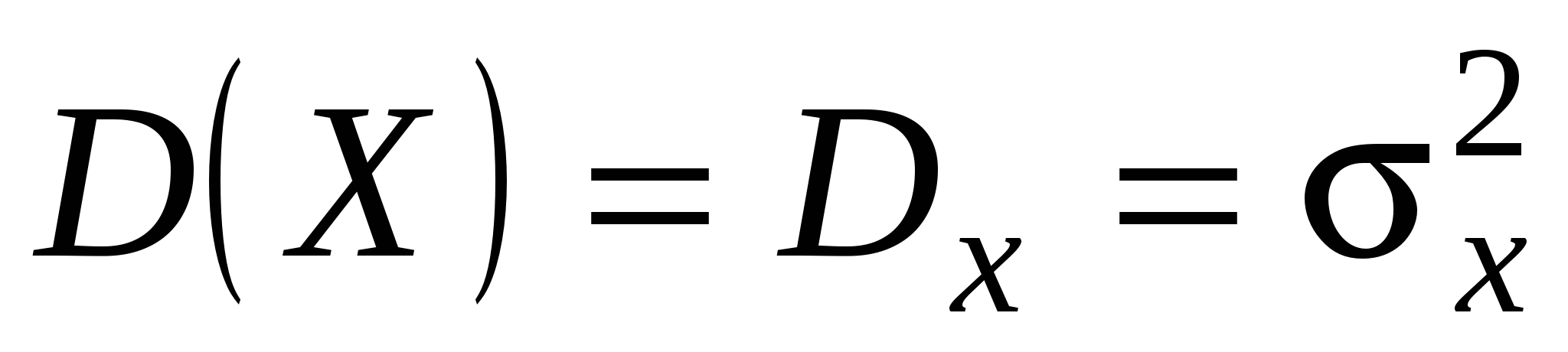 . .
В систематизированном виде основными условиями результативной обработки случайных процессов являются:
-
необходимость существенных априорных сведений. Об ожидаемых процессах судят по общим характеристикам и назначению объекта исследования, на основании расчетных данных и сопоставления с аналогами; на основе предварительных оценочных измерений, изучения характера внешних возмущающих воздействий и многократного анализа записей реализаций случайного процесса;
-
перед измерениями необходимо установить класс и характер исследуемых процессов, для чего приходится осуществлять теоретическое и натурное моделирование;
-
требуются знания теоретических основ обработки потоков стохастических сигналов;
-
необходимо для выбранной модели исследуемого процесса установить зависимость погрешности измерений от условий проведения эксперимента, в частности длительности его проведения;
-
в отличие от случая измерения детерминированных сигналов никакая вероятностная характеристика случайного процесса не может быть измерена единичной выборкой;
-
в тех случаях, когда это возможно, экспериментатор должен проверить приемлемость применения к изучаемому процессу гипотезы о стационарности, эргодичности и нормальности процесса.
В систематизированном виде основные задачи, решаемые при планировании и организации экспериментальных исследований, представлены в таблице.
В лекционном курсе анализируются базовые алгоритмы и типовые структуры устройств обработки информации в радиофизических системах, предназначенных для ядерно-физического эксперимента, масс-спектрометрии, спектрометрии ядерного магнитного и электронного парамагнитного резонанса, Месбауэровской спектроскопии, в системах сейсморазведки, в ультразвуковых расходомерах-счетчиках газа. Отмечаются особенности обработки информации в системах автоматического управления.
3. ОСНОВНЫЕ ЗАДАЧИ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ИНФОРМАЦИИ НА РАЗЛИЧНЫХ ЭТАПАХ ПРОЦЕССА ПЛАНИРОВАНИЯ И ОРГАНИЗАЦИИ
ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ
Таблица
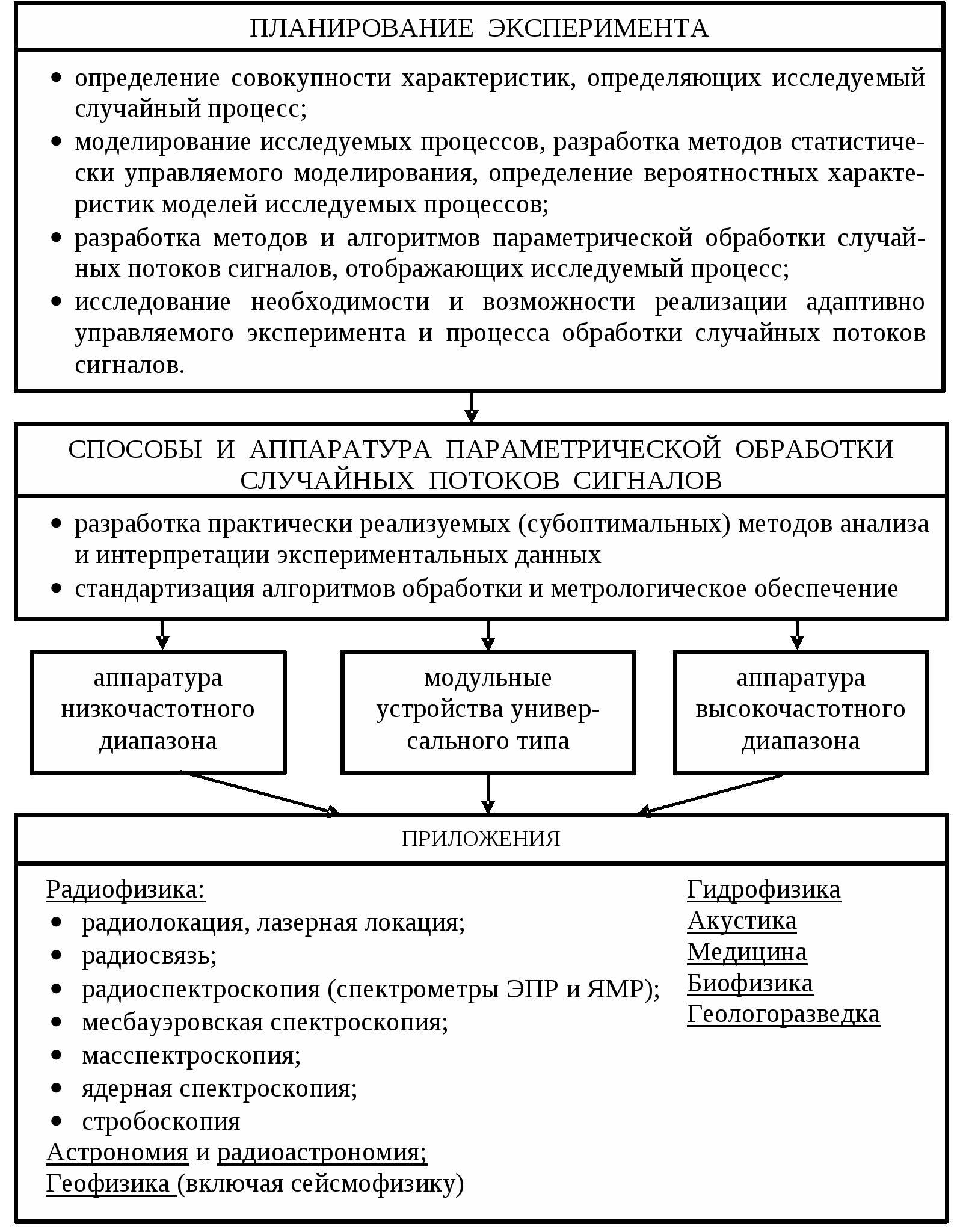
4. Основные разновидности систем статистической обработки результатов экспериментальных исследований
Для большинства задач цифровой обработки информации в обобщенном виде функциональную схему устройства обработки можно представить следующим образом (рис. 3):
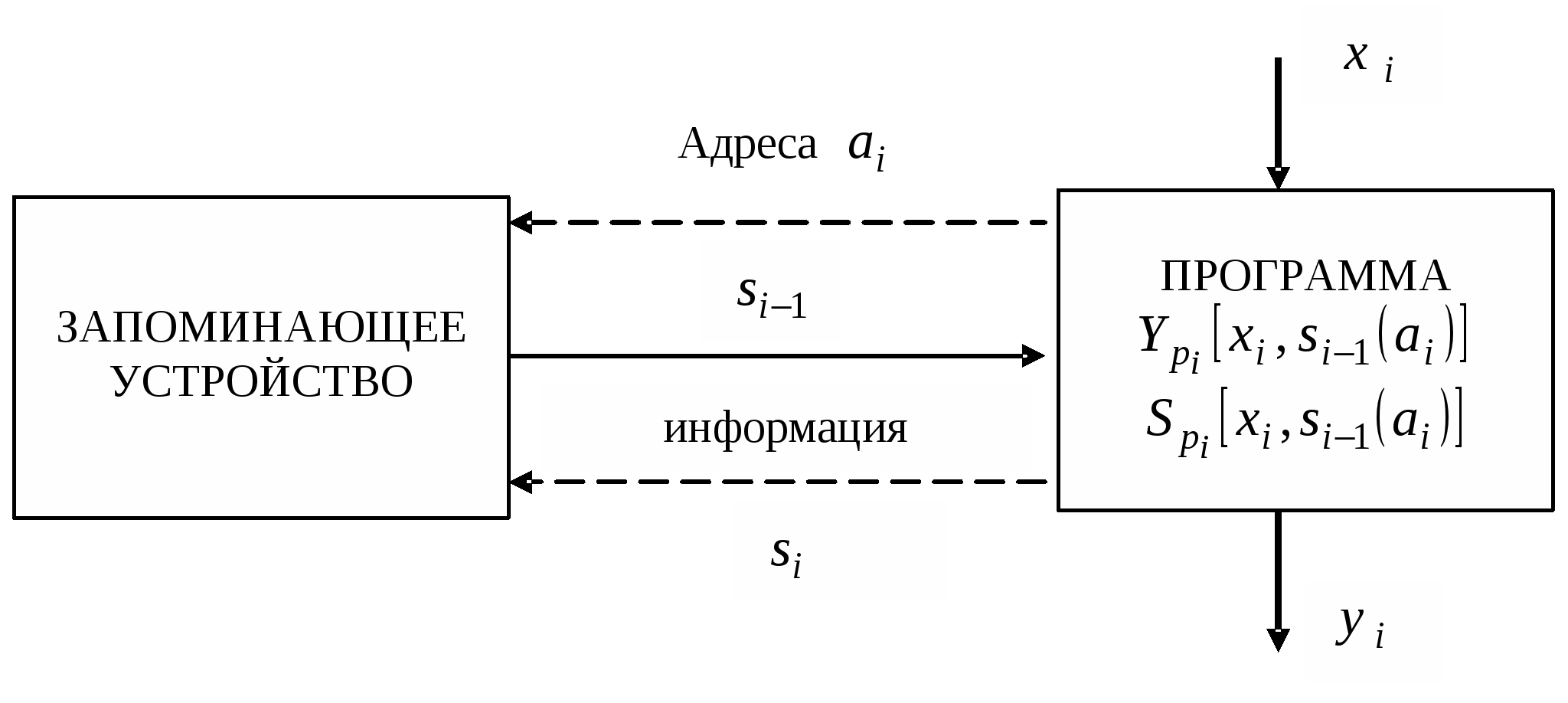
Рис. 3. Функциональная схема устройства обработки информации
При обработке информации воспринимается, истолковывается и познается лишь небольшая доля всего имеющегося, достаточно большого разнообразия данных об изучаемом объекте, при этом выделяются только наиболее существенные зависимости. Общее количество информации в процессе обработки, как правило, уменьшается за счет устранения избыточности, зато ценность и содержательность ее возрастает.
Элементами входных xi и выходных yi массивов данных могут быть результаты экспериментальных исследований (измерений), экономические показатели и отдельные реквизиты, сематические множители и коды документов в документалистике и др.
Массив входных данных представляется следующим образом:
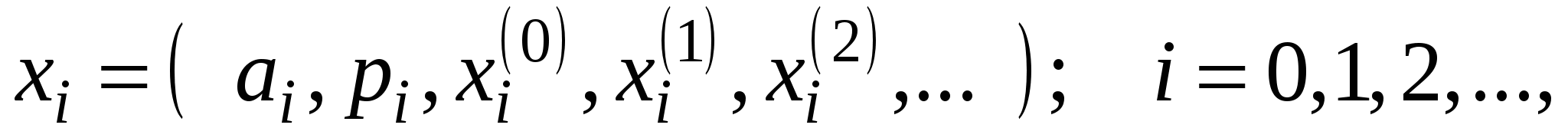
где 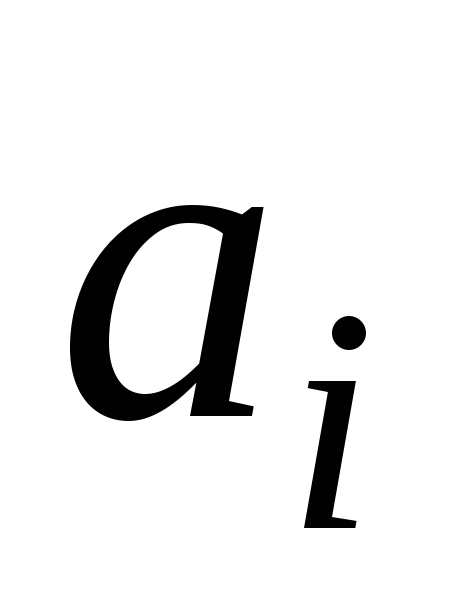 – адрес ячейки ЗУ, содержимое которой необходимо для обработки входных данных; – адрес ячейки ЗУ, содержимое которой необходимо для обработки входных данных; 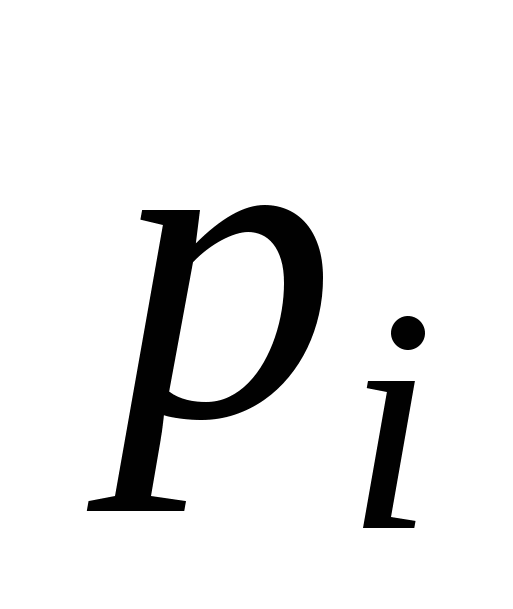 – номер программы, позволяющий определить, по какой из программ следует обрабатывать входной массив; – номер программы, позволяющий определить, по какой из программ следует обрабатывать входной массив; 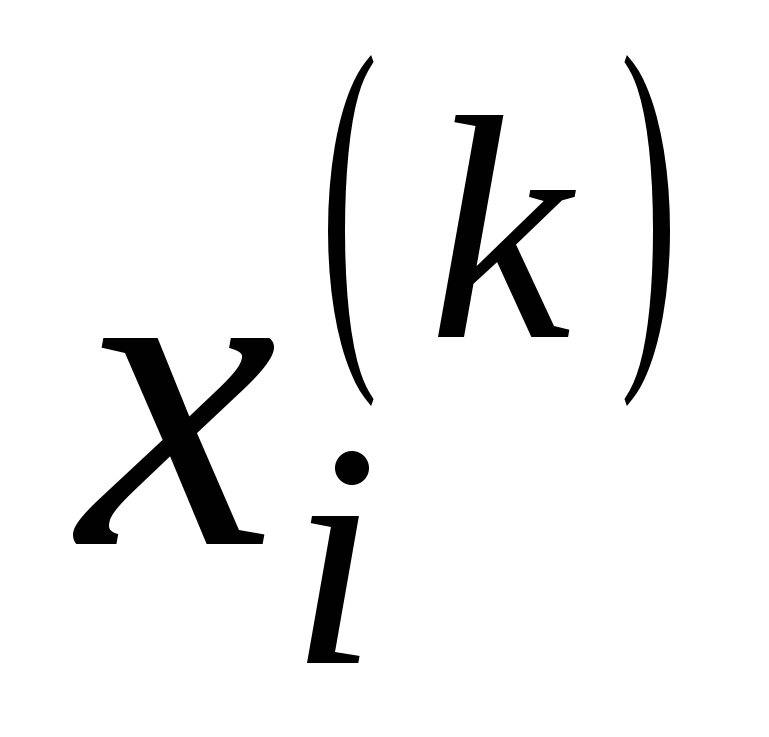 – множество входных элементов в массиве – множество входных элементов в массиве 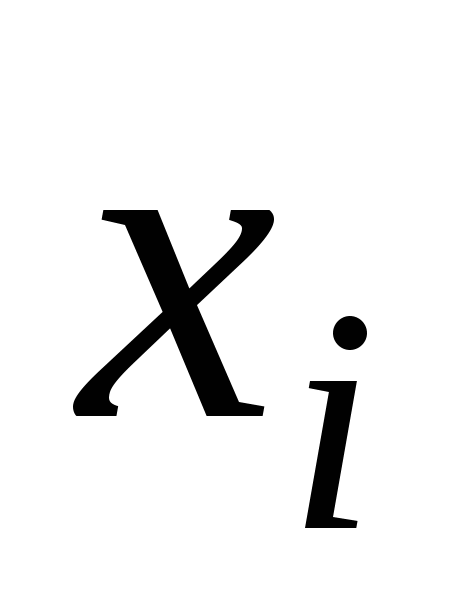 . .
В результате обработки получают два новых массива:
-
массив выходных данных 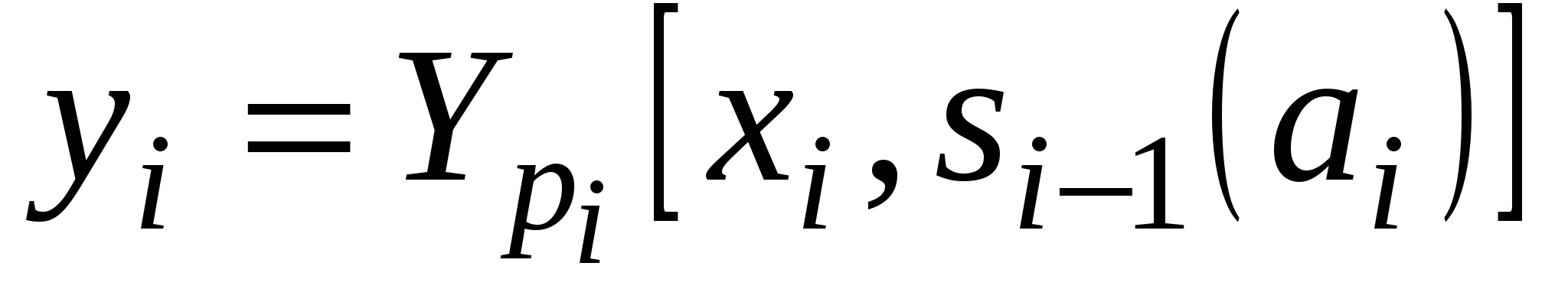 ; ;
-
массив памяти 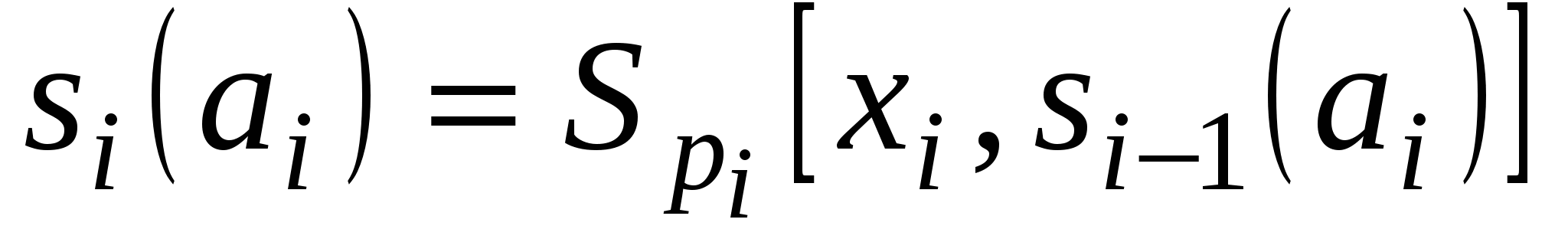 , где , где 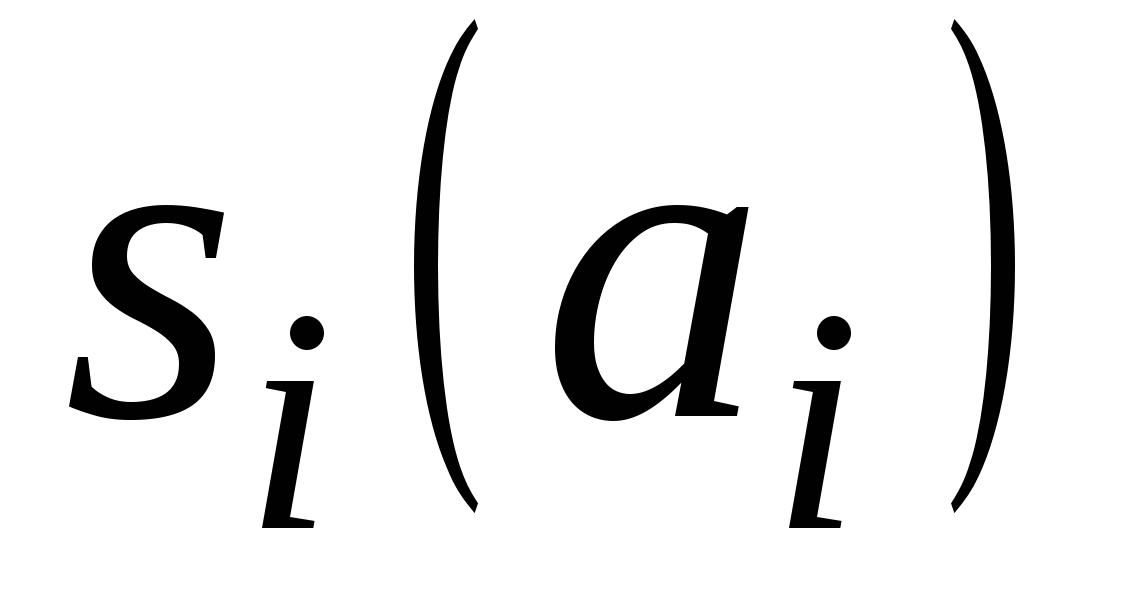 и и 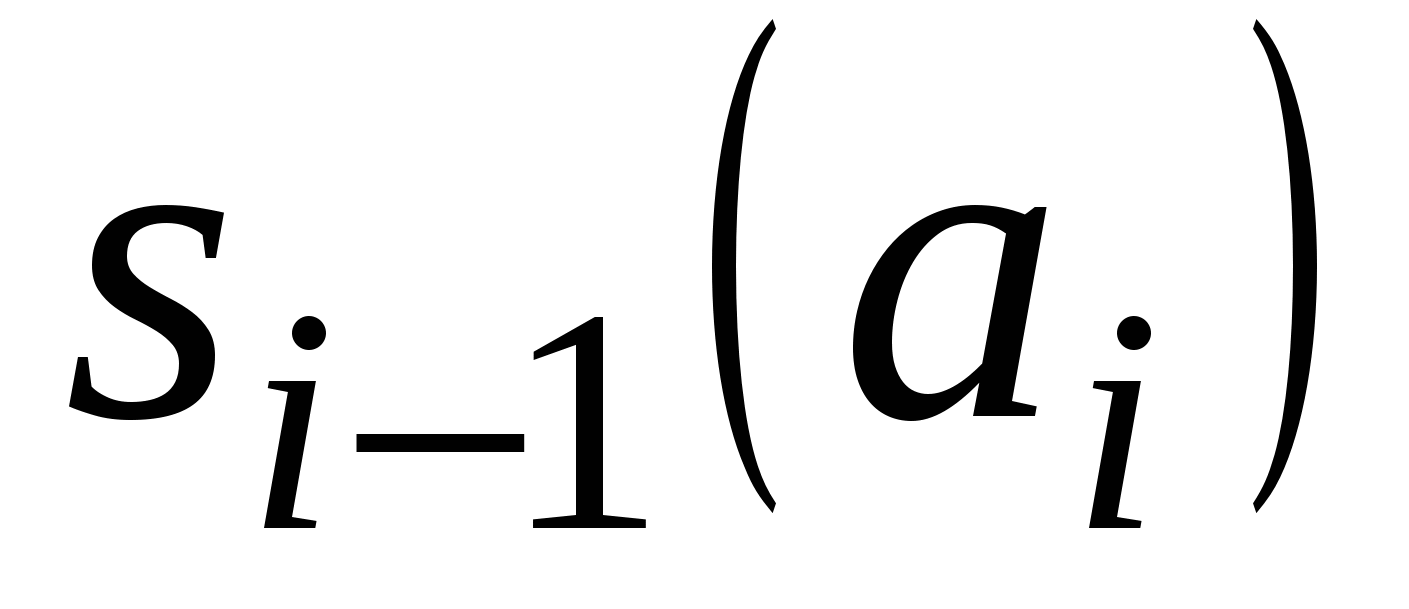 – содержимое – содержимое 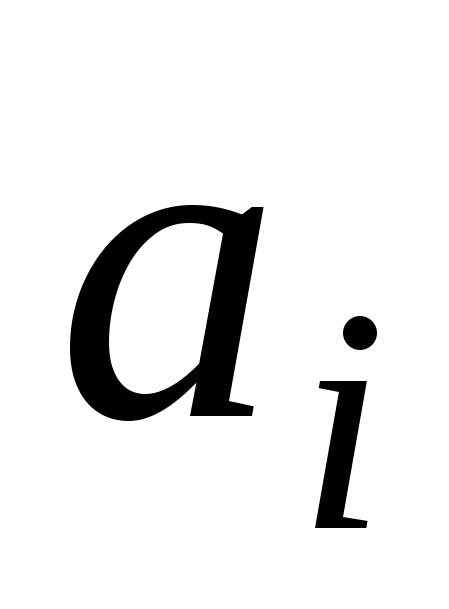 -ячейки ЗУ после и до обработки, соответственно. -ячейки ЗУ после и до обработки, соответственно.
Если содержимое ЗУ в процессе обработки изменяется (имеет место операция 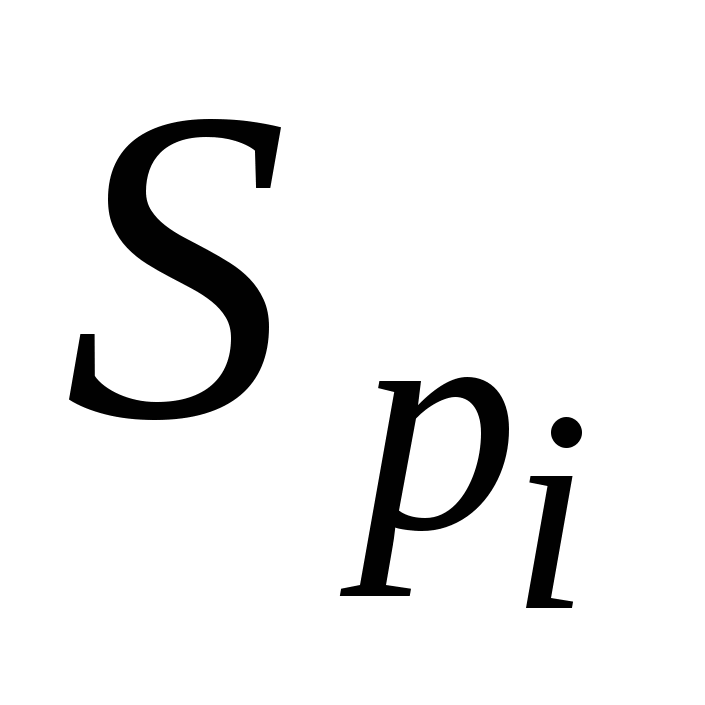 ), то такое устройство называется информационной системой статистической обработки результатов эксперимента. ), то такое устройство называется информационной системой статистической обработки результатов эксперимента.
Если содержимое ЗУ в процессе обработки не изменяется (отсутствует операция 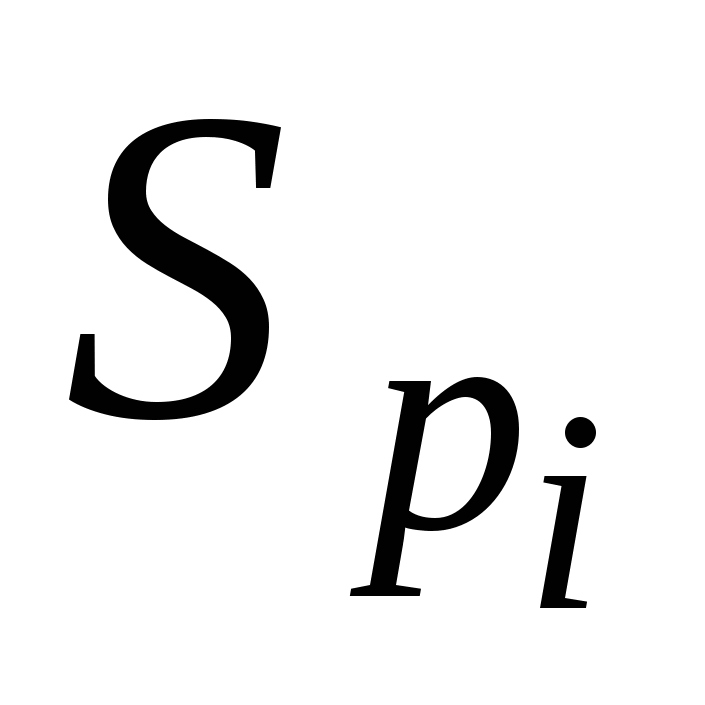 ), то такие устройства называются информационно-поисковыми и информационно-логическими системами. ), то такие устройства называются информационно-поисковыми и информационно-логическими системами.
страница 1
|