страница 1
Учреждение образования
“Гродненский государственный университет имени Янки Купалы”
УТВЕРЖДАЮ
Декан факультета математики и информатики
_____________ Е.Н. Ливак
_____________ 2011 г.
Регистрационный № УД- _______/р.
|
Практикум по решению задач школьного курса математики: модуль 5
Учебная программа для специальности:
(рабочий вариант)
1-31 03 01-02 Математика (научно-педагогическая деятельность)
Факультет математики и информатики
Кафедра алгебры, геометрии и методики преподавания математики
Курс 5
Семестр 9
Лекции 14
(количество часов)
|
Экзамен
(семестр)
|
Практические (семинарские)
занятия 32
(количество часов)
|
Зачёт 9
(семестр)
|
Лабораторные
занятия
(количество часов)
|
Курсовая работа (проект)
(семестр)
|
Всего аудиторных часов
по дисциплине 46
(количество часов)
|
|
Всего часов
по дисциплине 76
(количество часов)
|
Форма получения
высшего образования дневная
|
Составил Ю.П. Золотухин, кандидат физико-математических наук, доцент
2011 г.
Учебная программа (рабочий вариант) составлена на основе учебной программы для специальностей: 1-31 03 01-02 Математика (научно-педагогическая деятельность) по дисциплине «Практикум по решению задач школьного курса математики: модуль 5», утверждённой 21.05.2008 Советом факультета математики и информатики
Рассмотрена и рекомендована к утверждению в качестве рабочего варианта на заседании кафедры алгебры, геометрии и методики преподавания математики
01.06.2011 г., протокол N°7
Заведующий кафедрой
____________________ А.А. Гринь
Одобрена и рекомендована к утверждению на заседании Методической комиссии факультета математики и информатики
_____2011 г., протокол №_____
Председатель
___________________ Н.П. Макарова
Одобрена и рекомендована к утверждению на заседании Совета факультета математики и информатики
_____2011 г., протокол №_____
Учёный секретарь
___________________ _______________
1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
1.1. Цели и задачи учебной дисциплины
Практикум нацелен на повышение качества профессионально-педагогической подготовки студентов, развитие их учебно-познавательной компетенции. В частности, он призван максимально содействовать выработке устойчивых навыков решения задач школьной математики, доведению их до уровня необходимого для квалифицированного преподавания математики в учреждениях среднего образования любого типа.
Кроме того, прохождение практикума должно актуализировать знания, умения и навыки, приобретенные студентами в процессе изучения высшей математики, укрепить внутрипредметные связи, продемонстрировать преемственность различных разделов математической науки. Предполагается также, что курс будет способствовать созданию предметной основы для изучения методических дисциплин и прохождения педагогической практики.
Преподавание дисциплины предполагает также развитие ключевых образовательных компетенций студентов – ценностно-смысловой, общекультурной, информационной, коммуникативной, социально-трудовой, личностного самосовершенствования.
1.2. Формы и методы обучения и воспитания
Объяснительно-иллюстративный метод, метод проблемного обучения, метод самостоятельной работы, индивидуальный подход, деятельностный подход, контекстный подход.
1.3. Рекомендации по организации самостоятельной работы студентов
Содержательно самостоятельная работа студентов определяется образовательным стандартом специальности, программой дисциплины, содержанием рекомендуемых учебников, учебных пособий и методических руководств.
После практического занятия каждый студент должен самостоятельно выполнить обязательную домашнюю работу. По желанию студенты могут выполнять дома дополнительные задания по теме модуля (имеются в раздаточных материалах). Резервные тесты рекомендуется использовать для проведения дополнительной самостоятельной работы. Прежде чем приступить к выполнению домашнего теста студент должен повторить теоретический материал по соответствующей теме. Каждый студент должен иметь справочное пособие по математике, содержащее необходимые формулы и факты по теме модуля.
Тест считается выполненным, если правильно решены все задания и представлены их подробные, обоснованные решения. Тест считается выполненным по графику, если он выполнен к началу занятия, следующего за аудиторным занятием, на котором было разобрано последнее задание соответствующего теста.
1.4. Требования к компетентности
В результате изучения учебной дисциплины студент должен:
– знать: понятие функции, область определения функции, множество значений функции, график функции, явное и неявное задание функций, сложные функции, взаимно-обратные функции, чётные и нечётные функции, ограниченные и неограниченные функции, нули функции и промежутки знакопостоянства, монотонные функции, экстремумы, наибольшее и наименьшее значения функции, периодические функции, свойства и графики линейной, квадратичной, дробно-линейной функции, показательной, логарифмической функций, степенных функций с чётным, нечётным и дробным показателями, тригонометрических и обратных тригонометрических функций;
– уметь: исследовать свойства функций, встречающихся в школьном курсе математики, строить их графики, применять функциональные методы решения математических задач, решать простейшие функциональные уравнения;
– владеть навыками: исследования свойств функций, встречающихся в школьном курсе математики, построения их графиков, применения функциональных методов решения математических задач, решения простейших функциональных уравнений.
2. СОДЕРЖАНИЕ УЧЕБНОГО МАТЕРИАЛА
№
|
Наименование
раздела дисциплины
|
Содержание в соответствии с
учебной программой
|
|
Введение
|
Место и роль темы “Функции” в школьном курсе математики
|
1
|
Основные понятия и общие свойства функций
|
Понятие функции. Область определения и множество значений функции. Явное и неявное задание функций. Сложная функция. Взаимно обратные функции. Четные и нечетные функции. Ограниченные функции. Нули функции и промежутки знакопостоянства. Монотонные функции. Экстремумы. Наибольшее и наименьшее значения функции.
|
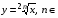 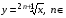 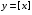 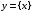 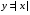 2 2
|
Основные классы функций школьного курса мвтематики
|
Постоянная функция. Линейная функция. Квадратичная функция. Обратная пропорциональность. Степенные функции с четным и нечетным показателями. Функции N, и N. Степенные функции с дробными показателями. Показательная и логарифмическая функции. Функции и . Функция .
Построение графиков функций с помощью геометрических преобразований.
|
3
|
Производная и ее применения к исследованию функций
|
Производная функции. Геометрический смысл производной. Касательная прямая. Физический смысл производной. Производная сложной функции. Производная обратной функции. Применение производной к исследованию функций на монотонность и нахождение экстремумов. Применение производной к нахождению наибольших и наименьших значений функций и построению их графиков. Изображение множеств точек на плоскости, заданных уравнениями и неравенствами.
|
4
|
Применение функций для решения математических задач
|
Функциональный и графический методы решения задач. Применение функций для доказательства тождеств, сравнения чисел, вычисления сумм, доказательства неравенств. Применение функций для решения уравнений и неравенств (нахождение областей определения и множеств значений, использование свойств ограниченности, монотонности, четности, периодичности). Задачи с параметрами.
Простейшие функциональные уравнения и неравенства.
|
3. ТРЕБОВАНИЯ К КУРСОВОЙ РАБОТЕ (ПРОЕКТУ)1
Учебным планом учреждения высшего образования не предусмотрено выполнение курсовой работы (проекта) по данной дисциплине.
3.1. Цель курсовой работы (проекта) по дисциплины
__________________________________________________________________________________________________________________________________________________
3.2. Объем задания2
__________________________________________________________________________________________________________________________________________________
3.3. Примерная тематика курсовых работ (проектов)
__________________________________________________________________________________________________________________________________________________
4. УЧЕБНО-МЕТОДИЧЕСКАЯ КАРТА УЧЕБНОЙ ДИСЦИПЛИНЫ
№
|
Тэмы заняткаў
Пытанні, якія вывучаюцца на занятках
|
Заняткі (гадзіны)
|
Форма кантролю ведаў
| |
Лекцыі
|
Практыч (семінар)
|
Метадычныя дапаможнікі, сродкі навучання
|
Лiтаратура
|
Кіруемая самааст. праца
|
1
|
2
|
3
| -
| -
| -
| -
| -
| -
|
1
|
Понятие функции. Область определения функции
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
2
|
Множество значений функции
|
1
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
3
|
Явное и неявное задание функций
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
4
|
Линейная, квадратичная и дробно-линейная функции: свойства и графики
|
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
5
|
Степенные функции с чётным, нечётным и дробным показателями
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
6
|
Показательная и логарифмическая функции
|
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
7
|
Тригонометрические и обратные тригонометрические функции: свойства и графики
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
8
|
Функция y=|x|, функция y=[x] и y={x}: свойства и графики
|
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
9
|
Сложные функции
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
10
|
Простейшие функциональные уравнения
|
|
|
Раздатачны матэрыял
|
[1] – [10]
|
2
|
Тестирование
|
11
|
Взаимно-обратные функции
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
12
|
Чётные и нечётные функции
|
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
13
|
Применение свойств чётных и нечётных функций
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
14
|
Ограниченные и неограниченные функции. Точные и неточные оценки
|
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
15
|
Нули функции и промежутки знакопостоянства
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
16
|
Монотонные функции
|
1
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
17
|
Применение свойств монотонных функций
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
18
|
Экстремумы. Наибольшее и наименьшее значения функции
|
1
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
19
|
Применение наибольших и наименьших значений
|
1
|
1
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
20
|
Периодические функции
|
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
21
|
Применение свойств периодических функций
|
1
|
2
|
Раздатачны матэрыял
|
[1] – [10]
|
|
Тестирование
|
|
Всего
|
14
|
30
|
|
|
2
|
|
5. ИНФОРМАЦИОННО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
ПО ДИСЦИПЛИНЕ
5.1. Перечень рекомендуемой литературы
№
п/п
| Перечень материалов | Основная литература |
1
|
Сборник экзаменационных материалов по математике за курс средней школы / МО РБ; Авт.-сост.: Будников Е.Г., Казаков В.В., Шестаков Ю.Н. – 6-е изд., доп. – Минск: Нар. асвета, 2006. – 319с.
|
2
|
А.И.Азаров, С.А.Барвенов. Функциональный и графический методы решения экзаменационных задач. – Минск: Аверсэв, 2000 – 222с.
|
3
|
В.В.Вавилов, И.И.Мельников и др. Задачи по математике. Начала анализа. – Москва: Наука, 1990. – 608с
|
4
|
Математика: Пособие для подготовки к экзамену и централизованному тестированию за курс ср. школы / А.И. Азаров, В.И. Булатов, А.И. Жук и др. – Мн.: «Аверсэв», 2003. – 396с. – (Школьникам, абитуриентам, учащимся).
|
5
|
В.П.Супрун. Математика для старшеклассников. Нестандартные методы решения задач. – Минск: Аверсэв, 2003. – 258с.
|
Дополнительная литература
|
6
|
В.А.Гусев, А.Г.Мордкович. Математика: Справочные материалы. – Москва: Просвещение, 1988. – 416с.
|
7
|
И.Ф.Шарыгин, В.И.Голубев. Факультативный курс по математике. Учеб.пособие для 11 кл. сред. шк. – Москва: Просвешение, 1991. – 384с.
|
8
|
К.О.Ананченко, Г.Н.Петровский. Алгебра и начала анализа. Учеб. пособие для 11 кл. общеобр. шк. с углубл. изучением математики. – Минск: Нар. асвета, 1997. – 375с.
|
9
|
Е.П.Кузнецова, Г.Л.Муравьева и др. Алгебра и начала анализа. Учеб. пособие для 11 кл. общеобр. шк. / Под ред. Л.Б.Шнепермана. – Минск: Нар. асвета, 2000. – 310с.
|
10
|
А.И.Азаров, В.И.Булатов. Функции, их свойства и графики. – Минск: Универсал Пресс, 2004. – 400с.
|
5.2. Перечень средств диагностики результатов учебной деятельности
Тестирование
6. ПРОТОКОЛ СОГЛАСОВАНИЯ УЧЕБНОЙ ПРОГРАММЫ
ПО ИЗУЧАЕМОЙ УЧЕБНОЙ ДИСЦИПЛИНЕ
С ДРУГИМИ ДИСЦИПЛИНАМИ СПЕЦИАЛЬНОСТИ
3Название дисциплины, с которой требуется согласование
|
Название кафедры
|
Предложения об изменениях в содержании учебной программы по изучаемой учебной дисциплине
|
Решение, принятое кафедрой, разработавшей учебную программу
(с указанием даты и номера протокола)
|
1.
|
|
|
|
|
|
|
| -
ДОПОЛНЕНИЯ И ИЗМЕНЕНИЯ К УЧЕБНОЙ ПРОГРАММЕ
на ____ / _____ учебный год
№
п/п
|
Дополнения и изменения
|
Основание
|
|
|
|
|
|
|
|
|
| Учебная программа пересмотрена и одобрена на заседании кафедры
____________________________ (протокол № __ от _____ 20___ г.)
(название кафедры)
Заведующий кафедрой
__________________________ ____________________ ______________________________ (ученая степень, ученое звание) (подпись) (И.О.Фамилия)
УТВЕРЖДАЮ
Декан факультета
__________________________ ____________________ ______________________________ (ученая степень, ученое звание) (подпись) (И.О.Фамилия)
страница 1
|