страница 1
Комплексные числа
Определение комплексного числа
Рассматривается множество упорядоченных пар z = (x, y). Первое число из такой пары называется вещественной частью и обозначаются x = Re z, второе число называется мнимой частью y = Im z.
Два элемента z1 , z2 равны z1 = z2 , если равны их вещественные и мнимые части z1 = z2 { Re z1 = Re z2, Im z1 = Im z2 }.
Определяются две операции:
Сложение z = (x,y), w = (u,v), z + w = (x + u,y + v).
Умножение zw = ( xu – yv, xv + yu).
Это множество с такими операциями называется множеством комплексных чисел и обозначается C (комплексная плоскость).
Геометрическая интерпретация. Комплексное число z=(x,y) можно интерпретировать, как радиус вектор в точку (x,y).
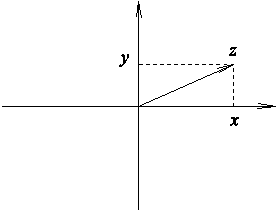
Свойства комплексных чисел
Ниже перечисленные свойства проверяются исходя из определения операций сложения и умножения комплексных чисел.
1) z1 +z2 = z1 + z2
2) z1 +(z2 + z3) = (z1 + z2) + z3
3) обозначим 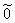 = (0, 0), тогда для любого z будет выполнено z + = (0, 0), тогда для любого z будет выполнено z + 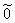 = z = z
4) zC можно определить противоположный элемент -z=(-x,-y), который обладает следующим свойством z+(-z)=
Можно доказать, что 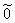 - единственный, противоположный для z также единственен. - единственный, противоположный для z также единственен.
5) z1 z2 = z2 z1
6) z1 ( z2 z3) = (z1 z2) z3
7) определим 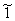 =(1,0) , тогда z: z =(1,0) , тогда z: z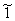 = z = z
8) z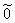 (обратный элемент) z-1: z z-1 = (обратный элемент) z-1: z z-1 = 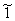
Существование обратного числа. Пусть z=(x,y). Будем искать число
z-1=(u,v), удовлетворяющее нужным свойствам: xu - yv=1,yu+xv=0 (z z-1 =  ). Решая эту систему, получим u=x/(x2+y2),v=-y/(x2+y2). ). Решая эту систему, получим u=x/(x2+y2),v=-y/(x2+y2).
Частное двух комплексных чисел определяется по формуле w/z=wz-1.
9) z1(z2+z3)=z1z2+z1z3
Алгебраическая форма записи
Рассмотрим отображение c(x) из R в C: 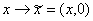 , где xR, , где xR,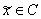 . Множество комплексных чисел (x,0), обозначим . Множество комплексных чисел (x,0), обозначим 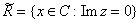 . Отображение c(x) взаимно-однозначно, причем . Отображение c(x) взаимно-однозначно, причем
c(x+y) = c(x)+c(y)
c(xy) = c(x)c(y)
c(0) = 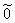
c(1) = 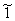
Следствие: c(-x)=-c(x), c(x-1)=c(x)-1 или c(1/x)=1/c(x).
Эти свойства позволяют отождествлять числа 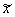 с вещественными числами x. В дальнейшем волну будем опускать. Множество чисел (x,0) называется вещественной осью. с вещественными числами x. В дальнейшем волну будем опускать. Множество чисел (x,0) называется вещественной осью.
Мнимая единица. Введем обозначение i=(0,1).
Отметим, что x+iy=(x,0)+(0,1)(y,0)=(x,y)=z , таким образом можно записать z=(x,y)=x+iy. Представление комплексного числа z=(x,y)=x+iy называется алгебраической формой записи комплексного числа. Множество чисел (0,y)=iy называется мнимой осью.
Модуль и аргумент комплексного числа. Комплексное сопряжение. Тригонометрическая форма записи комплексных чисел.
Некоторые определения и свойства
Для z=(x,y), определяется комплексно сопряженное число 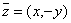 , ,
модуль комплексного числа 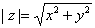 . .
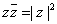
Определение аргумента комплексного числа
Главным значением аргумента комплексного числа называется угол между положительным направлением вещественной оси и радиус вектором комплексного числа, лежащий в диапазоне [0,2). Главное значение аргумента обозначается arg z. Аргумент комплексного числа Arg z = arg z +2k. Например, для первой четверти arg z = arctg y/x , а для четвертой четверти, arg z = 2+arctg y/x .
Тригонометрическая форма представления комплексного числа
z = x + iy = r( cos + i sin ), (1)
где =Arg z.
Формулы Эйлера. Введем обозначения
ei = cos + i sin , откуда следует, что
cos = 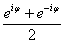 , sin = , sin = 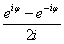 . .
Замечание. Определение комплексного числа ez в общем случае z=x+iy производится по формуле 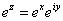 . .
Свойства символа ei. Непосредственно из определения следует
ei(+) = ei ei, (ei)n=ein
Используя ei комплексное число можно представить в виде
z = rei (2)
Выражения (1) и (2) - тригонометрические формы записи комплексного числа
Формула Муавра
zn=rnein=rn( cos n + i sin n) (3)
Доказывается индукцией по n. Решим уравнение
zn=w, z = rei, w = ei
Имеем rnein=ei n=+2k, kZ, r=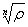 . Формулы . Формулы
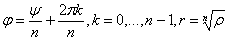
используются для вычисления корней из комплексного числа. Процесс нахождения корня n – ой степени из комплексного числа z можно описать следующим образом. Если это число не ноль, то таких корней будет ровно n – штук. Все они будут являться вершинами правильного n – угольника, вписанного в окружность радиуса 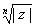 . Одна из вершин этого многоугольника имеет аргумент, равный . Одна из вершин этого многоугольника имеет аргумент, равный 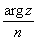 . .
Замечание: Знаки сравнения <, > не определены в C.
страница 1
|