страница 1
Министерство образования Республики Беларусь
УО « Волковысский государственный строительный профессиональный лицей»


ПРЕПОДАВАТЕЛЬ
Левданская Д. Р.
2011 - 2012 учебный год
АННОТАЦИЯ
Одной из главных задач преподавания математики является формирование и развитие у учащихся пространственных представлений, способности и умения производить различные операции над пространственными объектами. Решающую роль в формировании и развитии у учащихся пространственных представлений играет изучение стереометрии.
Конструктивные задачи на построение можно и следует решать уже на первых уроках стереометрии, после прохождения аксиом стереометрии и следствий из них.
В качестве материала для задач следует использовать наиболее известные учащимся геометрические тела: куб, треугольные и четырехугольные призмы и пирамиды.
Задача может состоять из нахождения точки пересечения данной прямой с данной плоскостью или из нахождения линии пересечения двух данных плоскостей, из построения сечения многогранника данной плоскостью. При этом вначале данные точки надо брать на ребрах, а прямые на гранях данного многогранника. Затем задания могут усложняться.
Такого рода задачи, связанные с хорошо известными учащимся геометрическими телами, сравнительно легко усваиваются ими благодаря известной наглядности.
В результате их решения у учеников создаются необходимые пространственные представления и приобретаются полезные навыки выполнения проекционных чертежей.
ЦЕЛИ УРОКА:
-
Образовательные:
-
обеспечить в ходе урока усвоение алгоритма решения задач на построение сечений куба, параллелепипеда, призмы;
-
обеспечить обобщение знаний учащихся по первым разделам стереометрии: взаимное расположение точек, прямых и плоскостей в пространстве;
-
создать условия для контроля (самоконтроля) усвоения знаний и умений.
-
Развивающие:
-
развитие умения применять полученные знания по стереометрии на практике;
-
формирование умения анализировать и обобщать знания в процессе решения задач на построение сечений, устанавливать связь между элементами темы.
-
Воспитательные:
-
воспитание осознанной потребности в знаниях;
-
совершенствование учебных умений и навыков;
-
воспитывать познавательный интерес к предмету через приобретение пространственного воображения и умения видеть красоту окружающего мира.
ТИП УРОКА: урок закрепления и корректировки знаний.
ОБОРУДОВАНИЕ: интерактивно - мультимедийная система, презентация «Построение сечений куба, параллелепипеда, призмы», карточки с заданиями, учебник В. В. Шлыков «Геометрия 10 класс».
ВИД УРОКА: урок с применением компьютера.
МЕТОД: комбинированный (словестно-наглядно-практический).
ХОД УРОКА
-
Организационная часть.
1.1 Актуальность темы.
1.2 Постановка задачи.
1.3 Навыки и умения, необходимые для успешной работы на уроке.
II. Проверка домашнего задания (проверка с помощью компьютерной презентации: слайды 4-6).
Домашнее задание было по трём уровням сложности
Задача 1 - первый уровень
Задача 2 – второй уровень
Задача 3 – третий уровень
Задача 1. АВСА1С1 – треугольная призма, точка F – середина ребра АВ, точка О лежит на продолжении ребра ВС так, что С расположена между В и О. Постройте сечение призмы плоскостью В1FO.
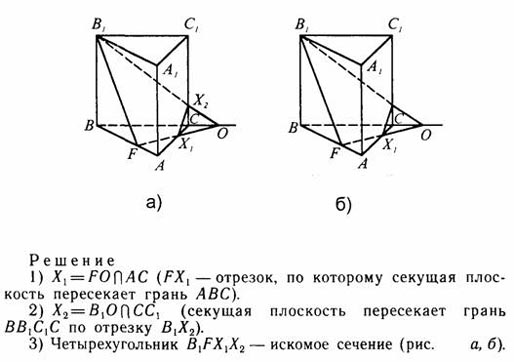
Задача 2. Построить сечение треугольной призмы АВСА1В1С1 плоскостью, проходящей через точки M Є АC, N Є СС1 и K Є ВВ1.
Решение
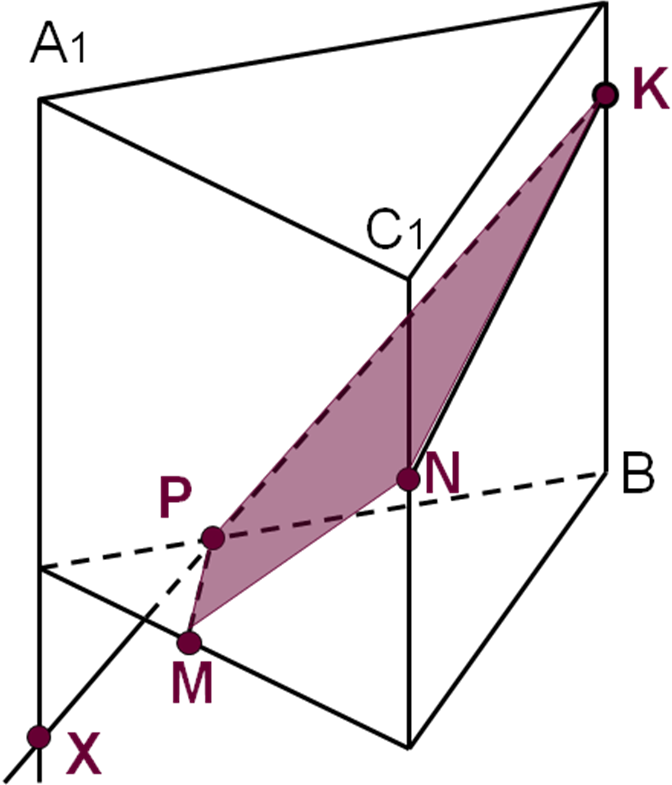 
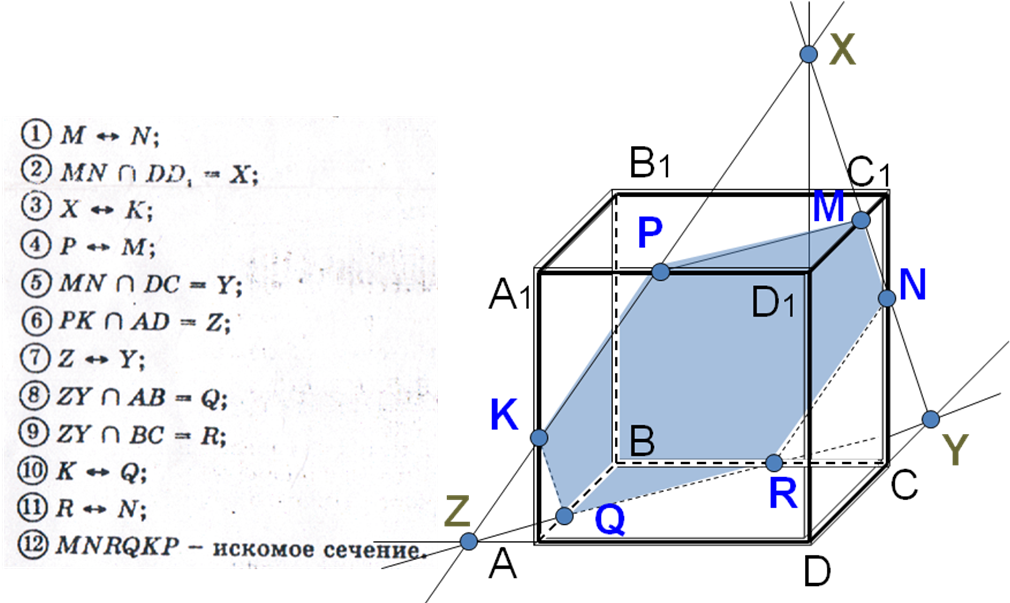
Задача 3. Построить сечение куба АВСDА1В1С1D1 плоскостью, проходящей через точки M Є D1C1, N Є CС1 и K Є AA1.
Решение
-
Актуализация знаний (слайд 7)
-
Какая плоскость называется секущей плоскостью многогранника?
-
Какая фигура называется сечением многогранника?
-
Поясните, как можно построить отрезок, по которому секущая плоскость пересекает грань многогранника.
-
Что необходимо построить для того, чтобы построить прямую, по которой пересекаются две плоскости?
-
Работа по готовым чертежам (слайды 8-11)
Предлагаются задачи по уровням сложности. Учащиеся выбирают уровень сложности, выполняют данные задания, а затем коллективное обсуждение хода решения.
Условие: являются ли закрашенные фигуры сечениями изображённых многогранников плоскостью PQR? В тех случаях, когда сечение показано неправильно, найдите правильное решение.
На рисунках изображены правильные параллелепипеды.
Задание первого уровня:
 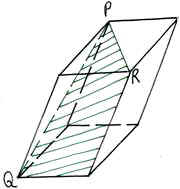 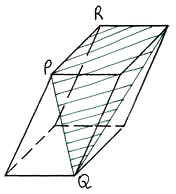
Задание второго уровня:
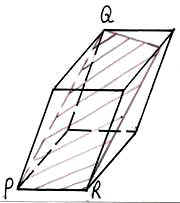 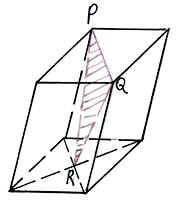 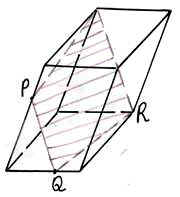
Задание третьего уровня:
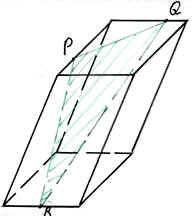 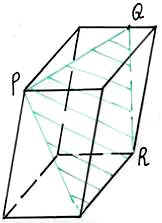 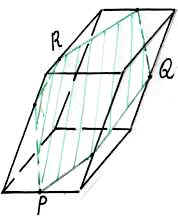
-
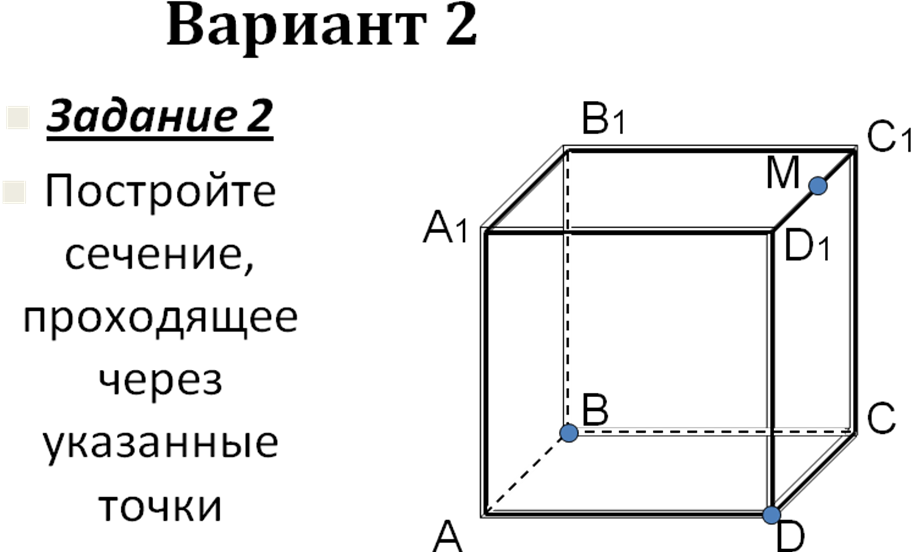
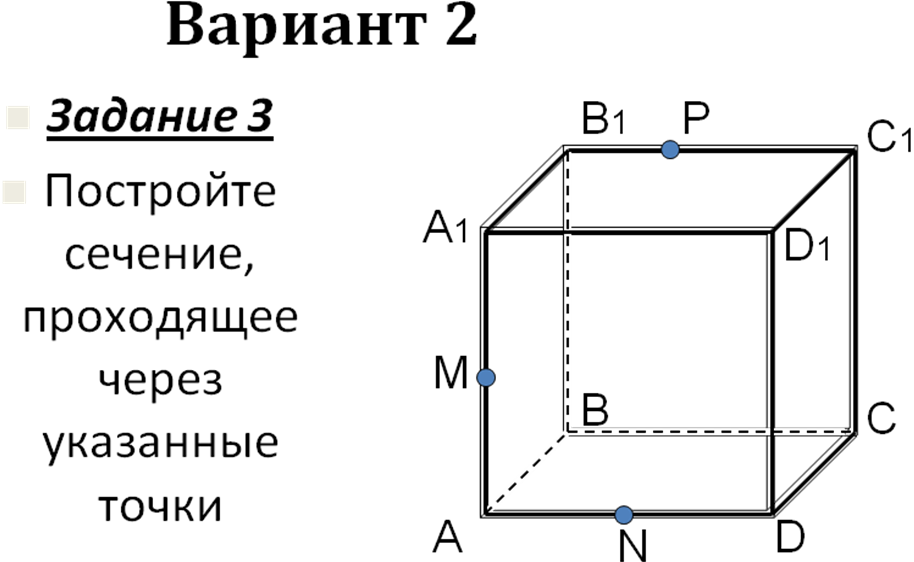
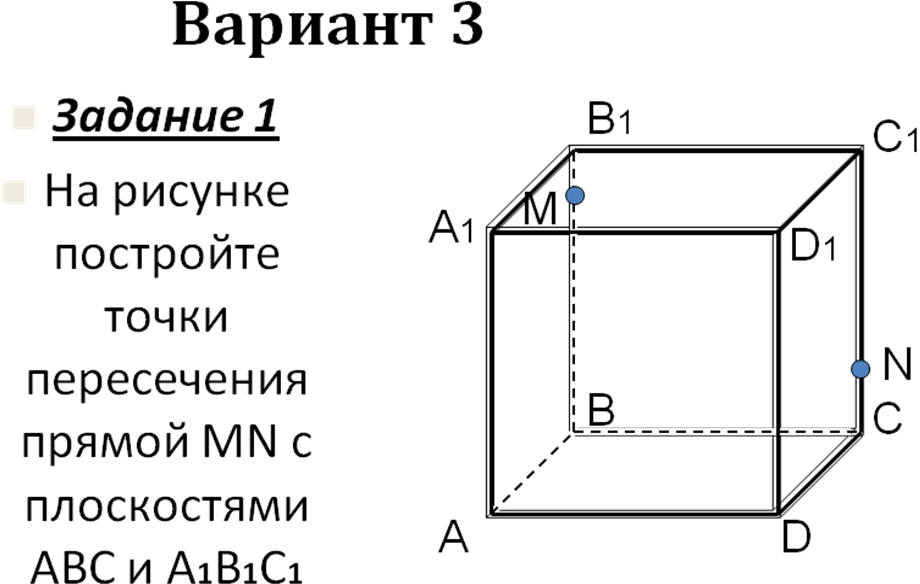
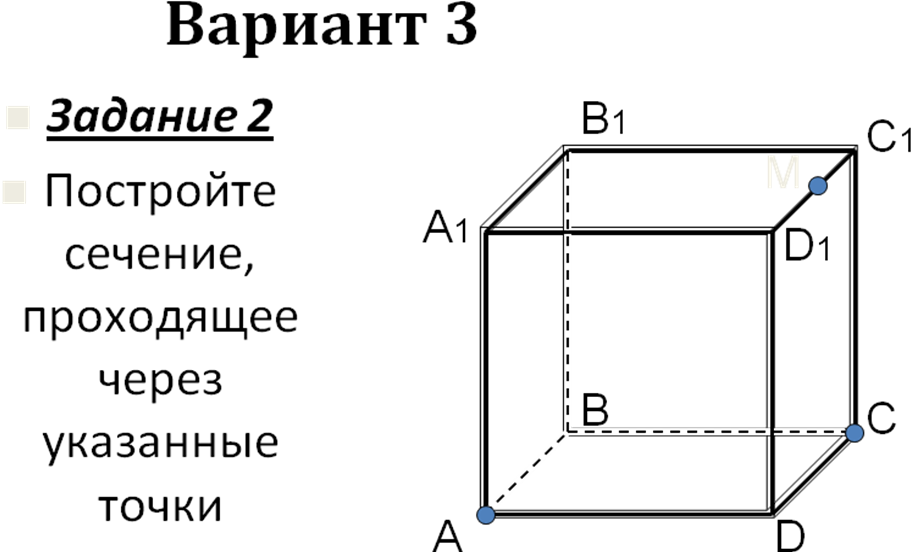
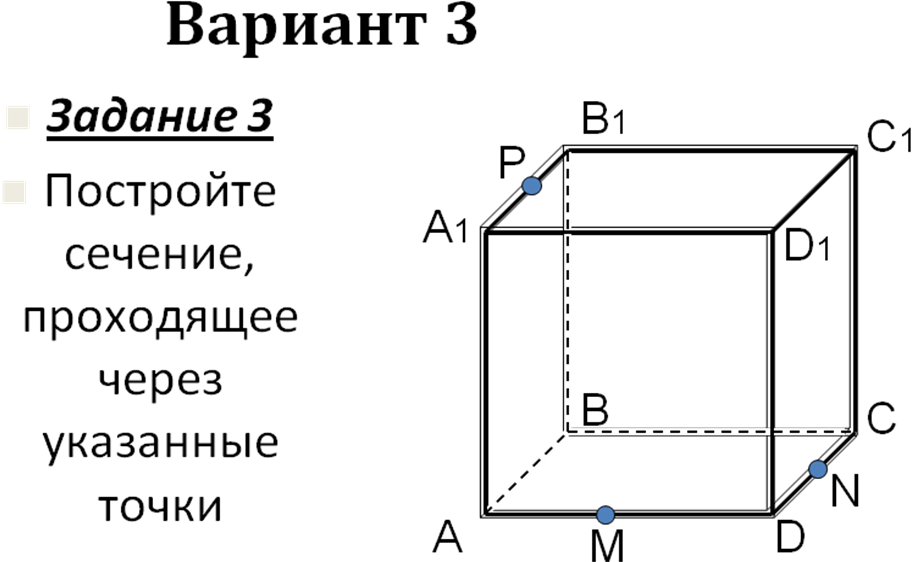
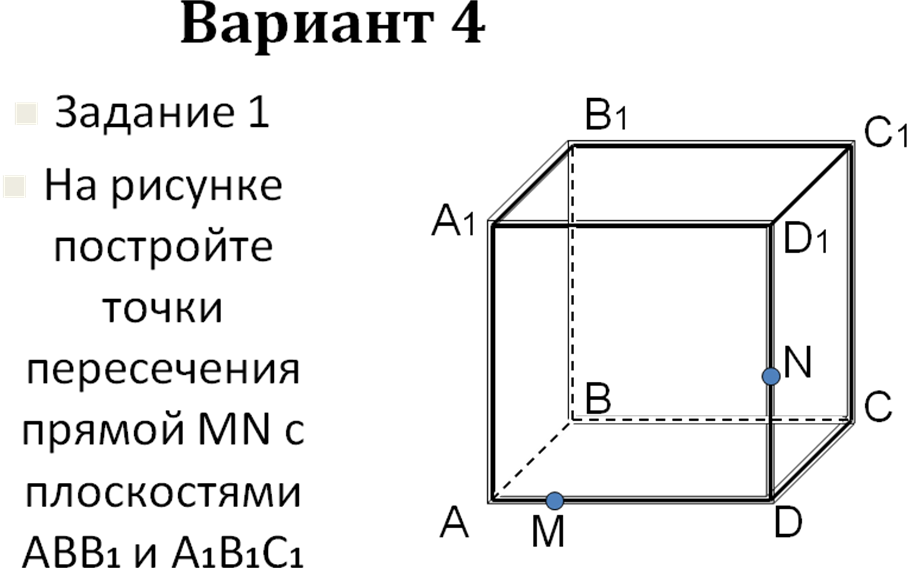
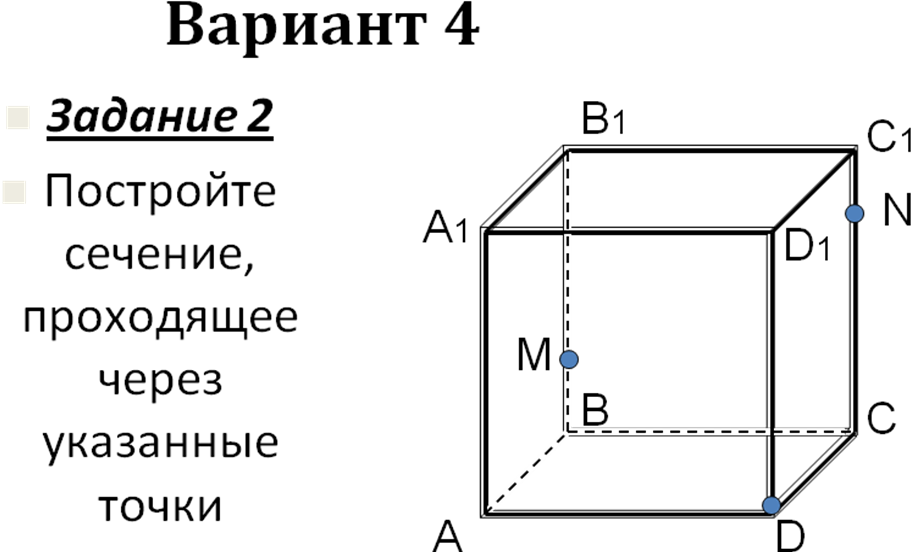
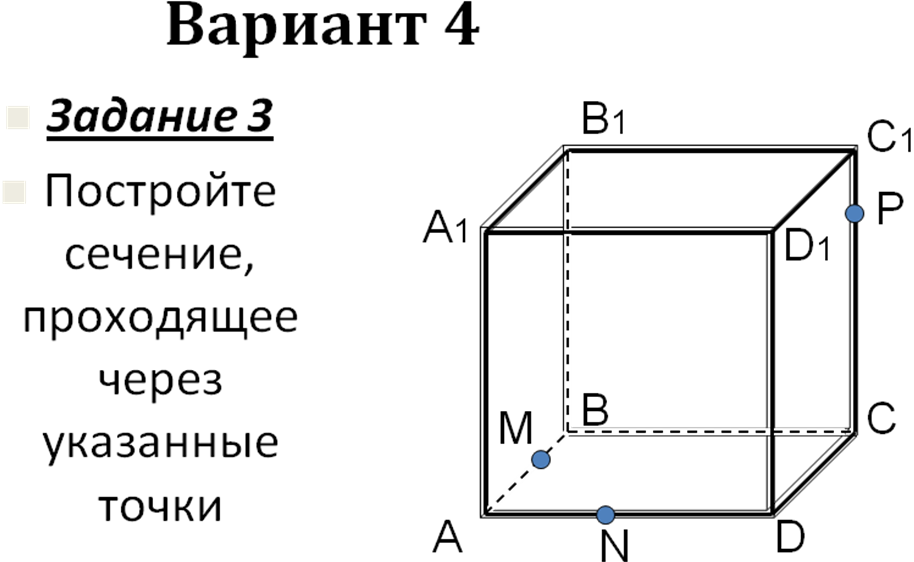
Самостоятельная работа на 4 варианта (слайды 12- 36) с последующей проверкой на компьютере.
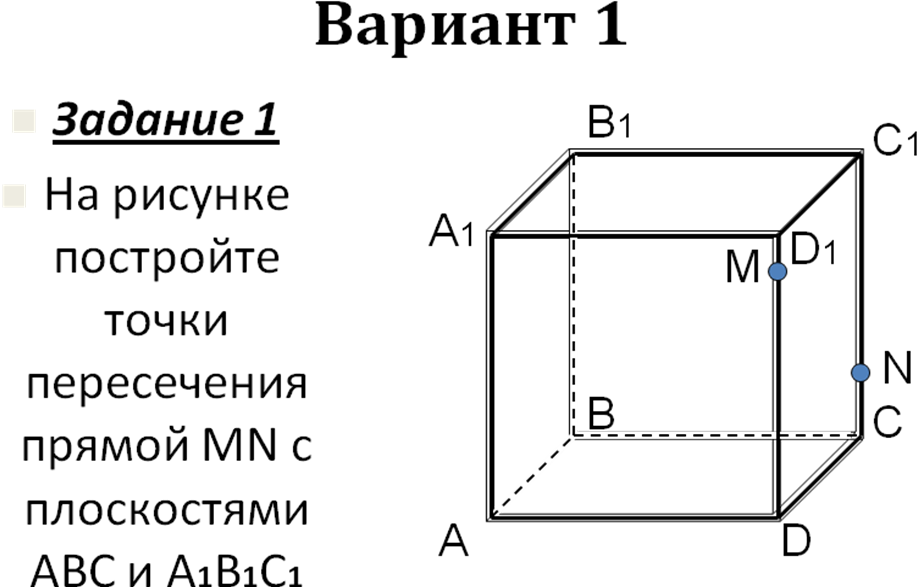
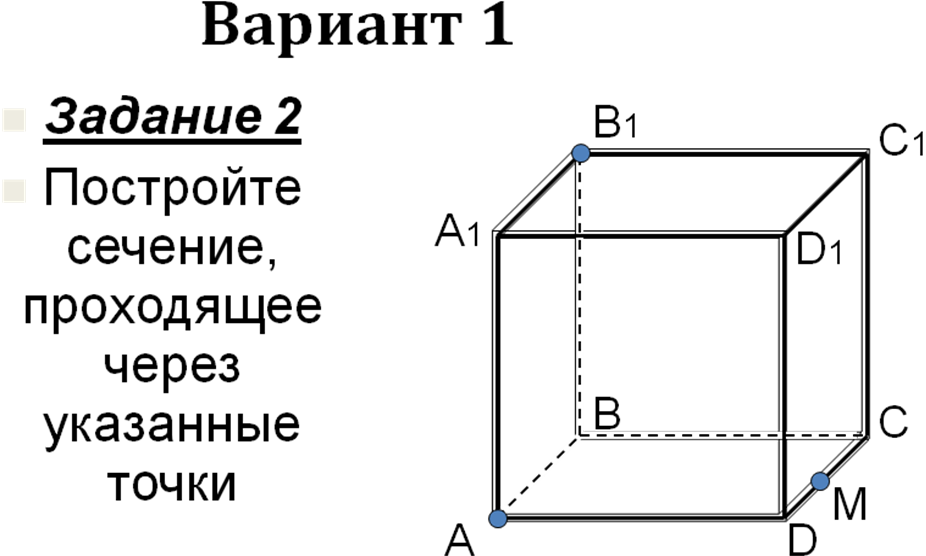
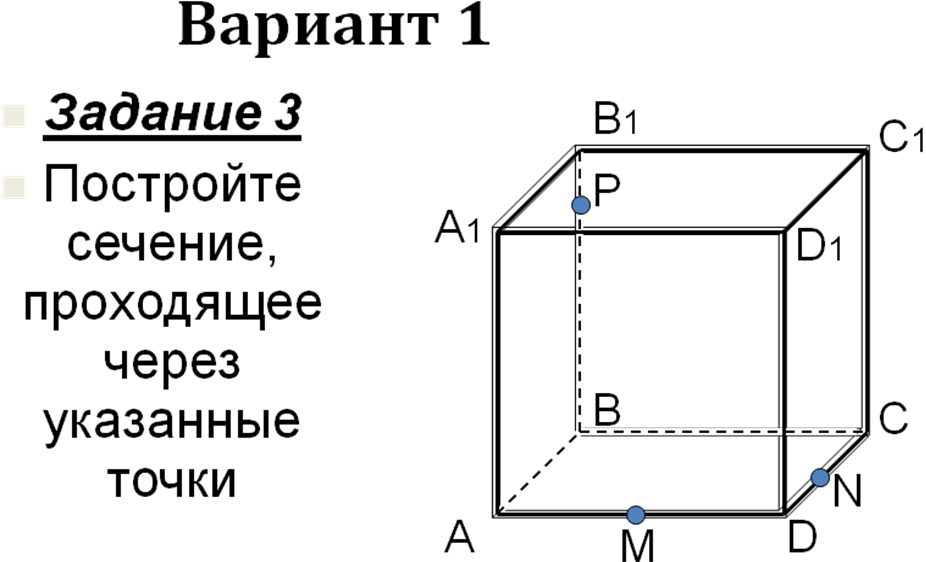
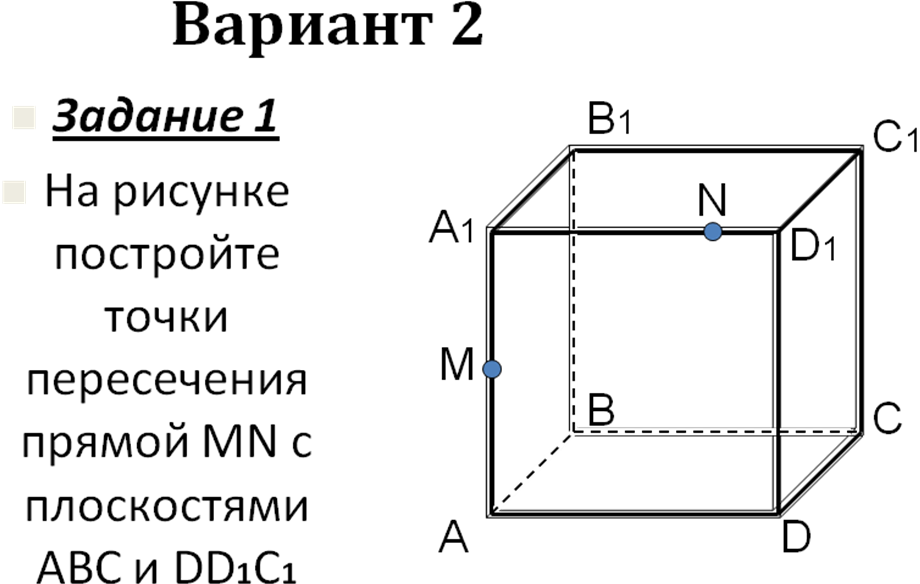
-
Краткий инструктаж по домашнему заданию (по учебнику глава 1, §4 №26, №35 ).
-
Рефлексия. Подведение итогов урока.
страница 1
|