В настоящее время традиционным методом аналитического контроля вещественного состава различных полезных ископаемых (уголь, железные, медные и полиметаллические руды, известняк, доломит и т.д.) является химический анализ. Однако в силу высокой трудоемкости и относительно низкой производительности (анализу подвергается проба, измельченная до аналитической крупности) химический анализ малоэффективен для массового контроля качества.
Инструментальный рентгенорадиометрический метод (РРМ), основанный на возбуждении и регистрации рентгеновской флуоресценции определяемых элементов, выгодно отличается от химического анализа повышенной экспрессностью и производительностью. Основной недостаток РРМ связан со сравнительно низкой величиной возбуждающего и регистрируемого гамма-излучения (а, следовательно, и малой глубинностью). В связи с этим объект исследований при рентгенорадиометрическом анализе также ограничен пробами аналитической крупности.
Более перспективным для анализа проб повышенной крупности является гамма-альбедный метод, основанный на облучении пробы первичным и регистрации рассеянного гамма-излучения. При использовании в качестве первичного гамма-излучения с энергией менее 150200 кэВ интенсивность рассеянного гамма-излучения Ns в основном является функцией эффективного порядкового номера облучаемой среды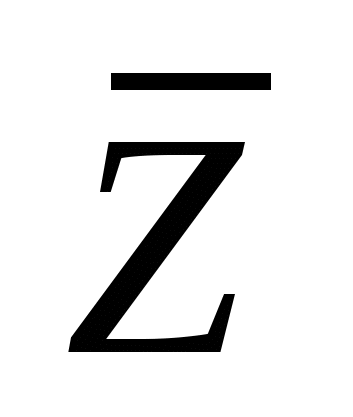 
, который при благоприятных условиях связан тесной корреляционной зависимостью с массовой концентрацией тяжелого компонента среды Сок. Степень тесноты данной связи влияет на величину методической погрешности, основной составляющей которой при реализации гамма-альбедного метода является погрешность, определяемая матричным эффектом. В данном случае под матричным эффектом понимается изменение 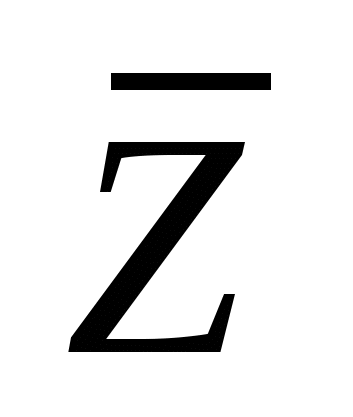(а, следовательно, и Ns), не связанное с изменением Сок, то есть когда перераспределение составных компонентов сложной среды происходит при неизменной концентрации определяемого компонента.
Для аналитического описания явления матричного эффекта анализируемую сложную среду в первом приближении можно аппроксимировать следующей моделью: [определяемый компонент (ок) + наполнитель легкий (нл) + наполнитель тяжелый (нт)] с соответствующими массовыми концентрациями Cок, Cнл, Cнт (рис. 1).
Интенсивность рассеянного данной средой гамма-излучения может быть определена как [1]
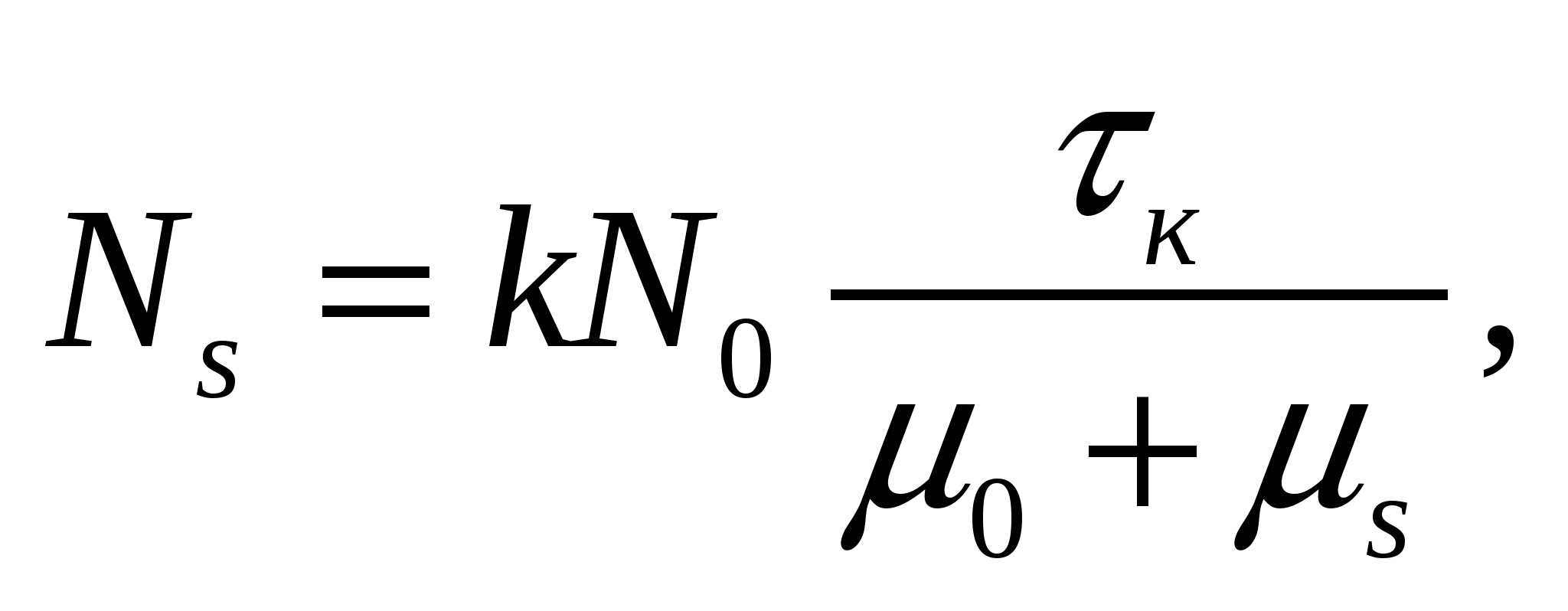(1)
где k — константа, зависящая от геометрических условий измерений;
N0 — интенсивность первичного гамма-излучения;
τк — массовый коэффициент некогерентного (комптоновского) рассеяния средой;
μ0, μs — общие массовые коэффициенты ослабления первичного и рассеянного гамма-излучения средой, соответственно.
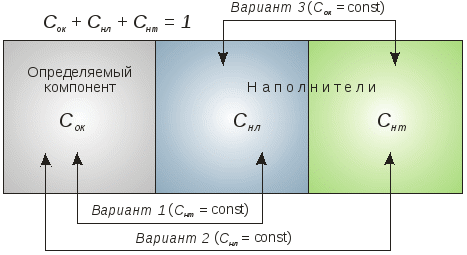
Рис. 1. Модель анализируемой среды
Для рассматриваемой модели среды общие массовые коэффициенты ослабления первичного и рассеянного гамма-излучения рассчитывают, исходя из принципа аддитивности, следующим образом
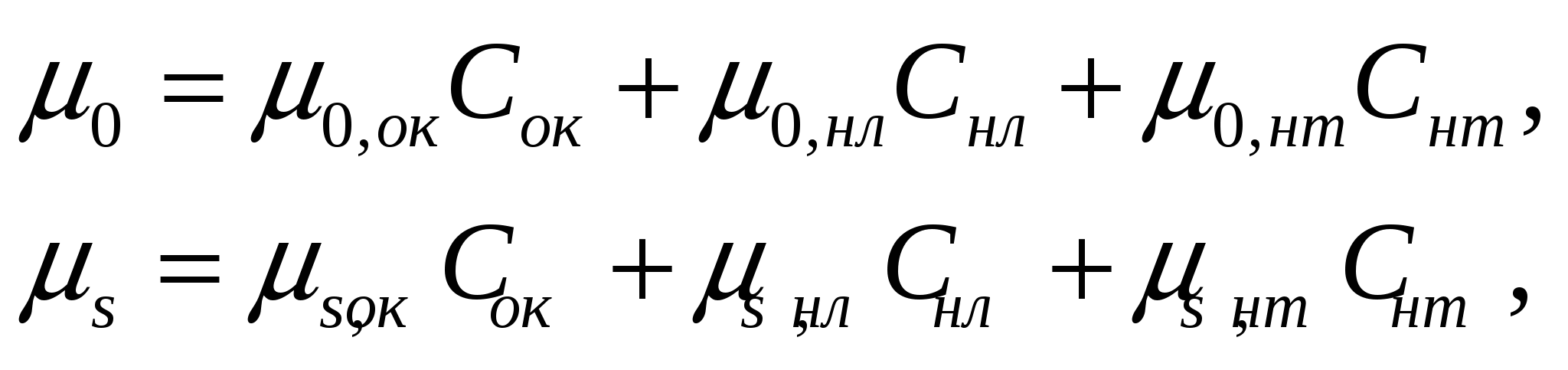(2)
где μ0,ок, μ0,нл, μ0,нт — общие массовые коэффициенты ослабления первичного гамма-излучения определяемым компонентом, легким и тяжелым наполнителями, соответственно;
μs,ок, μs,нл, μs,нт — общие массовые коэффициенты ослабления рассеянного гамма-излучения определяемым компонентом, легким и тяжелым наполнителями, соответственно.
Энергия рассеянного гамма-излучения Es определяется формулой Комптона [2]
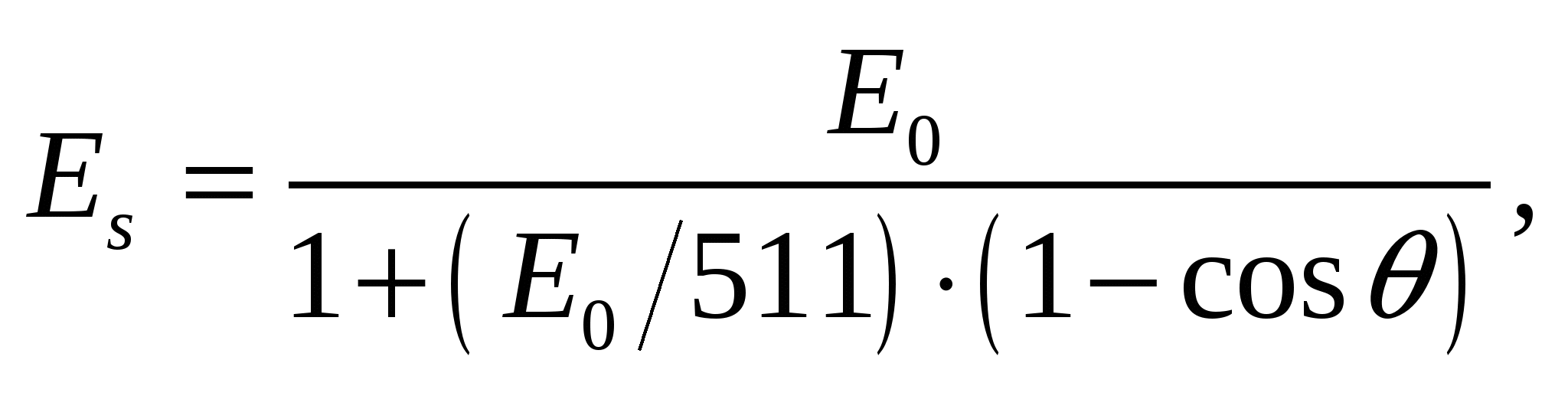кэВ, (3)
где E0 — энергия первичного гамма-излучения, кэВ;
511 — энергия покоя электрона, кэВ;
θ — угол рассеяния.
Методическая погрешность может быть определена по формуле [3]
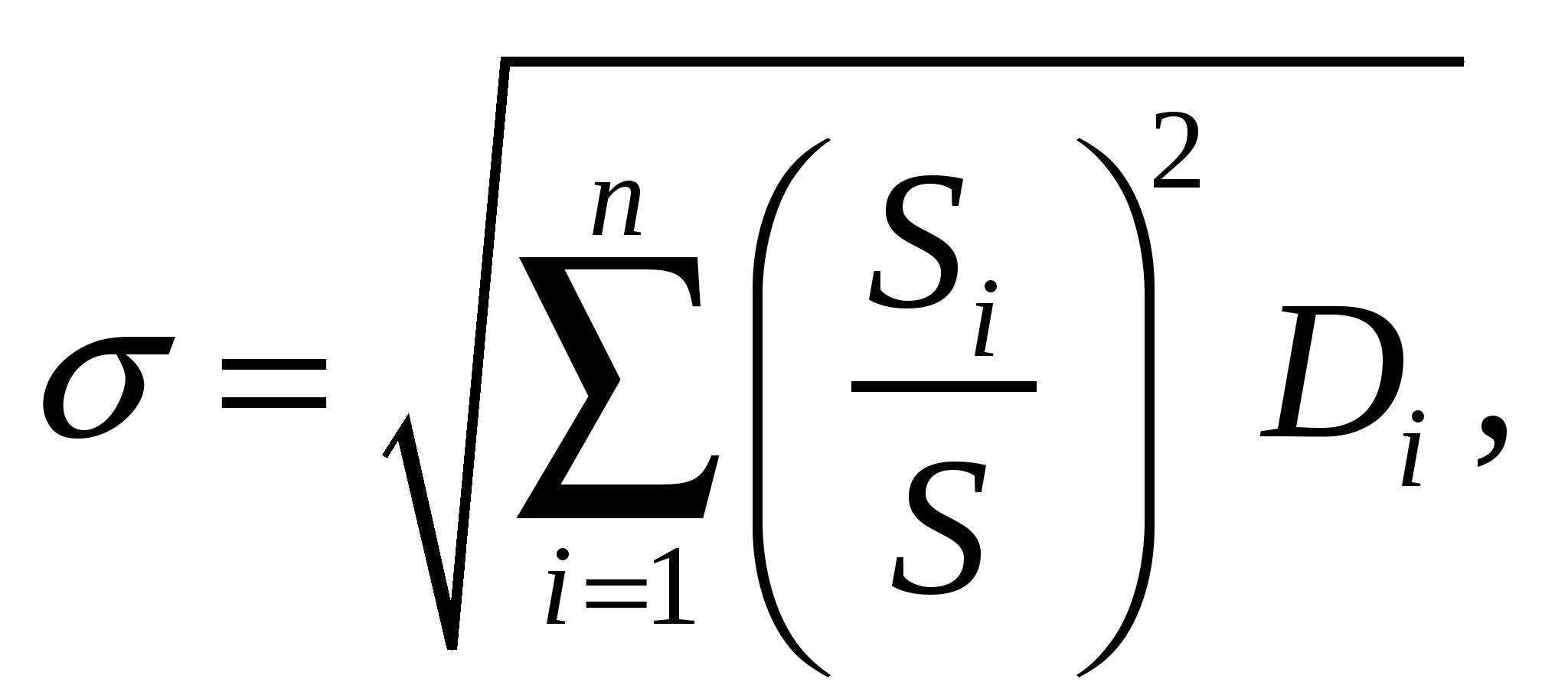(4)
где S, Si — относительные чувствительности метода к определяемому и мешающим параметрам, соответственно;
Di — дисперсия i-го мешающего параметра;
n — количество мешающих параметров.
В свою очередь, чувствительность метода к i-му влияющему параметру определяется как
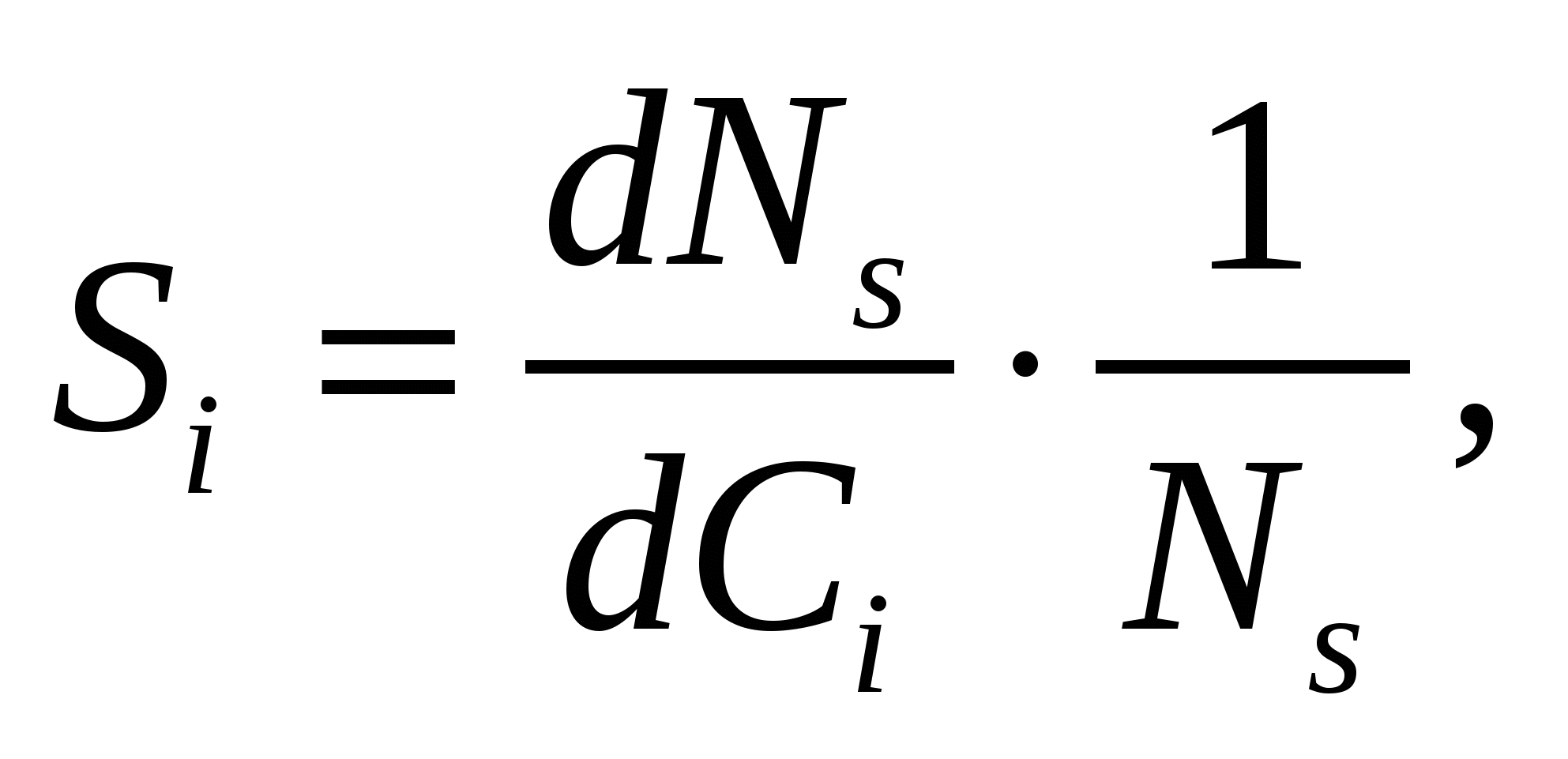(5)
где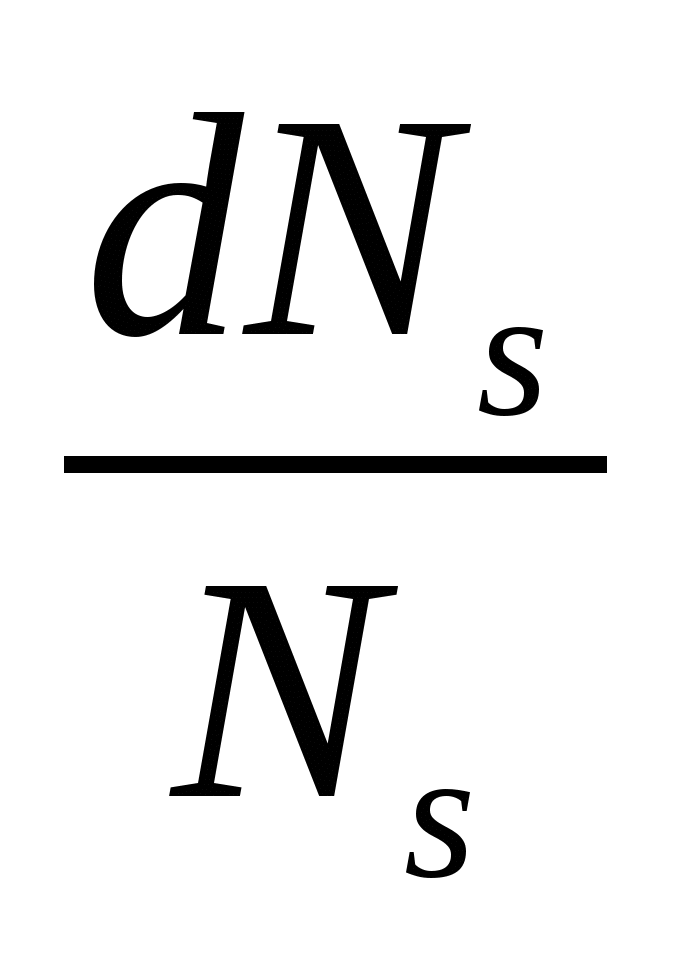 
— относительное приращение интенсивности рассеянного гамма-излучения при единичном изменении (dCi) влияющего параметра.
Применительно к погрешности матричного эффекта при n = 1 и единичной дисперсии мешающего параметра формула (4) приобретает вид
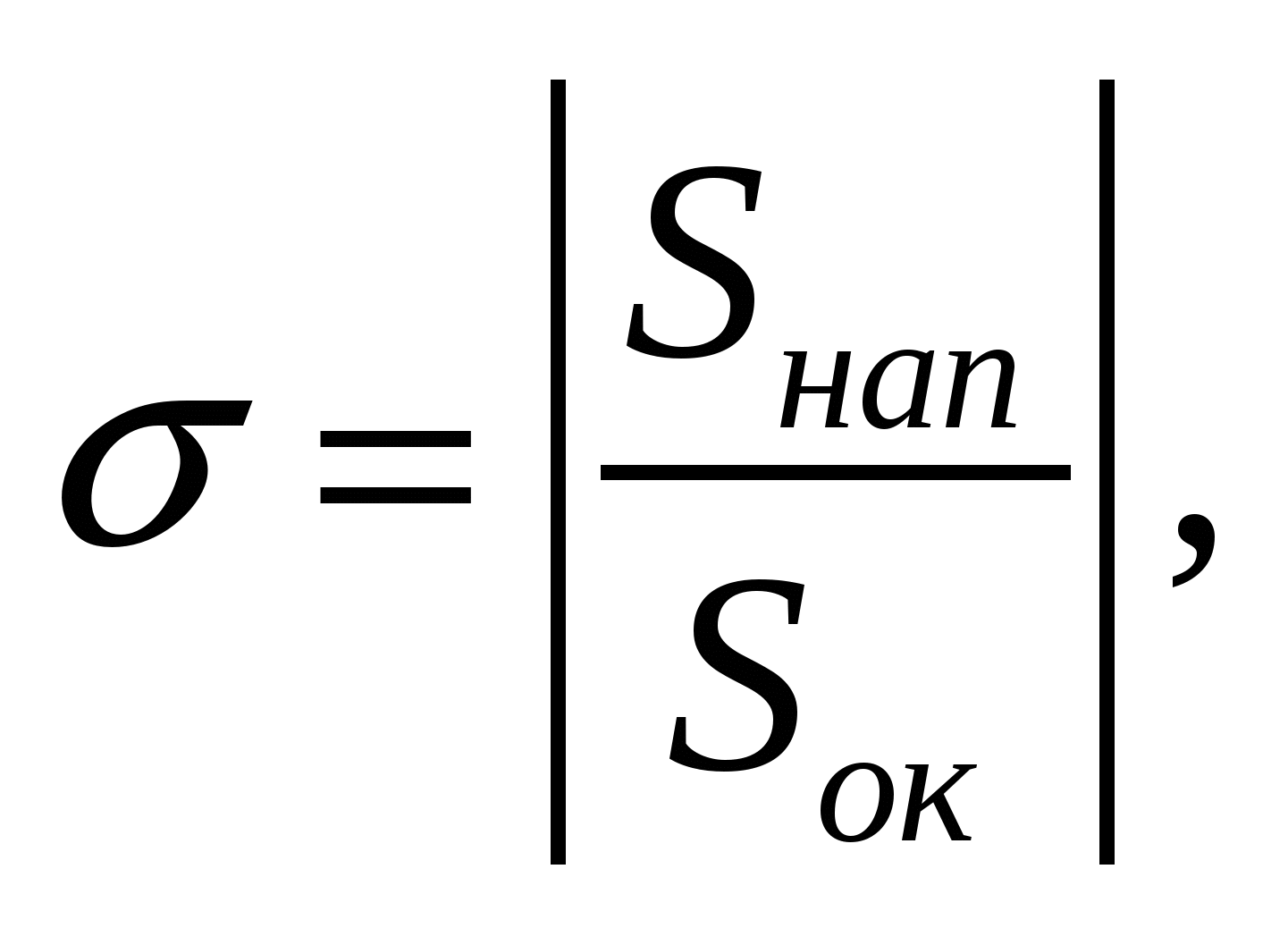(6)
где Sок, Sнап — относительные чувствительности метода к определяемому компоненту и наполнителю, соответственно.
Для рассматриваемой модели возможны три предельных варианта замещения составных компонентов (рис. 1).
1. Перераспределение определяемого компонента и легкого наполнителя при постоянстве тяжелого наполнителя.
2. Перераспределение определяемого компонента и тяжелого наполнителя при постоянстве легкого наполнителя.
3. Перераспределение легкого и тяжелого наполнителей при постоянстве определяемого компонента.
Варианты 1 и 2 являются благоприятными: влияющим параметром для них в обозначениях формулы (5) является Cок (вариант 1: Cнт = const; вариант 2: Cнл = const).
Вариант 3 определяет матричный эффект: влияющими параметрами являются Cнл или Cнт (Cок = const).
Дифференцируя (1) по dCопр с учетом (2), (5) и очевидного равенства
Cок + Cнл + Cнт = 1, (7)
получим формулы для расчета чувствительностей метода к определяемому параметру по первым двум вариантам:
Вариант 1:
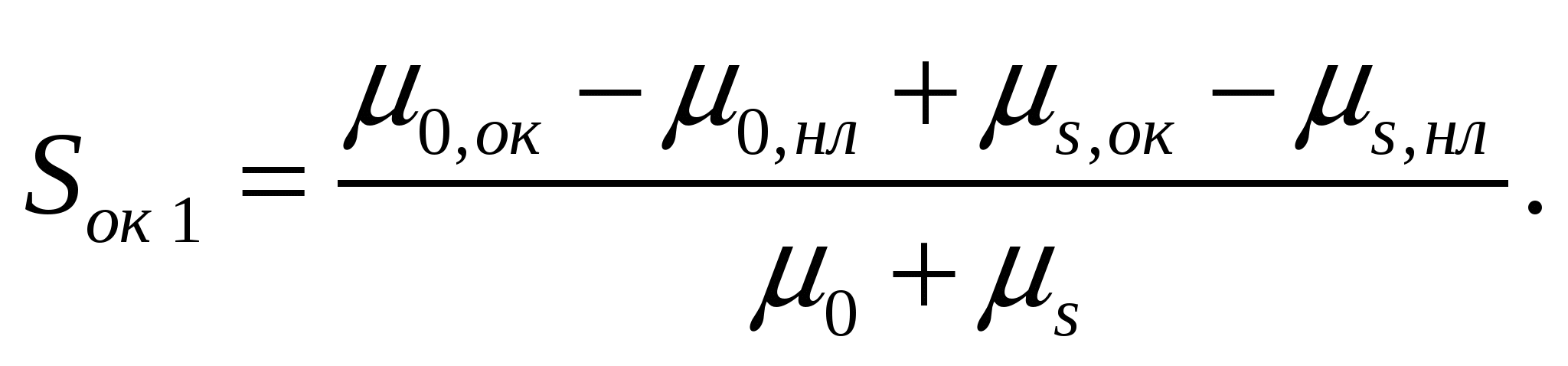(8)
Вариант 2:
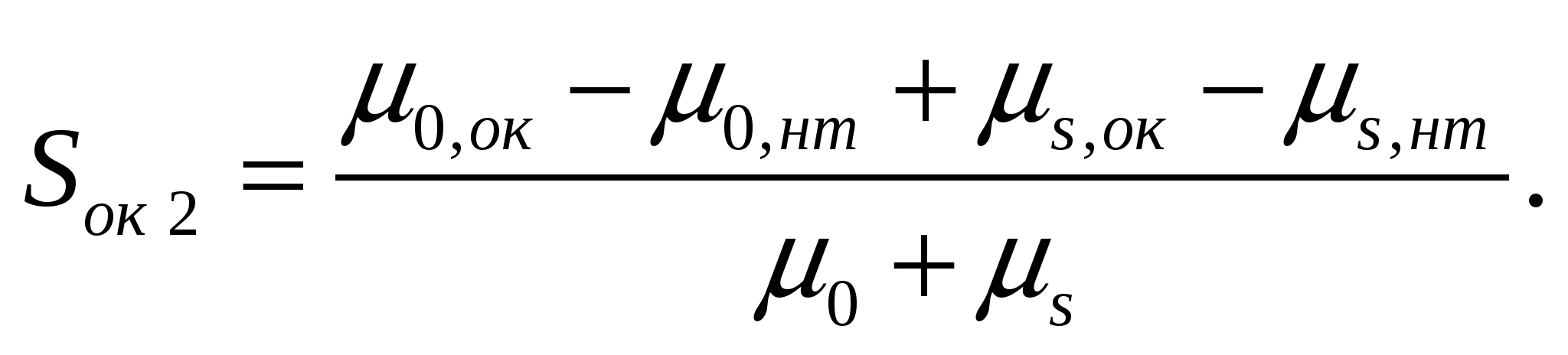(9)
Дифференцируя (1) соответственно по dCлегк и dCтяж с учетом (2), (5) и (7), получим формулы для расчета чувствительностей метода к мешающим компонентам по варианту 3:
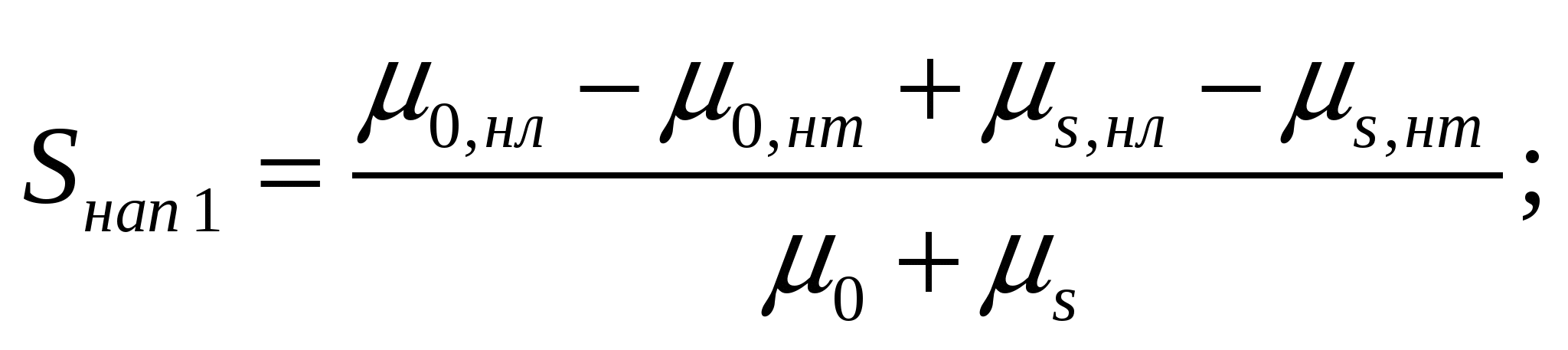(10)
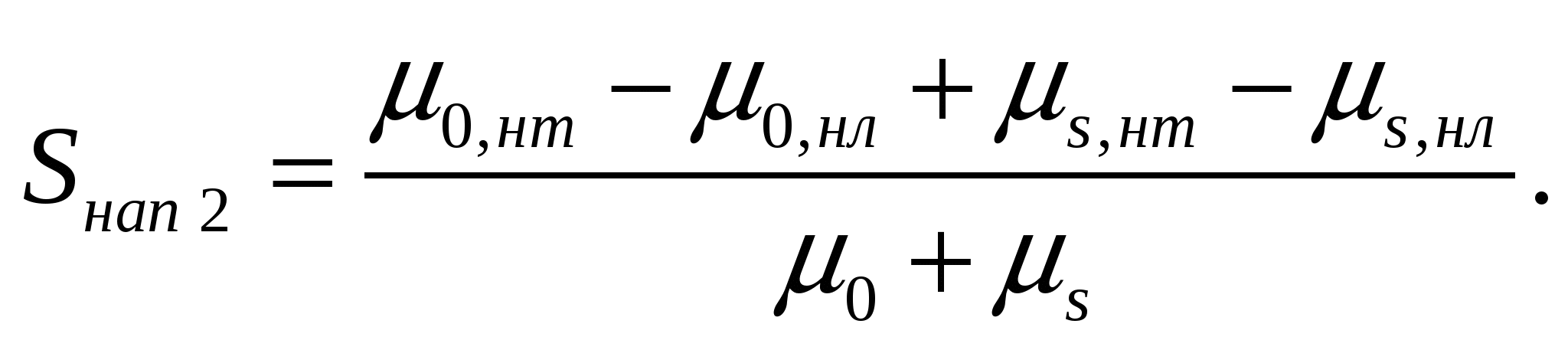(11)
Анализируя выражения (10) и (11), можно прийти к выводу, что чувствительности Sнап 1 и Sнап 2 различаются только знаком, совпадая при этом по абсолютной величине, то есть
(12)
Подставляя (8)-(12) в (6), получим аналитические выражения для расчета погрешностей:
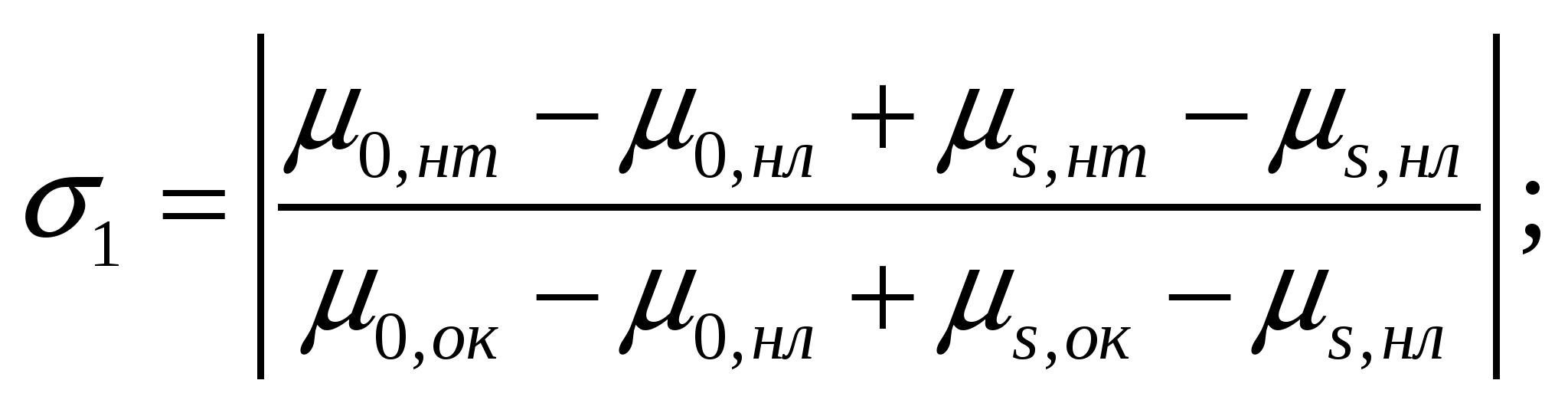(13)
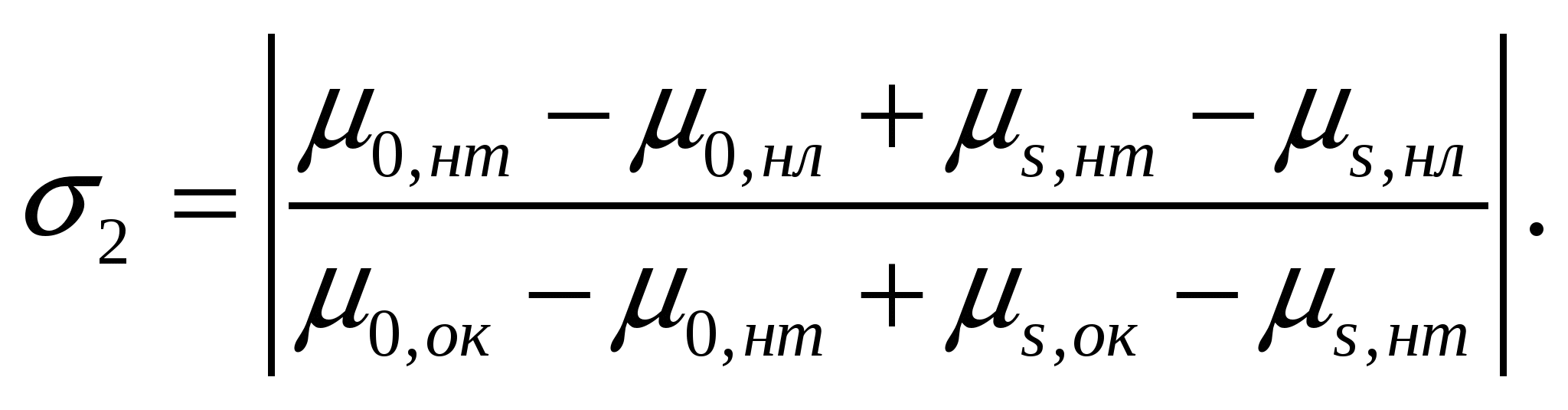(14)
За искомую методическую погрешность следует принимать большую из полученных величин σ1 или σ2 (наименее благоприятный вариант).
В рассматриваемом диапазоне энергий потеря энергии гамма-квантов при рассеянии относительно невелика (3), то есть можно принять, что Es E0. Тогда выражения для погрешностей σ1 и σ2 упрощаются
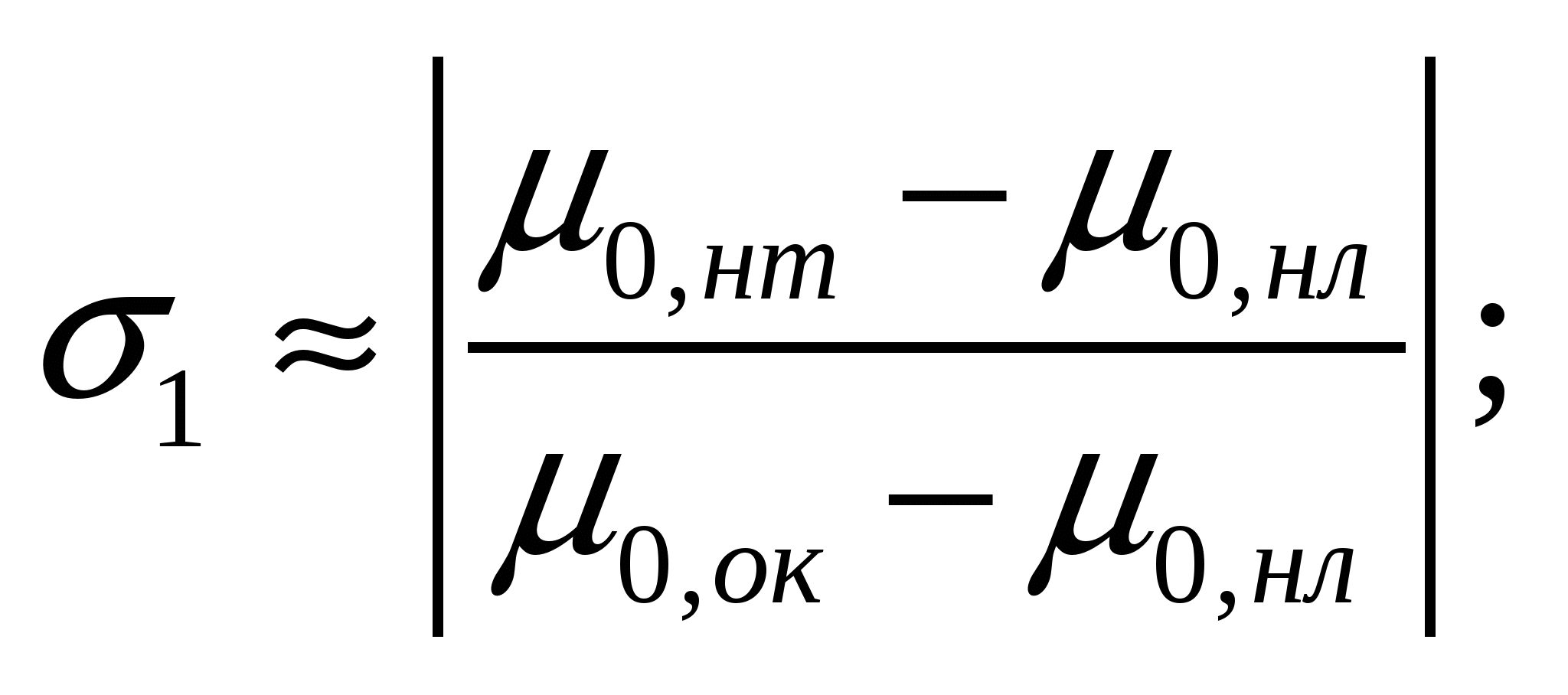(15)
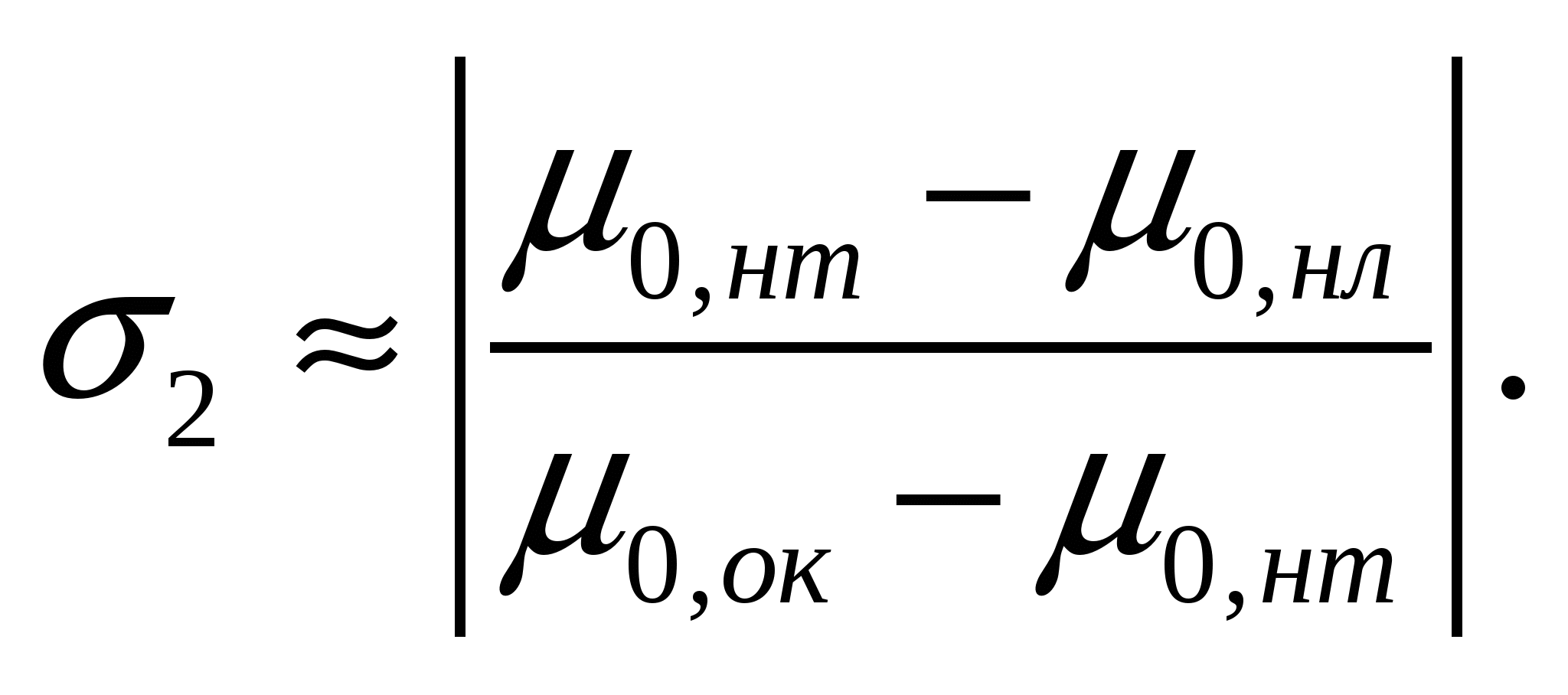(16)
На рис. 2 представлены зависимости σ1 и σ2 от энергии первичного гамма-излучения, рассчитанные по формулам (15) и (16) для железной руды, аппроксимированной смесью: Fe2O3 — определяемый компонент, SiO2 — легкий наполнитель, CaO — тяжелый наполнитель.
Во всем рассматриваемом диапазоне энергий величина погрешности σ2 больше погрешности σ1. Обе зависимости имеют инверсионный характер с минимумом при E0~90÷110 кэВ. Данный диапазон энергий следует считать оптимальным с точки зрения минимума погрешности за счет матричного эффекта.
Предложенная методика может быть использована при оптимизации параметров гамма-гамма метода при контроле вещественного состава и других различных сложных сред.
