Развитие информационных систем — измерительных, вычислительных, автоматических систем управления — расширило область интереса к информационным процессам далеко за пределы процесса передачи информации. Становление теории информации в середине ХХ века, связанной с работами В.А. Котельникова и К. Шеннона, также было вызвано потребностями практики — техники связи.
С развитием и усложнением информационных систем встал вопрос и об определении энергетической сложности различных информационных процессов, выяснении предельных соотношений при получении, хранении и обработке информации. На начальном этапе развития кибернетики и теории информации существовало мнение, что малая энергоемкость информационных процессов существенно отличает их от энергетических. Это послужило основой для известного высказывания фон Неймана: «…термодинамика является той частью теоретической физики, которая в некоторых из своих аспектов наиболее близка теории обработки и измерения информации…». Таким образом, потребности техники и развитие науки привели к возникновению термодинамики информационных процессов, основы которой были заложены в 1956 г. Л. Бриллюэном [1]. Однако существенного внимания со стороны исследователей вопросы термодинамики информационных процессов не получили.
Исключение составляют основополагающие работы Р.П. Поплавского [2]. Он подчеркивал, что термодинамика информационных процессов, в отличие от равновесной термодинамики и термодинамики открытых систем, является термодинамикой переходных процессов. Им были также установлены предельные соотношения между информационными (точность, количество информации) и термодинамическими (энергия, энтропия) характеристиками.
1980-90-е гг. ХХ века стали временем бурного развития синергетики, основу которой составляет термодинамика отрытых систем, в связи с выявлением глубокой связи между информацией и самоорганизацией материи.
Тем не менее, развитие информационно-измерительных систем (телемеханики и т.д.) настоятельно требует выявления тех или иных термодинамических ограничений как на структуру самих систем, так и на информационные процессы, включая управление или активное измерение.
Предложенный нами подход [3] отличается от подхода Р.П. Поплавского только в части математической формулировки задачи, но не выходит за рамки идеологии переходных процессов, связанных с наличием термостата. Такой подход оправдал себя применительно к процессам совершенно различной природы [2].
Термодинамика многомерных
информационных систем
В работе [3] мы получили выражение для вероятности диссипативных процессов в многомерных распределителях импульсов.
Принципы неравновесной термодинамики, предложенные в [3], используются нами для анализа многомерных информационно-измерительных систем.
Обозначим Em через Q, разложим экспоненту в ряд и, ограничиваясь существенными членами, получим
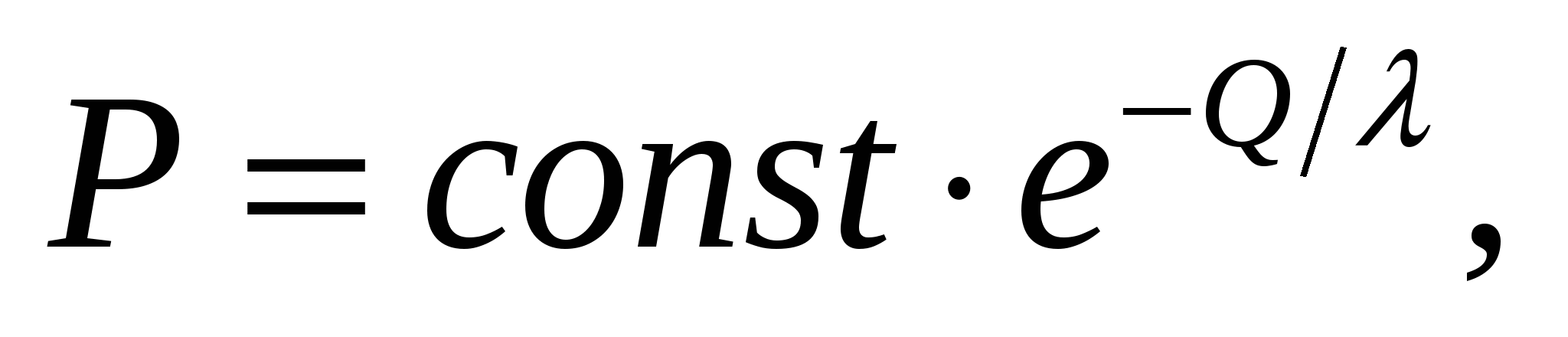
где λ — некоторая постоянная.
Эффективность распределителя импульсов η определим как отношение «сигнал-шум». В нашем случае
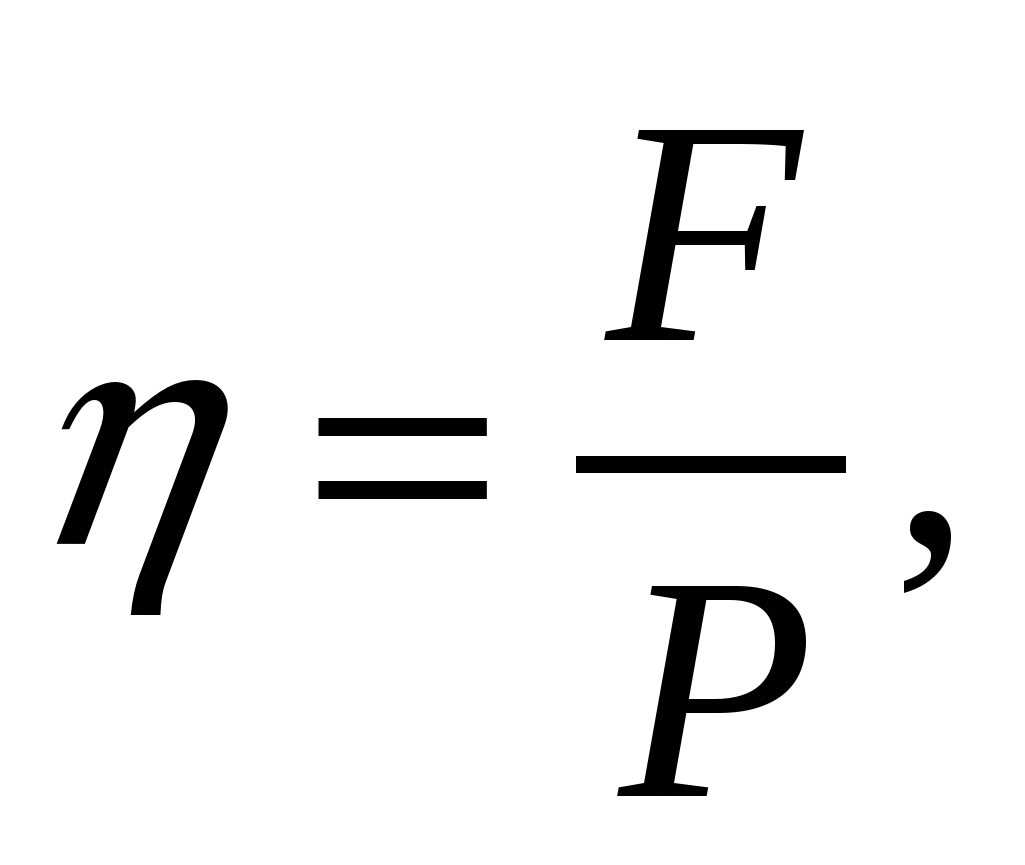
где F = 1/τ, τ — длительность «тактовых» импульсов.
Из приведенных выше соотношений получим
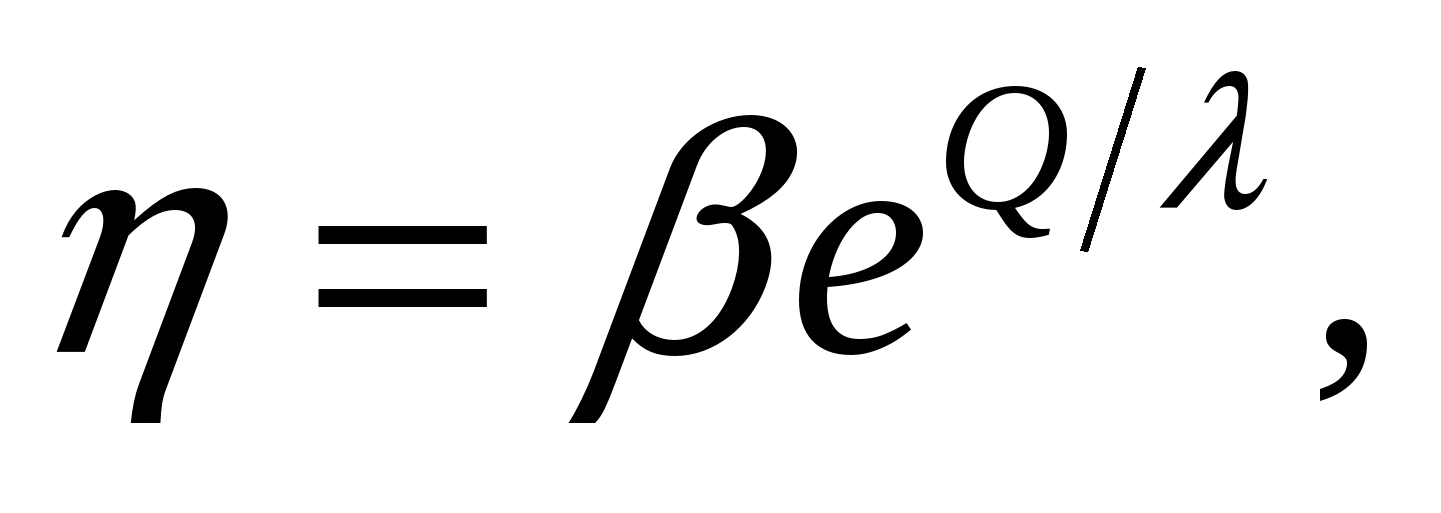
где β, λ — const.
График этой функции показан на рис. 1. Очевидна экспоненциальная зависимость эффективности распределителя импульсов от канальной емкости. Это значительно более сильная зависимость, чем следует из обычных подходов. Важность полученного результата подчеркивает необходимость создания многомерных распределителей импульсов на элементной базе, обладающей большой канальной емкостью.
Полученное выражение для вероятности диссипативного процесса может быть записано в виде
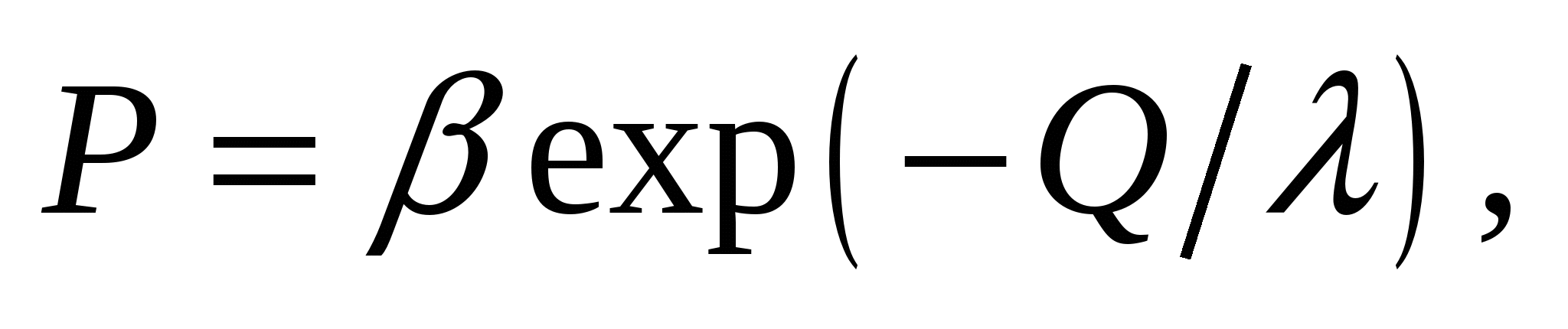
где β, λ — параметры информационно-измерительной системы;
Q — канальная емкость.
Вводя эффективность системы как отношение «сигнал-шум» η = F/P и учитывая, что η пропорциональна объему передаваемой информации, можно получить следующее выражение для канальной емкости
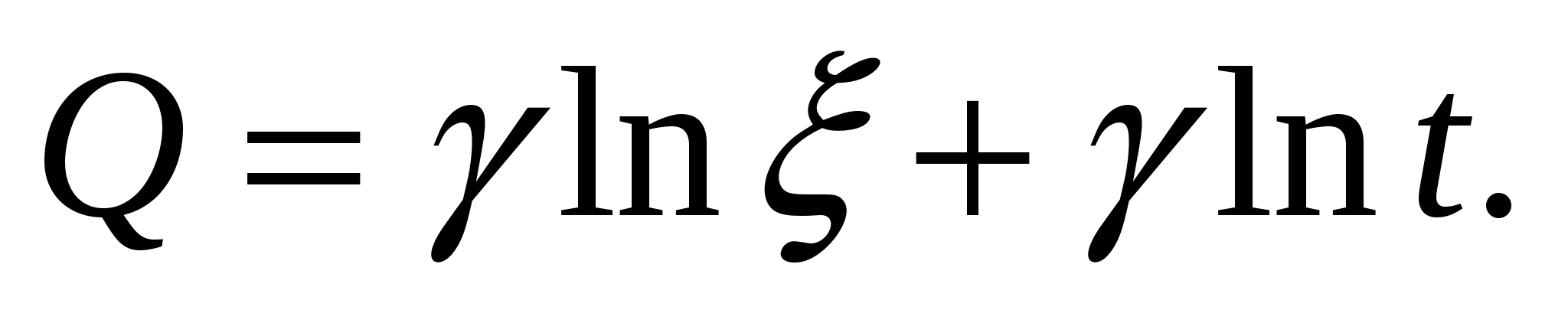
График этой зависимости схематично представлен на рис. 2.
Очевидно, что после резкого начального подъема зависимость Q от t выходит на насыщение, т.е. канальная емкость перестает зависеть от времени передачи информации. Видно также, что канальная емкость зависит от скорости передачи информации в единицу времени ξ.
Основной характеристикой устройств телеизмерения является точность.
Точность работы информационных систем определяется динамическими характеристиками (быстродействием), помехоустойчивостью, разрешающей способностью. Она определяется как внутренними факторами (структура системы, алгоритм функционирования и обработки сигналов и т.п.), так и внешними условиями (распространение радиоволн, наличие естественных помех и т.п.).
В (*) Em, ΔS, τ, N относятся к внутренним параметрам системы, а G0, T — к внешним. Из анализа (*) мы сразу приходим к выводу о термодинамических ограничениях точности информационно-измерительных систем. Действительно, из (*) следует, что средние потери R пропорциональны росту энтропии ΔS и обратно пропорциональны времени информационного процесса.
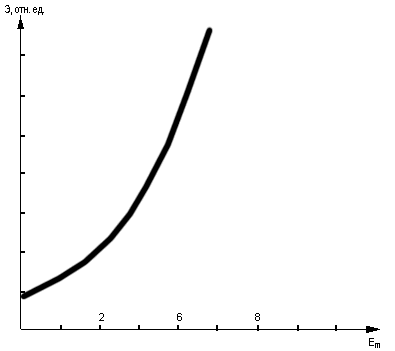
Рис. 1. Зависимость эффективности распределителя
импульсов от канальной емкости
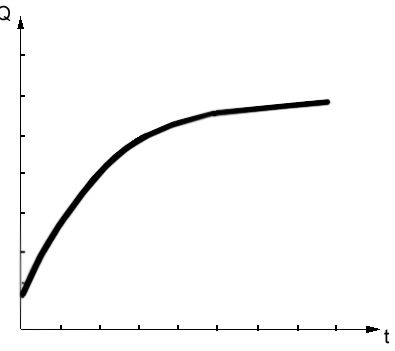
Рис. 2. Зависимость канальной емкости от времени передачи сигнала
На каждом этапе элементарного информационного взаимодействия рост энтропии термостата ΔS лежит в пределах
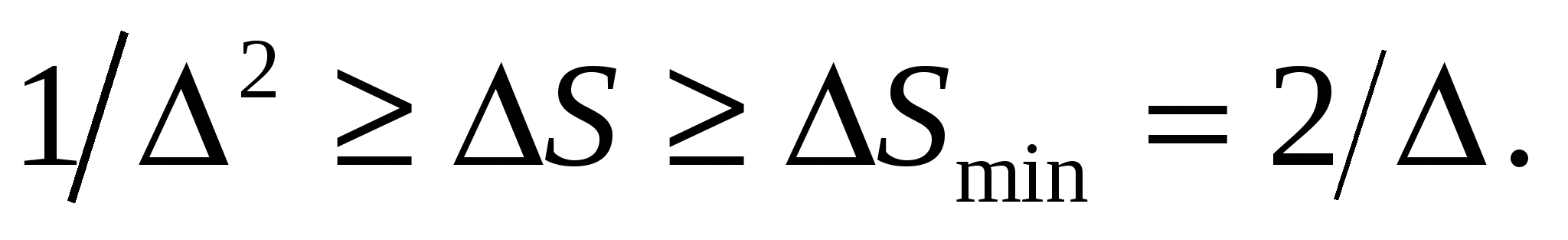
Левая граница соответствует предельно необратимой реализации переходного процесса, а правая — оптимальному замедлению его.
Необходимо сделать замечание. Действительно, как это следует из (*), при замедлении переходного процесса (т.е. при увеличении τ), вероятность диссипативных процессов уменьшается. Однако на практике такой путь неприемлем и, наоборот, современные и будущие информационно-измерительные системы должны обладать большим быстродействием для передачи большого массива информации.
С другой стороны, негэнтропийный эффект (эффект упорядочивания в системе, ΔK = –ΔS)
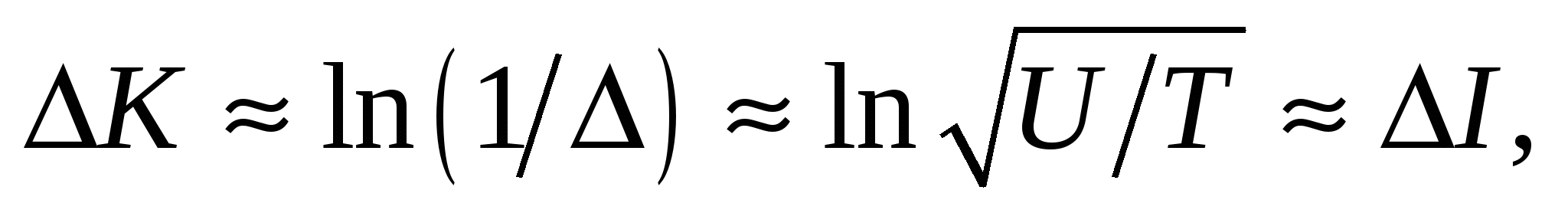
где ΔI — полученное в процессе измерения количество информации.
Таким образом, энтропийная эффективность информационно-измерительного процесса
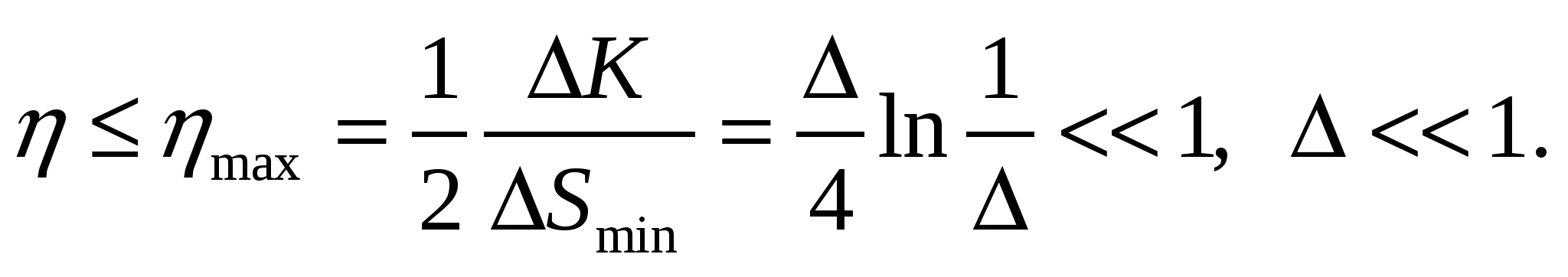
Потеря части информации в информационно-измерительных системах снижает ее достоверность. Несоответствие между принятой и переданной информацией может иметь место из-за искажений, возникающих по следующим причинам:
- несовершенство методов преобразования передаваемого сообщения в сигнал и технического их осуществления;
- несовершенство методов передачи и приема сигналов и технической реализации этих методов;
- несовершенство методов преобразования принимаемого сигнала в сообщение и технической реализации этих методов;
- особенности распространения сигнала по линии связи;
- недостаточная помехозащищенность сигнала.
Все эти причины приводят к трем видам искажений: линейным, нелинейным и случайным.
Однако на определенном уровне погрешность измерения ограничивается не техническими, а принципиальными физическими явлениями — квантовыми свойствами объектов и приборов.
Эффективность (или точность) информационно-измерительной системы определим соотношением:
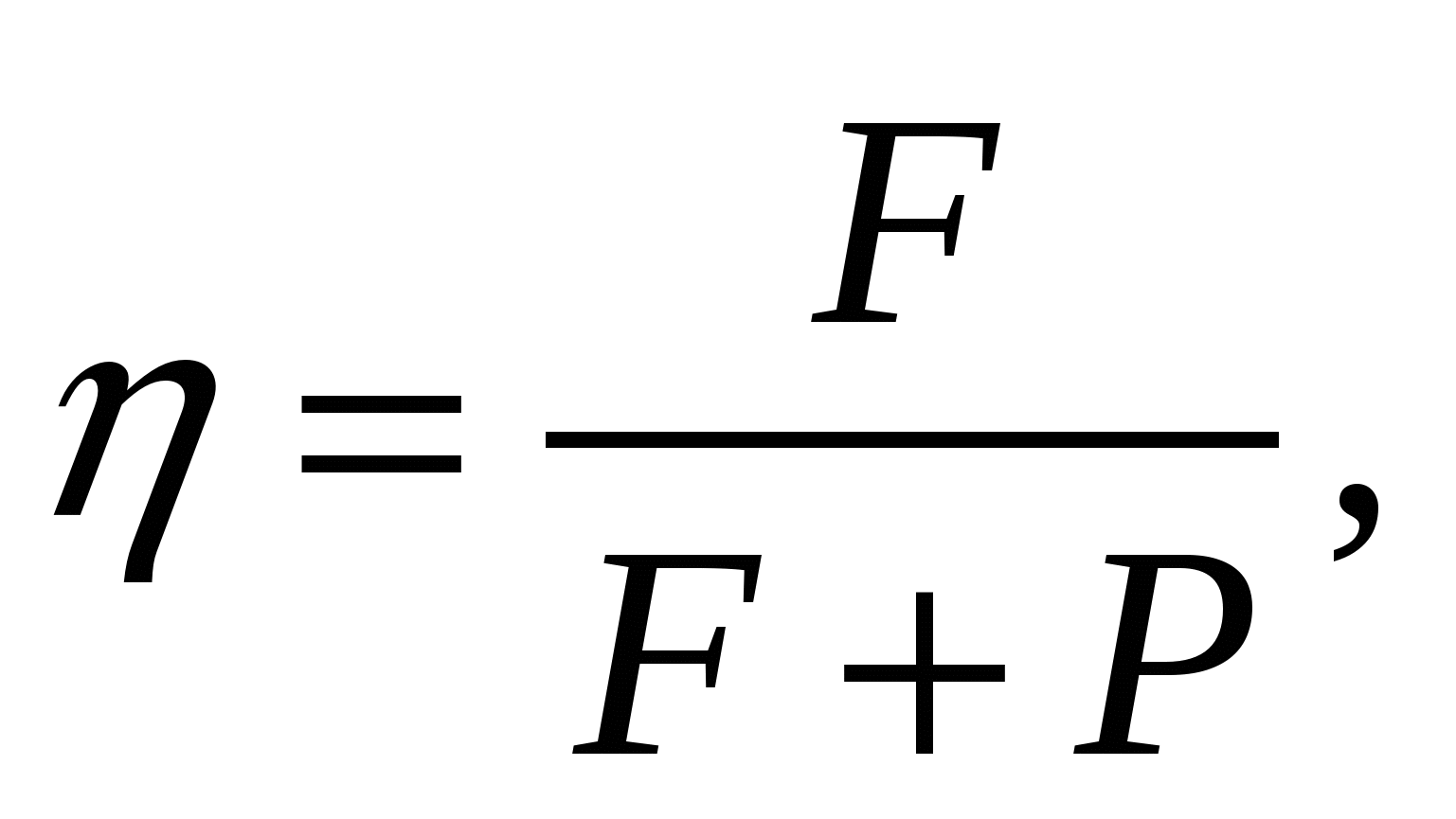
где F — вероятность перехода системы из начального в конечное состояние за время τp; F = 1/τp. С учетом (*) это выражение примет вид:
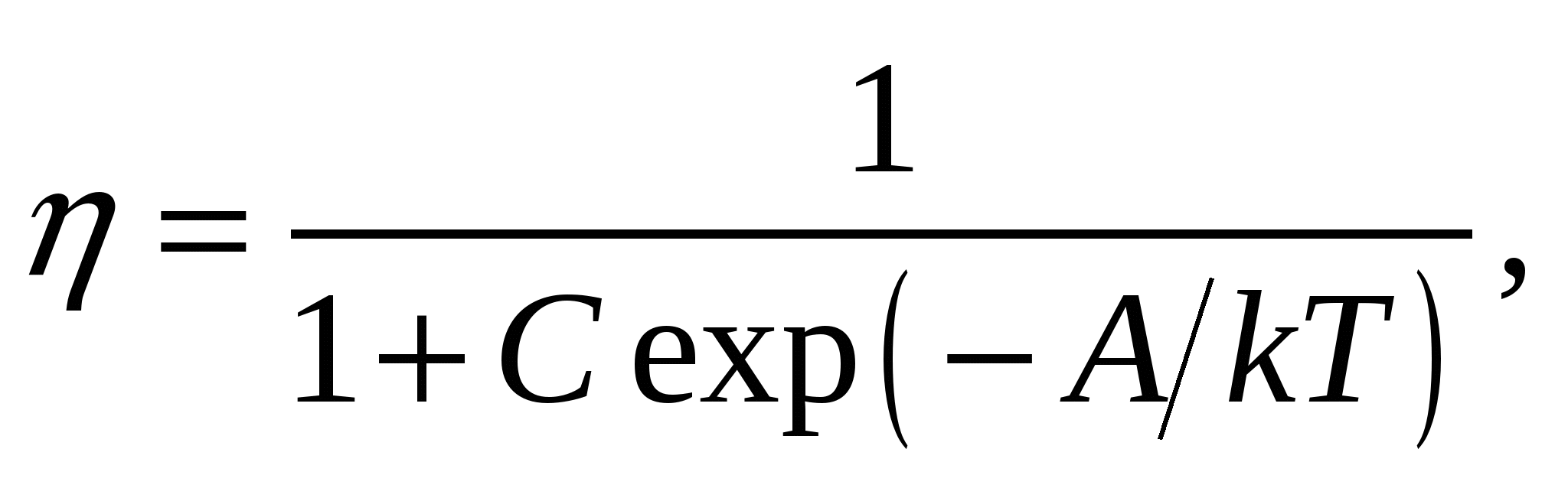
где 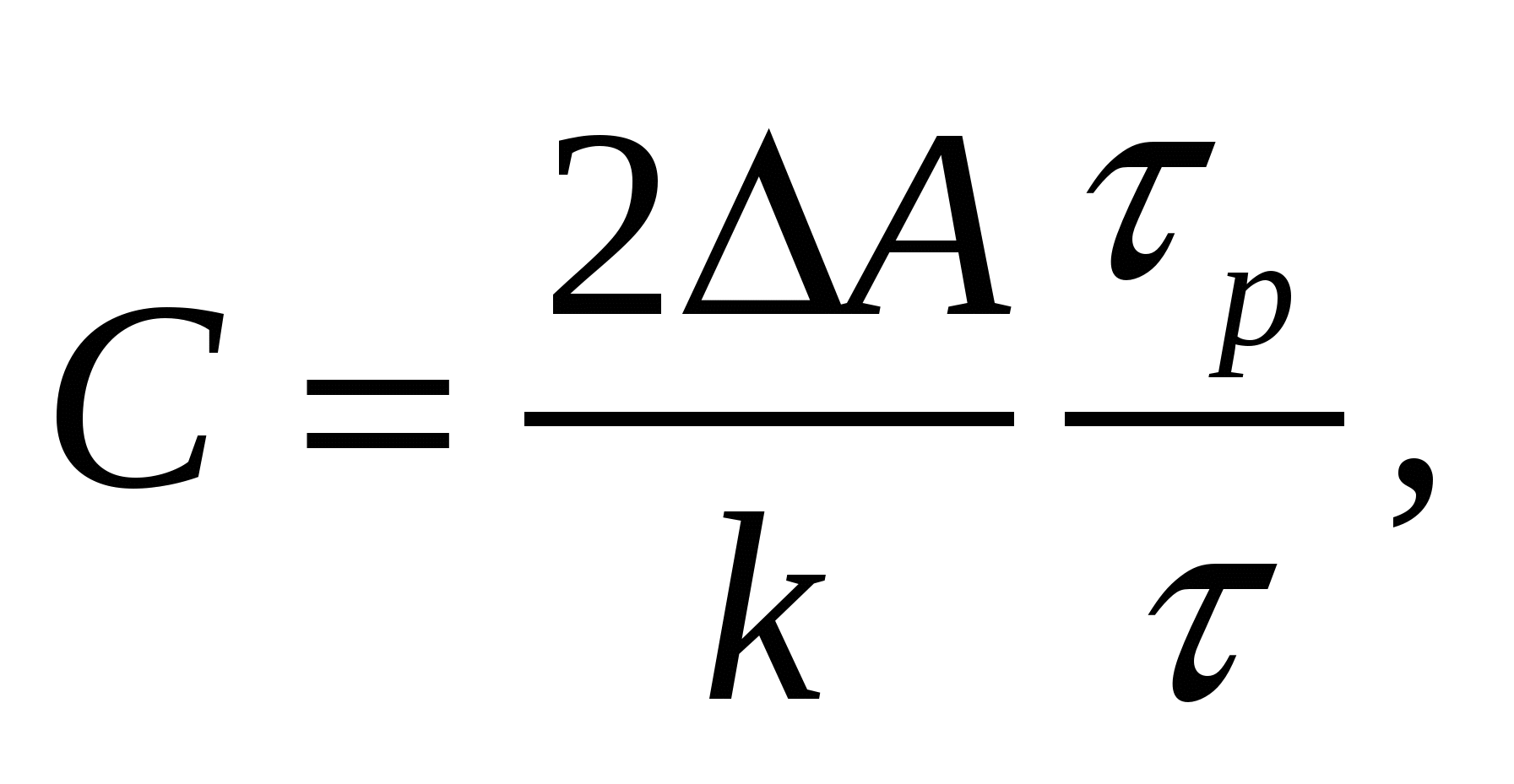 A = Em – G0/N. Заметим сразу, что, поскольку ΔS > 0, η < 1. Зависимость от температуры показана на рис. 3.
A = Em – G0/N. Заметим сразу, что, поскольку ΔS > 0, η < 1. Зависимость от температуры показана на рис. 3.
Аналогичная зависимость наблюдается для η(N), т.е. имеются термодинамические ограничения на число информационных каналов. При Tкр или Nкр информационно-измерительная система начинает «работать плохо» и потери информации резко возрастают.
Информационные характеристики
процесса измерения
Начнем с определения точности характеристик измерения. Пусть истинное значение измеряемой скалярной величины l, измеренное значение l', их разность
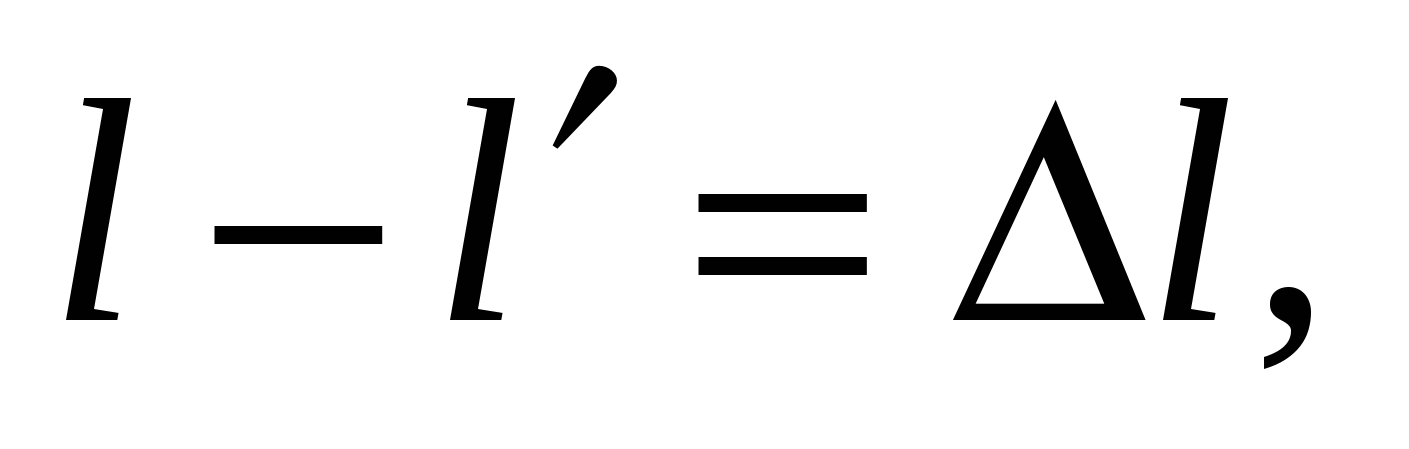 (1)
(1)
где Δl — погрешность данной реализации измерения.
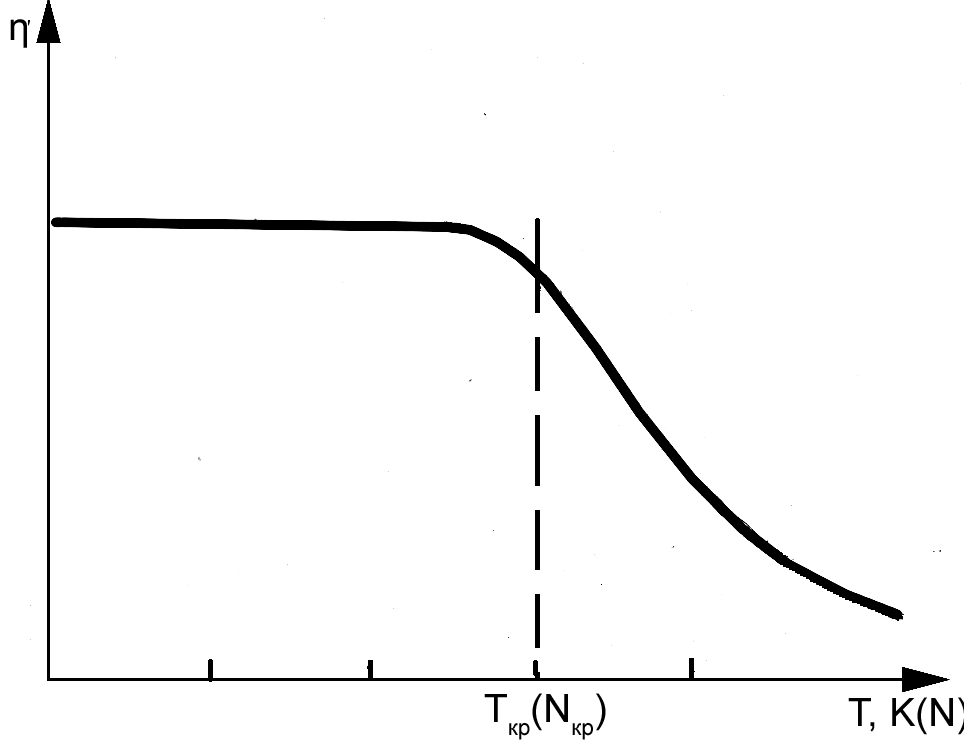
Рис. 3. Зависимость эффективности информационно-измерительной системы от температуры
Измерение в области или оценка случайной величины характеризуется тем, что заранее известна область (отрезок) длины δlm:
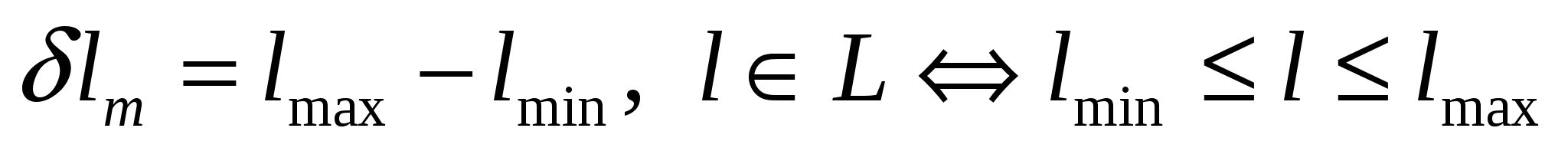 (2)
(2)
и задано априорное распределение Р(l) в L.
Погрешность Δl данной реализации измерения, естественно, не может служить критерием его качества; для этого следует выбрать некоторую величину, усредненную по совместному распределению P(l, l') = P(l)P(l'/l). Физическое измерение характеризуется обычно свойством однородности, т.е. тем, что P(l'/l) = P(|l – l'|) = P(|Δl|) и не зависит от l.
Усреднение по всем флуктуациям (т.е. по P(|Δl|) будем обозначать чертой сверху, а усреднение по априорному распределению — треугольными скобками 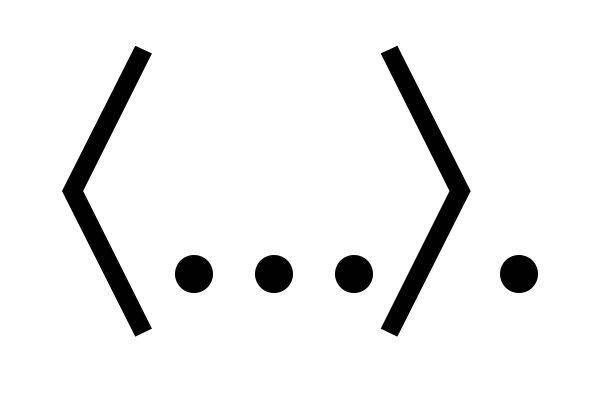
Тогда средний квадрат флуктуации
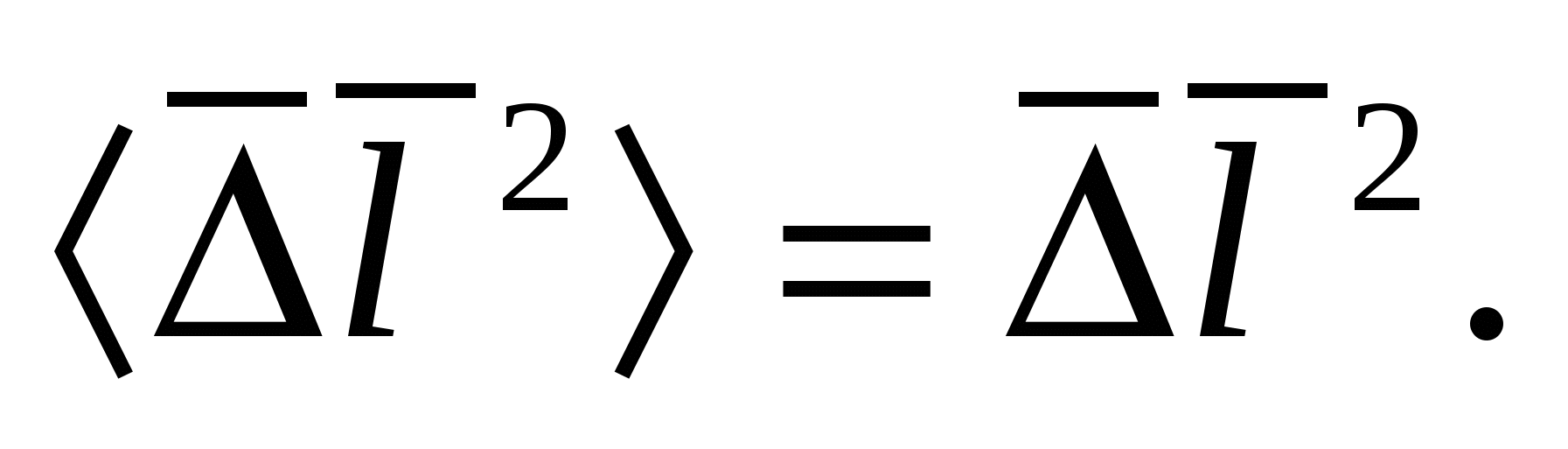 (3)
(3)
Кроме того, измерение часто характеризуется [106, 107] интервалом Δlp, имеющим смысл минимального разрешаемого интервала, или цены деления.
Заметим, что введение в рассмотрение интервала Δlp вызывается, как правило, необходимостью дискретизации (квантования) переменной l. Такое квантование всегда требуется при переходе от скалярного к векторному (позиционному) представлению чисел.
Следует подчеркнуть, что Δlp, в отличие от  , является неоднозначной характеристикой, так как
, является неоднозначной характеристикой, так как
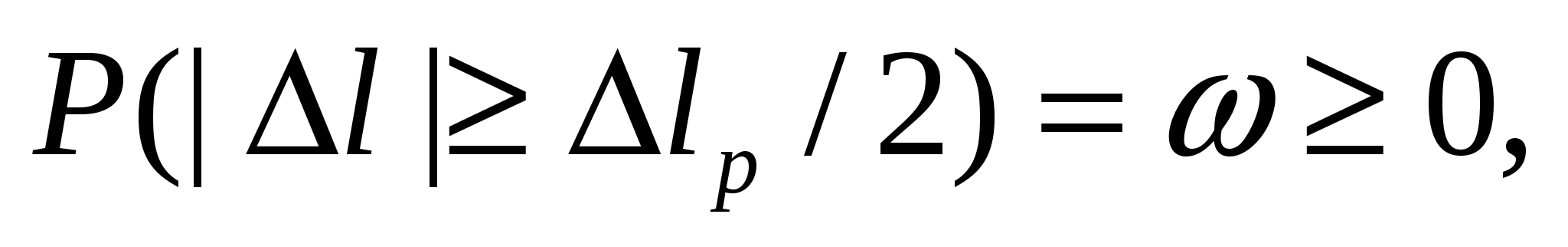 (4)
(4)
т.е. имеется ненулевая вероятность ω ошибки (превышения интервала Δlp). В связи с этим возникает вопрос о связи погрешности с надежностью эксперимента. Измерение по схеме (1) характеризуется линейным преобразованием
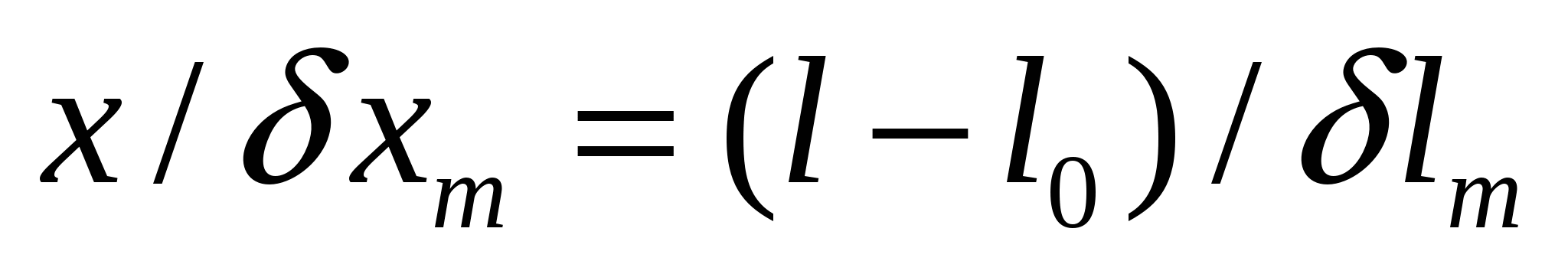 (5)
(5)
отрезка L(3) в отрезок X длиной δхm. При этом, как известно, распределения l и х принадлежат одному и тому же типу и различаются лишь параметрами расположения: масштабным δlm/δxm и центрирующим l0.
Будем в дальнейшем рассматривать лишь симметричные относительно < l > распределения Р(1) и, соответственно, случай симметричного измерения
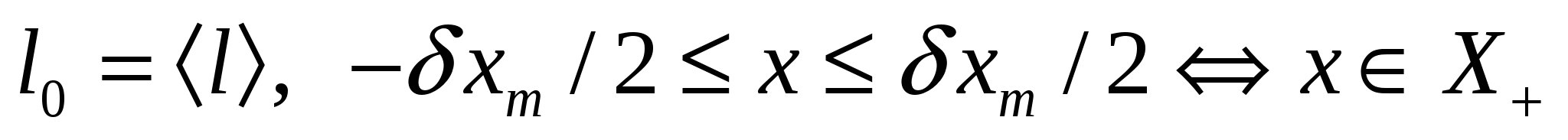 (6)
(6)
и асимметричного измерения
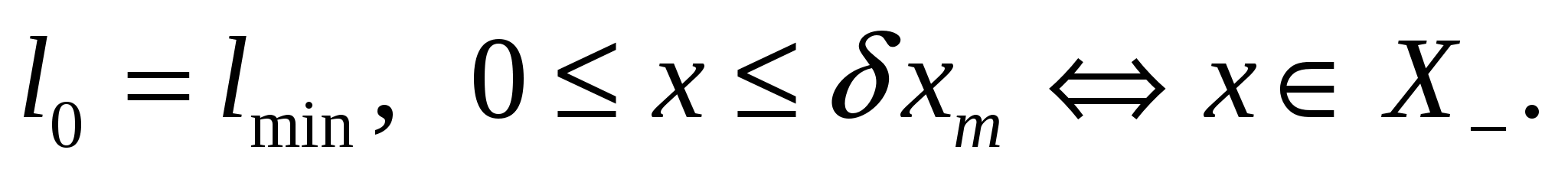 (7)
(7)
Рассматривая одновременно оба случая (6) и (7), запишем: 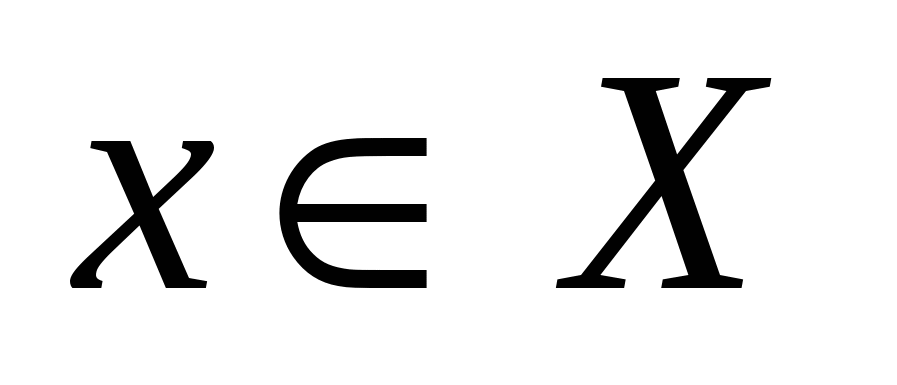 , имея в виду либо Х+, либо Х–.
, имея в виду либо Х+, либо Х–.
Преобразование (6) связано в общем случае с тем, что в датчике используется некоторая эталонная обобщенная сила Fэт, которая совместно с F(l) дает:
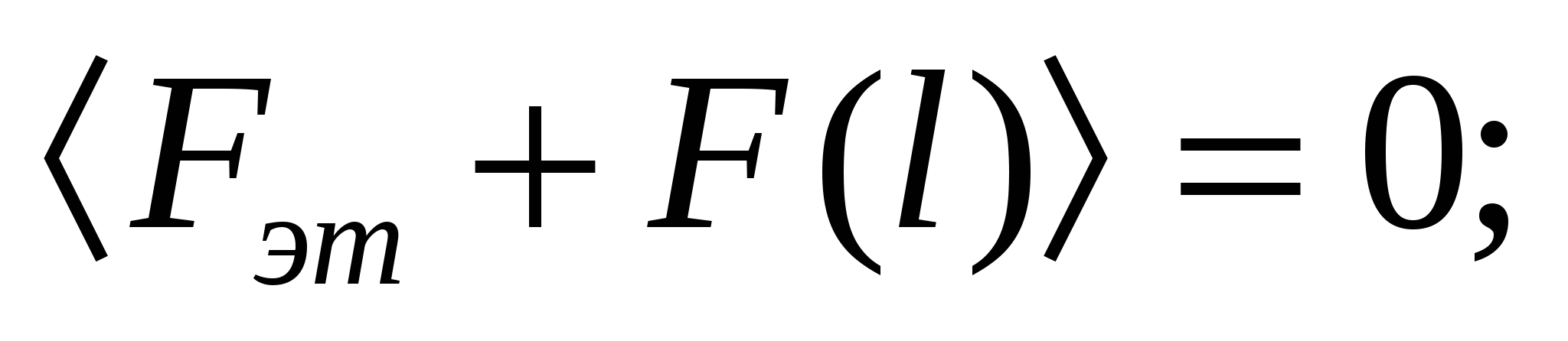 (8)
(8)
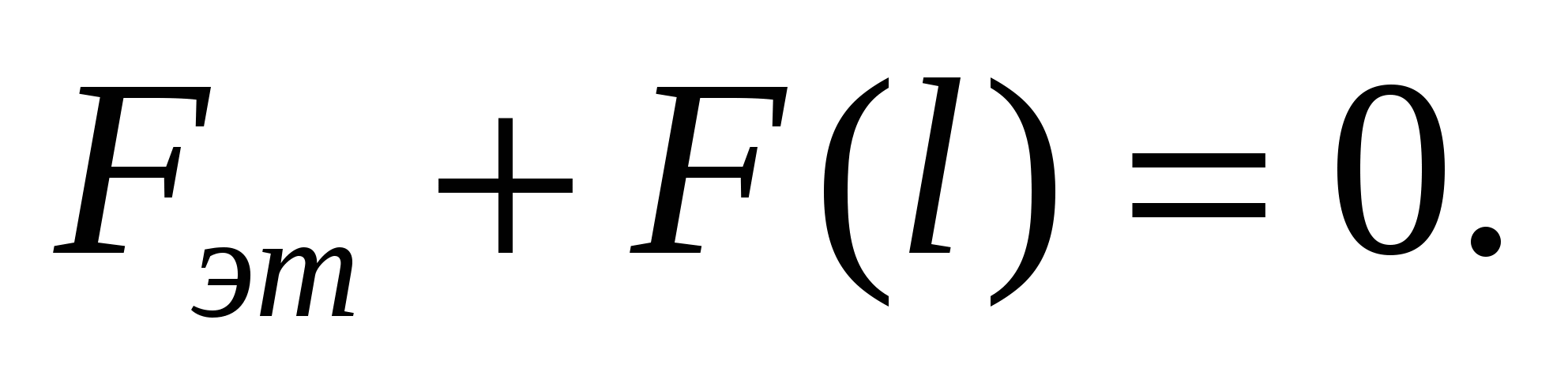 (9)
(9)
Обратим внимание на то, что совершенствование экспериментов обычно связывается с увеличением их чувствительности, т.е. различимости малых разностей l1 – l2.
Поэтому естественно, что в этих случаях основное внимание уделяется снижению абсолютной погрешности  (4). При этом, когда говорят о повышении точности, имеется в виду уменьшение погрешности, хотя формально размерная величина
(4). При этом, когда говорят о повышении точности, имеется в виду уменьшение погрешности, хотя формально размерная величина 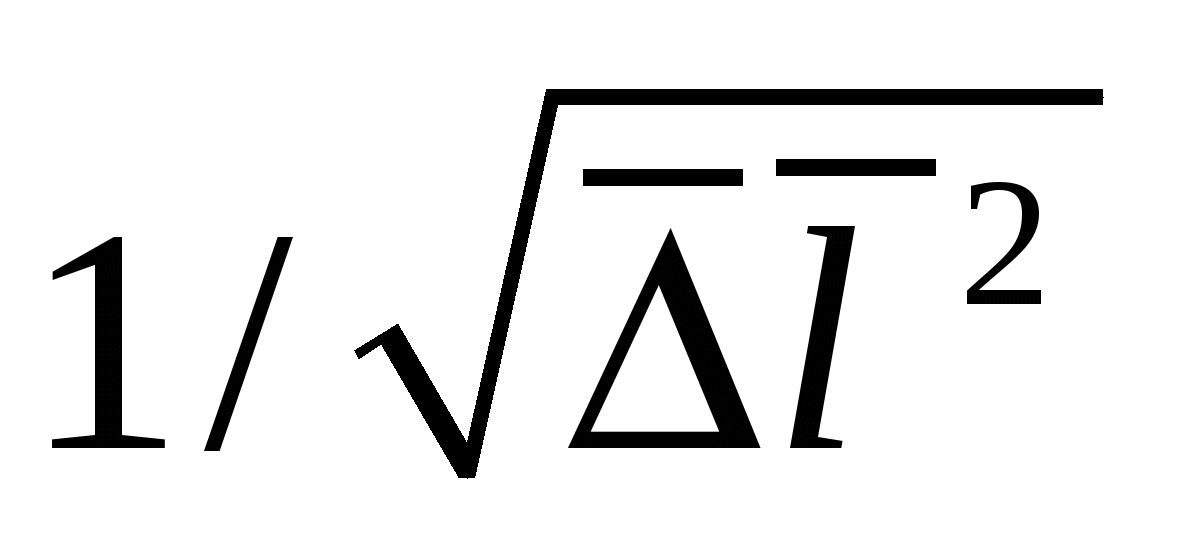 вряд ли может быть названа абсолютной точностью.
вряд ли может быть названа абсолютной точностью.
В противоположность этому относительная точность может быть формально определена как обратная относительной погрешности величина. Как будет видно из дальнейшего, именно эта безразмерная величина играет определяющую роль в термодинамике информационных процессов.
Определим относительную точность 1/σx однократного измерения
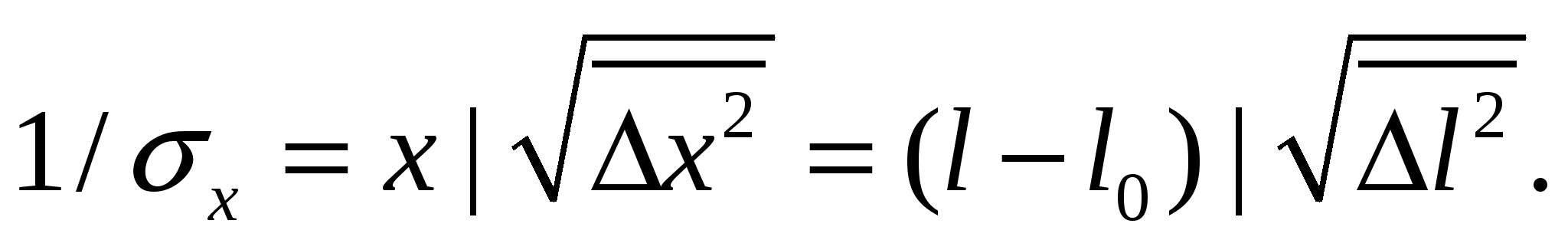 (10)
(10)
Эта величина имеет смысл либо как характеристика одной реализации измерения в области, либо при оценке постоянной величины. В последнем случае, говоря о точности величины l, обычно предполагают, что в (10) и (8) l0 = lmin = 0. В первом же случае
для характеристики всего процесса измерения в области определим среднюю относительную точность 1/σ как отношение априорной среднеквадратической погрешности к апостериорной:
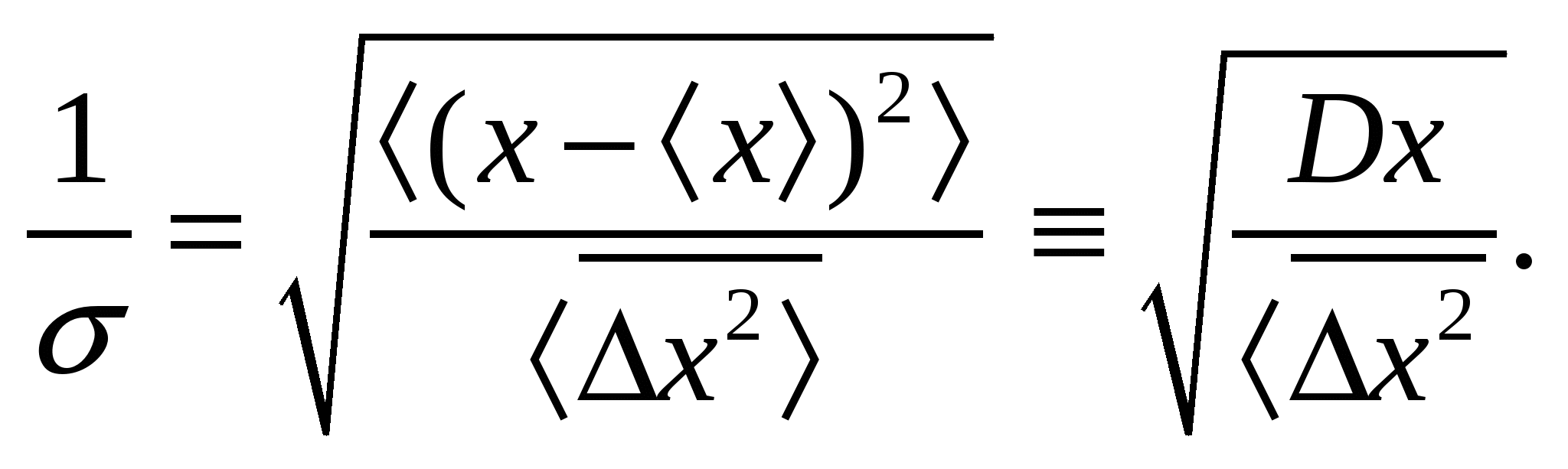 (11)
(11)
Часто вводят относительную погрешность 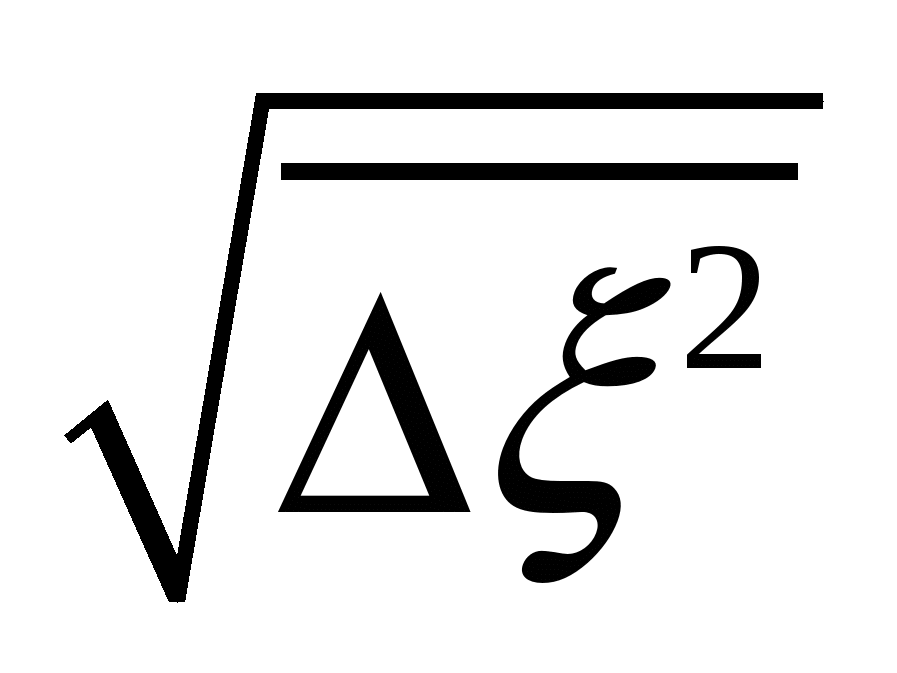 через безразмерную переменную
через безразмерную переменную
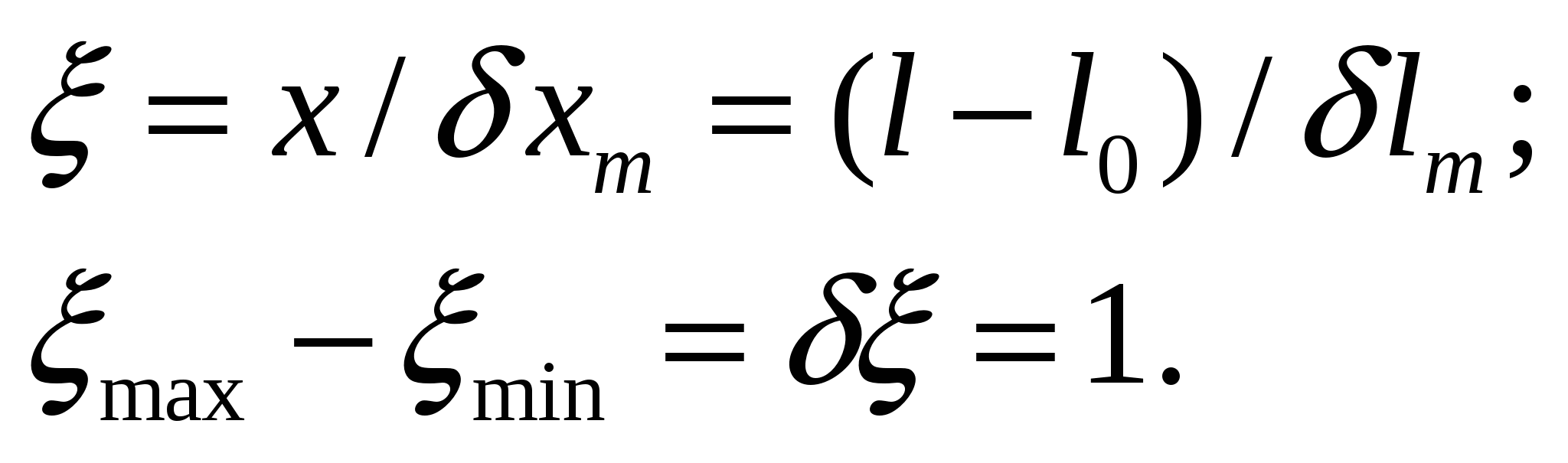 (12)
(12)
Тогда
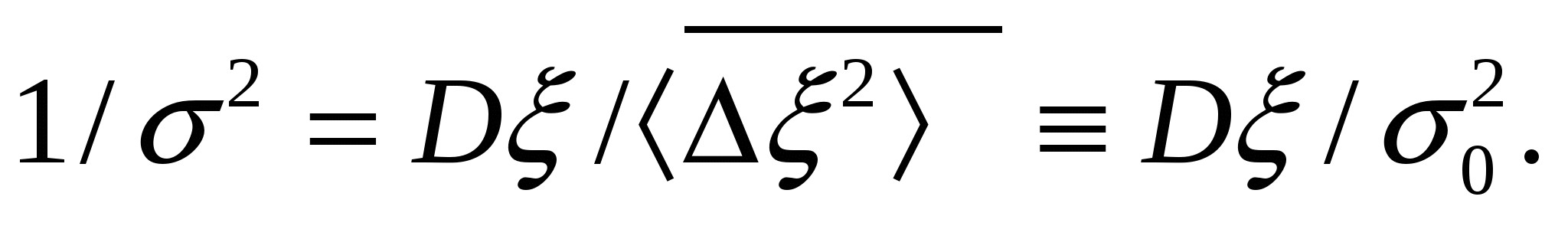 (13)
(13)
Введем еще относительный (приведенный) разрешаемый интервал
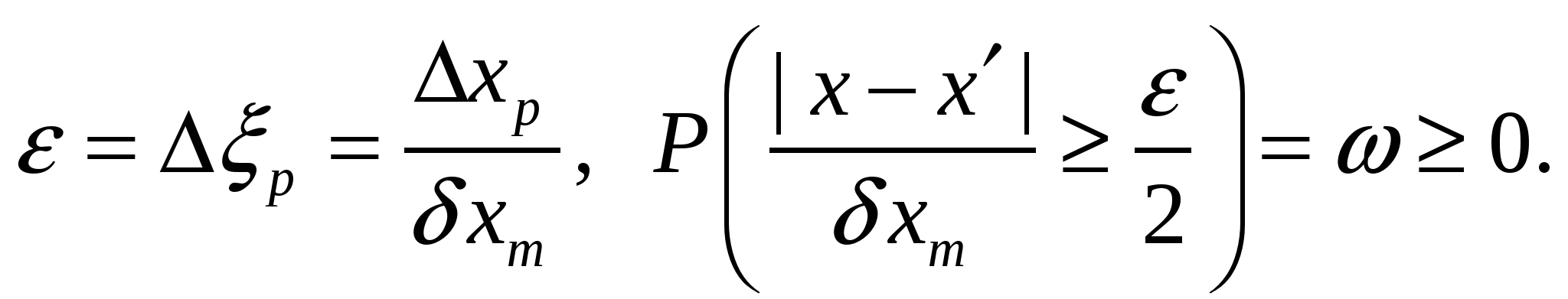 (14)
(14)
Будем называть 1/ε разрешающей способностью, 1/ω — надежностью, 1/σ, 1/σ0 — точностью измерения.
Остается определить среднее количество информации I(х, х'), характеризующее процесс измерения.
Имеем:
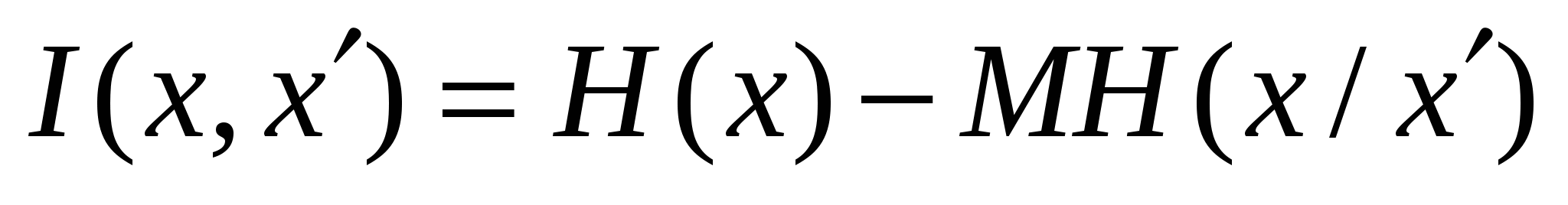 (15)
(15)
где H(x) — начальная энтропия, выражающая неопределенность априорного распределения Р(х);
Н(х/х') — условная энтропия, характеризующая апостериорную неопределенность х при измеренном значении х' (т.с. неопределенность распределения Р(х1х');
МН(х/х') — усредненное по Р(х') значение условной энтропии Н(х/х').