В системах автоматического управления прокатным станом имеются разнообразные датчики, предназначенные для сбора и передачи информации о температуре металла, давлении металла на валки, о параметрах прокатываемого профиля. Информация от датчиков поступает на ЭВМ, где обрабатывается, после чего выдаются управляющие сигналы на исполнительные механизмы прокатного стана. Одна из главных задач состоит в автоматизации регулирования размеров прокатываемого профиля, осуществляемого путем соответствующего автоматического изменения междувалкового пространства на основании показаний датчиков размеров профиля. Вследствие высоких скоростей прокатки (35-60 м/сек) требуется своевременная корректировка междувалкового пространства.
С этой целью проводилось моделирование алгоритмов обнаружения отклонений междувалкового пространства от заданного поля допусков.
Существующий интегральный метод не позволяет своевременно обнаруживать отклонения от заданного поля допусков.
Сущность интегрального метода заключается в том, что в качестве основного критерия для обнаружения отклонений (существенной нестационарности) в контролируемом процессе x(t) принимается площадь S(t), ограниченная x(t) и сглаженной реализацией y(t). Если величина площади отклонения S(t) больше некоторого критического значения ξ, то принимается решение о наличии отклонения.
В работе предлагается использование оценки дисперсии случайного процесса в качестве критерия обнаружения существенной нестационарности, которая значительно быстрее реагирует на изменения в контролируемом процессе, чем интегральный метод.
Как видно на рис. 1, вычисление дисперсии Di позволяет определить момент наступления существенной нестационарности в условиях аддитивных помех гораздо быстрее, чем интегральным методом. Площадь отклонения S(t) вычисляется для дисперсии случайного процесса. Решение о начале нестационарности принимается при условии S(t) > ξ. Величина ξ уточняется в процессе эксплуатации системы в реальных условиях.
Для решения задач обнаружения нестационарностей и накопления статистических данных необходимо вычислить сглаженные значения и дисперсии случайных процессов изменения контролируемых параметров.
Один из известных способов, используемых для получения оценок среднего значения и дисперсии на основе n-независимых измеренных значений случайного процесса, заключается в вычислении оценок по формулам
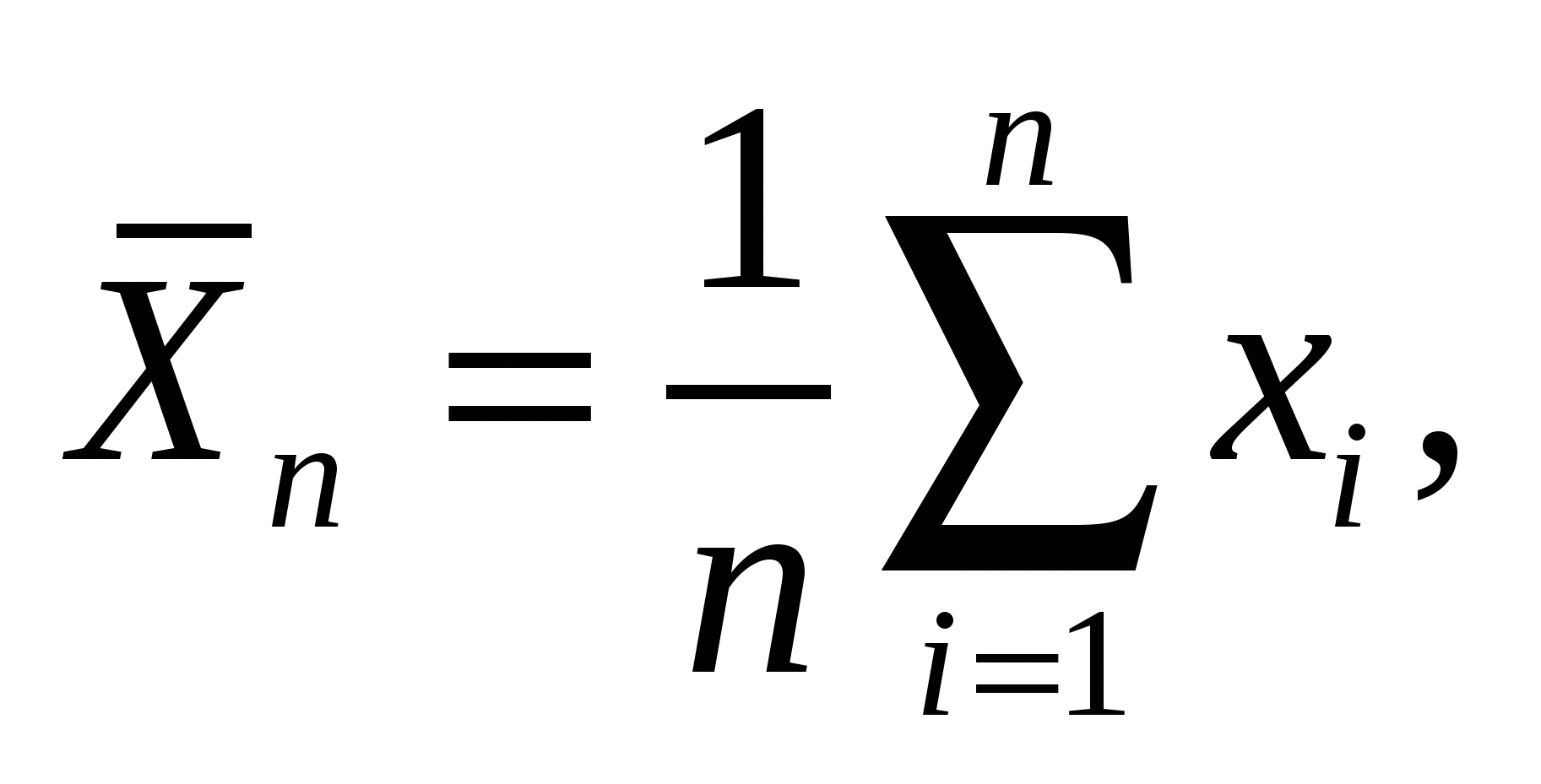
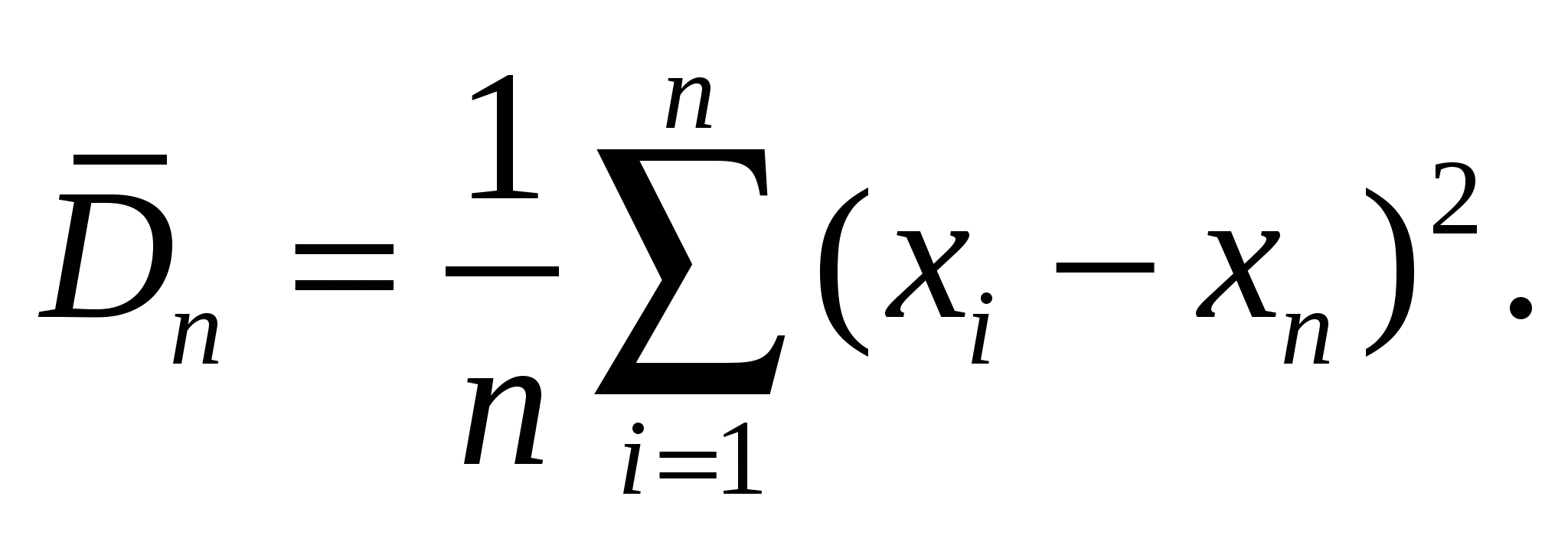(1)
Недостатком вычислений параметров по формулам (1) является необходимость накапливания значения данных за определенный промежуток времени, что приводит к задержке обнаружения существенных нестационарностей в контролируемом случайном процессе.
Оценку сглаженного значения можно вычислять с помощью известного оператора экспоненциального сглаживания
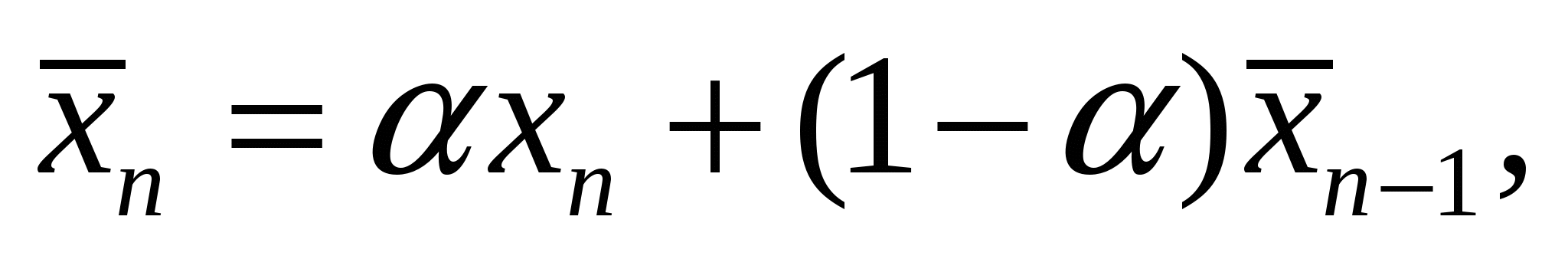(2)
где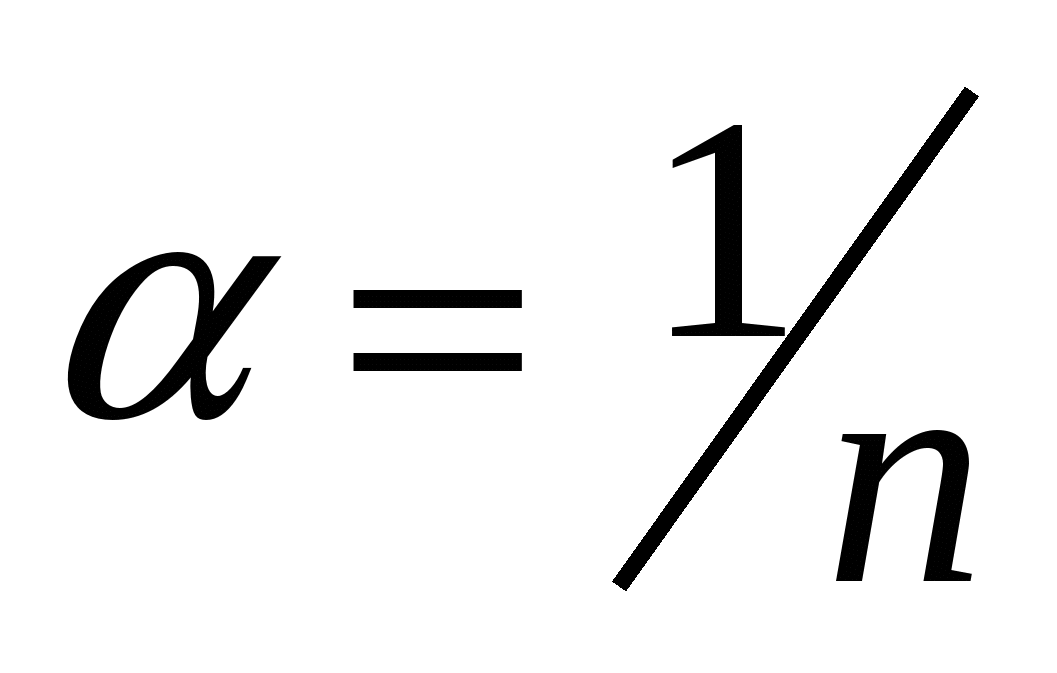 
.
Формула (2) позволяет вычислять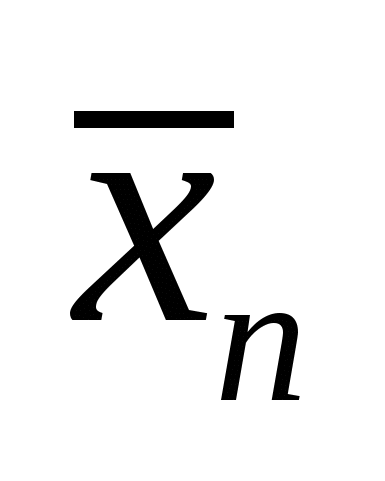 
в режиме реального времени без накопления промежуточных данных, т.е. без задержки.
В работе получено выражение для определения оценки дисперсии без накопления сумм
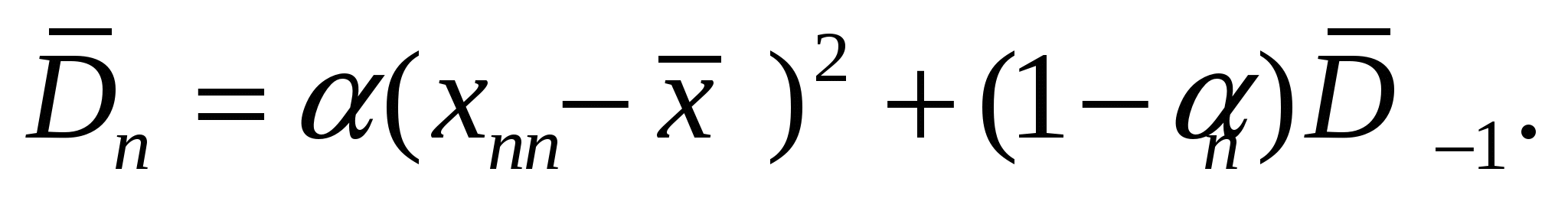(3)
При моделировании вычислялись оценки среднего значения и дисперсии по формулам (2), (3). В том случае, когда замеры xi снимаются через равные промежутки времени (Δt = const), имеем α = const.
Для повышения быстродействия автоматической системы обнаружения отклонений от заданного поля допусков используется адаптивная дискретизация контролируемых процессов (Δt ≠ const), при которой частота опроса разнотипных контролируемых датчиков меняется в зависимости от их параметров и показаний.
При адаптивной дискретизации необходимо выразить коэффициент α для выражений (2), (3) через параметры Δt, ТСГ.
Оператор (2) является дискретным аналогом апериодического звена первого порядка с постоянной времени ТСГ и коэффициентом усиления, равным единице. Решение дифференциального уравнения, описывающего такое звено, имеет вид:
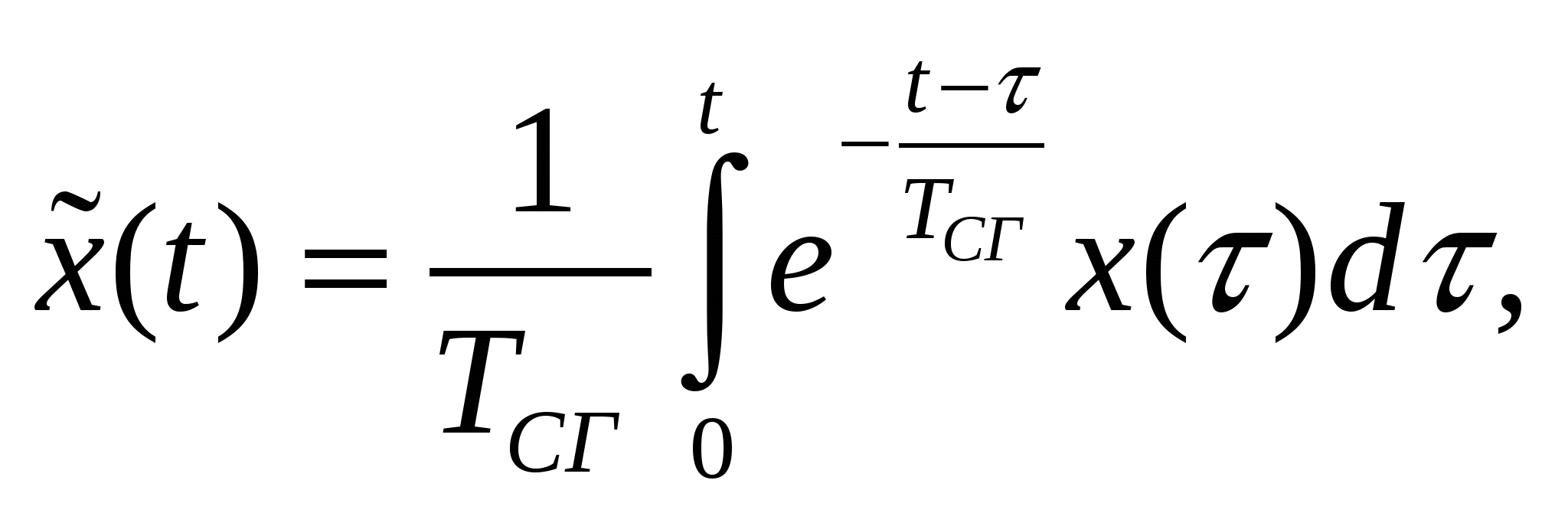(4)
где x(t),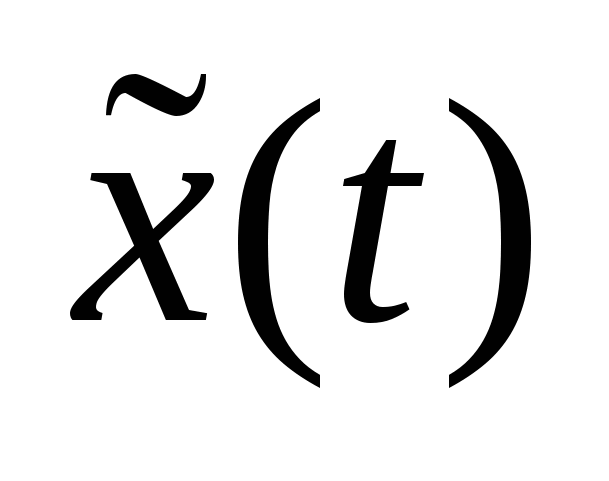 
— процессы на входе и выходе звена, соответственно.
При подаче на вход звена единичной ступенчатой функции x(t) = 1 из выражения (4) получим
X(t) = 1 – e-t/Tcg.
Переходя к дискретному представлению при tn = n*Δt и раскрывая рекуррентную формулу (2) при xi = 1, I = 1,2,…n, получим
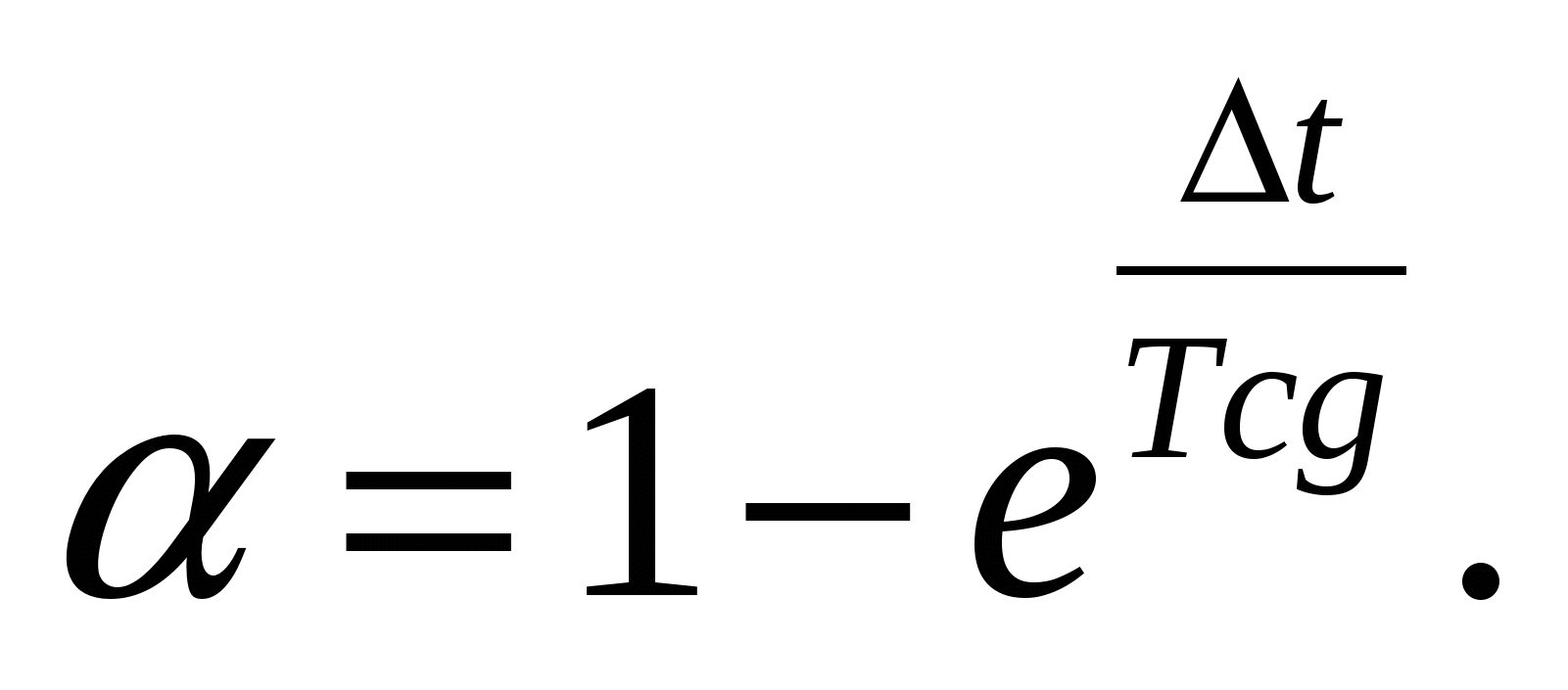(5)
Формула (5) характеризует зависимость коэффи-
циента сглаживания α от заданной постоянной времени Tcg сглаживания при изменяющемся интервале времени Δt.
Полученные результаты позволяют использовать формулы (2), (3), (5) для обнаружения существенных нестационарностей в случайных контролируемых процессах при адаптивной дискретизации.
Быстрое обнаружение отклонений междувалкового пространства от заданного поля допусков позволяет своевременно выработать управляющие воздействия на исполнительные механизмы прокатного стана, что повышает качество готовой продукции.
