страница 1
ИСПОЛЬЗОВАНИЕ МНОГОСЕТОЧНОГО МЕТОДА
ДЛЯ РЕШЕНИЯ УРАВНЕНИЯ ПУАССОНА В ЗАДАЧЕ
МОДЕЛИРОВАНИЯ ПРИБОРНЫХ СТРУКТУР МЕТОДОМ
МОНТЕ-КАРЛО
Д. С. Сперанский
Как известно, при численном моделировании различных полупроводниковых приборов, в частности методом Монте-Карло, - необходимо учитывать непрерывное изменение во времени и пространстве электрического поля. Решение уравнения Пуассона при определенных заданных граничных условиях позволяет получить адекватное реальному распределение потенциала и напряженности электрического поля в приборе [1]. Так как метод Монте-Карло требует больших затрат машинного времени, то при разработке программ моделирования должны использоваться эффективные алгоритмы решения уравнения поля.
Целью данной работы явилась демонстрация возможности использования многосеточного метода для решения уравнения Пуассона, а также его сравнительная оценка с некоторыми наиболее часто используемыми методами при моделировании полупроводниковых приборных структур методом Монте-Карло.
УРАВНЕНИЕ ПУАССОНА
Е сли ввести в области решения прямоугольную сетку с шагом h, то исходную дифференциальную задачу можно аппроксимировать пятиточечной конечно-разностной схемой [2]: сли ввести в области решения прямоугольную сетку с шагом h, то исходную дифференциальную задачу можно аппроксимировать пятиточечной конечно-разностной схемой [2]:
ш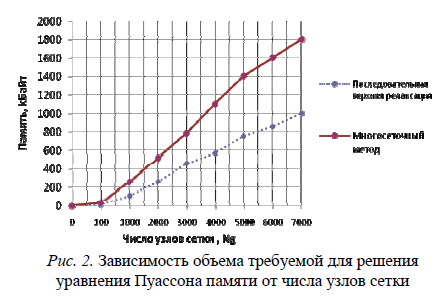 ений в узлах сетки, w -вектор значений правой части уравнения (1) в узлах сетки. ений в узлах сетки, w -вектор значений правой части уравнения (1) в узлах сетки.
Сегодня для решения
уравнения Пуассона чаще
всего используют методы
последовательной верхней
релаксации (ПВР), или
какой-либо из методов
быстрого решения эллиптических
уравнений (БРЭУ методы). Однако их производительности становиться недостаточно при моделировании двухмерных систем со сложными граничными условиями или трехмерных систем.
Существенно ускорить решение уравнения Пуассона позволяет многосеточный метод (МС), который можно отнести к итерационным методам. Он основан на использовании последовательности уменьшающихся сеток и операторов перехода от одной сетки к другой для эффективного подавления низкочастотных составляющих ошибки [3, 4]. Помимо этого, алгоритм многосеточного метода удачно вписывается в современную концепцию объектно-ориентированной методологии (ООМ), и дает возможность распараллеливания вычислений [5].
МНОГОСЕТОЧНЫЙ МЕТОД
Е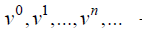 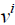 сли - последовательность приближенных решений системы (2), сходящихся к точному решению u,а - приближенное решение на шаге i, то можно определить невязку r' [2, 6]: сли - последовательность приближенных решений системы (2), сходящихся к точному решению u,а - приближенное решение на шаге i, то можно определить невязку r' [2, 6]:


для уточнения предыдущей аппроксимации v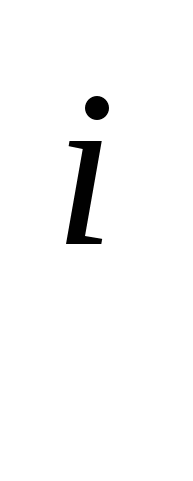 полученной на исходной сетке Ωn,[3, 6]: полученной на исходной сетке Ωn,[3, 6]:
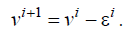 (6) (6)
Самая простая схема многосеточного алгоритма, использующая две сетки, для i-й итерации имеет следующий вид [6]:
-
Приближенное решение viсистемы (2) на сетке Ωn сглаживается на
исходной сетке с использованием подходящей релаксационной схемы;
-
Вычисленная на сетке Ωn согласно уравнению (3) невязка перено
ситься на более грубую сетку Ωn-1
-
Находится точное решение уравнения (5) на грубой сетке;
-
Н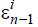 айденноеинтерполируется с сетки Ωn-1на сетку Ωn.Вычисля айденноеинтерполируется с сетки Ωn-1на сетку Ωn.Вычисля
етсяvi+1;
-
Осуществляется окончательное сглаживание приближенного реше
нияvi+1на сетке Ωn.
Для того, чтобы приведенную выше схему распространить на последовательность все более и более грубых сеток, необходимо применять весь алгоритм в рекурсивном порядке на шаге 3. Рекурсия прекращается, когда достигается самая грубая сетка Ω0, где уравнение (5) решается с заданной точностью.
Реализация многосеточного алгоритма, требует больших затрат памяти по сравнению с алгоритмом ПВР. Разница в основном связана с тем, что метод ПВР предполагает хранение значений в узловых точках единственной сетки, в то время как многосеточный алгоритм оперирует с рассчитанными данными в узлах всей последовательности уменьшающихся сеток. Помимо этого, схема многосеточного алгоритма подразумевает использование рассчитанных коэффициентов операторов интерполяции и сглаживания. На рис. 2 показана зависимость среднего объема памяти, требующейся для хранения промежуточной информации при реализации методов ПВР и МС, от числа узлов сетки Ng.
Несмотря на то, что многосеточный метод требует больших ресурсов памяти, чем метод последовательной верхней релаксации, он обладает гораздо более быстрой сходимостью [3, 6]. Для сравнения быстродействия многосеточного метода и чаще всего используемых в Монте-Карло моделировании методов последовательной верхней релаксации, а также метода быстрого преобразования Фурье с циклической редукцией, было проведено решение модельной задачи, соответствующей прямоугольной области приборной структуры с граничными условиями Дирихле на границе контакт-полупроводник, и Неймана на остальных границах (рис. 1). В этом случае решалась система уравнений (2) за временной шаг коррекции поля Δtв прямоугольной области с равномерной сеткой. На рис. 3 приведена зависимость времени решения уравнения Пуассона различными методами
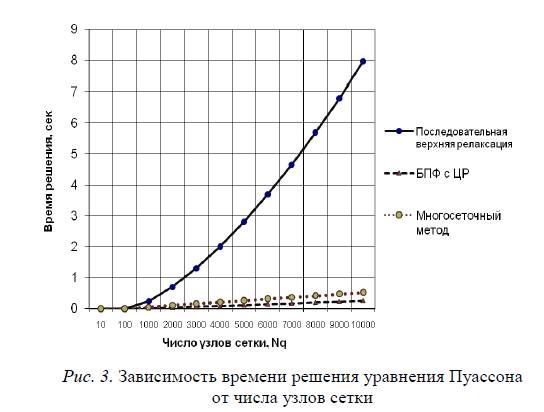
от Ng, при заданной точности 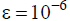 для итерационных методов. для итерационных методов.
Из рис. 3 видно, что многосеточный метод уступает по быстроте решения системы (2) методу быстрого преобразования Фурье с циклической редукцией (БПФ с ЦР). Это очевидно, поскольку как метод БПФ с ЦР, так и другие специализированные методы этого класса, доказывают свою эффективность лишь при моделировании упрошенных модельных задач. Если же учитывать сложные граничные условия, то необходимо использование дополнительной процедуры матрицы емкости, что ведет к значительному увеличению времени решения системы (2).
ЗАКЛЮЧЕНИЕ
Таким образом, можно сделать вывод о том, что многосеточный метод для рассмотренных условий является значительно более быстрым, чем метод последовательной верхней релаксации с ускорением по Чебышеву и более универсальным, чем специализированный метод БПФ с ЦР. Также видно, что зависимость времени решения для многосеточного метода от числа узлов является практически линейной. Благодаря этому его можно также успешно применять не только для решения двумерного уравнения Пуассона, но и при трехмерном моделировании приборных структур методом Монте-Карло.
В дальнейшем предполагается включить многосеточный алгоритм в программный пакет моделирования n-канального МОП-транзистора методом Монте-Карло на основе ООМ GSB-MOSFET. Представляется, что это позволит значительно увеличить скорость расчетов при сохранении необходимой точности.
Литература
-
Хокни Р., ИствудД. Численное моделирование методом частиц. М.: Мир, 1987. 640 с.
-
Самарский, А. А., ГулинА. В. Численные методы. М.: Наука, 1989. 432 с.
-
Trottenberg U., OsterleeC. W., Schuller A. Multigrid // Academic Press. 2000.
-
William L. Briggs, Van Emden Henson, and Steve F. McCormick. A Multigrid Tutorial.
Second Edition. SIAM, 2000.
-
Сперанский Д. С, Борздов В. М. Моделирование полупроводниковых приборных
структур методом Монте-Карло. Подход с использованием технологии объектно-
ориентированного программирования // Доклады БГУИР. 2008. № 4. С. 66-71.
-
Saraniti M., Rein A., Zandler G., Vogl P., Lugli P. An Efficient Multigrid Poisson
Solver for Device Simulations // IEEE Trans. on comp. 1996. Vol. 15, N 2. P. 141-150.
-
Борздов В. М. Моделирование методом Монте-Карло приборных структур инте
гральной электроники / В. М. Борздов, О. Г. Жевняк, Ф. Ф. Комаров, В. О. Гален-
чик. Минск, БГУ. 2007.
страница 1
|