страница 1
ТЕМА №2
Количественные показатели надежности.
Известно, что даже у двух идентичных элементов или систем, работающих в аналогичных условиях, отказы происходят в различные, случайные моменты времени, т.е. отказы могут быть описаны только в терминах теории вероятности. Таким образом, определения показателей надежности должны основываться главным образом на понятиях теории вероятности.
Вообще отказ это случайное событие, хотя причина его вызвавшая несет определенный и совсем не случайный характер. Если считать, что 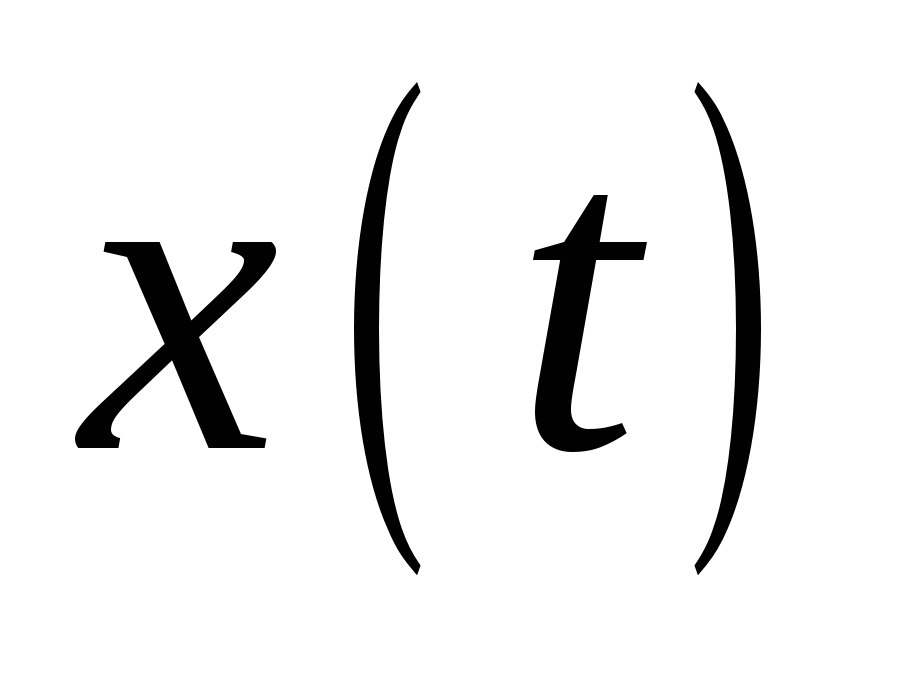 - это какое то определенное состояние изделия, то графически отказ можно изобразить следующим образом (рис. 2.1.), где - это какое то определенное состояние изделия, то графически отказ можно изобразить следующим образом (рис. 2.1.), где  - предельное состояние данного изделия (критерий отказа). - предельное состояние данного изделия (критерий отказа).
Надежность различных изделий оценивается критерием надежности, количественное значение которого называют характеристикой или количественным показателем надежности. Для практического использования очень удобны временные показатели надежности, важнейшим из которых является время безотказной работы прибора. Это вызвано тем, что моменты отказов совокупности приборов случайным образом распределены во времени в силу того, что сами приборы имеют определенный разброс своих параметров. Последний связан с неоднородностью исходных материалов и колебаниями технологических процессов их изготовления, приводящими к разбросу их внутренних геометрических размеров и физических характеристик.
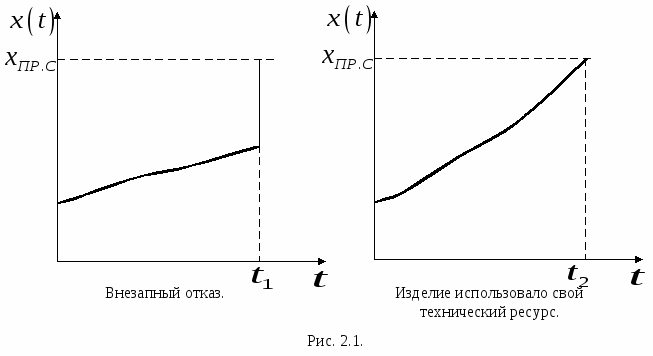
Кроме этого при эксплуатации приборов в составе аппаратуры, на нее воздействуют самые различные сочетания внешних факторов. Все вместе взятое приводит к неоднозначности результатов, когда переходят к рассмотрению надежностных характеристик отдельных приборов. Поэтому время безотказной работы прибора, или наработка до отказа, рассматривается как непрерывные случайные величины, описываемые интегральной функцией распределения.
Основным показателем безотказности является вероятность безотказной работы изделия - 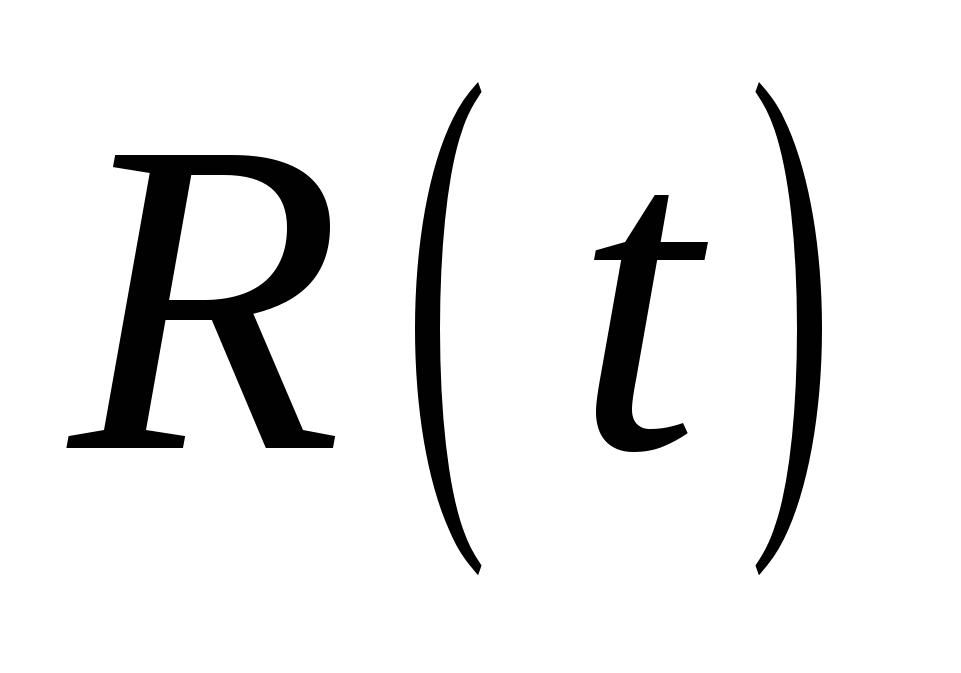 , под которым понимается, что при заданных режимах и условиях работы в заданном интервале времени, отказ прибора не возникает (естественно первоначальное предположение, что в начальный момент времени прибор был работоспособен). , под которым понимается, что при заданных режимах и условиях работы в заданном интервале времени, отказ прибора не возникает (естественно первоначальное предположение, что в начальный момент времени прибор был работоспособен).
Согласно определению вероятность безотказной работы
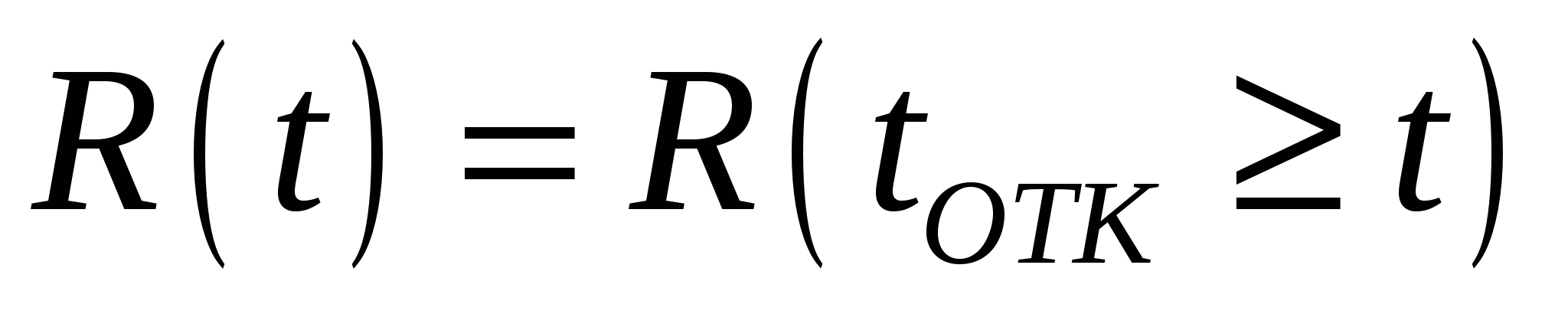 , (2.1) , (2.1)
где 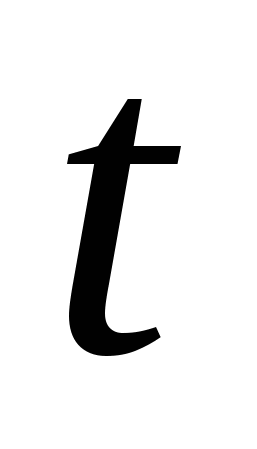 - текущее время, - текущее время, 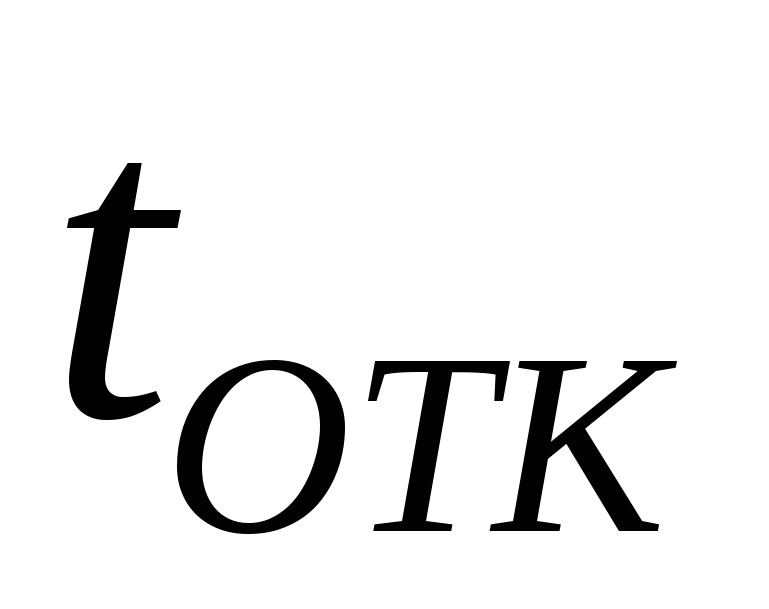 - время появления отказа (случайная величина), - время появления отказа (случайная величина), 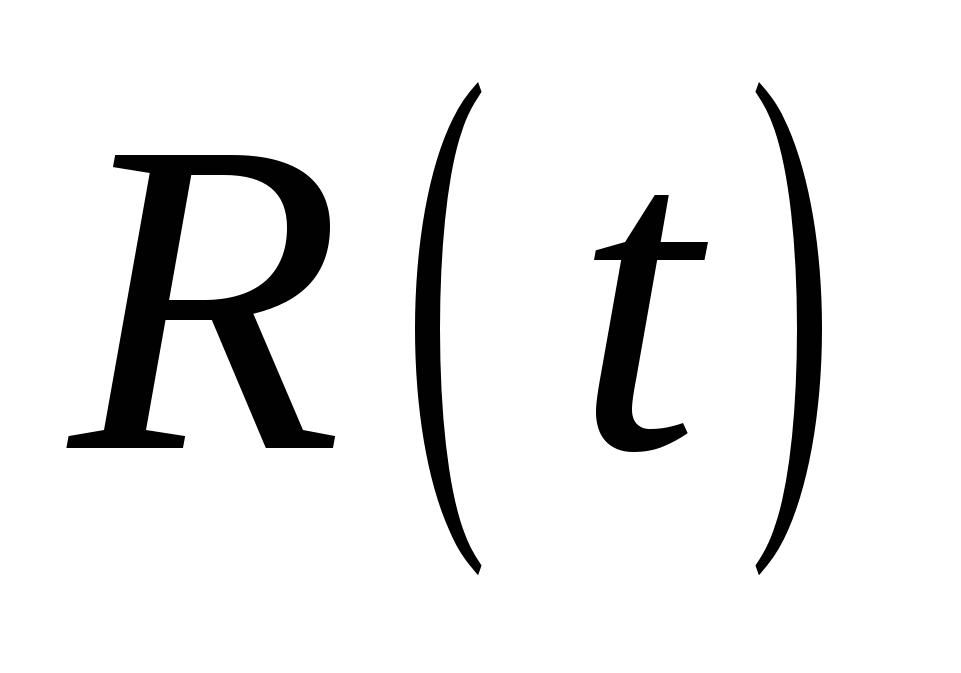 - вероятность. - вероятность.
Как функция распределения 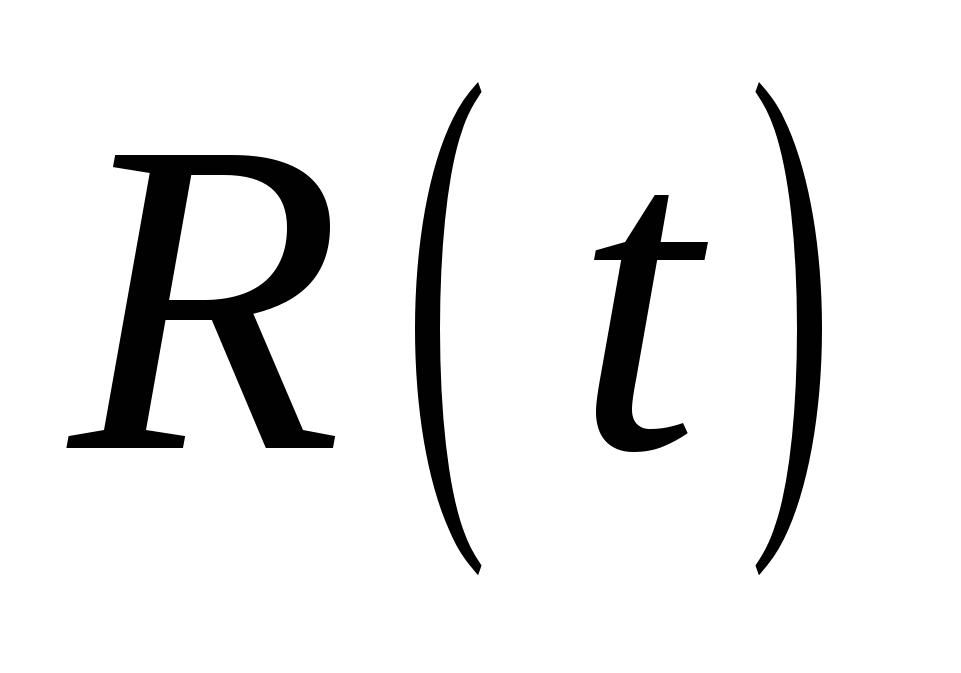 обладает следующими свойствами: обладает следующими свойствами:
-
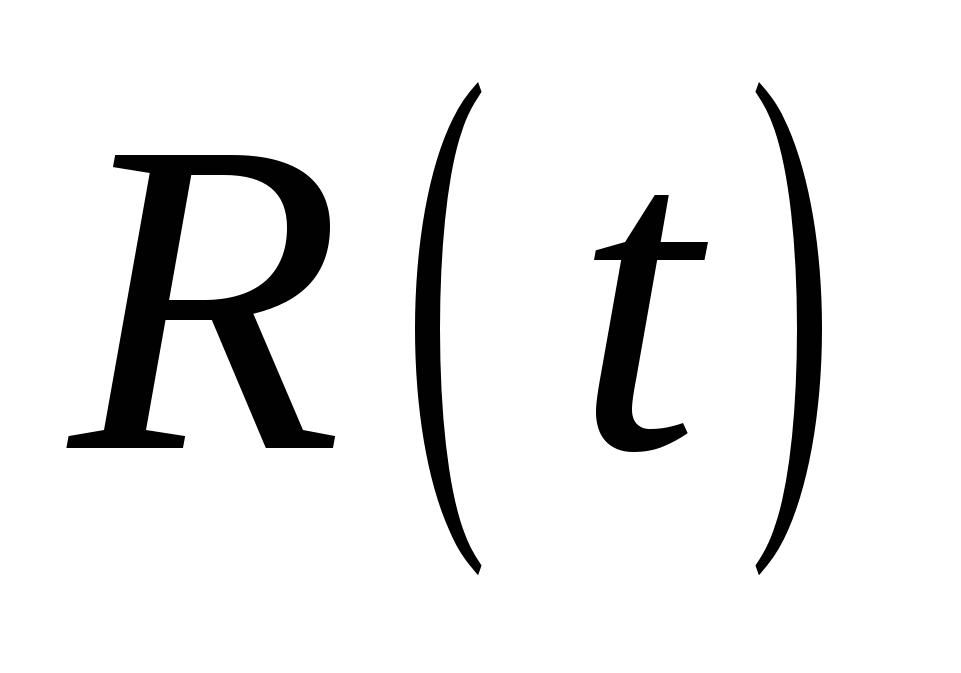 - монотонно невозрастающая функция, т.е. при - монотонно невозрастающая функция, т.е. при 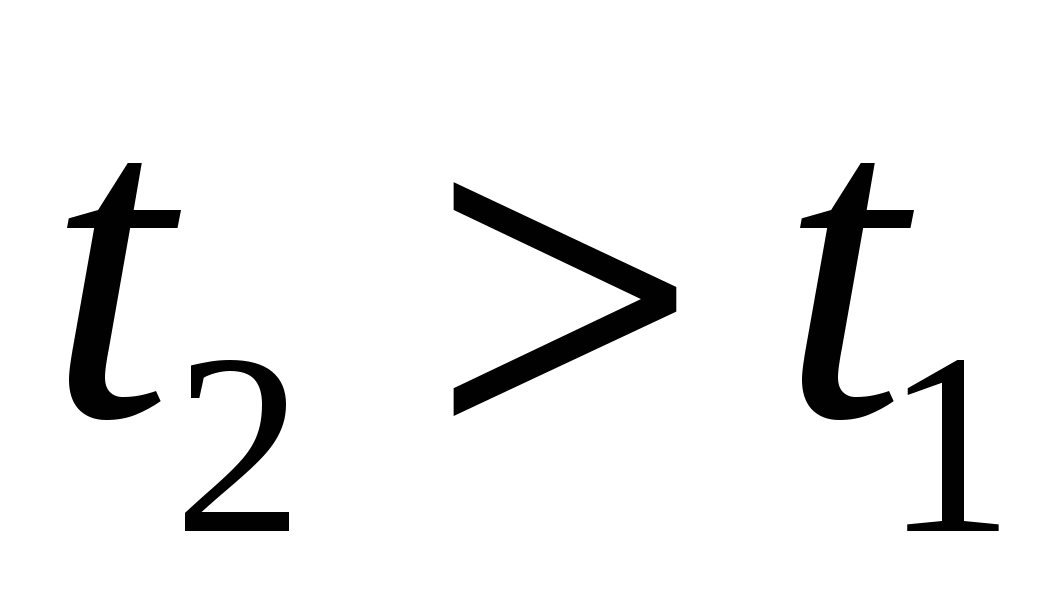 получаем получаем 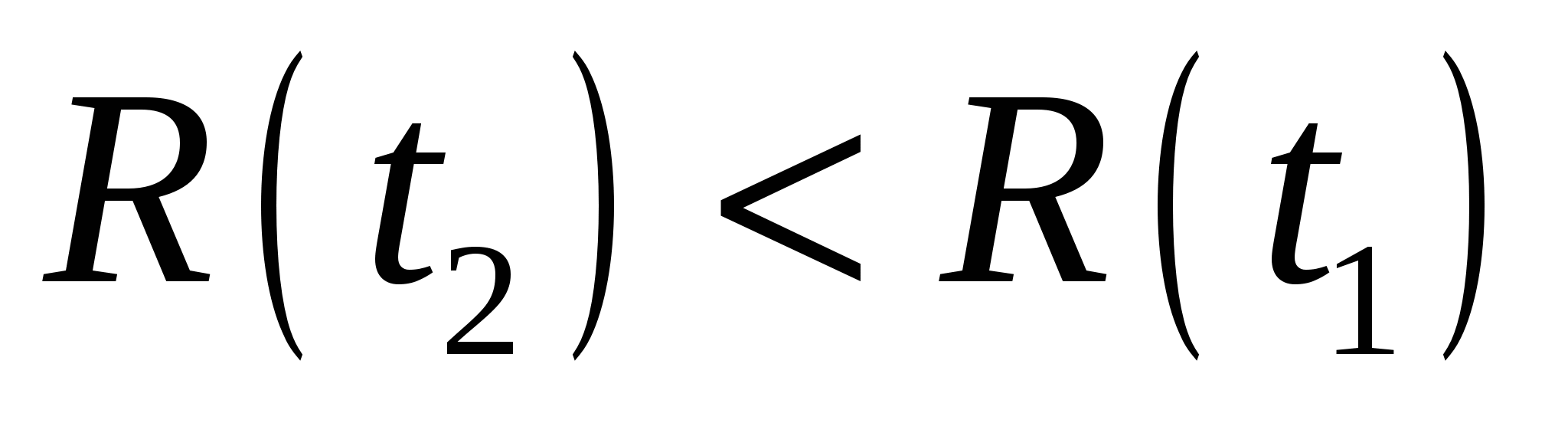 ; ;
-
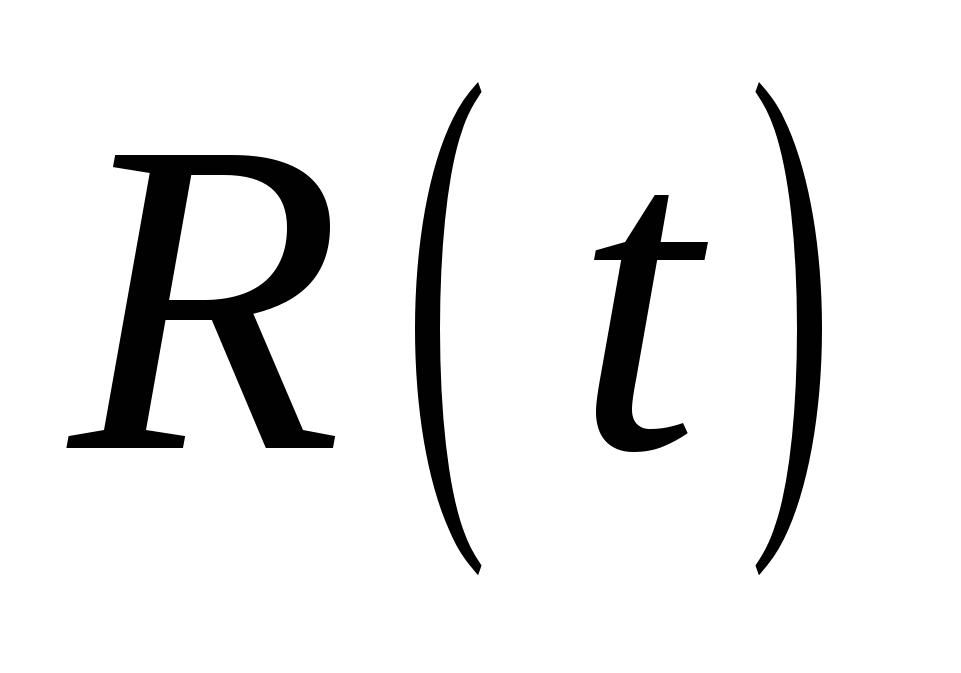 изменяется в пределах изменяется в пределах 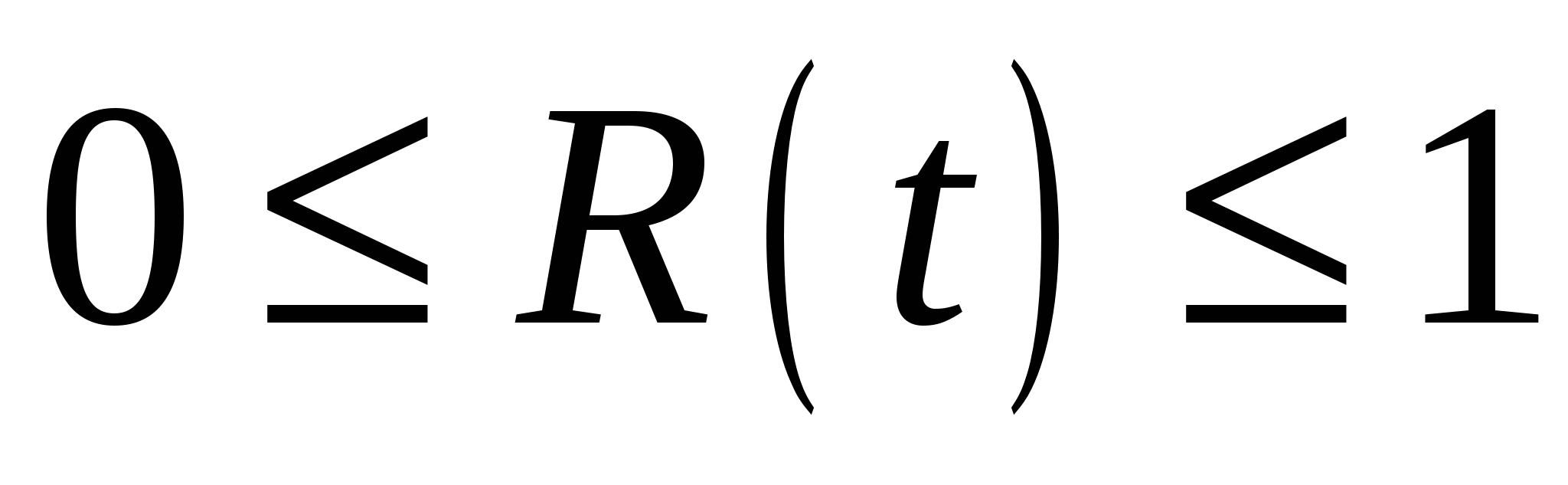 ; ;
-
В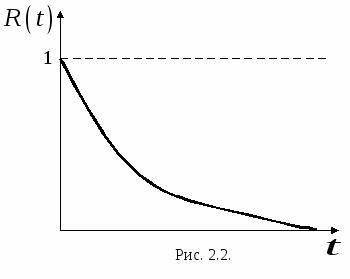
начальный момент времени 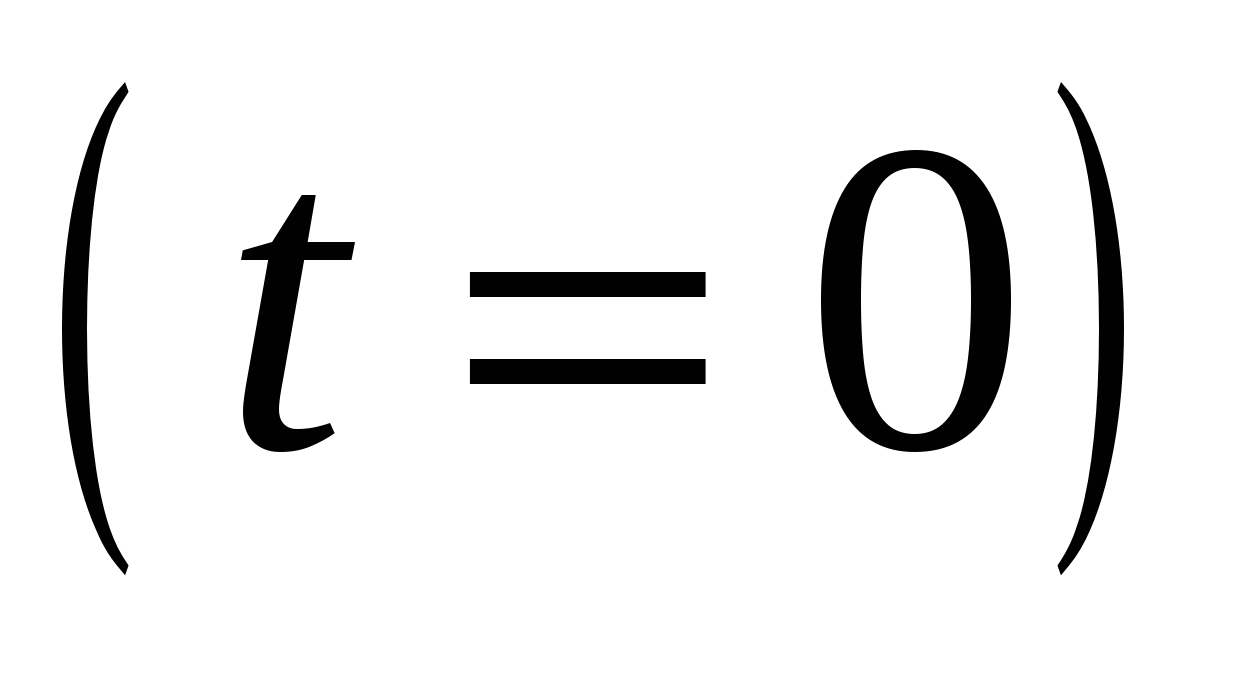 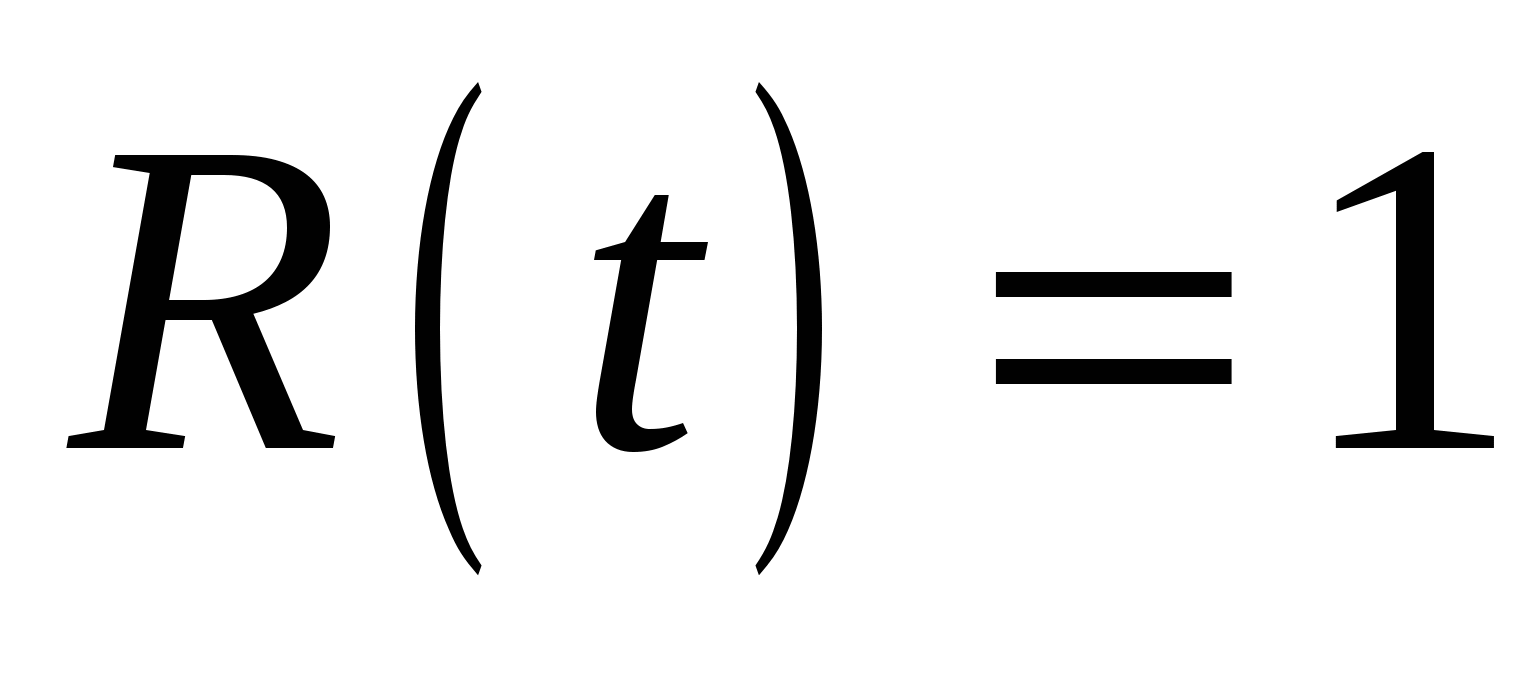 , в пределе, когда , в пределе, когда 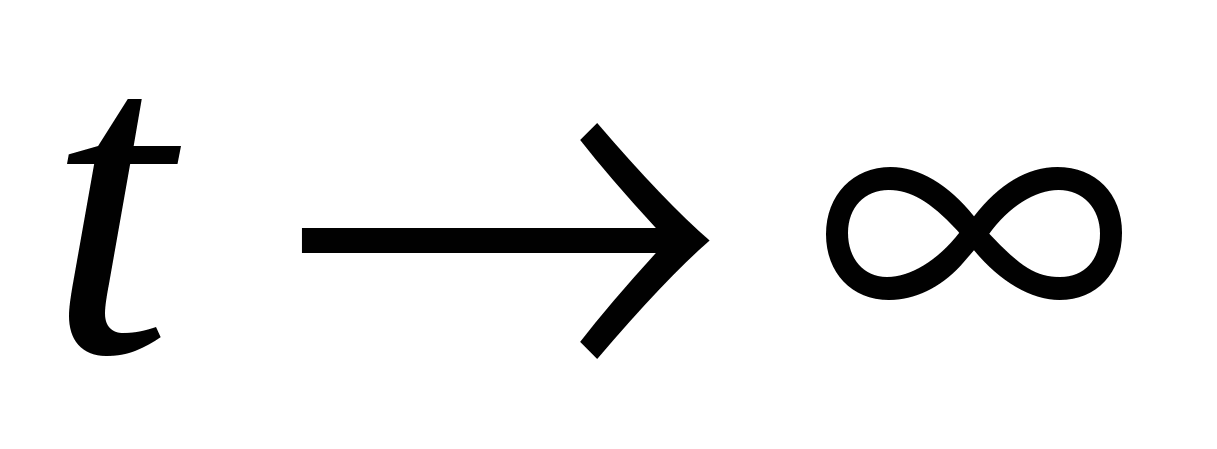 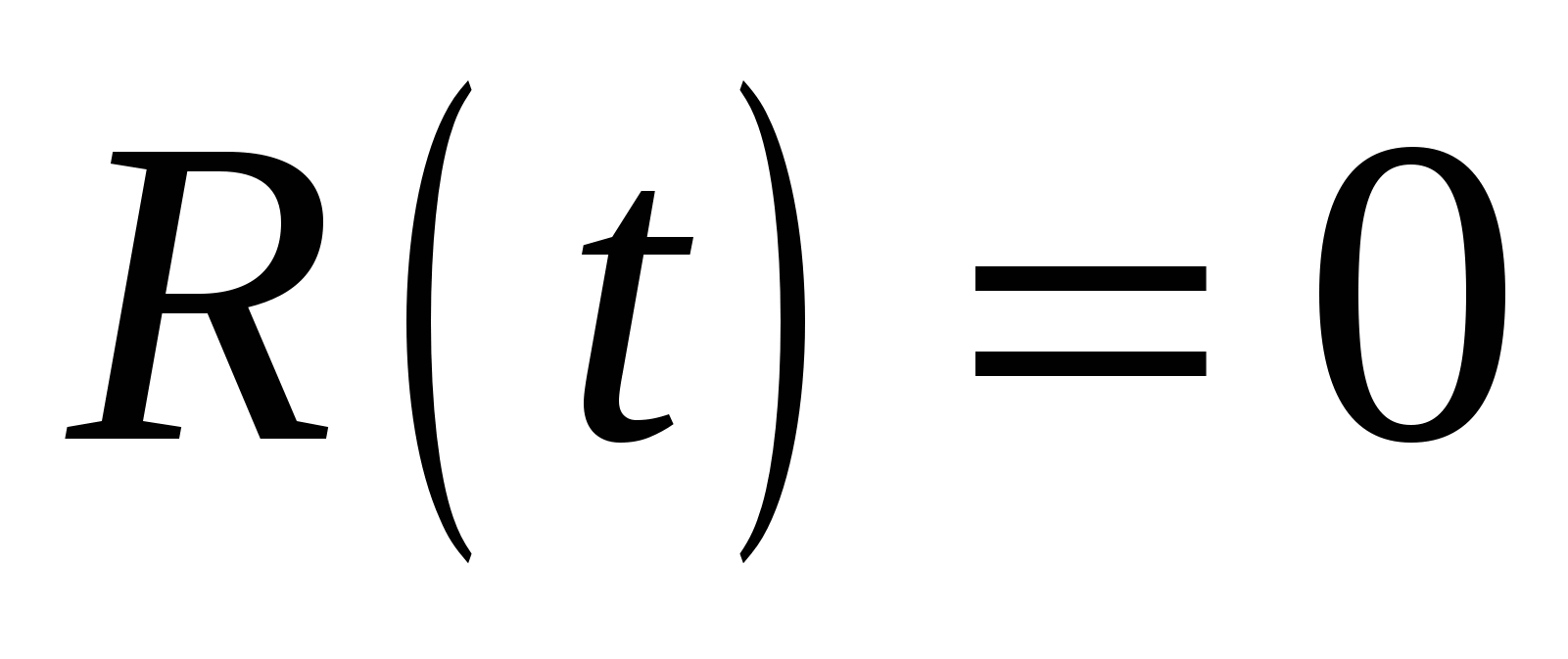 . .
Графическое изображение изменения зависимости 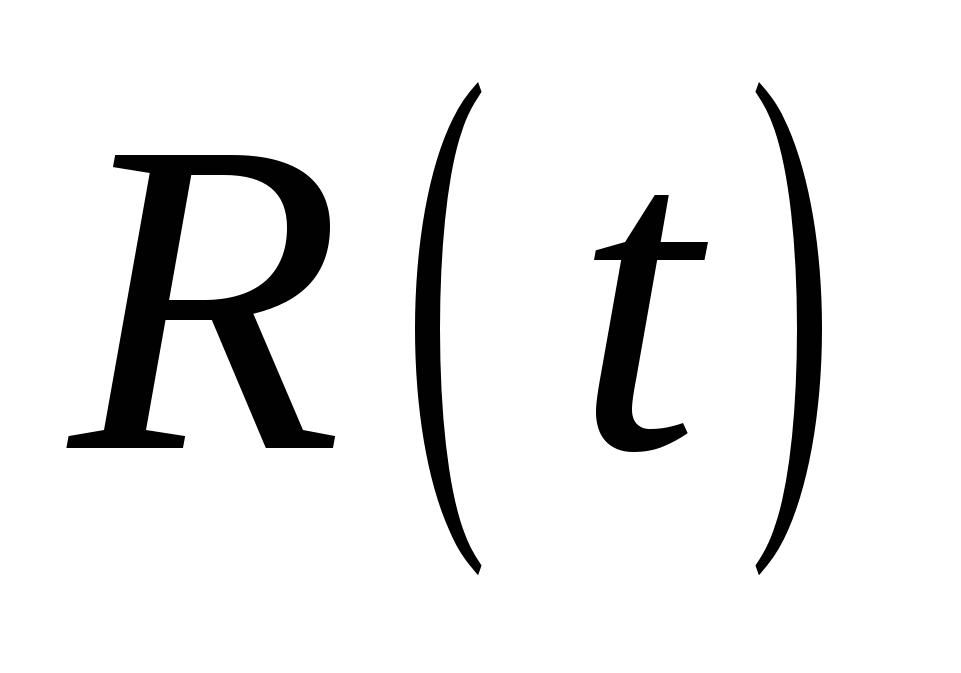 от времени представлено на рис. 2.2. от времени представлено на рис. 2.2.
Интегральная функция распределения 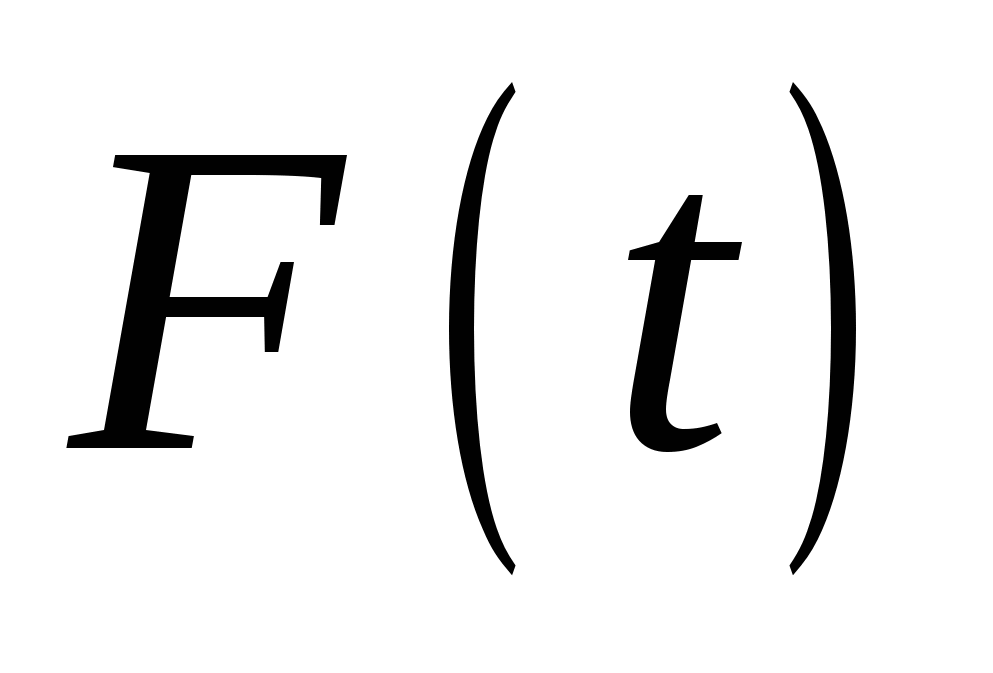 определяет вероятность отказа как вероятность того, что прибор откажет в течение заданного времени работы, будучи работоспособным в начальный момент времени и определяется выражением определяет вероятность отказа как вероятность того, что прибор откажет в течение заданного времени работы, будучи работоспособным в начальный момент времени и определяется выражением
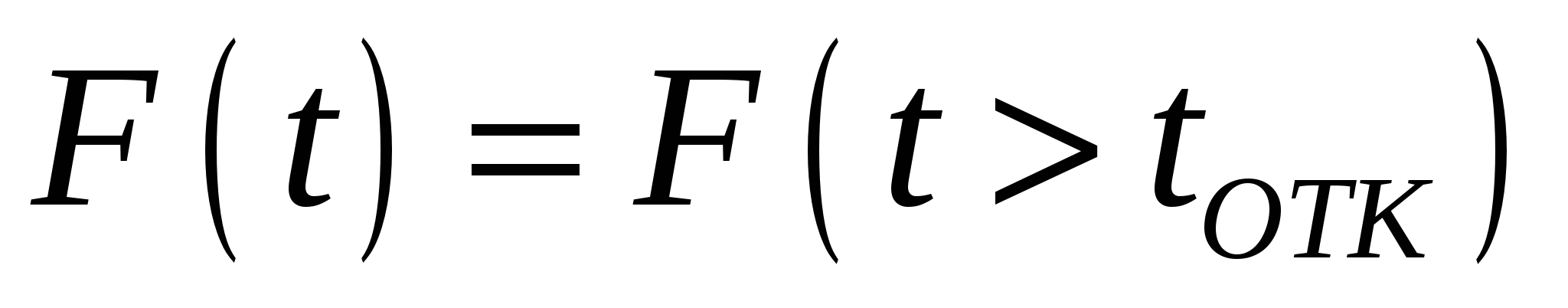 . (2.2) . (2.2)
Функция 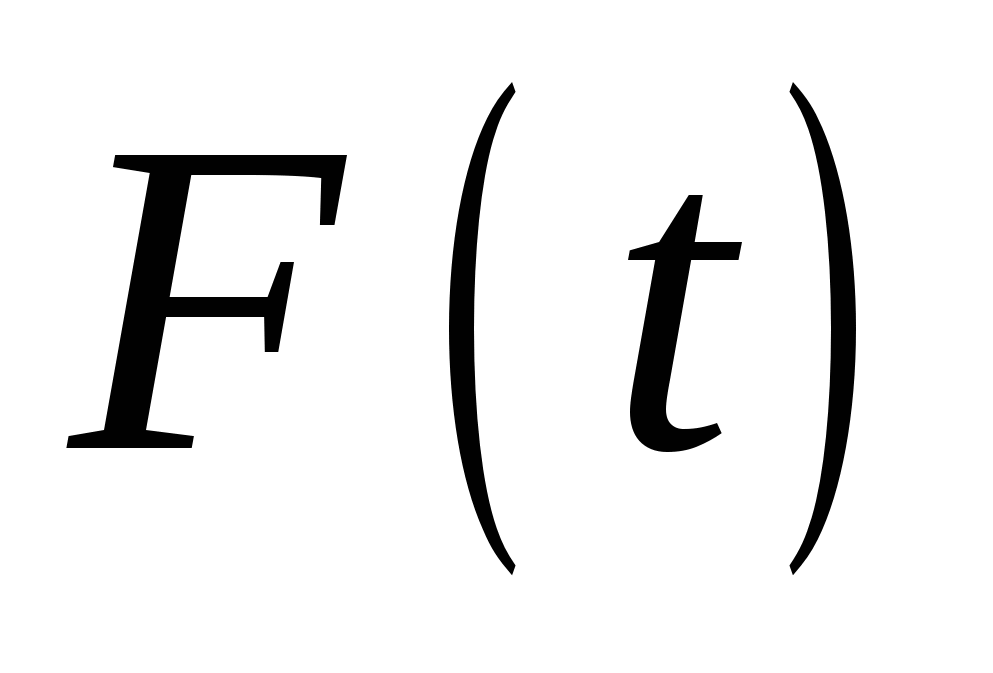 обладает следующими свойствами: обладает следующими свойствами:
-
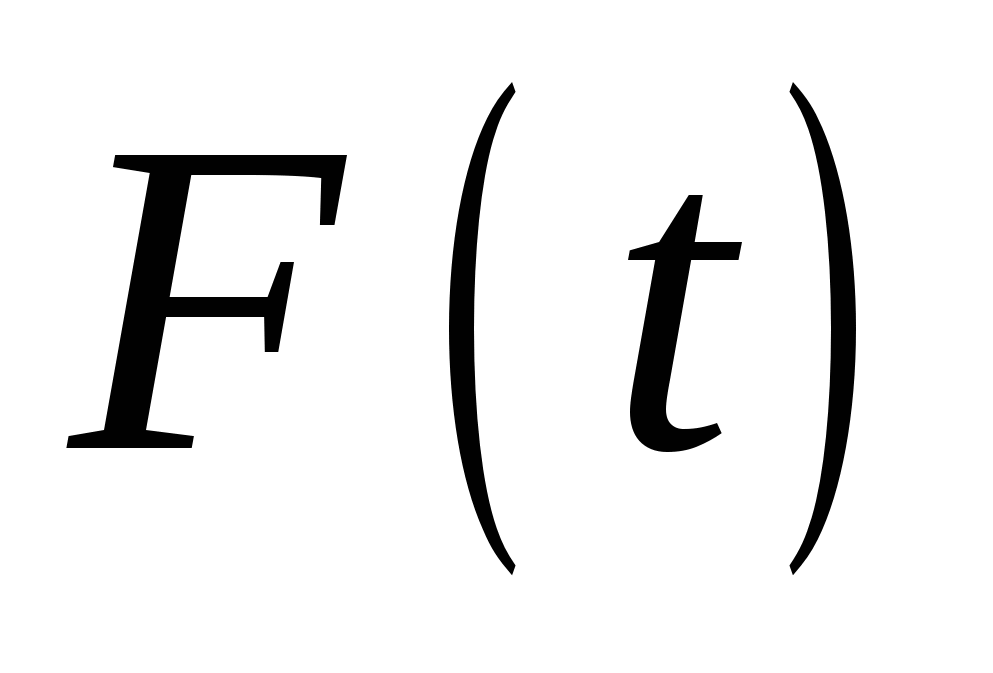  - монотонно неубывающая, т.е. при - монотонно неубывающая, т.е. при 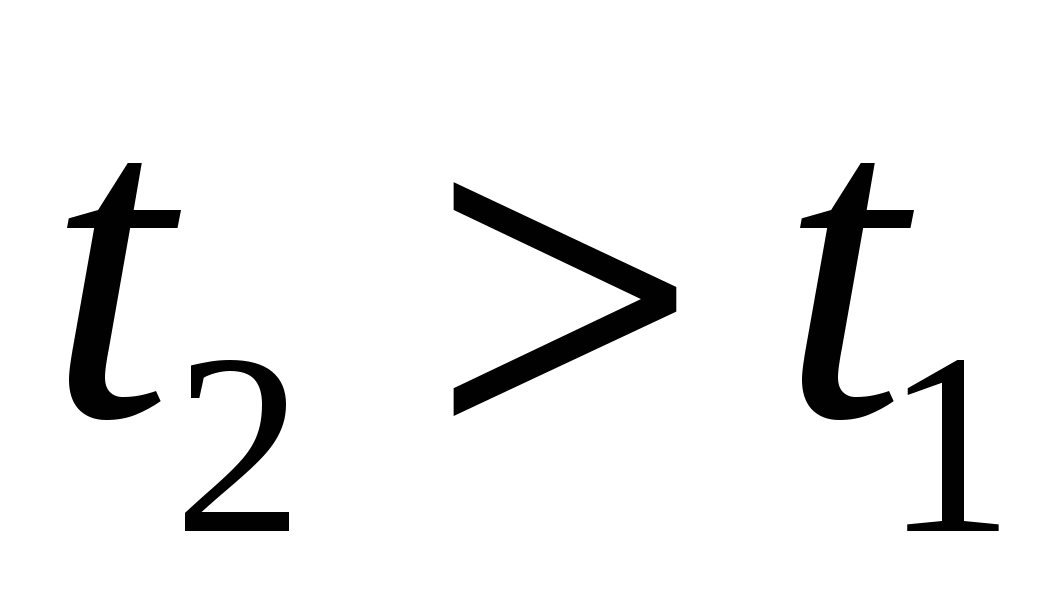 имеем имеем 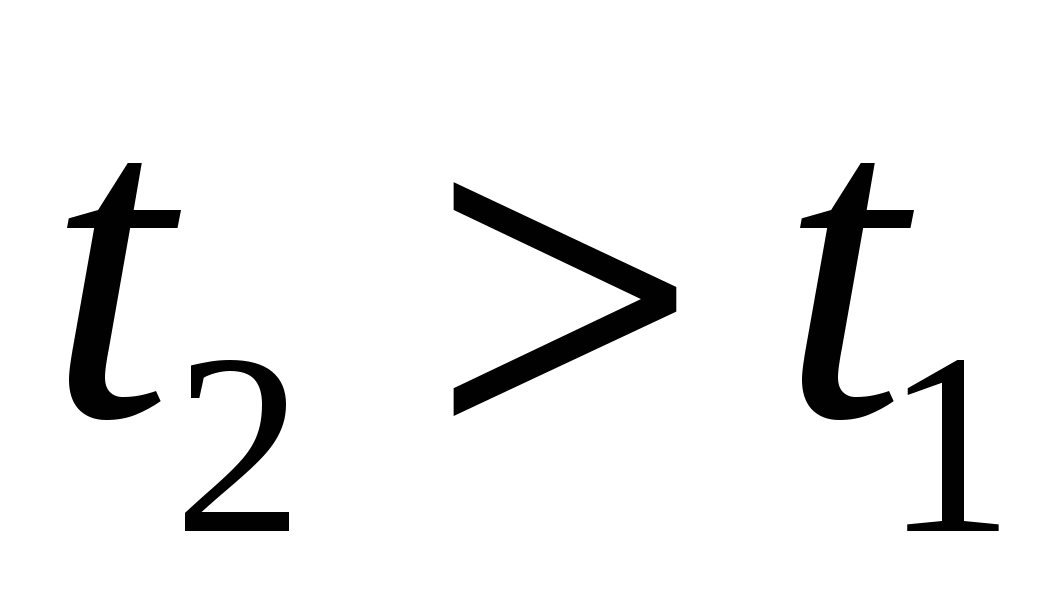 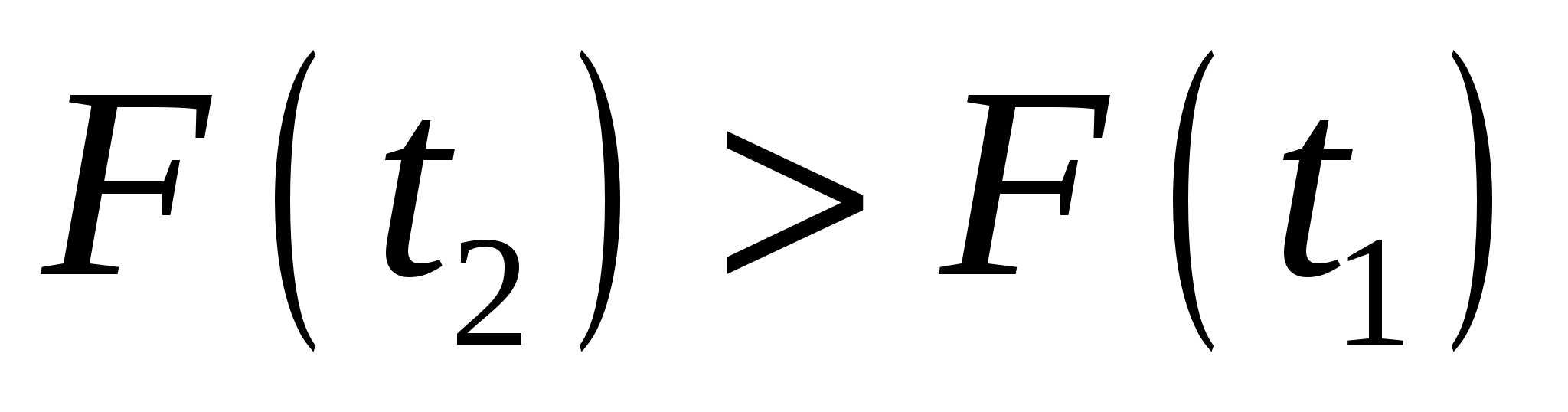 ; ;
-
Величина 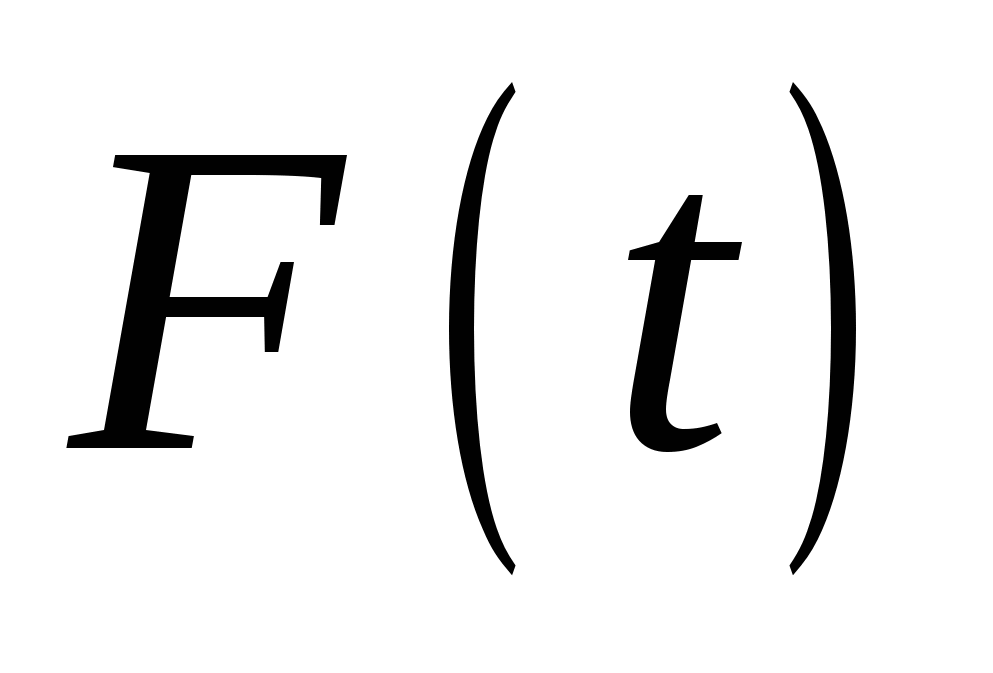 находится в пределах находится в пределах 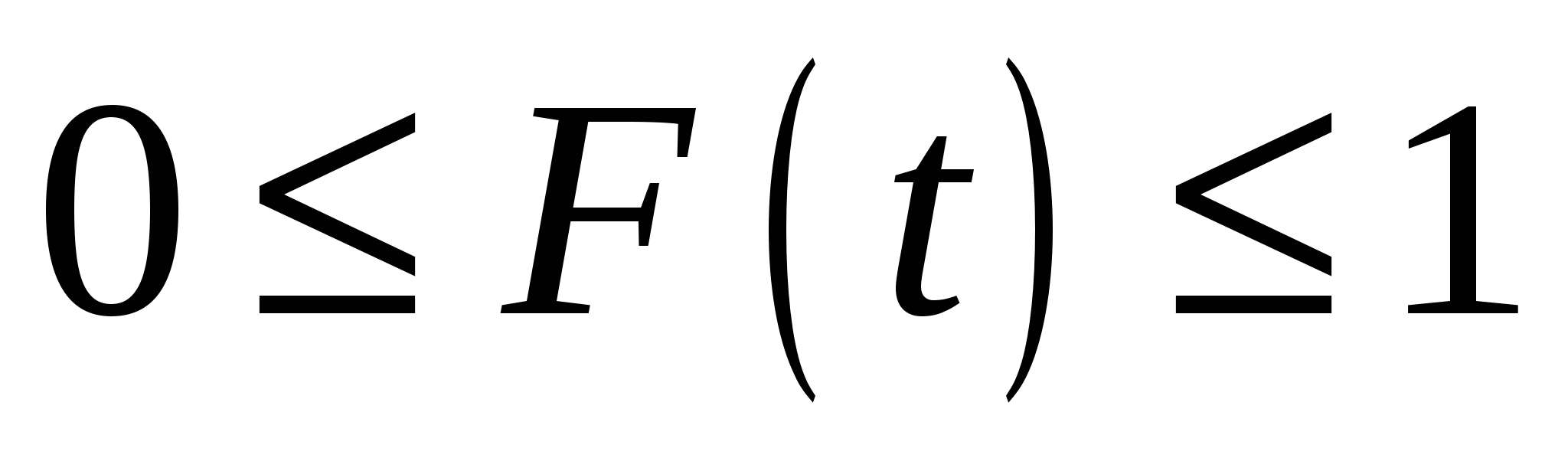 ; ;
-
При 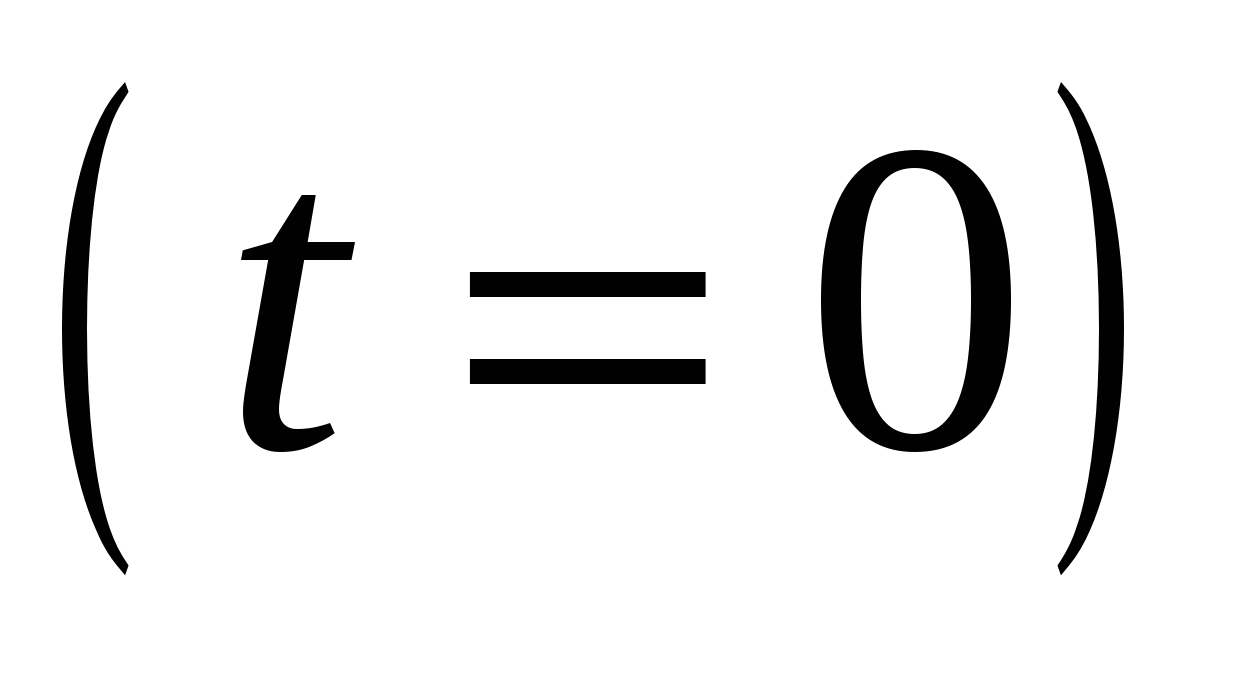 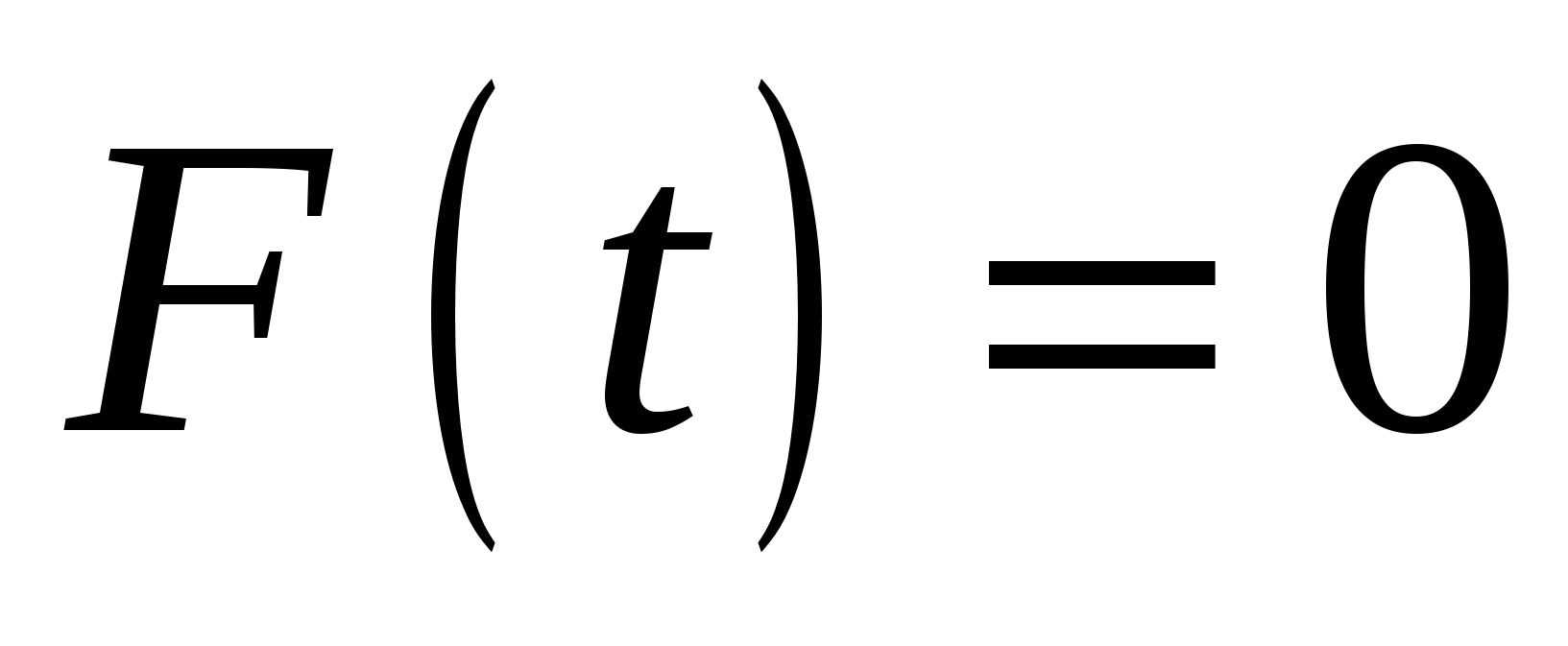 и и
при 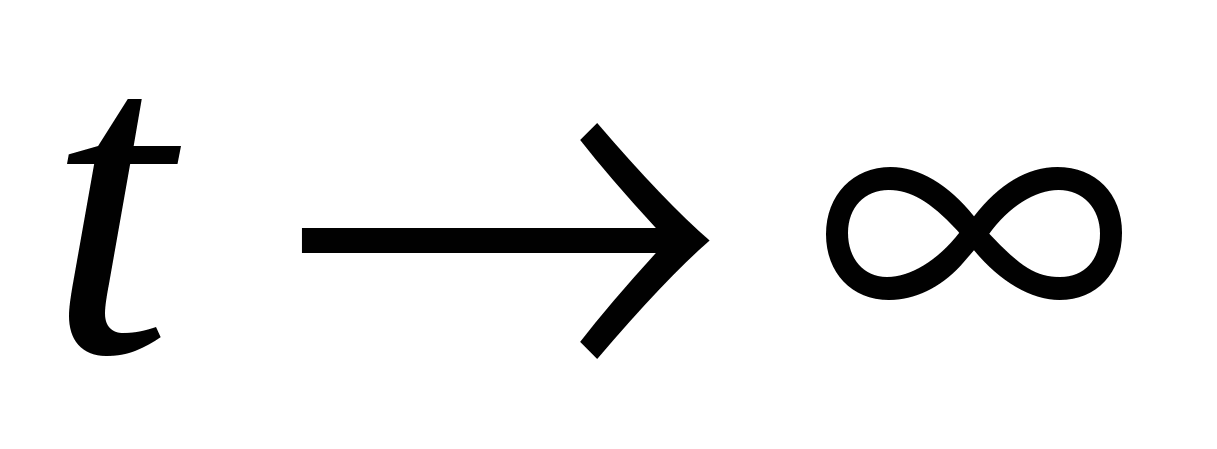 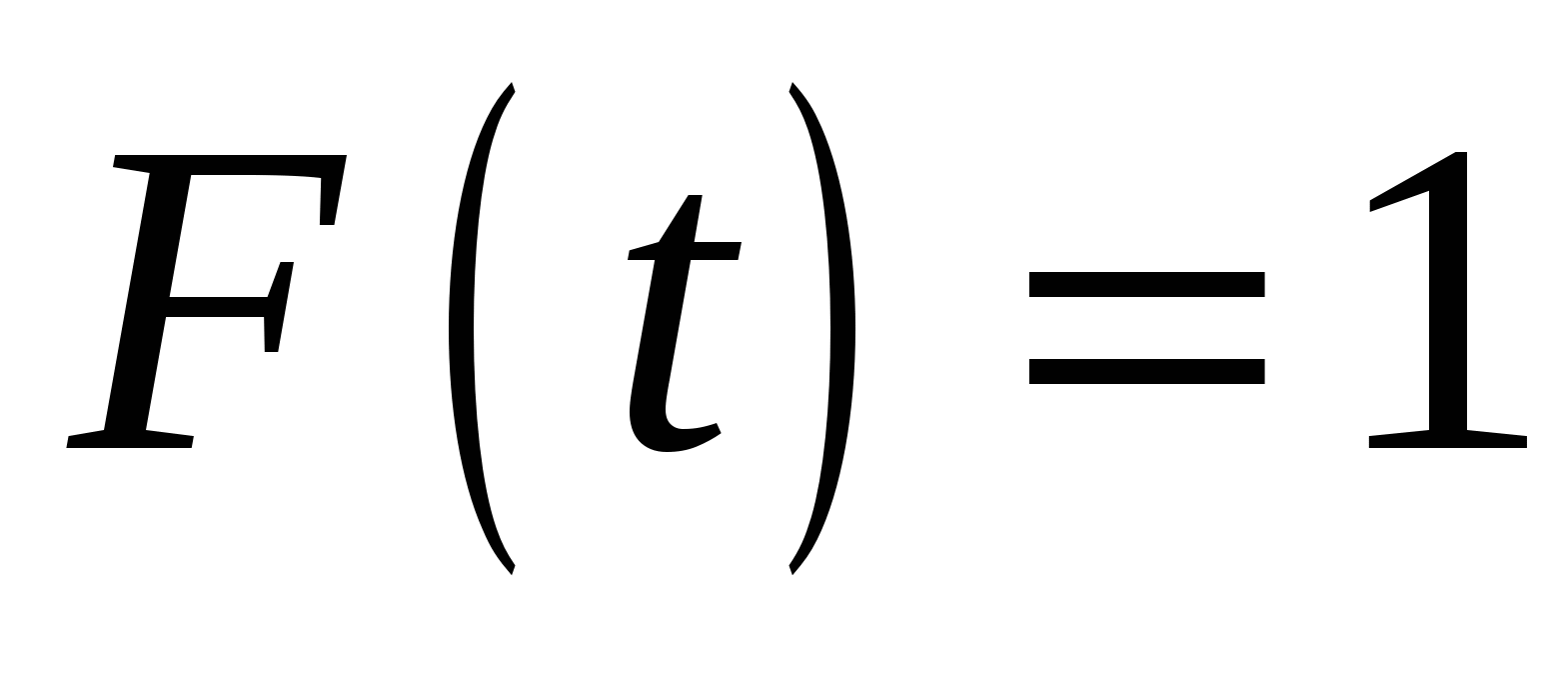 . .
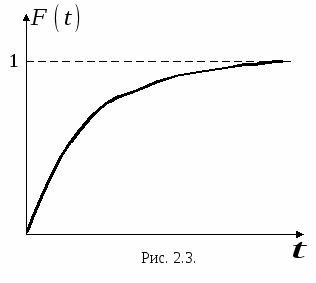
Графически изображение функции 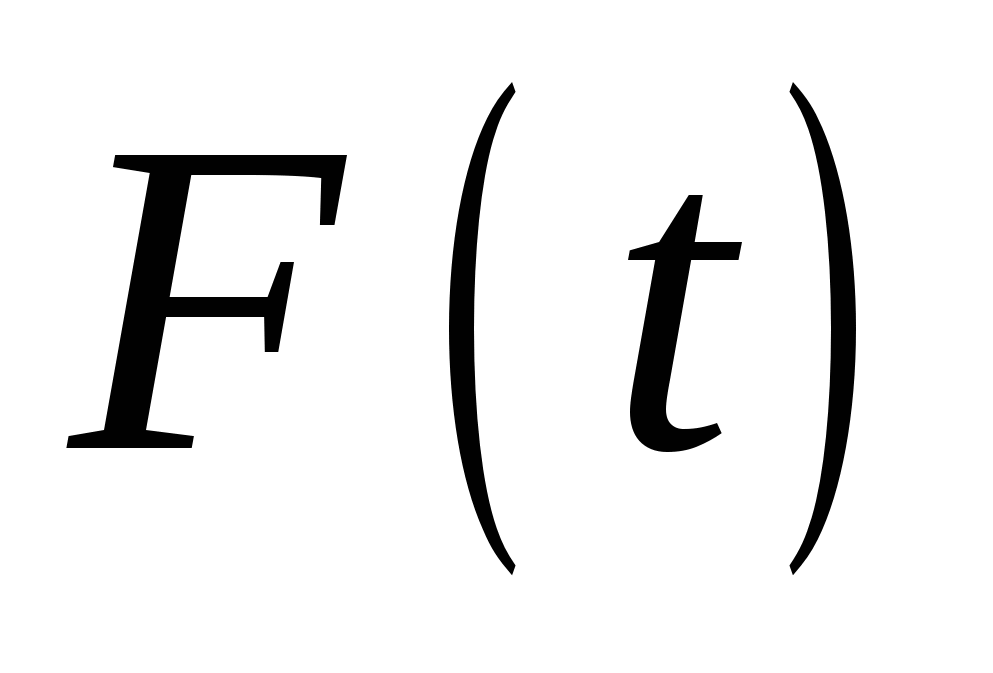 от времени представлено на рис. 2.3. Поскольку изделие может быть либо исправно либо неисправно (отказ) то можем записать от времени представлено на рис. 2.3. Поскольку изделие может быть либо исправно либо неисправно (отказ) то можем записать
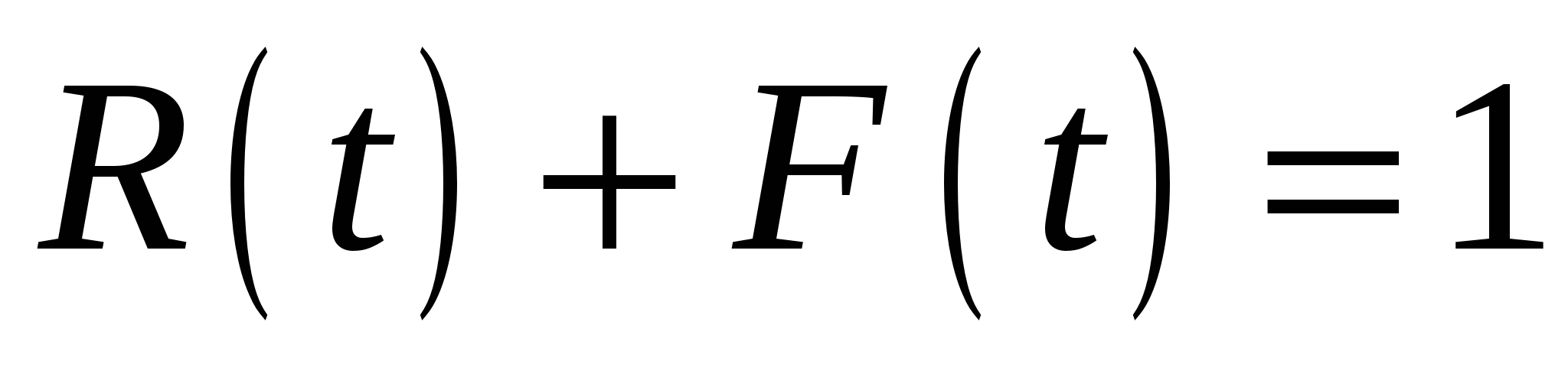 . (2.3) . (2.3)
Кроме интегральных характеристик, которыми являются функции 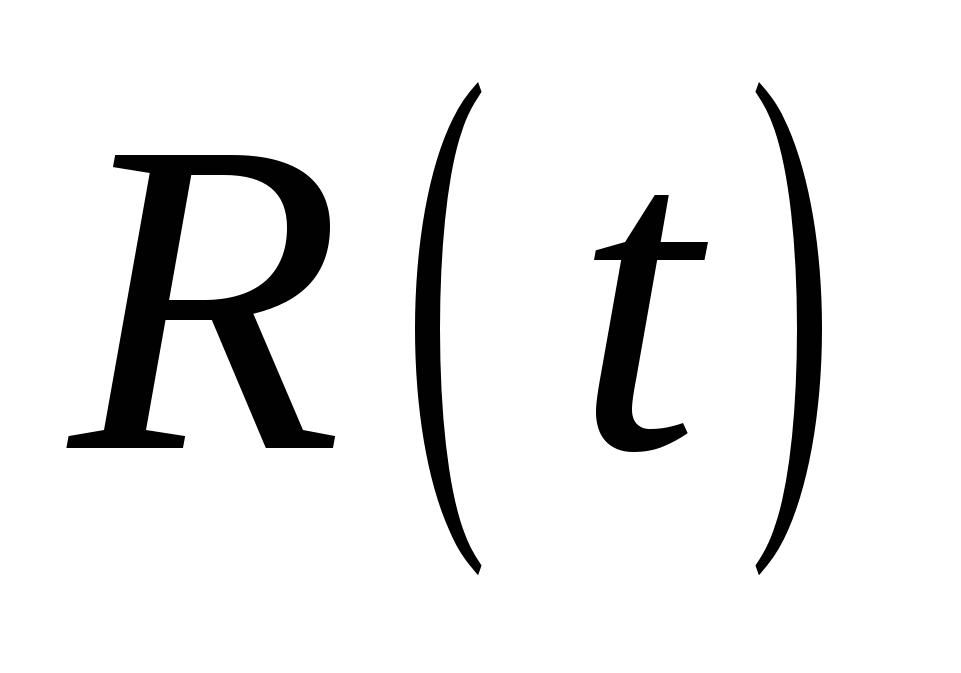 и и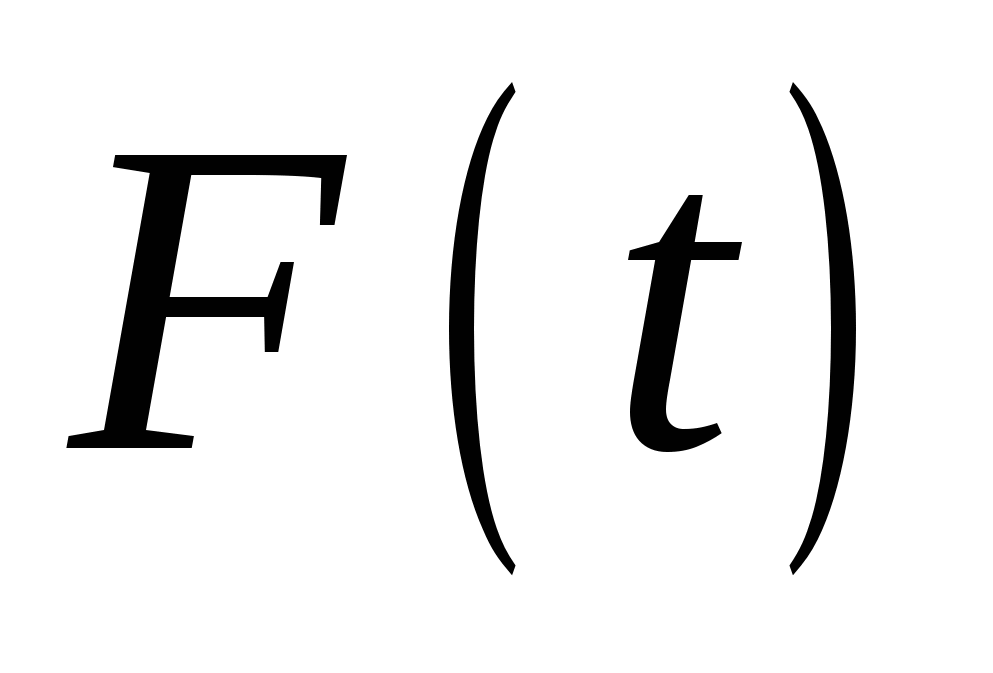 , для описания мгновенных значений показателей надежности и вероятности отказа дополнительно вводятся дифференциальные функции. Функция плотности распределения наработки до отказа , для описания мгновенных значений показателей надежности и вероятности отказа дополнительно вводятся дифференциальные функции. Функция плотности распределения наработки до отказа 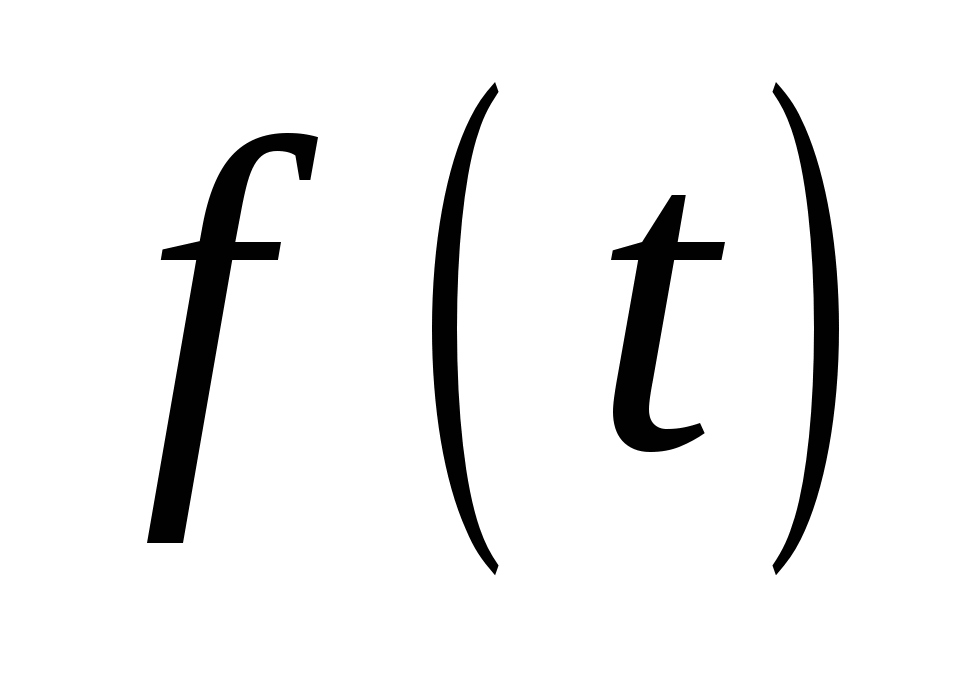 определяется выражением определяется выражением
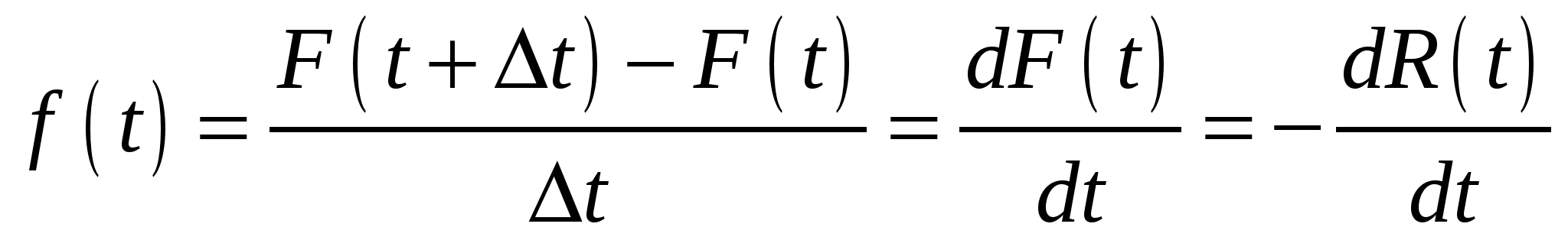 . (2.4) . (2.4)
Другой дифференциальной характеристикой является интенсивность отказов 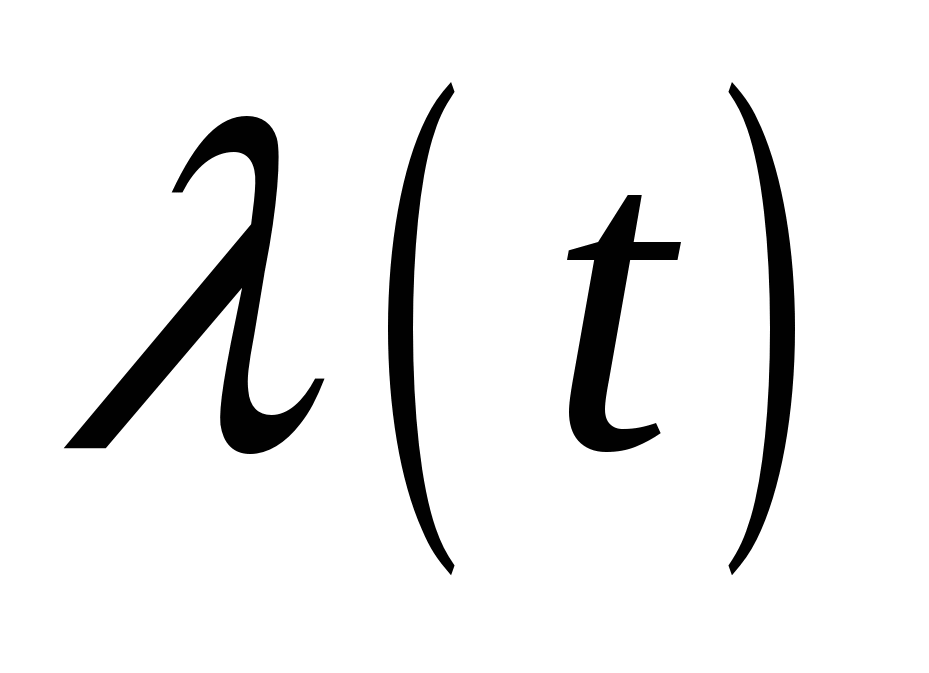 . Под ней понимается условная плотность вероятности возникновения отказа прибора, определяемая для рассматриваемого момента времени при условии, что до этого момента времени отказ не возникал. В соответствии с определением, интенсивность отказов есть отношение плотности вероятности наработки до отказа к вероятности безотказной работы приборов . Под ней понимается условная плотность вероятности возникновения отказа прибора, определяемая для рассматриваемого момента времени при условии, что до этого момента времени отказ не возникал. В соответствии с определением, интенсивность отказов есть отношение плотности вероятности наработки до отказа к вероятности безотказной работы приборов
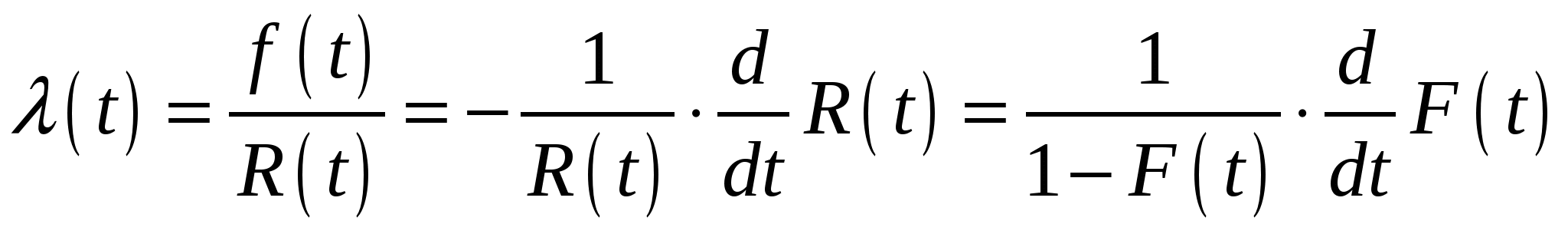 . (2.5) . (2.5)
При статистическом подходе вероятность безотказной работы определяется как
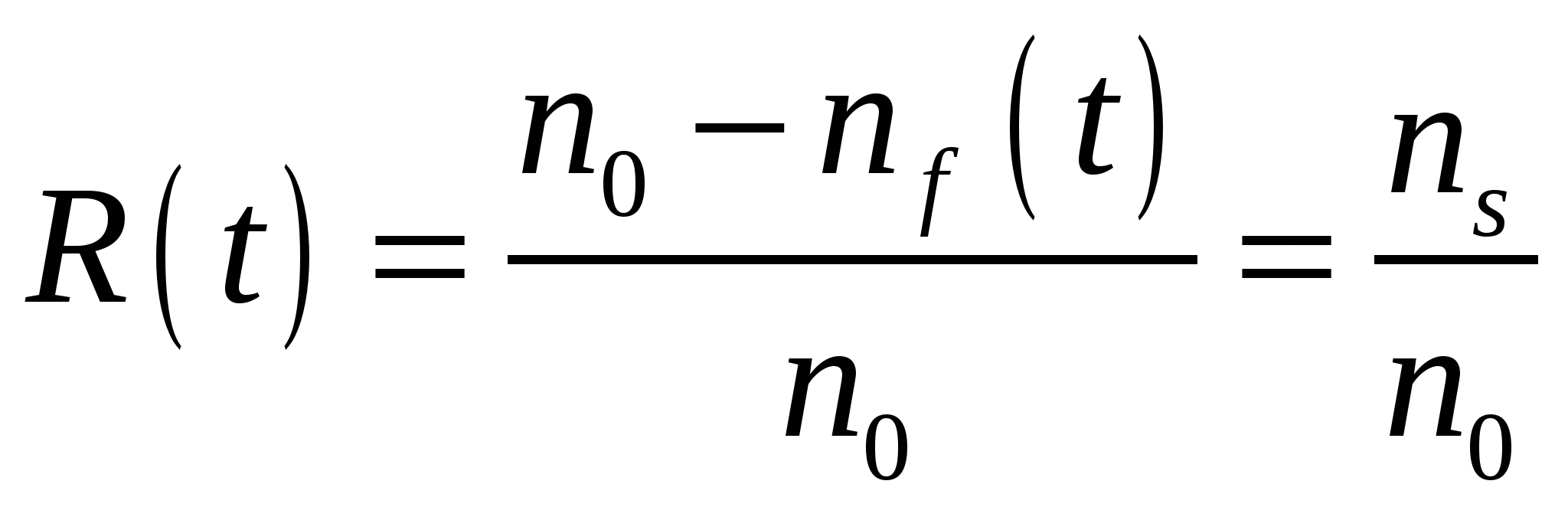 , (2.6) , (2.6)
где 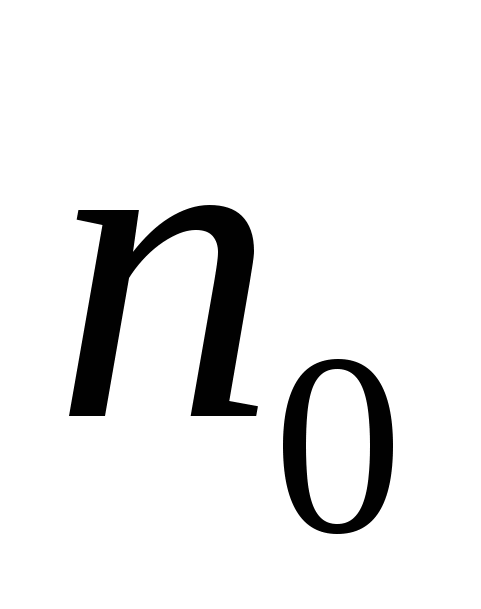 - число элементов, работоспособных в начальный момент времени, - число элементов, работоспособных в начальный момент времени, 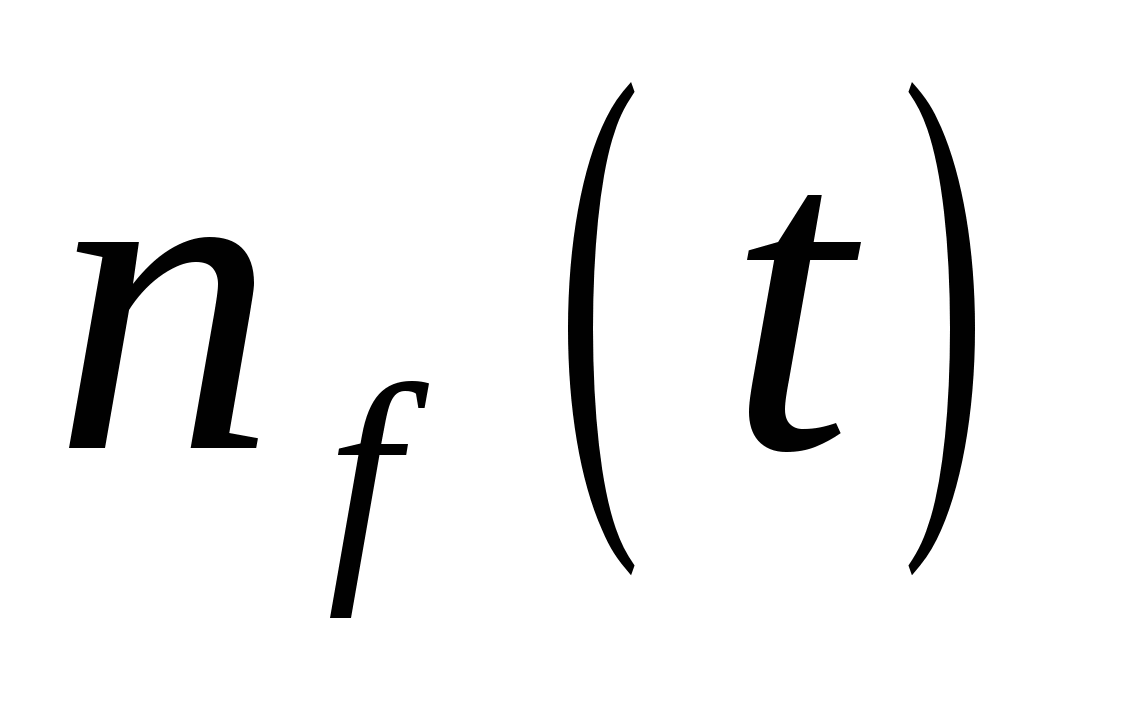 - число отказавших элементов к моменту времени - число отказавших элементов к моменту времени 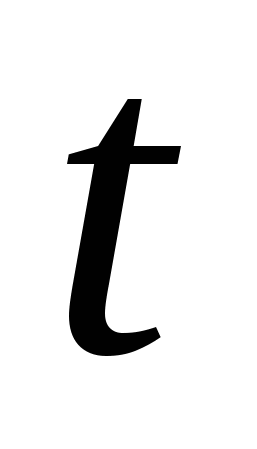 , , 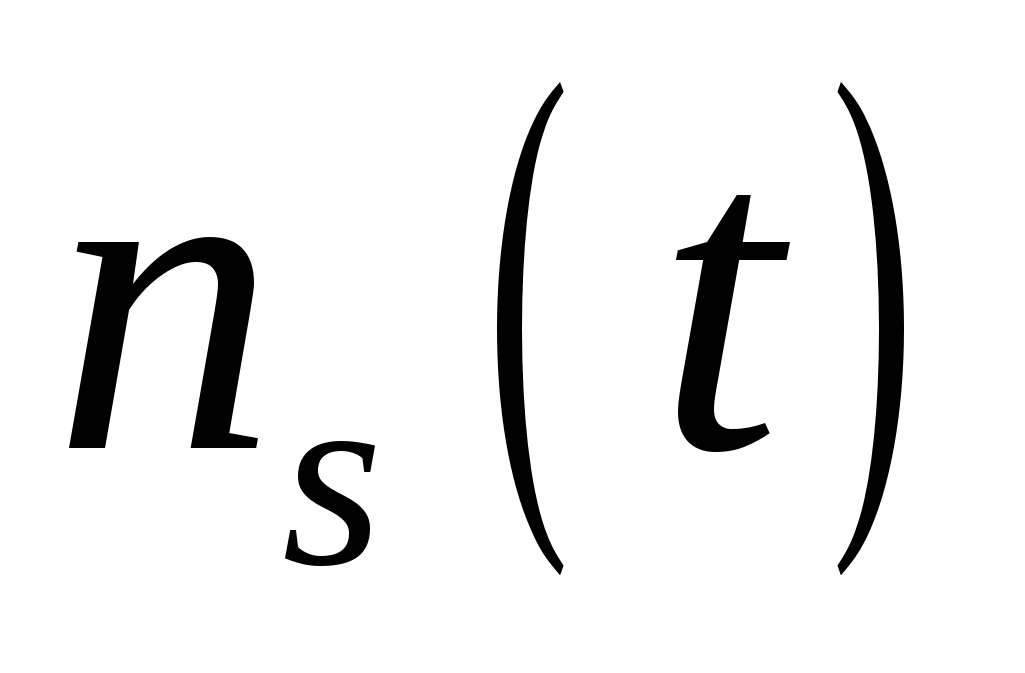 - число исправных элементов к моменту времени - число исправных элементов к моменту времени 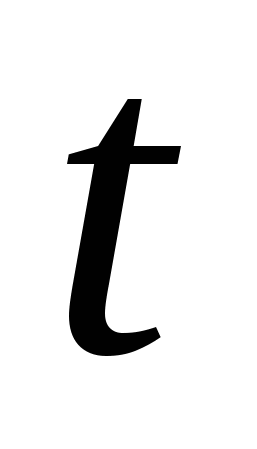 . .
Тогда для вероятности отказа можем записать:
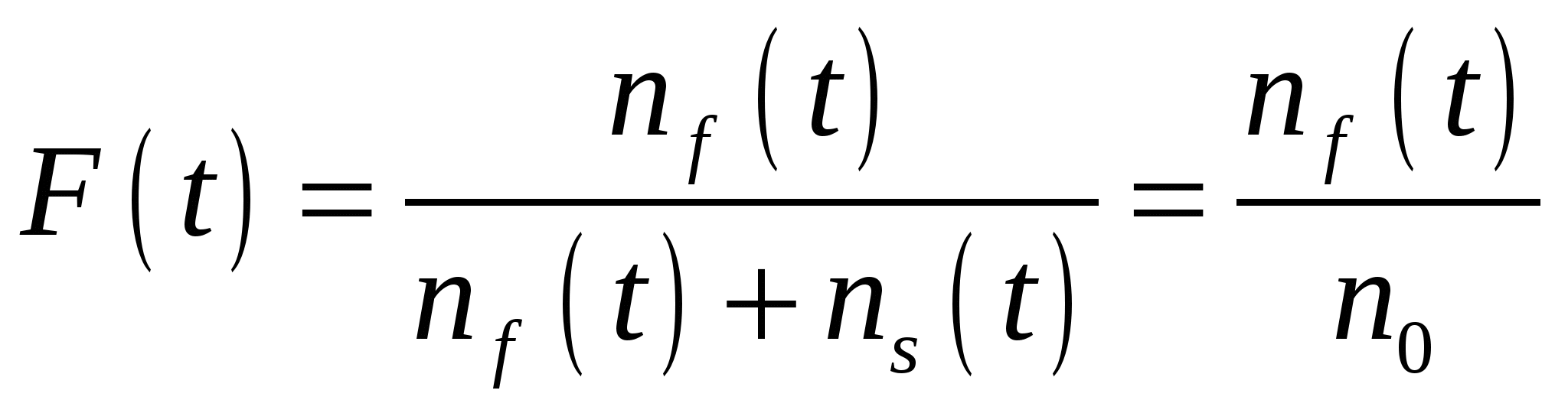 . (2.7) . (2.7)
Дифференциальная характеристика плотности распределения наработки до отказа определяется как
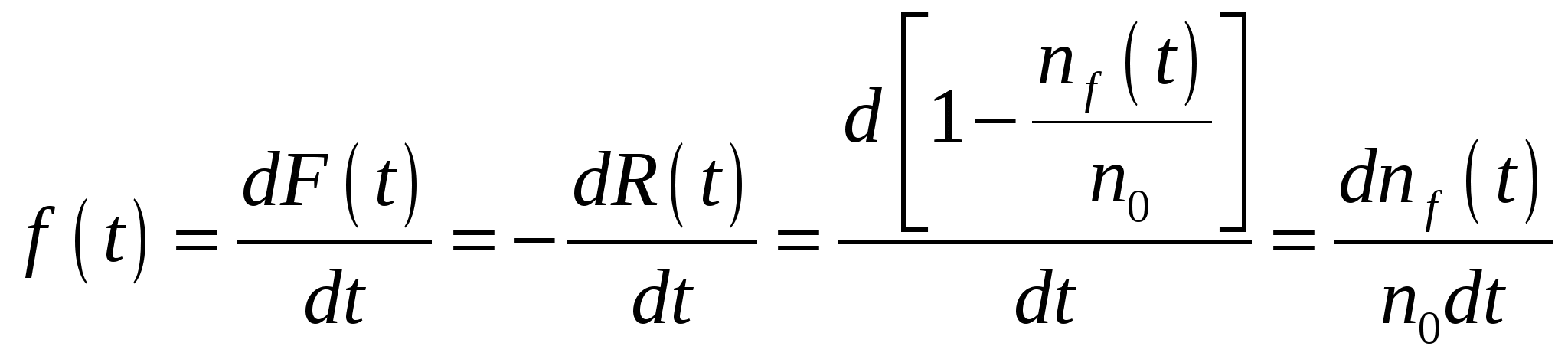 , (2.8) , (2.8)
а интенсивность отказов в этом случае равна
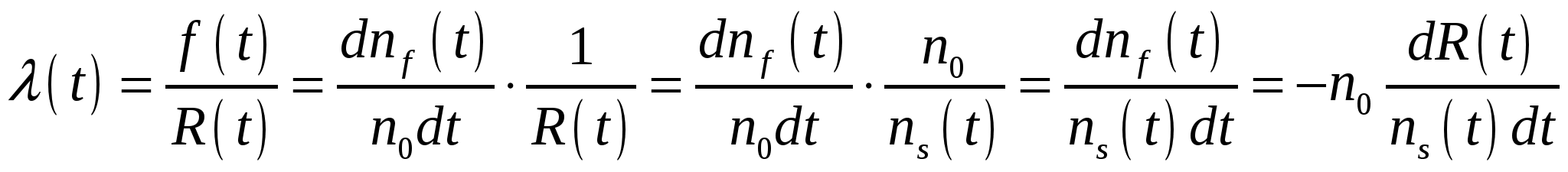 . (2.9) . (2.9)
Выведем зависимость 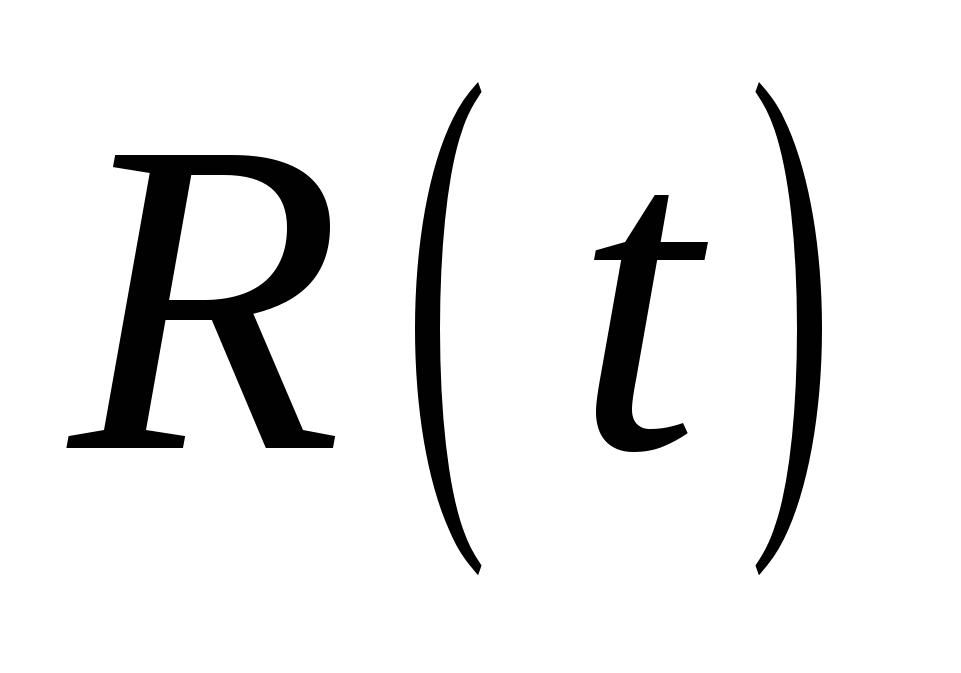 от от 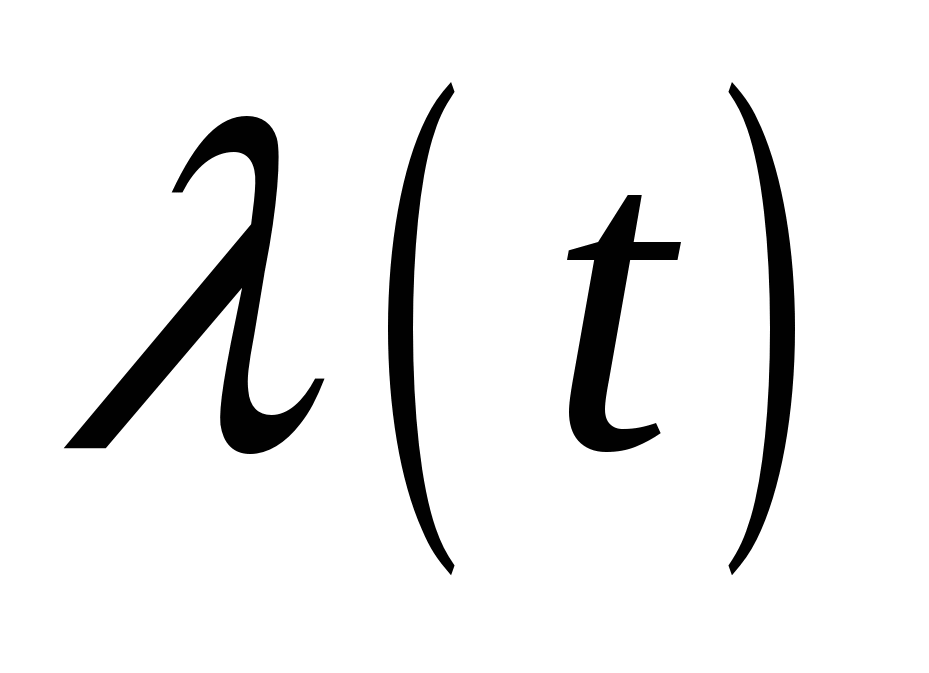 . Из выражения (2.9) можем записать . Из выражения (2.9) можем записать
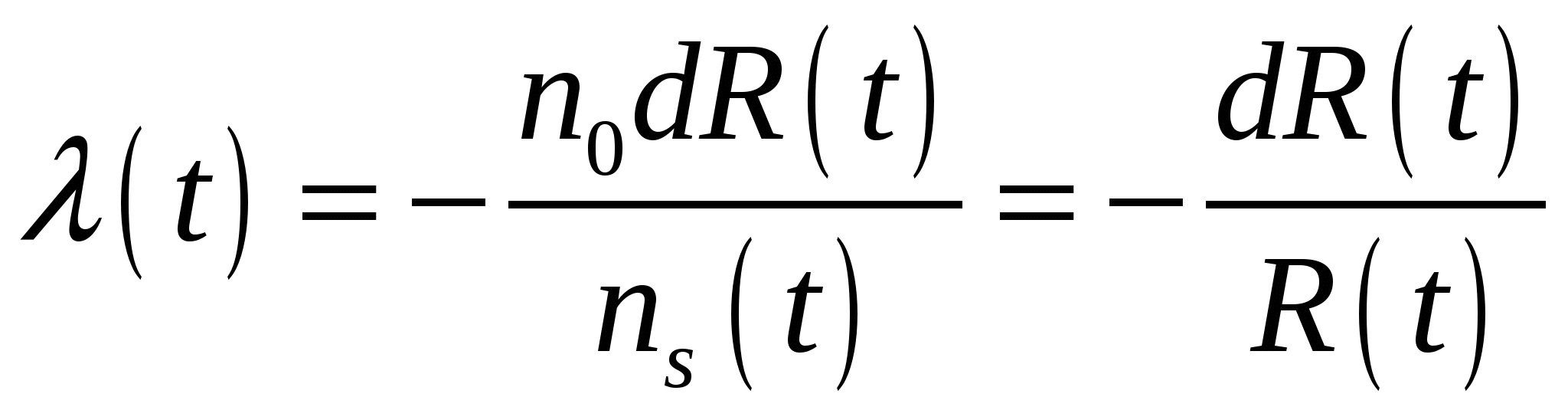 . (2.10) . (2.10)
Используя (2.10) и проинтегрировав ее в пределах от 0 до t, получим
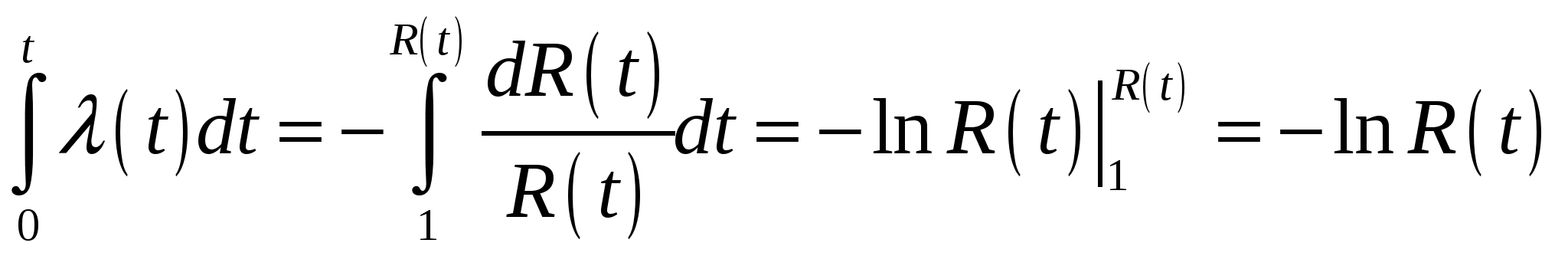 , (2.11) , (2.11)
и окончательно для 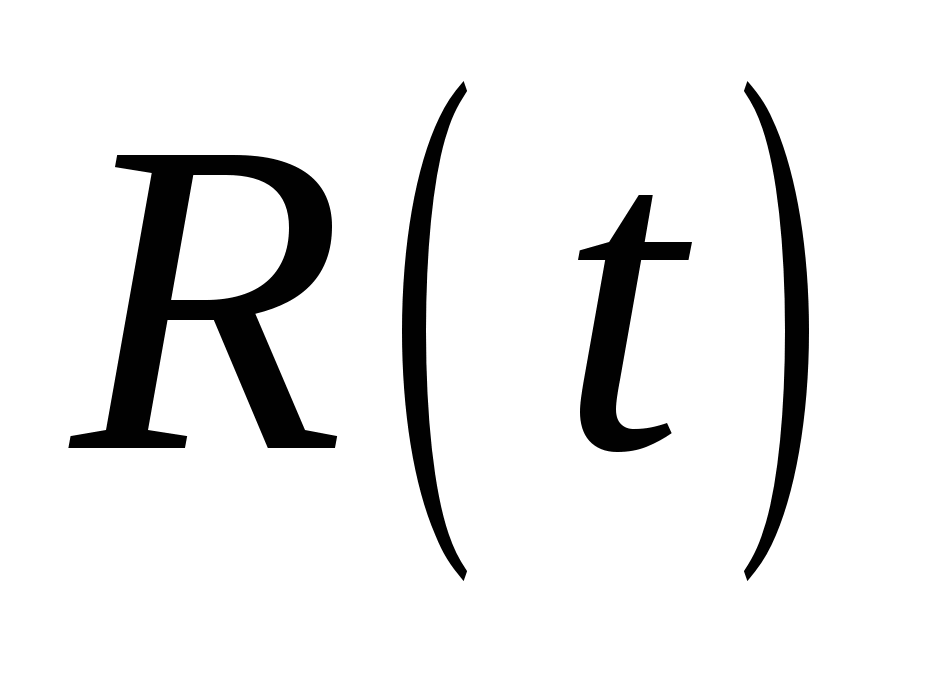 имеем имеем
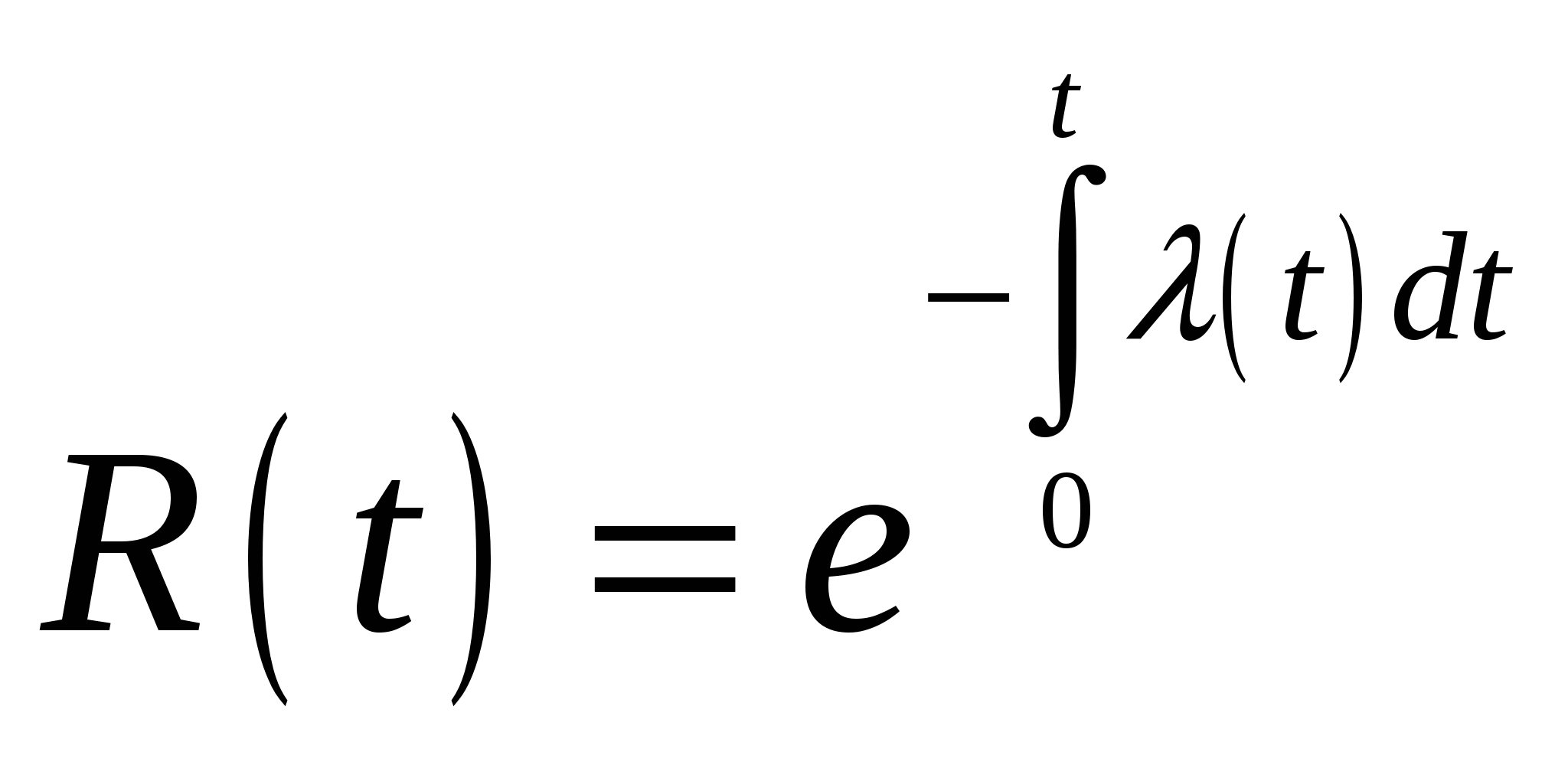 . (2.12) . (2.12)
Из соотношения (2.12) получим
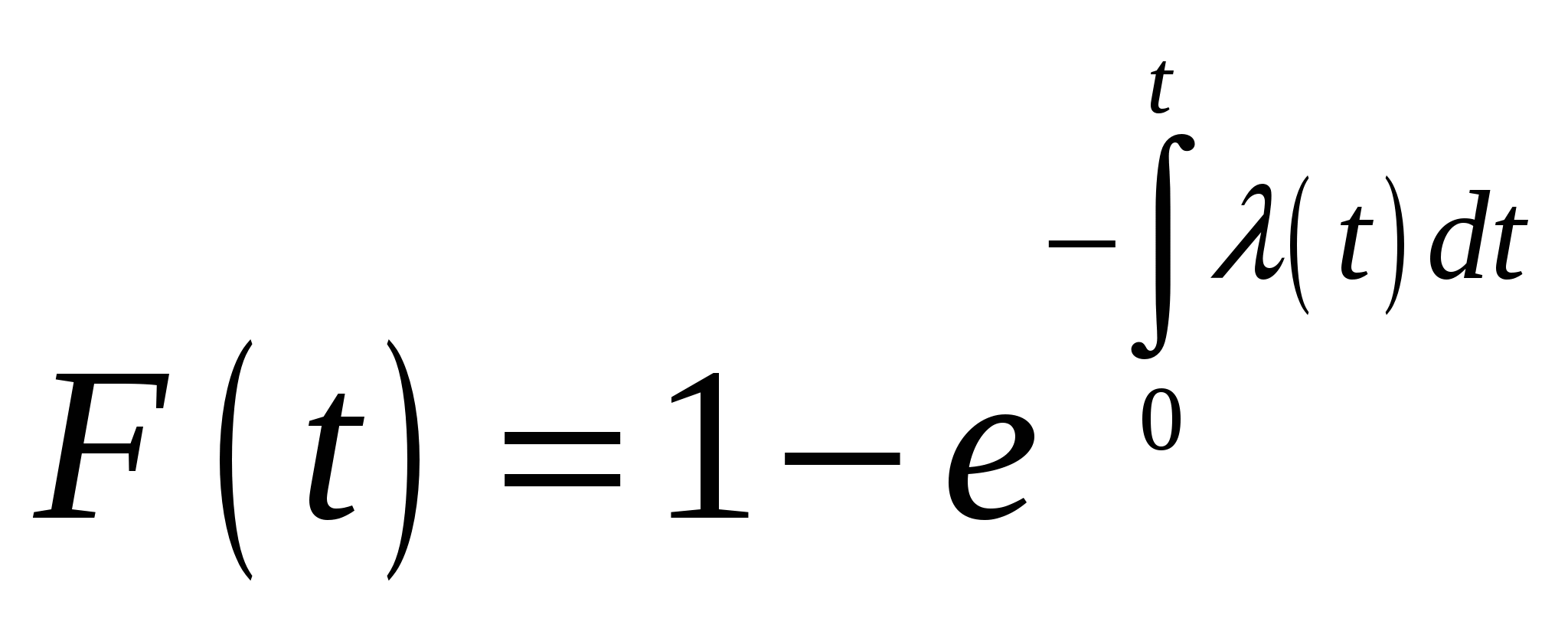 (2.13) (2.13)
и тогда
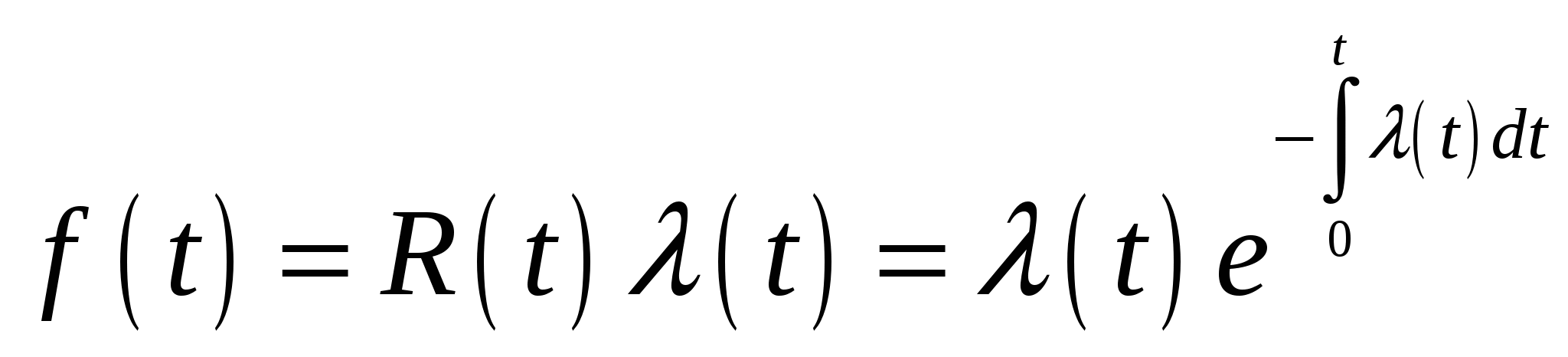 . (2.14) . (2.14)
Взаимосвязь между величинами 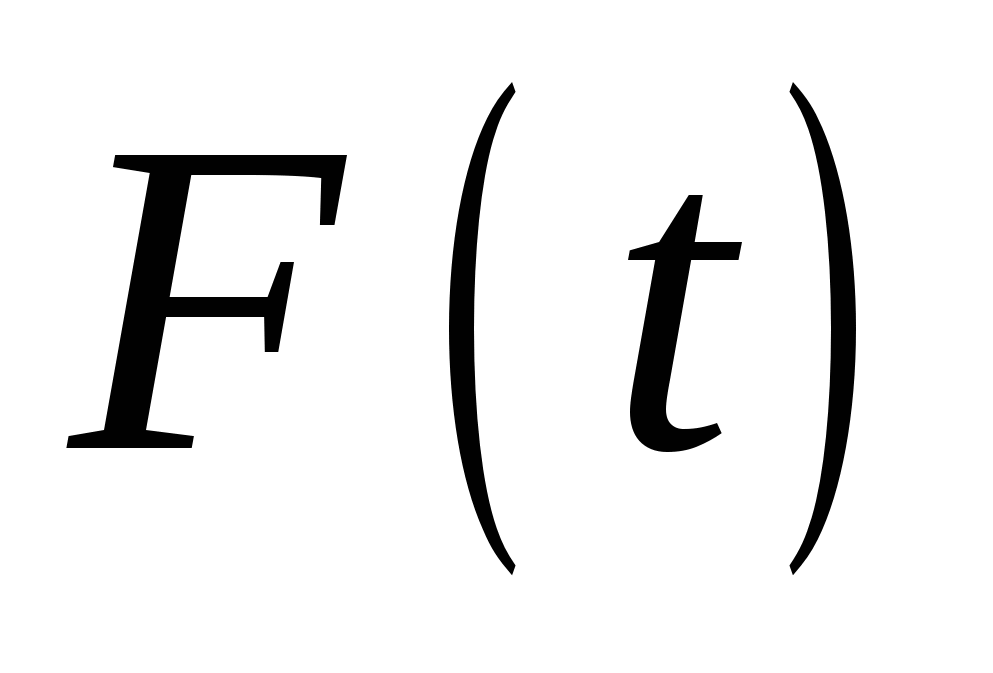 , , 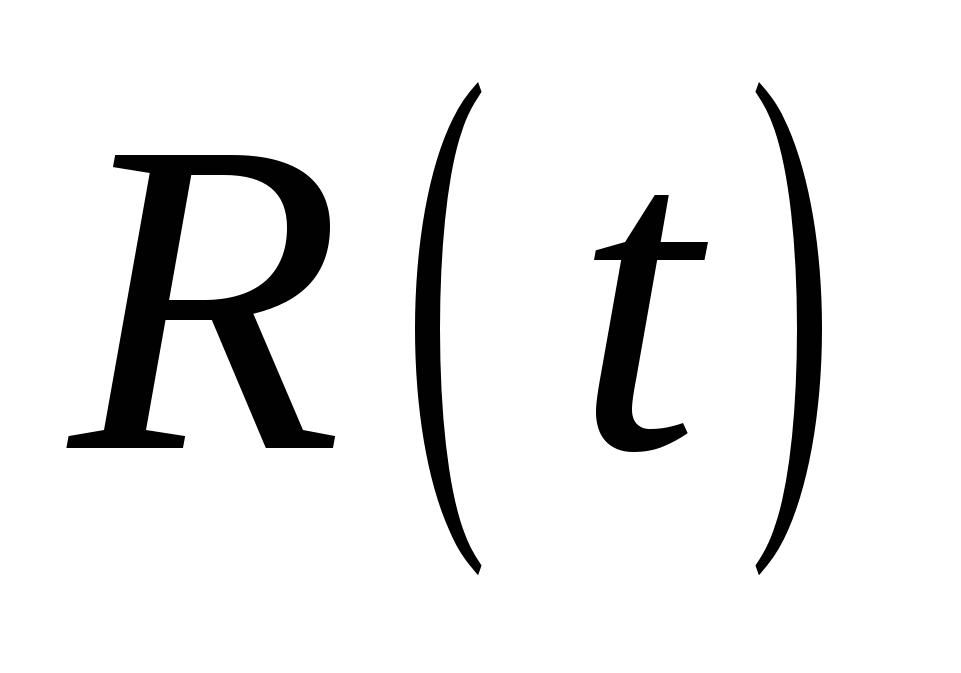 , , 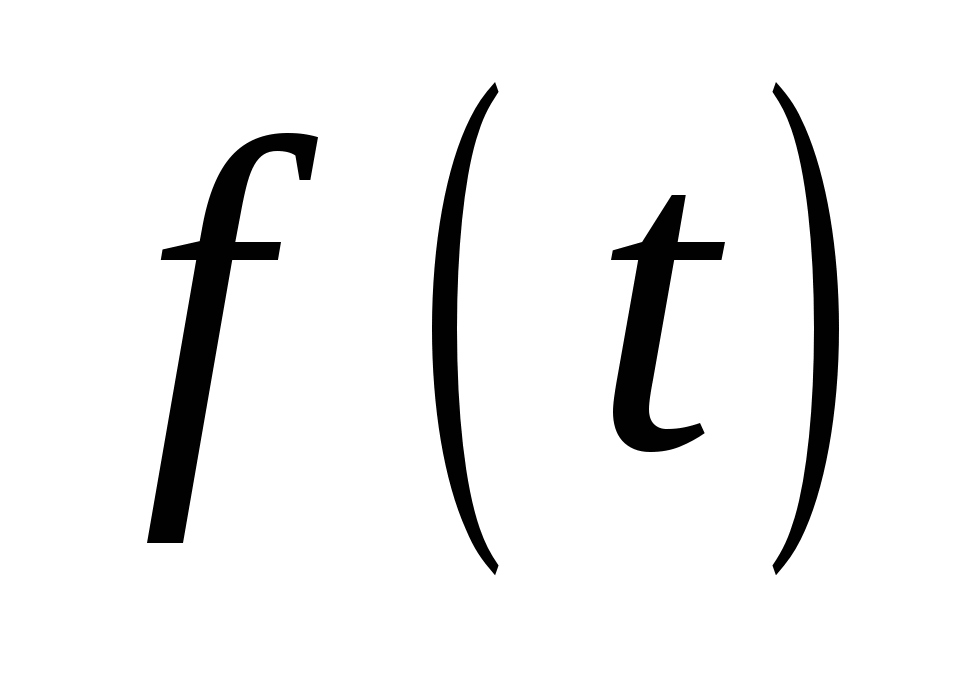 и и 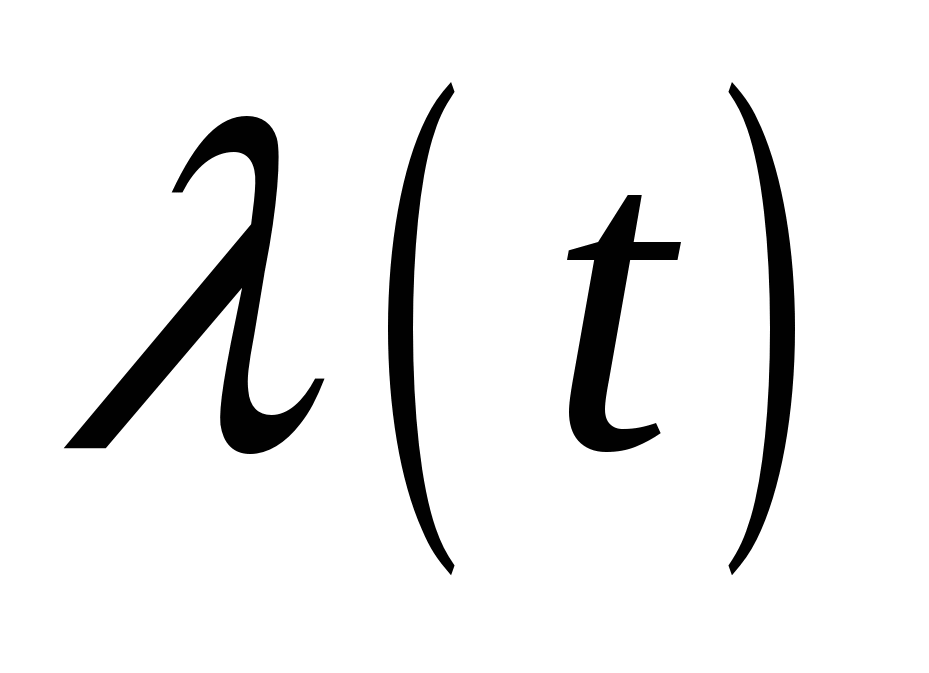 приведена в табл. 2.1. приведена в табл. 2.1.
Таблица 2.1.
Необходимо заметить, что интенсивность отказов как показатель безотказности применима только в случае невосстанавливаемых объектов, к которым и относятся полупроводниковые приборы и ИМС. Безотказность различной радиоэлектронной аппаратуры, в подавляющем большинстве своем относится к восстанавливаемым объектам и характеризуется потоком отказов. Поток отказов представляет собой отношение среднего числа отказов за произвольно малую его наработку к значению этой наработки.
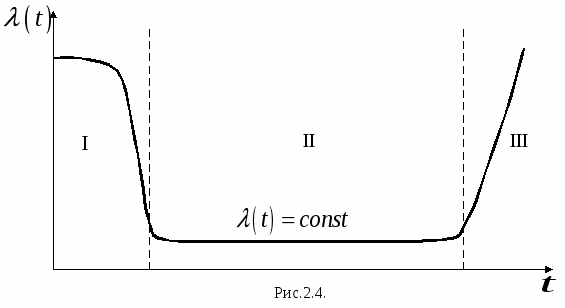
Исследования долговечности большого количества различных изделий (в том числе полупроводниковых приборов и ИМС) позволили определить общую зависимость интенсивности отказов от времени, которая приведена на рис. 2.4. В начальный период времени (I) интенсивность может значительно изменяться, так как эти отказы в основном обусловлены различными производственными дефектами, и они выявляются в процессе испытаний или специальной тренировки. Во второй период времени (II) интенсивность отказов практически постоянна и обусловлена случайными отказами. Это наиболее значительный временной период и он характеризует полезный срок работы изделия. Последний период (III) характеризует отказы, вызванные износом при длительной эксплуатации и, как видим из рисунка, интенсивность отказов в данный промежуток времени значительно возрастает.
Среднее время безотказной работы изделия (средняя наработка до отказа), т.е. математическое ожидание наработки до первого отказа, рассчитывается по формуле
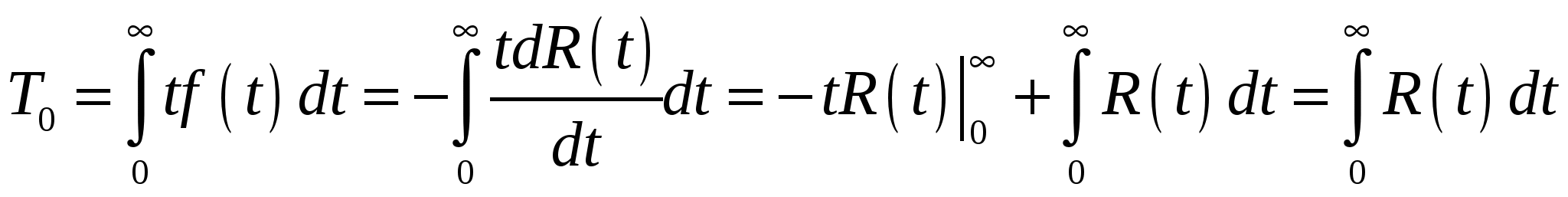 . (2.15) . (2.15)
Одним из показателей безотказности является гамма-процентная наработка до отказа
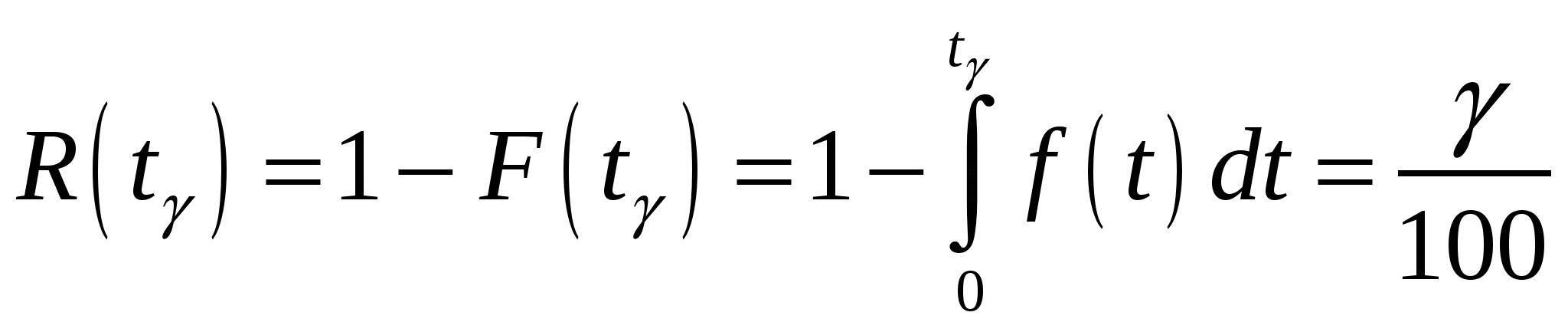 , (2.16) , (2.16)
определяемая как наработка, в течение которой отказ прибора не возникнет с вероятностью 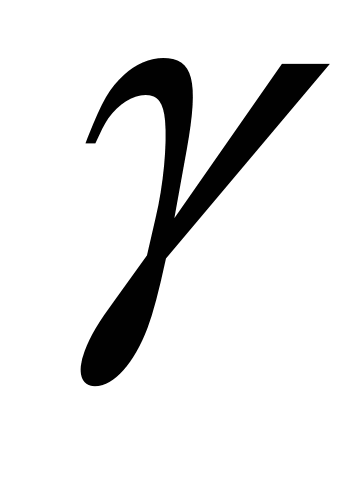 , выраженной в процентах. , выраженной в процентах.
Контрольные вопросы -
Как графически изобразить отказ изделия?
-
Какой смысл понятия вероятность безотказной работы?
-
Какой смысл понятия вероятность отказа?
-
Какими свойствами обладает функция 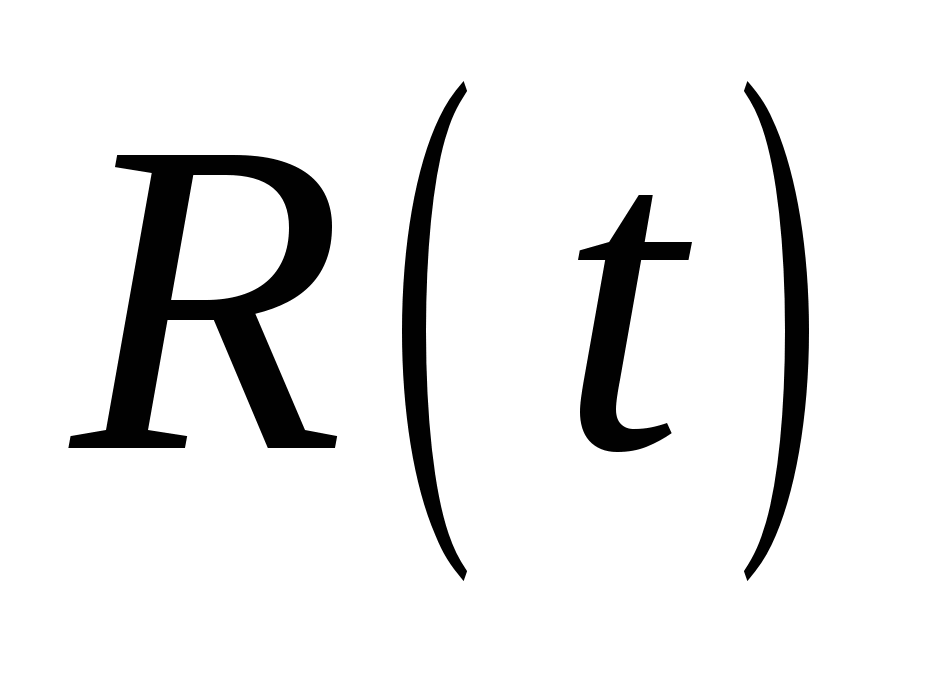 ? ?
-
Какими свойствами обладает функция 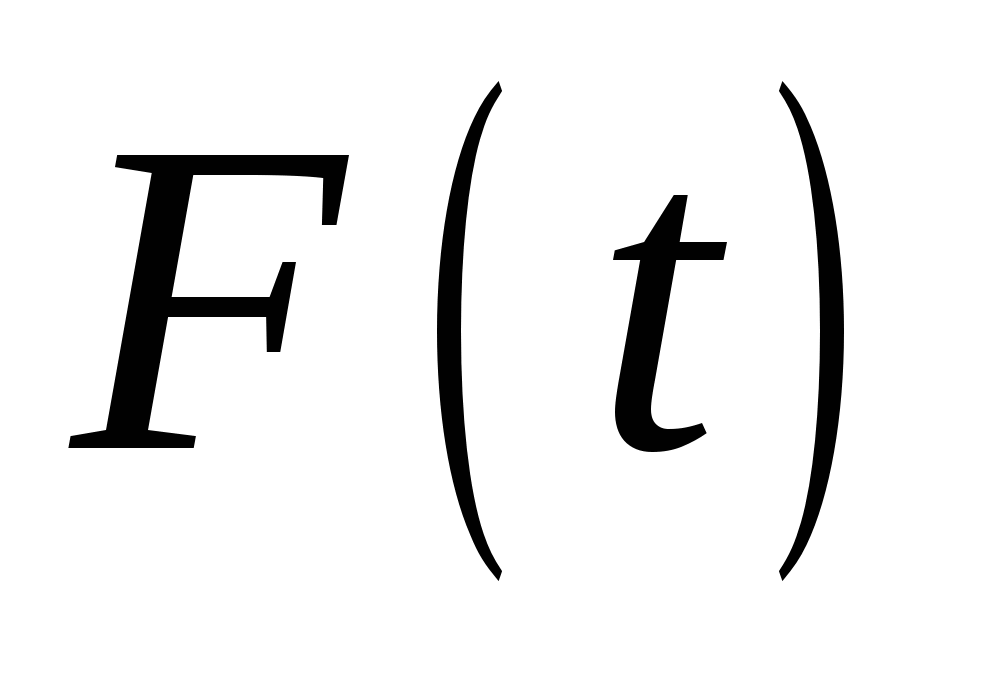 ? ?
-
Какие вводятся дифференциальные функции для описания мгновенных значений показателей надежности и вероятности отказа?
-
Какой смысл имеет понятие: функция плотности распределения наработки до отказа?
-
Какой смысл имеет понятие: функция интенсивность отказов?
-
Какой вид имеет зависимость интенсивности отказов от времени?
-
Каким выражением задается среднее время безотказной работы?
-
На какие периоды времени можно разделить зависимость интенсивности отказов, чем эти периоды характеризуются?
-
Какой период времени зависимости интенсивности отказов является полезным сроком работы изделия?
страница 1
|