страница 1
Радиационная безопасность. 2006г.
Лекция 3.
Вопросы:
-
Взаимодействие нейтронов с веществом.
-
Основное и возбужденное состояние атомного ядра
-
Упругое рассеяние нейтронов на ядрах атомов мишени
-
Неупругое рассеяние нейтронов
-
Ядерные реакции (n, γ), (n, p), (n, α), (n, 2n).
-
Реакции деления (n, f).
-
Энергия отделения нейтрона
-
Капельная модель ядра и формула Вайцзеккера
-
Эффект спаривания нуклонов
-
Деление атомных ядер и оболочечная модель структуры ядра
-
Механизм деления атомного ядра
-
Сечения рассеяния и поглощения тепловых нейтронов на ядрах некоторых биологически важных элементов
-
. Основное и возбуждённое состояние атомного ядра.
Атомное ядро – система с фиксированной полной энергией. Состояния таких систем – стационарные. Состояние с наибольшей энергией связи – основное. Но это же состояние характеризуется наименьшей полной энергией. Все остальные состояния с большей полной энергией – возбуждённые. Диаграмма ядерных уровней энергии строится так:
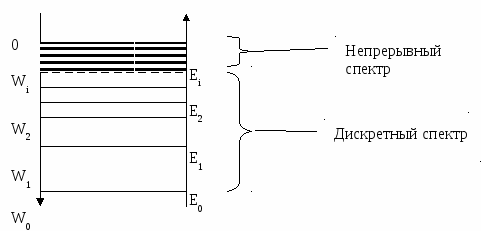
Нижнему по энергии (наибольшему по энергии связи –W) состоянию приписывается нулевой индекс и энергия E0=0:
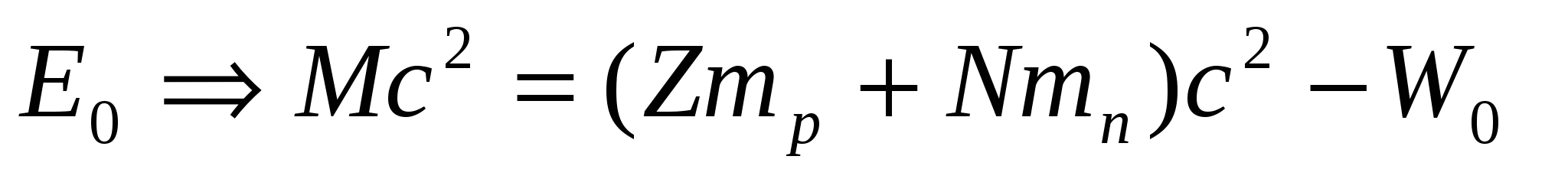 , где W0 – энергия связи ядра в основном состоянии. , где W0 – энергия связи ядра в основном состоянии.
Энергии Ei (i=1, 2,…) остальных состояний определяются как  , т.е. отсчитываются от основного состояния. Это – энергии возбуждения. Нижние уровни энергии ядра дискретны. При ядерных превращениях и рспадах происходят переходы между различными стационарными состояниями ядер. , т.е. отсчитываются от основного состояния. Это – энергии возбуждения. Нижние уровни энергии ядра дискретны. При ядерных превращениях и рспадах происходят переходы между различными стационарными состояниями ядер.
-
. Упругое рассеяние нейтронов на ядрах атомов мишени.
Для элементов с низким атомным номером первый возбуждённый уровень ядра обычно на 1МэВ выше основного состояния. Поэтому в случае лёгких элементов упругое рассеяние нейтронов с En< 1МэВ более вероятно, чем неупругое рассеяние.
Схема упругого рассеяния нейтрона на ядре массы М:

 - импульс ядра отдачи, - импульс ядра отдачи,
 - импульс рассеянного нейтрона, - импульс рассеянного нейтрона,
 - импульс падающего нейтрона, - импульс падающего нейтрона,
 и и  - углы определяющие направление движения рассеянного нейтрона и ядра отдачи. - углы определяющие направление движения рассеянного нейтрона и ядра отдачи.
Рис. 5. Упругое рассеяние нейтрона на тяжёлом ядре.
Из законов сохранения энергии и импульса можно получить выражения для модуля импульса и энергии ядра отдачи:
 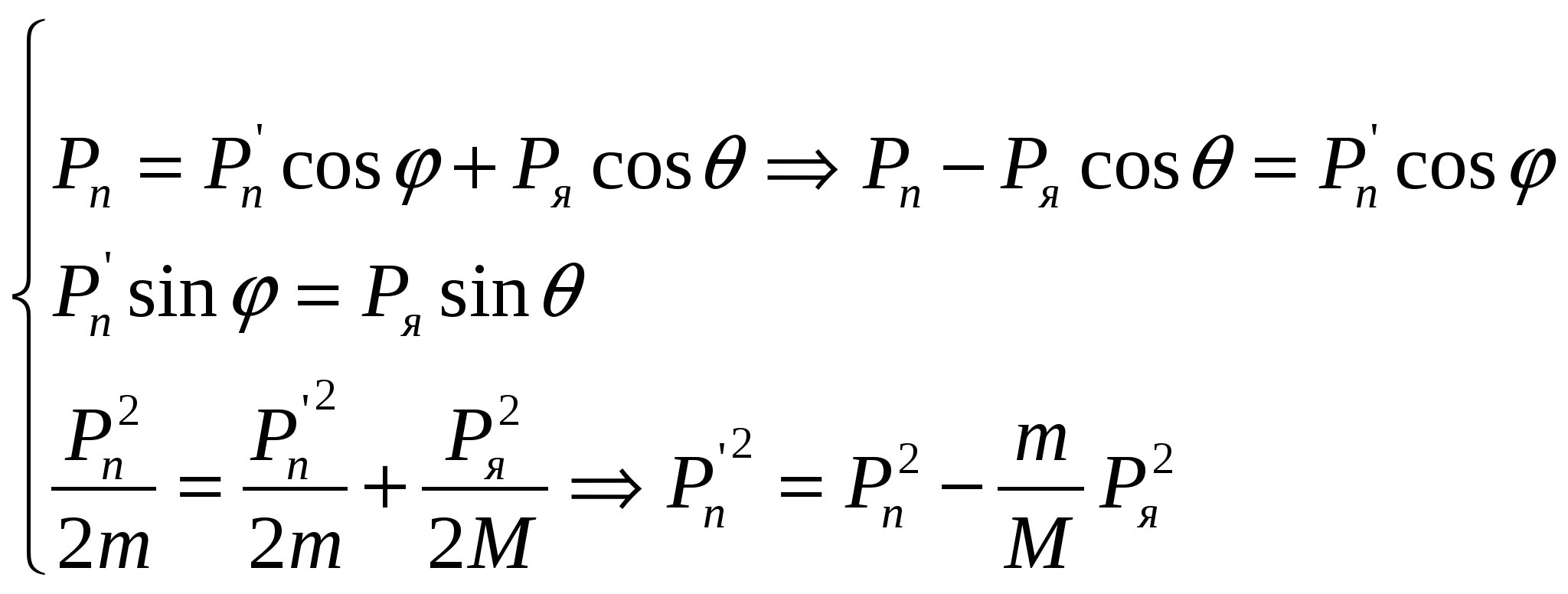


(  и и 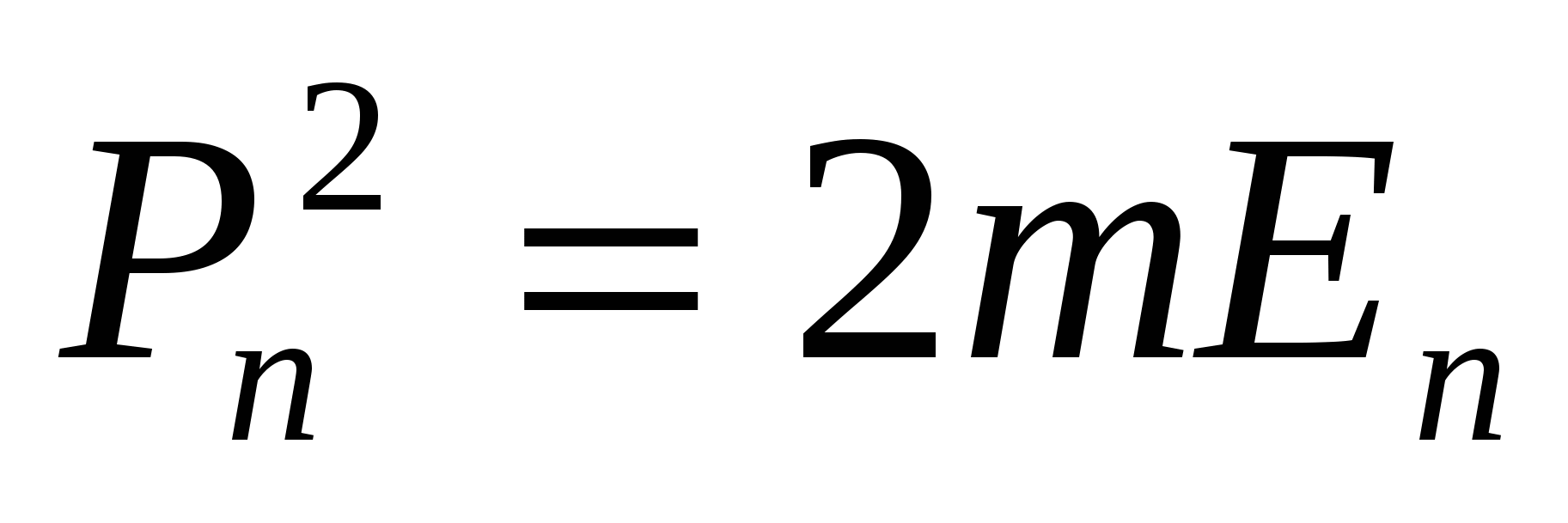 , m и M масса нейтрона и ядра отдачи) , m и M масса нейтрона и ядра отдачи)
П
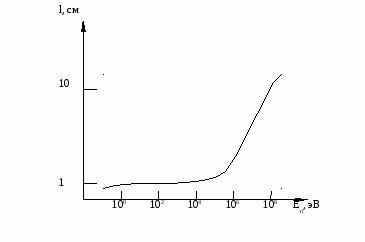
Рис. 6. Зависимость длины пробега нейтрона в биологической ткани от его энергии.
ри рассеянии нейтрона на протоне (mn≈mp) энергия протона отдачи равна Ep=Encos2θ. В таких столкновениях протоны получают большой импульс, т.е. возникают сильно ионизирующие протоны отдачи. Максимальный перенос энергии нейтрона уменьшается с ростом массы ядра отдачи. При рассеянии на ядрах C, O, N (входящих в состав биологических тканей) нейтроны теряют 10-15% своей энергии в упругих соударениях и от 85 до 95% энергии взаимодействующих нейтронов переносится к ядрам водорода. Несмотря на небольшой пробег протонов в биологических тканях, их образование происходит на различной ( в том числе и достаточно большой) глубине, т.к. пробег незаряженных нейтронов относительно велик (рис. 6).
-
. Неупругое рассеяние (n, n’).
С увеличением атомного номера мишени минимальная энергия возбуждения ядра уменьшается ~ до 0,1 МэВ, и нейтроны с большей энергией могут испытывать как упругое, так и неупругое рассеяние, причём вероятность последнего увеличивается с ростом En. В реакциях (n, n’) быстрые нейтроны сначала соединяются с ядром мишени, образуя составное ядро, затем этим ядром испускается нейтрон с меньшей энергией, а само ядро-мишень остаётся в возбужденном состоянии. Обычно это возбуждение очень быстро снимается испусканием  -квантов. В зависимости от энергии испущенного в этом процессе нейтрона в дальнейшем будет наблюдаться его упругое или неупругое рассеяние. -квантов. В зависимости от энергии испущенного в этом процессе нейтрона в дальнейшем будет наблюдаться его упругое или неупругое рассеяние.
1.4. Ядерные реакции (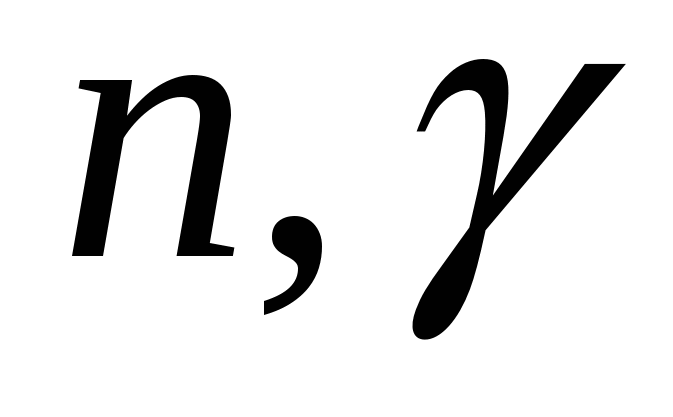 ), ( ), (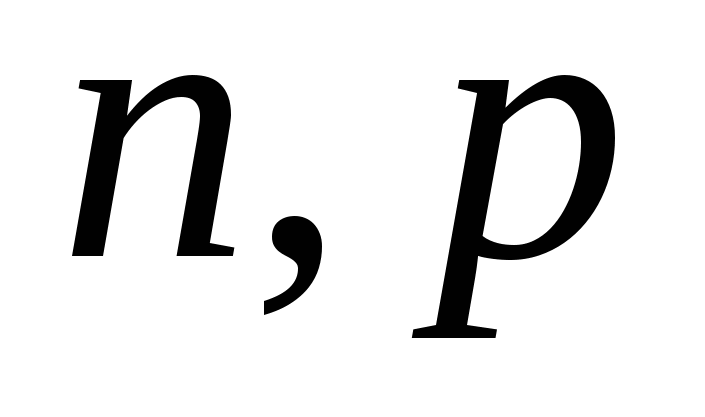 ), ( ), ( ), ( ), ( ). ).
Захват нейтронов ядрами (М) с зарядовым числом Z и массовым числом А часто приводит к ядерным реакциям, в результате которых возникает явление искусственной радиоактивности.
Радиационный захват нейтрона (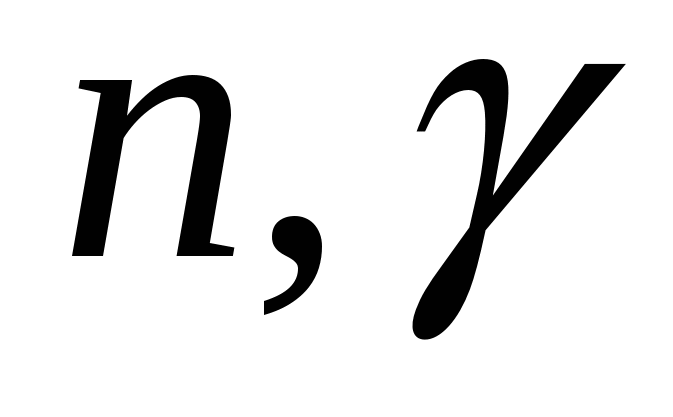 ). Согласно Ферми полное эффективное сечение этого процесса обратно пропорционально скорости нейтронов: ). Согласно Ферми полное эффективное сечение этого процесса обратно пропорционально скорости нейтронов:
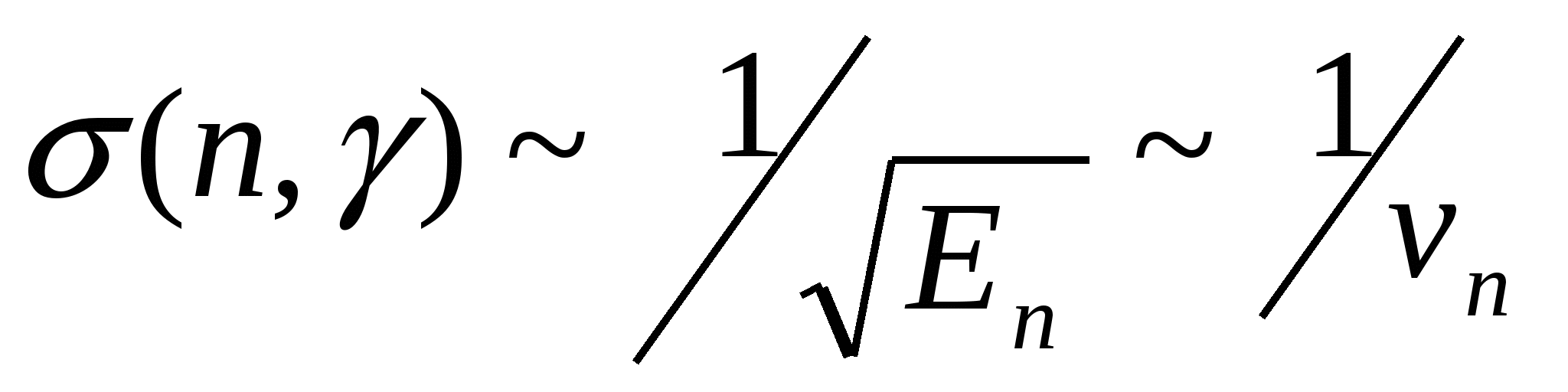 . .
Из этого видно, что подобные реакции эффективно протекают под действием медленных нейтронов:
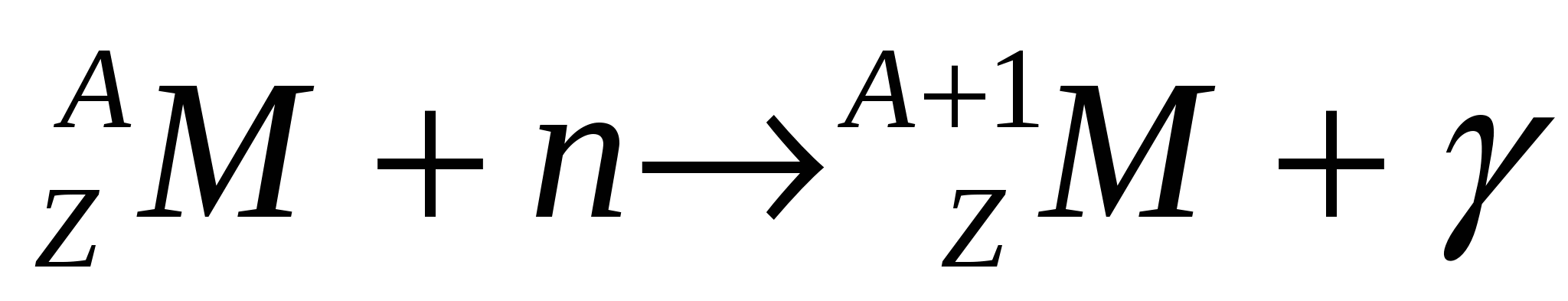
Возникающее ядро  радиоактивно, т.к. отношение числа нейтронов к числу протонов в нем увеличивается. Это ядро переходит в стабильное состояние за счет радиоактивно, т.к. отношение числа нейтронов к числу протонов в нем увеличивается. Это ядро переходит в стабильное состояние за счет 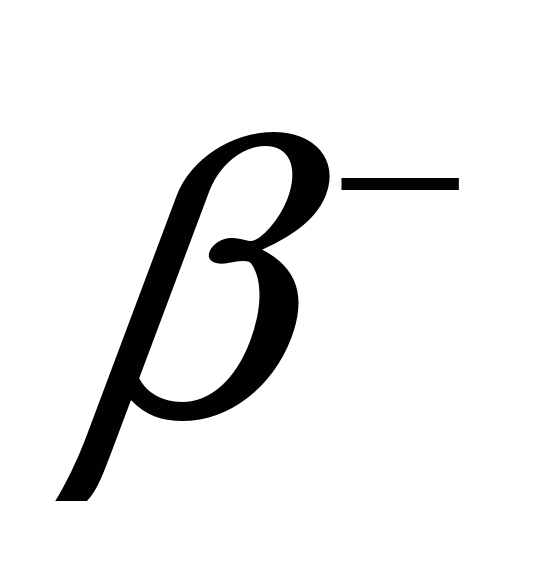 -распада: -распада:
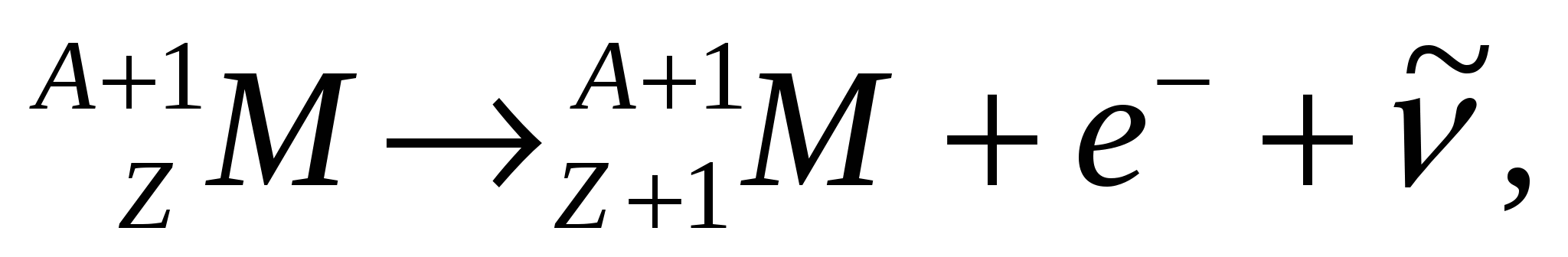 ( (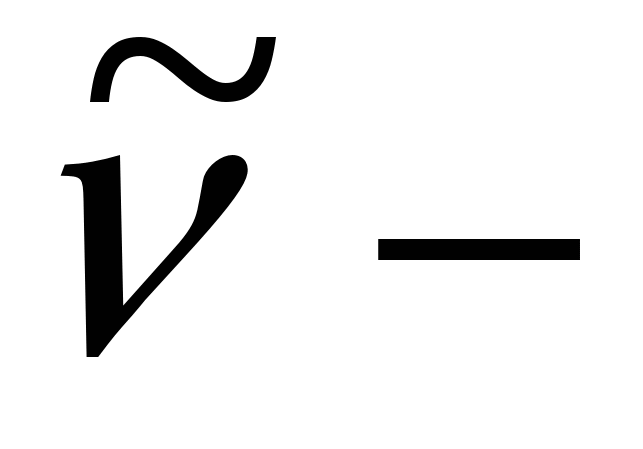 антинейтрино). антинейтрино).
Реакции с образованием протонов (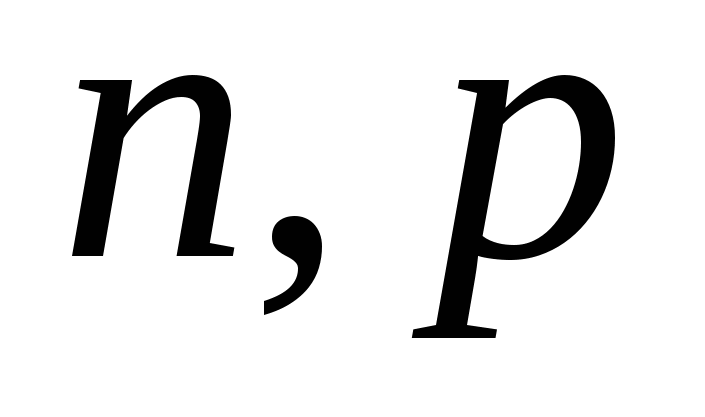 ). ).
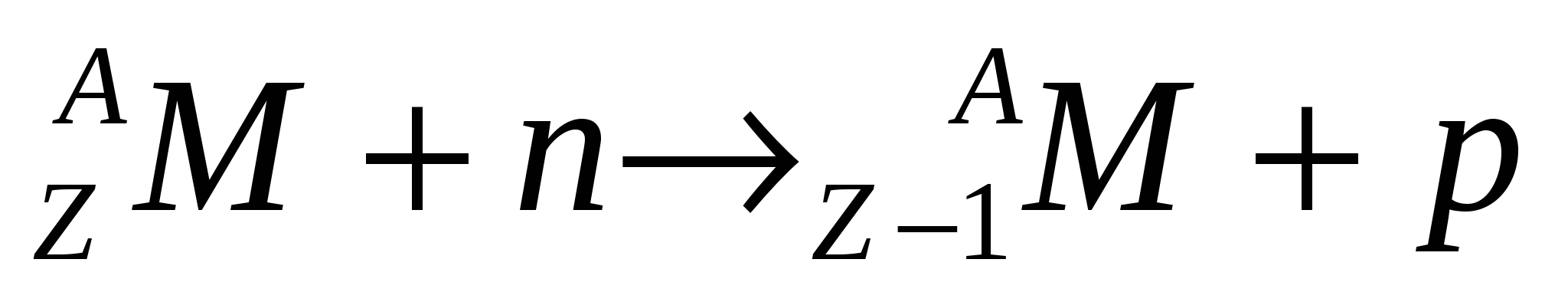
Образованные ядра   обычно радиоактивны, протекают они, как правило, с участием быстрых нейтронов (En>1МэВ). Лишь на легких ядрах они могут протекать и под действием тепловых нейтронов, когда потенциальный барьер, препятствующий вылету протона, относительно низок, например, на ядре обычно радиоактивны, протекают они, как правило, с участием быстрых нейтронов (En>1МэВ). Лишь на легких ядрах они могут протекать и под действием тепловых нейтронов, когда потенциальный барьер, препятствующий вылету протона, относительно низок, например, на ядре  : : 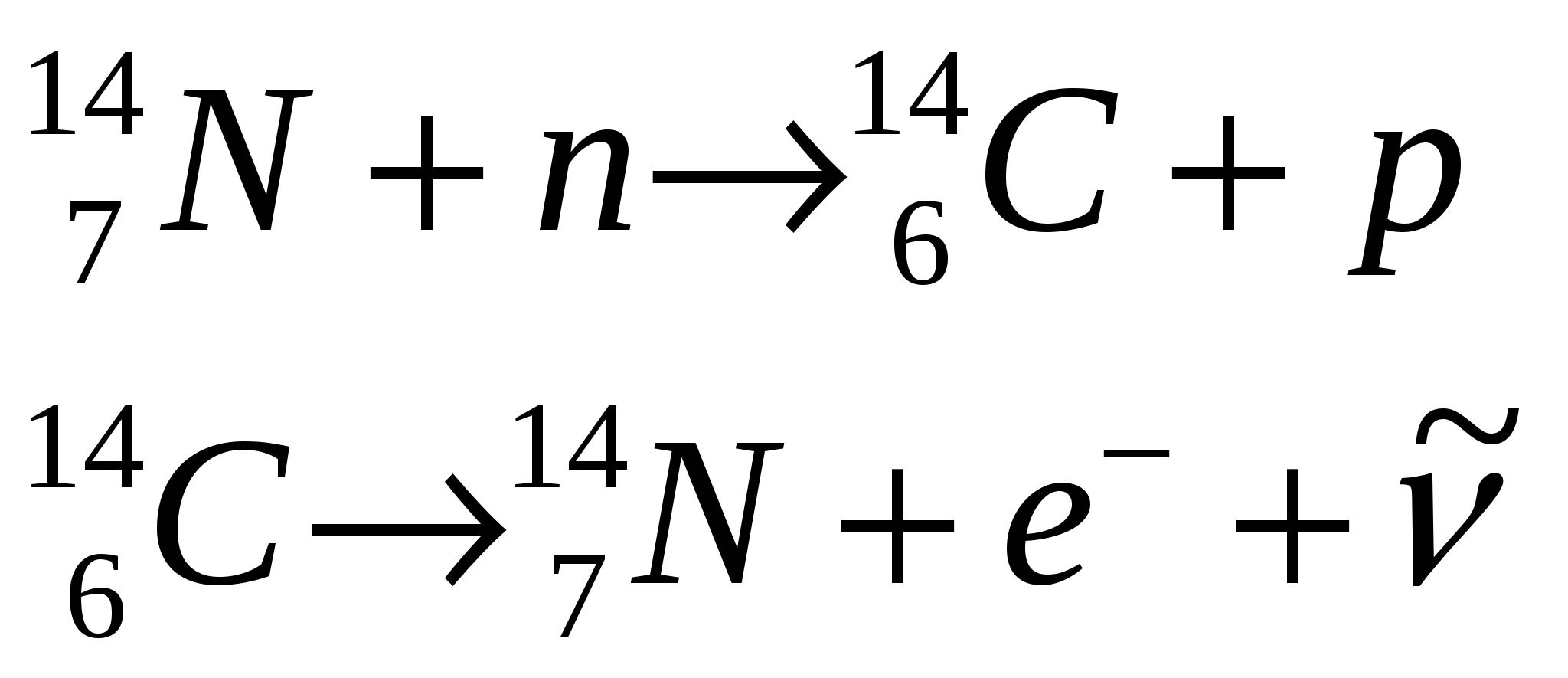
Конечный продукт идентичен первоначальному изотопу мишени. Реакции этого типа протекают в верхних слоях атмосферы.
Реакции с образованием  -частиц ( -частиц ( ). ).
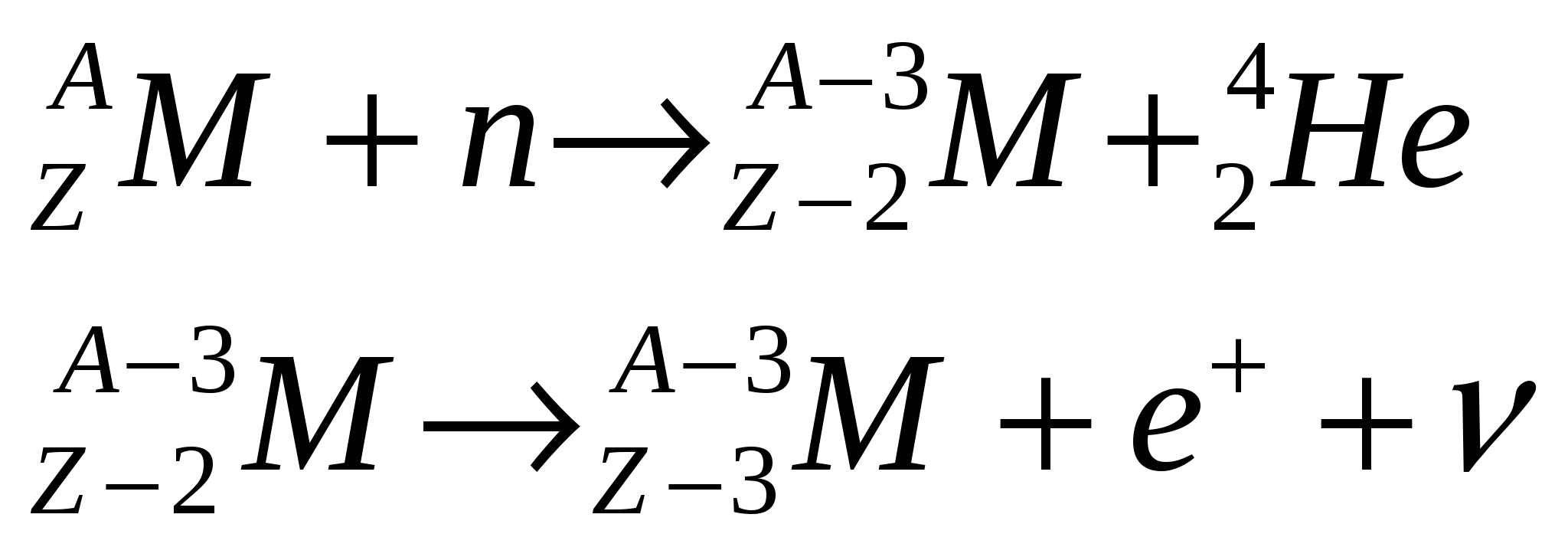 ( ( -нейтрино) -нейтрино)
Такие реакции при малых энергиях нейтронов идут только на легких ядрах, на тяжелых требуются большие Еn. Характерным примером является реакция на ядрах 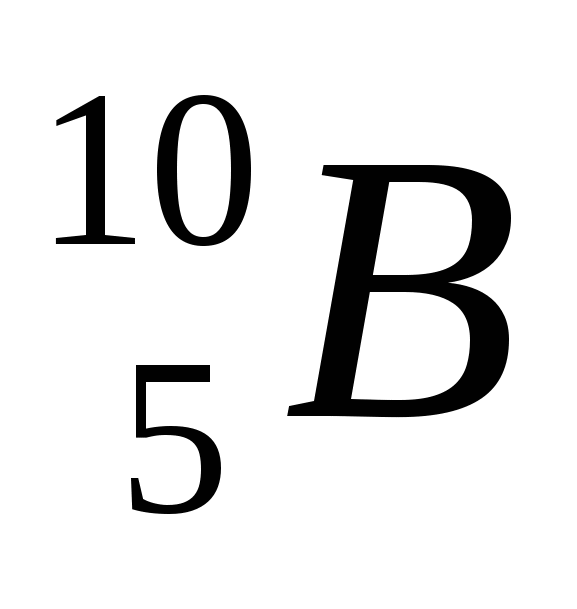 : :
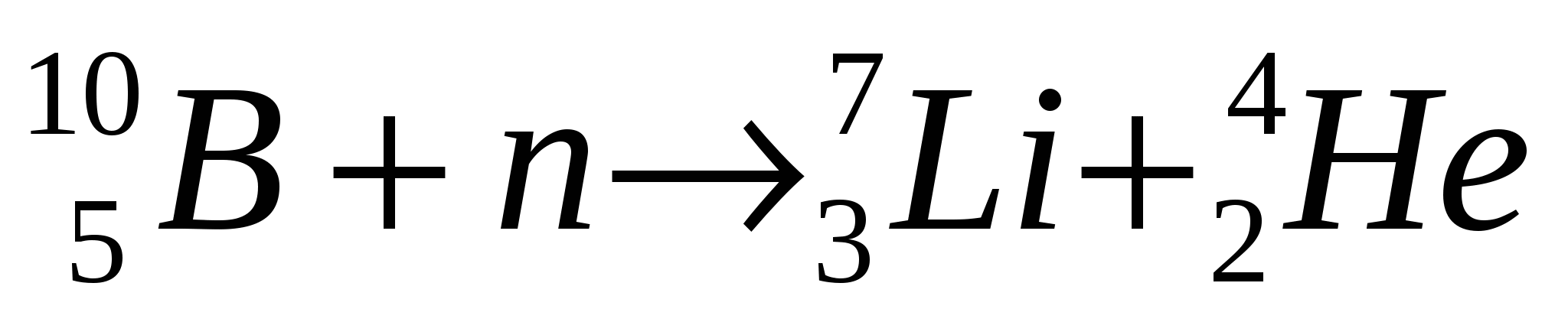
Реакции с образованием двух (или большего числа) нуклонов ( ), ( ), (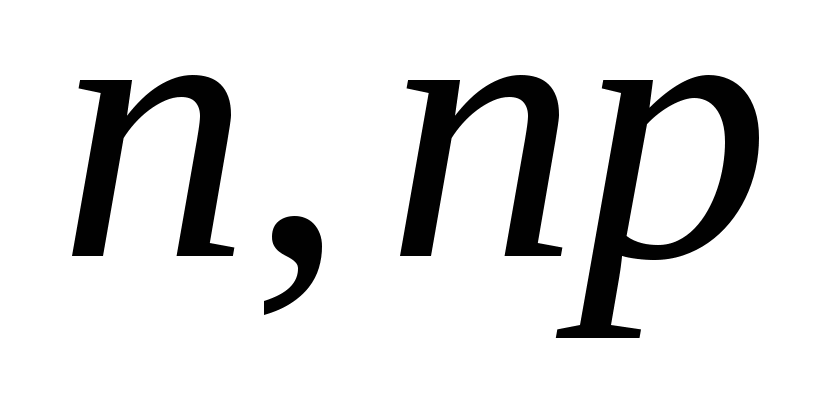 ), ( ), (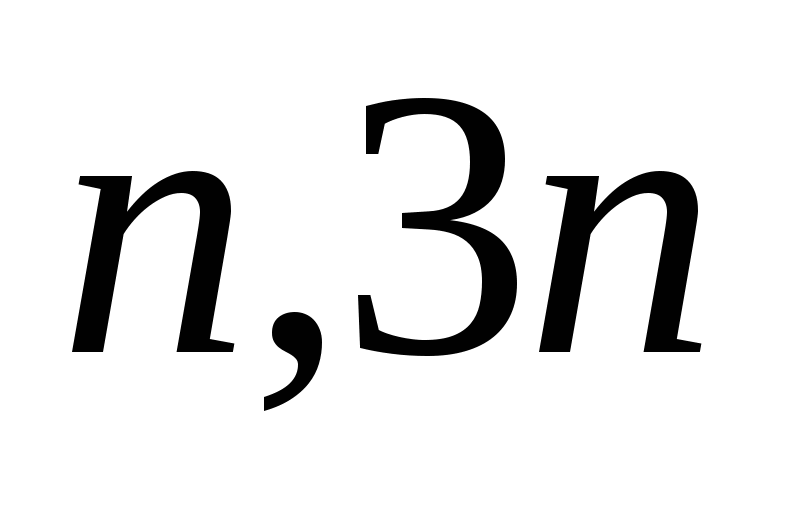 ). ).
Это пороговые реакции, которые идут при энергии нейтронов Еn>10МэВ, и вероятность которых растет с ростом Еn:

например: 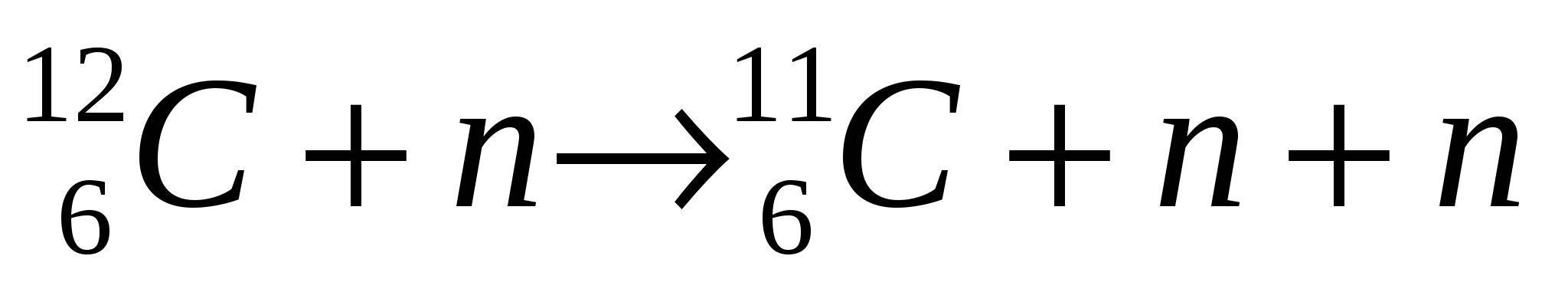
В этих реакциях часто возникают радиоактивные ядра с увеличенным процентным содержанием протонов. Их переход в стабильное состояние сопровождается 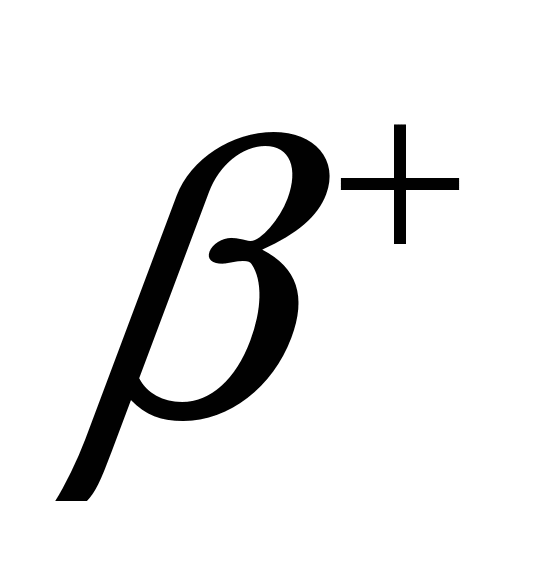 -распадом: -распадом:
 . .
1.5. Реакции деления (n,f).
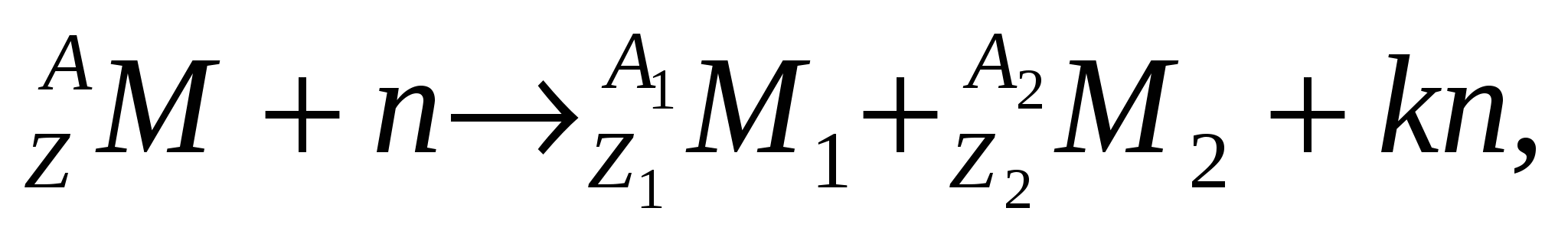 k=2÷3 k=2÷3
На некоторых тяжелых ядрах эта реакция может протекать под действием быстрых (Еn>1МэВ) нейтронов, на других – под действием тепловых нейтронов (Еn≈0.025эВ).
1.5.1. Энергия отделения нейтрона.
Ядро – система связанных нуклонов и чтобы его разделить на составные части (нуклоны) надо затратить энергию связи ядра W(A,Z):
W(A,Z)=(Zmpc2+Nmnс2) - M(A,Z)c2
M, mn,, mp – масса ядра, нейтрона и протона соответственно, с – скорость света, Z, N – число протонов и число нейтронов в ядре, A – массовое число (суммарное число нуклонов в ядре).
Энергия отделения нейтрона Bn равна:
Bn=M(A-1,Z)c2+mnc2-M(A,Z)c2=W(A,Z)-W(A-1,Z)-W(1,0)=[W(1,0)=0]=W(A,Z)-W(A-1,Z).
Энергия отделения протона Bp:
Bp=M(A-1,Z-1)c2+mpc2-M(A,Z)c2=W(A,Z)-W(A-1,Z-1)-W(1,1)=[W(1,1)=0]=W(A,Z)-W(A-1,Z-1).
И для вырывания любой частицы X(a,z):
Bx=W(A,Z)-W(A-a,Z-z)-W(a,z); W(a,z)≠0.
W(A,Z) тем больше, чем больше A. Для рассмотрения этих процессов удобно использовать удельную энергию связи:
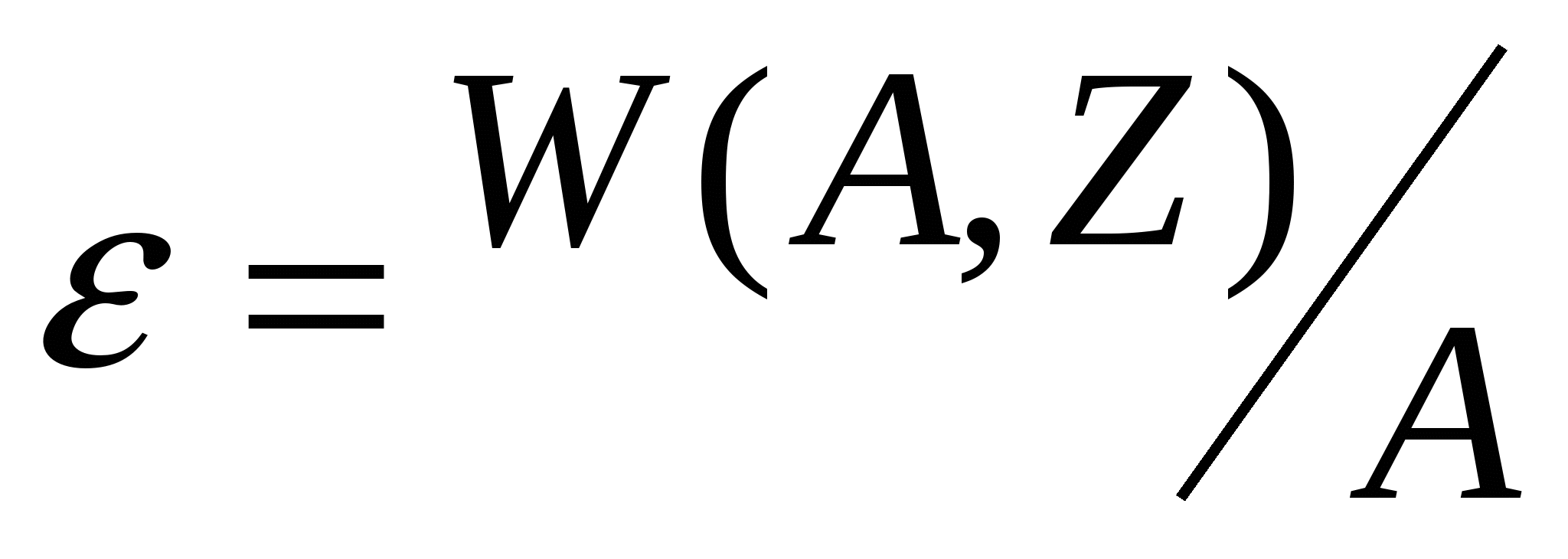 . .
Для стабильных и наиболее долгоживущих тяжелых элементов  (после А=20) изменяется относительно слабо (рис.7) и (после А=20) изменяется относительно слабо (рис.7) и   ≈8±1МэВ: ≈8±1МэВ:
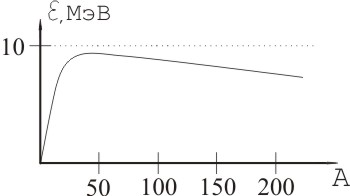
Рис.7. Зависимость удельной энергии связи ядра от
массового числа (А).
Для сравнения: на разрыв химической связи (электромагнитные силы) нужна энергия ~ в 106 раз меньшая. С точки зрения запаса энергии 1г ядерного топлива соответствует ~ 1т химического элемента. Эту энергию можно получить либо при синтезе легких ядер, либо при делении тяжелых ядер. В обоих случаях совершается переход к ядрам, в которых  больше и часть энергии связи при этом высвобождается. больше и часть энергии связи при этом высвобождается.
Если разделить ядро с А≈240 ( ≈7,6МэВ) на 2 осколка А1=А2=120 ( ≈7,6МэВ) на 2 осколка А1=А2=120 ( ≈8,5МэВ), то освободится энергия ≈240 · (8,5-7,6)МэВ≈220МэВ. Значения ≈8,5МэВ), то освободится энергия ≈240 · (8,5-7,6)МэВ≈220МэВ. Значения  характеризуют величину сильного (ядерного) взаимодействия. Для сравнения: энергия гравитационного взаимодействия 2х нуклонов в ядре: характеризуют величину сильного (ядерного) взаимодействия. Для сравнения: энергия гравитационного взаимодействия 2х нуклонов в ядре:

 NN>=2Фм, G=1,3*10-42 Фм*с4/МэВ NN>=2Фм, G=1,3*10-42 Фм*с4/МэВ
где с-скорость света, G-гравитационная постоянная.
Кулоновская энергия 2х протонов внутри ядра 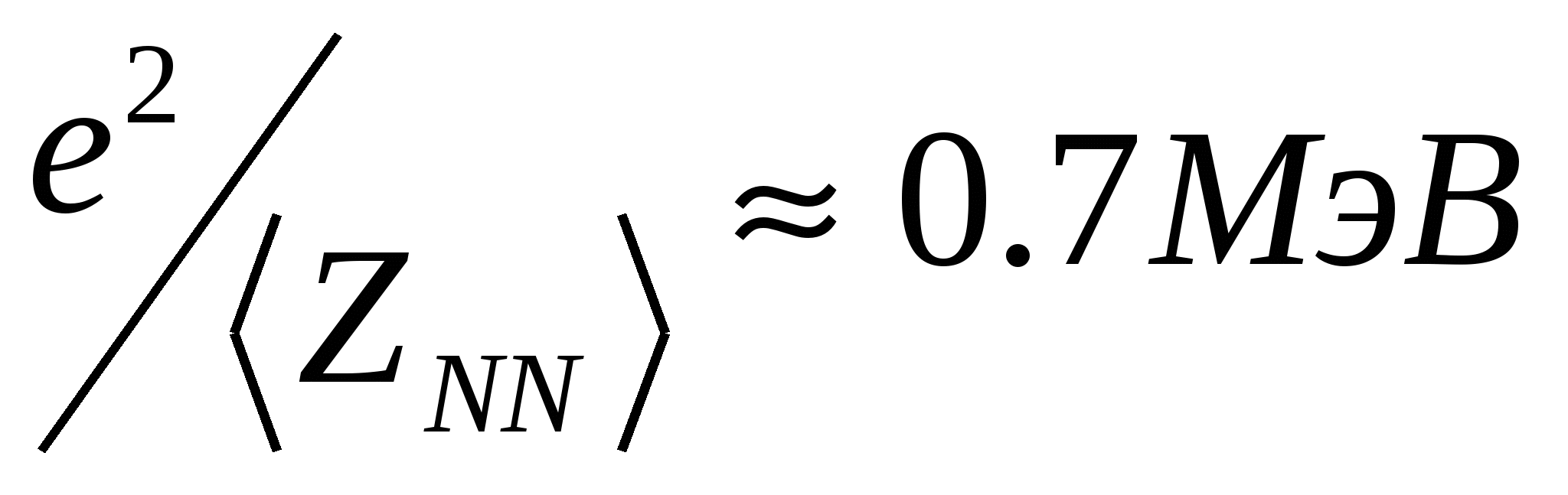 , т.е. примерно, в 10 раз меньше ядерной. , т.е. примерно, в 10 раз меньше ядерной.
1.5.2. Капельная модель ядра и формула Вайцзеккера.
Для ядер с А>20 энергия связи W≈ . Это говорит о том, что нуклон в ядре взаимодействует не со всеми, а лишь с ближайшими нуклонами. Это свойство насыщения ядерных взаимодействий, вытекающее из их короткодействия и отталкивания нуклонов на малых расстояниях, делает ядро похожим на каплю жидкости. Используя нерелятивистскую квантовую теорию, Вайцзеккер предложил капельную модель ядра, в которой можно не учитывать структуру нуклонов, да и трудности самой ядерной физики (в решении уравнения Шредингера для ядра: NN – взаимодействие до конца не изучено, не решена проблема сильно взаимодействующих тел для А >4) делают эту модель удобной и полезной. Сходство жидкой капли и ядра: в обоих случаях энергия связи пропорциональна числу составляющих частиц и радиальная форма NN – потенциала (VNN) аналогична потенциалу Леннард-Джонса для взаимодействующих атомов. . Это говорит о том, что нуклон в ядре взаимодействует не со всеми, а лишь с ближайшими нуклонами. Это свойство насыщения ядерных взаимодействий, вытекающее из их короткодействия и отталкивания нуклонов на малых расстояниях, делает ядро похожим на каплю жидкости. Используя нерелятивистскую квантовую теорию, Вайцзеккер предложил капельную модель ядра, в которой можно не учитывать структуру нуклонов, да и трудности самой ядерной физики (в решении уравнения Шредингера для ядра: NN – взаимодействие до конца не изучено, не решена проблема сильно взаимодействующих тел для А >4) делают эту модель удобной и полезной. Сходство жидкой капли и ядра: в обоих случаях энергия связи пропорциональна числу составляющих частиц и радиальная форма NN – потенциала (VNN) аналогична потенциалу Леннард-Джонса для взаимодействующих атомов.
В формуле Вайцзеккера для энергии связи ядра фигурируют:
1) объемная энергия (энергия связи тем больше, чем больше объем ядра (число нуклонов): Eоб.=av*A, где постоянная аz=15,6МэВ;
2) поверхностная энергия (нуклоны на поверхности связаны слабее, чем внутри ядра, т.к. взаимодействуют с меньшим числом своих партнеров, чем внутренние нуклоны. Число потерянных связей пропорционально числу нуклонов на поверхности, а, значит, и самой поверхности S=4 R2=4 R2=4 r r A2/3; R=r0A1/3; r0=1.2Фм. Итак, за счет поверхности, энергия связи уменьшается на величину аSA2/3: EПОВ.=аSA2/3, где постоянная аS=17,2МэВ. На нуклон, находящийся на поверхности, действует результирующая сила, направленная внутрь ядра. Поэтому поверхностные нуклоны стремятся сжать ядро, создавая, как в капле, поверхностное натяжение, энергия которого и определяется этим выражением); A2/3; R=r0A1/3; r0=1.2Фм. Итак, за счет поверхности, энергия связи уменьшается на величину аSA2/3: EПОВ.=аSA2/3, где постоянная аS=17,2МэВ. На нуклон, находящийся на поверхности, действует результирующая сила, направленная внутрь ядра. Поэтому поверхностные нуклоны стремятся сжать ядро, создавая, как в капле, поверхностное натяжение, энергия которого и определяется этим выражением);
3) кулоновская энергия (для заряда, равномерно распределенного по сфере:
 , ,
энергия кулоновского отталкивания, уменьшающая энергию связи:
ЕКУЛ=3/5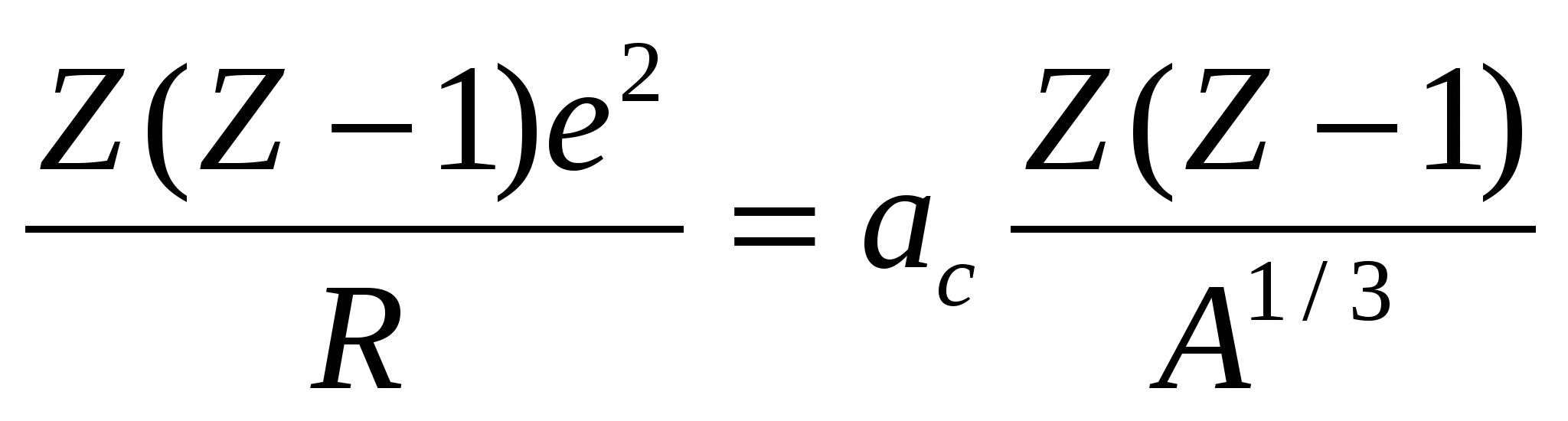 , ,
где ас – константа, ас=0,72МэВ);
4) энергия симметрии (этот член в формуле Вайцзеккера возникает при учете квантовой природы ядерной капли. Ядро состоит из фермионов, следовательно, необходимо учесть принцип Паули. Каждый уровень энергии в ядре характеризуется лишь одним набором квантовых чисел и потому в соответствии с принципом Паули может быть занят лишь одним нуклоном каждого типа. Ядра, у которых нуклонов одного типа больше, чем другого, имеют меньшую энергию связи, чем ядра с одинаковым числом протонов и нейтронов. Член в формуле Вайцзеккера, который учитывает стремление ядра иметь в основном состоянии симметричное расположение по уровням энергии нейтронов и протонов (энергия симметрии):

где аsym— константа, аsym=23,6МэВ. Квадрат в числителе отражает тот факт, что энергия симметрии должна возрастать при росте относительного числа нуклонов любого типа. Появление 1/A связано с реальным сближением ядерных уровней с ростом А. (Отклонение от симметрии уменьшает энергию связи, поэтому у этого члена знак “ — “ как и в двух предыдущих).
Представленные значения констант av, aS, aC и aSYM дают хорошие результаты при подгонке под экспериментальные данные.
1.5.3. Эффект спаривания нуклонов.
На зависимости Bn от N (рис.8) наблюдаются “пульсации” на уровне 1-2 МэВ.
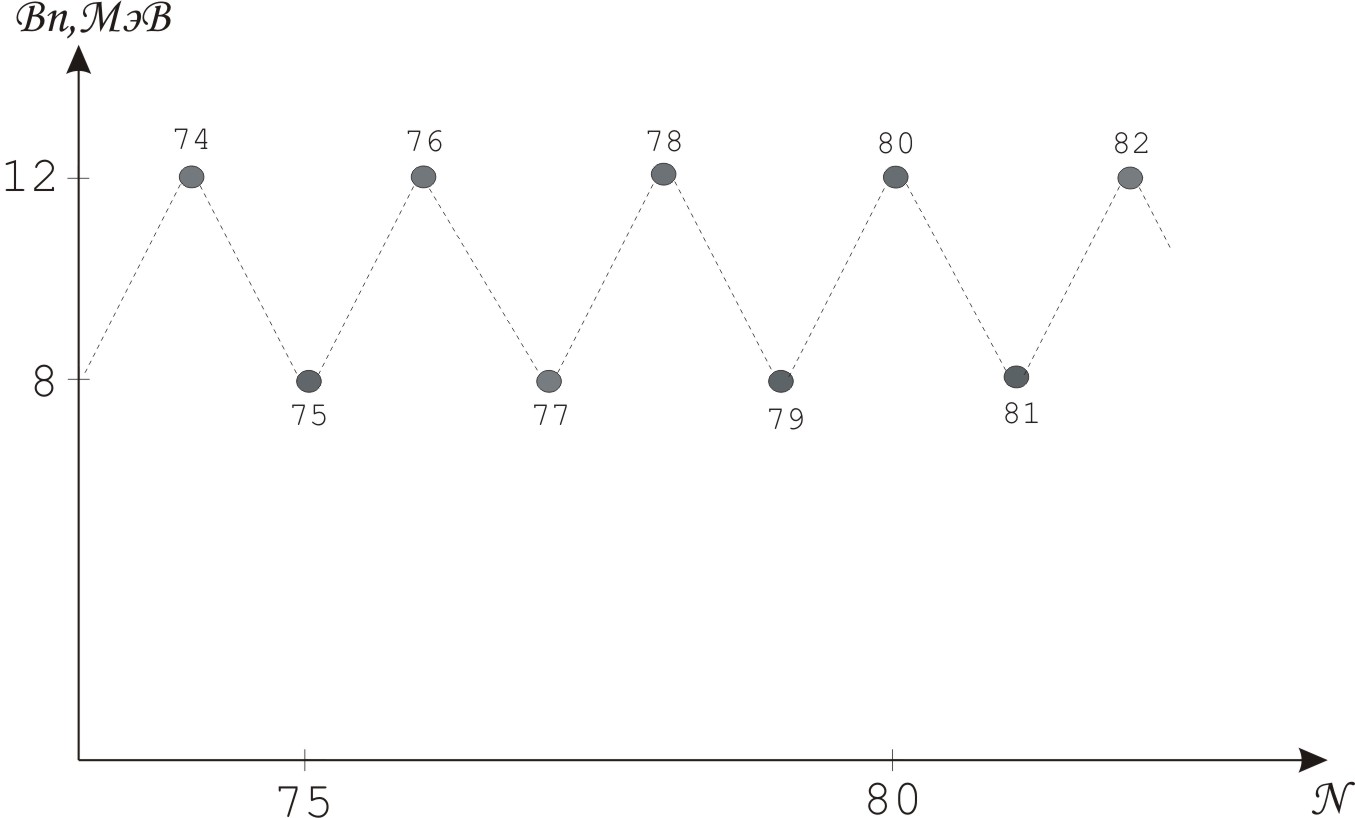
Рис.8. Зависимость энергии отделения нейтронов (Bn) от числа нейтронов (N) в ядре.
Это связанно со специфическим свойством NN – взаимодействия: в основном состоянии ядра возникает дополнительная связь между двумя нуклонами одного типа (двумя протонами или двумя нейтронами). Энергия Bn возрастает на 2-3 МэВ, когда число нейтронов становится четным. У четно-четных ядер все нуклоны в основном состоянии спарены и положительная добавка к энергии связи наибольшая. Условились энергию спаривания (Eспар) записывать так, чтобы для нечетных ядер (один нуклон в основном состоянии не спарен) она равнялась “0”. С экспериментом согласуется выражение:
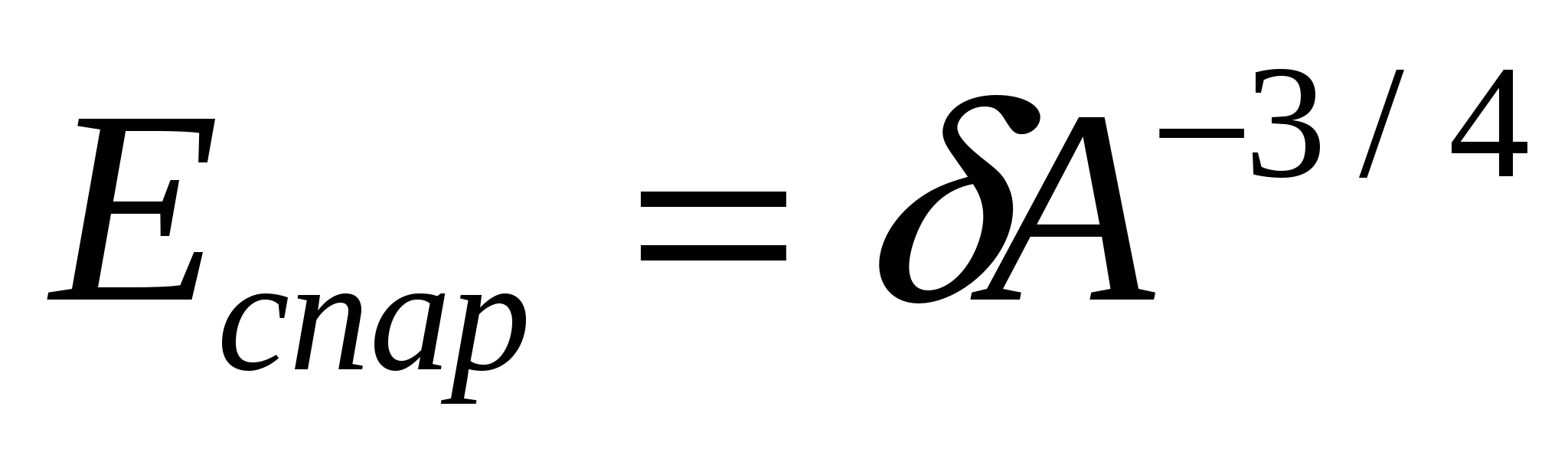 , ,
в котором  =0 (нечетные ядра); =0 (нечетные ядра);  = + = +  (четно-четные); (четно-четные);  = - = -  (нечетно-нечетные ядра). (нечетно-нечетные ядра).
Итак, окончательное выражение для энергии связи ядра в формуле Вайцзеккера:
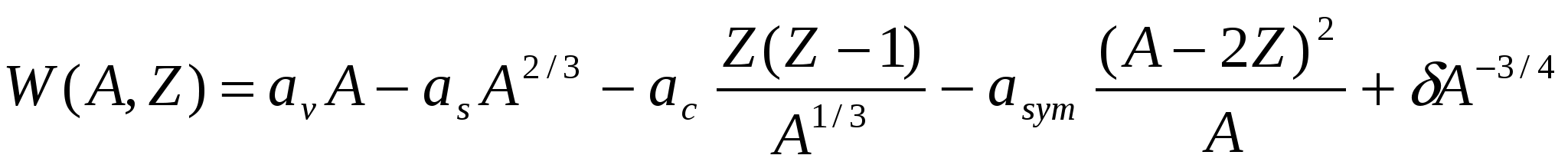 . .
1.5.4. Деление атомных ядер и оболочечная модель структуры ядра.
То, что при делении тяжелых ядер выделяется энергия, следует из зависимости  от А. При делении тяжелого ядра совершается переход к более легким ядрам, в которых нуклоны связаны сильнее ( от А. При делении тяжелого ядра совершается переход к более легким ядрам, в которых нуклоны связаны сильнее ( больше, рис.7), и часть энергии высвобождается. Для энергии деления (Едел)можно записать: больше, рис.7), и часть энергии высвобождается. Для энергии деления (Едел)можно записать:
Eдел=M(A,Z)c2-[M1(A1,Z1)c2+M2(A2,Z2)c2]=W1(A1,Z1)+W2(A2,Z2)-W(A,Z).
(A=A1+A2; Z=Z1+Z2).
Для случая, когда ядро делится на 2 примерно равных осколка с А1=А2=А/2 и Z1=Z2=Z/2, пренебрегая энергией спаривания ( А-3/4) и полагая, что Z(Z-1)≈Z2, получим, используя формулу Вайцзеккера (слагаемые объемной энергии и энергии симметрии сокращаются): А-3/4) и полагая, что Z(Z-1)≈Z2, получим, используя формулу Вайцзеккера (слагаемые объемной энергии и энергии симметрии сокращаются):
Едел=2W( )-W(A,Z)≈[Eпов((A,Z)+Eкул(A,Z)]-2[Eпов( )-W(A,Z)≈[Eпов((A,Z)+Eкул(A,Z)]-2[Eпов( )+Eкул( )+Eкул( )]≈0,37ac )]≈0,37ac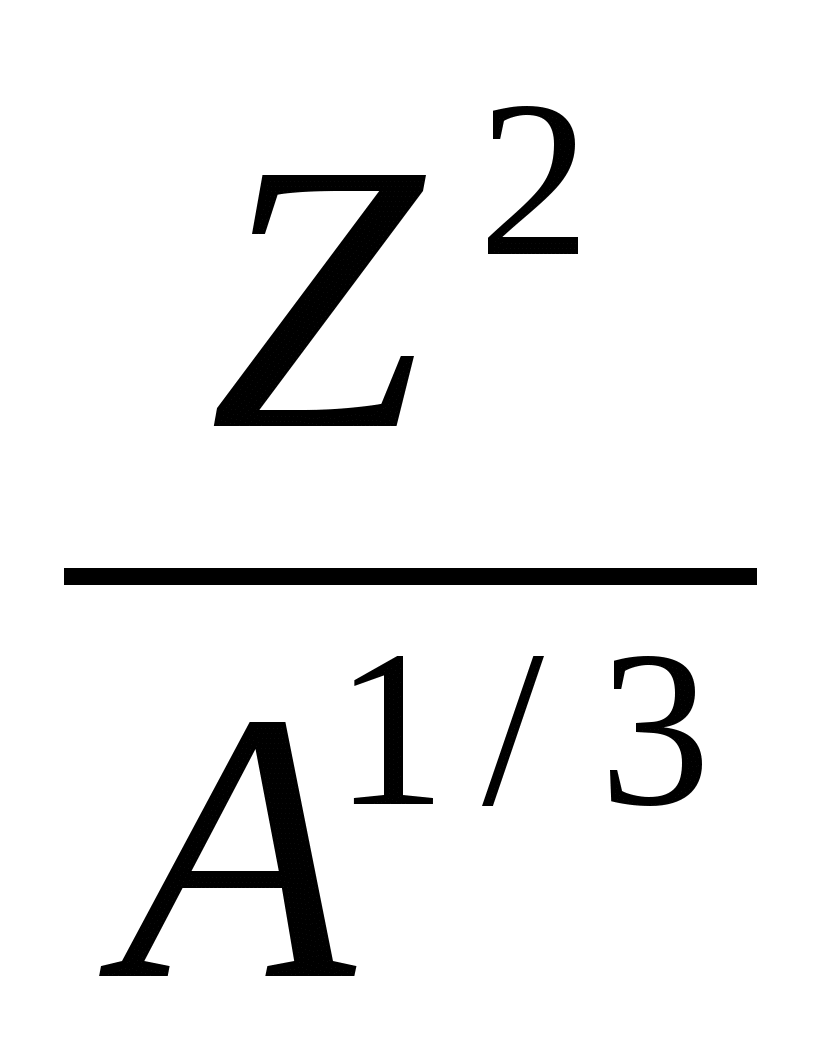 -0,26asA2/3. -0,26asA2/3.
Видно, что деление энергетически выгодно (Едел>0), если 0,37ас >0,26аsА2/3, т.е. когда >0,26аsА2/3, т.е. когда 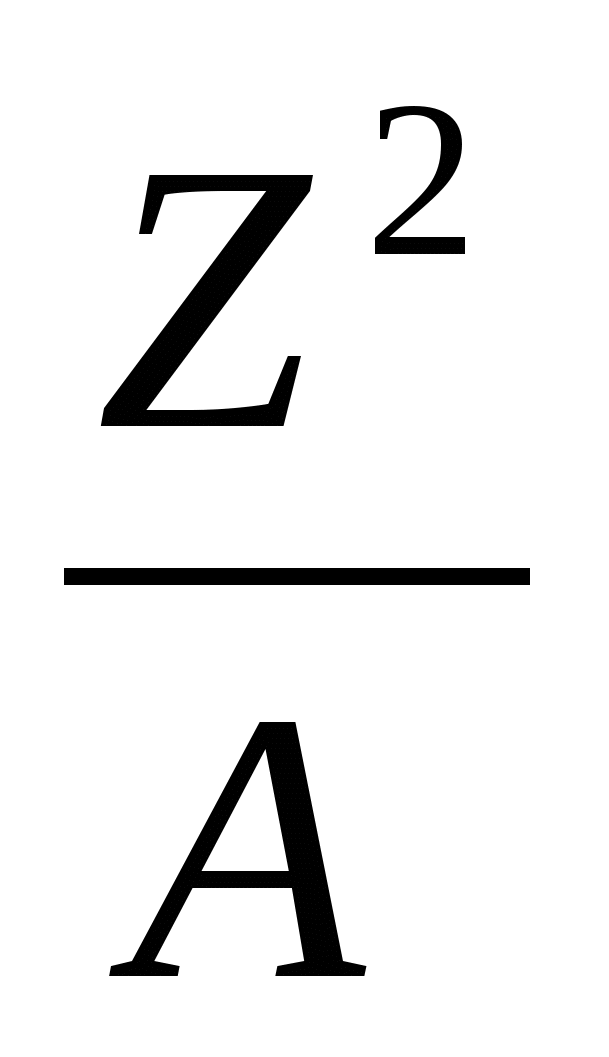 > >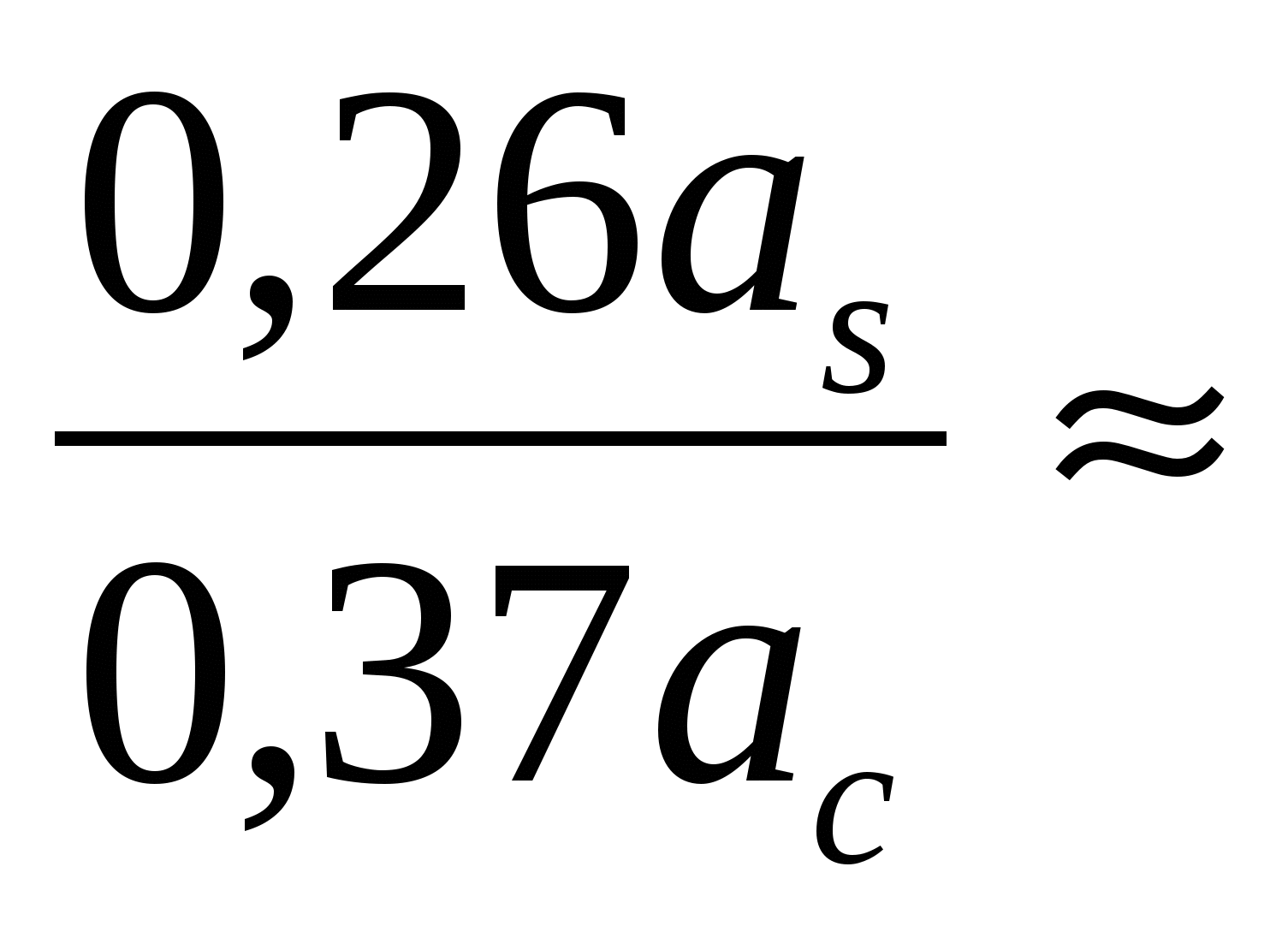 17. Величина 17. Величина 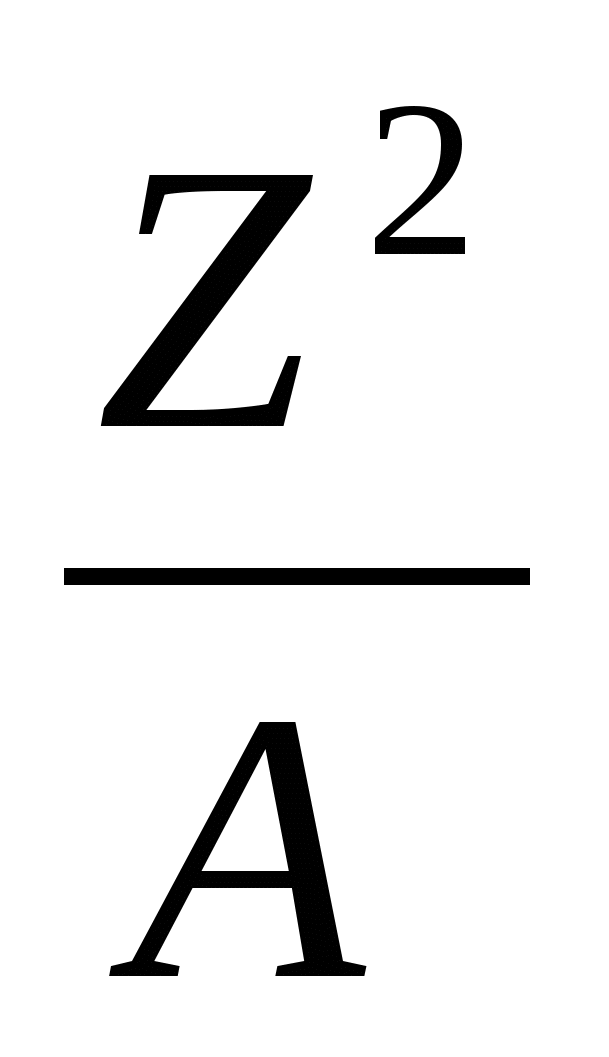 -- это параметр деления. Т.о. деление выгодно для ядер, которые тяжелее иттрия -- это параметр деления. Т.о. деление выгодно для ядер, которые тяжелее иттрия 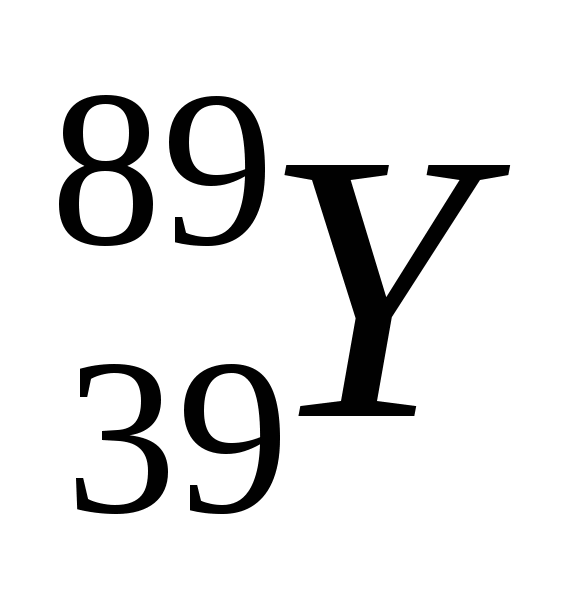 ( (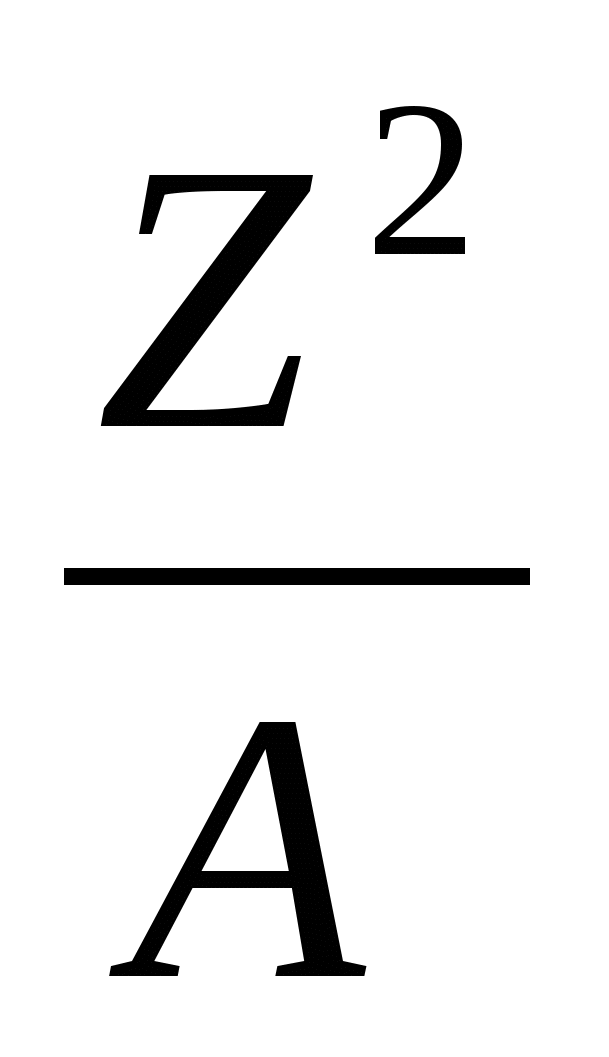 =17). =17).
При делении Епов возрастает, т.к. растет площадь ядерной поверхности, а Екул уменьшается, т.к. растет среднее расстояние между протонами. Чтобы при делении освобождалась энергия (Едел>0) нужно, чтобы уменьшение Екул превышало увеличение Епов. В примере деления ядра с А=240 на 2 равных осколка (1.5.1) это и происходит (уменьшение Екул превышает увеличение Епов примерно на 220МэВ).
Распределение энергии деления 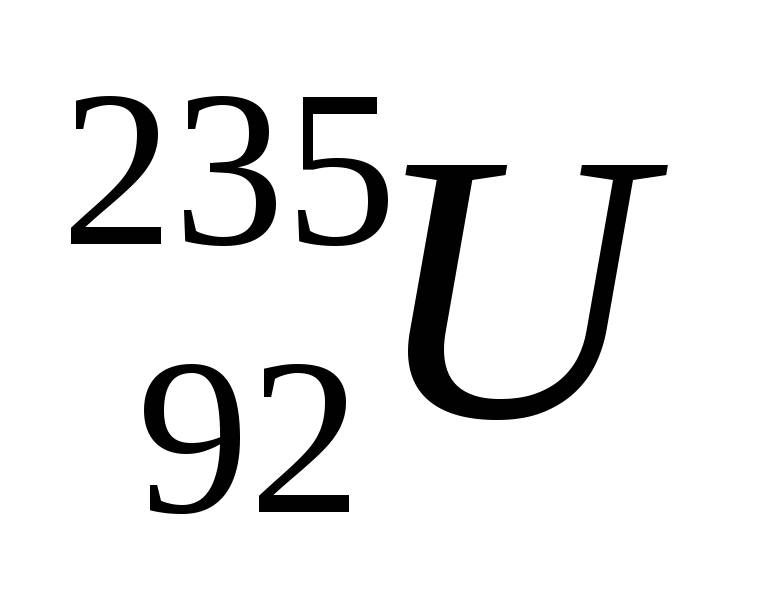 тепловыми нейтронами. тепловыми нейтронами.
При делении осколки в момент образования сильно перегружены нейтронами и находятся в состояниях с большой энергией возбуждения. Такие осколки неустойчивы к 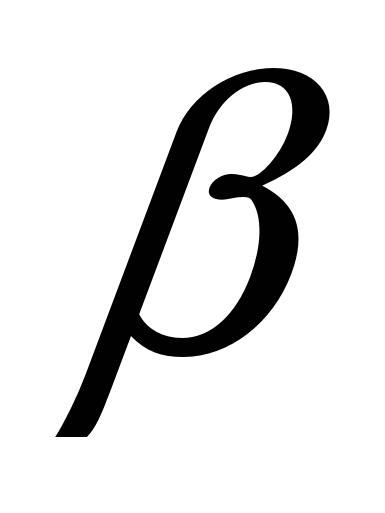 --распаду, который восстанавливает баланс между числом нейтронов и протонов в ядре. Снятие начального возбуждения осколков (возникшего из-за нарушения числа протонов и нейтронов) происходит также за счет вылета мгновенных нейтронов деления. Они испускаются за t < 4*10-14c. Энергетический спектр их имеет максимум около 1МэВ, средняя энергия мгновенных нейтронов ≈2МэВ. Около 1% нейтронов испускаются с запаздыванием (достигает ~1мин). Они испускаются остановившимися осколками после предварительного --распаду, который восстанавливает баланс между числом нейтронов и протонов в ядре. Снятие начального возбуждения осколков (возникшего из-за нарушения числа протонов и нейтронов) происходит также за счет вылета мгновенных нейтронов деления. Они испускаются за t < 4*10-14c. Энергетический спектр их имеет максимум около 1МэВ, средняя энергия мгновенных нейтронов ≈2МэВ. Около 1% нейтронов испускаются с запаздыванием (достигает ~1мин). Они испускаются остановившимися осколками после предварительного 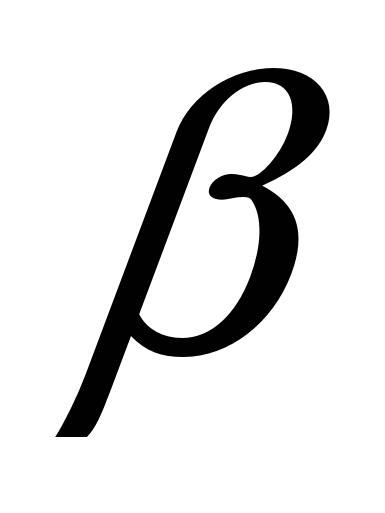 --распада и оказавшимися в результате этого распада в состоянии с энергией возбуждения >Bn. Часть энергии деления уносится --распада и оказавшимися в результате этого распада в состоянии с энергией возбуждения >Bn. Часть энергии деления уносится  -квантами из осколков сразу после вылета мгновенных нейтронов (“мгновенные” -квантами из осколков сразу после вылета мгновенных нейтронов (“мгновенные”  -кванты), а также -кванты), а также  -квантами после -квантами после 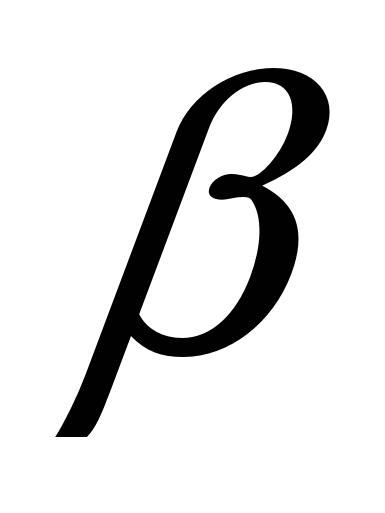 --распада осколков. --распада осколков.
При наиболее вероятном делении 23592U тепловыми нейтронами осколок с А=95 приобретает кинетическую энергию Т=100МэВ, а тяжёлый осколок (А=139) Т=67МэВ, в сумме 167 МэВ из полной энергии ~ 200 МэВ. Следовательно ~ 33 МэВ уносят другие частицы (n, e-, ΰ, γ). Из 200 МэВ в тепло можно превратить ~ 190 МэВ (в расчёте на ядро), т.к. следует исключить энергию, уносимую антинейтрино.
Распределение энергии деления 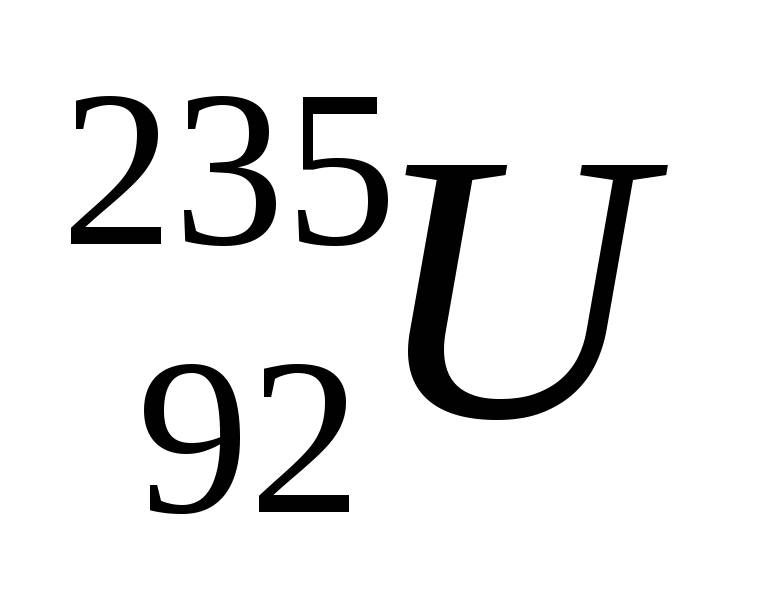 тепловыми нейтронами: тепловыми нейтронами:
кинетическая энергия осколков -- 167МэВ
мгновенные нейтроны -- 5 МэВ
электроны  --распада -- 5 МэВ --распада -- 5 МэВ
Антинейтрино  --распада -- 10МэВ --распада -- 10МэВ
мгновенное  -излучение -- 7 МэВ -излучение -- 7 МэВ
 -излучение продуктов распада -- 6 МэВ -излучение продуктов распада -- 6 МэВ
Характерной особенностью деления является то, что преобладает асимметричное деление (возникают разные по массе осколки). Так, в случае деления 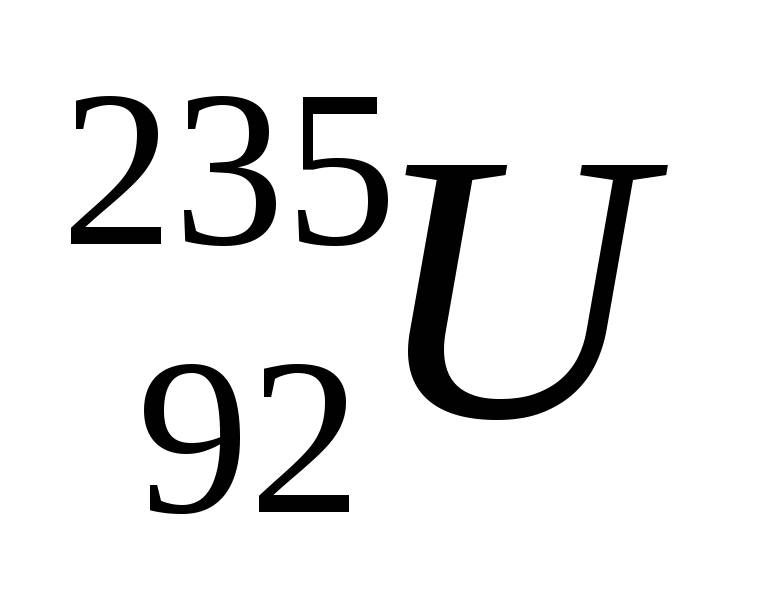 при захвате нейтрона (делится составное ядро при захвате нейтрона (делится составное ядро 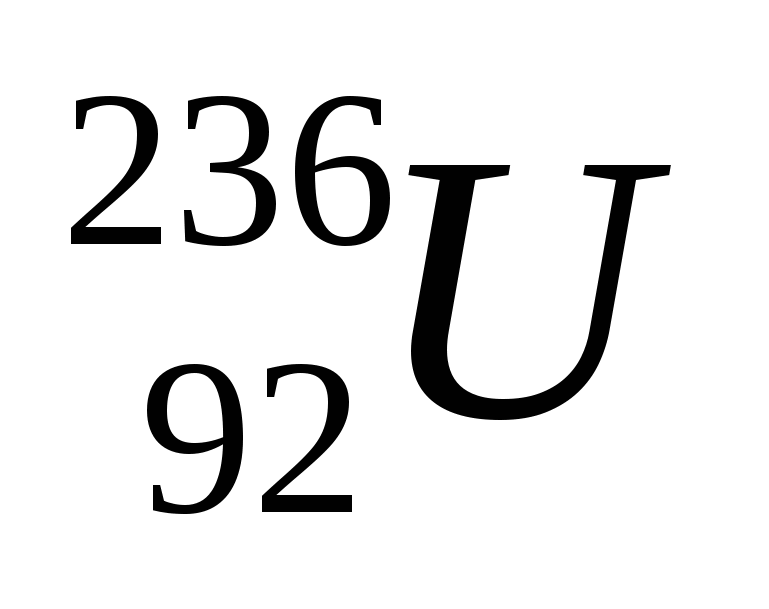 ) (рис.9): ) (рис.9):

Вероятность деления на равные осколки ≠0, но ~ на 3 порядка меньше, чем в случае наиболее вероятного деления на осколки с А=139 и 95. Капельная модель ядра не исключает возможность асимметричного деления, но не объясняет его основные закономерности. Асимметричное деление можно объяснить влиянием оболочечной структуры ядра. Ядро стремится разделиться таким образом, чтобы основная часть нуклонов каждого осколка образовала устойчивый магический остов.
Ядерное поле создается внутренними межнуклонными силами. Нуклоны в ядре должны часто сталкиваться и обмениваться энергиями. Средний пробег у нуклона должен быть меньше радиуса ядра. Это говорит о невозможности движения нуклонов внутри ядра по устойчивым орбитам, с долго сохраняющимися квантовыми числами, т.е. о невозможности нахождения их (нуклонов) на определённых оболочках.

Рис.9. Массовое распределение осколков деления урана.
Однако факты заставили оболочечную модель ввести. Было обнаружено, что ядра с числом нейтронов и/или протонов – 2, 8, 20, 50, 82, 126 (магические числа) обладают повышенной распространённостью, повышенной устойчивостью (с увеличением Bn), относительным уменьшением массы, резким увеличением энергии первого возбужденного состояния.
Оболочками в случае произвольного потенциала следует считать группы близко расположенных одночастичных уровней энергии.
Оболочечная структура ядра свидетельствует о том, что нуклоны в ядре во многом ведут себя как независимые частицы в потенциальной яме (одинаковый для всех нуклонов потенциал притяжения).
1.5.5. Механизм деления.
Если деление выгодно для ядра с Z2/A>17, т.е. с А≥90, то возникает вопрос: почему же большинство известных тяжёлых ядер устойчиво по отношению к спонтанному делению?
В ходе деления ядро проходит через стадии: шар, эллипсоид, гантель, 2 грушевидных осколка, 2 сферических осколка. Изменение энергии ядра на разных стадиях определяется изменением суммы поверхностной и кулоновской энергий начального ядра и осколков. При увеличении расстояния между центрами осколков (при делении 23692U из основного состояния на 2 асимметричных осколка) от начального значения r=0. Эта сумма сначала растёт, а затем уменьшается. Т.о. возникает потенциальный барьер, препятствующий мгновенному (за характерное ядерное время ~ 10-22с) спонтанному делению исходного ядра из основного состояния. Для 23692U величина этого барьера 6,5 МэВ. Барьер возникает потому, что поверхностная энергия с увеличением r (при r<10 Фм) растёт быстрее, чем уменьшается кулоновская энергия. Ядро 23692U в основном состоянии практически стабильно. Если ему добавить небольшую энергию, то оно может менять форму от сферической до эллипсоидальной, совершая небольшие колебания относительно исходного «сферического» состояния и не испытывая деления. Однако при передаче ядру энергии, большей величины барьера, амплитуда колебаний становится настолько большой, что ядро проскакивает максимальное значение потенциальной энергии и делится. Вершине барьера соответствует гантелевидная форма делящегося ядра. Как только ядро приобретает форму гантели деление становится необратимым.
Изменение полной энергии при переходе от сферы к эллипсоиду определяется соотношением:
 , где ε –малый параметр деформации ядра в выражениях для малой и большой осей эллипсоида: , где ε –малый параметр деформации ядра в выражениях для малой и большой осей эллипсоида: 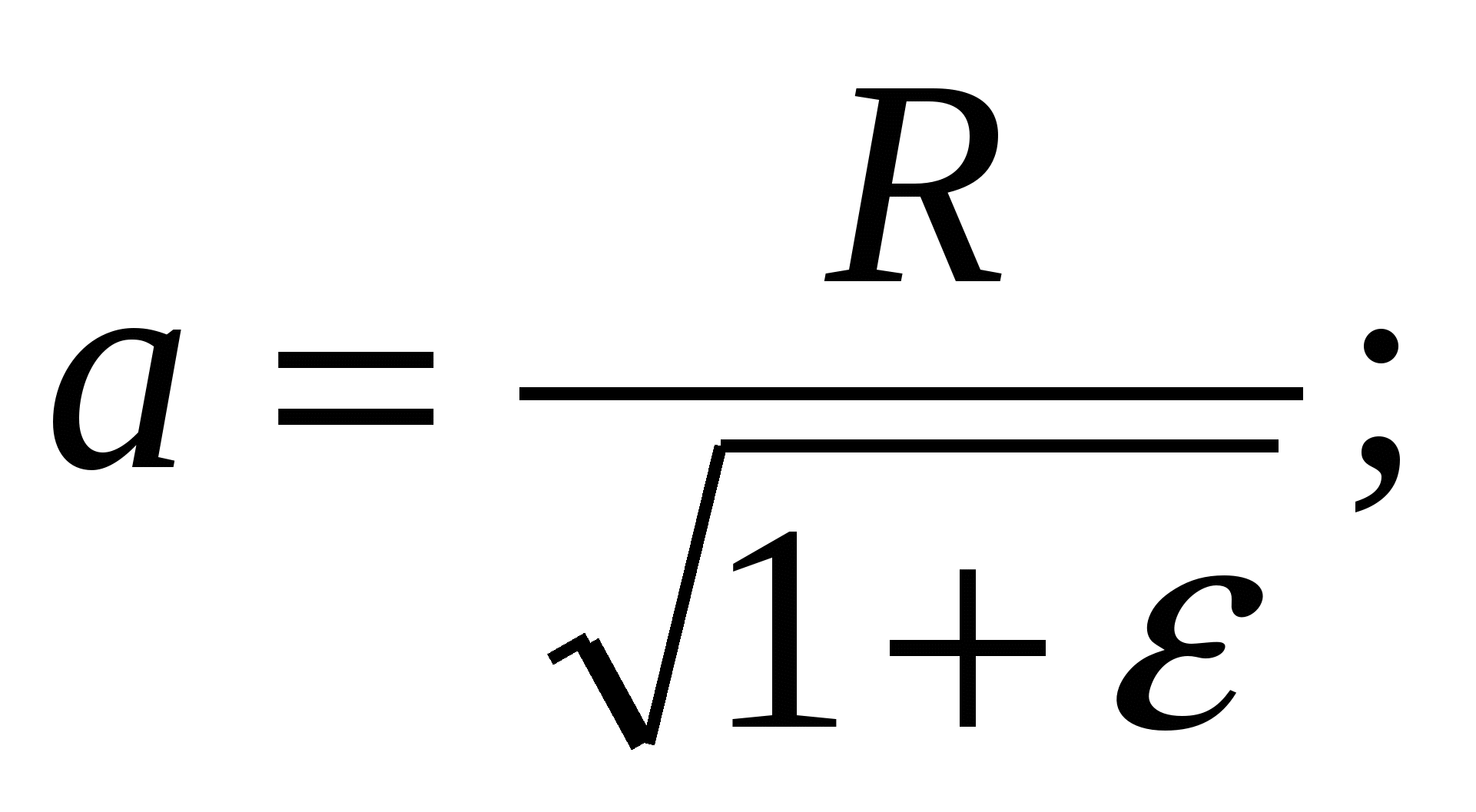  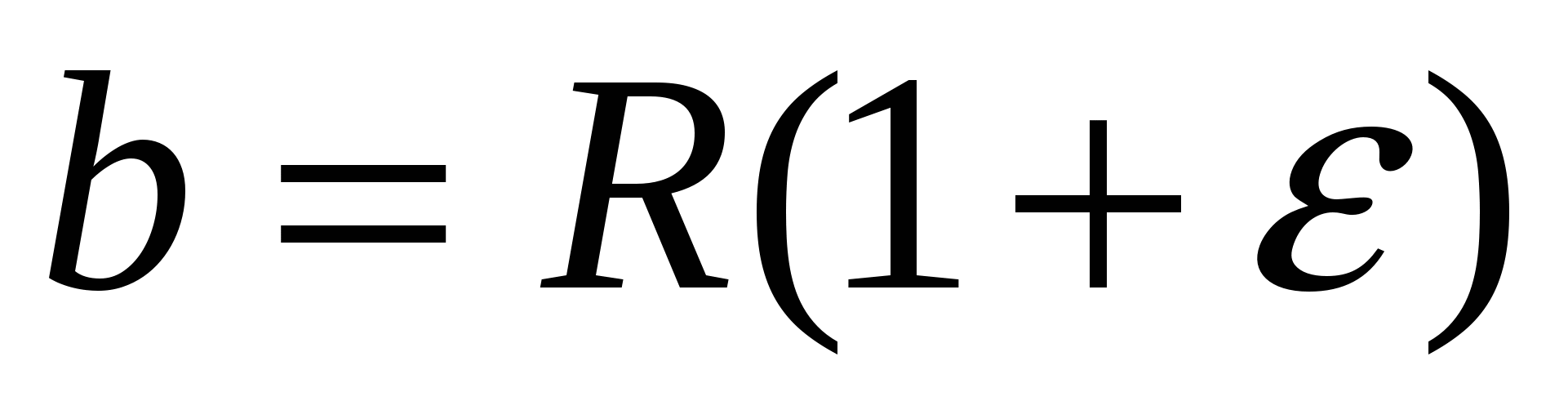 ; R – радиус исходного ядра. ; R – радиус исходного ядра.
Барьер возникает тогда, когда ΔE>0, т.е. при Z2/A<2as/ac≈48, причём высота барьера тем меньше, чем меньше выражение в скобках, т.е. чем больше параметр деления Z2/A. (Рис. 9)
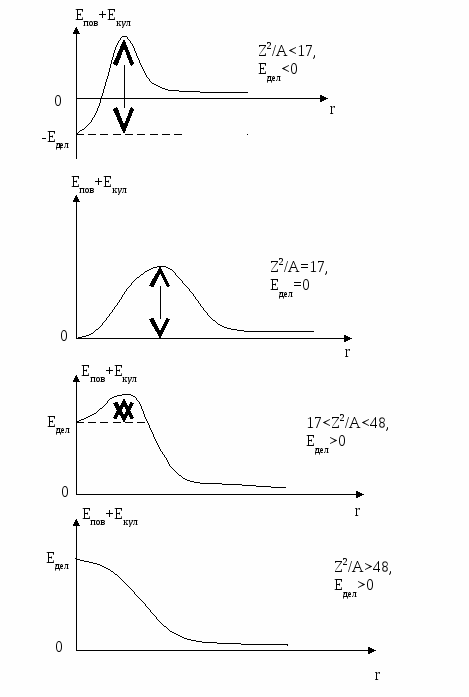
Рис. 10 Зависимость формы и высоты потенциального барьера, а также энергии деления от величины параметра Z2/A. Стрелками указана высота барьера.
При Z2/A≈48 барьер деления исчезает и ядра с таким или большим параметром деления неустойчивы к мгновенному (за время ~10-22с) спонтанному делению. Спонтанное деление ограничивает область существования устойчивых или долгоживущих ядер со стороны больших значений A и Z. Вероятность спонтанного деления растёт с увеличением Z2/A, т.е. с уменьшением высоты барьера. Период спонтанного деления уменьшается при переходе от менее тяжёлых ядер к более тяжёлым (от Т½>1021лет для 23290Th до 6 мс для 256104Rf). Также резко изменяется зависимость Т½ спонтанного деления от высоты барьера. При делении 23592U тепловыми нейтронами (n+23592U→23692U→9538Sr+13954Xe+2n) составное ядро 23692U получает энергию возбуждения, равную энергии отделения нейтрона (Bn) от ядра 23692U (кинетическая энергия Т теплового нейтрона ≈0,025эВ и добавкой к энергии возбуждения 23692U этой величины можно пренебречь). Т.к. Bn 23692U равна 6,8 МэВ, т.е. превышает барьер деления, то это ядро делится. Вынужденное деление может быть вызвано не только нейтронами, но и другими частицами. Однако использование нейтронов практически выгодно, т.к. их захвату ядром не препятствует кулоновский барьер и эффективное сечение захвата велико.
Итак, мерой способности к делению ядер в рамках капельной модели ядра может служить отношение кулоновского отталкивания протонов, стремящихся разорвать каплю, к энергии поверхностного натяжения, противодействующего растеканию капли: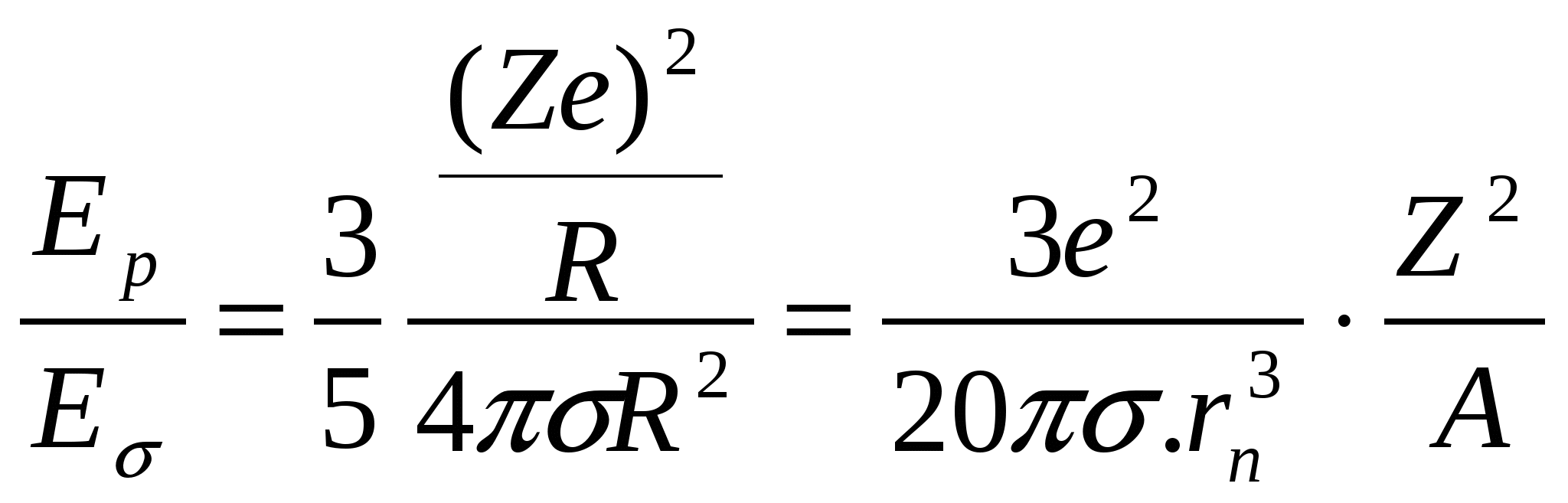 ; ;
σ- коэффициент поверхностного натяжения капли,
rn – радиус нуклона.
Z2/A – больше для 23692U, чем для 23992U следовательно, энергия активации (или величина барьера) реакции деления на ядрах 23692U меньше (6,5 МэВ), чем на ядрах 23992U (7,1 МэВ). Эти цифры характеризуют величину барьера, который должен быть преодолен при делении ядер 23692U и 23992U. Экспериментально было установлено, что энергия возбуждения у ядра 23992U – 5,5 МэВ, тогда как у 23692U – 6,8 МэВ, т.е. ядро 23692U должно делиться, находясь на энергетическом уровне более высоком, чем нужно для деления (6,8 МэВ-6,5 МэВ=0,3 МэВ), независимо от кинетической энергии падающего нейтрона, а ядро 23992U не будет делиться, если нейтрон не принесёт ещё дополнительную кинетическую энергию, равную 7,1-5,5=1,6 МэВ. Т.е. для деления ядер 23892U нужны быстрые нейтроны (с En>1,6 МэВ), тогда как ядра 23592U делятся тепловыми нейтронами.
1.6. Сечения рассеяния и поглощения тепловых нейтронов на ядрах некоторых биологически важных элементов.
Экспериментально определено, что даже для тепловых нейтронов сечение рассеяния больше сечения захвата (Табл. 3)
элемент
|
Сечение рассеяния, барн
|
С
Табл. 3. Сечение взаимодей-ствия тепловых нейтронов с
ядрами H, C, N, O.
ечение поглощения, барн
|
H
|
38
|
0,33 (n,γ)
|
C
|
4,8
|
0,0034 (n,γ)
|
N
|
10
|
1,75 (n,p)
|
0,13 (n,γ)
|
O
|
4,2
|
0,0002 (n,γ)
|
Сечение захвата быстро растёт при уменьшении En. Практически все нейтроны перд захватом при соударения внутри объекта замедляются до тепловой энергии. Самые большие сечения у ядер атомов водорода и азота.
Только небольшая часть биологического действия нейтронов вызывается этими двумя первичными процессами соударения и захвата. Большая часть радиационных повреждений происходит в результате действия ядер отдачи и вторичного излучения, которое индуцируется в процессе нейтронного захвата, т.е. основной ионизационный эффект будет определяться действием заряженных частиц. Поэтому нейтронное излучение относится к косвенно ионизирующим.
страница 1
|