страница 1
 Программа дисциплин Форма Программа дисциплин Форма
для студентов Ф СО ПГУ 7.18.2/06
Министерство образования и науки Республики Казахстан
Павлодарский государственный университет им. С. Торайгырова
Кафедра алгебры и математического анализа
ПРОГРАММА (ПДС)
обучения по дисциплине Действительный анализ
для студентов специальности(ей) 050601 Математика
Павлодар
 Лист утверждения к Форма Лист утверждения к Форма
программе дисциплины Ф СО ПГУ 7.18.2/11
для студентов
УТВЕРЖДАЮ
Декан ФФМиИТ
___________________Тлеукенов С.К.
«__»_______________20___г.
Составитель: к.ф.-м.н., профессор ПГУ им. С.Торайгырова Муканов Г.М. ____________
Кафедра алгебры и математического анализа
ПРОГРАММА (ПДС)
дисциплины «Действительный анализ» для студентов специальности 050601 Математика
Программа разработана на основании рабочей учебной программы, утверждённой
«___» _________200_г.
Рекомендована на заседании кафедры «____»________200__ г. Протокол №____
Заведующий кафедрой_____________________________И.И. Павлюк
(подпись)
Одобрена учебно-методическим советом факультета
«___»___________200__г. Протокол №______
Председатель УМС_______________________________ А.Т.Кишубаева
(подпись)
СОГЛАСОВАНО
Заведующий кафедрой ____________________Павлюк И.И.
(подпись)
«_____»___________________200_г.
Цели и задачи дисциплины, ее место в учебном процессе
Пререквизиты: курс опирается на дисциплины:
- высшая алгеба;
- геометрия;
- математически анализ.
Краткое описание дисциплины (аннотация)..Теория функций действительного переменного, иначе – действительный анализ, является одним из основополагающих разделов математического анализа в широком смысле. Она дополняет и обобщает классический математический анализ. Ее содержание составляет вопросы, зародившиеся в недрах классического анализа, и находившие свои решения в трудах крупных математиков во второй половине Х1Х и в первой четверти ХХ веков
1.1 Цель курса – изложение основных понятий и фактов этой теории, без знания которых была бы неполноценной аналитическая культура специалиста-математика, но также было бы затруднительно изучение многих разделов современной математической науки.
1.2 Задача курса – развить у студентов умение обращаться с объектами теории, помочь им в овладении аппаратом курса, ее своеобразными методами.
 Тематический план Форма Тематический план Форма
дисциплины СО ПГУ 7.18.2/07
ТЕМАТИЧЕСКИЙ ПЛАН ДИСЦИПЛИНЫ
|
№
п/п
|
Наименование тем
|
Количество часов
|
Лекц.
|
Прак.
|
СРC
|
1
|
2
|
3
|
4
|
6
|
1
|
Множества
|
2
|
4
|
|
2
|
Топологические классы множеств
|
2
|
4
|
|
3
|
Мера множеств
|
2
|
4
|
|
4
|
Измеримые функции
|
2
|
4
|
|
5
|
Интеграл Лебега
|
3
|
6
|
|
6
|
Восстановление функции по ее производной
|
1
|
2
|
|
7
|
Классы функции.
|
2
|
4
|
|
8
|
Мера и интеграл Лебега в 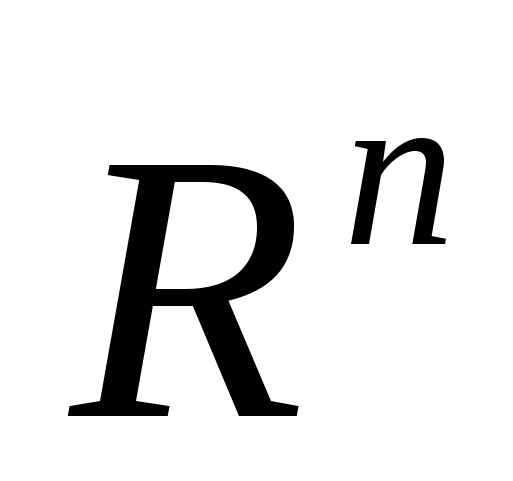
|
1
|
2
|
|
ИТОГО:
|
15
|
30
|
90
|
3 Содержание теоретического курса
3.1 Содержание лекции
Тема 1 Множества
Лекция №1. Примеры множества различной природы. Числовые множества N, Z, Q, I, R. Операции над множествами. Функции на множествах, взаимно однозначные отображения. Эквивалентные множества. Мощность множества. Конечные, счетные множества.
Лекция №2. Множества мощности континуума. Теоремы о счетных и континуальных множествах. Сравнение мощностей. Теорема Кантора-Бернштейна.
Тема 2 Топологические классы множеств.
Лекция №3. Открытые и замкнутые множества, их объединения и пересечения. Строение открытых и замкнутых множеств во множестве R действительных чисел и их строение.
Лекция №4. Множества всюду плотные и нигде неплотные на данном множестве. Совершенное множество. Канторовы открытое и совершенное множество.
Тема 3 Мера множества
Лекция №5. Мера открытых множеств, ее аддитивное свойство. Внешняя мера на R, ее монотонность и счетная полуаддитивность. Определение меры Лебега для числовых множеств. Множество меры нуль и связанные с ним свойства. Примеры простейших измеримых множеств.
Лекция №6. Измеримость множества по Каратеодори. Эквивалентность различных определений измеримости множества. Доказательство замкнутости системы всех измеримых множеств относительно конечных и счетных операций.
Тема 4 Измеримые функции
Лекция №7. Определение и простейшие примкры измеримых функций. Измеримость суммы, пройзведения и частного измеримых функций. Сходимость почти всюду и по мере последовательности измеримых функций. Измеримость предела последовательности, сходящейся почти всюду.
Лекция №8. Основные виды сходимостей (всюду, равномерная, почти всюду и по мере) и их сравнение.
Тема 5 Интеграл Лебега
Лекция №9. Определение интеграла Лебега от ограниченной функции на множестве конечной меры и его существование. Основные свойства. Теорема Лебега о предельном переходе под знаком интеграла Лебега. Сравнение интеграла Лебега с интегралом Римана.
Лекция №10.. Функций ограниченной вариации и их свойства. Абсолютно непрерывные функции и их свойства
Лекция №11. Мера Лебега-Стилтьеса. Интегралы Лебега-Стилтьеса и Римана-Стилтьеса.
Тема 6 Восстановление функции по ее производной
Лекция №12. Абсолютная непрерывность неопределенного интеграла Лебега. Теорема Лебега о восстановлении абсолютно непрерывной функции по ее пройзводной. Граница применимости формулы Ньютона-Лейбница.
Тема 7 Классы функций
Лекция №13. Класс суммируемых по Лебегу функций. Шкала лебеговских классов. Сходимость последовательности измеримых функций в среднем.
Лекция №14. Сравнение сходимости в среднем с другими видами сходимостей. Класс функций, суммируемых в среднем квадратическом.
Тема 8 Мера и интеграл Лебега в пространстве 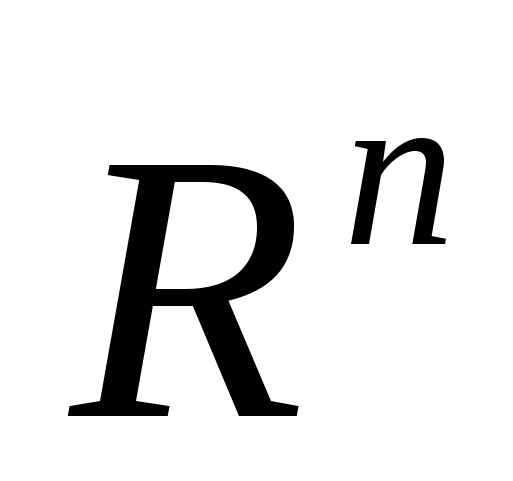
Лекция №15. Функции многих переменных, определенные на множествах конечномерного действительного пространства. Произведение линейных мер. Суммируемые функции многих переменных. Теорема Фубини.
3.2 Содержание практических занятий
Тема 1 Множества
Занятие №1. Примеры множеств различной природы. Операции над множествами.
Вопросы, подлежащие освоению:
* понятие множества (на примерах N, Z, Q, I, R и другие);
* операции над множествами.
* Решение примеров. [8] 1 – 25 (решить 5, 6 примеров по выбору);
Литература [1], 17 – 21.
Занятие №2. Функции па множествах
Вопросы, подлежащие освоению:
* взаимно однозначное отображение;
* эквивалентные множества;.
* Решение примеров. [8] 27 – 44 (решить 5, 6 примеров по выбору );
Литература [1], 21 – 26.
Занятие №3. Мощность множества
Вопросы, подлежащие освоению:
* понятие мощности множества;
* конечная мощность;
* счетная мощность;
* свойства счетной мощности;
* Решение примеров. [8] 61 – 68 (решить 5, 6 примеров пл выбору);
Литература [1], 26 – 30.
Занятие №4. Сравнение мощностей
Вопросы, подлежащие освоению:
* множество мощности континуума;
* сравнение мощностей (определение нонятий: «больше», «меньше» и «равно» между мощностями);
* доказательство того, что мощность континуума больше счетной мощности;
* теорема Кантора-Бернштейна;
* теорема о неограниченности совокупности всех мощностей;
* континуум - гипотеза Кантора
* Решение примеров. [8] 27 – 44 (решить 5, 6 примеров по выбору.);
Литература [1], 30 – 34.
Тема 2 Топологические классы множеств
Занятие №5
Вопросы, подлежащие освоению:
* основные типы точек (точка прикосновения, предельная точка, точка еонденсеции, изолированная точка, внутренняя точка, внешняя точка, граничная точка);
* окрестность точки числовой прямой;
* основные типы множеств (открвтые, замкнутые, всюду плотные, плотные в себе, совершенные);
* Канторово совершенное множество 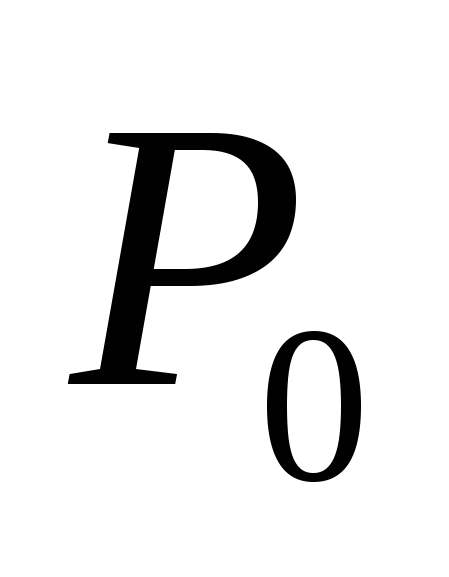 , его мощность. , его мощность.
* Решение примеров. [8] 225.
Литература [1], 67 – 78, 288 – 303.
Занятие №6
Вопросы, подлежащие освоению:
* Канторово открытое множество Р как дополнение Каторово совершенного множества Р0 до сегмента [0,1]
* Структура ограниченного открытого, Замкнутого и совнршенного множества.
* Решение примеров. [8] 213 - 216.
Литература [1], 288 – 303.
Занятие №7
Вопросы, подлежащие освоению:
* всюду плотные множества;
* нигде неплотные множества;
* нигде неплотность канторова совершенного множества.
* Решение примеров. [8] 217 – 220.
Литература [1], 288 – 323
Занятие №8
Вопросы, подлежащие освоению:
* Арифметическая структура канторво совершенного множества.
* Решение примеров. [8] 225 – 230.
Литература [1], 288 – 323.
Тема 3 Мера множеств
Занятие №9
Вопросы, подлежащие освоению:
* мера открытых множеств;
* аддитивность меры открытого множества;
* Внешняя мера на R;
* счетная полуаддитивность внешней меры;
* Решение примеров. [8] 408 – 411.
Литература [1], 288 – 323.
Занятие №10
Вопросы, подлежащие освоению:
* определение меры Лебега для числовых множеств;
* множество меры нуль и связанные с ним свойства;
* примеры простейших измеримых множеств;
* Решение примеров. [8] 416 – 418.
Литература [1], 288 – 323.
Занятие №11
Вопросы, подлежащие освоению:
* измеримость множеств по Каратеодори;
* Эквивалентность различнвх определений измеримости множеств.
* Решение примеров. [8] 419, 420.
Литература [1], 323 – 334.
Занятие №12
Вопросы, подлежащие освоению:
* Доказательство замкнутости системы всех измеримых множеств относительно конечных и счетных операций.
* Решение примеров. [8] 421 – 425. Литература [1], 323 – 334.
Тема 4 Измеримые функции
Занятие №13
Вопросы, подлежащие освоению:
* определение измеримой функции;
* измеримость суммы измеримых функций;
* пройзведения и частного измеримых функций.
* Решение примеров. [8] 679 – 685.
Литература [1], 323 – 334.
Занятие №14
Вопросы, подлежащие освоению:
* сходимость последовательности почти всюду;
* сходимость последовательности по мере;
* сходимость последоательности всюду;
* равномерная сходимость последовательности;
* Решение примеров. [8] 696, 699.
Литература [1], 323 – 334.
Занятие №15
Вопросы, подлежащие освоению:
* измеримость предела последовательности, сходящейися почти всюду.
* сравнение сходимости по мере со сходимостию почти всюду (теорема Лебнга, пример Рисса, теорема Рисса).
* Решение примеров № 699, 700.
Литература [1], 323 – 334.
Занятие №16
Вопросы, подлежащие освоению:
* сравнение сходимости пости вюду с равномерной сходимостью (т. Егорова Д.Ф.);
* сруктура измеримой функции (т. Лузина Н.Н., или С-свойство).
Литература [1], 323 – 334.
Тема 5 Интеграл Лебега
Занятие №17
Вопросы, подлежащие освоению:
* определение интеграла Лебега от ограниченной функции;
* основные свойства интеграла Лебега;
* Решение примеров. [8] 710, 709, 710.
Литература [1], 334 – 355.
Занятие №18
Вопросы, подлежащие освоению:
* существование интеграла Лебега от измеримой ограничнной функции;
* Решение примеров. [8] 713, 714.
Литература [1], 334 – 355.
Занятие №19
Вопросы, подлежащие освоению:
* сравнение интегала Лебега с интегралом Римана.
* Решение примеров. [8] Решить примеры: № 715 – 718
Литература [1], 334 – 355.
Занятие №20
Вопросы, подлежащие освоению:
* интеграл Лебега от неотрицательной измеримой функции;
* суммируемые функции любого знака.
* Решение примеров. [8] 719, 723 – 725.
Литература [1], 334 – 355.
Занятие №21
Вопросы, подлежащие освоению:
* предельный переход под знаком интеграла Лебега.
* Решение примеров. [8] 732 – 735.
Литература [1], 334 – 355.
Занятие №22
Вопросы, подлежащие освоению:
* функции с ограниченным иизменением;
* мера Лебега-Стилтьеса;
* интеграл Лебега-Стилтьеса;
* интеграл Римана-Стилтьеса.
* Решение примеров. [8] 736, 745, 746.
Литература [1], 368 – 423.
Тема 6 Восстановление функции по ее пройзводной
Занятие №23
Вопросы, подлежащие освоению:
* представимость монотонной функции как разность двух монотонно неубыващих функции;
* абсолютно непрерывная функция;
* функция скачков;
* сингулярная функция;
* представимлсть функции с ограниченным изменением в виде суммы трех компанент – функции скачков, абсолютно непрерывной функции и сингулярной функции.
Литература [1], 368 – 423.
Занятие №24
Вопросы, подлежащие освоению:
* восстановление функции по ее производной;
* граница применимости формулы Ньютона-Лейбница.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Тема 7 Классы функции
Занятие №25
Вопросы, подлежащие освоению:
* класс интегрируемых по Лебегу функций;
* классы функций Лебега 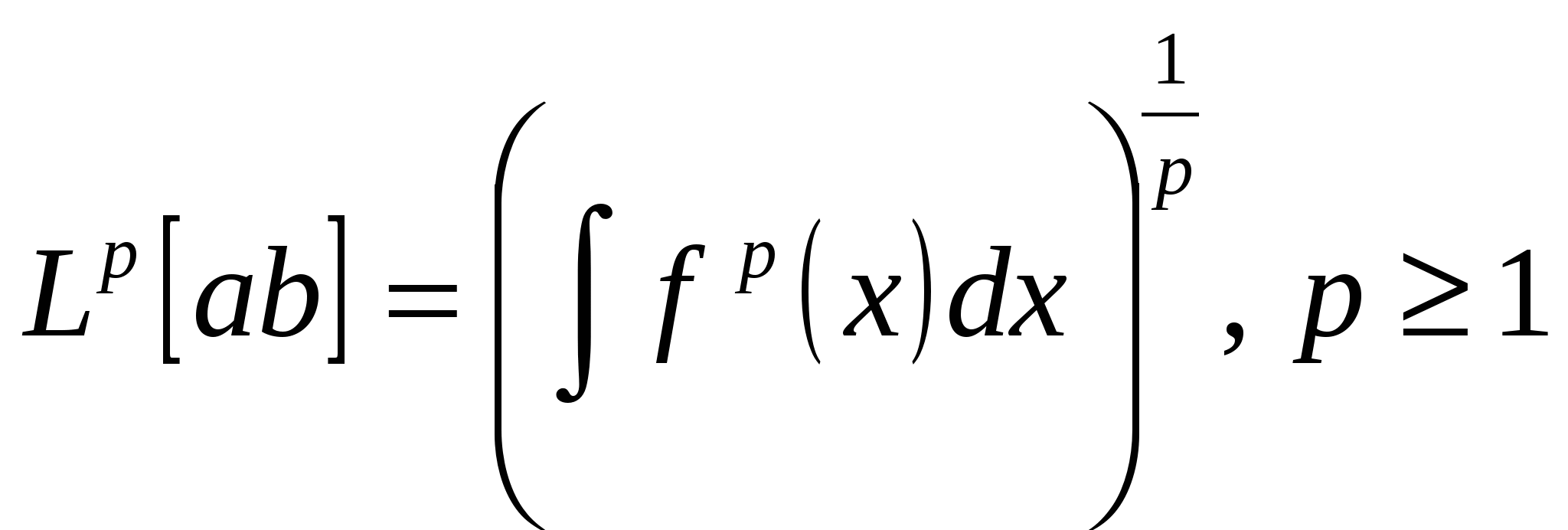 ; ;
* сходимость последовательности суммируемых по Лебегу функций в среднем;
* сравнение сходимости в среднем со сходимостью по мере.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Занятие №26
Вопросы, подлежащие освоению:
* сходимость в классе функций с суммируемым квадратом;
* сравнение сходимости в среднеквадратическом с другими видами сходимости.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Занятие №27
Вопросы, подлежащие освоению:
* тригонометрическая система функций;
* коэффициенты Фурье функции с суммируемым квадратом;
* ряд Фурье функции с суммируемым квадратом.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Занятие №28
Вопросы, подлежащие освоению:
* примеры на разложение функции в ряд Фурье.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 368 – 423.
Тема 8 Мера и интеграл Лебега в Rn
Занятие №29
Вопросы, подлежащие освоению:
* функции, определенные на множествах пространства Rn;
* произведение линейных мер;
* определение кратного интеграла.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 355 –363.
Занятие №30
Вопросы, подлежащие освоению:
* суммируемые функции многих переменных;
* теорема Фубини.
* Решение примеров. [8] 1 – 25 (решить примеры :№ 27 – 44, по выбору 5, 6 пр.);
Литература [1], 355 – 363.
3.3 Содержание СРC
№
|
Вид СРC
|
Форма отчётности
|
Вид контроля
|
Объем в часах
|
1
|
Подготовка к лекционным занятиям
|
Наличие конспекта
|
Участие на занятии
|
10
|
2
|
Подготовка к практическим занятиям, выполнение домашних заданий
|
Рабочая тетрадь
|
контрольные вопросы, отчет
|
12
|
3
|
Изучение материала, не вошедшего в содержание аудиторных занятий
|
Конспект
|
Участие на практических занятиях, контрольных мероприятиях
|
14
|
4
|
Выполнение индивидуальных заданий
|
Наличие тетради с решениями
|
Защита ИЗ
|
12
|
5
|
Подготовка к контрольным мероприятиям
|
|
РК 1, РК 2, коллоквиум (тестирование и другие)
|
12
|
Всего:
|
90
|
Темы для самостоятельного изучения
Тема 1 Множества
Лекция №1. Примеры множества различной природы. Числовые множества N, Z, Q, I, R. Операции над множествами. Функции на множествах, взаимно однозначные отображения. Эквивалентные множества. Мощность множества. Конечные, счетные множества.
Лекция №2. Множества мощности континуума. Теоремы о счетных и континуальных множествах. Сравнение мощностей. Теорема Кантора-Бернштейна.
Рекомендуемая литература: [1], [2], [3]
Тема 2 Топологические классы множеств.
Лекция №3. Открытые и замкнутые множества, их объединения и пересечения. Строение открытых и замкнутых множеств во множестве R действительных чисел и их строение.
Лекция №4. Множества всюду плотные и нигде неплотные на данном множестве. Совершенное множество. Канторовы открытое и совершенное множество.
Рекомендуемая литература: [2], [3], [4]
Тема 3 Мера множества
Лекция №5. Мера открытых множеств, ее аддитивное свойство. Внешняя мера на R, ее монотонность и счетная полуаддитивность. Определение меры Лебега для числовых множеств. Множество меры нуль и связанные с ним свойства. Примеры простейших измеримых множеств.
Лекция №6. Измеримость множества по Каратеодори. Эквивалентность различных определений измеримости множества. Доказательство замкнутости системы всех измеримых множеств относительно конечных и счетных операций.
Рекомендуемая литература: [1], [2], [3]
Тема 4 Измеримые функции
Лекция №7. Определение и простейшие примкры измеримых функций. Измеримость суммы, пройзведения и частного измеримых функций. Сходимость почти всюду и по мере последовательности измеримых функций. Измеримость предела последовательности, сходящейся почти всюду.
Лекция №8. Основные виды сходимостей (всюду, равномерная, почти всюду и по мере) и их сравнение.
Рекомендуемая литература: [4], [5], [6]
Тема 5 Интеграл Лебега
Лекция №9. Определение интеграла Лебега от ограниченной функции на множестве конечной меры и его существование. Основные свойства. Теорема Лебега о предельном переходе под знаком интеграла Лебега. Сравнение интеграла Лебега с интегралом Римана.
Лекция №10.. Функций ограниченной вариации и их свойства. Абсолютно непрерывные функции и их свойства
Лекция №11. Мера Лебега-Стилтьеса. Интегралы Лебега-Стилтьеса и Римана-Стилтьеса.
Рекомендуемая литература: [3], [4], [6]
Тема 6 Восстановление функции по ее производной
Лекция №12. Абсолютная непрерывность неопределенного интеграла Лебега. Теорема Лебега о восстановлении абсолютно непрерывной функции по ее пройзводной. Граница применимости формулы Ньютона-Лейбница.
Рекомендуемая литература: [6], [7], [8]
Тема 7 Классы функций
Лекция №13. Класс суммируемых по Лебегу функций. Шкала лебеговских классов. Сходимость последовательности измеримых функций в среднем.
Лекция №14. Сравнение сходимости в среднем с другими видами сходимостей. Класс функций, суммируемых в среднем квадратическом.
Рекомендуемая литература: [3], [5], [7]
Тема 8 Мера и интеграл Лебега в пространстве 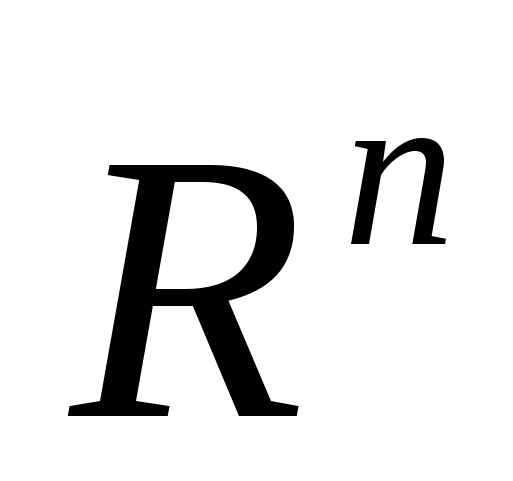
Лекция №15. Функции многих переменных, определенные на множествах конечномерного действительного пространства. Произведение линейных мер. Суммируемые функции многих переменных. Теорема Фубини.
Рекомендуемая литература: [7], [8], [9]
Литература
Основная:
-
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М: Наука, 1989.
-
Натансон И.П. Терия функций вещественной переменной. М: Наука, 1974.
-
Дьяченко М.И. , Ульянов П.П. Мера и интеграл. М: Факторная, 1998.
-
Теміргалиев Н. Математикалық анализ, т.2. Алматы: Ана тілі, 1991.
-
Лузин Н.Н. Теория функций действительного переменного . - М.: ГУНИ,
-
Брудно А.Л. Теория функций действительного переменного . - М.: Наука, 1971.
-
Толстов Г.П. Мера и интеграл. – М.: Наука, 1976.
-
Очан Ю.С. Сборник задач по математическому анализу. М. 1981.
-
Теляковский С.А. Сборник задач по теории функций действительного переменного. М: Наука, 1980.
Дополнительная:
-
Александров П.С. ВВедение в теорию множеств и общую топологию.М,1977.
-
Хаусдорф Ф. Терия множеств. М. ОНТИ, 1937.
-
Халмош П. Теория меры. М: ИЛ, 1953.
-
Сахс С. Теория интеграла. М.: ИЛ, 1949.
-
Рудин У. Основы математическогго анлиза. М. : Мир, 1966.
-
Лузин Н.Н. Интеграл и тригонометрический ряд . М.: ГИТТЛ, 1951.
-
Камне Е. Интеграл Лебега- Стилтьеса. М.: Физматгиз, 1959.
17. Ғ. М. Мұқанов, Нақты айнымалы функциялар теориясының негіздері.
 Выписка из рабочего Форма Выписка из рабочего Форма
учебного плана Ф СО ПГУ 7.18.1/10
специальности(ей)
Выписка из рабочего учебного плана специальности
050601 Математика
Наименование дисциплины Действительный анализ
Форма обучения
|
Формы контроля
|
Объём работы обучающихся, в часах
|
Распределение часов по курсам и семестрам (часов)
|
экз.
|
зач.
|
КП
|
КР
|
РГР
|
контр.
раб
|
всего
|
лек
|
пр.
|
лаб
|
СРС
|
лек
|
пр.
|
лаб
|
СРС
|
общ
|
ауд
|
СРС
| |
очная на базе ОСО
|
4
|
|
|
|
|
|
135
|
45
|
90
|
семестр 3
|
семестр 4
|
|
|
|
|
15
|
30
|
|
90
|
Политика курса
В политике курса выполнение всех практических и самостоятельных заданий являются обязательным условием.
Посещение занятий является обязательным. Уважительные причины пропуска занятий не освобождают студента от выполнения всего комплекса практических и самостоятельных работ.
В случае опоздания на занятие студент не допускается к занятию.
За любые нарушения правил поведения на занятиях устанавливаются штрафные санкции — вычитается 5 баллов за одно занятие!
Все аудиторное время будет поделено на лекции, выполнение практических работ. Подготовка к каждому занятию обязательна, также как и прочтение всего заданного материала. Ваша подготовка будет проверяться контрольными работами, тестами и заданиями рубежного контроля.
Самостоятельная работа должна быть выполнена соответственно вашему варианту, иначе работа не будет зачтена. Вариант задания указывает преподаватель.
Все задания должны выполняться к установленному времени. Задания, выполненные с опозданием, будут автоматически оцениваться ниже. Списывание на любом из видов контроля, а также на экзамене запрещено. Штрафные санкции составят в этом случае 80% от балла за данный вид контроля.
Если в силу каких-либо причин вы отсутствовали во время проведения контрольного мероприятия, вам предоставляется возможность пройти его на консультациях преподавателя в течении одной последующей недели в соответствии с установленным графиком.
Виды контроля
|
Максимальное число баллов
|
|
ТУ1
|
ТУ2
|
|
|
|
1 Посещение занятий, подготовка к занятиям и работа в группе
|
24
|
22
|
2 Выполнение и защита практических работ
|
38
|
36
|
3 Выполнение и защита заданий на СРС (РГР, рефераты и др.)
|
38
|
42
|
Итого
|
100
|
100
|
Оценка рубежного контроля (РК) так же определяется по 100
балльной шкале.
К рубежному контролю по дисциплине допускаются студенты, имеющие баллы по ТУ.
По итогам оценки ТУ и РК определяется рейтинг (Р1 и Р2) студента
по дисциплине
Р1(2) = ТУ 1(2)*0,7 + РК1(2)*0,3.
Если в учебном плане предусмотрены экзамен и зачёт, то зачёт следует учесть при определении Р2 как второй рубежный контроль.
Рейтинг не определяется, если студент не прошел РК или получил по РК менее 50 баллов. В данном случае декан устанавливает индивидуальные сроки сдачи РК.
Оценка рейтинга допуска студента по дисциплине за семестр равна
РД = (Р1+Р2)/2.
К итоговому контролю (ИК) по дисциплине допускаются студенты,
выполнившие все требования рабочей учебной программы (выполнение и сдача всех лабораторных работ, работ и заданий по СРС), получившие положительную оценку за защиту курсового проекта (работы) и набравшие рейтинг допуска (не менее 50 баллов).
Уровень учебных достижений студентов по каждой дисциплине (в
том числе и по дисциплинам, по которым формой итогового контроля ГЭ)
определяется итоговой оценкой (И), которая складывается из оценок РД и
ИК (экзамена, дифференцированного зачета или курсовой работы/проекта) с
учетом их весовых долей (ВДРД и ВДИК).
И = РД*0,6 + ИК*0,6
Итоговая оценка по дисциплине подсчитывается только в том случае,
если обучающийся имеет положительные оценки, как по рейтингу допуска,
так и по итоговому контролю. Не явка на итоговый контроль по
неуважительной причине приравнивается к оценке «не удовлетворительно».
Результаты экзамена и промежуточной аттестации по дисциплине доводятся
до студентов в тот же день или на следующий день, если письменный
экзамен проводился во второй половине дня.
Пересдача положительной оценки по итоговому контролю (в том
числе на ГЭ) с целью ее повышения не разрешается.
Виды контроля: ПР – практическая работа, СРС- самостоятельная работа студента, РК – рубежный контроль
Итоговая оценка знаний обучающихся
Итоговая оценка в баллах (И)
|
Цифровой эквивалент баллов (Ц)
|
Оценка в буквенной системе
|
Оценка по традиционной системе
|
Экзамен, диф.зачет
|
Зачет
|
95-100
|
4
|
A
|
Отлично
|
Зачтено
|
90-94
|
3,67
|
A-
|
85-59
|
3,33
|
B+
|
Хорошо
|
80-84
|
3,0
|
B
|
75-79
|
2,67
|
B-
|
70-74
|
2,33
|
C+
|
Удовлетворительно
|
65-69
|
2,0
|
C
|
60-64
|
1,67
|
C-
|
55-59
|
1,33
|
D+
|
50-54
|
1,0
|
D
|
0-49
|
0
|
F
|
Не удовлетворительно
|
Не зачтено
|
Календарный график контрольных мероприятий текущей успеваемости
дисциплина: Геометрия
1 рейтинг
|
Недели
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Всего
|
Максимальный балл за неделю
|
5
|
11
|
12
|
10
|
10
|
12
|
30
|
10
|
100
|
Посещение и подготовка к лекциям
|
Вид контр.
|
У
|
У
|
У
|
У
|
У
|
У
|
У
|
У
|
17
|
Макс.балл
|
1
|
1
|
1+1,5
|
1+1,5
|
1+1,5
|
1+1,5
|
1+1,5
|
1+1,5
|
Посещение и подготовка к практическим занятиям
|
Вид контр.
|
У
|
У
|
У
|
У
|
У
|
У
|
У
|
У
|
32
|
Макс.балл
|
3
|
5
|
5
|
3
|
5
|
5
|
3
|
3
|
Изучение материала, не вошедшего в содержание аудиторных занятий.
|
Вид контр.
|
|
И
|
|
И
|
И
|
И
|
|
|
19
|
Макс.балл
|
|
4
|
|
5
|
5
|
5
|
|
|
Выполнение
индивидуальных заданий.
|
Форма контр.
|
|
|
ТЗТФ1
|
|
|
|
ТЗТФ2
|
|
7
|
Макс.балл
|
|
|
3
|
|
|
|
4
|
|
Подготовка к контр. мероприятиям.
|
Форма контр.
|
|
|
|
|
|
|
|
К1
|
25
|
Макс.балл
|
|
|
|
|
|
|
|
25
|
2 рейтинг
|
Недели
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
-
|
Всего
|
Максимальный балл за неделю
|
11
|
12
|
11
|
12
|
10
|
12
|
32
|
|
100
|
Посещение и подготовка к лекциям
|
Вид контр.
|
У
|
У
|
У
|
У
|
У
|
У
|
У
|
|
14
|
Макс.балл
|
2
|
1+1
|
1+1
|
1+1
|
1+1
|
1+1
|
1+1
|
|
Посещение и подготовка к практическим занятиям
|
Вид контр.
|
У
|
У
|
У
|
У
|
У
|
У
|
У
|
|
37
|
Макс.балл
|
6
|
5
|
6
|
5
|
5
|
5
|
5
|
|
Изучение материала, не вошедшего в содержание аудиторных занятий.
|
Вид контр.
|
И
|
|
И
|
|
И
|
|
|
|
15
|
Макс.балл
|
5
|
|
5
|
|
5
|
|
|
|
Выполнение
индивидуальных заданий.
|
Форма контр.
|
|
ТЗТФ3
|
|
ТЗТФ4
|
|
ТЗТФ5
|
|
|
9
|
Макс.балл
|
|
3
|
|
3
|
|
3
|
|
|
Подготовка к контр. мероприятиям.
|
Форма контр.
|
|
|
|
|
|
|
К2
|
|
25
|
Макс.балл
|
|
|
|
|
|
|
25
|
|
Условные обозначения: У - участие в учебном процессе, ТЗТФ – тематические задания в тестовой форме, И – индивидуальных заданий, КР – контрольная работа по темам первого рейтинга, Т – тестирование по темам второго рейтинга.
страница 1
|