|
|
|
страница 1
Вопросы к экзамену по курсу
«МАТЕМАТИЧЕСКИЙ АНАЛИЗ»
(специальность – Физика. Техническое творчество. 2 курс 4 семестр)
-
Площадь поверхности. Сторона поверхности.
-
Площадь криволинейной поверхности.
-
Вычисление площади поверхности.
-
Поверхностный интеграл первого рода.
-
Поверхностный интеграл второго рода.
-
Выражение объема тела поверхностным интегралом.
-
Формула Стокса.
-
Формула Гаусса-Остроградского.
-
Скалярные векторные поля.
-
Поток вектора через поверхность.
-
Дивергенция, циркуляция, специальные поля.
-
Понятие комплексного числа. Операции сложения, умножения, вычитания и деления комплексных чисел.
-
Алгебраическая форма комплексного числа. Геометрическое представление комплексного числа.
-
Тригонометрическая форма комплексного числа. Действия над комплексными числами, заданными в тригонометрической форме.
-
Множества точек на комплексной плоскости.
-
Определение функции комплексного переменного.
-
Геометрическая интерпретация понятия функции комплексного переменного.
-
Отображение подобия.
-
Отображение вращения.
-
Определение предела функции комплексного переменного.
-
Теоремы о пределах.
-
Непрерывность функций комплексного переменного. Свойства непрерывных функций.
-
Определение производной функции комплексного переменного. Дифференциал.
-
Условия Коши-Римана.
-
Сопряженные гармонические функции.
-
Геометрический смысл модуля и аргумента производной.
-
Понятие конформного отображения.
-
Основные функции комплексного переменного.
-
Определение интеграла от функции комплексного переменного.
-
Связь интеграла комплексной переменной с криволинейным интегралом второго рода
-
Свойства интегралов по комплексному переменному.
-
Основная теорема Коши.
-
Неопределенный интеграл в комплексной области.
-
Формула Коши.
-
Теорема о среднем для аналитических функций.
-
Принцип максимума модуля аналитической функции.
-
Интеграл типа Коши.
-
Теорема Коши-Лиувилля. Теорема Морера.
-
Ряды с комплексными числами.
-
Ряды функций комплексного переменного.
-
Равномерная сходимость функционального ряда. Признак Вейерштрасса.
-
Степенные ряды.
-
Ряд Тейлора. Голоморфные функции.
-
Ряд Лорана.
-
Разложение аналитической функции в ряд Лорана.
-
Классификация изолированных особых точек аналитической функции.
-
Устранимая особая точка.
-
Полюс.
-
Существенно особая точка.
-
Разложение аналитической функции в ряд Лорана в окрестности бесконечно удаленной точки.
-
Определение вычета. Основная теорема Коши о вычетах
-
Вычисление вычетов функции относительно полюса.
-
Логарифмический вычет.
-
Принцип аргумента.
-
Основная теорема алгебры.
-
Вычет функции относительно бесконечно удаленной точки. Теорема о сумме вычетов.
-
Вычисление определенных интегралов типа 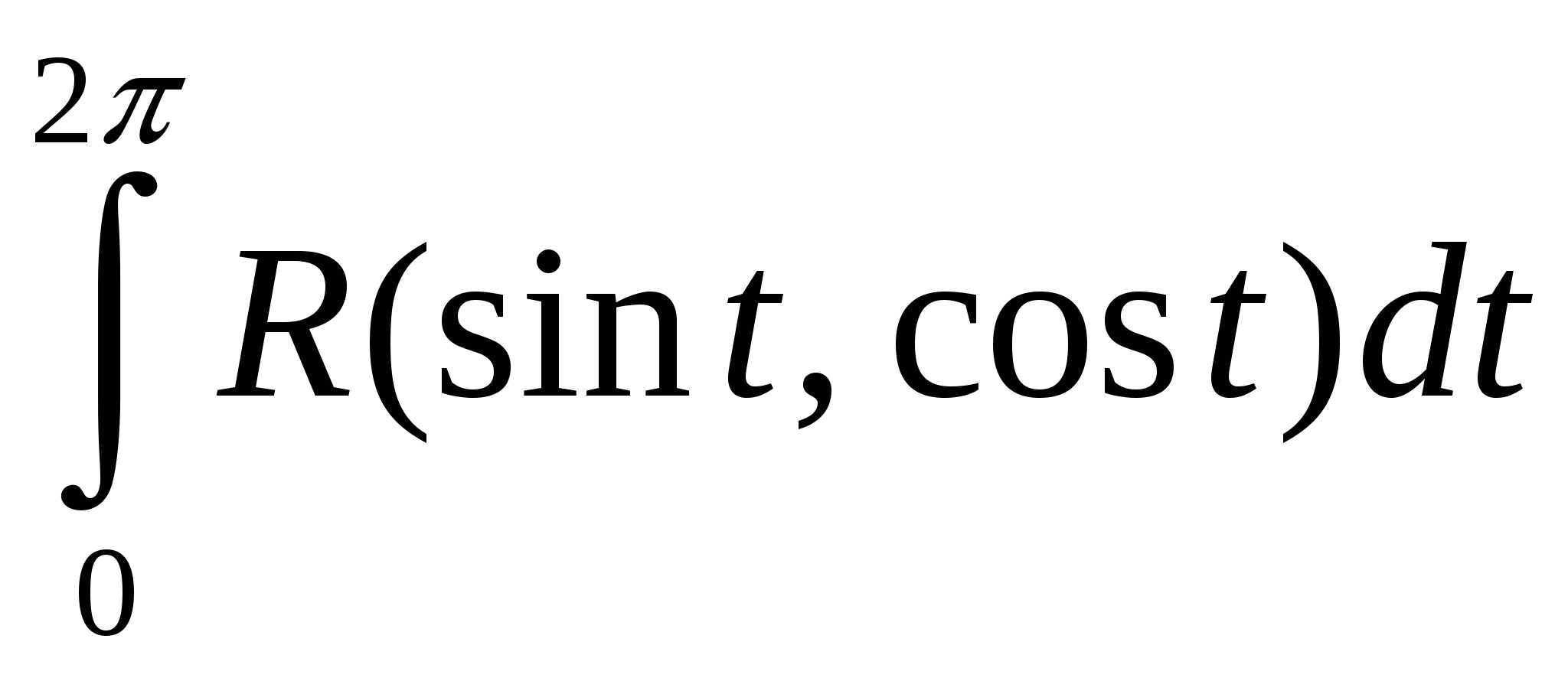 с помощью вычетов. с помощью вычетов.
-
Теорема Руше.
-
Вычисление несобственных интегралов с помощью вычетов.
-
Определение преобразования Лапласа.
-
Свойства оригиналов.
-
Свойства изображений.
-
Обратное преобразование Лапласа.
-
Свойства преобразования Лапласа: линейность, подобие, запаздывание.
-
Свойства преобразования Лапласа: опережение, затухание (смещение).
-
Дифференцирование оригинала.
-
Дифференцирование изображения.
-
Изображение оригинала (интегрирование оригинала).
-
Интегрирование изображения.
-
Умножение изображений. Формула Дюамеля.
-
Умножение оригиналов. Формула Парсеваля.
-
Решение линейных дифференциальных уравнений с постоянными коэффициентами операционным методом.
-
Решение систем линейных дифференциальных уравнений с постоянными коэффициентами операционным методом.
страница 1
|
Смотрите также:
Специальность Физика. Техническое творчество
28,14kb. 1 стр.
Критерии оценки вступительных испытаний для специальности 1-18 01 01 «Народное творчество (по направлениям)», направление специальности 1-18 01 01–01 «Народное творчество
36,1kb. 1 стр.
Программа для поступающих в магистратуру по специальности 1-31 80 05
152,73kb. 1 стр.
|
|