страница 1
Управление образования Гродненского облисполкома
Учреждение образования « Волковысский государственный строительный профессиональный лицей»
«Тригонометрические функции»
Методическая разработка
2010
Материал подготовила Д.Р. Левданская, преподаватель математики Волковысского государственного строительного профессионального лицея
Методическая разработка предназначена для проведения урока обобщения и систематизации знаний, умений и навыков по математике после изучения тем «Тригонометрические выражения. Тригонометрические функции».
Разработка содержит кроссворд, вопросы и задания по данным темам, задания творческого характера. Учёт результативности учащихся на уроке фиксируется на листе учёта знаний.
Урок – соревнование по математике
Тема урока: « Тригонометрические функции."
ЦЕЛИ УРОКА:
-
Образовательные:
-
Повторить, обобщить и систематизировать материал по теме;
-
Создать условия для контроля (самоконтроля) усвоения знаний и умений.
-
Развивающие:
-
Способствовать формированию умений сравни-
вать, обобщать;
-
Развивать математический кругозор, речь, мышление, внимание, память, умения анализировать и устанавливать связь между элементами темы.
-
Воспитательные:
-
Воспитывать активность, мобильность, ответст-
венность, умение общаться;
-
Развивать интерес к математике, дух соперничества, уважение друг к другу.
ТИП УРОКА: урок обобщения и систематизации
знаний, умений и навыков.
ОБОРУДОВАНИЕ: часы; маркеры; карточки с
заданиями; листы учета знаний команд (индивидуальный); таблички с названиями команд; табло; на плакатах написаны тема урока, девиз урока, зашифрованная фраза; нарисован кроссворд; графики функций.
ХОД УРОКА
-
Организационный момент.
Группа делится на три команды: «Синус», «Косинус», «Тангенс». Выбираются капитаны команд (до начала занятия). Команды садятся за свои «круглые столы».
На столе каждой команды лежит «Лист учета знаний», где капитан команды напротив каждой фамилии ставит (в случае правильного ответа) знак «+».
По итогам каждого конкурса подсчитываются знаки «+» и в строке «Всего» ставится их количество на команду.
В строке напротив фамилии суммируются знаки «+» и можно выставить оценку каждому за работу на уроке.
Лист учета знаний.
№
п/п
|
Фамилия, имя учащегося
| Конкурсы | Сумма
плюсов
| Оценка
за урок
|
1
|
2
|
3
|
4
|
5
|
1.
2.
3.
4.
…
|
|
|
|
|
|
|
|
|
|
Всего:
|
|
|
|
|
|
|
|
Слово учителя.
Добрый день! Мы снова вместе для совместной работы. Я рада и, судя по вашим глазам, вашим улыбкам, вы рады тоже. Спасибо.
Сегодня у нас урок необычный: присутствуют гости. Позвольте от вашего имени и от себя поприветствовать их. Ну а вам, ребята, я хочу пожелать успехов. Садитесь.
Французский писатель Анатоль Франс (1844-1924) однажды заметил: «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Так вот, давайте будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в вашей дальнейшей жизни.
Сегодня у нас обобщающий урок по теме «Тригонометрические функции». Проведем его в необычной форме – в форме соревнования, девиз которого «Будь настойчив, и успех обязательно придет». Повторяем, обобщаем, приводим в систему изученные тригонометрические формулы, виды, методы и приемы решения тригонометрических уравнений. Перед вами задача – показать свои знания и умения в данной области.
До начала занятий группа была разделена на три команды: команда «Синус» - капитан команды … , команда «Косинус» - капитан … , команда «Тангенс» – капитан … .
На столе каждой команды лежит «Лист учета знаний», где капитан команды напротив каждой фамилии ставит в случае правильного ответа знак «+», подсчитывает количество «+» по итогам каждого конкурса, выставляет оценку каждому за работу на уроке. Капитан команды также руководит работой, распределяет задания между членами команды.
-
Первый конкурс «Разминка».
Начинаем первый конкурс «Математическая разминка». Перед вами кроссворд. Каждой команде нужно ответить на 4 вопроса. Если какая-то команда не сможет ответить на поставленный вопрос, право на ответ передается другой команде. Таким образом, команда может заработать себе дополнительные баллы.
|
1
|
|
|
2
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
|
9
|
|
|
|
|
|
|
10
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
|
|
|
|
|
|
|
|
12
|
|
|
|
|
|
|
|
|
|
|
-
Как называется раздел математики, в котором изучаются тригонометрические функции? (Тригонометрия).
-
Какая английская мера длины используется для измерения небольших расстояний, где нужна большая точность? (Фут).
-
Что является графиком функции у=х2? (Парабола).
-
Что является графиком функции у=sinx? (Синусоида).
-
Что является графиком функции y=tgx? (Тангенсоида).
-
Близ города Великие Луки в бывшей Витебской губернии прошло детство и юность всемирно известной женщины-математика. Назовите ее. (Софья Васильевна Ковалевская).
-
Соответствие между множествами Х и У, при котором каждому значению из множества Х поставлено в соответствие единственное значение из множества У, носит название …(Функция).
-
Есть в каждом слове, у растения и может быть у уравнения. (Корень).
-
Какая мера длины произошла от римской меры «двойной шаг»? (Миля).
-
Синоним слова «дюжина». (12).
-
Древнерусская мера длины, равная приблизительно 71 см. (Аршин).
-
Ученый, который известен, как создатель школы математиков. Он открыл замечательное свойство прямоугольных треугольников. (Пифагор).
Капитаны команд подсчитывают верные ответы. Результаты заносятся в табло.
-
Второй конкурс “Дальше, дальше…”.
Каждая команда за 2 минуты должна ответить на наибольшее количество вопросов. За каждый верный ответ – 1 балл. Если команда успеет ответить верно на все вопросы (их 12) досрочно, она получает дополнительно 3 балла.
ВОПРОСЫ 1-Й КОМАНДЕ -
Выразить в градусной мере П/2. (90°)
-
Выразить в радианной мере1200 .(2П/3)
-
sin(П/2-α). (cosα)
-
tgα ctgα. (1)
-
tg2α. (2tgα/(1-tgα)
-
sin300 . (1/2)
-
Знак синуса в 4-й четверти. (-)
-
Наименьший положительный период функции у=sinх. (2П)
-
k-функция для косинуса. (sin)
-
Arcsin½. (П/6)
-
Arccos(-√2/2). (3П/4)
-
Arctg(-1). (-П/4)
ВОПРОСЫ 2-Й КОМАНДЕ
-
Выразить в градусной мере П. (180°)
-
Выразить в радианной мере 1500. (5П/6)
-
сos(П/2-α). (sinα)
-
sin2 α+cos2 α. (1)
-
sin2α. (2sinα cosα)
-
cos300 . (√3/2)
-
Знак косинуса в 4-й четверти. (+)
-
Наименьший положительный период функции у=cosx. (2П)
-
k-функция для тангенса. (ctg)
-
Arcsin1. (П/2)
-
Arccos(-½). (3п/4)
-
Arctg0. (0)
ВОПРОСЫ 3-Й КОМАНДЕ
-
Выразить в градусной мере 2П. (360° )
-
Выразить в радианной мере 2700. (3П/2)
-
tg(П/2-α). (ctgα)
-
1-sin2 α. (cos2α)
-
cos2α. (cos2 α-sin2 α)
-
sin600 . (√3/2)
-
Знак синуса в 1-й четверти. (+)
-
Наименьший положительный период функции у=tgx. (П)
-
k- функция для синуса. (cos)
-
Arcsin√2/2. (П/4)
-
Arccos(-1). (П)
-
Arctg(-√3). (-П/3)
Капитаны команд сообщают учителю количество верных ответов. Результаты заносятся в табло.
-
3-й конкурс «Спешите видеть».
Каждая команда за 3 минуты должна начертить эскиз графика функции. За верное построение команда получает по 2 балла.
Задание 1-й команде
f-четная функция; хmin=0; xmax=3; f(0)=0; f(3)=6.
Задание 2-й команде
f-нечетная функция; x min =-1; xmax =-4; f(-1)=-1; f(-4)=6.
Задание 3-й команде
f-нечетная функция; xmax =1; xmin =4; f(1)=3; f(4)=-5.
Все команды изображают графики на миллиметровой бумаге. Результаты конкурса заносятся в табло.
-
4-й конкурс «Составьте фразу».
Зашифрованная фраза перед вами на доске. Каждой команде нужно решить по 9 заданий. После решения на доске нужно найти правильный ответ, рядом с которым написана буква. Номер карточки соответствует порядковой букве во фразе. На конкурс отводится 8 минут.
№ n/n
|
Задания
|
Ответы
|
1.
|
Вычислить: sin(П/2-α)-cos(П-α)
|
2cosα
|
2.
|
Вычислить: cos2α+2sin2(П-α)
|
1
|
3.
|
Вычислить: sin(3П/2-α)-cos(П+α)
|
0
|
4.
|
Вычислить: sin(П+α)+cos(П+α)
|
-2sinα
|
5.
|
Решить уравнение: cos2х=1
|
Пk
|
6.
|
Вычислить: tg(3П/2+α)+ctg(П+α)
|
-ctgα
|
7.
|
Вычислить: arcsin√3/2+arctg0
|
П/3
|
8.
|
Решить уравнение: tg2х=√3
|
П/6+Пk/2
|
9.
|
Вычислить: arcsin1/2-arcsin1
|
-П/3
|
10.
|
Вычислить: arccos√3/2+arccos(-√3/2)
|
П
|
11.
|
Вычислить: sin2α+(sinα-cosα)2
|
1
|
12.
|
Вычислить:arccos√3/2-arccos0
|
-П/3
|
13.
|
Вычислить: 4arctg√3
|
4П/3
|
14.
|
Вычислить: arctg1/√3-arcsin1
|
-П/3
|
15.
|
Вычислить: arctg√3+arcctg(-√3)
|
П
|
16.
|
Решить уравнение: cos3x=1/2
|
±П/9+2/3Пk
|
17.
|
Решить уравнение: sin2x=1/2
|
(-1)k П/12+Пk/2
|
18.
|
Вычислить: 4arcsin√3/2
|
4П/3
|
19.
|
Вычислить: 2arccos(-1/2)
|
4П/3
|
20.
|
Вычислить: arctg√3-arcsin0
|
П/3
|
21.
|
Решить уравнение: sinx=-1
|
-П/2+2Пk
|
22.
|
Решить уравнение: sinx=0
|
Пk
|
23.
|
Решить уравнение: sinx=1
|
П/2+2Пk
|
24.
|
Вычислить: arccos1/2+arccos1
|
П/3
|
25.
|
Вычислить: arccos(-1)+arctg0
|
П
|
26.
|
Решить уравнение: cosx=-1
|
П+2Пk
|
27.
|
Вычислить: cos(П+α)-sin(2П-α)
|
0
|
Зашифрованная фраза
1
|
2
|
3
|
4
|
5
|
|
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
13
|
14
|
15
|
16
|
17
|
18
|
ж
|
и
|
з
|
н
|
ь
|
|
и
|
д
|
о
|
в
|
е
|
р
|
и
|
е
|
т
|
е
|
р
|
я
|
ю
|
т
|
19
|
20
|
21
|
22
|
23
|
24
|
|
25
|
26
|
27
|
т
|
о
|
л
|
ь
|
к
|
о
|
р
|
а
|
з
|
Ответы
Значение |
Буква
|
Значение
|
Буква
|
0
|
З
|
Пk
|
Ь
|
4П/3
|
Т
|
-2sin α
|
Н
|
-ctg α
|
Д
|
±П/9+2/3Пk
|
Я
|
П
|
Р
|
-П/3
|
Е
|
П/3
|
О
|
П/2+2Пk
|
К
|
1
|
И
|
(-1)k П/12+Пk/2
|
Ю
|
2cos α
|
Ж
|
П/6+Пk/2
|
В
|
П+2Пk
|
А
|
- П/2+2Пk
|
Л
|
Результаты конкурса заносятся в табло.
Вопрос группе: «Как вы, ребята, понимаете данное выражение».
6.5-й конкурс «Гонка за лидером».
Каждая команда получает карточку, в которой по 2 задания: одно – в форме теста, другое – своеобразный математический ребус. За каждое верно решенное задание команда получает 2 балла. Максимальная оценка конкурса – 8 баллов. На конкурс отводится 5 минут.
КАРТОЧКА №1
-
Какой является функция f(х)=sinx+tgx.
Варианты ответов:
А) четная;
Б) нечетная;
В) не является ни четной, ни нечетной.
-
(Приложение1).
Ответ:
№1- б;
№2- 3; 0,5; 4/5.
КАРТОЧКА №2
-
Какой является функция f(х)=cos2x+x2.
Варианты ответов:
А) не является ни четной, ни нечетной.
Б) нечетная;
В) четная.
-
(Приложение 2).
Ответ:
№1- в;
№2- 4; 0; 12/13.
КАРТОЧКА №3
-
Какой является функция f(x)=х3+sin3х.
Варианты ответов:
А) нечетная;
Б) не является ни четной, ни нечетной;
В) четная.
-
(Приложение 3).
Ответ:
№1- а;
№2- 2; 1,5; 3/5.
Результаты конкурса заносятся в табло.
7. Поведение итогов.
Подсчитываются баллы, полученные командой за весь урок. Распределяются места. Капитаны сообщают о работе каждого учащегося на уроке, выставляют оценки.
Рефлексия.
-
С какими трудностями вы встретились сегодня на уроке?
-
Как с ними справились?
-
Что удивило на уроке?
-
С каким настроением покидаете урок?
Слово учителя:
Подводя итог урока, мне хочется сказать, что вы сегодня все много поработали, показали неплохие знания в области тригонометрии: хорошо усвоены темы…, надо поработать над… .
Дается домашнее задание каждой команде отдельно (в зависимости от усвоения тем).
Математика – важная и нужная наука, особенно в наш 21 век. И поэтому урок мне хочется закончить следующим стихотворением:
Есть о математике молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даешь
Для победы трудностей закалку.
Учится с тобою молодежь
Развивать и волю, и смекалку.
И за то, что в творческом труде
Выручаешь в трудные моменты,
Мы сегодня искренне тебе
Посылаем гром аплодисментов.
Спасибо за работу. Урок закончен.
ПРИЛОЖЕНИЕ 1
  
 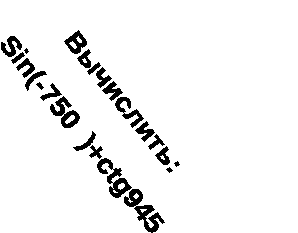

 
 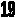

 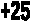
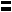
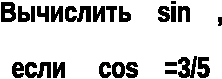
ПРИЛОЖЕНИЕ 2
   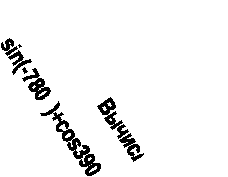



ПРИЛОЖЕНИЕ 3
 
 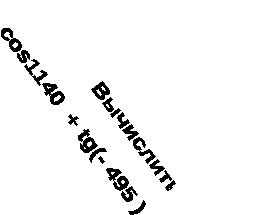


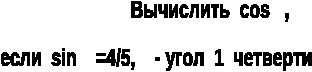
страница 1
|