страница 1
Содержание
Введение……………………………….…………………............
|
5
|
Требования образовательного стандарта ………………………
|
7
|
Учебная программа курса «Математический анализ»…………
|
8
|
Лекционный курс…………………………………………………
|
17
|
Раздел 1 Числовые множества ……………………………….
|
17
|
Тема 1 Множества……………………………………………….
|
17
|
Тема 2 Грани числовых множеств……………………………...
|
21
|
Тема 3 Множество комплексных чисел………………………..
|
23
|
Раздел 2 Теория пределов……………………………………..
|
29
|
Тема 1 Числовые последовательности………………………….
|
29
|
Тема 2 Предел последовательности…………………………….
|
32
|
Тема 3 Предел функции…………………………………………
|
34
|
Тема 4 Бесконечно малые функции…………………………….
|
42
|
Тема 5 Непрерывность функции………………………………..
|
45
|
Раздел 3 Дифференциальное исчисление функции действительной переменной……………………………………………...
|
53
|
Тема 1 Определение производной……………………………...
|
53
|
Тема 2 Производная обратной и сложной функции…………..
|
62
|
Тема 3 Производные и дифференциалы высших порядков…..
|
63
|
Тема 4 Теоремы о среднем. Правило Лопиталя……………….
|
67
|
Тема 5 Формула Тейлора………………………………………..
|
71
|
Тема 6 Локальные и глобальные экстремумы функции……...
|
72
|
Тема 7 Исследование функции…………………………………
|
76
|
Тема 8 Построение графиков функций…………………………
|
79
|
Тема 9 Векторные функции …………………………………….
|
82
|
Тема 10 Кривизна кривой ………………………………………
|
93
|
Раздел 4 Интегральное исчисление функции действительной переменной…………………………………………………..
|
101
|
Тема 1 Первообразная и неопределенный интеграл…………..
|
101
|
Тема 2 Общие методы интегрирования………………………..
|
105
|
Тема 3 Интегрирование рациональных функций……………...
|
107
|
Тема 4 Интегрирование иррациональностей…………………..
|
109
|
Тема 5 Интегрирование трансцендентных функций ………….
|
113
|
Тема 6 Определенный интеграл и формула Ньютона-Лейбница
|
116
|
Тема 7 Геометрические приложения определенного интеграла..
|
125
|
Тема 8 Физические приложения определенного интеграла…..
|
129
|
Тема 9 Несобственные интегралы………………………………
|
136
|
Раздел 5 Теория рядов…………………………………………
|
146
|
Тема 1 Ряды с неотрицательными членами…………………...
|
146
|
Тема 2 Знакопеременные ряды…………………………………
|
150
|
Тема 3 Функциональные ряды…………………………………
|
153
|
Тема 4 Степенные ряды…………………………………………
|
158
|
Тема 5 Ряд Тейлора ……………………………………………..
|
161
|
Задания к практическим занятиям с решениями типовых примеров.........................................................................................
|
166
|
Раздел 1 Числовые множества ……………………………….
|
166
|
Раздел 2 Теория пределов…………………………………….
|
174
|
Раздел 3 Дифференциальное исчисление функции действительной переменной……………………………………………...
|
195
|
Раздел 4 Интегральное исчисление функции действительной переменной…………………………………………………..
|
249
|
Раздел 5 Теория рядов…………………………………………
|
287
|
Задания к контрольным работам...................................................
|
313
|
Тестовые задания…………………………………………………
|
318
|
Примерный перечень вопросов экзамену………………………
|
323
|
Типовые задачи к экзамену ……………………………………..
|
326
|
Литература………………………………………………………..
|
329
|
Введение
Учебно-методический комплекс «Математический анализ» написан в соответствии с действующей программой по данной дисциплине для физических специальностей.
Данный комплекс представлен тремя частями: «Функции действительной переменной. Ряды», «Функции многих переменных», «Функции комплексной переменной». В первую часть входят разделы теория пределов, дифференциальное и интегральное исчисление функции действительной переменной, числовые и функциональные ряды, которые излагаются в 1-м семестре. Во второй части представлены разделы 2-го семестра: непрерывность и дифференцируемость функции многих переменных, криволинейные, кратные и поверхностные интегралы; векторный анализ; интегралы, зависящие от параметра. Третья часть содержит материал 3-го семестра: ряды и интеграл Фурье, непрерывность, дифференцируемость и интегрируемость функции комплексной переменной, вычеты и их приложения, операционное исчисление.
Структура каждой части содержит требования образовательного стандарта, учебную программу, тематический план. По изучаемым разделам математического анализа приводится краткий лекционный курс, материал которого разбит на части, соответствующие темам. Каждая тема содержит перечень вопросов, подлежащих изучению, основные определения, утверждения и теоремы (доказательства теорем излагаются в литературе, приведенной в пособии). В конце каждого раздела краткого лекционного курса предлагаются вопросы для самоконтроля, которые могут быть использованы студентами при самоподготовке по дисциплине, а также преподавателями при проведении устных опросов и математических диктантов. В пособии по каждому разделу приводятся примерные задания к практическим занятиям с решениями типовых примеров. Для осуществления контроля знаний предлагаются примерные задания контрольных работ по каждому разделу, тестовые задания итогового контроля, примерный перечень вопросов к экзамену и типовые задачи к нему. Нумерация таблиц и рисунков дана самостоятельно в каждом разделе; нумерация заданий к практическим занятиям своя в каждой теме.
При написании комплекса авторы использовали литературу, список которой приводится в конце каждой части комплекса.
Учебно-методический комплекс по курсу «Математический анализ» предназначен, с одной стороны, для организации учебного процесса дневного отделения физического факультета по специальности: 1-31 04 03 – Физическая электроника, а также может быть использован в качестве учебно-методического обеспечения для специальностей 1-31 04 01 02 – Физика (производственная деятельность), 1-31 04 01 03 – Физика (научно-педагогическая деятельность), 1-31 04 01 04 – Физика (управленческая деятельность), 1-02 05 04 04 – Физика. Техническое творчество. С другой стороны, изложенные вопросы разделов математического анализа, позволяют студентам использовать методы математического анализа в решении задач из различных областей математики и физики.
Требования
образовательного стандарта
(руководящий документ Республики Беларусь
РД РБ 021005.038–98)
Высшее образование
специальности 1-31 04 03 – Физическая электроника,
Дисциплина «Математический анализ»
Числовые последовательности. Основные теоремы о пределах последовательностей. Предельные точки последовательности. Общий критерий сходимости. Предел функции. Критерий Коши существования предела функции. Непрерывность функции. Точки разрыва. Замечательные пределы. Производная. Основные правила и формулы дифференцирования. Дифференциал. Производные и дифференциалы высших порядков. Неопределенный интеграл. Основные методы и формулы интегрирования. Основные теоремы о непрерывных функциях. Основная теорема о неопределенном интеграле. Понятие определенного интеграла. Свойства определенного интеграла. Оценки интегралов. Функция нескольких переменных. Частные производные. Дифференцируемость сложной функции. Производная по направлению. Градиент. Производные и дифференциалы высших порядков. Формула Тейлора. Неявные функции. Числовые ряды. Абсолютная и условная сходимости. Функциональные ряды. Интегрирование и дифференцирование функциональных рядов. Несобственные интегралы и признаки сходимости. Эйлеровы интегралы. Двойной интеграл и его основные свойства. Тройные и n-кратные интегралы. Несобственные кратные интегралы. Криволинейные интегралы. Интегралы на поверхности. Интегралы, зависящие от параметра. Ряд Фурье по ортогональной системе элементов гильбертова пространства. Неравенство Бесселя. Комплексная форма ряда Фурье. Понятие о кратных рядах Фурье. Интеграл Фурье и его комплексная форма. Комплексная переменная. Функция комплексной переменной. Аналитические функции. Степенные ряды. Ряд Тейлора. Ряд Лорана.
Требования к знаниям и умениям:
иметь представление: о месте и роли математики в системе естественнонаучного знания; о математике как особом способе познания мира; о содержании основных разделов высшей математики, об отличии прикладной математики от фундаментальной;
знать и уметь использовать: методы математического анализа;
владеть: дифференцированием и интегрированием функций.
Учебная программа курса «математический анализ»
Цели и задачи курса
Курс «Математический анализ» представляет собой совокупность фундаментальных разделов математики: действительный и комплексный анализ.
Целью курса «Математический анализ» является формирование у студентов теоретических знаний и практических навыков по теории множеств, теории пределов, дифференциального и интегрального исчислений функций одной м многих переменных, теории рядов, элементам векторного анализа, теории функций комплексной переменной и операционного исчисления.
Основной задачей курса «Математический анализ» является реализация требований установленных образовательным стандартом Высшего образования к подготовке специалистов в области естественно-научных дисциплин.
Задачами курса являются изучение: языка теории множеств; последовательностей и функций посредством предельного перехода; аппарата дифференциального и интегрального исчислений для функций одной и многих действительных переменных; числовых и функциональных рядов, рядов Фурье; элементов векторного анализа; функций комплексной переменной; операционного исчисления.
Содержание курса “Математический анализ” определяет совокупность необходимых знаний, навыков и умений, которыми должен овладеть студент в соответствии с требованиями образовательного стандарта высшего образования РБ.
По завершении обучения по курсу «Математический анализ» студент обязан:
– иметь представление: о месте и роли математики в системе естественнонаучного знания; о содержании основных разделов высшей математики, об отличии прикладной математики от фундаментальной;
– знать: основные понятия и теоретические положения;
– уметь: применять изучаемые теоретические сведения для решения задач;
– иметь навыки: решения типовых задач.
Данный курс отличается глубокими внутренними связями и поэтому имеет высокую степень автономности. При этом он тесно связан с дисциплинами «Аналитическая геометрия», «Алгебра», «Дифференциальный уравнения». Теоретические основы и практические навыки широко используются во многих других математических теориях и учебных дисциплинах.
Содержание курса (1 семестр)
Раздел 1 Числовые множества
Тема 1 Множества
Язык теории множеств. Логические символы. Операции над множествами. Эквивалентность множеств. Множество натуральных чисел. Множество целых чисел. Множество рациональных чисел. Множество действительных чисел. Принцип Архимеда.
Тема 2 Грани числовых множеств
Ограниченные и неограниченные множества. Наибольший и наименьший элементы. Верхняя и нижняя грани. Точная верхняя и точная нижняя грани. Существование точной верхней (нижней) грани. Метод математической индукции. Принцип вложенных отрезков. Бином Ньютона.
Тема 3 Множество комплексных чисел
Понятие комплексного числа. Геометрическое изображение комплексных чисел. Модуль и аргумент комплексного числа. Действия над комплексными числами в алгебраической форме. Тригонометрическая и показательная формы комплексного числа. Действия над комплексными числами в тригонометрической и показательной формах комплексного числа.
Раздел 2 Теория пределов
Тема 1 Числовые последовательности
Определение числовой последовательности. Арифметические действия над последовательностями. Ограниченные и неограниченные последовательности. Монотонные последовательности. Бесконечно малые последовательности их свойства. Бесконечно большие последовательности.
Тема 2 Предел последовательности
Определение предела числовой последовательности. Свойства сходящихся последовательностей. Арифметические свойства сходящихся последовательностей. Предельный переход в неравенствах. Критерий Коши сходимости последовательности. Определение монотонной последовательности. Теорема Вейерштрасса. Число 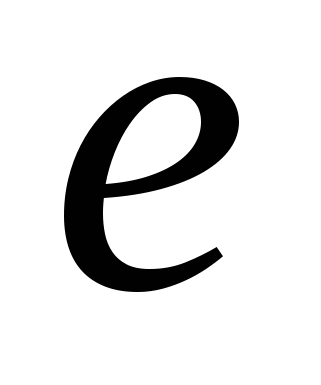 . Подпоследовательности. Принцип выбора. Фундаментальные последовательности. Критерий Коши. . Подпоследовательности. Принцип выбора. Фундаментальные последовательности. Критерий Коши.
Тема 3 Предел функции
Понятие функции. Способы задания функции. Основные свойства функций. Сложная функция. Обратная функция. Основные числовые функции. Классификация функций. Основные функции, заданные параметрическими уравнениям. Полярная система координат. Основные линии, заданные в полярной системе координат. Определение предела функции по Гейне и по Коши. Эквивалентность этих определений. Свойства предела функции. Односторонние пределы функции. Конечный предел функции при  , , 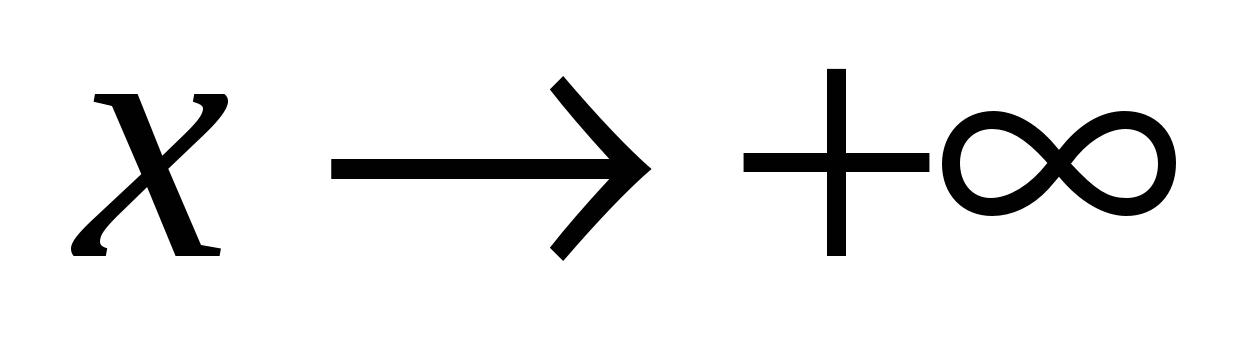 и и 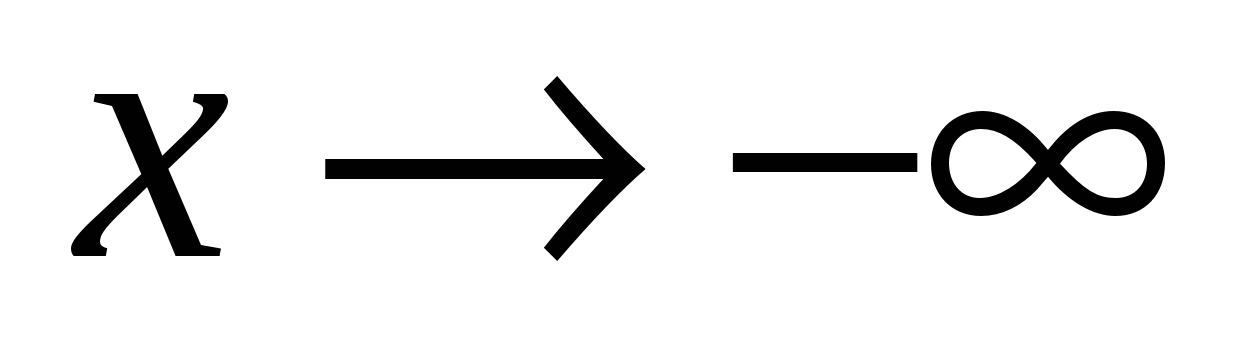 . Бесконечные пределы функции при . Бесконечные пределы функции при 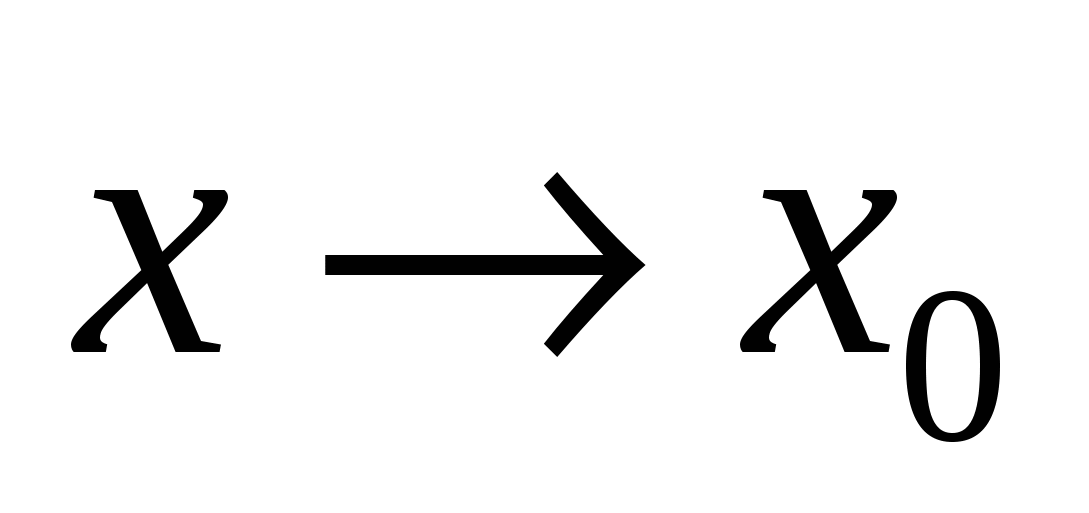 . Бесконечный предел функций при . Бесконечный предел функций при 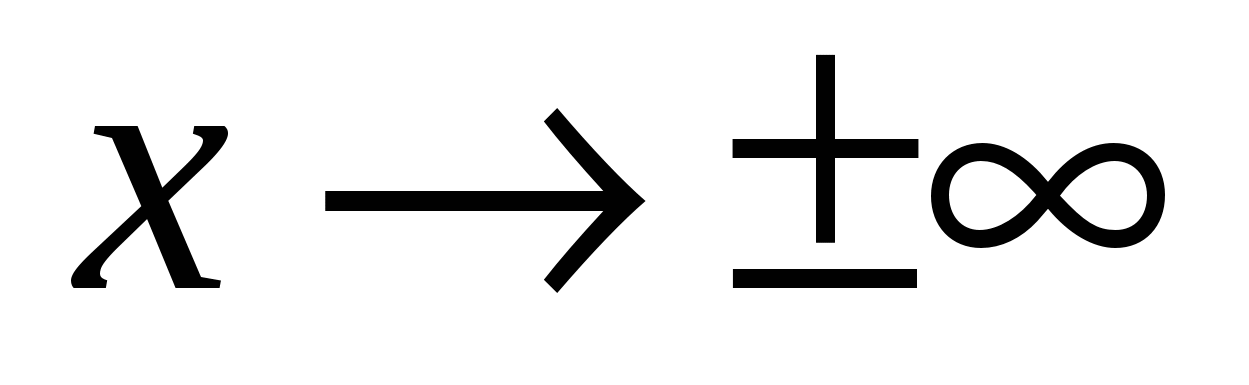 . Критерий Коши существования предела . Критерий Коши существования предела
Тема 4 Бесконечно малые функции
Определение бесконечно малой функции. Свойства бесконечно малых функций. Сравнение асимптотического поведения функций. Первый замечательный предел. Второй замечательный предел.
Тема 5 Непрерывность функции
Определение непрерывности функции. Арифметические действия над непрерывными функциями. Точки разрыва и их классификация. Непрерывность монотонной функции. Непрерывность сложной функции. Непрерывность обратной функции.Теорема об устойчивости знака непрерывной функции. Прохождение непрерывной функции через любое промежуточное значение. Теоремы Больцано-Коши. Ограниченность непрерывных функций. Первая теорема Вейерштрасса. Достижение непрерывной функцией своих точных граней. Вторая теорема Вейерштрасса. Определение равномерной непрерывности функции. Теорема Кантора.
Раздел 3 Дифференциальное исчисление функции действительной переменной
Тема 1 Определение производной
Определение производной. Правая и левая производная. Дифференцируемость функции. Дифференциал. Геометрический смысл производной дифференциала. Уравнение касательной и нормали. Физический смысл производной и дифференциала. Свойства производных, связанные с арифметическими операциями.
Тема 2 Производная обратной и сложной функции
Производная обратной функции. Производная и дифференциал сложной функции. Логарифмическая производная. Инвариантность формы первого дифференциала. Таблица производных.
Тема 3 Производные и дифференциалы высших порядков
Производная функции, заданной параметрическими уравнениями. Производная неявной функции. Производные высших порядков. Механический смысл второй производной. Дифференциалы высших порядков.
Тема 4 Теоремы о среднем.. Правило Лопиталя
Теорема Ферма. Теорема Роля. Теорема Лагранжа. Теорема Коши. Правило Лопиталя. Раскрытие неопределенностей вида 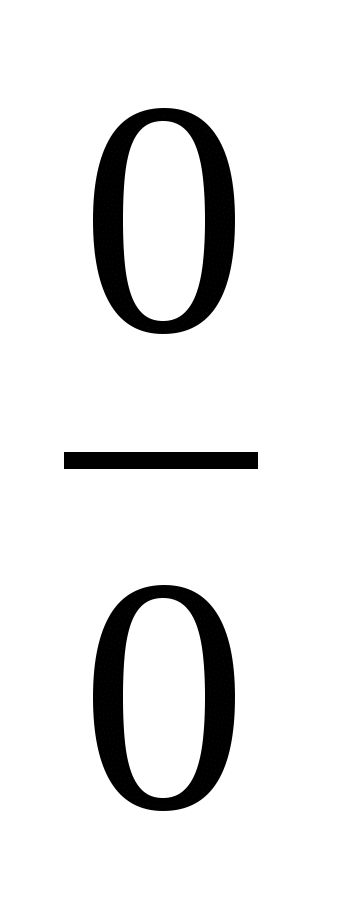 и и 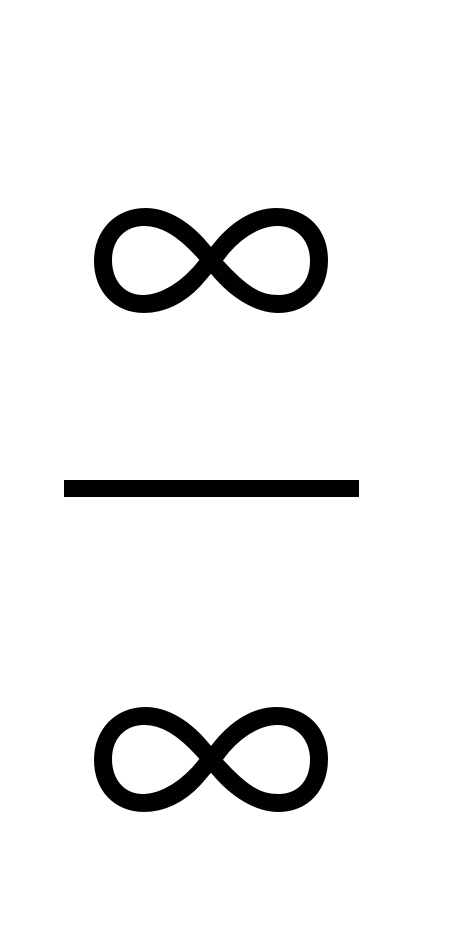 . Другие виды неопределенностей и их раскрытие. . Другие виды неопределенностей и их раскрытие.
Тема 5 Формула Тейлора
Определение многочлена Тейлора. Формула Тейлора с остаточным членом в виде Лагранжа. Формула Тейлора с остаточным членом в виде Пеано. Примеры разложения функций по формуле Тейлора. Формула Маклорена. Разложение по формуле Маклорена элементарных функций. Использование формулы Тейлора для выделения главной части функции для вычисления пределов. Использование формулы Тейлора для вычисления приближенных значений функции.
Тема 6 Локальные и глобальные экстремумы функции
Признаки монотонности функции. Точки локального экстремума функции. Необходимое условие существования локального экстремума функции. Точка возврата. Угловая точка. Стационарные точки. Достаточное условие существования локального экстремума. Наибольшее и наименьшее значение функции на отрезке.
Тема 7 Исследование функций
Выпуклость и вогнутость функции. Точки перегиба. Необходимое условие точки перегиба. Достаточное условие точки перегиба. Асимптоты графика функции. Общая схема исследования функции. Исследование функции, заданных: а) параметрическими уравнениями; б) неявно; в) в полярных координатах.
Тема 8 Векторные функции
Определение векторной функции. Годограф. Радиус-вектор. Предел и непрерывность векторной функции. Производная и дифференциал векторной функции. Свойства дифференцируемых функций. Геометрический и механический смысл производной. Понятие кривой. Носитель кривой. Способы задания кривой. Ориентированная кривая. Точа самопересечения. Замкнутая кривая. Простой замкнутый контур. Касательная к кривой. Определение длины кривой. Гладкие и кусочно-гладкие кривые. Натуральное уравнение гладкой кривой. Уравнение нормальной плоскости. Единичный вектор касательной.
Тема 9 Кривизна кривой
Определение кривизны кривой. Вычисление кривизны кривой. Главная нормаль. Радиус, круг и координаты центра кривизны плоской кривой. Эволюта Ии эвольвента плоской кривой. Соприкасающаяся плоскость. Трехгранник Френе.
Раздел 4 Интегральное исчисление функции действительной переменной
Тема 1 Первообразная и неопределенный интеграл
Определение первообразной функции и ее свойства. Неопределенный интеграл и его геометрический смысл. Дифференцирование неопределенного интеграла. Линейность неопределенного интеграла. Инвариантность формул интегрирования. Таблица неопределенных интегралов.
Тема 2 Общие методы интегрирования
Непосредственное интегрирование. Интегрирование заменой переменной. Подведение множителя под знак дифференциала. Метод интегрирования по частям. Некоторые особенности использования метода интегрирования по частям.
Тема 3 Интегрирование рациональных функций
Рациональные дроби. Разложение рациональной дроби на простейшие дроби. Метод неопределенных коэффициентов. Метод частных значений. Интегрирование простейших рациональных дробей. Интегрирование рациональных дробей.
Тема 4 Интегрирование некоторых иррациональностей
Интегралы вида 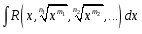 ( (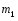 , ,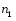 , ,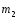 ,… ,… 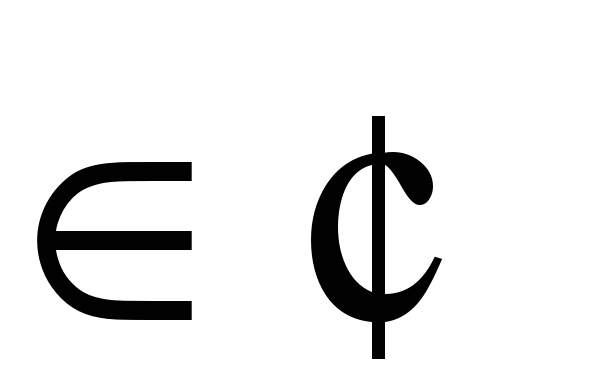 ). Интегралы вида ). Интегралы вида 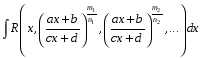 ( (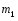 , , 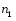 , ,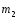 , , 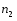 , … , …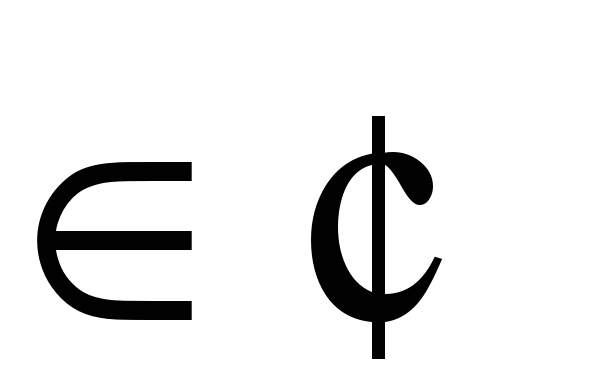 ). Интегралы вида ). Интегралы вида 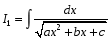 , , 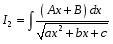 , , 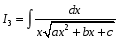 . Интеграл от дифференциального бинома . Интеграл от дифференциального бинома 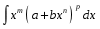 ( (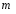 , ,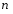 , ,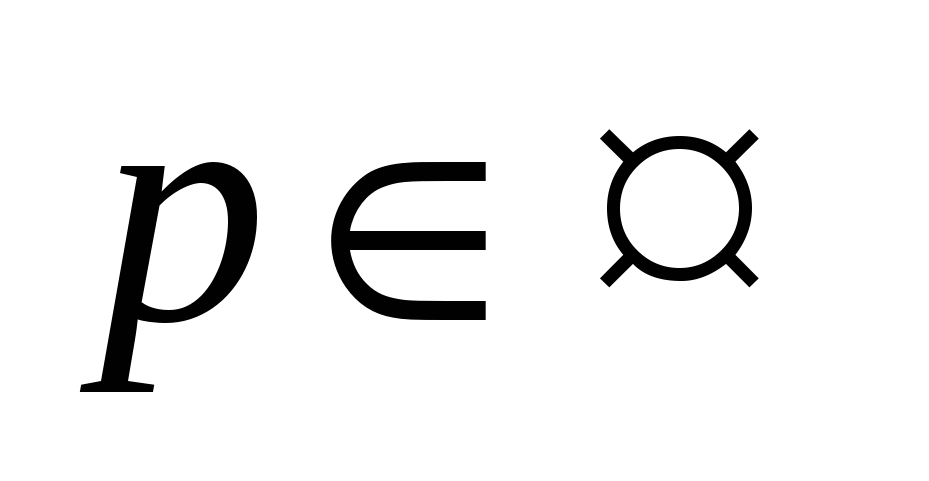 , , 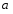 , ,  ). Интегралы, не выражающиеся через элементарные функции. ). Интегралы, не выражающиеся через элементарные функции.
Тема 5 Интегрирование трансцендентных функций
Интегралы вида 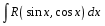 . Универсальная тригонометрическая подстановка. Интегралы вида . Универсальная тригонометрическая подстановка. Интегралы вида 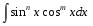 ( (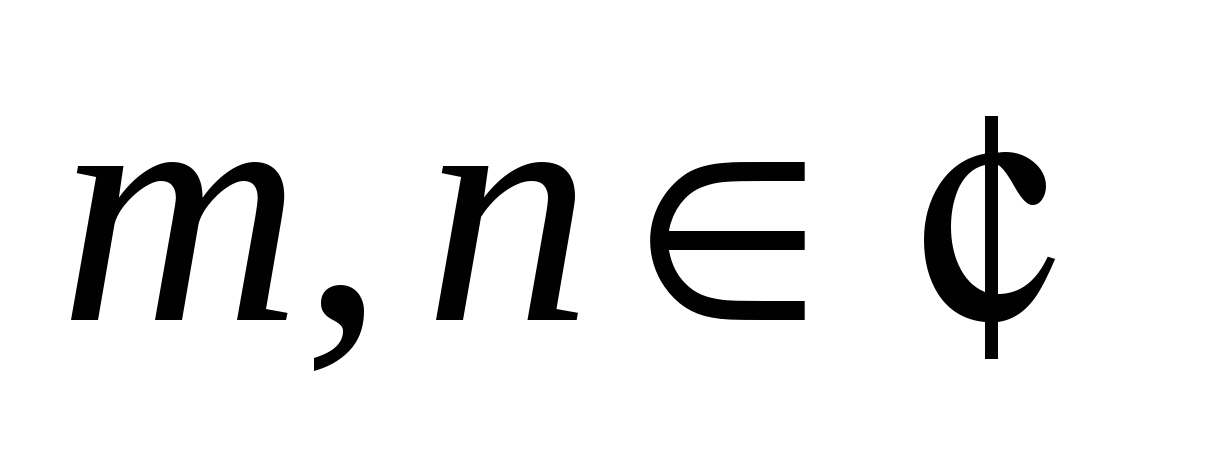 , , 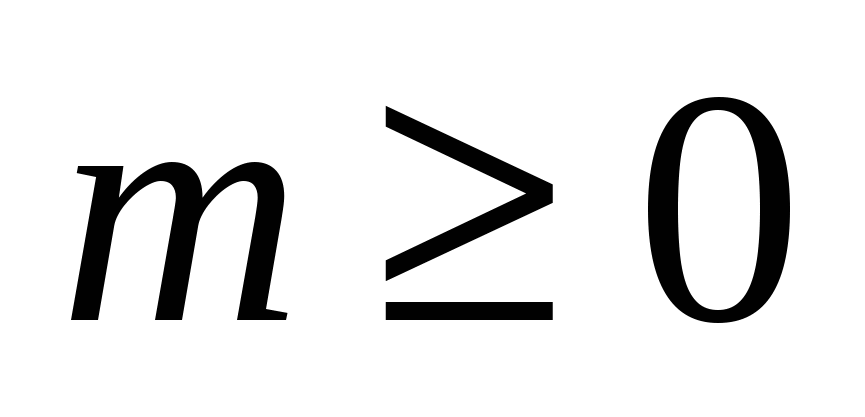 , , 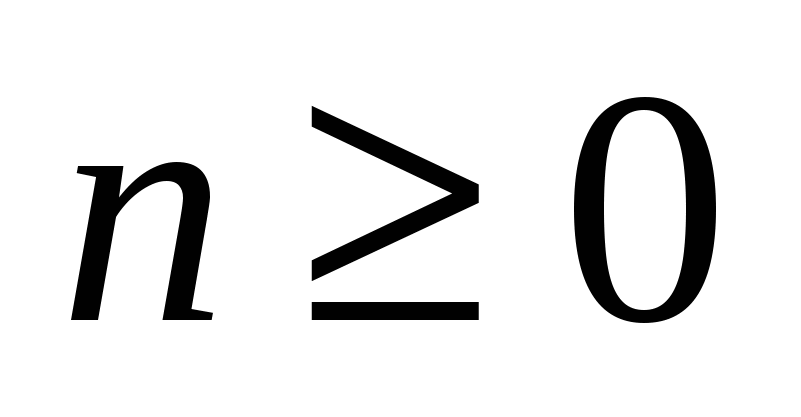 ). Интегралы вида ). Интегралы вида 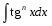 , , 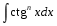 ( (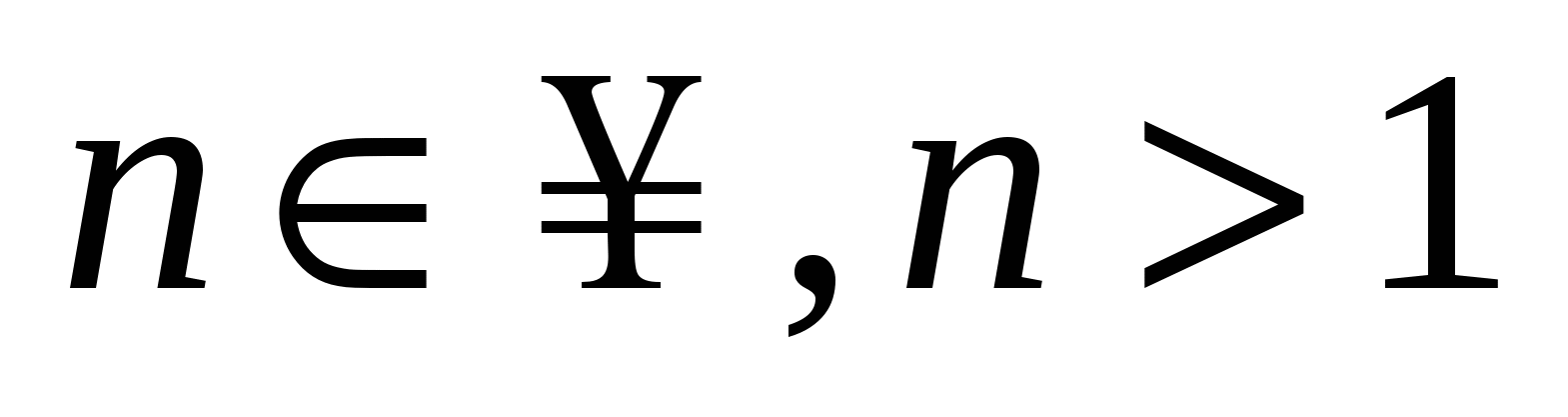 ). Интегралы вида ). Интегралы вида 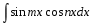 , , 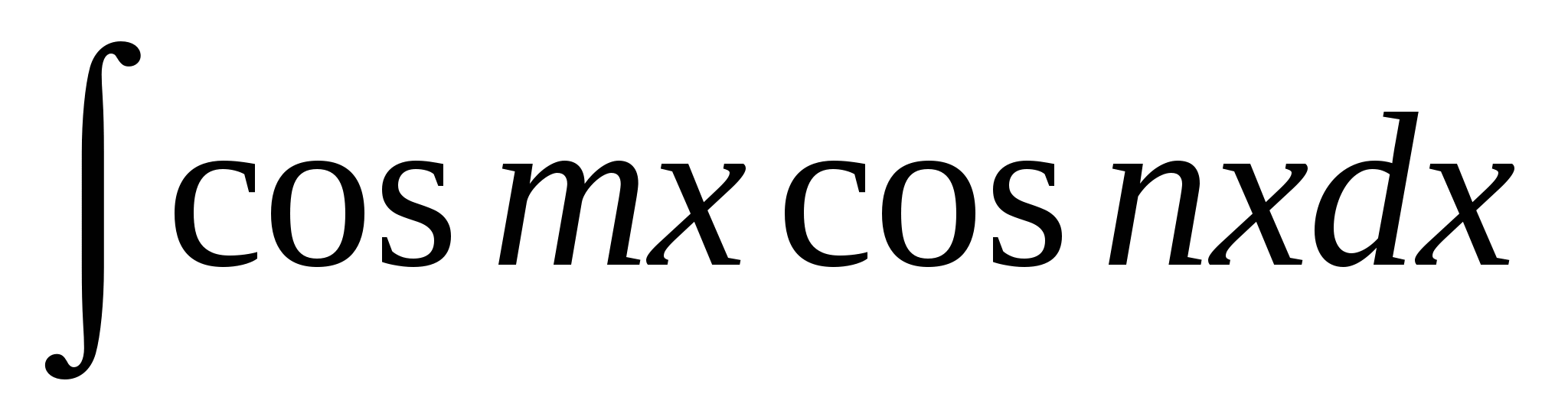 , , 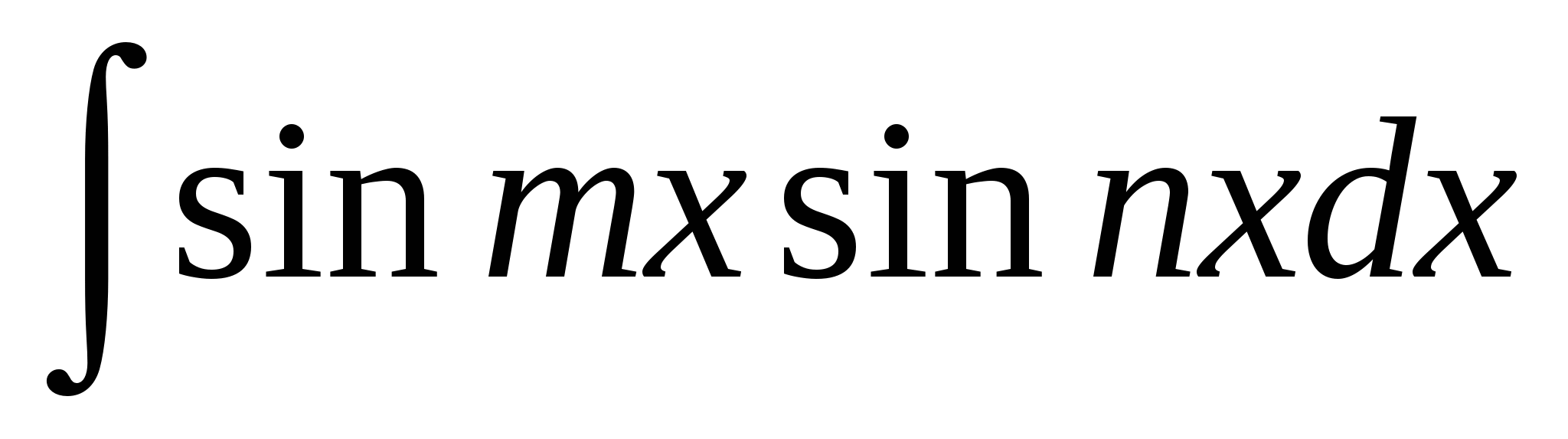 ( (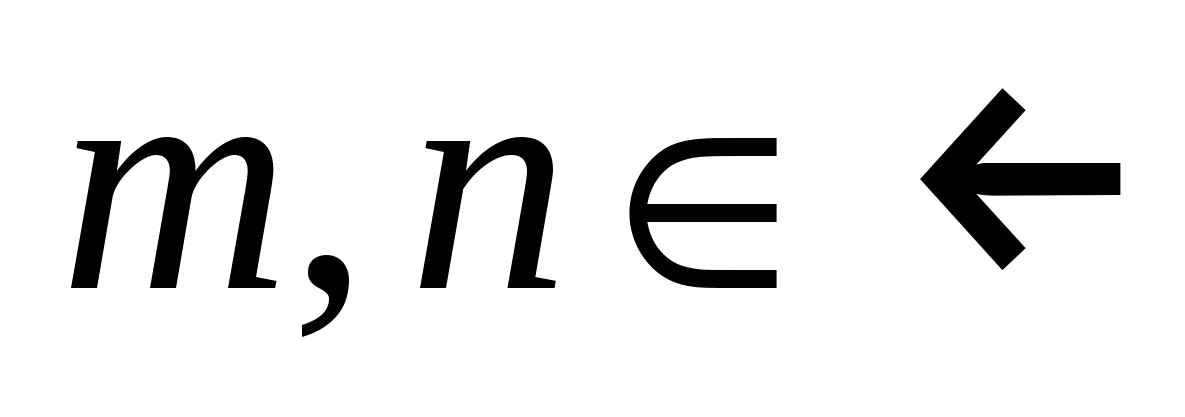 ). Интегралы вида ). Интегралы вида 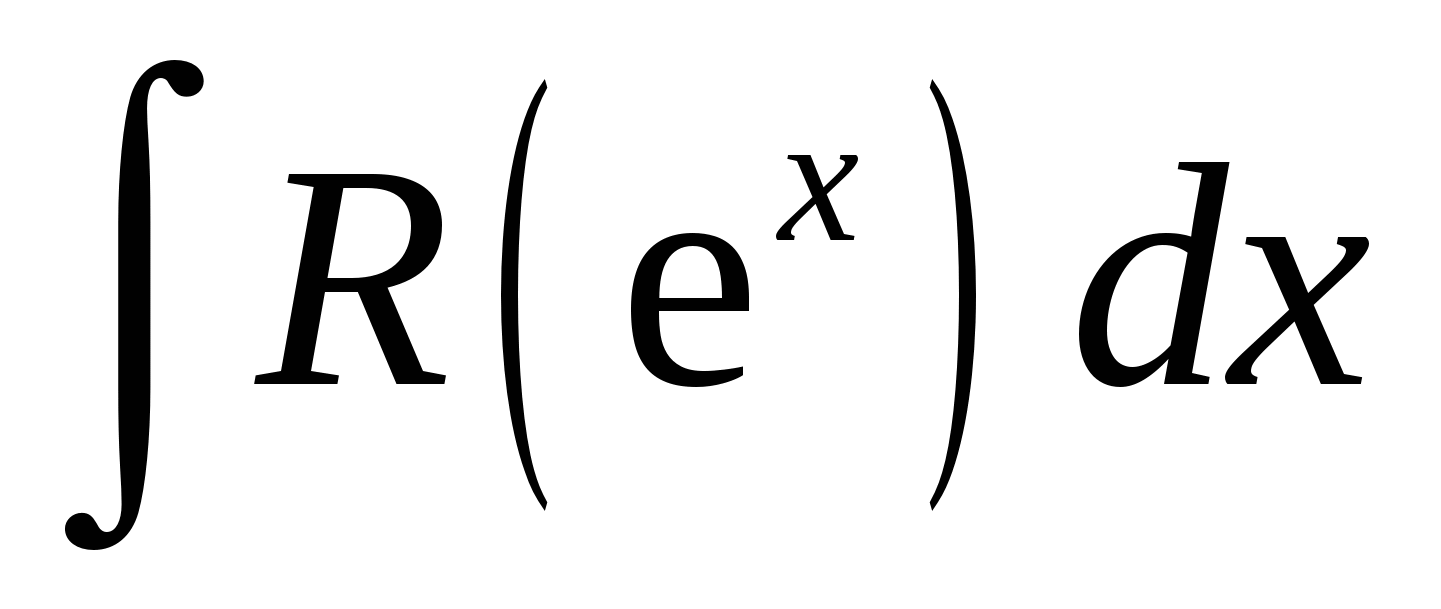 . Интегралы от гиперболических функций. . Интегралы от гиперболических функций.
Тема 6 Определенный интеграл
Задачи, приводящие к понятию определенного интеграла. Определение определенного интеграла Римана. Необходимое условие интегрируемости функций. Верхние и нижние суммы Дарбу. Верхние и нижние интегралы. Критерий интегрируемости Дарбу. Основные свойства определенного интеграла. Оценки интеграла. Теорема о среднем. Дифференцируемость интеграла по переменному верхнему пределу. Существование первообразной. Формула Ньютона-Лейбница. Формула замены переменной в определенном интеграле. Интегрирование по частям в определенном интеграле.
Тема 7 Геометрические приложения определенного интеграла
Вычисление площадей криволинейных трапеций. Вычисление длины кривой. Вычисление площади поверхности. Вычисление объемов пространственных тел. Вычисление площади и объема поверхности вращения.
Тема 8 Физические приложения определенного интеграла
Вычисление работы переменной силы; работы электродвигателя переменной мощности; вычисление силы давления; вычисление статических моментов, моментов инерции и координат центра масс плоской кривой; вычисление статических моментов, моментов инерции и координат центра масс плоской фигуры.
Тема 9 Несобственные интегралы
Несобственные интеграл с бесконечными пределами интегрирования. Несобственные интеграл от неограниченной функции. Формулы для несобственных интегралов. Критерий Коши сходимости несобственного интеграла. Интегралы от неотрицательных функций. Признаки сравнения несобственных интегралов. Абсолютная и условная сходимость. Признаки Дирихле и Абеля. Метод средних прямоугольников. Метод трапеций. Метод Симпсона.
Раздел 5 Теория рядов
Тема 1 Ряды с неотрицательными членами
Определение числового ряда. Необходимый признак сходимости числового ряда. Простейшие свойства числовых рядов. Линейные операции над сходящимися рядами. Критерий Коши сходимости числового ряда. Ряда с неотрицательными членами. Гармонический ряд. Ряд Дирихле. Интегральный признак Коши. Признаки сравнения. Признак Даламбера. Признак Коши.
Тема 2 Знакопеременные ряды
Определение знакочередующегося ряда. Признак Лейбница. Абсолютно сходящиеся ряды. Определение знакопеременного числового ряда. Условно сходящиеся ряды. Признаки сходимости Дирихле и Абеля знакопеременных рядов.
Тема 3 Функциональные ряды
Поточечная и равномерная сходимость функциональных последовательностей. Функциональные ряды. Поточечная сходимость функциональных рядов. Равномерная сходимость функциональных рядов. Признаки равномерной сходимости функциональных рядов. Свойства равномерно сходящихся функциональных рядов: непрерывность, дифференцируемость, интегрируемость.
Тема 4 Степенные ряды
Определение степенного ряда. Теорема Абеля. Радиус сходимости и интервал сходимости. Область сходимости. Свойства степенных рядов: непрерывность, дифференцируемость, интегрируемость.
Тема 5 Ряд Тейлора
Определения ряда Тейлора. Теорема о разложении функции в ряд Тейлора. Ряд Маклорена. Разложение элементарных функций в ряд Маклорена. Использование ряда Тейлора для вычисления пределов, для вычисления приближенных значений функции, для решения обыкновенных дифференциальных уравнений.
Тематический план
Учебный процесс по курсу осуществляется в виде лекций, практических занятий, групповых и индивидуальных консультаций, самостоятельной учебной работы студентов. Итоговой формой контроля знаний является экзамен. Распределение часов по разделам и темам представлена в таблице 1.
Таблица 1.1 – Распределение часов по разделам и темам курса
№
пп
|
Название темы
|
Всего
часов
|
В том числе
|
Форма контроля знаний
|
Лекции
|
Практические
|
СУРС
| -
|
Раздел 1 Числовые множества
|
14
|
8
|
6
|
|
| -
|
Тема 1 Множества
|
6
|
4
|
2
|
|
| -
|
Тема 2 Грани числовых2множеств
|
4
|
2
|
2
|
|
| -
|
Тема 3 Множество комплексных чисел
|
4
|
2
|
2
|
|
| -
|
Раздел 2 Теория пределов
|
30
|
20
|
10
|
|
| -
|
Тема 1 Числовые последовательности
|
4
|
2
|
2
|
|
| -
|
Тема 2 Предел последовательности
|
6
|
4
|
2
|
|
| -
|
Тема 3 Предел функции
|
8
|
6
|
2
|
|
| -
|
Тема 4 Бесконечно малые функции
|
4
|
2
|
2
|
|
К/р по разделу «Теория пределов»
| -
|
Тема 5 Непрерывность функции
|
8
|
6
|
2
|
|
| -
|
Раздел 3 Дифференциальное исчисление функции действительной переменной
|
48
|
26
|
22
|
|
| -
|
Тема 1 Определение производной
|
4
|
2
|
2
|
|
| -
|
Тема 2 Производная обратной и сложной функции
|
4
|
2
|
2
|
|
| -
|
Тема 3 Производные и дифференциалы высших порядков
|
4
|
2
|
2
|
|
| -
|
Тема 4 Теоремы о среднем. Правило Лопиталя
|
6
|
4
|
2
|
|
| -
|
Тема 5 ФормулаТейлора
|
6
|
4
|
2
|
|
| -
|
Тема 6 Локальные и глобальные экстремумы функции
|
6
|
4
|
2
|
|
| -
|
Тема 7 Исследование функции
|
4
|
2
|
2
|
|
| -
|
Тема 8 Построение графиков функций
|
4
|
–
|
4
|
|
К/р по разделу «Дифференциальное исчисление функции действительной переменой»
| -
|
Тема 9 Векторные функции
|
6
|
4
|
2
|
|
| -
|
Тема 10 Кривизна кривой
|
4
|
2
|
2
|
|
| -
|
Раздел 4 Интегральное исчисление функции действительной переменной
|
44
|
24
|
20
|
|
| -
|
Тема 1 Первообразная и неопределенный интеграл
|
4
|
2
|
2
|
|
| -
|
Тема 2 Общие методы интегрирования
|
4
|
2
|
2
|
|
| -
|
Тема 3 Интегрирование рациональных функций
|
4
|
2
|
2
|
|
| -
|
Тема 4 Интегрирование иррациональностей
|
4
|
2
|
2
|
|
| -
|
Тема 5 Интегрирование трансцендентных функций
|
4
|
2
|
2
|
|
| -
|
Тема 6 Определенный интеграл и формула Ньютона Лейбница
|
6
|
4
|
2
|
|
| -
|
Тема 7 Геометрические приложения определенного интеграла
|
4
|
2
|
2
|
|
| -
|
Тема 8 Физические приложения определенного интеграла
|
4
|
2
|
2
|
|
| -
|
Тема 9 Несобственные интегралы
|
10
|
6
|
4
|
|
К/р по разделу «Интегральное исчисление функции действительной переменной»
| -
|
Раздел 5 Теория рядов
|
24
|
12
|
12
|
|
| -
|
Тема 1 Ряды с неотрицательными членами
|
6
|
4
|
2
|
|
| -
|
Тема 2 Знакопеременные ряды
|
4
|
2
|
2
|
|
| -
|
Тема 3 Функциональные ряды
|
4
|
2
|
2
|
|
| -
|
Тема 4 Степенные ряды
|
4
|
2
|
2
|
|
К/р по разделу «Теория рядов»
| -
|
Тема 5 Ряд Тейлора
|
6
|
2
|
4
|
|
Итоговый тест
| -
|
Итого
|
160
|
90
|
70
|
0
|
|
Лекционный курс
Раздел 1 Числовые множества
Тема 1 Множества
1.1 Язык теории множеств
1.2 Операции над множествами
1.3 Числовые множества
1.4 Понятие функции
Понятие множества считается первоначальным, неопределяемым. Под множеством понимается совокупность определенных и отличных друг от друга объектов, объединенных общим характерным признаком в единое целое. Объекты, из которых состоит множество, называются элементами множества.
Способы задания множеств:
– перечислением его элементов – если множество  состоит из элементов состоит из элементов  , , 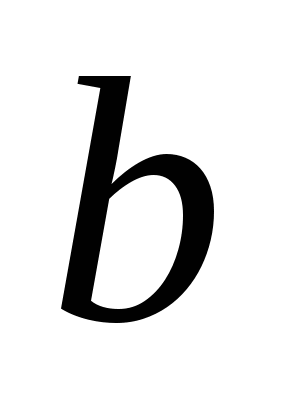 , , 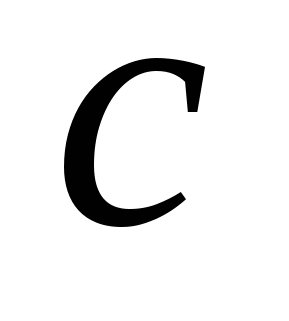 , , 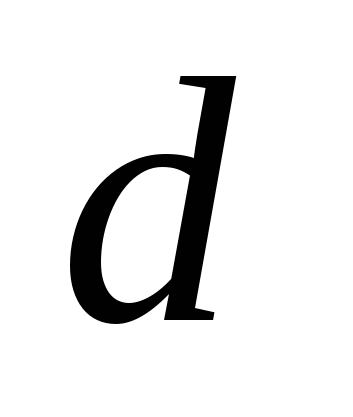 , то пишут , то пишут 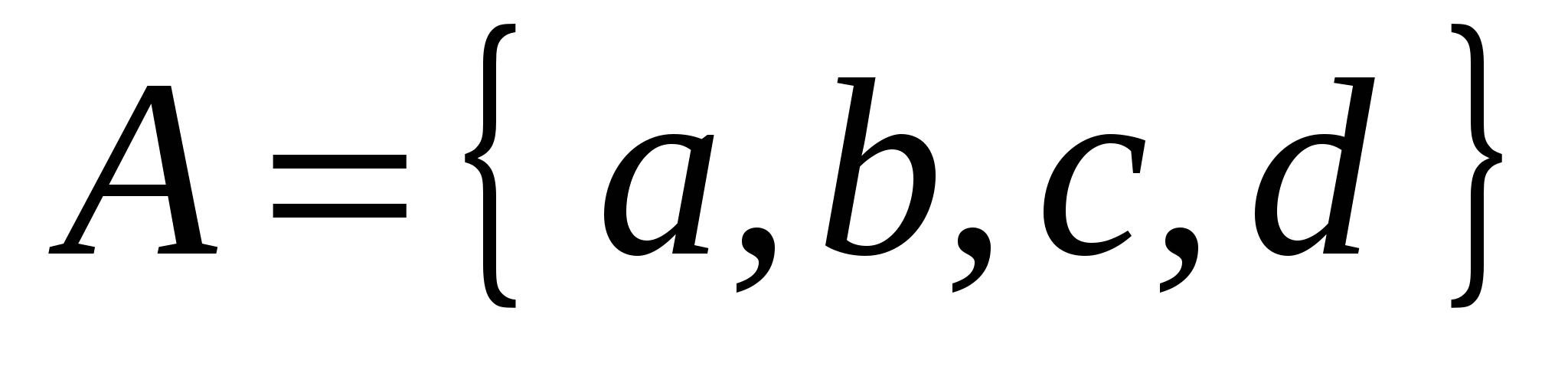 ; ;
– указанием характеристики свойств элементов – если множество  задается указанием характерного свойства задается указанием характерного свойства 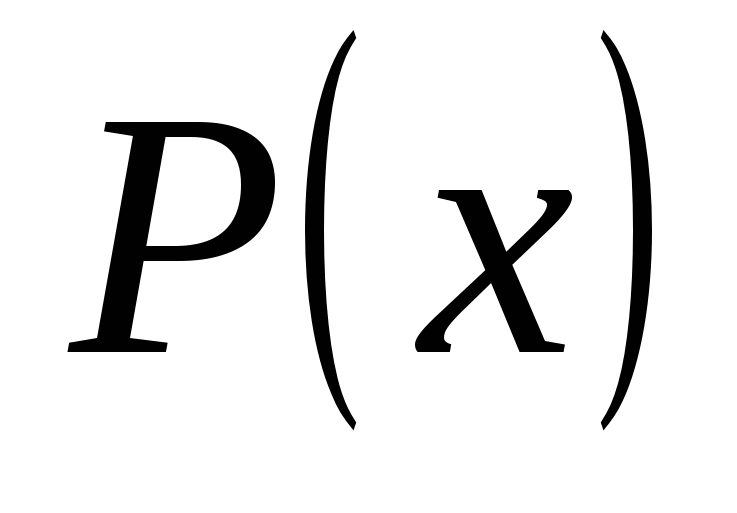 его элементов, то пишут его элементов, то пишут 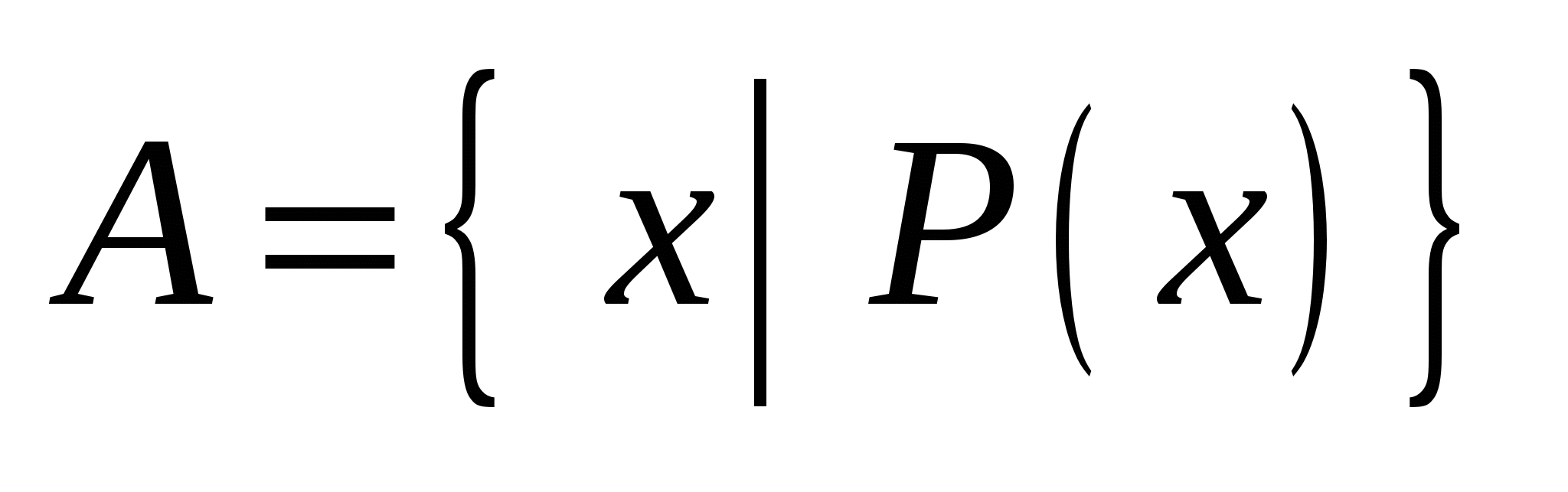 . .
– диаграммы Эйлера-Венна – множество изображается в виде кругов, треугольников или геометрических фигур произвольной формы, внутри которых располагаются элементы множества.
Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø.
Множества  и и 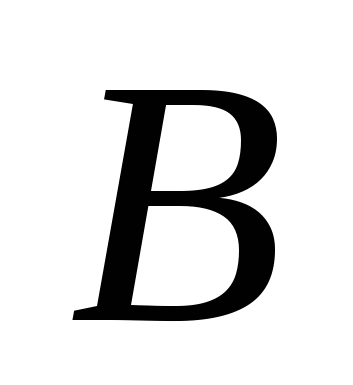 называются равными, если каждый элемент множества называются равными, если каждый элемент множества  является элементом множества является элементом множества 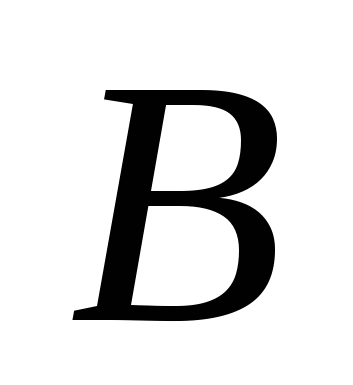 и, наоборот, каждый элемент множества и, наоборот, каждый элемент множества 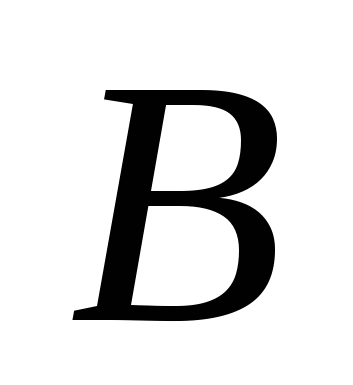 является элементом множества является элементом множества  . Равенство множеств . Равенство множеств  и и 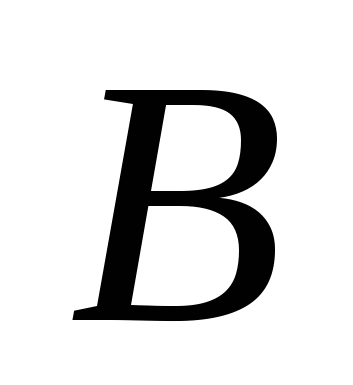 обозначают обозначают 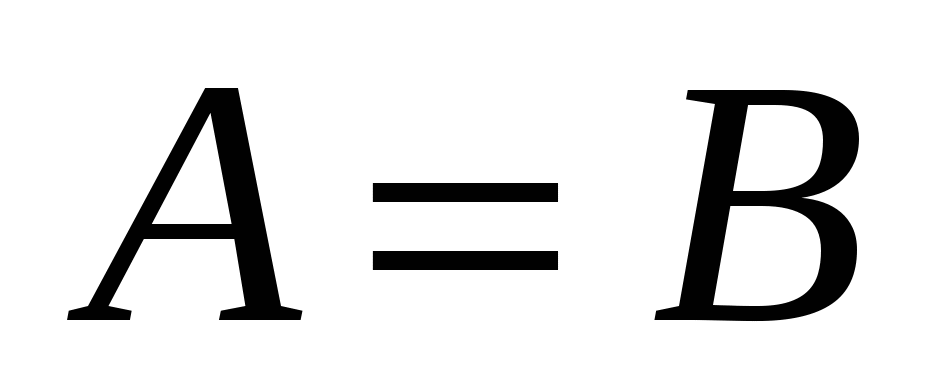 . Равные множества состоят из одних и тех же элементов. Если множество . Равные множества состоят из одних и тех же элементов. Если множество  не равно множеству не равно множеству 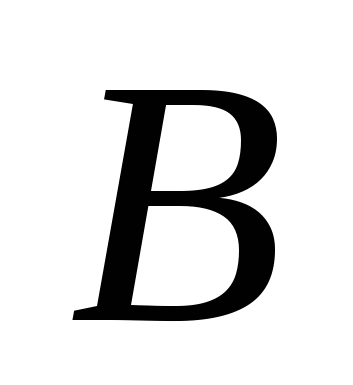 , то пишут , то пишут 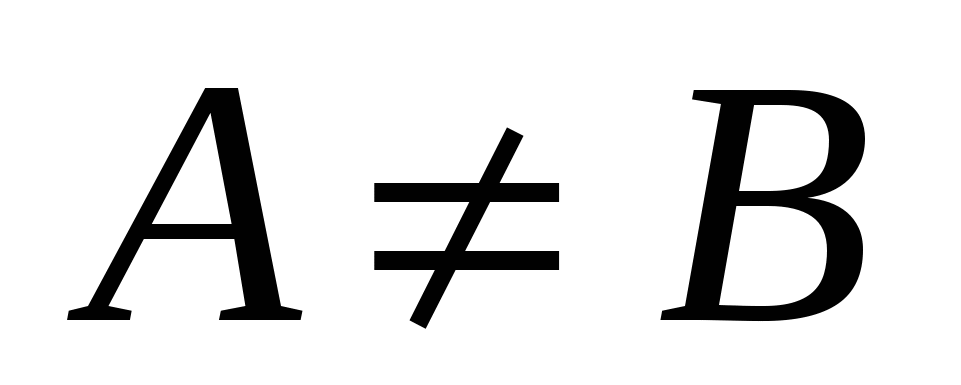 . .
Множество  , , 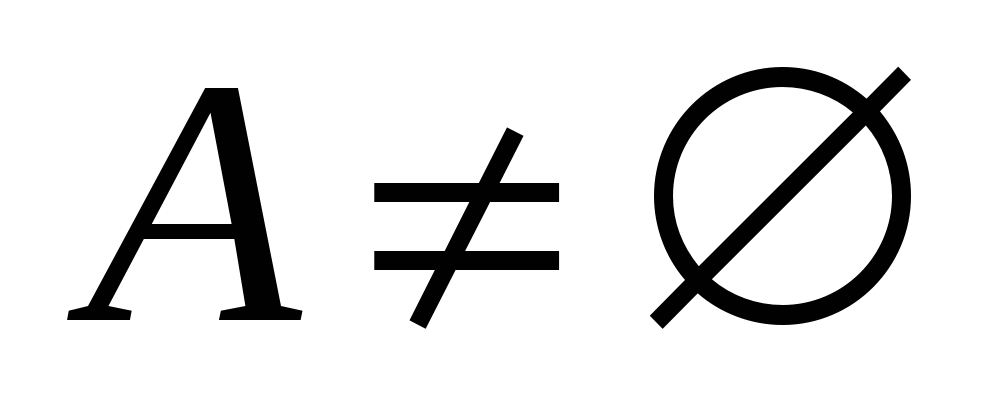 , называется подмножеством множества , называется подмножеством множества 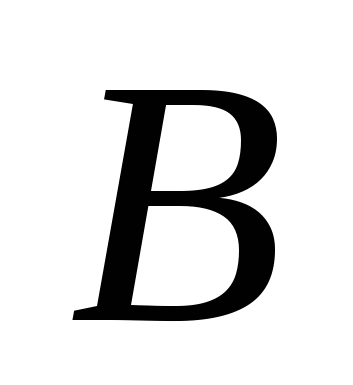 , , 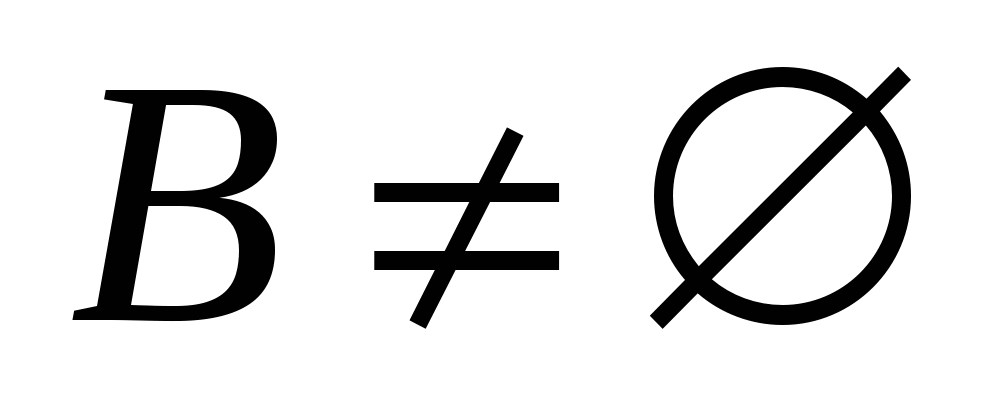 , если каждый элемент множества , если каждый элемент множества  является элементом множества является элементом множества 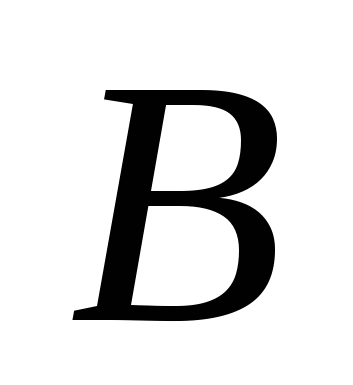 . Если . Если  – подмножество множества – подмножество множества 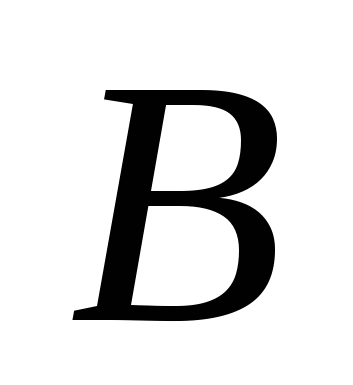 , то пишут , то пишут 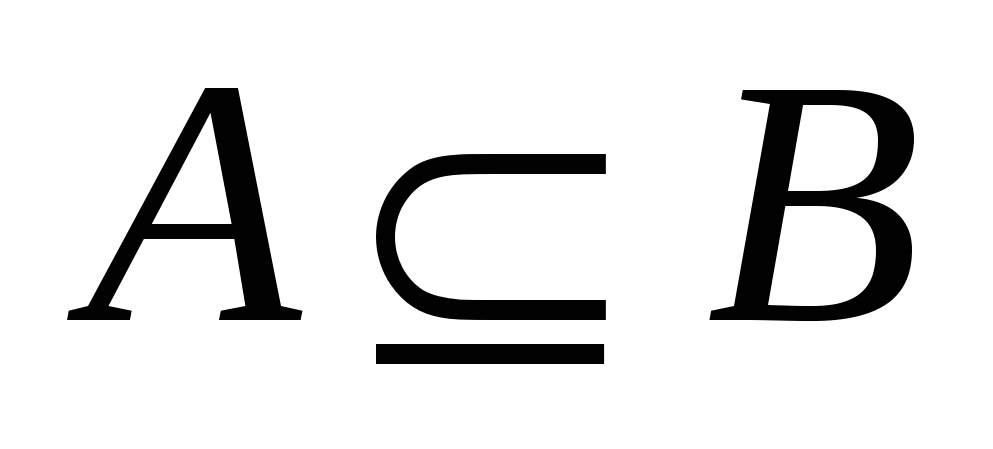 . .
Понятие подмножества определяет между двумя множествами отношение включения. Если 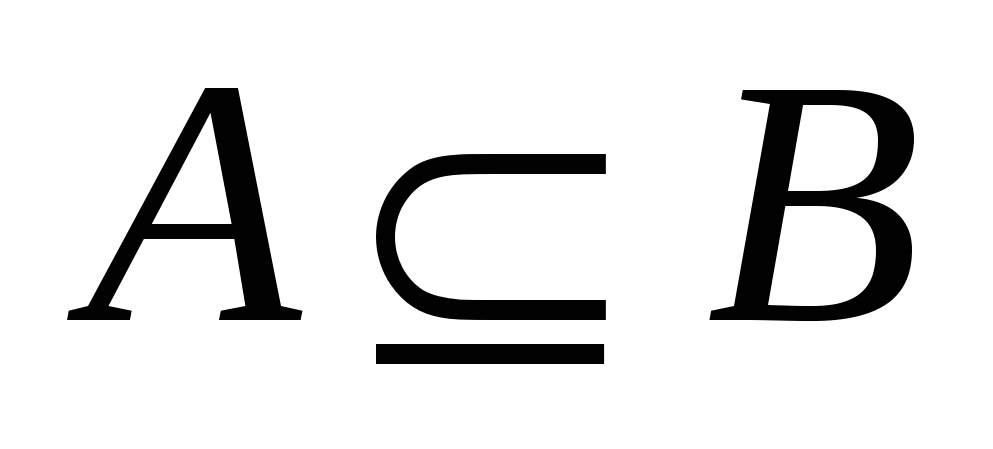 и и 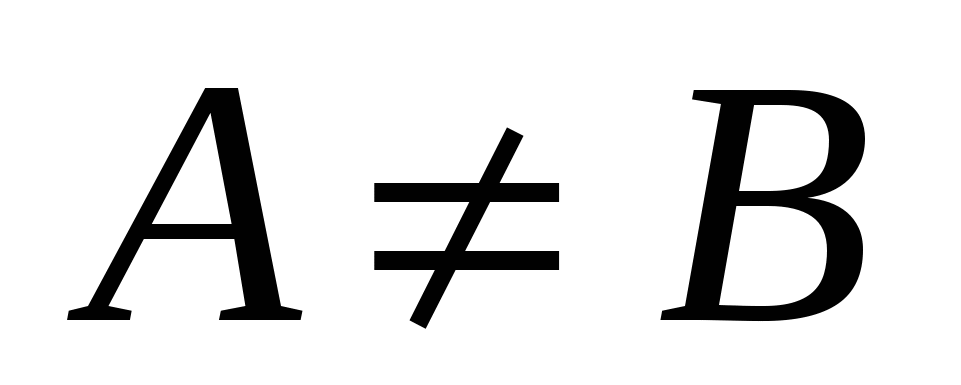 ,то ,то  называется собственным подмножеством множества называется собственным подмножеством множества 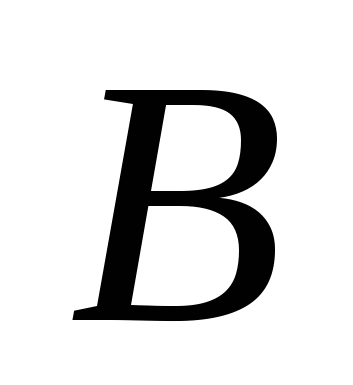 и обозначается и обозначается 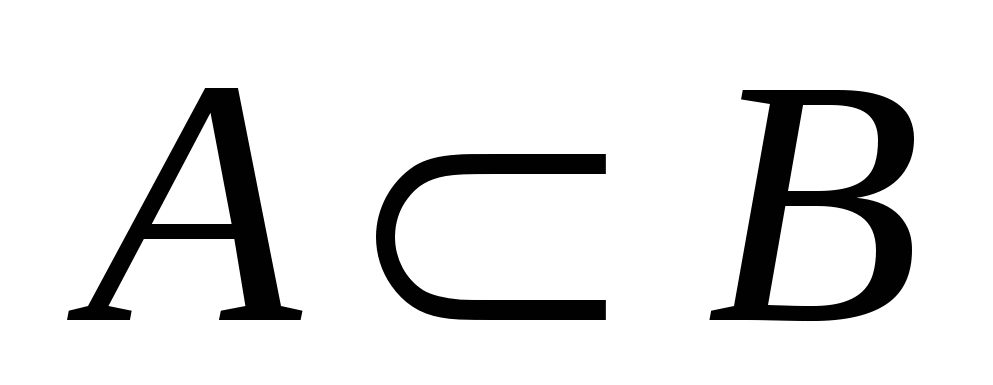 . .
Будем рассматривать всевозможные подмножества одного и того же множества, которое называется основным или универсальным. Обозначается универсальное множество буквой 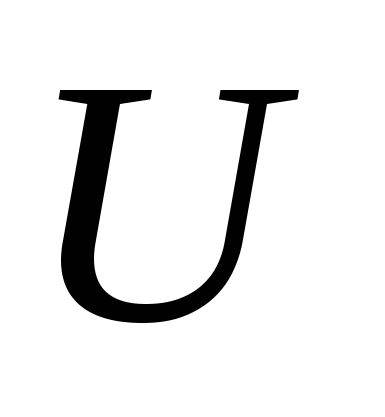 . .
Объединением множеств  и и 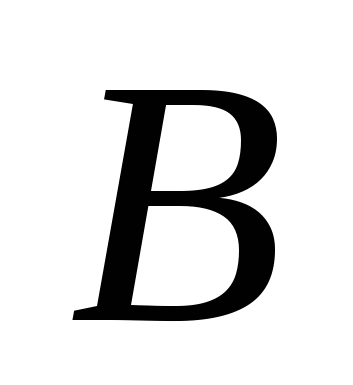 называется множество называется множество  , содержащее те и только те элементы, которые принадлежат хотя бы одному из множеств , содержащее те и только те элементы, которые принадлежат хотя бы одному из множеств  или или 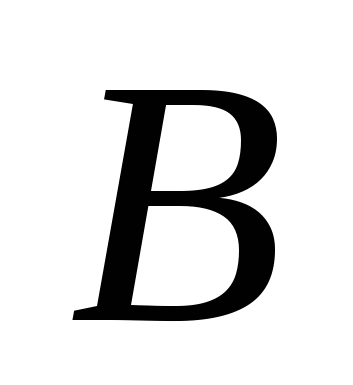 (или обоим одновременно): (или обоим одновременно):
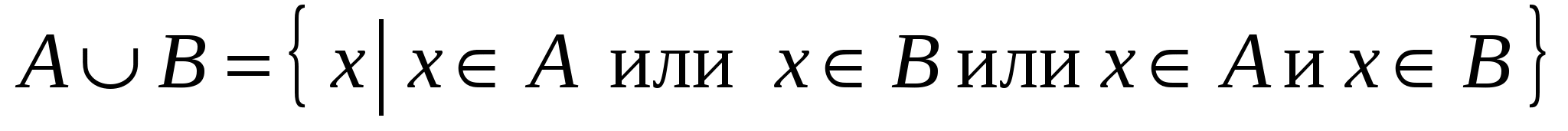 . .
Пересечением множеств  и и 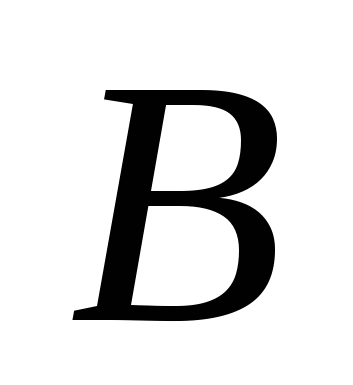 называется множество называется множество 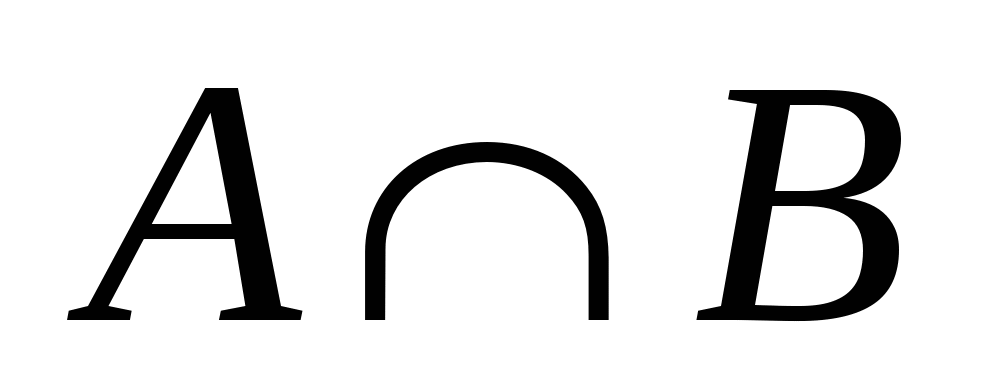 , состоящее из всех тех и только тех элементов, каждый из которых принадлежит обоим множествам одновременно: , состоящее из всех тех и только тех элементов, каждый из которых принадлежит обоим множествам одновременно:
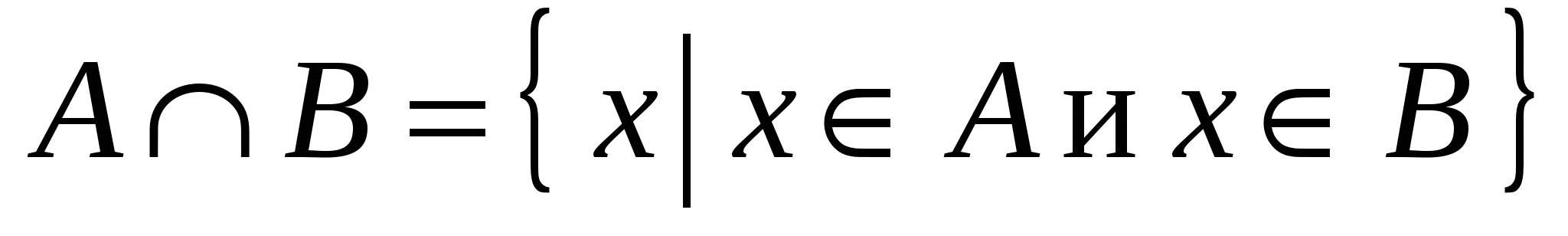 . .
Разностью двух множеств 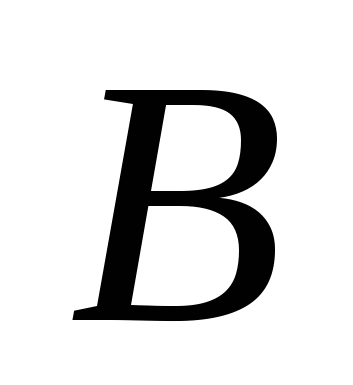 и и  называется множество называется множество 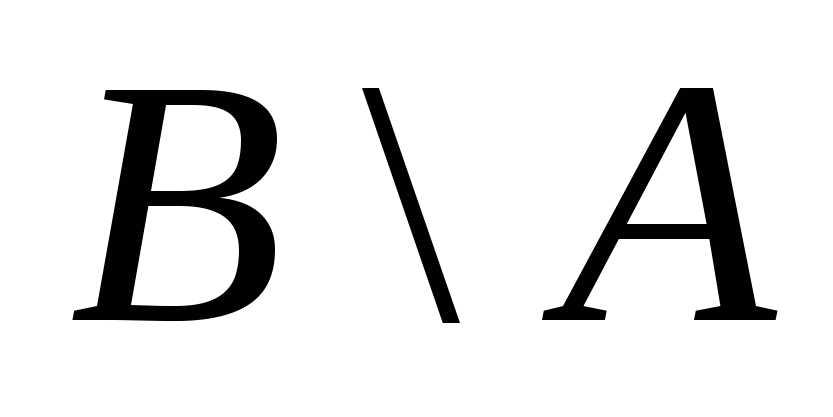 , состоящее из всех тех и только тех элементов, которые принадлежат , состоящее из всех тех и только тех элементов, которые принадлежат 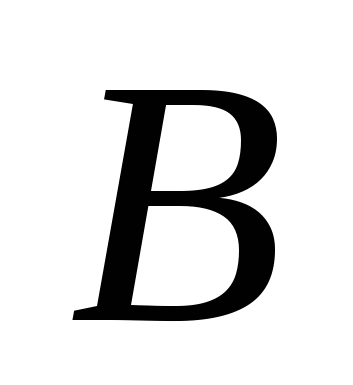 , но не принадлежат , но не принадлежат  : :
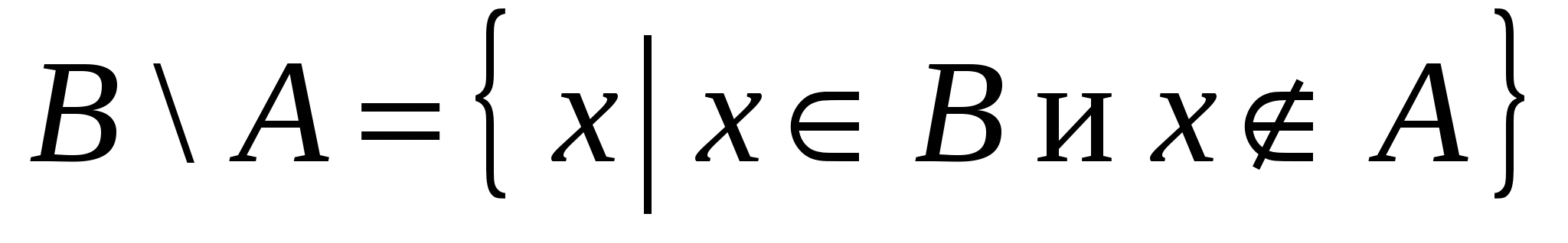 . .
Разность  называется дополнением множества называется дополнением множества  до универсального множества до универсального множества 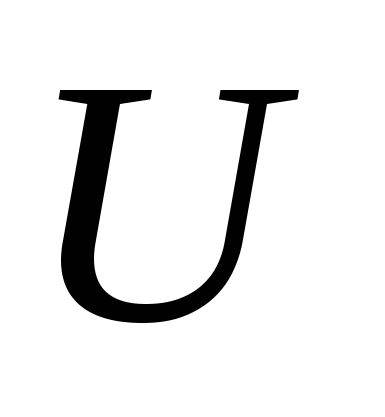 и обозначается и обозначается  : :
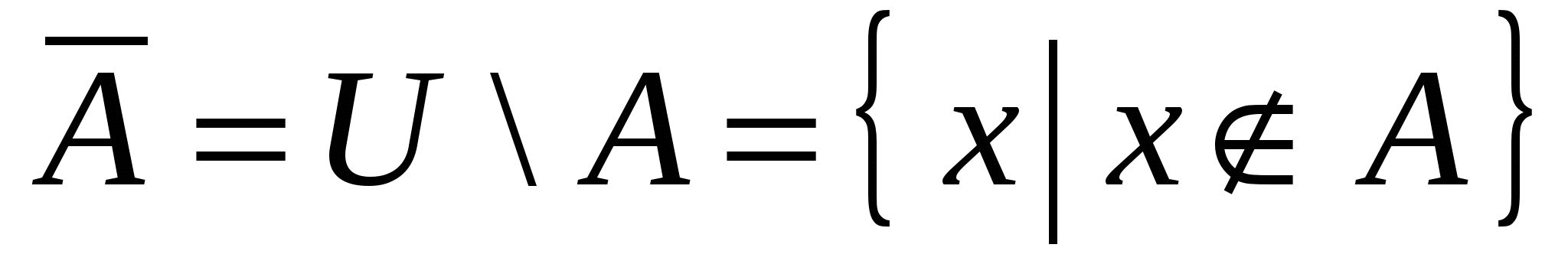 . .
Пара элементов 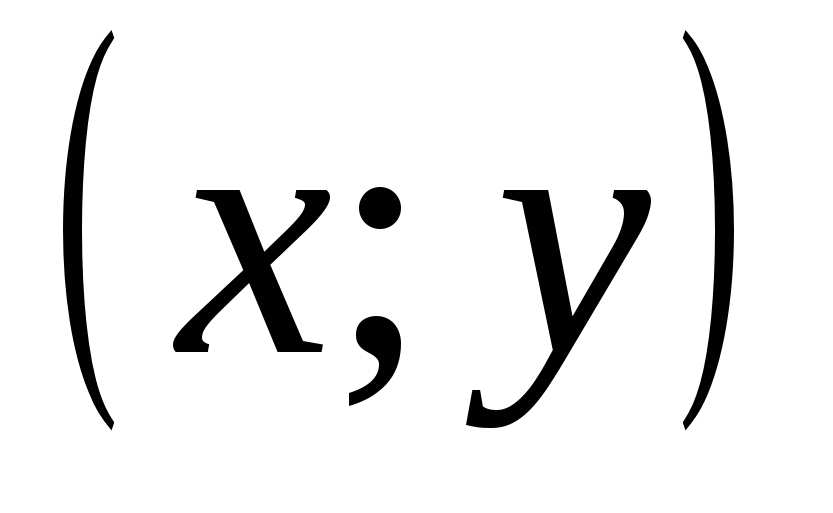 , , 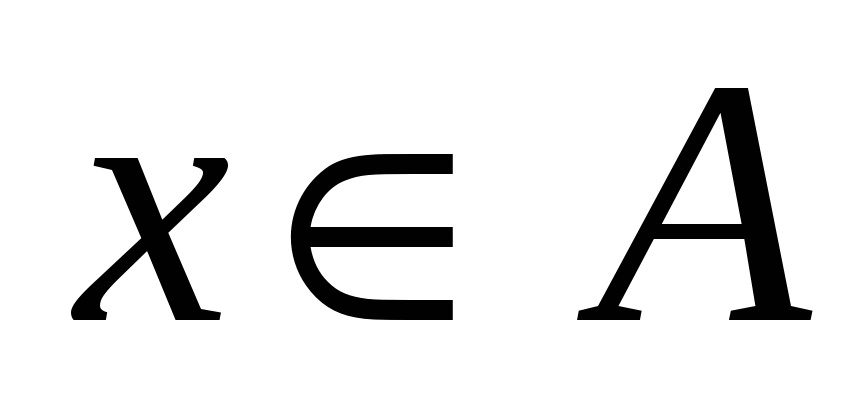 , , 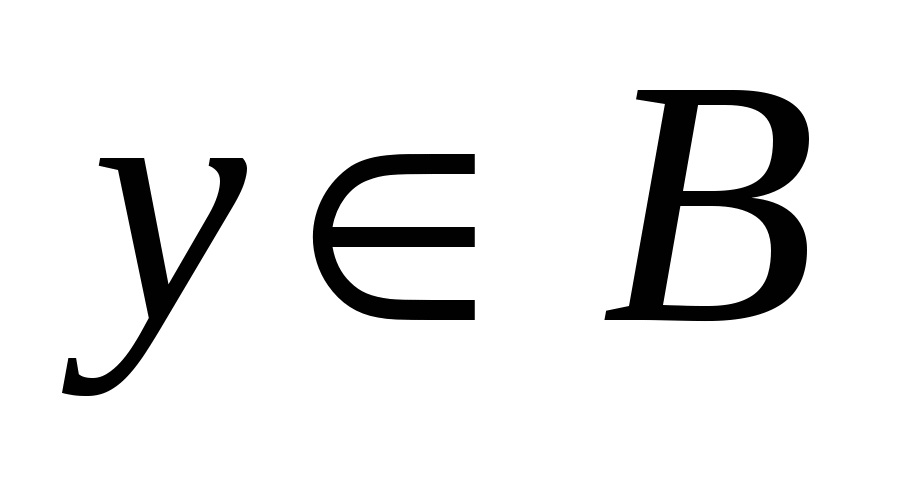 , называется упорядоченной, если указан порядок записи элементов , называется упорядоченной, если указан порядок записи элементов 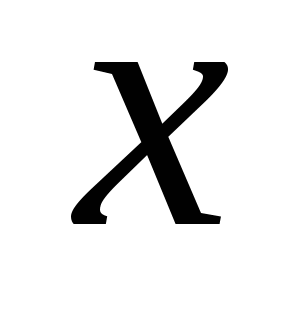 и и 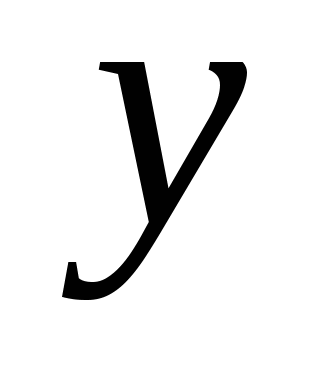 . Элементы . Элементы 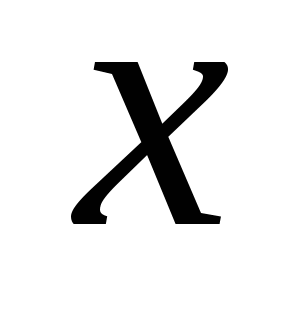 и и 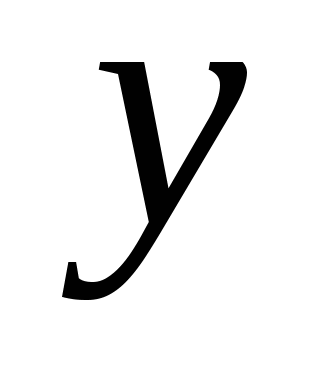 упорядоченной пары упорядоченной пары 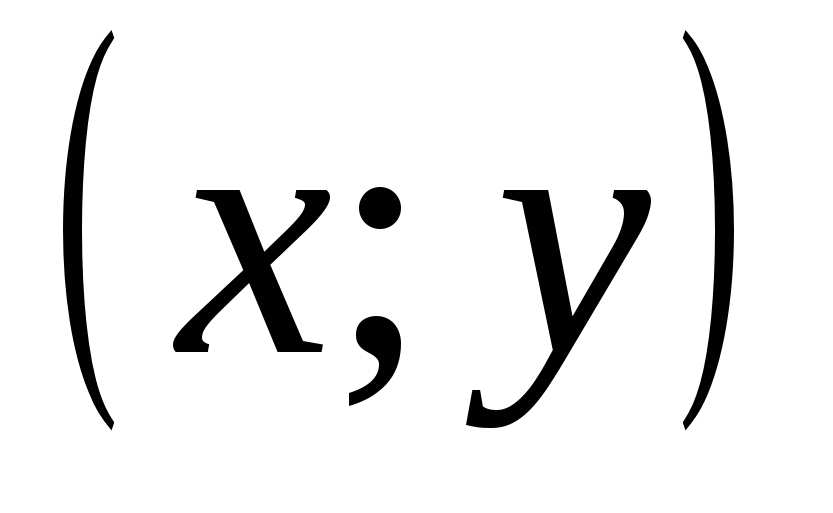 называются координатами, при этом называются координатами, при этом 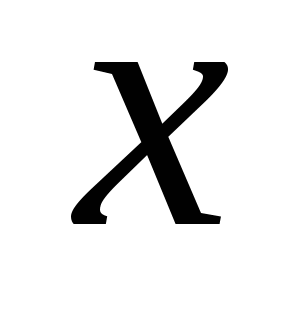 – первая координата, – первая координата, 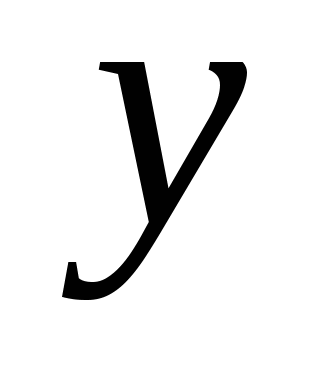 – вторая. При этом – вторая. При этом 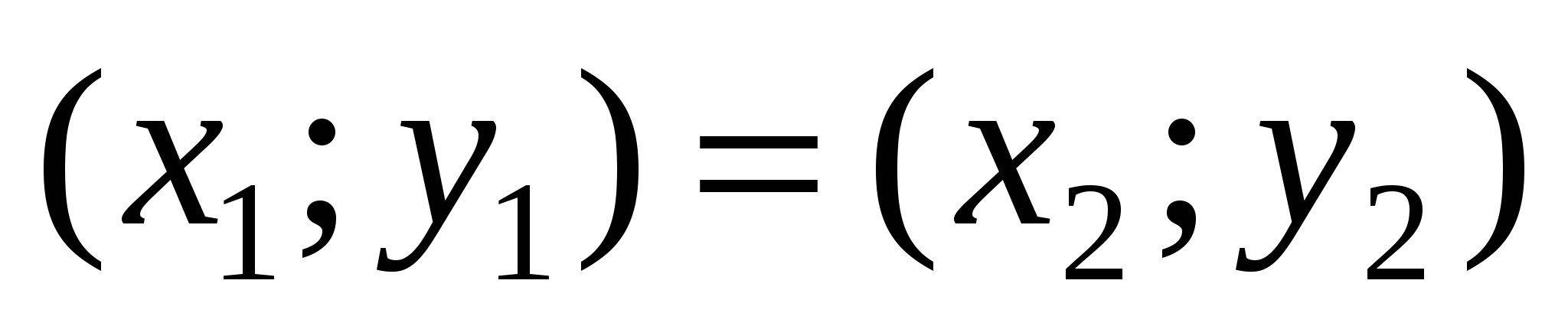 тогда и только тогда, когда тогда и только тогда, когда 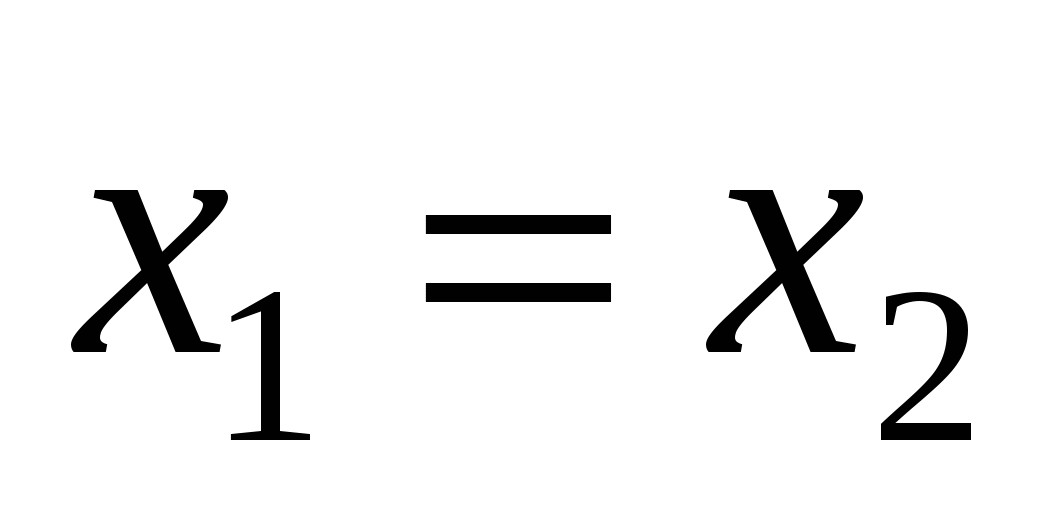 и и 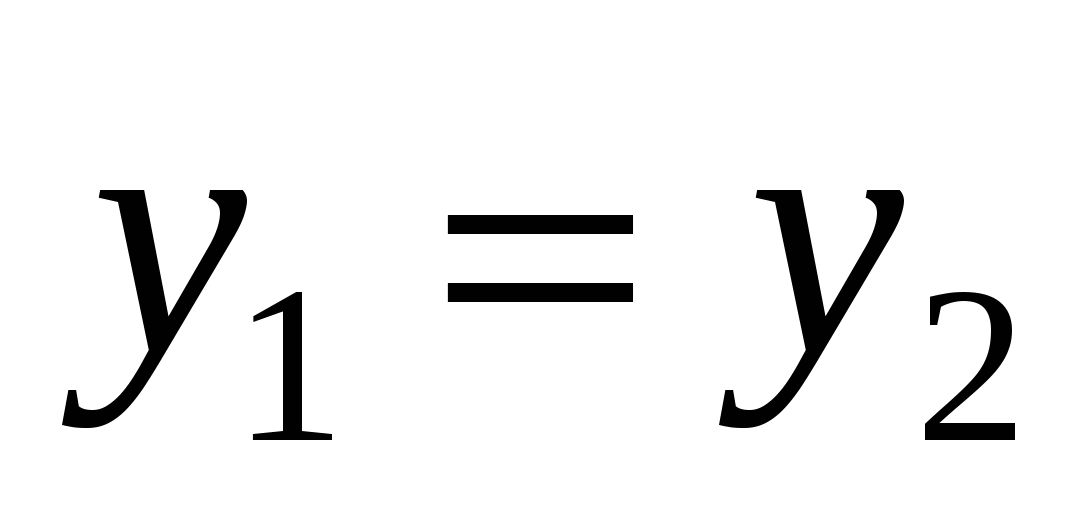 . .
Основные числовые множества:
– множество натуральных чисел, т.е. чисел, которые используются при счете:
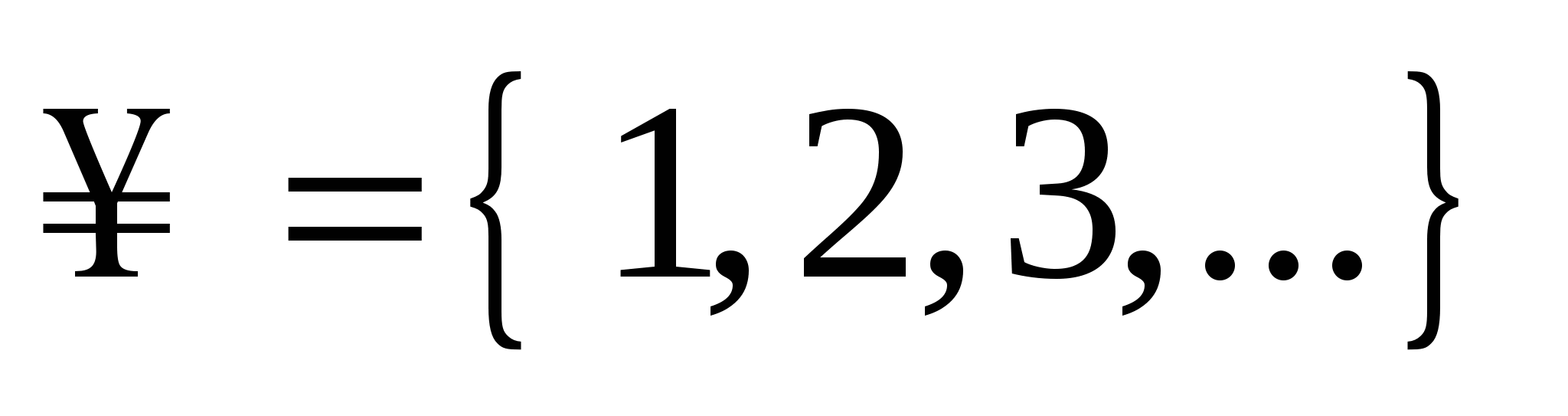 ; ;
– объединение натуральных чисел, чисел, им противоположных и нуля составляет множество целых чисел:
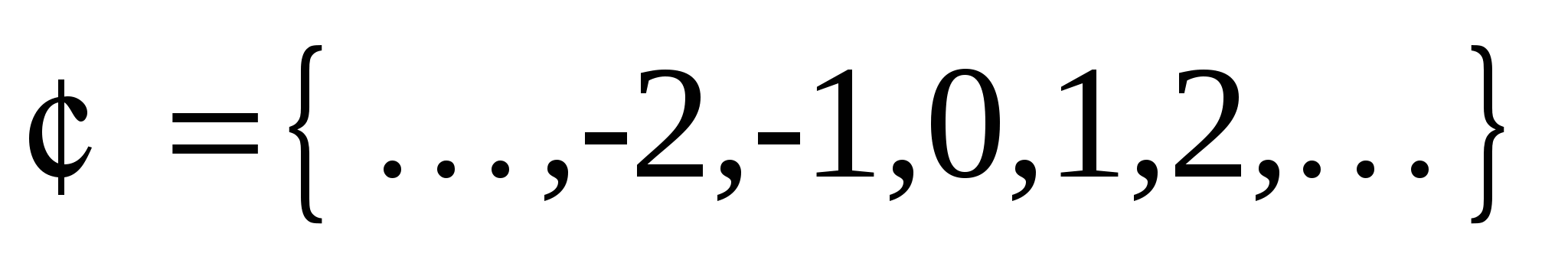 ; ;
– множество чисел вида 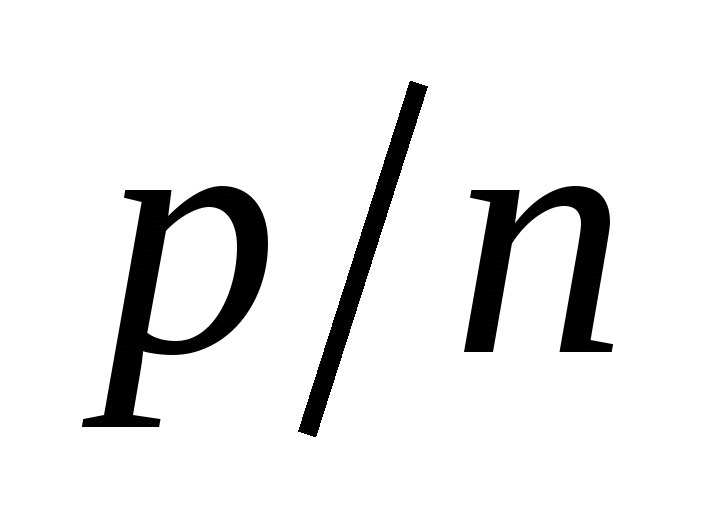 , где , где 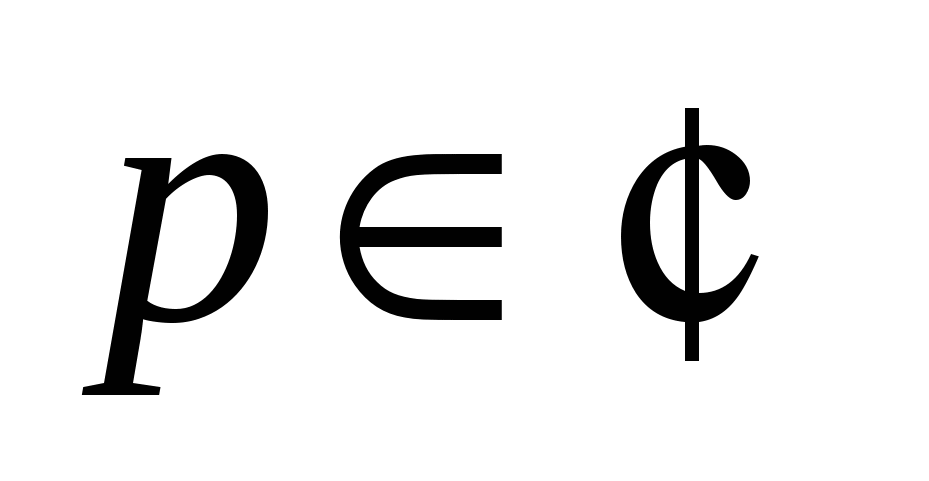 ; ; 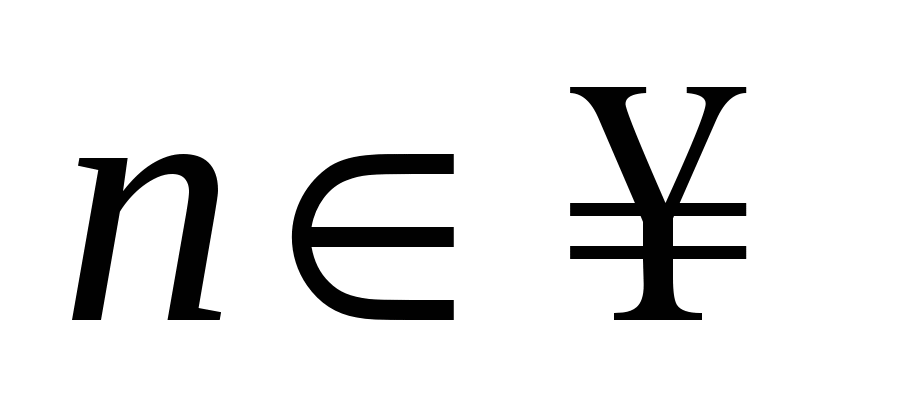 , называется множеством рациональных чисел: , называется множеством рациональных чисел:
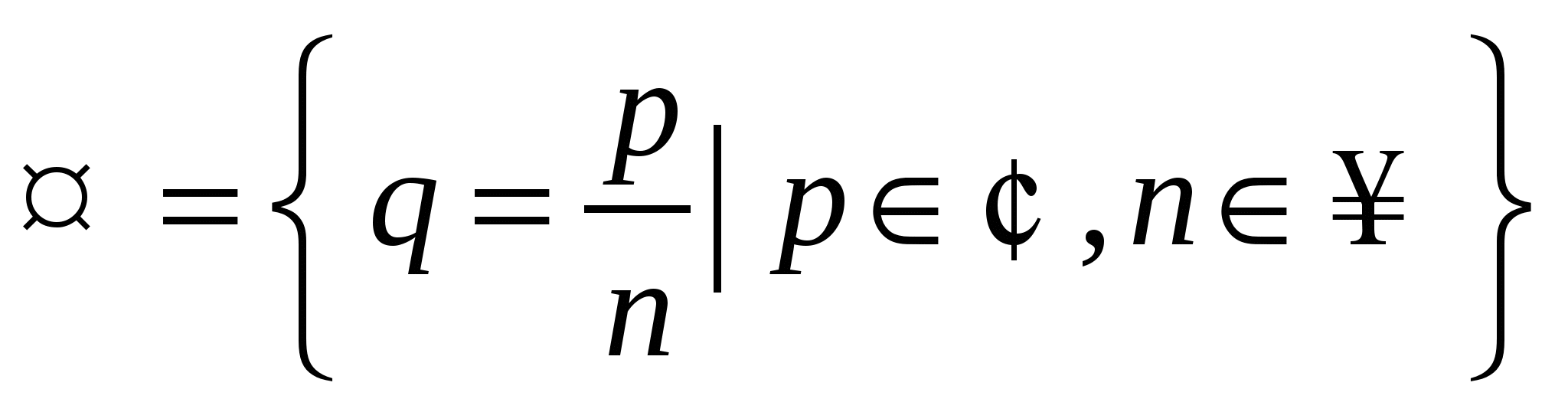 ; ;
– числа, которые представимы в виде бесконечной непериодической десятичной дроби называются иррациональными;
– объединение рациональных и иррациональных чисел составляет множество действительных чисел  . .
Очевидно, 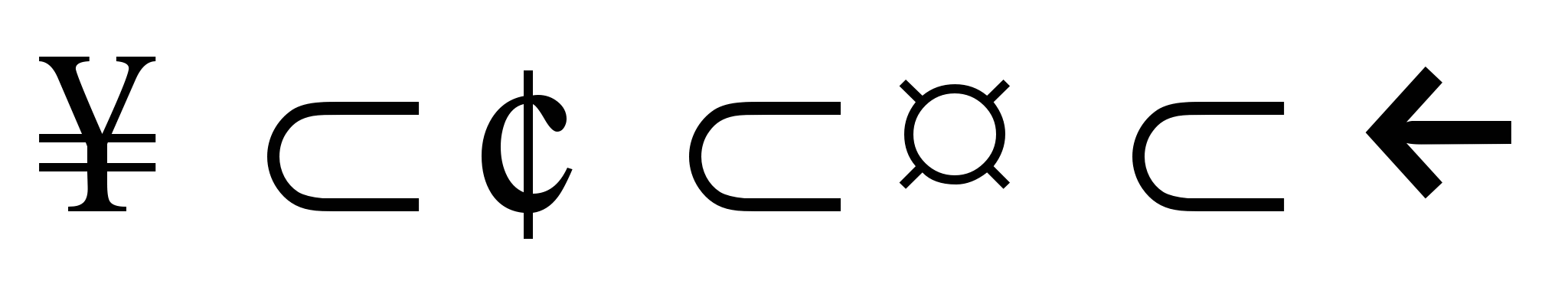 . .
Множество действительных чисел  , пополненное символами , пополненное символами 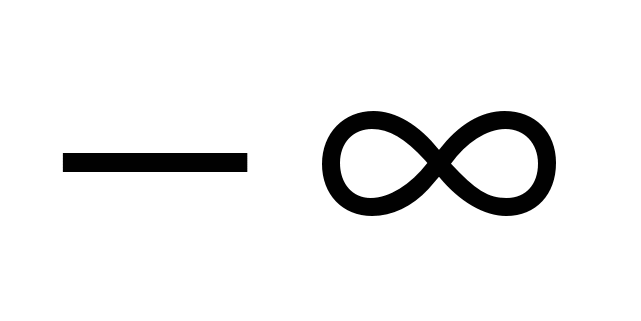 и и 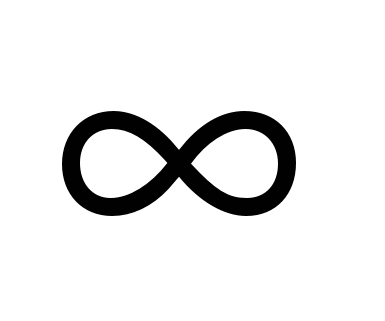 , обозначается , обозначается 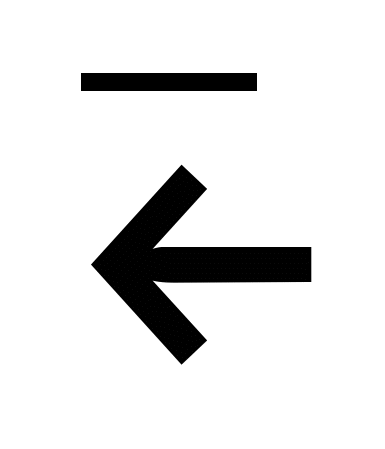 и называется расширенным множеством действительных чисел, бесконечности и называется расширенным множеством действительных чисел, бесконечности 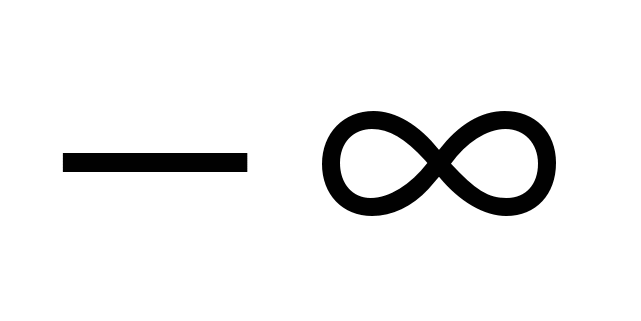 и и 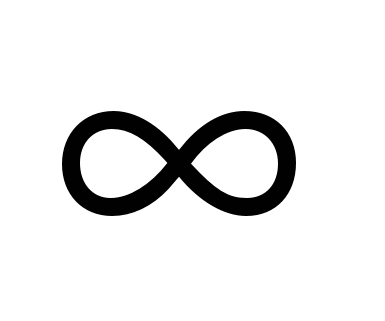 называются бесконечно удаленными точками числовой прямой, остальные точки – конечными точками числовой прямой. называются бесконечно удаленными точками числовой прямой, остальные точки – конечными точками числовой прямой.
Основными промежутками во множестве 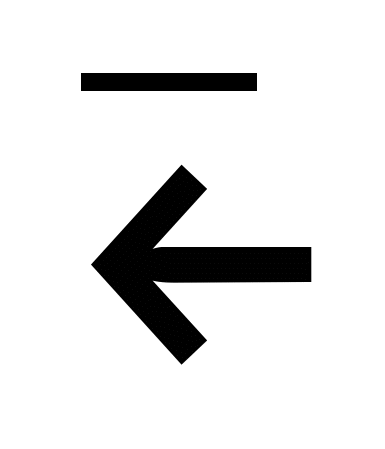 являются: являются:
– интервал с концами  и и 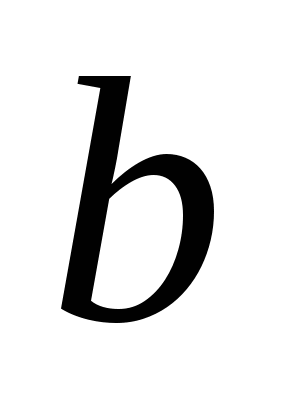 : : 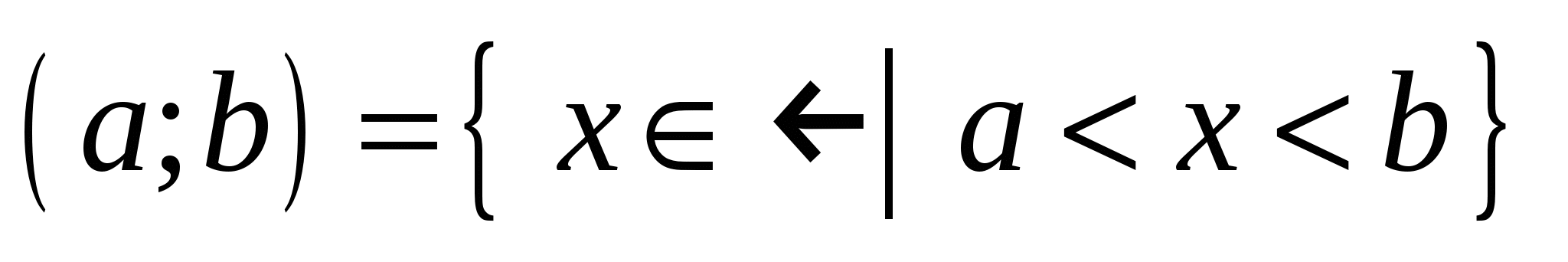 ; ;
– отрезок с концами  и и 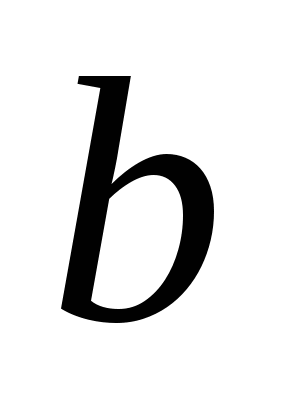 : : 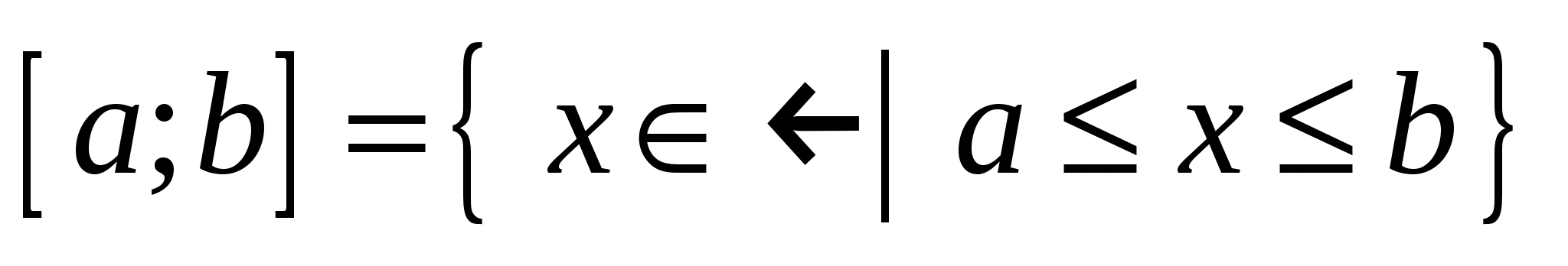 ; ;
– полуинтервалы:
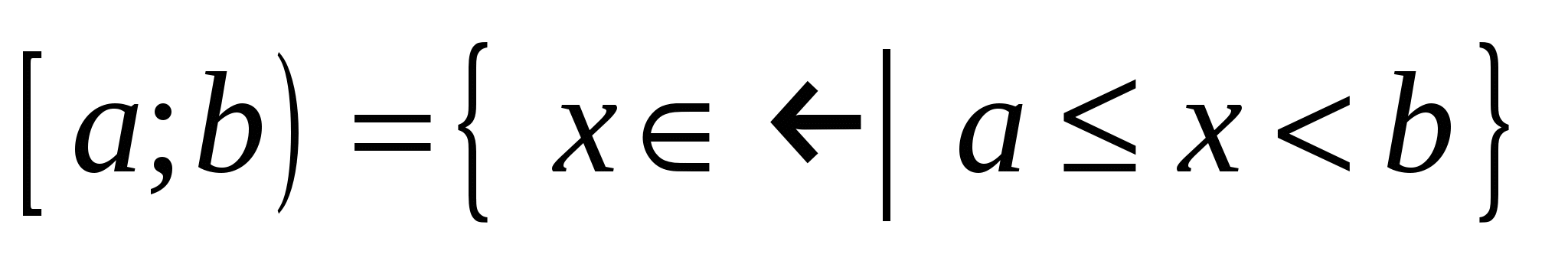 , , 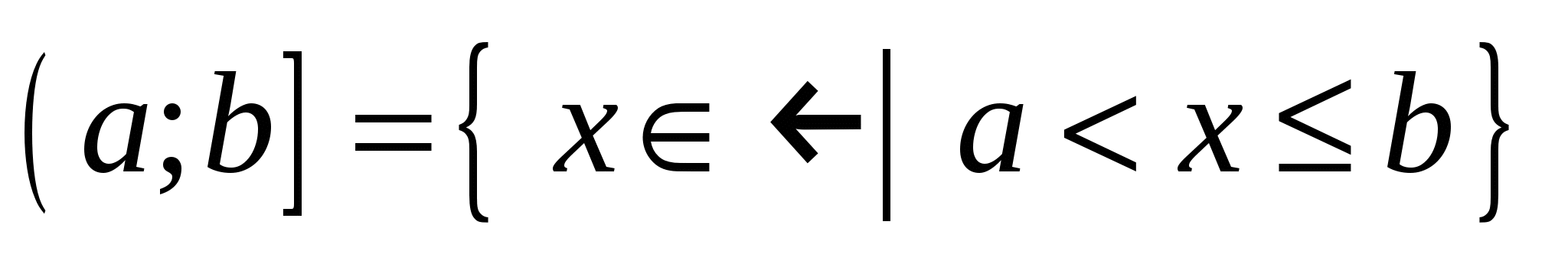 ; ;
– бесконечные интервалы и полуинтервалы:
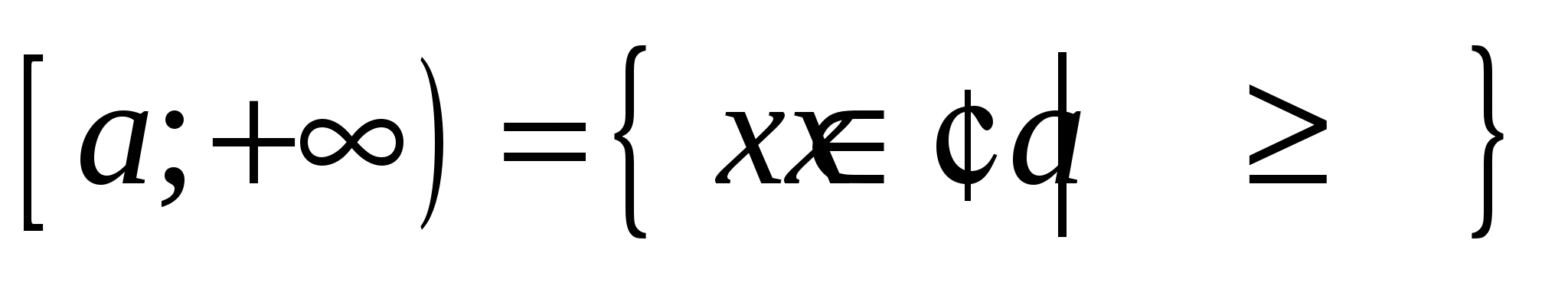 , , 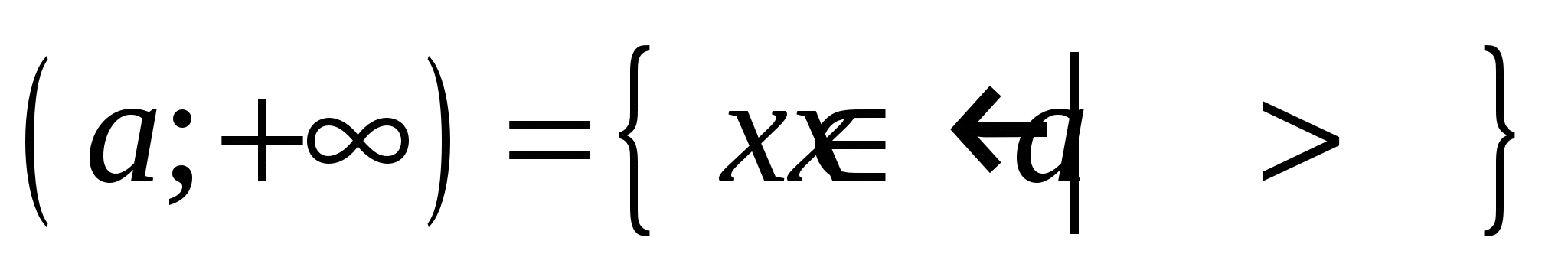 , ,
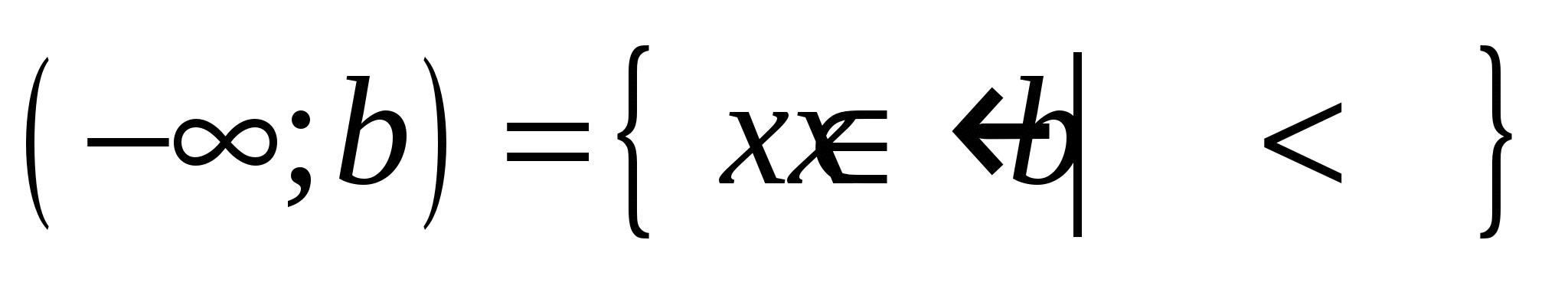 , , 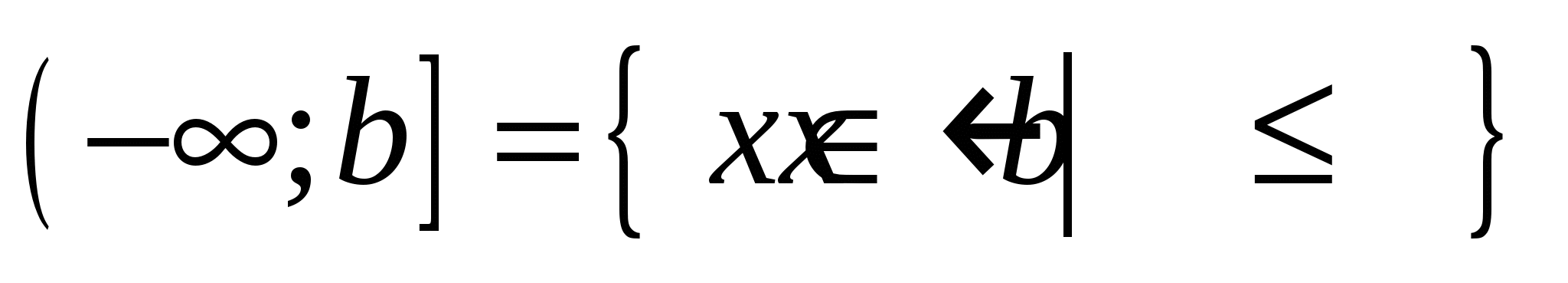 , ,
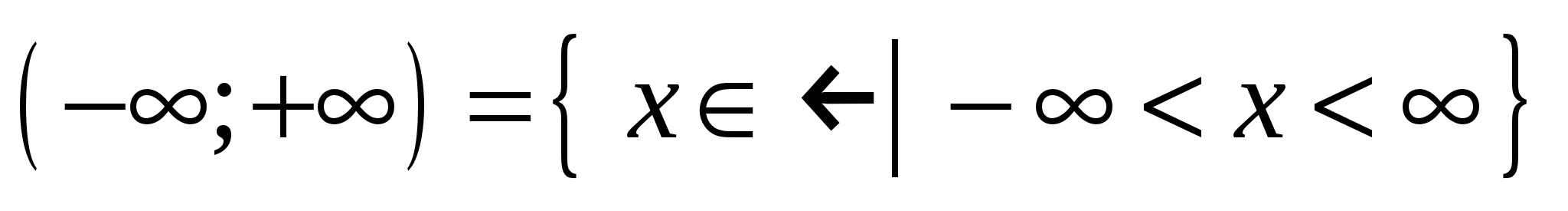 . .
Декартовым произведением двух множеств  и и 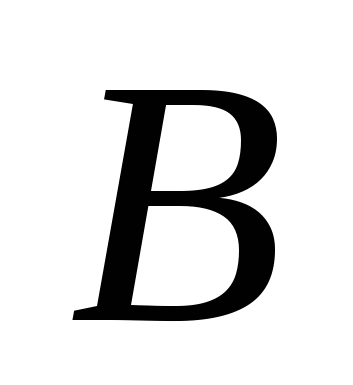 называется множество, обозначаемое называется множество, обозначаемое 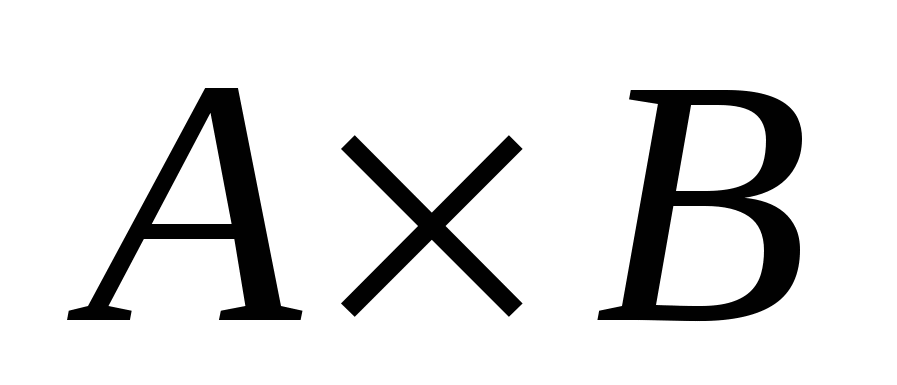 , состоящее из всевозможных упорядоченных пар , состоящее из всевозможных упорядоченных пар 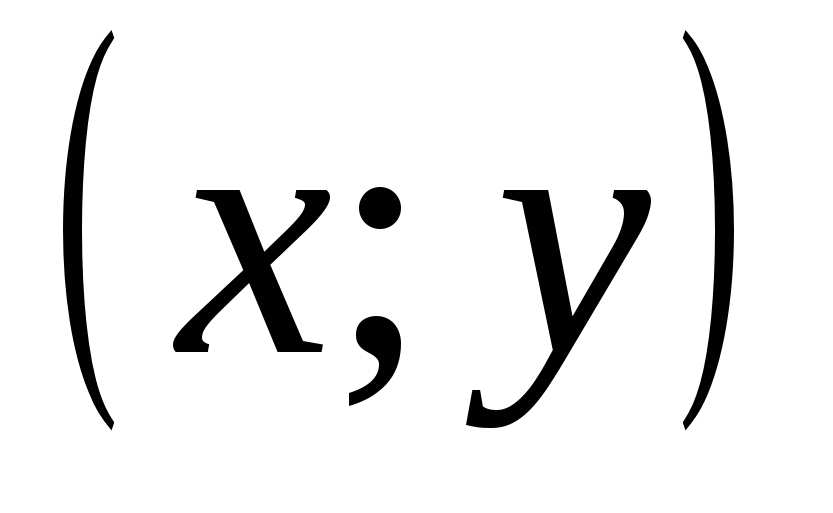 : :
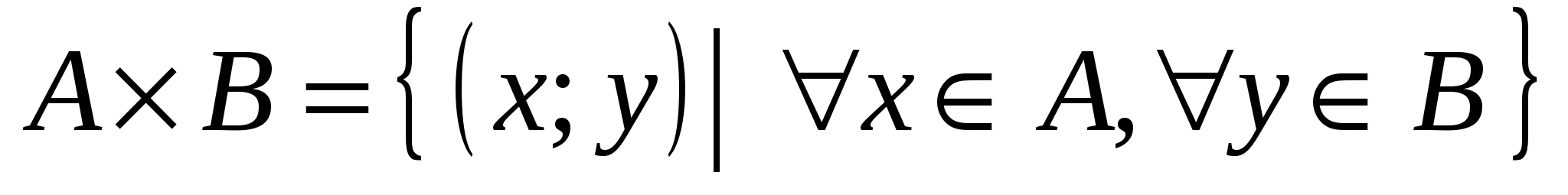 . .
Если 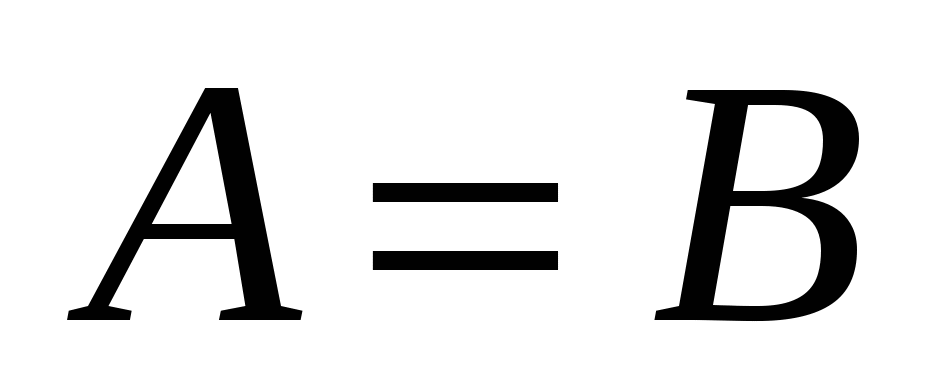 , то , то 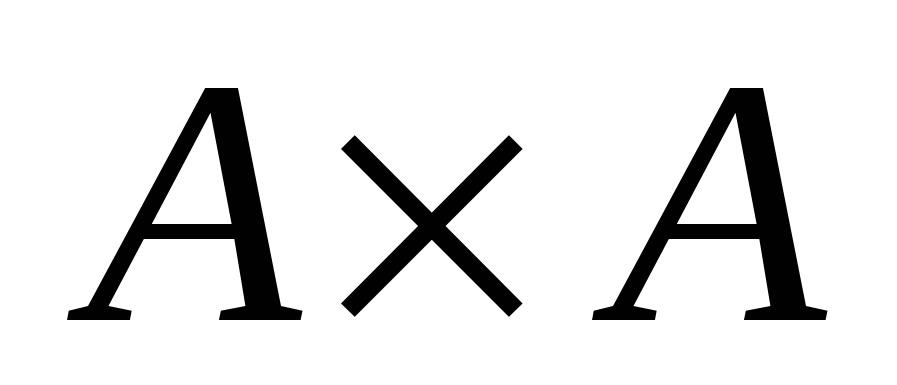 называется декартовым квадратом и обозначается называется декартовым квадратом и обозначается  , т.е. , т.е. 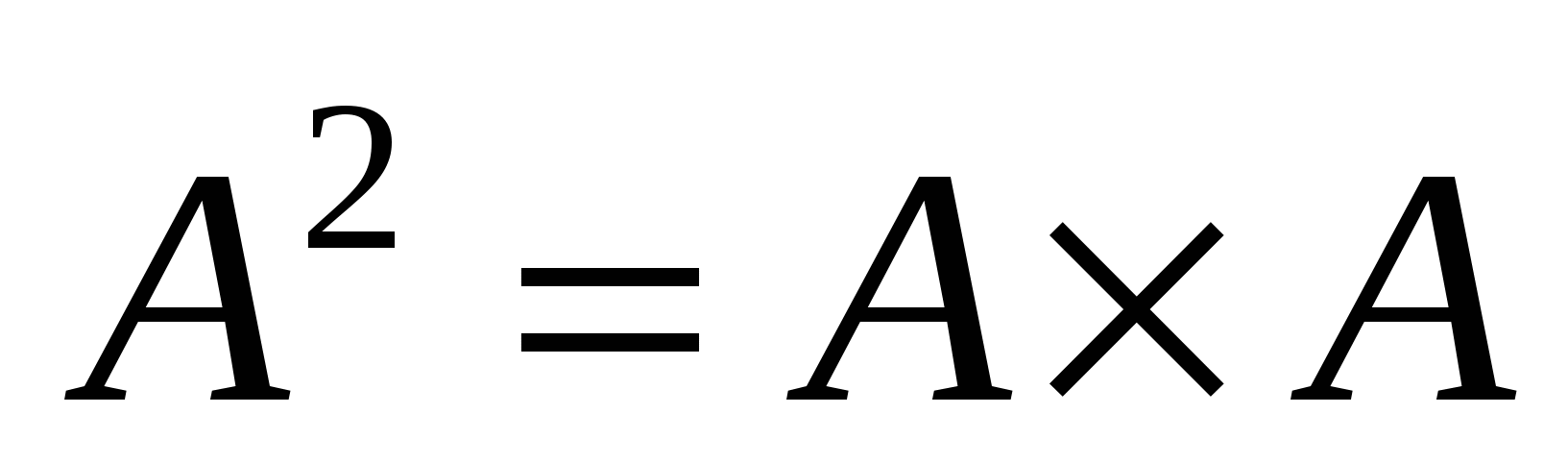 . .
Пусть 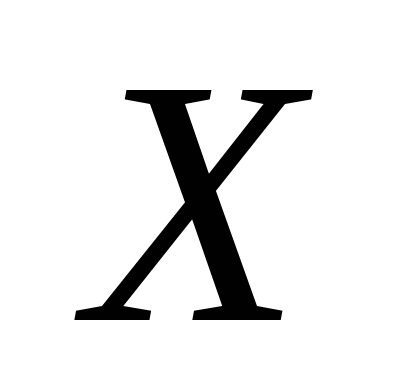 , , 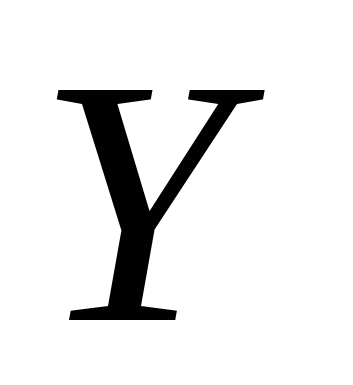 – произвольные множества. Соответствие, при котором каждому элементу – произвольные множества. Соответствие, при котором каждому элементу 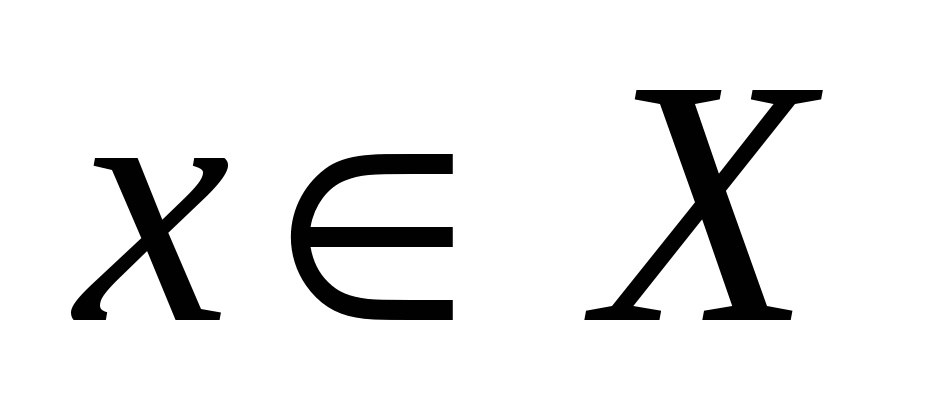 ставится в соответствие единственный элемент ставится в соответствие единственный элемент 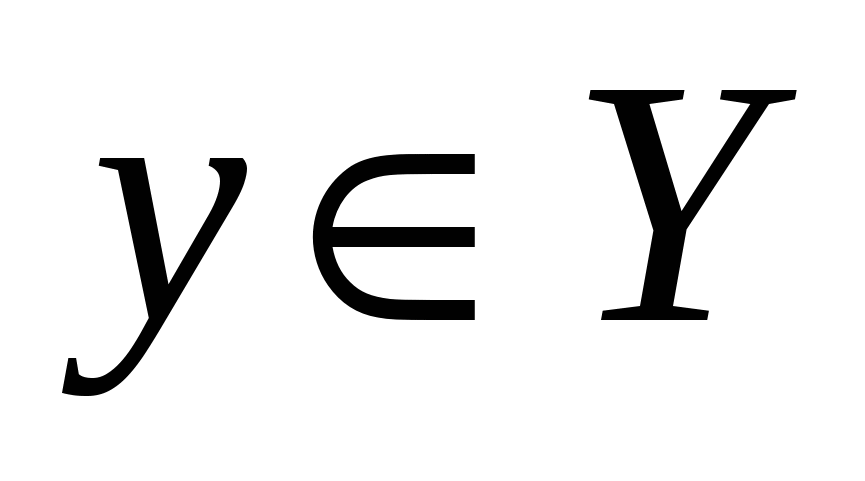 , называется функцией (отображением), заданной на множестве , называется функцией (отображением), заданной на множестве 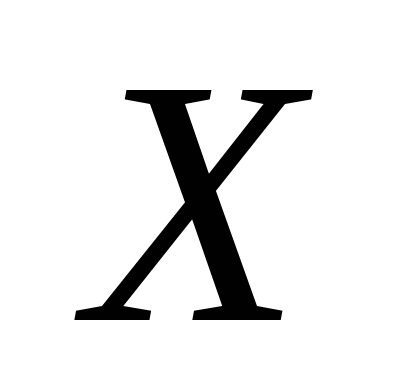 со значениями во множестве со значениями во множестве 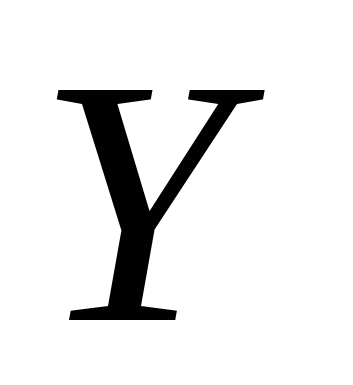 , при этом элемент , при этом элемент 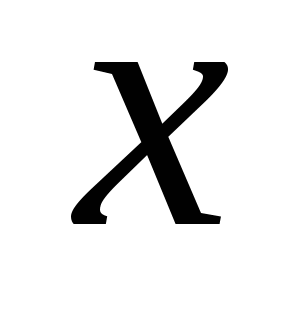 называется независимой переменной (аргументом), элемент называется независимой переменной (аргументом), элемент 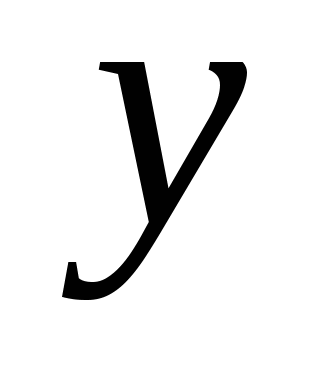 – зависимой переменной и обозначается: – зависимой переменной и обозначается:
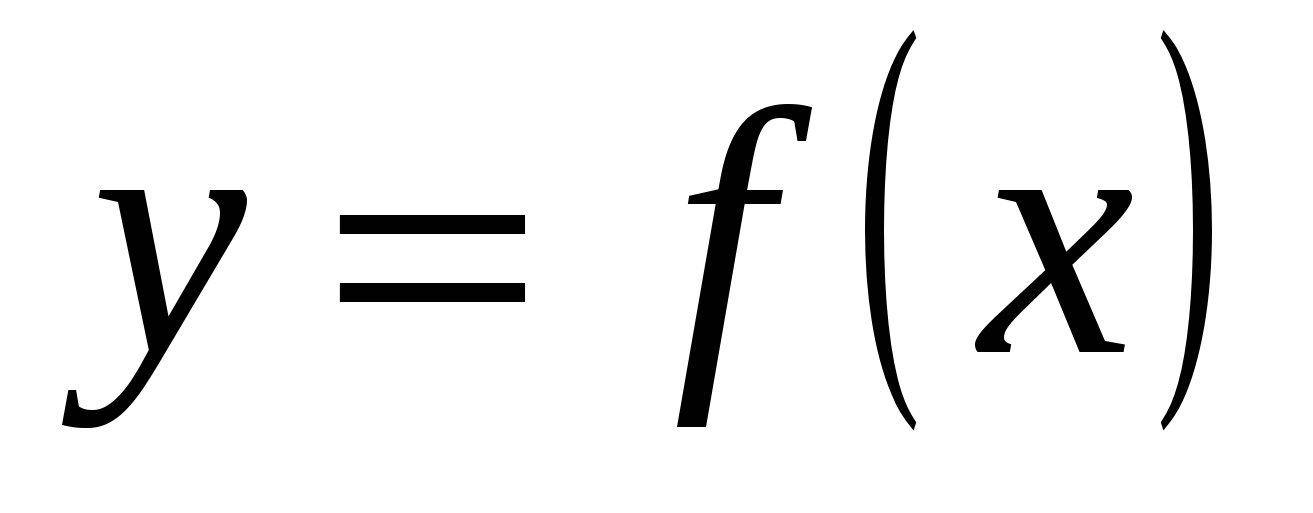 , , 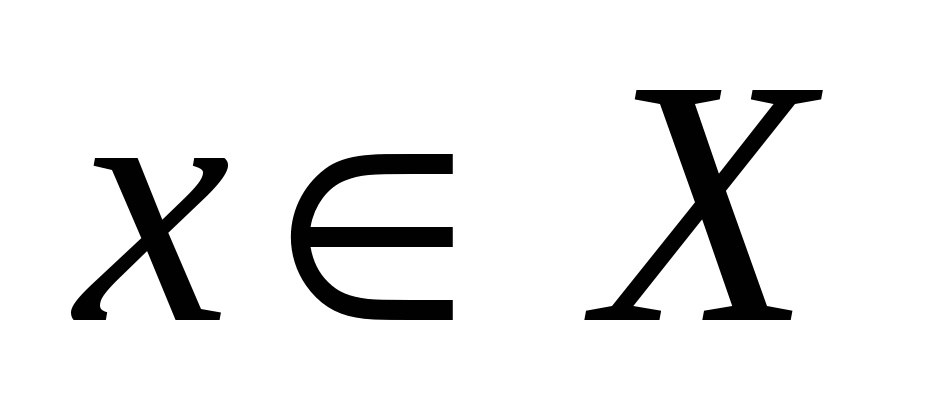 , , 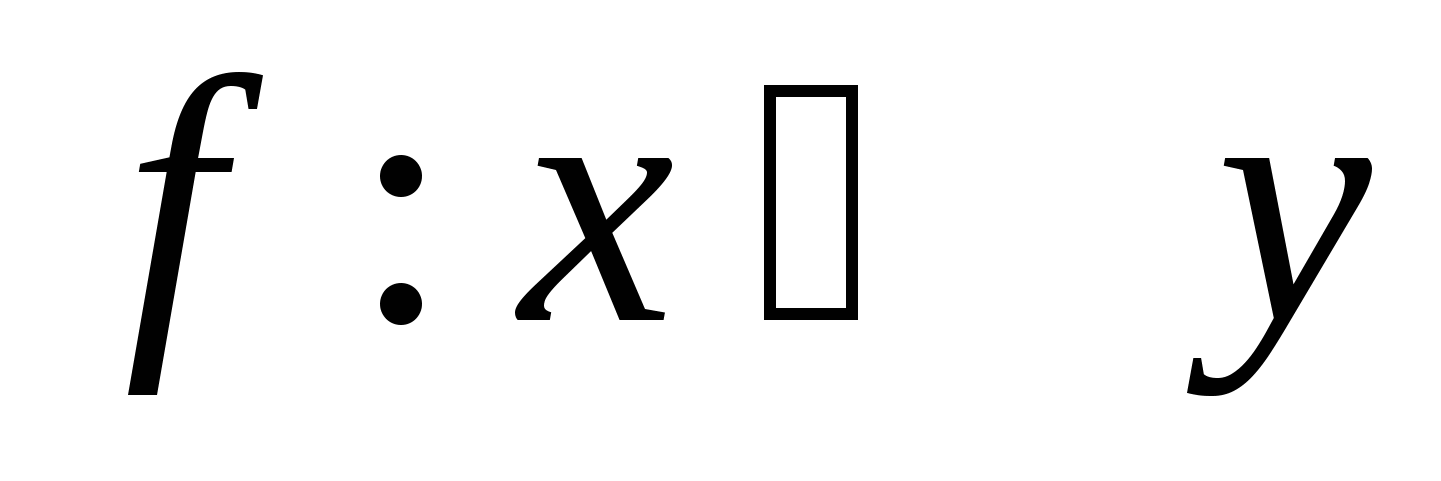 при при 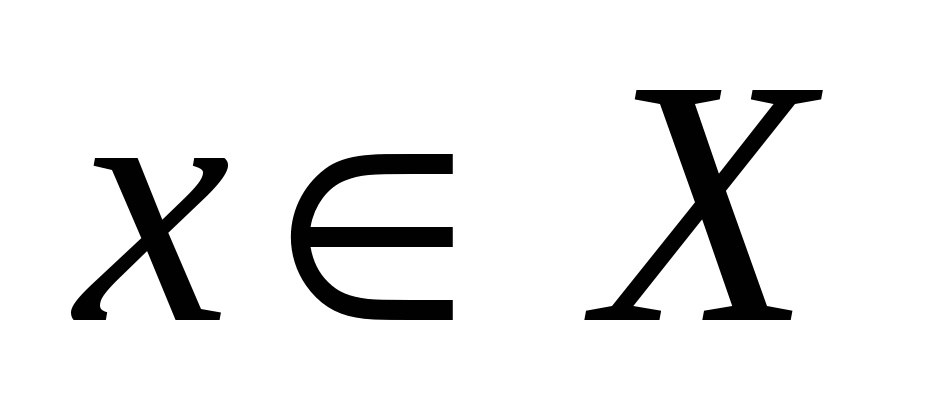 и и 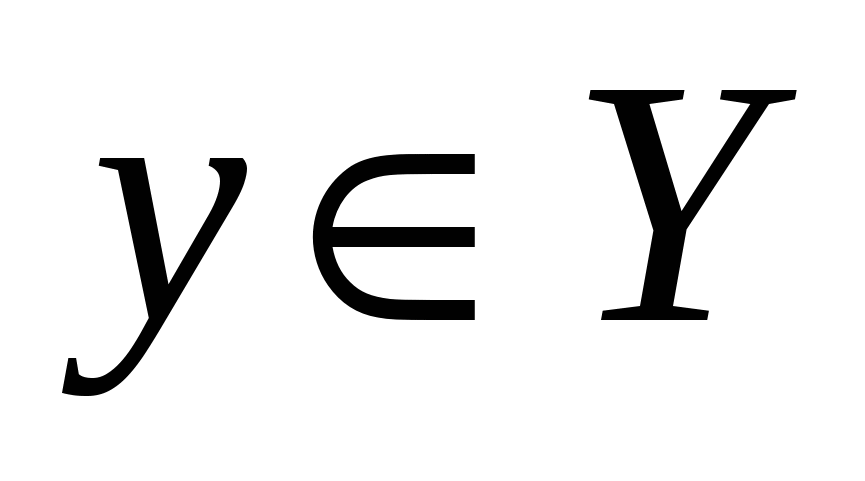 ; ; 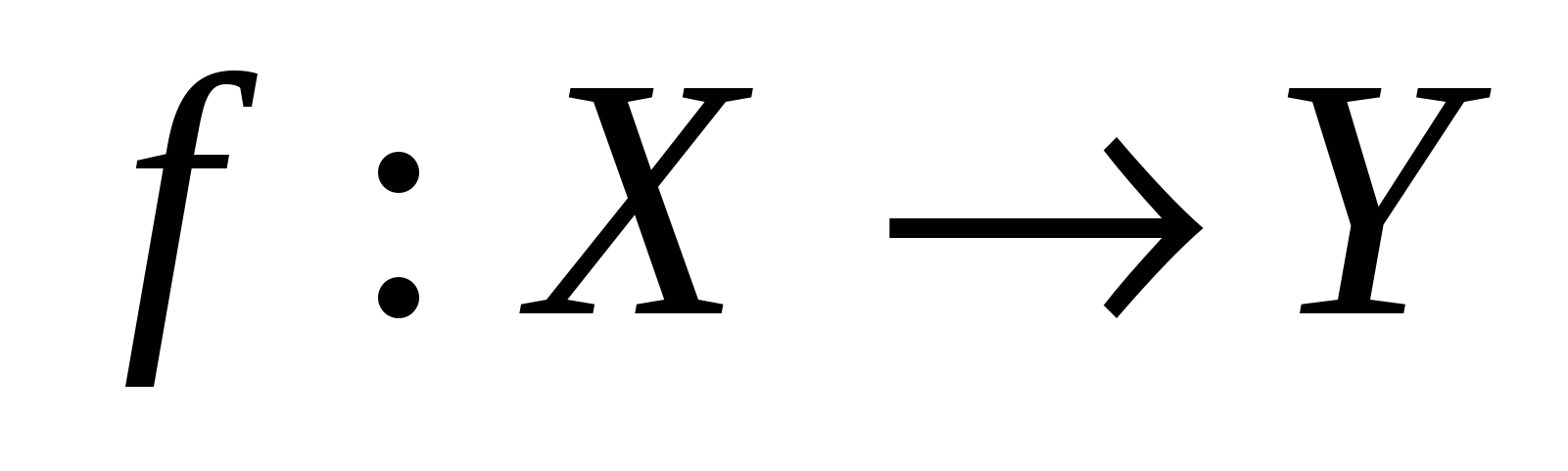 . .
Множество 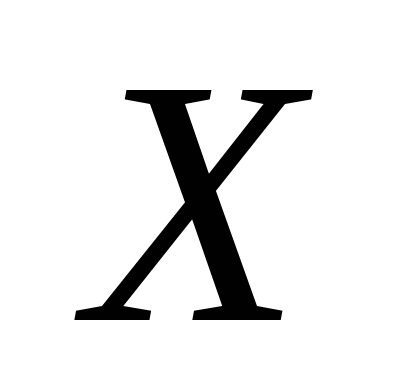 называется областью определения функции называется областью определения функции 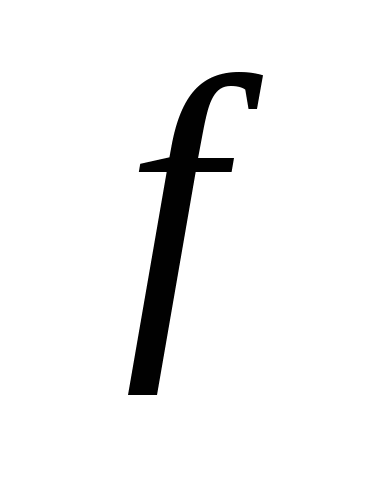 и обозначается и обозначается 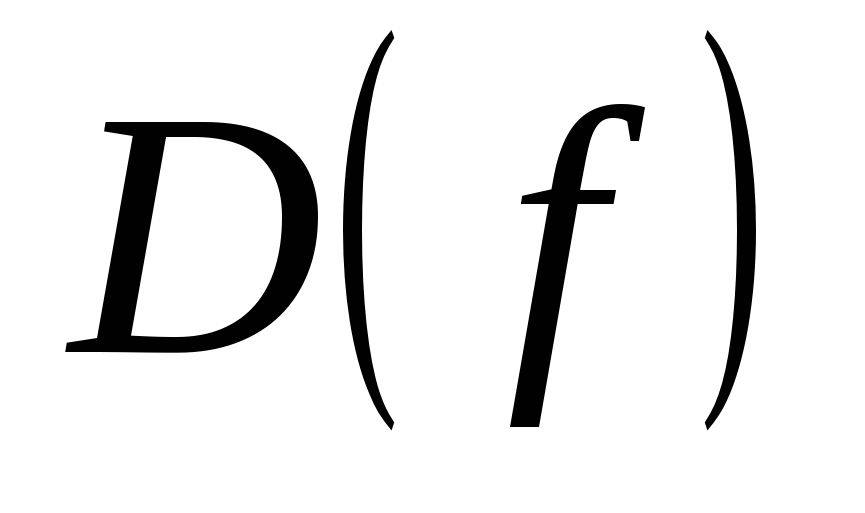 . Множество тех . Множество тех 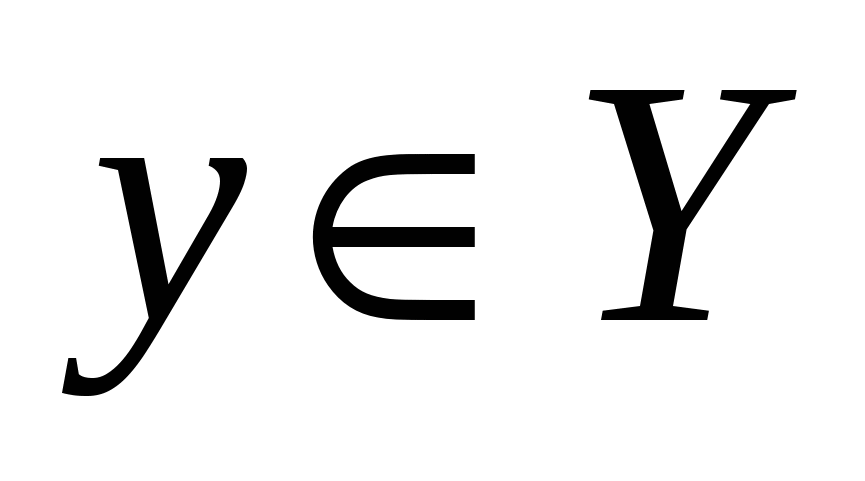 , каждый из которых поставлен в соответствие хотя бы одному , каждый из которых поставлен в соответствие хотя бы одному 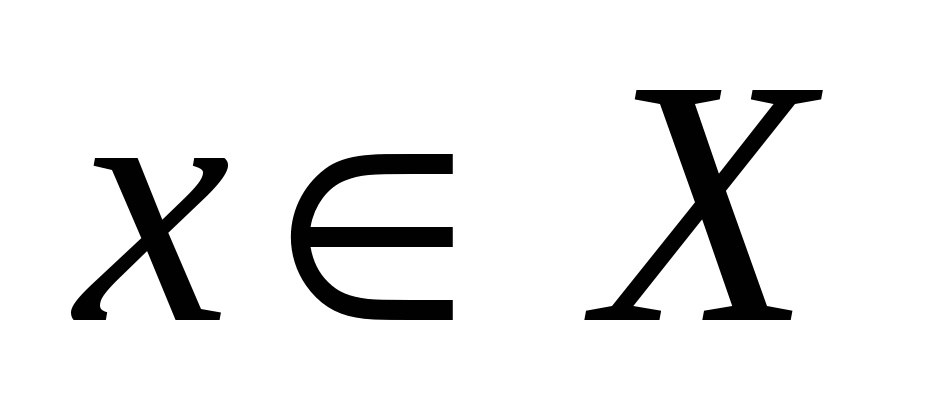 , называется множеством значений функции , называется множеством значений функции 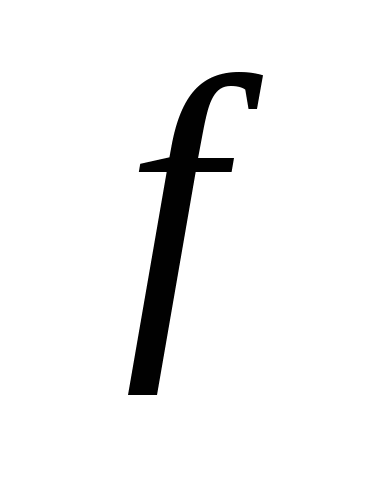 и обозначается и обозначается 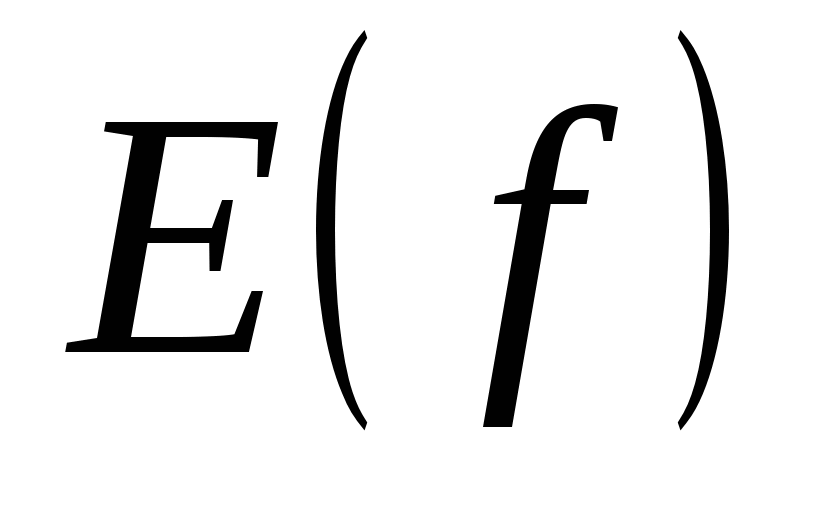 . Очевидно, что . Очевидно, что 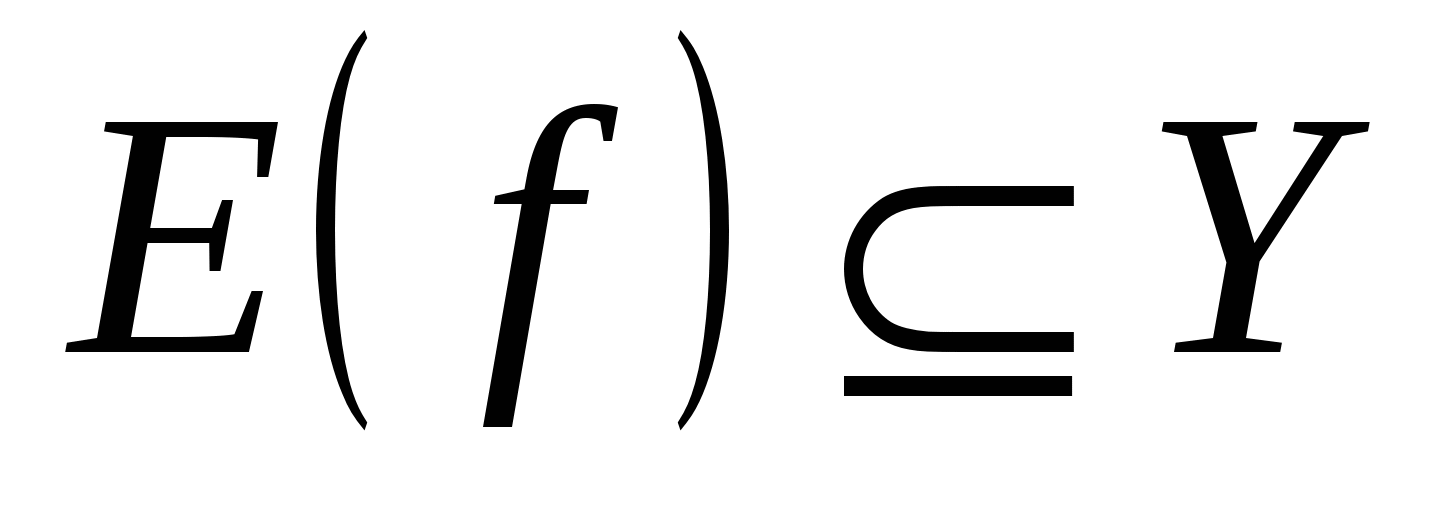 . .
Определение функции с помощью логических символов записывается в виде:
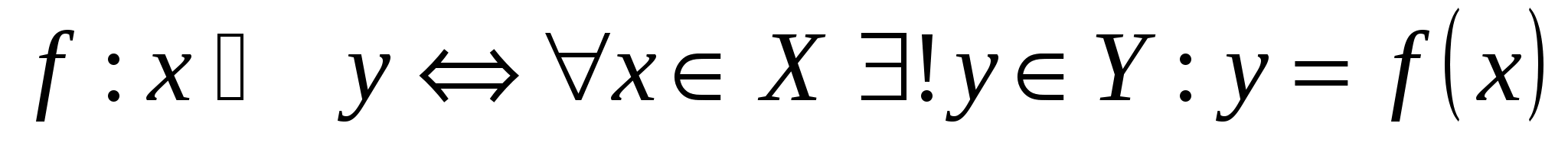 . .
Элемент 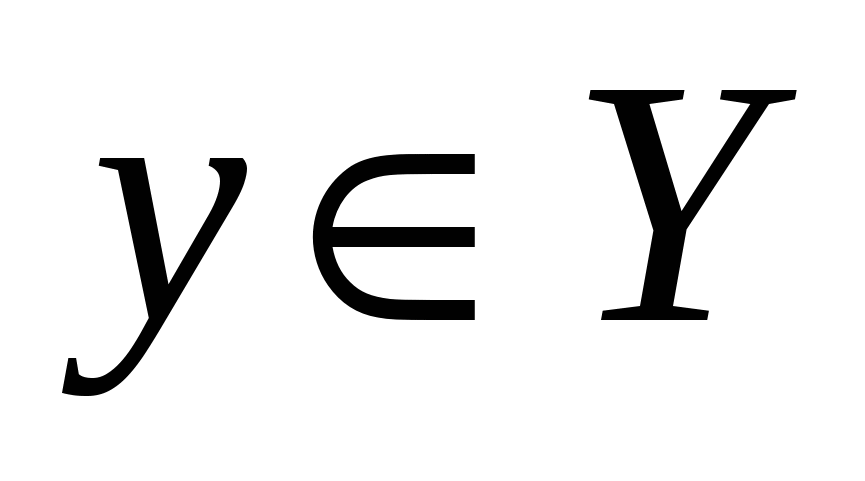 , в который отображен , в который отображен 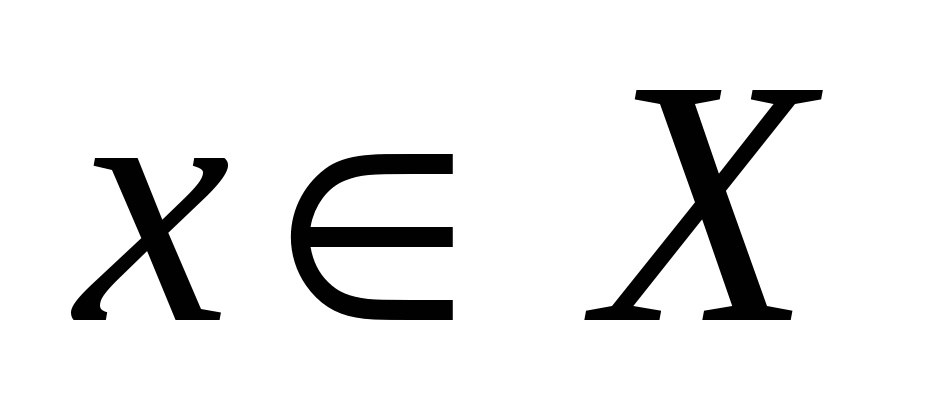 , называется образом элемента , называется образом элемента 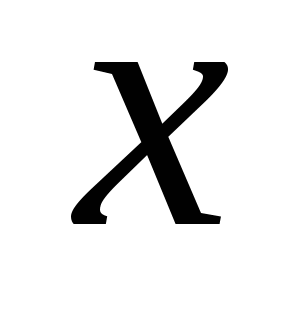 при отображении при отображении 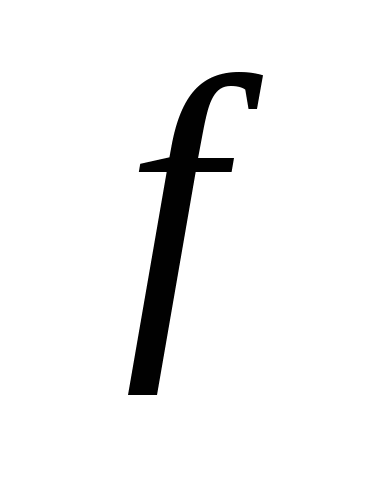 и обозначается и обозначается 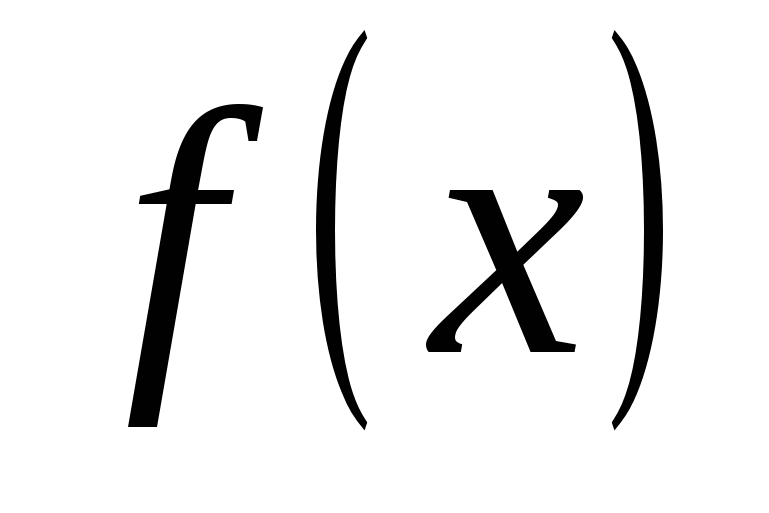 . Элемент . Элемент 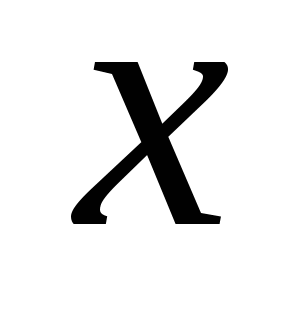 называется прообразом элемента называется прообразом элемента 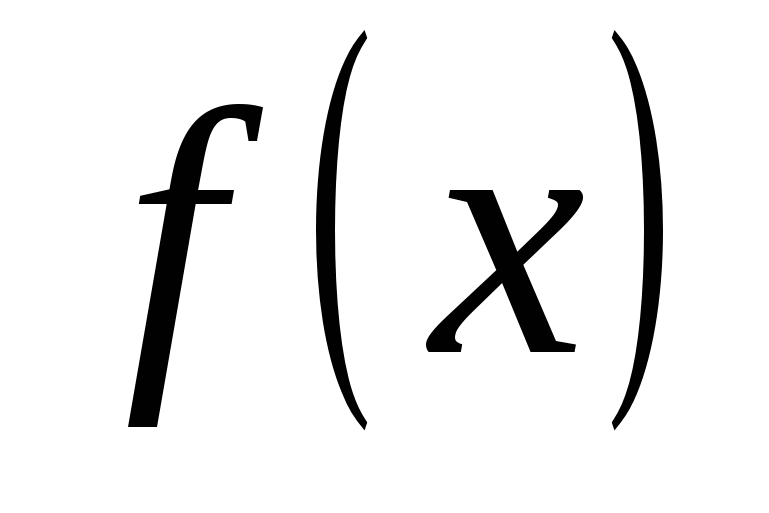 . Поэтому отображение удобно записывать в виде . Поэтому отображение удобно записывать в виде 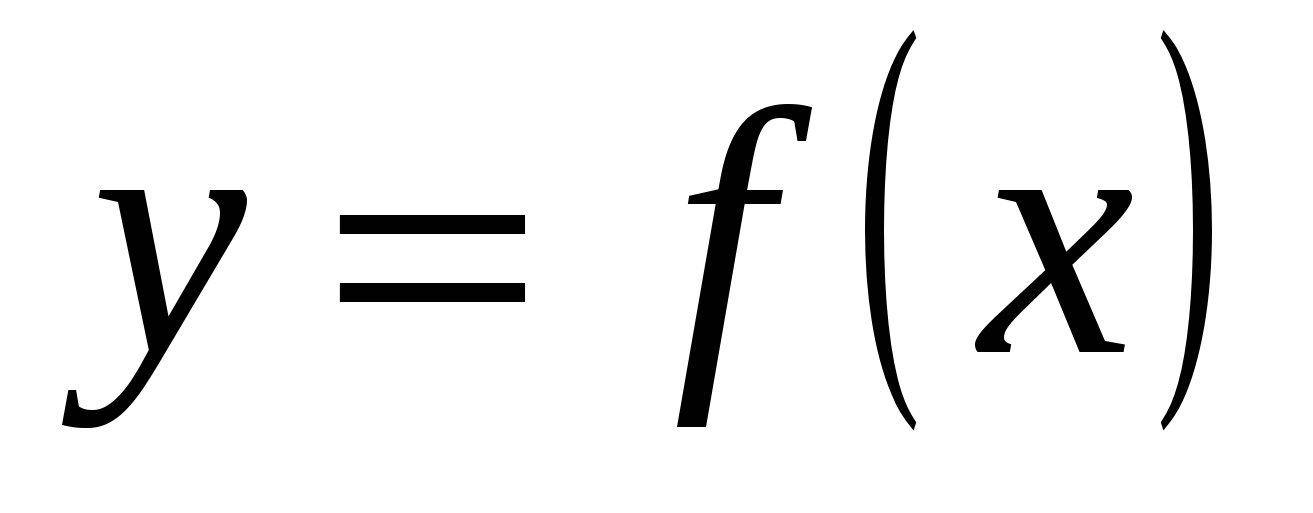 , , 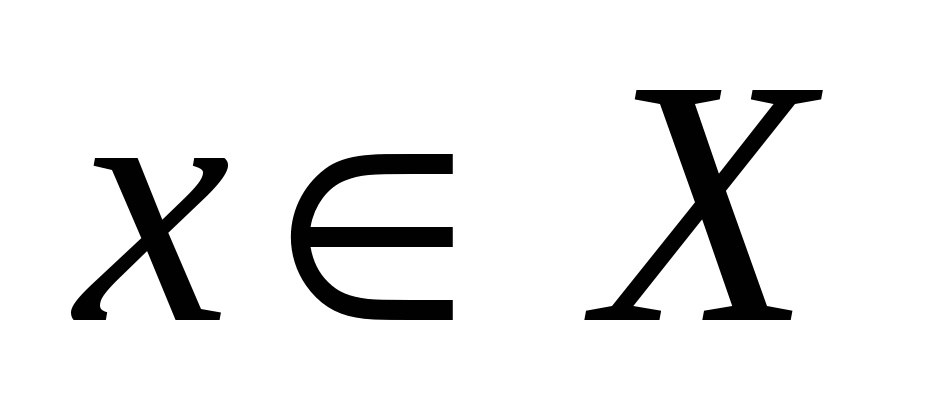 . .
Множество образов всех элементов 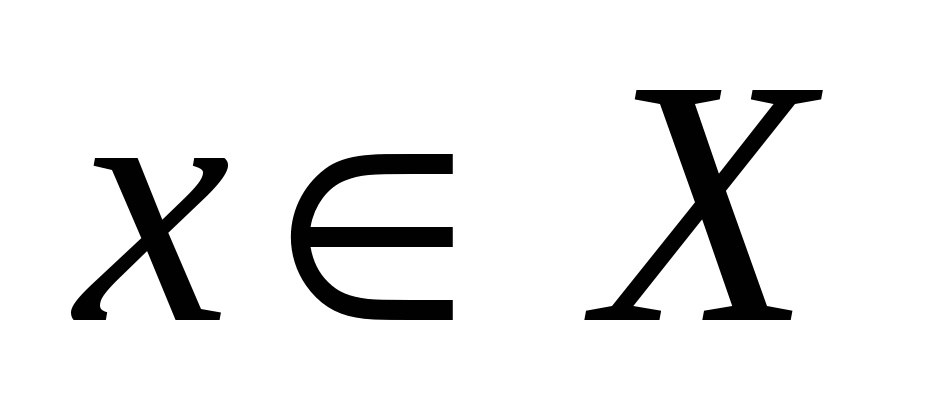 при отображении при отображении 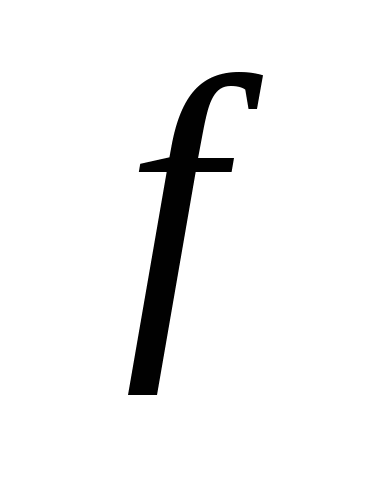 называется образом множества называется образом множества 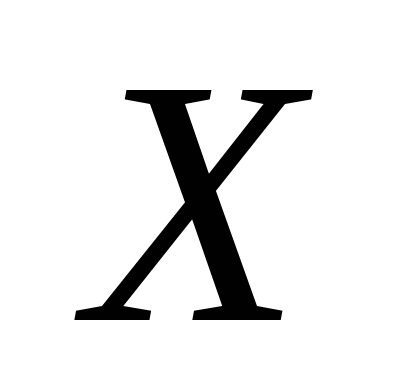 при этом отображении: при этом отображении:
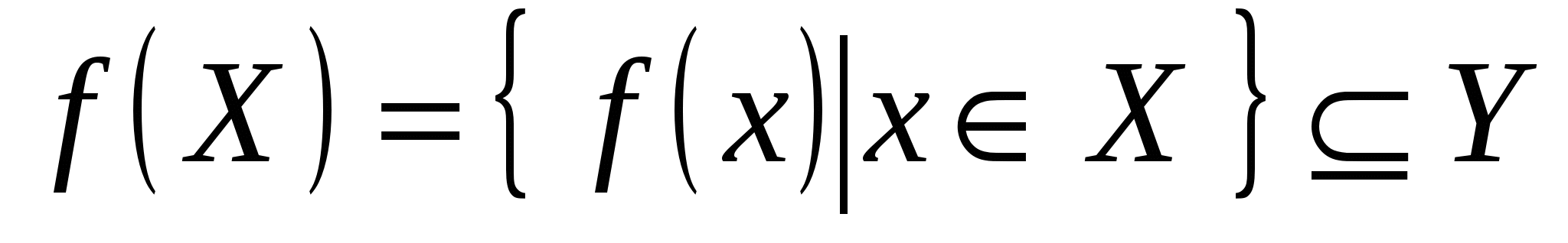 . .
Полным прообразом множества 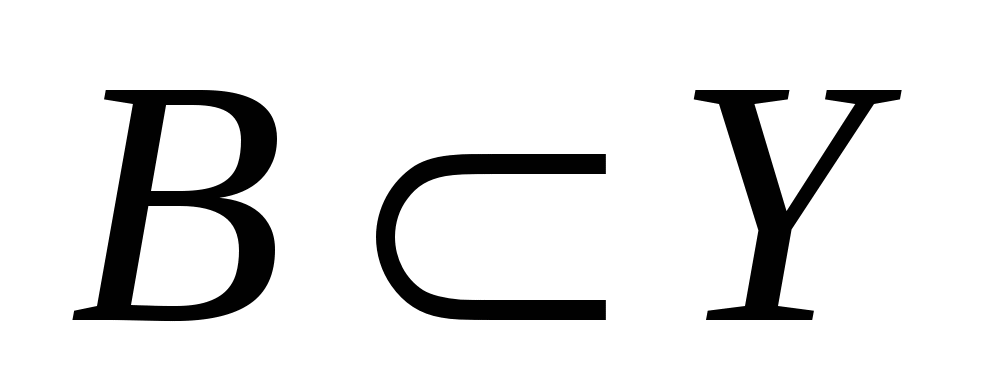 при отображении при отображении 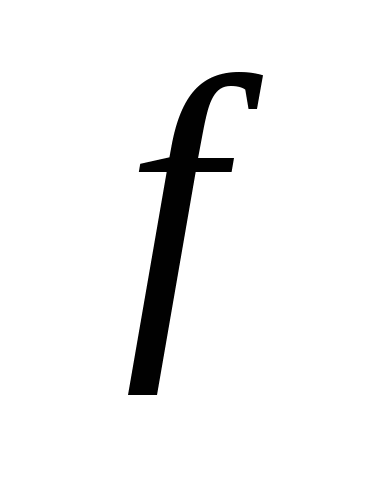 называется множество называется множество 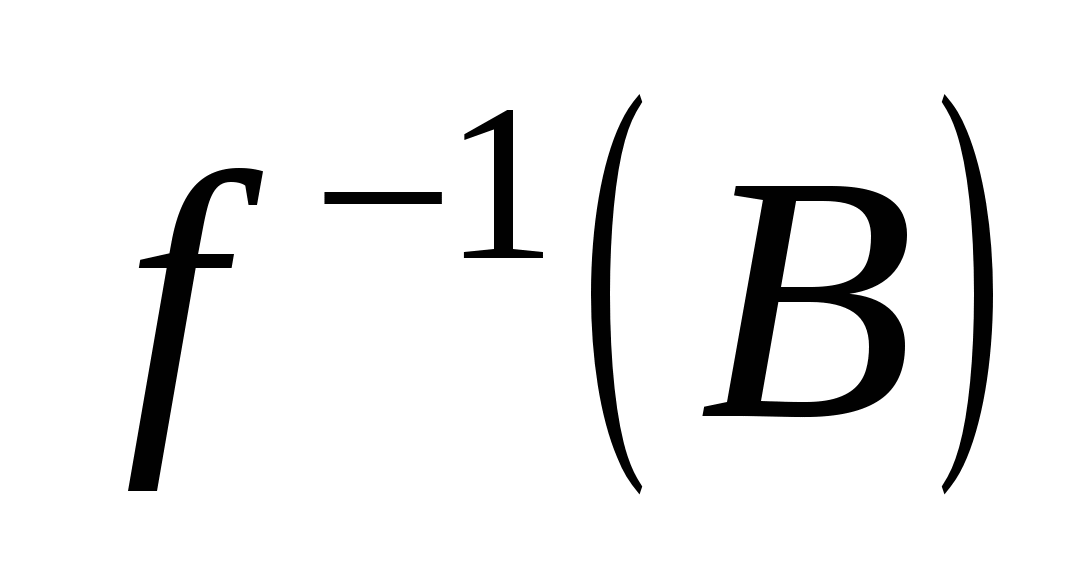 , состоящее из всех прообразов всех элементов множества , состоящее из всех прообразов всех элементов множества 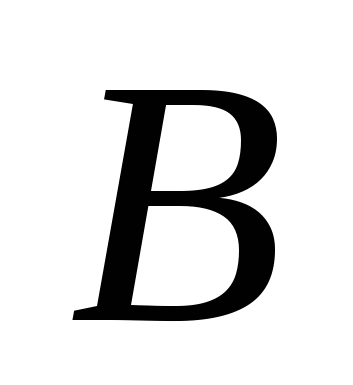 : :
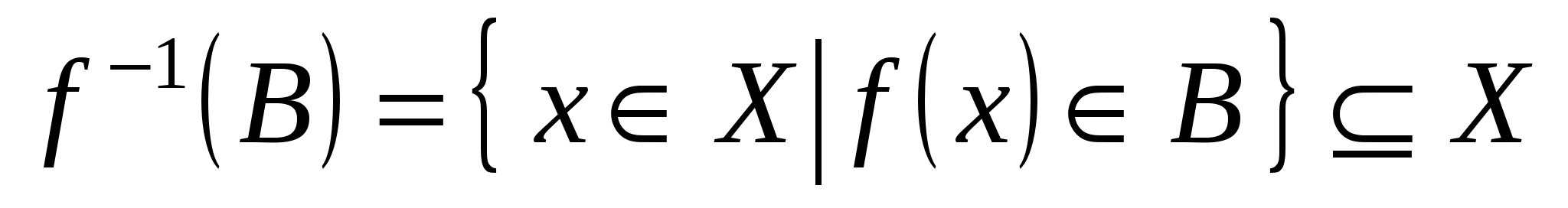 . .
Функция 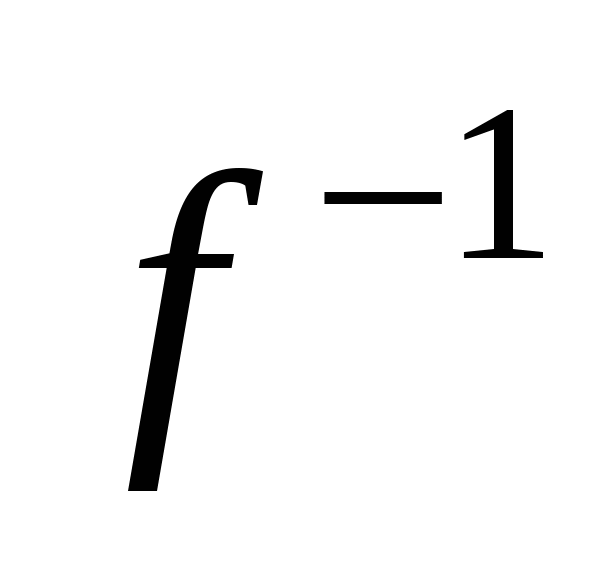 называется обратной к функции называется обратной к функции 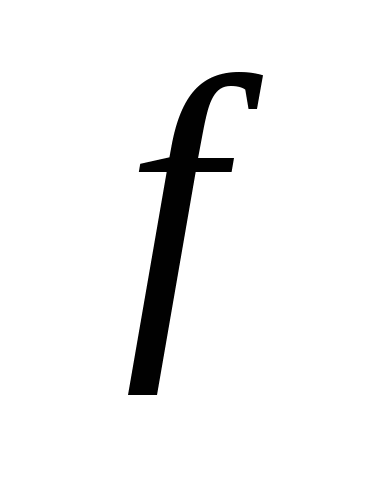 , если элементу , если элементу 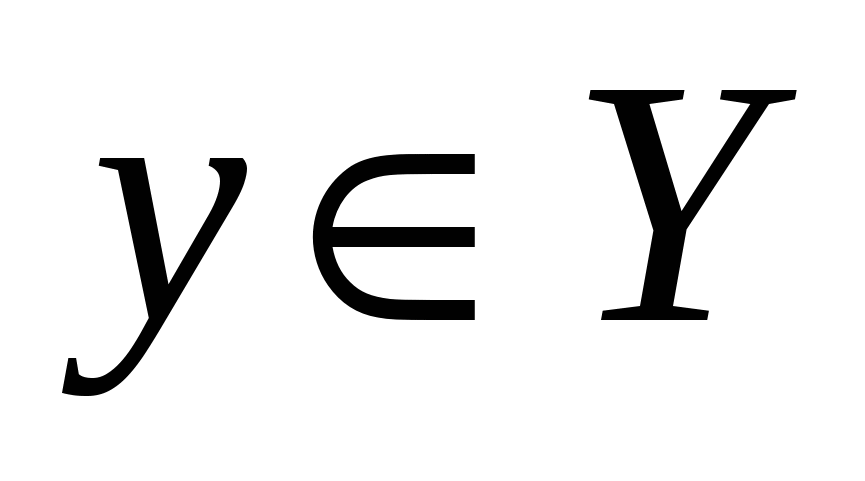 ставится в соответствие тот элемент ставится в соответствие тот элемент 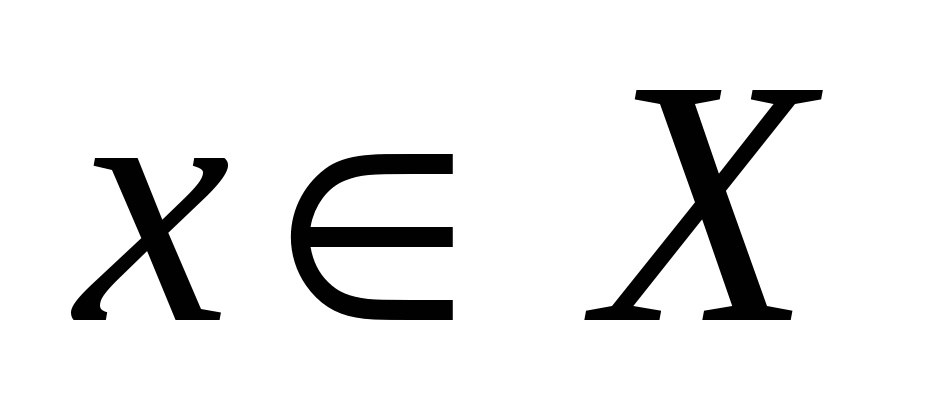 , образом которого при отображении , образом которого при отображении 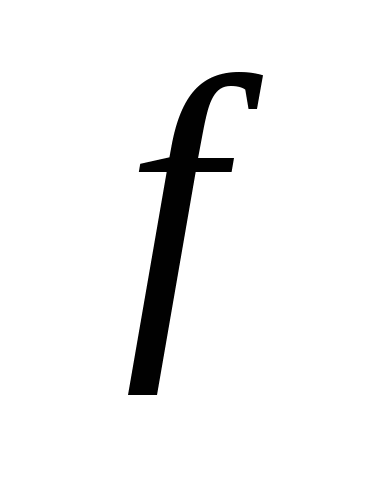 является является 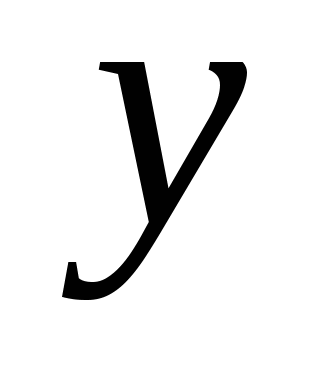 . .
Определение обратной функции с помощью логических символов записывается в виде:
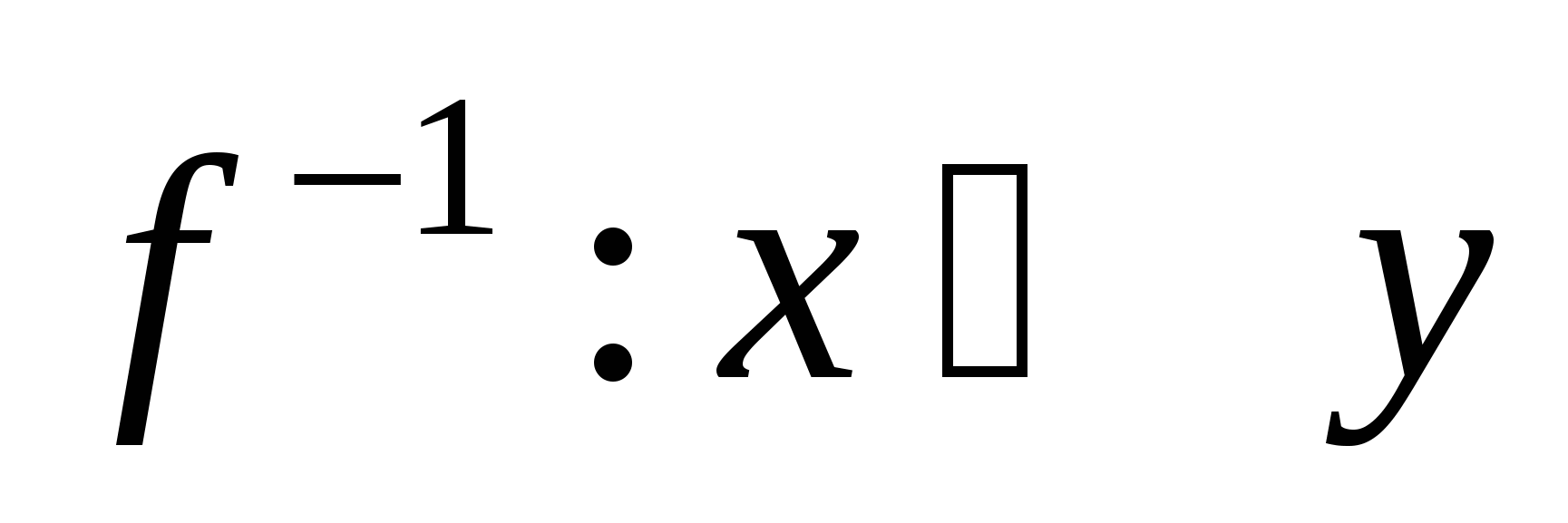  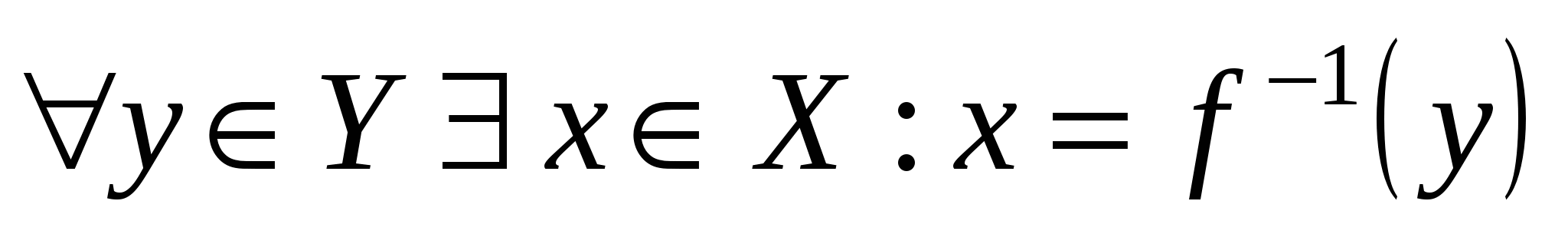 . .
Если 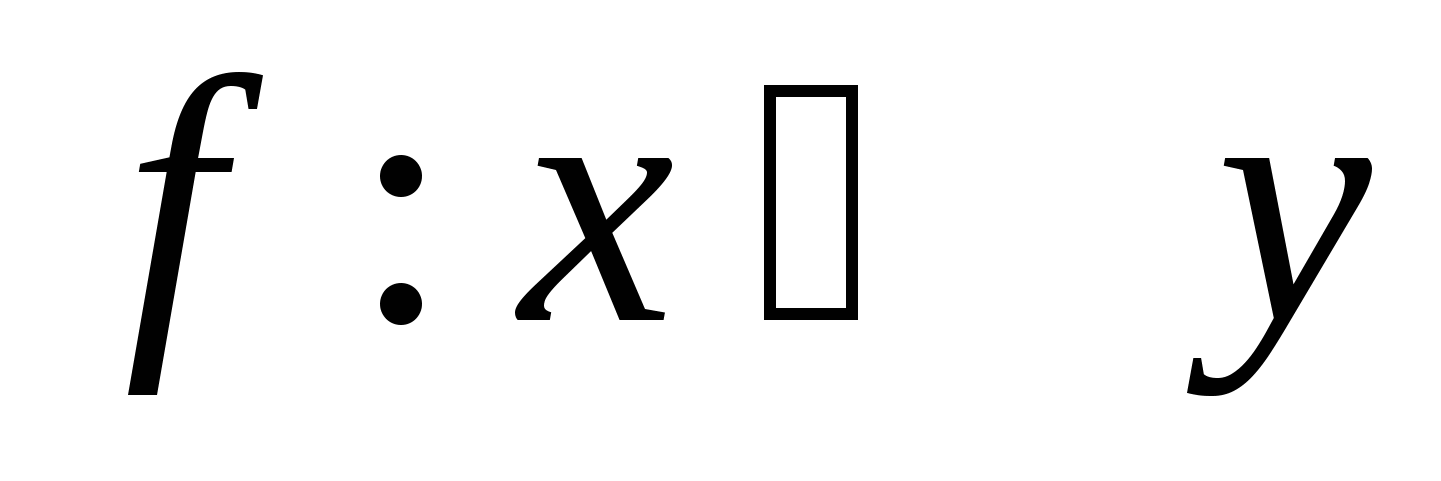 и и 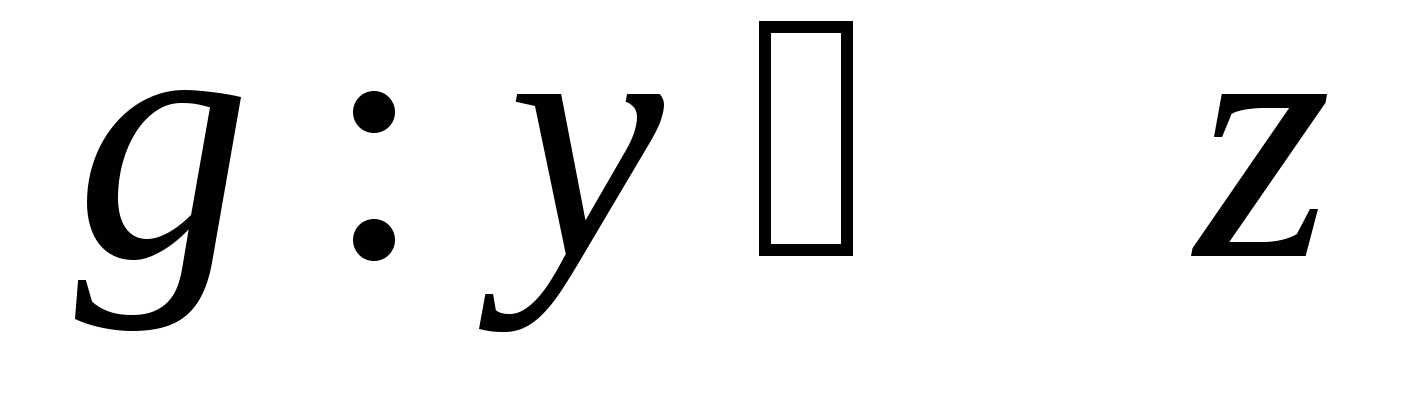 функции, то функция функции, то функция 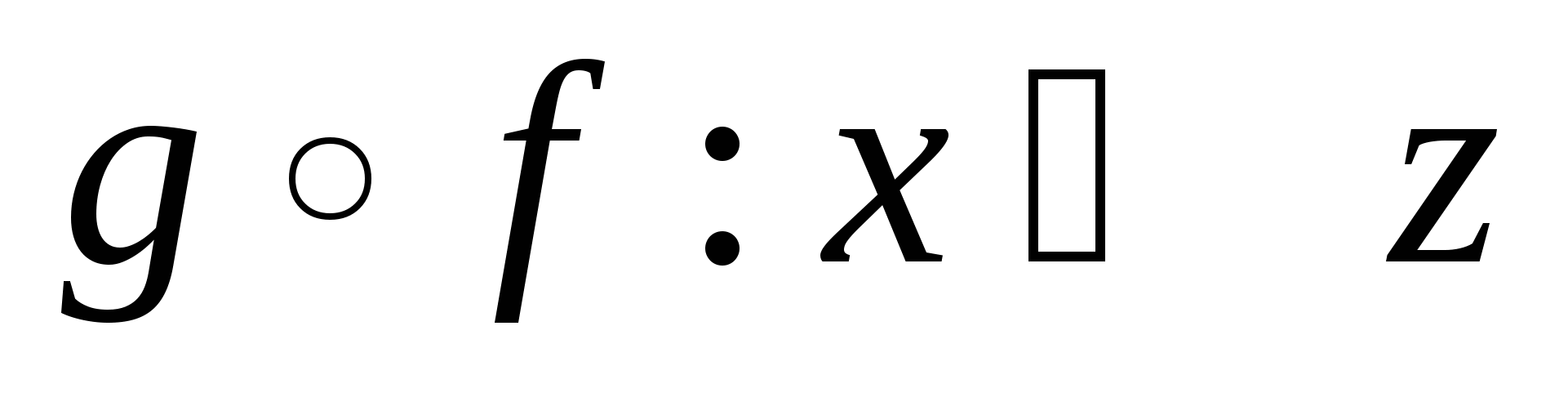 , ставящая в соответствие каждому элементу , ставящая в соответствие каждому элементу 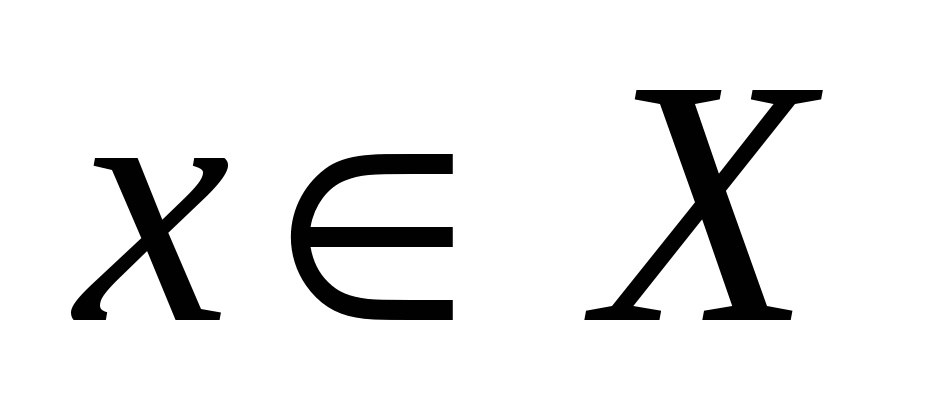 элемент элемент 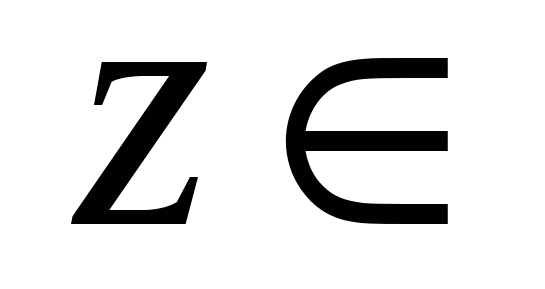  , , 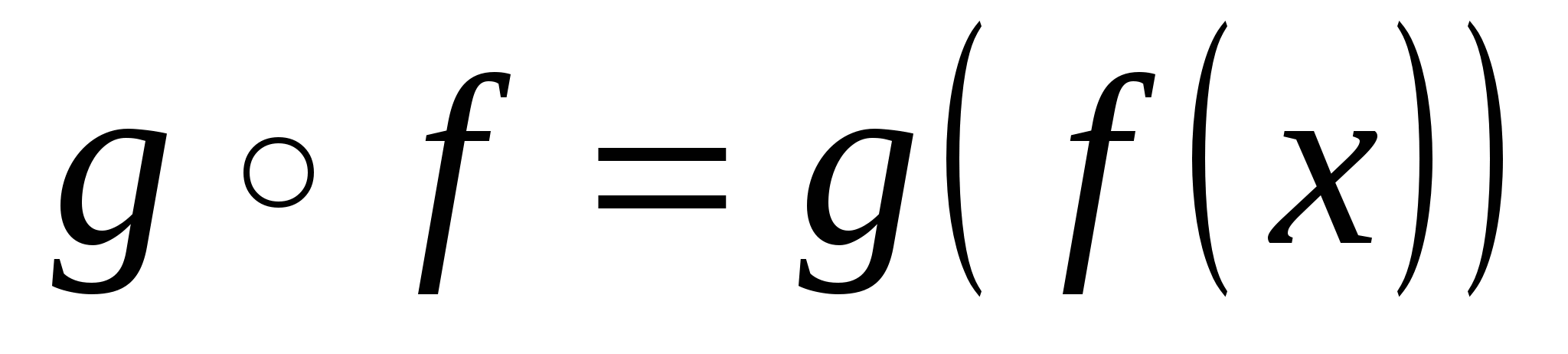 , называется сложной функцией или композицией функций , называется сложной функцией или композицией функций 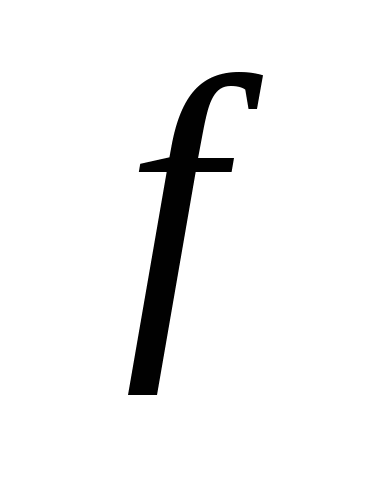 и и 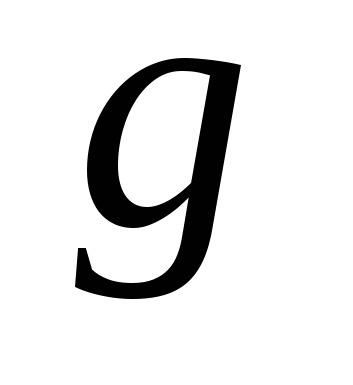 . .
Два множества  и и 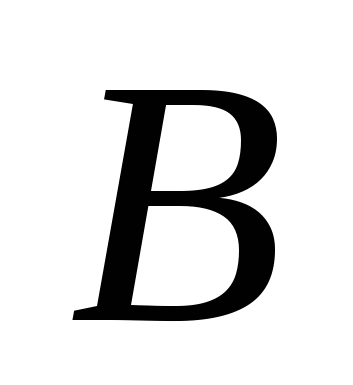 называются эквивалентными (равномощными), если существует хотя бы одно взаимно однозначное отображение одного множества на другое. Обозначается: называются эквивалентными (равномощными), если существует хотя бы одно взаимно однозначное отображение одного множества на другое. Обозначается:  ~ ~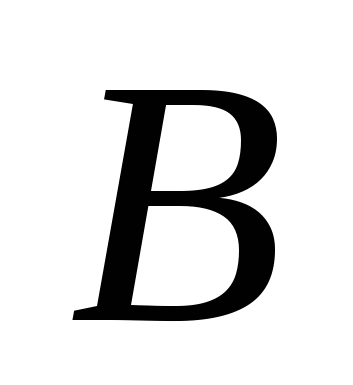 . .
Всякое множество, эквивалентное множеству натуральных чисел, называется счетным. Если множество счетное, то его элементы можно занумеровать. Множества, состоящие из конечного числа элементов, называются конечными. Множество, не являющееся конечным, называется бесконечным. Если  – конечное множество, то число его элементов обозначается – конечное множество, то число его элементов обозначается  или или 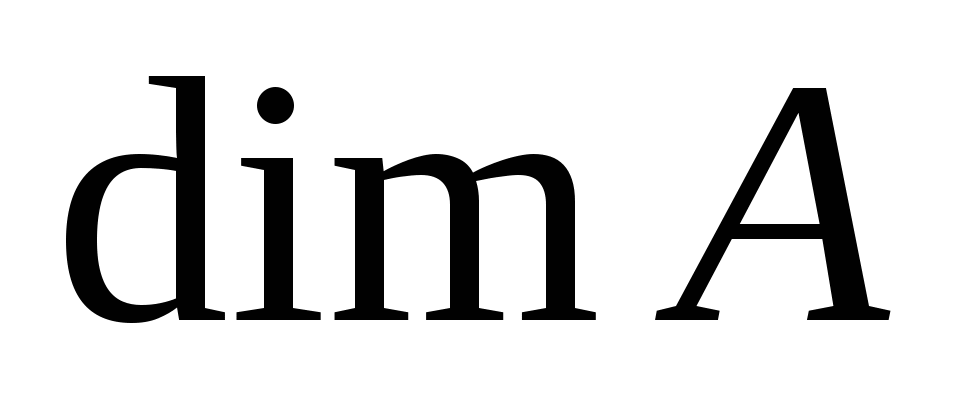 и называется мощностью множества и называется мощностью множества  . .
Тема 2 Грани числовых множеств
2.1 Точные грани числовых множеств
2.2. Система вложенных отрезков
2.3 Метод математической индукции
2.4 Бином Ньютона
Рассмотрим произвольное числовое множество 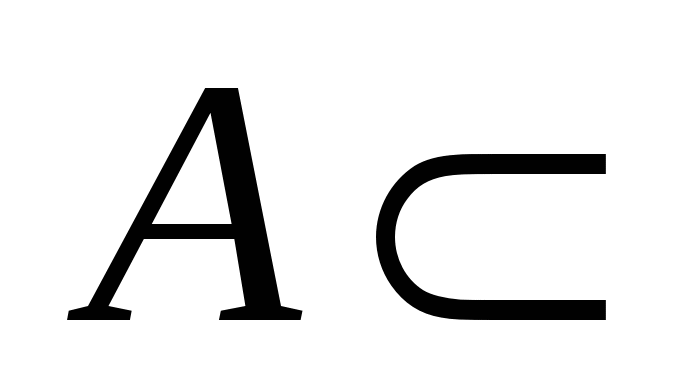  . .
Множество действительных чисел  называется ограниченным сверху, если существует такое действительное число называется ограниченным сверху, если существует такое действительное число 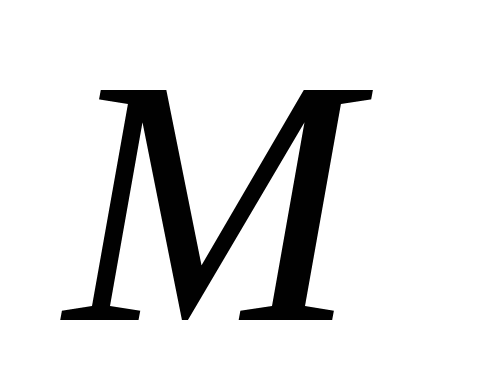 , что каждое число , что каждое число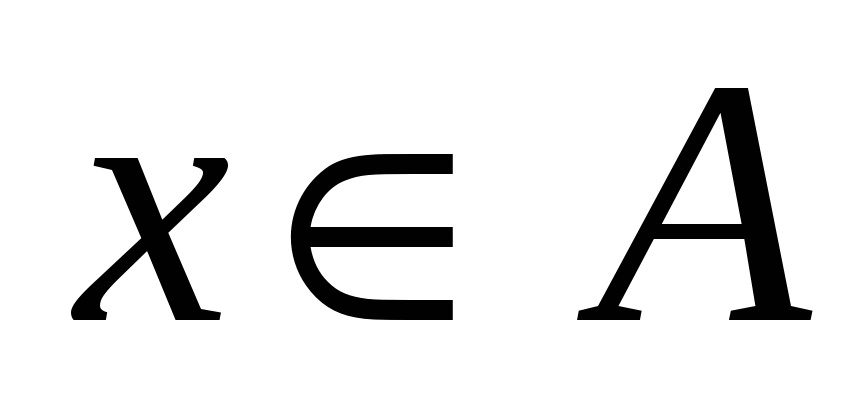 удовлетворяет неравенству удовлетворяет неравенству 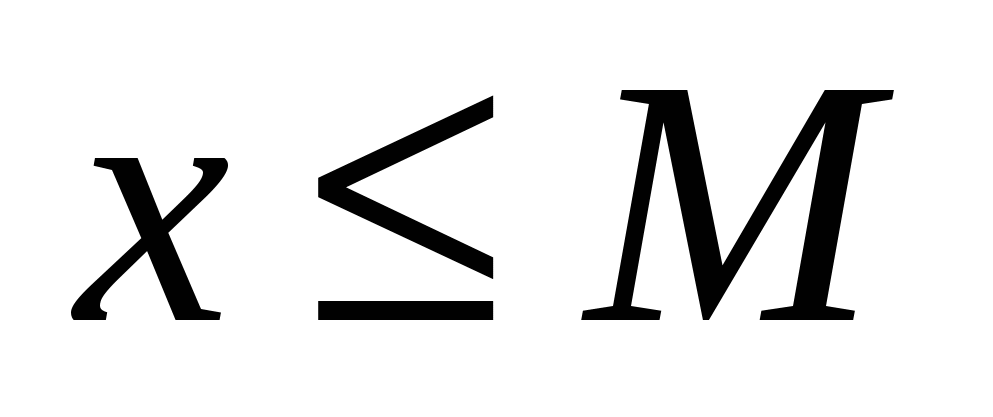 , т. е. , т. е.
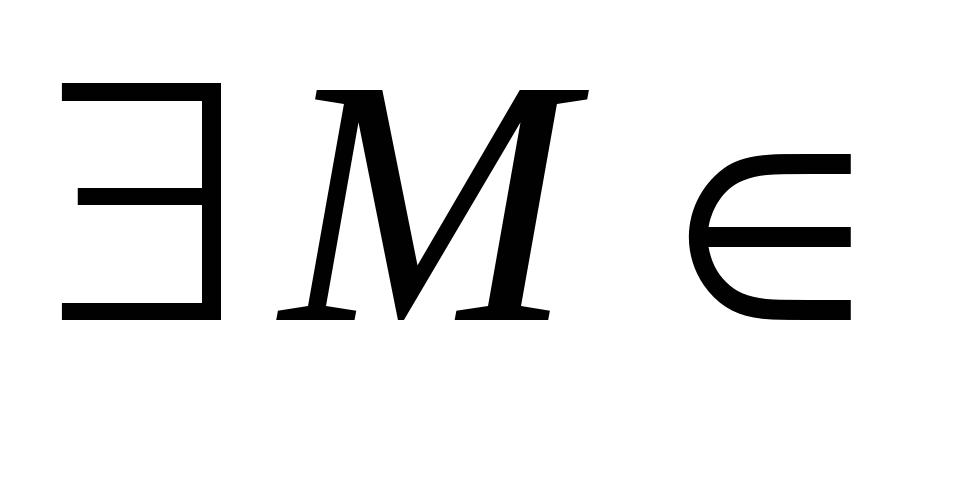  : : 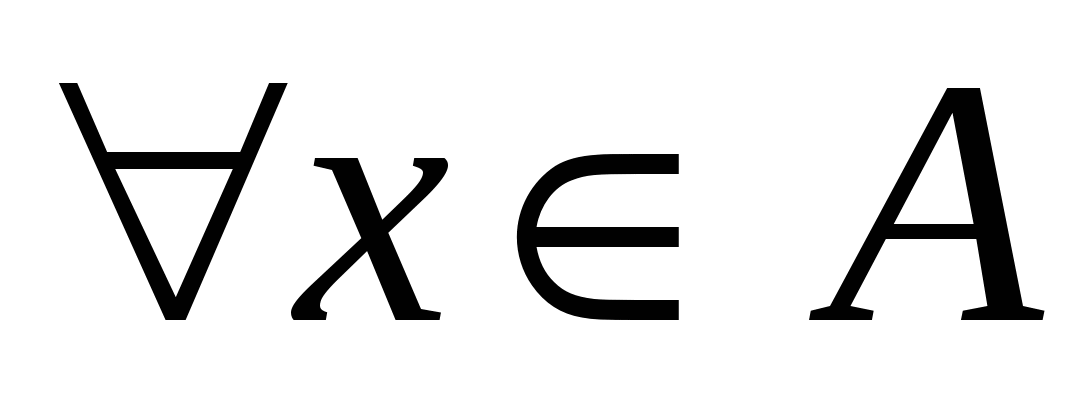 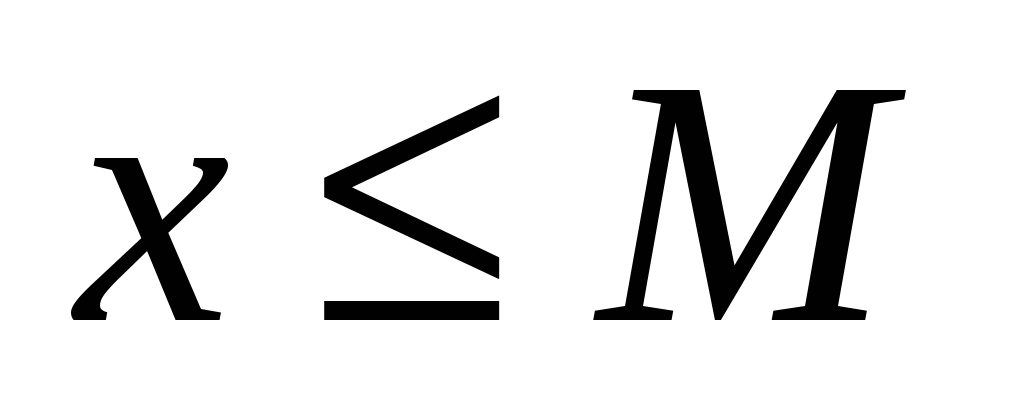 . .
При этом число 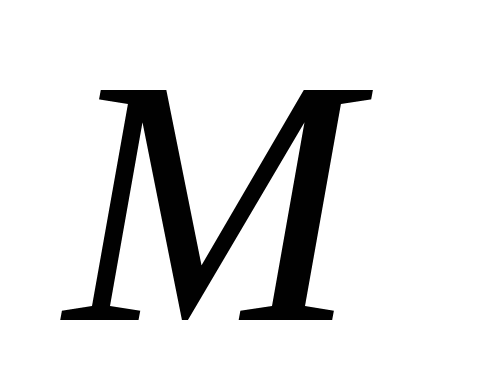 называется верхней гранью множества называется верхней гранью множества  . .
Множество  неограничено сверху, если неограничено сверху, если
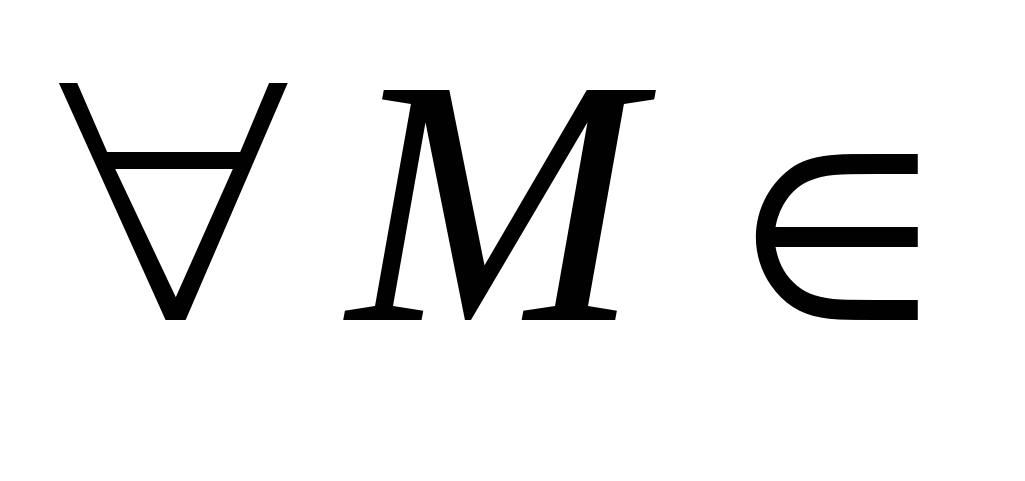  : : 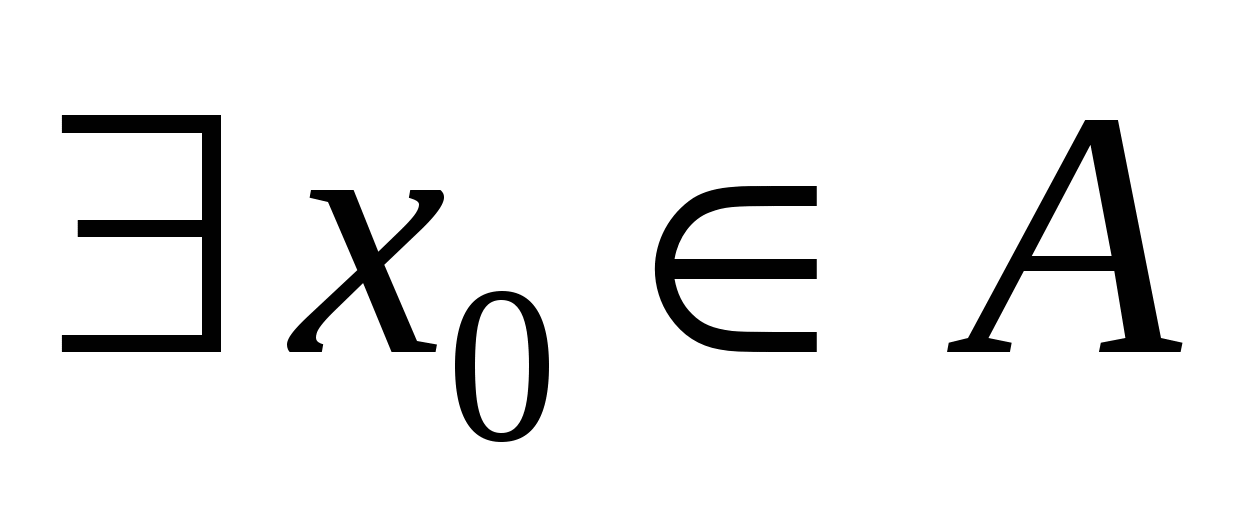 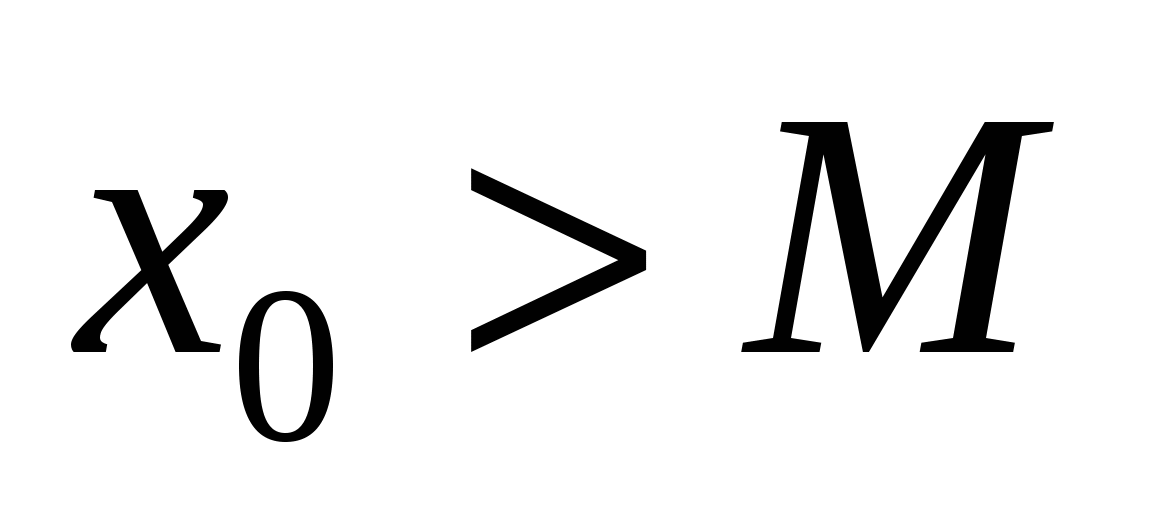 . .
Элемент 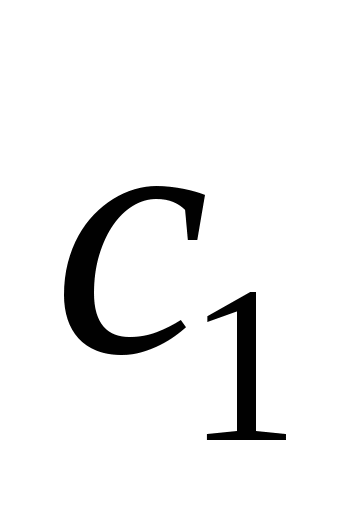 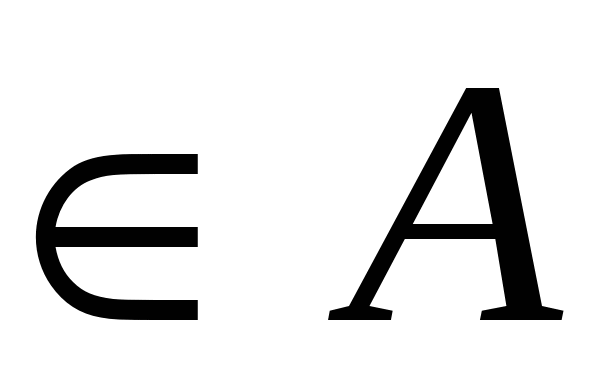 называется наибольшим элементом множества называется наибольшим элементом множества  , если , если 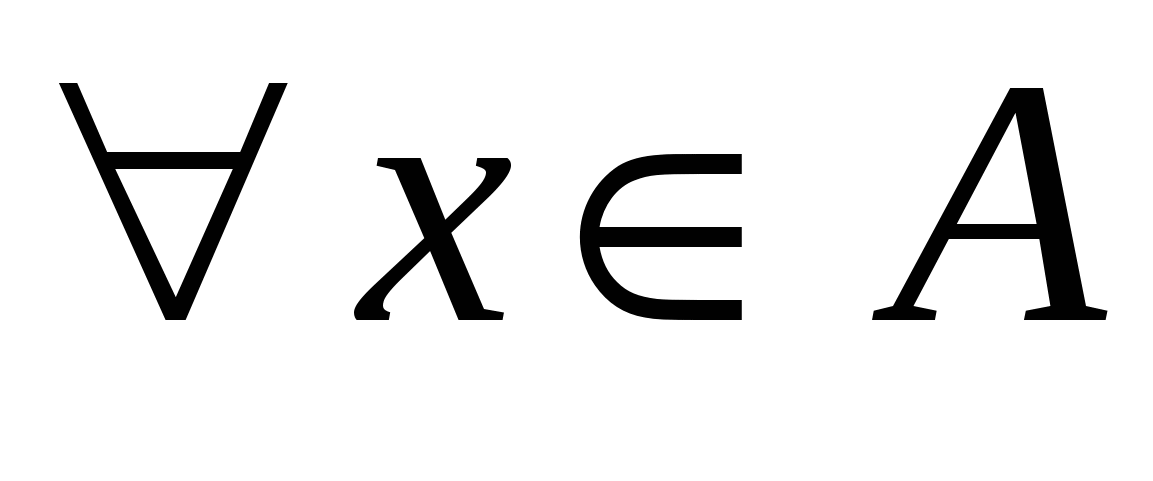 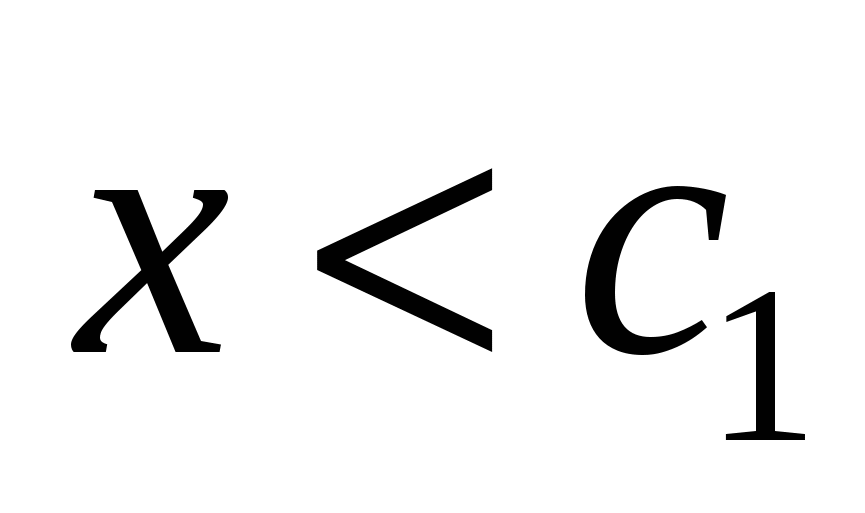 . .
Наименьшая из всех верхних граней ограниченного сверху множества 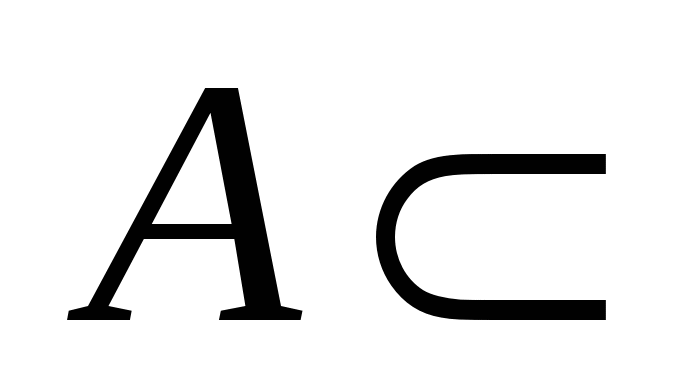  называется точной верхней гранью и обозначается называется точной верхней гранью и обозначается 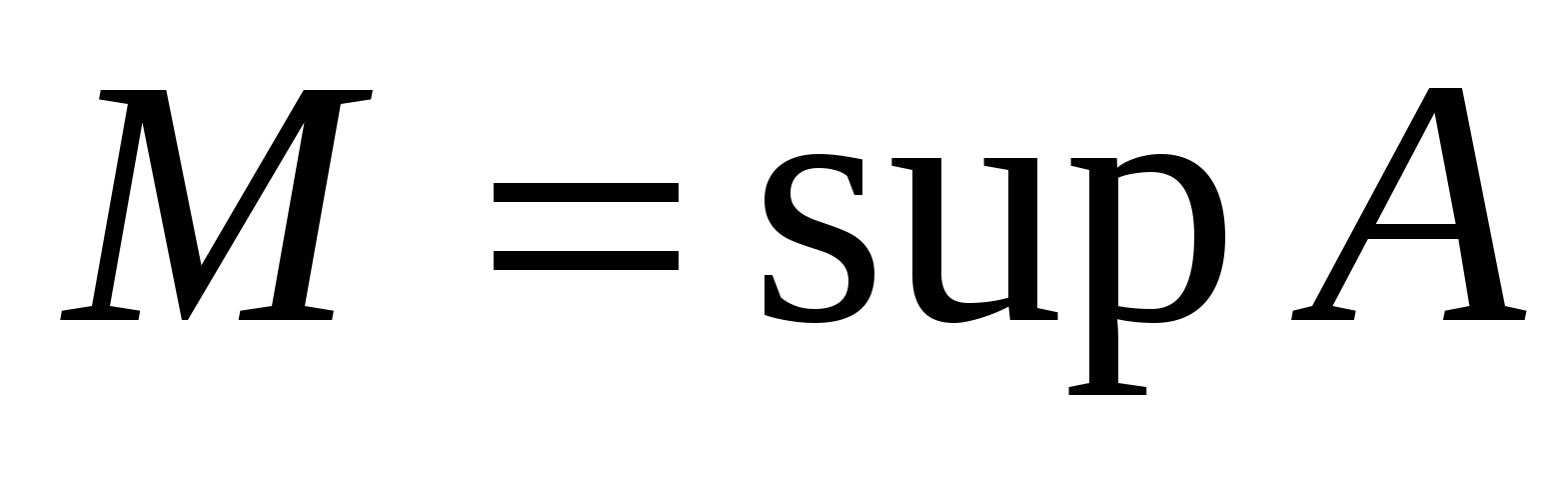 : :
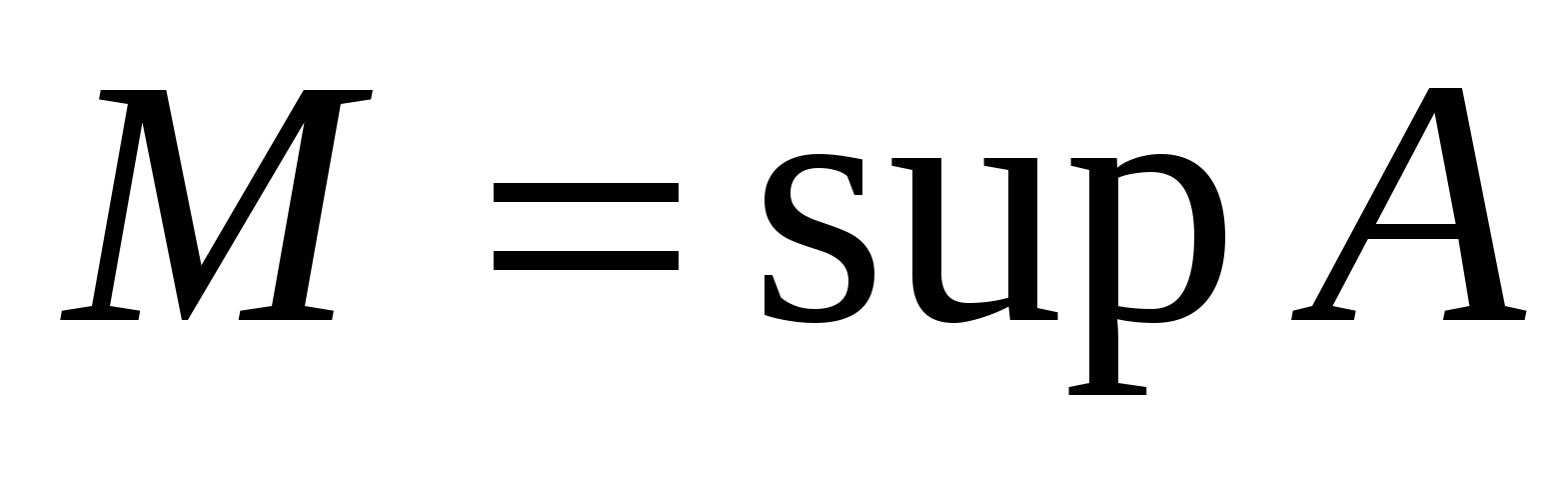  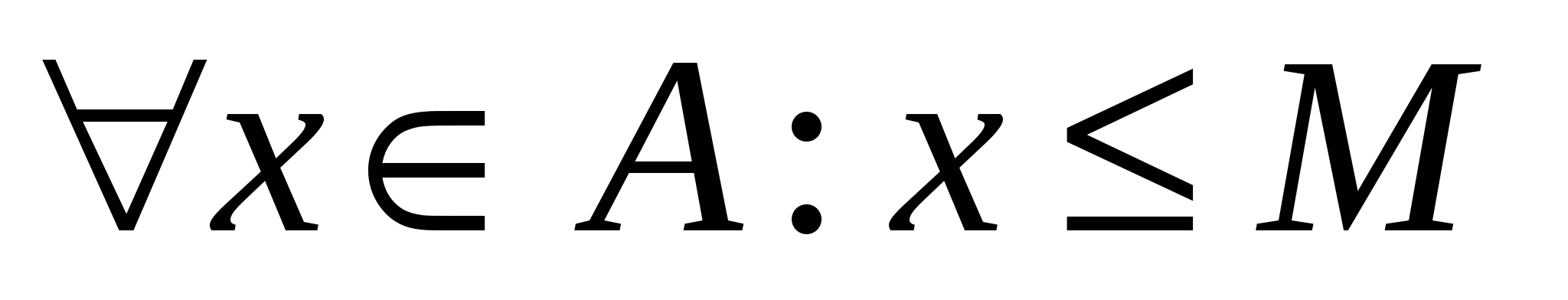 и и 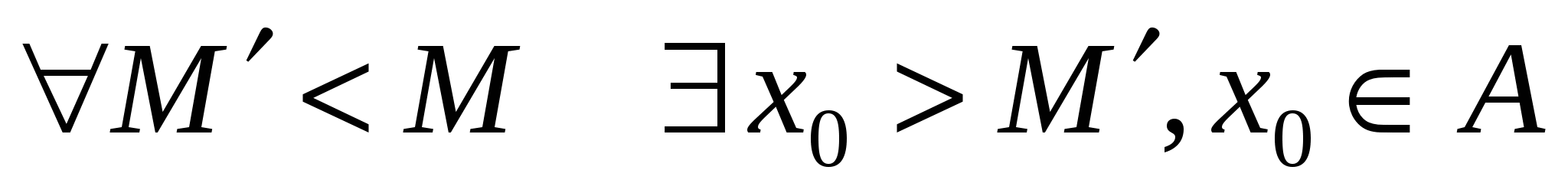 . .
Множество действительных чисел  называется ограниченным снизу, если существует такое действительное число называется ограниченным снизу, если существует такое действительное число 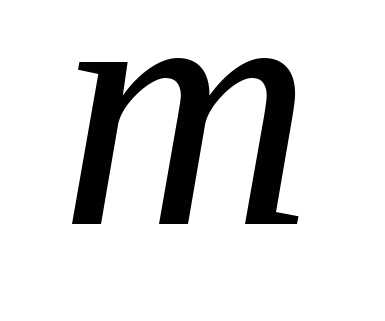 , что каждое число , что каждое число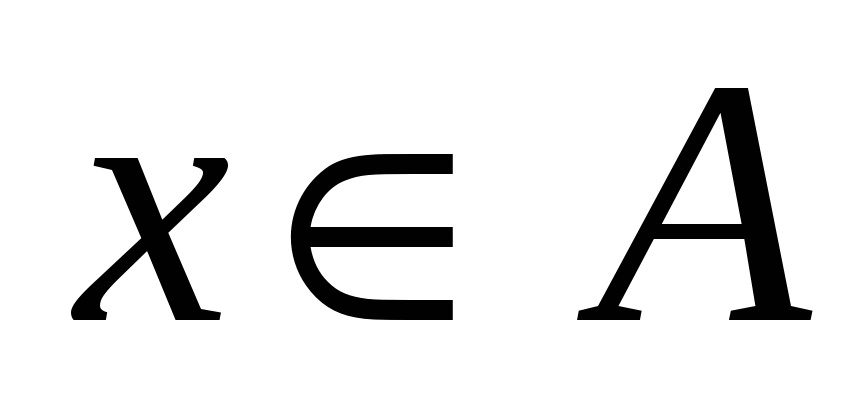 удовлетворяет неравенству удовлетворяет неравенству 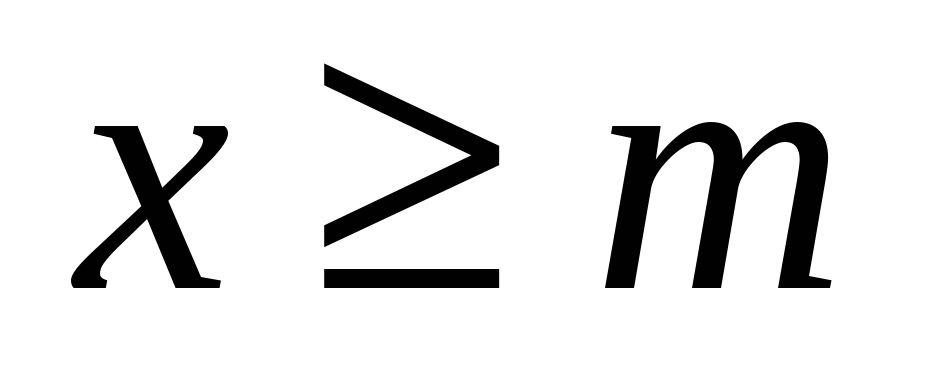 , т. е. , т. е.
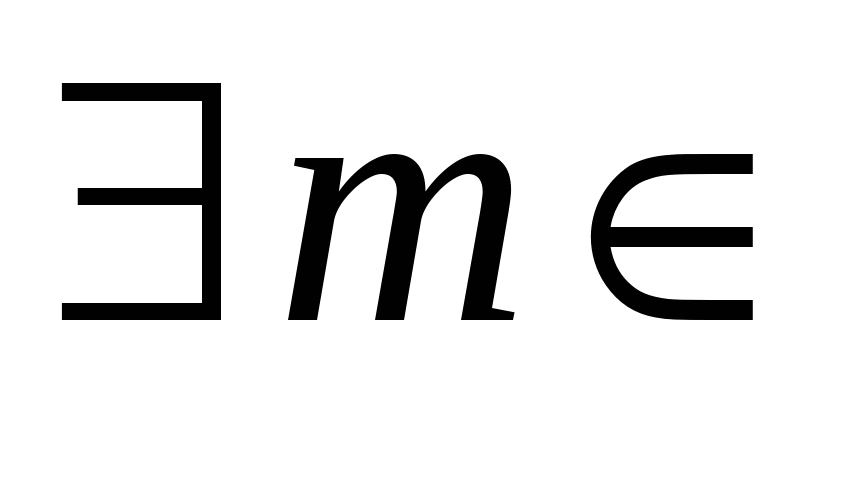  : : 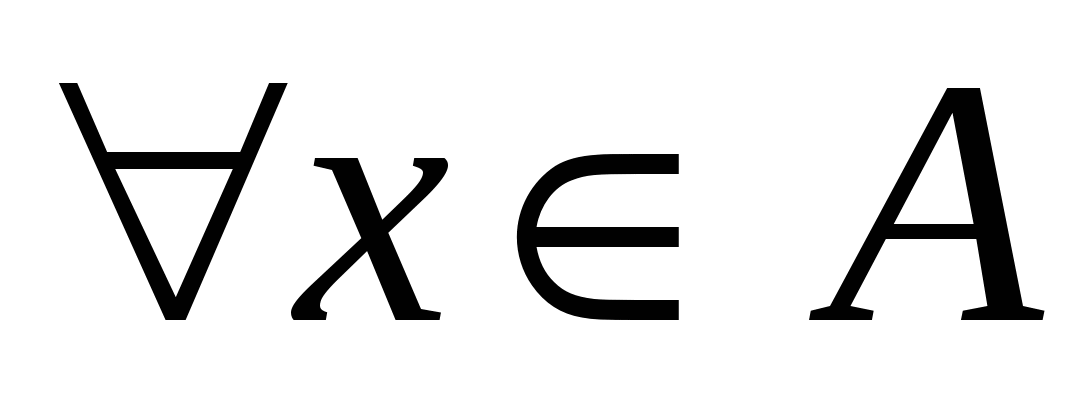 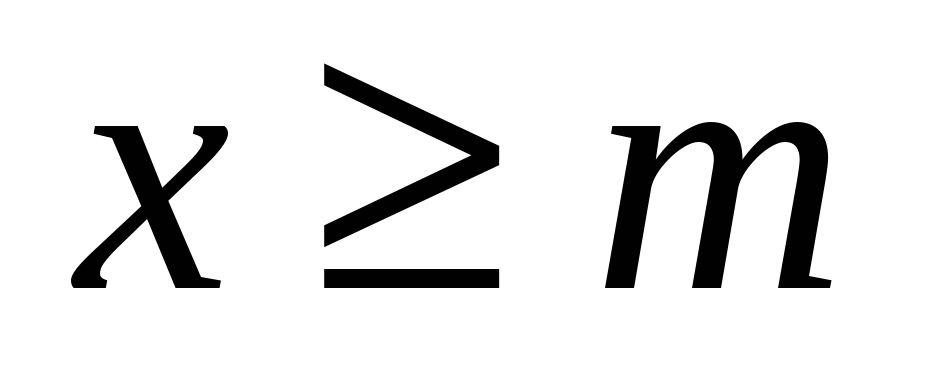 . .
При этом число 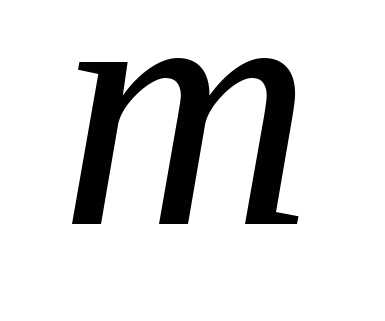 называется нижней гранью множества называется нижней гранью множества  . .
Множество  неограничено снизу, если неограничено снизу, если
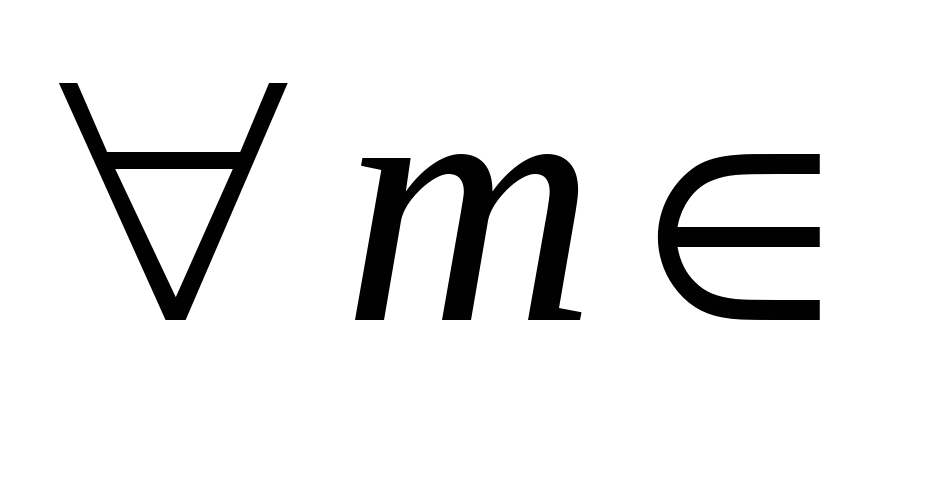  : : 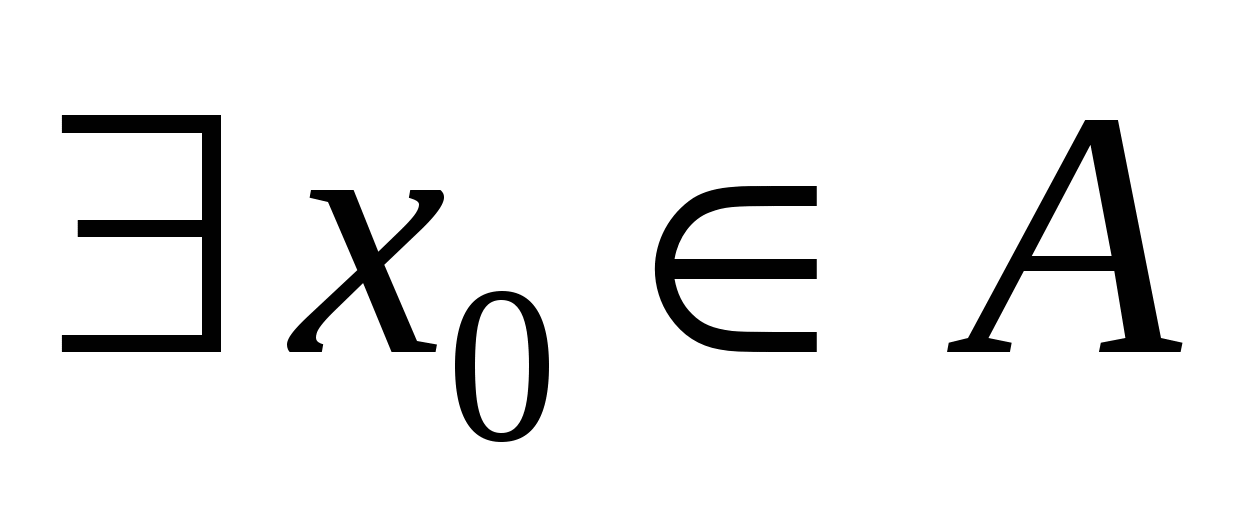 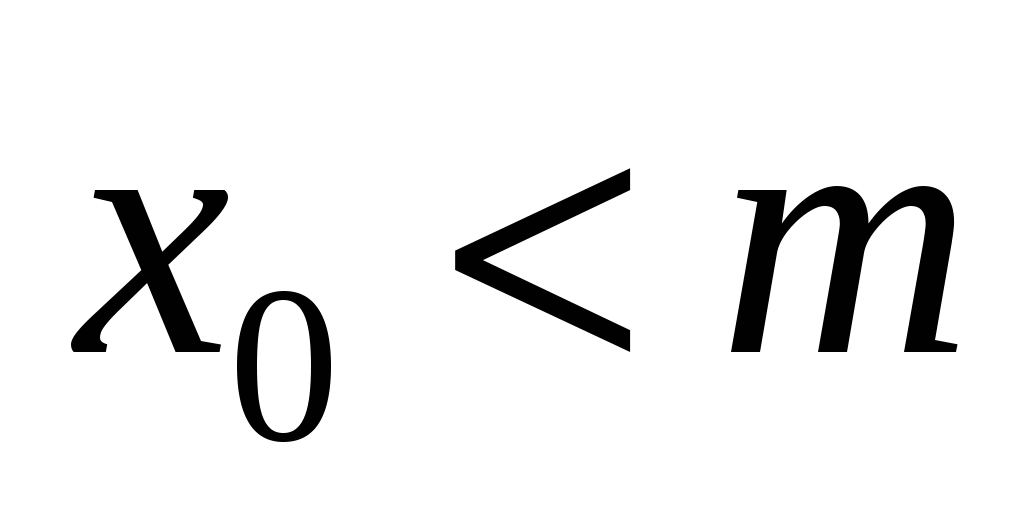 . .
Элемент 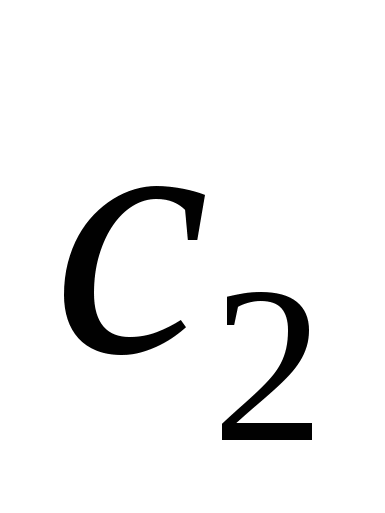 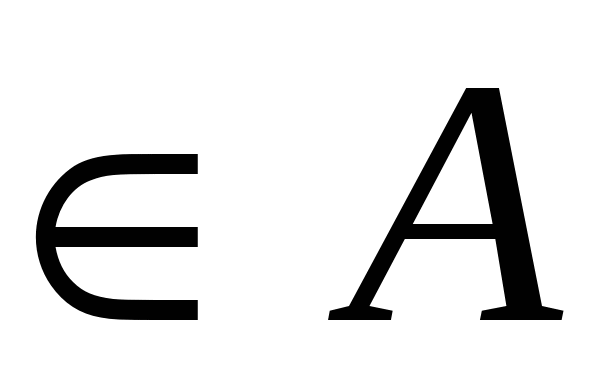 называется наименьшим элементом множества называется наименьшим элементом множества  , если , если 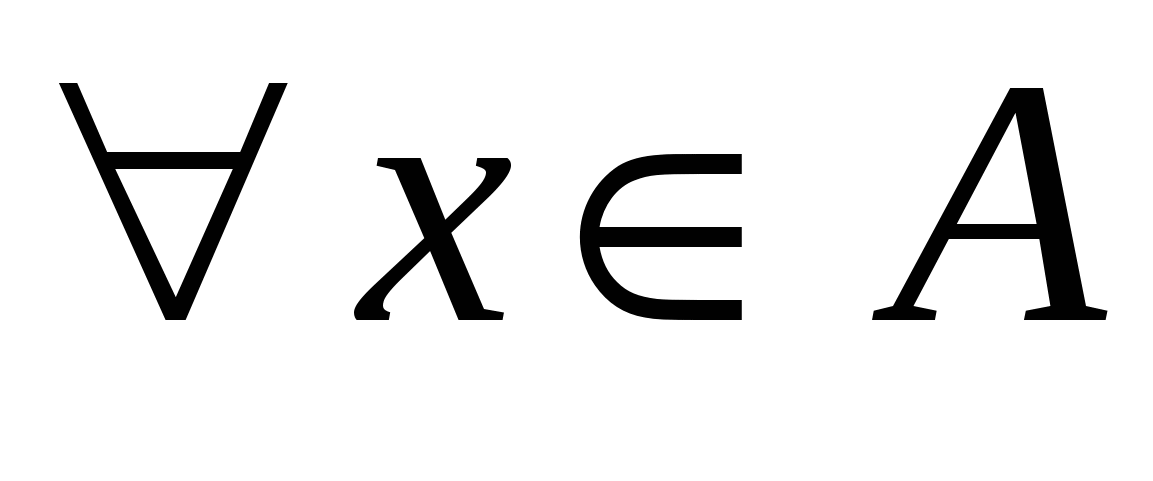 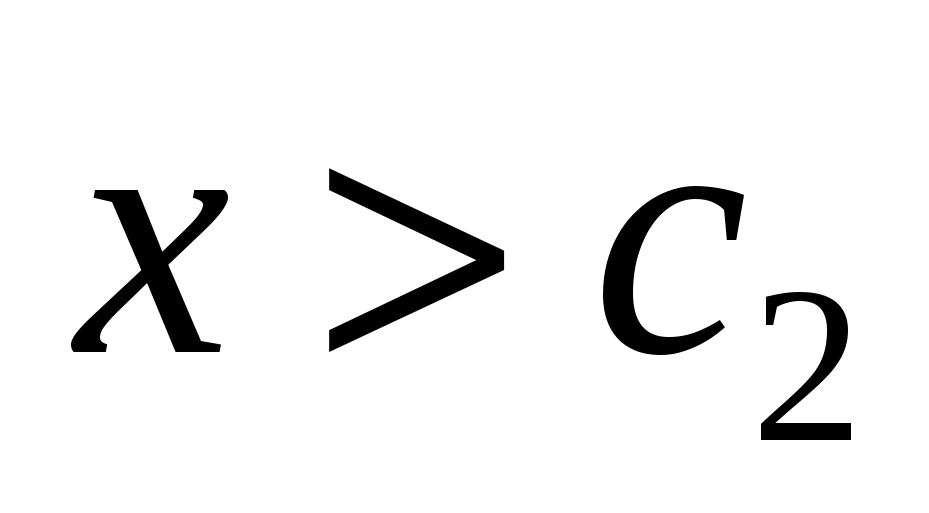 . .
Наибольшая из всех нижних граней ограниченного снизу множества 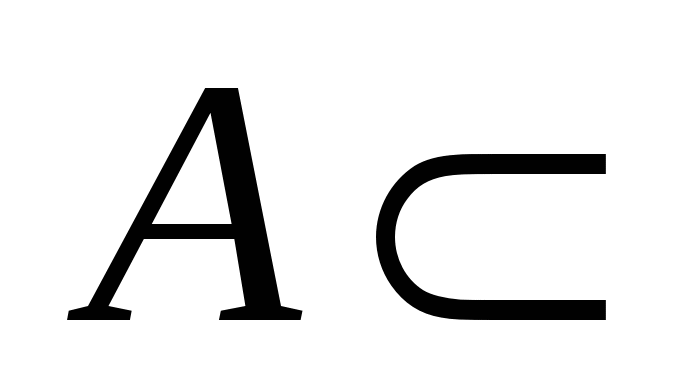  называется точной нижней гранью. называется точной нижней гранью.
Обозначается:
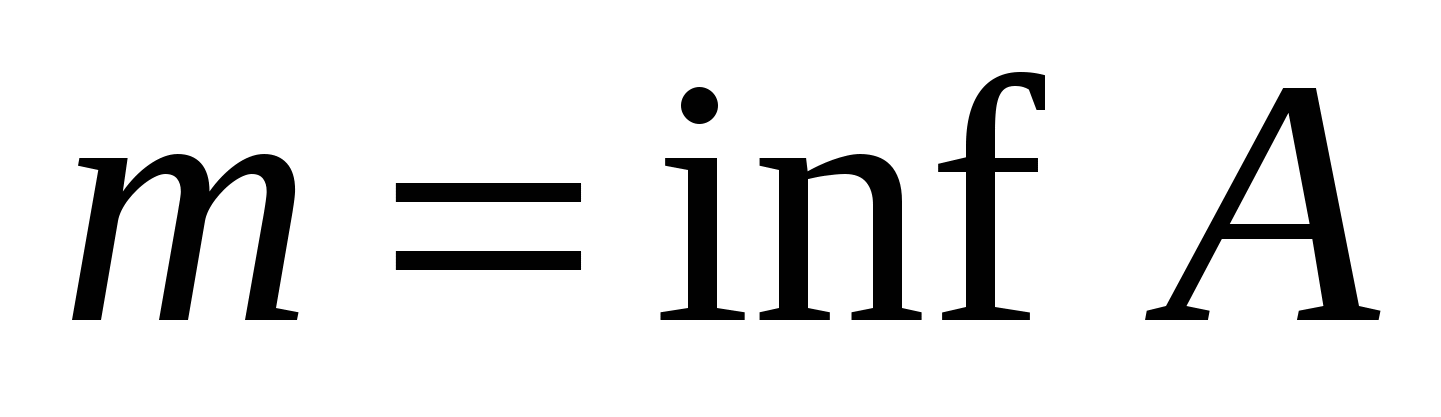  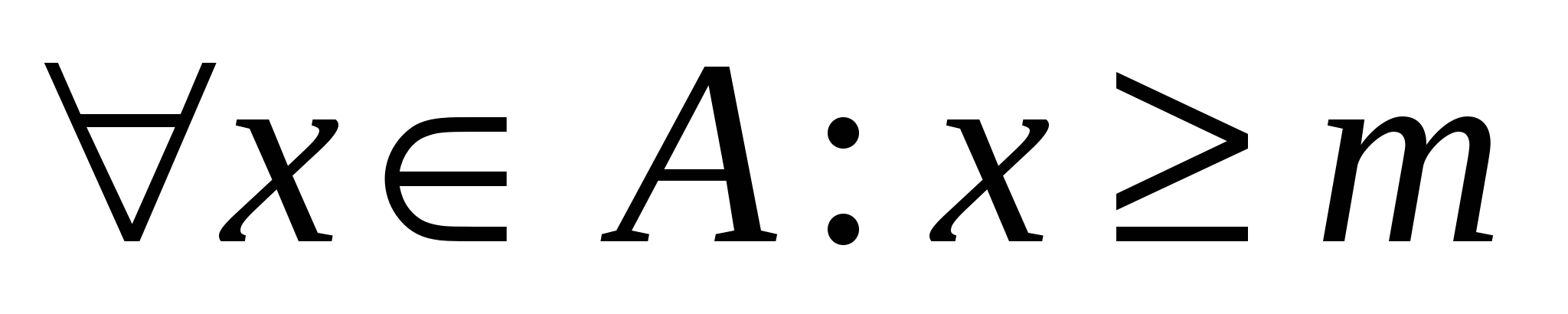 и и 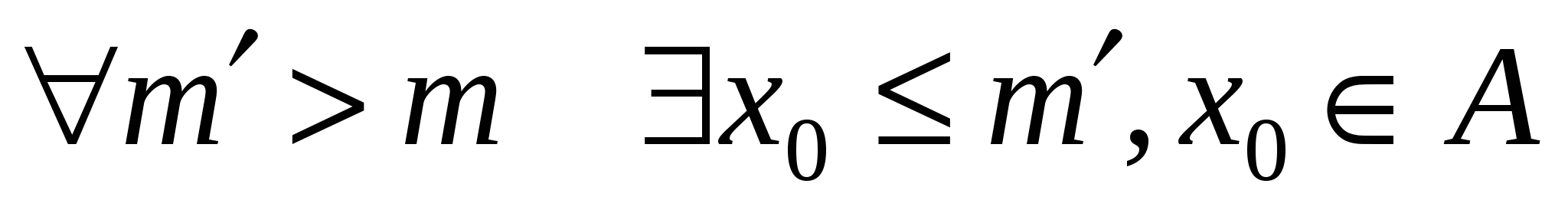 . .
Множество, ограниченное сверху и снизу, называется ограниченным: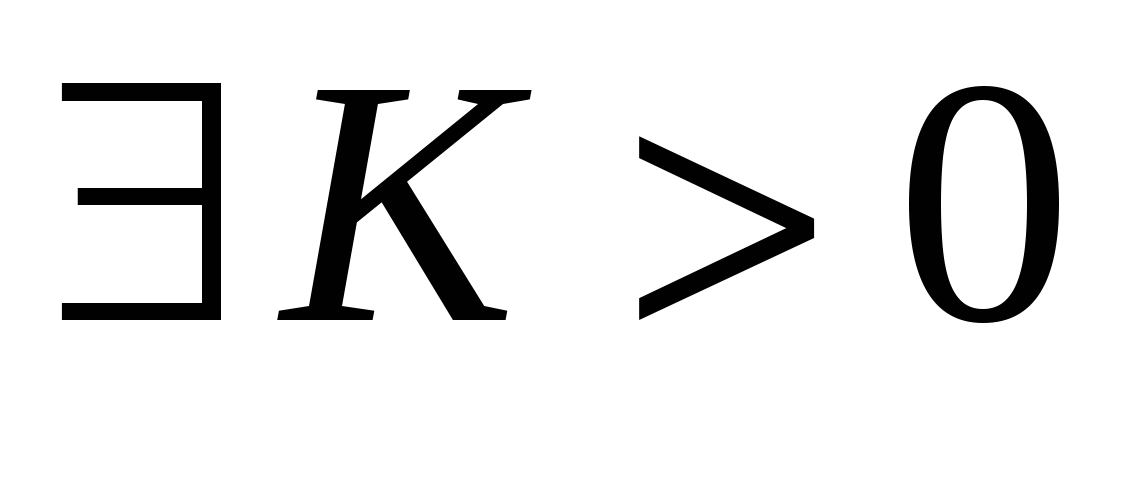 : : 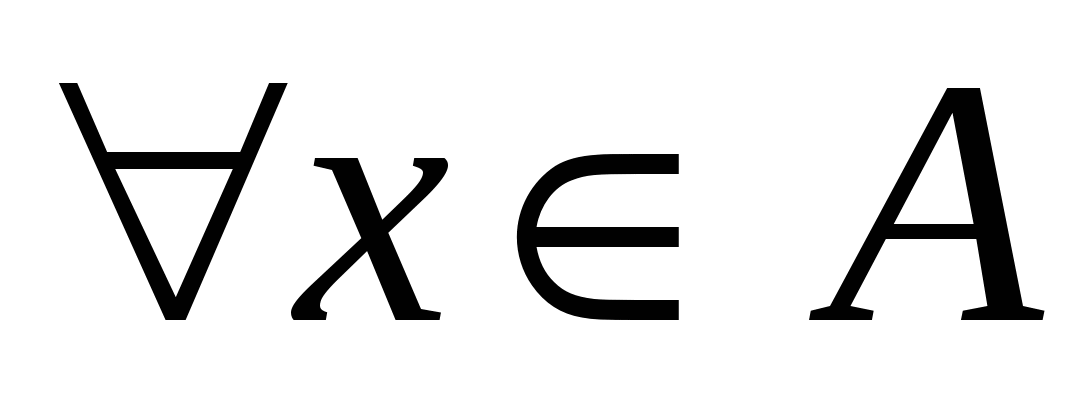 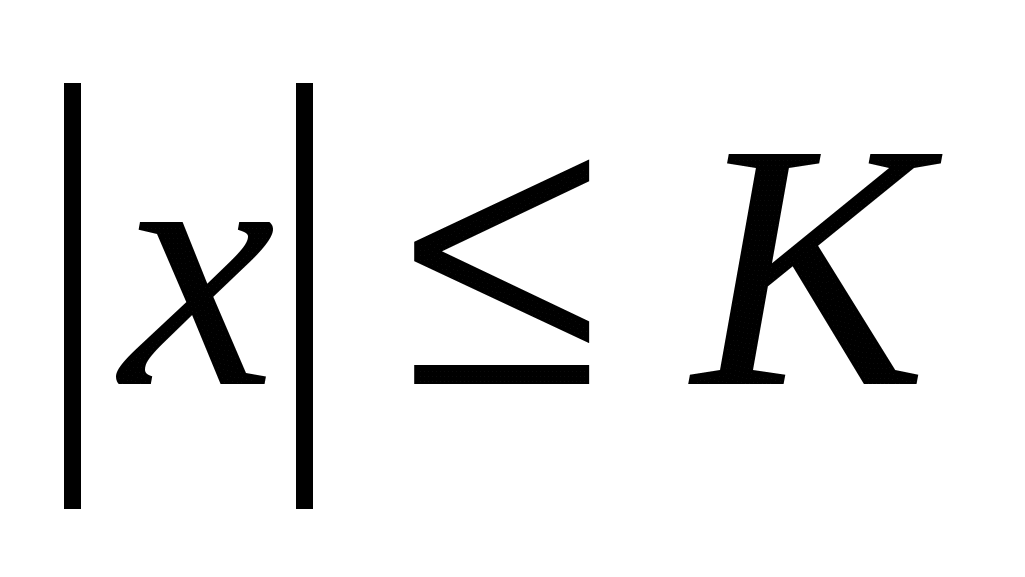 . .
Теорема (о существовании верхней грани) Ограниченное сверху (снизу) непустое множество имеет точную верхнюю (нижнюю) грань.
Система числовых отрезков
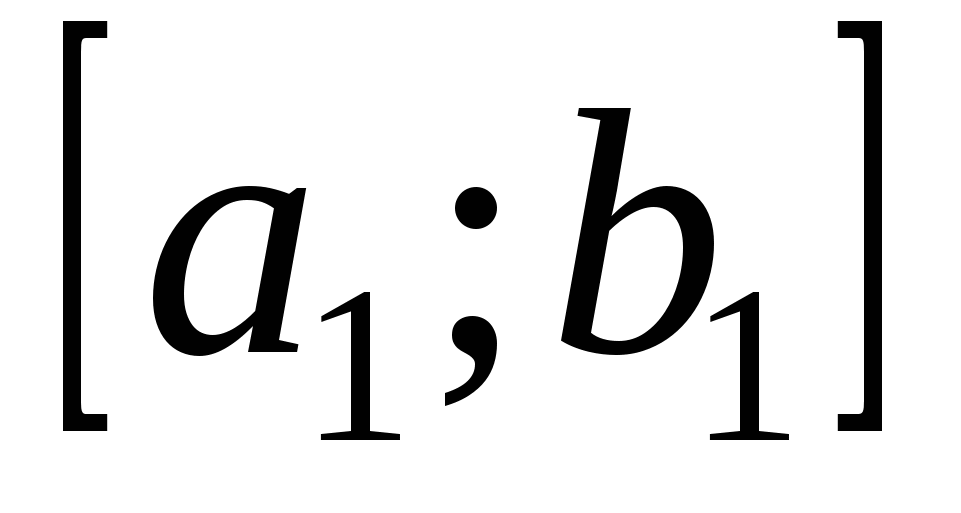 , , 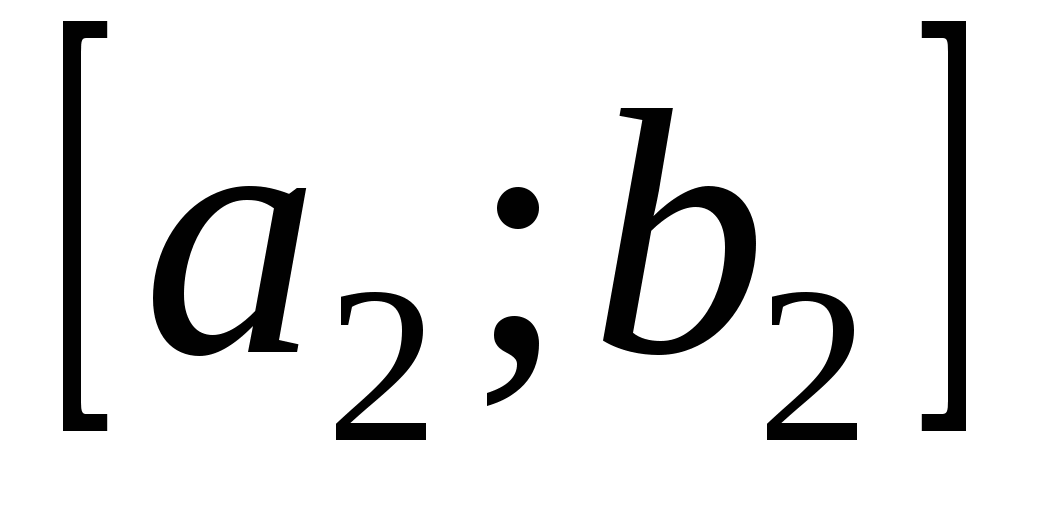 , ,  , , 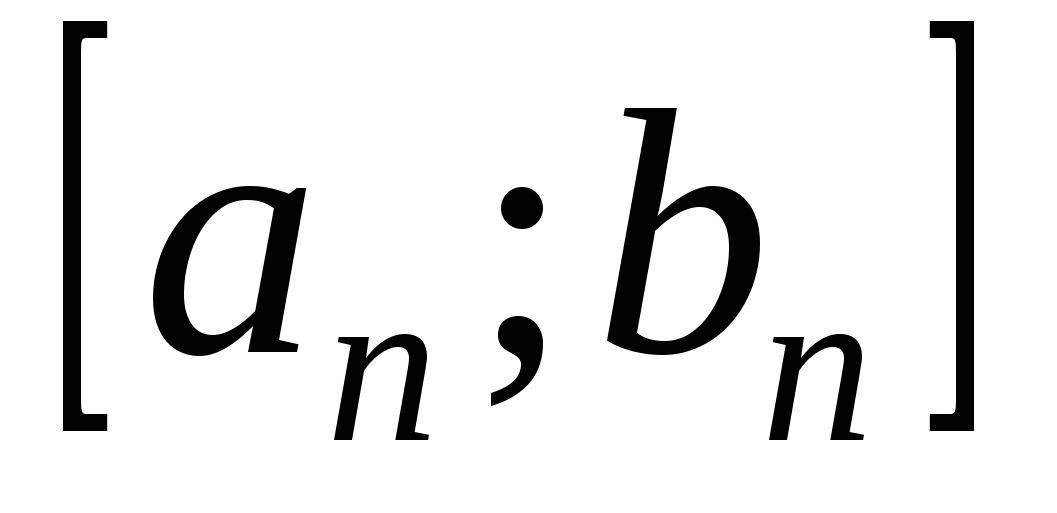 , , , , 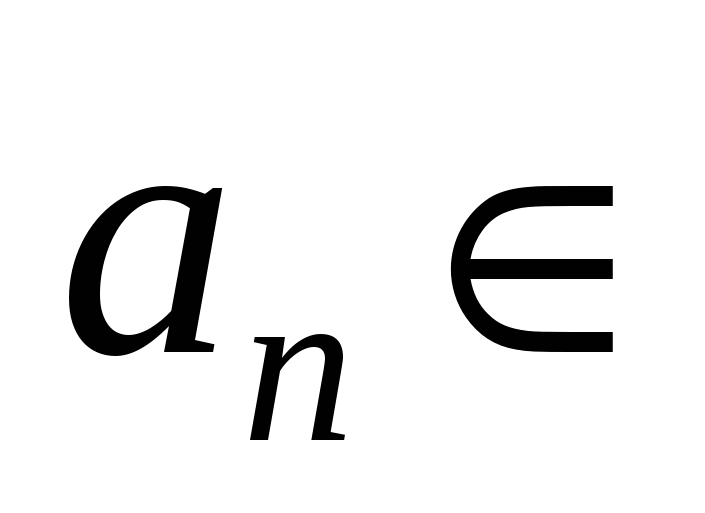  , , 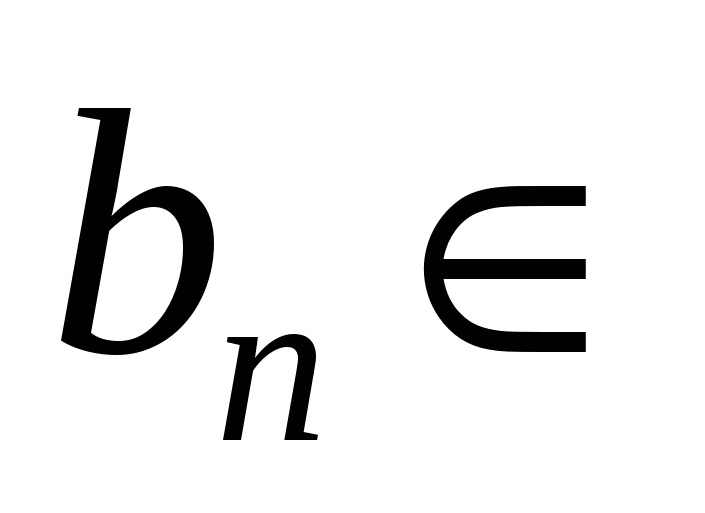  , ,
называется системой вложенных отрезков, если
1) каждый следующий отрезок содержится в предыдущем
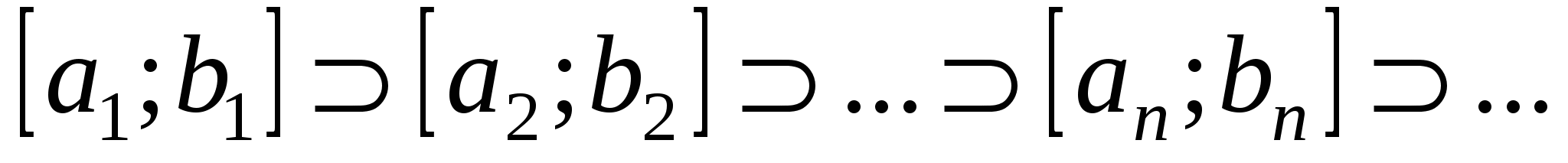 ; ;
2) концы отрезков 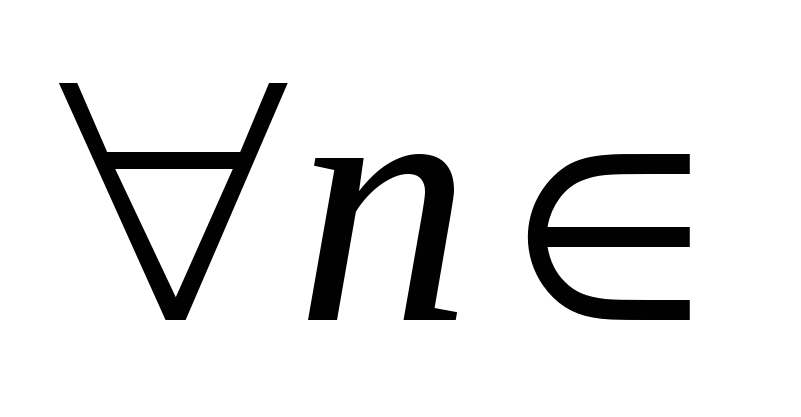 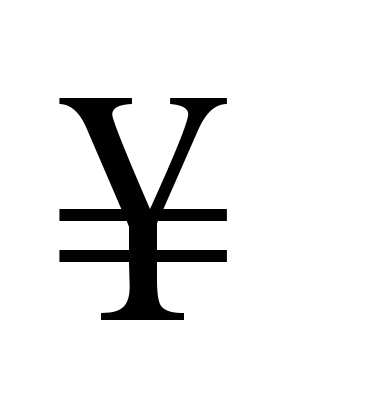 удовлетворяют неравенству удовлетворяют неравенству
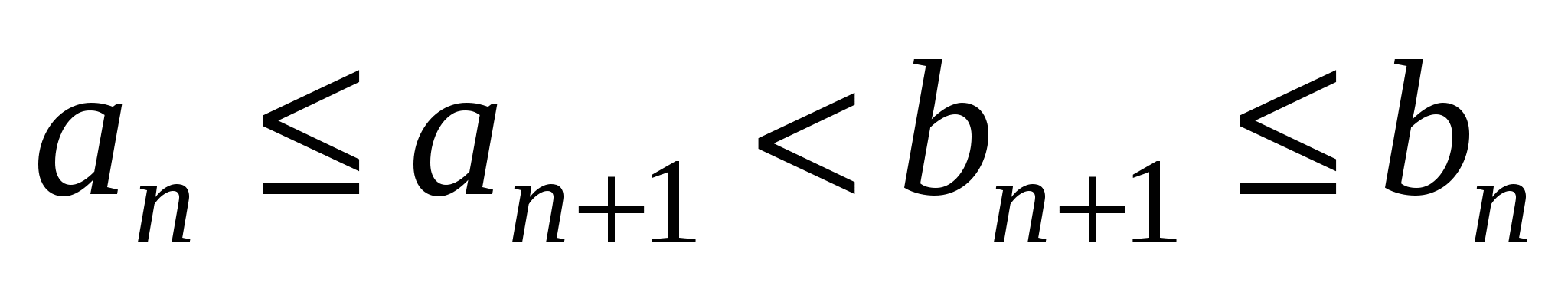 . .
Длины 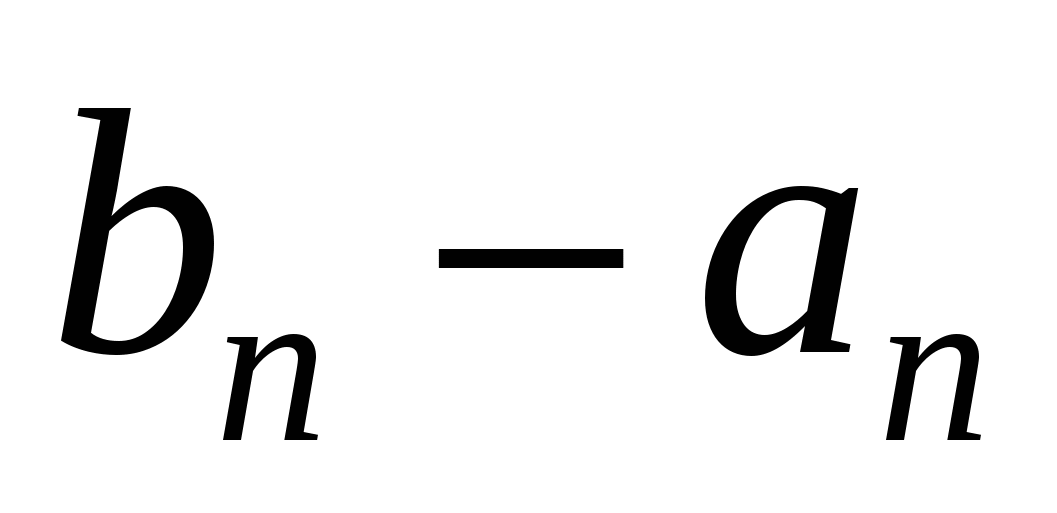 отрезков отрезков 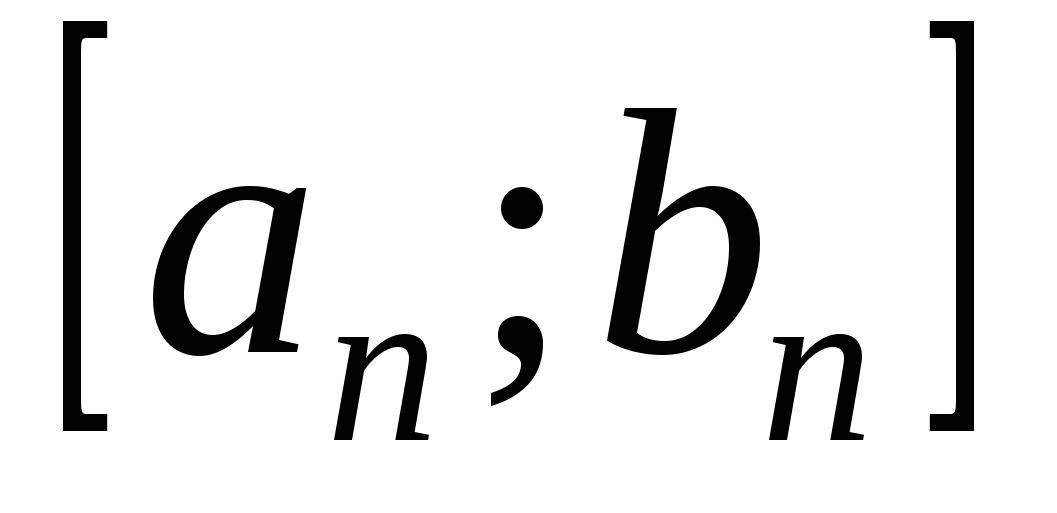 , , 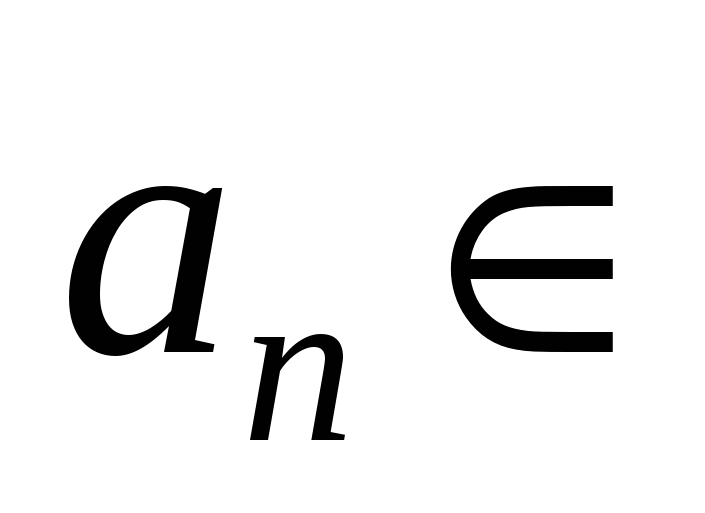  , , 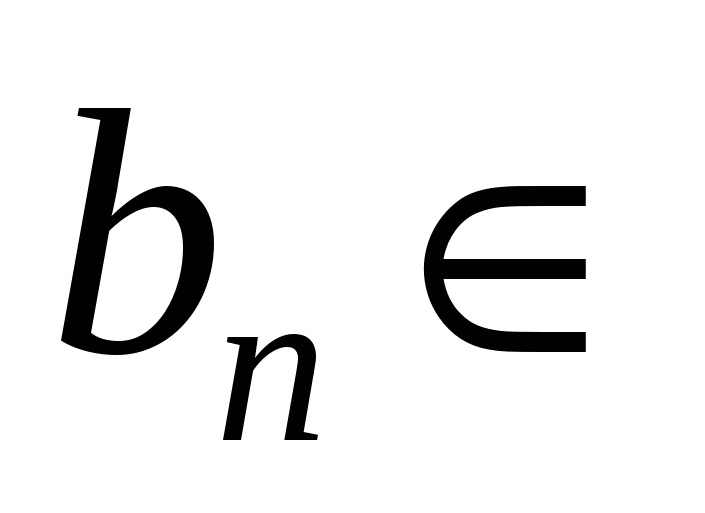  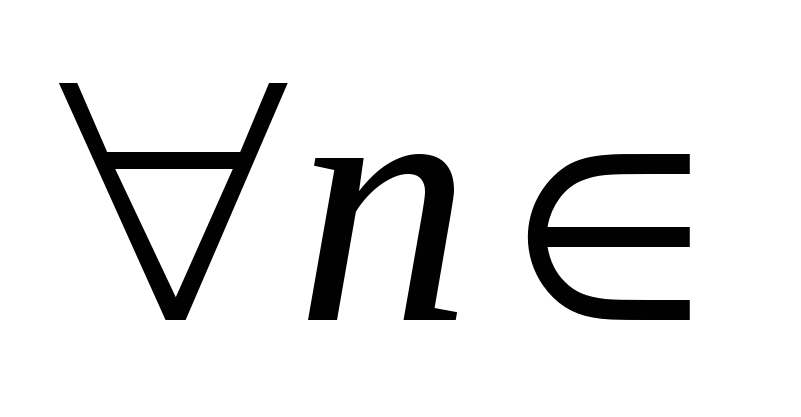 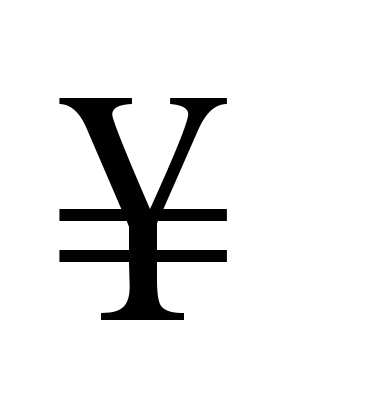 , называются стремящимися к нулю, если для любого числа , называются стремящимися к нулю, если для любого числа 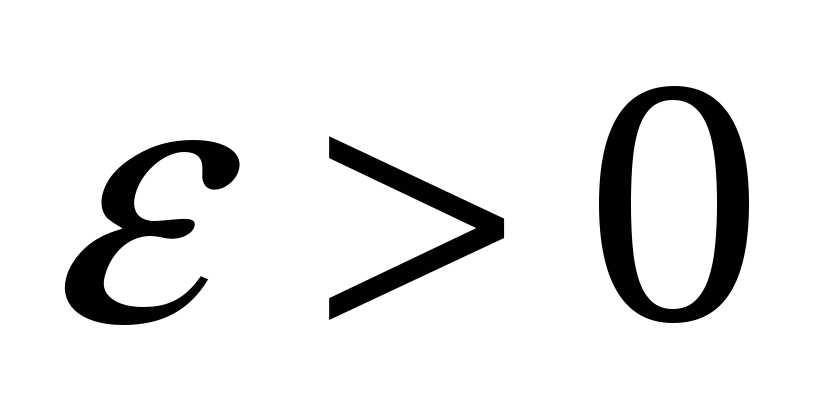 существует такой номер существует такой номер 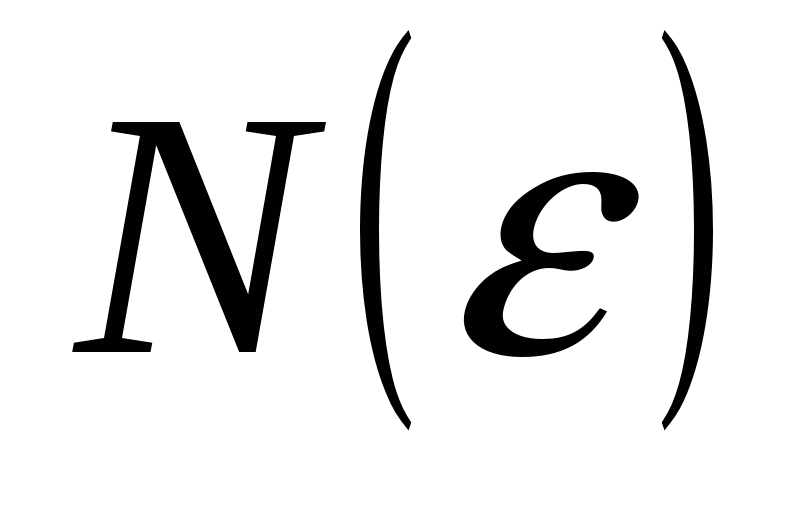 , что для всех номеров , что для всех номеров 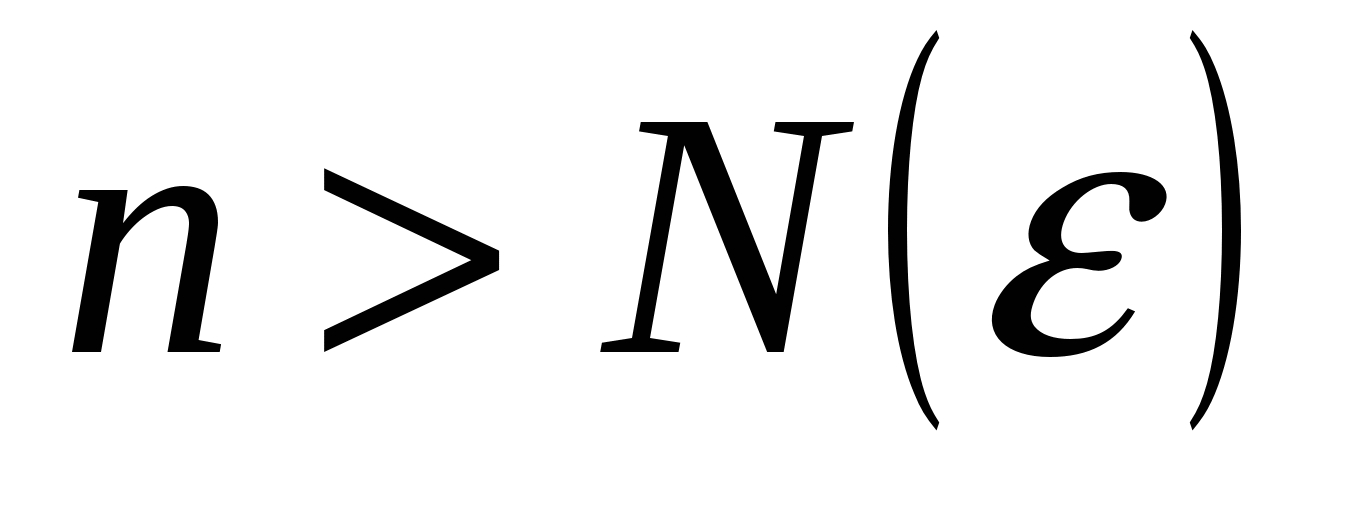 выполняется неравенство выполняется неравенство 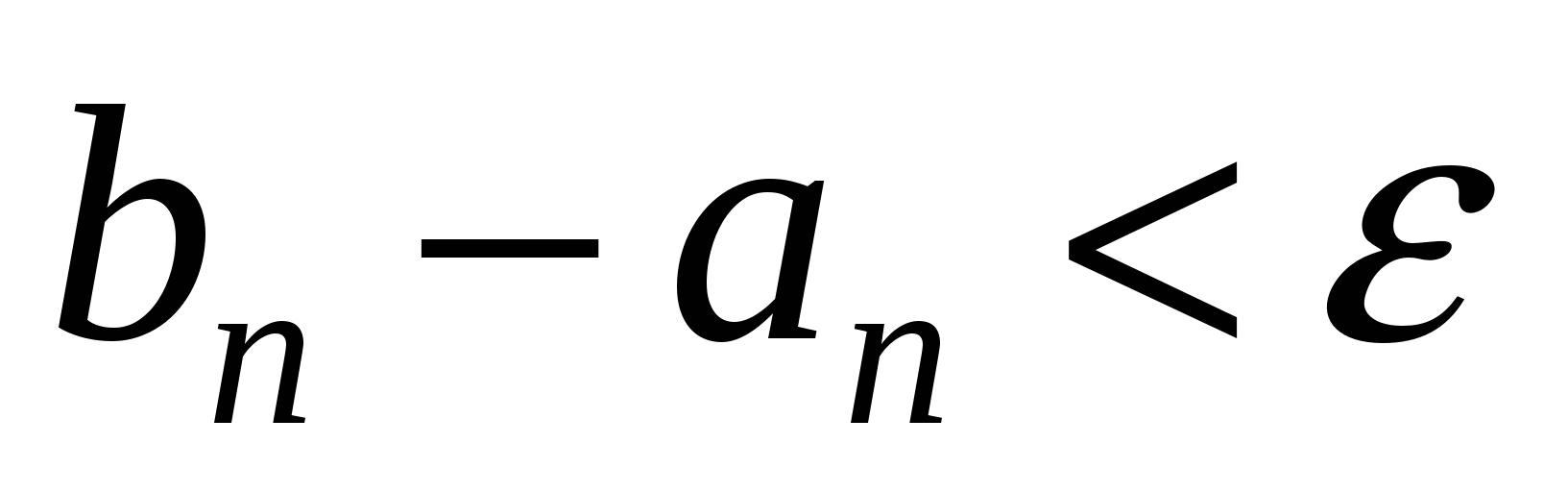 . .
Лемма (о вложенных отрезках) Всякая система вложенных числовых отрезков, длины которых стремятся к нулю, имеет единственную точку, принадлежащую всем отрезкам.
Метод математической индукции используется при доказательстве утверждений, зависящих от натурального аргумента. Для доказательства необходимо:
1) проверить верность утверждения при 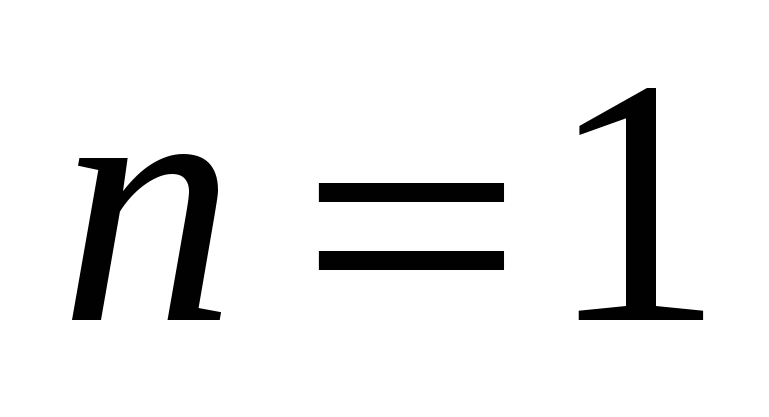 (либо для первого натурального числа, для которого доказывается утверждение); (либо для первого натурального числа, для которого доказывается утверждение);
2) в предположении, что утверждение верно для 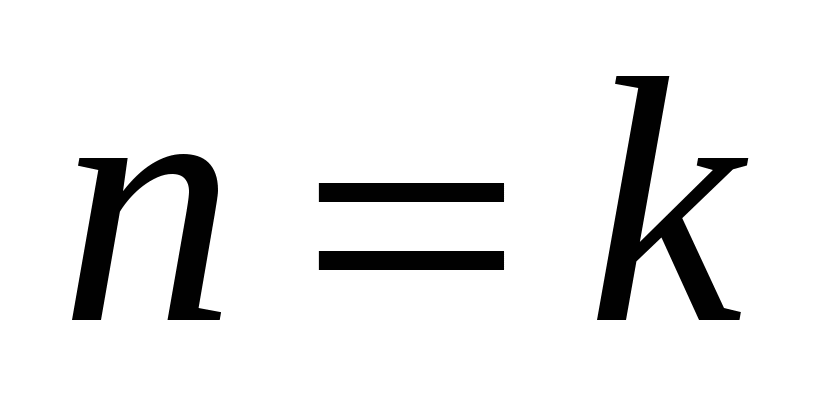 , доказать его справедливость для следующего натурального числа , доказать его справедливость для следующего натурального числа 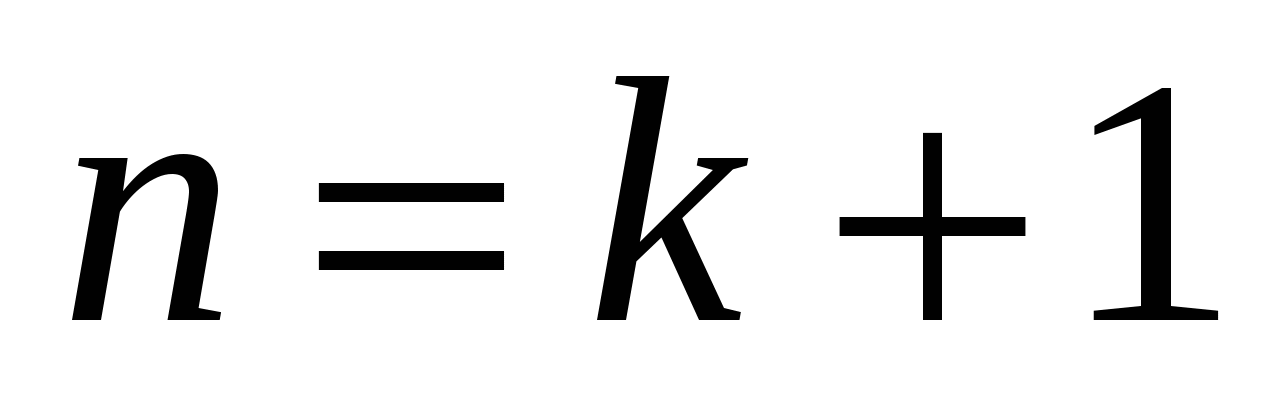 . .
При решении задач часто используется бином Ньютона.
Пусть задано конечное множество элементов. Группы элементов, состоящие их одних и тех элементов и отличающиеся друг от друга только их порядком, называются перестановками. Число возможных перестановок из 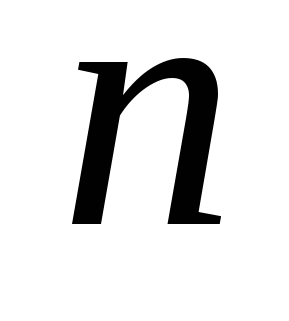 элементов равно элементов равно
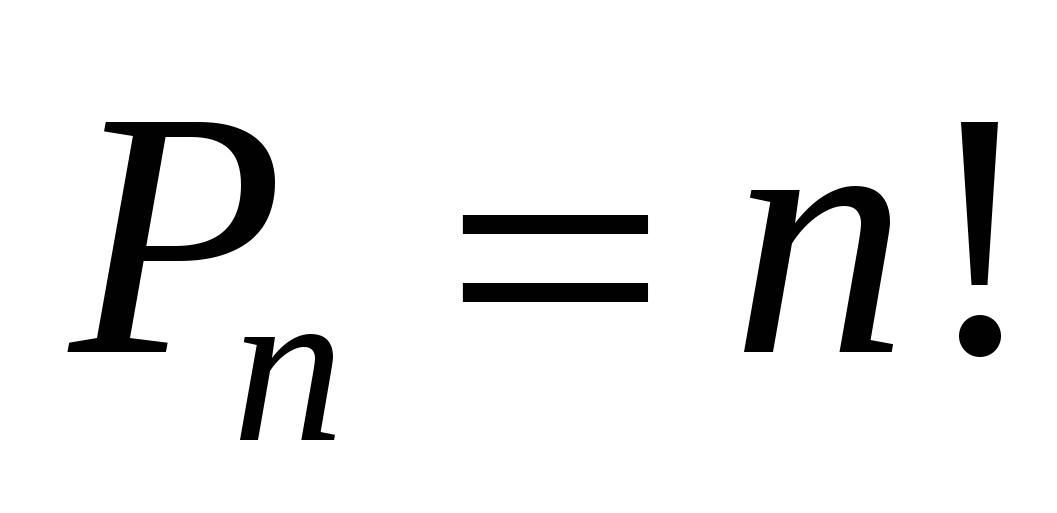 , , 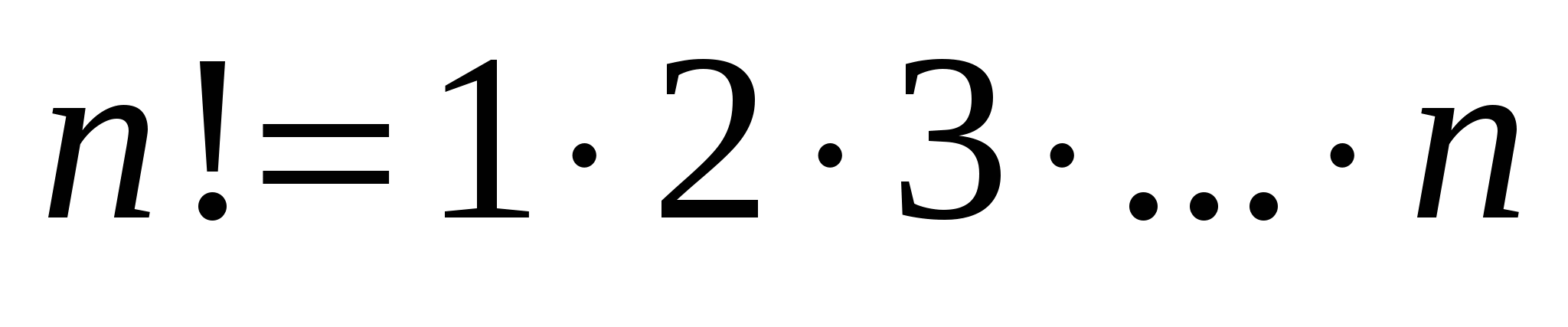 , , 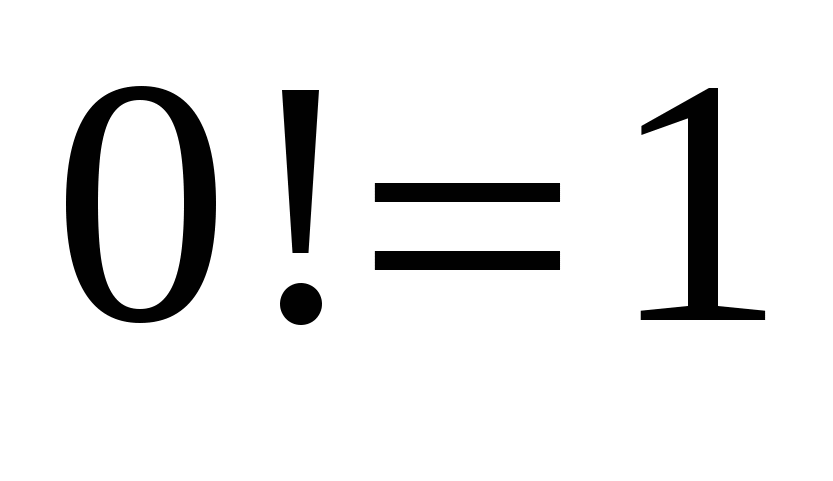 . .
страница 1
|