Итого: 60 баллов

- текущего контроля (проводится еженедельно)

- рубежного контроля (5, 10 и 15 недели)

- итогового контроля (проводится один раз в конце периода, т.е. экзамен).

Текущий контроль подразумевает оценку работы студента на лабораторных и лекционных занятиях (выполнение домашних заданий, самостоятельное выполнение задач, лабораторных работ, ответы на теоретические вопросы лекционного курса), итоги индивидуальных заданий и т.д..

Рубежный контроль – это выполнение тестов и контрольных работ в аудитории в присутствии преподавателя, а также сдачу коллоквиумов.

Итоговый контроль проводится после окончания изучения всех тем, по которым студент должен показать целостное видение законченной, замкнутой части изученной дисциплины.

6. 
   Рейтинг-шкала
   

1) Не опаздывать на занятия.

3) Не пропускать занятия, в случае болезни предоставить справку.

4) Пропущенные занятия отрабатывать в определенное преподавателем время.

5) Отключить сотовый телефон.

6) В случае невыполнения заданий итоговая оценка снижается.

7) Своевременно и старательно выполнять лабораторные и домашние задания.

8) Активно участвовать в учебном процессе, быть пунктуальным и обязательным.

10) Быть терпимым, открытым и доброжелательным к сокурсникам и преподавателям.

II. УЧЕБНО – МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ПО ДИСЦИПЛИНЕ

1. 
   Тематический план курса «Математика для химиков»
   

- основные понятия (элементы, строка, столбец, индекс, главная диагональ, квадратная, диагональная, единичная, нулевая, треугольная, вектор-столбец, вектор-строка, транспонированная матрица, равные матрицы, эквивалентные матрицы);

действия над матрицами; (операция сложения матриц вводится только

для матриц одинаковых размеров, а операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы, умножение матриц не обладает перестановочным свойством);

- определители (детерминант) 2-го и 3-го, n-го порядков; минор, алгебраическое дополнение, способы вычисления определителей (правила треугольников или Саррюса, разложения определителя по элементам некоторого ряда); свойства определителей;

- вырожденная и невырожденная, союзная матрицы, обратная матрица (определитель не равен нулю); ранг матрицы.

- основные понятия и определения теории систем уравнений;

- система n линейных уравнений с n неизвестными;

- метод обратной матрицы;

- метод Крамера;

- метод Гаусса;

- теорема Кронекера-Капелли;

- система n линейных уравнений с m неизвестными;

- однородные системы линейных уравнений;

- фундаментальная система решений;

- структура общего решения.

Основная литература: 1,2,3,6,7,8.

Дополнительная литература: 10,11,,12,14,18.

Тема 3: Элементы векторной алгебры и матричного анализа.

Тезисы лекции:

- векторы на плоскости и в пространстве (направленный отрезок или параллельный перенос, модуль вектора, единичный вектор, орт, равные, коллинеарные, компланарные векторы);

- линейные операции над векторами (умножение, вычитание и умножение вектора на число, правило треугольника, правило параллелограмма);

- скалярное произведение векторов, свойства, выражение скалярного произведения через координаты, приложения (угол между векторами, проекция вектора на заданное направление, работа постоянной силы);

- линейно зависимые и линейно независимые системы векторов; базис и координаты; размерность линейного пространства; Евклидово пространство; линейные операторы; собственные значения и собственные векторы линейного оператора; квадратичные формы.

- векторное произведение векторов, свойства, выражение векторного произведения через координаты, приложения (установление коллинеарности, нахождение площади параллелограмма и треугольника, определение момента силы относительно точки;

- смешанное произведение векторов, свойства, выражение смешанного произведения через координаты, приложения

Основная литература: 2,6,8.

Дополнительная литература: 10,12,18.

Тема 4: Элементы аналитической геометрии.

Тезисы лекции:

- система координат (декартова система координат, абсцисса, ордината, аппликата, координата точки, полярная система координат, полюс, полярная ось, единичный вектор), метод координат, преобразование системы координат (параллельный перенос и поворот осей координат);

- уравнения линии на плоскости (с угловым коэффициентом, общее уравнение, уравнение прямой в отрезках, уравнение прямой проходящей через две точки, полярное уравнение прямой, нормальное уравнение прямой, уравнение прямой, проходящей через данную точку перпендикулярно данному вектору), различные формы уравнения прямой на плоскости;

- угол между двумя прямыми; условия параллельности и перпендикулярности двух прямых; расстояние от точки до прямой;

- кривые второго порядка: окружность, эллипс, гипербола, парабола, основные понятия, их уравнения и геометрические свойства;

- уравнения плоскости и прямой в пространстве (поверхности).

- определение функции (соответствие), ее область существования, способы задания (аналитический, табличный, графический); основные характеристики функции, обратная и сложная функции, основные элементарные функции, их свойства и графики;

- числовые последовательности и их пределы, предельный переход в неравенствах; число е, натуральные логарифмы, предел функции в точке и на бесконечности; бесконечно малые и бесконечно большие величины и их свойства, связь между функцией, ее пределом и бесконечно малой функцией;

- основные теоремы о пределах; признаки существования пределов, замечательные пределы;

- непрерывность функции в точке и на интервале; свойства непрерывных функций.

Основная литература: 1,2,3,6,7,8.

Дополнительная литература: 10,11,13.

Тема 6: Дифференциальное исчисление функции одной

переменной.

- задачи, приводящие к понятию производной (скорость прямолинейного движения, касательная к прямой);

приращение аргумента, приращение функции, определение производной; геометрический (угловой коэффициент) и физический смысл (скорость протекания процесса) производной; понятие дифференцируемой функции (функция, имеющая производную в каждой точке интервала);

- основные правила дифференцирования;

- производные основных элементарных функций;

- производная сложной и обратной функции;

- дифференцирование неявных и параметрически заданных функций;

- логарифмическое дифференцирование;

- производные высших порядков.

Основная литература: 1,2,3,6,7,8.

Дополнительная литература: 10,11,12,13,15.

Тема 7: Приложение производной.

Тезисы лекции:

- основные теоремы дифференциального исчисления (теоремы Ролля, Коши, Лагранжа, Ферма);

- правило Лопиталя; раскрытие неопределенностей;

- возрастание и убывание функции; экстремум функции; выпуклость и вогнутость графика функции; наибольшее и наименьшее значения функции на отрезке, аналитические признаки выпуклости и вогнутости; точки перегиба; вертикальные, горизонтальные и наклонные асимптоты графика функции;

- общая схема исследования функции и построение ее графика.

Основная литература: : 1,2,3,6,7,9.

Дополнительная литература: 10,11,12,13,15.

Тема 8: Неопределенный интеграл.

Тезисы лекции:

- первообразная (определение, основное свойство, признак постоянства, правила нахождения первообразной);

- неопределенный интеграл, его свойства; таблица интегралов;

- основные методы интегрирования: непосредственное интегрирование, разложение, замена переменной (подстановка), интегрирование по частям;

- интегрирование рациональных функций (полиномы, рациональные дроби); интегрирование иррациональностей (квадратичные иррациональности, дробно-линейная подстановка, тригонометрическая подстановка, интегрирование дифференциального бинома) и выражений, содержащих тригонометрические функции (универсальная тригонометрическая подстановка, интегралы типа 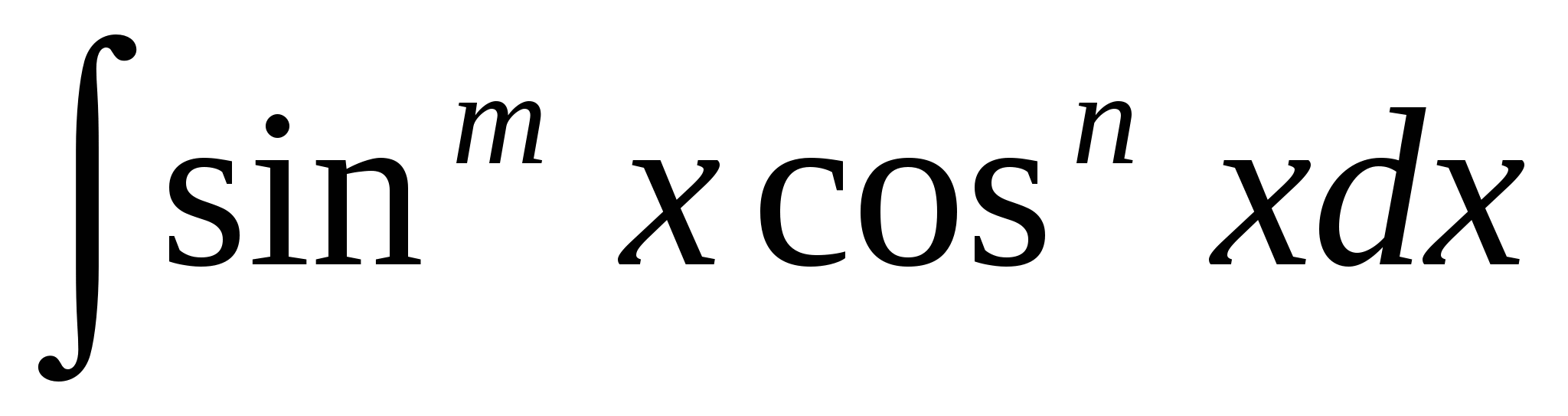, использование тригонометрических преобразований);

- «Берущиеся» и «неберущиеся» интегралы (таблица неопределенных интегралов М.Л.Смолянского, интеграл Пуассона, интегральный логарифм, интегралы Френеля, интегральные синус и косинус, интегральная показательная функция).

- задачи, приводящие к понятию определенного интеграла; интегральная сумма;

- понятие определенного интеграла, его свойства; определенный интеграл как функция верхнего предела;

- геометрический и физический смысл определенного интеграла;

- формула Ньютона Лейбница;

- применение (геометрическое) определенного интеграла к вычислению площадей плоских фигур; вычисление объемов тел и длин дуг кривых;

- механические приложения определенного интеграла (работа переменной силы, путь, пройденный телом, давление жидкости на вертикальную пластинку, вычисление статических моментов и координат центра тяжести)

- несобственные интегралы с бесконечными пределами и от неограниченных функций;

- приближенное вычисление определенного интеграла (формулы прямоугольников, трапеций, парабол (Симпсона)).

Основная литература: 1,2,3,7,8,9.

Дополнительная литература: 10-12.

Тема 10: Функции нескольких переменных.

Тезисы лекции:

- определение функции нескольких переменных;

- предел и непрерывность;

- частные производные и дифференциал функции; производная по направлению, градиент;

- касательная плоскость и нормаль к поверхности;

- экстремум функции нескольких переменных; наибольшее и наименьшее значения функции; условный экстремум, метод Лагранжа.

- основные понятия дифференциальных уравнений;

- решение уравнение, задача Коши; общее и частное решения;

- дифференциальные уравнения с разделяющимися переменными;

- однородные дифференциальные уравнения 1-го порядка;

- линейные дифференциальные уравнения 1-го порядка (метод И.Бернулли, метод Лагранжа, уравнение Я.Бернулли);

- уравнение в полных дифференциалах, интегрирующий множитель, уравнения Лагранжа и Клеро;

- дифференциальные уравнения 2-го порядка, допускающие понижение порядка;

- линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами: однородные и неоднородные.

Основная литература: 1,2,3,6,9.

Дополнительная литература: 10-14.

Тема 12: Ряды. Числовые ряды.

Тезисы лекции:

- числовые ряды; сходимость и сумма ряда, ряд геометрической прогрессий;

- необходимое условие сходимости; гармонический ряд;

- ряды с положительными членами; достаточные признаки сходимости (сравнения рядов, признак Даламбера, радикальный признак Коши, интегральный признак Коши);

- знакочередующиеся ряды; теорема Лейбница;

- знакопеременные ряды (общий достаточный признак); абсолютная и условная сходимость числовых рядов;

- степенные ряды: основные понятия, сходимость степенных рядов, разложение функций в степенные ряды (ряды Тейлора и Маклорена), некоторые приложения степенных рядов.

Основная литература: 1,2,3,6,9.

Дополнительная литература: 10-15.

Тема 13: Элементы теории вероятностей.

Тезисы лекции:

- предмет теории вероятностей, классификация событий, пространство элементарных событий, алгебра событий;

- понятие случайного события, относительные частоты, закон устойчивости относительных частот;

- классическое и геометрическое определение вероятности, понятие об аксиоматическом построении теории вероятностей;

- методы исчисления вероятностей;

- схема Бернулли;

- дискретные и непрерывные случайные величины, функция их распределения и свойства, математическое ожидание и дисперсия случайной величины;

- нормальное распределение и его свойства;

- числовые характеристики;

Основная литература: 1,3-6,8,.

Дополнительная литература: 13-15.

Тема 14.Элементы математической статистики.

Тезисы лекции:

- генеральная совокупность и выборка, вариационный ряд, гистограмма и эмпирическая функция распределения, выборочная средняя и дисперсия;

- статистические оценки генеральной средней и доли, погрешность оценки, доверительная вероятность и доверительный интервал, определение необходимого объема выборки;

- понятие о критериях согласия, проверка статистических гипотез; дисперсионный анализ; корреляционный анализ; регрессионный анализ;

- временные ряды; модели временных рядов и их составляющие.

Основная литература: 1,4-6,8.

Дополнительная литература: 13,15.

2.3 Планы практических (семинарских) занятий.

Тема1: Матрицы и определители.

Контрольные вопросы:

1) Что называется матрицей?

2) Какая матрица называется: квадратной, нулевой, вектором-столбцом, треугольной, вектором-строкой, присоединенной, диагональной, невырожденной, единичной, ступенчатой?

3) Перечислите операции, которые можно производить над матрицами.

4) Чем отличается операция умножения матриц от операции умножения чисел? Когда умножение матрицы А на матрицу В определено?

5) Что такое транспонирование матрицы?

6) Что называется определителем матрицы?

7) Как возвести матрицу в степень?

8) Как определяется размер матрицы?

9) Какие матрицы называются равными?

10) Как вычислить определитель 3-го порядка?

11) Что называется минором элемента а_ij матрицы n-го порядка?

12) Что называется алгебраическим дополнением элемента а_ij матрицы n-го порядка?

13) Сформулируйте теорему Лапласа. Какое значение она имеет для вычисления определителей?

14) Сформулируйте основные свойства определителей.

15) Какая матрица называется обратной? Сформулируйте необходимое и достаточное условие существования обратной матрицы.

16) Каков алгоритм вычисления обратной матрицы?

17) Что такое ранг матрицы?

18) Какие преобразования матрицы называются элементарными? Что происходит с рангом матрицы при элементарных преобразованиях?

19) Что называется линейной комбинацией строк матрицы?

20) Какие строки матрицы называются линейно-зависимыми; линейно-независимыми?

21) Сформулируйте теорему о ранге матрицы.

Решение задач (здесь и далее необходимое учебное обеспечение практических занятий выделяется косыми чертами, номер источника приводится по разделу 1.5 настоящей программы): №№ 1.15 – 1.29 /С. 36-37/1/.