страница 1 | страница 2 страница 3
Тема 2: Системы линейных уравнений.
Контрольные вопросы:
1) Что называется решением системы m линейных уравнений с n переменными?
2) Какая система уравнений называется совместной, несовместной?
3) Когда совместная система уравнений называется определенной; неопределенной?
4) В каком случае две системы уравнений называются
равносильными?
5) Какой вид имеет система m линейных уравнений с n неизвестными, записанная в матричной форме?
6) Как решить систему линейных уравнений, используя метод обратной матрицы?
7) Сформулируйте теорему Крамера.
8) В чем заключается метод Гаусса решения систем линейных уравнений?
9) Каковы достоинства метода Гаусса?
10) Какая матрица называется расширенной матрицей системы линейных уравнений?
11) Сформулируйте теорему Кронекера-Капелли.
12) Какое решение системы линейных уравнений называется базисным?
13) Когда система m линейных уравнений с n переменными называется однородной?
14) Какими свойствами обладают решения системы линейных однородных уравнений?
15) Что такое фундаментальная система решений системы линейных однородных уравнений?
16) Какой вид имеет общее решение системы линейных однородных уравнений?
Решение задач: №№ 2.11 – 2.28 /С.60-62/1/
Тема 3: Элементы векторной алгебры и матричного анализа.
Контрольные вопросы:
-
Что называется вектором?
-
Что называется длиной и направлением вектора?
-
Какой вектор называется нулевым? Имеет ли он направление?
-
Как называется угол между двумя векторами?
-
Какой вектор называется суммой двух данных векторов? Сформулируйте правило треугольника сложения двух векторов.
-
В чем состоит правило многоугольника сложения нескольких векторов? Какой вектор называется разностью двух векторов?
-
Что называется произведением вектора на число?
-
Какие два вектора называются коллинеарными?
-
Что называется скалярным произведением двух векторов?
-
Как найти угол между векторами, используя скалярное произведение?
-
Дайте определение n-мерного вектора.
-
Что такое векторное пространство?
-
Что называется линейной комбинацией векторов?
-
Дайте определение линейной зависимости и линейной
независимости векторов линейного пространства.
-
Как определяется размерность линейного пространства?
-
Что называют базисом линейного пространства?
-
Сформулируйте теорему о единственности представления вектора линейного пространства.
-
Сформулируйте теорему о размерности и базисе пространства.
-
Какое пространство называется евклидовым?
-
Дайте определение нормы вектора в евклидовом пространстве.
-
Когда два вектора называются ортогональными?
-
Какой базис называется ортонормированным?
-
Дайте определение линейного оператора.
-
Сформулируйте теорему о зависимости между матрицами оператора в разных базисах.
-
Дайте определение собственного вектора и собственного значения линейного оператора.
-
Сформулируйте теорему о о матрице оператора в базисе, состоящем из его собственных векторов.
-
Что такое квадратичная форма? каноническая форма?
-
Сформулируйте критерий Сильвестра.
Решение задач: №№ 3.14 – 3.35 /С. 93-94/1/.
Тема 4: Элементы аналитической геометрии.
Контрольные вопросы:
1) Дайте определение уравнения линии на плоскости.
2) Какими способами можно задать прямую на плоскости?
3) Как записывается уравнение прямой, проходящей через две данные точки?
4) Какое уравнение называется уравнением прямой в отрезках?
5) Как записывается уравнение прямой , проходящей через данную точку в данном направлении?
6) Какое уравнение называется общим уравнением прямой?
7) Какая прямая, заданная общим уравнением, проходит через начало координат?
8) Как записывается уравнение прямой с угловым коэффициентом?
9) Как вычисляется угол между прямыми, заданными уравнениями с угловым коэффициентом?
10) Сформулируйте условия параллельности и перпендикулярности двух прямых, заданных уравнениями с угловыми коэффициентами.
11) Как находится расстояние от точки до прямой?
12) Что называется окружностью?
13) Какой вид имеет общее уравнение окружности? Какое уравнение окружности называется нормальным?
14) Что называется эллипсом?
15) Какой вид имеет каноническое уравнение эллипса?
16) Какие точки плоскости называются фокусами эллипса? Сколько фокусов у эллипса? Как называется расстояние между фокусами?
17) Какие точки эллипса называются его вершинами?
18) Что называется эксцентриситетом эллипса?
19) Что называется гиперболой?
20) Какие точки плоскости называются фокусами гиперболы?
21) Какой вид имеет каноническое уравнение гиперболы?
22) Какие прямые называются асимптотами гиперболы?
23) Что называется параболой?
24) Какая точка плоскости называется фокусом параболы? Что называется директрисой параболы?
25) Что называется вершиной параболы?
26) Почему окружность, гипербола, эллипс и парабола называются кривыми второго порядка?
Решение задач: №№ 4.14 – 4.32 /С. 121-122/1/.
Тема 5: Введение в анализ.
Контрольные вопросы:
1) Что такое функция?
2) Какие способы задания функции вы знаете?
3) Что такое область определения функции; область
значений функции?
4) Перечислите основные свойства функций.
5) Какие основные элементарные функции вы знаете?
6) Что значит, что функция задана явно; неявно?
7) Какая функция называется обратной?
8) Что такое суперпозиция функций?
9) Дайте определение числовой последовательности?
10) Что такое предел числовой последовательности?
11) В чем заключается геометрический смысл предела числовой последовательности?
12) Дайте определение предела функции в бесконечности; предела функции в точке.
13) Какая функция называется бесконечно малой величиной; бесконечно большой величиной?
14) Перечислите основные свойства бесконечно малых и бесконечно больших величин. Какова связь между этими величинами?
15) Сформулируйте основные теоремы о пределах.
16) Какие замечательные пределы вы знаете?
17) Дайте определение непрерывности функции в точке.
18) Перечислите свойства функций, непрерывных в точке.
19) Какая функция называется непрерывной на промежутке?
20) Сформулируйте свойства функций непрерывных на отрезке.
Решение задач: №№ 5.8 – 5.22 /С. 140/1/; №№ 6.15 – 6.41 С.
174-175/1/.
Тема 6: Дифференциальное исчисление функции одной переменной.
Контрольные вопросы:
-
Сформулируйте определение производной функции. В чем заключается геометрический и физический смысл производной?
2) Что значит, что функция дифференцируема в точке; на промежутке?
3) Как связаны между собой понятия непрерывности и
дифференцируемости функции?
4) Сформулируйте основные правила дифференцирования.
5) Таблица производных основных элементарных функций.
6) Сформулируйте теорему о производной сложной функции.
7) Сформулируйте теорему о производной обратной функции.
8) Как найти производную функции, заданной неявно?
9) Дайте определение производной n-го порядка.
10) Сформулируйте определение дифференциала функции.
В чем заключается геометрический смысл дифференциала функции?
11) Перечислите основные свойства дифференциала функции.Таблица дифференциалов.
12) Сформулируйте теорему об инвариантности формы первого
дифференциала.
13) как применяется дифференциал в приближенных вычислениях?
14) Сформулируйте определение дифференциала n-го порядка.
Решение задач: № 7.20 – 7.53 /С. 206-208/1/; № 9.6 – 9.13 /
С.250/1/.
Тема 7: Приложение производной.
Контрольные вопросы:
1) Сформулируйте теоремы для дифференцируемых функций:
а) теорему Ферма; б) теорему Ролля; в) теорему Лагранжа.
2) Сформулируйте правило Лопиталя.
3) Сформулируйте условие монотонности функции.
4) Какая точка называется точкой максимума (минимума) функции?
5) Что такое экстремум функции?
6) Сформулируйте необходимое условие экстремума.
7) Какие точки называются стационарными?
8) Как исследовать функцию на экстремум, применяя первое достаточное условие экстремума?
9) Как исследовать функцию на экстремум, используя второе д достаточное условие экстремума?
10)Как найти наибольшее и наименьшее значение функции на отрезке?
11) Дайте определение функции выпуклой вверх; выпуклой вниз.
12) Сформулируйте достаточные условия выпуклости и вогнутости.
13) Какая точка графика функции называется точкой перегиба?
14) Сформулируйте необходимое и достаточное условие
существования точек перегиба.
15) Приведите схему нахождения точек перегиба.
16) Что такое асимптота графика функции?
17) Сформулируйте условия существования асимптот.
18) Приведите общую схему исследования функций и построения их графиков.
Решение задач: №№ 8.19 – 8.53 /С. 242-243/1/.
Тема8: Неопределенный интеграл.
Контрольные вопросы:
1) Дайте определение первообразной функции.
2) Что называется неопределенным интегралом?
3) Сформулируйте основные свойства неопределенного интеграла.
4) Таблица основных неопределенных интегралов.
5) Охарактеризуйте следующие методы интегрирования:
а) непосредственное интегрирование;
б) интегрирование подведением под знак дифференциала;
в) интегрирование по частям; д) метод подстановки
6) По какой схеме проводится интегрирование:
а) рациональных дробей; б) выражений, содержащих иррациональности; в) тригонометрических функций.
Решение задач: №№ 10.29 – 10.70 /С. 280-282/1/.
Тема9: Определенный интеграл.
Контрольные вопросы:
1) Что такое интегральная сумма функции y=f(x) на данном промежутке?
2) Дайте определение определенного интеграла.
3) В чем заключается геометрический смысл определенного интеграла?
4) Сформулируйте условие интегрируемости функций.
5) Сформулируйте основные свойства определенного интеграла.
6) Связь между определенным и неопределенным интегралами. Формула Ньютона-Лейбница.
7) По какой формуле проводится интегрирование по частям определенном интеграле?
8) Сформулируйте правило замены переменной в определенном интеграле.
9) Приведите формулы для вычисления: а) площадей плоских фигур; б) объемов тел вращения.
10) Сформулируйте определение несобственного интеграла
с бесконечным пределом интегрирования. Схема вычисления такого интеграла.
11) Сформулируйте определение несобственного интеграла от неограниченной функции и схему его вычисления.
Решение задач: №№ 11.25 – 11.62 /С. 323-324/1/.
Тема10: Функции нескольких переменных.
Контрольные вопросы:
1) Дайте определение функции нескольких переменных?
2) Что такое график функции двух переменных?
3) Что такое линия уровня?
4) Дайте определение предела функции двух переменных в точке (х0,у0).
5) Какая функция от двух переменных называется непрерывной в точке (х0, у0)?
6) Дайте определение частной производной функции нескольких переменных.
7) Сформулируйте правило вычисления частных производных.
8) Сформулируйте определение дифференциала функции нескольких переменных.
9) Что такое производная по направлению?
10) Что такое градиент?
11) Какая точка называется точкой максимума (минимума) функции двух переменных?
12) Сформулируйте необходимый признак экстремума функции двух переменных.
13) Сформулируйте достаточное условие экстремума функции двух переменных.
14) Приведите схему исследования функции двух переменных на экстремум.
15) Как найти наибольшее и наименьшее значения функции двух переменных?
16) Какая точка называется точкой условного экстремума?
17) В чем заключается сущность метода множителей Лагранжа?
Решение задач: №№ 15.23 – 15.34 /С. 435-436/1/.
Тема11: Дифференциальные уравнения
Контрольные вопросы:
1) Какие уравнения называются дифференциальными?
2) Как определяется порядок дифференциального уравнения?
3) Что называется решением дифференциального уравнения? Какое решение называется общим; частным?
4) Сформулируйте теорему о существовании и единственности частного решения дифференциального уравнения 1-го порядка.
5) В чем заключается геометрический смысл дифференциального уравнения и его частного и общего решений?
6) Приведите основные типы уравнений 1-го порядка:
а) с разделяющимися переменными; б) однородные;
в) линейные.
7) Сформулируйте алгоритм решения дифференциальных уравнений 2-го порядка, допускающих понижение порядка.
8) Какой вид имеет линейное дифференциальное
уравнений 2-го порядка? В каком случае оно называется
однородным; неоднородным?
9) Сформулируйте основные свойства решений линейного
однородного уравнения.
10) Сформулируйте теорему о структуре общего решения линейного однородного уравнения 2-го порядка.
11) Как найти общее решение линейного однородного уравнения 2-го порядка?
12) В чем заключается сущность метода вариации произвольных постоянных?
13) Сформулируйте теорему о структуре общего решения
неоднородного линейного уравнения.
14) В чем заключается сущность метода неопределенных
коэффициентов?
Решение задач: №№ 12.29 – 12.48 /С. 354-355/1/.
№№ 12.49 – 12.64 /С. 355/1/.
Тема12: Числовые ряды.
Контрольные вопросы:
1) Что такое числовой ряд?
2) Что называется суммой ряда?
3) Что называется частичной суммой ряда?
4) Какой ряд называется сходящимся; расходящимся?
5) Сформулируйте основные свойства сходящихся рядов.
6) Сформулируйте необходимый признак сходимости.
7) Какой ряд называется гармоническим?
8) Сформулируйте достаточные признаки сходимости
знакоположительных рядов: а) признак сравнения;
б) предельный признак сравнения; в) признак Даламбера;
г) интегральный признак.
9) Какой ряд называется знакочередующимся?
10) Сформулируйте признак Лейбница.
11) Какой ряд называется знакопеременным?
12) Сформулируйте достаточный признак сходимости
знакопеременного ряда.
13) Какой ряд называется абсолютно сходящимся?
14) Какой ряд называется условно сходящимся?
Решение задач: №№ 13.16 – 13.45 /С. 377-378/1/.
Тема13: Элементы теории вероятностей
Контрольные вопросы:
1) Что называют событием?
2) Какое событие называют случайным в данном опыте?
3) Что называют случайной величиной?
4) Как задают закон распределения дискретной случайной величины, принимающей конечное множество значений?
5) Какую случайную величину называют непрерывной?
6) Какой вид имеет график функции распределения?
7) Что называют плотностью распределения случайной величины?
8) Как определяется математическое ожидание дискретной случайной величины, принимающей конечное множество значений?
9) Каковы свойства математического ожидания случайной величины?
10) Как определяется дисперсия случайной величины?
11) Что характеризует дисперсия случайной величины?
12) Какое распределение вероятностей случайной величины называют нормальным?
13) Назовите методы вычисления вероятностей.
Решение задач: №№ 15 – 31 /С. 128-129/2/.
Тема14: Элементы математической статистики.
Контрольные вопросы:
1) Что называют генеральной совокупностью и выборкой?
2) Что означают вариационный ряд, гистограмма и эмпирическая функция распределения?
3) Как определяются выборочная средняя и дисперсия?
4) Что характеризуют статистические оценки генеральной средней и доли?
5) Что такое погрешность оценки?
6) В чем заключается разница между доверительной вероятностью и доверительным интервалом?
7) Как определяется необходимый объем выборки?
8) Что знаете о критериях согласия?
9) Как осуществляется проверка статистических гипотез?
10) Каковы особенности дисперсионного анализа; корреляционного анализа; регрессионного анализа?
11) Что означают временные ряды; модели временных рядов и их составляющие?
Решение задач: №№ 15 – 31 /С. 128-129/2/.
Методические рекомендации: Подготовку к каждому практическому занятию следует начинать с повторения основных моментов темы (по учебнику или конспектам), ответов на контрольные вопросы и детального разбора примеров, рассмотренных на лекции или в учебниках. Очень полезно, взяв условия примера из текста учебника, самостоятельно произвести для него все требующиеся расчеты, а затем сверить их с расчетами в учебнике.
Основные типы задач решаются на аудиторных практических занятиях. Здесь разрабатывается полный и подробный план решения задач.
Основная и дополнительная литература приведена в подразделе 2.2. Курс содержит много формул. Чтобы запомнить эти формулы, необходимо хорошо разбираться в принципах их построения. Содержание каждой темы надо кратко законспектировать, записывая основные определения и все без исключения формулы и характеризуя их смысл. Записи следует вести в особой тетради (т.е. для практических работ). В ней же следует решать основные типы задач по каждой теме (можно записывать решение примеров из учебника). Эта тетрадь затем не только окажет большую помощь при повторении курса перед экзаменом, но и может быть использована как справочный материал в дальнейшей работе во всех случаях, когда придется иметь дело с математическими методами. Тема может считаться усвоенной, если студента не затруднят ответы на контрольные вопросы и решение задач, помещенных в рекомендованных учебниках.
2.5 Планы занятий в рамках самостоятельной работы студентов под руководством преподавателя.
Менее сложный для освоения материал выносятся на СРСП (т.е. самостоятельную работу студента под руководством преподавателя), которые будут проходить в форм индивидуальных или групповых консультаций или лабораторных занятии с преподавателем.
В течение изучения дисциплины студент должен самостоятельно выполнить тринадцать заданий, причем три из них (1; 4; 6) имеют теоретический характер, остальные на выполнение лабораторных работ (2; 7; 10), собственных разработок (5; 12) и решение задач (№3; 8; 9; 11; 13). Цель выполнения этих заданий – усвоить, закрепить и углубить материал, изученный на лекциях и практических занятиях.
Тематика заданий:
Тема 1: Матрицы и определители.
1Вычисление определителей методом эффективного понижения порядка.
2. Приведение определителя к треугольному виду.
3. Коммутирующие матрицы.
4. Метод единиц и нулей.
5. Метод окаймляющих миноров.
Форма проведения СРСП: Семинар.
Тема 2: Системы линейных уравнений.
1. Матричный метод решения систем.
2. Доказательство совместности систем с помощью теоремы Кронекера – Капелли.
3. Исследование систем уравнений на совместность.
Форма проведения СРСП: Лабораторная работа
Тема 3: Элементы векторной алгебры и матричного анализа.
1. Линейные операции над векторами.
2. Деление отрезка в данном отношении.
3. Векторное и смешанное произведения векторов и их приложения.
Форма проведения СРСП: Практикум по решению задач
Тема 4: Элементы аналитической геометрии.
1.Различные способы задания плоскости и соответствующие им виды ее уравнения.
2. Прямая в пространстве. Прямая и плоскость.
3. Линии, заданные уравнениями в полярных координатах и параметрическими уравнениями.
Форма проведения СРСП: Семинар
Тема 5: Введение в анализ.
1. Представление сложных функций в виде композиции функций, являющихся основными элементарными функциями.
2. Раскрытие неопределенностей.
3. Сравнение бесконечно малых функций.
4. Точки разрыва функции.
Форма проведения СРСП: Защита проектов
Тема 6: Дифференциальное исчисление функции одной переменной.
1. Логарифмическое дифференцирование.
2. Производные и дифференциалы высших порядков.
Форма проведения СРСП: Семинар
Тема 7: Приложение производной.
1.Практические задачи на экстремум.
2. Дифференциал длины дуги и кривизна плоской линии.
Форма проведения СРСП: Лабораторная работа
Тема 8: Неопределенный интеграл.
1. Интегрирование функций, содержащих квадратный трехчлен.
2. Метод неопределенных коэффициентов.
Форма проведения СРСП: Практикум по решению задач.
Тема 9: Определенный интеграл.
1. Несобственные интегралы.
2. Приложение определенных интегралов к задачам геометрии.
3. Приложение определенных интегралов к решению задач
физического и экономического содержания.
Форма проведения СРСП: Практикум по решению задач.
Тема 10: Функции нескольких переменных.
1. Полный дифференциал. Дифференцирование сложных и неявных функций.
2. Частные производные высших порядков.
3. Касательная плоскость и нормаль к поверхности.
Форма проведения СРСП: Лабораторная работа
Тема 11: Дифференциальные уравнения
1. Уравнение Бернулли.
2. Метод Бернулли.
3. Уравнения в полных дифференциалах.
4. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
5. Линейные дифференциальные уравнения с постоянными
коэффициентами.
6. Задача Коши.
Форма проведения СРСП: Практикум по решению задач.
Тема 12: Числовые ряды. Степенные ряды.
1. Исследование рядов на сходимость.
2. Степенные ряды. Интервал сходимости. Теорема Абеля.
3. Ряд Тейлора.
4. Разложения функций в ряд Маклорена.
Форма проведения СРСП: Защита проектов.
Тема 13: Элементы математической статистики.
1. Проверка статистических гипотез.
2. Дисперсионный анализ.
3. Корреляционный анализ. Регрессионный анализ.
Форма проведения СРСП: Практикум по решению задач.
Методические рекомендации к выполнению: Чтобы научиться решать задачи того или иного типа, рекомендуется сначала изучить план решения в общем виде (алгоритм), затем рассмотреть пример реализации плана в конкретном случае и, по аналогии с ним, решить несколько задач из числа предлагаемых для самостоятельного решения. Чтобы приобрести устойчивый навык решения типовых задач, необходимо решить не менее трех – пяти задач каждого типа.
Рекомендуемая литература: Индивидуальные задания по высшей математике. / Под ред. А.П. Рябушко. – Минск: Высшая школа, 2000. Ч1, 2.
2.6 Планы занятий в рамках самостоятельной работы студентов.
В ходе изучения дисциплины каждый студент получает индивидуальные задания (ИЗ), которые охватывают основные разделы курса и позволяют выяснить, насколько хорошо усвоены теоретические положения и может ли студент применять их для решения практических задач.
График выполнения и сдачи индивидуальных заданий по дисциплине «Математика для химиков»
Таблица 5
Неделя
|
Выполненная работа
|
1
|
Установочная неделя. Определение типов и видов заданий.
|
2
|
Раздача заданий.
|
3
|
Работа над заданиями. Консультации.
|
4
|
Сдача первого задания (домашняя контрольная работа)
|
5
|
Работа над заданиями. Консультации.
|
6
|
Работа над заданиями. Консультации.
|
7
|
Сдача второго задания (ИЗ по изученным темам).
|
8
|
Работа над заданиями. Консультации.
|
9
|
Работа над заданиями. Консультации.
|
10
|
Сдача третьего задания (коллоквиум).
|
11
|
Сдача четвертого задания (задачи).
|
12
|
Работа над заданиями. Консультации.
|
13
|
Сдача пятого задания (задачи).
|
14
|
Работа над заданиями. Консультации.
|
15
|
Сдача шестого задания (коллоквиум).
|
В течение изучения дисциплины студент должен самостоятельно выполнить шесть заданий, причем два из них (№3 и №6) имеют теоретический характер, остальные на выполнение упражнений и решение задач. Цель выполнения этих заданий – усвоить, закрепить и углубить материал, изученный на лекциях и практических занятиях.
Тематика заданий:
№1: Матрицы и определители. Системы линейных уравнений. Элементы векторной алгебры и матричного анализа.
№2: Уравнение линии. Предел и непрерывность. Производная и дифференциал функции.
№3: Коллоквиум – письменный опрос по пройденным темам.
№4: Приложение производной. Неопределенный и определенный интеграл. Дифференциальные уравнения 1-го порядка.
№5: Дифференциальные уравнения 2-го порядка. Числовые ряды. Функции нескольких переменных.
№6: Коллоквиум – устный опрос по пройденным темам.
Методические рекомендации к выполнению: каждое ИЗ должно быть выполнено в тетради (или на листах формата А4) , на обложке которой указывается специальность, курс, группа, фамилия и имя студента, номер варианта и дата сдачи работы.
Работа должна быть написана разборчивым почерком, на страницах следует оставить поля.
Решение задач необходимо сопровождать краткими пояснениями, обязательно приводить все формулы, используемые в задаче.
Решение задач ни в коем случае не следует откладывать на последний вечер перед занятиями, как, к сожалению, нередко поступают студенты. В этом случае более сложные и притом наиболее содержательные и полезные задачи заведомо не могут быть решены.
Задания, выполненные с опозданием, будут оцениваться ниже.
Содержание заданий будет сообщено каждому студенту индивидуально.
Рекомендуемая литература: Индивидуальные задания по высшей математике. / Под ред. А.П. Рябушко. – Минск: Высшая школа, 2000. Ч1, 2.
2.7 Тематика письменных работ по курсу.
Контрольная работа № 1: матрицы, определители, системы линейных уравнений, векторная алгебра.
Контрольная работа № 2: аналитическая геометрия, пределы, производные и их приложения.
Контрольная работа № 3: неопределенные интегралы, определенный интеграл и его приложение, дифференциальные уравнения.
Тематика рефератов: №1. Элементы аналитической геометрии.
./1 – 3,7,8,10,17,18/
№2. Производная и дифференциал./1 – 3,7 - 10,16/
№3. Элементы теории вероятностей./1- 8, 10,16/.
2.8 Тестовые задания для самоконтроля.
1. Найдите произведение матриц: 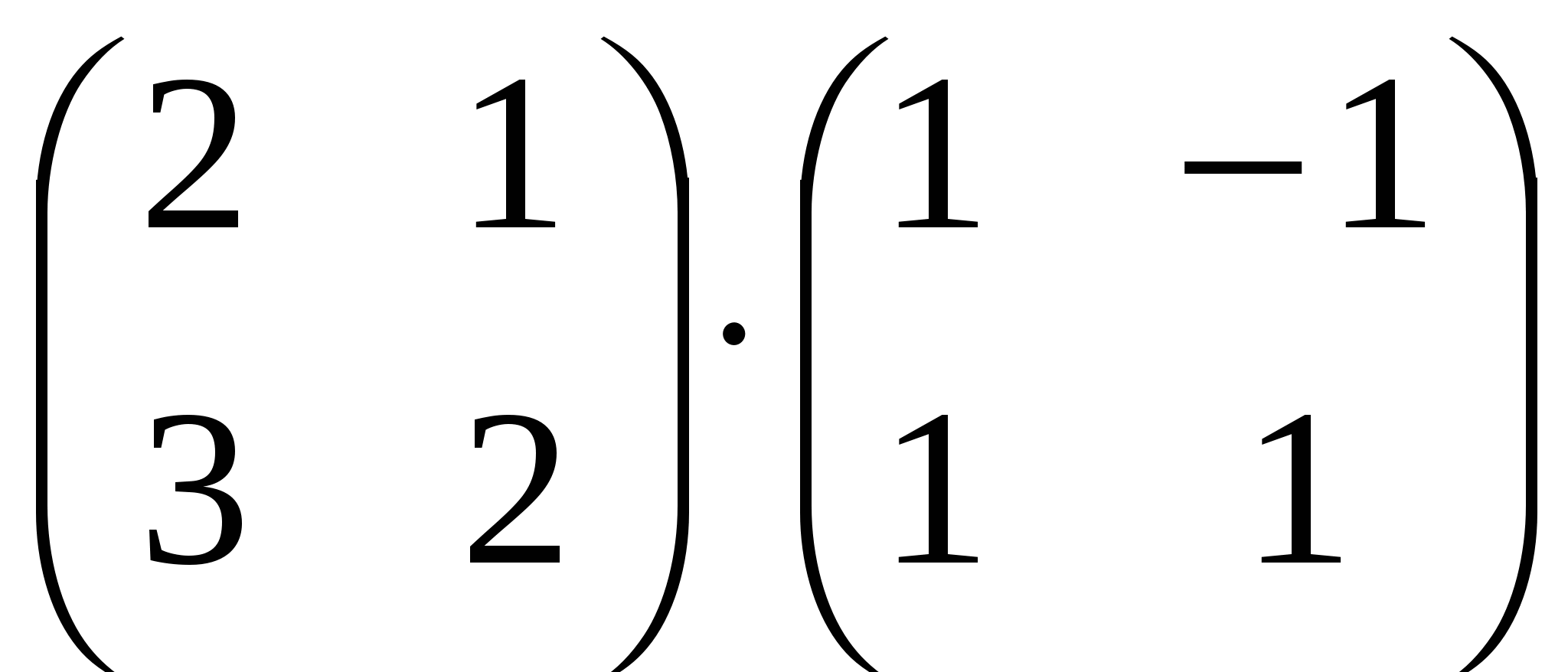 ; ;
А. 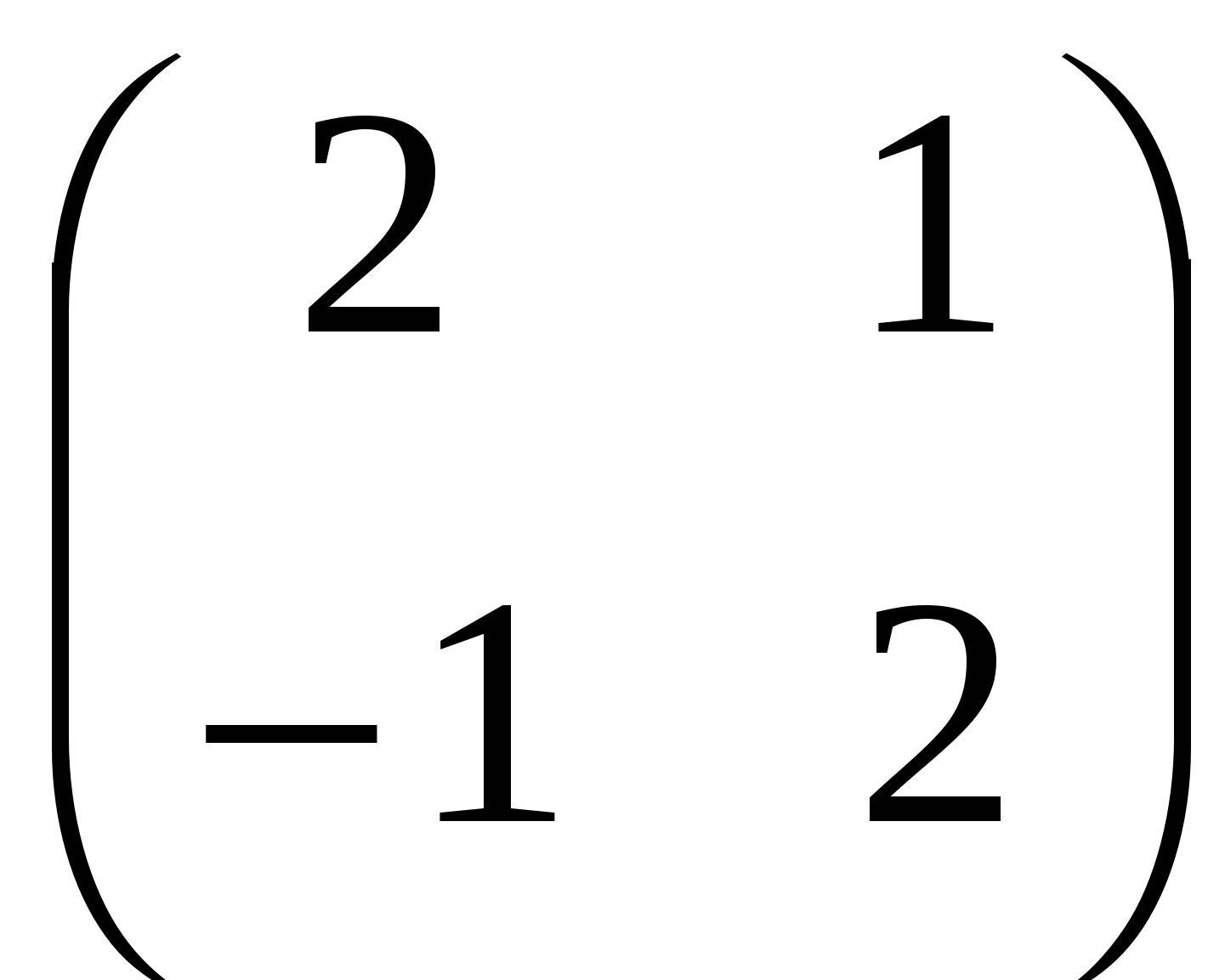 ; ;
Б. 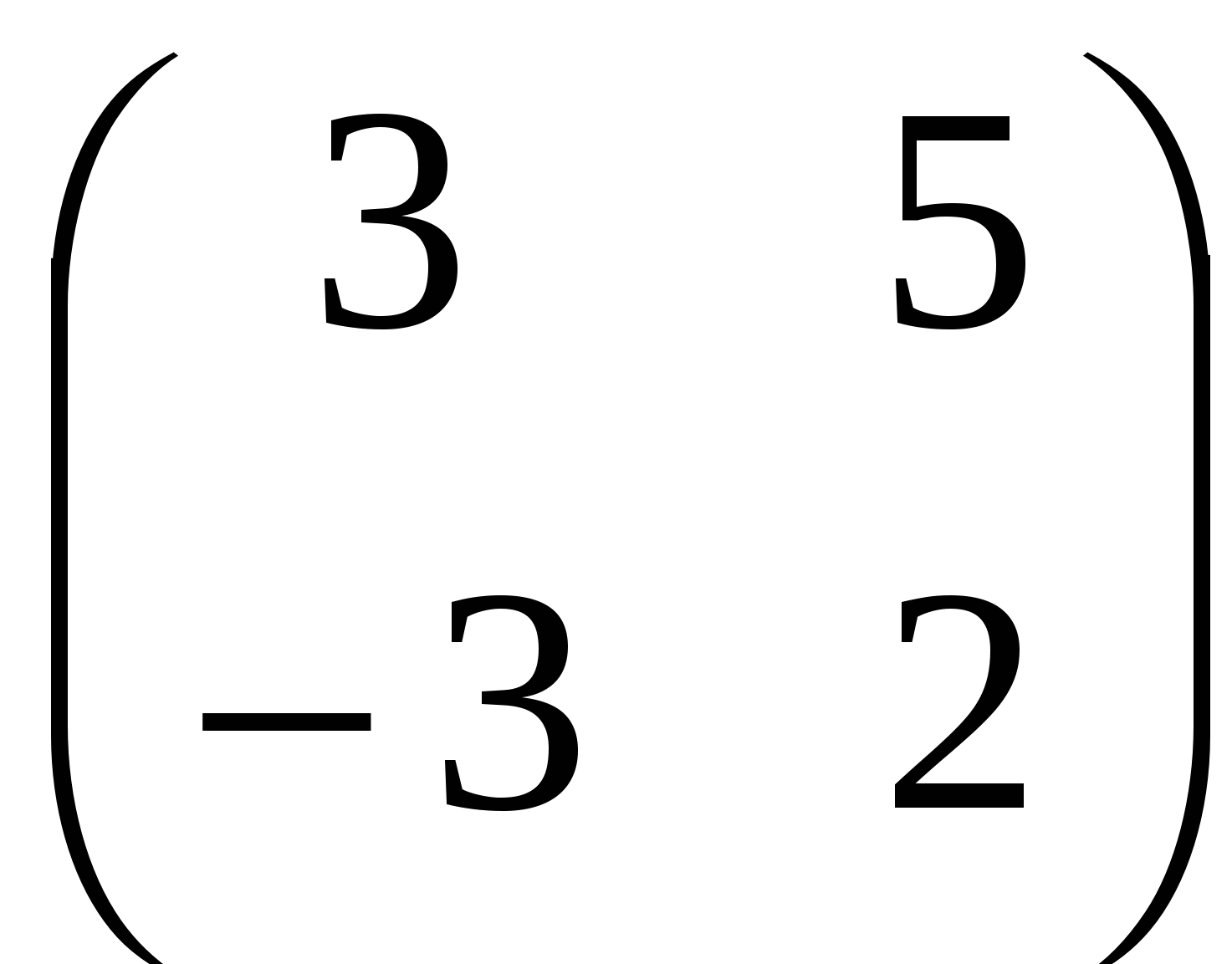 ; ;
В.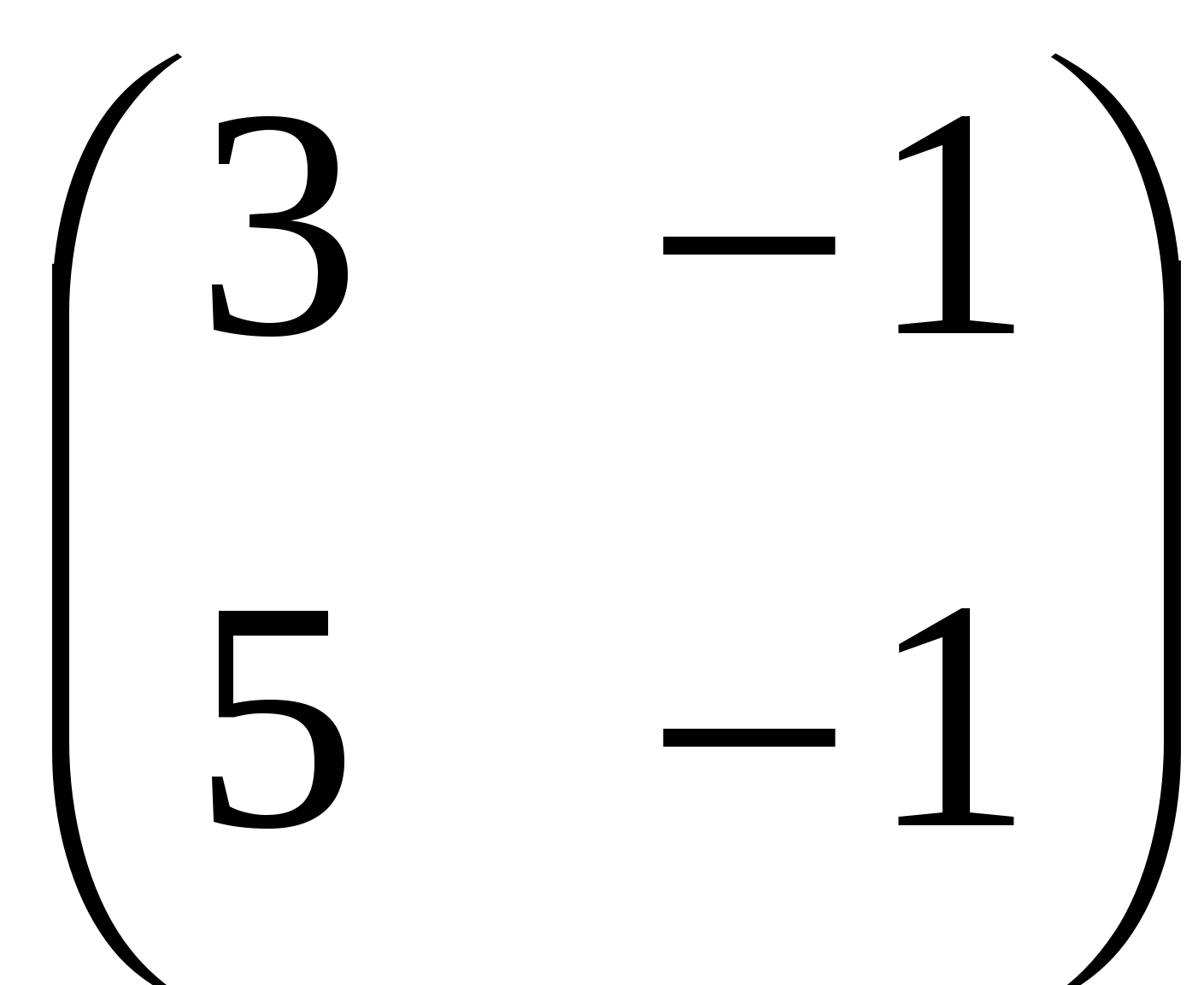 ; ;
С.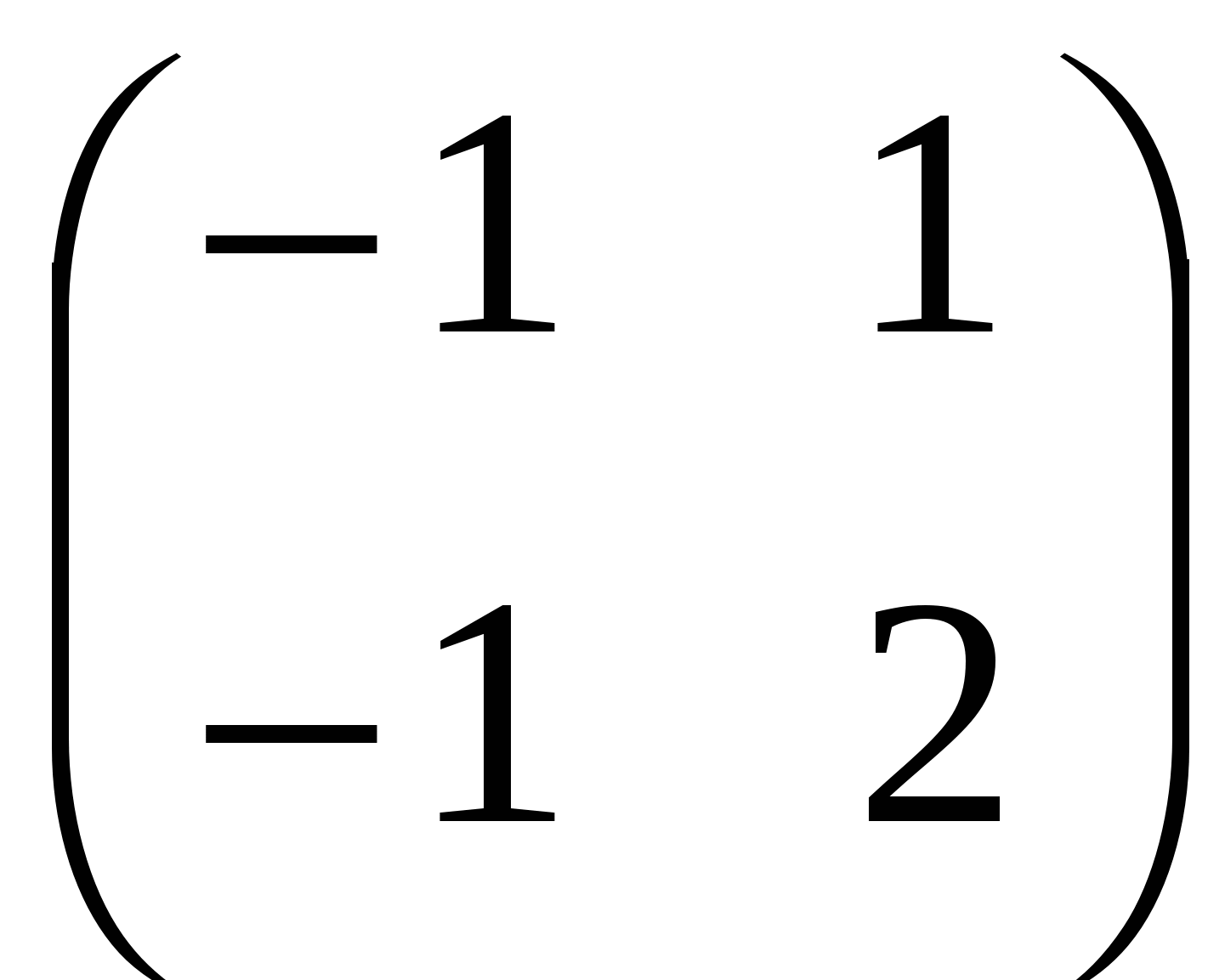 ; ;
D. 0.
2. Найдите произведение матриц: 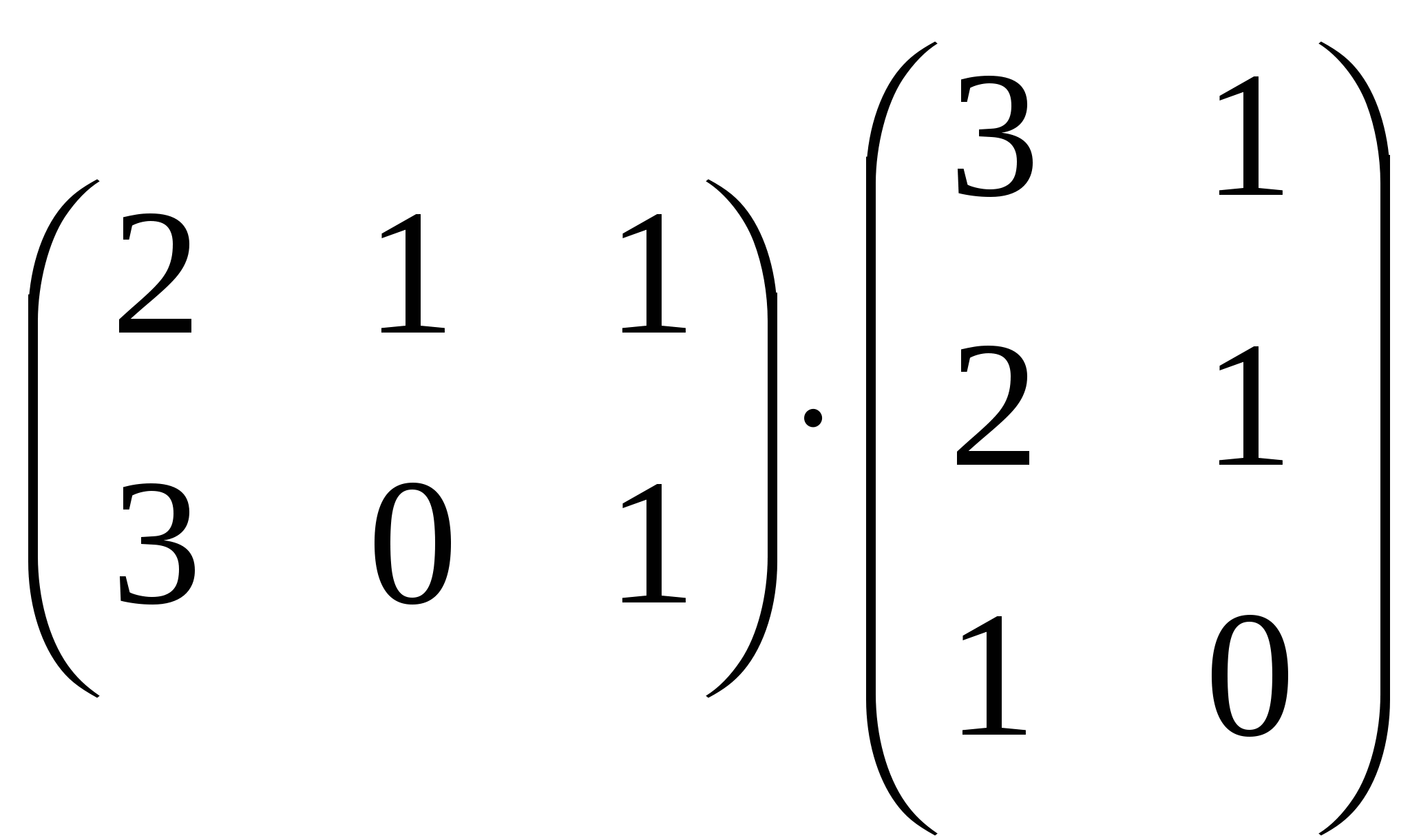 ; ;
А. 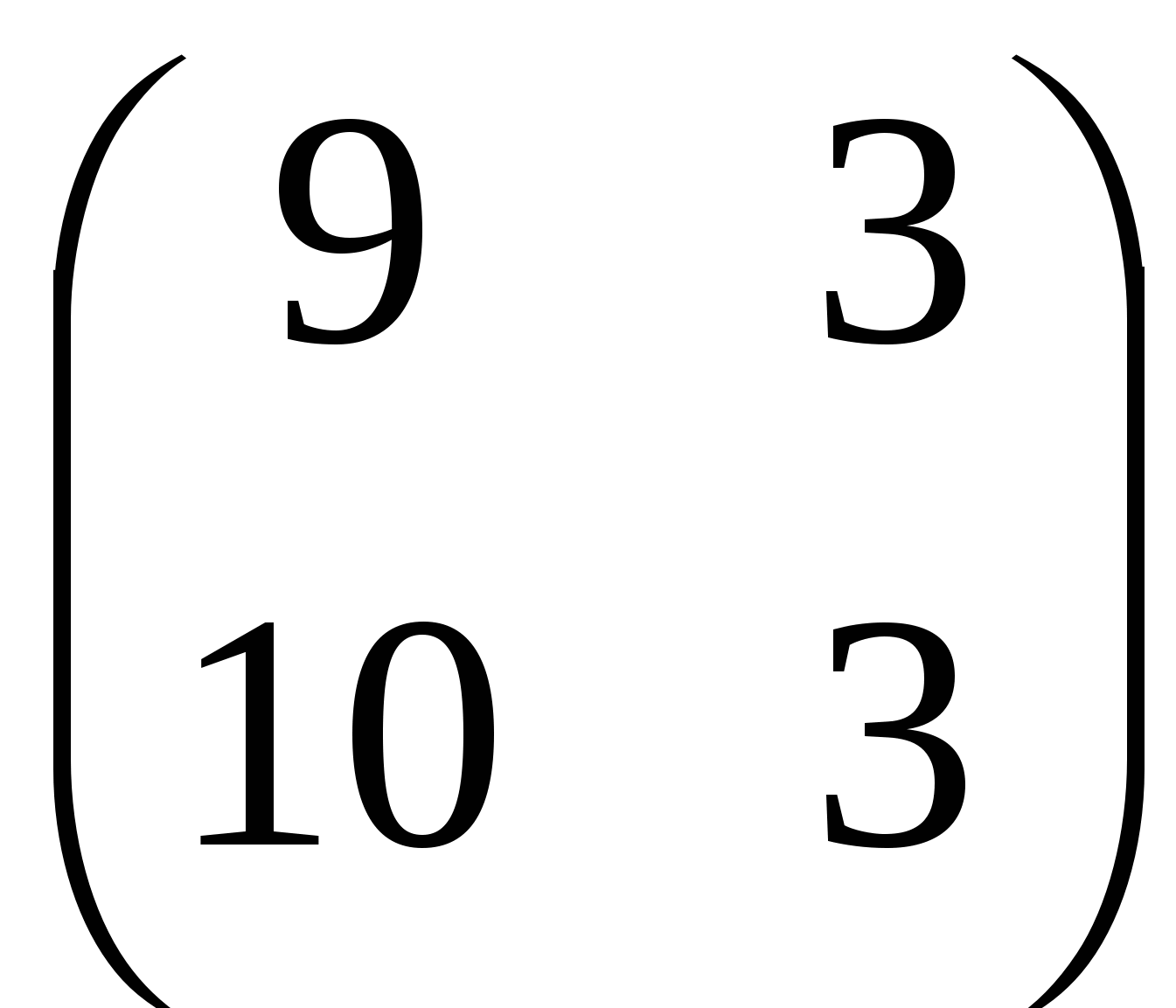 ; ;
Б. 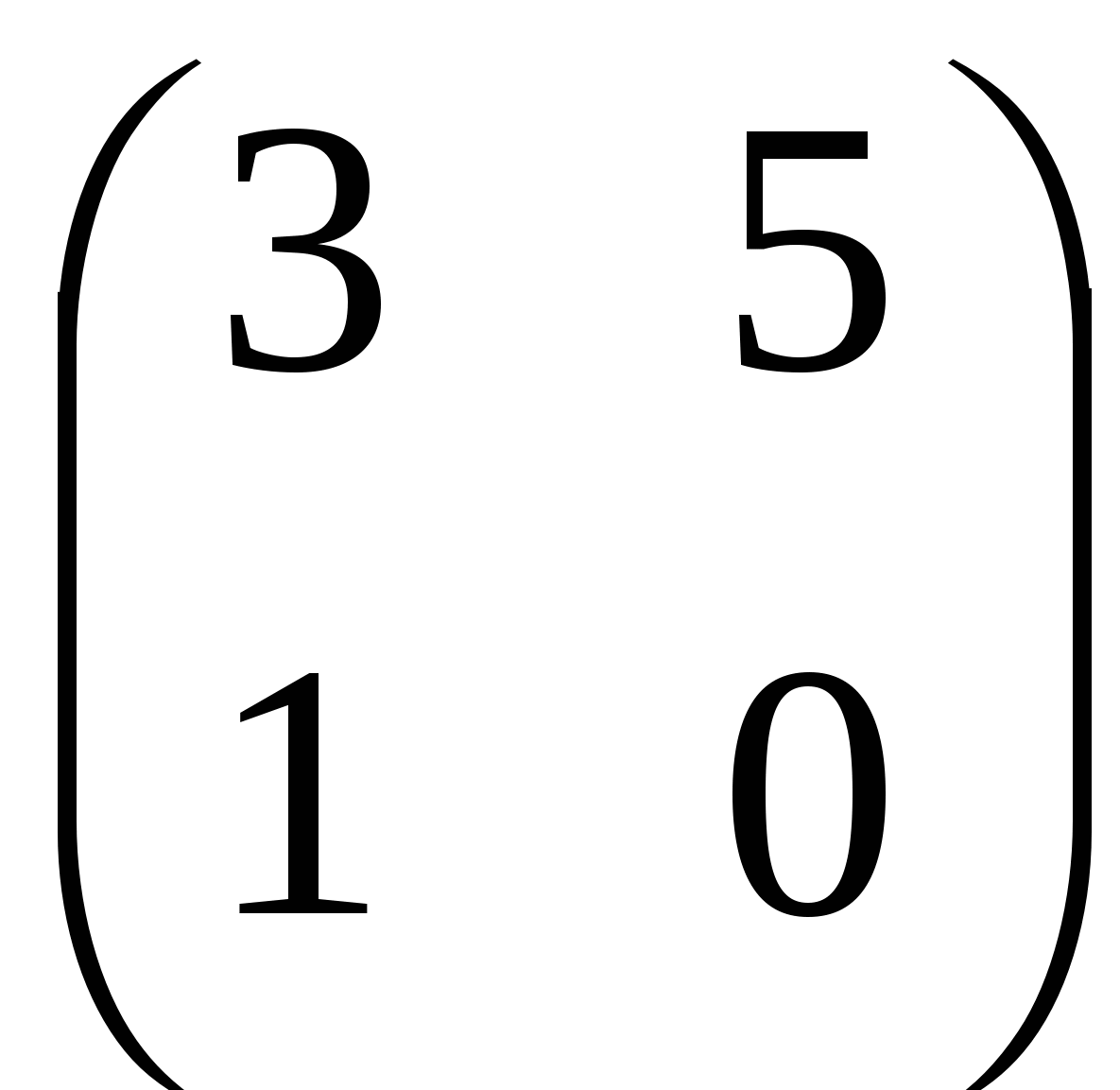 ; ;
В. ; ;
С. 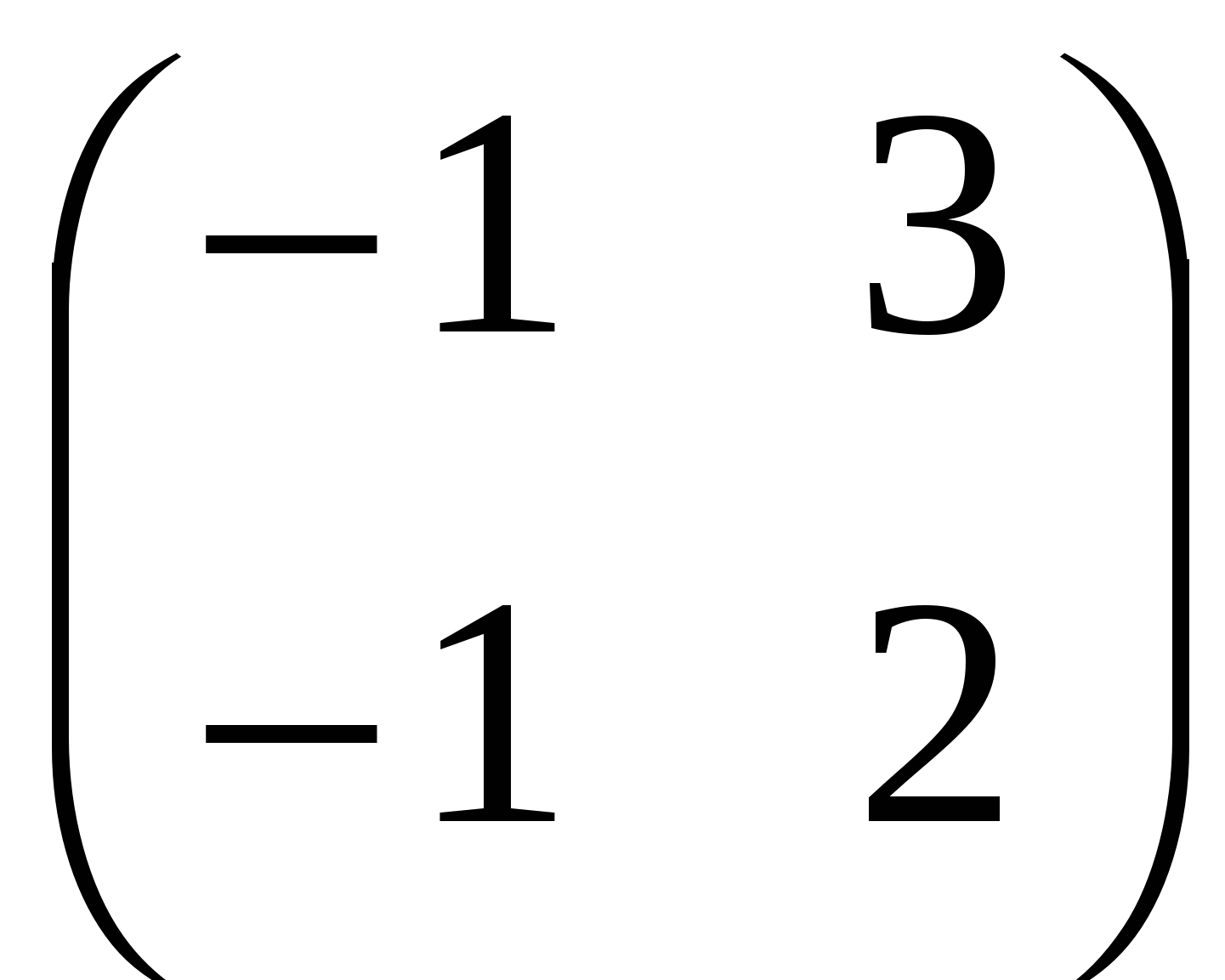 ; ;
D. 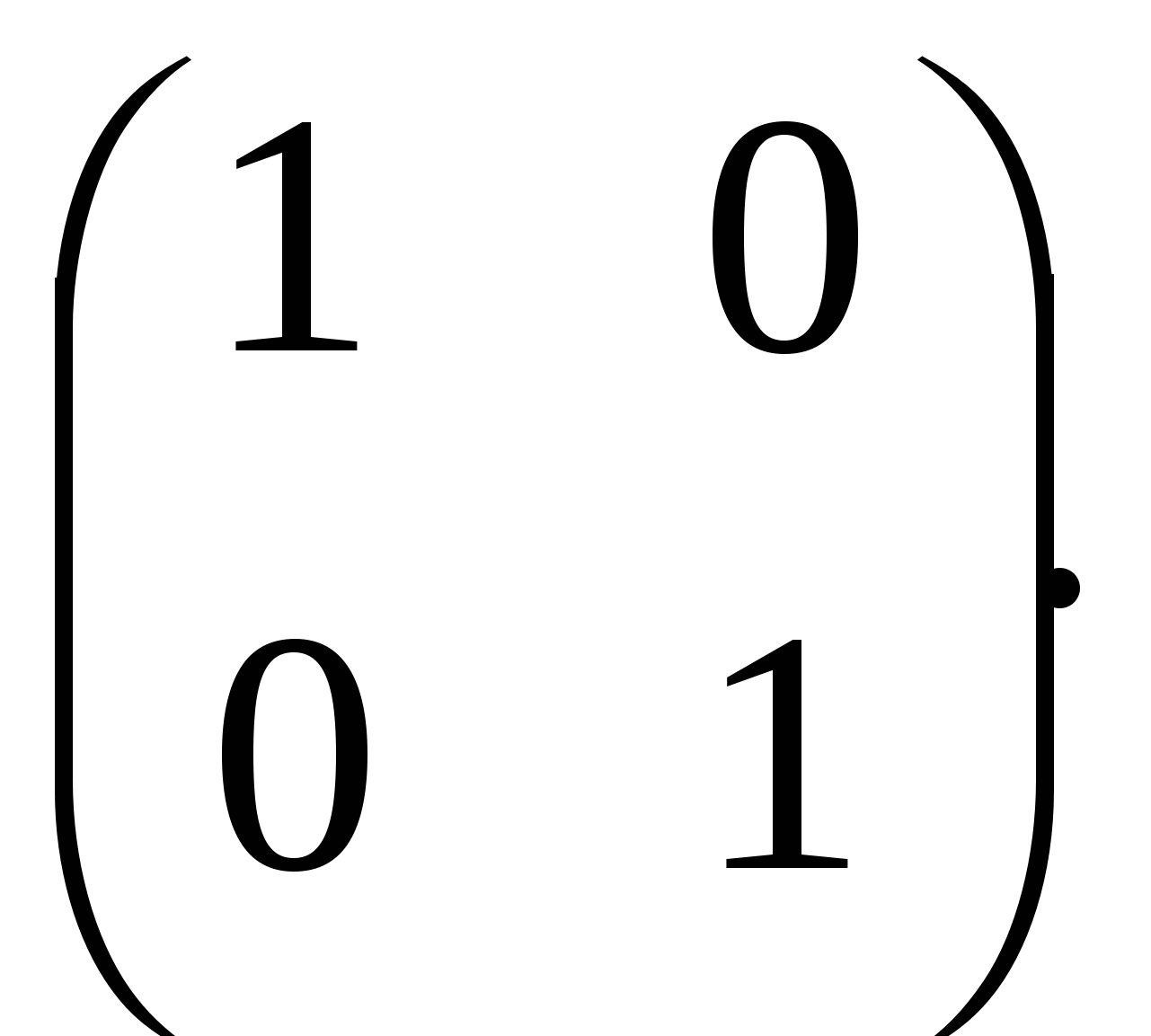 . .
3. Выполните действия:
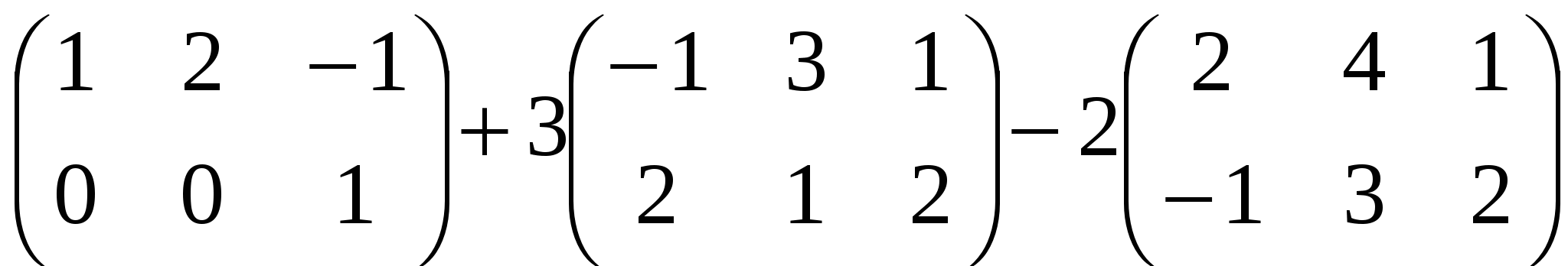
А. 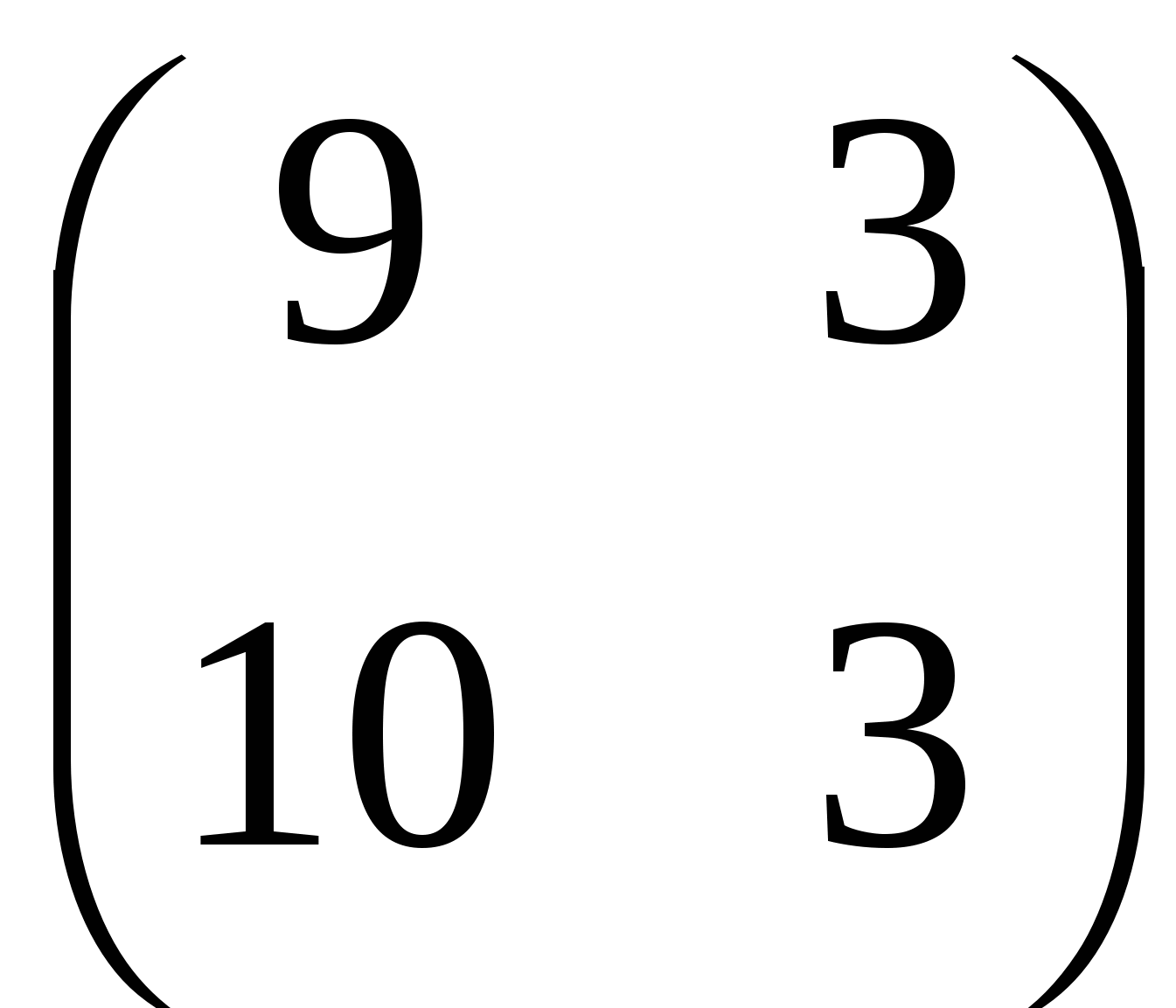 ; ;
Б. 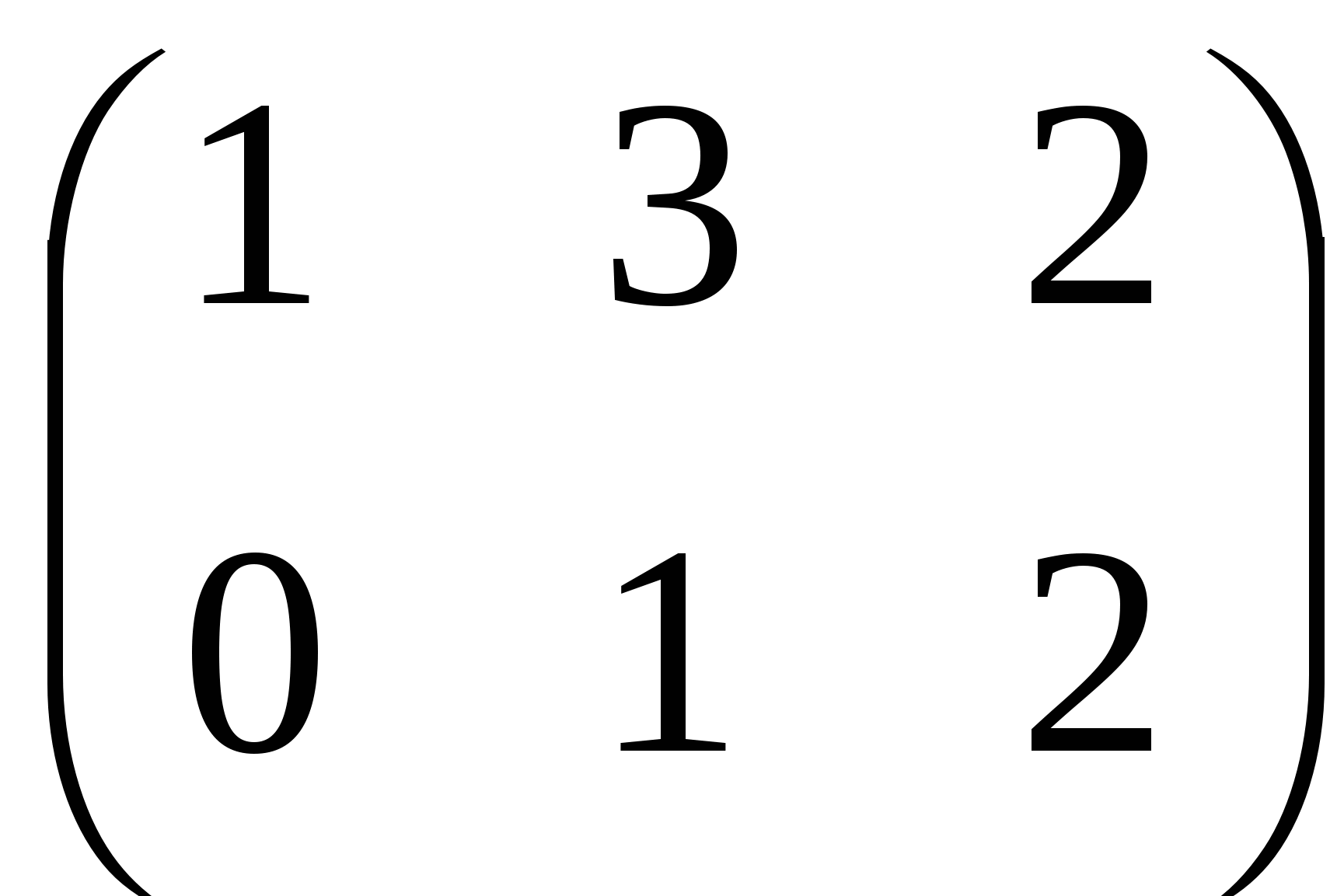 ; ;
В. ; ;
С. 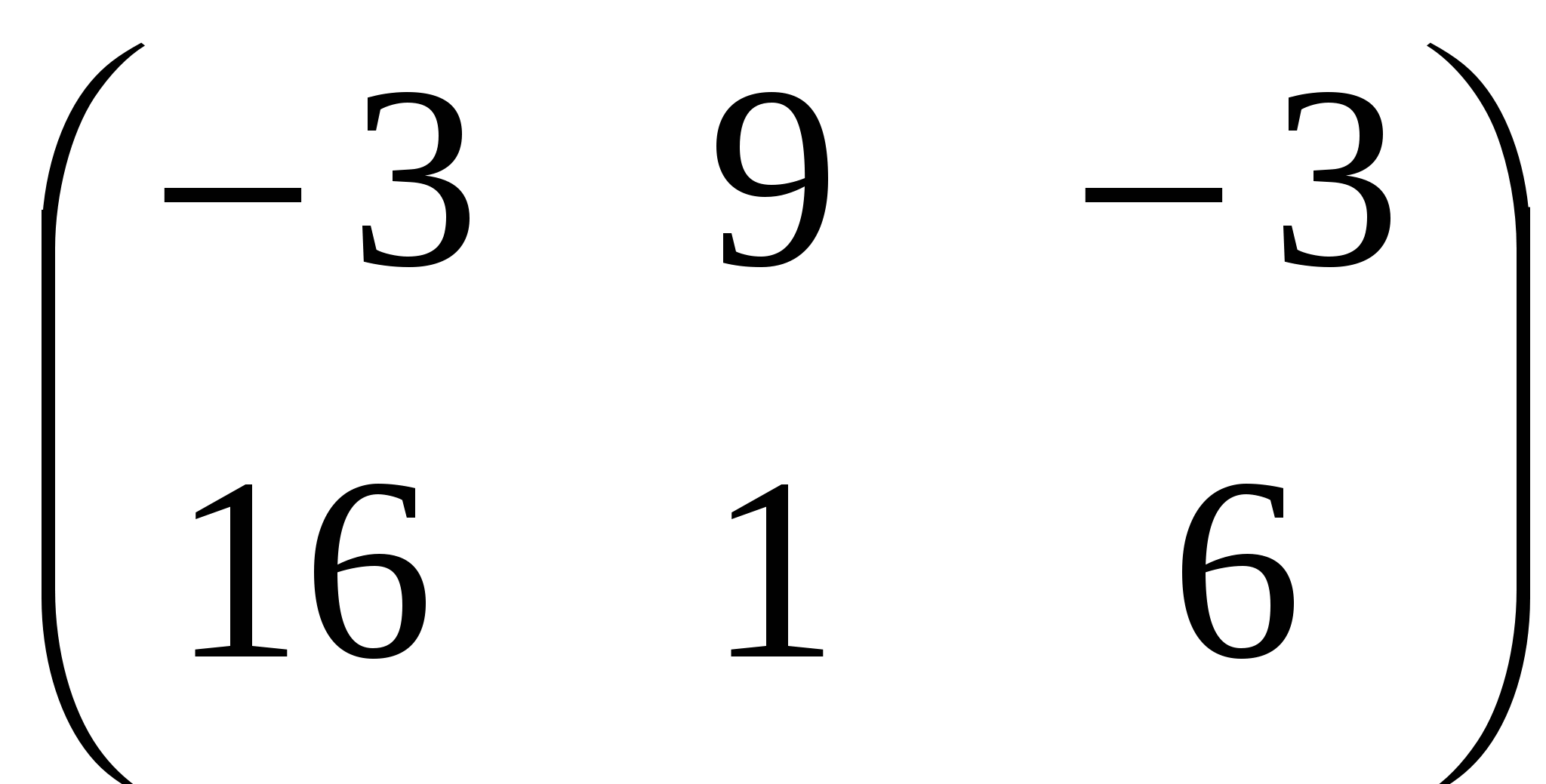 ; ;
D. 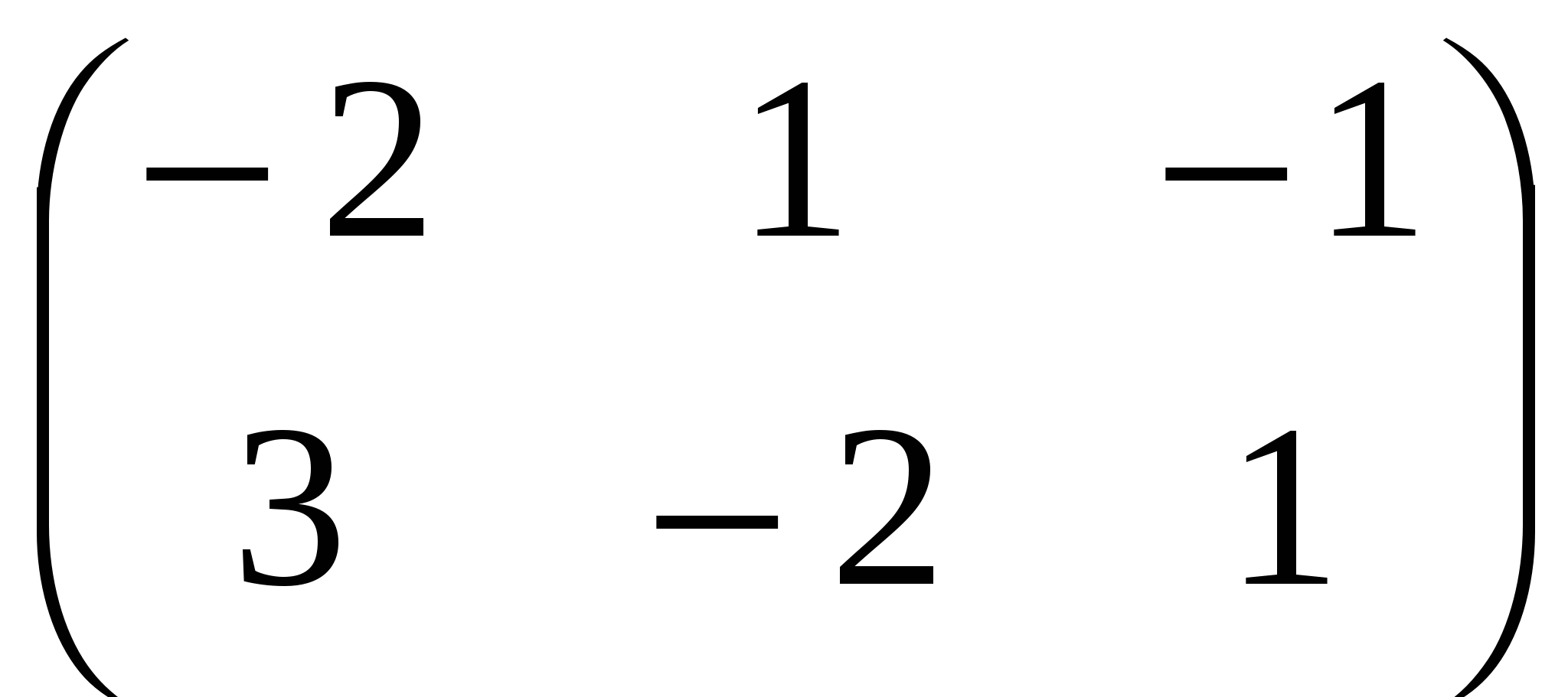 . .
4. Выполните действия : 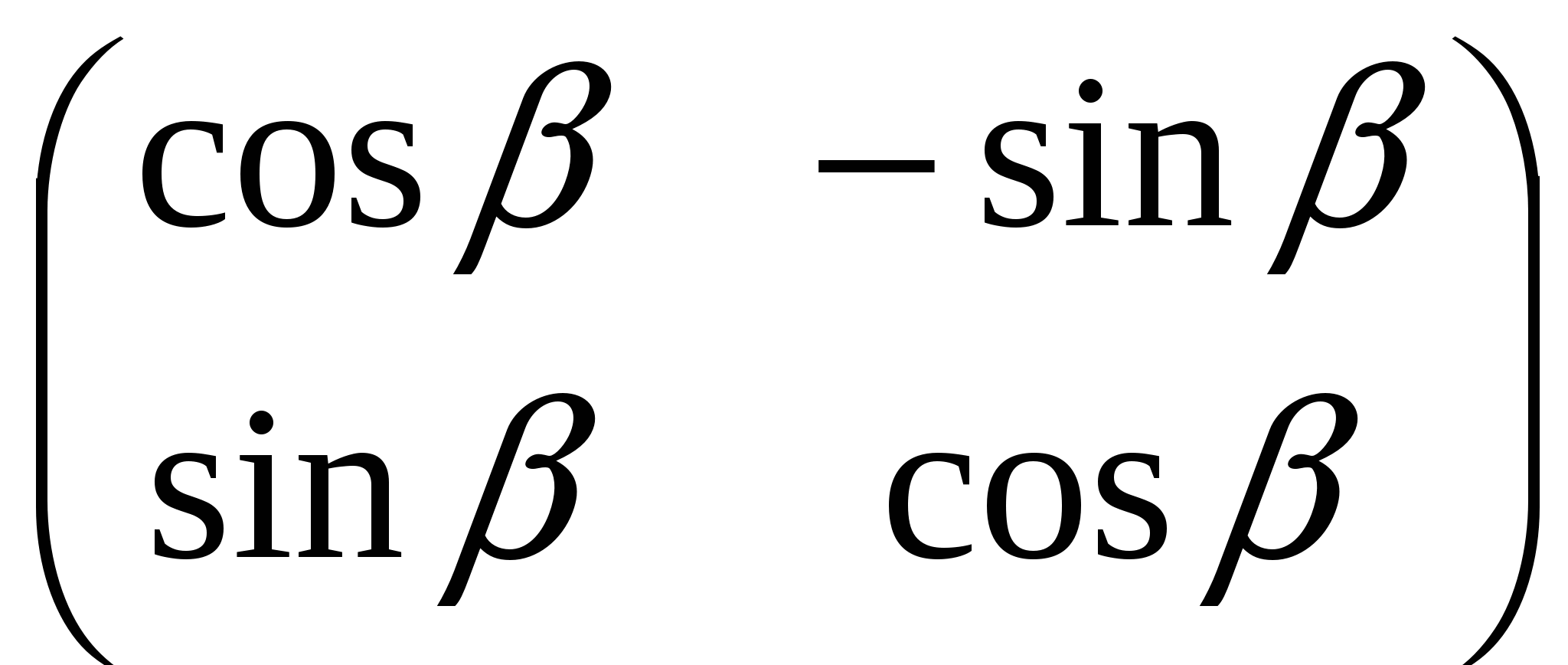 ; ;
А. 1.
Б. 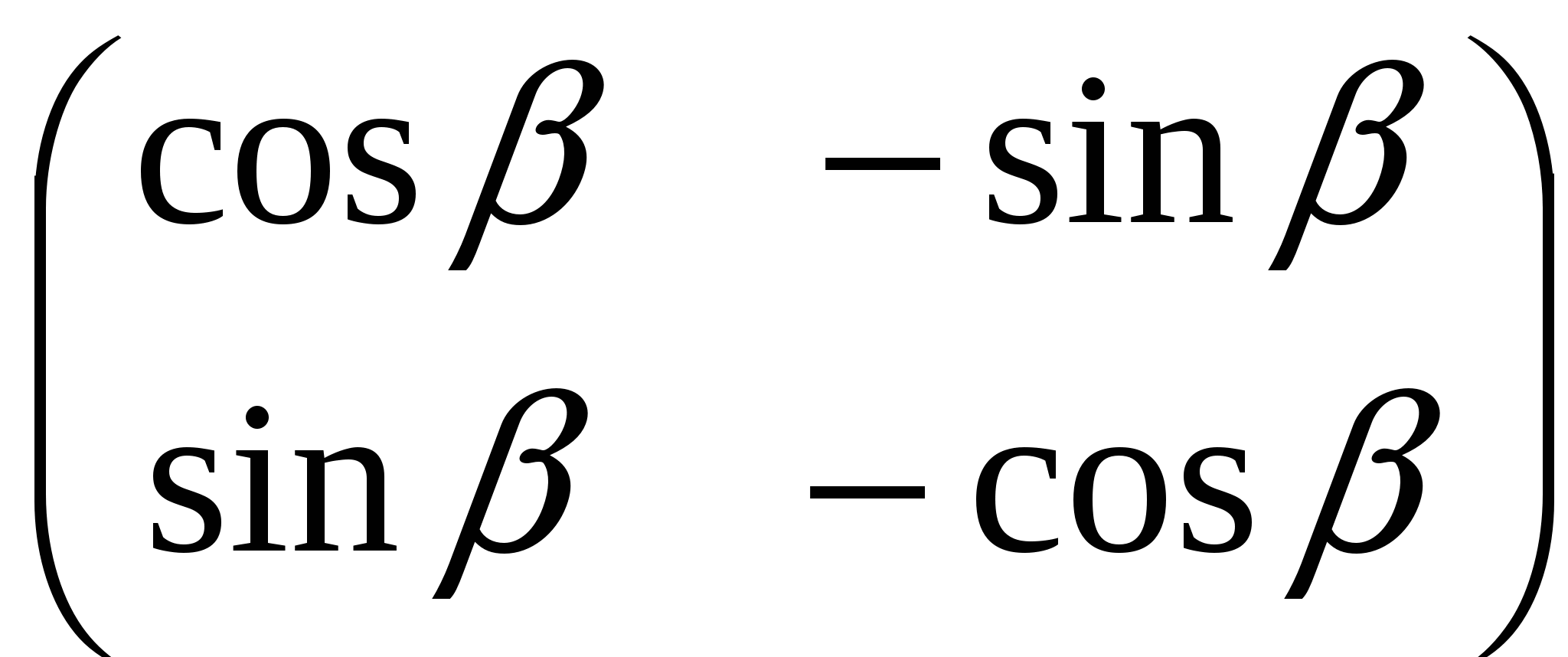 ; ;
В. 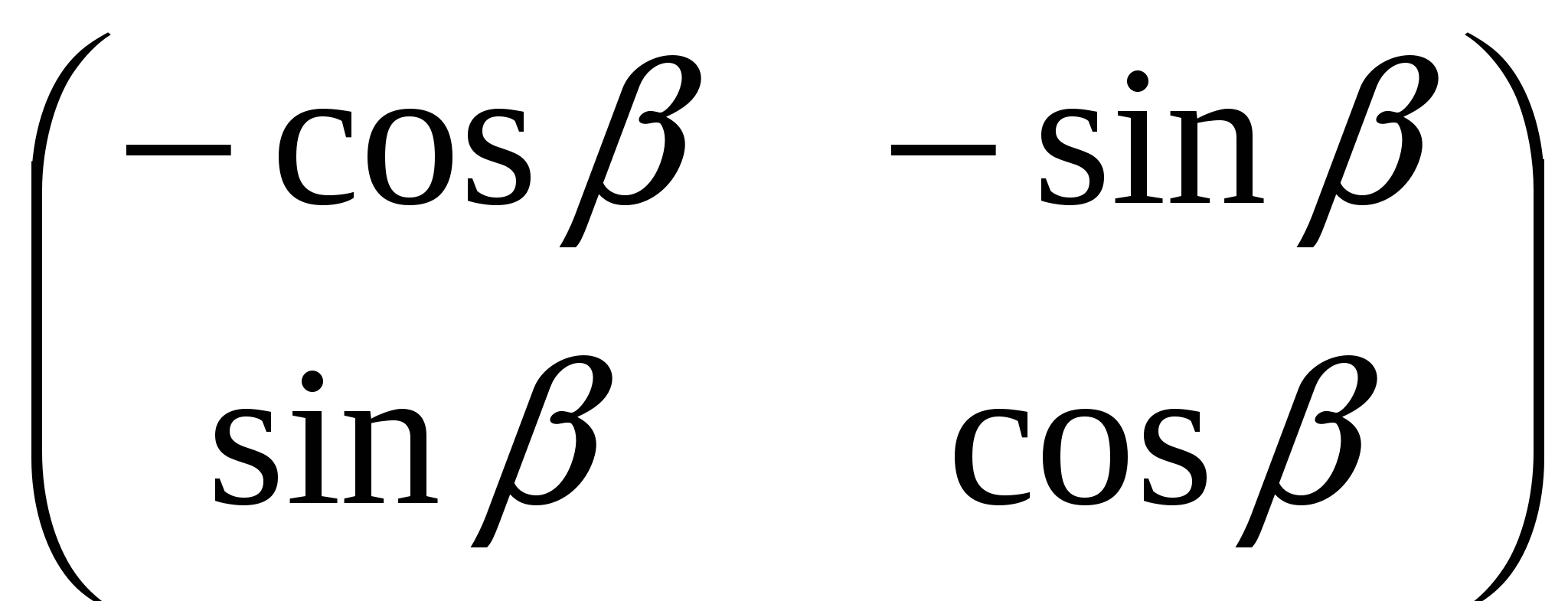 ; ;
С.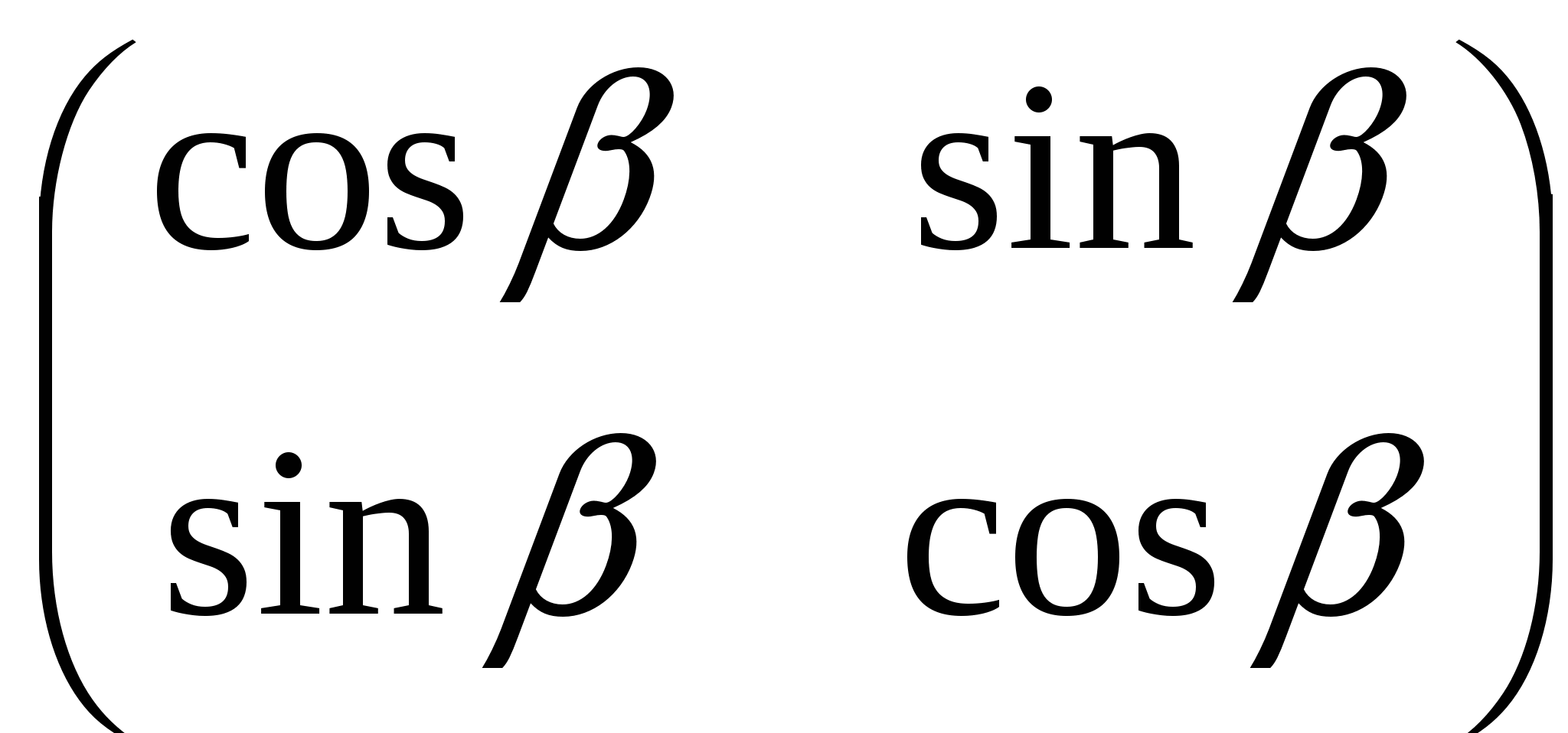 ; ;
D. 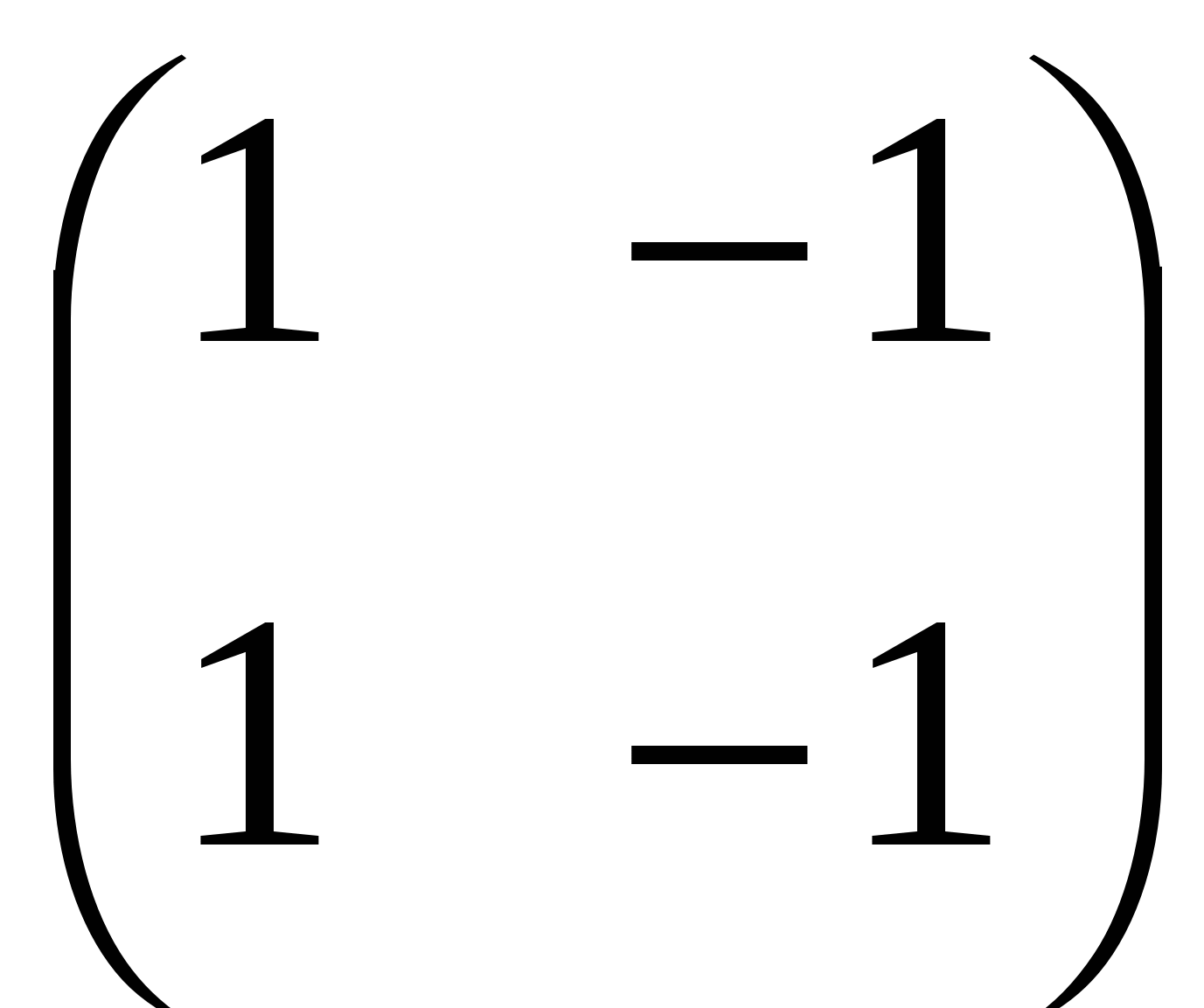 . .
5. Выполните действия: 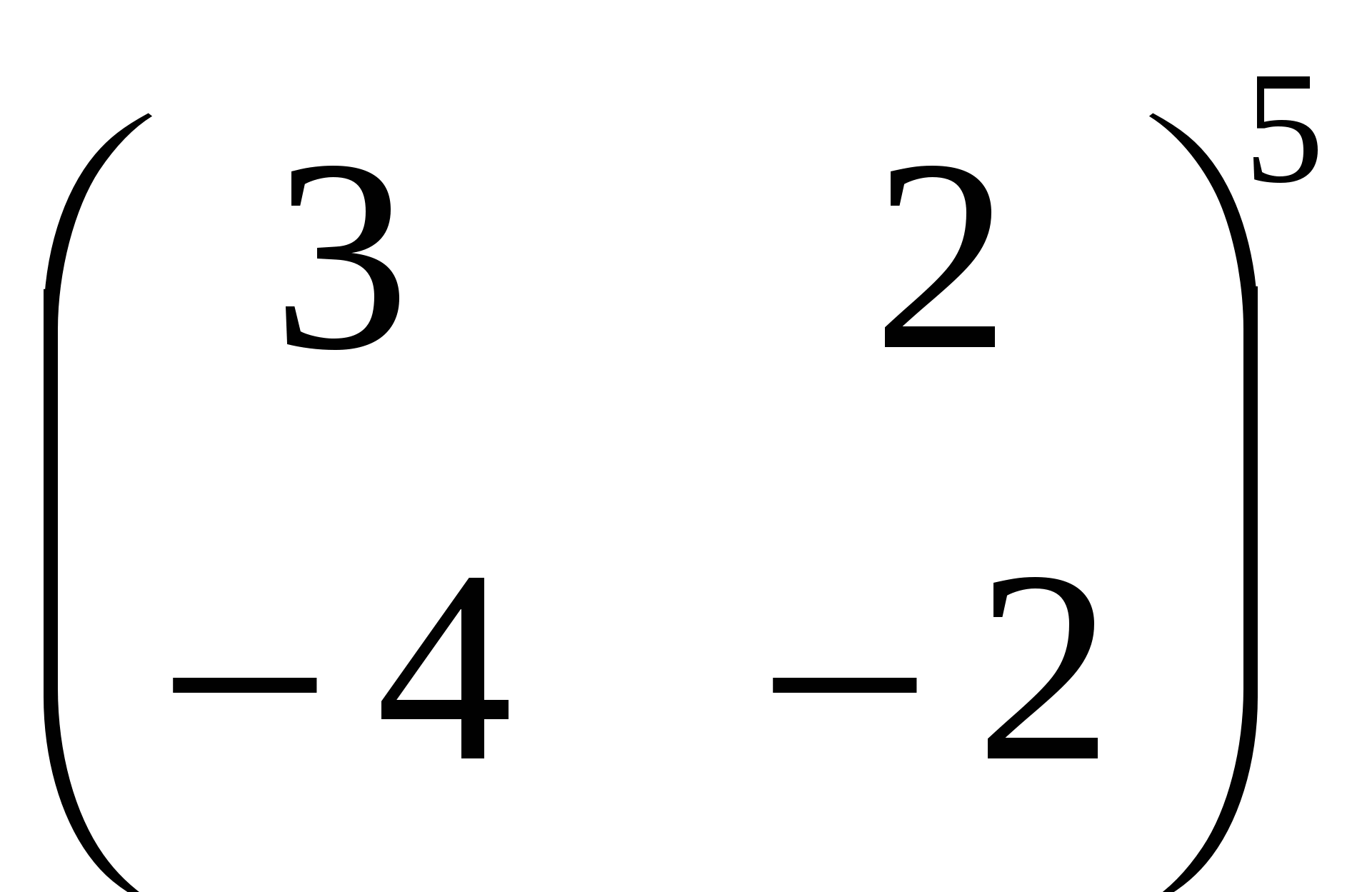 ; ;
А. 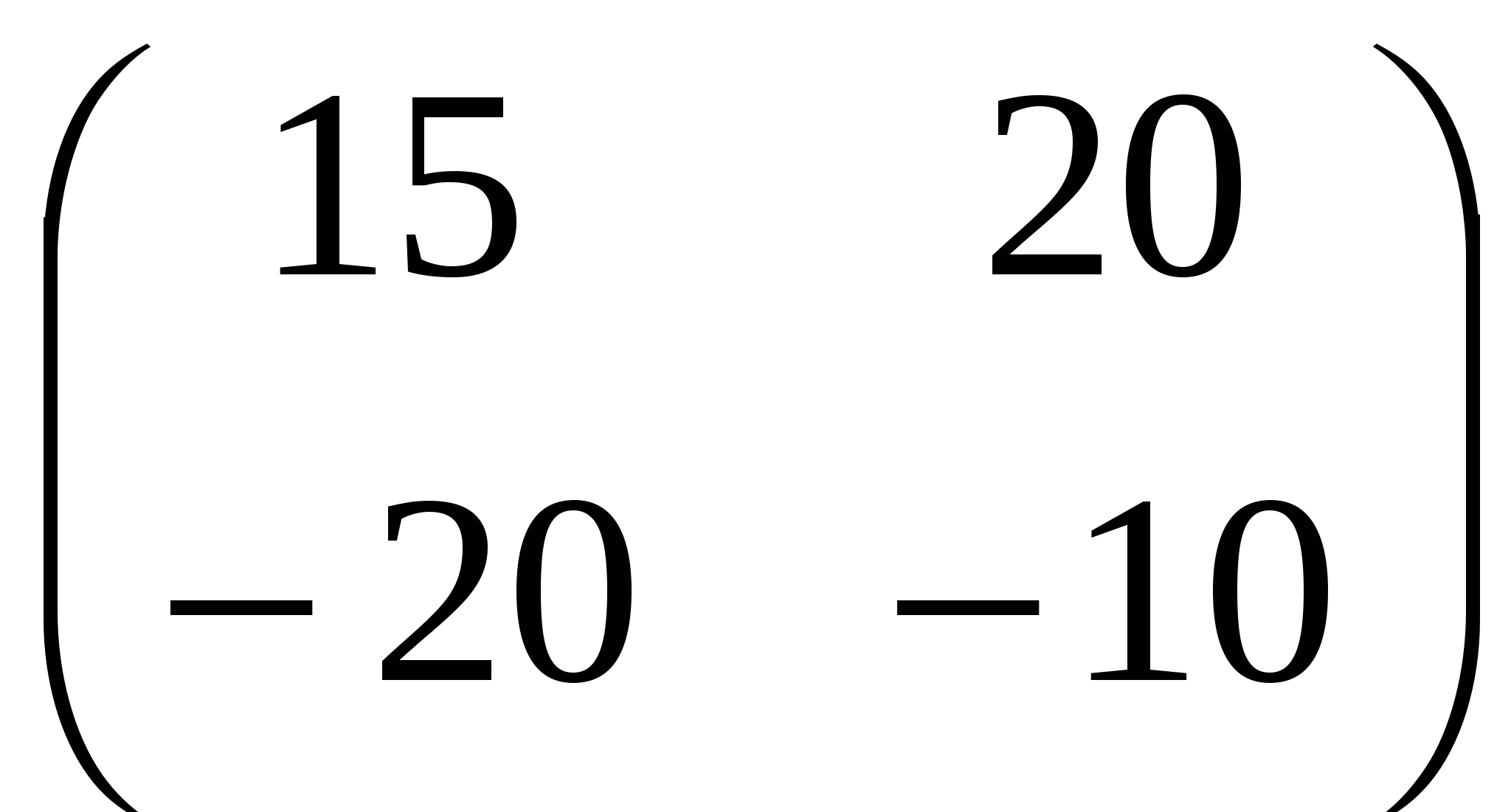 ; ;
Б. 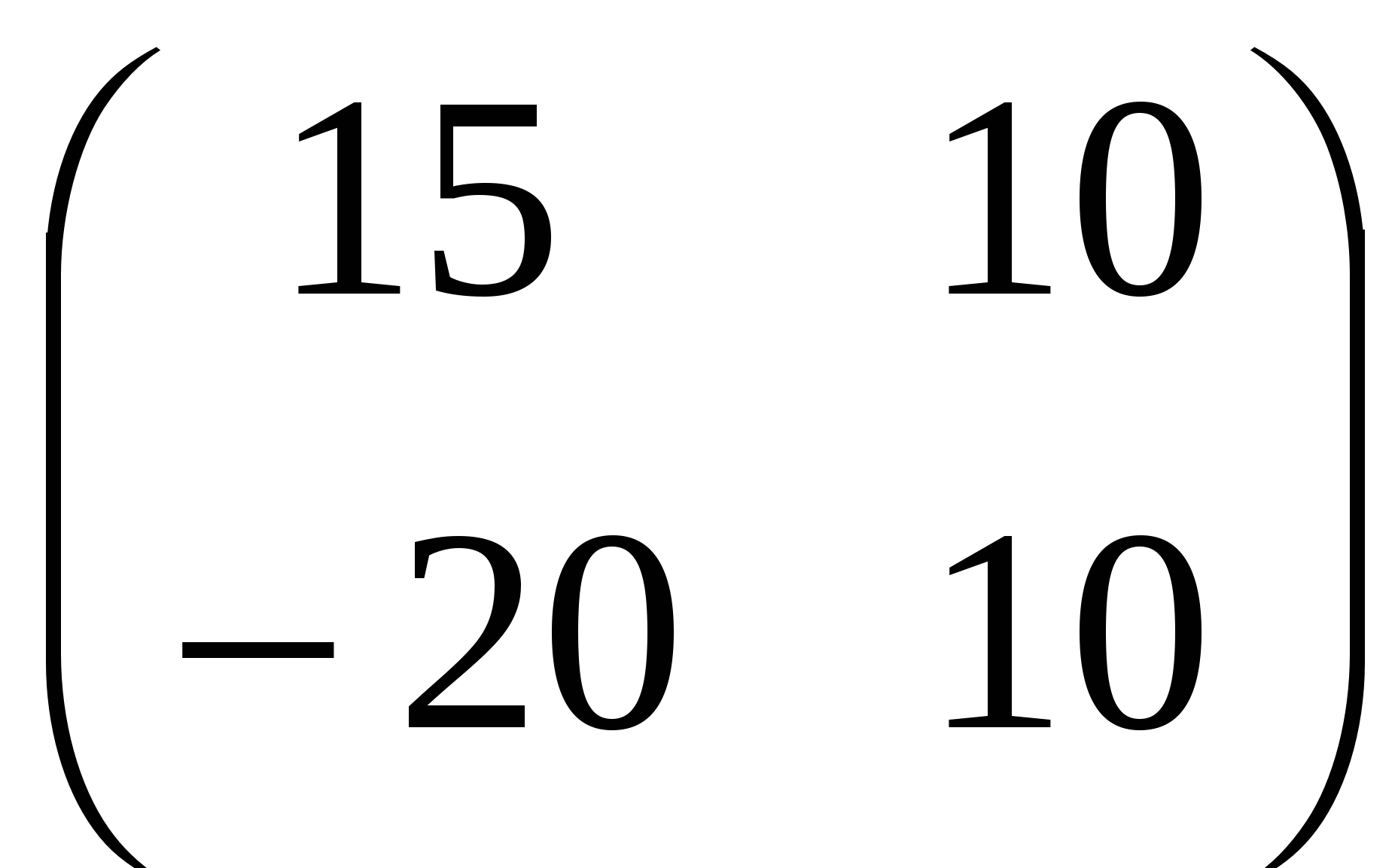 ; ;
В. ; ;
С. 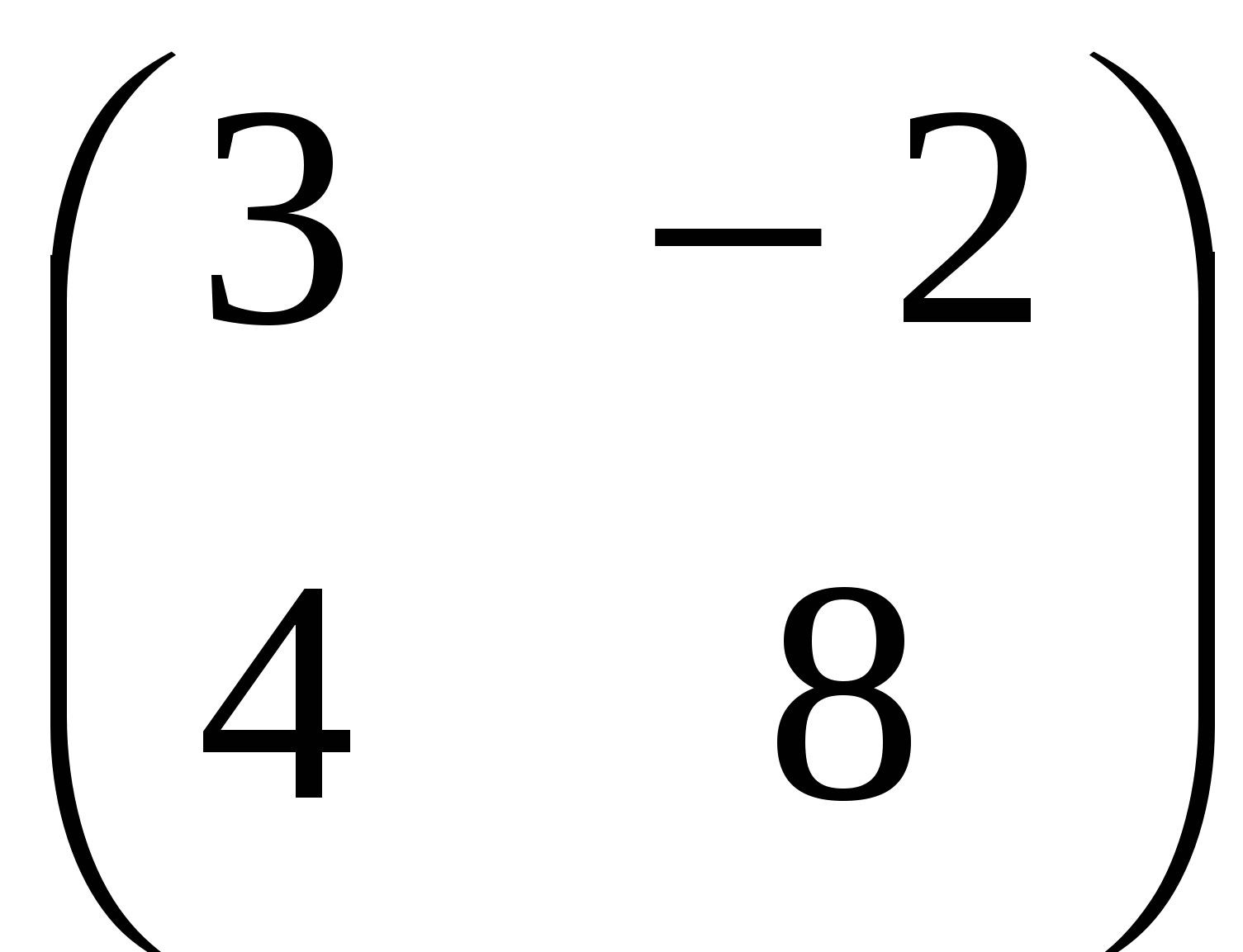 ; ;
D. 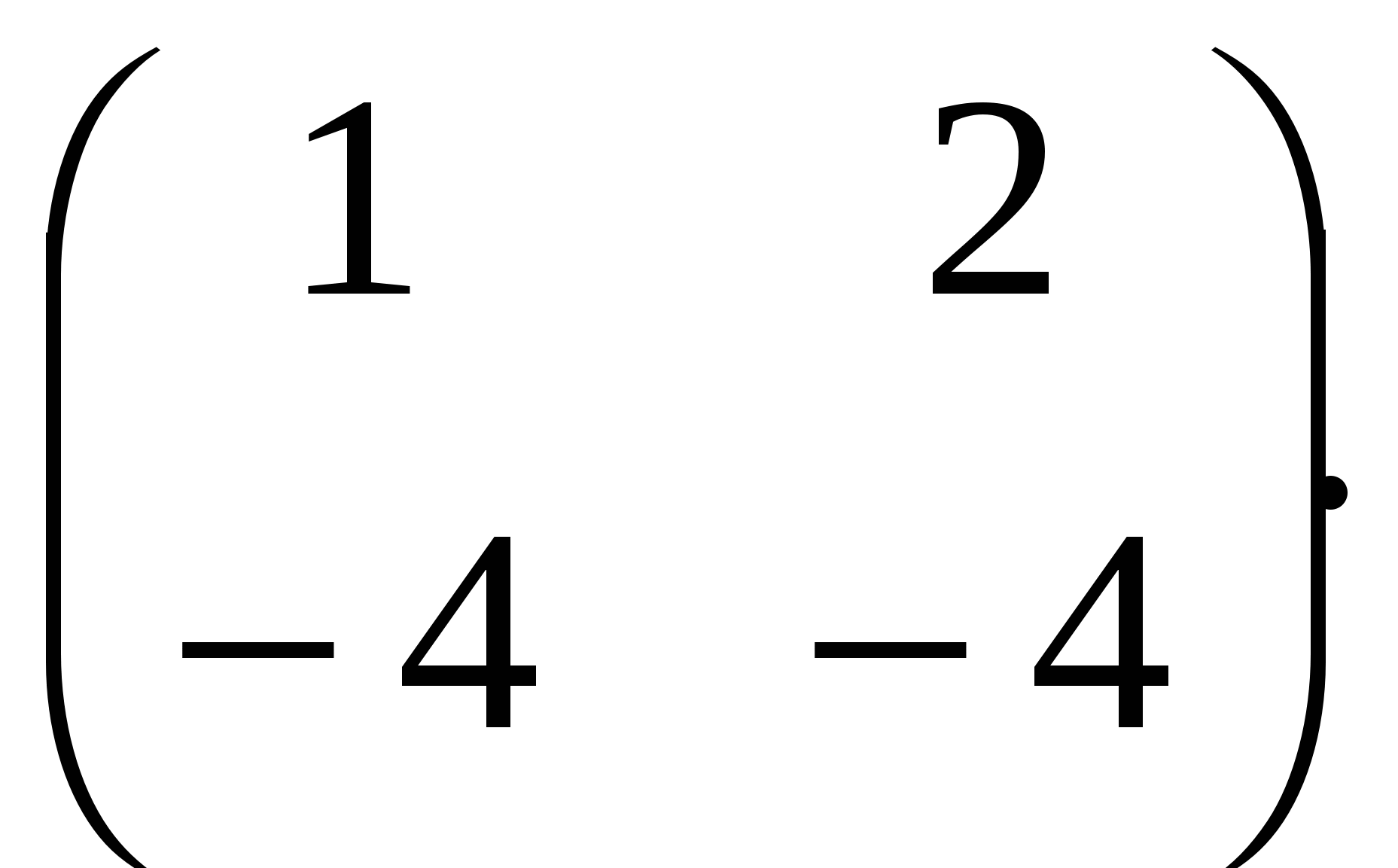
6. Вычислите, если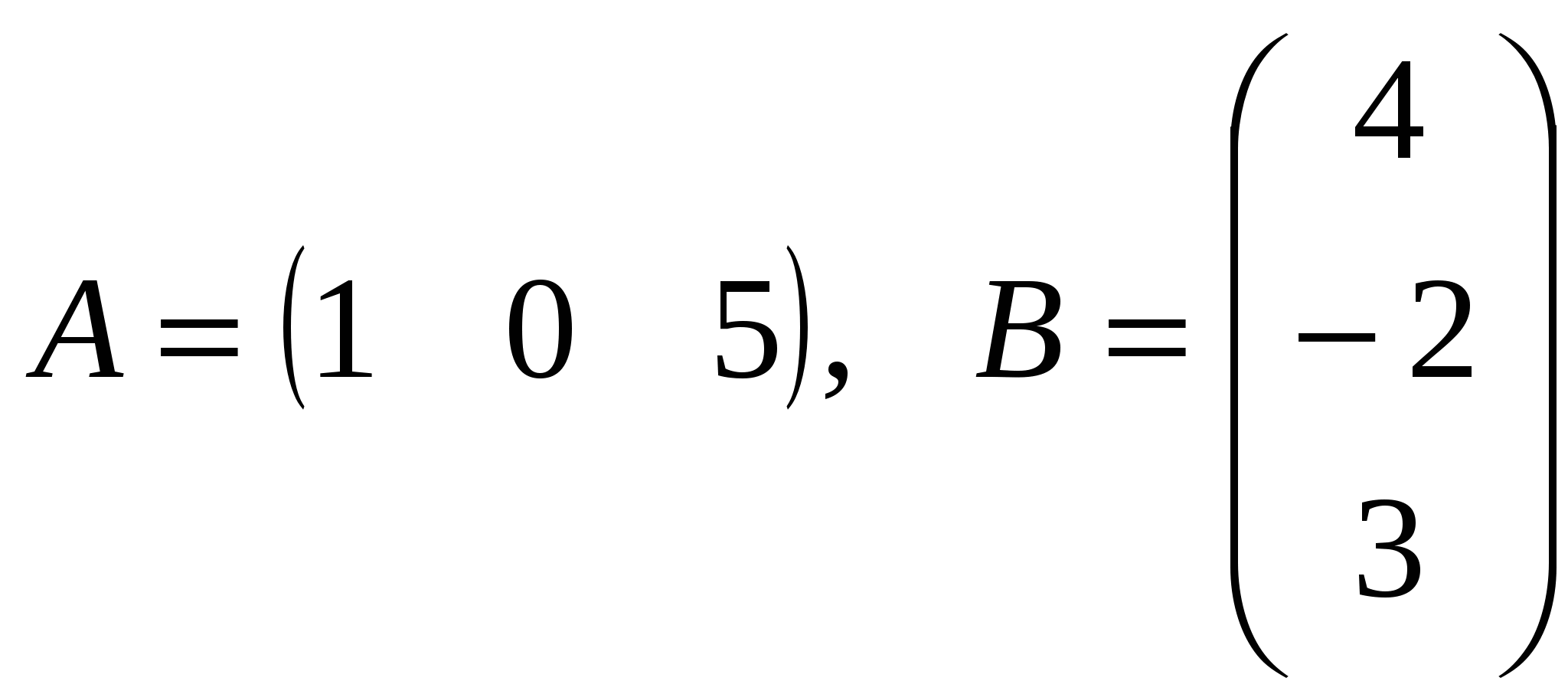 и и
существует 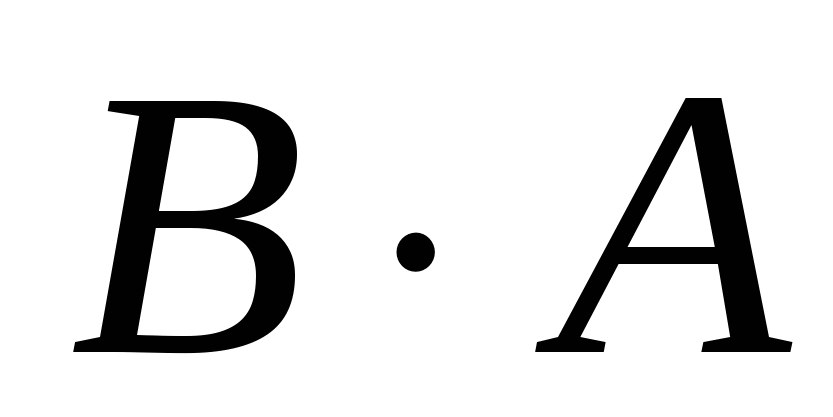 . .
А.Е;
Б.(1);
В. 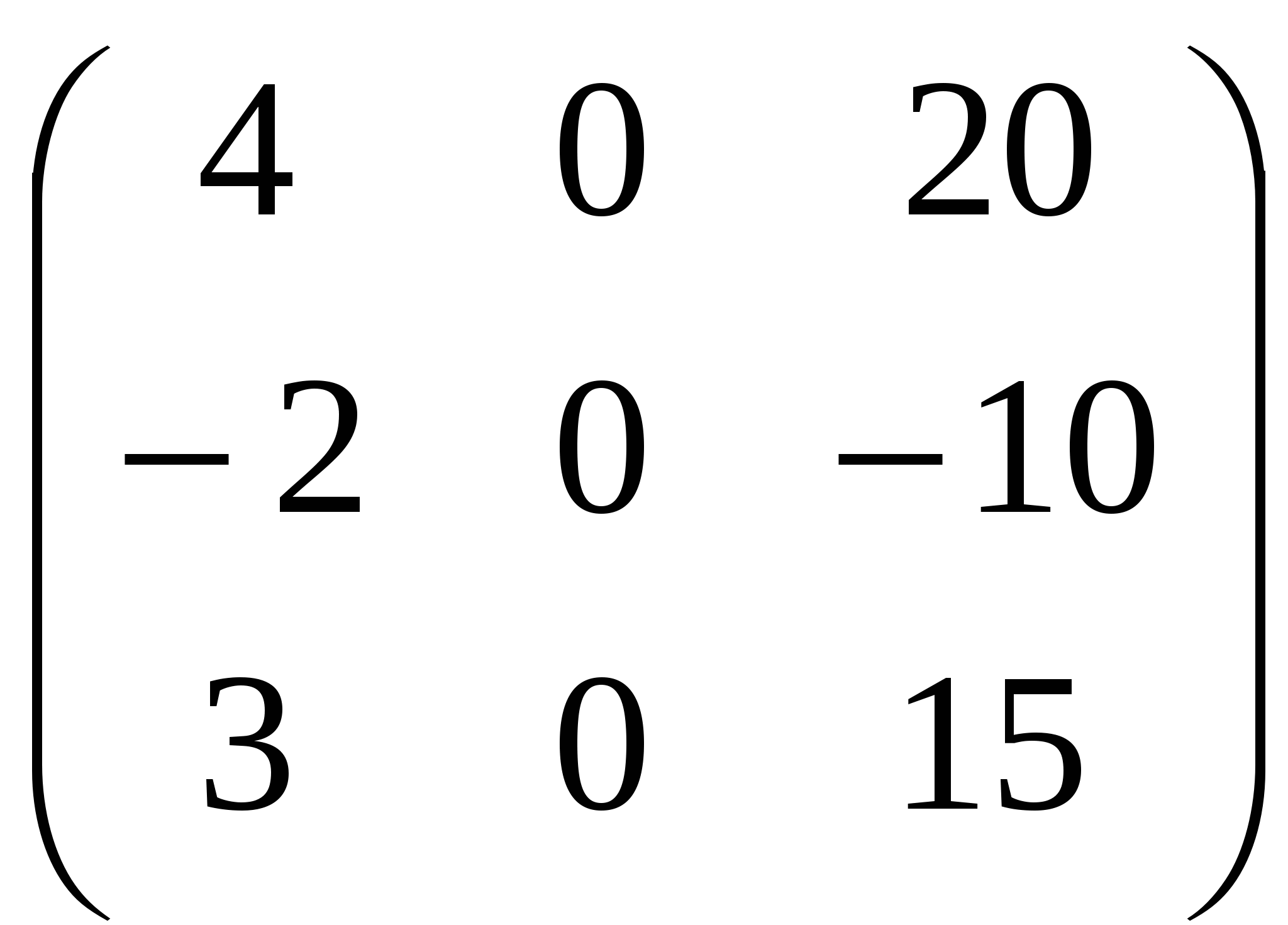 ; ;
С. 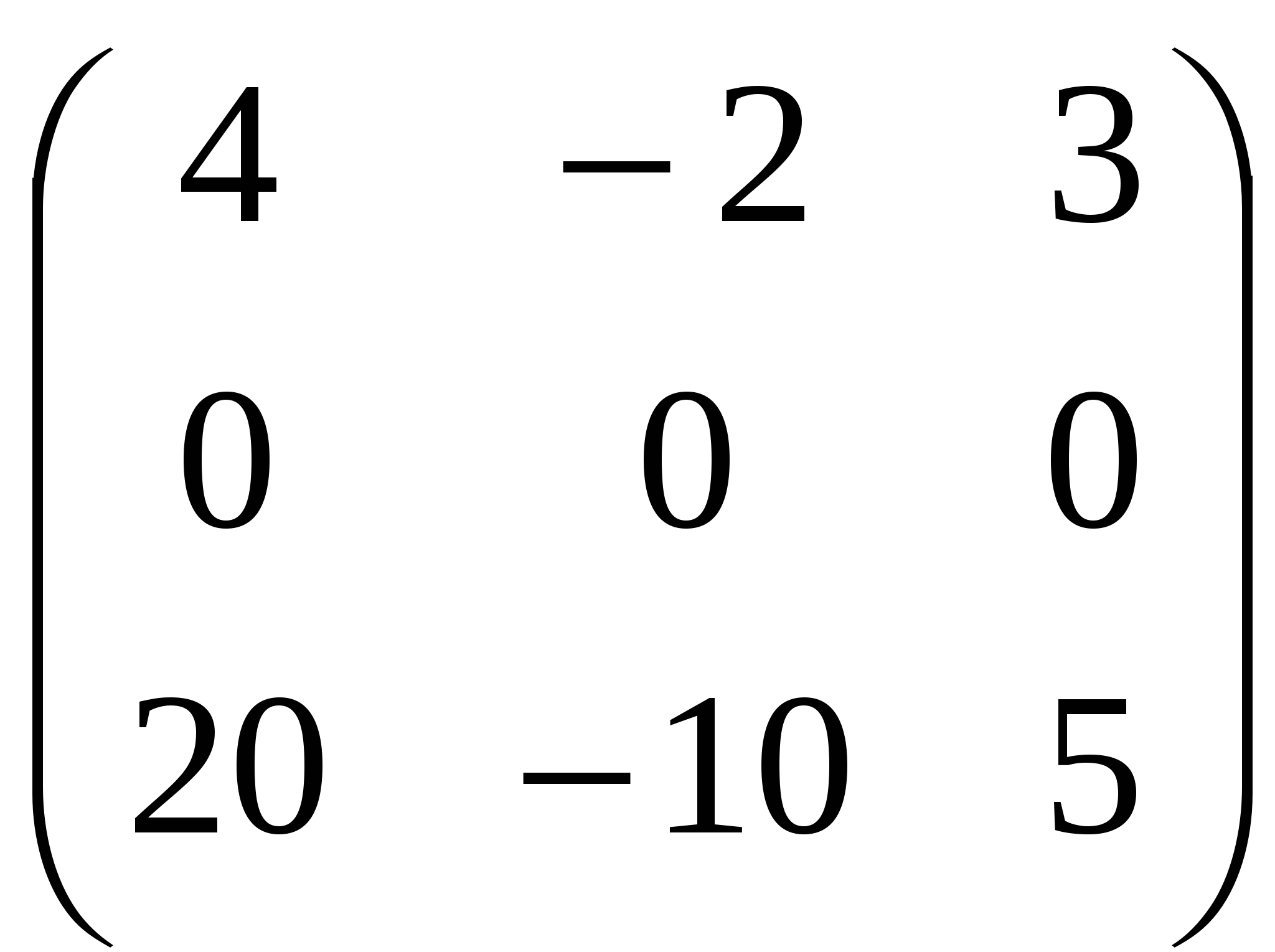 ; ;
D. (19).
7. Вычислите определитель: 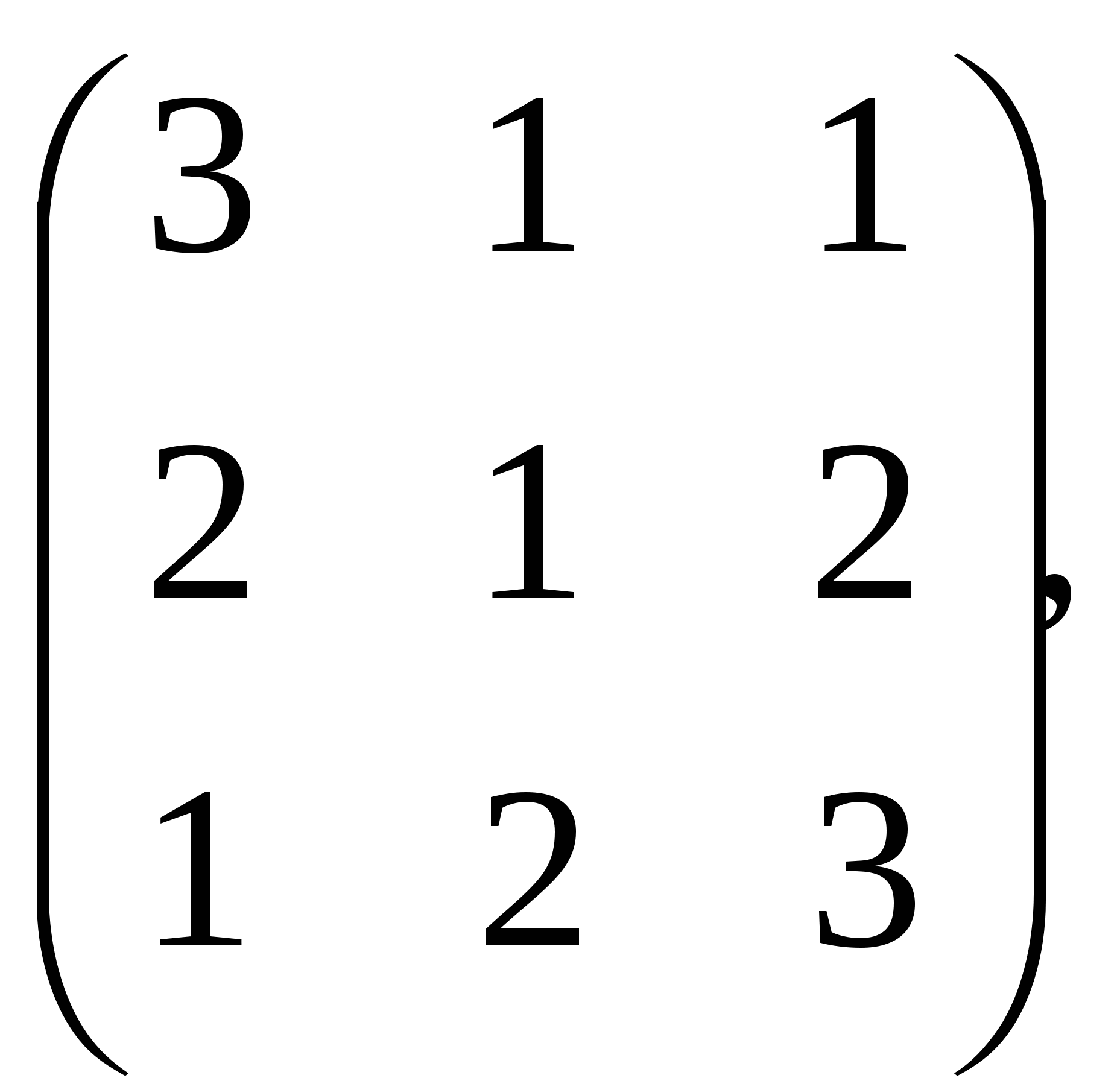
А. -4;
Б. 1;
В. 1,5;
С. 2;
D. -5.
8. Вычислите определитель: 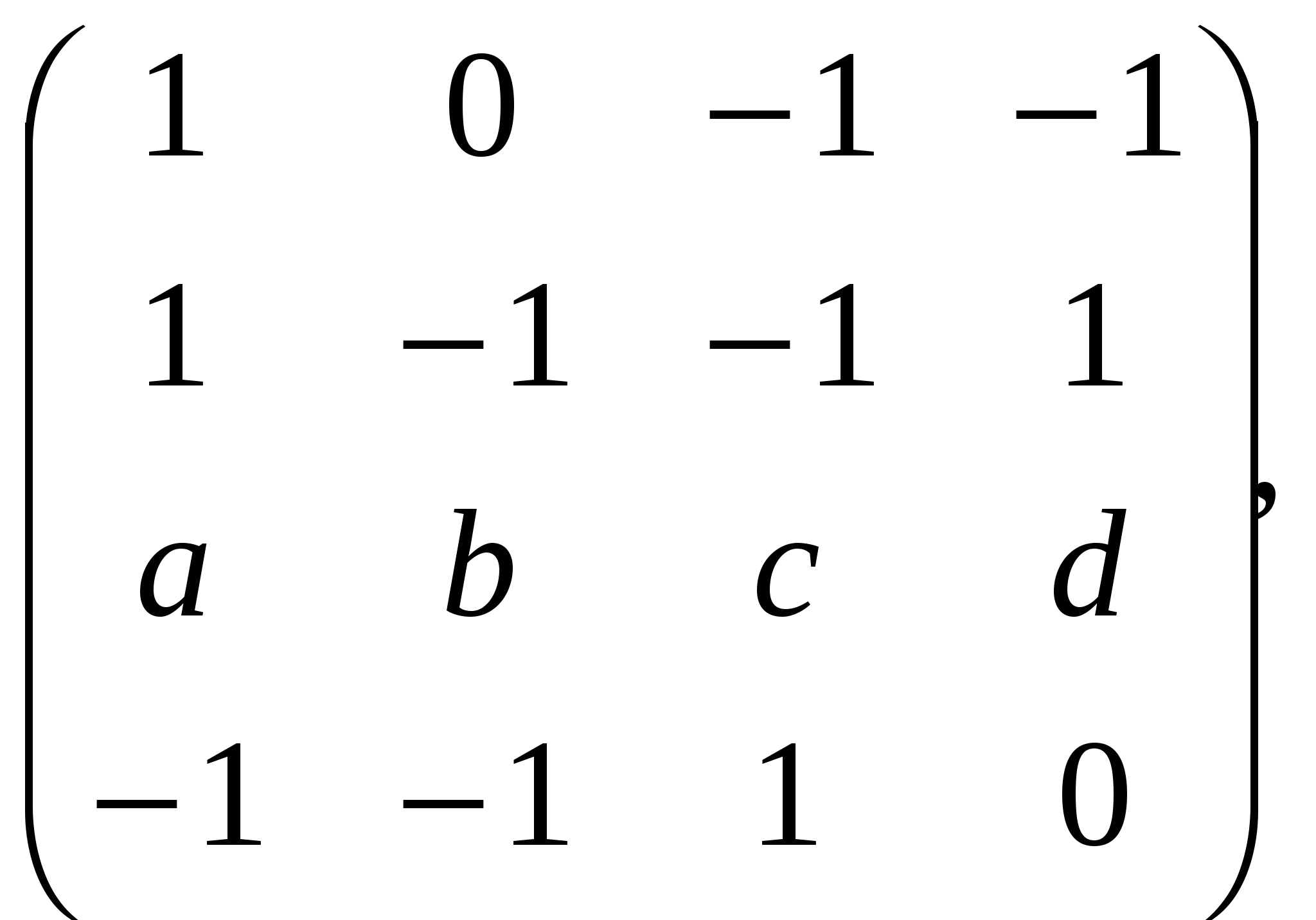
А. 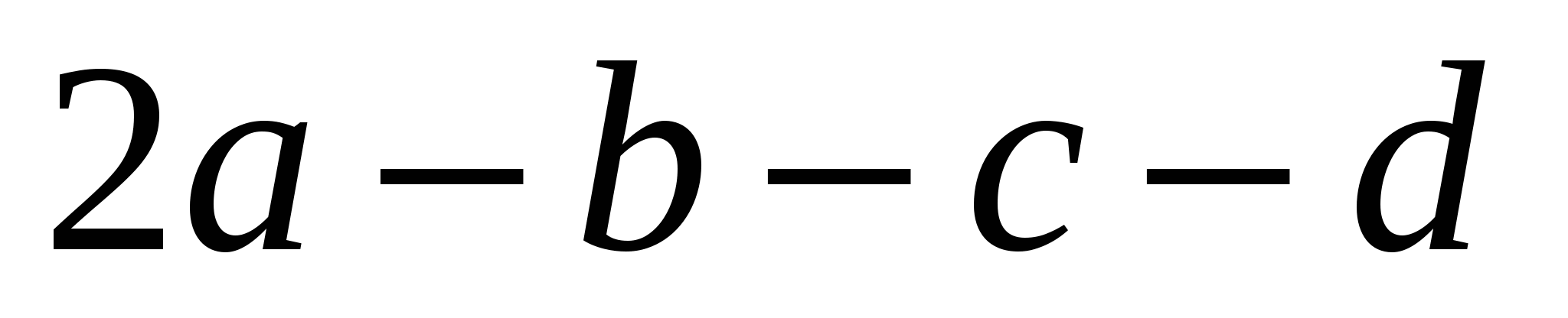 ; ;
Б. 1;
В. 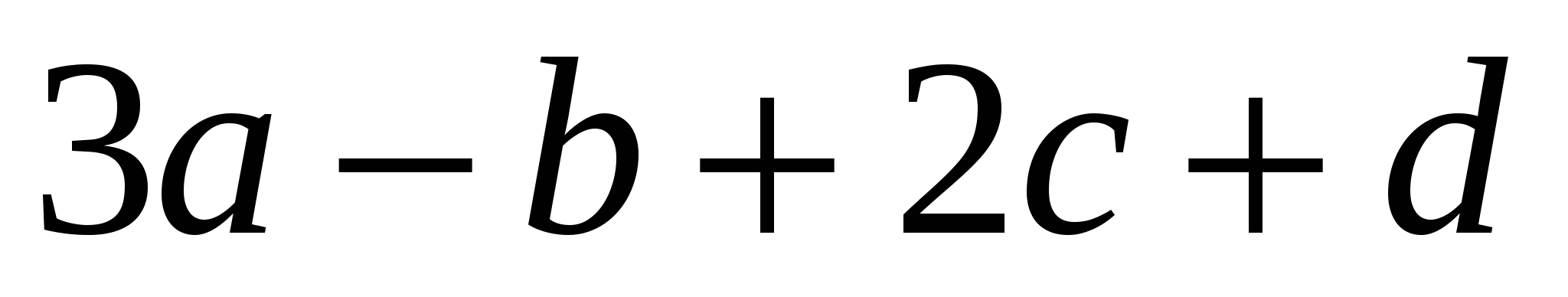 ; ;
С. 0;
D. 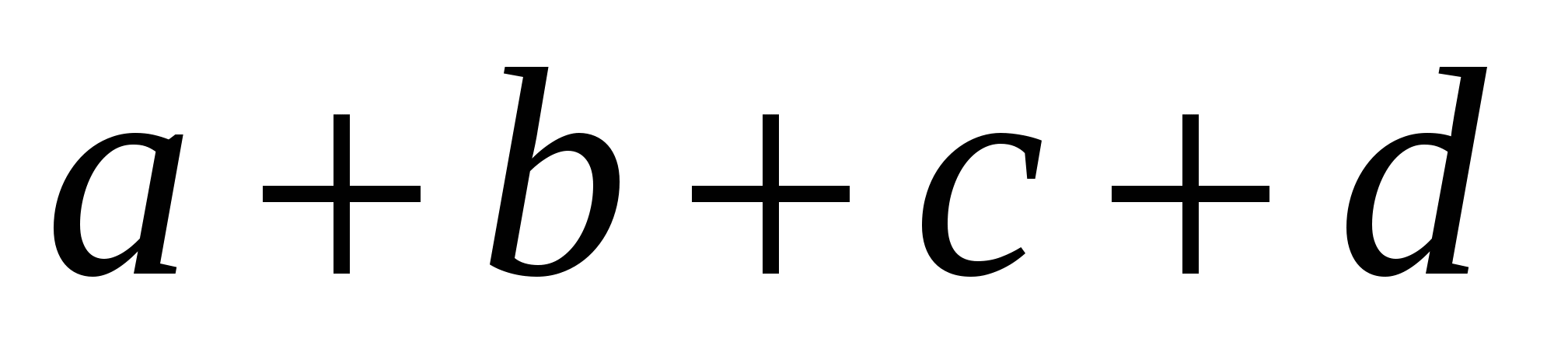 . .
9. Решите уравнение:
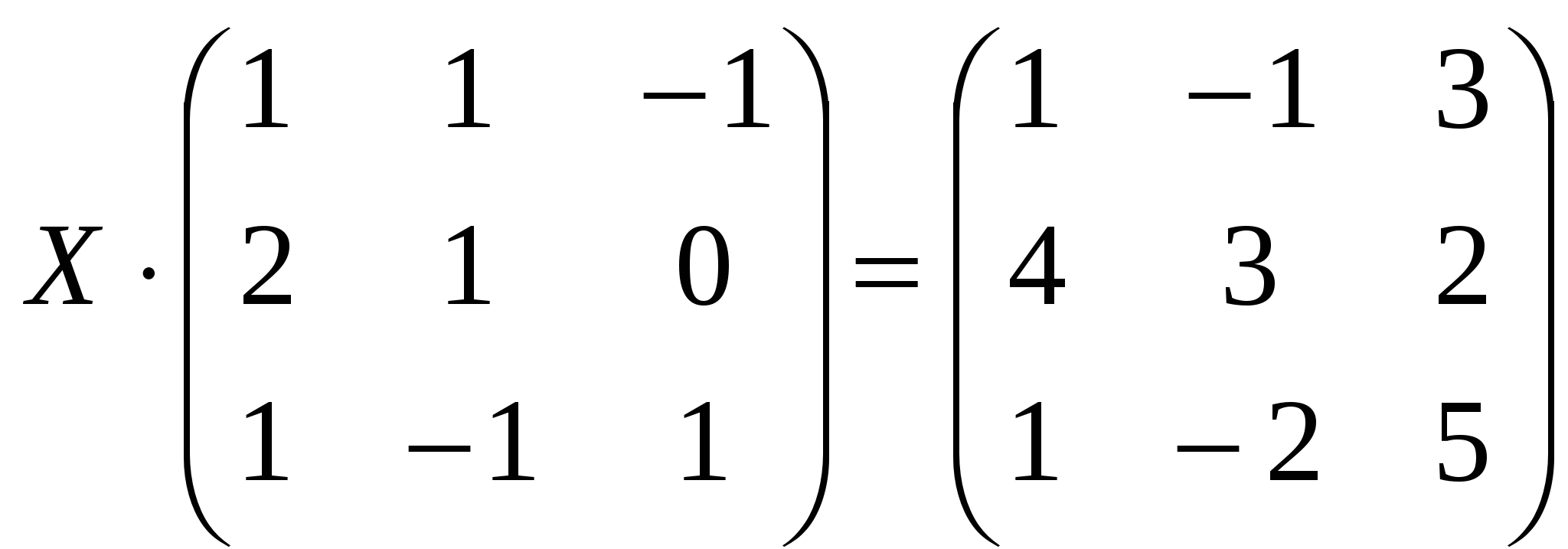 ; ;
А. 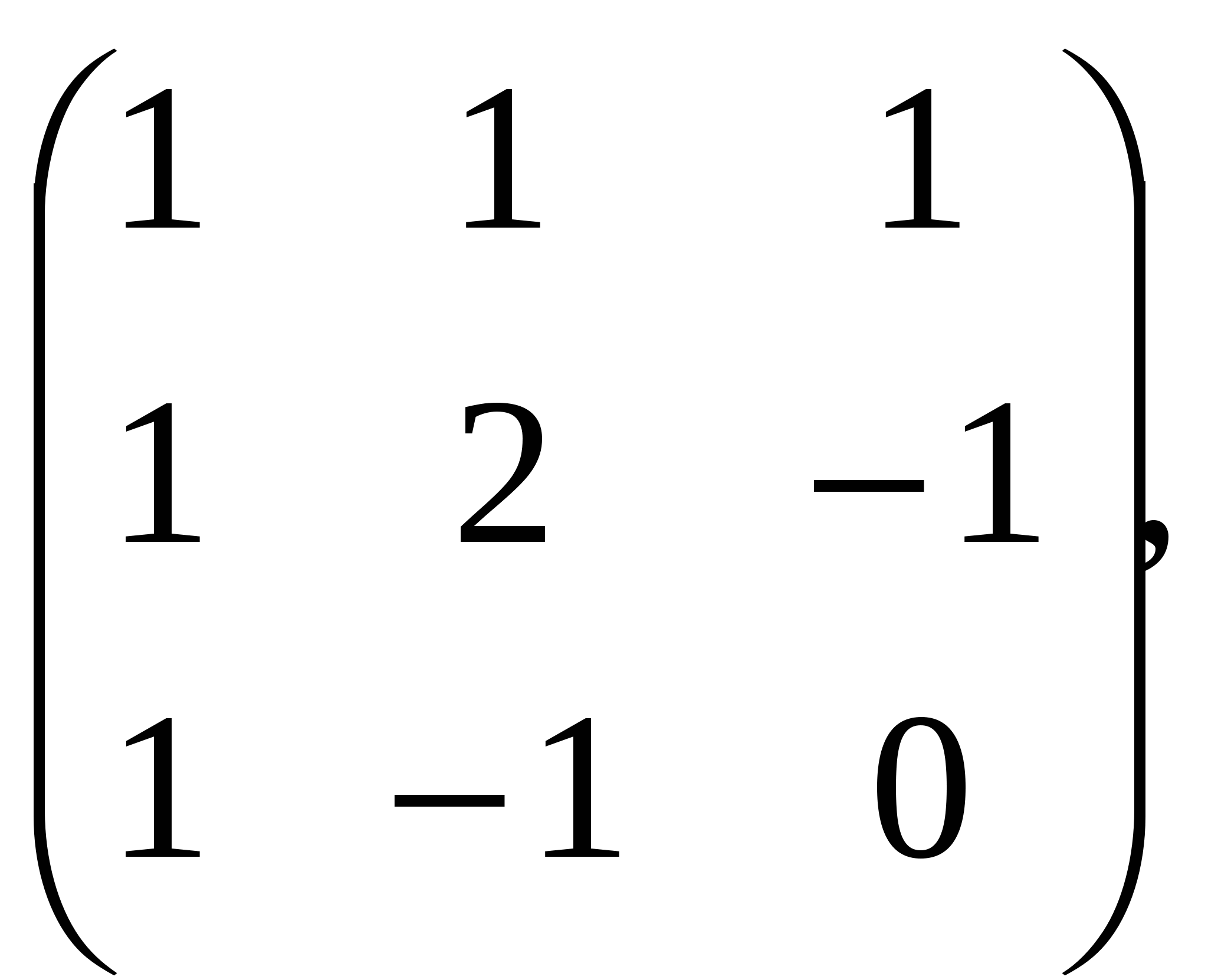
Б. 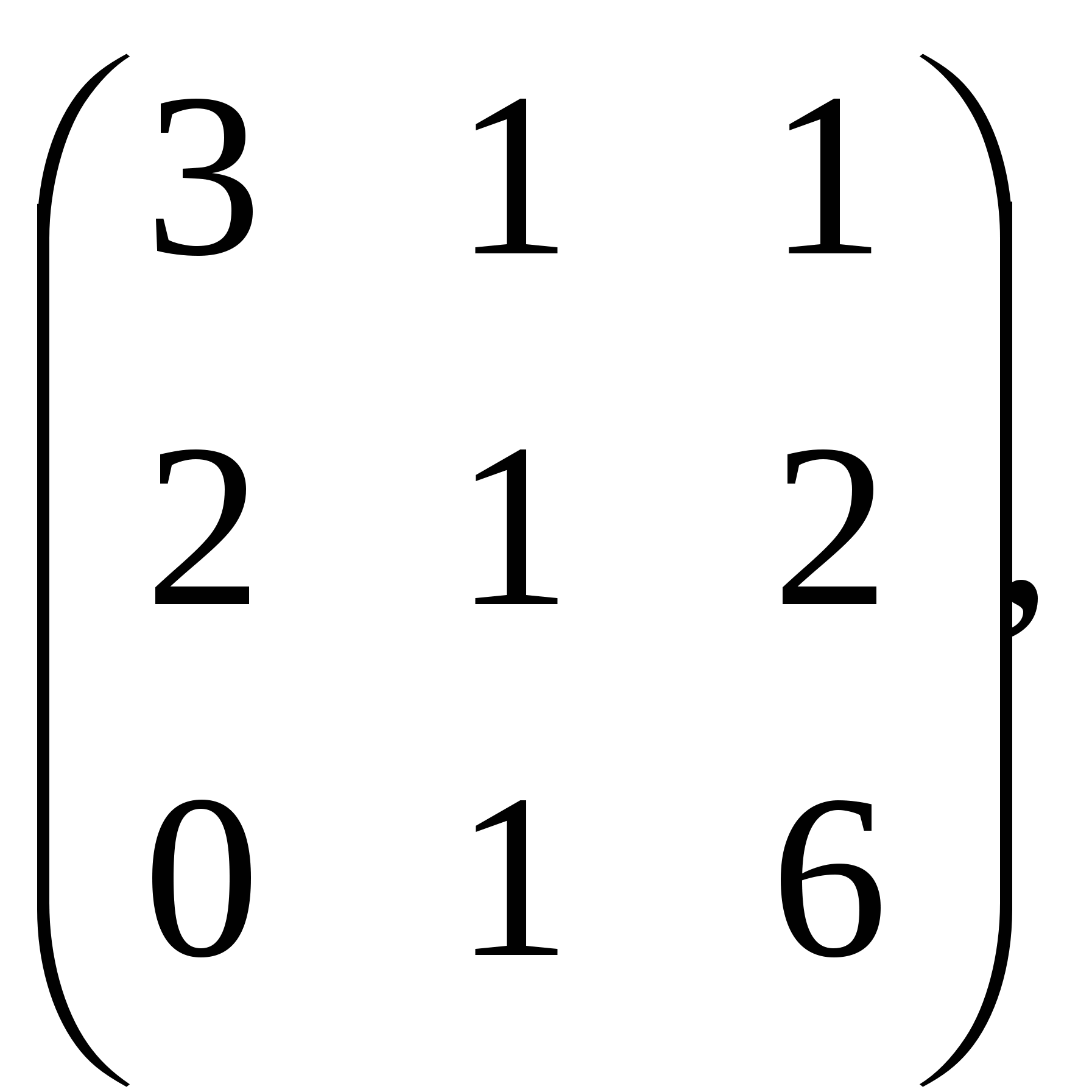
В. 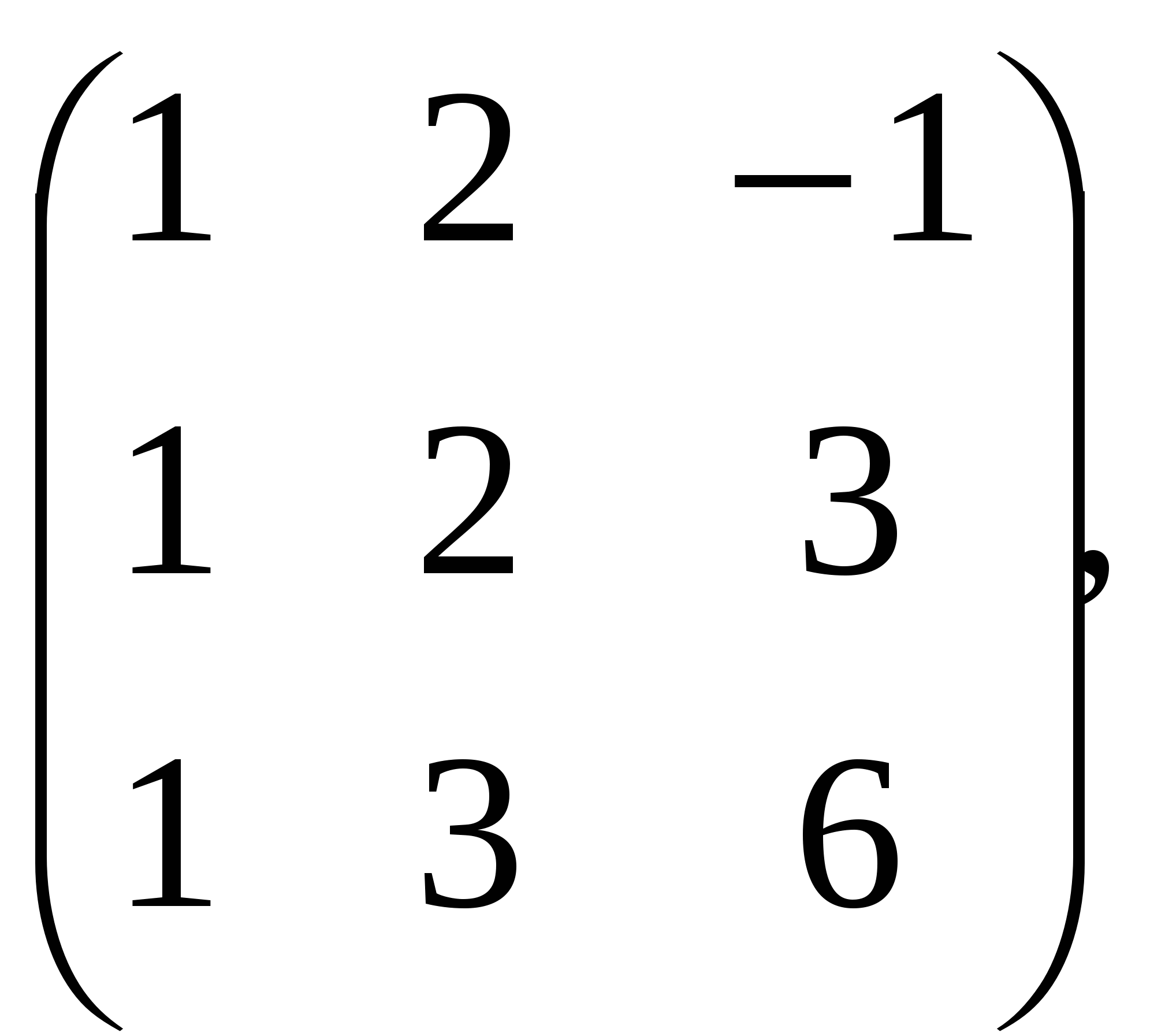
С.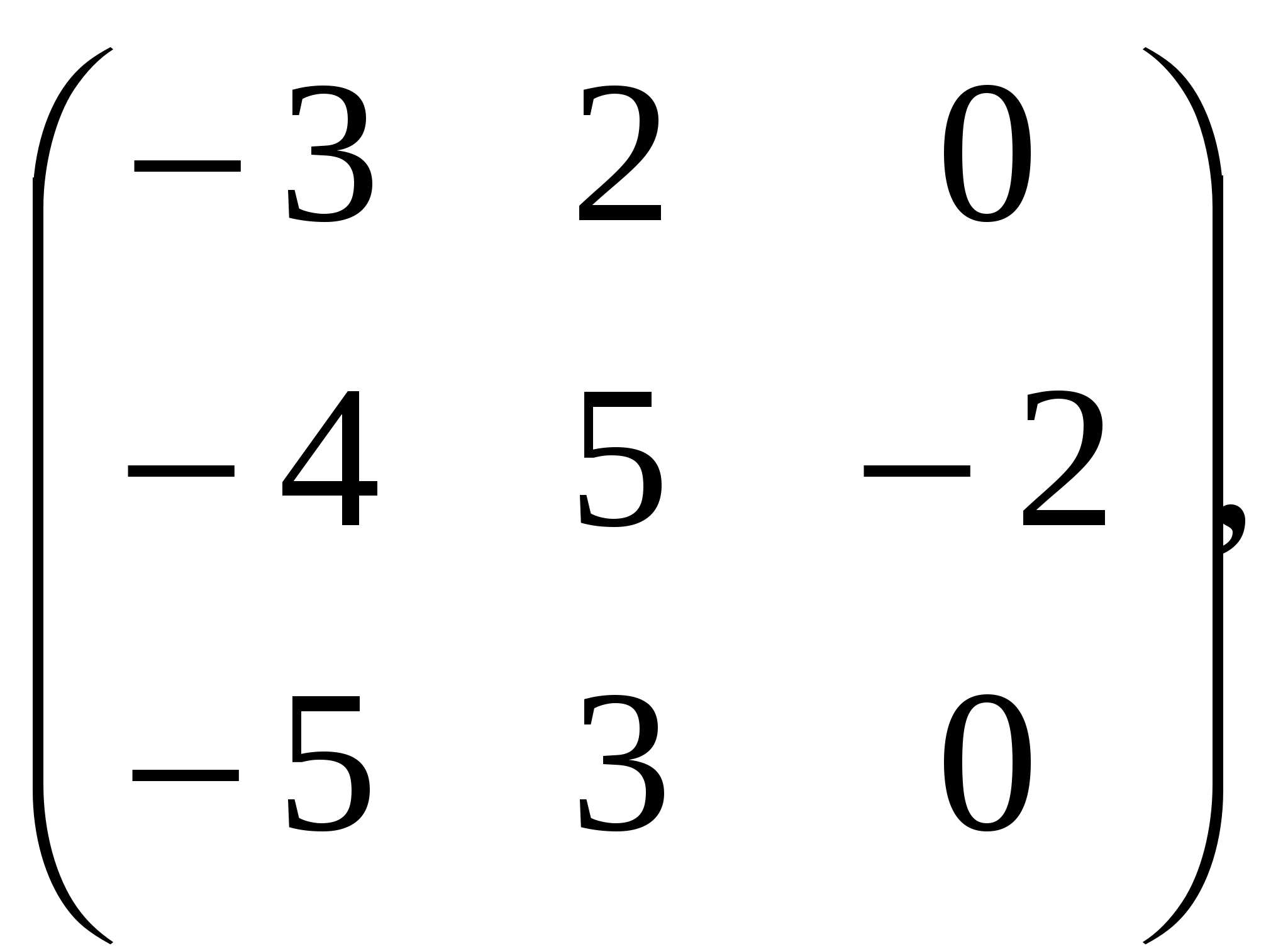 ; ;
D.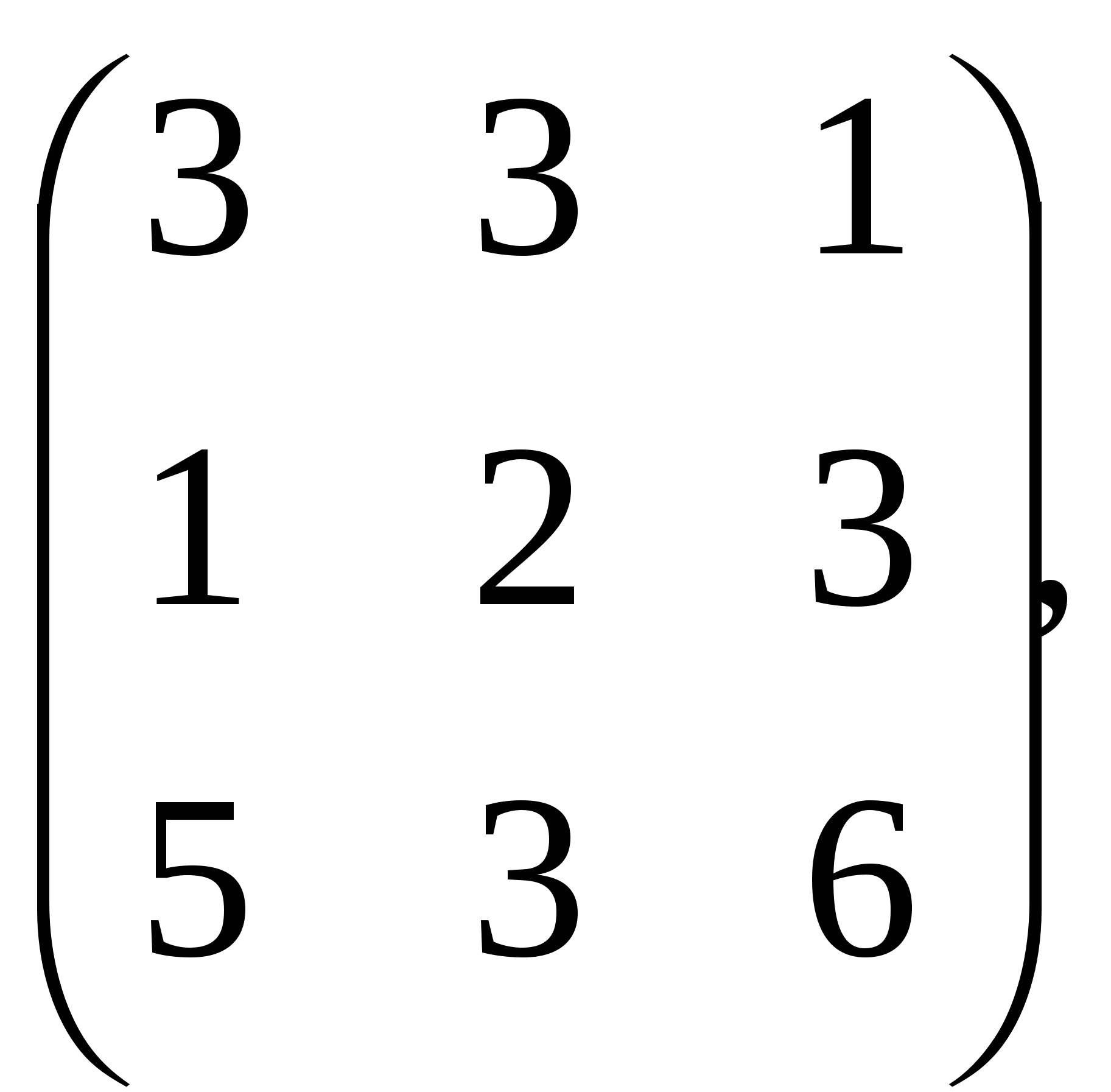
10. Найдите обратную матрицу : 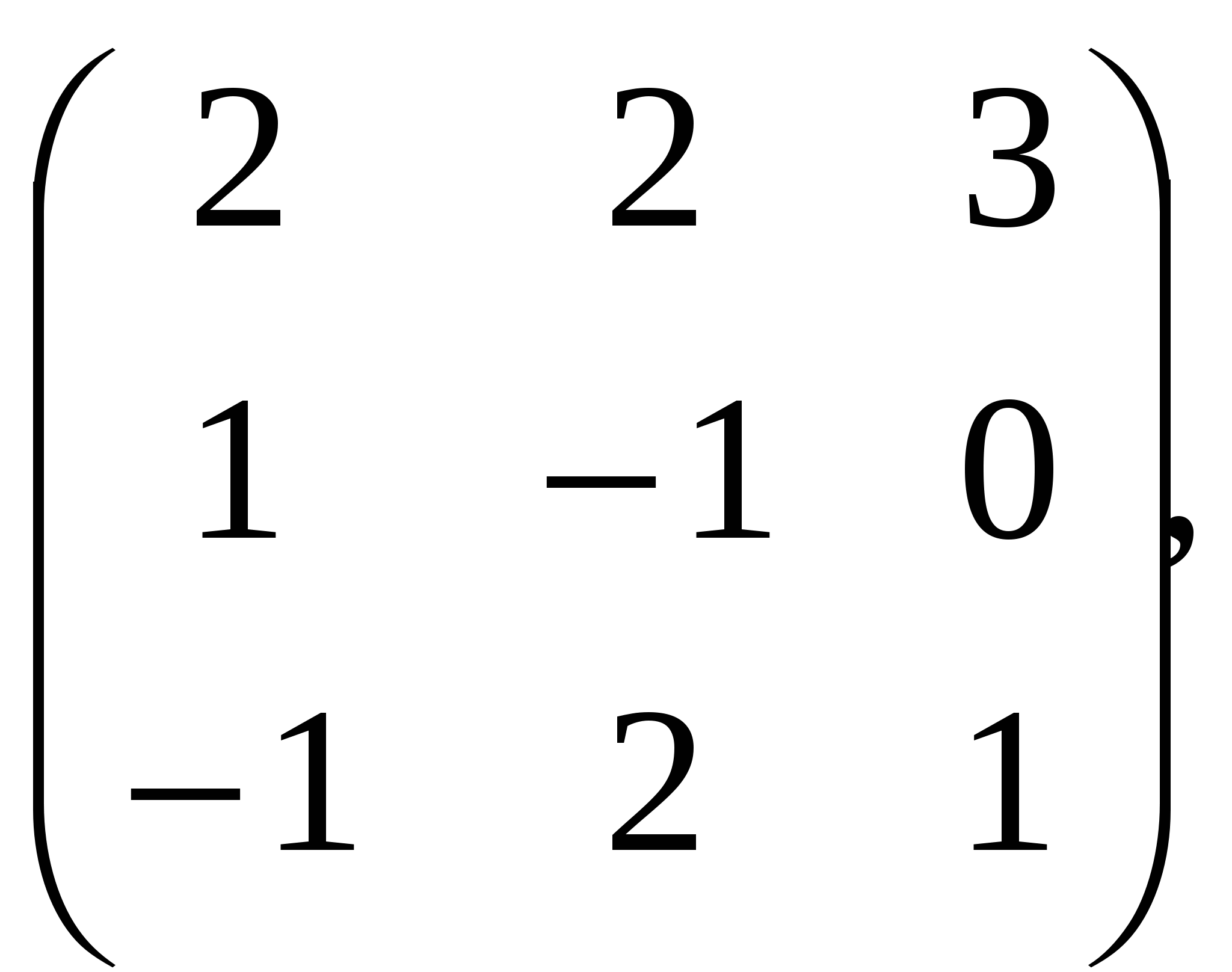
А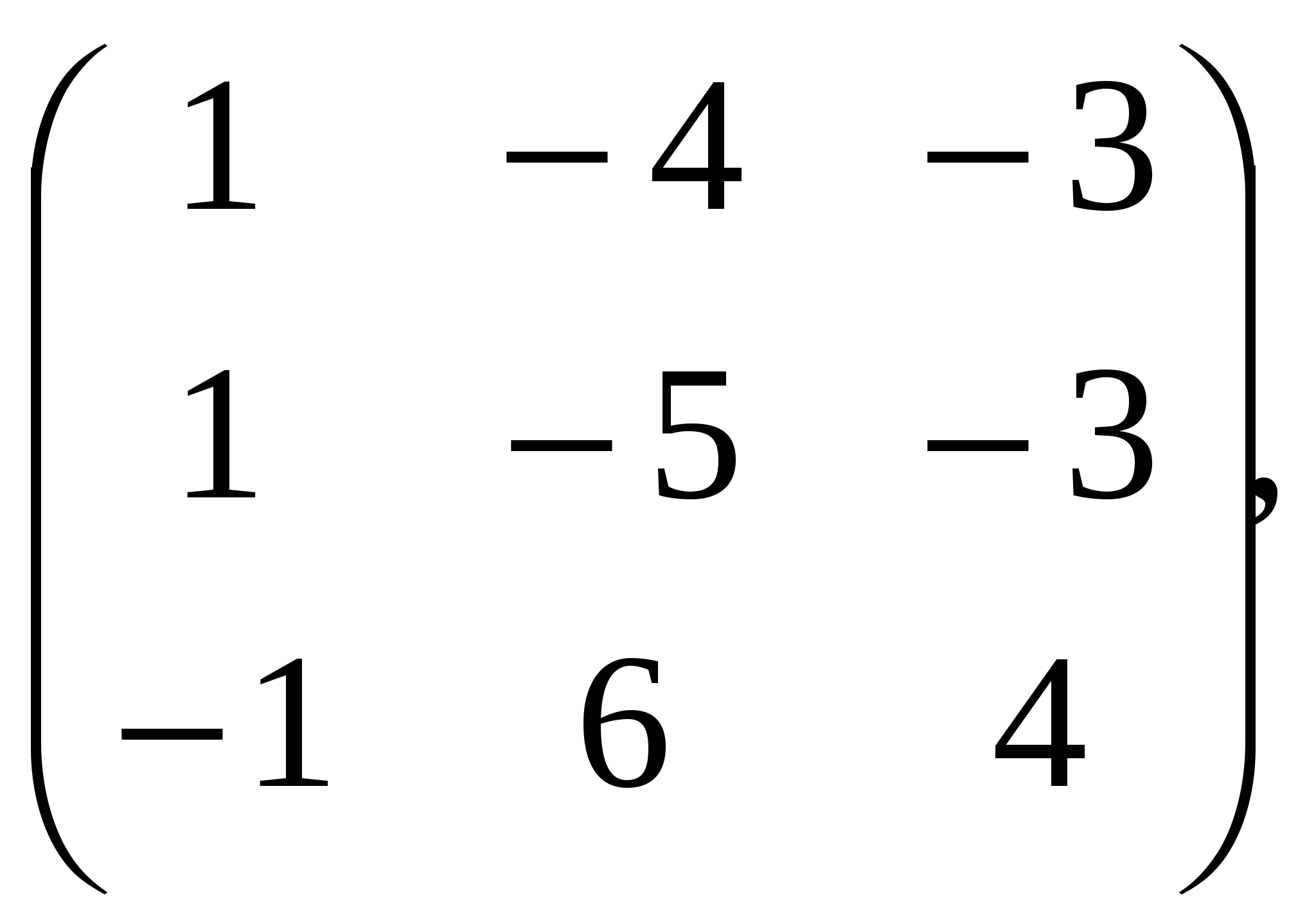
Б.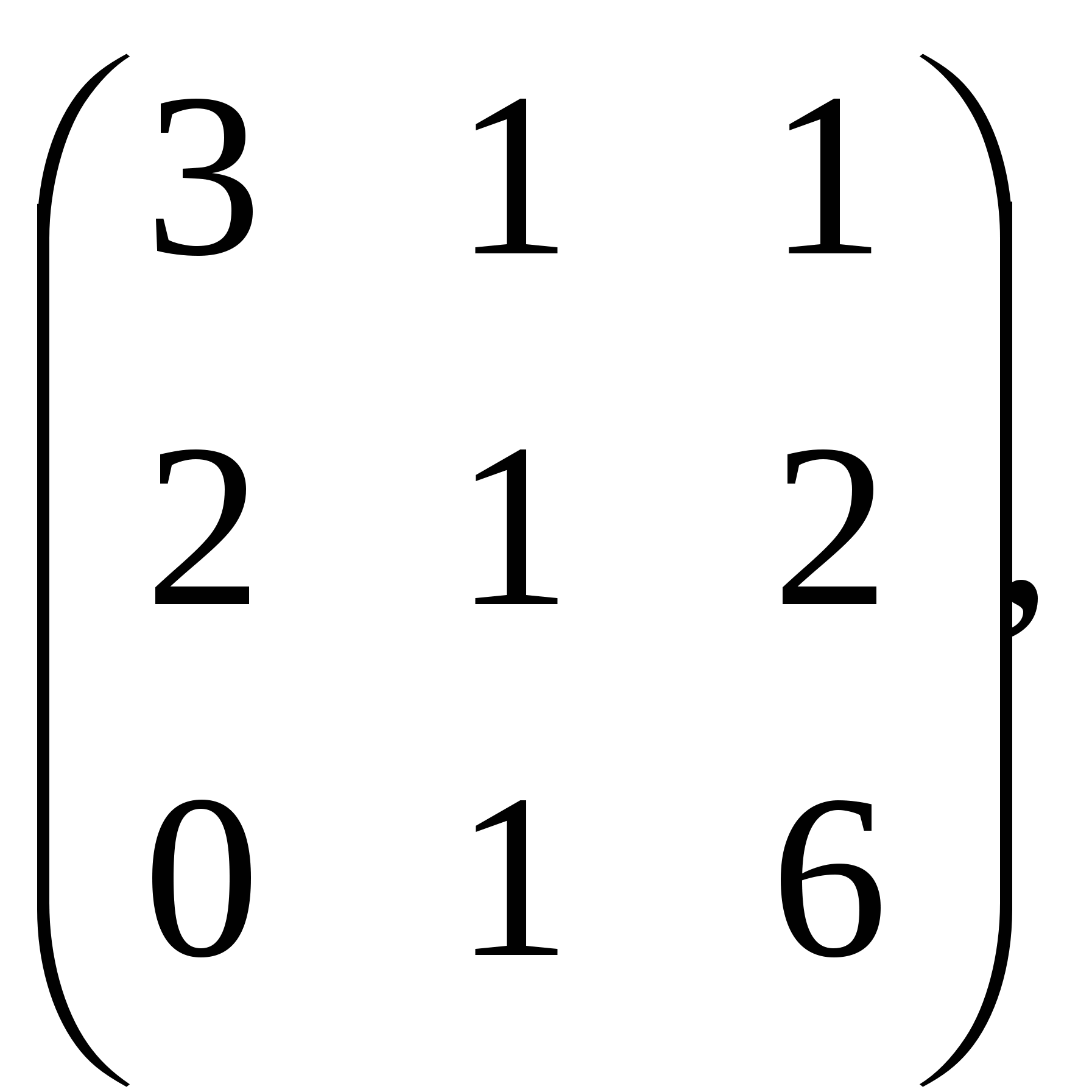
В.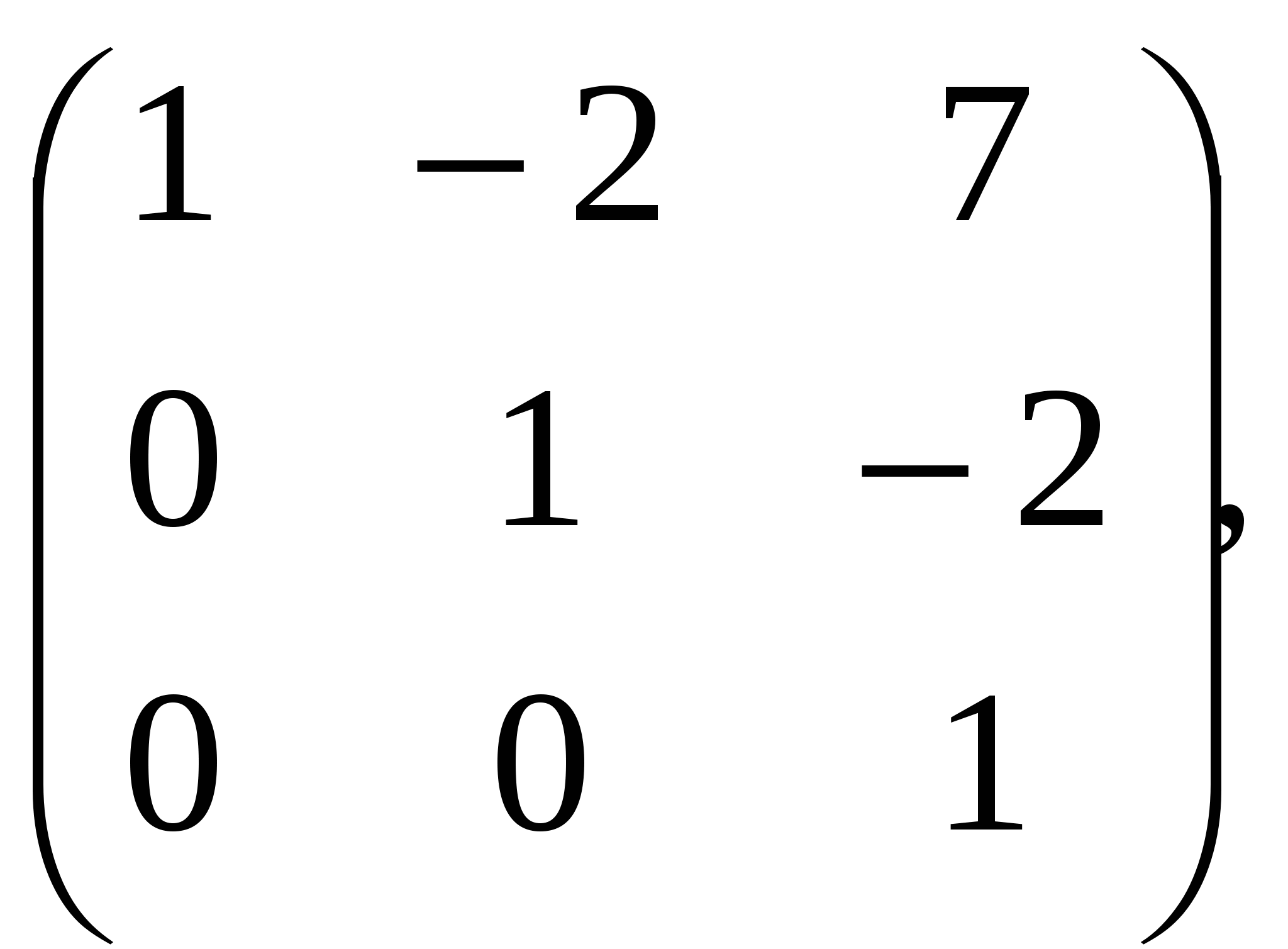
С.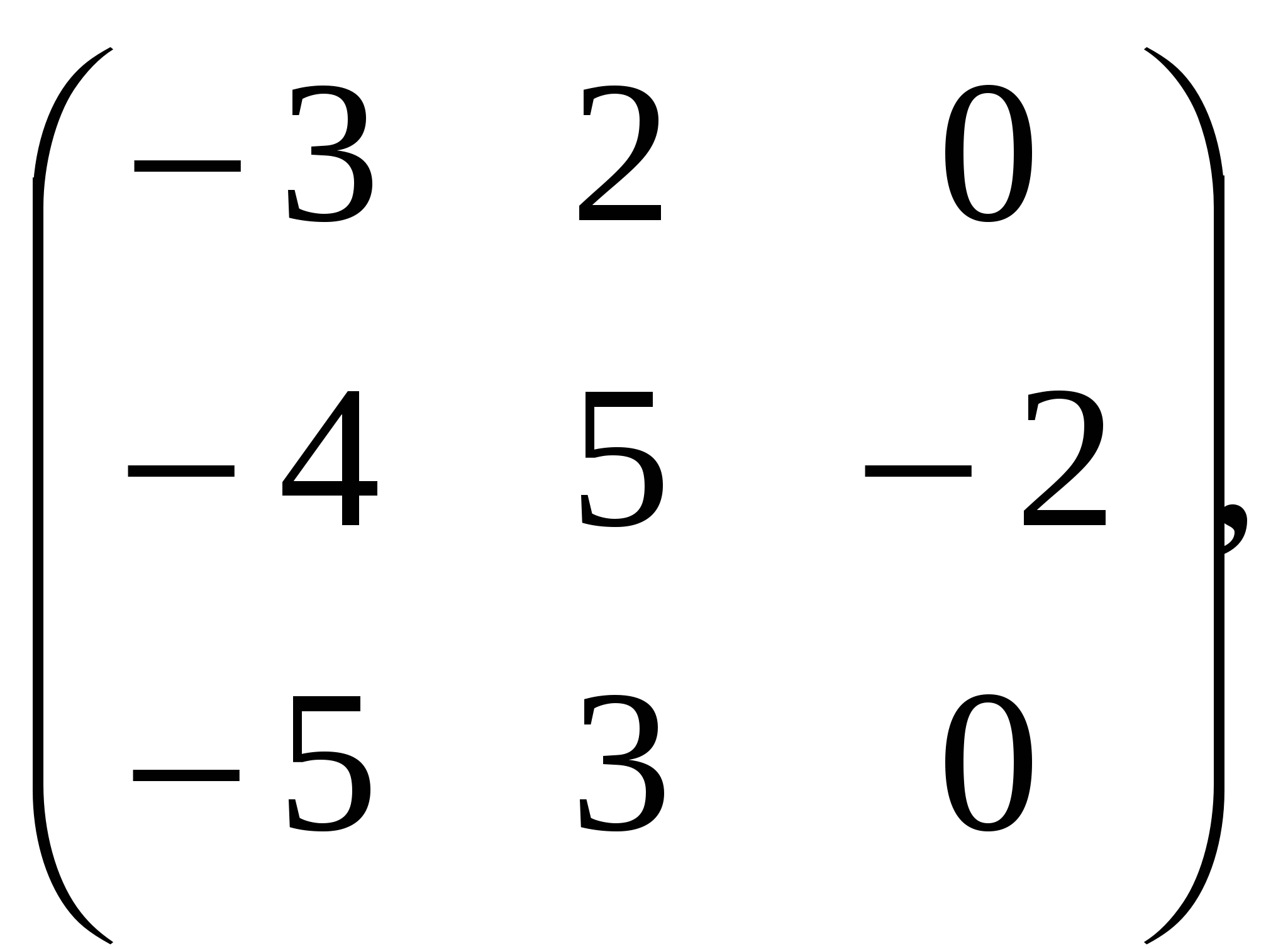 ; ;
D.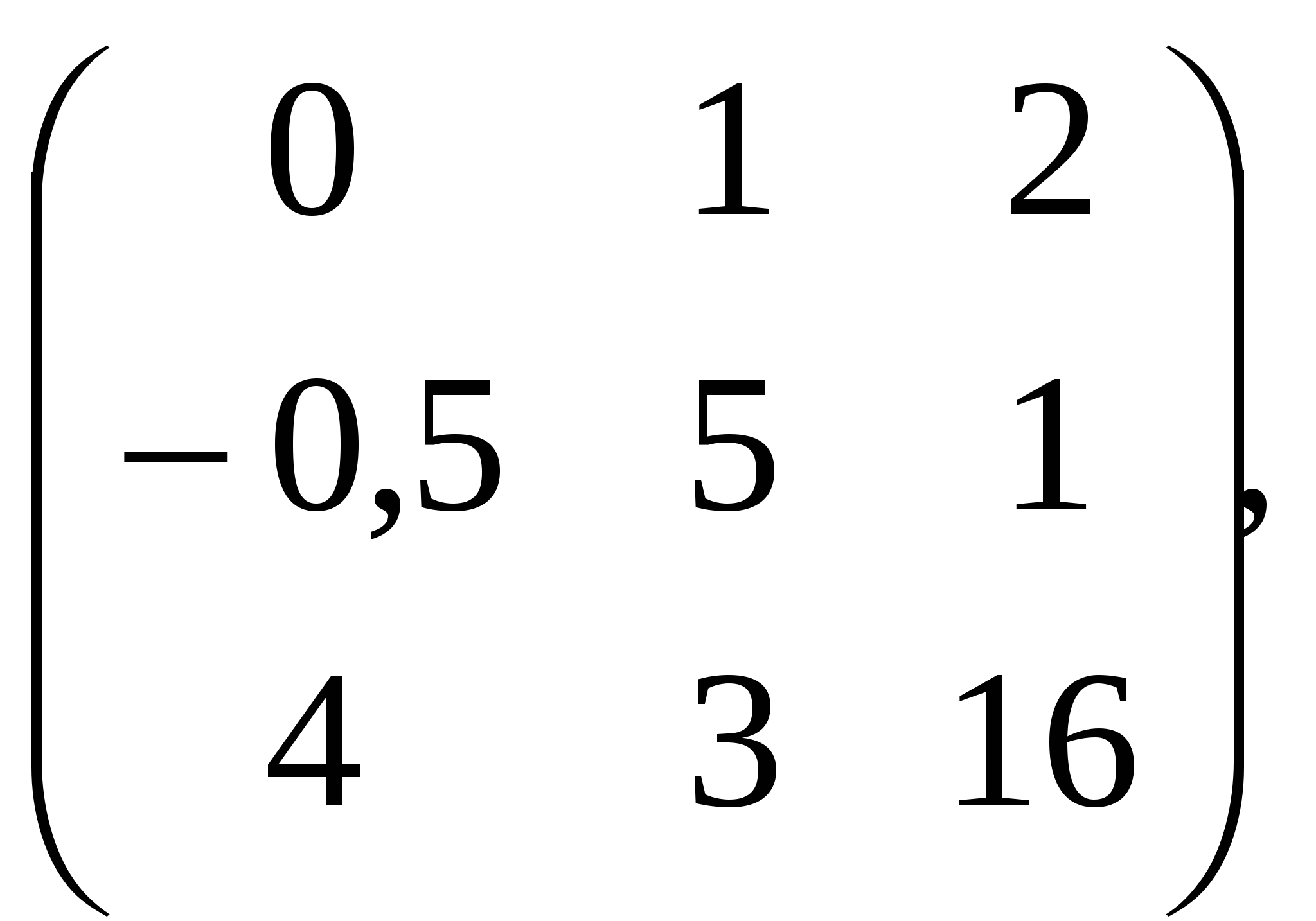
11. Вычислите ранг матрицы.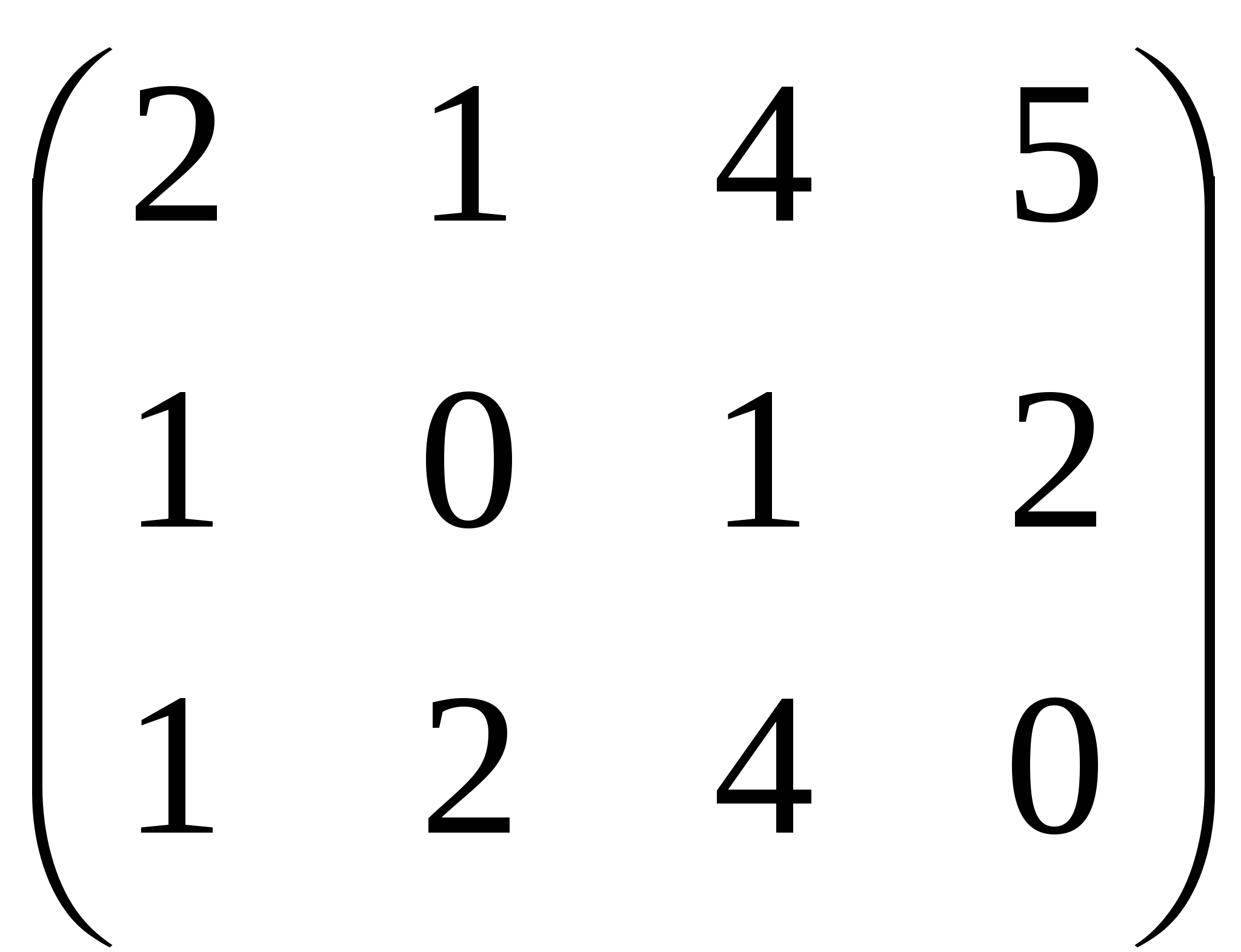 ; ;
А. 3;
Б. 1;
В. 1,5;
С. 2;
D. 4.
12.Решите систему: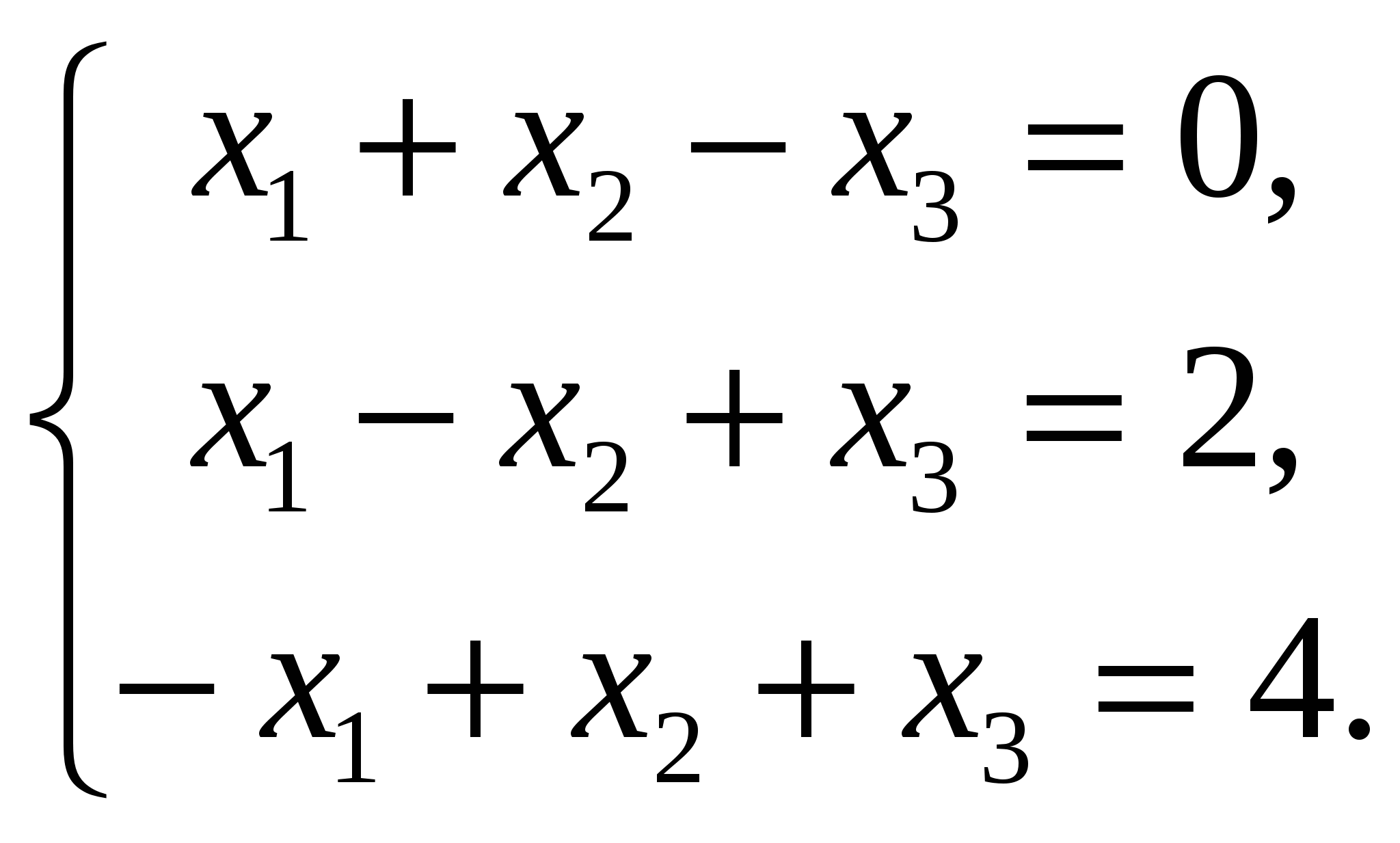
А. 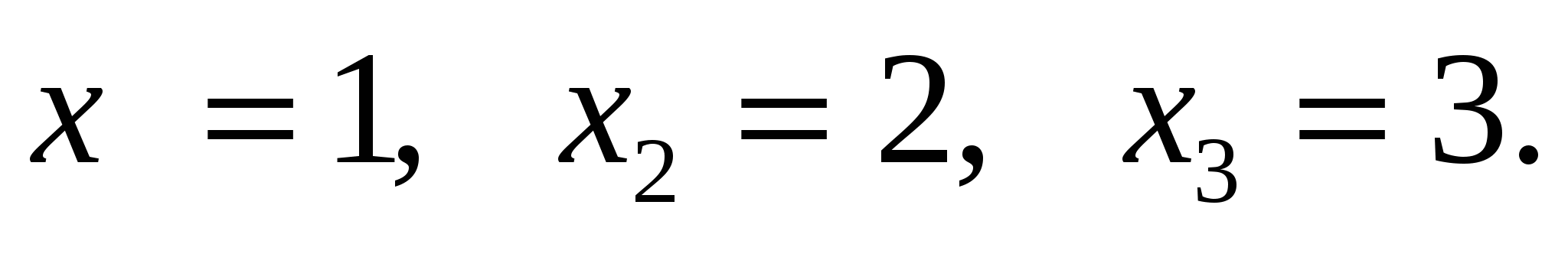
Б. 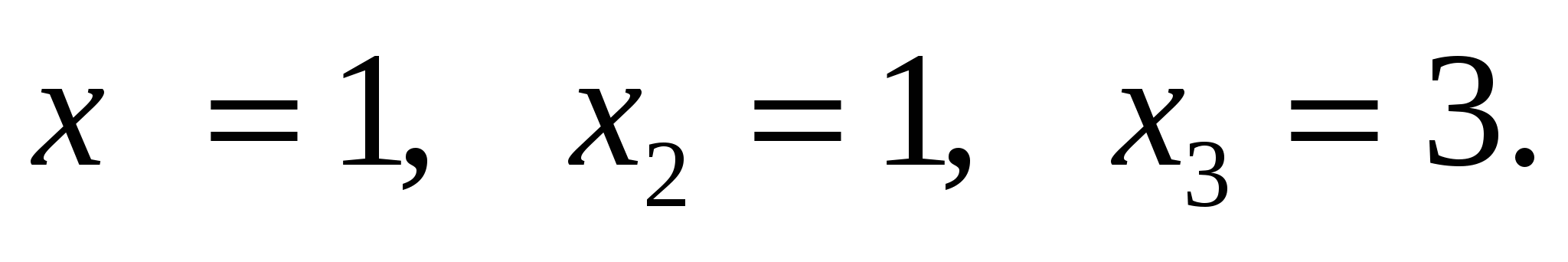
В.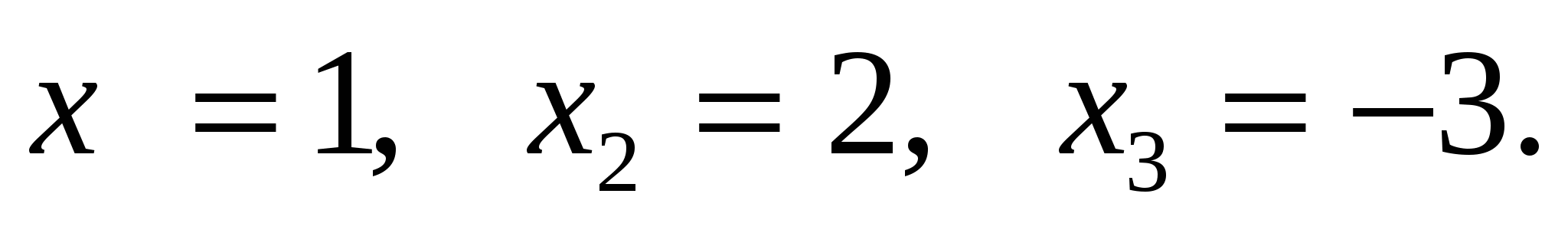
С.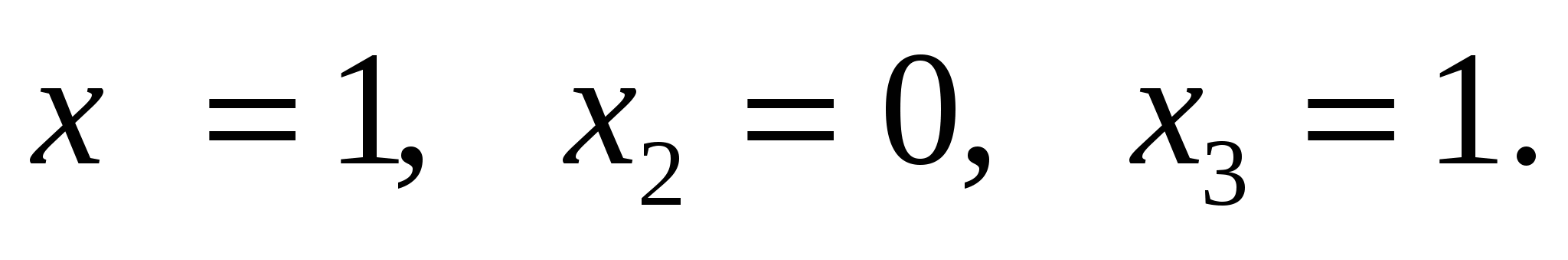
D.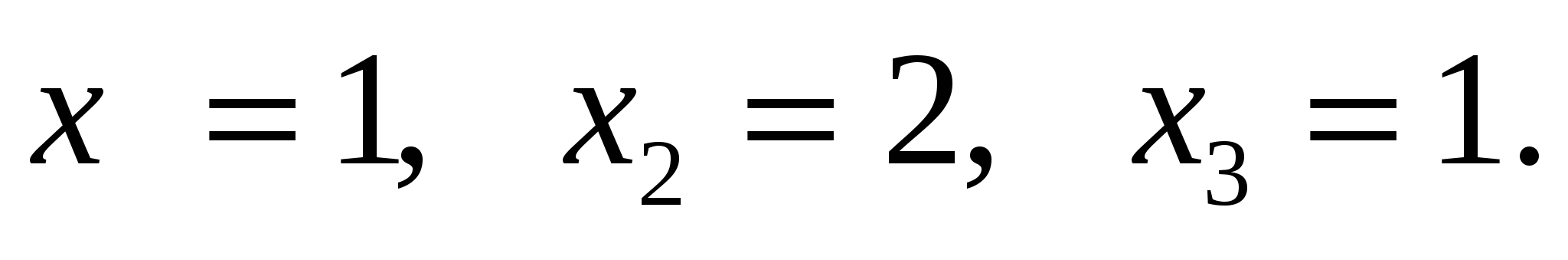
13. Даны векторы 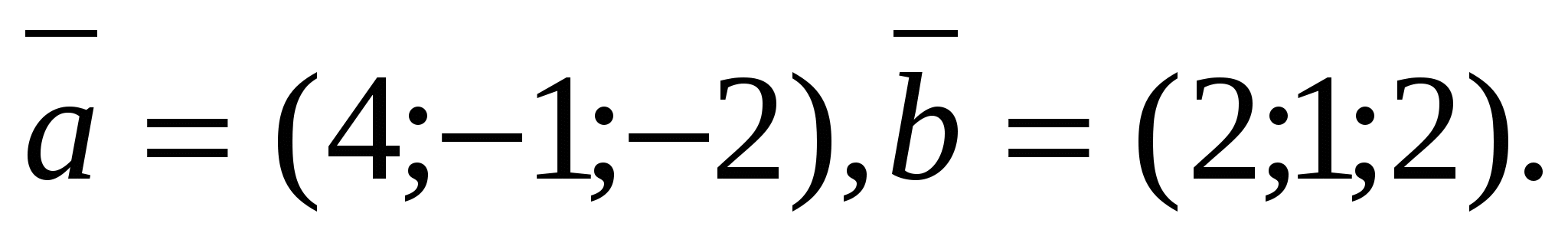 Найдите скалярное произведение этих векторов. Найдите скалярное произведение этих векторов.
А. 12;
Б. 10;
В. 8;
С. 1;
D. 3.
14. Найдите площадь треугольника с вершинами А(1;2;0), В(3;2;1), С(-2;1;2).
А. 3;
Б. 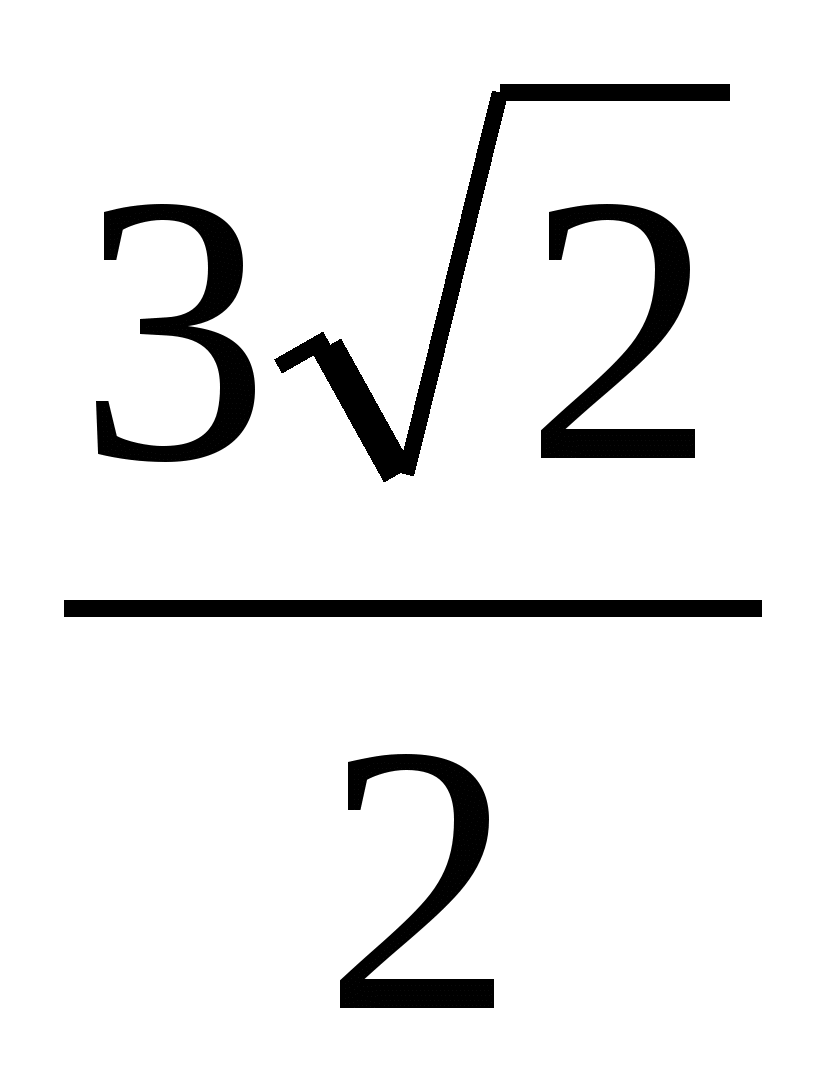 ; ;
В. 1;
С. 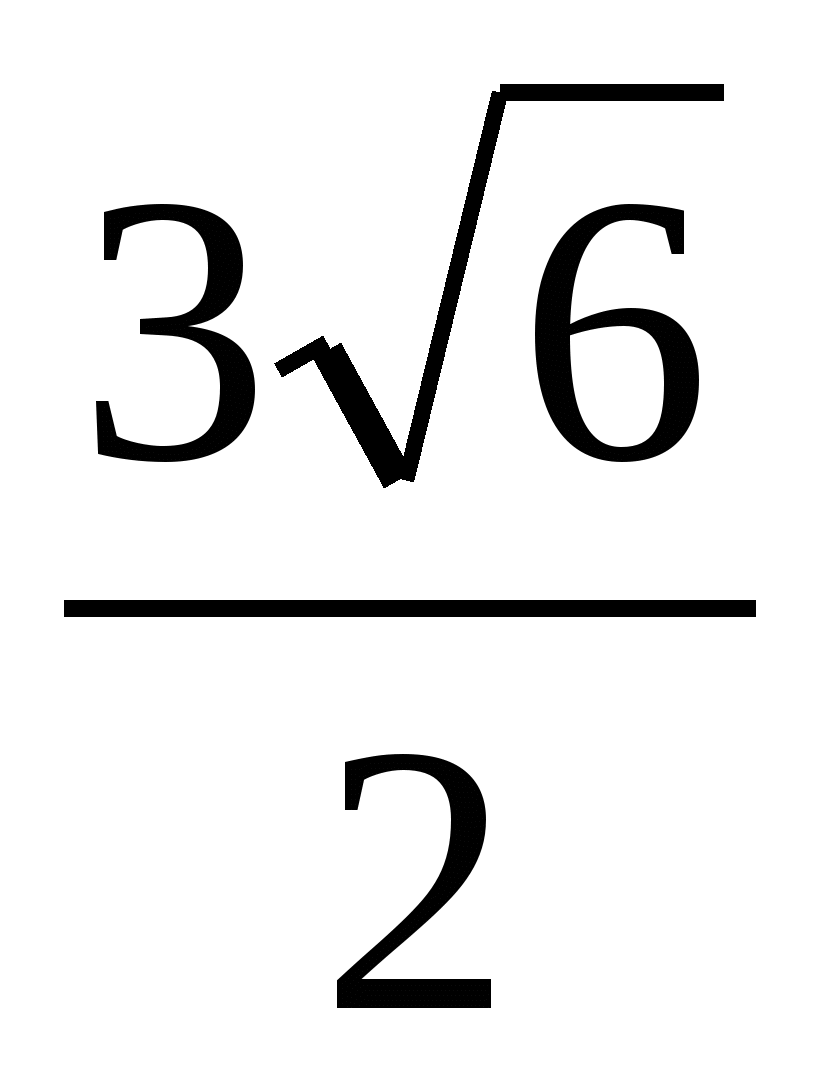 ; ;
D. 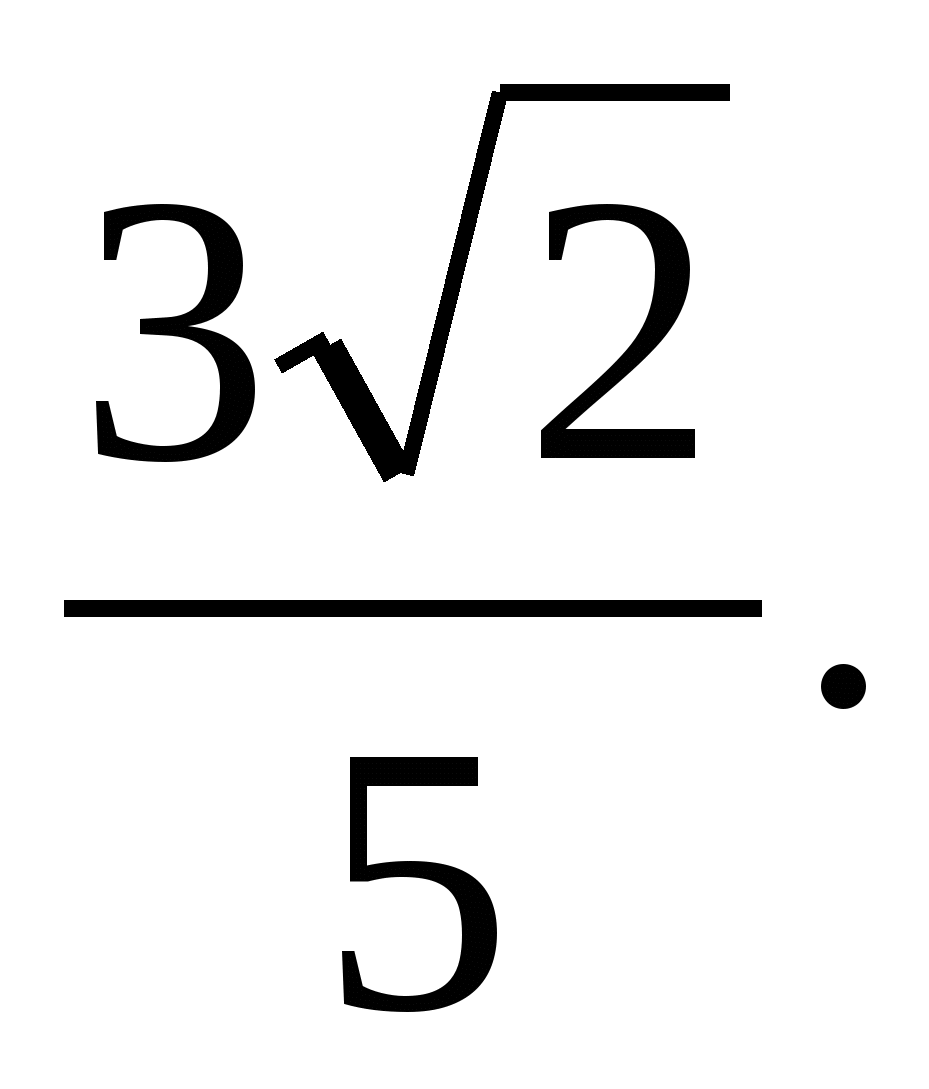
15. Найдите точку, в которой прямая, проходящая через точки А(5; 5) и В(1; 3), пересечет ось Ох.
А. (1; 1);
Б. (5; 0);
В. (-5; -1);
С. (-5; 0);
D. (0; 5).
16. Найдите точки пересечения линий  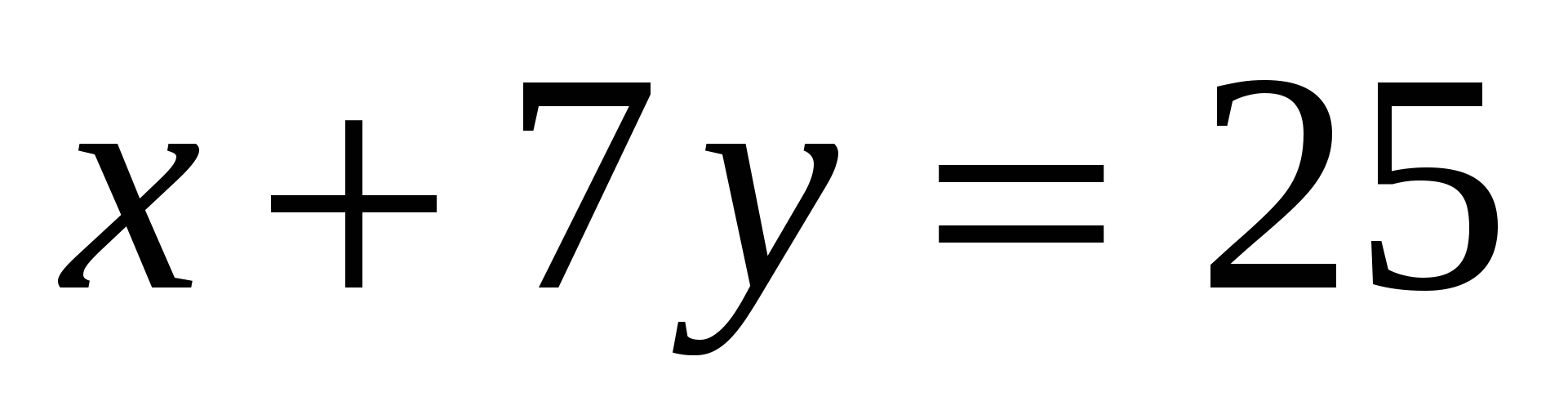 и и 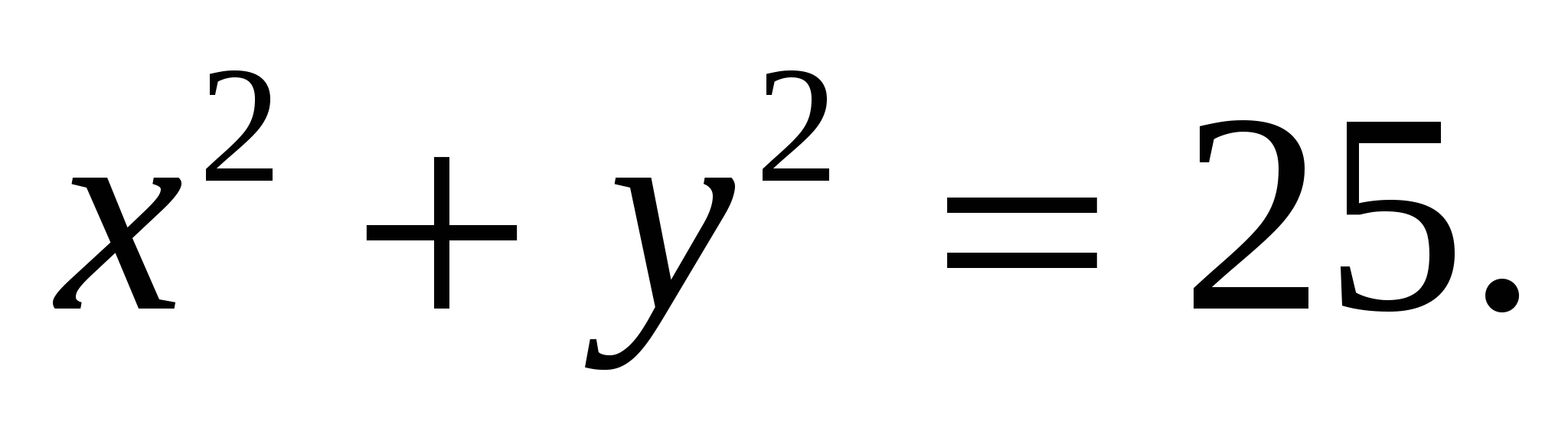
А. (1; 1);
Б. (5; 0), (-3;-4);
В. (-5; -1);
С. (-5; 0), (0; 5);
D. (-3; 4), (4; 3).
17. Найдите угол между прямыми 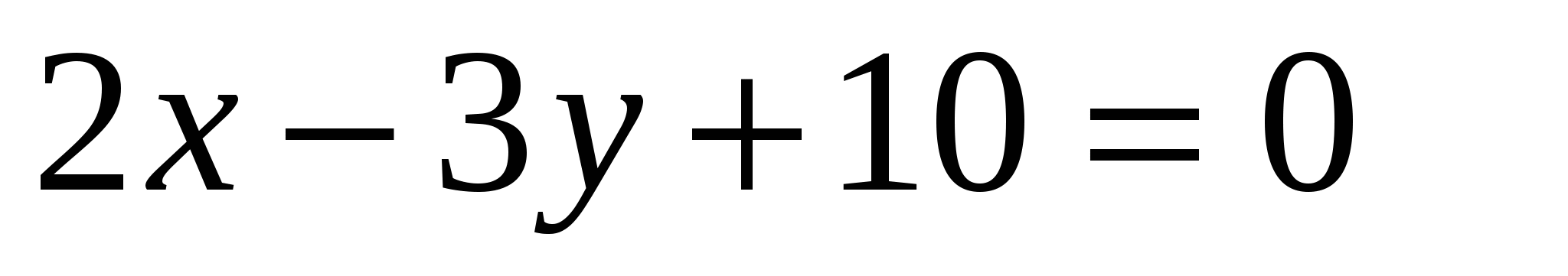 и и 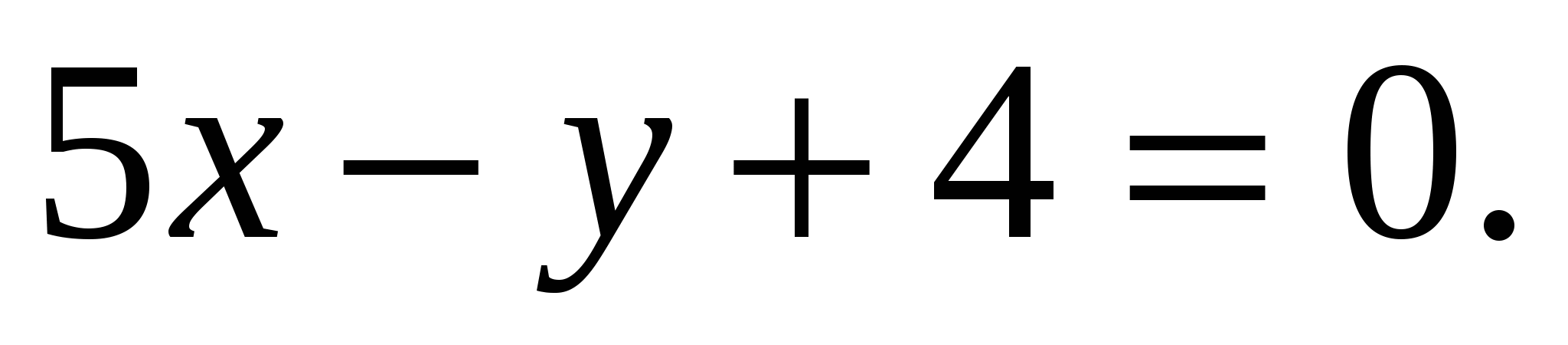
А.  ; ;
Б.  /4; /4;
В.  /2; /2;
С.  /3; /3;
D. 0.
18. Найдите координаты ценра и радиус окружности 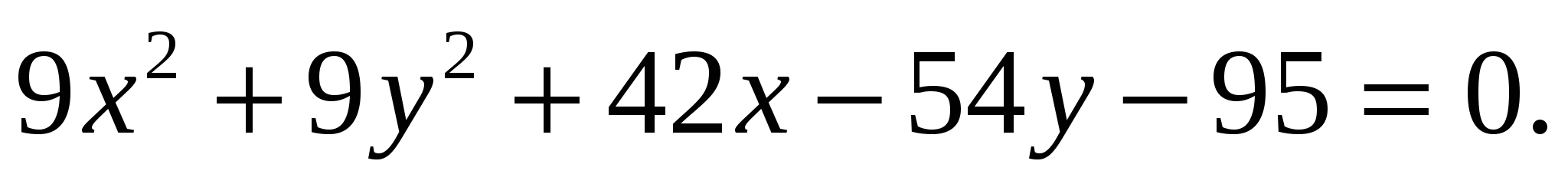
А.(3; 2) и R=5.
Б. (2; 2) и R=2.
В. (-3; -2) и R=3.
С. (3/7; 2) и R=5.
D. (-7/3; 3) и R=5.
19. На оси Оу найти точку С(ч; у; z), равноудаленную от двух точек А(2; 3; 1) и В(-1; 5; -2).
А. (1; 1; 4);
Б. (5; 0;1);
В. (-2; -1; 2);
С. (0;4; 0);
D. (0; 0;5).
20. Найдите параметрические уравнения прямой, проходящей через точку (1; 0; -1) и параллельной вектору 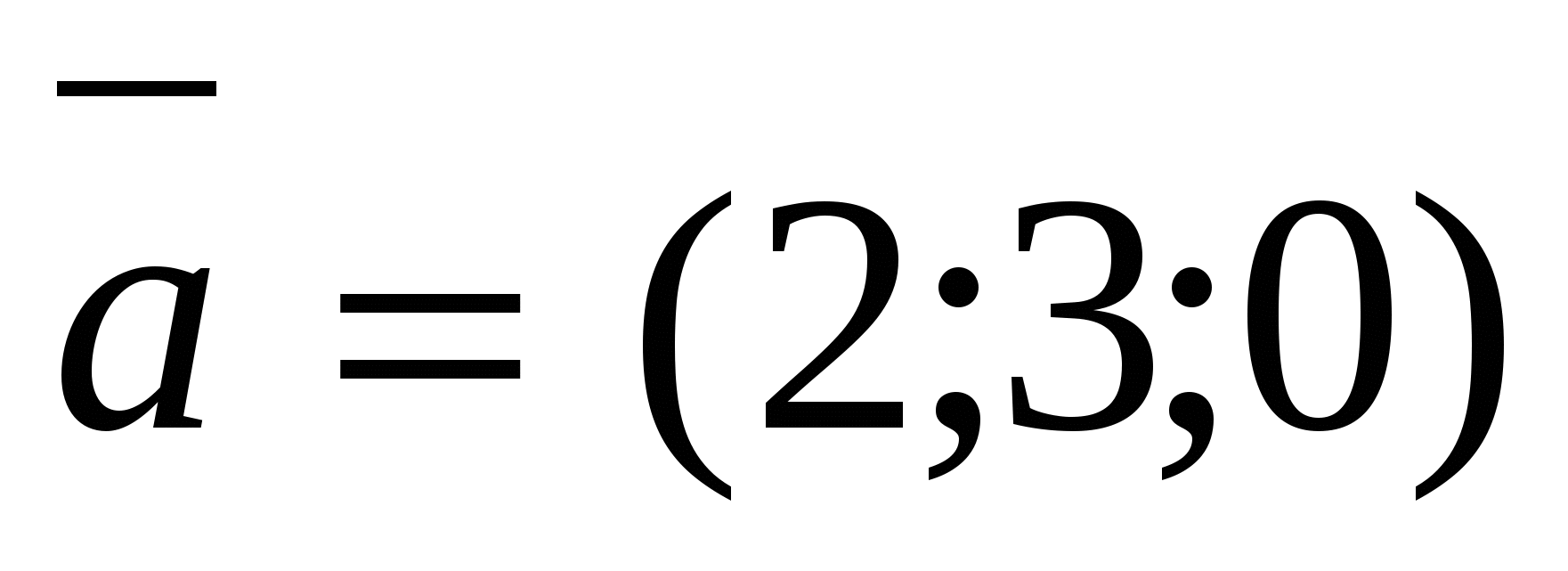 . .
А. 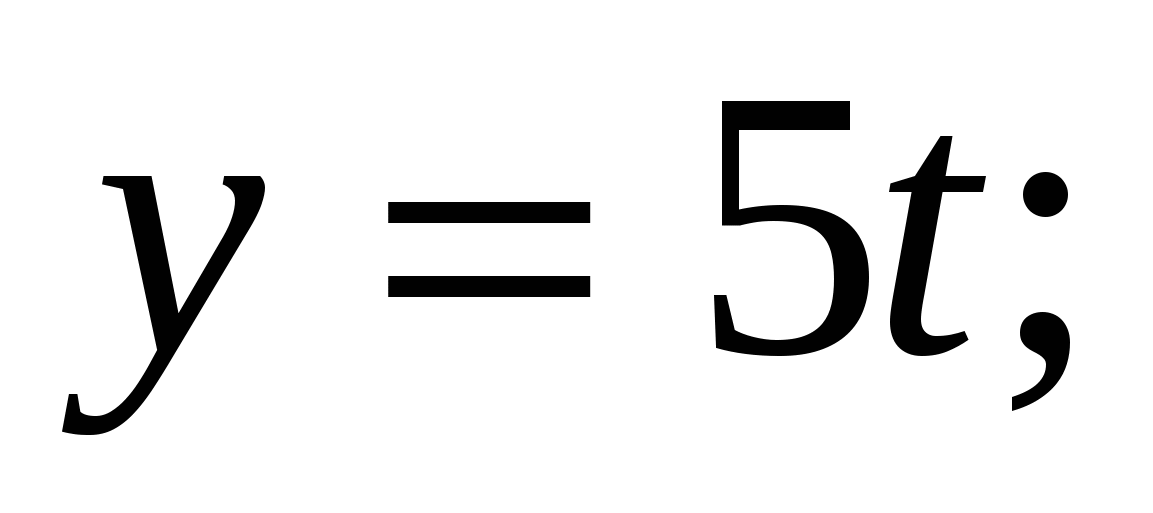 Б. Б. 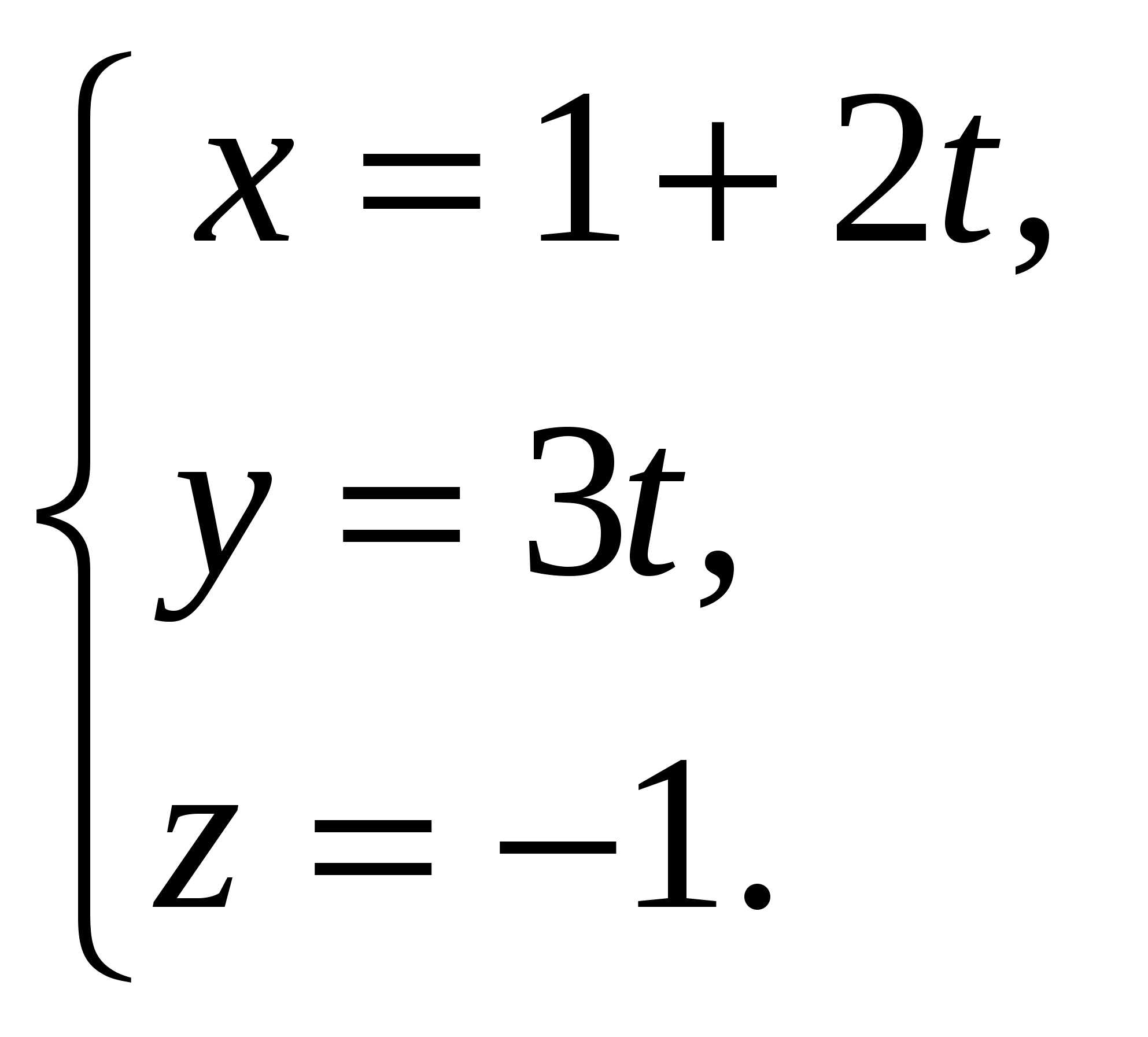 В. В. 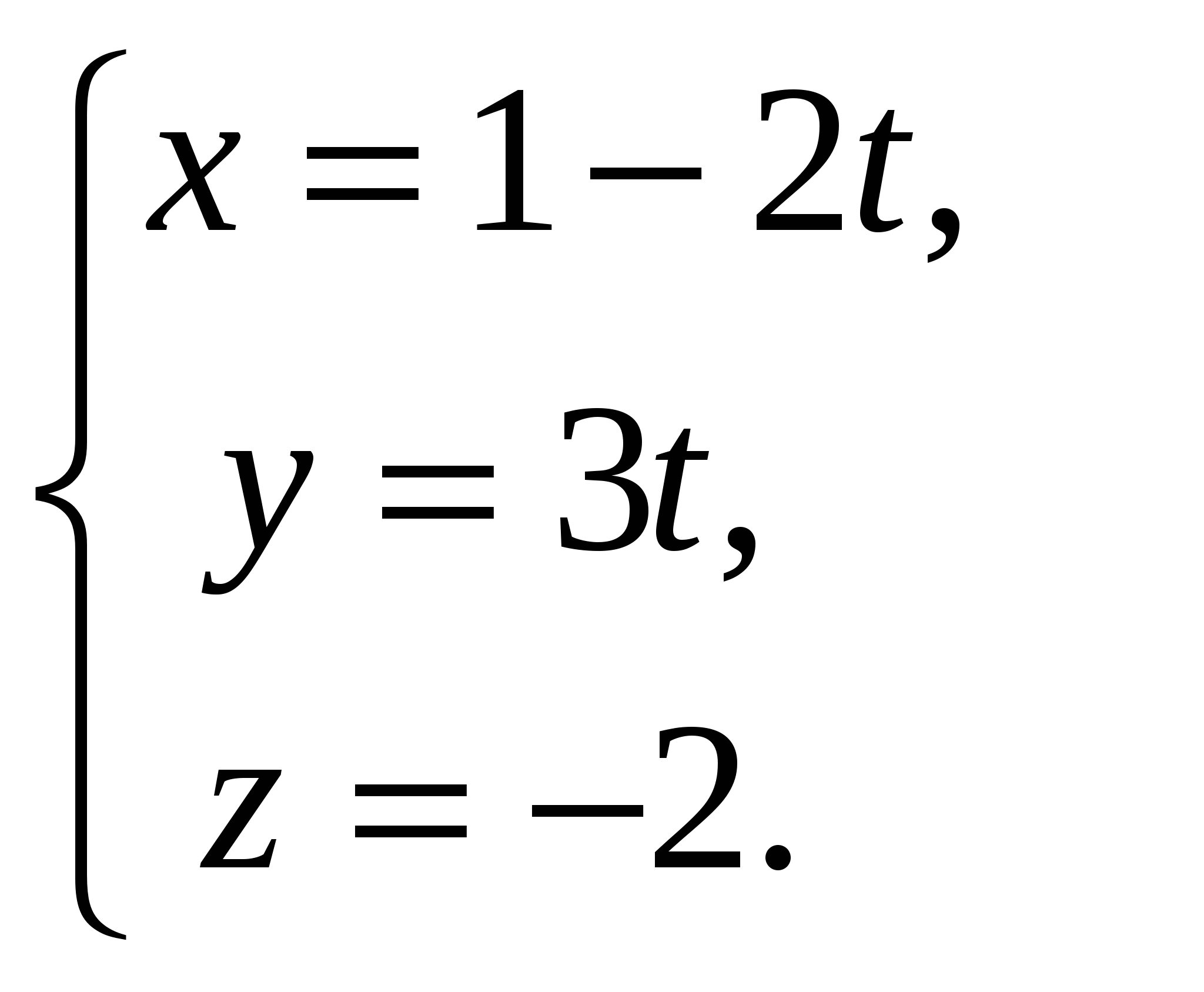
С. 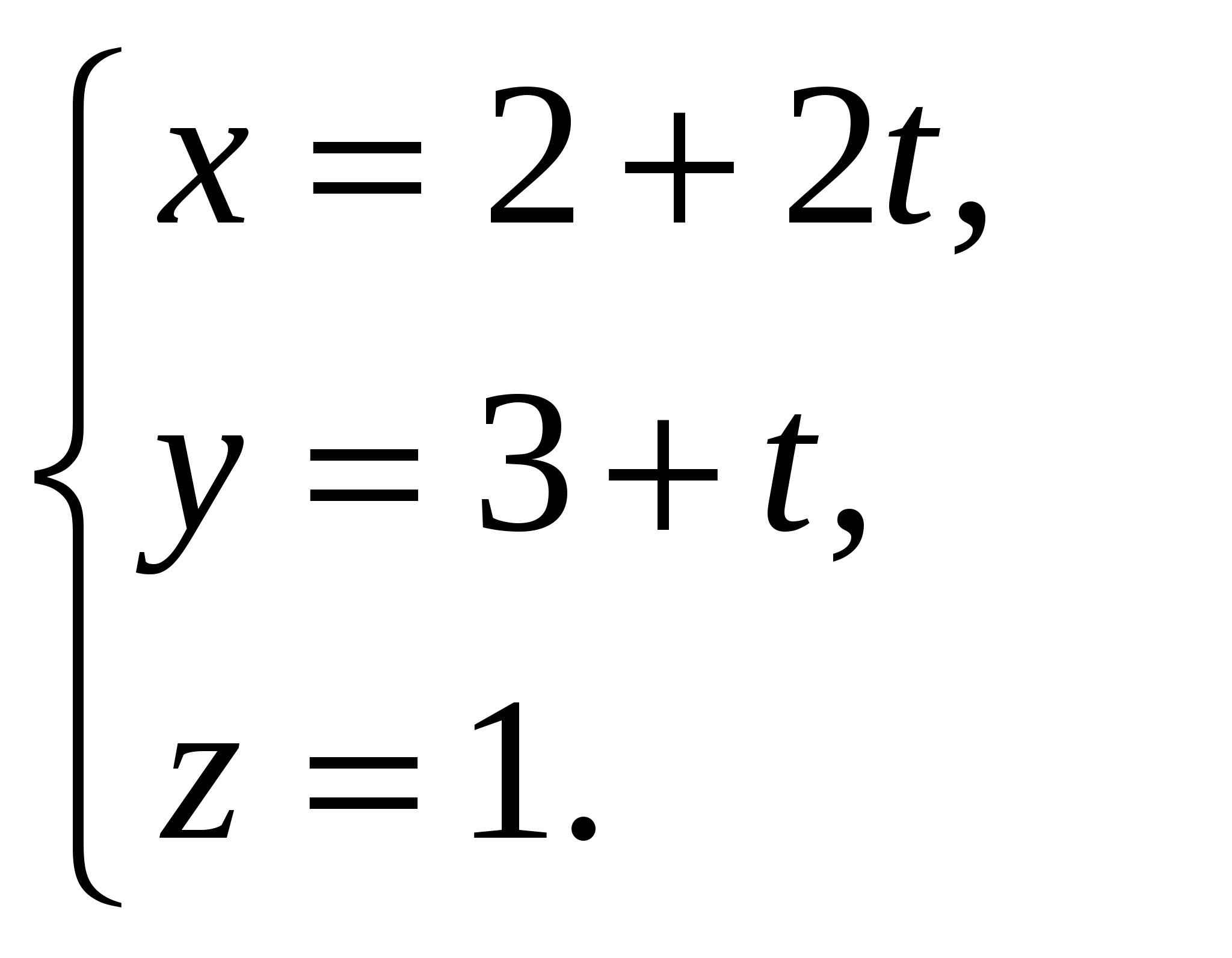 D. D. 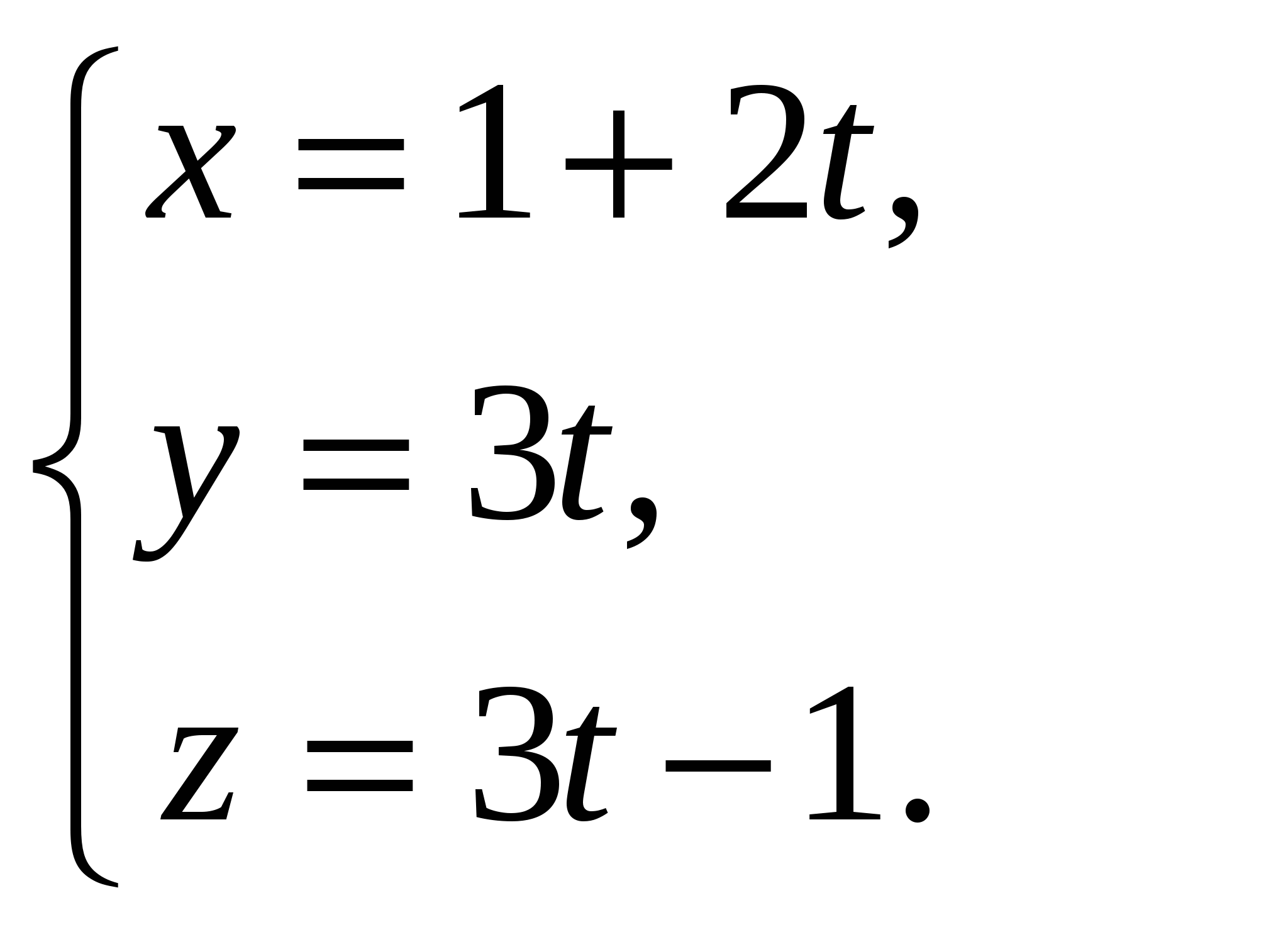
Ключи правильных ответов
№
|
Правильные
ответы
|
№
|
Правильные
ответы
|
1
|
В
|
11
|
А
|
2
|
А
|
12
|
А
|
3
|
С
|
13
|
D
|
4
|
А
|
14
|
С
|
5
|
С
|
15
|
С
|
6
|
В
|
16
|
D
|
7
|
А
|
17
|
Б
|
8
|
В
|
18
|
D
|
9
|
С
|
19
|
C
|
10
|
А
|
20
|
Б
|
2.8 Экзаменационные вопросы по курсу: по курсу:
1. Матрицы. Действия над матрицами.
2. Обратная матрица. Ранг матрицы.
3. Определители квадратных матриц. Вычисление определителей.
4. Свойства определителей (одно из них доказать).
5. Системы линейных уравнений. Метод обратной матрицы и  формулы Крамера. формулы Крамера.
6. Метод Гаусса.
7. Векторы на плоскости и в пространстве.
8. Векторное пространство. Размерность и базис.
9. Линейные операторы.
10. Квадратичные формы.
11. Уравнение прямой на плоскости и в пространстве.
12. Кривые 2-го порядка: окружность и эллипс.
13. Кривые 2-го порядка: парабола и гипербола.
14. Понятие функции. Основные свойства функций.
15. Предел числовой последовательности и предел функции.
16. Основные теоремы о пределах.
17. Замечательные пределы.
18. Непрерывность функции.
19. Определение производной. Основные правила дифференцирования (одно из них доказать).
20. Производная сложной и обратной функции.
21. Основные теоремы дифференциального исчисления.
22. Правило Лопиталя.
23. Общая схема исследования функций и построения их графиков.
24. Дифференциал функции, его применение в приближенных вычислениях.
25. Неопределенный интеграл, его свойства.
26. Метод интегрирования по частям.
27. Понятие определенного интеграла, его свойства. Формула Ньютона –Лейбница.
28. Несобственные интегралы.
29. Дифференциальные уравнения 1-го порядка, виды и методы решений.
30. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
31. Числовые ряды. Необходимый признак сходимости.
32. Признаки сходимости рядов с положительными членами.
33. Признаки сходимости рядов с членами произвольного знака.
34. Степенные ряды.
35. Функции нескольких переменных, частные производные и дифференциал.
36. Наибольшее и наименьшее значения функции нескольких переменных.
37. Экстремум функции нескольких переменных.
38. Условный экстремум. Метод Лагранжа.
страница 1 | страница 2 страница 3
|