страница 1 | страница 2 страница 3 страница 4 | страница 5 | страница 6
Задание 4
1. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,5. Определить вероятность того, что из 10 выданных кредитов будут возвращены в установленный договором срок: а) 5 кредитов; б) менее 5 кредитов; в) по крайней мере, один кредит.
2. В ходе аудиторской проверки строительной компании, аудитор случайным образом отбирает 10 документов. При условии, что в среднем 5 % документов содержат ошибки, найти вероятность того, что: а) менее 3 документов содержат ошибки; б) хотя бы один документ содержит ошибки; в) более 3 документов содержат ошибки.
3. Тестовое задание состоит из 10 вопросов, предусматривающих ответы «да» или «нет». Предположим, тестируемый не знает ответ ни на один из вопросов и выбирает ответы наугад. Какова вероятность того, что: а) он даст не менее 8 правильных ответов, необходимых для сдачи теста; б) найдите наиболее вероятное число правильных ответов, которые даст тестируемый, и вероятность получения этого наиболее вероятного числа ответов.
4. В городе 10 коммерческих банков, работающих независимо друг от друга. У каждого банка риск банкротства в течение года составляет 10 %. Определить вероятность того, что в течение года обанкротится: а) менее 2 банков; б) хотя бы один банк; в) не менее 2 банков.
5. Записи страховой компании показали, что 10 % держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. В случайном порядке было отобрано 10 человек старше 50 лет, имеющих полисы. Определить вероятность того, что из 10 человек потребуют возмещения страховых сумм: а) более 3 человек; б) хотя бы один человек; в) найдите наиболее вероятное число держателей страховых полисов, которые потребуют возмещение страховых сумм, и вероятность, соответствующую этому числу.
6. Телевизионный канал рекламирует новый вид автомобилей. Вероятность того, что телезритель увидит эту рекламу, оценивается в 10 %. Какова вероятность того, что из 20 телезрителей, отобранных в случайном, порядке рекламу увидят: а) ровно 5 человек; б) более 5 человек; в) найдите наиболее вероятное число телезрителей, увидевших рекламу автомобилей.
7. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,6. Определить вероятность того, что из 12 выданных кредитов будут возвращены в установленный договором срок: а) 6 кредитов; б) менее 6 кредитов; в) по крайней мере, один кредит.
8. В ходе аудиторской проверки строительной компании, аудитор случайным образом отбирает 8 документов. При условии, что в среднем 4 % документов содержат ошибки, найти вероятность того, что: а) менее 2 документов содержат ошибки; б) хотя бы один документ содержит ошибки; в) более 2 документов содержат ошибки.
9. Тестовое задание состоит из 15 вопросов, предусматривающих ответы «да» или «нет». Предположим, тестируемый не знает ответ ни на один из вопросов и выбирает ответы наугад. Какова вероятность того, что: а) он даст не менее 12 правильных ответов, необходимых для сдачи теста; б) найдите наиболее вероятное число правильных ответов, которые даст тестируемый, и вероятность получения этого наиболее вероятного числа ответов.
10. В городе 8 коммерческих банков, работающих независимо друг от друга. У каждого банка риск банкротства в течение года составляет 8 %. Определить вероятность того, что в течение года обанкротится: а) менее 3 банков; б) хотя бы один банк; в) не менее 3 банков.
11. Записи страховой компании показали, что 15 % держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. В случайном порядке было отобрано 20 человек старше 50 лет, имеющих полисы. Определить вероятность того, что из 20 человек потребуют возмещения страховых сумм: а) более 5 человек; б) хотя бы один человек; в) найдите наиболее вероятное число держателей страховых полисов, которые потребуют возмещение страховых сумм, и вероятность, соответствующую этому числу.
12. Телевизионный канал рекламирует новый вид автомобилей. Вероятность того, что телезритель увидит эту рекламу, оценивается в 9 %. Какова вероятность того, что из 10 телезрителей, отобранных в случайном, порядке рекламу увидят: а) ровно 6 человек; б) более 6 человек; в) найдите наиболее вероятное число телезрителей, увидевших рекламу автомобилей.
13. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,55. Определить вероятность того, что из 13 выданных кредитов будут возвращены в установленный договором срок: а) 7 кредитов; б) менее 7 кредитов; в) по крайней мере, один кредит.
14. В ходе аудиторской проверки строительной компании, аудитор случайным образом отбирает 16 документов. При условии, что в среднем 2 % документов содержат ошибки, найти вероятность того, что: а) менее 3 документов содержат ошибки; б) хотя бы один документ содержит ошибки; в) более 3 документов содержат ошибки.
15. Тестовое задание состоит из 18 вопросов, предусматривающих ответы «да» или «нет». Предположим, тестируемый не знает ответ ни на один из вопросов и выбирает ответы наугад. Какова вероятность того, что: а) он даст не менее 16 правильных ответов, необходимых для сдачи теста; б) найдите наиболее вероятное число правильных ответов, которые даст тестируемый, и вероятность получения этого наиболее вероятного числа ответов.
16. В городе 19 коммерческих банков, работающих независимо друг от друга. У каждого банка риск банкротства в течение года составляет 4 %. Определить вероятность того, что в течение года обанкротится: а) менее 2 банков; б) хотя бы один банк; в) не менее 2 банков.
17. Записи страховой компании показали, что 7 % держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. В случайном порядке было отобрано 20 человек старше 50 лет, имеющих полисы. Определить вероятность того, что из 20 человек потребуют возмещения страховых сумм: а) более 5 человек; б) хотя бы один человек; в) найдите наиболее вероятное число держателей страховых полисов, которые потребуют возмещение страховых сумм, и вероятность, соответствующую этому числу.
18. Телевизионный канал рекламирует новый вид автомобилей. Вероятность того, что телезритель увидит эту рекламу, оценивается в 12 %. Какова вероятность того, что из 20 телезрителей, отобранных в случайном, порядке рекламу увидят: а) ровно 8 человек; б) более 8 человек; в) найдите наиболее вероятное число телезрителей, увидевших рекламу автомобилей.
19. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,4. Определить вероятность того, что из 14 выданных кредитов будут возвращены в установленный договором срок: а) 6 кредитов; б) менее 6 кредитов; в) по крайней мере, один кредит.
20. В ходе аудиторской проверки строительной компании, аудитор случайным образом отбирает 9 документов. При условии, что в среднем 2 % документов содержат ошибки, найти вероятность того, что: а) менее 3 документов содержат ошибки; б) хотя бы один документ содержит ошибки; в) более 3 документов содержат ошибки.
21. Тестовое задание состоит из 10 вопросов, предусматривающих ответы «да» или «нет». Предположим, тестируемый не знает ответ ни на один из вопросов и выбирает ответы наугад. Какова вероятность того, что: а) он даст не менее 9 правильных ответов, необходимых для сдачи теста; б) найдите наиболее вероятное число правильных ответов, которые даст тестируемый, и вероятность получения этого наиболее вероятного числа ответов.
22. В городе 22 коммерческих банков, работающих независимо друг от друга. У каждого банка риск банкротства в течение года составляет 3 %. Определить вероятность того, что в течение года обанкротится: а) менее 5 банков; б) хотя бы один банк; в) не менее 5 банков.
23. Записи страховой компании показали, что 10 % держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. В случайном порядке было отобрано 8 человек старше 50 лет, имеющих полисы. Определить вероятность того, что из 8 человек потребуют возмещения страховых сумм: а) более 6 человек; б) хотя бы один человек; в) найдите наиболее вероятное число держателей страховых полисов, которые потребуют возмещение страховых сумм, и вероятность, соответствующую этому числу.
24. Телевизионный канал рекламирует новый вид автомобилей. Вероятность того, что телезритель увидит эту рекламу, оценивается в 11 %. Какова вероятность того, что из 15 телезрителей, отобранных в случайном, порядке рекламу увидят: а) ровно 5 человек; б) более 5 человек; в) найдите наиболее вероятное число телезрителей, увидевших рекламу автомобилей.
25. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,8. Определить вероятность того, что из 20 выданных кредитов будут возвращены в установленный договором срок: а) 15 кредитов; б) менее 15 кредитов; в) по крайней мере, один кредит.
26. В ходе аудиторской проверки строительной компании, аудитор случайным образом отбирает 13 документов. При условии, что в среднем 1 % документов содержат ошибки, найти вероятность того, что: а) менее 4 документов содержат ошибки; б) хотя бы один документ содержит ошибки; в) более 4 документов содержат ошибки.
27. Тестовое задание состоит из 14 вопросов, предусматривающих ответы «да» или «нет». Предположим, тестируемый не знает ответ ни на один из вопросов и выбирает ответы наугад. Какова вероятность того, что: а) он даст не менее 12 правильных ответов, необходимых для сдачи теста; б) найдите наиболее вероятное число правильных ответов, которые даст тестируемый, и вероятность получения этого наиболее вероятного числа ответов.
28. В городе 17 коммерческих банков, работающих независимо друг от друга. У каждого банка риск банкротства в течение года составляет 10 %. Определить вероятность того, что в течение года обанкротится: а) менее 5 банков; б) хотя бы один банк; в) не менее 5 банков.
29. Записи страховой компании показали, что 17 % держателей страховых полисов старше 50 лет потребовали возмещения страховых сумм. В случайном порядке было отобрано 20 человек старше 50 лет, имеющих полисы. Определить вероятность того, что из 20 человек потребуют возмещения страховых сумм: а) более 6 человек; б) хотя бы один человек; в) найдите наиболее вероятное число держателей страховых полисов, которые потребуют возмещение страховых сумм, и вероятность, соответствующую этому числу.
30. Телевизионный канал рекламирует новый вид автомобилей. Вероятность того, что телезритель увидит эту рекламу, оценивается в 12 %. Какова вероятность того, что из 10 телезрителей, отобранных в случайном, порядке рекламу увидят: а) ровно 4 человека; б) более 4 человек; в) найдите наиболее вероятное число телезрителей, увидевших рекламу автомобилей.
Задание 5
1. Вероятность того, что малое предприятие региона обанкротится за время Т равна 0,2. Определить вероятность того, что из 100 малых предприятий региона, работающих независимо друг от друга, за время Т приостановят свою деятельность: а) ровно 40 предприятий; б) от 40 до 80 предприятий.
2. Предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по 200 адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие составляет 5 %. Какова вероятность того, что из 200 разосланных анкет «возвратятся»: а) менее 5 анкет; б) найдите наиболее вероятное число анкет, «возвратившихся» на предприятие и соответствующую этому значению вероятность.
3. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,5. Определить вероятность того, что из 100 выданных кредитов, будут возвращены в установленный договором срок: а) ровно 80 кредитов; б) от 80 до 100 кредитов.
4. Вероятность того, что выпускник экономического факультета «откроет свое дело» равна 0,05. Определить вероятность того, что из 100 выпускников экономического факультета свое дело откроют: а) менее 5 выпускников; б) не менее 5 выпускников; в) хотя бы один выпускник.
5. В банк поступает выручка из магазинов. Среди поступающей денежной массы купюр достоинством 5 тыс. руб. в среднем 8 % . Какова вероятность того, что из случайно отобранных 500 купюр: а) ровно 70 купюр достоинством 5 тыс. руб.; б) от 80 до 400 купюр достоинством 5 тыс. руб.
6. В выставке фирм, реализующих компьютерную технику и комплектующих для нее, участвуют 200 представителей фирм. Вероятность того, что в определенный день представителем фирмы будет заключен контракт на продажу продукции, равна 0,2. Определить вероятность того, что из 200 представителей фирм в определенный день заключат контракты: а) более 20 представителей; б) ровно 20 представителей.
7. Вероятность того, что малое предприятие региона обанкротится за время Т равна 0,1. Определить вероятность того, что из 200 малых предприятий региона, работающих независимо друг от друга, за время Т приостановят свою деятельность: а) ровно 50 предприятий; б) от 40 до 100 предприятий.
8. Предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по 300 адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие составляет 7 %. Какова вероятность того, что из 300 разосланных анкет «возвратятся»: а) менее 10 анкет; б) найдите наиболее вероятное число анкет, «возвратившихся» на предприятие и соответствующую этому значению вероятность.
9. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,6. Определить вероятность того, что из 200 выданных кредитов, будут возвращены в установленный договором срок: а) ровно 70 кредитов; б) от 70 до 150 кредитов.
10. Вероятность того, что выпускник экономического факультета «откроет свое дело» равна 0,07. Определить вероятность того, что из 90 выпускников экономического факультета свое дело откроют: а) менее 6 выпускников; б) не менее 6 выпускников; в) хотя бы один выпускник.
11. В банк поступает выручка из магазинов. Среди поступающей денежной массы купюр достоинством 10 тыс. руб. в среднем 7 % . Какова вероятность того, что из случайно отобранных 600 купюр: а) ровно 100 купюр достоинством 10 тыс. руб.; б) от 120 до 500 купюр достоинством 10 тыс. руб.
12. В выставке фирм, реализующих компьютерную технику и комплектующих для нее, участвуют 150 представителей фирм. Вероятность того, что в определенный день представителем фирмы будет заключен контракт на продажу продукции, равна 0,3. Определить вероятность того, что из 150 представителей фирм в определенный день заключат контракты: а) более 40 представителей; б) ровно 40 представителей.
13. Вероятность того, что малое предприятие региона обанкротится за время Т равна 0,15. Определить вероятность того, что из 170 малых предприятий региона, работающих независимо друг от друга, за время Т приостановят свою деятельность: а) ровно 80 предприятий; б) от 90 до 120 предприятий.
14. Предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по 170 адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие составляет 3 %. Какова вероятность того, что из 170 разосланных анкет «возвратятся»: а) менее 4 анкет; б) найдите наиболее вероятное число анкет, «возвратившихся» на предприятие и соответствующую этому значению вероятность.
15. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,55. Определить вероятность того, что из 130 выданных кредитов, будут возвращены в установленный договором срок: а) ровно 80 кредитов; б) от 80 до 130 кредитов.
16. Вероятность того, что выпускник экономического факультета «откроет свое дело» равна 0,08. Определить вероятность того, что из 80 выпускников экономического факультета свое дело откроют: а) менее 9 выпускников; б) не менее 9 выпускников; в) хотя бы один выпускник.
17. В банк поступает выручка из магазинов. Среди поступающей денежной массы купюр достоинством 20 тыс. руб. в среднем 9 % . Какова вероятность того, что из случайно отобранных 700 купюр: а) ровно 90 купюр достоинством 20 тыс. руб.; б) от 80 до 600 купюр достоинством 20 тыс. руб.
18. В выставке фирм, реализующих компьютерную технику и комплектующих для нее, участвуют 90 представителей фирм. Вероятность того, что в определенный день представителем фирмы будет заключен контракт на продажу продукции, равна 0,27. Определить вероятность того, что из 90 представителей фирм в определенный день заключат контракты: а) более 30 представителей; б) ровно 30 представителей.
19. Вероятность того, что малое предприятие региона обанкротится за время Т равна 0,3. Определить вероятность того, что из 190 малых предприятий региона, работающих независимо друг от друга, за время Т приостановят свою деятельность: а) ровно 90 предприятий; б) от 70 до 130 предприятий.
20. Предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по 260 адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие составляет 5 %. Какова вероятность того, что из 260 разосланных анкет «возвратятся»: а) менее 13 анкет; б) найдите наиболее вероятное число анкет, «возвратившихся» на предприятие и соответствующую этому значению вероятность.
21. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,4. Определить вероятность того, что из 250 выданных кредитов, будут возвращены в установленный договором срок: а) ровно 100 кредитов; б) от 100 до 200 кредитов.
22. Вероятность того, что выпускник экономического факультета «откроет свое дело» равна 0,07. Определить вероятность того, что из 110 выпускников экономического факультета свое дело откроют: а) менее 8 выпускников; б) не менее 10 выпускников; в) хотя бы один выпускник.
23. В банк поступает выручка из магазинов. Среди поступающей денежной массы купюр достоинством 5 тыс. руб. в среднем 4 % . Какова вероятность того, что из случайно отобранных 400 купюр: а) ровно 80 купюр достоинством 5 тыс. руб.; б) от 150 до 400 купюр достоинством 5 тыс. руб.
24. В выставке фирм, реализующих компьютерную технику и комплектующих для нее, участвуют 160 представителей фирм. Вероятность того, что в определенный день представителем фирмы будет заключен контракт на продажу продукции, равна 0,9. Определить вероятность того, что из 160 представителей фирм в определенный день заключат контракты: а) более 25 представителей; б) ровно 25 представителей.
25. Вероятность того, что малое предприятие региона обанкротится за время Т равна 0,1. Определить вероятность того, что из 200 малых предприятий региона, работающих независимо друг от друга, за время Т приостановят свою деятельность: а) ровно 60 предприятий; б) от 30 до 130 предприятий.
6. Предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по 100 адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие составляет 1 %. Какова вероятность того, что из 100 разосланных анкет «возвратятся»: а) менее 2 анкет; б) найдите наиболее вероятное число анкет, «возвратившихся» на предприятие и соответствующую этому значению вероятность.
27. Вероятность возвращения клиентом банковского кредита в установленный договором срок равна 0,65. Определить вероятность того, что из 230 выданных кредитов, будут возвращены в установленный договором срок: а) ровно 200 кредитов; б) от 100 до 200 кредитов.
28. Вероятность того, что выпускник экономического факультета «откроет свое дело» равна 0,04. Определить вероятность того, что из 90 выпускников экономического факультета свое дело откроют: а) менее 7 выпускников; б) не менее 8 выпускников; в) хотя бы один выпускник.
29. В банк поступает выручка из магазинов. Среди поступающей денежной массы купюр достоинством 50 тыс. руб. в среднем 12 % . Какова вероятность того, что из случайно отобранных 700 купюр: а) ровно 200 купюр достоинством 50 тыс. руб.; б) от 300 до 600 купюр достоинством 50 тыс. руб.
30. В выставке фирм, реализующих компьютерную технику и комплектующих для нее, участвуют 150 представителей фирм. Вероятность того, что в определенный день представителем фирмы будет заключен контракт на продажу продукции, равна 0,7. Определить вероятность того, что из 150 представителей фирм в определенный день заключат контракты: а) более 40 представителей; б) ровно 50 представителей.
Задание 6
1. Товаровед проверяет изделия на стандартность, но проверяет не более пяти изделий. Составить закон распределения числа проверенных изделий, если вероятность того, что изделие будет признано стандартным, равна 0,6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение полученной случайной величины.
2. В лотерее на 1000 билетов разыгрываются три вещи, стоимости которых 50, 30 и 20 рублей. Составить закон распределения суммы выигрыша для лица, имеющего два билета. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение полученной случайной величины.
3. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые посетит студент, если в городе пять библиотек. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение полученной случайной величины.
4. Вероятность того, что вошедший в магазин покупатель сделает покупку, равна 0,4. Предполагая, что покупатель делает не более одной покупки, составить закон распределения числа покупок, сделанных в магазине, если вошло 5 человек. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение, полученной случайной величины.
5. Имеются 4 ключа из которых только один подходит к замку. Составить закон распределения числа попыток открывания замка, если испробованный ключ в последующих попытках не участвует. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
6. В магазине имеются 20 телевизоров, из них 7 имеют дефекты. Необходимо: а) составить закон распределения числа телевизоров с дефектами среди выбранных наудачу пяти; б) найти математическое ожидание и дисперсию этой случайной величины: в) определить вероятность того, что среди выбранных нет телевизоров с дефектами.
7. Распределение дискретной случайной величины  задано формулой p{=k} =Ck2, где k=1, 2, 3, 4, 5. Найти: а) константу С; б) вероятность события |–2| 1.
8. Дискретная случайная величина – число мальчиков в семьях с 4 детьми. Предполагая равновероятными рождения мальчика и девочки: а) найдите закон распределения ; б) найдите вероятности событий: А – в семье не менее 2, но не более 3 мальчиков; В – не более 3 мальчиков; С – более одного мальчика. Найти среднее квадратическое отклонение случайной величины .
9. C вероятностью попадания при одном выстреле 0,8 охотник стреляет по дичи до первого попадания, но успевает сделать не более 3 выстрелов. Дискретная случайная величина – число промахов. а) Найдите закон распределения . б) Найдите вероятности событий: <2; 2; 1 < 3. в) Найти математическое ожидание М[], дисперсию D[], среднее квадратическое отклонение [].
10. 2 стрелка делают по одному выстрелу в мишень. Вероятность попадания для первого стрелка при одном выстреле – 0,6, для второго – 0,7. Дискретная случайная величина – число попаданий в мишень. а) Найдите закон распределения . б) Найдите вероятность события 1.в) Найти математическое ожидание М[], дисперсию D[], среднее квадратическое отклонение [].
11. В коробке имеется 8 карандашей, из которых 3 красных. Из этой коробки наудачу извлекаются 3 карандаша. а) Найдите закон распределения случайной величины , равной числу красных карандашей в выборке. б) Найдите вероятность события 0<2. в) Найти математическое ожидание М[], дисперсию D[], среднее квадратическое отклонение [].
12. Автомат штампует детали. Контролируется длина детали , которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактическая длина изготовленных деталей не менее 48 мм и не более 52 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 49 мм; б) меньше 51 мм. (Указание: из равенства Р(48<<52) = 1 предварительно найти ).
13. В партии из 10 деталей имеется 5 стандартных. Из этой партии наудачу взято 3 детали. Найдите закон распределения случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание М[], дисперсию D[], среднее квадратическое отклонение [].
14. Два стрелка стреляют по одной мишени, делая независимо друг от друга по два выстрела. Вероятность попадания в мишень для первого стрелка – 0,5, для второго – 0,6. Найдите закон распределения случайной величины , равной общему числу попаданий в мишень. Найти математическое ожидание М[], дисперсию D[], среднее квадратическое отклонение [].
15. Рабочий обслуживает 3 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка – 0,7, для второго – 0,8, для третьего – 0,9. Найдите закон распределения случайной величины , равной числу станков, которые не потребуют внимания рабочего. Найти математическое ожидание М[], дисперсию D[], среднее квадратическое отклонение [].
16. Случайная величина , сосредоточенная на интервале [2;6], задана функцией распределения F(x) =1/16(x2–4x+4). Найти вероятность того, что случайная величина Х примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.
17. Случайная величина , сосредоточенная на интервале [–1,3], задана функцией распределения F(x)=0,25x+0,25. Найти вероятность попадания случайной величины в интервал [0; 2]. Построить график функции F(x).
18. Случайная величина , сосредоточенная на интервале [2;6], задана функцией распределения F(x)=1/16(x2–4x+4). Найти вероятность того, что случайная величина примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.
19. Вероятность попадания стрелком при каждом выстреле равна 0,4. Имея в запасе 6 патронов, он ведет стрельбу до первого попадания в мишень или до израсходования всех патронов. Найдите закон распределения случайной величины , равной числу израсходованных патронов. Найти математическое ожидание М[], дисперсию D[], среднее квадратическое отклонение [].
20. Случайная величина , сосредоточенная на интервале [2;6], задана функцией распределения F(x)=1/16(x2–4x+4). Найти вероятность того, что случайная величина примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.
21. Торговый агент имеет 5 телефонных номеров потенциальных покупателей и звонит им до тех пор, пока не получит заказ на покупку товара. Вероятность того, что потенциальный покупатель сделает заказ, равна 0,4. Составить закон распределения числа телефонных разговоров, которые предстоит провести агенту. Найти математическое ожидание и дисперсию этой случайной величины.
22. Стрелок ведет стрельбу по цели с вероятностью попадания при каждом выстреле 0,2. За каждое попадание он получает 5 очков, а в случае промаха очков ему не начисляют. Составить закон распределения числа очков, полученных стрелком за 3 выстрела. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
23. Охотник, имеющий 4 патрона, стреляет по дичи до первого попадания или до израсходования всех патронов. Вероятность попадания при первом выстреле равна 0,6, при каждом последующем – уменьшается на 0,1. Необходимо: а) составить закон распределения числа патронов, израсходованных охотником; б) найти математическое ожидание и дисперсию этой случайной величины.
24. Экзаменатор задает студенту вопросы, пока тот правильно отвечает. Как только число правильных ответов достигнет четырех либо студент ответит неправильно, экзаменатор прекращает задавать вопросы. Вероятность правильного ответа на один вопрос равна 2/3. Составить закон распределения числа заданных студенту вопросов. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
25. Каждый поступающий в институт должен сдать 3 экзамена. Вероятность успешной сдачи первого экзамена 0,9, второго – 0,8, третьего – 0,7. Следующий экзамен поступающий сдает только в случае успешной сдачи предыдущего. Составить закон распределения числа экзаменов, сдававшихся поступающим в институт. Найти математическое ожидание и дисперсию этой случайной величины.
26. По данным длительной проверки качества запчастей определенного вида брак составляет 3%. Изготовлено 1000 запчастей. Определить математическое ожидание и среднее квадратическое отклонение числа годных запчастей.
27. Найти вероятность того, что в течение смены произойдет не более двух отказов оборудования, при условии, что среднее число отказов в течение смены равно 1,6. (Предполагается, что число отказов имеет распределение Пуассона.)
28. Вероятность сдачи первого экзамена для данного студента равна 0.7, второго экзамена – 0.8, третьего – 0.7. С.в. – число сданных экзаменов. Найти ряд распределения и математическое ожидание с.в. . Вычислить значение функции распределения с.в. в точках 0; 1; 2,5; 10.
29. Вероятность выпуска прибора, удовлетворяющего требованиям качества, равна 0,9 . В контрольной партии четыре прибора. С.в. – число приборов, удовлетворяющих требованиям качества. Найти ряд распределения и математическое ожидание с.в. . Вычислить значение функции распределения с.в. X в точках 0; 1; 2,5; 10.
30. Функция распределения случайной величины имеет вид:
 
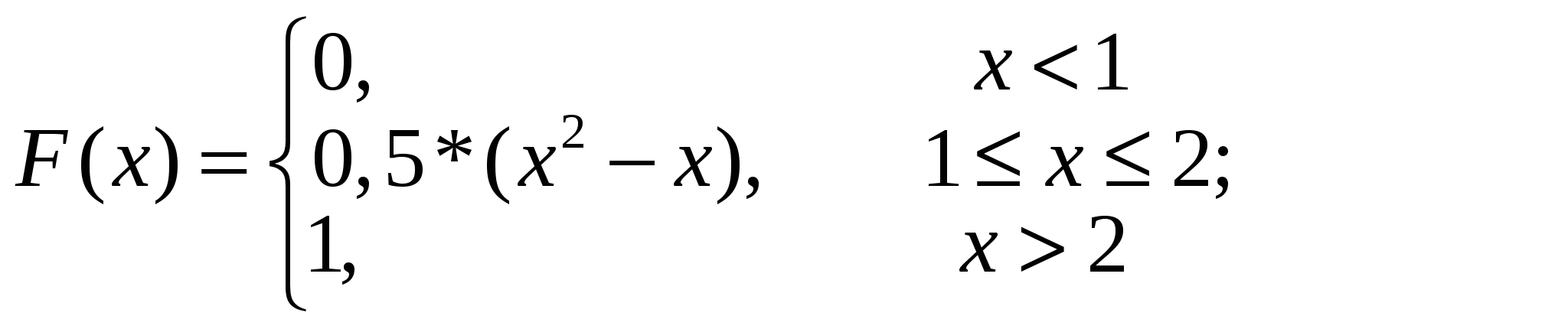
Найти функцию плотности распределения с.в. и построить ее график. Найти медиану с.в. . Вычислить значение функции распределения с.в. в точках 0; 1; 2,5; 10. Найти вероятность попадания значения с.в. в интервал (1.2, 1,5).
Задание 7
1. Все значения равномерно распределенной случайной величины принадлежат отрезку [2, 8]. Найти вероятность попадания случайной величины в отрезок [3, 5].
2. Найти среднее время безотказной работы устройства, если известно, что для данного устройства вероятность работы без сбоев в течение 100 часов равна 0,2. (Предполагается, что время безотказной работы распределено по экспоненциальному закону).
3. Время безотказной работы механизма подчинено показательному закону с плотностью распределения вероятностей 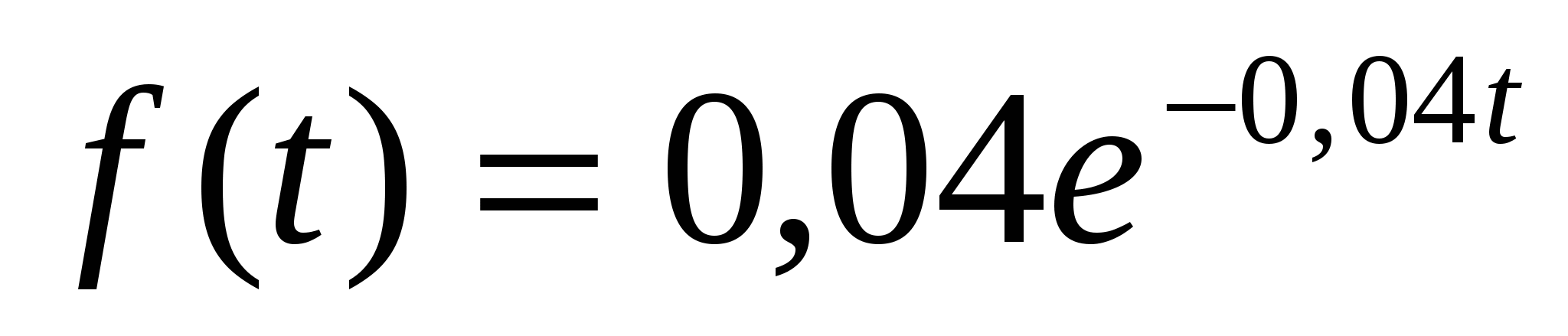 при t > 0 (t – время в часах). Найти вероятность того, что механизм проработает безотказно не менее 100 часов.
4. Время простоя оборудования в ожидании ремонта распределено по показательному (экспоненциальному) закону с математическим ожиданием, равным 2 часа. Найти вероятность простоя более трех часов.
5. Предполагая, что время, необходимое для ремонта поступившего вагона, распределено по показательному (экспоненциальному) закону с параметром =0,125 [час-1], найти вероятность того, что для ремонта одного вагона понадобится не более шести часов.
6. В результате проверки точности работы прибора установлено, что 60% ошибок не вышло за пределы 20 мм, а остальные ошибки вышли за эти пределы. Определите среднее квадратическое отклонение ошибок прибора, если известно, что систематических ошибок прибор не дает, а случайные ошибки распределены по нормальному закону.
7. Случайная величина распределена нормально с математическим ожиданием М[]=25 и дисперсией D[]=100. Напишите выражение для плотности вероятности f(x) и функции распределения F(x). Чему равна вероятность события 1535?
8. Взвешивание на весах производится без систематических ошибок. Случайные ошибки имеют с дисперсию, равную 100 г2. Полагая, что ошибки распределены по нормальному закону, определить вероятность того, что ошибка при взвешивании предмета по абсолютной величине не превысит 50 г.
9. Производится измерение вала без систематических ошибок. Случайные ошибки измерения подчинены нормальному закону распределения со средним квадратическим отклонением, равным 1 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 1,5 мм.
10. Автоматический станок производит однотипные изделия, номинальный размер которых равен 3 см. Фактический размер изделий имеет разброс, подчиненный нормальному закону с []=0,05 см. Систематические отклонения размера отсутствуют. При контроле отбраковываются все изделия, размер которых отличается от номинального больше, чем на 0,12 см. Определить, какой процент изделий в среднем будет отбраковываться.
11. Случайная величина распределена нормально с математическим ожиданием М[]=25 и дисперсией D[]=100. Напишите выражение для плотности вероятности f(x) и функции распределения F(x). Чему равна вероятность события 1535?
12. Производится измерение вала без систематических ошибок. Случайные ошибки измерения подчинены нормальному закону распределения со средним квадратическим отклонением, равным 1 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 1 мм.
13. Случайная величина , сосредоточенная на интервале [2;6], задана функцией распределения F(x)=1/16(x2–4x+4). Найти вероятность того, что случайная величина примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.
14. Все значения равномерно распределенной случайной величины принадлежат отрезку [3; 9]. Найти вероятность попадания значения случайной величины : а) в отрезок [1; 5]; б) в отрезок [4; 10 ].
15. Автоматический станок производит однотипные изделия, номинальный размер которых равен 3 см. Фактический размер изделий имеет разброс, подчиненный нормальному закону с []=0,05 см. Систематические отклонения размера отсутствуют. При контроле отбраковываются все изделия, размер которых отличается от номинального больше, чем на 0,12 см. Определить, какой процент изделий в среднем будет отбраковываться.
16. Завод изготовляет шарики для подшипников, номинальный диаметр которых равен 10 мм, а фактический диаметр случаен и распределен по нормальному закону с математическим ожиданием, равным 10 мм и средним квадратическим отклонением 0,4 мм. При контроле бракуются все шарики, не проходящие через круглое отверстие диаметром 10,7 мм, и все, проходящие через круглое отверстие диаметром 9,3 мм. Какой процент шариков в среднем будет отбраковываться?
17. Случайная величина – ошибка измерительного прибора распределена по нормальному закону с дисперсией, равной 16 мкм и математическим ожиданием, равным нулю. Найти вероятность того, что величина ошибки при одном измерении не превзойдет по абсолютной величине 6 мкм.
18. Измерительный прибор имеет систематическую ошибку, равную 5 м и среднее квадратическое отклонение случайной ошибки – 75 м. (Предполагается, что возникающие ошибки распределены по нормальному закону.) Какова вероятность того, что ошибка измерения не превзойдет по абсолютной величине 5 м?
19. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением, равным 100 м. Найти вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м.
20. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением, равным 100 м. Найти вероятность того, что измеренная дальность не превзойдет истинной.
21. Коробки с шоколадом упаковываются автоматически: их средняя масса равна 1,06 кг. Найти среднее квадратическое отклонение, если известно, что 5% коробок имеют массу, меньшую 1 кг. Предполагается, что масса коробок распределена по нормальному закону.
22. Размер деталей подчинен закону нормального распределения с математическим ожиданием 15 мм и дисперсией 0,25 мм2. Определить ожидаемый процент брака, если допустимые размеры деталей находятся в пределах от 14 до17 мм.
23. Найти среднее время безотказной работы устройства, если известно, что для данного устройства вероятность работы без сбоев в течение 100 часов равна 0,2. (Предполагается, что время безотказной работы распределено по экспоненциальному закону.)
24. Считается, что изделие – высшего качества, если отклонение его размеров от номинальных не превосходит по абсолютной величине 3,6 мм. Случайные отклонения размера изделия от номинального подчиняются нормальному закону со средним квадратичным отклонением, равным 3 мм. Систематические отклонения отсутствуют. Определить среднее число изделий высшего качества среди 100 изготовленных.
25. Время безотказной работы механизма подчинено показательному закону с плотностью распределения вероятностей  при t>0 (t – время в часах). Найти вероятность того, что механизм проработает безотказно 100 часов.
26. Считается, что отклонение длины изготавливаемых деталей от стандартной является случайной величиной, распределенной по нормальному закону. Систематические отклонения размера детали от номинала отсутствуют. Зная, что длина стандартной детали 40 см, а среднее квадратичное отклонение равно 0,4 см, определить, какую точность длины изделия можно гарантировать с вероятностью 0,8.
27. Случайная ошибка измерения дальности импульсным радиодальнометром имеет нормальное распределение со средним квадратическим отклонением, равным 50 м. Найти вероятность того, что измеренное значение дальности будет отличаться по абсолютной величине от истинного не более чем на 30 м, если систематическая ошибка дальнометра равна +20 м.
28. Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,04А.
29. Валик, изготовленный автоматом, считается стандартным, если отклонение его диаметра от проектного размера не превышает 2 мм. Случайные отклонения диаметра валиков подчиняются нормальному закону со средним квадратичным отклонением 1,6 мм и математическим ожиданием, равным 0. Сколько стандартных валиков (в %) изготовляет автомат?
30. Предполагая, что время, необходимое для ремонта поступившего вагона, распределено по экспоненциальному закону с параметром =0,25[час-1], найти вероятность того, что для ремонта одного вагона понадобится не более шести часов.
Задание 8
В результате наблюдений над некоторой случайной величиной получена следующая выборка. Используя эти данные, необходимо:
1) сделать механическую выборку, отобрав 25 значений (каждое пятое считая в порядке записи сверху вниз по колонкам и по этой выборке);
2) записать эмпирическую функцию распределения;
3) построить интервальный вариационный ряд;
4) построить гистограмму и эмпирическую кривую распределения;
5) предполагая, что генеральная совокупность имеет нормальное распределение с плотностью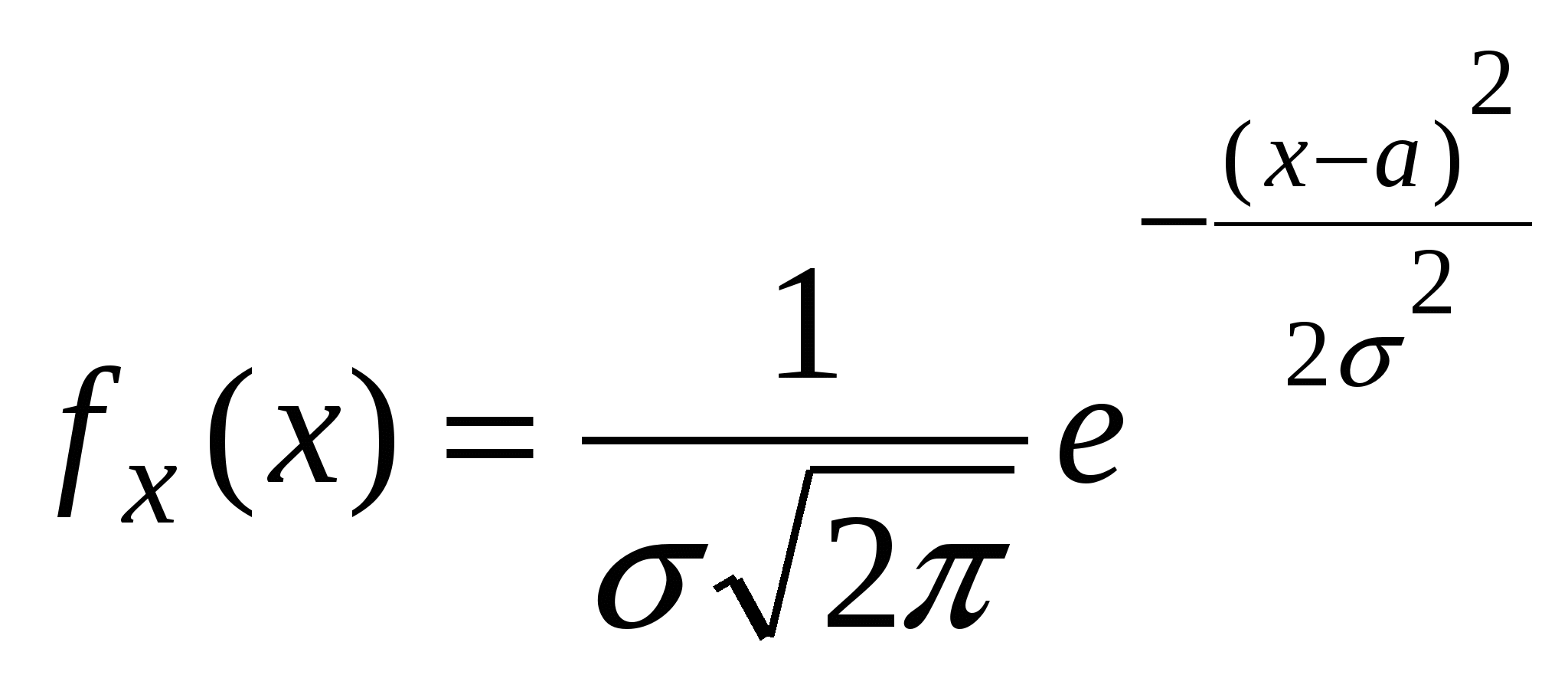 
найти методом моментов по выборке из 1) статистические оценки неизвестных параметров а и  ;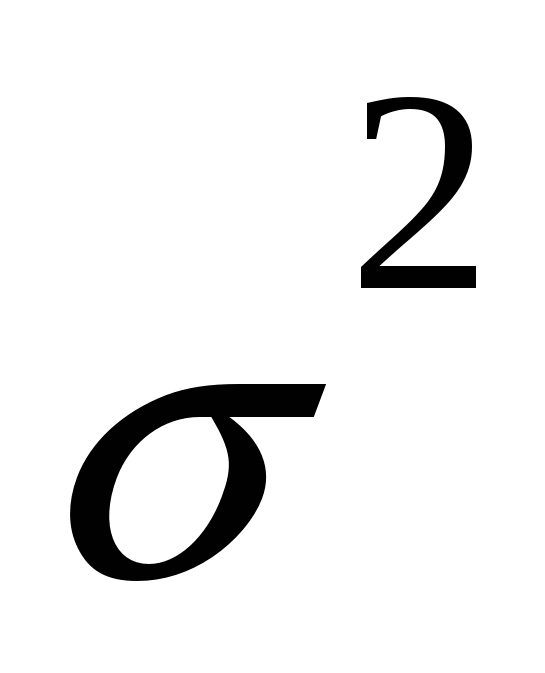
6) найти доверительные интервалы для а и 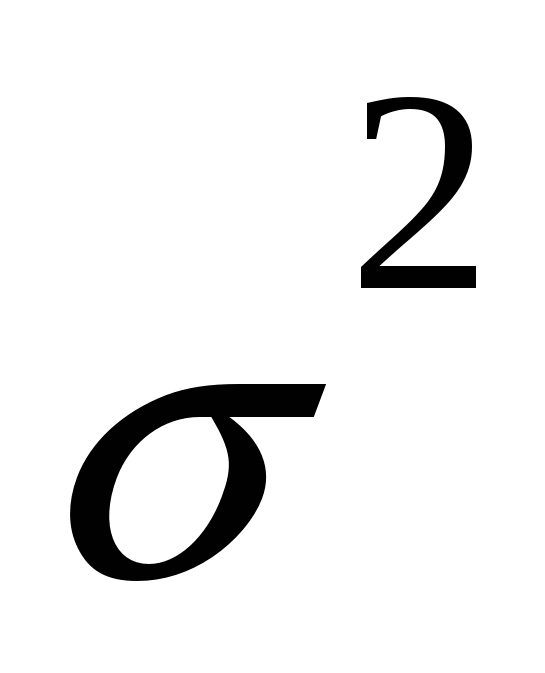с доверительной вероятностью 0,95.
8.1
Случайная величина характеризует продолжительность безотказного функционирования устройства (в часах).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.2
Случайная величина характеризует продолжительность выполнения технологической операции (в часах).
( 1) 35.7985 (11) 33.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 37.2978 (12) 39.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 38.5226 (13) 35.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 38.7486 (14) 34.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 34.3587 (15) 35.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 33.2306 (16) 35.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 34.4744 (17) 38.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 36.7948 (18) 40.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 37.9989 (19) 37.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 35.6923 (20) 35.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.3
Случайная величина характеризует продолжительность безотказного функционирования устройства (в часах).
( 1) 45.7985 (11) 43.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 47.2978 (12) 49.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 48.5226 (13) 45.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 48.7486 (14) 44.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 44.3587 (15) 45.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 43.2306 (16) 45.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 44.4744 (17) 48.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 46.7948 (18) 40.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 47.9989 (19) 47.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 45.6923 (20) 45.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.4
Случайная величина характеризует продолжительность безотказного функционирования устройства определенного вида (в сутках).
( 1) 25.7985 (11) 33.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 39.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 35.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 34.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 35.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 35.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 38.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 37.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 35.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.5
Случайная величина характеризует массу изготовленной детали определенного вида (в кг).
( 1) 25.7985 (11) 23.6532 (21) 37.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 38.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 34.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 37.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 38.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 36.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 35.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 37.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 38.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 35.1591 (40) 29.6166 (50) 26.7133
8.6
Случайная величина характеризует продолжительность безотказного функционирования устройства (в часах).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 39.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 39.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 39.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 33.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 37.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 34.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 39.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 39.6166 (50) 26.7133
8.7
Случайная величина характеризует продолжительность устранения дефекта определенного вида (в часах).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 35.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 33.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 34.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 33.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 34.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 39.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 39.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 36.7133
8.8
Случайная величина характеризует продолжительность безотказного функционирования устройства (в часах).
( 1) 45.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 47.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 48.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 48.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 44.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 43.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 44.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 46.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 47.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 45.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.9
Случайная величина характеризует продолжительность выполнения технологической операции (в часах).
( 1) 25.7985 (11) 43.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 49.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 45.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 44.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 45.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 45.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 48.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 40.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 47.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 45.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.10
Случайная величина характеризует продолжительность устранения дефекта определенного вида (в часах).
( 1) 25.7985 (11) 23.6532 (21) 47.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 48.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 44.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 47.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 48.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 46.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 45.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 47.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 48.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 45.1591 (40) 29.6166 (50) 26.7133
8.11
Случайная величина характеризует продолжительность ожидания детали в накопителе до отправки на упаковочный конвейер (в мин.).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 49.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 40.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 40.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 49.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 49.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 43.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 47.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 44.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 49.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 49.6166 (50) 26.7133
8.12
Случайная величина характеризует время простоя устройства в ожидании переналадки (в минутах).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 40.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 45.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 43.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 44.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 43.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 40.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 44.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 49.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 49.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 46.7133
8.13
Случайная величина характеризует продолжительность устранения дефекта определенного вида (в часах).
( 1) 21.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 22.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 23.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 24.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 25.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 26.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 27.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 28.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 29.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 20.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.14
Случайная величина характеризует продолжительность безотказного функционирования устройства определенного вида (в сутках).
( 1) 25.7985 (11) 21.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 22.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 23.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 26.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 27.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 38.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 29.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 20.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.15
Случайная величина характеризует продолжительность выполнения технологической операции.
( 1) 25.7985 (11) 23.6532 (21) 21.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 22.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 23.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 24.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 25.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 27.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 28.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 29.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 20.1591 (40) 29.6166 (50) 26.7133
8.16
Случайная величина характеризует продолжительность устранения дефекта определенного вида (в часах).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 21.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 32.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 33.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 24.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 25.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 26.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 28.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 20.6166 (50) 26.7133
8.17
Случайная величина характеризует среднемесячную заработную плату работников некоторого предприятия (в условных ден. един.).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 31.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 22.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 25.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 36.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 27.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 28.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 20.7133
8.18
Случайная величина характеризует время пребывания детали на общем конвейере (в часах).
( 1) 22.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 22.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 22.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 22.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 22.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 22.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 22.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 22.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 22.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 22.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.19
Случайная величина характеризует среднемесячную заработную плату работников некоторого предприятия (в условных ден. един.).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 23.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 23.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 23.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 23.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 23.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 23.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 33.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 23.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 23.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.20
Случайная величина характеризует продолжительность выполнения определенной технологической операции (в минутах).
( 1) 25.7985 (11) 23.6532 (21) 24.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 24.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 24.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 24.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 24.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 24.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 24.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 24.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 24.1591 (40) 29.6166 (50) 26.7133
8.21
Случайная величина характеризует время пребывания детали на общем конвейере (в минутах).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 25.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 35.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 35.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 25.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 25.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 25.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 25.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 25.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 25.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 25.6166 (50) 26.7133
8.22
Случайная величина характеризует продолжительность выполнения определенной технологической операции (в часах).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 36.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 26.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 26.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 26.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 26.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 36.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 26.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 26.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 26.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.23
Случайная величина характеризует время обработки детали определенного вида на станке (в минутах).
( 1) 27.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 27.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 27.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 27.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 27.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 27.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 27.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 27.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.24
Случайная величина характеризует внутренний радиус изготовленной на станке детали (в мм).
( 1) 25.7985 (11) 28.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 28.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 28.8035 (23) 24.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 28.9188 (24) 27.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 28.3773 (25) 28.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 28.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 38.6574 (28) 27.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 28.0493 (29) 28.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 28.5494 (30) 25.1591 (40) 29.6166 (50) 26.7133
8.25
Случайная величина характеризует время простоя оборудования в ожидании ремонта.
( 1) 25.7985 (11) 23.6532 (21) 29.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 29.6561 (32) 30.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 29.4059 (33) 30.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 29.5624 (34) 29.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 29.9174 (35) 29.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 29.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 29.9613 (37) 27.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 29.0814 (38) 24.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 29.8153 (39) 29.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 29.1591 (40) 29.6166 (50) 26.7133
8.26
Случайная величина характеризует время, затрачиваемое на доставку продукции от поставщика потребителю.
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 21.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 31.2499 (42) 25.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 31.9916 (43) 23.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 21.3445 (44) 24.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 21.9391 (45) 23.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 21.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 21.1893 (47) 24.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 21.8246 (48) 29.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 21.3138 (49) 29.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 21.6166 (50) 26.7133
8.27
Случайная величина характеризует время простоя оборудования в ожидании ремонта.
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 30.7951
( 2) 27.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 20.0384
( 3) 28.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 20.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 20.7476
( 5) 24.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 20.3705
( 6) 23.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 30.4135
( 7) 24.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 20.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 20.6136
( 9) 27.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 20.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 20.7133
8.28
Случайная величина характеризует время обработки детали определенного вида на станке (в минутах).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 35.7951
( 2) 25.2978 (12) 29.4075 (22) 28.6561 (32) 30.2499 (42) 25.0384
( 3) 25.5226 (13) 25.8035 (23) 24.4059 (33) 30.9916 (43) 25.8167
( 4) 25.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 25.7476
( 5) 25.3587 (15) 25.3773 (25) 28.9174 (35) 29.9391 (45) 25.3705
( 6) 25.2306 (16) 25.3216 (26) 26.6193 (36) 23.6529 (46) 35.4135
( 7) 25.4744 (17) 28.7622 (27) 25.9613 (37) 27.1893 (47) 25.2096
( 8) 25.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 25.6136
( 9) 25.9989 (19) 27.0493 (29) 28.8153 (39) 29.3138 (49) 25.7766
(10) 25.6923 (20) 25.5494 (30) 25.1591 (40) 29.6166 (50) 25.7133
8.29
Случайная величина характеризует удельный вес прореагировавшего в течение одной минуты вещества (в процентах).
( 1) 25.7985 (11) 26.6532 (21) 27.4098 (31) 26.1856 (41) 30.7951
( 2) 27.2978 (12) 26.4075 (22) 28.6561 (32) 36.2499 (42) 25.0384
( 3) 28.5226 (13) 26.8035 (23) 24.4059 (33) 36.9916 (43) 23.8167
( 4) 28.7486 (14) 26.9188 (24) 27.5624 (34) 26.3445 (44) 24.7476
( 5) 24.3587 (15) 26.3773 (25) 28.9174 (35) 26.9391 (45) 23.3705
( 6) 23.2306 (16) 26.3216 (26) 26.6193 (36) 26.6529 (46) 30.4135
( 7) 24.4744 (17) 26.7622 (27) 25.9613 (37) 26.1893 (47) 24.2096
( 8) 26.7948 (18) 36.6574 (28) 27.0814 (38) 26.8246 (48) 29.6136
( 9) 27.9989 (19) 26.0493 (29) 28.8153 (39) 26.3138 (49) 29.7766
(10) 25.6923 (20) 26.5494 (30) 25.1591 (40) 26.6166 (50) 26.7133
8.30
Случайная величина характеризует продолжительность ожидания детали в накопителе до отправки на упаковочный конвейер (в мин.).
( 1) 25.7985 (11) 23.6532 (21) 27.4098 (31) 29.1856 (41) 31.7951
( 2) 27.2978 (12) 29.4075 (22) 27.6561 (32) 30.2499 (42) 21.0384
( 3) 28.5226 (13) 25.8035 (23) 27.4059 (33) 30.9916 (43) 21.8167
( 4) 28.7486 (14) 24.9188 (24) 27.5624 (34) 29.3445 (44) 21.7476
( 5) 24.3587 (15) 25.3773 (25) 27.9174 (35) 29.9391 (45) 21.3705
( 6) 23.2306 (16) 25.3216 (26) 27.6193 (36) 23.6529 (46) 31.4135
( 7) 24.4744 (17) 28.7622 (27) 27.9613 (37) 27.1893 (47) 21.2096
( 8) 26.7948 (18) 30.6574 (28) 27.0814 (38) 24.8246 (48) 21.6136
( 9) 27.9989 (19) 27.0493 (29) 27.8153 (39) 29.3138 (49) 21.7766
(10) 25.6923 (20) 25.5494 (30) 27.1591 (40) 29.6166 (50) 21.7133
Задание 9
Получить механическую выборку из данных, приведенных в задании 7, отобрав 25 значений (каждое второе, считая в порядке записи сверху вниз по колонкам и по этой выборке). Используя критерий согласия Пирсона, проверить согласие выборочных значений с гипотезой о нормальном распределении генеральной совокупности с параметрами, оцененными предварительно по выборке.
Задание 10
Получить две механические выборки, объемом по 25 значений, из данных, приведенных в задании 7, включая в первую значения, стоящие на нечетных местах, а во вторую – на четных (нумерация производится по колонкам).
Найти выборочное уравнение линейной регрессии Y на Х по результатам двух выборок, считая первую выборку значениями X ,а вторую – Y. Проверить гипотезу о значимости коэффициента корреляции.
страница 1 | страница 2 страница 3 страница 4 | страница 5 | страница 6
|