страница 1 страница 2 страница 3 | страница 4
в
Рисунок 2.8 – Разгонные характеристики, приведенные к единому масштабу по времени
Таблица 2.1 – Обработка разгонных характеристик (температура нагреваемого продукта на выходе из печи)
t, мин
|
Т, оС
|
∆Т=
Т-То
|
h(t)= =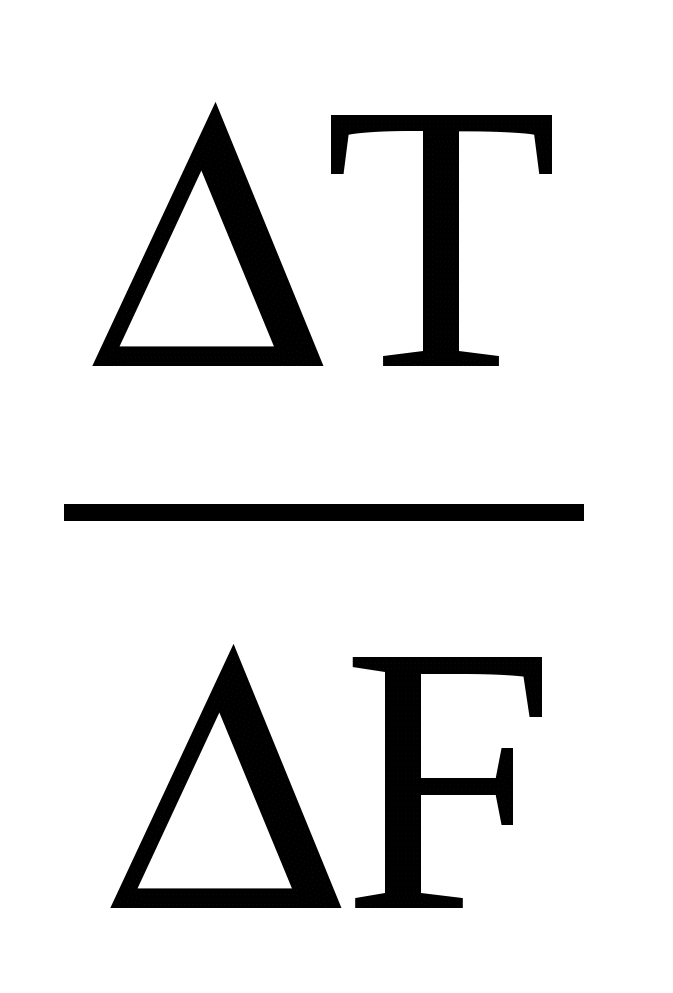
|
Т, оС
|
∆Т
|
h(t)
|
Т, оС
|
∆Т
|
h(t)
|
∑h
|
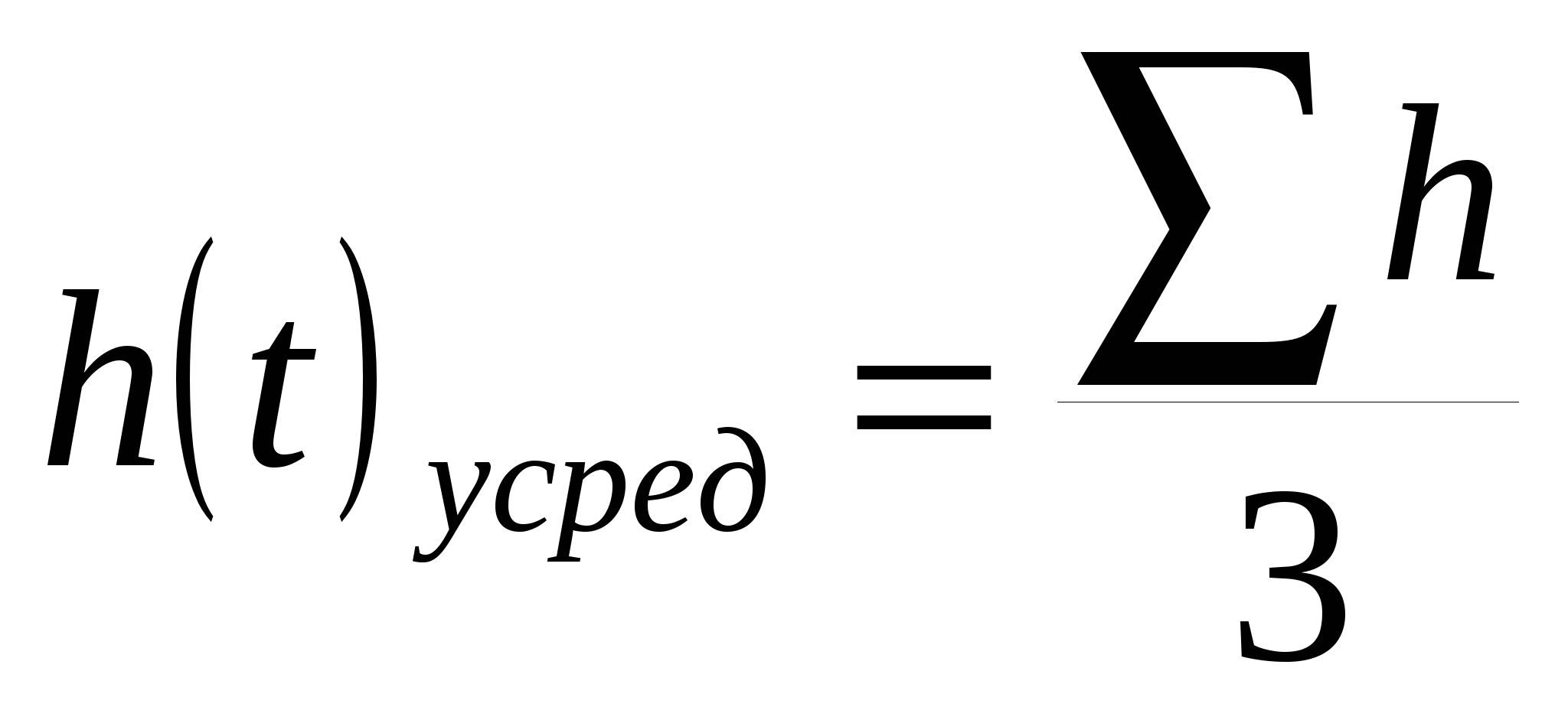
|
|
∆F=7 м3/мин
|
∆F=4 м3/мин
|
∆F=2 м3/мин
|
0
|
43
|
0
|
0
|
155
|
0
|
0
|
195
|
0
|
0
|
0
|
0
|
1
|
48
|
5
|
0,71
|
154
|
-1
|
-0,25
|
194
|
-1
|
-0,5
|
-0,04
|
-0,01
|
2
|
50
|
7
|
1,00
|
153
|
-2
|
-0,50
|
192
|
-3
|
-1,5
|
-1,00
|
-0,33
|
3
|
51
|
8
|
1,14
|
151
|
-4
|
-1,00
|
194
|
-1
|
-0,5
|
-0,36
|
-0,12
|
4
|
52
|
9
|
1,29
|
152
|
-3
|
-0,75
|
198
|
3
|
1,5
|
2,04
|
0,68
|
5
|
53
|
10
|
1,43
|
162
|
7
|
1,75
|
209
|
14
|
7,0
|
10,18
|
3,39
|
6
|
54
|
11
|
1,57
|
165
|
10
|
2,50
|
215
|
20
|
10,0
|
14,07
|
4,69
|
7
|
55
|
12
|
1,71
|
169
|
14
|
3,50
|
217
|
22
|
11,0
|
16,21
|
5,40
|
...
|
|
|
|
|
|
|
|
|
|
|
...
|
26
|
199
|
156
|
22,29
|
222
|
67
|
16,75
|
213
|
18
|
9,00
|
|
16,01
|
27
|
203
|
160
|
22,86
|
223
|
68
|
17,00
|
210
|
15
|
7,50
|
|
15,79
|
Разброс точек усредненной характеристики h(t)усред. значительно меньше, чем исходных. Если увеличить число экспериментальных характеристик, то усреднённая характеристика станет ещё более сглаженной. Рекомендуется использовать редактор MS Excel.
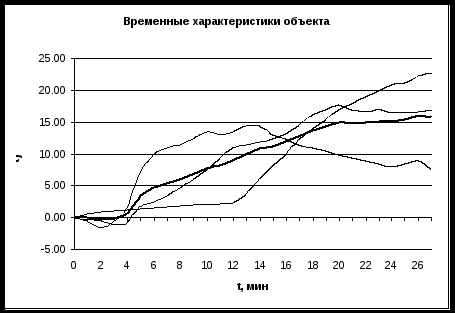
Рисунок 2.9 – Исходные и усредненная (жирная линия) характеристики
По приведённой кривой разгона можно сделать вывод, что рассматриваемый объект управления является статическим объектом с самовыравниванием и запаздыванием, т. е. описывается двумя типовыми звеньями (инерционное звено и звено транспортного запаздывания) и передаточной функцией (2.1).
По временной характеристике (рисунок 2.9) определяем параметры, характеризующие динамические свойства объекта:
- запаздывание τоб. Если в точке максимальной скорости изменения выходной величины провести касательную к графику и продолжить её до пересечения с линией начального установившегося значения выходной величины, то отрезок времени от момента внесения возмущения до точки пересечения касательной с осью абсцисс определит общее запаздывание объекта управления τоб, которое составляет 2 мин или 120 с;
- постоянная времени Тоб. Отрезок времени от момента пересечения касательной с линией начального установившегося значения до момента её пересечения с линией нового установившегося значения называется постоянной времени объекта Тоб, она равна 20 2 = 18 мин или 1080 с;
- коэффициент передачи kоб, определяемый по кривой разгона. Для статического объекта kоб представляет собой изменение выходной величины объекта при переходе из начального в новое установившееся состояние, отнесённое к единичному возмущению на входе. В нашем случае коэффициент усиления объекта kоб определяем по установившемуся значению усреднённой характеристики, приведенной на рисунке 2.9, kоб = 15,5 °С/(м3/мин).
Следовательно, подставляя найденные значения в формулу (2.2), получаем передаточную функцию объекта управления в САР температуры – при измерении времени в минутах
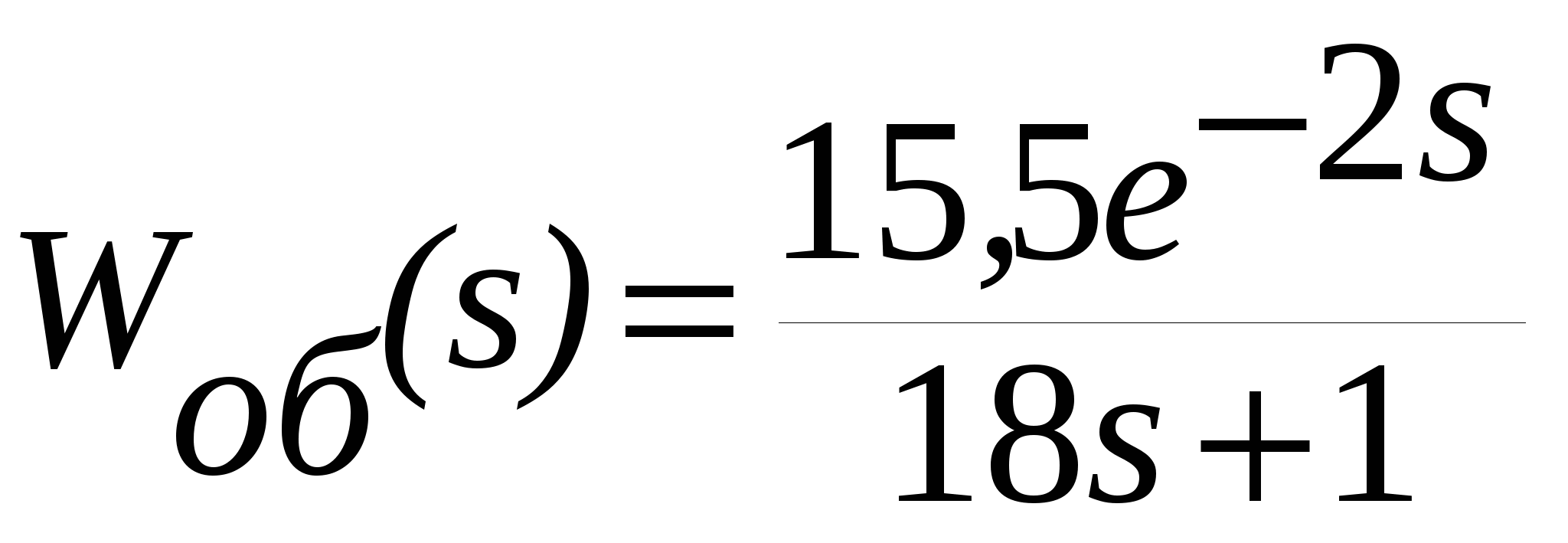
и секундах
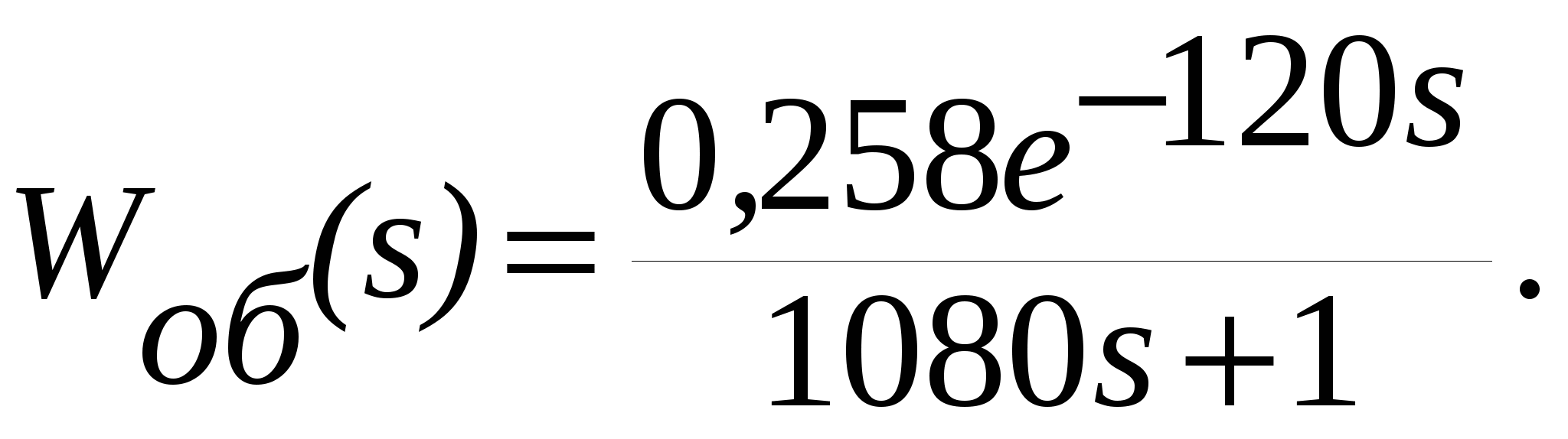
Очевидной проблемой является проведение эксперимента на действующем оборудовании и в существующей замкнутой системе регулирования, из-за чего фактически снимаются характеристики не отдельно объекта, а с влиянием всех остальных элементов САР. Зачастую в состав объекта регулирования попадает и регулирующий орган и датчик, их невозможно выделить при эксперименте. Если в процессе модернизации САР датчик и исполнительный орган планируется заменить, одновременно должен решаться вопрос о корректировке характеристик объекта регулирования.
2.2 Построение модели с применением ЭВМ
Если замена сложного дифференциального уравнения объекта более простым неприемлема, то для определения коэффициентов дифференциального уравнения без учета запаздывания используют графо-аналитический метод площадей (метод М. П. Симою). Этот метод легко программируется и позволяет получать более точное математическое описание объекта (погрешность модели определяется точностью исходной информации, т. е. точностью экспериментального определения кривой разгона).
Программа Ident_4.xls, разработанная на кафедре автоматизации и управления ПГУ, реализует метод Симою, выполнена с использованием макросов VBA в среде MS Excel (рисунок 2.10) и позволяет произвести идентификацию объекта управления до четвертого порядка по кривой разгона моделью в виде передаточной функции
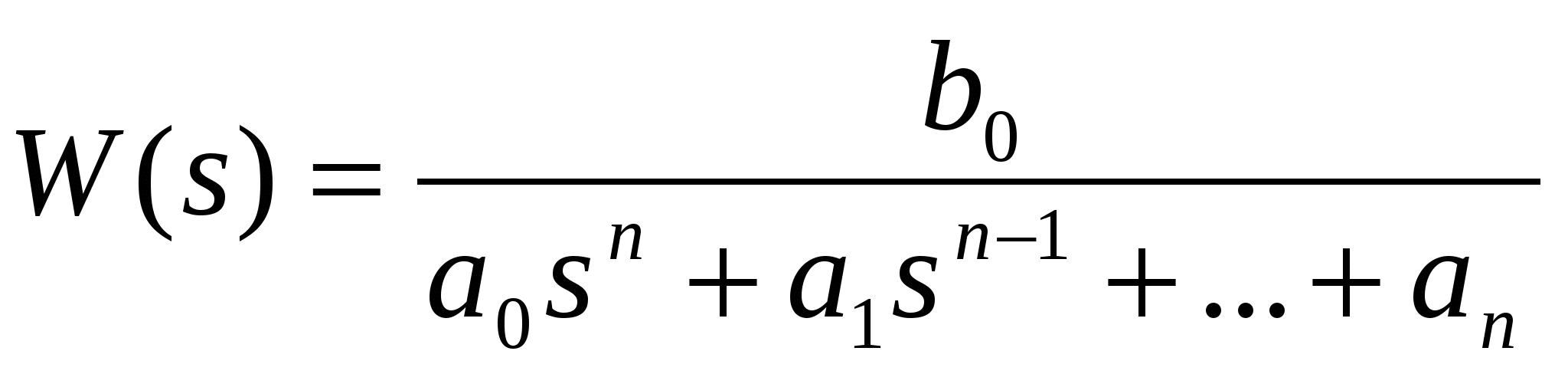 . (2.13) . (2.13)
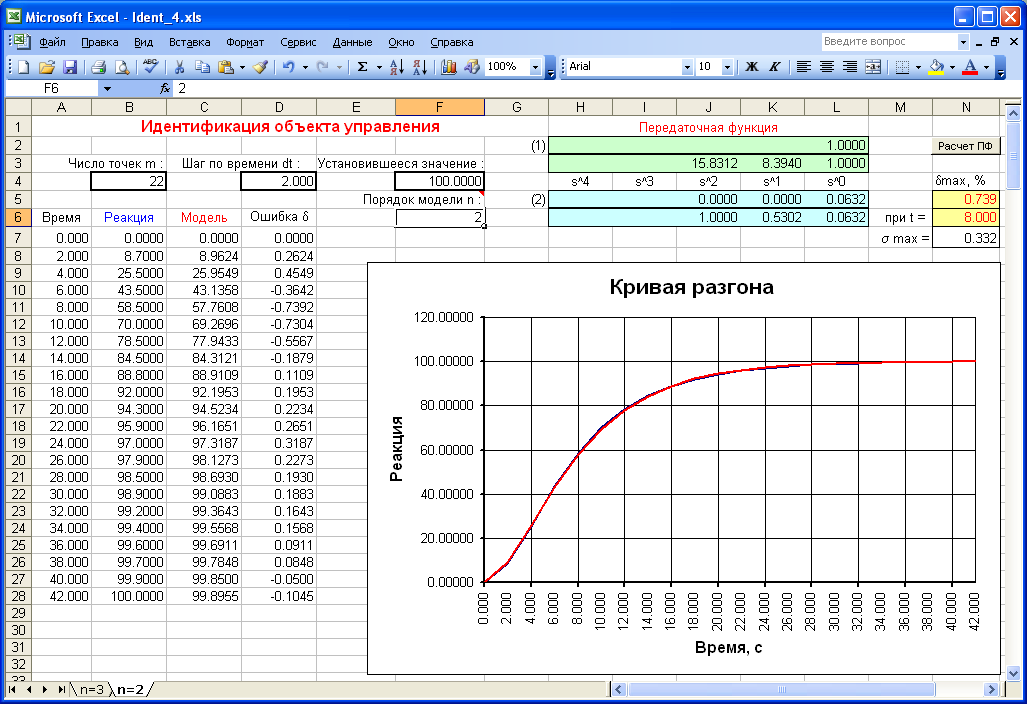
Рисунок 2.10
Программа предназначена для объектов с самовыравниванием. При открытии книги не следует отключать макросы. Транспортное запаздывание в кривой разгона не учитывается, оно высчитывается самостоятельно пользователем и просто умножается на передаточную функцию модели в форме показателя экспоненты (см. формулу 2.2). Удалять и вводить исходные данные следует вручную, всегда подразумевается воздействие типа «единичный скачок».
Необходимо задать число точек отсчета m и шаг по времени dt, в колонку А занести значения времени, в колонку В – значения координат кривой разгона. Ввести установившееся значение hуст, которое не обязательно точно совпадает с конечным отсчетом кривой разгона. Кривая разгона может быть ненормированной, но должна быть снята с равномерным шагом. Указать предполагаемый порядок модели n, щелкнуть кнопку "Расчет ПФ".
Передаточная функция выводится нормированной по свободному члену (форма 1) и по старшему коэффициенту (форма 2). По полученной ПФ модели методом Рунге-Кутта рассчитывается переходная функция и ошибка (разница исходной и полученной кривых в каждой точке отсчета). Максимальное значение ошибки max (в процентах) указывается вместе с соответствующим ему моментом времени. На диаграмме отображаются обе кривых, что, вместе со значением ошибки, позволяет выбрать приемлемый порядок модели по наименьшему значению ошибки, изменяя предполагаемый порядок модели. Кроме абсолютной разницы max высчитывается также средне-квадратичное отклонение σmax.
Коэффициент передачи объекта должен вычисляться пользователем самостоятельно по отношению hуст к величине входного ступенчатого воздействия, при которой получена кривая разгона объекта управления, он умножается на передаточную функцию в форме 1.
Для объекта (рисунок 2.10) число точек m = 22, шаг по времени 2 с, установившееся значение 100. Адекватность модели второго порядка
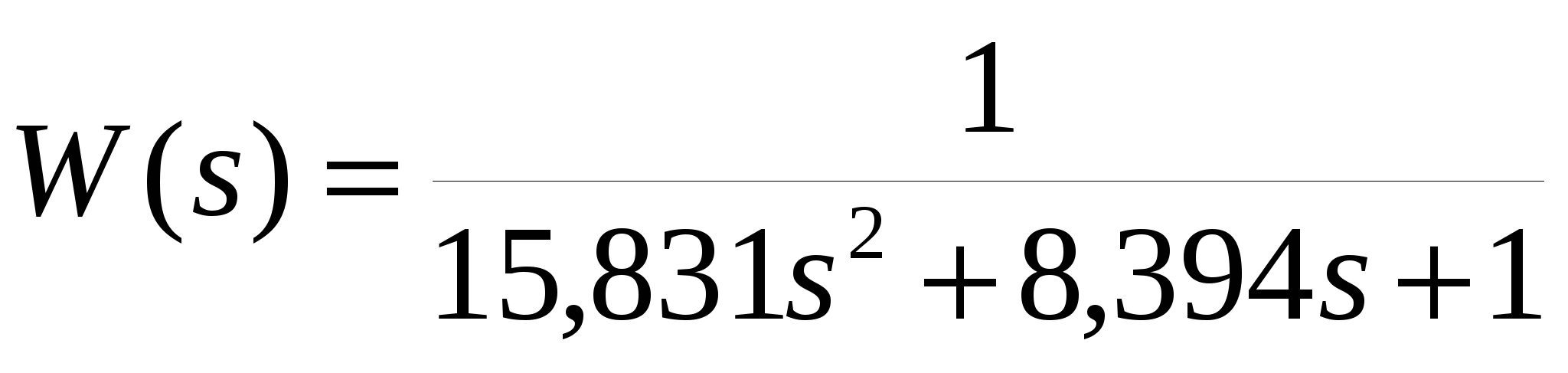
оценивается ошибкой max = 0,739 % и отклонением σmax = 0,332, адекватность модели третьего порядка
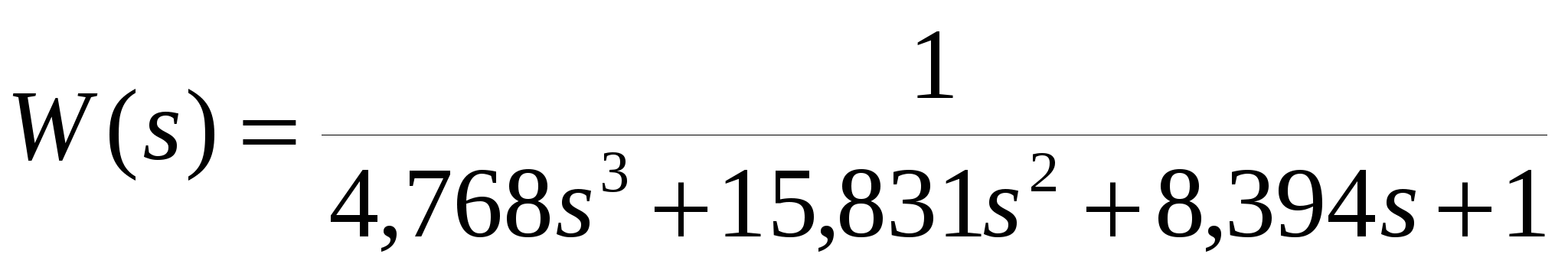
ошибкой max = 1,056 % и отклонением σmax = 0,266. В обоих случаях ошибка меньше 3 %, выбираем модель второго порядка, как более простую и имеющую меньшее значение ошибки max. Окончательно, с учетом коэффициента передачи kуст = hуст/1(t) = 100/1 = 100
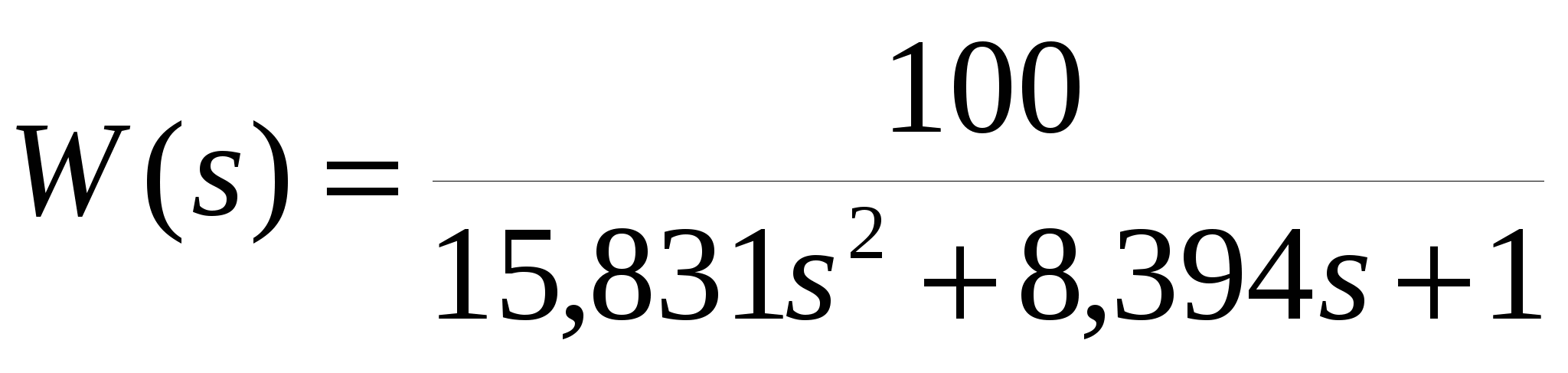 . .
Для объекта (рисунок 2.11) число точек кривой разгона m = 201, шаг по времени 0,125 с, установившееся значение 1. Адекватность модели второго порядка
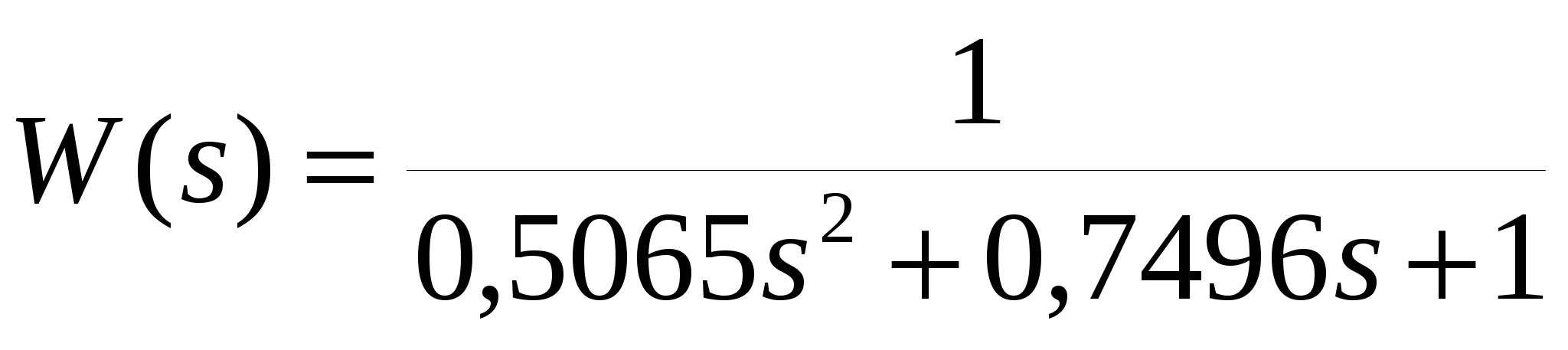
оценивается ошибкой max = 34,363 %, модели третьего порядка
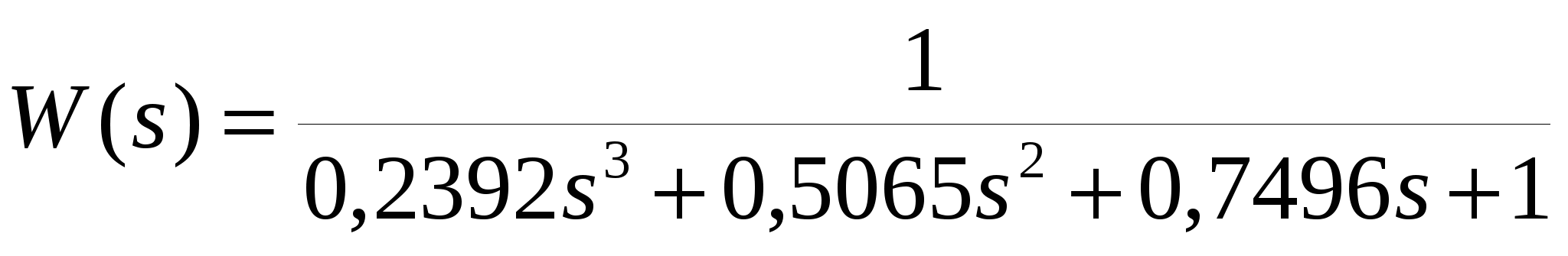
ошибкой max = 3,514 %, модель четвертого порядка неустойчива. Выбираем модель третьего порядка, коэффициент kуст = hуст/1(t) = 1.
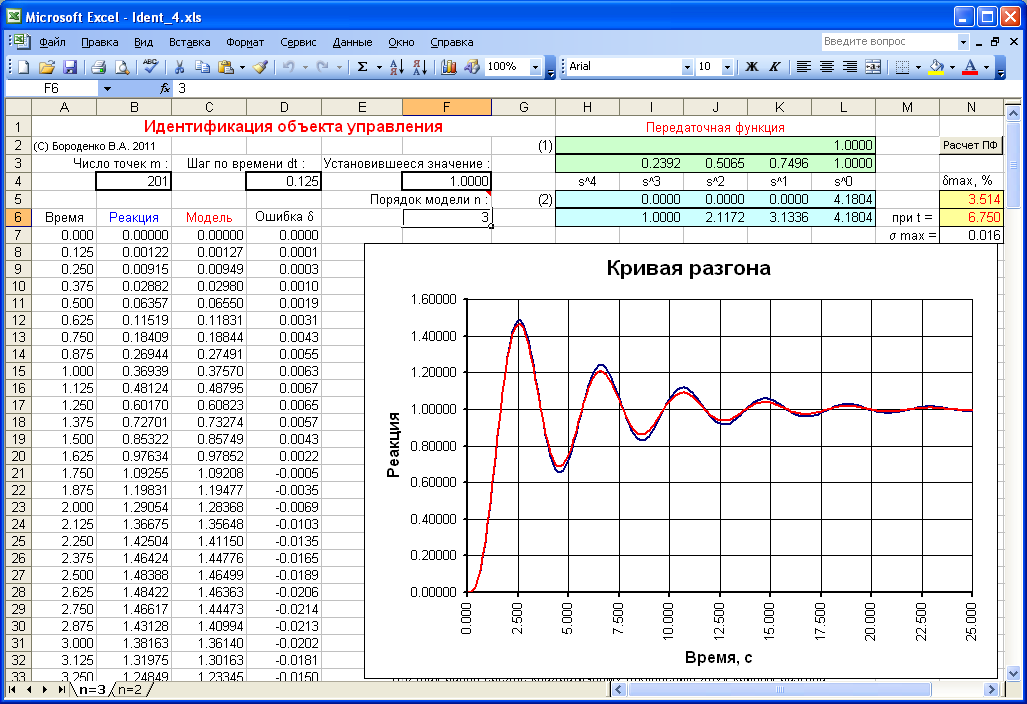
Рисунок 2.11
Рассмотрим пример идентификации объекта регулирования в среде MATLAB. Принципиальное отличие от предыдущей программы заключается в том, что здесь нужно вводить для анализа значения возмущающего испытательного воздействия, что особенно ценно, если оно не соответствует по форме типовому.
MATLAB позволяет решить задачу идентификации объекта (построения его модели в виде передаточной функции или описания переменными состояния), если для объекта известен закон изменения входа u(t) и выхода y(t) во времени. Формируем массив данных для идентификации объекта управления, представленного на рисунке 2.11 (продолжение массива y на следующей строке обеспечивается троеточием в конце предыдущей строки)
>> t=0:0.125:25; ‘ шаг и интервал взяты из предыдущего примера
>> u=exp(0*t); ‘ это единичный скачок
>> y =[0 0.0012 0.0092 0.0288 0.0636 0.1152 0.1841 0.2694 0.3694...
0.4812 0.6017 0.7270 0.8532 0.9763 1.0925 1.1983 1.2905 1.3667 ...
1.4250 1.4642 1.4839 1.4842 1.4662 1.4313 1.3816 1.3198 1.2485 ...
1.1709 1.0902 1.0095 0.9318 0.8599 0.7961 0.7426 0.7008 0.6718 ...
0.6561 0.6538 0.6644 0.6869 0.7200 0.7620 0.8109 0.8648 0.9214 ...
0.9784 1.0338 1.0856 1.1320 1.1715 1.2030 1.2257 1.2391 1.2430 ...
1.2378 1.2241 1.2027 1.1747 1.1414 1.1043 1.0650 1.0250 0.9857 ...
0.9486 0.9151 0.8861 0.8625 0.8450 0.8340 0.8296 0.8317 0.8399 ...
0.8537 0.8723 0.8948 0.9202 0.9475 0.9756 1.0033 1.0298 1.0540 ...
1.0752 1.0927 1.1061 1.1149 1.1192 1.1188 1.1141 1.1054 1.0931 ...
1.0779 1.0605 1.0416 1.0220 1.0024 0.9836 0.9661 0.9507 0.9377 ...
0.9276 0.9206 0.9169 0.9163 0.9189 0.9244 0.9324 0.9426 0.9544 ...
0.9675 0.9811 0.9949 1.0083 1.0208 1.0320 1.0416 1.0492 1.0547 ...
1.0579 1.0588 1.0575 1.0542 1.0490 1.0422 1.0341 1.0252 1.0156 ...
1.0059 0.9964 0.9875 0.9794 0.9724 0.9667 0.9625 0.9598 0.9588 ...
0.9593 0.9613 0.9646 0.9691 0.9746 0.9808 0.9874 0.9941 1.0009 ...
1.0073 1.0131 1.0182 1.0225 1.0257 1.0278 1.0288 1.0287 1.0276 ...
1.0255 1.0225 1.0188 1.0146 1.0100 1.0053 1.0005 0.9960 0.9918 ...
0.9880 0.9849 0.9825 0.9808 0.9799 0.9798 0.9804 0.9817 0.9837 ...
0.9861 0.9890 0.9922 0.9955 0.9988 1.0020 1.0051 1.0078 1.0101 ...
1.0119 1.0132 1.0140 1.0142 1.0139 1.0131 1.0118 1.0102 1.0082 ...
1.0061 1.0038 1.0014 0.9991 0.9970 0.9950 0.9933 0.9919 0.9909 ...
0.9903 0.9900 0.9902];
>> da=iddata(y',u',0.125)
Time domain data set with 201 samples.
Sampling interval: 0.125
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
Обе временные функции должны быть представлены вектором-столбцом значений одинаковой размерности, поэтому вектор-строка u, y транспонирован в вектор-столбец. При создании набора данных da функцией iddata() последним указано значение шага дискретности (Sampling interval) по времени ts = 0.125 с. Далее по набору da формируется непрерывная (ts = 0) модель методом предсказаний Prediction Error Method в пространстве состояний ′ss′ с каноническим представлением ′can′. В итоге получена модель в виде передаточной функции объекта второго порядка.
>> sys=pem(da,'ts',0,'ss','can'); ‘ пространство состояний
>> w=tf(sys); w=w(1) ‘ передаточная функция
Transfer function from input "u1" to output "y1":
-0.4775 s + 2.421
----------------------
s^2 + 0.3503 s + 2.421
Адекватность модели проверяется по максимальной ошибке delta, либо по средне-квадратичному отклонению sigma
>> yt=step(w(1),t);
>> delta=max(abs(y-yt))*100/1
delta = ‘ максимальная разница двух кривых в процентах от установившегося значения, равного 1
44.4735
>> sigma=sqrt(sum((y-yt).^2)/200)
sigma =
0.1242
В данном случае максимальная ошибка лучше характеризует недостаточную точность модели (рисунок 2.12), однако подобный результат может быть принят, если получить параметры модели иным образом не представляется возможным. Жирной линией отображена переходная характеристика исходного объекта, тонкой – характеристика полученной модели.
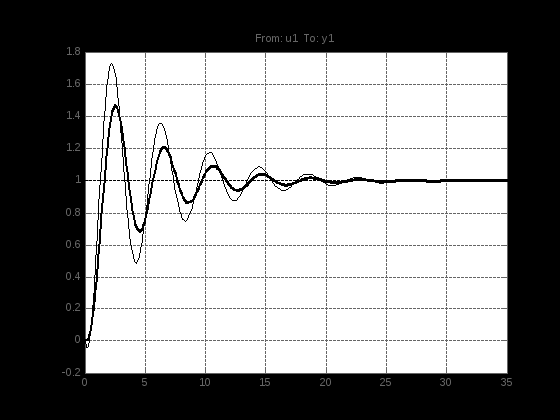
Рисунок 2.12
3 Выбор параметров регулятора
3.1 Выбор регулятора по данным объекта
Выбор типа и параметров регулятора производится либо вручную, без использования систем автоматизированного проектирования, либо с применением компьютерного моделирования, что будет рассмотрено далее на основе программы MATLAB.
Основной проблемой при выборе регуляторов является вопрос правильности определения характеристики регулятора применительно к динамическим свойствам объекта.
При отсутствии регулятора внесенное возмущение вынуждает регулируемую величину объекта изменяться по некоторой кривой, определяемой свойствами данного объекта. Максимальное отклонение регулируемой величины в этих условиях зависит от значений возмущения f и оператора 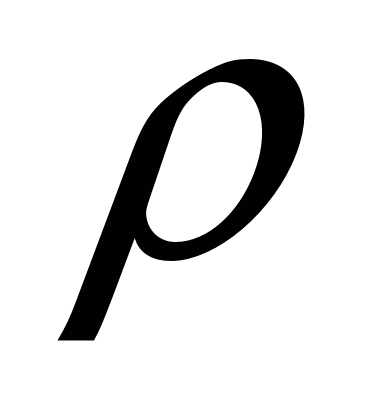 , отражающего свойства объекта , отражающего свойства объекта 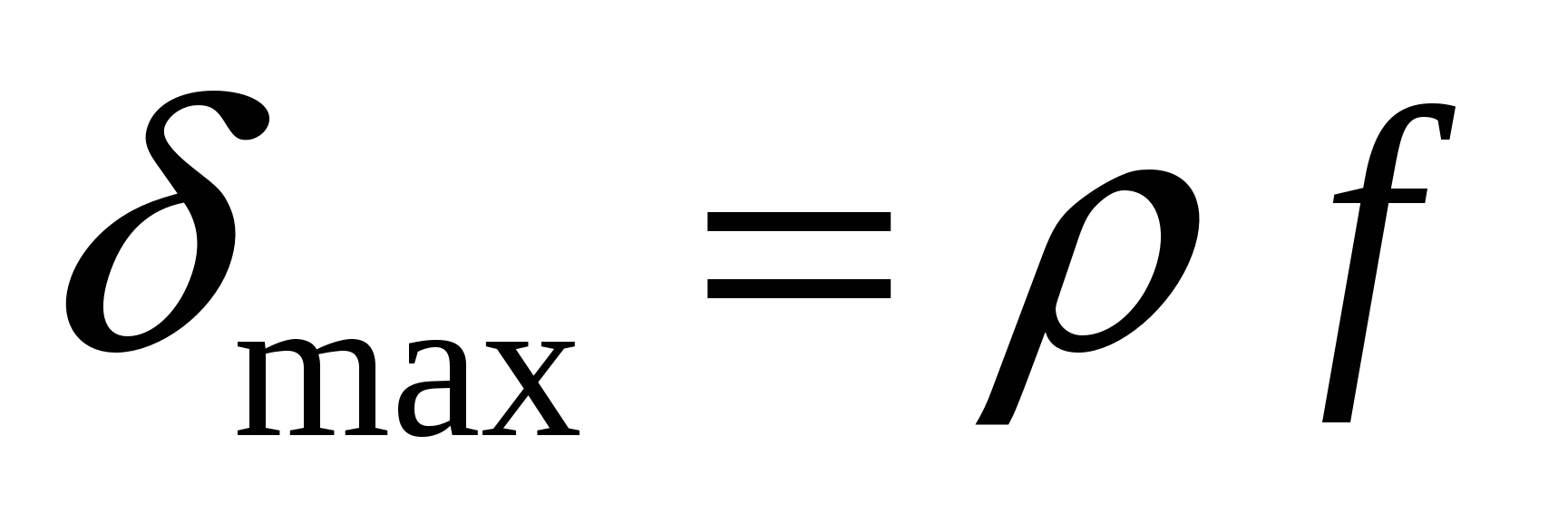 . .
Продолжительность отклонения регулируемой величины определяется временем действия возмущения на объект. Если включить регулируемый объект в систему регулирования, то можно уменьшить абсолютное значение отклонения 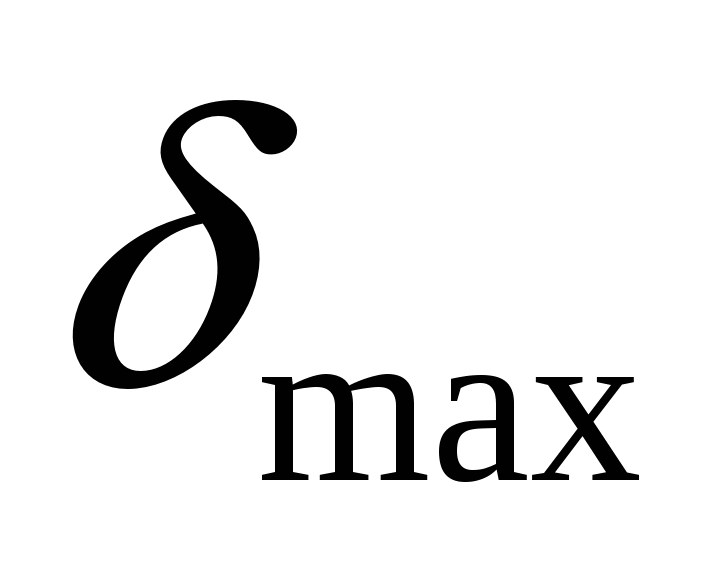 и время, в течение которого это отклонение будет продолжаться. и время, в течение которого это отклонение будет продолжаться.
Однако регуляторы с различными характеристиками обеспечивают разные результаты регулирования, что вызывает необходимость их выбора в соответствии со свойствами регулируемого объекта. При правильно выбранном регуляторе и соответствующей его настройке степень затухания процесса регулирования должна быть примерно равна 0,75 (при этом значении обеспечивается наиболее благоприятное изменение регулируемой величины).
При отсутствии сведений о динамических свойствах проектируемого объекта выбор регуляторов следует производить по аналогии с действующими объектами или же на основании предположительных соображений о свойствах данного объекта, учитывая при этом критерии, приведенные в таблице 3.1.
Таблица 3.1 – Критерии выбора регуляторов по роду действия
Тип регулятора
|
Импульсный
|
Релейный
|
Непрерывный
|
Критерий
|
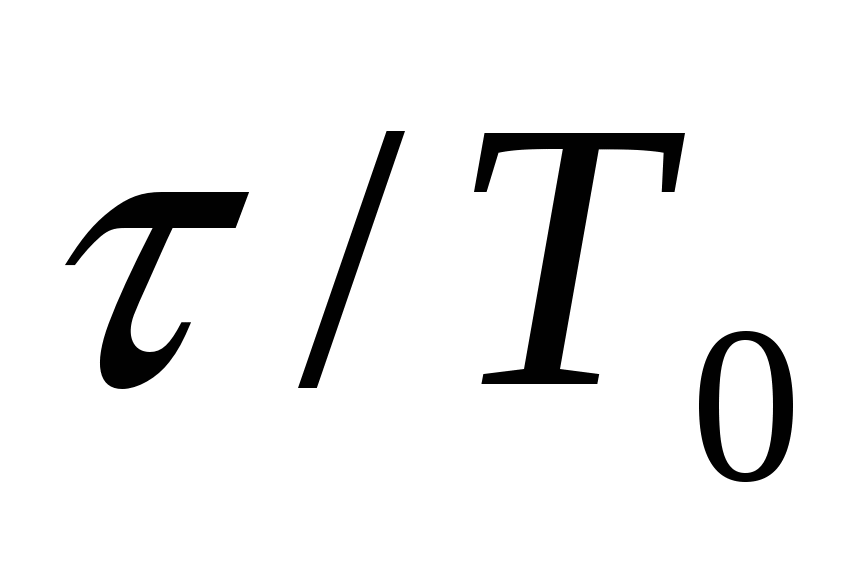 0,5…1,0 0,5…1,0
|
0 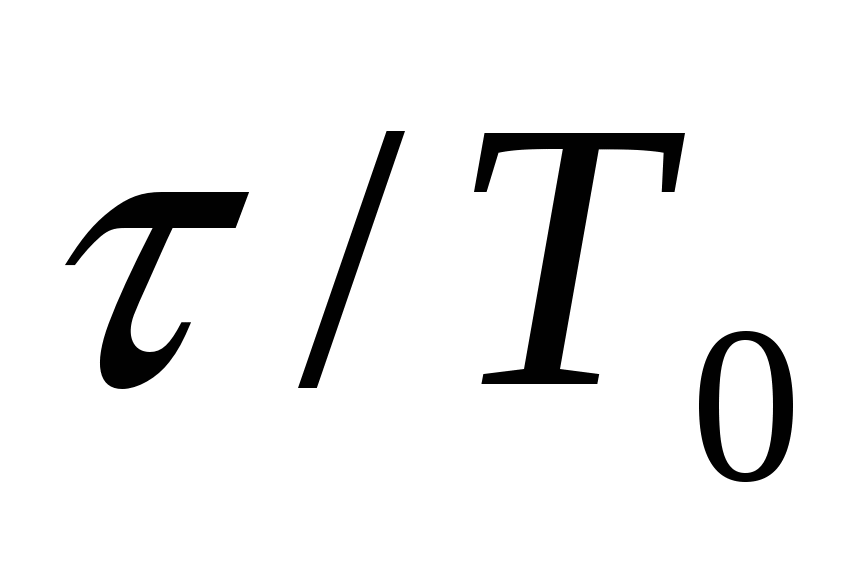 0,2 0,2
|
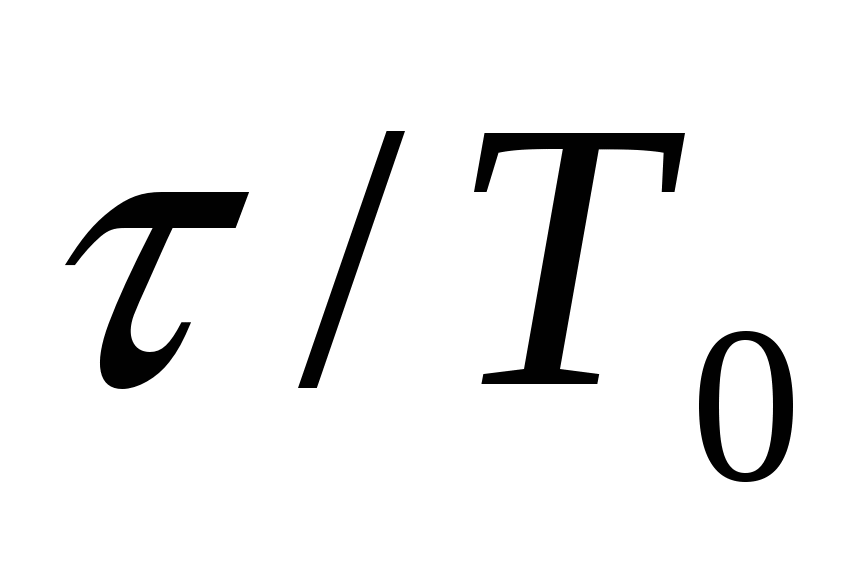 0 0
|
Здесь τ – время чистого запаздывания, Т0 – постоянная времени.
Импульсные регуляторы применяются для объектов без большого запаздывания, обладающих средней емкостью, при постоянной или плавно и мало меняющейся нагрузке.
Двухпозиционные (релейные) регуляторы применяются для объектов без большого запаздывания, обладающих большой емкостью, при постоянной или очень мало меняющейся нагрузке. Эти регуляторы применяются также для объектов с одной емкостью, не обладающих свойством самовыравнивания. Хорошая работа двухпозиционных регуляторов во многом зависит от инерционности чувствительного элемента, которая должна соответствовать инерционности объекта. Для двух- и более емкостных объектов двухпозиционное регулирование применяется редко, только в тех случаях, когда не требуется большая точность поддержания регулируемой величины.
Идеальные регуляторы непрерывного действия имеют следующие передаточные функции:
- П-регулятор 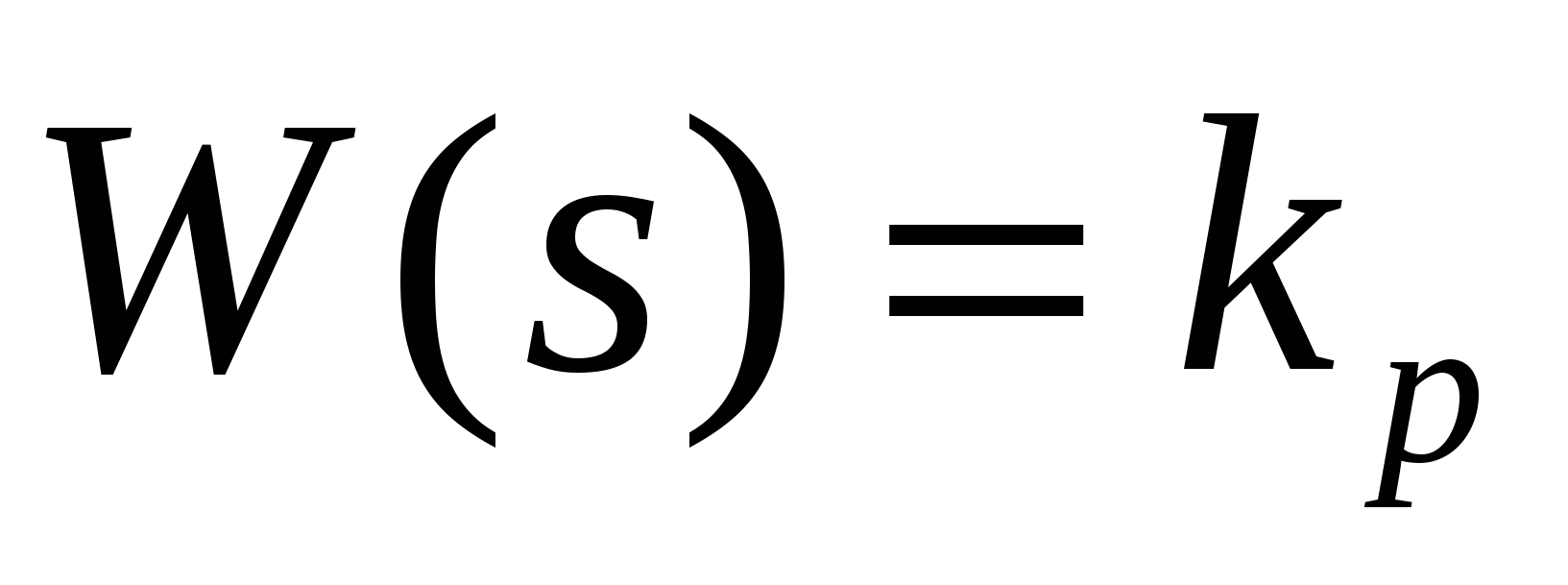 ; ;
- И-регулятор 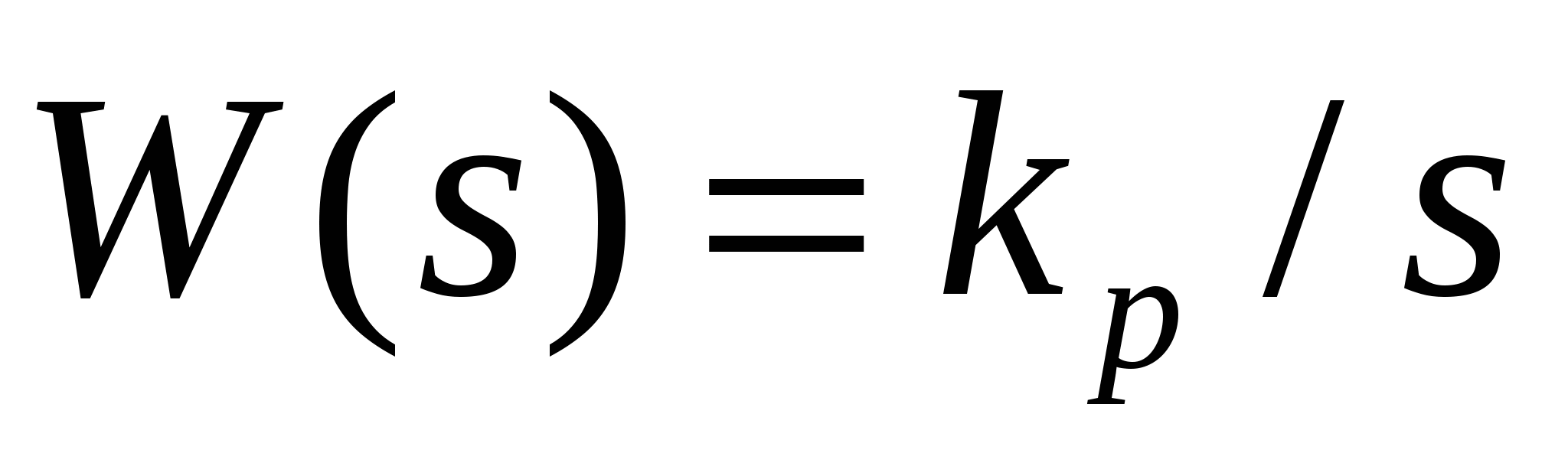 ; ;
- ПИ-регулятор 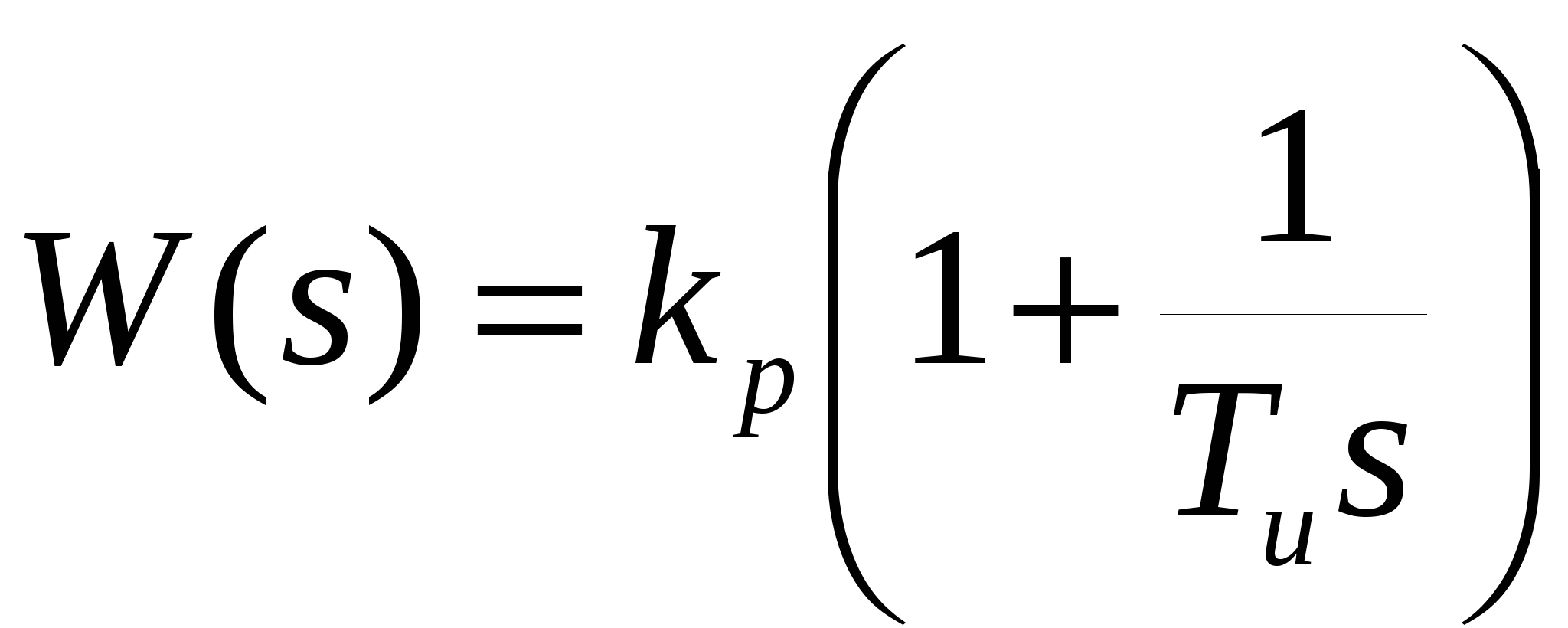 ; ;
- ПД-регулятор 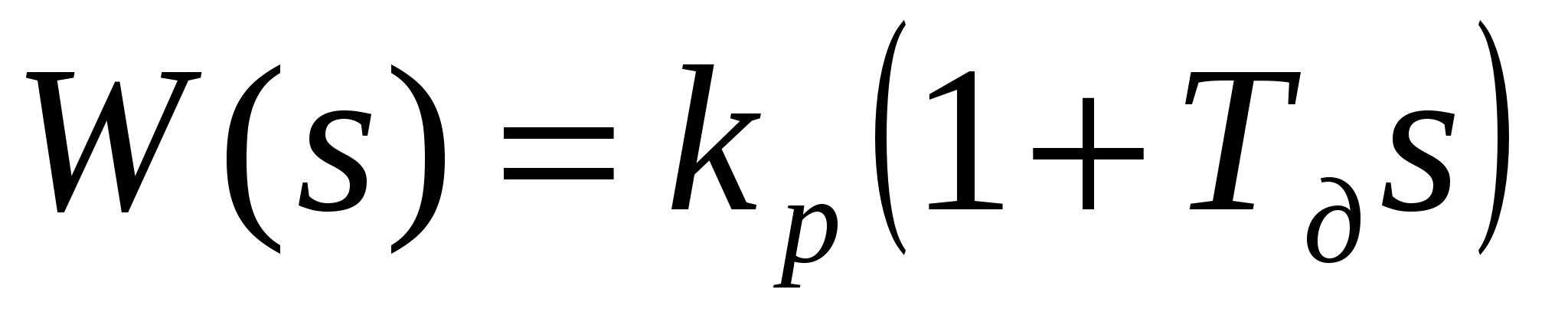 . .
- ПИД-регулятор 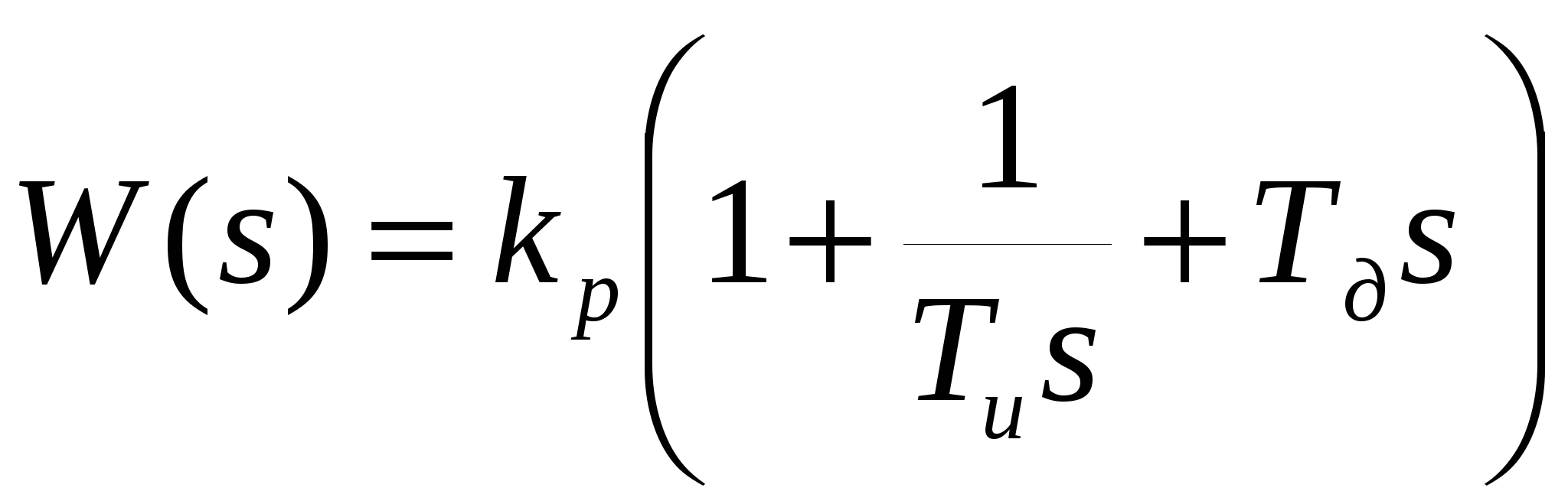 . .
П-регуляторы применяются в объектах со средней емкостью, небольшим запаздыванием и при небольших изменениях нагрузки. Большей частью они применяются для одноемкостных объектов, реже для двухъемкостных. Для многоемкостных объектов пропорциональные регуляторы применяются ограниченно.
П-регуляторы могут обеспечить устойчивое регулирование объекта с самовыравниванием при условии
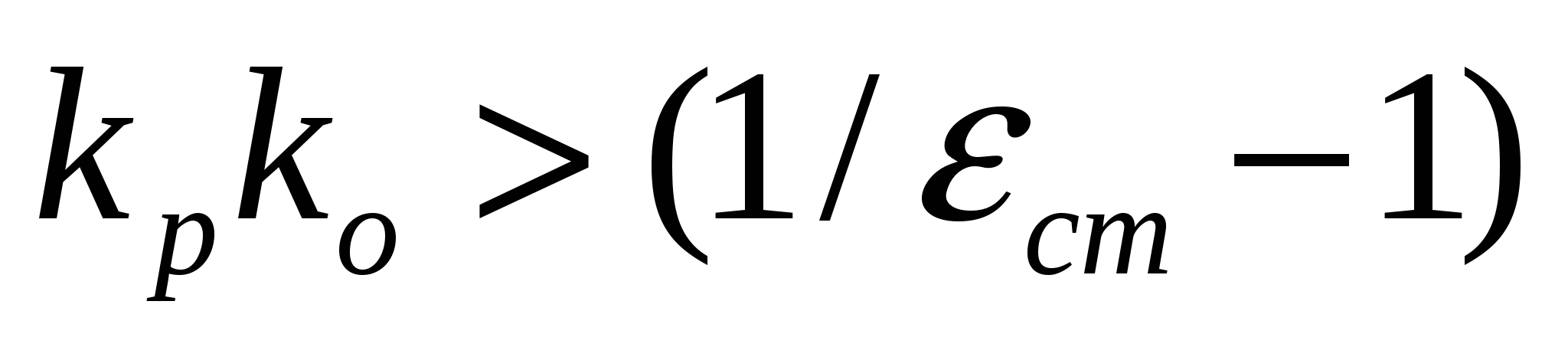 , (3.1) , (3.1)
где 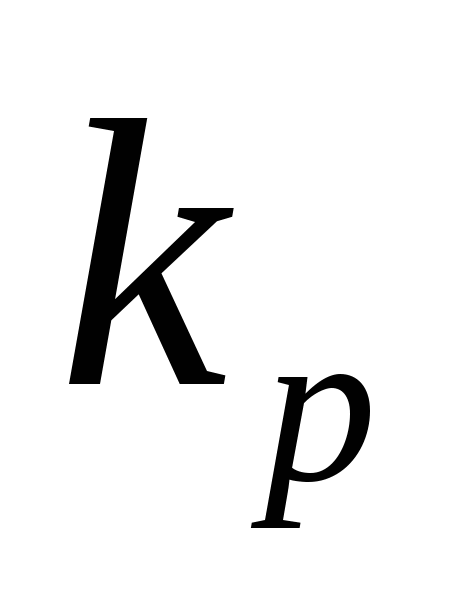 и и 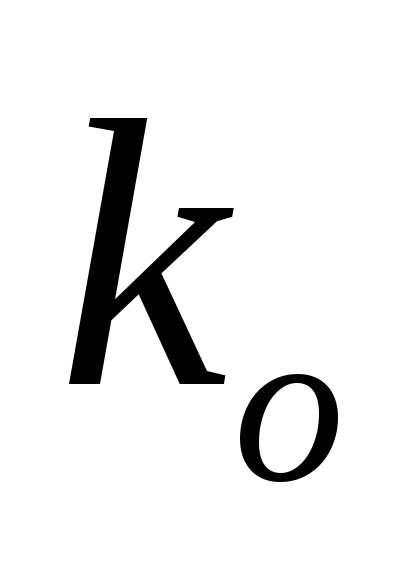 – соответственно коэффициенты передачи регулятора и объекта; – соответственно коэффициенты передачи регулятора и объекта;
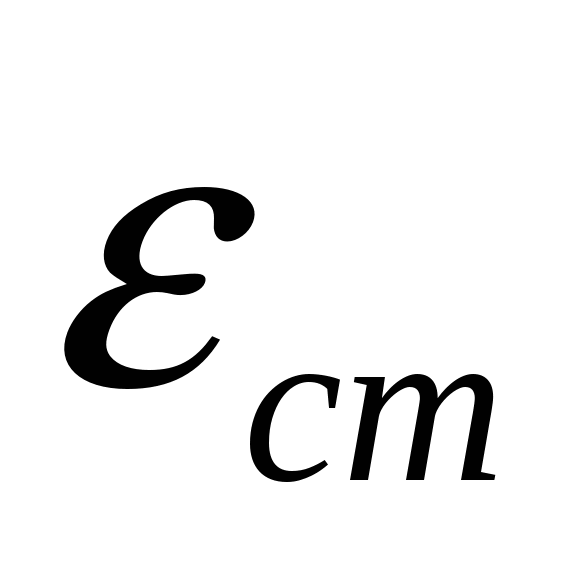 – статическая ошибка, – статическая ошибка,
и объекта без самовыравнивания при условии
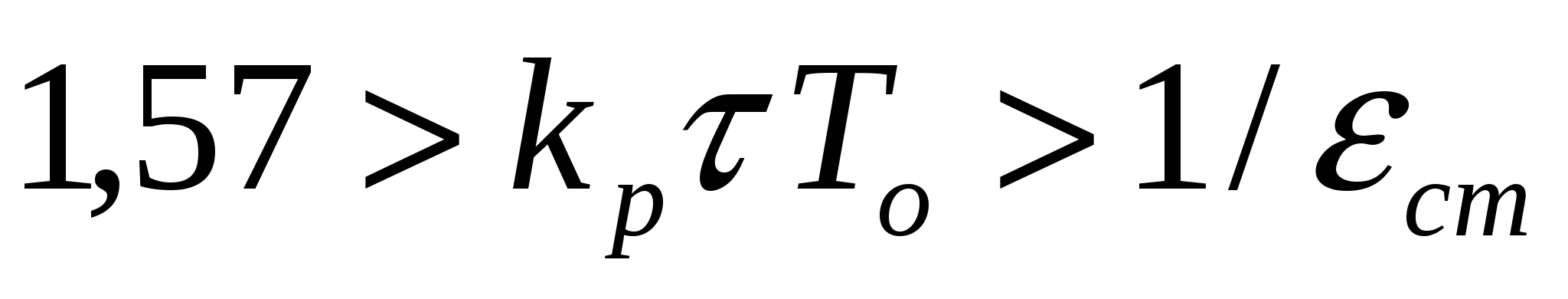 . (3.2) . (3.2)
И-регуляторы применяются для объектов с самовыравниванием, небольшим запаздыванием, имеющих любую мощность, при медленно меняющейся нагрузке.
Для получения оптимального переходного процесса в системе астатического регулирования необходимо выполнение следующих условий:
- объект должен быть статическим;
- постоянная времени объекта Т0 должна быть в пределах
2 ...40 с;
- время емкостного запаздывания процесса в системе регулирования должно составлять не более 1/10 от постоянной времени объекта, т. е . 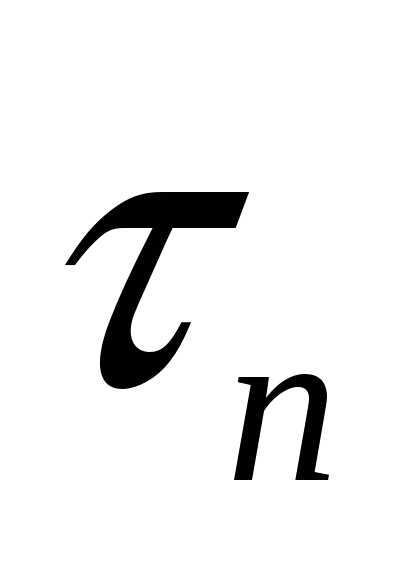 < 0,17; < 0,17;
- скорость перемещения регулирующего органа и коэффициент усиления регулятора должны выбираться в соответствии с емкостью объекта.
Также И-регуляторы с постоянной скоростью хорошо работают в объектах регулирования уровня, давления и температуры, но при обязательном условии, что чистое запаздывание τ и время разгона Тр малы, а постоянная времени объекта Т0 составляет не более 30...40 с. При этом чем больше емкость объекта, тем больше должна быть скорость перемещения регулирующего органа, а следовательно, и скорость регулирования.
И-регулятор с постоянной скоростью перемещения регулирующего органа может применяться только при наличии у него некоторой зоны нечувствительности; в этом случае регулирование становится устойчивым, что достигается также при условии
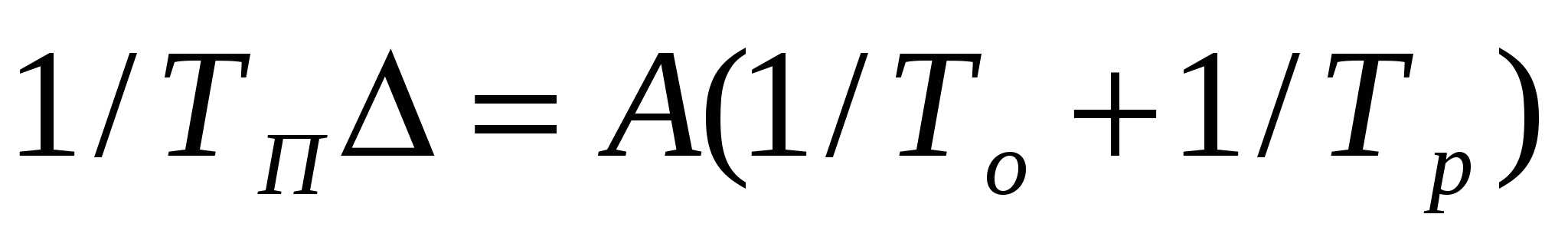 , (3.3) , (3.3)
где 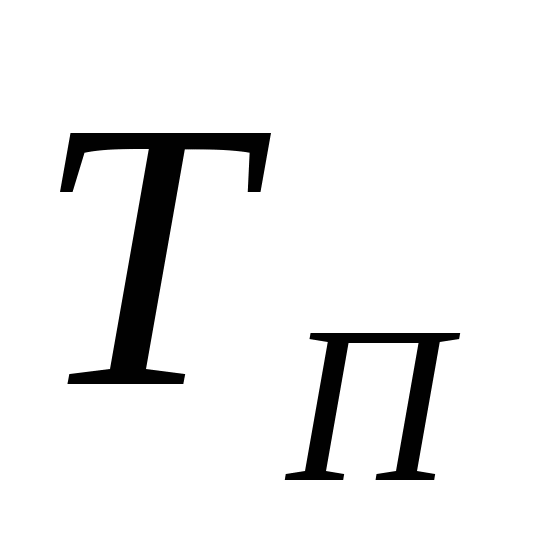 – время перемещения регулирующего органа; – время перемещения регулирующего органа;
 – зона нечувствительности регулятора; – зона нечувствительности регулятора;
А – некоторая постоянная, зависящая от свойств объекта и характера возмущения.
При этом чем меньше 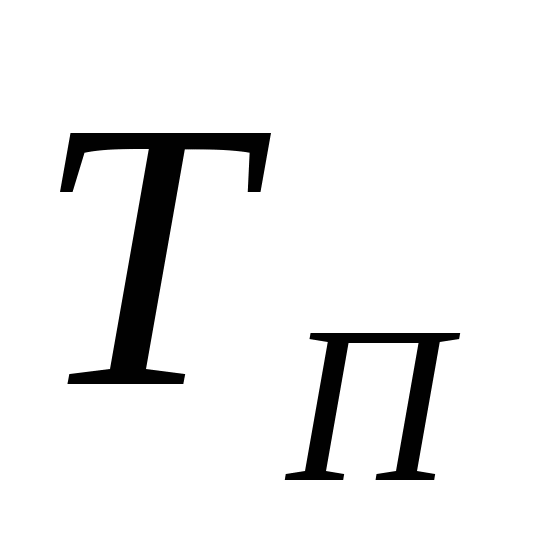 , тем больше должна быть зона нечувствительности , тем больше должна быть зона нечувствительности  . .
Устойчивое регулирование И-регулятор обеспечивает при условии
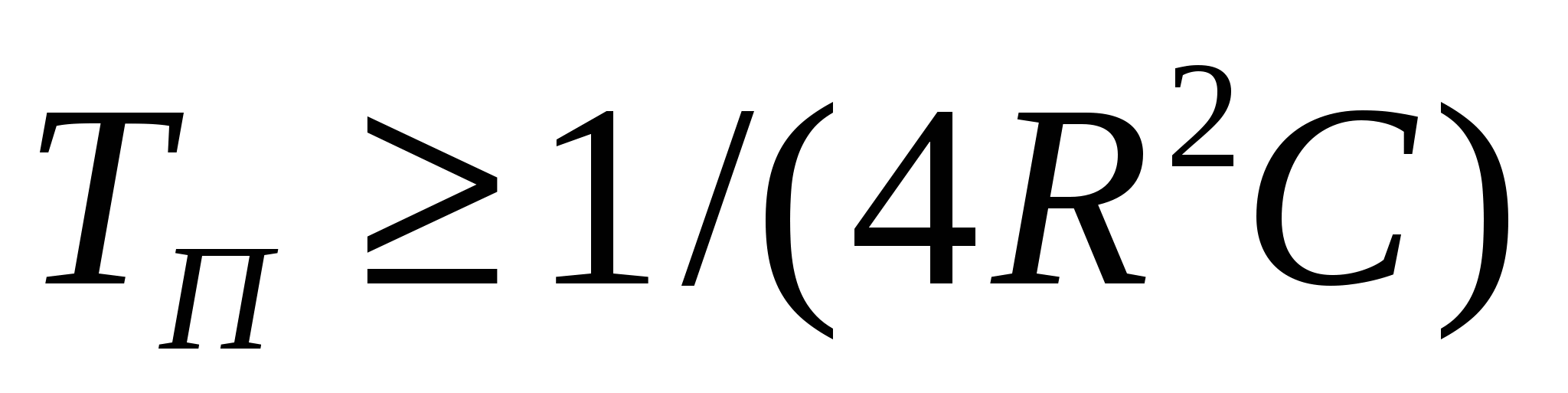 , (3.4) , (3.4)
где R – коэффициент сопротивления (по выходу);
С – коэффициент емкости объекта.
Например, при регулировании уровня воды в баке коэффициент сопротивления
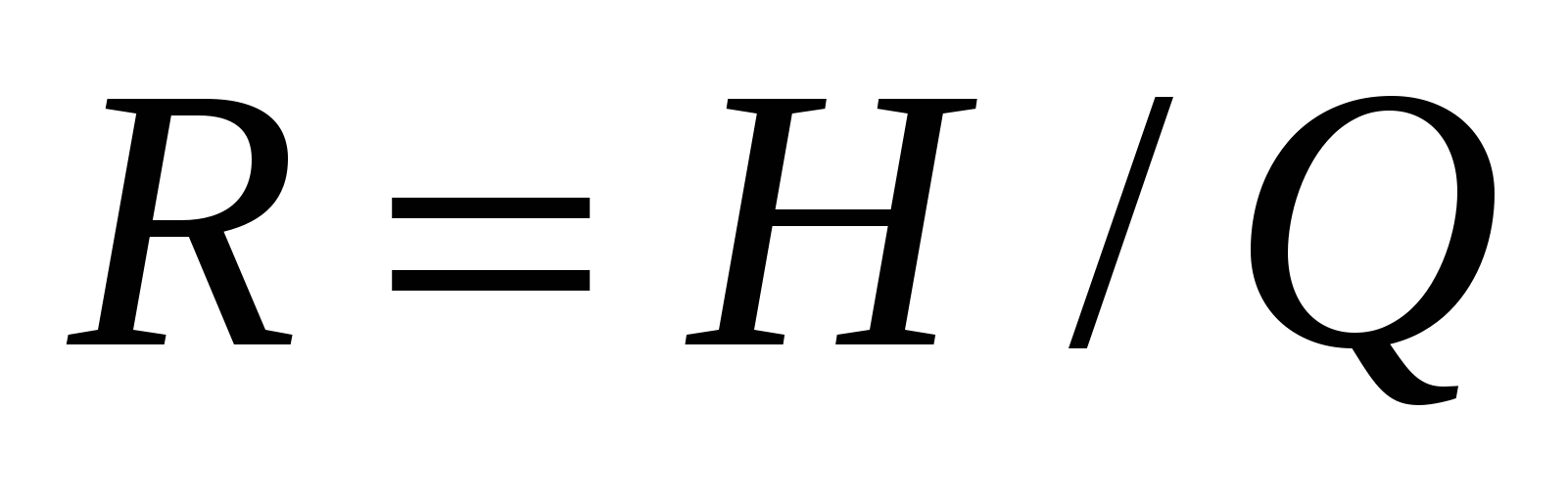 , ,
где Н – уровень воды;
Q – расход воды.
При регулировании температуры жидкости в баке коэффициент сопротивления
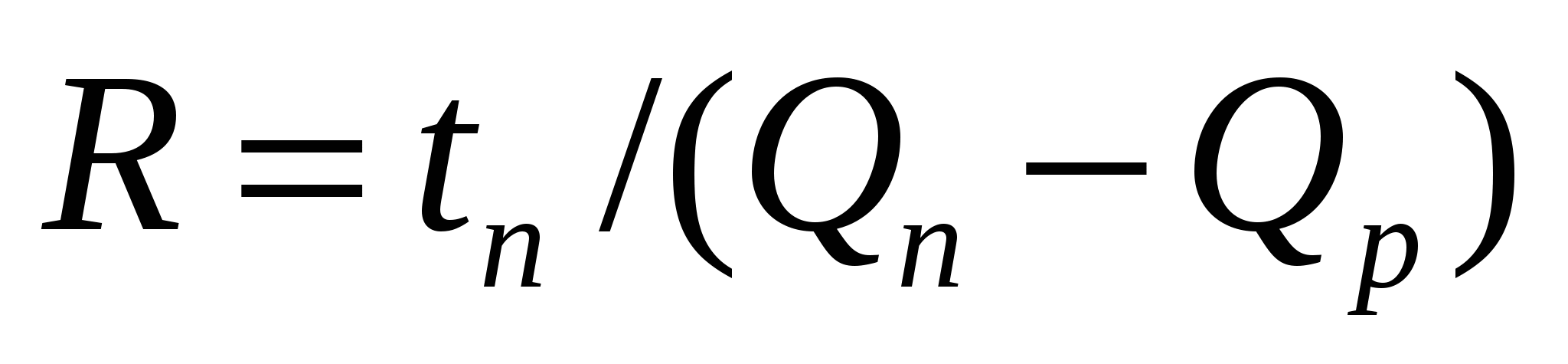 , ,
где 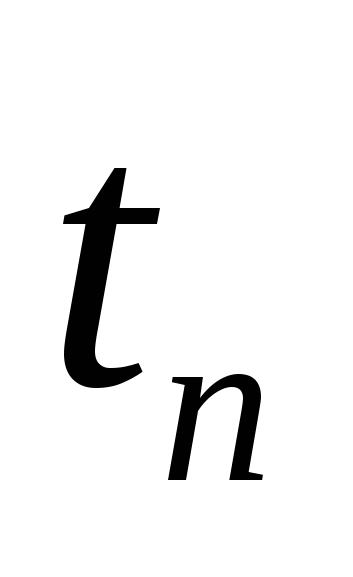 – потенциальное значение температуры; – потенциальное значение температуры;
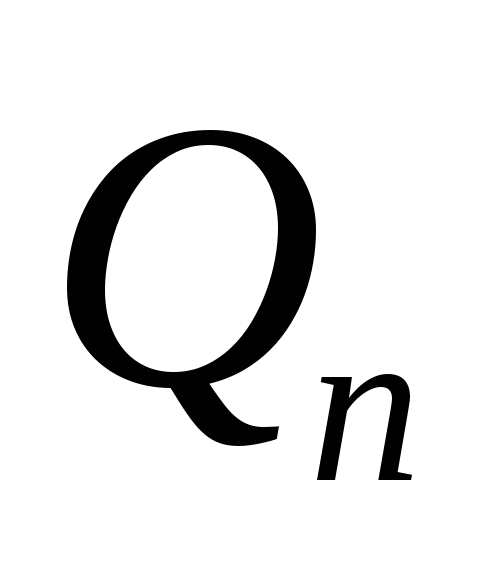 – количество теплоты, вносимое в объект; – количество теплоты, вносимое в объект;
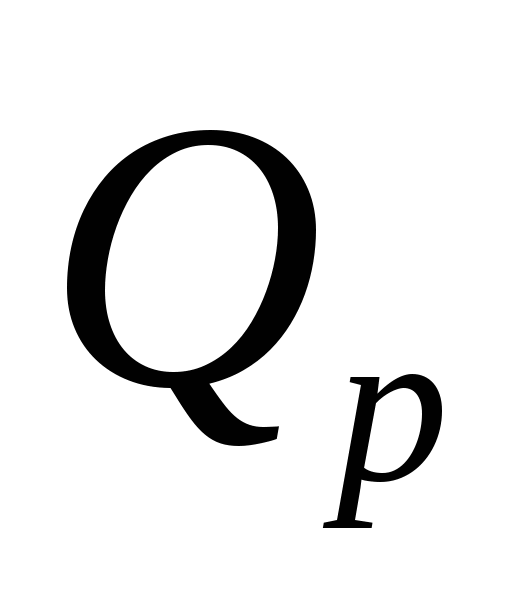 – количество теплоты, уносимое из объекта. – количество теплоты, уносимое из объекта.
ПИ-регуляторы применяются в объектах с любой емкостью, большим запаздыванием и при большой, но медленно меняющейся нагрузке.
Для объектов многоемкостных эти регуляторы применяются при 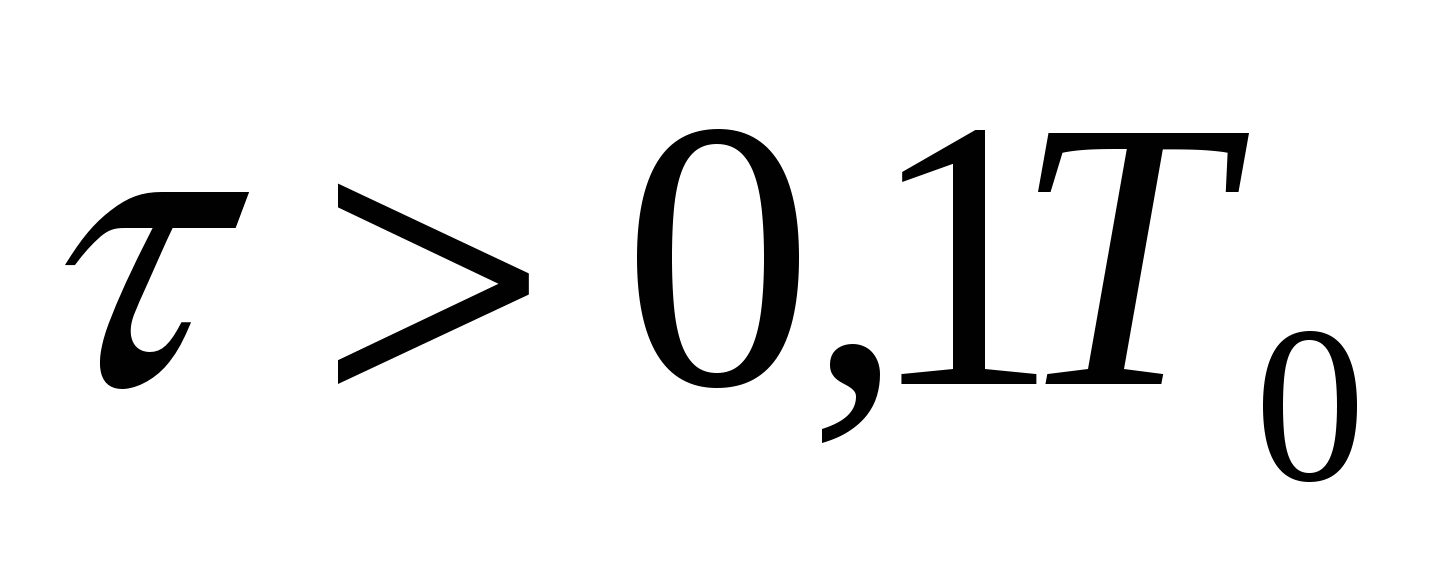 . .
ПД-регуляторы применяются в объектах со средней емкостью, при большом времени запаздывания и при малых изменениях нагрузки.
ПИД-регуляторы применяются в объектах с любой емкостью, очень большим запаздыванием и при больших и резких изменениях нагрузки. Эти регуляторы нецелесообразно применять для объектов, в которых 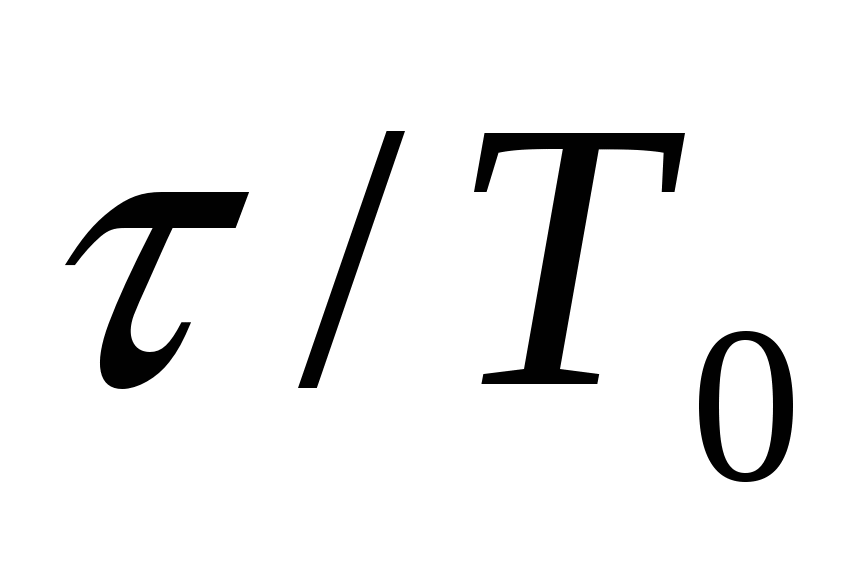 > 1. > 1.
3.2 Выбор регуляторов на основании расчета
Для действующего объекта при наличии кривых разгона либо частотных характеристик, либо для вновь проектируемого объекта, для которого кривые разгона сняты с аналогичного действующего объекта, выбор регуляторов следует производить на основании расчета.
При известных 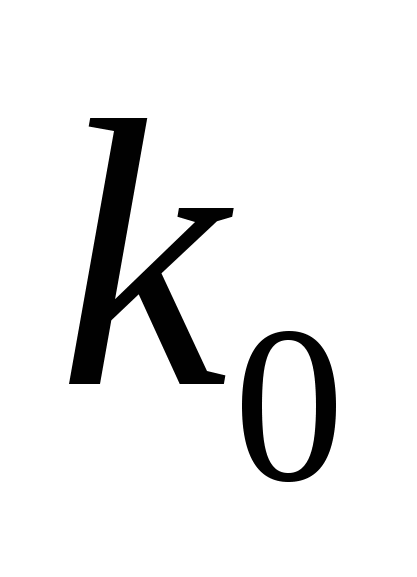 , , 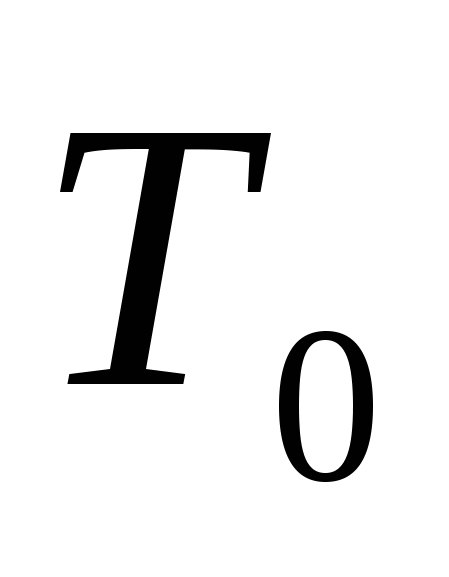 и и  переходный процесс системы регулирования (рисунок 3.1) для объектов с самовыравниванием, динамические свойства которых описываются дифференциальным уравнением первого порядка, может быть рассчитан по формуле переходный процесс системы регулирования (рисунок 3.1) для объектов с самовыравниванием, динамические свойства которых описываются дифференциальным уравнением первого порядка, может быть рассчитан по формуле
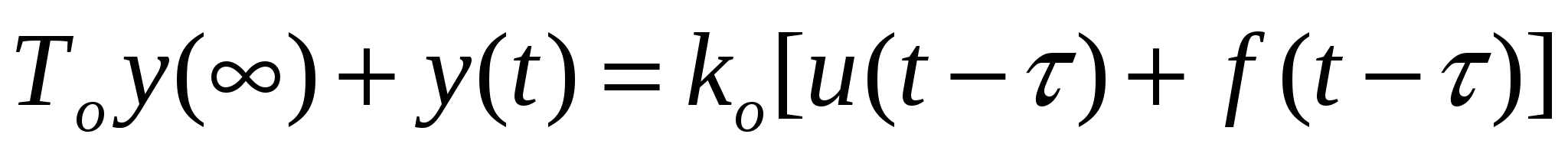 , (3.5) , (3.5)
а для объектов без самовыравнивания – по формуле
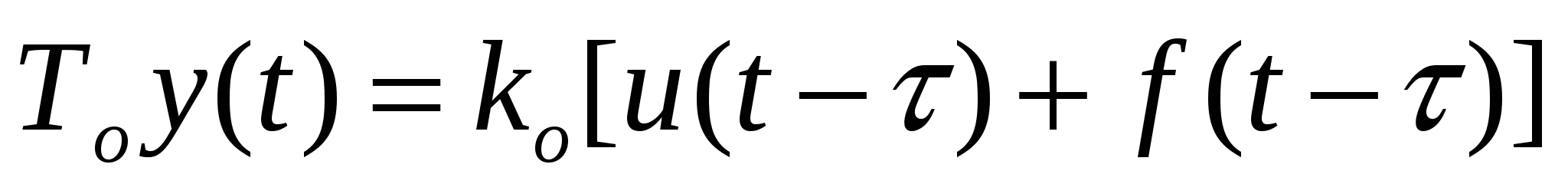 , (3.6) , (3.6)
где y – фактическое отклонение регулируемой величины;
 – текущее время; – текущее время;
u– регулирующее воздействие,
f– возмущение по нагрузке.

 Рисунок 3.1 – Структурная схема системы регулирования Рисунок 3.1 – Структурная схема системы регулирования
Характер переходного процесса, т. е. показатель качества регулирования, определяется динамическими свойствами объекта, выбранным законом регулирования и коэффициентами управления этого закона (параметрами настройки).
В соответствии с технологическими требованиями к системе автоматического регулирования необходимо выбрать такой закон регулирования, который в совокупности со свойствами регулируемого объекта обеспечил бы выполнение этих требований. Технологические требования к переходным процессам системы регулирования зависят от требований к конкретному технологическому процессу и его режима.
Большинству технологических требований удовлетворяют три характерных переходных процесса: апериодический, с перерегулированием 20 % и с минимальной квадратичной площадью отклонения регулируемого параметра.
Показателями переходных процессов являются:
– апериодического – 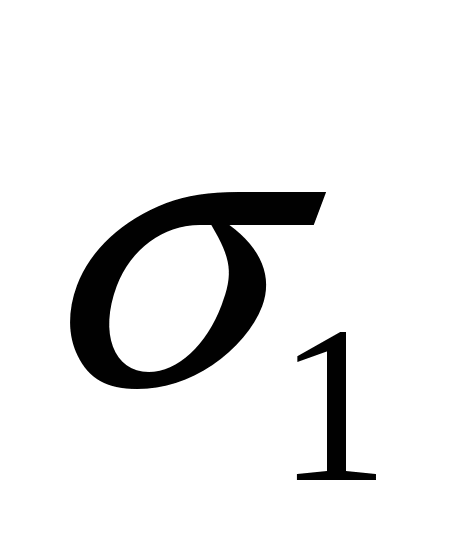 и и 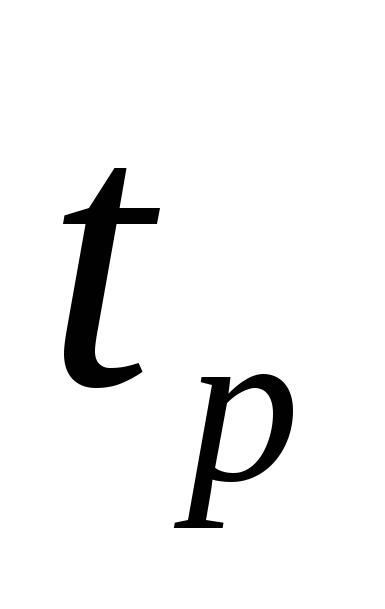 (принимается (принимается 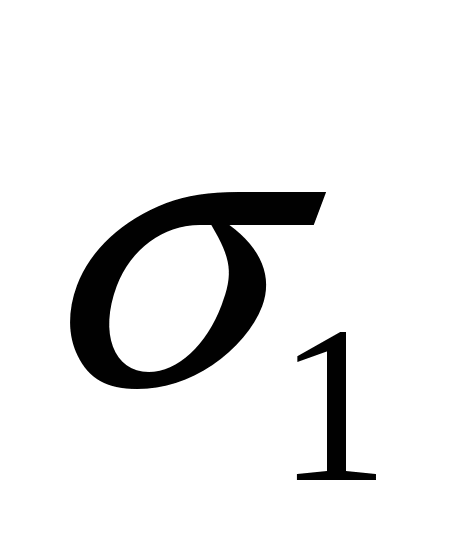 > > 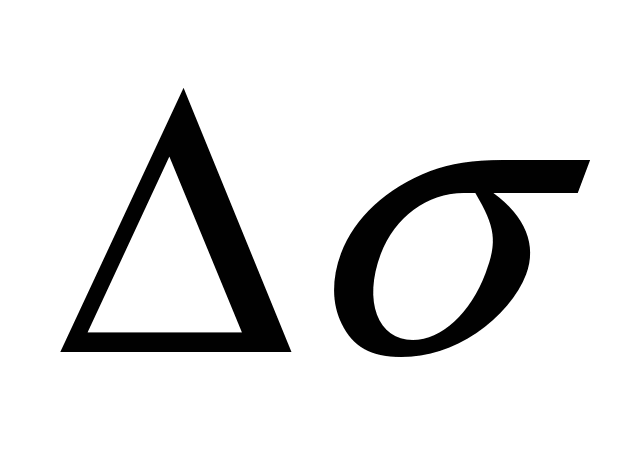 = 0,05); = 0,05);
– с перерегулированием 20 % – 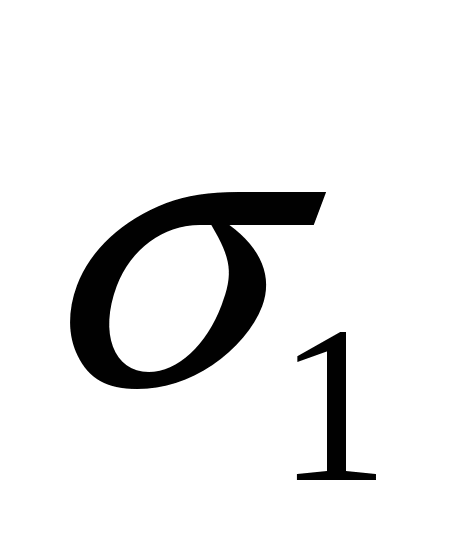 , , 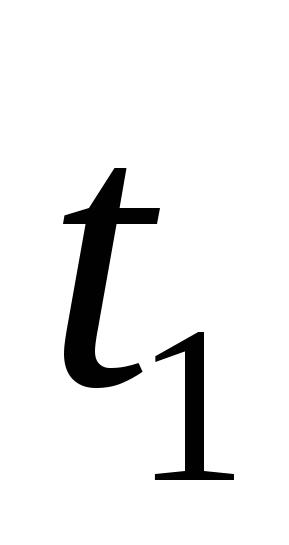 , , 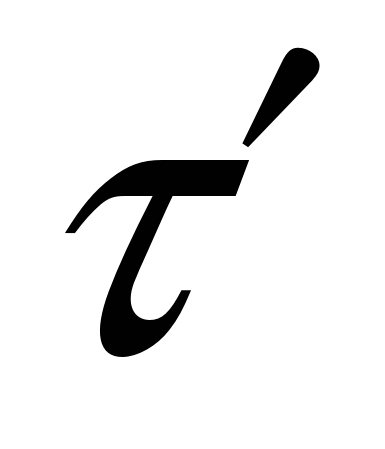 ( (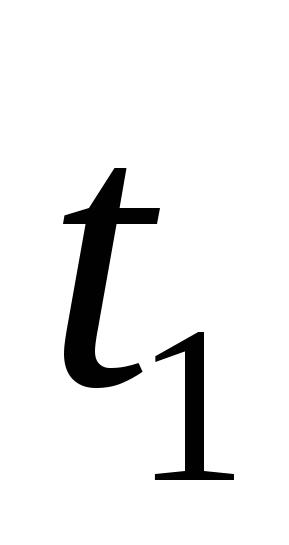 – время первого полупериода колебаний; – время первого полупериода колебаний; 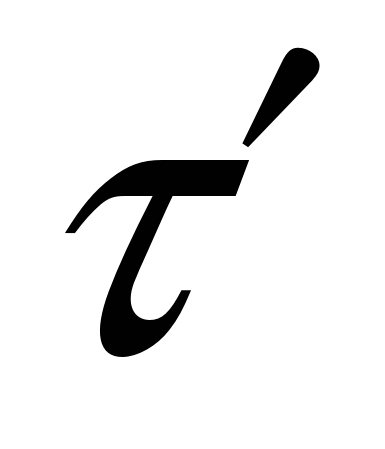 – время вхождения регулируемой величины в заданную зону); – время вхождения регулируемой величины в заданную зону);
– с минимальной квадратичной площадью отклонения регулируемого параметра – 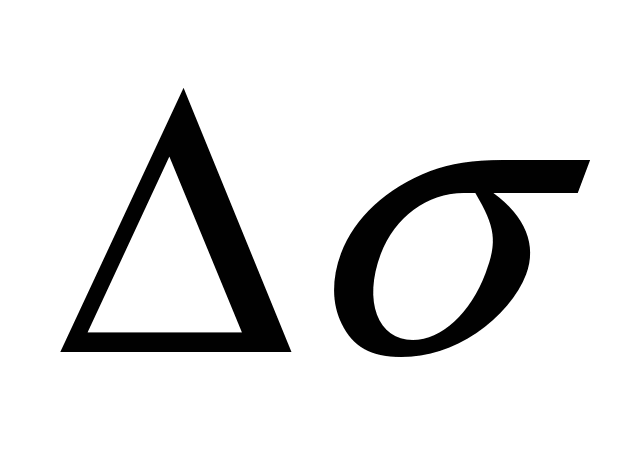 , S, , S, 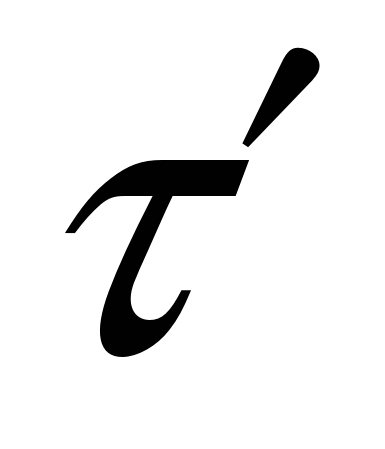 ( (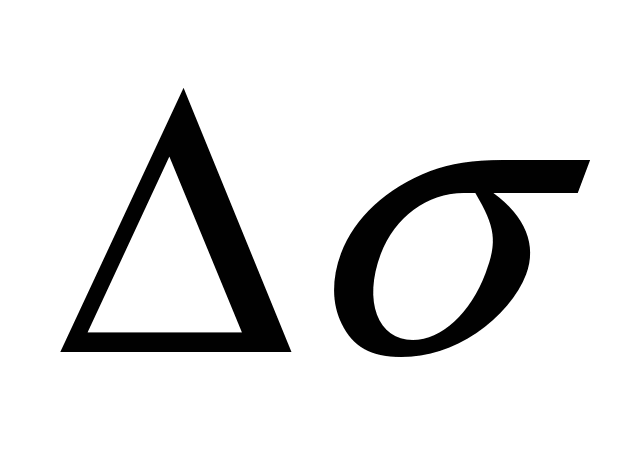 – динамическое отклонение регулируемой величины; S – чувствительность регулятора). – динамическое отклонение регулируемой величины; S – чувствительность регулятора).
После выбора регулятора производят следующие поверочные расчеты:
– уточняют по кривым, показанным на рисунке 3.2, значение Rд, которое должно быть меньше расчетного;
– по форме переходного процесса определяют максимальное динамическое отклонение регулируемой величины 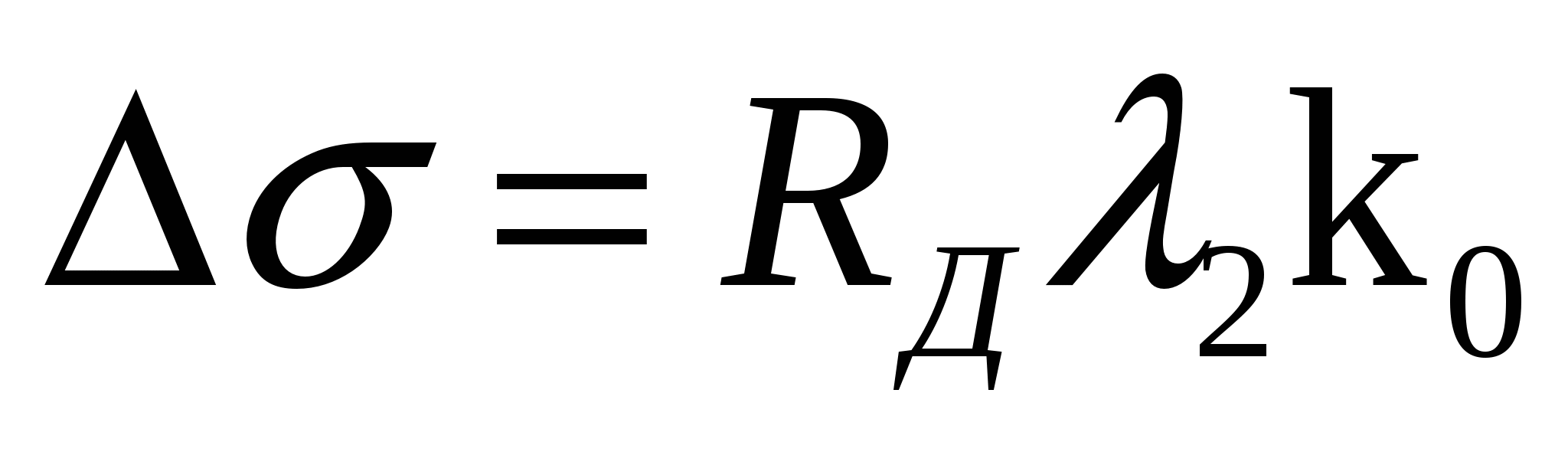 ; ;
- по графикам, изображенным на рисунке 3.3, находят относительное время регулирования 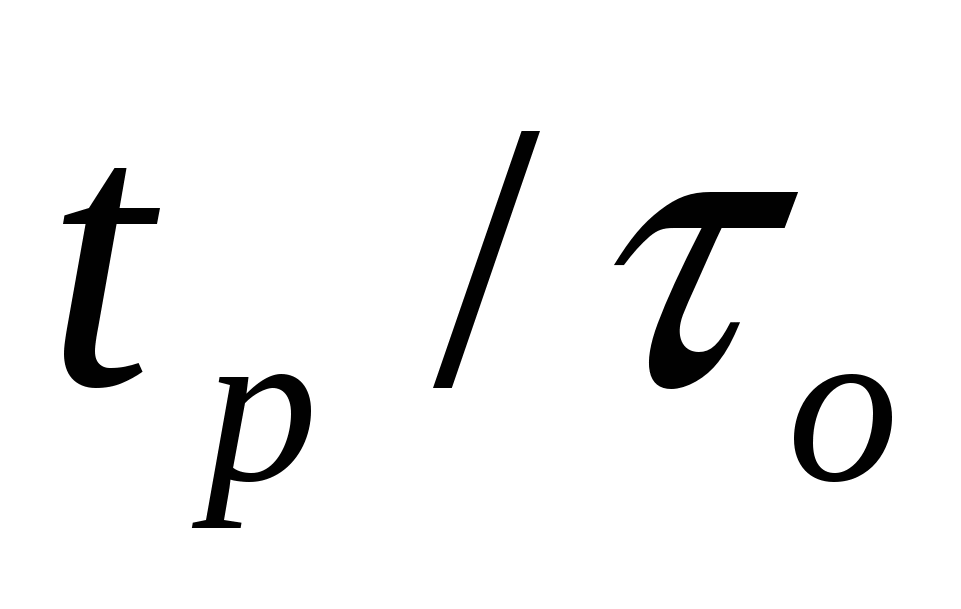 , которое должно быть меньше заданного по технологическим требованиям. , которое должно быть меньше заданного по технологическим требованиям.
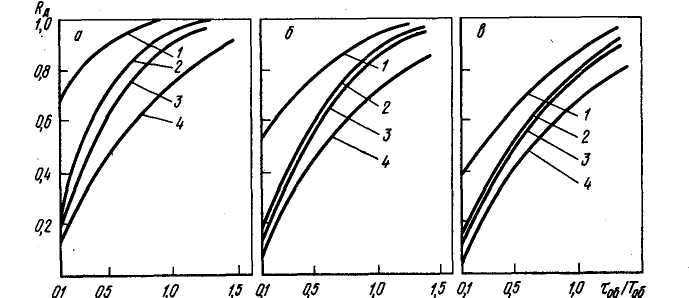
а – апериодическом; б – с 20 % перерегулированием; в – с min∫Δσ2dt; 1 – И-регулятор; 2 – П-регулятор; 3 –ПИ-регулятор; 4 – ПИД-регулятор
Рисунок 3.2 – Динамические коэффициенты регулирования на статических объектах при различных процессах
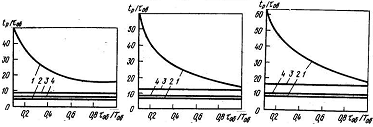
а) б) в)
а – апериодический; б – с 20 % перерегулированием; в – с min∫Δσ2dt; 1 – И-регулятор; 2 – П-регулятор; 3 –ПИ-регулятор; 4 – ПИД-регулятор
Рисунок 3.3 – Время регулирования на статических объектах при различных процессах
Таким образом, выбранный регулятор обеспечит технологические режимы регулирования.
3.3 Выбор оптимальных значений параметров регуляторов
Для каждого объекта с его характерными динамическими свойствами необходима соответствующая настройка регулятора. Оптимальные значения параметров настройки можно определить по специальным кривым, а также путем расчета. Однако на практике найденные значения параметров настройки корректируются при наладке регулятора по кривым регистрации регулируемой величины.
При инженерных методах выбора и расчета регулятора приближенные значения настроек для обеспечения типовых переходных процессов можно получить по формулам, приведенным в таблице 3.2.
Таблица 3.2 – Определение параметров настройки регулятора
Тип
регулятора
|
Вид
объекта
|
Вид переходного процесса
|
апериодический
|
с 20% перерегулированием
|
с миним. динамической ошибкой
|
П
|
с самовыравниванием
|
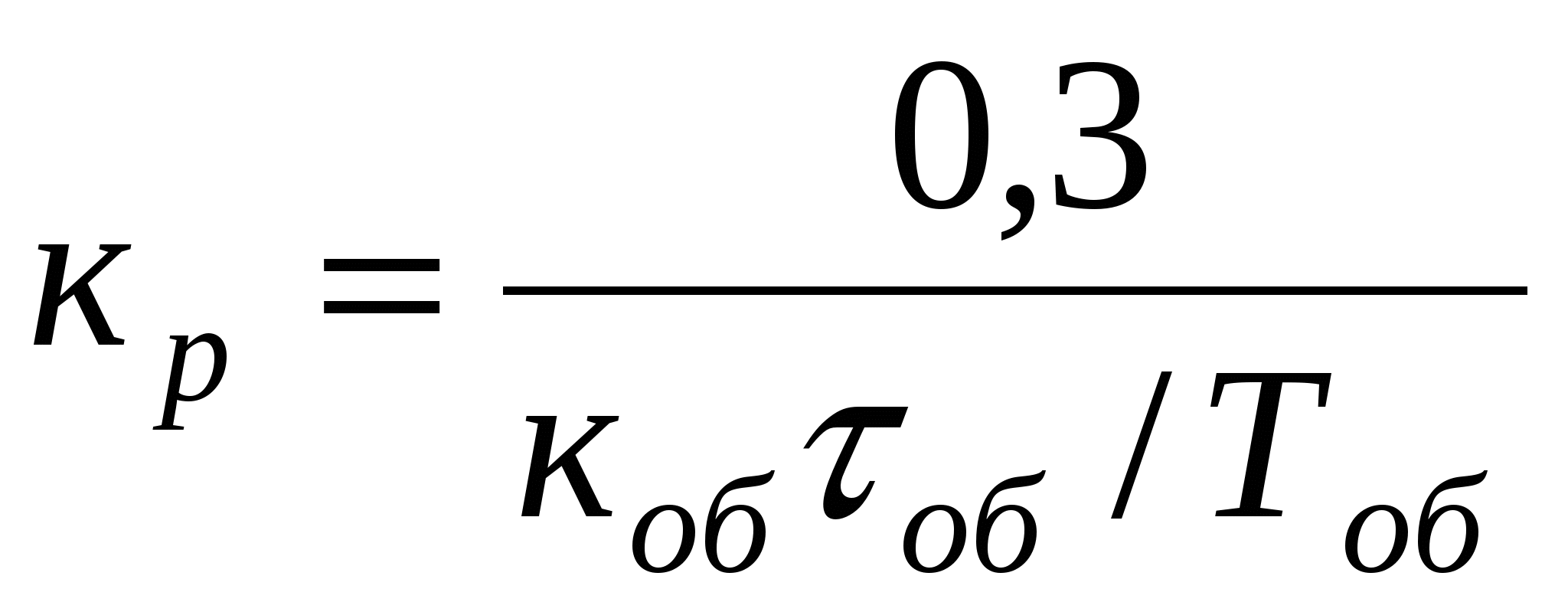
|
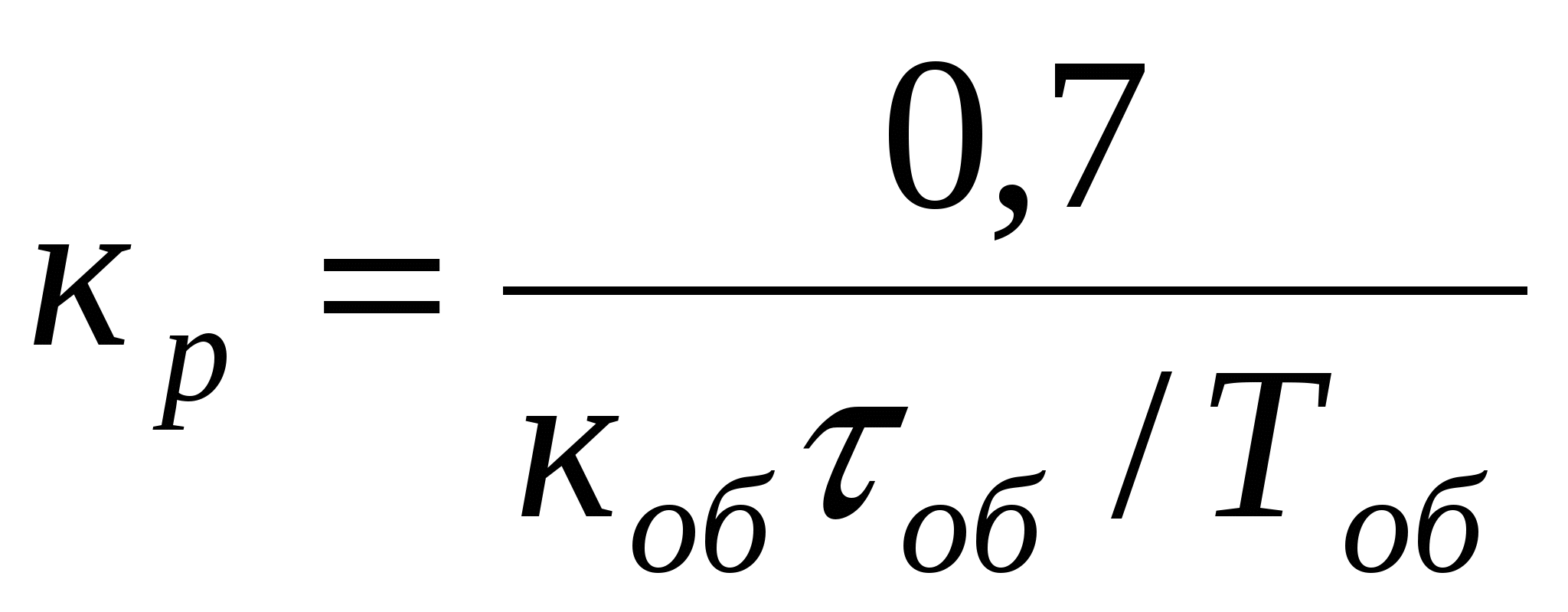
|
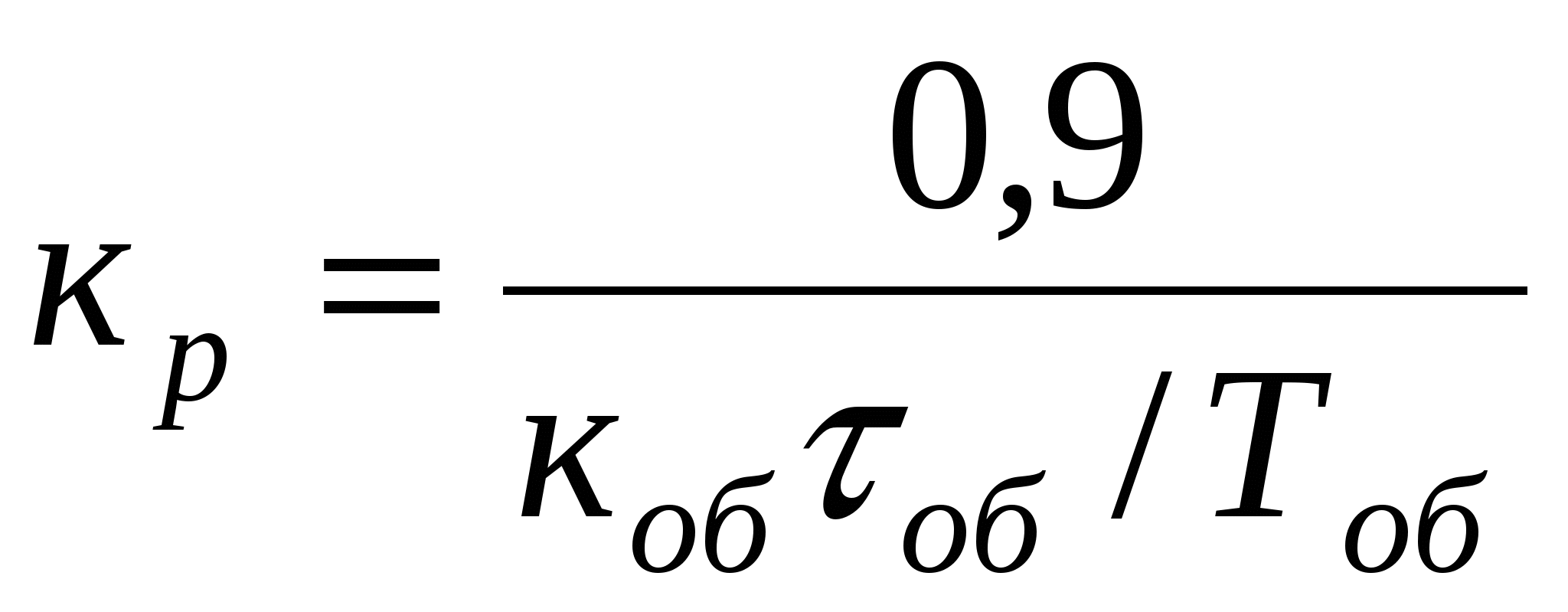
|
ПИ
|
с самовыравниванием
|
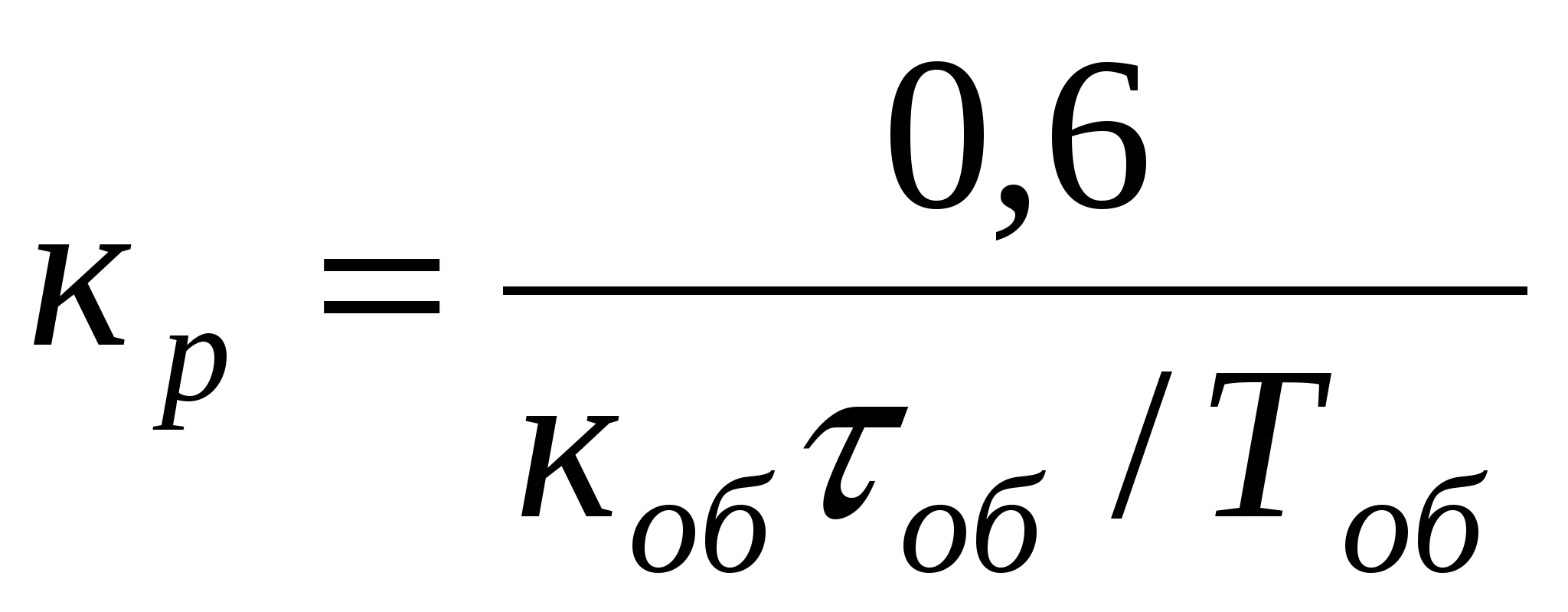 Ти=0,6 Тоб Ти=0,6 Тоб
|
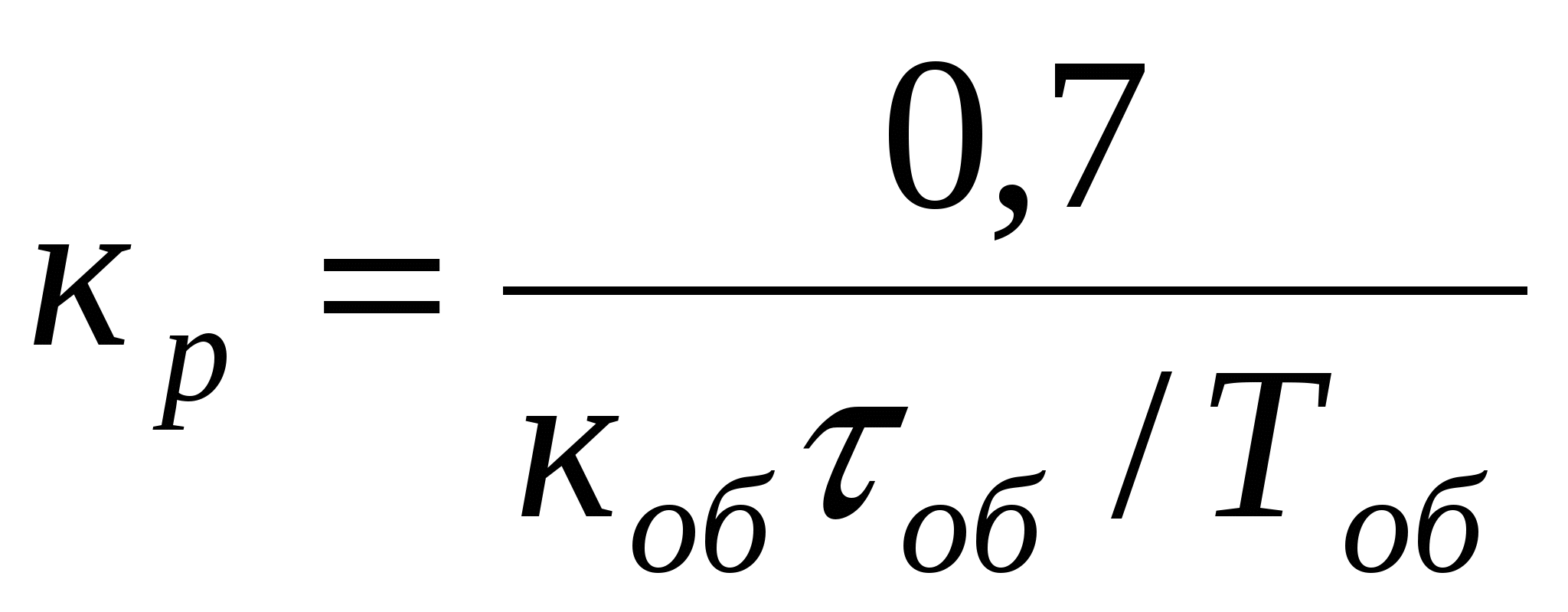 Ти=0,7 Тоб Ти=0,7 Тоб
|
 Ти= Тоб Ти= Тоб
|
ПИД
|
с самовыравниванием
|
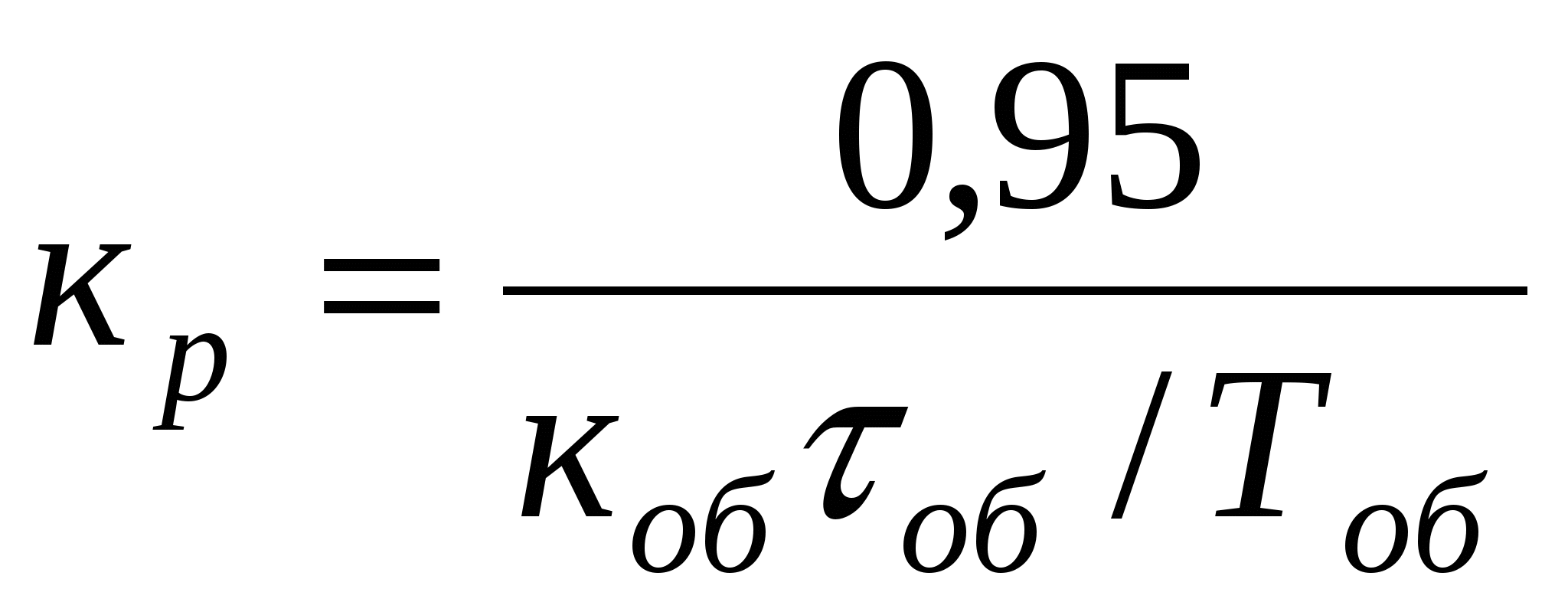 Ти=2,4 τоб Ти=2,4 τоб
Тд=0,4 τоб
|
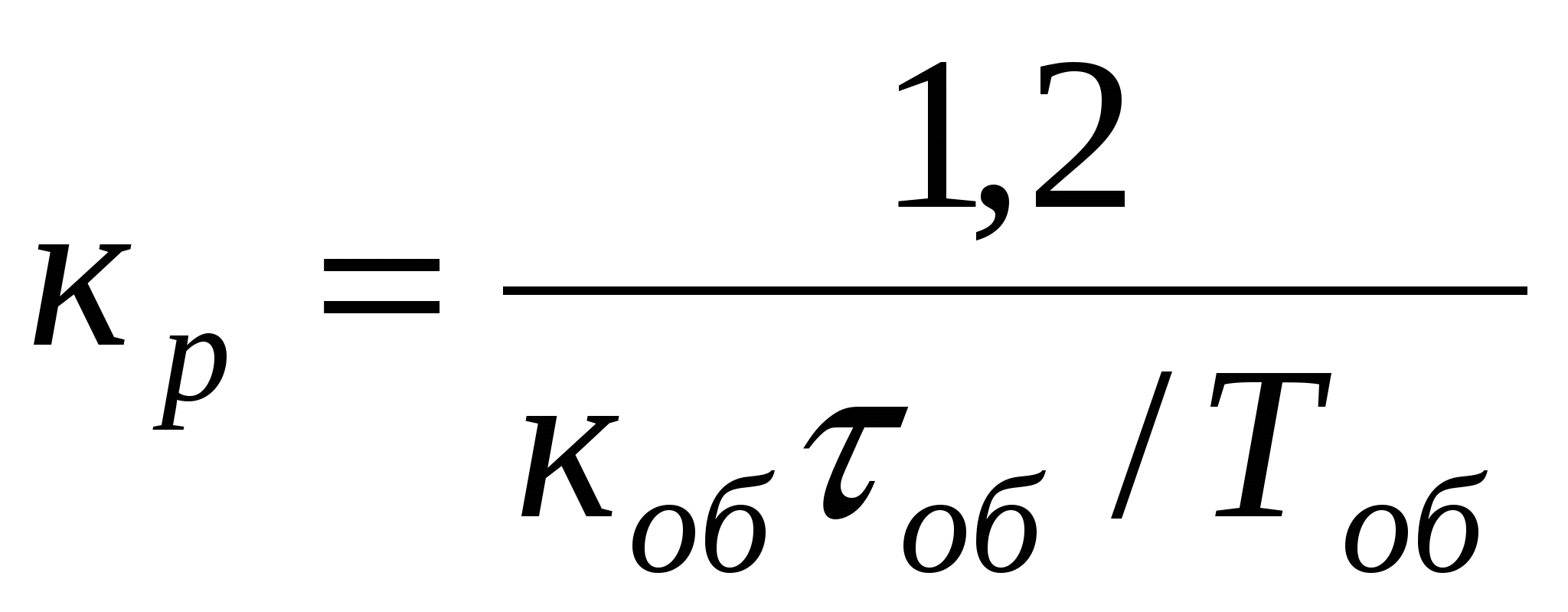 Ти=2 τоб Ти=2 τоб
Тд=0,4 τоб
|
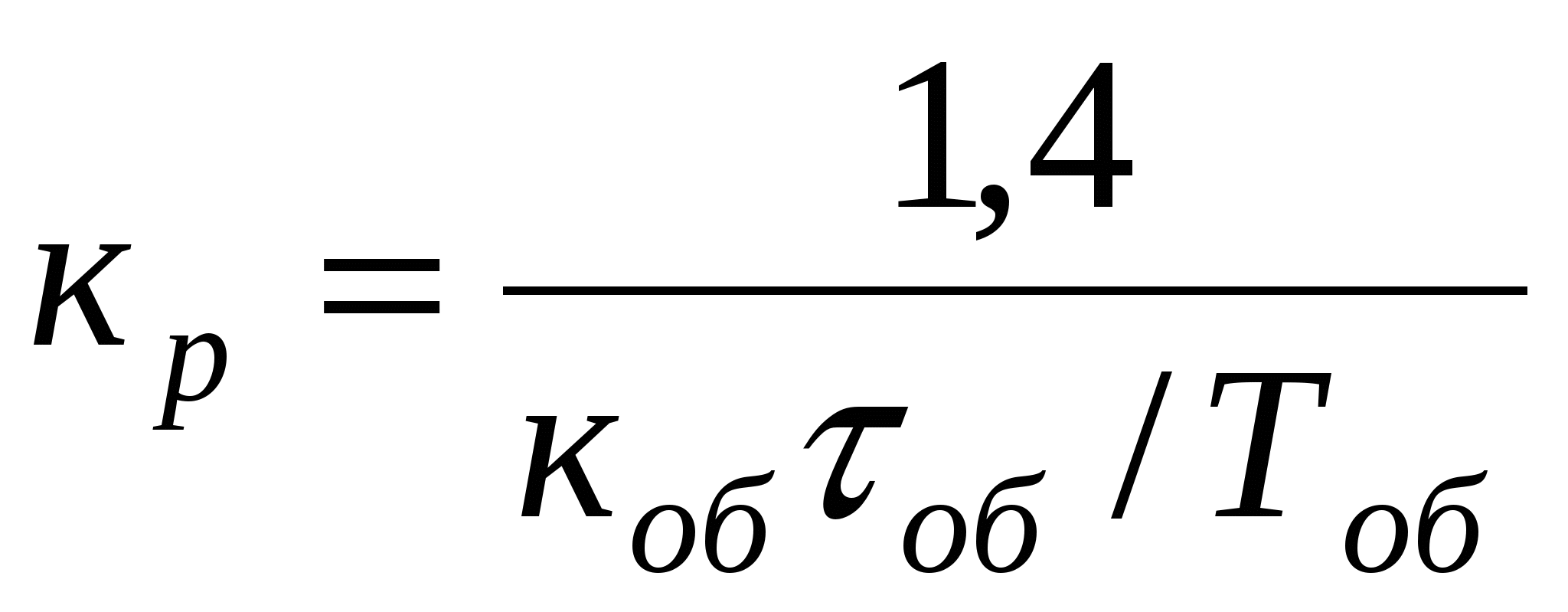 Ти=1,3 τоб Ти=1,3 τоб
Тд=0,5 τоб
|
П
|
без самовыравнивания
|
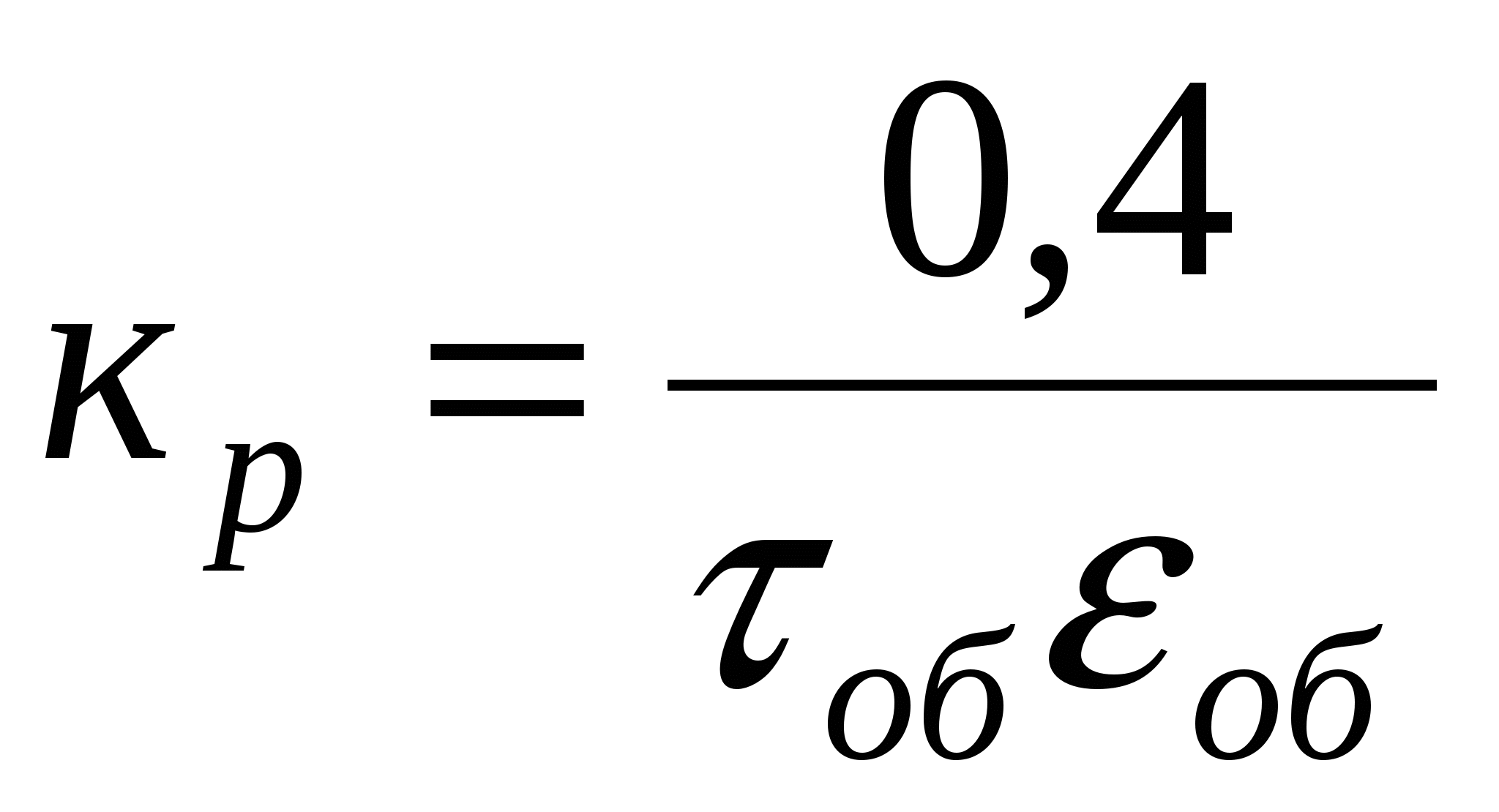
|
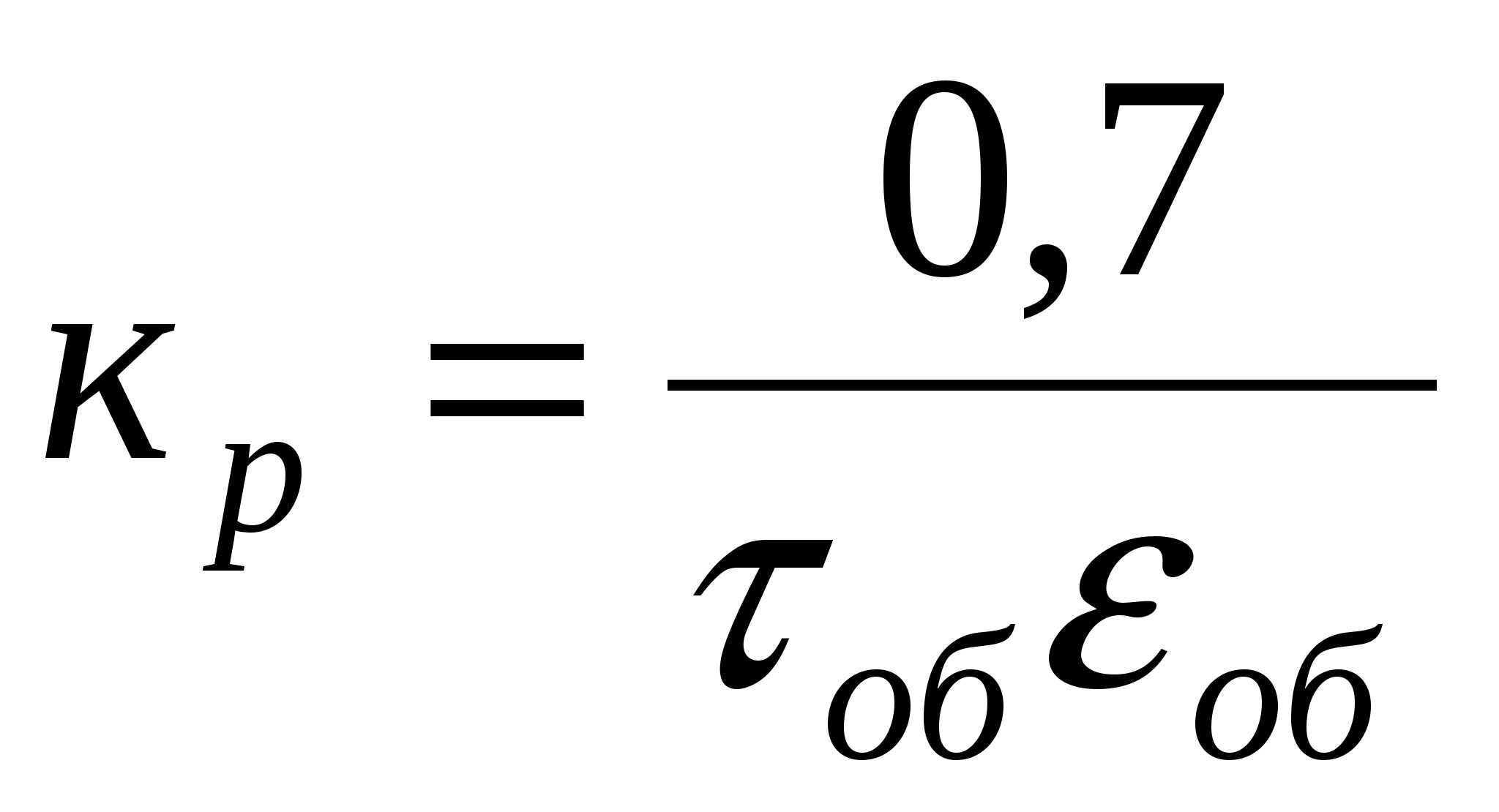
|
-
|
ПИ
|
без самовыравнивания
|
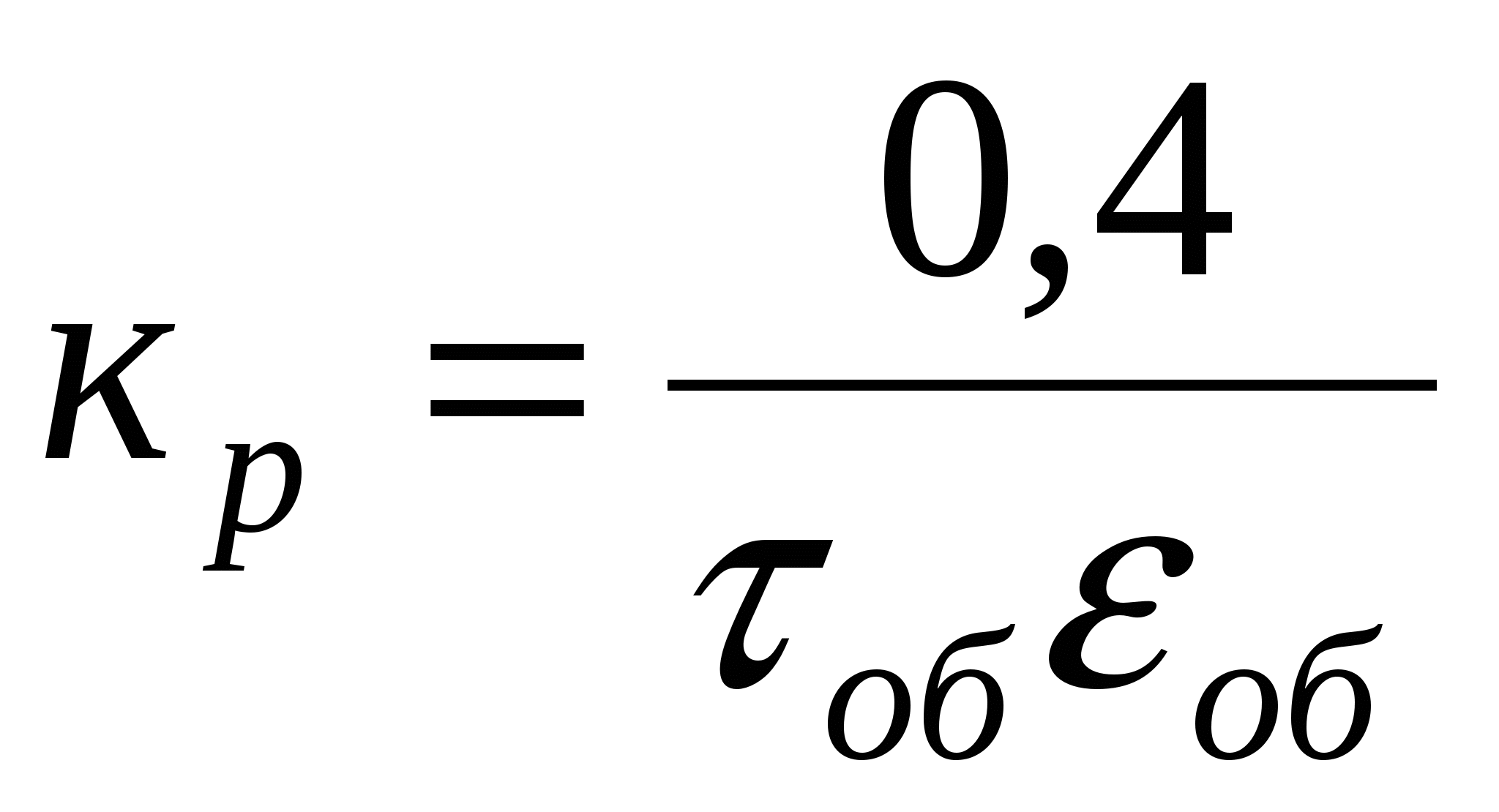
Ти=6 τоб
|
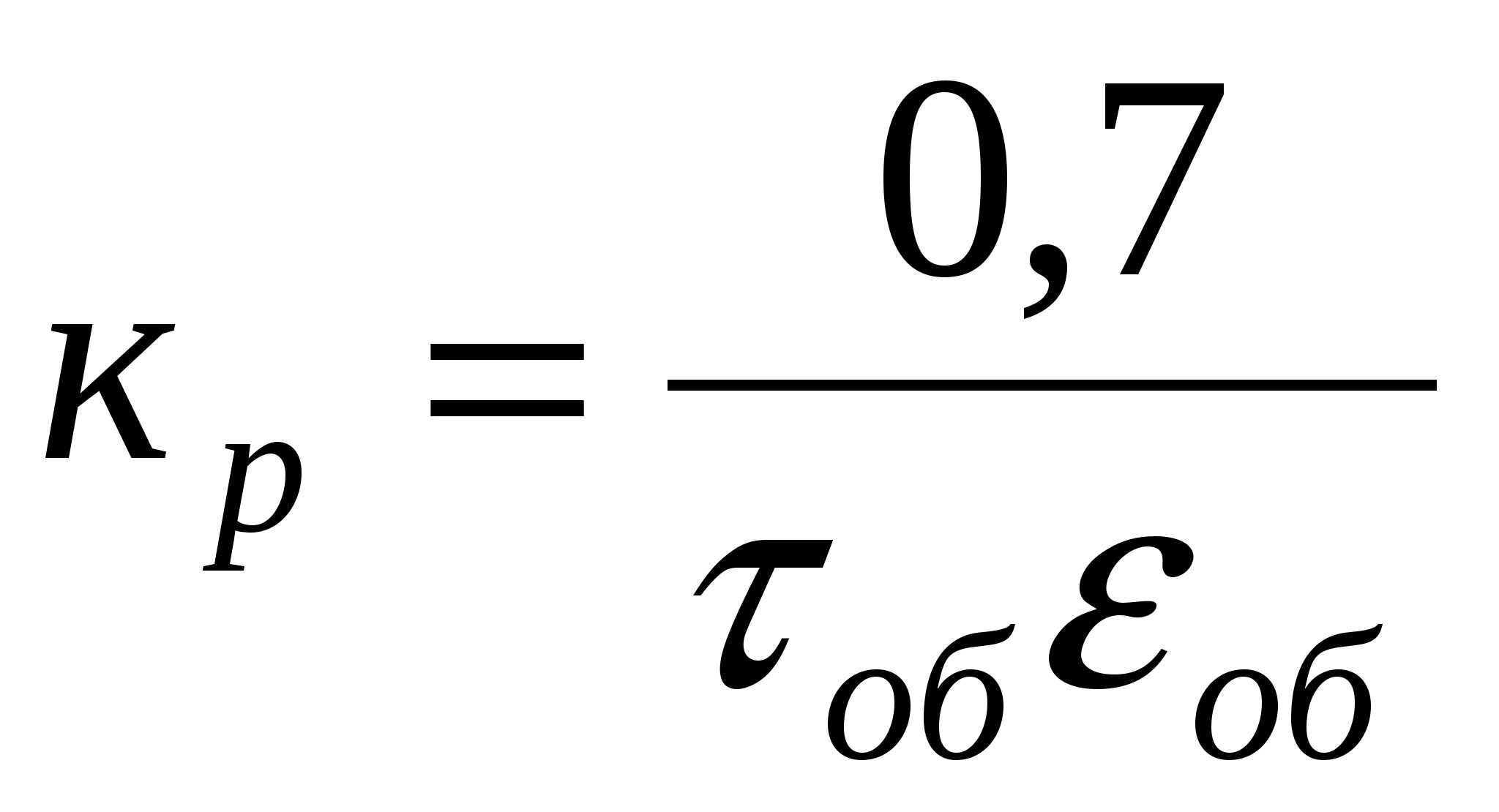
Ти=3 τоб
|
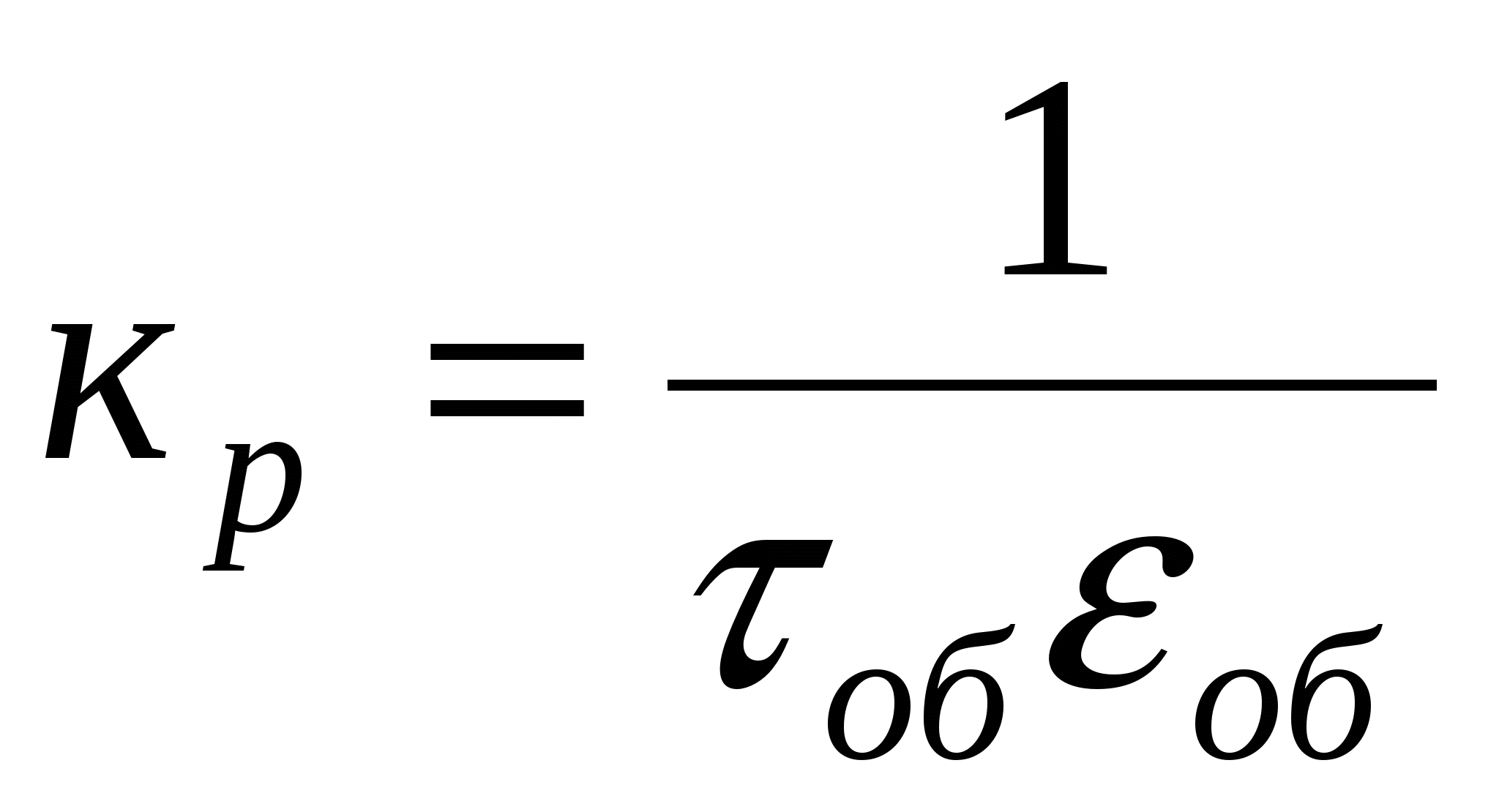
Ти=4 τоб
|
ПИД
|
без самовыравнивания
|
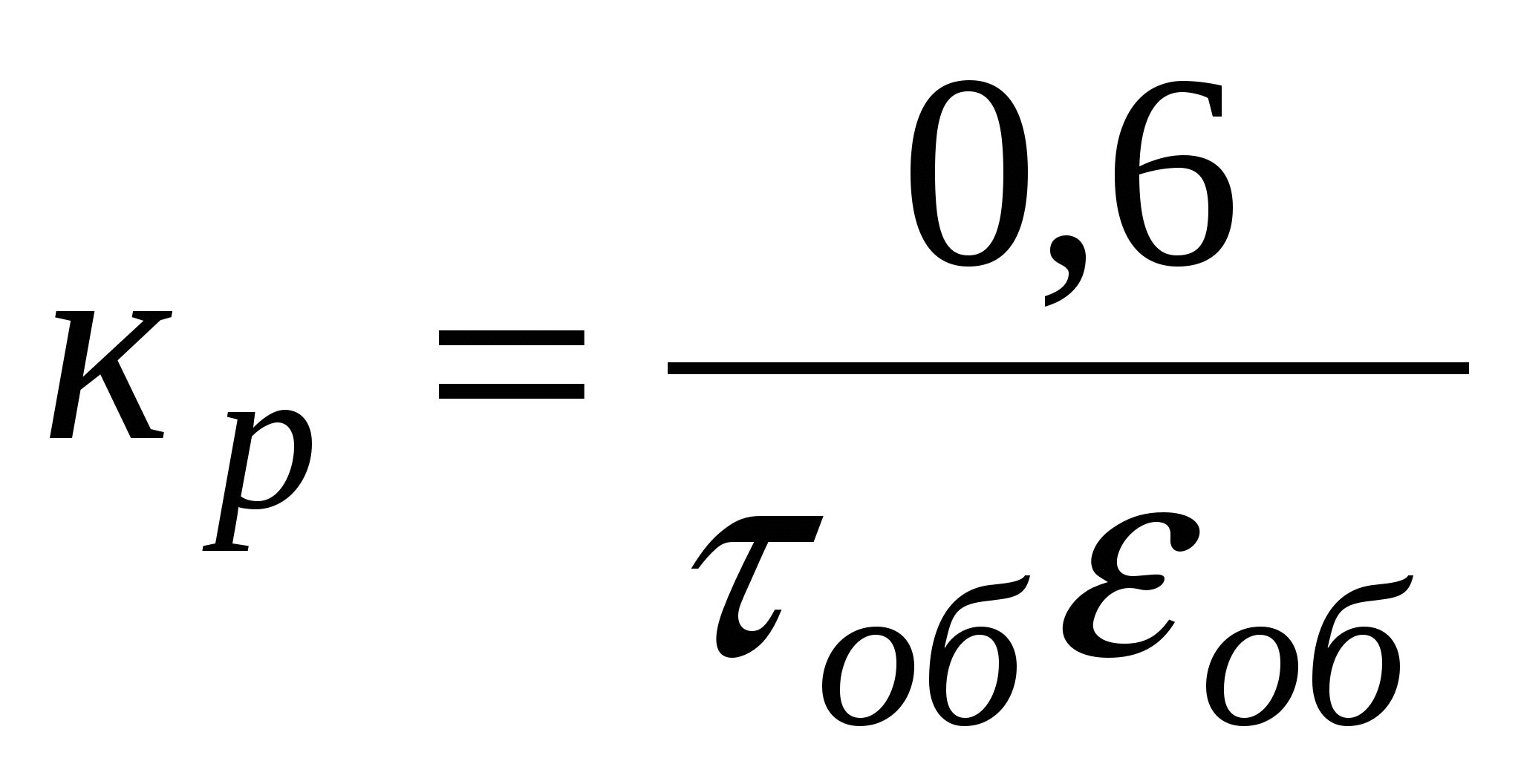
Ти=5 τоб
Тд=0,2 τоб
|
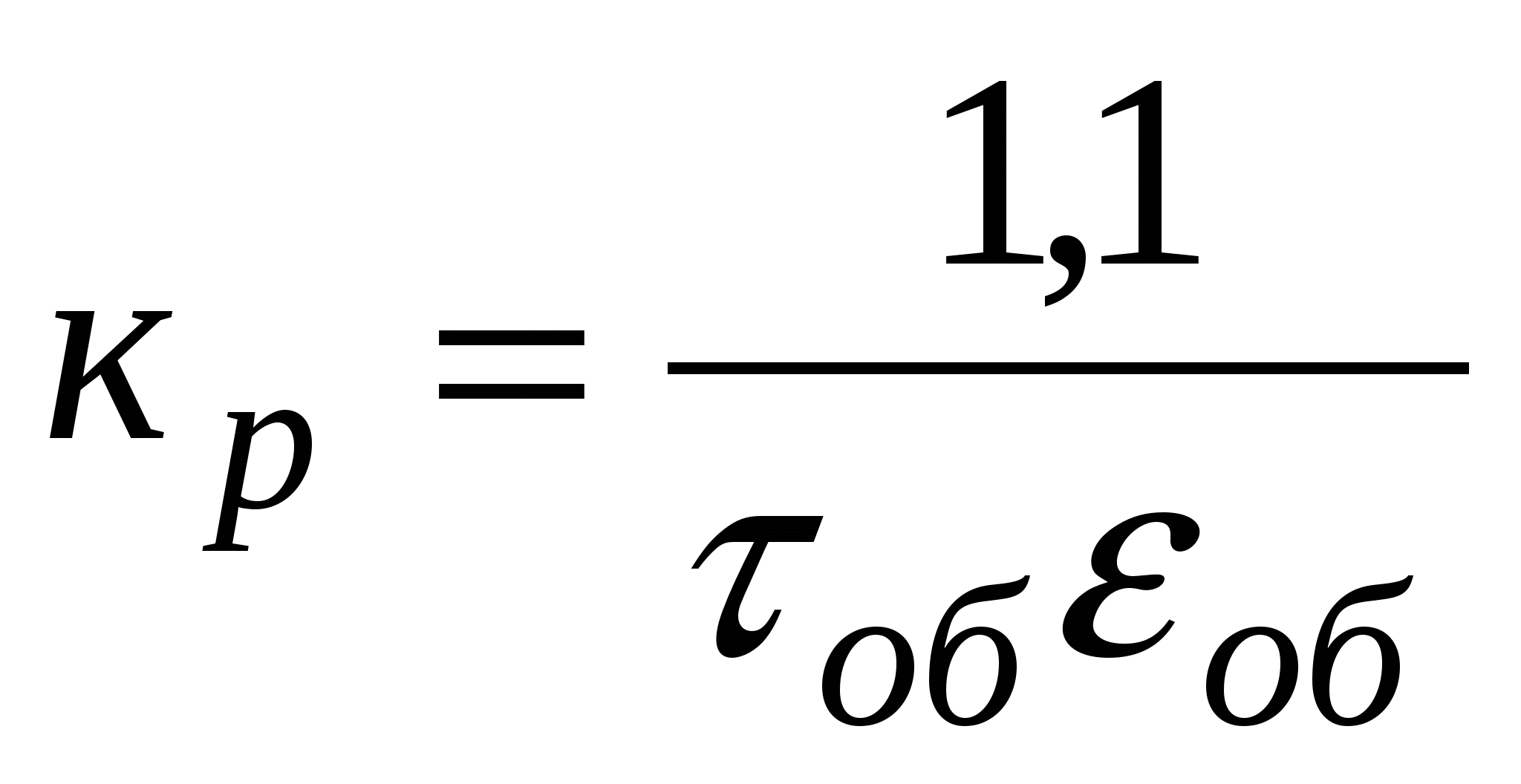
Ти=2 τоб
Тд=0,4 τоб
|
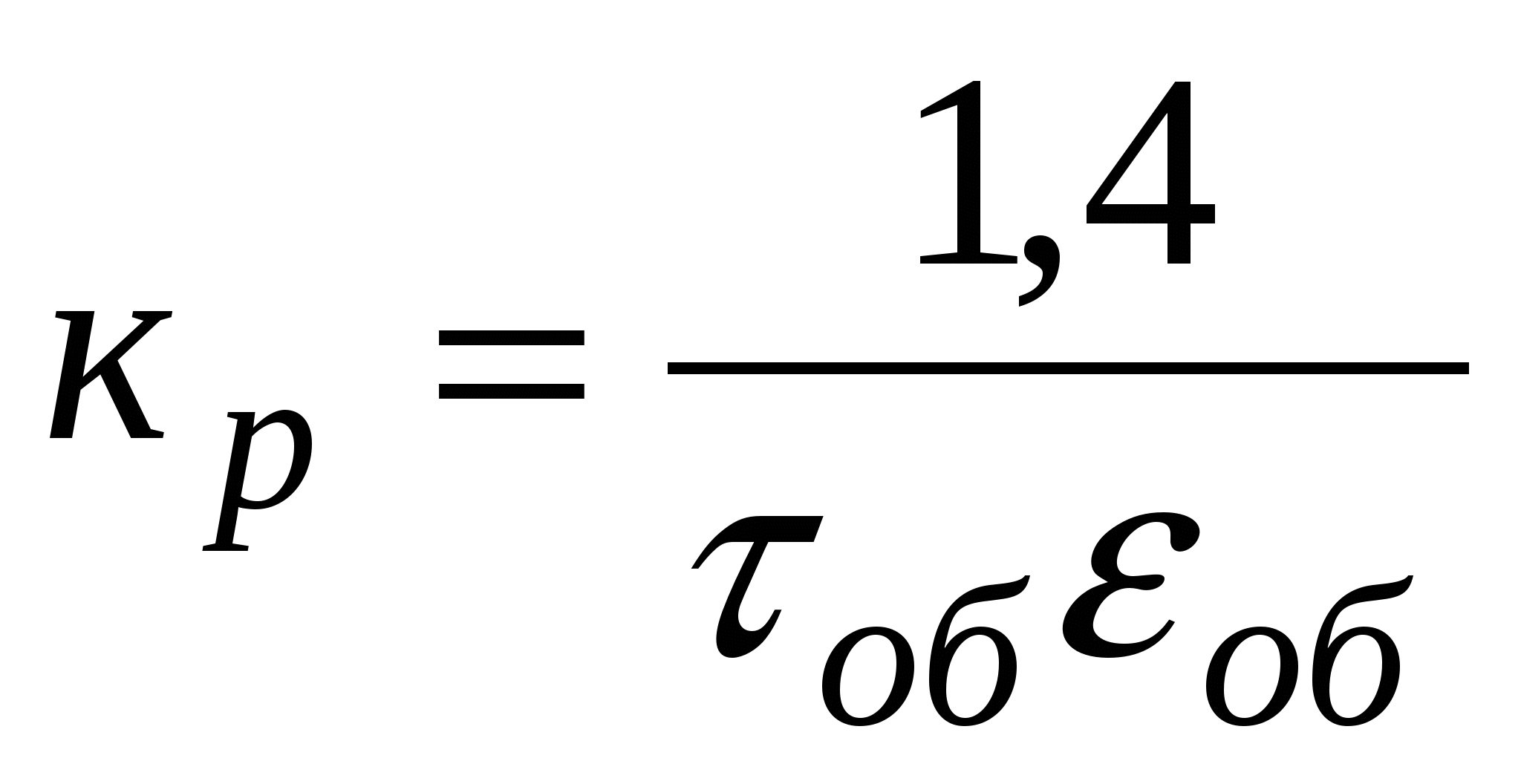
Ти=1,6 τоб
Тд=0,5 τоб
|
Приведем сведения, необходимые для приближенного определения значений параметров настройки.
П-регулятор. Чем больше предел пропорциональности, тем больше остаточное отклонение регулируемой величины. Чем меньше предел пропорциональности, тем больше амплитуда затухающих колебаний и больше время переходного процесса, но остаточное отклонение регулируемой величины в этом случае меньше.
Для пропорциональных регуляторов увеличение емкости объекта благоприятно влияет на качество регулирования, но при этом следует уменьшить пределы пропорциональности.
При наличии запаздывания надо увеличить пределы пропорциональности. Чем больше скорость перемещения регулирующего органа, тем выше устойчивость, а следовательно, и качество регулирования.
Необходимый предел пропорциональности
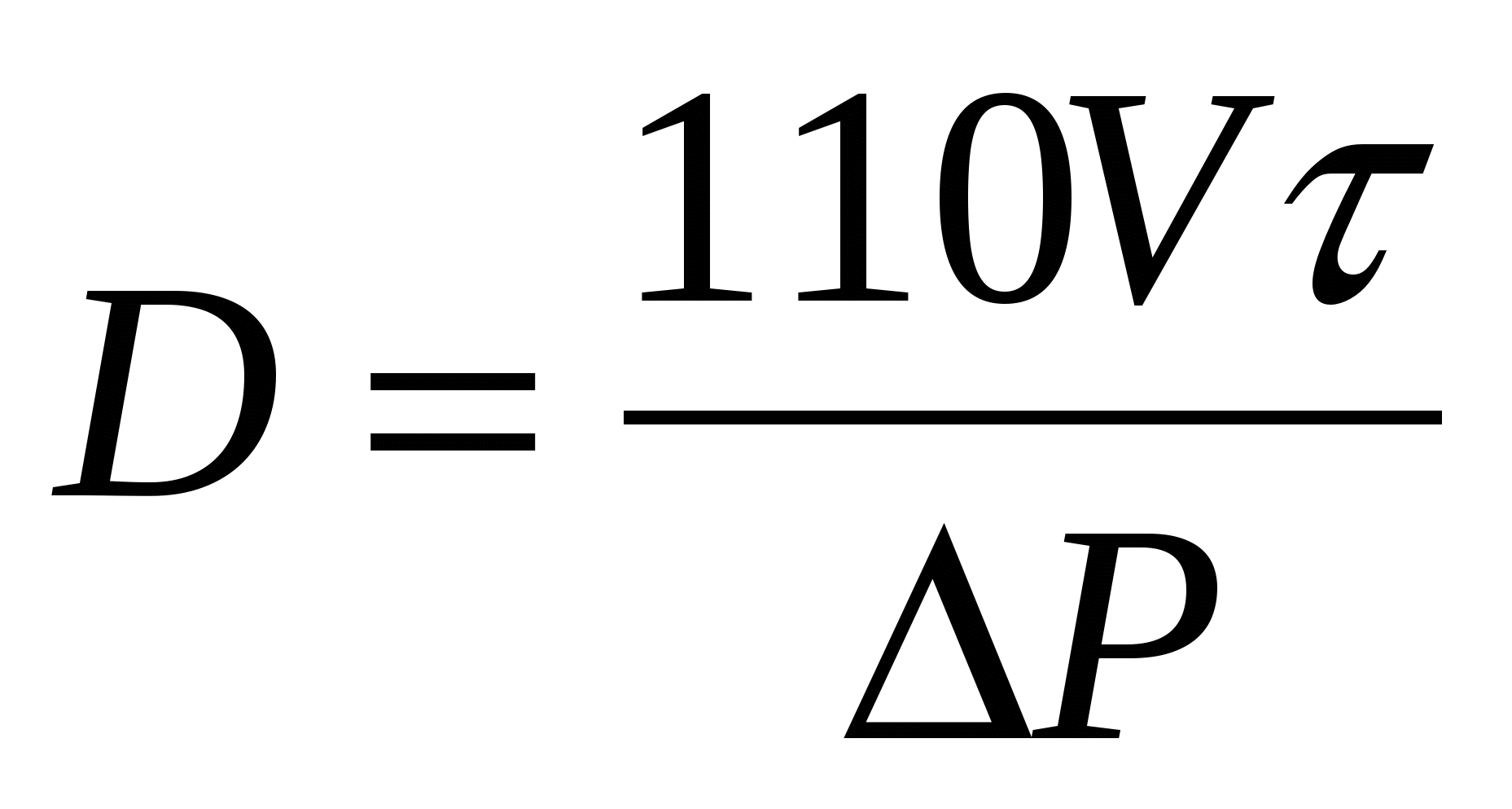 , (3.7) , (3.7)
где V – скорость изменения регулируемой величины, выраженная в процентах приращения в единицу времени;
ΔР – перемещение регулирующего органа в процентах полного хода, вызвавшее возмущение.
Для объектов без самовыравнивания предел пропорциональности можно определить по формуле
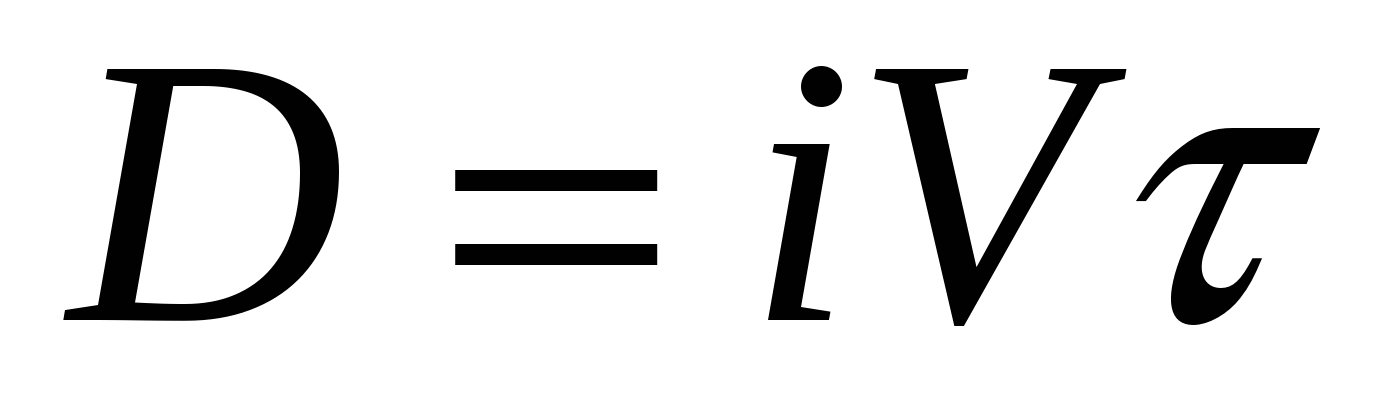 , (3.8) , (3.8)
где 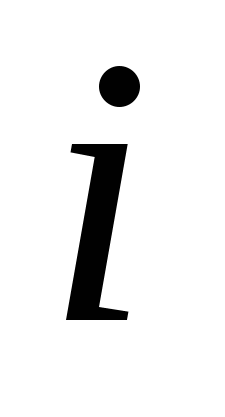 – коэффициент чувствительности измерительной части регулятора. – коэффициент чувствительности измерительной части регулятора.
Для объектов с самовыравниванием предел пропорциональности определяется по формуле
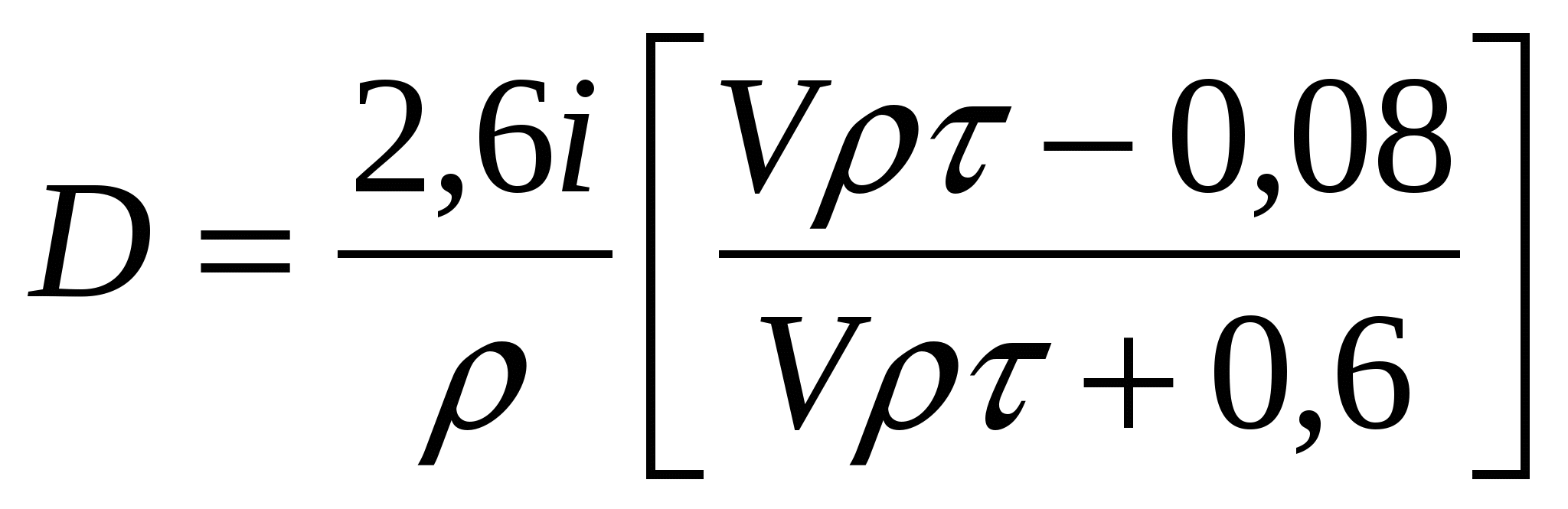 . (3.9) . (3.9)
И-регулятор. С увеличением пределов пропорциональности уменьшается переходный период. Необходимый предел пропорциональности определяется по формуле
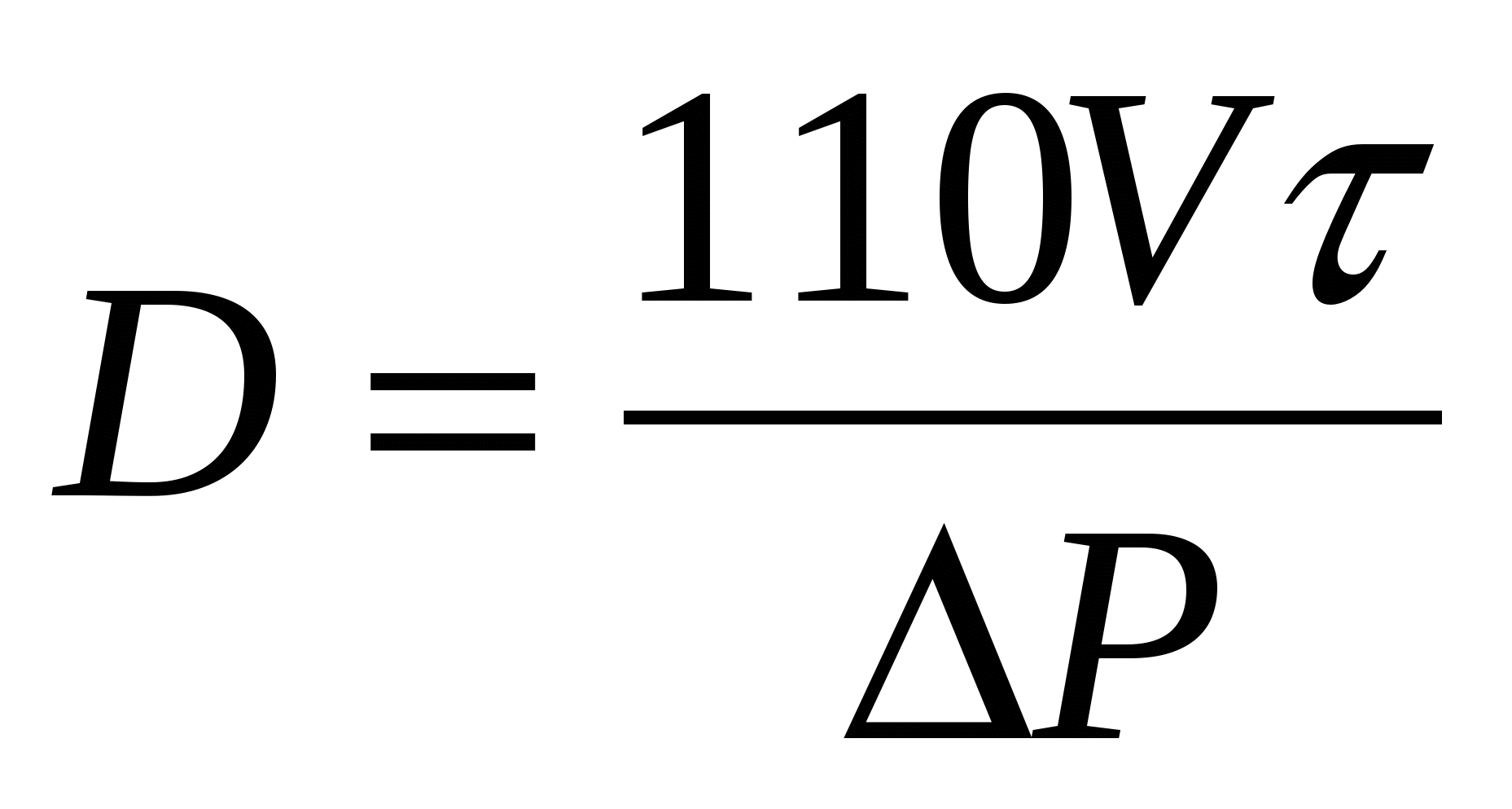 . (3.10) . (3.10)
ПИД-регулятор. Необходимый предел пропорциональности для этих регуляторов приближенно определяют по формуле
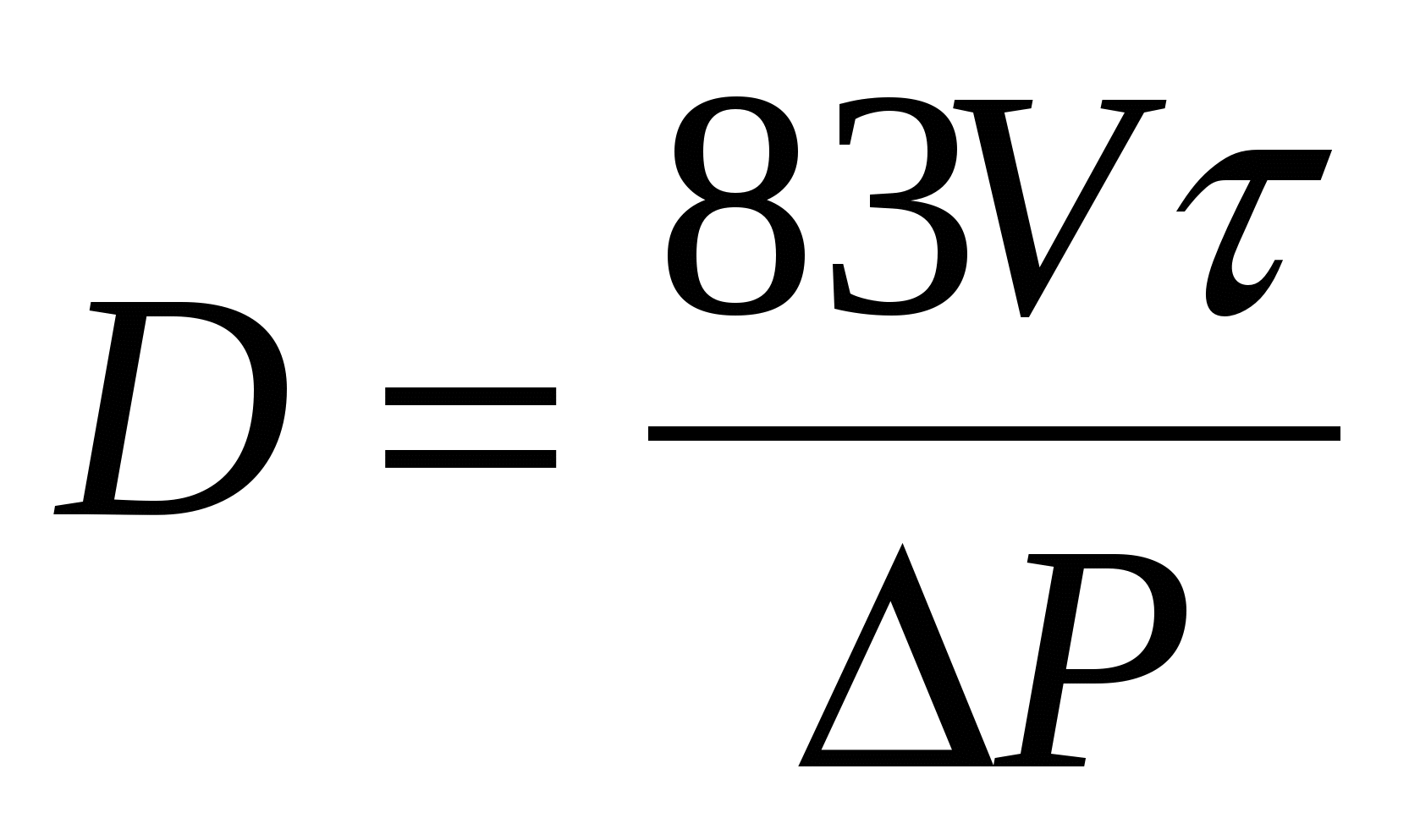 . (3.11) . (3.11)
Не менее важным фактором для хорошей работы регулятора является рациональный выбор пределов зоны нечувствительности и скорости регулирования.
Регулятор не реагирует на отклонение регулируемой величины, если оно меньше значения Δ /2. Большая зона нечувствительности, равная Δ, ухудшает качество регулирования, так как регулятор в этих пределах не может обнаружить возмущение. Регулятор начнет реагировать лишь тогда, когда значение регулируемой величины выйдет за пределы этой зоны. Наличие большой зоны нечувствительности вызывает увеличение запаздывания регулятора. Однако для регулятора с электроприводом зона нечувствительности не должна быть чрезмерно малой, так как в этом случае будут происходить излишне частые включения, что приведет к быстрому износу привода.
При наличии запаздывания регулятора или выбега исполнительного механизма колебания регулируемой величины значительно превысят ширину зоны нечувствительности; в этих случаях полезно иметь несколько большую зону нечувствительности. Однако при этом увеличится запаздывание регулятора.
Для многоемкостных объектов со значительным переходным запаздыванием зону нечувствительности следует сокращать. Это улучшит качество регулирования и не приведет к излишне частым включениям исполнительного механизма, так как график регулирования сравнительно большое время не будет выходить из зоны нечувствительности Δ. При этом следует учитывать длительно допустимые отклонения σдлит регулируемой величины. Следовательно, зона нечувствительности должна быть в пределах 0,3 ...0,5σдлит.
Скорость регулирования выбирается сравнительно небольшой при работе объекта на малых нагрузках. При переходе на большую нагрузку скорость регулирования увеличивается. Снижение скорости регулирования может повысить устойчивость регулирования лишь в очень редких случаях, например при астатическом регуляторе на объекте большой емкости.
3.4 Проектирование регулятора в MATLAB
Для решения этой задачи в MATLAB предусмотрены средства PID Tuner и SISO Design Tool.
ПИД регулятор представляется в параллельной PID и стандартной PIDSTD формах. Функция comp = pid(Kp,Ki,Kd,Tf) формирует непрерывный параллельный регулятор с независимыми пропорциональным Kp, интегральным Ki, дифференциальным Kd коэффициентами усиления и постоянной времени инерции Tf дифференциального фильтра (реального дифференцирующего звена)
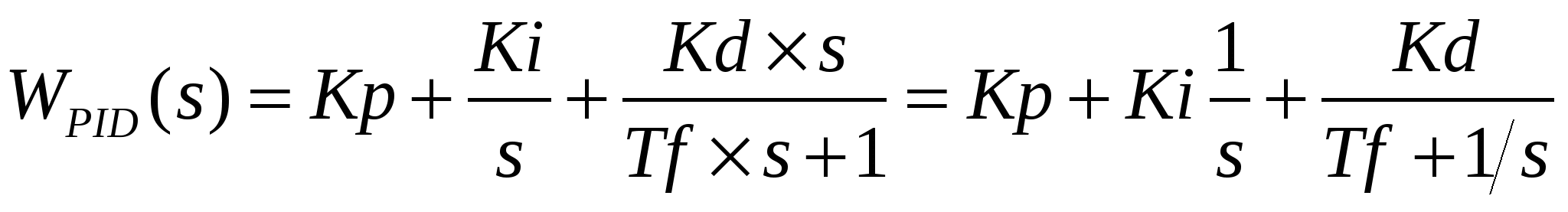 . (3.12) . (3.12)
Все числа должны быть вещественными, конечными, а постоянная времени – неотрицательной, по умолчанию Kp=1, Ki=0, Kd=0 и Tf=0. Задавая лишь часть параметров, получаем разный тип регулятора, например, П-регулятор при задании pid(Kp), ПИ-регулятор при задании pid(Kp,Ki), И-регулятор при задании pid(0,Ki), ПИД-регулятор при задании pid(Kp,Ki,Kd), ПИД-регулятор с реальным дифференцирующим звеном (PIDF) при задании pid(Kp,Ki,Kd,Tf).
Функция comp=pidstd(Kp,Ti,Td,N) создает непрерывный PID регулятор в стандартной форме с общим пропорциональным коэффициентом усиления Kp, постоянными времени интегрирования Ti и дифференцирования Td и делителем N инерционной постоянной времени
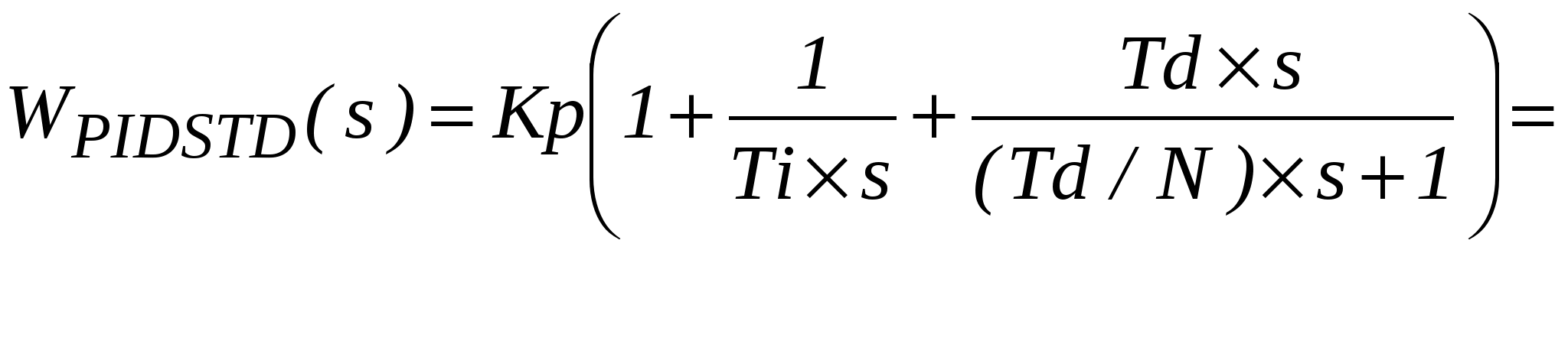
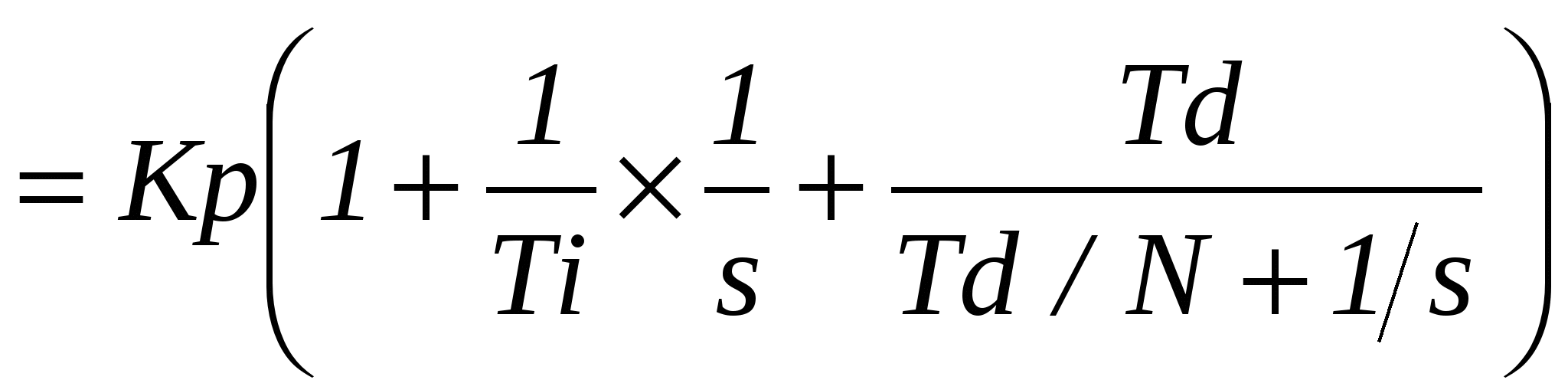 . (3.13) . (3.13)
Все числа должны быть вещественными, Kp и Td – конечными, постоянная времени Td – неотрицательной, постоянная времени Ti и делитель N – положительными. По умолчанию Kp=1, Ti=Inf, Td=0 и N=Inf. Задавая часть параметров, получаем разный тип регулятора, например, П-регулятор при задании pidstd(Kp), ПИ-регулятор при задании pidstd(Kp,Ti), ПИД-регулятор при задании pidstd(Kp,Ti,Td), ПИД-регулятор с реальным дифференцирующим звеном (PIDF) при задании pidstd(Kp,Ti,Td,N). И-регулятор реализуется приблизительно, коэффициенты составляющих равны Ki = Kp/Ti, Kd = Kp*Td.
Функции pid(sys) и pidstd(sys) преобразуют систему sys в PID или PIDSTD объект, если это допускают параметры системы, для массива объектов sys формируется массив PID или PIDSTD объектов. Создадим PID и PIDSTD объекты regp и regs, исследуем их свойства.
>> regp=pid(3,0.1,0.01)
Continuous-time PID controller in parallel form:
1
Kp + Ki * --- + Kd * s
s
страница 1 страница 2 страница 3 | страница 4
|