страница 1 | страница 2 страница 3 страница 4
with Kp = 3, Ki = 0.1, Kd = 0.01
>> get(regp)
Kp: 3
Ki: 0.1000
Kd: 0.0100
Tf: 0
IFormula: ''
DFormula: ''
InputDelay: 0
OutputDelay: 0
Ts: 0
TimeUnit: ''
InputName: {''}
InputUnit: {''}
InputGroup: [1x1 struct]
OutputName: {''}
OutputUnit: {''}
OutputGroup: [1x1 struct]
Name: ''
Notes: {}
UserData: []
>> regs=pidstd(3,0.1,0.01)
Continuous-time PID controller in standard form:
1 1
Kp * (1 + ---- * --- + Td * s)
Ti s
with Kp = 3, Ti = 0.1, Td = 0.01
>> get(regs)
Kp: 3
Ti: 0.1000
Td: 0.0100
N: Inf
IFormula: ''
DFormula: ''
...и так далее
Как видно из распечатки, индивидуально задаются свойства Kp, Ki, Kd, Tf – для объекта типа PID, Kp, Ti, Td, N – для объекта типа PIDSTD; свойства Iformula, Dformula необходимы только для дискретных регуляторов и в непрерывных моделях игнорируются. Остальные свойства те же, что и для других LTI объектов.
Как и у других LTI-объектов, можно извлечь характеризующие регулятор параметры или преобразовать структуру регулятора
>> [Kp,Ki,Kd,Tf]=piddata(regp)
Kp =
3
Ki =
0.1000
Kd =
0.0100
Tf =
0
>> [Kp,Ti,Td,N]=pidstddata(regs)
Kp =
3
Ti =
0.1000
Td =
0.0100
N =
Inf
>> [Kp,Ti,Td,N]=pidstddata(regp) % из другой формы
Kp =
3
Ti =
30
Td =
0.0033
N =
Inf
>> rg=pid(regs) % преобразование формы регулятора
Continuous-time PID controller in parallel form:
1
Kp + Ki * --- + Kd * s
s
with Kp = 3, Ki = 30, Kd = 0.03
Конструктор PID Tuner предназначен для проектирования в интерактивном режиме PID регулятора в прямой цепи замкнутой одномерной (SISO) системы регулирования с главной единичной отрицательной обратной связью (рисунок 3.4)
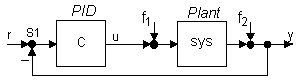
Рисунок 3.4
Для регулятора С необходимо задать его тип (P, I, PI, PD, PDF, PID, PIDF) и форму описания (параллельная parallel или стандартная standard). Команда pidtool(plant, 'type') вызывает конструктор для имеющегося объекта управления plant с указанием типа регулятора в виде строковой переменной 'type', по умолчанию используется параллельная форма. При обращении pidtool(plant, cbase) проектирование ведется в сравнении с образцовым регулятором cbase и результируется в виде регулятора того же типа и формы.
Выводимое диалоговое окно позволяет выбирать способ синтеза Design Mode (Basic, Extended), форму описания Form (Parallel, Standard), тип регулятора Type (P, I, PI, PD, PDF, PID, PIDF), тип графика Plot (Step, Bode) и вид анализируемой реакции в меню Response:
- Reference tracking – влияние задания на управляемую величину замкнутой системы (от r к y);
- Controller effort – влияние задания на управляющее воздействие замкнутой системы (от r к u);
- Input disturbance Rejection – влияние возмущения на входе объекта на управляемую величину замкнутой системы (от f1 к y)
- Output disturbance Rejection – влияние возмущения на выходе объекта (например, шумов измерения) на управляемую величину замкнутой системы (от f2 к y);
- Open-loop – характеристики разомкнутой системы (необходимы при частотных методах исследования устойчивости, например, по ЛЧХ);
- Plant – характеристики только объекта управления.
Спроектируем для объекта W(s) = 10/(s3 + 2s2 + 3s + 4) ПИ-регулятор, получим диалоговое окно (рисунок 3.5)
>> plant=tf(10,[1 2 3 4]); pidtool(plant,'pi')
После запуска PID Tuner отображает по умолчанию переходную характеристику замкнутой системы с регулятором, параметры которого выбраны сбалансированно между требованиями наименьшего времени регулирования и удовлетворительной робастности (приемлемых запасов устойчивости).
Все стандартные показатели качества (установившееся значение, время нарастания, время регулирования, перерегулирование, время максимума) можно вызвать щелчком правой кнопки мыши на графике. Если значения показателей не удовлетворяют предъявляемым техническим требованиям к системе, их можно откорректировать посредством движка Response time в сторону Slower (медленнее) или Faster (быстрее), непосредственно наблюдая изменения в табличках возле соответствующих маркеров. Время Response time не связано со стандартными понятиями время регулирования, время нарастания.
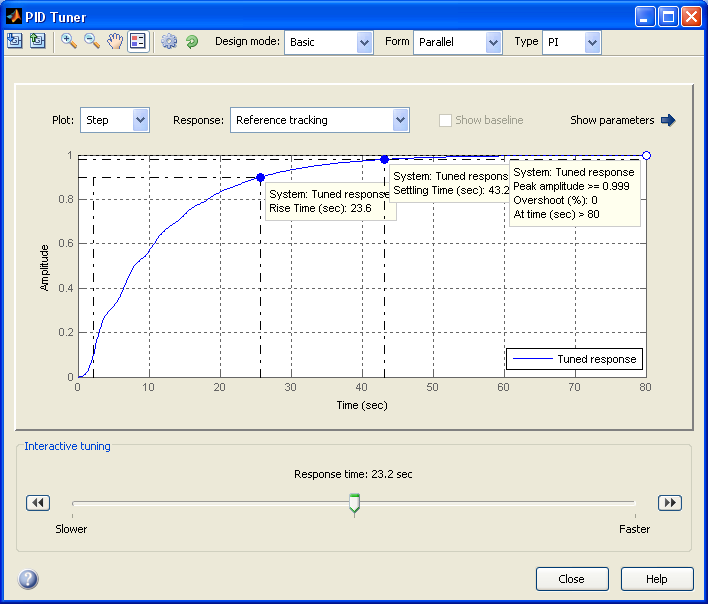
Рисунок 3.5
Кнопка Show parameters вызывает дополнительное поле с панелями Controller parameters и Performance and robustness. В частности, выбранные параметры регулятора равны Kp = 0, Ki = 0.034485; остальные показатели Rise time = 23.6 c, Settling time = 43.2 c, Overshoot = 0 %, Peak = 0.999, запас по амплитуде Gain margin = 15.3 дБ на частоте 1.41 рад/с, запас по фазе Phase margin = 86.3 град на частоте 0.172 рад/с, замкнутая система устойчива. Хотя задан был ПИ-регулятор, окончательно выбран И-регулятор, т. к. Кр = 0.
Следует иметь в виду, что на панели справа выводятся параметры всегда только для стандартных установок MATLAB: время нарастания по диапазону 0.1-0.9, время регулирования по уровню 2 %, тогда как на графике слева те же параметры отображаются при фактических установках, заданных в окне Control System Toolbox Preferences пользователем. Соответственно, значения Rise time и Settling time для одной и той же системы слева и справа могут быть разными.
В форме Standard параметры регулятора равны Kp = 3.9935e-005 и Ti = 0.001158, что в итоге дает то же самое значение Ki = Kp/Ti = 0.0345 и те же показатели качества. Для независимой настройки полосы пропускания и запаса по фазе следует выбрать опцию Extended в меню Design Mode. В строке меню диалогового окна имеются кнопки импорта другого объекта регулирования Plant Model или образцового регулятора Baseline Controller (рисунок 3.6), экспорта полученного регулятора как объекта PID (если выбрано Form-Parallel) или PIDSTD (если выбрано Form-Standard) в рабочее пространство Workspace.
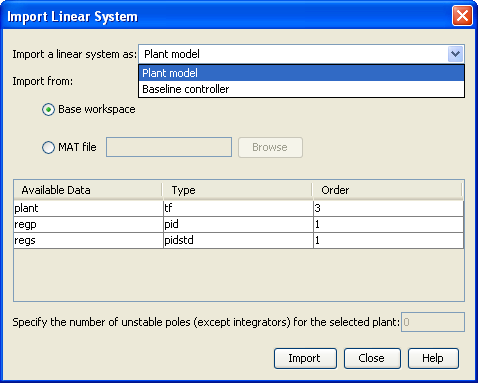
Рисунок 3.6
Для проектирования регулятора из командной строки используется функция pidtune в следующем виде:
- rgp=pidtune(plant,'type') – для SISO объекта plant проектируется регулятор параллельной формы указанного типа type (P, I, PI, PD, PID, PIDF), параметры которого выбраны сбалансированно между требованиями наименьшего времени регулирования и удовлетворительной робастности (запасов устойчивости);
- rgc=pidtune(plant,cbase) – проектирование ведется в сравнении с образцовым регулятором cbase и результируется в виде регулятора того же типа и формы;
- rgp=pidtune(plant,'type',options) и rgc=pidtune(plant,cbase,options) – определяет дополнительные параметры настройки;
- [rgp,info] = pidtune(plant,...) – возвращает дополнительные сведения по проектируемому регулятору.
Функция opt=pidtuneoptions позволяет увидеть предустановленные значения дополнительных параметров настройки или задать их в форме opt = pidtuneoptions('Option1',Value1,'Option2',Value2,...). Это:
- CrossoverFrequency – частота среза рад/с разомкнутой системы. Чем больше частота среза, тем шире полоса пропускания системы, меньше время регулирования, но хуже устойчивость;
- PhaseMargin – запас по фазе (норма 60 градусов), его значение определяется на частоте среза;
- NumUnstablePoles – число правых полюсов объекта регулирования (по умолчанию ноль). Их указание необходимо для FRD модели или SS объектов с внутренней задержкой для правильного выбора регулятора и обеспечения устойчивости системы.
Пример проектирования регулятора в командной строке для объекта с передаточной функцией W(s) = 10/(s3 + 2s2 + 3s + 4)
>> plant=tf(10,[1 2 3 4]);
>> [regp,info]=pidtune(plant,'pidf')
Continuous-time I-only controller:
1
Ki * ---
s
with Ki = 0.031884
info =
Stable: 1
CrossoverFrequency: 0.0798
PhaseMargin: 86.5704
Увеличим быстродействие, изменив частоту среза в 20 раз
>> Options=pidtuneoptions('CrossoverFrequency',...
20*info.CrossoverFrequency);
>> [regp,info]=pidtune(plant,'pidf',Options)
Continuous-time PIDF controller in parallel form:
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
with Kp = 0.073314, Ki = 0.0056516, Kd = 0.058519, Tf = 0.44043
info =
Stable: 1
CrossoverFrequency: 1.5964
PhaseMargin: 60.0000
Практический выбор параметров ПИД-регулятора, включенного последовательно с объектом, можно выполнить и в среде Simulink. Выбрав из библиотеки элементов Continuous ПИД-регулятор (PID Controller), составим структурную схему замкнутой системы регулирования с запаздыванием, как наиболее сложной для реализации (рисунок 3.7). На входе системы подключим источник ступенчатого сигнала Step (библиотека Sources), на выходе индикатор Scope (библиотека Sinks).
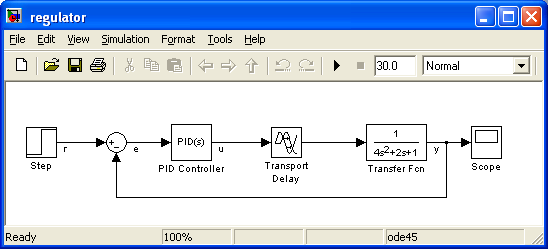
Рисунок 3.7
В блоке Step зададим момент скачка, равный нулю, время запаздывания в блоке Transport Delay ставим равным 1 с и обязательно указываем порядок аппроксимации, например, второй. Двойным щелчком на изображении регулятора открываем окно Function Block Parameters: PID Controller, где по умолчанию стоит тип регулятора PID, непрерывный Continuous-time, со значениями коэффициентов: пропорциональная часть Proportional (P): 1, интегральная часть Integral (I): 1, дифференцирующая часть Derivative (D): 0, постоянная времени дифференцирующего звена Filter coefficient (N): 100. Форм построения регулятора две: параллельная Parallel и идеальная Ideal (вместо Standard, как в командной строке для функции pidstd) c передаточной функцией
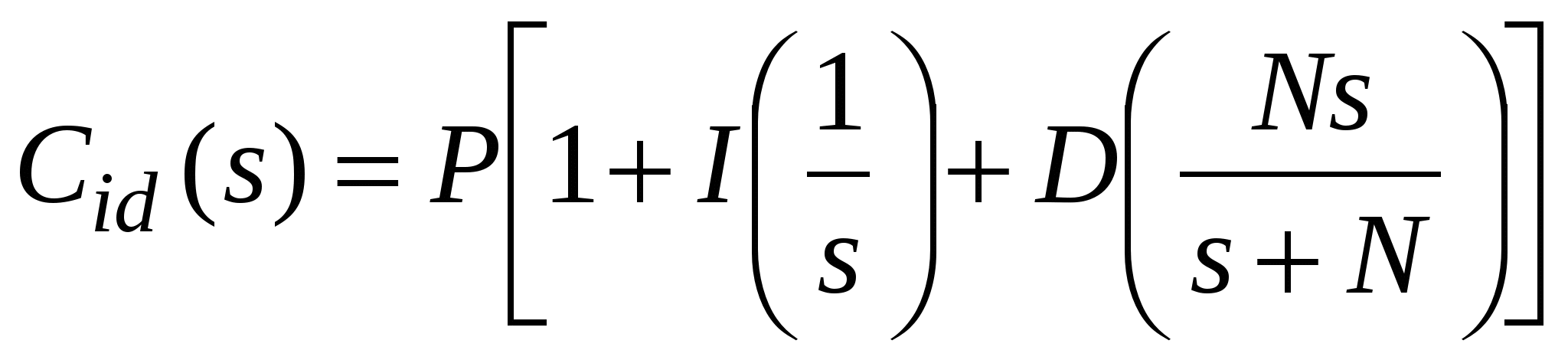 . (3.14) . (3.14)
Хотя по формуле всегда имеется единичная пропорциональная связь и создать чистый И-регулятор как будто невозможно, тем не менее в опциях окна параметров такой регулятор имеется (при условии весьма малого Р и значительного I). Все изменения должны завершаться кнопкой Apply.
После нажатия кнопки Tune последовательно линеаризируется объект управления, конструируется регулятор, запускается PID Tuner, выводится его диалоговое окно. Работа в данном окне описывалась ранее. Изменения автоматически вносятся в параметры регулятора, если выбрана опция Automatically update block parameters. Для объекта регулирования с передаточной функцией 1/(4*s^2+2*s+1) и задержкой 1 с выбраны параметры Parallel-регулятора P = 0, I = 0.087571, Ideal-регулятора P = 2.2204e-016, I = 394383924034772.3, обеспечивающие в обоих случаях время регулирования 34.9 с по зоне 2 %, время нарастания 17.5 с по диапазону 10-90 %, запас по амплитуде Gm = 12.2 дБ, запас по фазе Pm = 74.5°. Естественно, более удобными для задания являются параметры Parallel-регулятора.
Выбор параметров регулятора по установленным границам допустимой зоны позволяет осуществить блок ограничений Signal Constraint из библиотеки Simulink Design Optimization. Подключим его на выход блока Transfer Fcn рассматриваемой схемы параллельно Scope. Момент скачка (Step time) в блоке Step зададим нулевым, время запаздывания (Time delay) в блоке Transport Delay равным 1 с, порядок аппроксимации (Pade order) равным 2. Дважды щелкнув на изображении регулятора, впишем латинским шрифтом вместо чисел символические обозначения изменяемых коэффициентов Kp (окно Proportional), Ki (окно Integral), Kd (окно Derivative), тип регулятора PID, Parallel. В командном окне определим исходные значения Kp=.5, Ki=.5, Kd=0.
Двойным щелчком на изображении блока ограничений вызываем окно Block Parameters: Signal Constraint (рисунок 3.8), в котором линиями заданы границы рабочей зоны переходного процесса, определяемые тремя параметрами: время регулирования (узкая зона вдоль линии установившегося значения), время нарастания (первый выступ снизу) и перерегулирование (выступ сверху).
Грубо настройки зоны устанавливаются перетаскиванием границ мышью, точные значения координат границ задаются после открытия их свойств двойным щелчком мыши (рисунок 3.9). Значения 0.95 (внизу) и 1.05 (вверху) в завершающей части процесса обеспечивают 5 % зону для определения времени регулирования, значение 1.2 вверху в начале процесса задает величину перерегулирования 20 %.
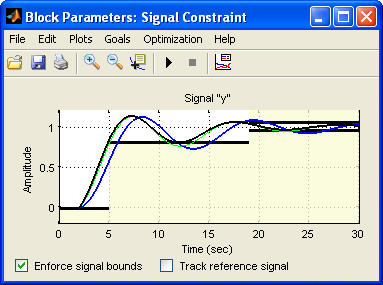
Рисунок 3.8
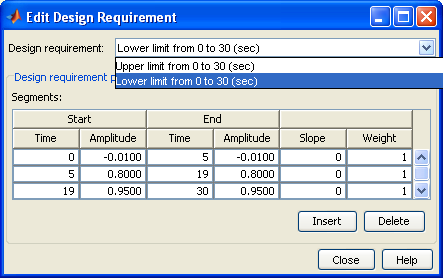
Рисунок 3.9
Через меню Optimization-Tuned Parameters открывается окно, в котором после импорта командой Add каждого из настраиваемых параметров можно указать их начальные значения (Initial guess), например, переменную Ki (тогда при каждой новой попытке подбор начнется с последнего значения на прошлом сеансе).
Кнопкой Start в блоке Block Parameters: Signal Constraint запускается процесс выбора параметров, отображаемый в окнах этого блока, окнах Scope (лучше с включенной опцией Autoscale) и Optimization Progress. Если за установленное число итераций решение не найдено, процесс подбора останавливается, а в случае успеха выводятся рекомендуемые значения коэффициентов.
max Directional First-order
Iter S-count f(x) constraint Step-size derivative optimality Procedure
0 1 0 1.76
1 14 0 0.7711 0.466 0 0.362
2 21 0 0.003325 0.164 0 0.0321
3 28 0 0.0002375 0.0116 0 0.000172 Hessian modified
Successful termination.
Found a feasible or optimal solution within the specified tolerances.
Ki =
0.2848
Kp =
0.9120
Kd =
0.5951
Интервал исследования задается в меню Optimization-Simulation Options или окне Simulation Stop Time, масштаб отображения в меню Edit-Axes Properties. Можно убрать старые графики командой Plots-Clear Plots, масштабировать по уровню 1.0 командой Edit-Scale Constraint, сбросить предыдущие установки командой Edit-Reset Constraint.
Запуская каждый раз процесс оптимизации кнопкой Start и изменяя при необходимости настройки допустимой зоны процесса регулирования, можно добиться минимальных перерегулирования, времени регулирования и нарастания.
3.5 Работа с SISO Design Tool
Другим путем создания SISO регулятора является использование конструктора SISO design Tool, который вызывается командой sisotool. Конструктор позволяет проектировать регулятор в стандартной форме PID, с наблюдателем в виде Internal Model Control Structure (IMC) или реализующий линейно-квадратичный гауссов закон (LQG) в интерактивном режиме, используя корневой годограф (Root Locus), диаграммы Боде и Николса.
По умолчанию подразумевается замкнутая система с четырьмя входами r, du, dy, n и двумя выходами y, u (рисунок 3.10), где G – объект регулирования (plant), H – датчик (sensor), С – настраиваемый регулятор (compensator или controller), F – настраиваемый задатчик или предварительный фильтр (prefilter), S1 – главный сумматор. Конструктор позволяет при открытии командой sisotool импортировать существующий объект регулирования sisotool(G), с регулятором sisotool(G, C) и прочими элементами схемы sisotool(G, C, H, F), заданными в виде TF, ZPK, SS или PID, PIDSTD одномерных объектов, из рабочего пространства или mat-файлов. Незаданные элементы имеют единичный коэффициент усиления.
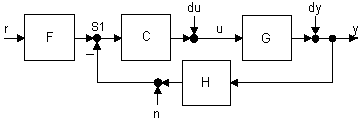
Рисунок 3.10
Возможно задание типа используемых при синтезе графиков командой sisotool({'график1','график2',…},G,…) из доступного набора 'rlocus', 'bode', 'nichols', 'filter', т. е. корневой годограф, диаграммы Боде и Николса для разомкнутой системы, диаграмма Боде для замкнутой системы и задатчика.
Все данные текущей сессии можно сохранить в виде mat-файла командой sisotool(sessiondata) и открыть повторно командой sisotool(initdata). Структуру initdata формируют с помощью команды initdata = sisoinit(config), где архитектура config выбирается из набора:
- config=1 – C в прямой цепи, F на входе;
- config=2 – C в главной обратной связи, F на входе;
- config=3 – C и F на входе включены параллельно;
- config=4 – сдвоенный регулятор без задатчика;
- config=5 – система IMC с наблюдателем (внутренней моделью);
- config=6 – подчиненное (каскадное) регулирование (два регулятора, два датчика).
По умолчанию используется конфигурация 1. Все указанные шаги можно выполнить и после открытия конструктора командой sisotool. Пример запуска инструмента с указанием объектов:
>> T=sisoinit(1) % задание и просмотр структуры для config=1
Name: ''
Configuration: 1
Description: 'Design snapshot.'
FeedbackSign: -1 % знак обратной связи
Input: {4x1 cell} % четыре входа
Output: {2x1 cell} % два выхода
G: [1x1 sisodata.system] % объект регулирования
H: [1x1 sisodata.system] % датчик
C: [1x1 sisodata.TunedZPKSnapshot] % регулятор
F: [1x1 sisodata.TunedZPKSnapshot] % задатчик
OL1: [1x1 sisodata.TunedLoopSnapshot] % Open Loop
CL1: [1x1 sisodata.TunedLoopSnapshot] % Close Loop
>> T.G.Value=ss([0 1;-2 -3],[0; 1],[3 0],0); % задаем объект G
>> T.C.Value=tf(1,[1 2]); % задаем регулятор С
>> T.OL1.View={'rlocus','nichols'}; % задаем графики, необходимые для настройки разомкнутой системы Open Loop OL1
>> sisotool(T) % запуск SISO Design Tool с установками initdata=T
Открываются диалоговые окна Control and Estimation Tools Manager и SISO Design for SISO Design Task.
Опция меню Edit-SISO Tool Preferences окна Control and Estimation Tools Manager вызывает диалоговое окно выбора единиц измерения Units, порядка аппроксимации Паде временных задержек Time Delays, шрифтов, цвета осей и предустановки сетки на вкладке Style, цвета графиков на вкладке Line Colors, формата представления регулятора на вкладке Options: через постоянные времени Time constant (по умолчанию), через частоты сопряжения Natural frequencies, через нули-полюса-коэффициент Zero-pole-gain. Здесь же можно отменить или установить показ корней объекта и датчика на частотных графиках Боде и Николса.
На вкладке Architecture в окне Control and Estimation Tools Manager кнопка Control Architecture позволяет выбрать структуру системы управления из перечисленных ранее config=1 … config=6, знак обратной связи сумматора, обозначения и имена для всех входов, выходов и блоков системы. Кнопка System Data открывает возможность импортировать данные из Workspace для всех элементов схемы.
Вкладка Graphical Tuning дает возможность изменить (выбрать) тип используемых в диалоговом окне графиков. Например, заменим диаграмму Боде для замкнутой системы на аналогичный график для разомкнутой, выбрав в строке Plot 3 вместо Close Loop 1 опцию Open Loop 1 и в колонке Plot Type тип графика Open-Loop Bode (рисунок 3.11).
Вкладка Analysis Plots позволяет выбрать дополнительно шесть типов графиков (Step, Impulse, Bode, Nyquist, Nichols, Pole/Zero), создаваемых графоанализатором LTI Viewer и расширяющих возможности настройки параметров системы с регулятором. В каждой из шести графических вставок окна LTI Viewer for SISO Design Task можно совместить до 10 графиков из списка объектов: в замкнутой системе от r к y, от r к u, от du к y (Input Sensitivity), от dy к y (Output Sensitivity), от n к y (Noise Sensitivity), разомкнутую систему Open Loop L = C*G*H (для конфигурации 1), отдельно регулятор С, задатчик F, объект G и датчик H. Например, выберем для окна Plot 1 вид графика Step и анализируемый объект Closed Loop r to y, т. е. переходную характеристику выхода замкнутой системы по заданию.
Опция меню Analysis окна SISO Design for SISO Design Task позволяет выбрать в качестве вспомогательных графиков предустановленные комбинации сигналов: Response to Step Command (переходная характеристика замкнутой системы по выходам y и u относительно r), Rejection of Step Disturbance (переходная характеристика замкнутой системы по выходу y относительно dy и du), Closed-Loop Bode и Compensator Bode (ЛЧХ для замкнутой системы и регулятора), Open-Loop Nyquist (АФЧХ для разомкнутой системы). Опция Other Loop Responses просто вызывает уже известное окно Analysis Plots.
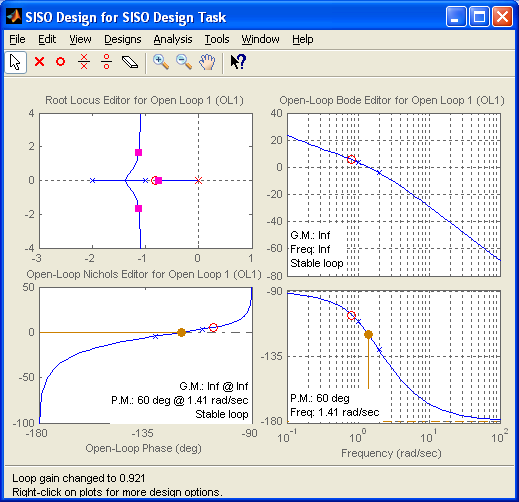
Рисунок 3.11
Опция File-Toolbox Preferences позволяет на вкладке Options задать величину зоны Δ для контроля времени регулирования (по умолчанию 2 %), интервал для контроля времени нарастания (по умолчанию 10-90 %) и ограничение фазового угла величиной 180° (снять флажок Unwrap Phase). Исходная система с заданным регулятором имеет запасы устойчивости по амплитуде Gm = 21.6 дБ при частоте 2.83 рад/с, по фазе Pm = Inf, показатели качества – перерегулирование 7.42 %, время регулирования 4.36 с по уровню 2 %, установившаяся ошибка 1 – 0.429 = 0.571. Текущие параметры точки под курсором и иные сведения отображаются в строке состояния внизу окна.
Если флажок Real-Time Update на графике LTI Viewer установлен, можно в интерактивном режиме подобрать желаемый вид переходной характеристики системы с заданными показателями качества, например, временем регулирования (соответствующий маркер вызывается, как обычно, в контекстном меню графика опцией Characteristics-Settling Time). Для этого левой кнопкой мыши двигают любой из частотных графиков для разомкнутой системы или полюс-нуль на корневом годографе, наблюдая непосредственно за изменением параметров качества и запасов устойчивости в обоих окнах. Отменить сделанные изменения можно в меню Edit-Undo. Изменить текущие параметры регулятора можно на вкладке Compensator Editor, например, задав необходимый коэффициент усиления для статической системы.
Для быстрой оценки приемлемости полученных результатов можно через опцию Design Requirements-New контекстного меню соответствующего графика задать допустимую зону – по запасам устойчивости для частотных графиков (рисунок 3.12) и по показателям качества для временных характеристик (рисунок 3.13), что приводит к установке ограничений (рисунок 3.14).
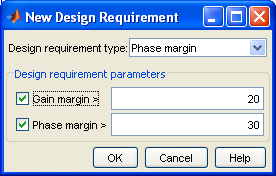
Рисунок 3.12
Воспользуемся автоматической настройкой, для чего на вкладке Automated Tuning можно выбрать метод настройки регулятора С из перечисленных: Optimization Based Tuning (по умолчанию), PID Tuning, IMC Tuning, LQG Synthesis и Loop Shaping.
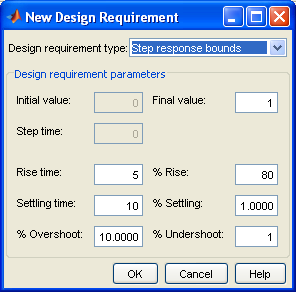
Рисунок 3.13
Выбрав опцию PID настройка, получим окно с выведенной передаточной функцией регулятора С, выбором метода настройки Classical design formulas (классическим) и Robust response time (по умолчанию), выбором режима проектирования Interactive (с участием пользователя) и Automatic (автоматически по балансу быстродействия и запасов устойчивости).
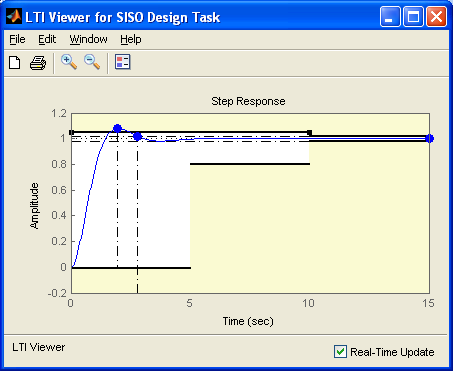
Рисунок 3.14
Оставим тип регулятора PIF (регулятор PI с установленным флажком «использовать реальное дифференцирующее звено – дифференцирующий фильтр первого порядка»). Нажав кнопку Update Compensator, получим систему с передаточной функцией регулятора
C = 1×(1 + 1.2s)/s, запасами устойчивости по амплитуде Gm = Inf, по фазе Pm = 60 ° при частоте 1.41 рад/с, нулевой установившейся ошибкой регулирования, перерегулированием 8.04 % и временем регулирования 2.79 с для зоны Δ = 2 % (рисунок 3.15, а).
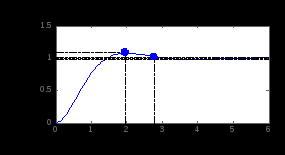
|
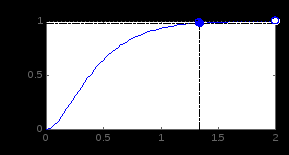
|
а б
Рисунок 3.15
При выборе метода настройки с внутренней моделью объекта IMC получили ПФ регулятора C= 1.45×(1+s)(1+0.5s)/s/(1+0.12s) и следующие параметры системы: запасы по амплитуде Gm = Inf и фазе Pm = 76.3 ° при частоте 2.11 рад/с, перерегулирование 0 %, время регулирования 1.34 с, нулевая установившаяся ошибка (рисунок 3.15, б).
Для метода Optimization Based Tuning необходимо выбрать оптимизируемый регулятор (C, C1, C2, F) и его параметры на вкладке Compensators, задать ограничения Design Requirements в соответствующем графике (можно вызвать график Show Plots или добавить ограничения кнопкой Add new design requirements) и запустить процесс, щелкнув Start Optimization. Метод требует установки пакета Simulink Design Optimization, полученный результат должен удовлетворять заданным ограничениям.
Контекстное меню, вызываемое правой кнопкой мыши на любом из графиков окна SISO Design for SISO Design Task (рисунок 3.16) позволяет самостоятельно корректировать структуру и параметры регулятора. Аналогичное меню появляется при щелчке правой кнопкой на поле Dynamics панели Pole/Zero вкладки Compensator Editor окна Control and Estimation Tools Manager. Отдельные кнопки Add real pole (добавить вещественный полюс, обозначается крестиком), Add real zero (добавить вещественный нуль, обозначается кружком), Add complex pole (добавить комплексный полюс), Add complex zero (добавить комплексный нуль), Delete pole/zero (удалить полюс/нуль) имеются в строке меню окна SISO Design for SISO Design Task.
В контекстном меню Add Pole/Zero предусмотрена также возможность добавить корректирующие звенья: интегратор, дифференциатор, фильтры Notch – режекторный (заграждающий), Lead – с опережением по фазе, Lag – с отставанием по фазе. Общий вид передаточной функции Lead и Lag фильтров (s – z)/(s – p), причем на отрицательной вещественной оси полюсы и нули этих фильтров располагаются последовательно |pd| > |zd| > |zg| > |pg|, где pd и zd – корни Lead фильтра, zg и pg – корни Lag фильтра. Lead регулятор с опережением по фазе за счет вносимого им положительного угла сдвигает корневой годограф на комплексной плоскости влево, он улучшает быстродействие системы и увеличивает запасы устойчивости. Lag регулятор с отставанием по фазе противоположен по влиянию на временные характеристики и устойчивость, зато повышает точность в установившемся режиме.
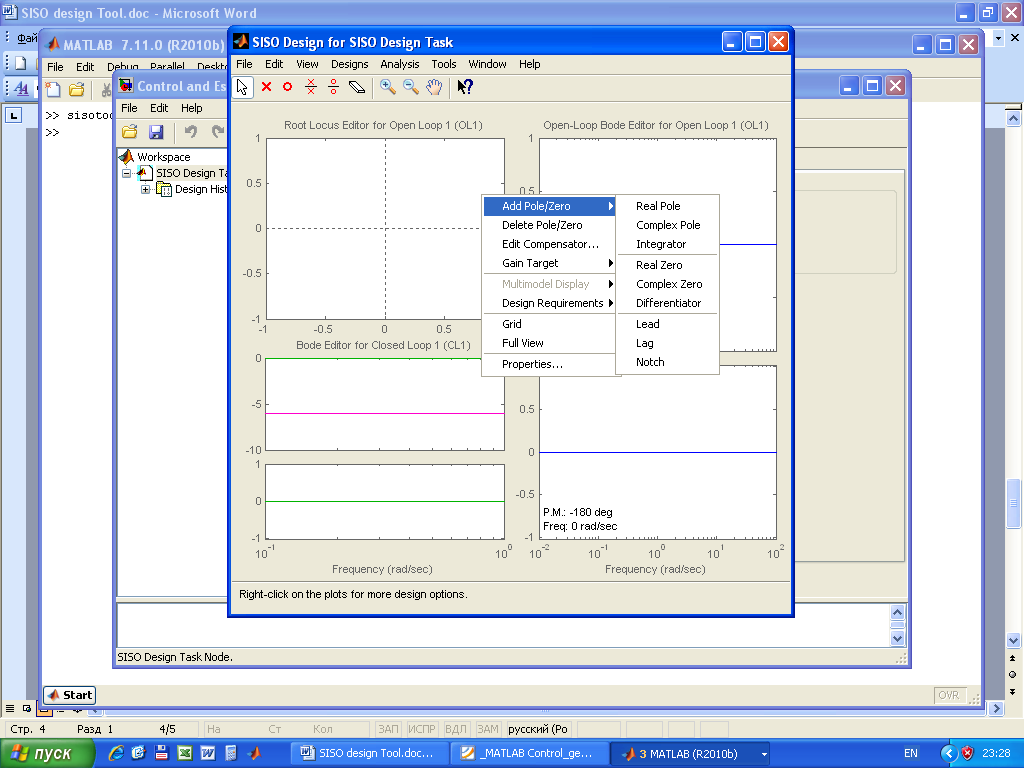
Рисунок 3.16
Средняя частота вносимого фильтрами фазового сдвига равна 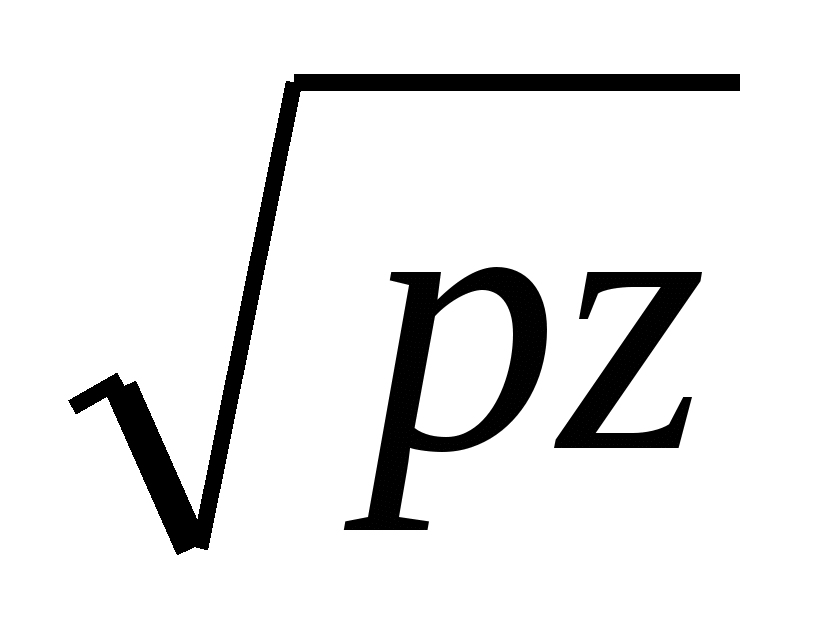 , сам сдвиг не может превышать 70°. , сам сдвиг не может превышать 70°.
Полоса подавления заграждающего Notch фильтра с передаточной функцией второго порядка
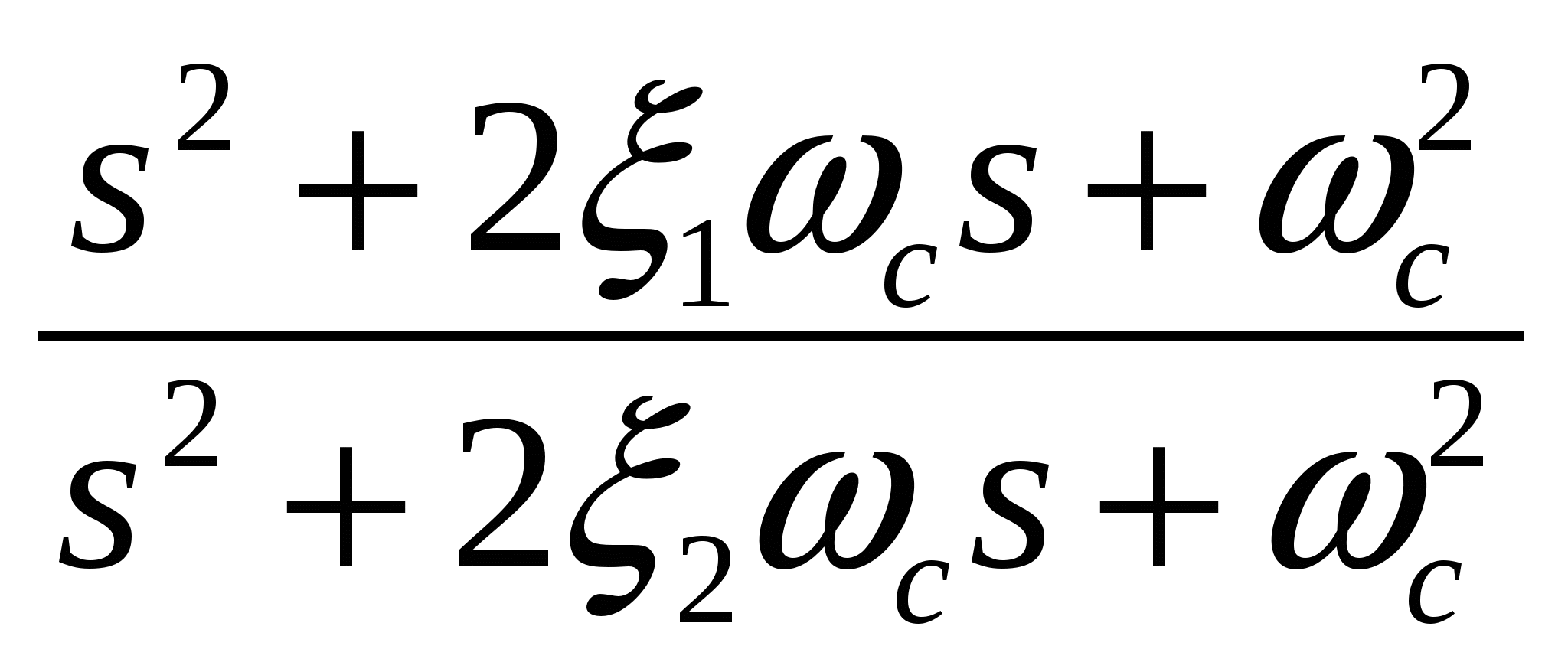
характеризуется шириной Notch Width ωH–ωL, глубиной Notch Depth Δ (дБ) и центральной частотой Natural Frequency ωс (рисунок 3.17).
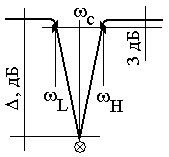
Рисунок 3.17
Глубина подавления определяется отношением коэффициентов демпфирования Damping ξ2/ξ1. При выборе в контекстном меню диаграммы Боде опции Notch появляется возможность выбрать место резкого локального снижения ЛАЧХ (щелкнув на графике и перемещая точку частоты подавления) и, тем самым, увеличить запас устойчивости по амплитуде. При выборе этой опции на вкладке Dynamics панели Pole/Zero окна Compensator Editor программа автоматически добавляет фильтр с параметрами Natural Frequency ωс = 1, Damping (Zero) ξ1 = 0.1, Damping (Pole) ξ2 = 1, Notch Depth Δ = -20 dB, Notch Width (Log) 0.54483. Затем можно самостоятельно изменить значения этих параметров желаемым образом или переместить частоту подавления (кружок с крестиком) и граничные частоты (черные ромбики) на графике.
Чтобы устранить статическую ошибку в исходной системе, введем в состав регулятора интегратор. Теперь установившаяся ошибка равна нулю, зато ухудшились прочие параметры: Gm = 5.67 дБ, Pm = 26.3 °, при колебательном переходном процессе перерегулирование 49.5 % и время регулирования 28.7 с. Вызвав на Open-Loop Bode диаграмме контекстное меню, добавим щелчком левой кнопки мыши в нужном месте графика Lead-фильтр, его параметры (значения вещественных нуля, полюса и собственного фазового сдвига в градусах) можно корректировать на панели редактирования регулятора (рисунок 3.18). При ПФ регулятора 0.5×(1+2.9s)/[s(1+0.5s)(1+0.1s)] обеспечены следующие показатели устойчивости и качества системы: Gm = 7.35 дБ, Pm = 41.3 °, статическая ошибка ε(∞) = 0, перерегулирование 21.8 %, время регулирования 9.3 с.
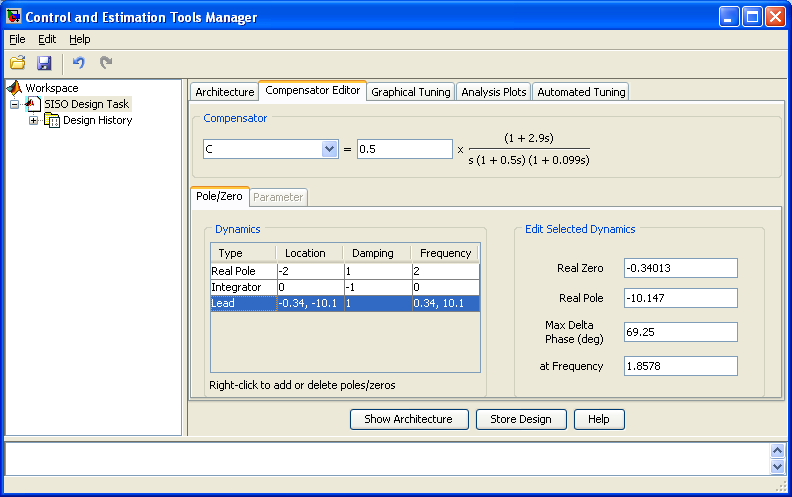
Рисунок 3.18
Полученные результаты через меню File-Export (рисунок 3.19) в виде отдельных объектов и структур можно передать в рабочее пространство Workspace или записать на диск как mat-файл. После двойного щелчка левой кнопкой мыши в колонке Export As можно задать собственное имя для выбранного объекта.
Если необходимо представить выбранный регулятор в стандартной форме с коэффициентами Kp, Ki, Kd пропорциональной, интегральной и дифференциальной составляющих, следует передать его параметры в Workspace, а затем преобразовать соответственно в PID или PIDSTD объект.
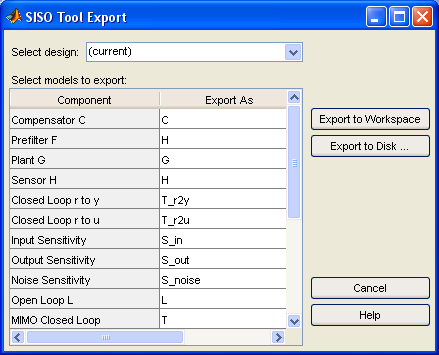
Рисунок 3.19
Через опцию Меню Tools-Draw Simulink Diagram возможно построение структурной схемы полученной системы с присвоенными именами блоков (рисунок 3.20). Если параметры блоков не переданы в Workspace, программа делает это самостоятельно.
Всю последовательность операций по проектированию регулятора (текущий сеанс) можно сохранить для использования в будущем через меню Design History-Store Design или File-Save Session. Кнопкой Retrieve Design загружают сеанс, выбрав при необходимости из нескольких существующих.
Команда rltool является упрощенной формой команды sisotool. В ней также можно сразу указать объект регулирования plant, регулятор comp, место установки регулятора forward (в прямой цепи последовательно с объектом) и feedback (в цепи обратной связи), знак обратной связи -1 (отрицательная) или 1 (положительная обратная связь).
>> plant=tf(1,[1 2 3 4]); comp=tf(1,[1 0]);
>> rltool(plant,comp,'forward',-1)
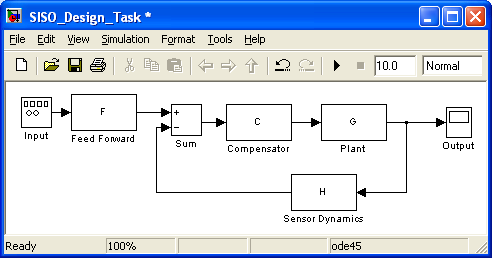
Рисунок 3.20
По умолчанию открывается единственное графическое окно с корневым годографом, однако все дальнейшие действия соответствуют работе с инструментом sisotool.
При работе с S-моделью в Simulink через меню Tools-Control Design-Compensator Design вызывают окно Control and Estimation Tools Manager c выделенной в левом окне задачей Simulink Compensator Design Task. Справа на вкладке Tunable Blocks следует нажать Select Blocks и из занесенных в список блоков выбрать подлежащий настройке – поставить птичку у PID Controller, OK.
Кликнув правой клавишей мыши соответствующую ветвь схемы S-модели, в контекстном меню Linearization Points выбирают тип контрольной точки (Input Point, Output Point), выбор отмечается на схеме входящей или исходящей стрелкой с кружком и записывается на вкладке Closed-Loop Signals открытого окна. На вкладке Operating Points (рисунок 3.21) можно выбрать область линеаризации – с существующей рабочей точкой Existing Operating Points или в заданный момент моделирования Simulation Snapshot (с указанием времени фиксации). Наконец, нажимают Tune blocks. Возможные действия в окне Control and Estimation Tools Manager описаны ранее.
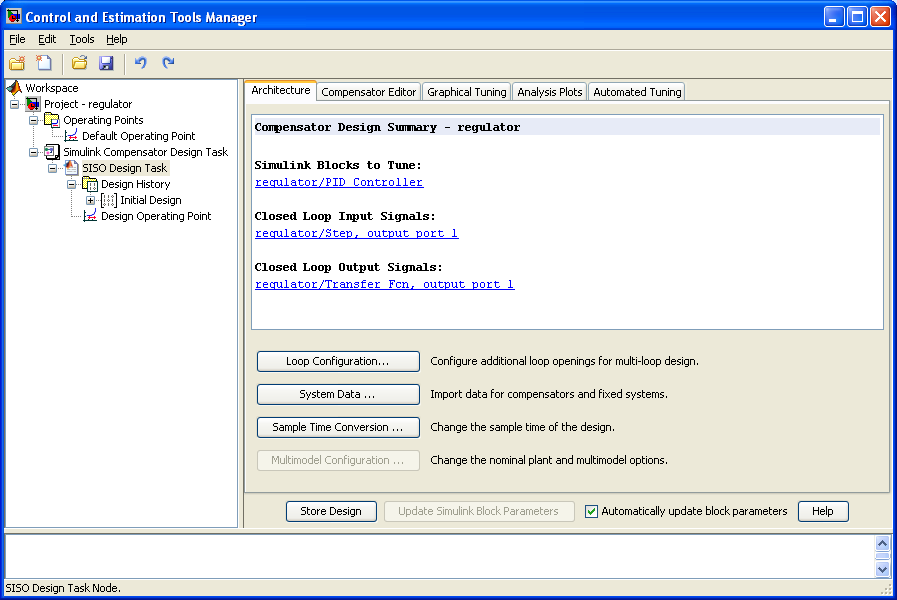
Рисунок 3.21
4 Оценка устойчивости и качества САР
4.1 Оценка запасов устойчивости САР
Проще всего устойчивость системы позволяют оценить критерии Гурвица, Рауса или в MATLAB функция isstable(имя_системы), возвращающая 1 (устойчива), 0 (неустойчива) или NaN (обычно для FRD систем), например
>> w=tf([1 2 3],[1 2 3 4 1]);
>> isstable(w)
ans =
1
Однако в дипломном проекте важно не просто оценить устойчивость создаваемой САР, а определить запасы устойчивости этой системы, для чего служат критерии Найквиста, Николса и логарифмический критерий Боде.
При оценке устойчивости по критерию Найквиста следует задавать для анализа передаточную функцию разомкнутой (Open-Loop) системы, а на графике оценивать положение особой точки с координатами (-1, j0) – АФЧХ неустойчивой в замкнутом состоянии (Closed-Loop) системы охватывает эту точку.
Если имеется уже замкнутая система, передаточную функцию разомкнутой системы можно получить одним из следующих способов:
- вычесть соответственно из коэффициентов полинома знаменателя передаточной функции замкнутой системы значения коэффициентов полинома числителя;
- разомкнуть систему, созданную в среде Simulink, убрав (Cut) главную обратную связь и подключив к точке разрыва выход Out1 (рисунок 4.1), после чего передать параметры линеаризированной модели в рабочее пространство MATLAB.
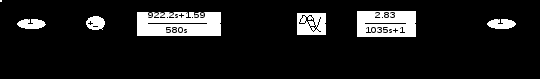
Рисунок 4.1
Первый способ может применяться только в случае охвата всей системы главной единичной отрицательной обратной связью, второй более универсален.
Сформировать в рабочем пространстве MATLAB модель по структурной схеме, созданной в конструкторе Simulink, позволяет команда [b,a]=linmod('имя_модели'), где b и a – полиномы соответственно числителя и знаменателя ПФ объекта. Пусть имя разомкнутой системы w12_open.
>> [b,a]=linmod('w12_open');
Returning transfer function model
Передаточная функция разомкнутой системы
>> w12_open=tf(b,a)
Transfer function:
-0.004348 s^2 + 4.365e-005 s + 8.819e-008
-----------------------------------------.
s^3 + 0.01273 s^2 + 1.137e-005 s
АФЧХ выводится опцией Plot Types-Nyquist в контекстном меню графоанализатора ltiview() или отдельной командой nyquist(), nyquistplot(). Рекомендуется убрать кривую для отрицательных частот командой в контекстном меню графика Show-Negative Frequences и подобрать масштаб по осям командой Properties-Limits (рисунок 4.2).
>> nyquist(w12_open)
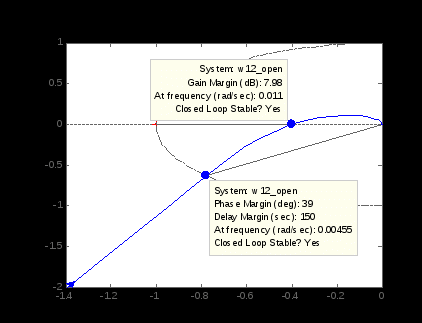
Рисунок 4.2
При выборе в контекстном меню графика опций Characteristics-Stability Margins в точках, отмеченных маркерами, указываются и соответствующие им частоты в рад/с, а также дается общая оценка устойчивости системы после замыкания единичной отрицательной обратной связью. Значение Inf говорит о том, что по данному параметру система имеет бесконечный запас устойчивости, отрицательные (для АФЧХ первого рода) или нулевые значения – об отсутствии запасов. Обратите внимание на то, что в СНГ максимальным значением запаса по фазе (100 %) считается не бесконечность как в MATLAB, а 180°. После перехода от All Stability Margins к Minimum Stability Margins необходимо самостоятельно снять флажок у первой опции, иначе изменений не произойдет.
АФЧХ исследуемой системы в разомкнутом состоянии не охватывает точку с координатами (-1, j0), следовательно, система в замкнутом состоянии будет устойчивой. Об этом гласит и заключение по каждому из запасов Closed Loop Stable? Yes. Запас устойчивости по амплитуде Gain Margin равен Gm = 7.98 дБ, по фазе Phase Margin равен Pm = 39 град, по запаздыванию Delay Margin равен Dm = 150 с. Это превышает стандартные нормы соответственно 6 дБ и 30 град и удовлетворяет предъявляемым к САР требованиям.
В СНГ запас устойчивости принято считать равным расстоянию от критической точки до точки пересечения АФЧХ с отрицательной действительной полуосью, в данном случае Ам = 1 – 0.4= 0.6, что превышает норму запаса 0,5. На диаграмме Найквиста запас по модулю Gm (дБ) вычисляется по отношению единицы к отсекаемому на указанной полуоси отрезку.
Особенность АФЧХ нейтральной в разомкнутом состоянии системы (системы с нулевым полюсом) заключается в том, что она стремится к началу координат, начинаясь в бесконечности. Нейтральной в разомкнутом состоянии будет система с астатическим объектом регулирования, либо с И, ПИ, ПИД регулятором.
Распространенным инструментом оценки устойчивости систем является диаграмма Боде или ЛЧХ, вызов которой производится из командной строки обращением bode(sys), bode(num,den), bode(a,b,c,d), bode(sys1,sys2,...), с указанием крайних частот bode(sys,{wmin, wmax}) или всего диапазона частот bode(sys, logspace(-2,2,100)), bode(sys, fr), из LTI Viewer опцией меню Plot Types-Bode. Дополнительными возможностями обладает функция bodeplot(). Выведем ЛЧХ для той же системы (рисунок 4.3) с отмеченными запасами устойчивости – опция Characteristics-Minimum Stability Margins. Для лучшей фиксации момента пересечения линии минус 180 град рекомендуется в опции контекстного меню Properties-Characteristics убрать флажок Unwrap Phase.
>> bode(w12_open), grid
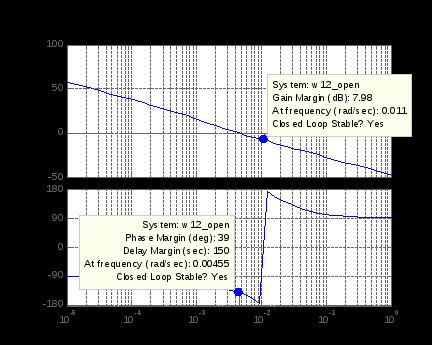
Рисунок 4.3
Диаграмма Николса является полной аналогией годографа Найквиста и предназначена для тех же целей. Она имеет три отличия:
- если годограф Найквиста строится в координатах действительная часть-мнимая часть на комплексной плоскости, то годограф Николса строится в дополняющих их координатах фаза (градусы)-амплитуда (децибелы);
- положение характеристики оценивается относительно точки с координатами (0 дБ, -180°);
- координатная сетка содержит как линии равных значений амплитуды, так и линии равных значений фазы замкнутой системы.
Для работы с экспериментальными данными диаграмма Николса удобнее годографа Найквиста, так как обычно в опытах производится замер отношения амплитуд и разности фаз гармонических сигналов на входе и выходе объекта. Построим график Николса для той же разомкнутой системы (рисунок 4.4).
>> nichols(w12_open)
Оценки запасов устойчивости полностью совпадают. Все проблемы оценки устойчивости систем в особых случаях, характерные для критерия Найквиста, относятся и к диаграмме Николса, но дополнительные условия, вроде правила штриховки, здесь не применяются.
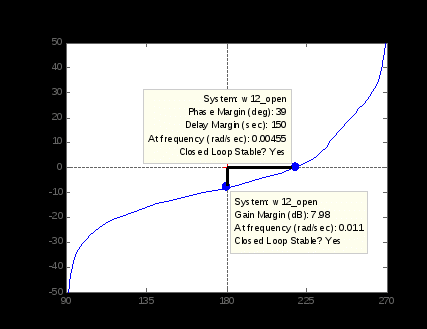
Рисунок 4.4
На диаграмме Николса (рисунок 4.5) неустойчивой в замкнутом состоянии системы кривая охватывает особую точку и запас устойчивости по амплитуде отрицателен, т. е. отсутствует.
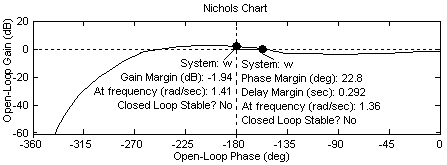
Рисунок 4.5
Замкнутая система устойчива, если годограф Николса разомкнутой системы проходит ниже точки с координатами (0 дБ, -180°). Запас устойчивости по амплитуде (Gain Margin) равен расстоянию от указанной точки до кривой по вертикали вниз, запас устойчивости по фазе (Phase Margin) – расстоянию от указанной точки до кривой по горизонтали вправо. В этой же точке рассчитывается запас по чистой задержке (Delay Margin).
Во многих случаях при оценке устойчивости дипломники допускают несколько характерных ошибок, которые легко обнаружить на графике Найквиста. Во-первых, забывают включить звено запаздывания вообще или указать порядок его аппроксимации рядом Паде (Pade Order) в Simulink.
Правильный график (рисунок 4.2) с порядком 1 аппроксимации рядом Паде заметно отличается от ошибочного с порядком аппроксимации 0, установленным по умолчанию (рисунок 4.6 а), поскольку имеет характерное закручивание по часовой стрелке относительно начала координат и гораздо меньшие запасы устойчивости.
а б
Рисунок 4.6
Другими характерными ошибками являются анализ замкнутой системы вместо разомкнутой и использование регулятора без И-составляющей, хотя в проекте заявлен именно И, ПИ или ПИД регулятор. При этом у систем с И-составляющей регулятора (нейтральных в разомкнутом состоянии) АФЧХ начинается в бесконечности (рисунок 4.2), чего не наблюдается у годографа Найквиста с ошибкой, если пользователь не разомкнул систему, либо вместо И, ПИ, ПИД регуляторов использовал фактически устройства без И-составляющей (рисунок 4.6 б), например, инерционное звено.
4.2 Оценка показателей качества регулирования
Для анализа качества регулирования исследуется замкнутая система w12_closed (рисунок 4.7) с заданным порядком аппроксимации рядом Паде 1 в блоке транспортной задержки.
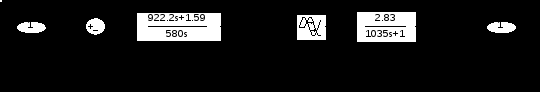
Рисунок 4.7
Получаем передаточную функцию замкнутой системы
[b,a]=linmod(‘w12_closed’); w12=tf(b,a)
Returning transfer function model
Transfer function:
-0.004348 s^2 + 4.365e-005 s + 8.819e-008
----------------------------------------------
страница 1 | страница 2 страница 3 страница 4
|