где Р = 0,5γ [H2(ctgλ – ctgα) – h2 ctgλ]; 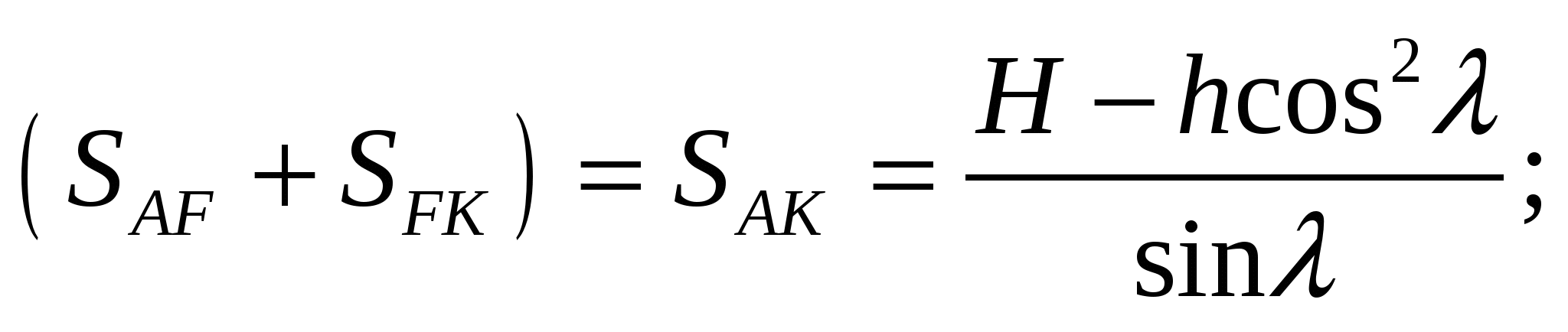
SDK = h cosλ,
где γ — плотность пород, 103 кг/м3;
Н — высота откоса, м;
α — угол наклона откоса, град;
h — минимальная глубина возникновения площадок скольжения по наиболее напряженному контакту, м, h = SDF.
H2a – h2b – Hd + hf = 0, (2)
где 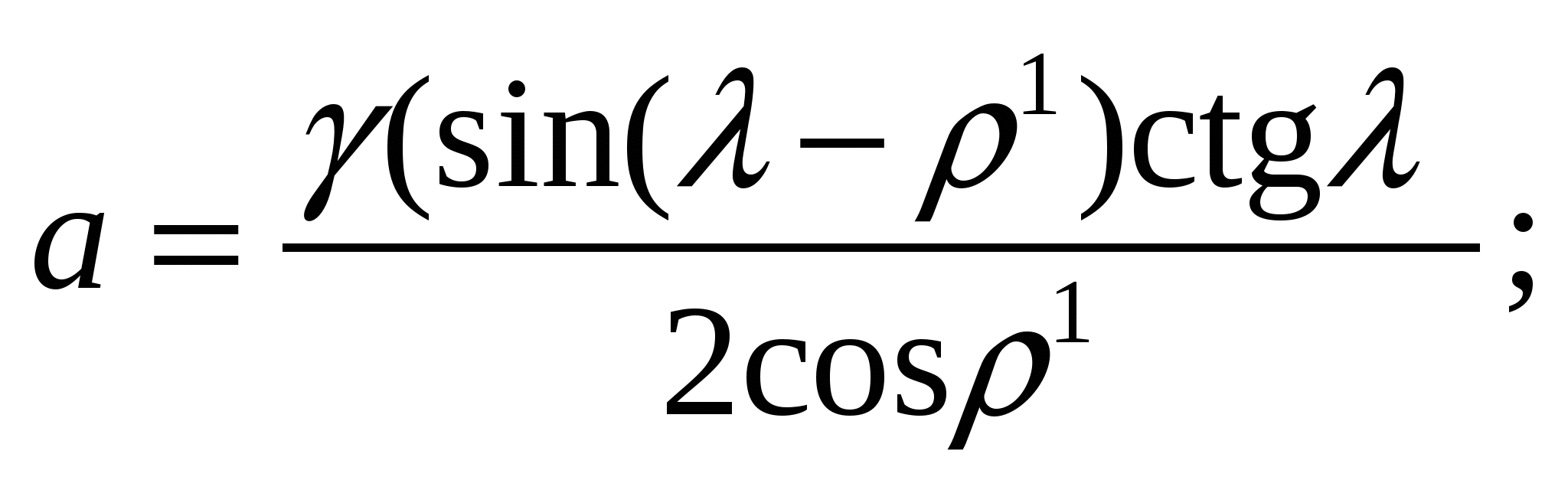
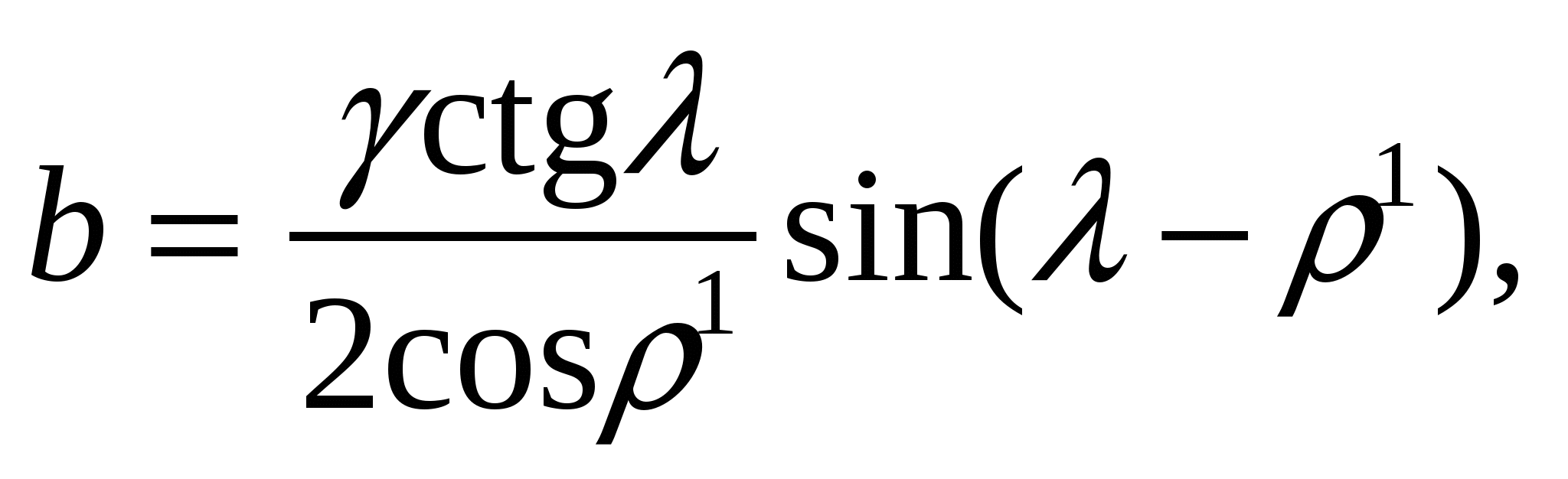
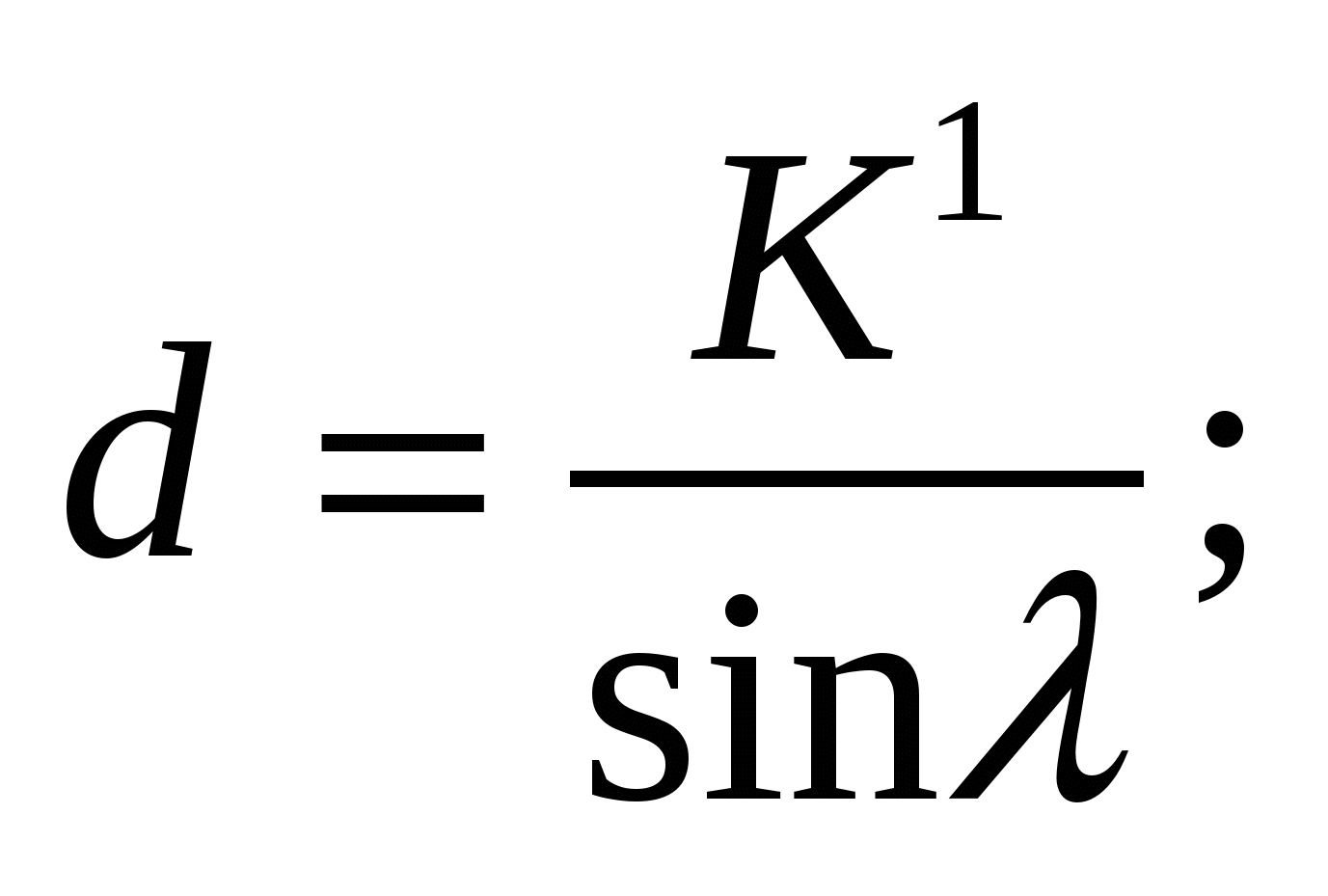
f = cosλ (К1ctgλ – σp).
Анализ выражения (2) показывает, что параметры Н и h связаны между собой параболической зависимостью. Определим такое значение h, при котором высота устойчивости откоса H = min. Тогда при dH/dh = 0, –2hb + f = 0 откуда h = 0,5f/b, и после подстановки f и b получаем выражение
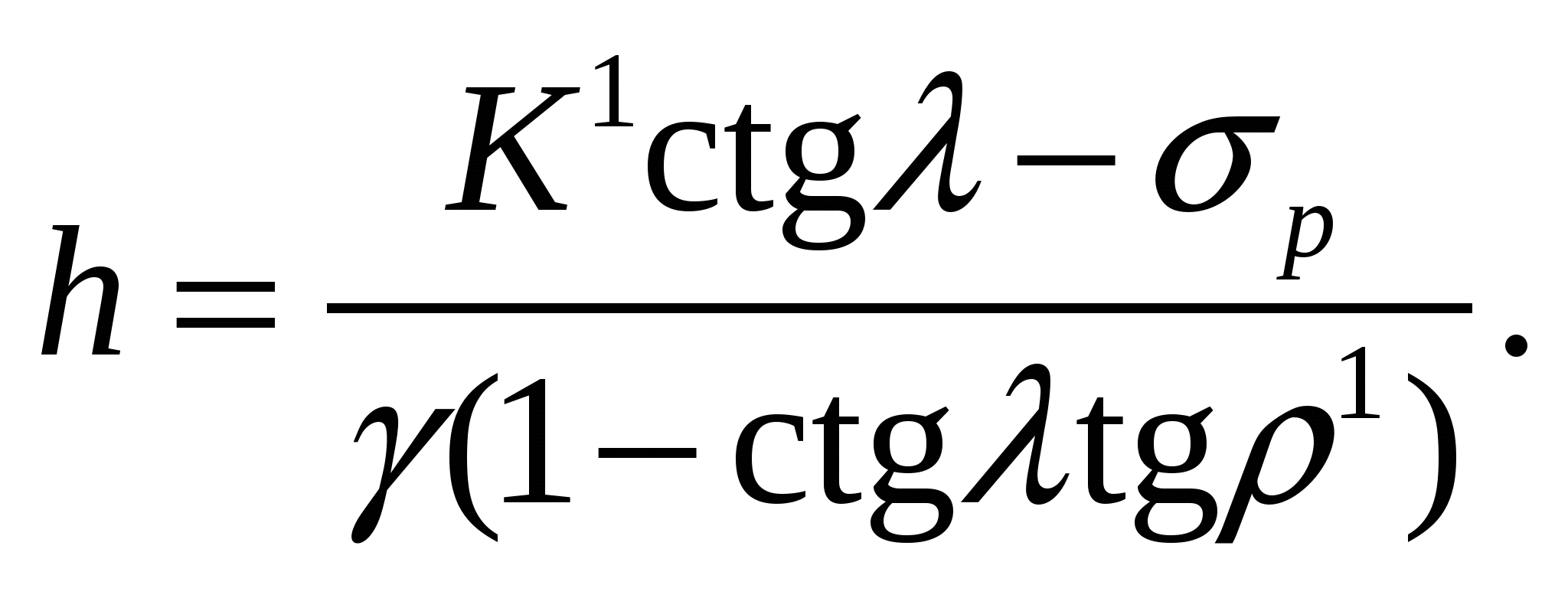 (3)
(3)
При σp = 0
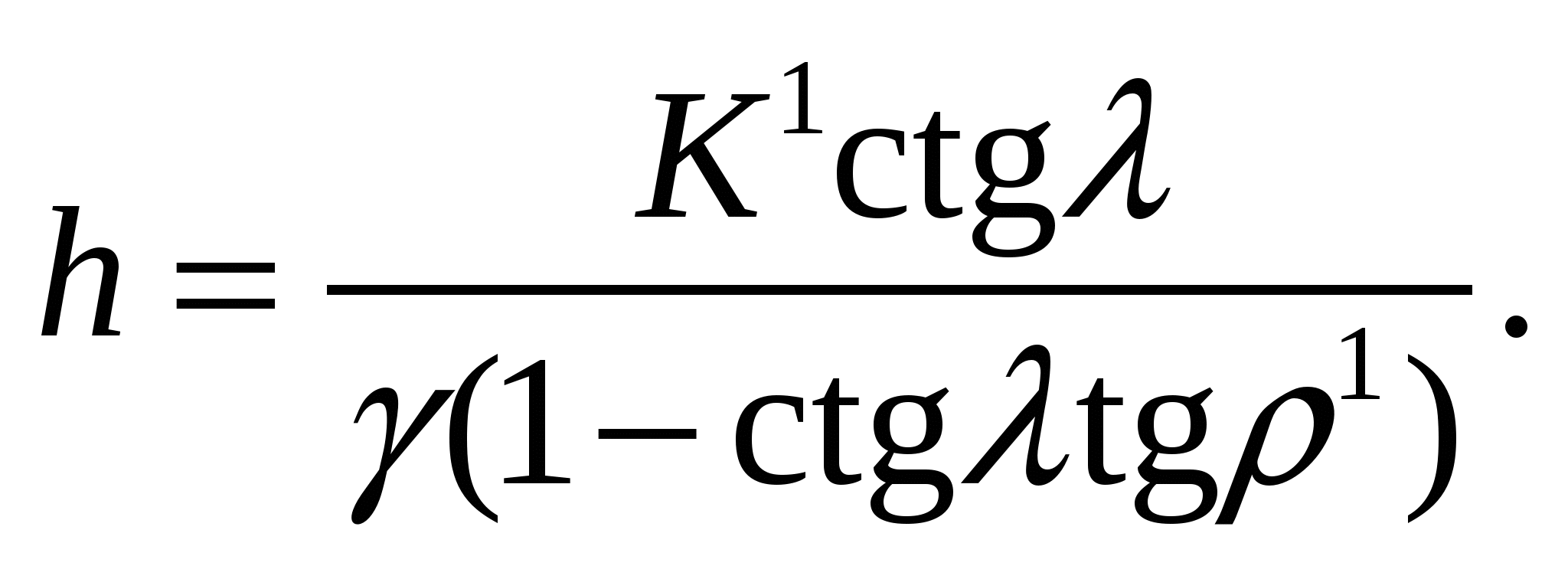 (4)
(4)
Сравнение результатов расчетов минимальной глубины возникновения площадок скольжения (минимальная высота вертикального откоса) показывает, что найденные по формуле (4) значение h меньше аналогичного параметра, определенного по рекомендациям (147), приведенным в [1], в 1/cos2λ раз. Это расхождение объясняется тем, что при выводе уравнения для h в работе [1] не учтено дополнительное сопротивление сдвигу массива за счет сцепления по элементарным площадкам ΔSFK. Действительно, если исключить из выражения (1) дополнительное сопротивление на сдвиг К1FK, можно получить
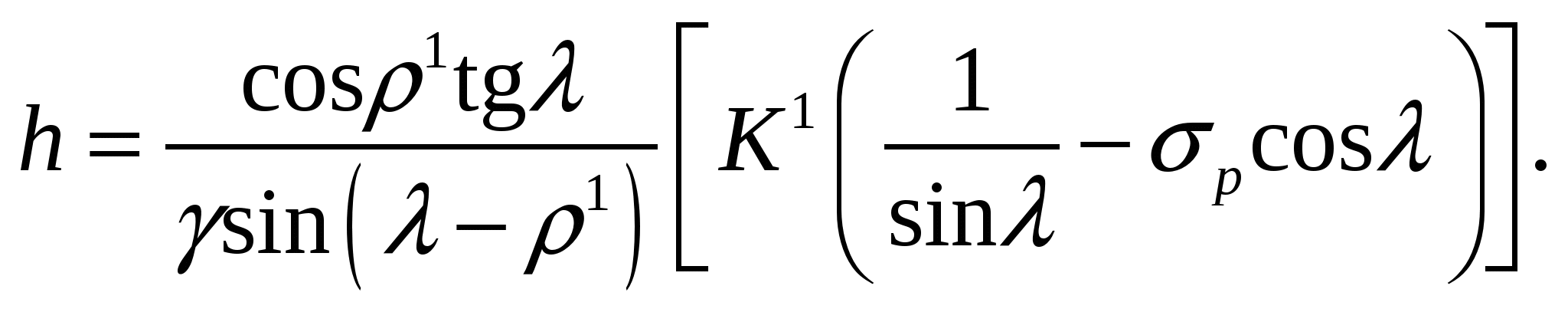 (5)
(5)
Из уравнения (5) при σp = 0 получается выражение, идентичное уравнению (147) в работе [1].
Поставив выражение для h из формулы (3) в уравнение (2), после соответствующих преобразований получаем
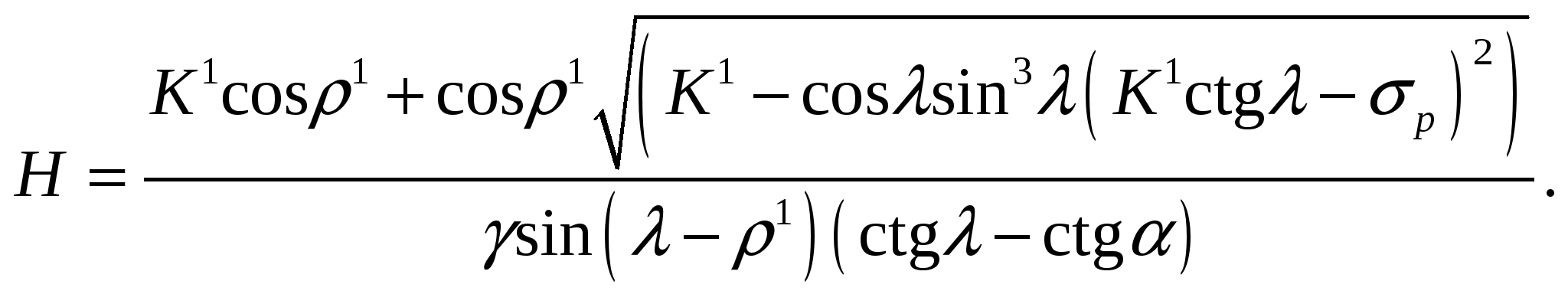 (6)
(6)
Проведем сравнительный анализ разных методик вычисления H.
Сравним величину Н, определенную по формуле (6), с численными значениями этого параметра, определенного по рекомендациям в [2] и [3]:
H = h [1 – (ctgα tgλ)1/2]–1, (7)
где h = K1cosρ1[γcosρ1 sin(λ – ρ1)]–1, на численном примере при следующих исходных данных: К1 = 0,05 МПа; ρ1 = 15°; γ = 2,5 103, кг/м3; λ = 45°; σp = 0; α = 50...90°.
Н = 2 К1 соsρ1 sinα [γsin(λ – ρ1)] sin(α – λ)]–1. (8)
Результаты расчета параметров Н по формулам (6), (7) и (8) приведены на рисунке 2.
Упрощенное решение по формуле (7) дает занижение высоты устойчивого откоса по сравнению с формулой (6), изменяющееся от 3 до 46,5 % с возрастанием угла наклона откоса α. Расхождение объясняется тем, что при выводе формулы (7) не учтено дополнительное сопротивление сдвигу массива за счет сцепления по элементарным площадкам ΔFK.
Определение значения Н по формуле (8) при полном клине обрушения дает незначительное завышение высоты откоса по сравнению с предлагаемым решением по формуле (6), изменяющееся от 1 до 6 % при увеличении угла α.
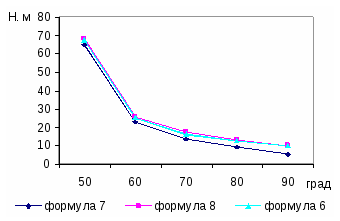
Рисунок 2 — График зависимости Н
Предлагаемая расчетная схема с решением по формуле (6) реализуется, когда h, определяемая по формуле (3), больше нуля, т.е. сопротивление породы на разрыв σp К1ctgλ. В противном случае, когда σp ≥ К1ctgλ, реализуется схема полного клина обрушения и высоту откоса необходимо определять по формуле (8).
Рассмотрим схему, когда откосом уступа подрезаны две системы диагональных поверхностей ослабления (рисунок 3). Здесь возможный сдвиг породной пирамиды будет происходить по линии скрещивания поверхностей скольжения с углом наклона ψ.
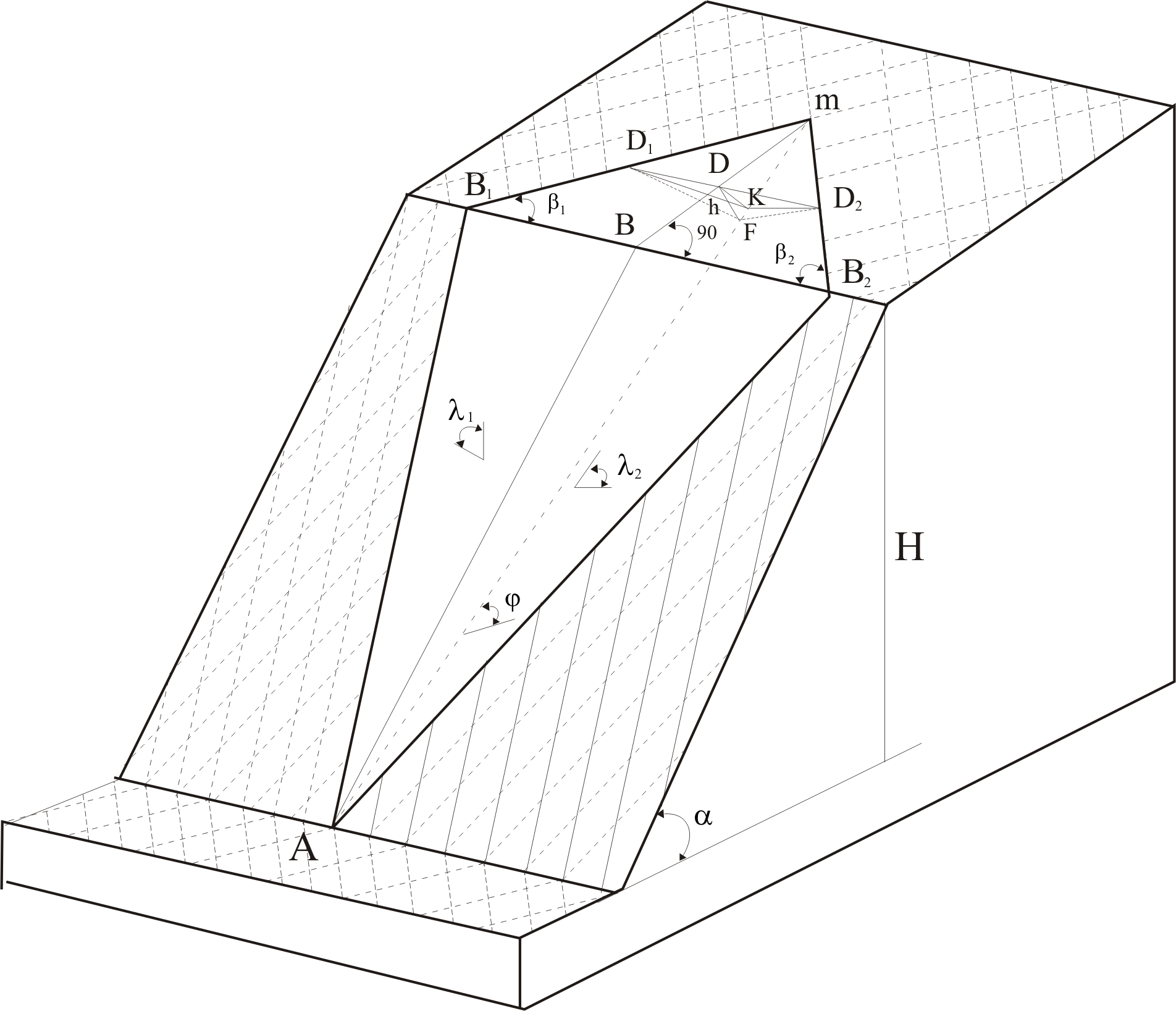
Рисунок 3 — Схема расчета устойчивости откосов при их подрезке системой диагональных трещин
В общем случае прочностные характеристики по поверхностям ослабления различны (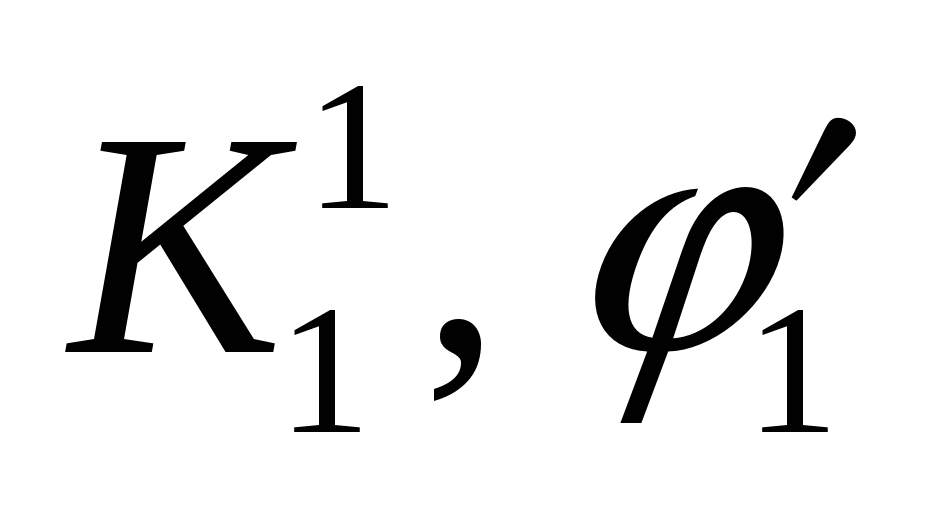 и
и 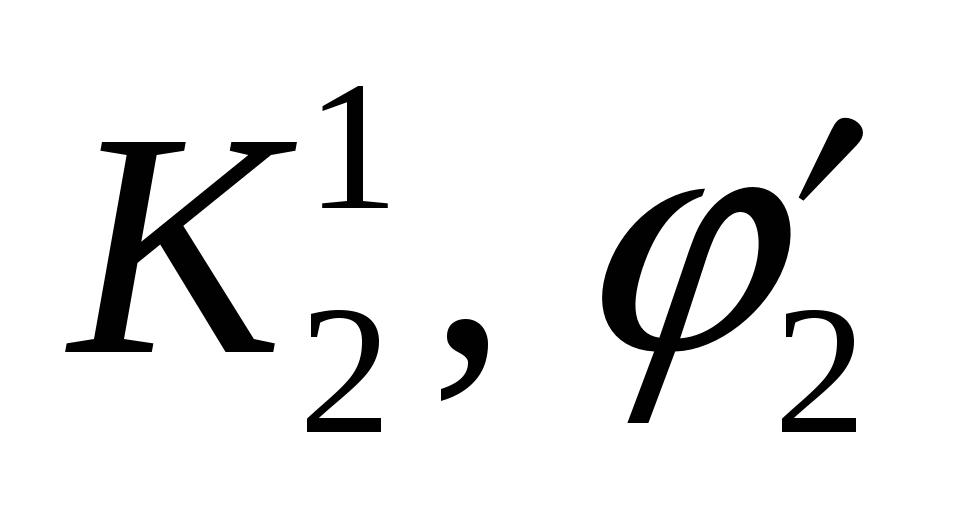 — сцепление и угол трения по 1-й и 2-й поверхностям). Так как размер поверхностей скольжения S1 и S2 и их прочность различны, то каждая из них способна удержать определенный вес Р1 и Р2. При этом должно соблюдаться условие, что полный вес пирамиды возможного обрушения Р = Р1 + Р2.
— сцепление и угол трения по 1-й и 2-й поверхностям). Так как размер поверхностей скольжения S1 и S2 и их прочность различны, то каждая из них способна удержать определенный вес Р1 и Р2. При этом должно соблюдаться условие, что полный вес пирамиды возможного обрушения Р = Р1 + Р2.
Рассуждая аналогично, условие предельного равновесия для рассматриваемой расчетной схемы можно записать в виде
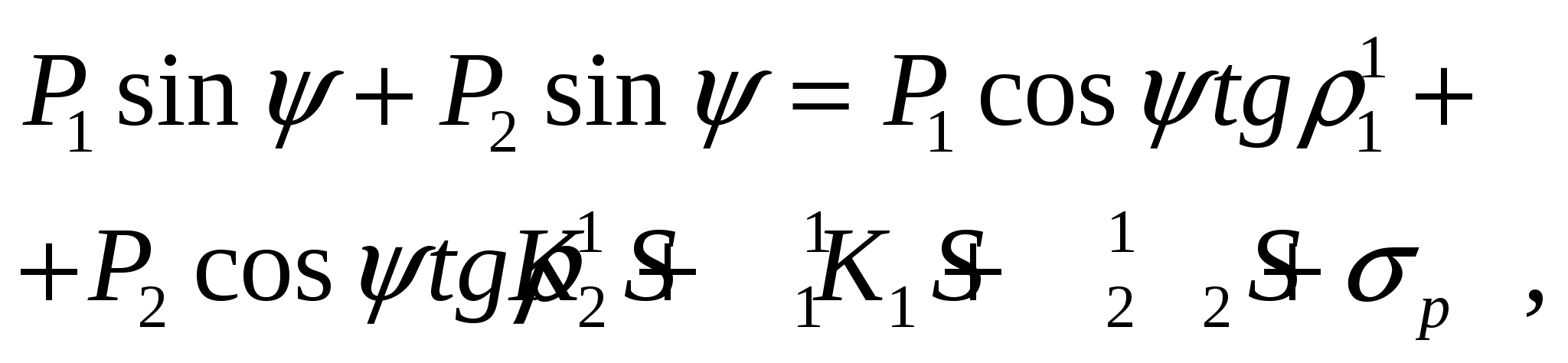 (9)
(9)
где S — площадь поверхности отрыва D1KD2, перпендикулярной к линии скрещивания Am. Площадь 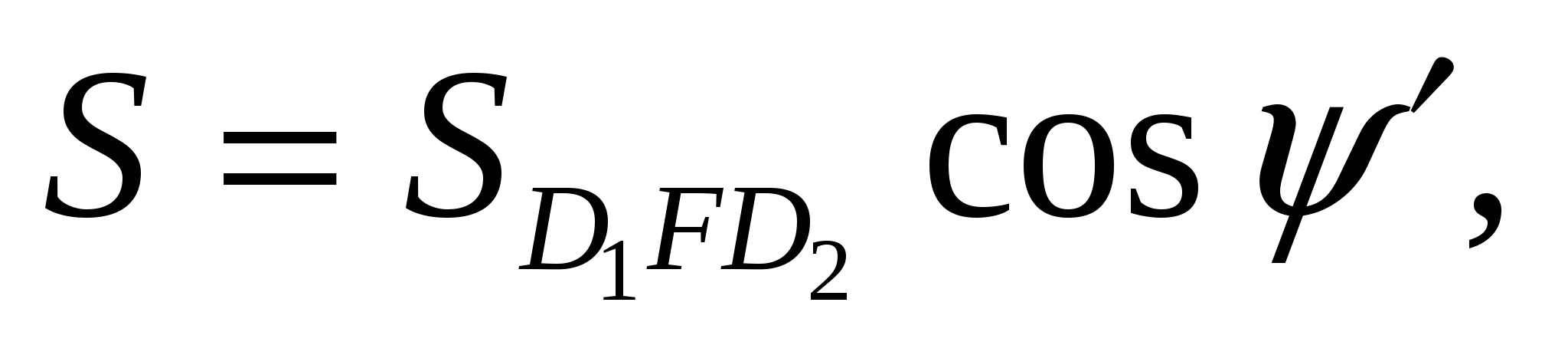 где ψ' — угол наклона линии скрещивания поверхностей ослабления в плоскости, перпендикулярной к откосу;
где ψ' — угол наклона линии скрещивания поверхностей ослабления в плоскости, перпендикулярной к откосу; 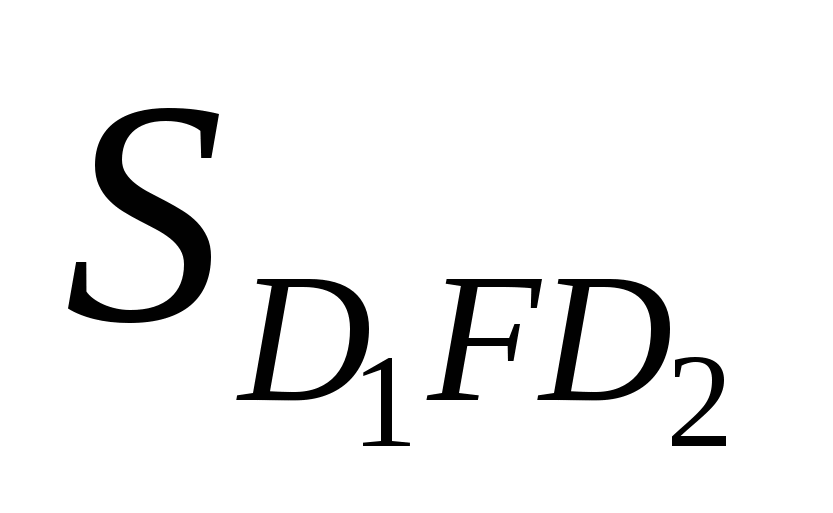 — ступенчатая поверхность отрыва, близкая к вертикальной и определяемая из выражения
— ступенчатая поверхность отрыва, близкая к вертикальной и определяемая из выражения 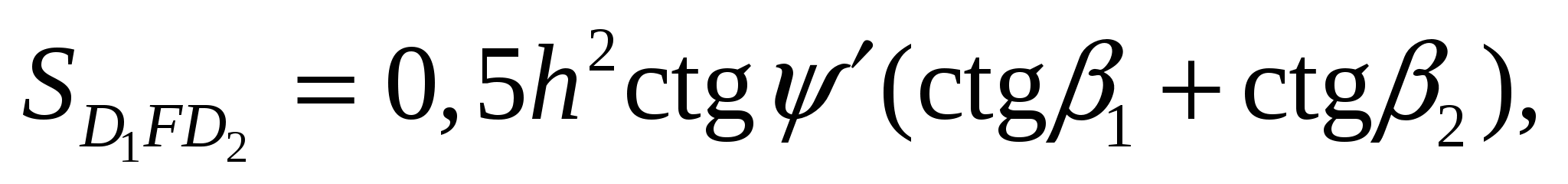 где h — минимальная глубина возникновения площадок скольжения; β1, β2 = углы разворота поверхностей ослабления относительно откоса в плане. Тогда окончательно S = 0,5h2ctgψ'cosψ'(ctgβ1 + ctgβ2). Площади скольжения S1 и S2 равны соответственно площадям поверхностей АВ1D1F и AB2D2F и находятся из выражений:
где h — минимальная глубина возникновения площадок скольжения; β1, β2 = углы разворота поверхностей ослабления относительно откоса в плане. Тогда окончательно S = 0,5h2ctgψ'cosψ'(ctgβ1 + ctgβ2). Площади скольжения S1 и S2 равны соответственно площадям поверхностей АВ1D1F и AB2D2F и находятся из выражений:
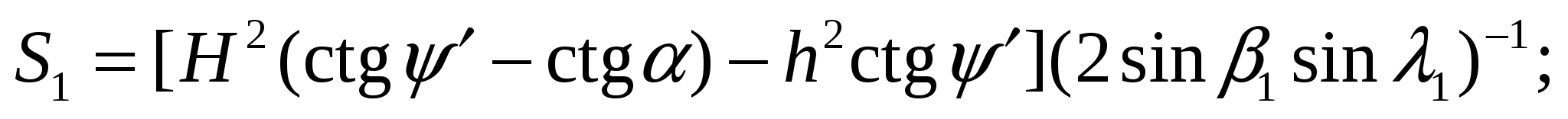
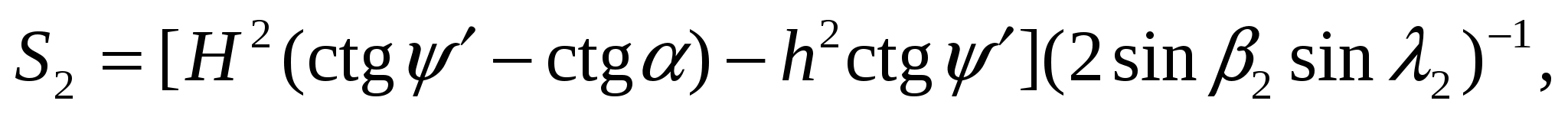
где λ1, λ2 — углы наклона поверхностей ослабления;
H, α — высота и угол наклона откоса.
В работе [4] по формуле веса Р1 и Р2 находятся из предположения их пропорциональности площадям проекций поверхностей скольжения на горизонтальную плоскость. Такое предположение полностью исключает несущую способность скольжения при угле их падения, равном 90°, что является совершенно неверным. В действительности же значение Р1 и Р2 должны быть пропорциональны несущим способностям поверхностей скольжения Р1нес и Р2нес и определяться из соотношений:
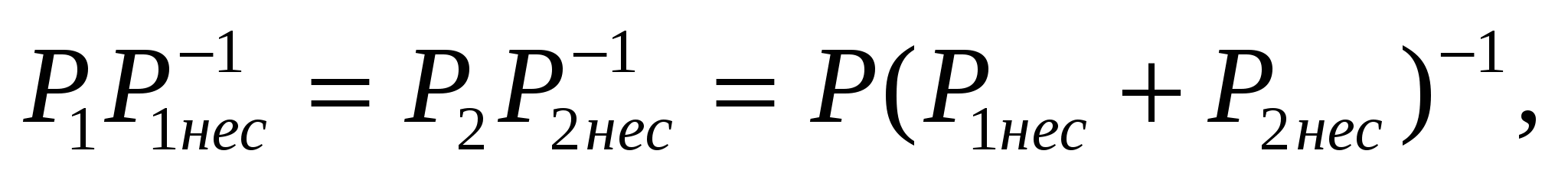 (10)
(10)
где P1 = PP1нес(P1нес + P2нес)–1;
P2 = PP2нес(P1нес + P2нес)–1.
Несущая способность поверхностей скольжения:
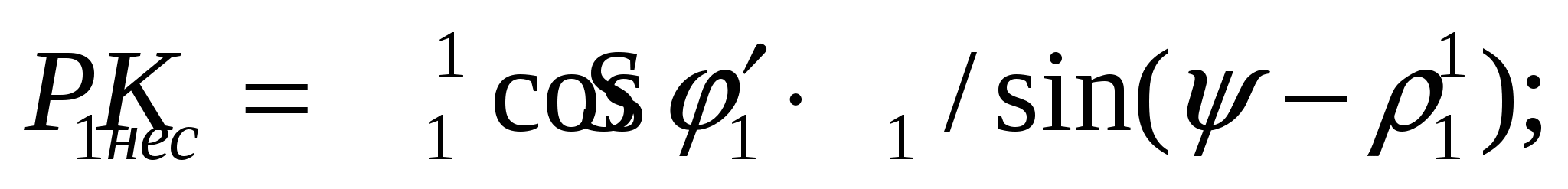
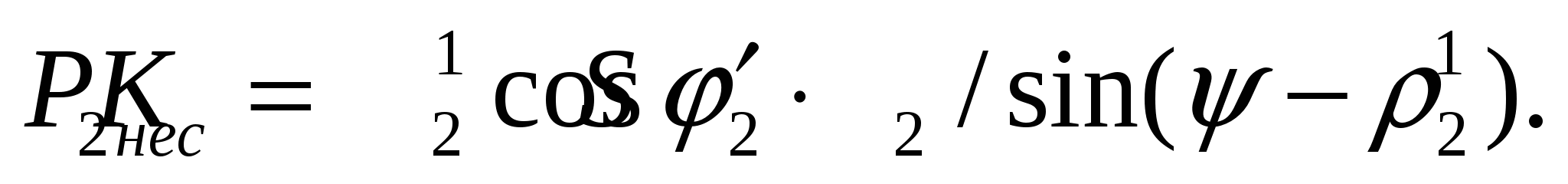
Общий вес породной призмы возможного обрушения ABD1D2FA
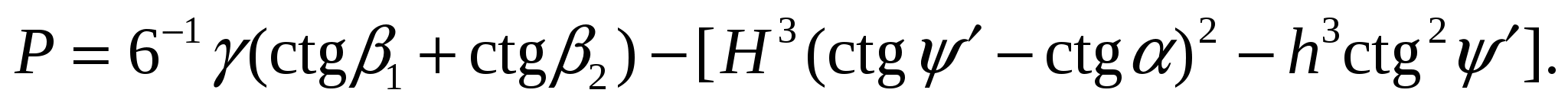
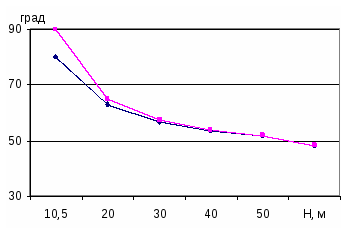
Рисунок 4 — График зависимости α от высоты уступа
После подстановки всех приведенных выражений для P1, P2, P, S1, S2, S в уравнение предельного равновесия (9) получаем зависимость H = f(h), записанную в неявном виде:
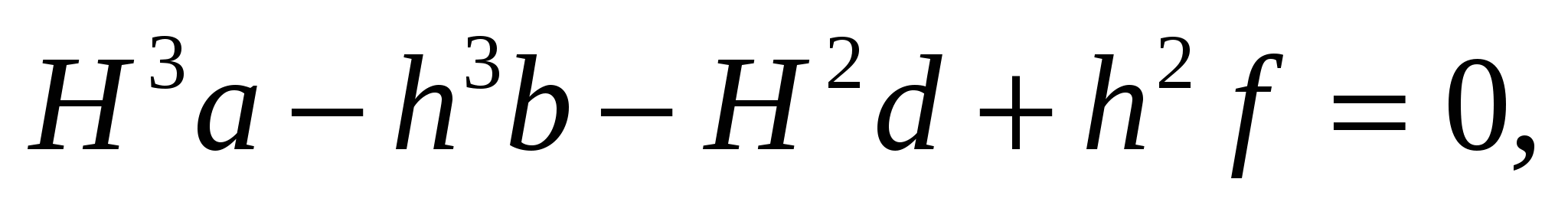 (11)
(11)
где 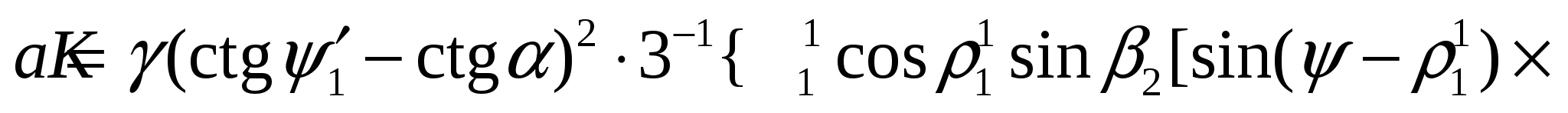
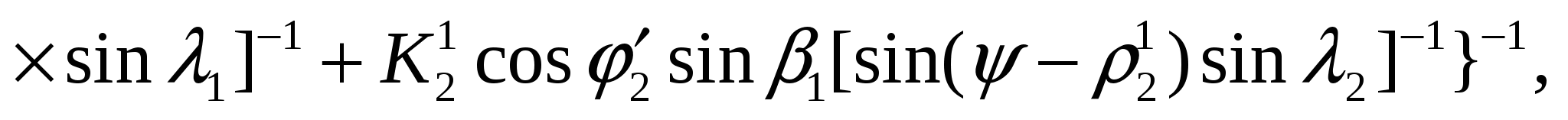
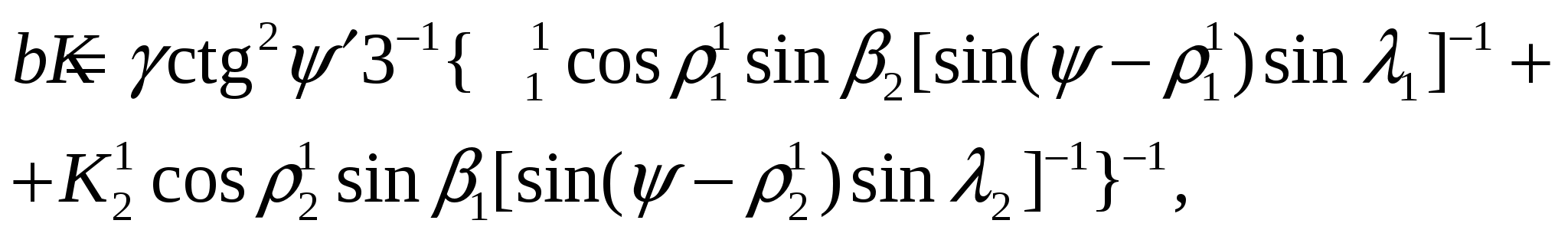
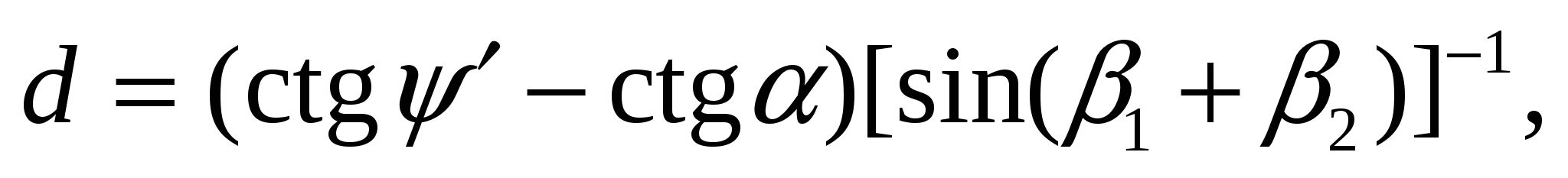
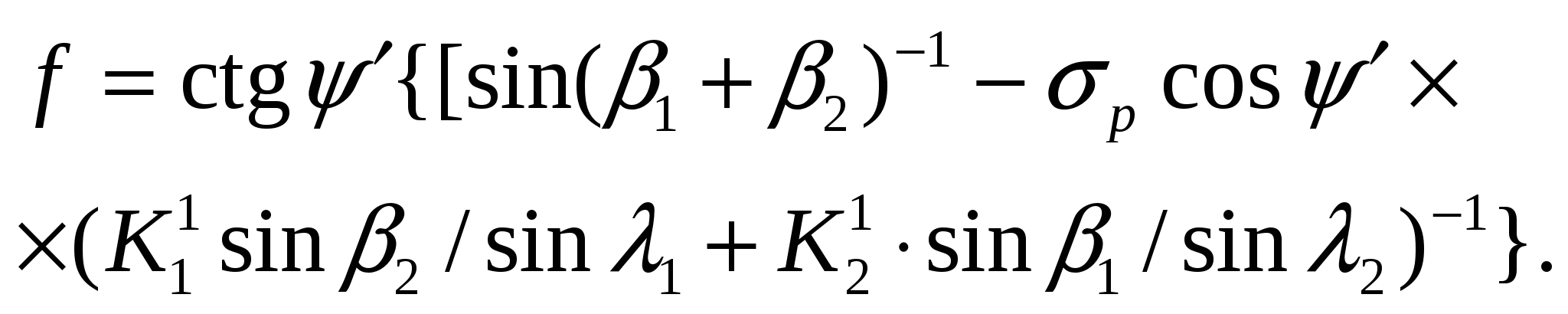
Найдем такое значение для h, при котором высота устойчивого откоса H = min, т.е. принимаем, что dH / dh = 0. Тогда из (11): –3h2b + 2hf =0, откуда h = 2f / (3b), или после подстановки значений f и b:
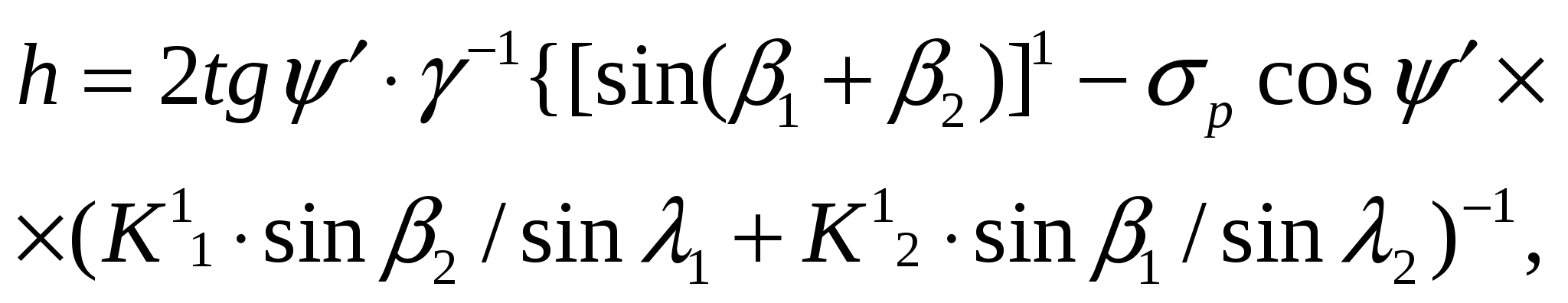
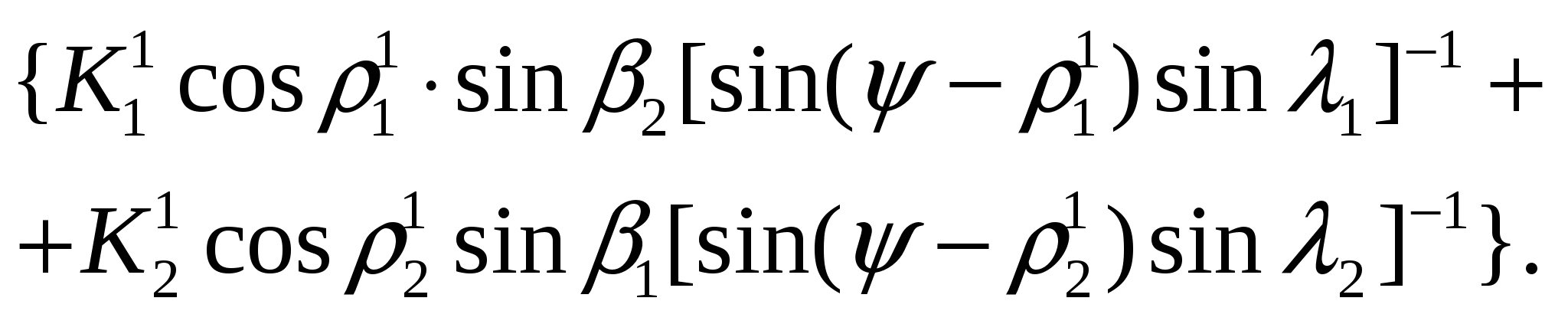 (12)
(12)
Подставим выражение для h через f и b в уравнение (11) и получим кубическое уравнение по определению высоты устойчивого откоса в виде
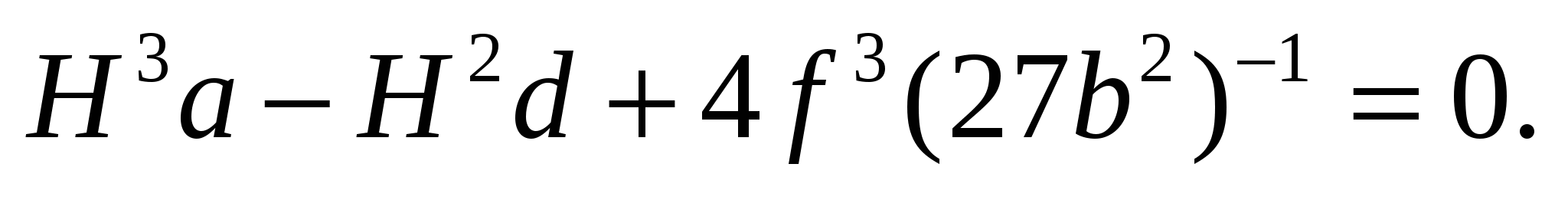 (13)
(13)
Так как это уравнение трудно решить математически через Н, разрешим его через угол наклона откоса α, для чего выделим из коэффициентов a и d выражение ctgψ' – ctgα и в результате получим преобразованное уравнение
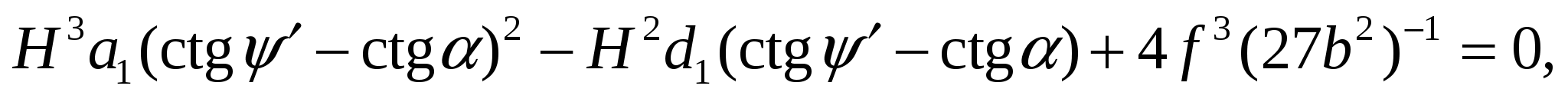 (14)
(14)
где 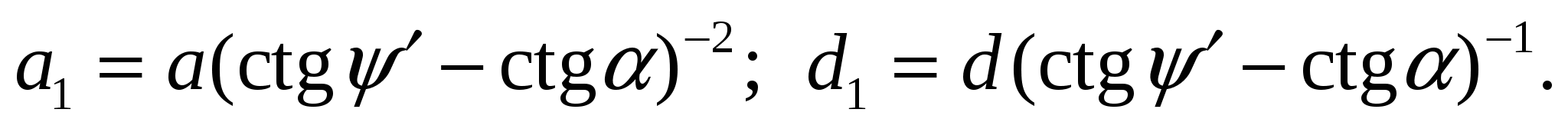
Находим единственный действительный корень квадратного уравнения (14) по формуле (ctgψ'–ctgα) = 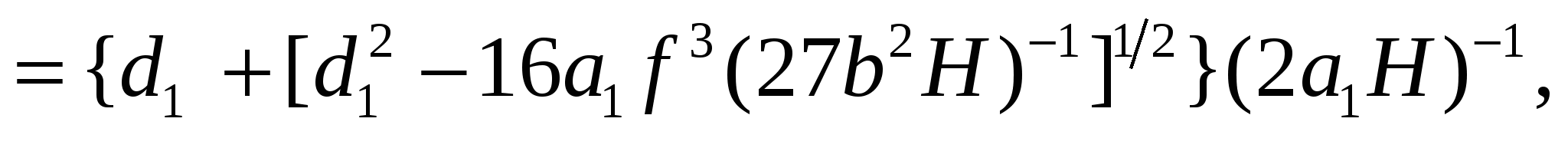 откуда с заменой коэффициентов d1, a1, f, b их выражениями
откуда с заменой коэффициентов d1, a1, f, b их выражениями
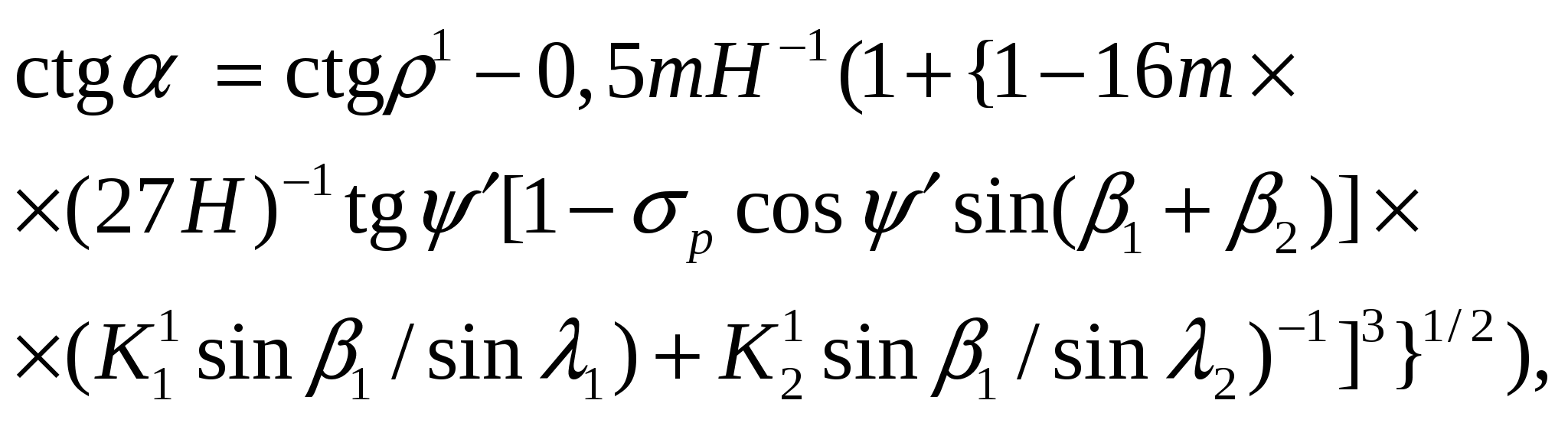 (15)
(15)
где 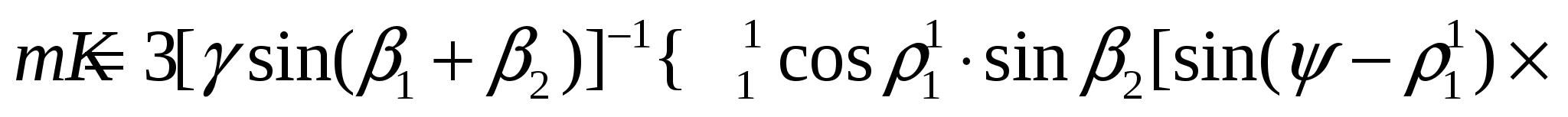
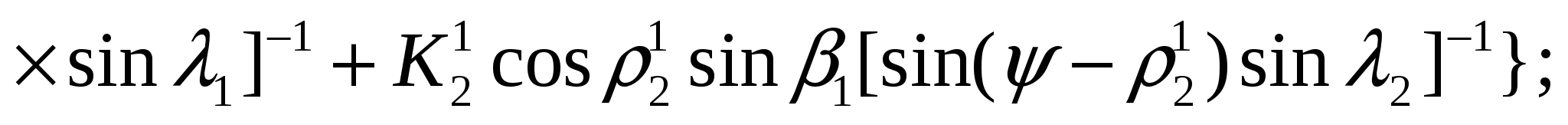
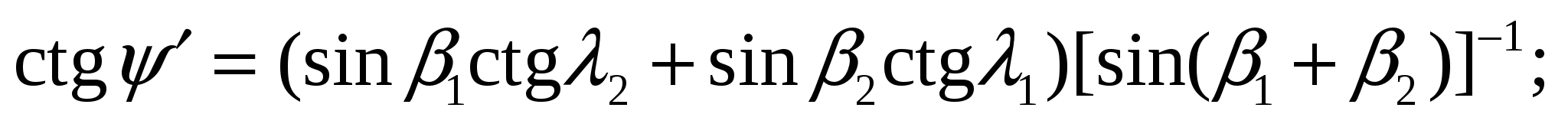
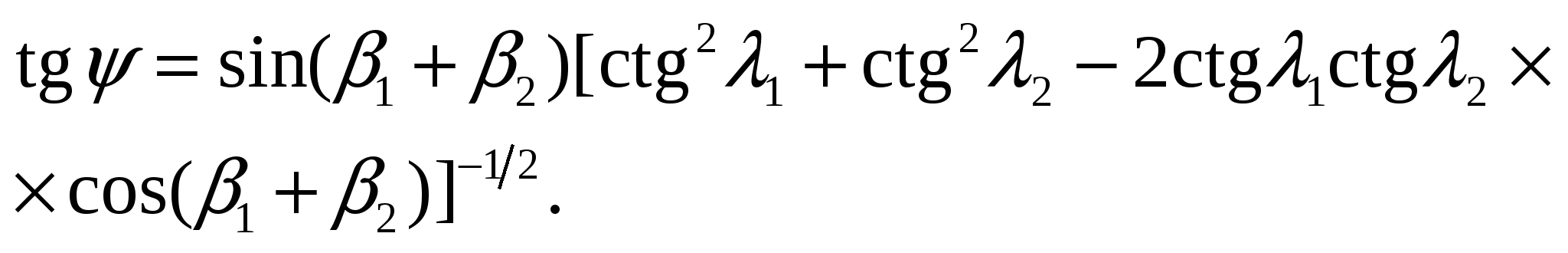
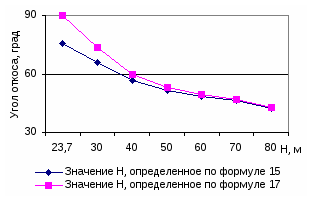
Рисунок 5 — График зависимости α от высоты уступа
Рассматриваемая схема реализуется так же, как и первая, при h > 0 в выражении (12). Это может быть только при условии
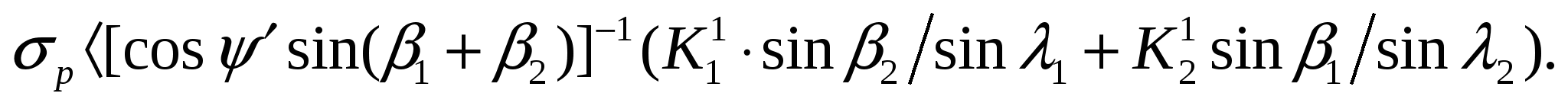
В противном случае реализуется схема полного обрушения породной пирамиды и при h = 0 из (11) вытекает, что
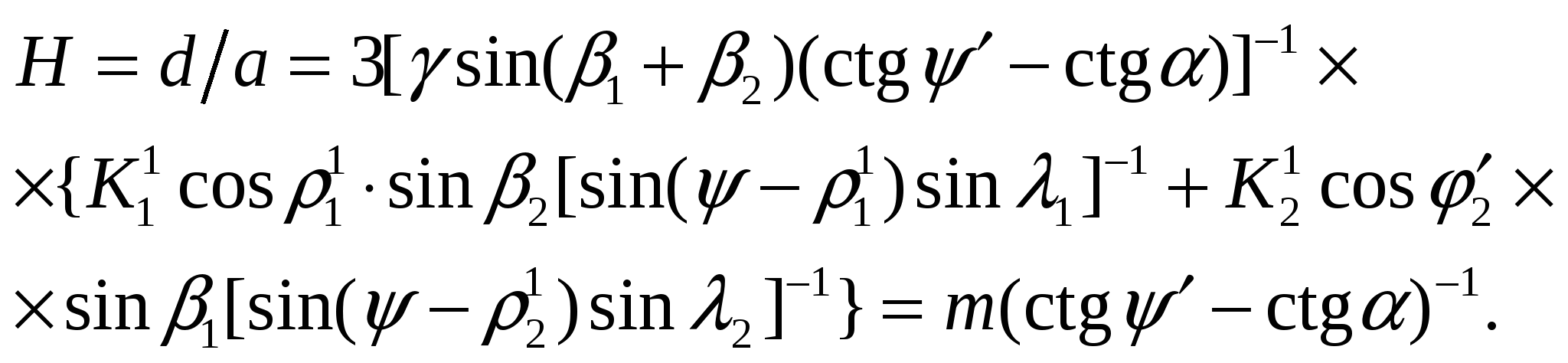 (16)
(16)
Выражение (16) идентично формуле (116) в работе [3], а параметр m есть не что иное, как ширина породной пирамиды полного обрушения r, определяемая по формуле (117) из [3]. Из (16) угол наклона устойчивого откоса α находим через Н:
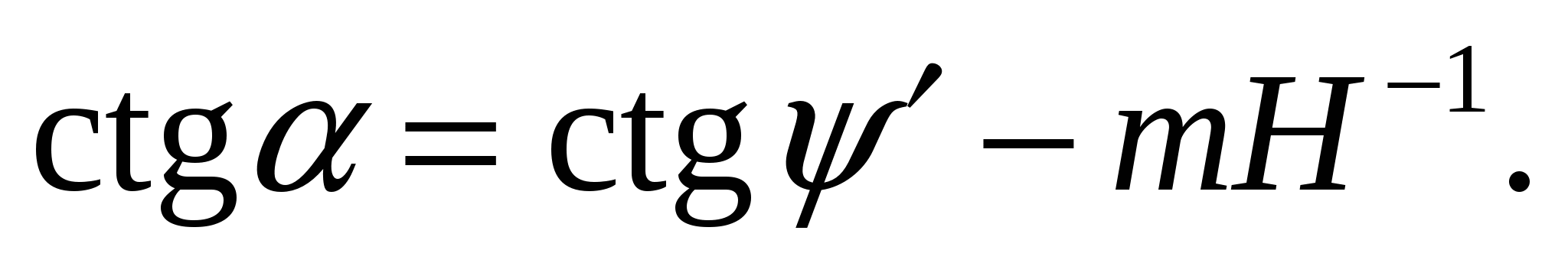 (17)
(17)
Численный сравнительный анализ выражений (15) и (17) (рисунок 4) при следующих исходных данных: 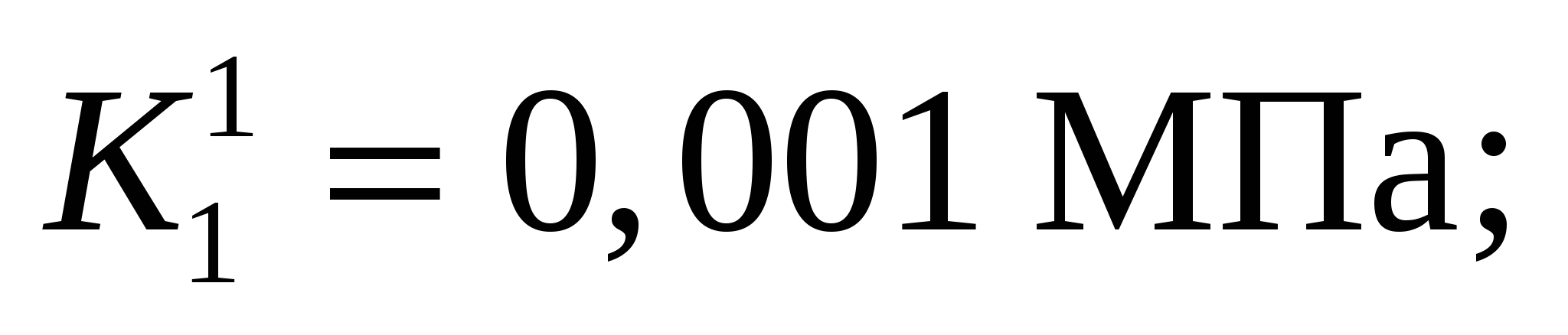
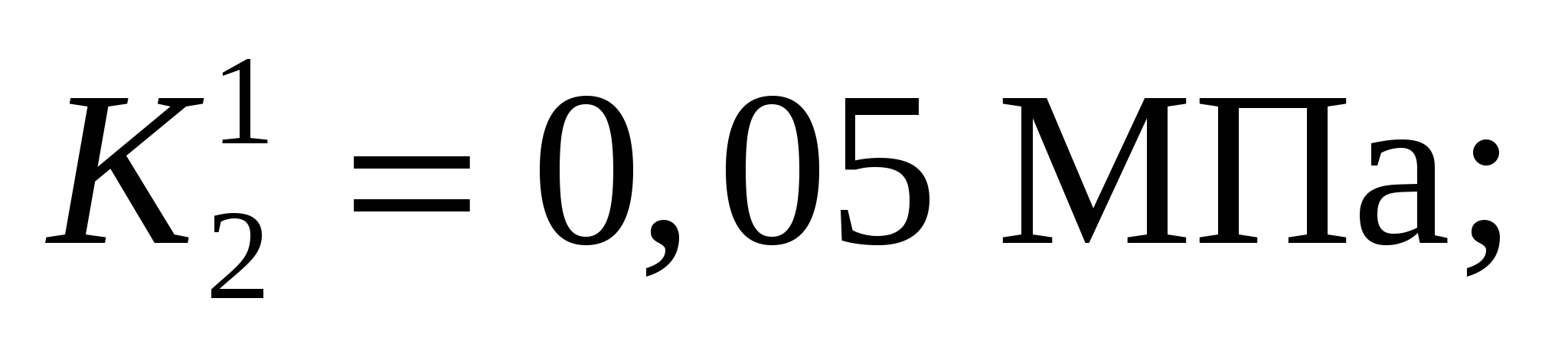
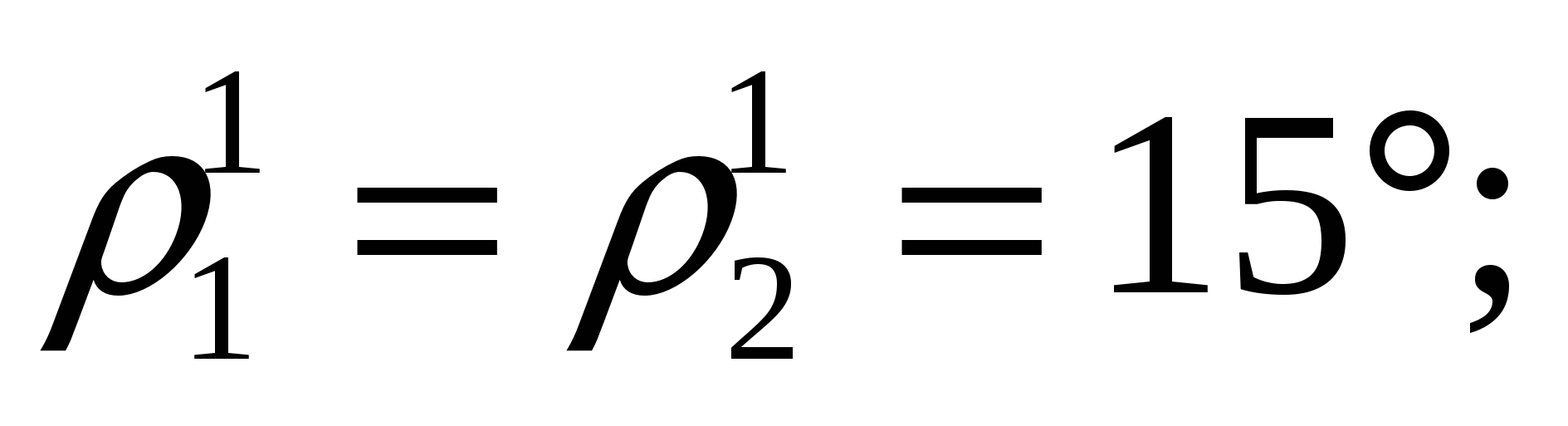 β1 = 10°; β = 20°; λ1 = 50°; λ2 = 40°; γ = 2,5·103 кг/м3; σз = 0 и (рисунок 5) при
β1 = 10°; β = 20°; λ1 = 50°; λ2 = 40°; γ = 2,5·103 кг/м3; σз = 0 и (рисунок 5) при 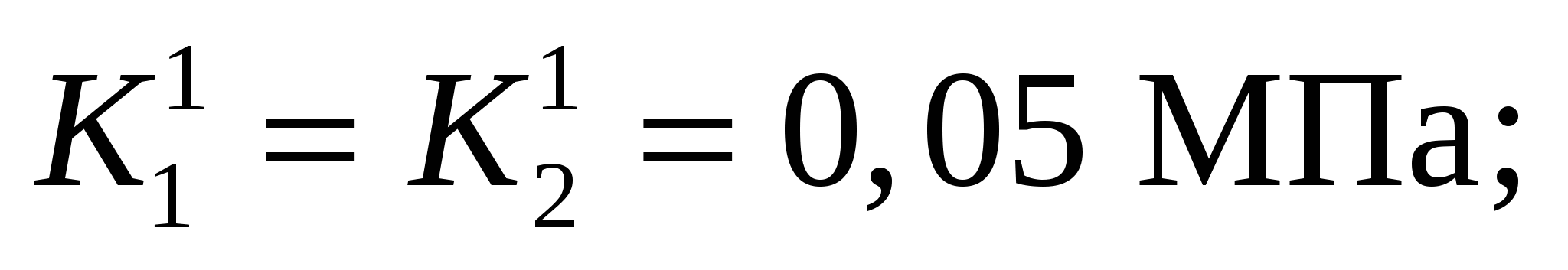
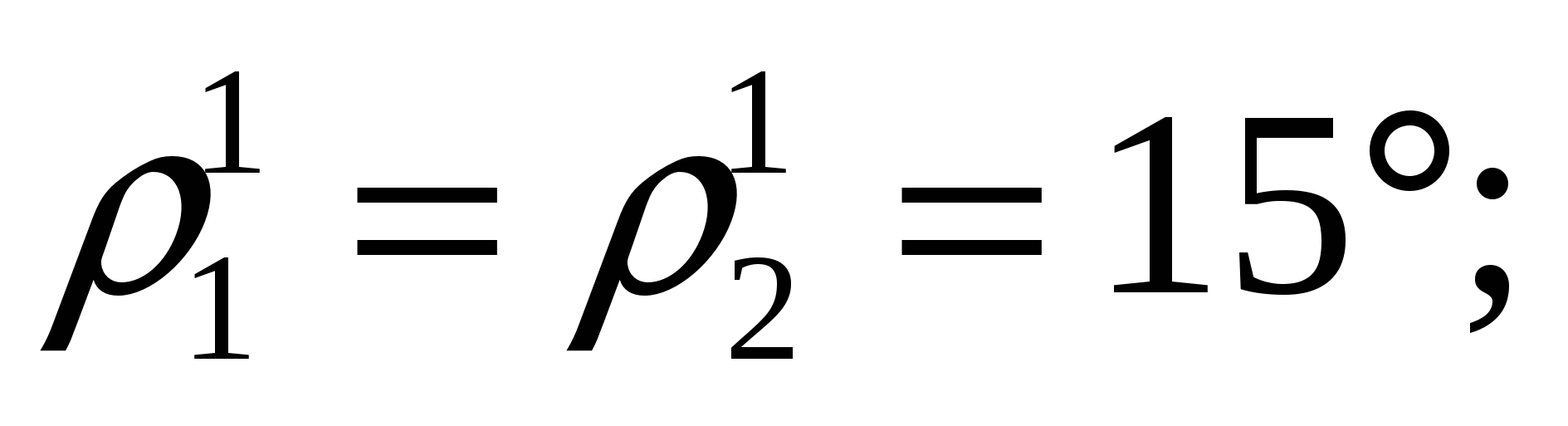 β1 = β2 = 45°; λ1 = λ2 = 45°; γ = 2,5·103 кг/м3; σp = 0.
β1 = β2 = 45°; λ1 = λ2 = 45°; γ = 2,5·103 кг/м3; σp = 0.
Как видно из рисунков 4 и 5, неучет фактора отрыва породного массива в районе верхней бровки при полном клине обрушения дает завышение угла наклона устойчивого откоса на 13…19 %, стремящееся к нулю при увеличении высоты откоса. Такое завышение является максимальным, когда σp = 0; оно становится меньше, когда имеет какое-то конкретное значение, и равно нулю, когда
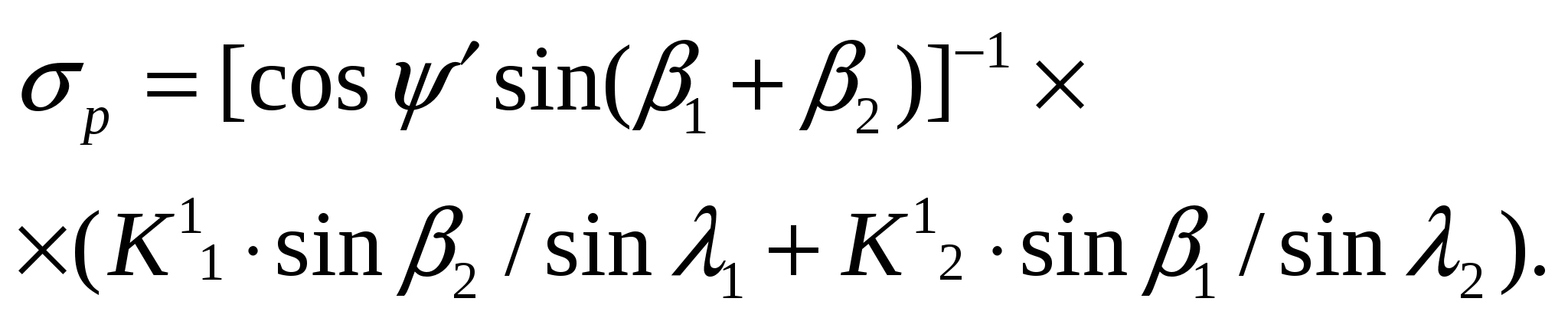
В последнем случае выражение (15) переходит в (17).
Таким образом, можно утверждать, что механизм деформирования породного массива с наличием поверхностей ослабления, подрезанных откосом, объясняется рассмотренными выше расчетными схемами, учитывающими разрыв призмы возможного обрушения и образование в результате этого нависей в районе верхней бровки. Эти схемы являются общими, а решения по ним — математически более строгими, чем известные ранее. В определенных условиях при сопротивлении породного массива на разрыв свыше выявленного нами предела схемы (рисунки 1 и 3) переходят в полный клин обрушения, решаемый по простым в математическом отношении формулам. Известное решение по формуле (12) в работе [2] является упрощенным и может применяться только при пологом и наклонном залегании откоса.
Жерасты сілтілеу әдісі (ЖС) 1962 жылдан бері әлем бойынша өндіріле бастады (ҚР, РФ, АҚШ, Канада және т.б.).
Жерасты сілтілеу — кенді оның жатқан орнында химиялық реагенттермен іріктеп еріту және одан кейін кенқұрамды ерітіндіден алу арқылы қазудың геотехнологиялық әдісі.
Геотехнология әдістерінің дәстүрлі қазу жүйесі алдындағы артықшылықтарын қарастырып көрейік [1, 2].
Жерасты сілтілеу әдісінің дәстүрлі ашық және жерасты қазып-өндіру алдыңдағы негізгі артықшылықтары келесідей:
1. Қазып-өндіруге кедей, кем бағалы және баланстан тыс кендерді келтіру, сондай-ақ, кеннің жату шарттары күрделі және соңғы өнім бірлігінің құны айтарлықтай тиімді болатын зор қорлары бар кен орындарын көңілге келтіру;
2. Кәсіпорын құрылысына күрделі шығындардың 2...4 есе төмендеуі, және сонын салдарынан, құрылыс мерзімінің қысқаруы;
3. Соңғы өнім бойынша еңбек өнімділігінің 2...4 есе өсуі және жұмыс атқарушылар санының сәйкес қысқаруы;
4. Кәсіпорындардағы еңбек шарттарының елеулі жақсаруы;
5. Қоршаған ортаға нашар әсер етуінің төмендеуі, әсіресе, жер бетіне және ауа бассейніне.
Осыған сәйкес геотехнология жүйесінің негізгі көрсеткіштерін анықтаймыз.
Негізгі көрсеткіштер үш нысандардың байланысымен анықталады, олар: қазылатын кен, кенді ашып-дайындау төтелдері, төтелдер арқылы кенді жылжымалы қалпына келтіретін ерітінді (ашытқыл, қышқыл, су және т.б.).
Мысалы, геотехнология өнімділігін қоймалы немесе этажды жүйелерге қарастырайық (Ақшатау, Ақсу, Бестөбе кен орындары тәріздес), яғни, белгілі шарттарды пайдаланып көрсеткіштерді есептейік.
Бұл көрсеткіштерді келесі формулалармен анықтауға болады [2, 3]:
1. Металдың өнімді қоспадағы шоғырлану шамасы:
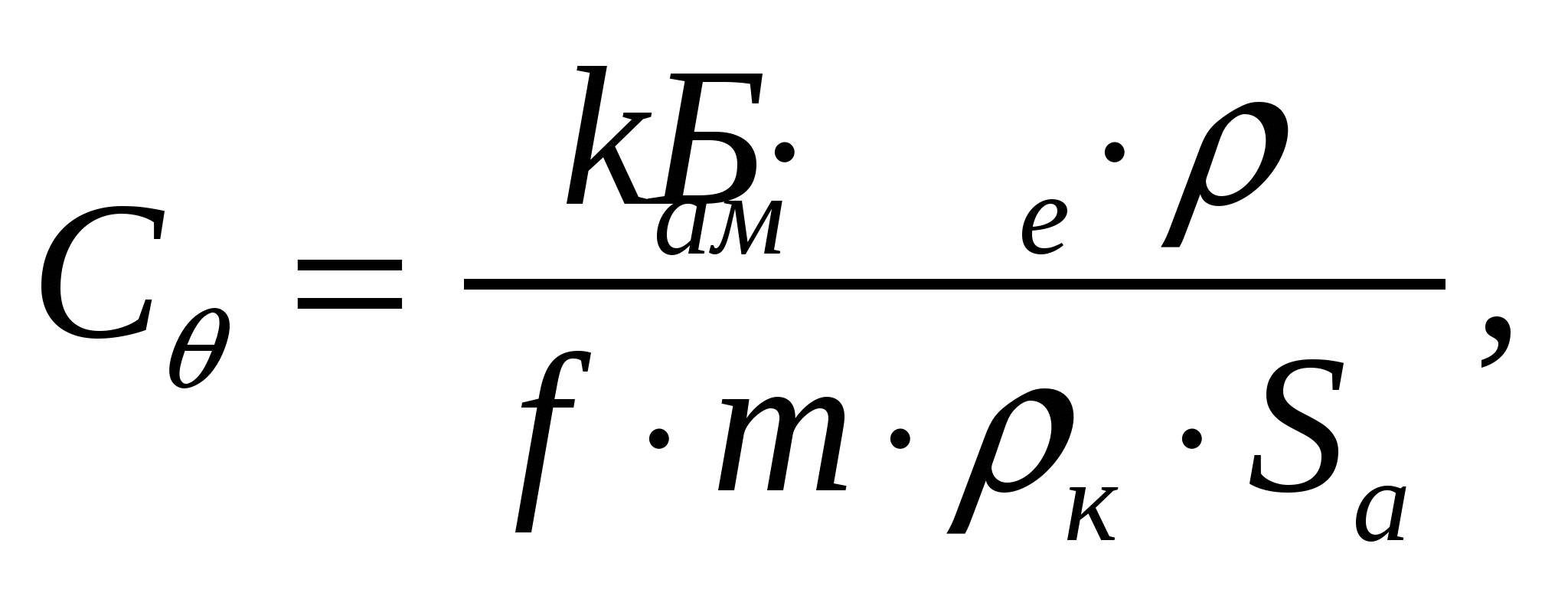 т/м3, (1)
т/м3, (1)
мұндағы ka — қазылған металдың кеннен алу шамасы, ka=0,6;
Бм — шоғырдағы металл барлығы, Бм=500т;
ρe — өнімді ерітіндінің тығыздығы, ρe=1,2 т/м3;
f — сілтілеу қоспасының кен массасына қатынасы, f=0,5;
т — шоғыр қалындығы, т=5 м;
ρк — кен тығыздығы, ρк=2,8 т/м3;
Sa — қазылатын алаң мөлшері, Sa=150000 м3.
Сонда
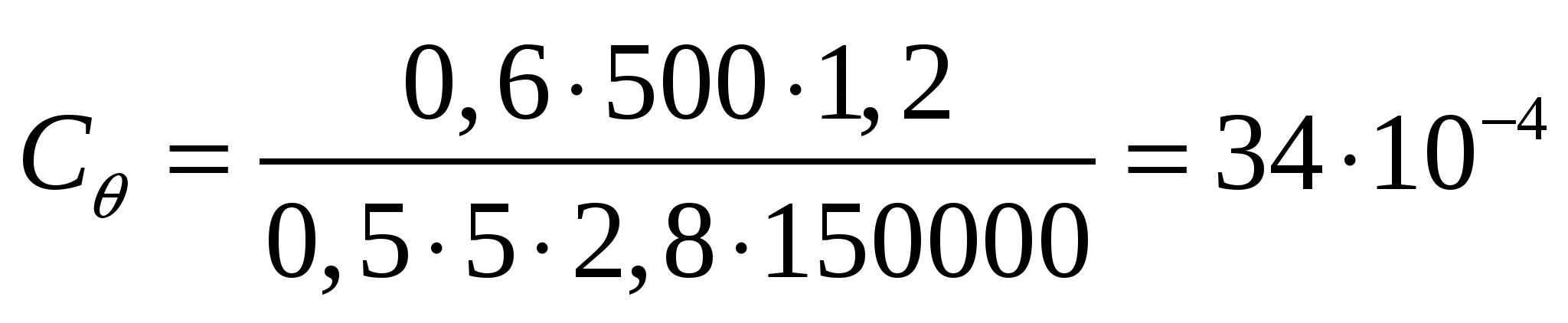 т/м3.
т/м3.
2. Төтелдің жалпы өнімділігі:
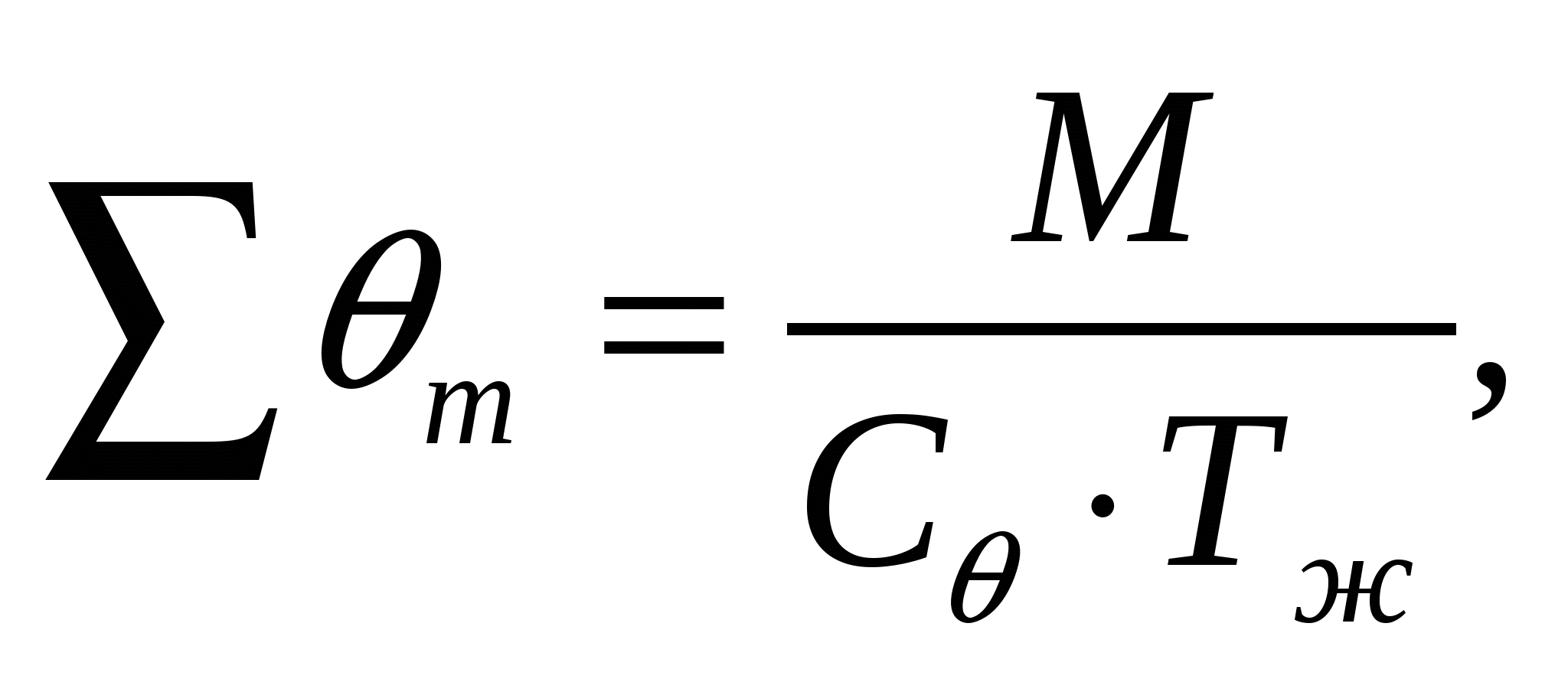 м3/тәу, (2)
м3/тәу, (2)
мұндағы М — метал жылдық қуаты, М=50 т;
Тж — жылдағы жұмыс тәулік саны, Тж=300 тәу.
Сонда
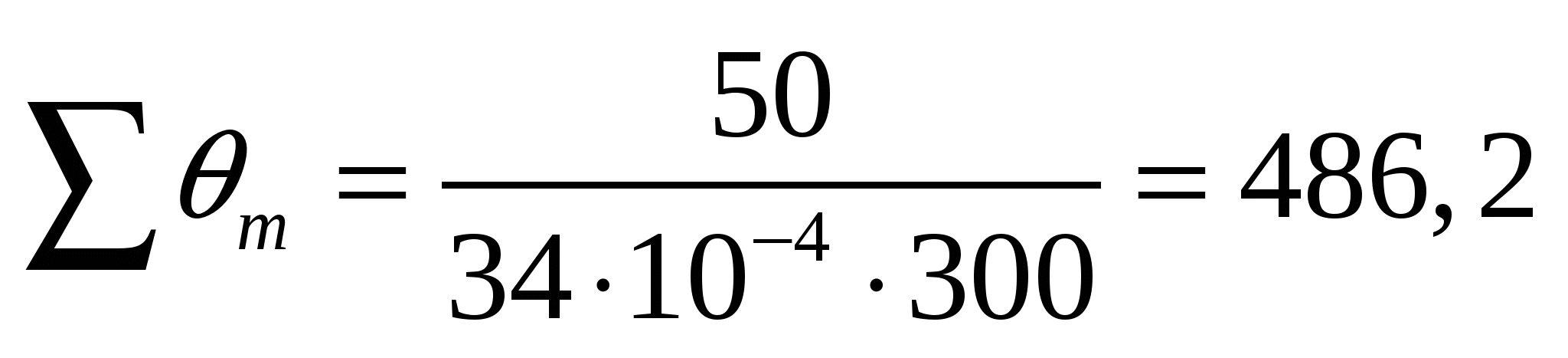 м3/тәу.
м3/тәу.
3. Төтел өнімділігі (қоспа шығару):
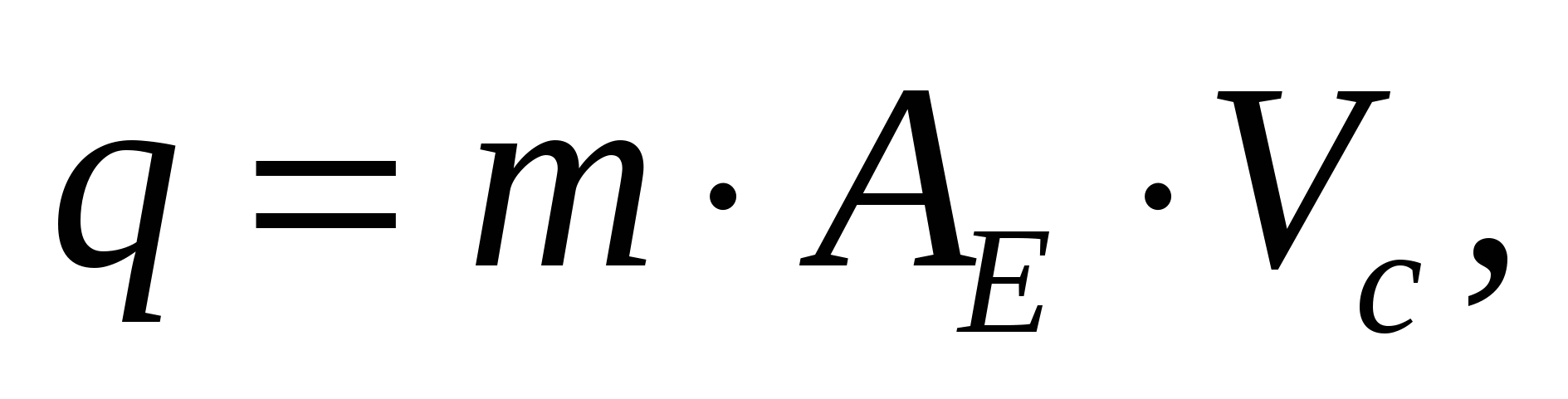 т/тәу, (3)
т/тәу, (3)
мұндағы АЕ — ерітінді (қоспа) ағын ен, АЕ=5 м;
Vc — сүзу жылдамдығы, Vc=2 м/тәу.
Сонда
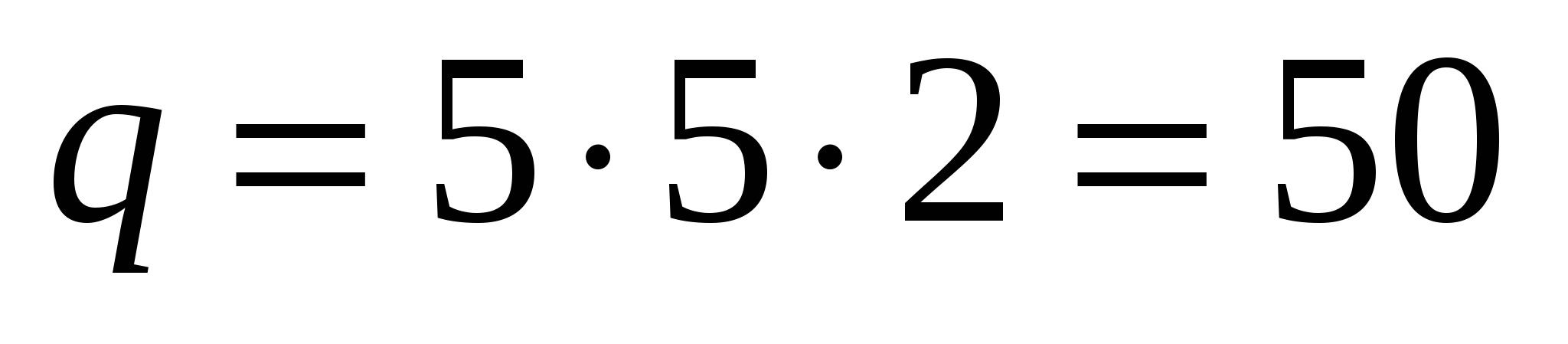 т/тәу.
т/тәу.
4. Бір мерзімде жұмыстағы төтелдер саны:
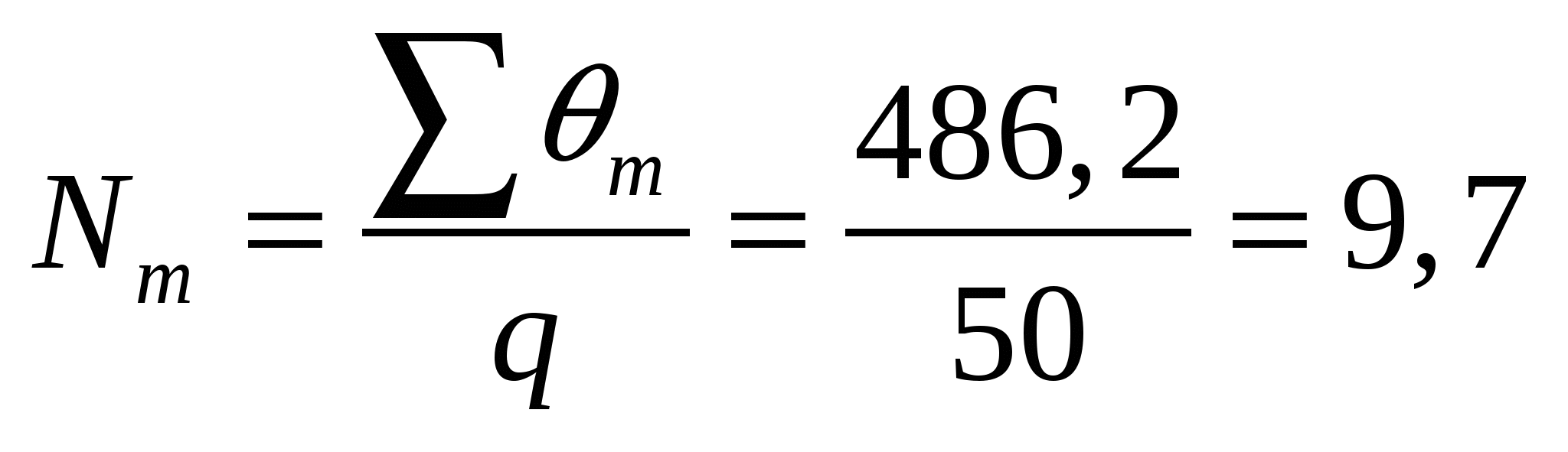 төтел. (4)
төтел. (4)
5. Бір төтел маңайындағы қорды қазу ұзақтылығы:
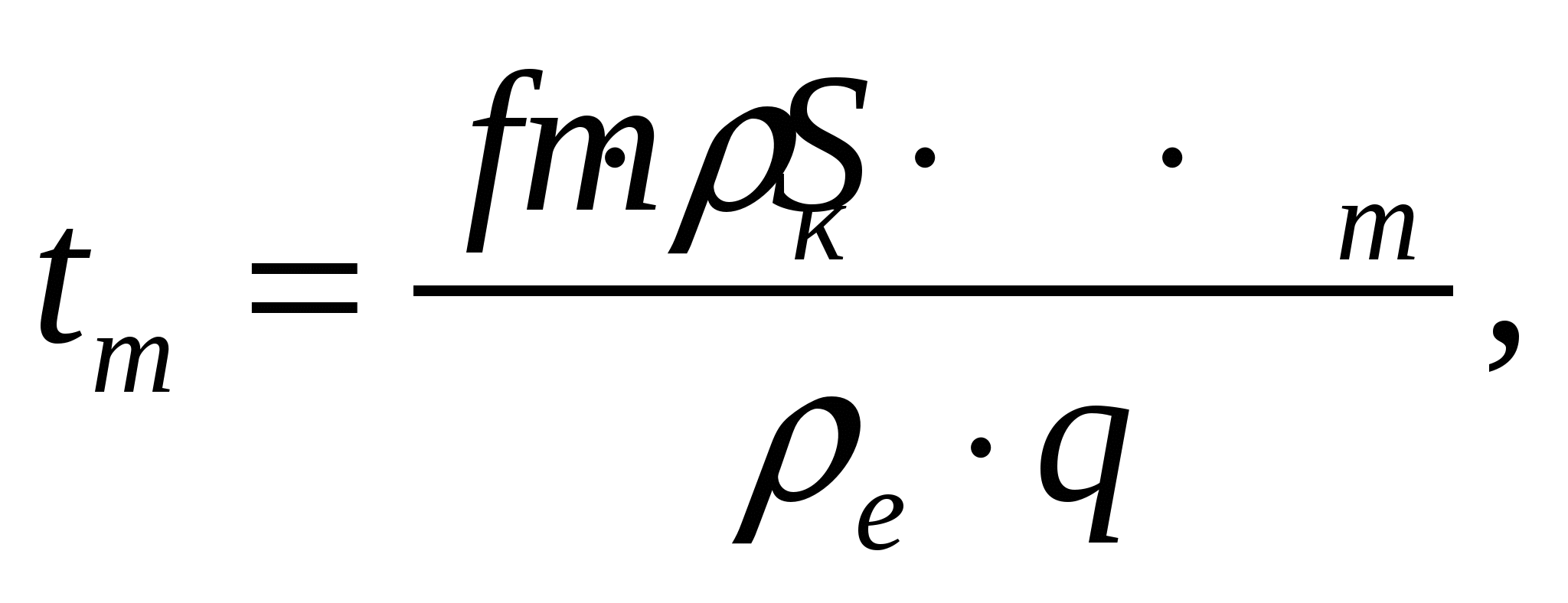 тәу, (5)
тәу, (5)
мұндағы Sт — төтел маңайындағы сілтілеу алаңы, Sт=150 м2.
Сонда
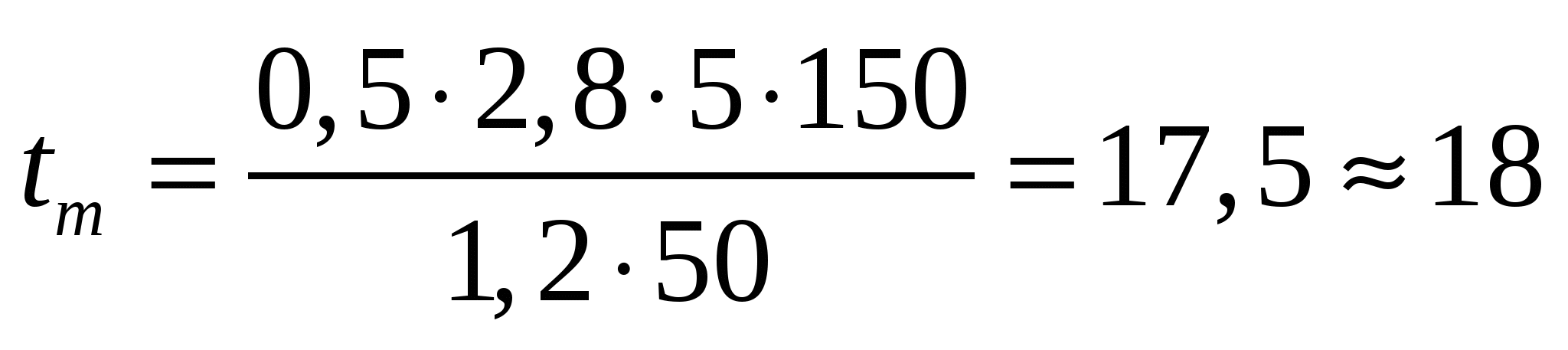 тәу.
тәу.
6. Шығару төтелдерде қоспаның пайда болу уақыты:
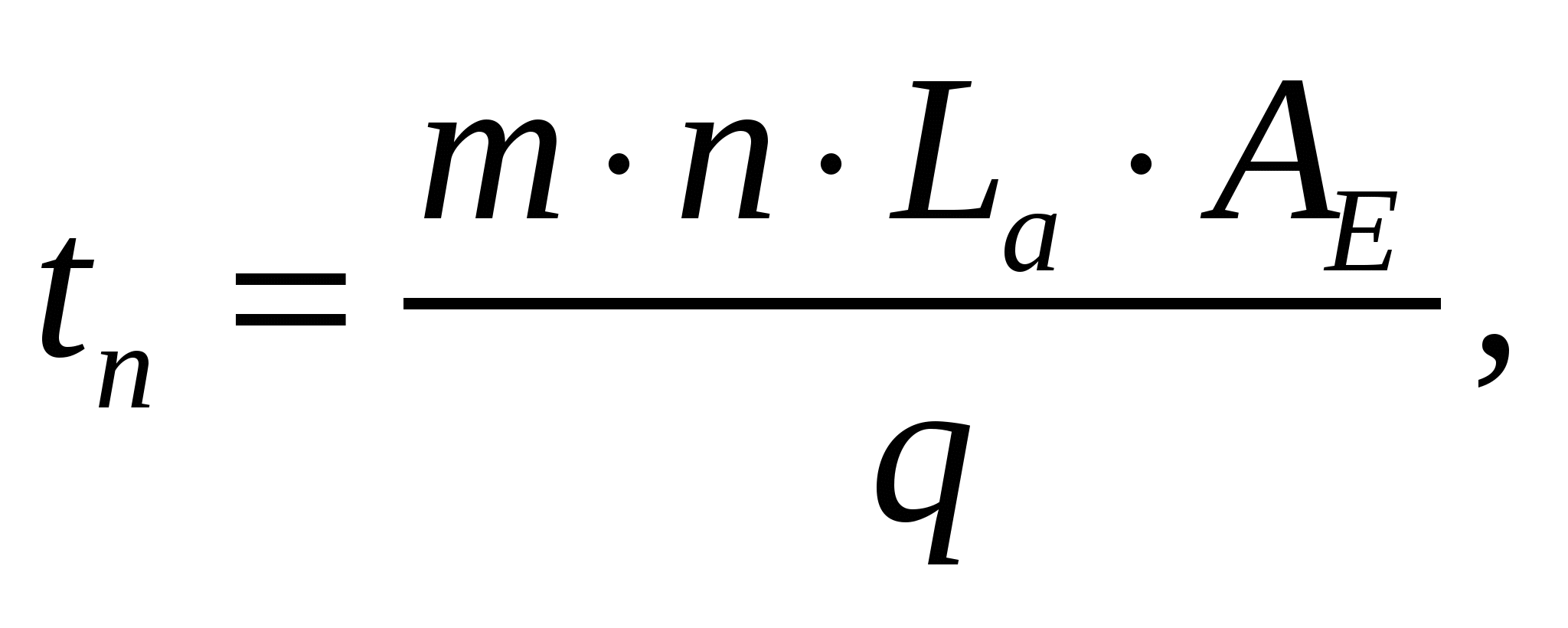 тәу, (6)
тәу, (6)
мұндағы п — тиімді жарықтану шамасы, п=0,4;
La — еріткіштің шоғырлану шамасы, La=10 м.
Сонда
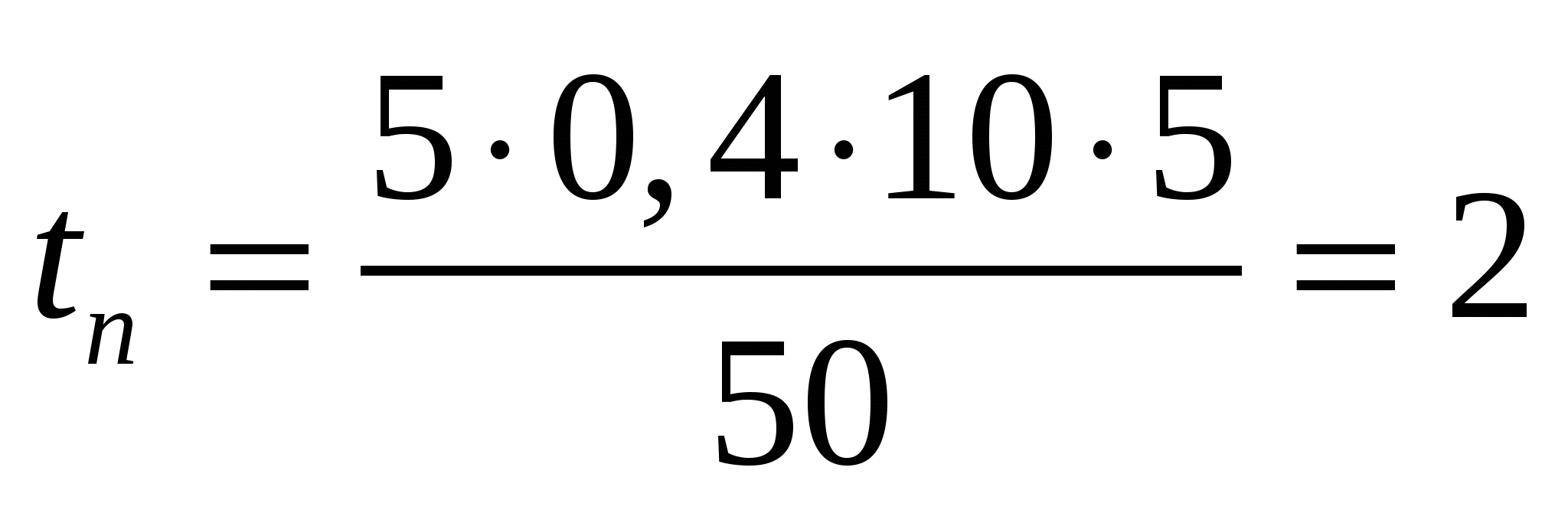 тәу.
тәу.
7. Қоспалардың өнімсіз көлемі:
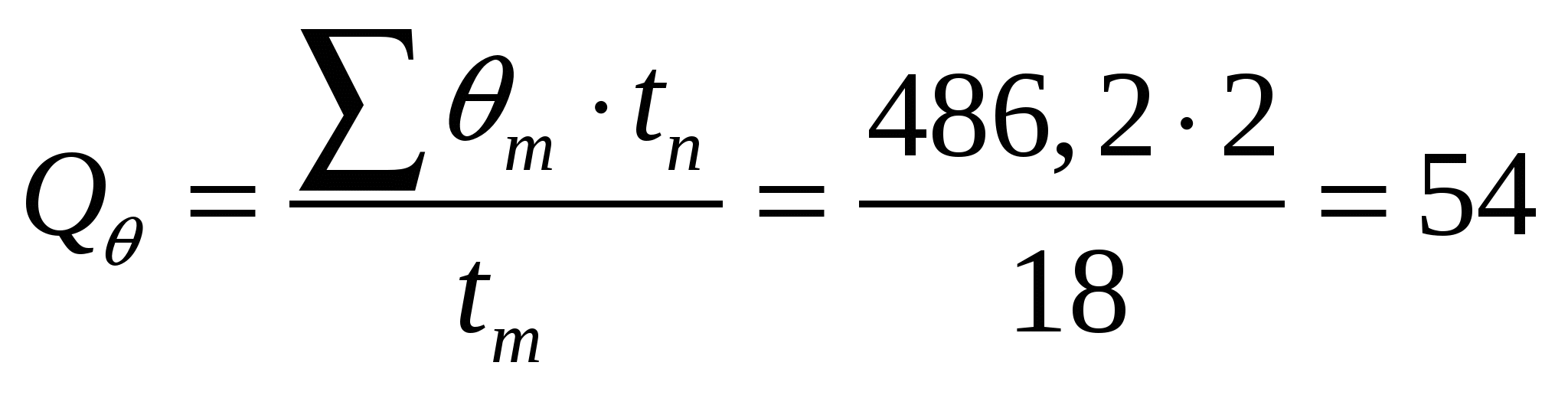 м3/тәу. (7)
м3/тәу. (7)
8. Ерітінді шығыны (керекті көлемі):
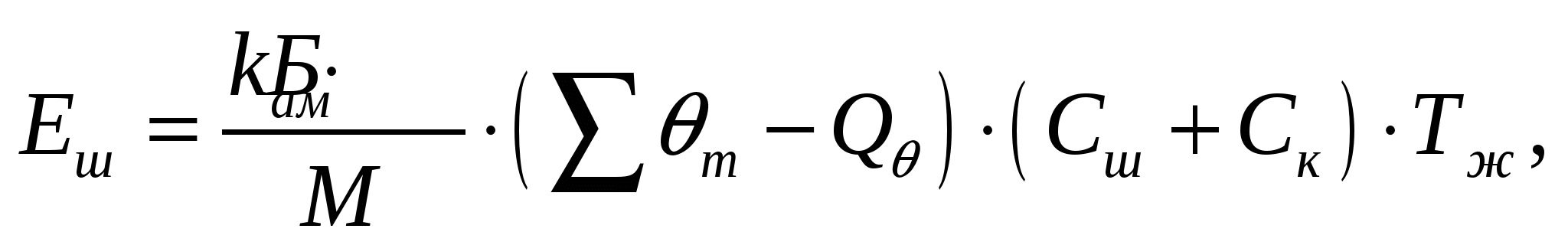 т, (8)
т, (8)
мұндағы Сш — еріткіштің шоғырлану шамасы, Сш=0,005;т
Ск — еріткіштің алынатын қоспадағы шоғырлану шамасы, Ск=0,002.
Сонда
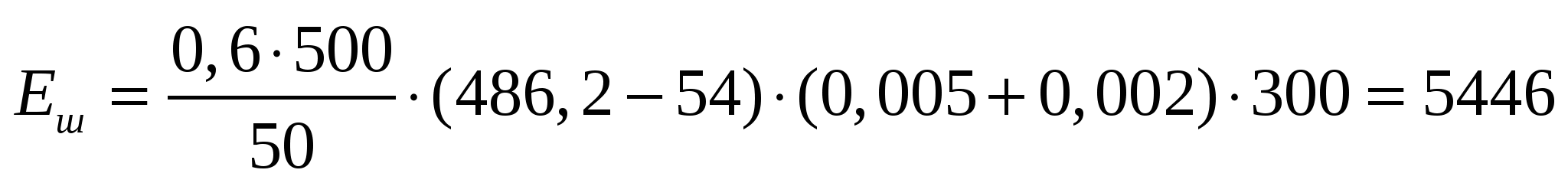 т.
т.
9. Нақты металдың шоғырлану шамасы:
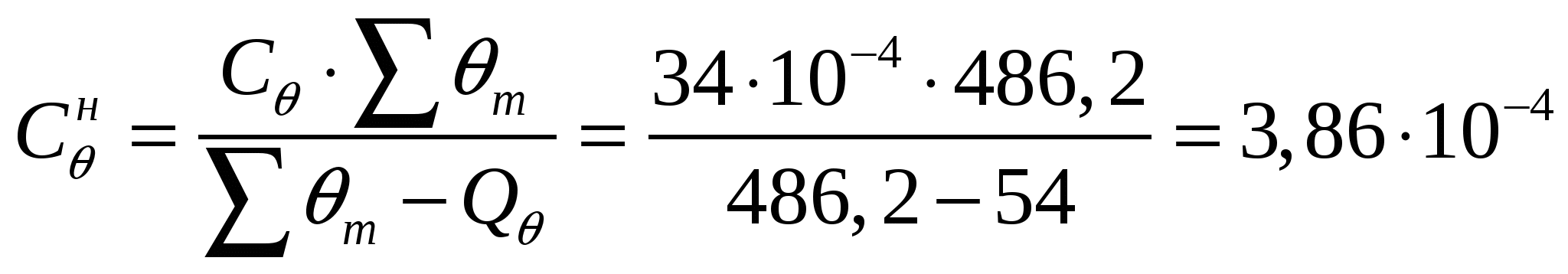 т/м3. (9)
т/м3. (9)
Есептелген көрсеткіштерді талдасақ, келесі түйін алуға болады:
- алынуға тиіс металл сілтілеу реагентінің осал сулы ерітінділерімен оңай бұзылатын минерал пішінінде кенде кездесуі керек, яғни, қышқылдың өзіндік шығыны анықталады;
- кеннің құрамына кіретін жыныстүзуші материалдар технологиялық ерітінділермен арақатынас шартында төмен қышқылсыйымдылықты болу керек;
- кендер не табиғи өткізгіш болуы керек, не болмаса жасанды уатудан кейін ерітіндіөткізгіш болуы керек, яғни, қопарылған блок кеніне қолдануы;
- кендердің жату шарттары және кен орнының аймағындағы тау-кен техникалық жағдай геотехнологияның барлық үдірістерін іске асыру үшін рационалды қолданылуы тиіс, яғни, төтелдердің саны, өнімділігі, шығарылған металл мөлшері мен құндылығы.