страница 1 страница 2 | страница 3 | страница 4
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ГОСУДАРСТВЕННЫЙ ИНСТИТУТ УПРАВЛЕНИЯ
И СОЦИАЛЬНЫХ ТЕХНОЛОГИЙ
Кафедра управления финансами и недвижимостью
ТАБЛИЧНЫЙ ПРОЦЕССОР
MICROSOFT EXCEL
Учебное пособие в 2-х частях
Часть 2. Лабораторный практикум
Минск
ГИУСТ БГУ
2009
А в т о р – с о с т а в и т е л ь:
Т. В. Борздова, кандидат технических наук, доцент
Утверждено Ученым советом
государственного института управления и социальных технологий БГУ
28 октября 2009 года, протокол № 2
Рецензенты:
кандидат экономических наук, доцент Кобзик Е. Г.
кандидат физико-математических наук, доцент Прокашева В. А.
Табличный процессор Microsoft Excel. Учебное пособие в 2-х частях. Часть 2. Лабораторный практикум// Сост. Т. В. Борздова. – Мн.: БГУ, 2009.– 65 c.
Часть 2 учебного пособия рассчитана на студентов 1 курса государственного института управления и социальных технологий. Она ориентирована на поддержку лабораторных и практических занятий по курсам “Информационные технологии” и “Основы информационных технологий”; содержит лабораторные работы, нацеленные на получение навыков использования программы Microsoft Excel, входящей в состав пользовательского пакета Microsoft Office. В нем также содержится перечень заданий для самостоятельной работы студентов.
УДК 330.115:681.14(075.8)
ББК 65с.я73
БГУ, 2009
ВВЕДЕНИЕ
Настоящее пособие предназначено для студентов Государственного института управления и социальных технологий Белорусского государственного университета и ориентировано на поддержку дисциплин “Основы информационных технологий”, “Современные информационные технологии” и “Информационные технологии”.
Часть 2 данного пособия – лабораторный практикум – состоит из одиннадцати лабораторных работ, предусматривающих освоение основных возможностей приложения Microsoft Excel. Каждая лабораторная работа содержит перечень индивидуальных заданий для выполнения, учитывающих будущую специализацию студентов.
Каждая лабораторная работа способствует закреплению и углублению знаний, полученных студентами на лекционных занятиях.
Данное пособие ориентировано на поддержку лабораторных и практических занятий в компьютерных классах; может также использоваться для самостоятельной работы, индивидуального и дистанционного обучения.
Лабораторная работа № 1. “СОЗДАНИЕ, ЗАПОЛНЕНИЕ
И РЕДАКТИРОВАНИЕ ТАБЛИЦ. АВТОЗАПОЛНЕНИЕ”
Задания
-
Выполнить следующие задания на первом листе рабочей книги, используя средство Автозаполнение с шагом 1:
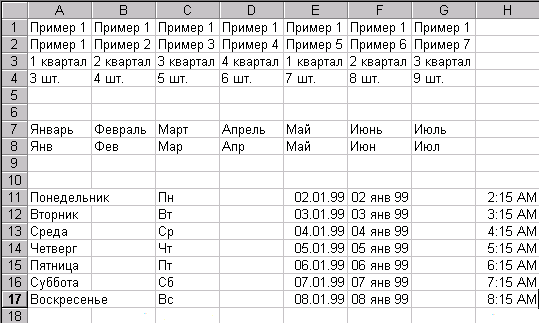
Дать листу имя Автозаполнение 1.
-
Выполнить следующие задания на втором листе книги, используя средство Автозаполнение с заданным шагом:
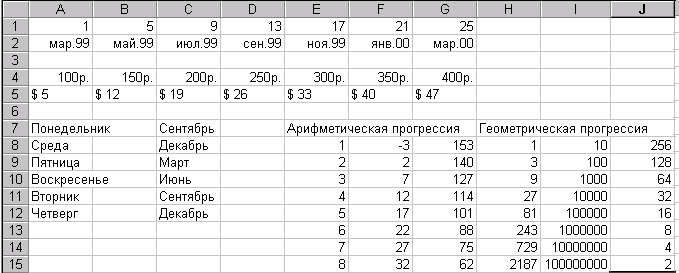
Дать листу имя Автозаполнение 2.
-
Создать на третьем листе следующие списки:
-
список городов-поставщиков фирмы;
-
список фирм-потребителей;
-
список отделов завода.
Дать листу имя Списки.
-
Используя средство Автозаполнение, на Листе 4 построить таблицу вычисления n-ого члена и суммы членов арифметической прогрессии (четвертый столбец в ней не заполнять).
Вычисление n-ого члена и
суммы членов
арифметической прогрессии
|
d
|
n
|
An
|
Sn
|
2
|
1
|
1
|
|
2
|
2
|
3
|
|
2
|
3
|
5
|
|
2
|
4
|
7
|
|
2
|
5
|
9
|
|
2
|
6
|
11
|
|
2
|
7
|
13
|
|
2
|
8
|
15
|
|
2
|
9
|
17
|
|
2
|
10
|
19
|
|
Дать листу имя Прогрессия.
-
Используя средство Excel Автозаполнение и Списки, на Листе 5 построить таблицу вида:
ОТЧЕТ
|
|
|
|
|
|
|
|
|
|
|
|
Март
|
Апрель
|
Май
|
Июнь
|
Июль
|
Август
|
Всего
|
|
Приход
|
32560
|
33038
|
33634
|
34037
|
34547
|
36066
|
|
|
Затраты на товары
|
19316
|
19490
|
19665
|
19842
|
20021
|
20201
|
|
|
Полная выручка
|
|
|
|
|
|
|
|
|
Статьи расходов
|
|
|
|
|
|
|
|
|
Реклама
|
4000
|
4000
|
4000
|
4000
|
4000
|
4000
|
|
|
Аренда помещений
|
500
|
500
|
500
|
500
|
500
|
500
|
|
|
Налоги и льготы
|
240
|
241
|
242
|
243
|
244
|
245
|
|
|
Проценты по кредитам
|
800
|
807
|
814
|
821
|
828
|
835
|
|
|
Расходы Всего
|
|
|
|
|
|
|
|
|
Прибыль
|
|
|
|
|
|
|
|
Дать листу имя Отчет.
-
Сохранить результат работы в своей папке под именем Лабораторная работа №1.
Лабораторная работа № 2. “ФОРМАТИРОВАНИЕ ТАБЛИЦ. ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ В ТАБЛИЦАХ.
АВТОСУММИРОВАНИЕ”
Задания
-
Открыть файл Лабораторная работа №1, открыть лист Прогрессия и скопировать таблицу с этого листа в новую книгу на Лист 1. Присвоить листу имя Прогрессия 1. Заполнить 4-ый столбец и отформатировать таблицу, воспользовавшись командой Автоформат.
Указание. Формула для вычисления суммы членов арифметической прогрессии: S=(a1 + an)*n/2
При конструировании формулы обратите внимание на использование абсолютного адреса для задания a1.
-
Составить на Листе 2 таблицу, аналогичную по структуре таблице из предыдущего задания (можно скопировать таблицу с листа Прогрессия 1), выписав в столбце 3 десять членов числовой последовательности по одному из следующих правил:
-
четные натуральные числа, не делящиеся на 4;
-
нечетные натуральные числа, делящиеся на 3;
-
натуральные числа, которые при делении на 10 дают остаток 9;
-
натуральные числа, делящиеся на 3 и 4;
-
натуральные числа, которые при делении на 7 дают остаток 3;
-
натуральные числа, которые при делении на 5 дают остаток 2;
-
четные натуральные числа, не делящиеся на 6;
-
нечетные натуральные числа, делящиеся на 9;
-
натуральные числа, делящиеся на 15;
-
натуральные числа, делящиеся на 45.
Присвоить листу имя Прогрессия 2.
При этом определить формулу для вычисления n-ого члена последовательности и использовать ее для вычисления значений в столбце 3.
Указание. Формула для вычисления n-ого члена арифметической прогрессии: an=a1+d(n-1).
Сохранить результат работы в своей папке под именем Лабораторная работа №2.
-
Открыть файл Лабораторная работа №1, открыть лист Отчет и скопировать таблицу с этого листа в новую книгу на Лист 3. Присвоить листу имя Отчет 1. Заполнить недостающие строки таблицы: "Полная выручка", "Расходы", "Всего", "Прибыль" и заполнить столбец "Всего".
Отформатировать таблицу, задав формат числовых данных в ячейках как в виде ###0 "тыс. руб.". Результат сохранить в своей папке в файле с именем Лабораторная работа №2.
-
Учетное ведомство фирмы "Запад" готовит десятилетний финансовый отчет. Необходимо оформить сведения за последние 10 лет в виде соответствующей таблицы и определить долю торговли от производства.
Для этого:
-
Ввести следующие данные в таблицу (на новом листе):
Фирма "Запад". Торговый оборот за 10 лет
Дата
Годовые показатели
Год
|
Торговля
|
Производство
|
Доля торговли
|
1998
|
66174
|
1230000
|
|
1999
|
86814
|
1260000
|
|
2000
|
113490
|
1300000
|
|
2001
|
125280
|
1350000
|
|
2002
|
145452
|
1380000
|
|
2003
|
178922
|
1370000
|
|
2004
|
200340
|
1400000
|
|
2005
|
262850
|
1500000
|
|
2006
|
299468
|
1690000
|
|
2007
|
350200
|
2000000
|
|
-
Присвоить листу имя Торговля и производство.
-
Просуммировать данные по показателям "Торговля" и "Производство".
-
Вычислить "Долю торговли".
Указание. При вычислении "Доли торговли" содержимое столбца "Торговля" делится на содержимое столбца Производство.
-
Отформатировать таблицу, применив к столбцам "Торговля" и "Производство" денежный формат, а к столбцу "Доля торговли" – процентный.
Таблица должна иметь следующий вид:
Год
|
Торговля
|
Производство
|
Доля торговли
|
1998
|
66 174тыс. руб.
|
1 230 000тыс. руб.
|
5,38%
|
1999
|
|
|
|
2000
|
|
|
|
2001
|
|
|
|
2002
|
|
|
|
2003
|
|
|
|
2004
|
|
|
|
2005
|
|
|
|
2006
|
|
|
|
2007
|
|
|
|
Всего
|
1 828 990тыс. руб.
|
14 480 000тыс. руб.
|
12,63%
|
Сохранить таблицу в своей папке в файле с именем Лабораторная работа №2.
-
Н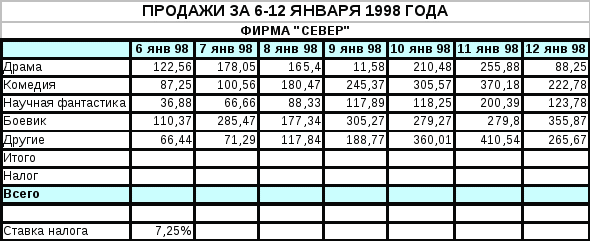
а новом листе книги с именем Север составить таблицу сведений о прибыли от продаж видеофильмов фирмы "Север" в следующем виде:
Замечание. При вычислении Налога использовать абсолютный адрес для ссылки на ячейку, содержащую %-ую ставку налога.
Результат сохранить в своей папке в файле с именем Лабораторная работа №2.
-
На листе с именем Автомобили создать таблицу и отформатировать ее:
Марка
|
4 – ый квартал 2008
|
4 – ый квартал 2009
|
Среднее
значение
|
| Объем |
Доля
|
Объем
|
Доля
|
|
БМВ
|
63
|
|
48
|
|
|
Форд
|
47
|
|
17
|
|
|
Мерседес
|
48
|
|
50
|
|
|
Пежо
|
31
|
|
23
|
|
|
Рено
|
22
|
|
12
|
|
|
Ауди
|
18
|
|
22
|
|
|
Опель
|
17
|
|
10
|
|
|
Феррари
|
12
|
|
7
|
|
|
Всего:
|
|
|
|
|
|
Для этого:
-
ввести формулы для вычисления сумм по столбцам 2 и 4;
-
вычислить "Долю" как отношение соответствующего объема продаж к значению "Всего";
-
вычислить "Среднее значение" как среднее между объемами продаж.
Результат сохранить в своей папке в файле с именем Лабораторная работа №2.
-
На листе Книги заполнить и отформатировать следующую таблицу:
Список книг, купленных в январе
-
№ п/п
|
Название
|
Цена за единицу
|
Количество
|
Стоимость в долл.
|
Стоимость в
бел. руб.
|
1
|
Маринина А.
"Чужая маска"
|
8,3
|
10
|
|
|
2
|
Бенцони Ж.
"Марианна"
|
7,2
|
8
|
|
|
3
|
Кинг Ст.
"Ночная смена"
|
14,2
|
20
|
|
|
4
|
Шелдон С.
"Расколотые сны"
|
10,0
|
15
|
|
|
5
|
Шелдон С.
"Интриганка"
|
12,0
|
25
|
|
|
6
|
Леонов Н.
"Бросок кобры"
|
8,9
|
29
|
|
|
7
|
Леонов Н.
"Стервятники"
|
8,4
|
30
|
|
|
8
|
Словин Л.
"Расстояние в
один вечер
|
6,3
|
22
|
|
|
9
|
Чейз Дж. Х.
"Мертвые молчат"
|
9,2
|
36
|
|
|
10
|
Незнанский Ф.
"Последний
маршал"
|
7,1
|
20
|
|
|
Для этого:
-
вычислить "Стоимость в долларах";
-
вычислить "Стоимость в бел. руб." следующими способами:
-
ввести в некоторую ячейку значение "Курса доллара" и использовать адрес этой ячейки в расчетах;
-
присвоить ячейке, содержащей "Курс доллара", имя и использовать его в расчетах.
Результат сохранить в своей папке в файле с именем Лабораторная работа №2.
-
Финансовая задача.
Постановка задачи.
В сберегательном банке имеются два вида денежных вкладов: простой и сложный (иногда называется капитализированным). Простой вклад составляет P1, сложный - Р2 процентов в месяц. При простом вкладе проценты начисляются от первоначально вложенной суммы S0. При сложном вкладе очередное начисление осуществляется по итогам предыдущего, т.е. происходит начисление процентов на проценты.
Исследуйте финансовую модель для ответа на вопросы:
-
Каким вкладом и в какие сроки выгодно пользоваться?
-
Каков будет ответ на предыдущий вопрос, если начиная с K-ого месяца, простой процент увеличился до S1, а сложный упал до S2?
-
Когда при таких изменениях сумма сложного вклада достигнет M рублей?
-
Когда сумма сложного вклада увеличится в 1,5 раза?
-
Проведите исследования для S0=1 000 000 руб; Р1=6; Р2=4; S1=6,5; S2=3,5; K=4; М=2 000 000.
Математическая модель.
Для поиска зависимости между исходными и конечными данными построим цепочку равенств:
Простой вклад
|
Сложный вклад
|
А0=S0
|
В0=S0
|
А1=А0+А0*Р1/100
|
B1=B0(1+P2/100)
|
А2=А1+А0*Р1/100
|
B3=B1(1+P2/100)
|
…
|
…
|
АN=AN-1+A0*P1/100
|
BN=BN-1(1+P2/100)
|
Соотношение простого и сложного вкладов через N месяцев определяется знаком разности АN - BN.
Математическая постановка задачи: Определить значение N, при котором изменяется знак разности АN - BN .
-
Экологическая задача.
Постановка задачи.
В результате сброса промышленных стоков возрос уровень загрязнения реки. Каким он будет через сутки, двое, трое и т.д. и через сколько суток уровень загрязнения воды станет допустимым, если известно, что за сутки он уменьшается в К раз, начальная концентрация вредных примесей С0, предельно допустимая концентрация примесей – Сдоп.
Провести исследование экологической модели при следующих значениях параметров:
Вещество
|
C0(мг/л)
|
Cдоп(мг/л)
|
K
| |
Свинец
|
5
|
0,03
|
1,12
|
Мышьяк
|
1,5
|
0,05
|
1,05
|
Фтор
|
0,2
|
0,05
|
1,01
|
-
Задача "Преступность и судимость".
На листе Преступность и судимость заполнить таблицу "Соотношение уровней зарегистрированных преступлений, выявленных правонарушителей и осужденных в России в 1985– 1997 годах":
Годы
|
Зарегистр.
преступления
|
Выявленные правонарушители
|
Осужденные
|
|
|
Абс.
число
|
%
к престу-
плениям
|
Абс.
число
|
%
к престу-
плениям
|
%
к право-
наруши-
телям
|
1985
|
1416935
|
1154496
|
|
837310
|
|
|
1986
|
1338424
|
1128439
|
|
797286
|
|
|
1987
|
1185914
|
969338
|
|
580074
|
|
|
1988
|
1220361
|
834673
|
|
427039
|
|
|
1989
|
1619181
|
847577
|
|
436988
|
|
|
1990
|
1839451
|
897229
|
|
537643
|
|
|
1991
|
2167964
|
956258
|
|
593823
|
|
|
1992
|
2760652
|
1148962
|
|
661392
|
|
|
1993
|
2799614
|
1262735
|
|
792410
|
|
|
1994
|
2632708
|
1441562
|
|
924754
|
|
|
1995
|
2755669
|
1595501
|
|
1035807
|
|
|
1996
|
2625081
|
1618394
|
|
1111097
|
|
|
1997
|
2397311
|
1372161
|
|
1007776
|
|
|
Отформатировать таблицу. Результат сохранить
Результат сохранить в своей папке в файле с именем Лабораторная работа №2.
Лабораторная работа №3. “Функции и сложные вычисления в Excel”
Задания
-
На листе “Функции” выполнить следующие ниже задания.
-
Вычислить в ячейках строки 1:
Sin 37o, Cos 25o, Tg 132o
-
Вычислить в ячейках строки 2:
Ln 5,25; Log2372,3; e7,05
-
Составить таблицу значений чисел
7,2293; -18,992971; 15,32143,
округленных обычным способом, с недостатком и с избытком. Сохранить при этом 3 знака после запятой.
-
Вывести в свободную ячейку сегодняшнюю дату.
-
Определить, каким днем недели было:
2 февраля 1907 года;
14 декабря 1938 года;
5 января 1992 года;
6 апреля 1996 года.
-
Решить следующие ниже финансовые задачи на листе “Задачи”.
-
Кредит взят на 6 лет под 28% годовых. Величина кредита 15000000. Подсчитать ежемесячные выплаты по кредиту.
-
Организации необходим кредит в сумме 10000000. Банк дает кредит под 39% годовых. Ежемесячно организация может выплачивать 425000. За сколько месяцев (лет) можно рассчитаться за кредит?
-
Станок стоит 15000000. После 4 лет работы его остаточная стоимость составляет 7000000. Подсчитать величину амортизационных выплат.
-
Предположим, что мы хотим получать доход, равный 10 млн. руб. в год, на протяжении четырех лет. Какая сумма обеспечит получение такого дохода, если ставка по срочным депозитам равна 10 % годовых?
-
Рассчитать величину ежегодного взноса на погашение кредита в сумме 40000 тыс. руб., предоставленного на 15 лет под 20% годовых.
-
Для обеспечения будущих предполагаемых расходов решено создать фонд. Для этого на счет в банке при ставке 15% годовых поступают взносы в виде постоянной ренты в течение 5 лет. Размер разового годового платежа 5 млн. руб. Определить размер фонда.
Результат сохранить в своей папке в файле с именем Лабораторная работа №3.
-
Выполнить следующее задание.
Создать на листе Погода в марте таблицу, структура которой представлена ниже.
ПОГОДА 1 МАРТА
|
|
|
Минск
|
Гродно
|
Брест
|
Гомель
|
Витебск
|
Могилев
|
Орша
|
Баранович
|
Бобруйск
|
Борисов
|
Москва
|
Санкт-Петербург
|
Киев
|
Рига
|
Вильнюс
|
Таллинн
|
|
Температура, по С
|
-5
|
-7
|
-9
|
-6
|
-3
|
0
|
0
|
2
|
4
|
-1
|
-6
|
-12
|
2
|
3
|
-1
|
5
|
|
Осадки
|
с
|
с
|
н
|
н
|
н
|
н
|
н
|
д
|
н
|
д
|
с
|
с
|
д
|
н
|
с
|
н
|
|
С - снег; Д - дождь; Н - без осадков
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Выделить средствами Excel цветом самый холодный день – синий цвет;
|
|
|
самый теплый – красный; нулевая температура – желтый
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Вычислить, используя формулы и функции:
|
|
|
|
1) среднюю температуру для всех городов списка;
|
|
|
|
|
|
|
|
|
|
2) количество городов, где шел снег;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) количество городов, где шел дождь;
|
|
|
|
|
|
|
|
|
|
|
|
|
4) каких городов больше: с положительной или с отрицательной температурой;
|
|
|
5) сколько городов имели температуру ниже средней;
|
|
|
|
|
|
|
|
|
|
6) сколько городов с отрицательной температурой было в Беларуси.
|
|
|
|
|
|
7) сколько городов с отрицательной температурой было в России.
|
|
|
|
|
|
8) сколько городов с отрицательной температурой было в Прибалтике.
|
|
|
|
|
9) среднюю температуру для всех городов Беларуси;
|
|
|
|
|
|
|
|
|
|
10) среднюю температуру для всех городов России;
|
|
|
|
|
|
|
|
|
|
11) среднюю температуру для всех городов Прибалтики.
|
|
|
|
|
|
|
|
|
Указание. При выполнении задания использовать условное форматирование, функции ЕСЛИ, СЧЕТЕСЛИ, СУММЕСЛИ.
IV. Выполнить следующее задание на таблицы, размещенные на разных листах.
Фирма осуществляет многостороннюю деятельность – торгово-закупочные операции, оказание услуг сторонним организациям др. Для учета всех видов операций ведется следующая документация:
-
список товаров и услуг, оказываемых фирмой, заданный таблицей 1:
Список товаров и услуг фирмы
|
|
| |
Код товара
|
Наименование товара и услуг
|
Характеристика
|
Цена у. е.
|
1
|
Компьютер
|
Pentium-133
|
800,5
|
2
|
Монитор
|
15''
|
113
|
3
|
Установка ПО
|
Microsoft Office
|
24
|
4
|
Замена платы
|
|
5,4
|
5
|
Мука
|
Высш. сорт
|
255
|
6
|
Окраска пола
|
Краска имп.
|
38,7
|
7
|
Сахар
|
Украина
|
19
|
-
список фирм-заказчиков, заданный таблицей 2:
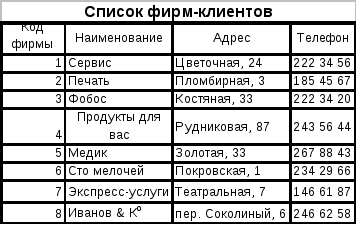
-
список договоров на поставку товаров и оказание услуг, заданный таблицей 3:
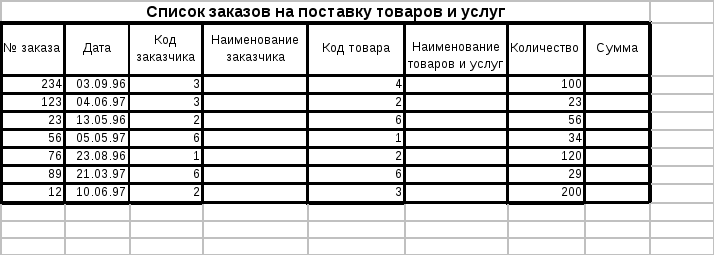
Выполнить следующие задания:
-
Создать "Таблицу 1" на листе "Товары".
-
Создать "Таблицу 2" на листе "Клиенты".
-
Создать "Таблицу 3" на Листе "Заказы".
-
Заполнить в таблице 3 столбцы 4, 6 и 8, используя информацию из таблицы 1 и таблицы 2, содержащихся на других листах.
-
Результат сохранить в своей папке в файле с именем Лабораторная работа №3.
Указание. Использовать функции ЕСЛИ и ПРОСМОТР в следующем виде:
-
для столбца 4 в ячейке D3:
=ЕСЛИ(С3<>"";ПРОСМОТР(С3;КЛИЕНТЫ!$A$3:$A$10; КЛИЕНТЫ!$B$3:$B$10));
-
для столбца 6 в ячейке F3:
=(С3<>"";ПРОСМОТР(С3;ТОВАРЫ!$A$3:$A$9;ТОВАРЫ!$B$3:$B$9))
-
для столбца 8 в ячейке H3:
=ПРОСМОТР(Е3;ТОВАРЫ!$A$3:$A$9;ТОВАРЫ!$D$3:$D$9)*G3.
V. Подготовить отчет о работе склада торгового дома "Олимп".
-
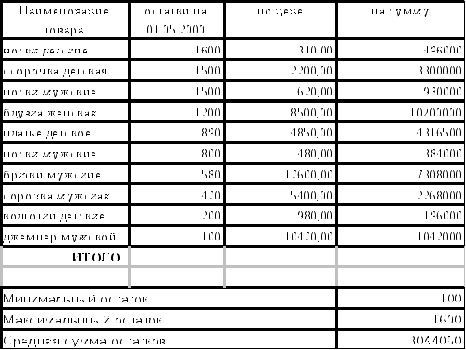
Для этого необходимо создать таблицу по приведенному ниже образцу и выполнить в ней соответствующие расчеты.
-
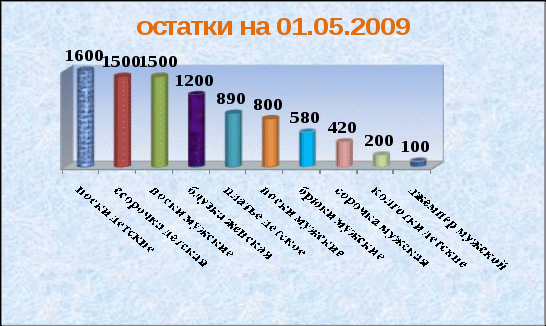
Под таблицей следует поместить диаграмму с названием «Остатки товаров на складе» согласно образцу.
Сведения о наличии товаров по складу №1
Лабораторная работа №4. “Функции и
сложные вычисления в Excel” (часть II)
Задания
Подготовить таблицу расчета зарплаты сотрудникам фирмы по следующей форме:
Ведомость зарплаты сотрудникам фирмы за январь 2009 года

Исходными данными при этом являются:
-
№ п/п;
-
ФИО;
-
должность;
-
оклад;
-
количество отработанных дней.
Эта исходная информация извлекается из файла, подготовленного в Word преподавателем, и "расщепляется" по столбцам в Excel с помощью Мастера текстов.
Дальнейшие вычисления проводятся в соответствии со следующими требованиями:
-
Начисления:
-
За отработанные дни.
Значение зарплаты за отработанные дни вычислить, используя абсолютный адрес. Ввести в некоторую свободную ячейку (например, О1) значение числа рабочих дней в месяце.
-
Премия.
Значение премии вычислить по следующему алгоритму:
премия равна 10% от "Начислено за отработанные дни", если отработал полный месяц, и 0 – в противном случае.
-
Другие начисления.
Значения в этом столбце подсчитать по следующему алгоритму:
другие начисления равны 5 000, если отработал полный месяц и оклад меньше среднего оклада по списку, и 0 – в противном случае. Тогда вычислить в некоторой ячейке (например, Р1) средний оклад по списку (статистическая функция СРЗНАЧ), присвоить имя СРЕДНИЙ_ОКЛАД ячейке Р1 и использовать его в формуле.
-
Всего.
Вычисляется как сумма всех начислений.
-
Удержания:
-
Подоходный налог.
Ставки подоходного налога:
до 52 800 руб.
|
9%
|
от 52 801 до 132 000 руб.
|
4 752+15% с суммы, превышающей 52 800
|
от 132 001 до 184 800 руб.
|
16 632+20% с суммы, превышающей 132 000
|
от 184 801 до 237 600 руб.
|
27 192+25% с суммы, превышающей 184 800
|
от 237 601 руб. и выше
|
40 392+30% с суммы, превышающей 237 600
|
-
Профсоюзный и пенсионный фонды.
Значения в столбцах вычисляются как 1% от "Всего начислено".
-
Всего.
Значения в столбце вычисляются как сумма всех удержаний.
-
К выдаче.
Значения в столбце вычисляются как разность между "Всего начислено" и "Всего удержано".
Лабораторная работа №5. “Построение и редактирование диаграмм, графиков и поверхностей”
Задания
-
На листе Графики построить графики функций, приведенных ниже, используя диаграмму типа График и Точечную диаграмму. Результаты сравнить.
-
y=x^3+2x^2+2
-
y=sin x
-
y= -6x^2+3x
-
y=1/x
-
y=ln(x-1)+5
-
y=|cos x|
-
y=|x|+3
-
3+2/(x-4)
-
y=1/(x^2+2x+1)
Результат сохранить в файле с именем Лабораторная работа №5.
-
Для таблицы, сформированной на листе "Преступность и судимость" в файле Лабораторная работа №2, по данным ее первого, второго, третьего и пятого столбцов построить графики, отражающие динамику основных криминологических показателей в России за 1985 – 1997 годы. Изменить на каждом графике маркеры значений данных и установить для каждого графика свою толщину линии.
-
Для таблицы, сформированной на листе "Торговля_и_Производство" в файле Лабораторная работа №2, выполнить следующие задания:
-
используя данные Год, Торговля, Производство за последние 10 лет, построить объемную гистограмму на отдельном листе с именем Развитие торговли;
-
отредактировать диаграмму:
-
изменить подтип гистограммы, чтобы ряды данных размещались один перед другим;
-
вставить основную сетку по всем трем осям диаграммы;
-
сместить легенду под область построения диаграммы;
-
ввести заголовок "Развитие торговли по отношению к производству за последние 10 лет";
-
изменить данные в некоторой строке и посмотреть, что произойдет с диаграммой;
-
вставить в таблицу новую строку и посмотреть, что произойдет с диаграммой;
-
по данным "Год" и "Доля" торговли построить круговую диаграмму на отдельном листе с именем "Доля_Торговли";
-
отредактировать диаграмму:
-
нанести на диаграмму показатели значений к каждому участку диаграммы;
-
выдвинуть участок круговой диаграммы, соответствующий самому большому значению Доли торговли.
-
Для таблицы "Продажа видеофильмов", сохраненной в файле Лабораторная работа №2, выполнить следующие задания:
-
построить объемную гистограмму с накоплением "Продажа видеофильмов за первые 3 дня по категориям" (по оси категорий – категории фильмов, по оси значений – число продаж по дням);
-
построить круговую диаграмму "Продажи за 6 января 1998 года", отображающую итоги продажи видеофильмов за 6 января 1998 года;
Результат сохранить в файле с именем Лабораторная работа №5.
Следующие задания выполняются по вариантам.
Номер варианта выполняемого задания совпадает с номером по списку группы (если номер по списку >10, то отнять от номера число 10, если номер по списку >20, то отнять от номера число 20).
Вариант 1
-
Построить в разных системах координат при 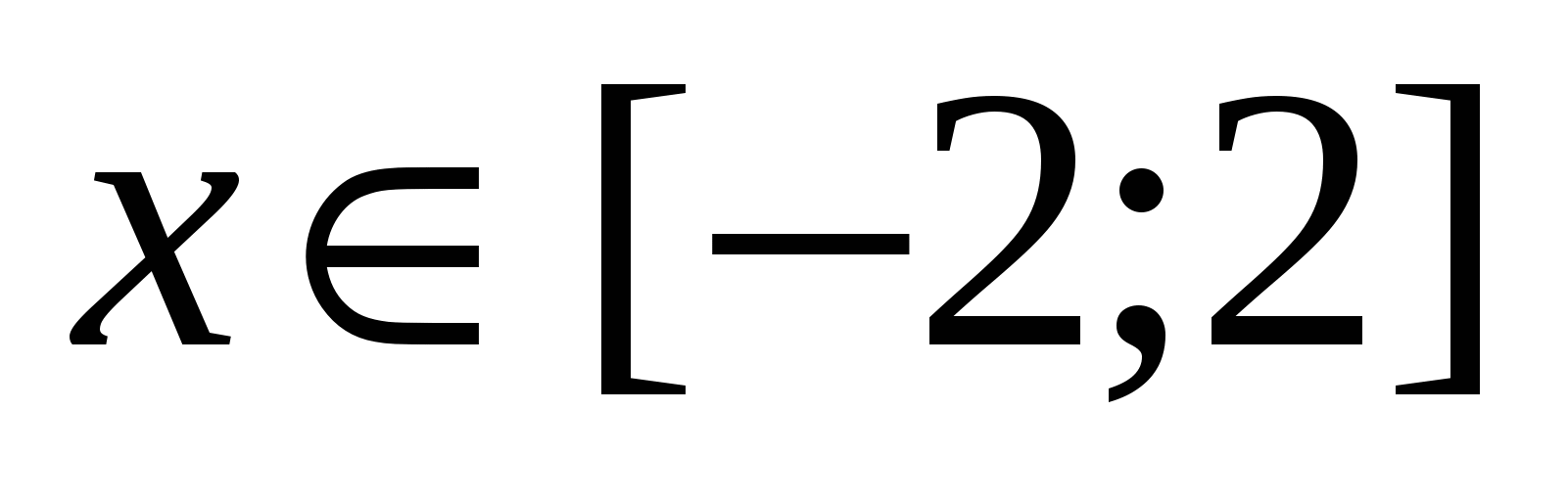 графики функций: графики функций:
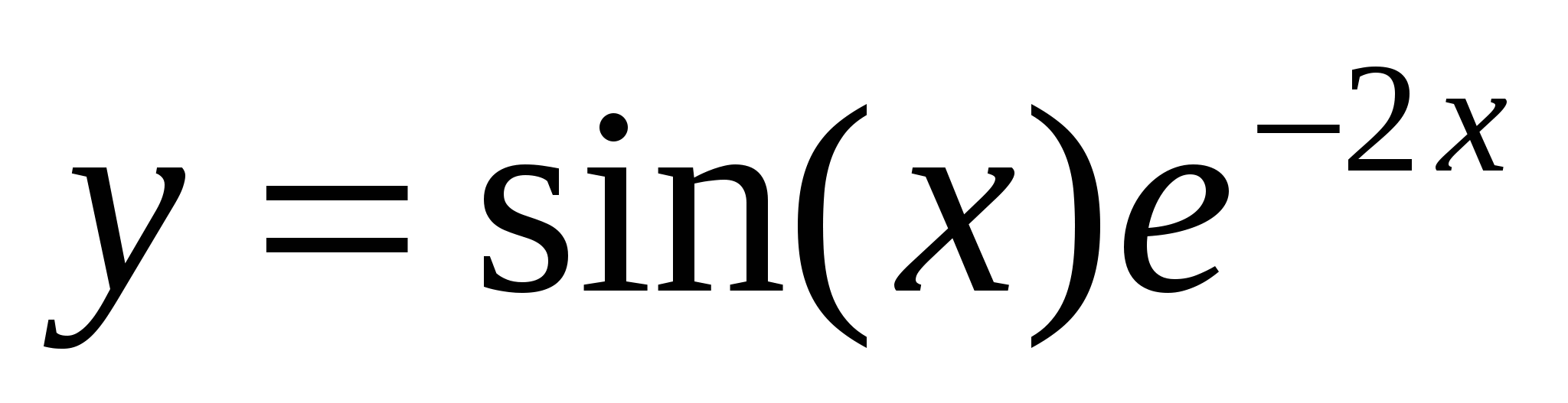
 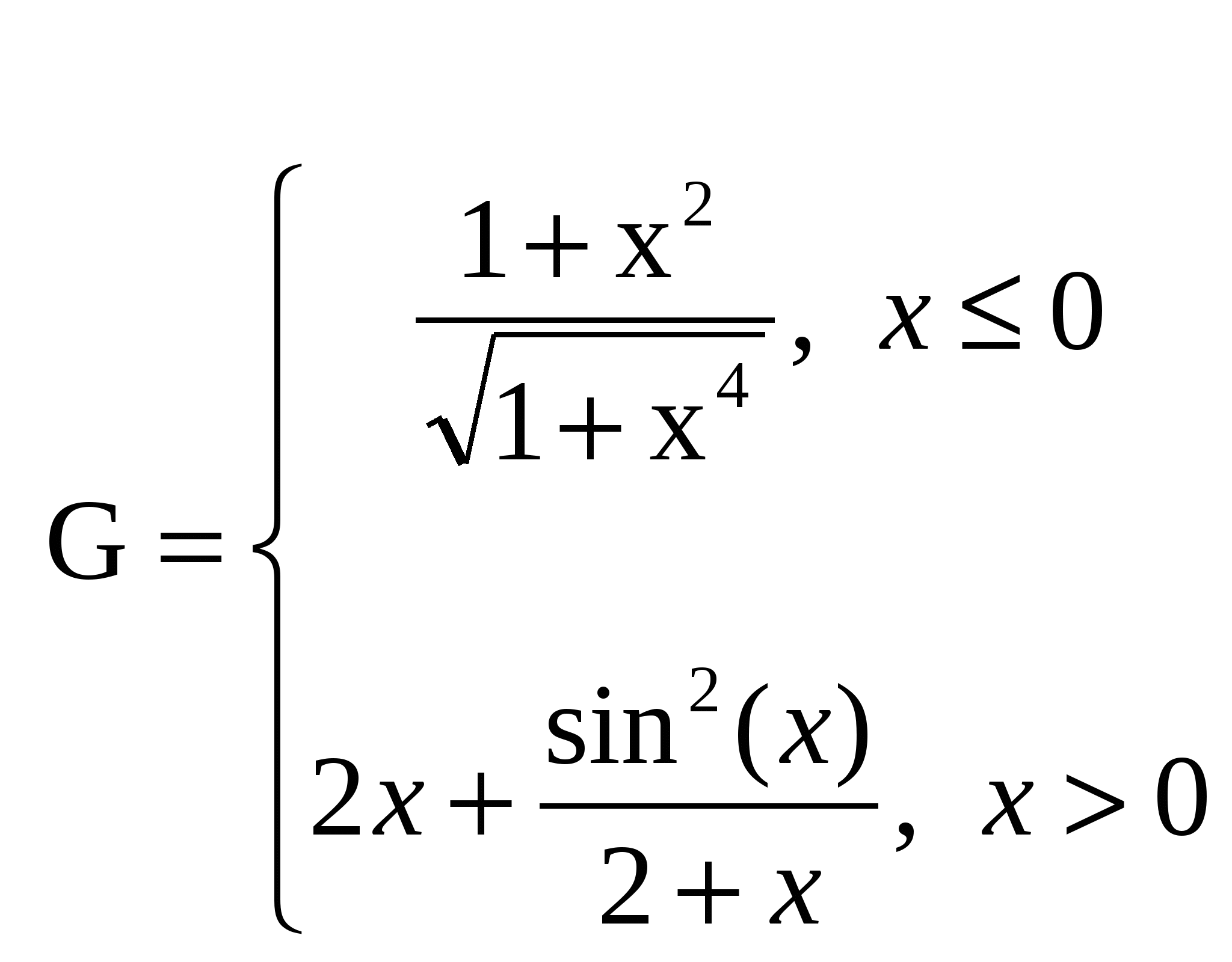 
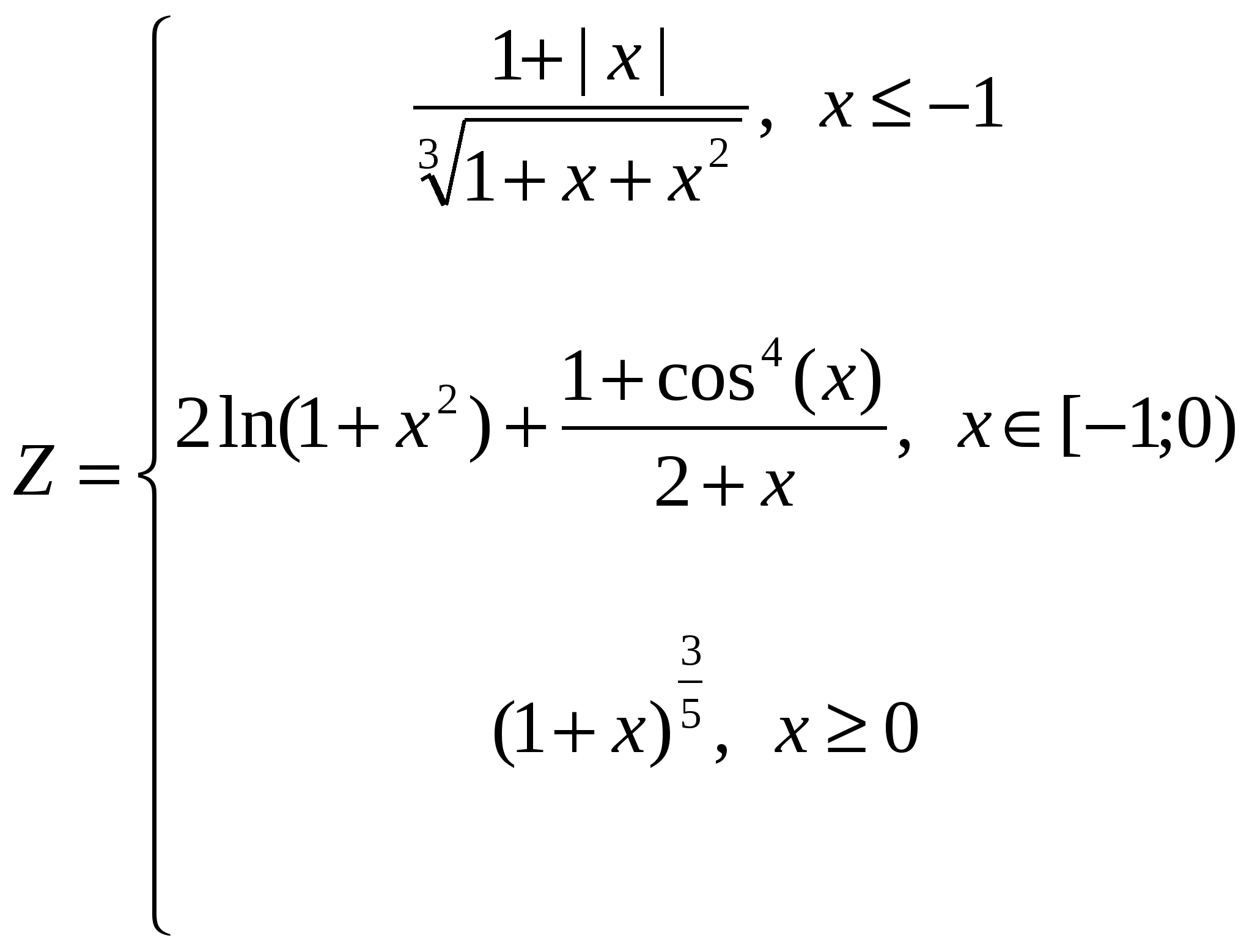
-
Построить в одной системе координат при 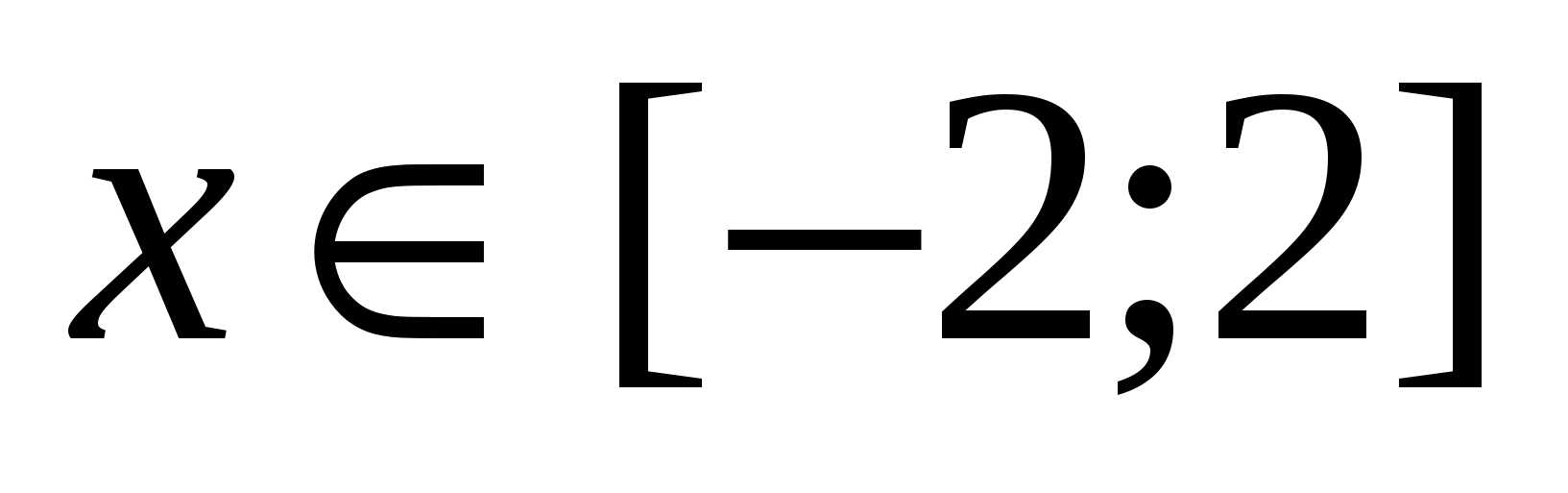 графики функций: графики функций:
-
Y=2sin(x)cos(x);
-
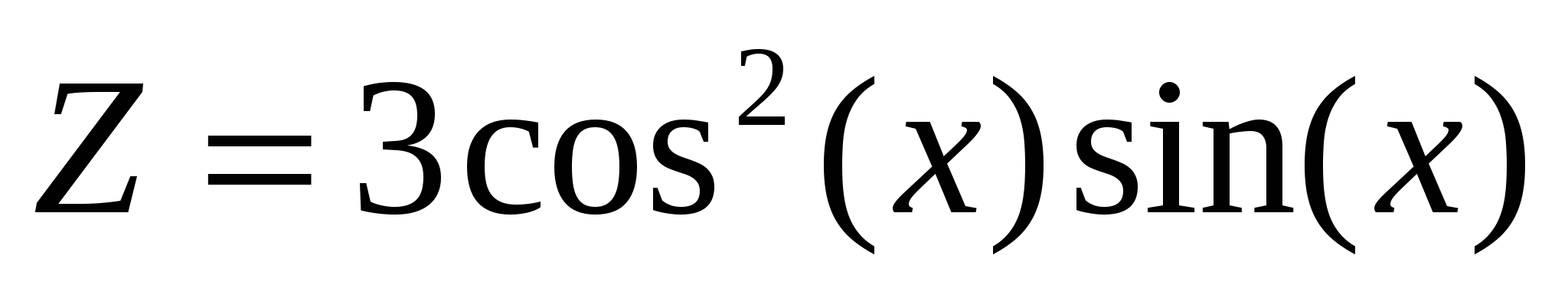 . .
-
Построить поверхность 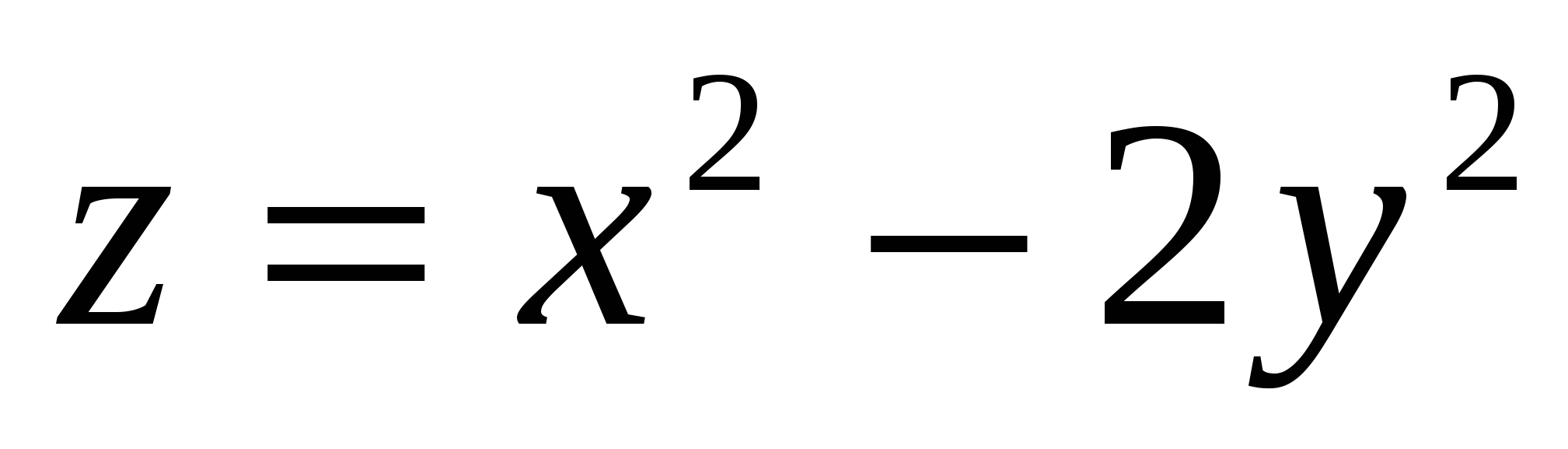 при при 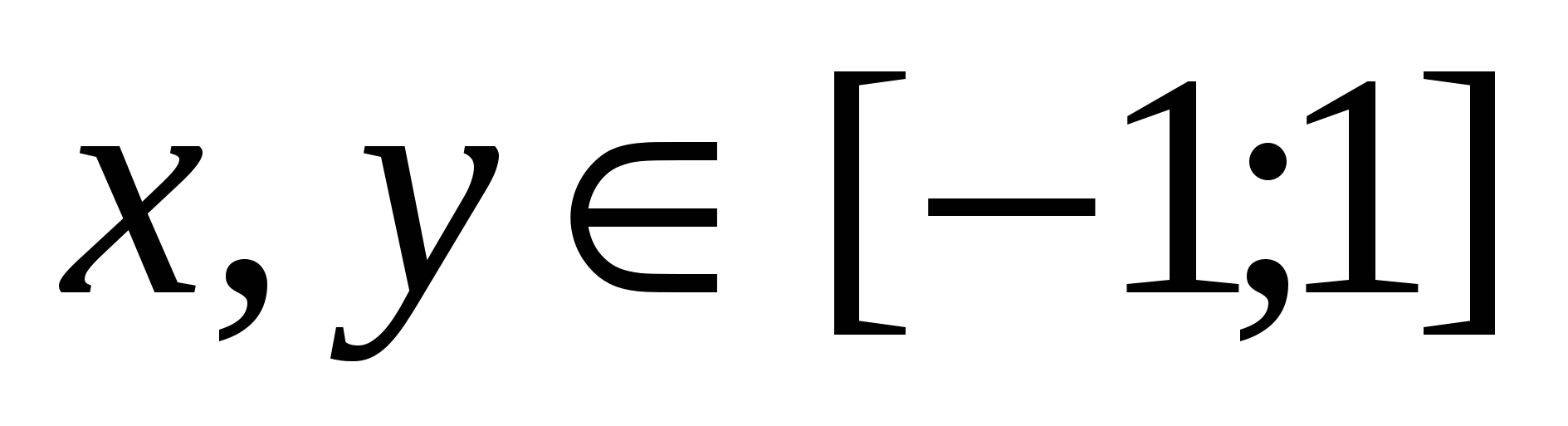 . .
Вариант 2
-
Построить в разных системах координат при 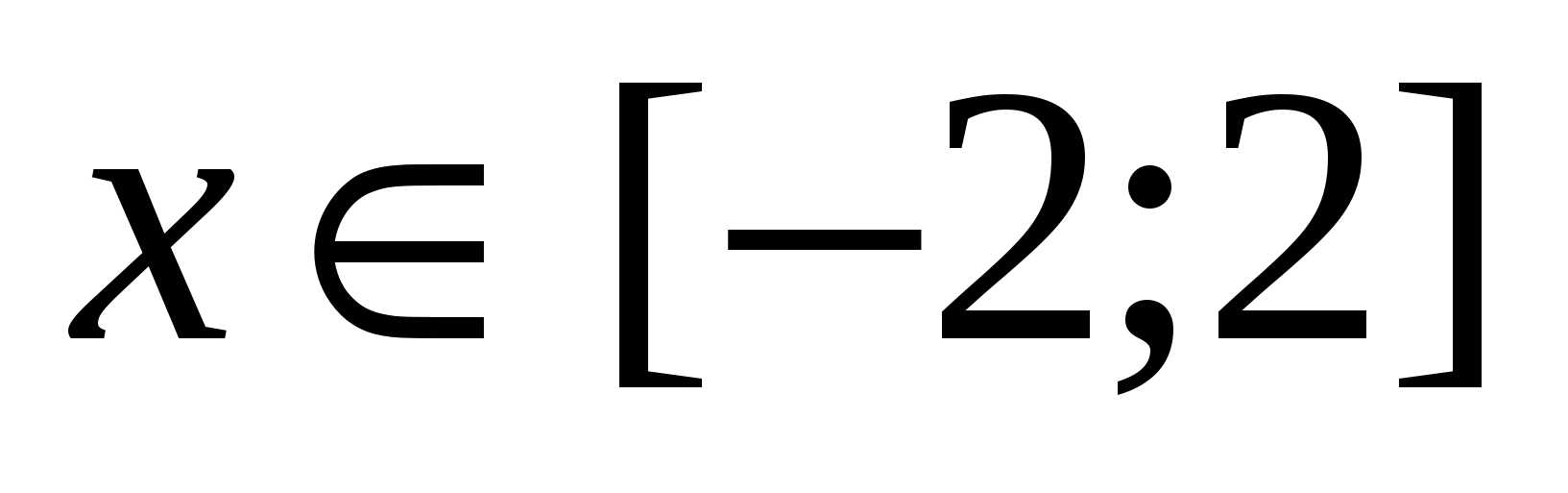 графики функций: графики функций:
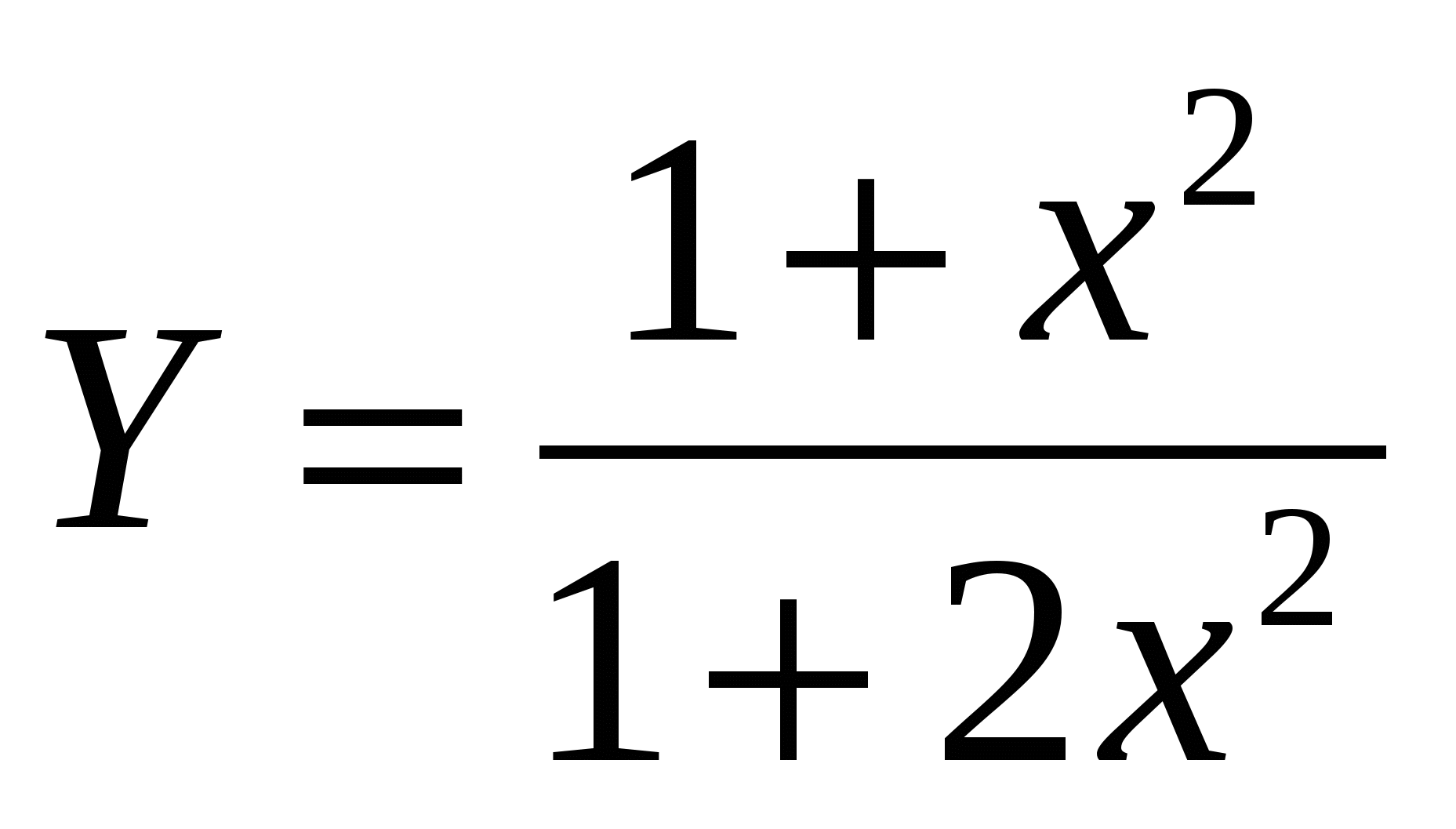
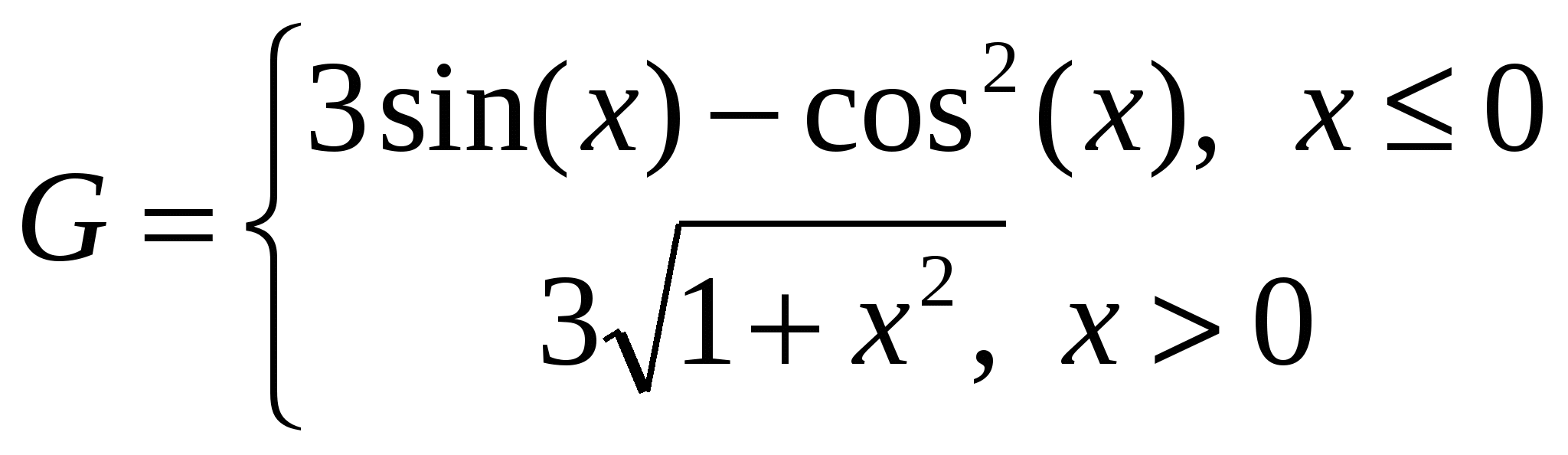
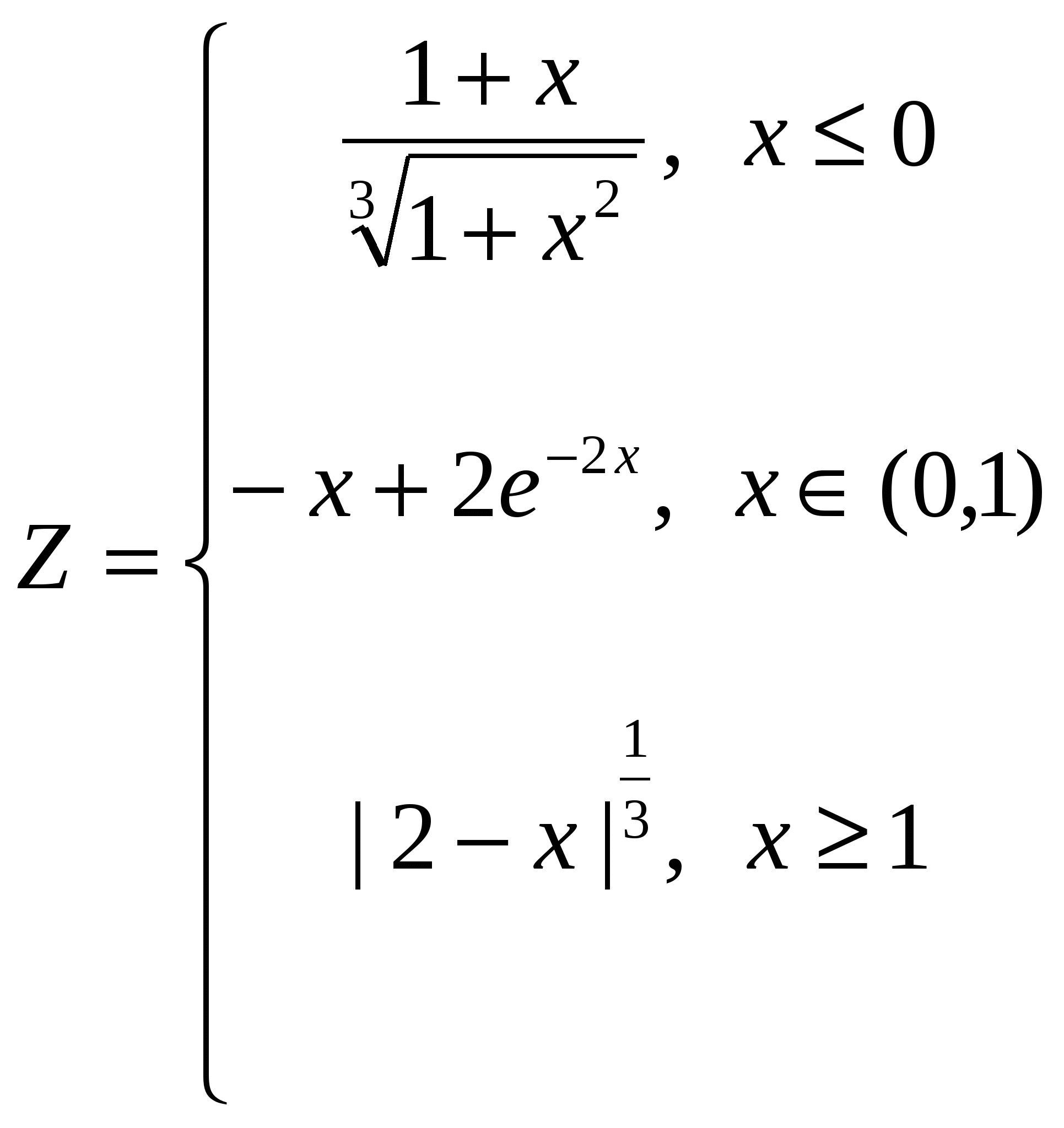
-
Построить в одной системе координат при 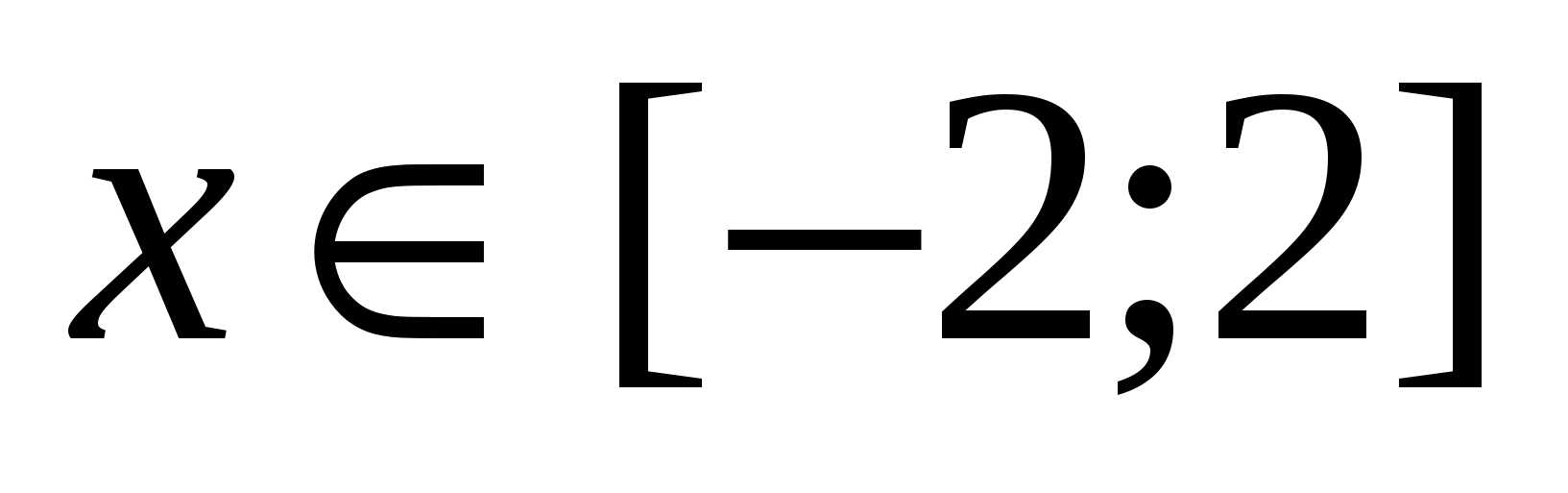 графики функций: графики функций:
-
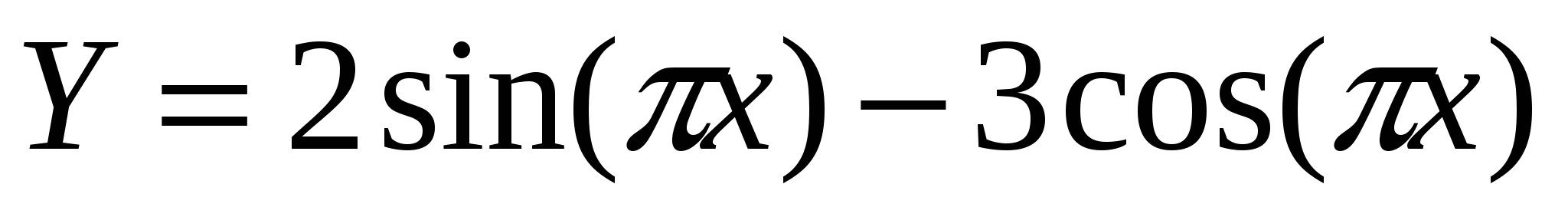
-
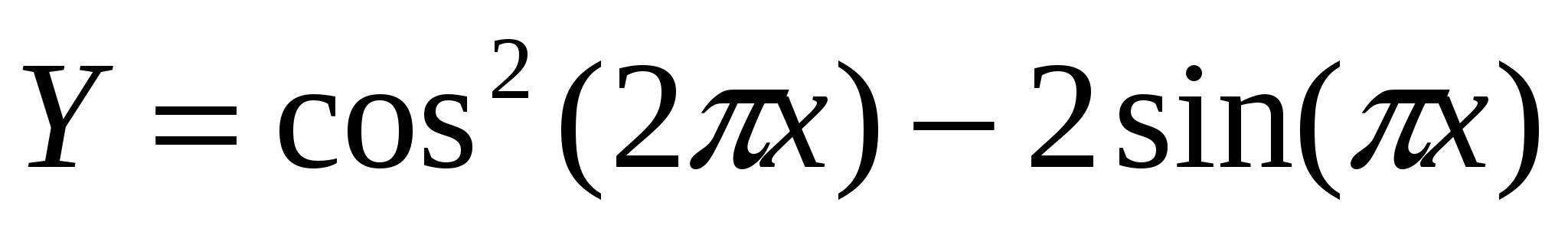 . .
-
Построить поверхность 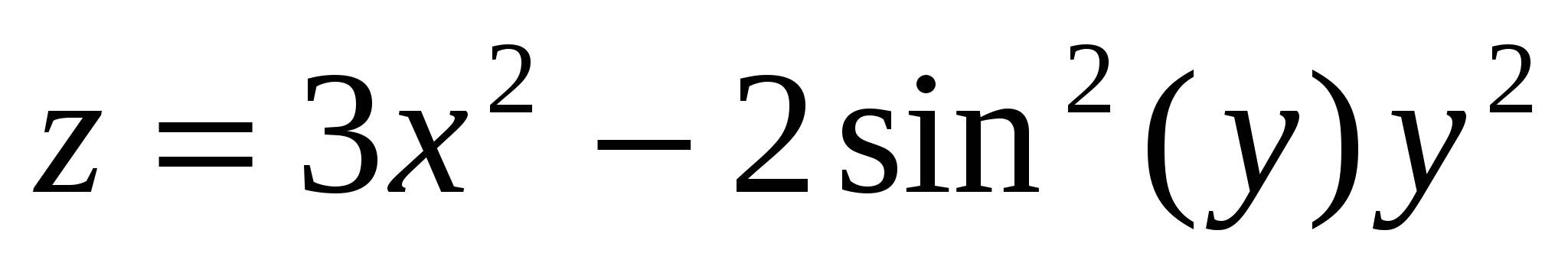 при при 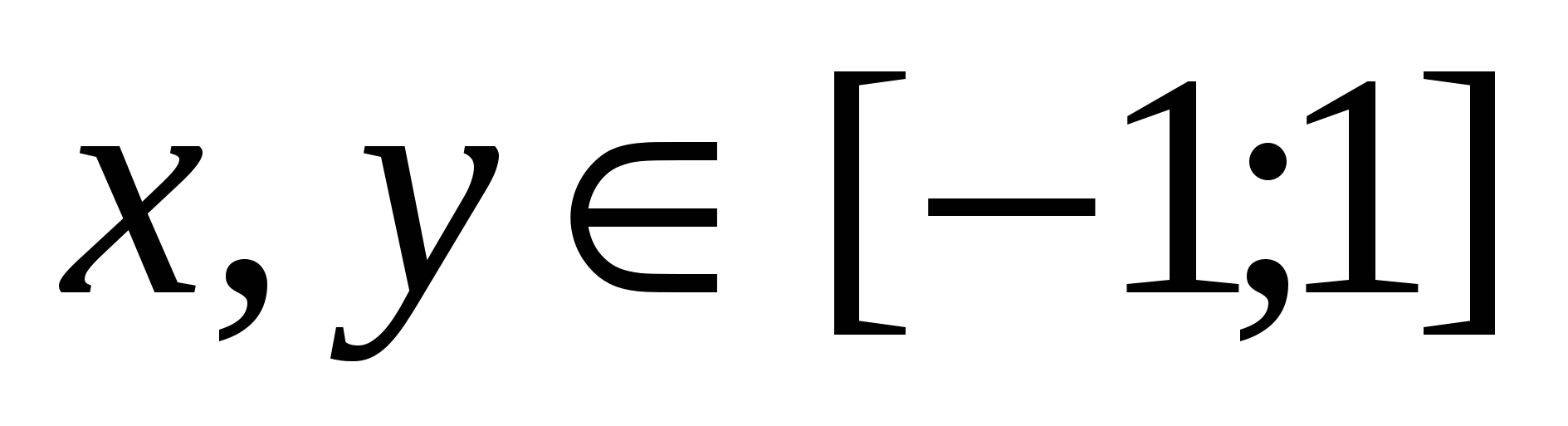 . .
Вариант 3
-
Простроить в разных системах координат при 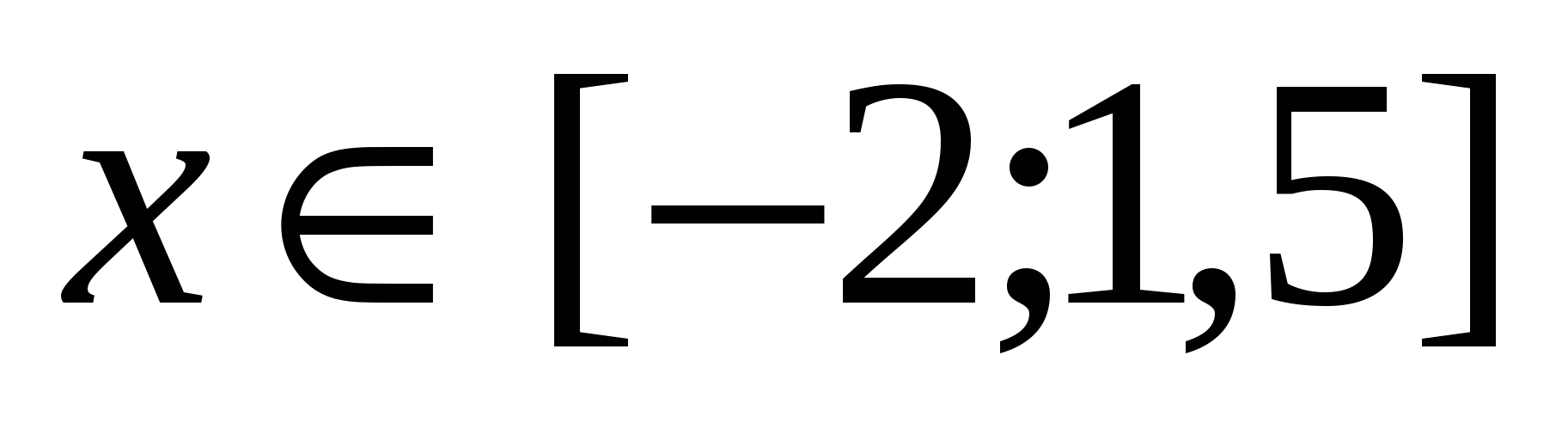 графики функций: графики функций:
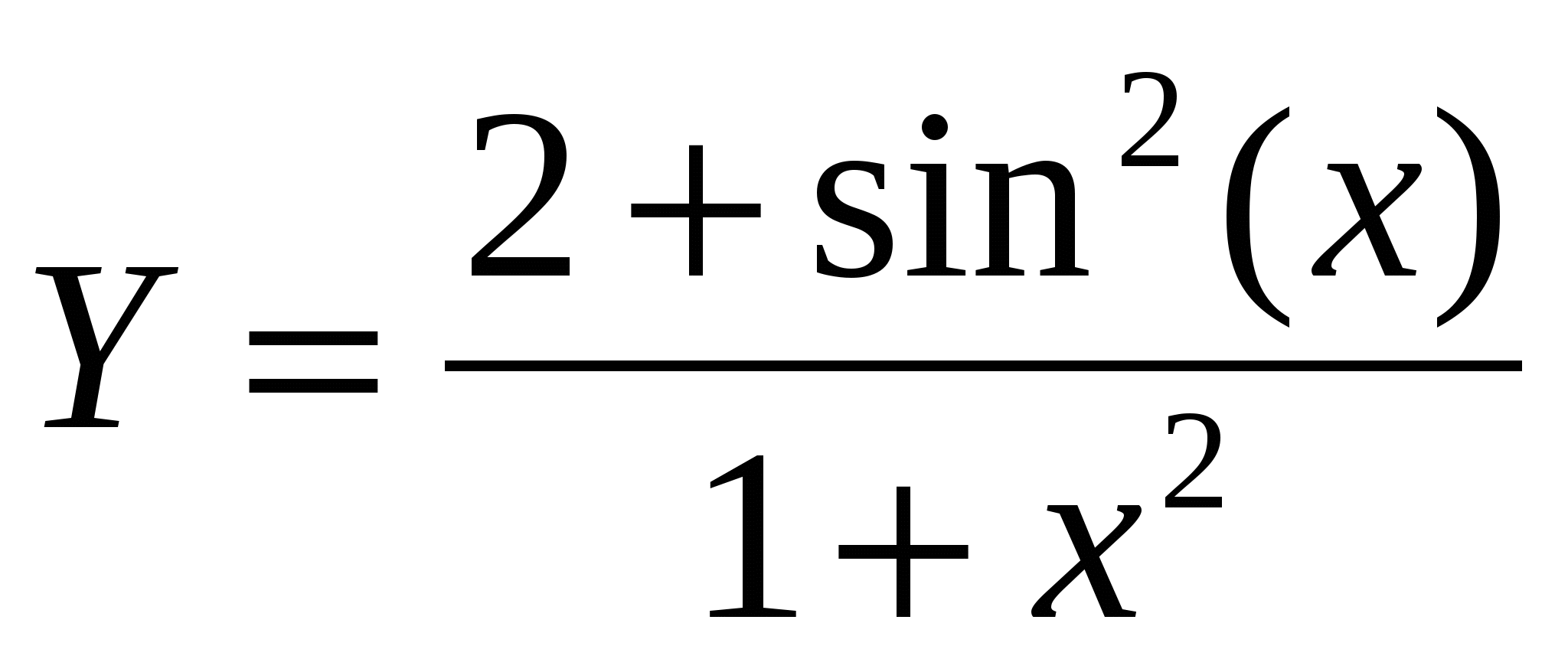
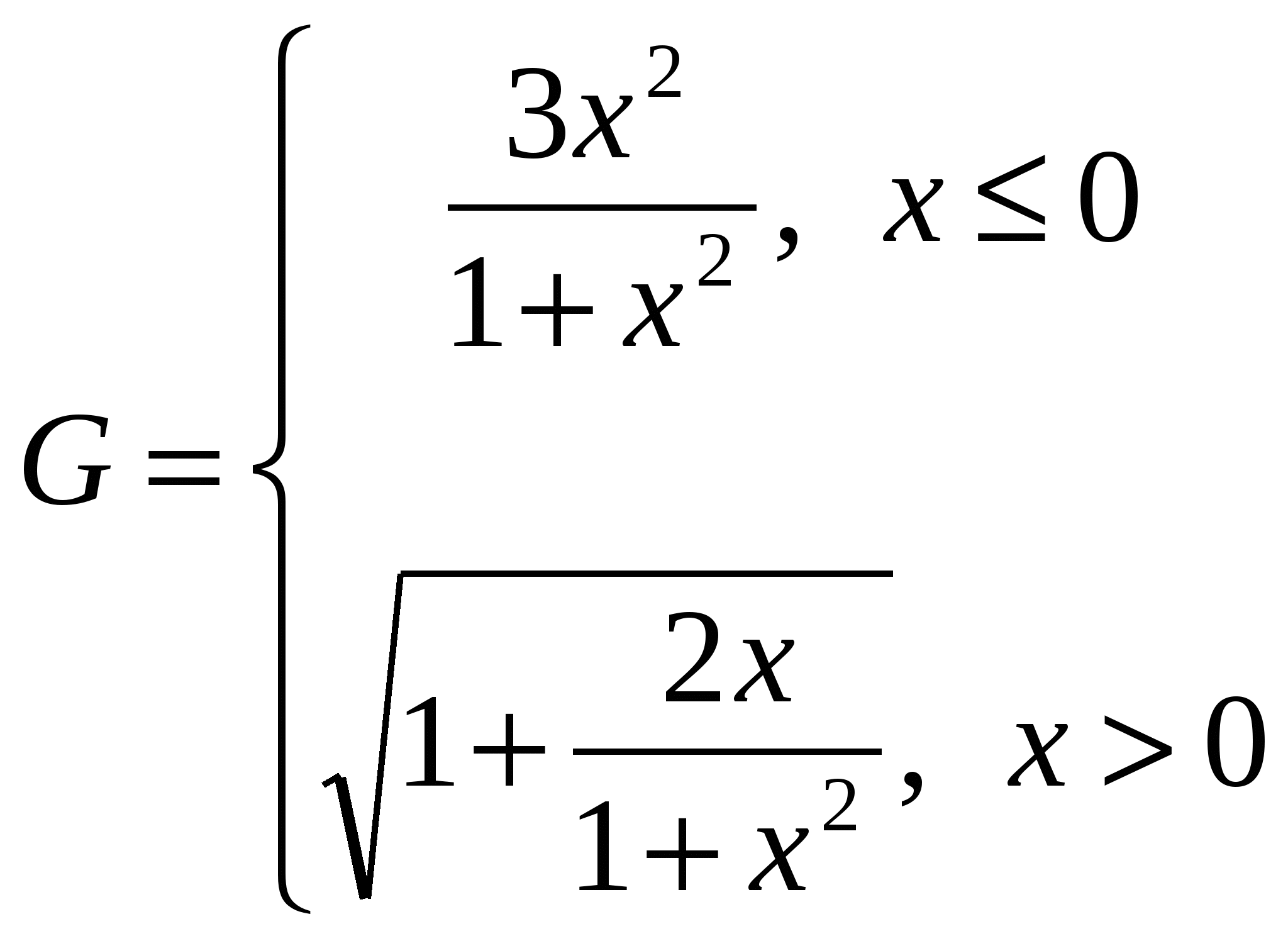
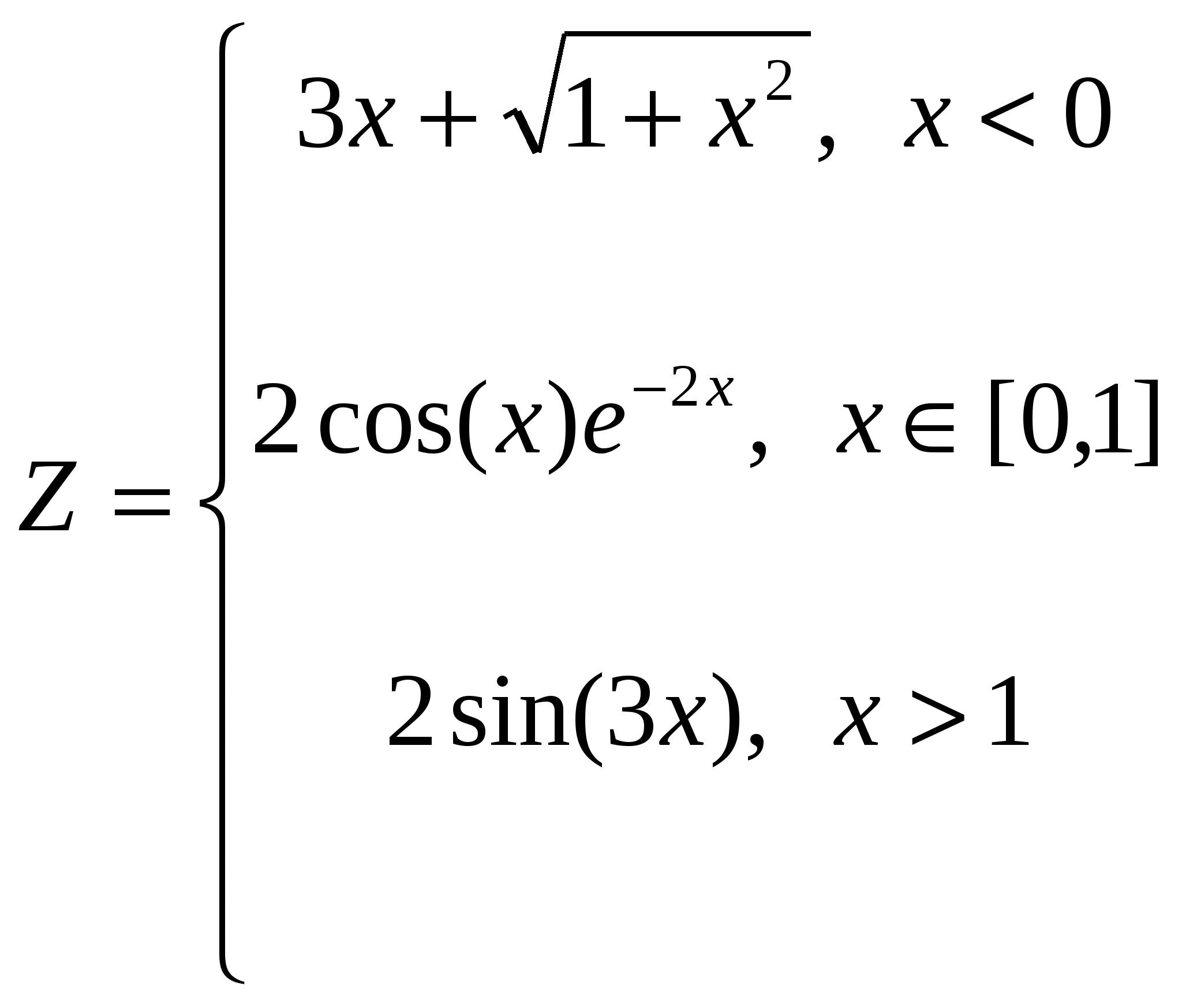 . .
-
Построить в одной системе координат при 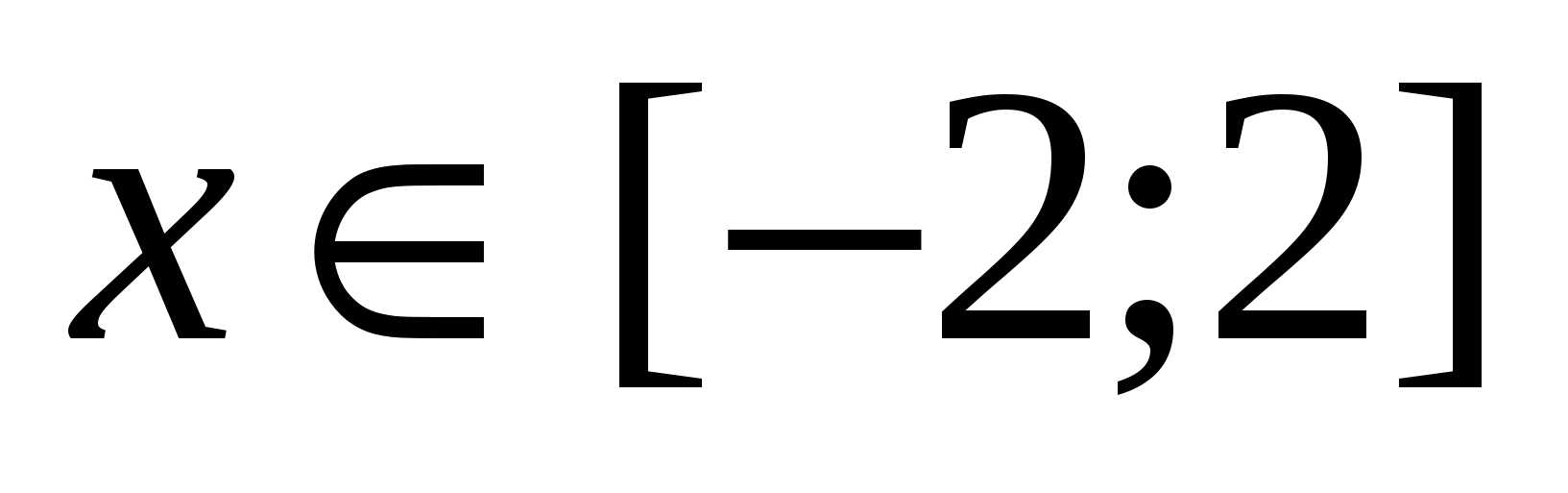 графики функций: графики функций:
-
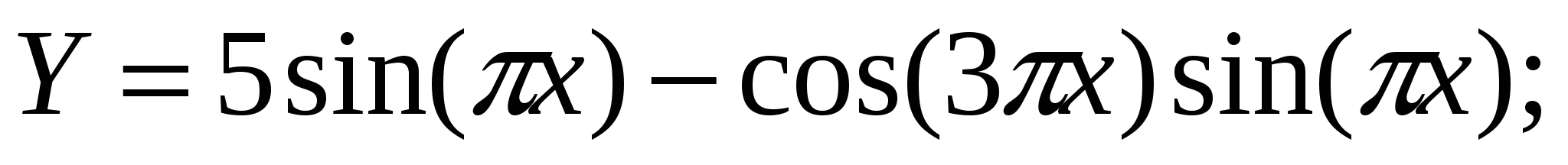
-
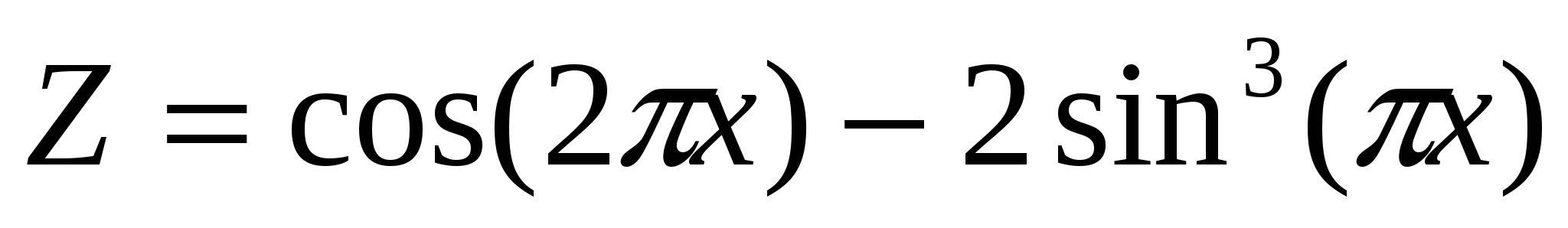 . .
-
Построить поверхность 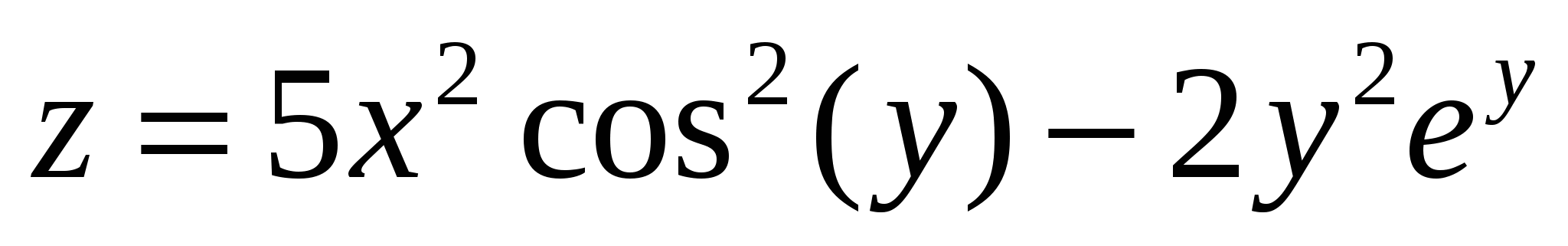 при x[-1;1]. при x[-1;1].
Вариант 4
1. Построить в разных системах координат при x [-1,5;1,5] графики функций: [-1,5;1,5] графики функций:
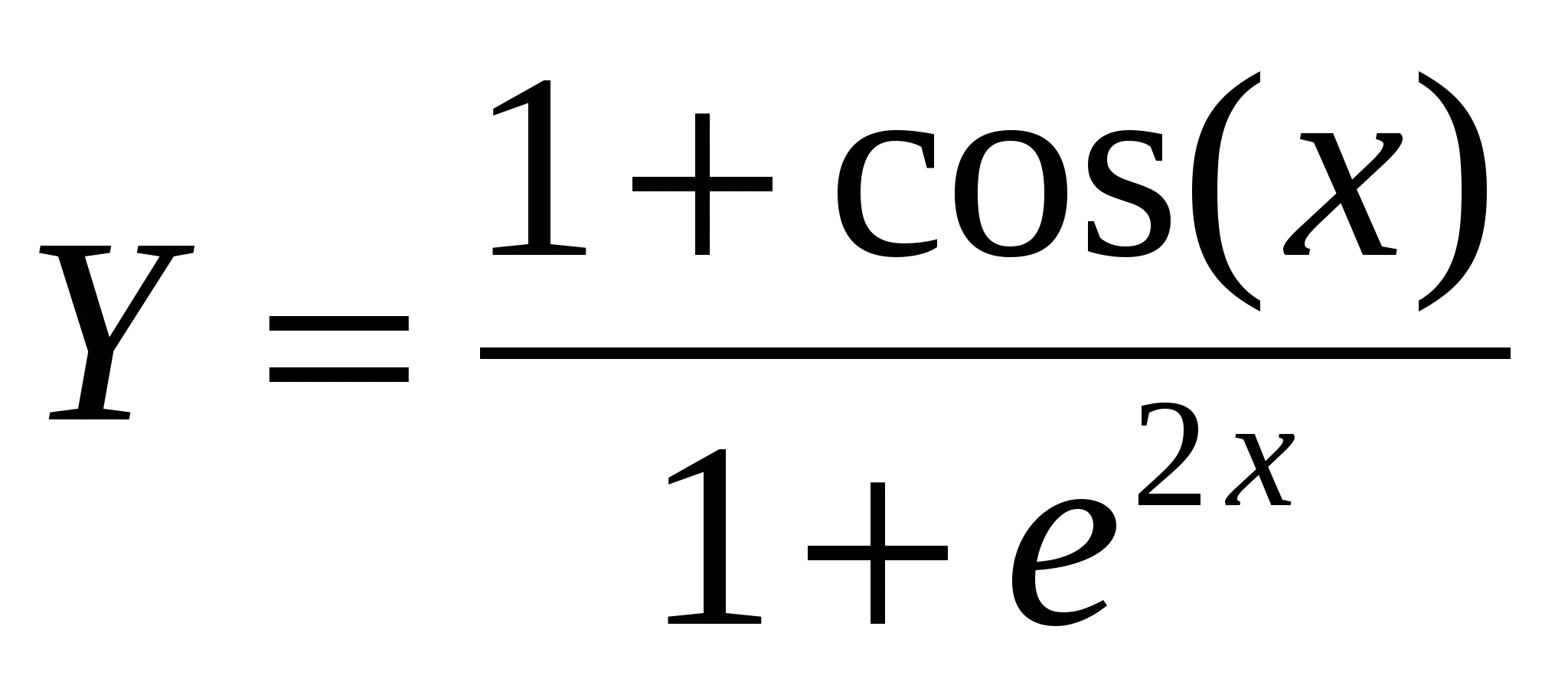
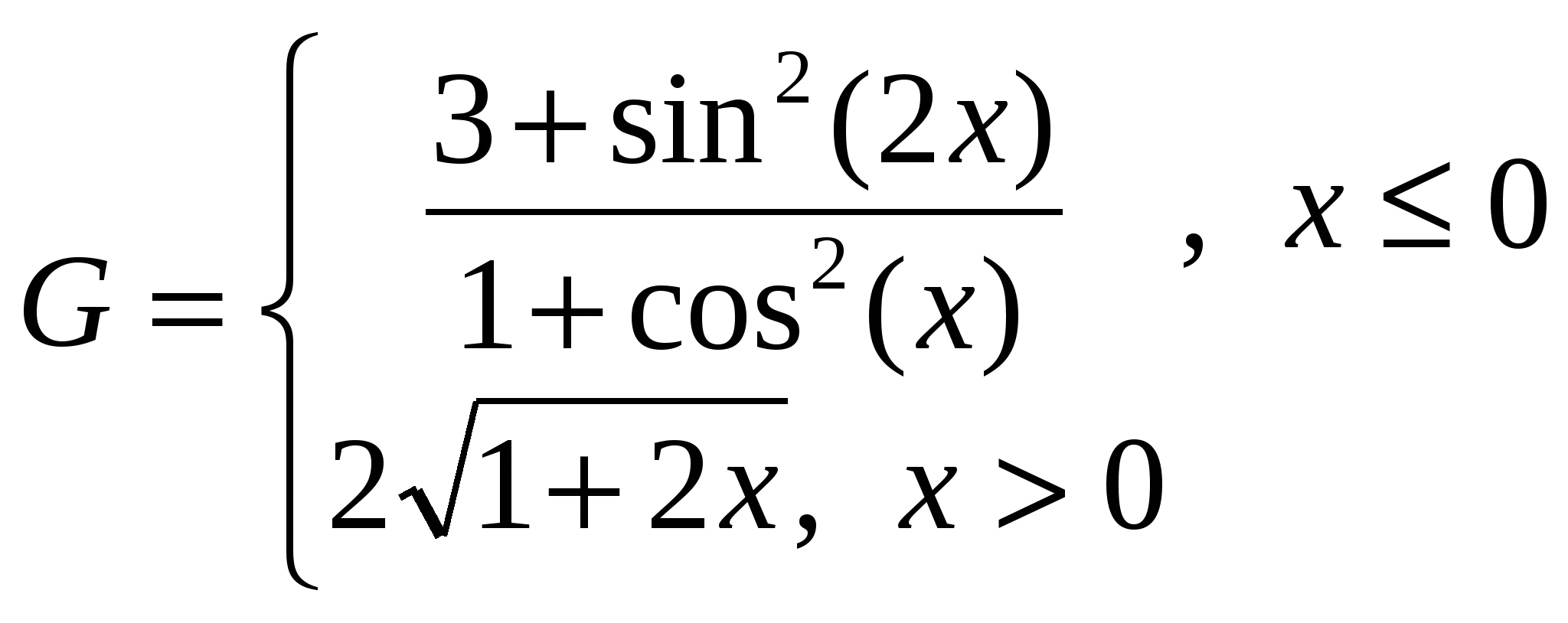
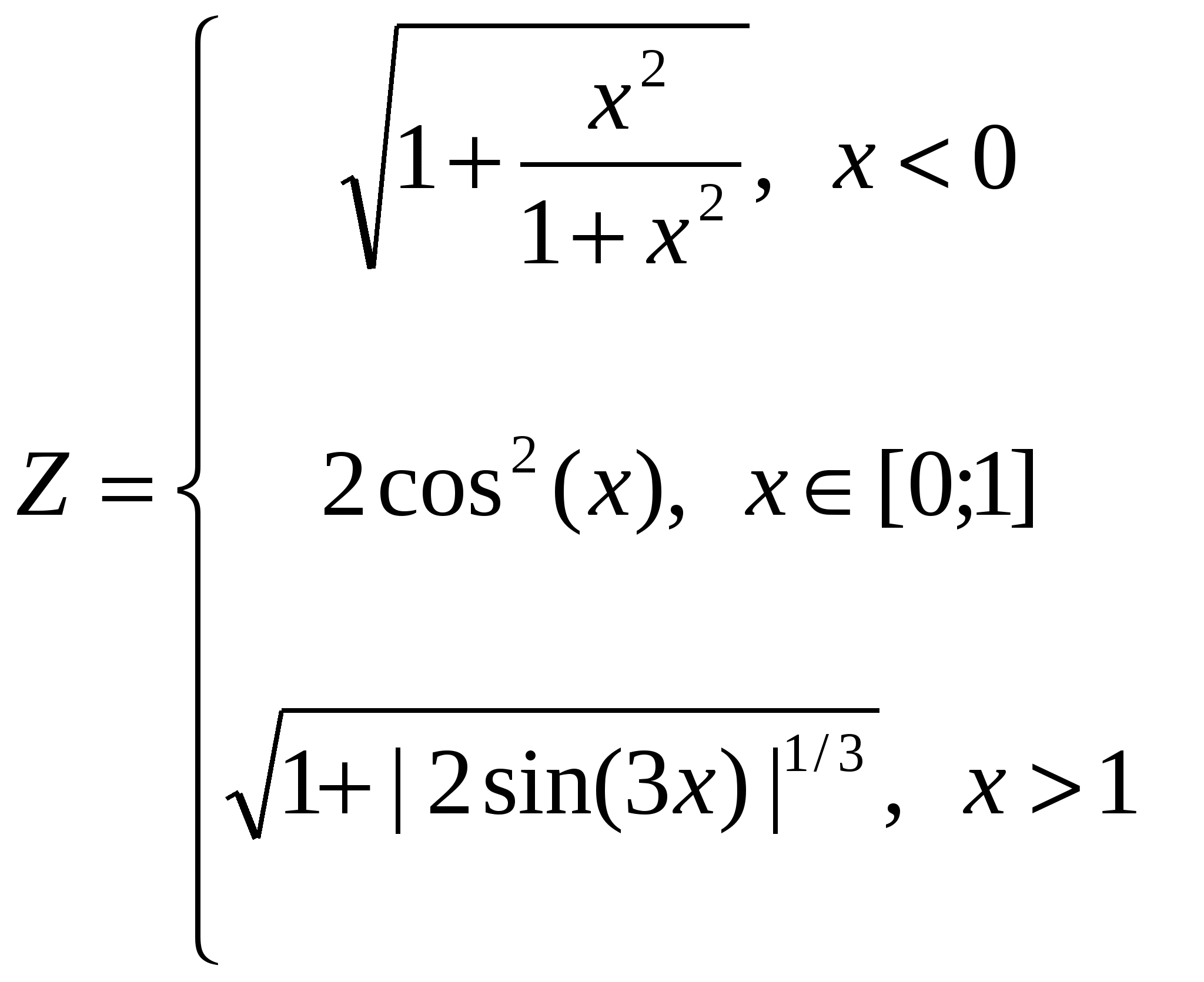  . .
2. Построить в одной системе координат при x [-2;2] графики функций: [-2;2] графики функций:
-
Y = 3sin(2 πx) cos(πx) – cos2 (3πx);
-
Z = 2cos2(2πx) – 3sin(3πx).
3. Построить поверхность при x, y [-1;1] [-1;1]
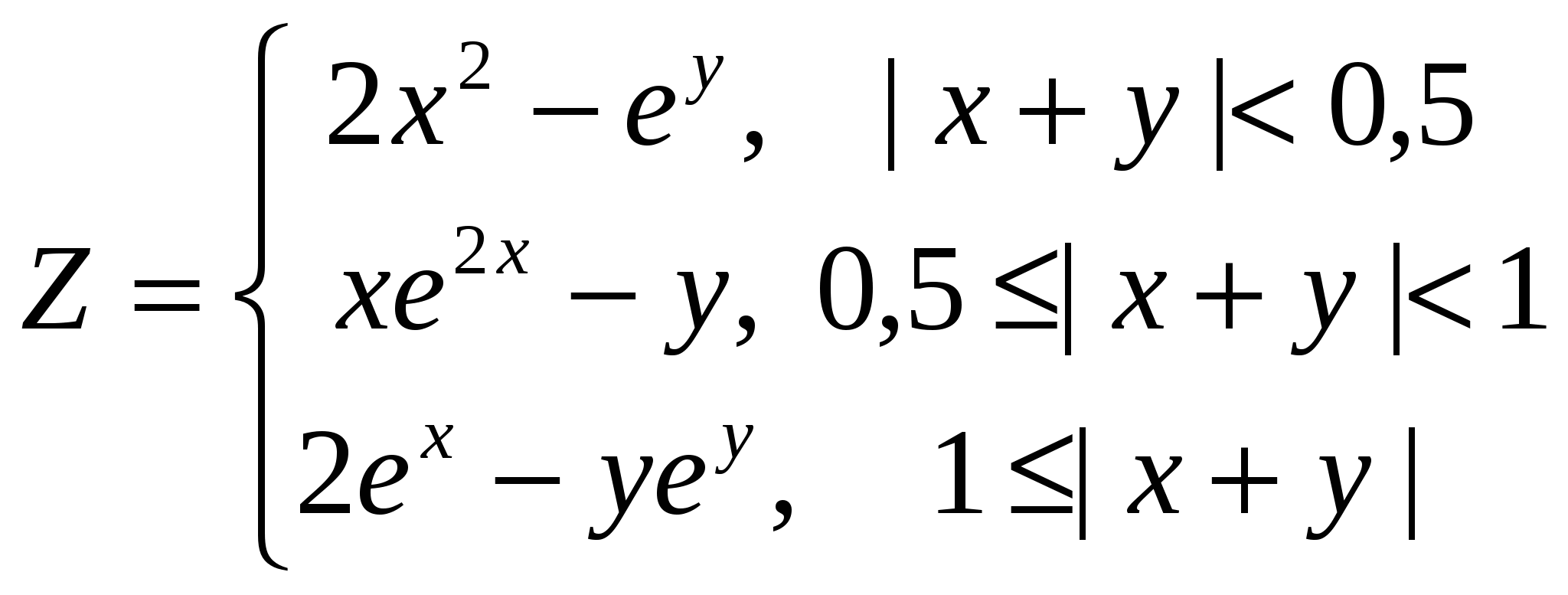 . .
Вариант 5
1. Построить в разных системах координат при x [-1,8;1,8] графики функций: [-1,8;1,8] графики функций:
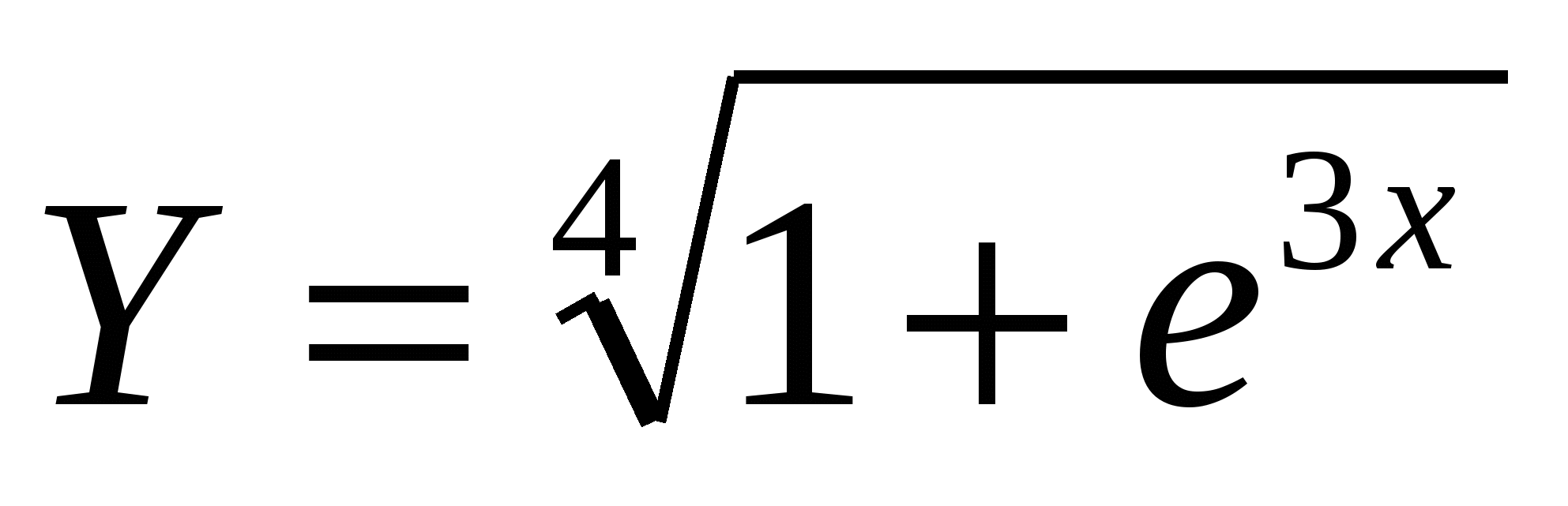
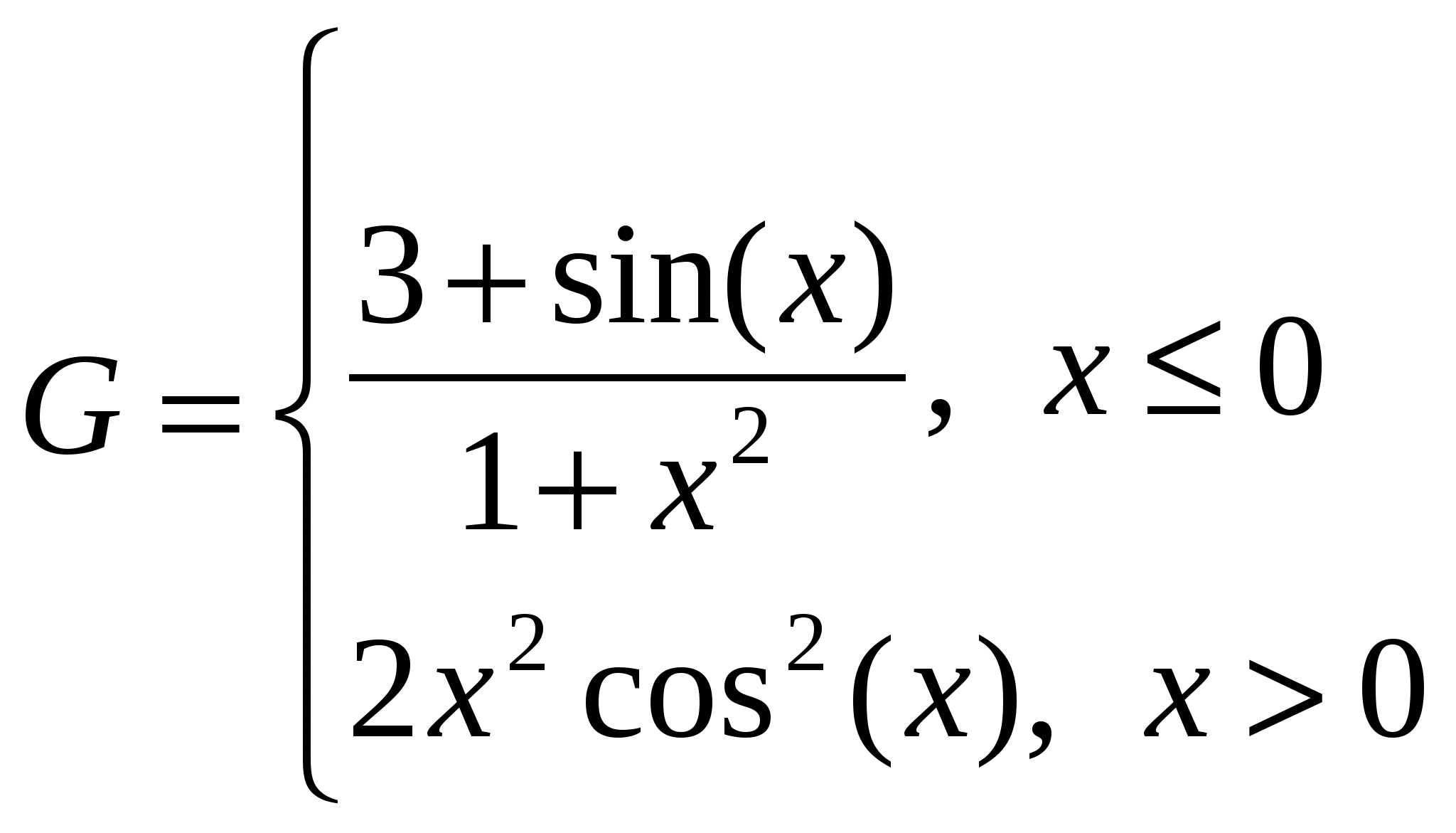
 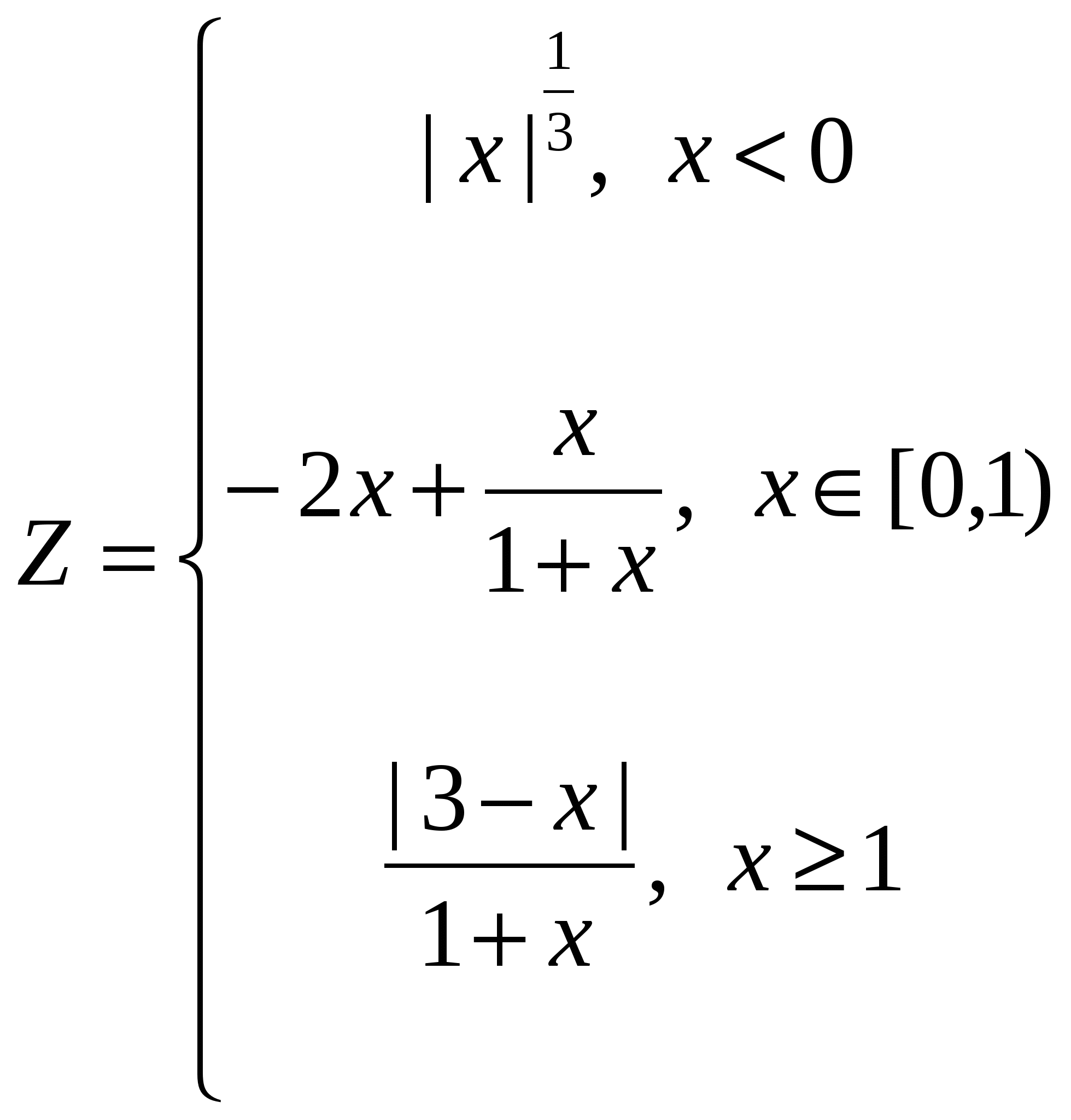
2. Построить в одной системе координат при x [0;3] графики функций: [0;3] графики функций:
-
Y = 2sin(πx)cos(πx);
-
Z = cos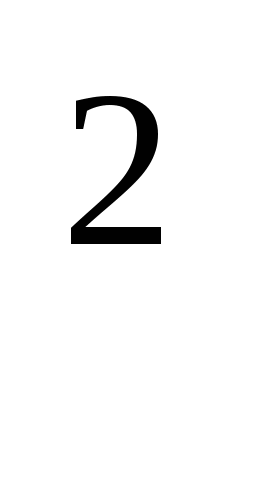 (πx)sin(3πx). (πx)sin(3πx).
3. Построить поверхность 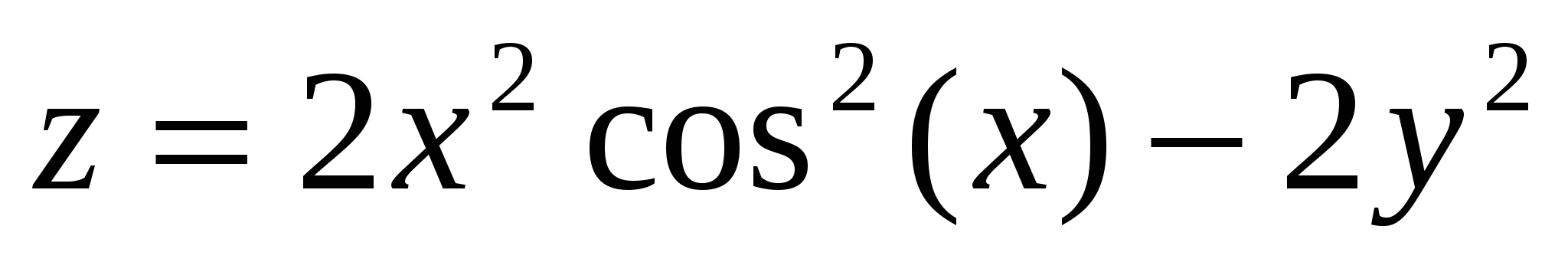 при x, y при x, y [-1;1]. [-1;1].
Вариант 6
1. Построить в разных системах координат при x [-2;1,8] графики функций: [-2;1,8] графики функций:
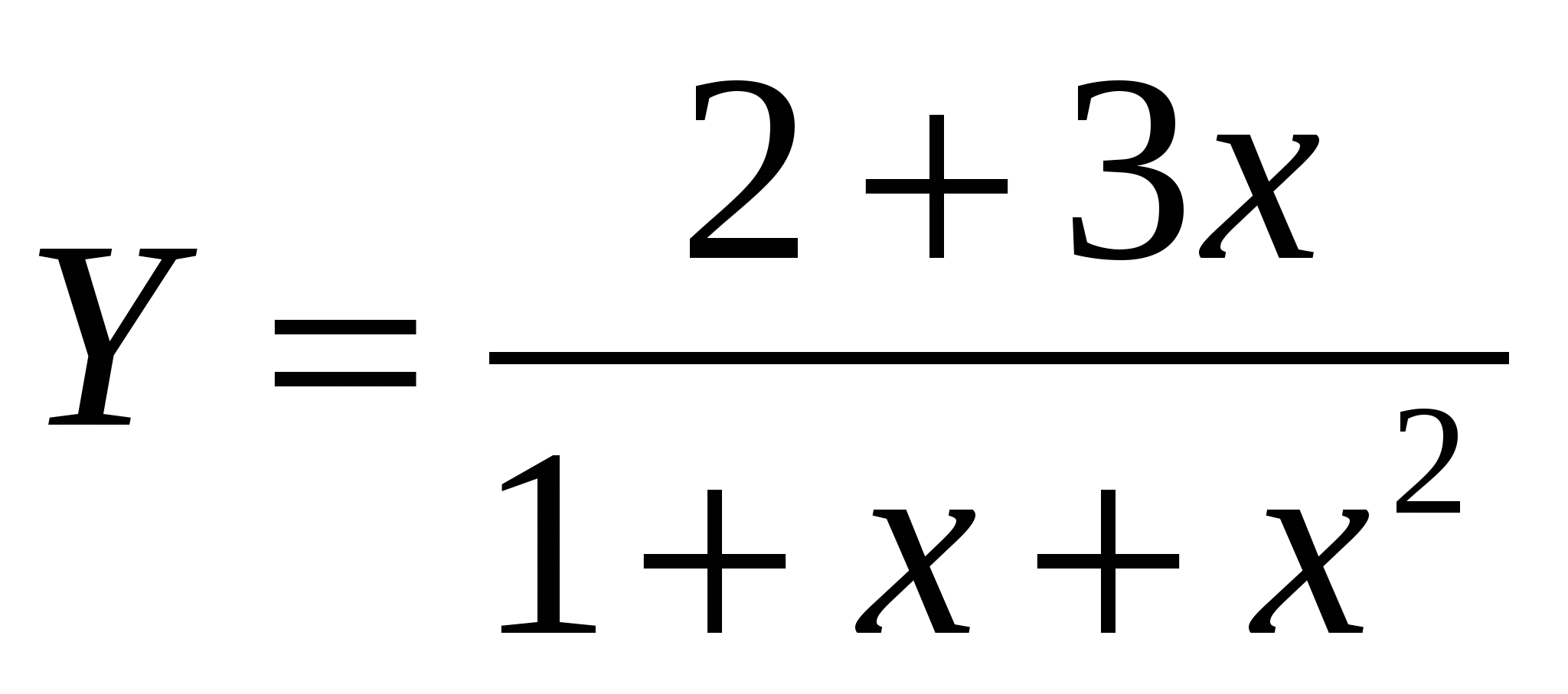
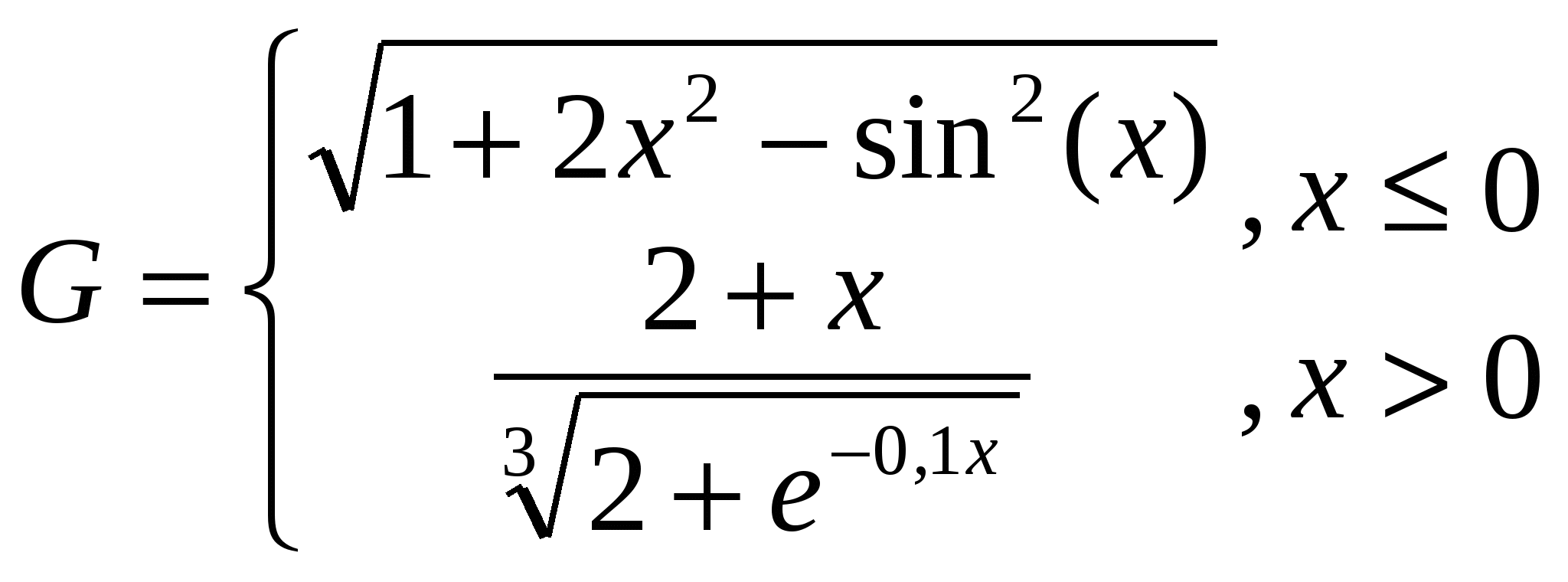
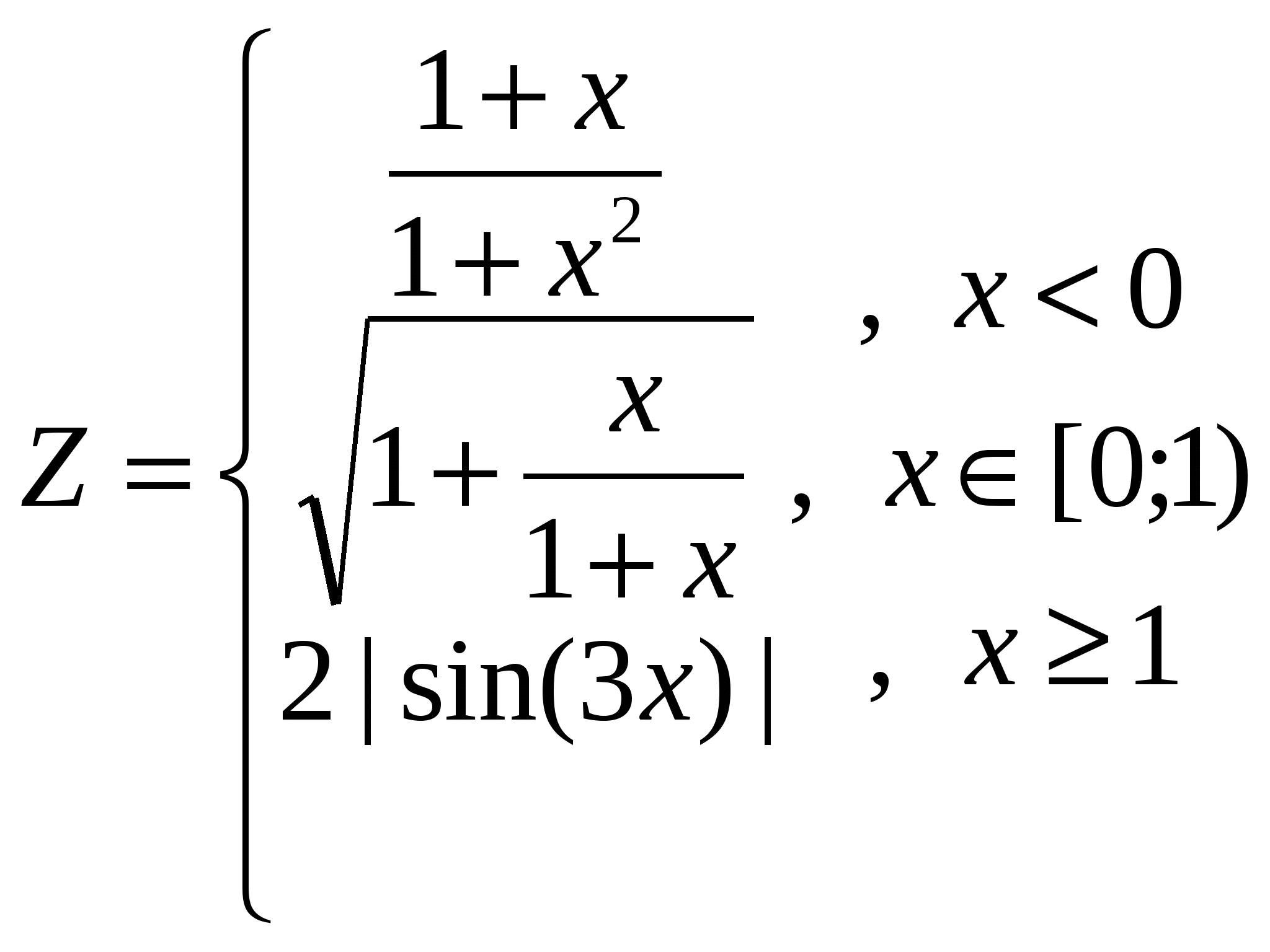 . .
2. Построить в одной системе координат при x [-3;0] графики функций: [-3;0] графики функций:
-
Y = 3sin(3πx)cos(2πx);
-
Z = cos3(4πx)sin(πx).
3. Построить поверхность 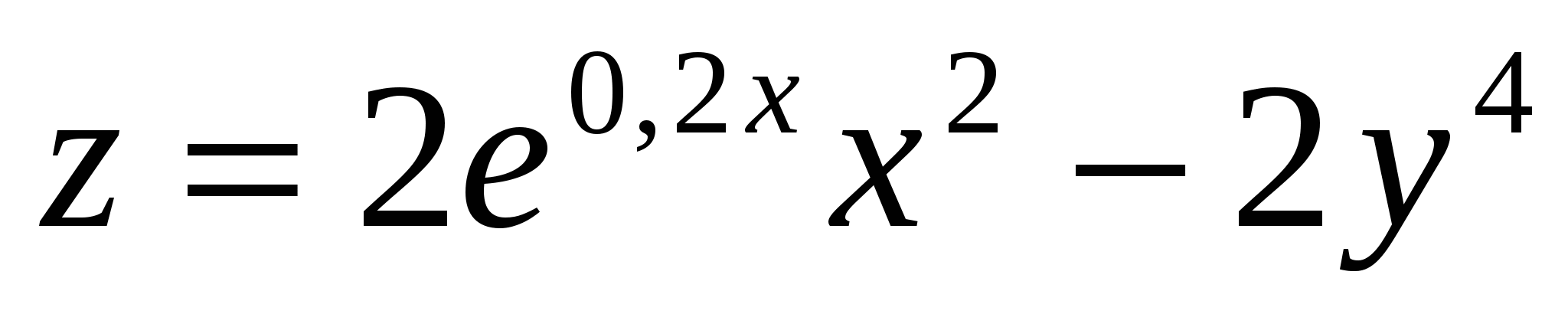 при x, y при x, y [-1;1]. [-1;1].
Вариант 7
1. Построить в разных системах координат при x [-1,7;1,5] графики функций: [-1,7;1,5] графики функций:
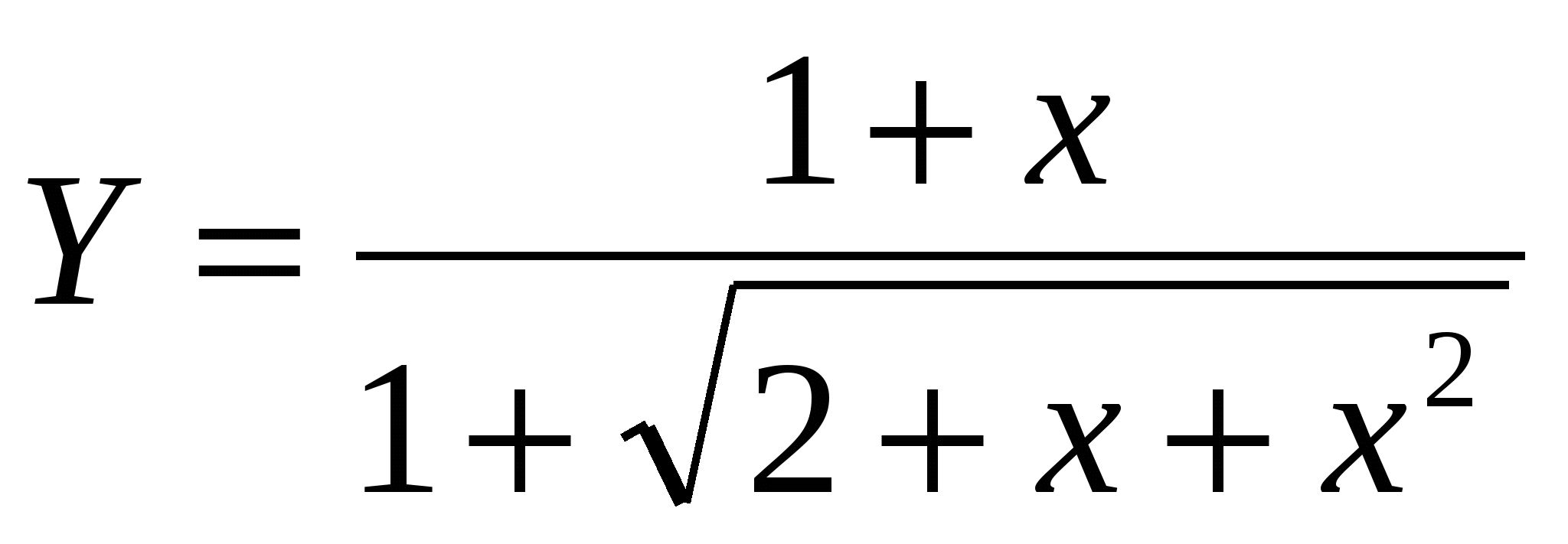
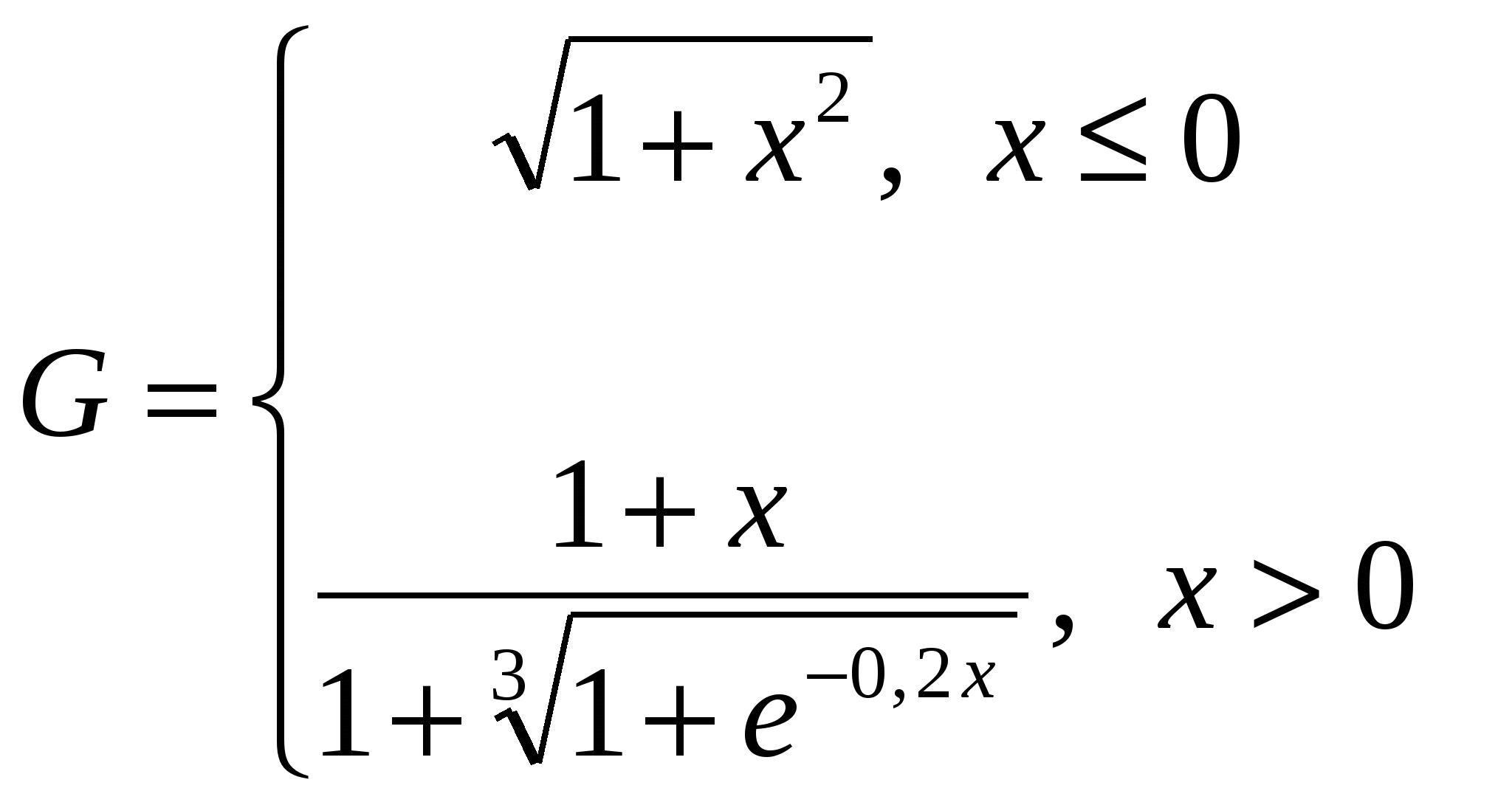
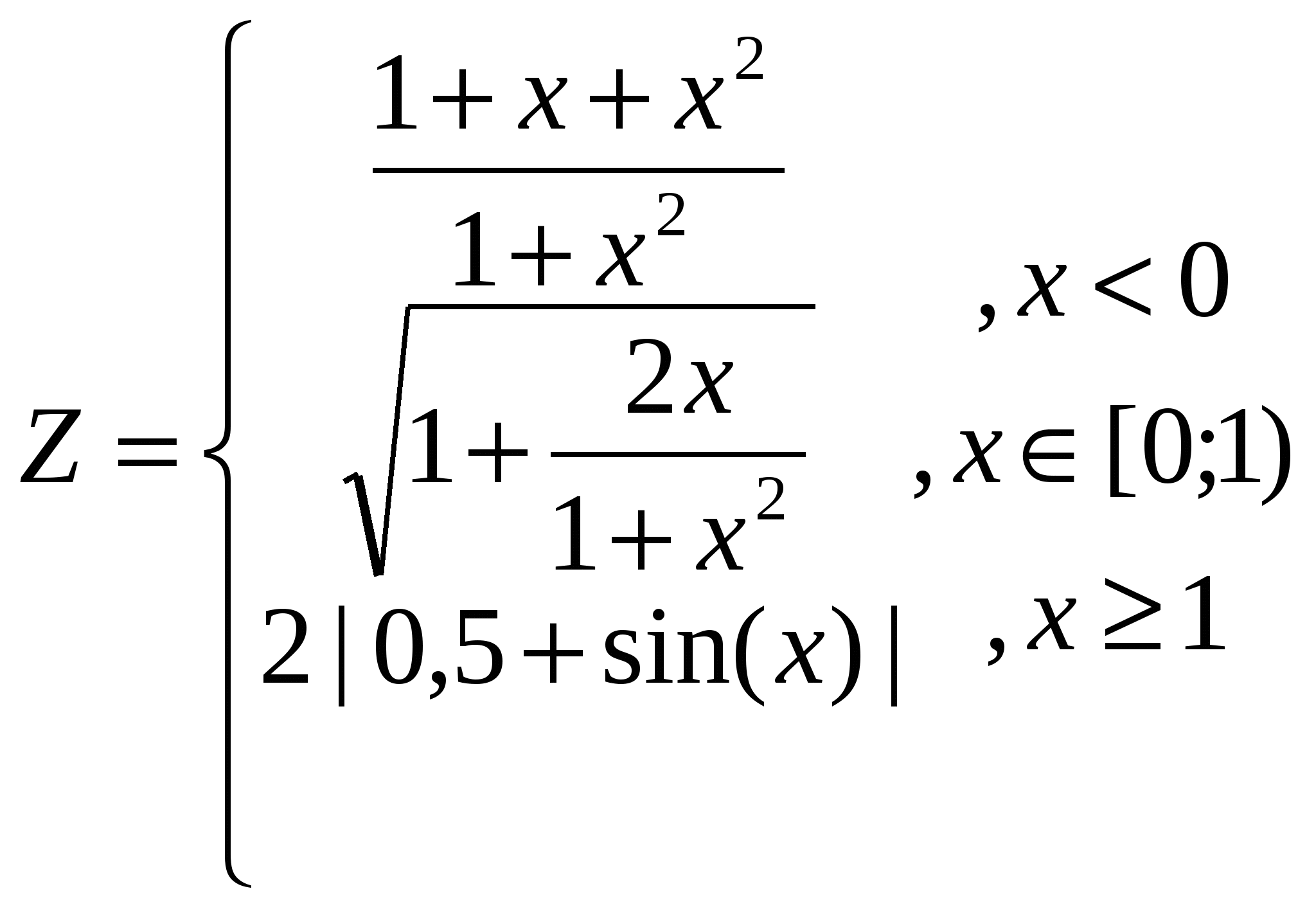  . .
2. Построить в одной системе координат при x [-3;0] графики функций: [-3;0] графики функций:
-
Y = 2sin(2πx)cos(4πx);
-
Z = cos2(3πx) – cos(πx)sin(πx).
3. Построить поверхность 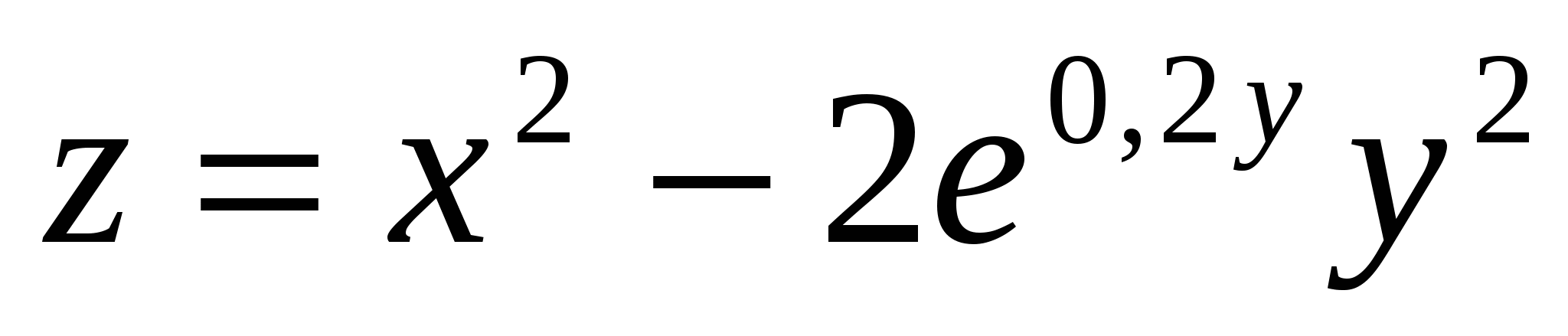 при x, y при x, y [-1;1]. [-1;1].
Вариант 8
-
Построить в разных системах координат при 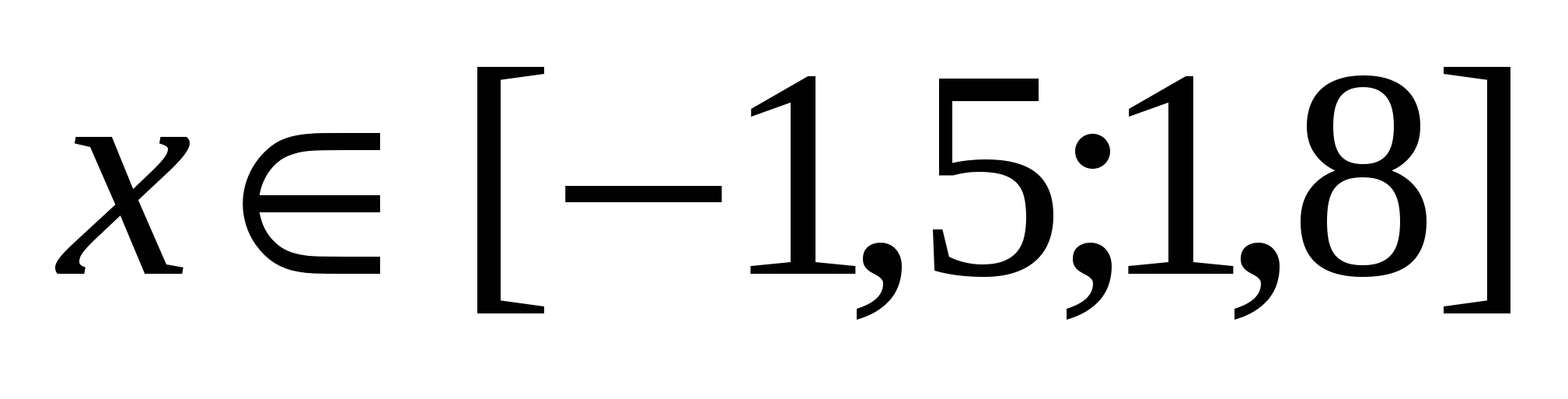 графики функций: графики функций:
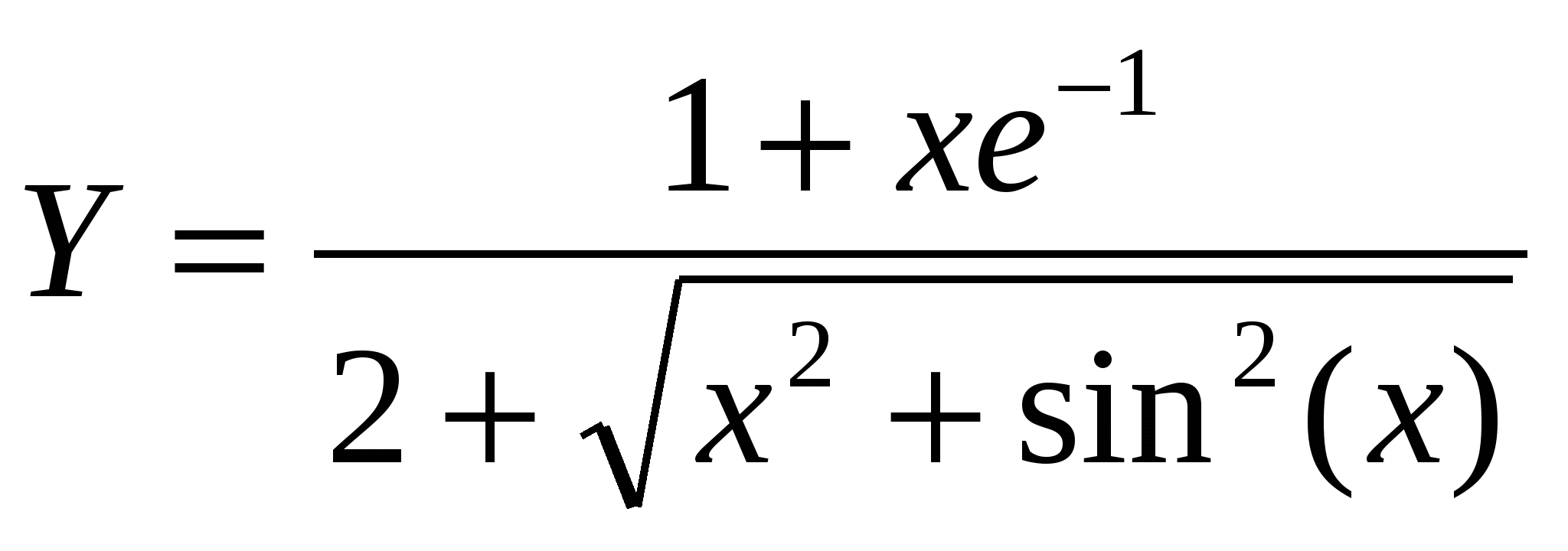
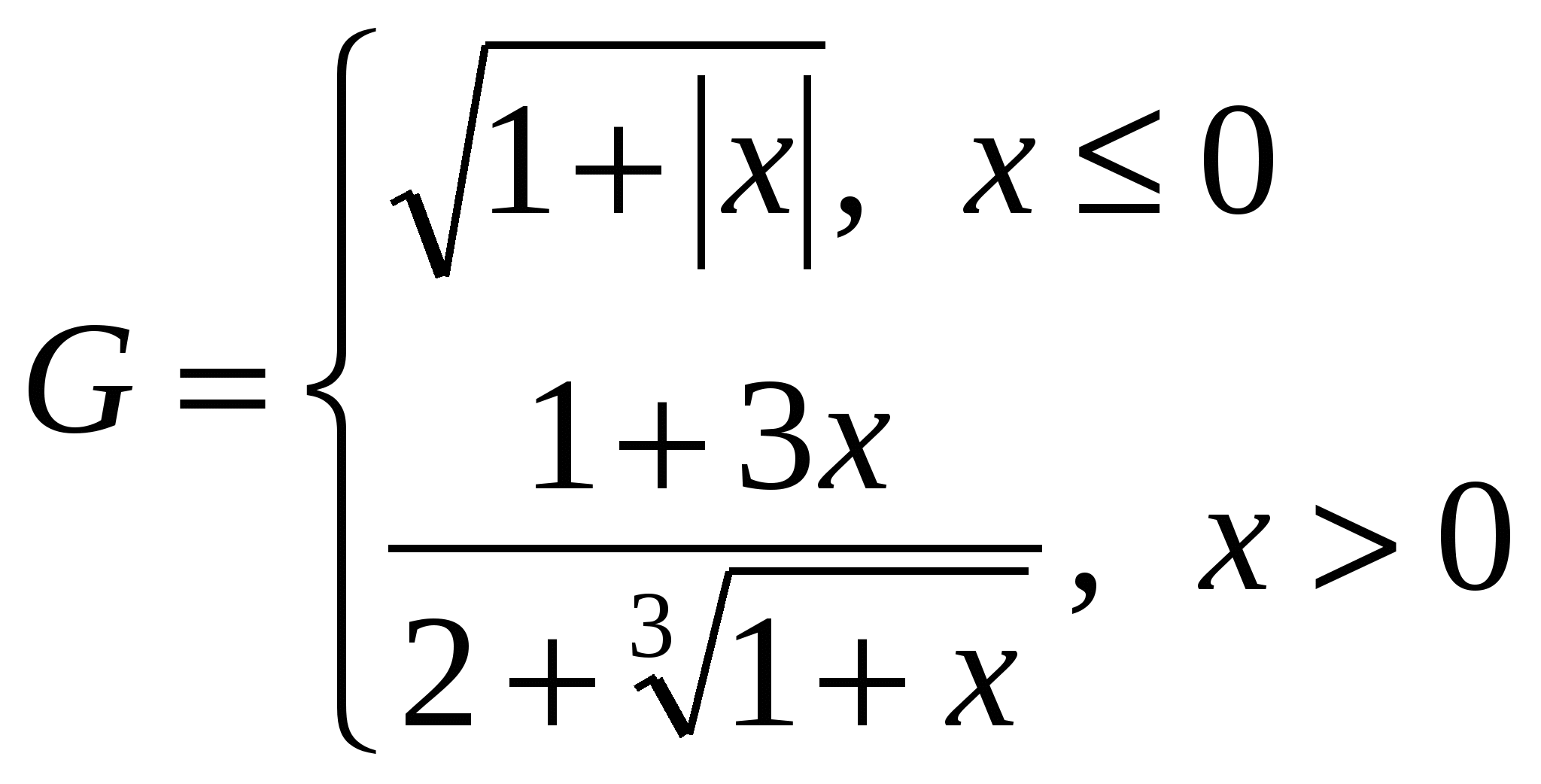
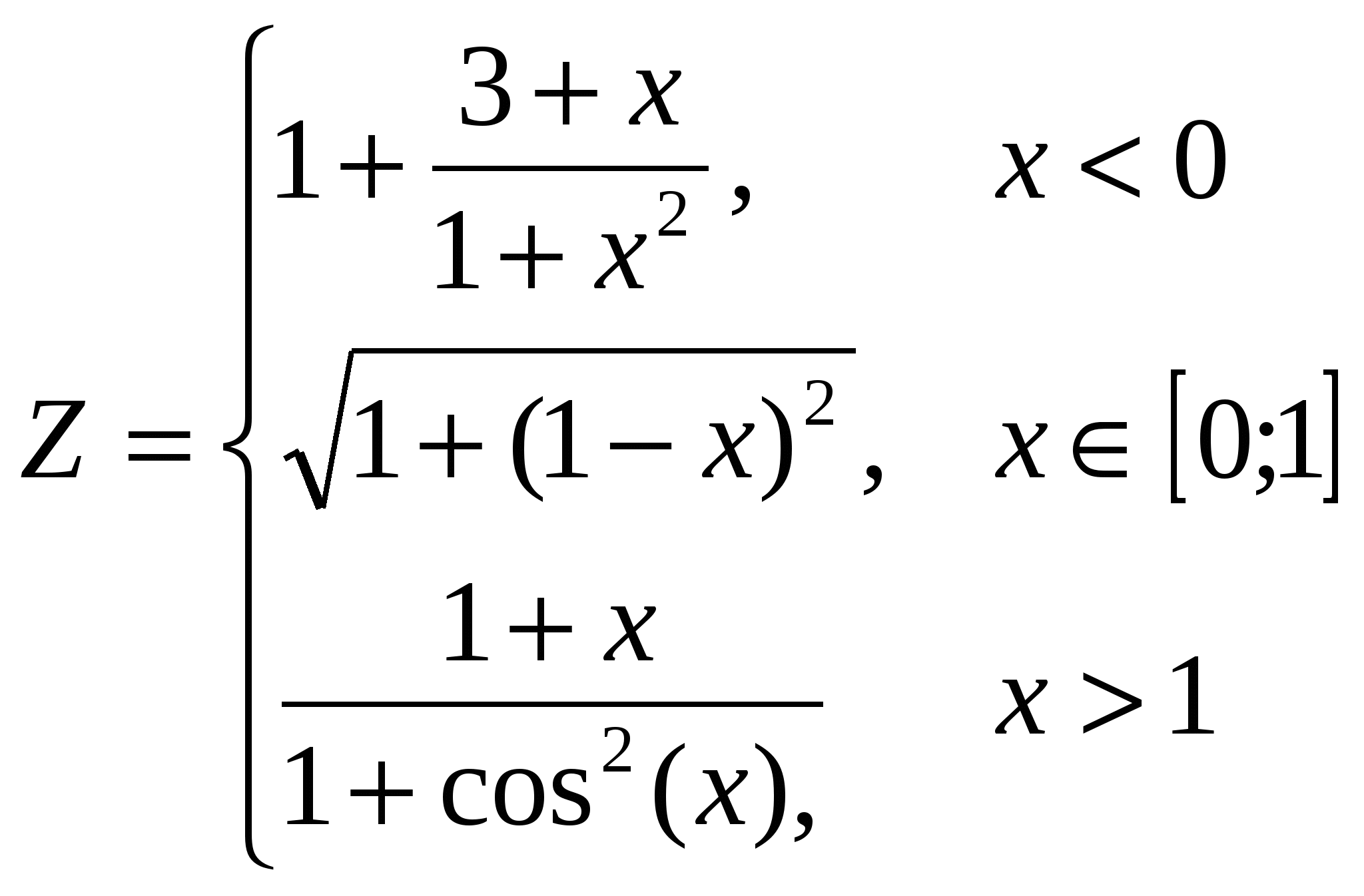 . .
-
Построить в одной системе координат при 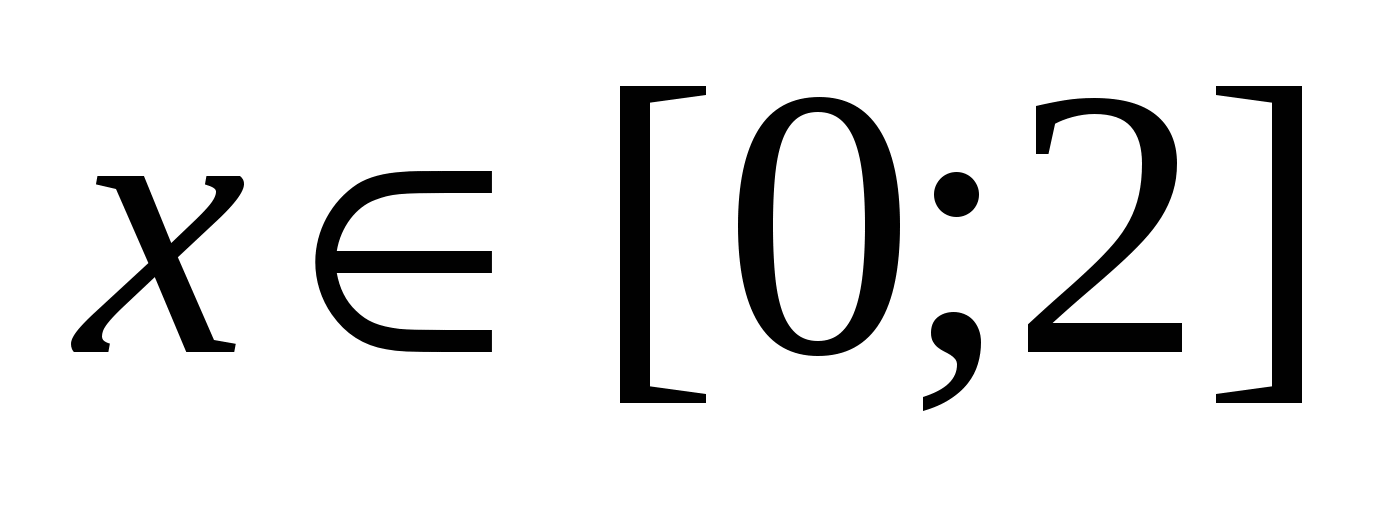 графики функции: графики функции:
-
Построить поверхность при 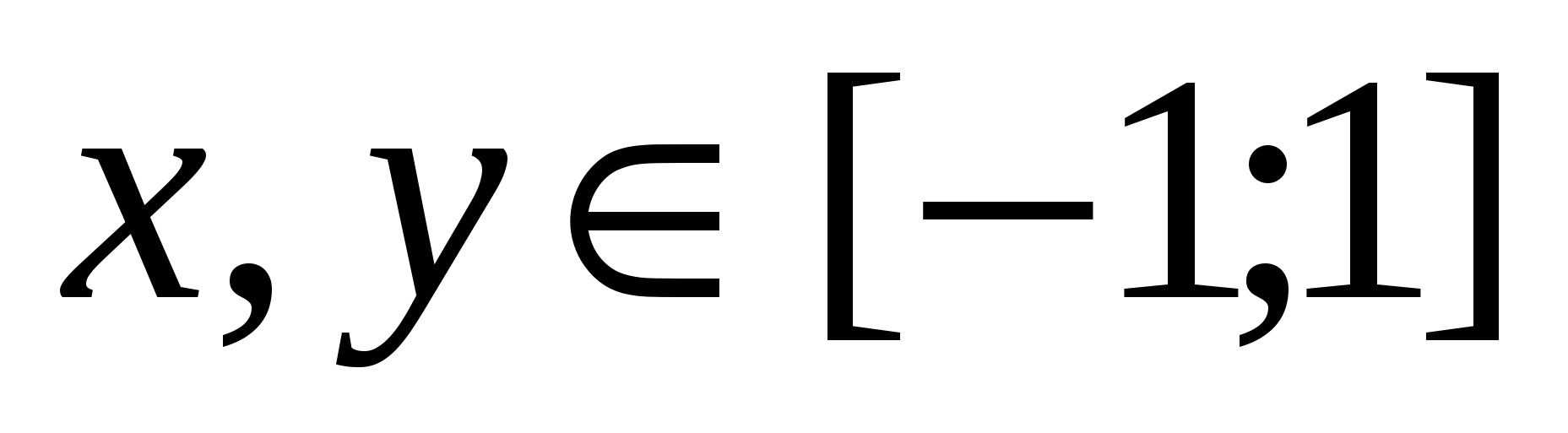
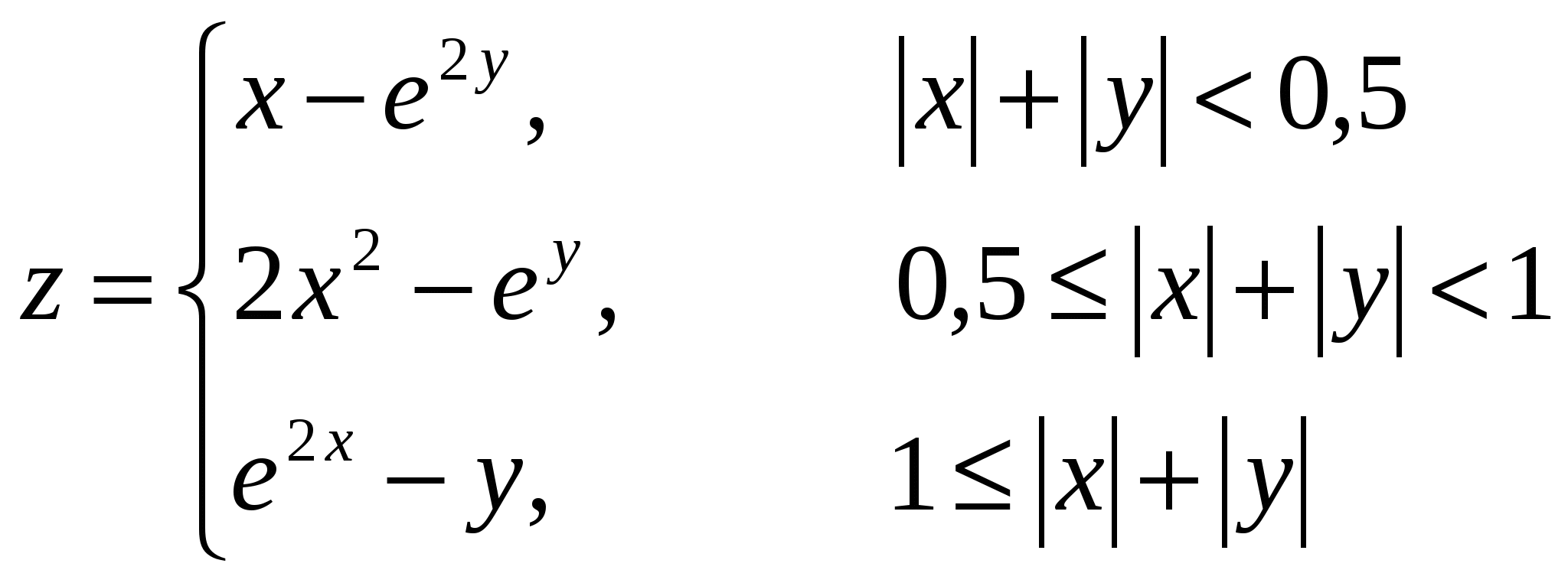
Вариант 9
1. Построить в разных системах координат при x[1,4;1,9] графики функций:
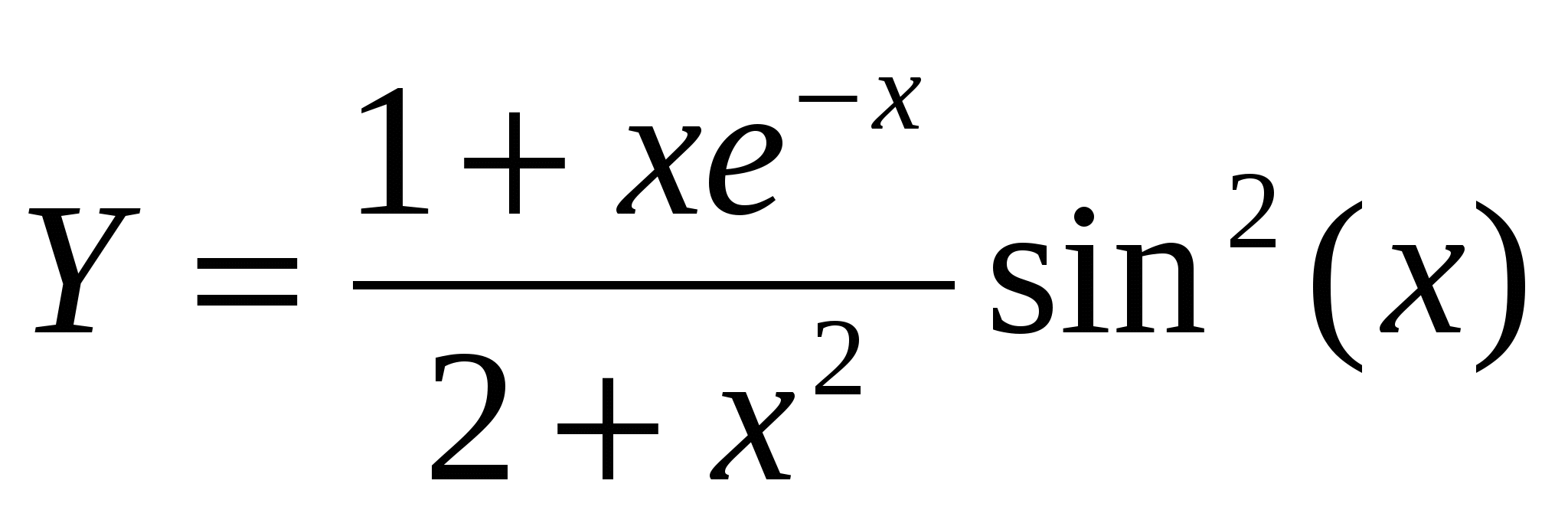
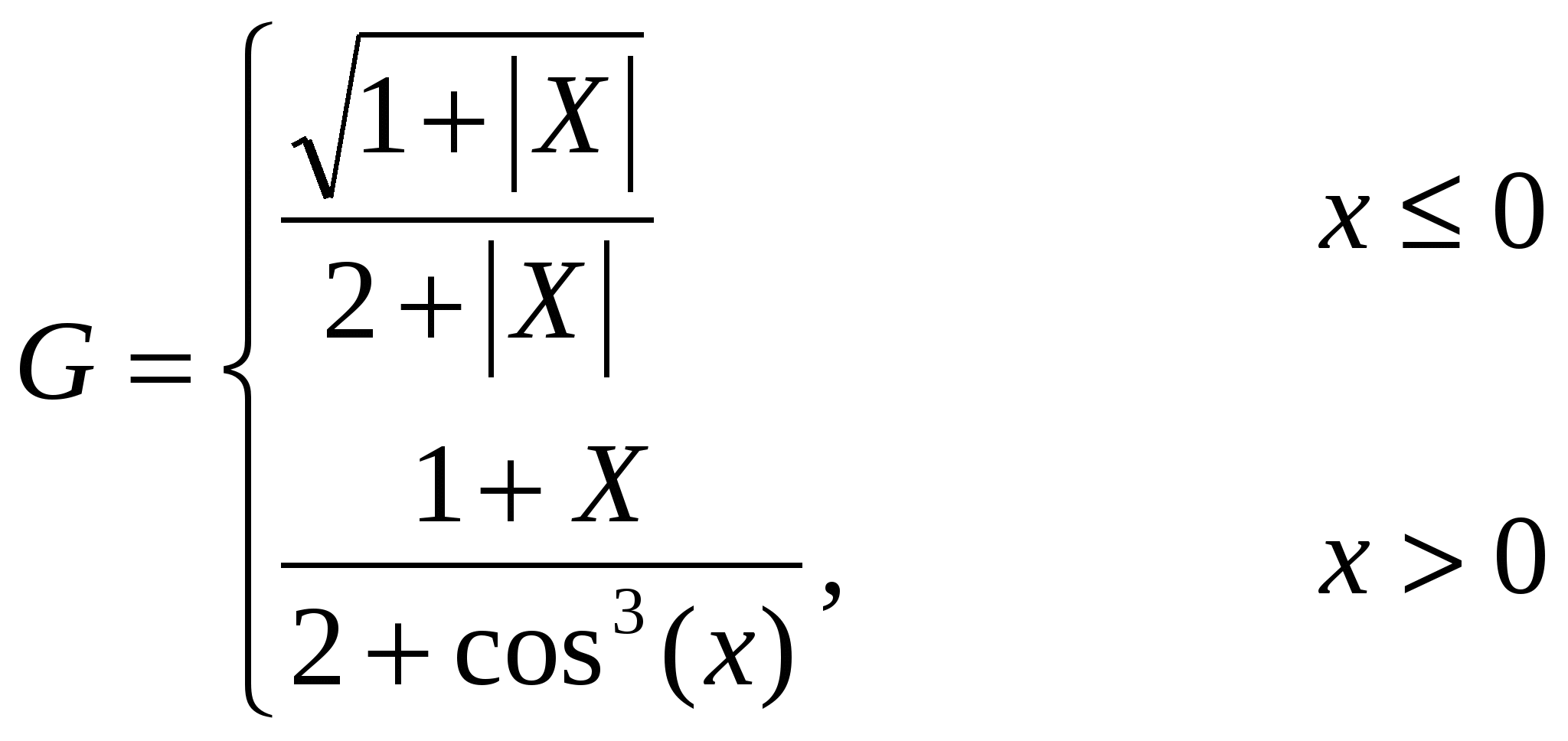  
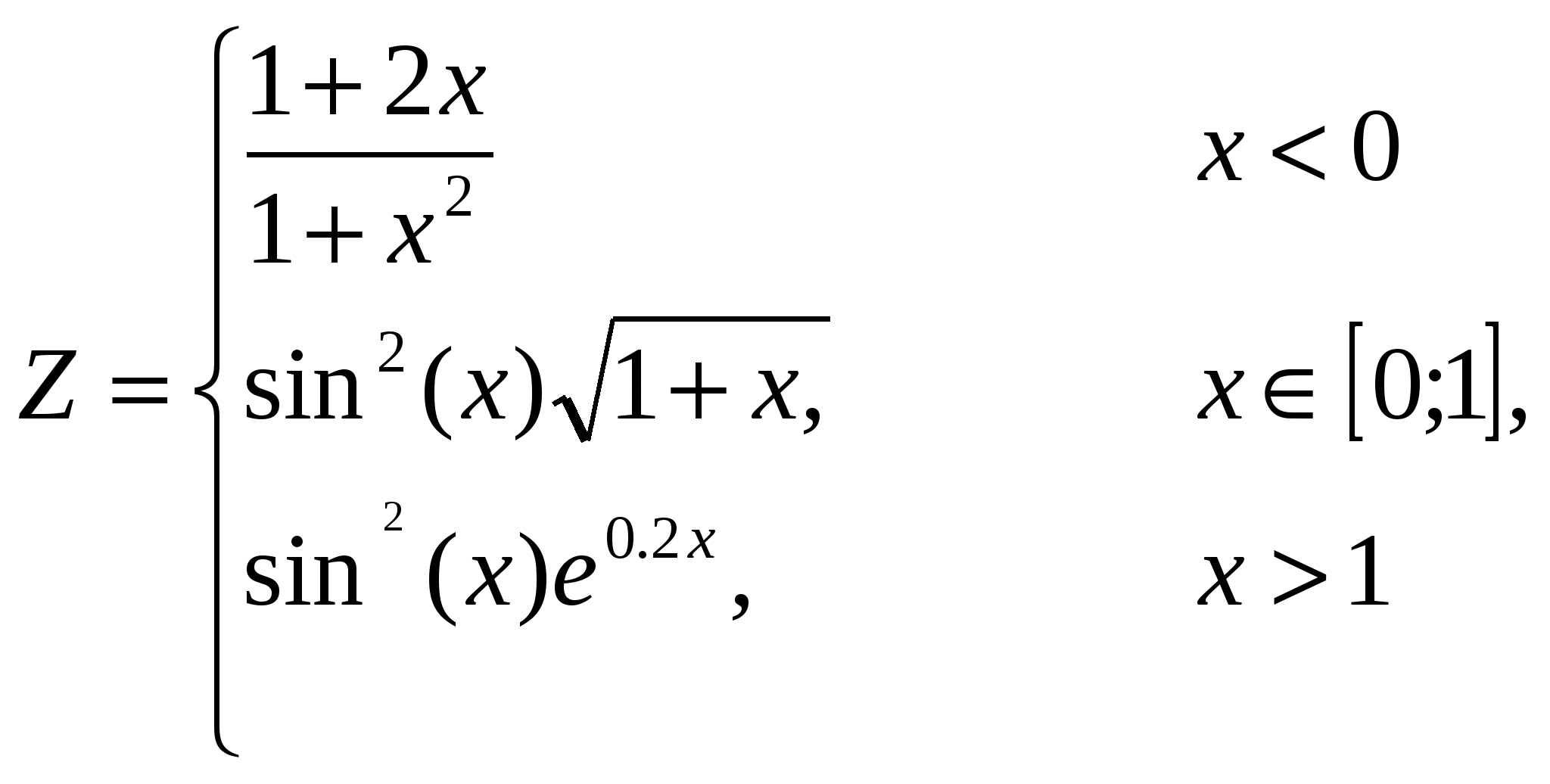
2. Построить в одной системе координат при х[0;2] графики функций:
-
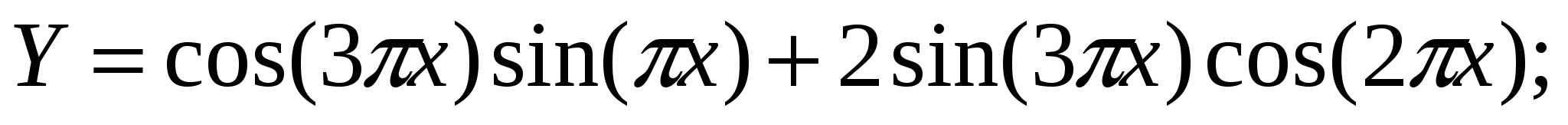
-
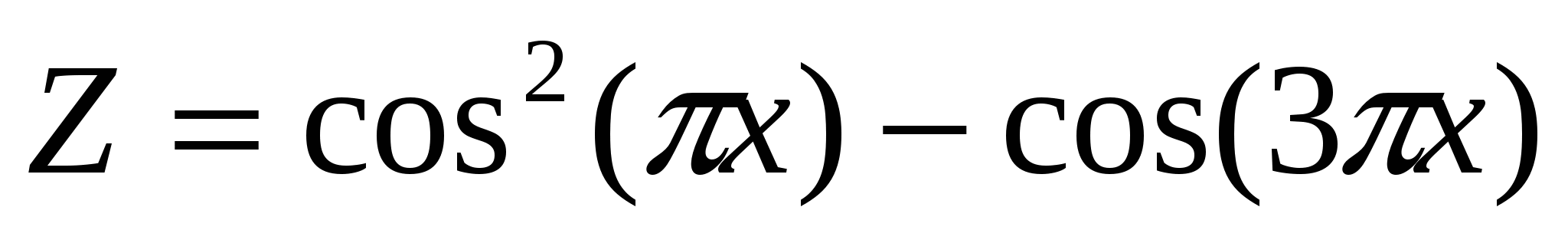 . .
-
Построить поверхность при х[-1;1]
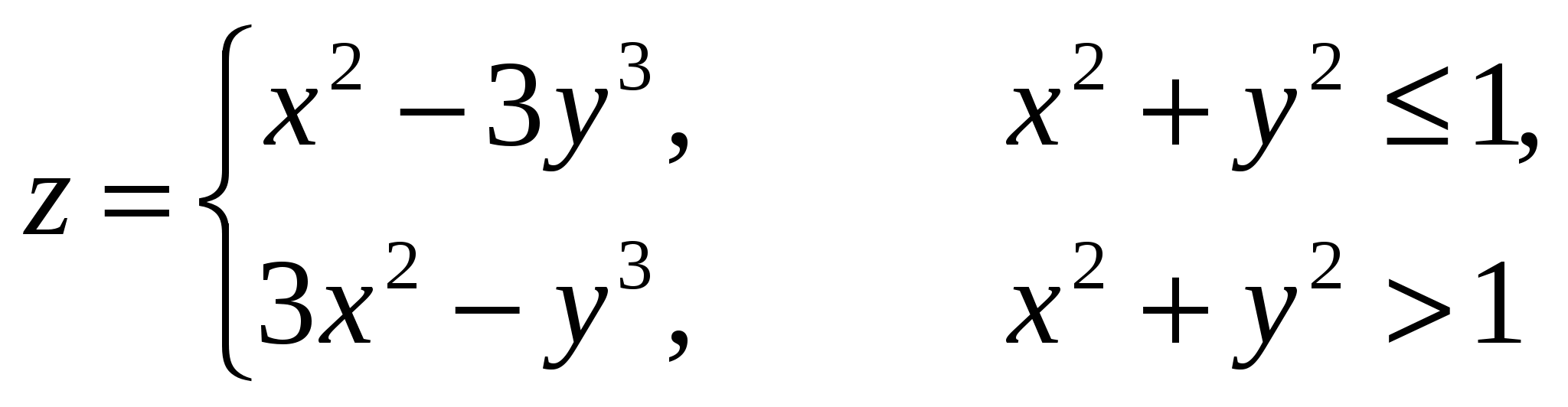 . .
Вариант 10
-
Построить в разных системах координат при 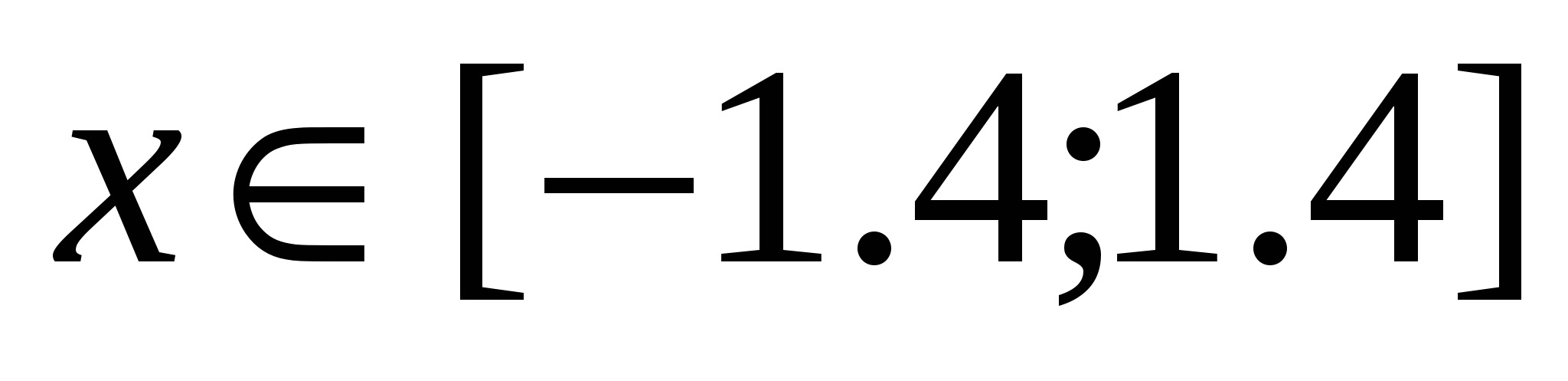 графики функций: графики функций:
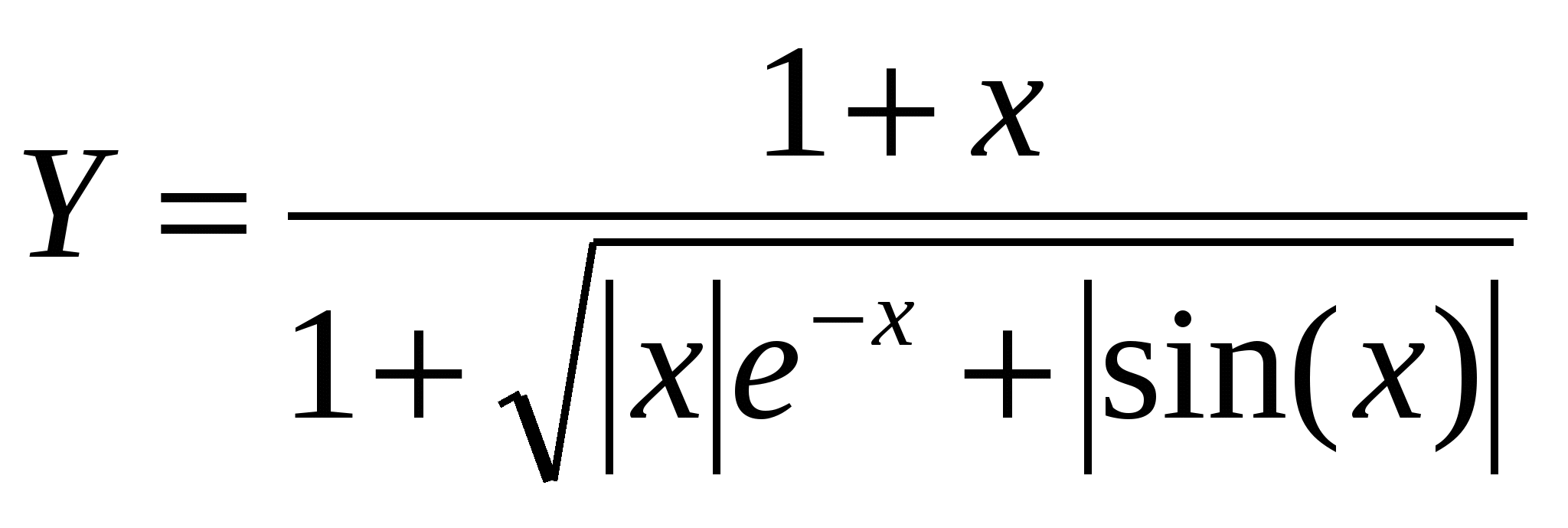
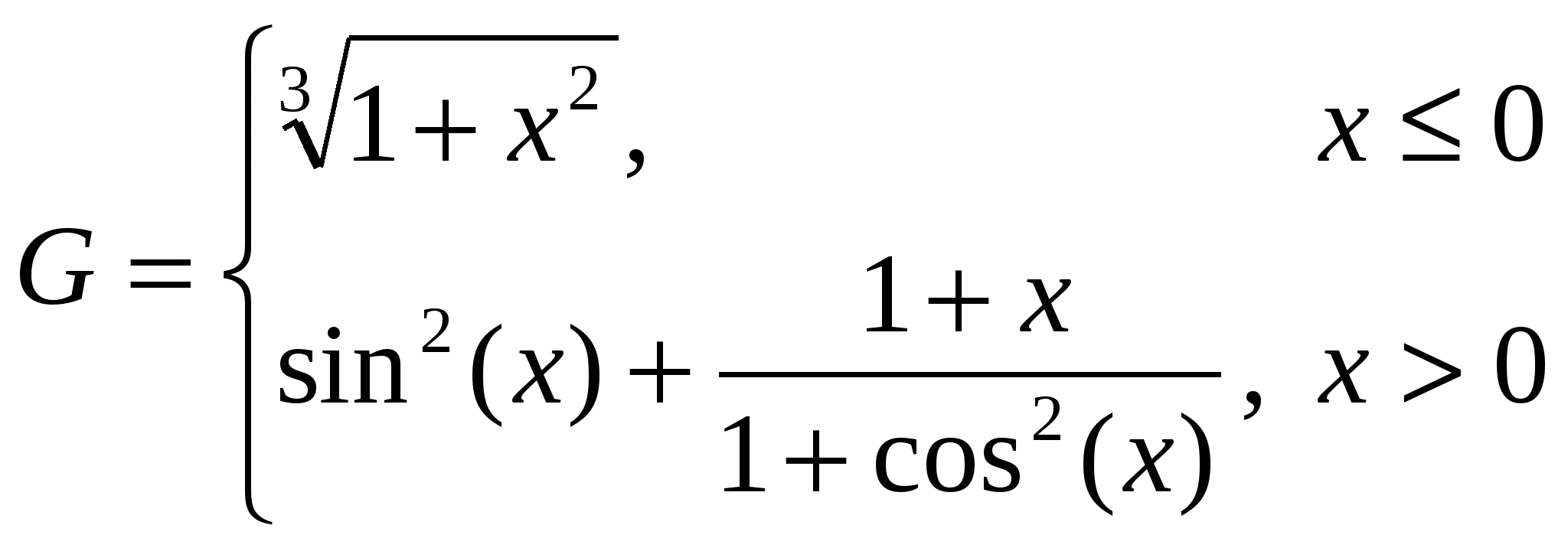
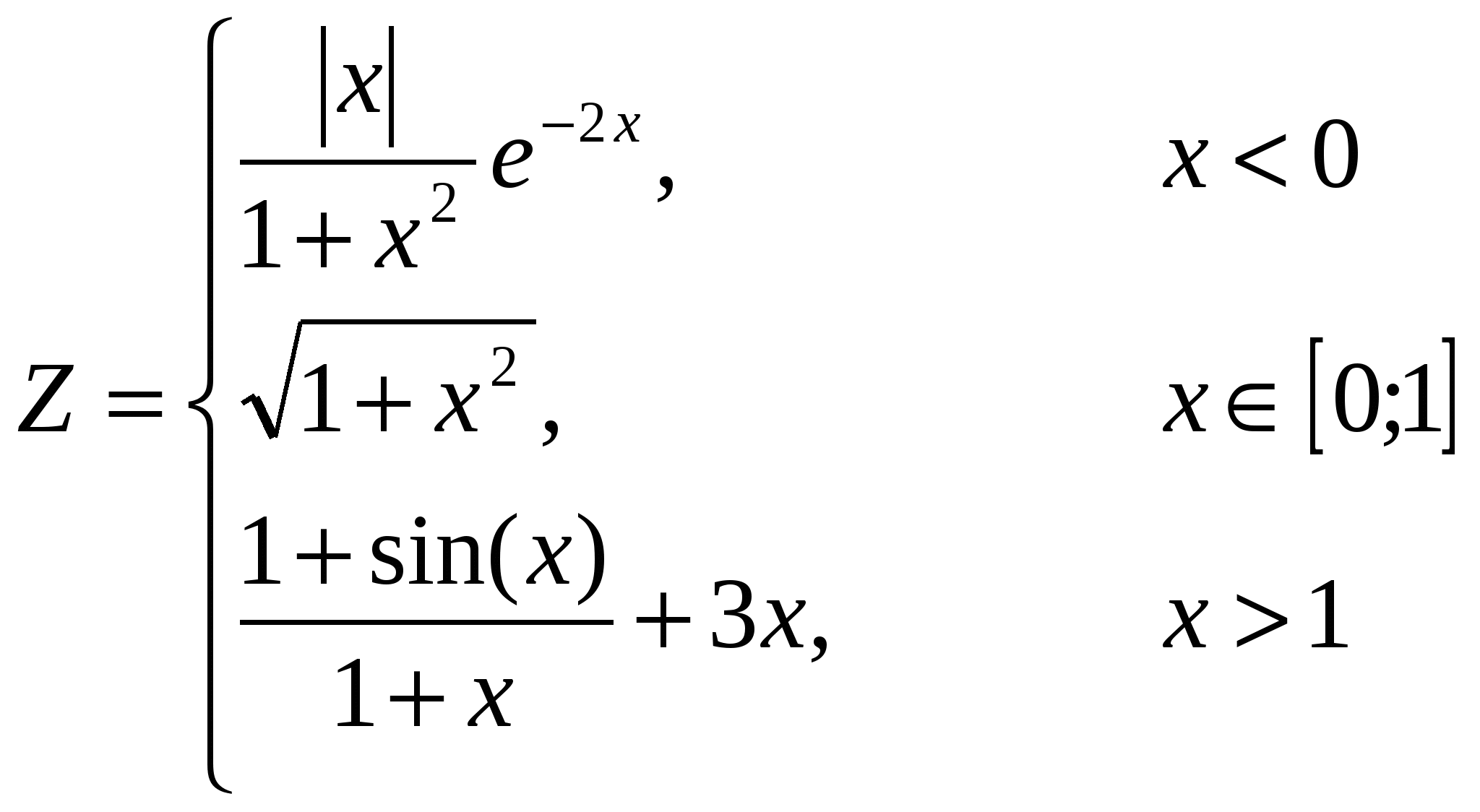
-
Построить в одной системе координат при 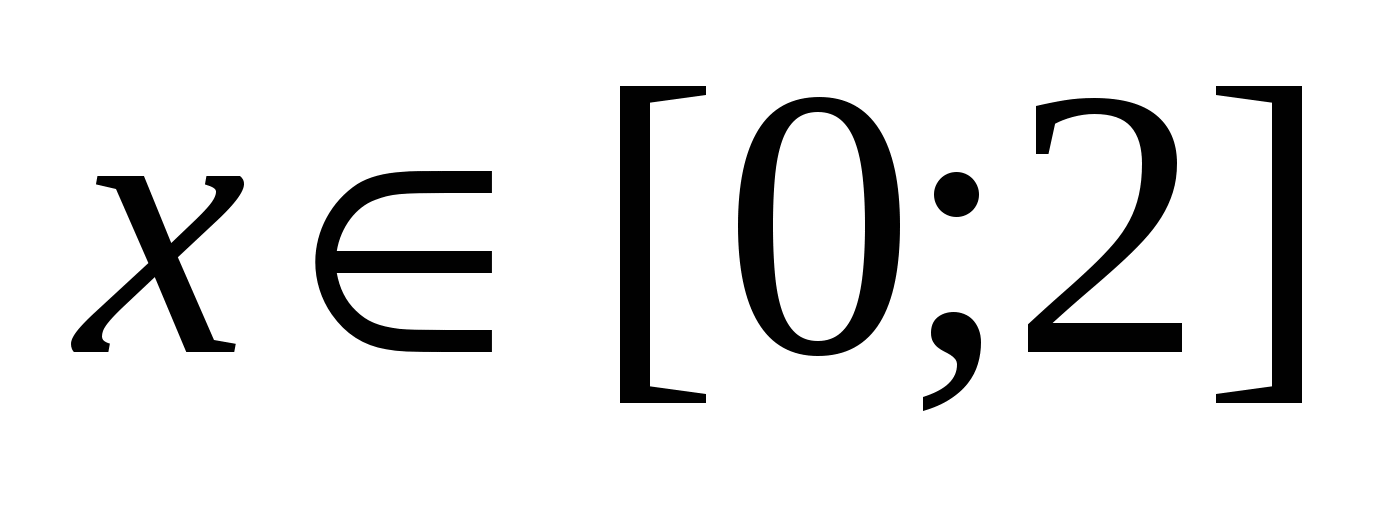 графики функций: графики функций:
-
Построить поверхность 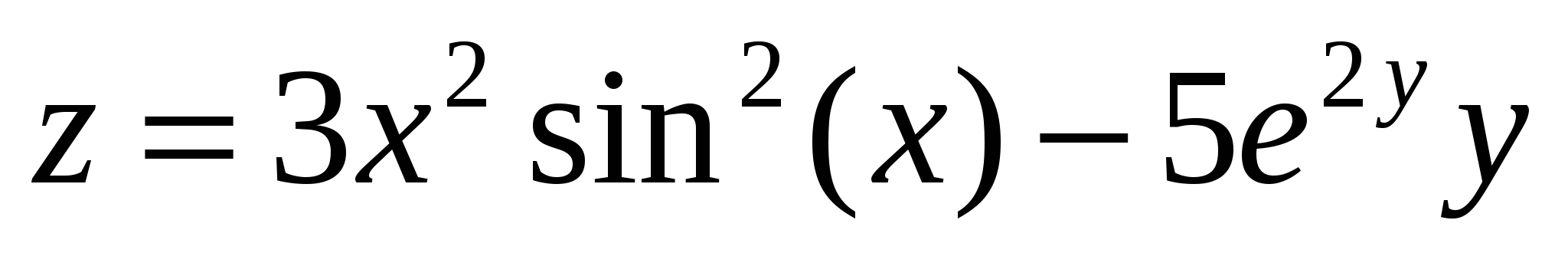 при при 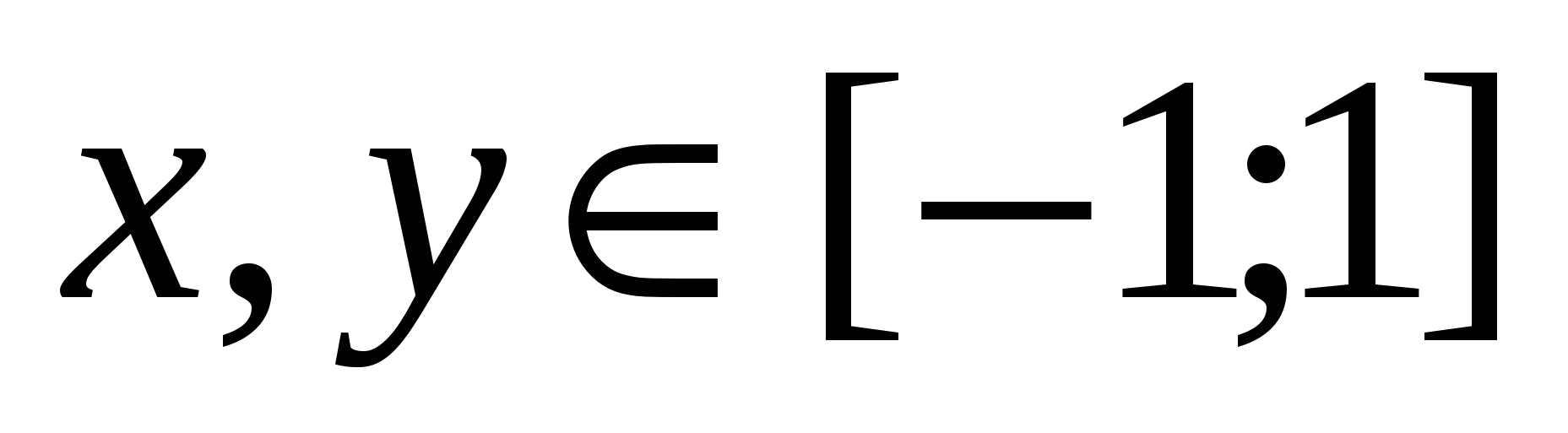 . .
Лабораторная работа №6. “Применение массивов
в решении экономических задач”
Задания
I. Выполнить следующие задания с помощью средств Microsoft Excel в соответствии с номером варианта (номер варианта выбирается по номеру студента в списке).
Вариант 1
-
Решить системы линейных уравнений AX=B, A3X=B и вычислить значение квадратичной формы Z=YTATA2Y, где
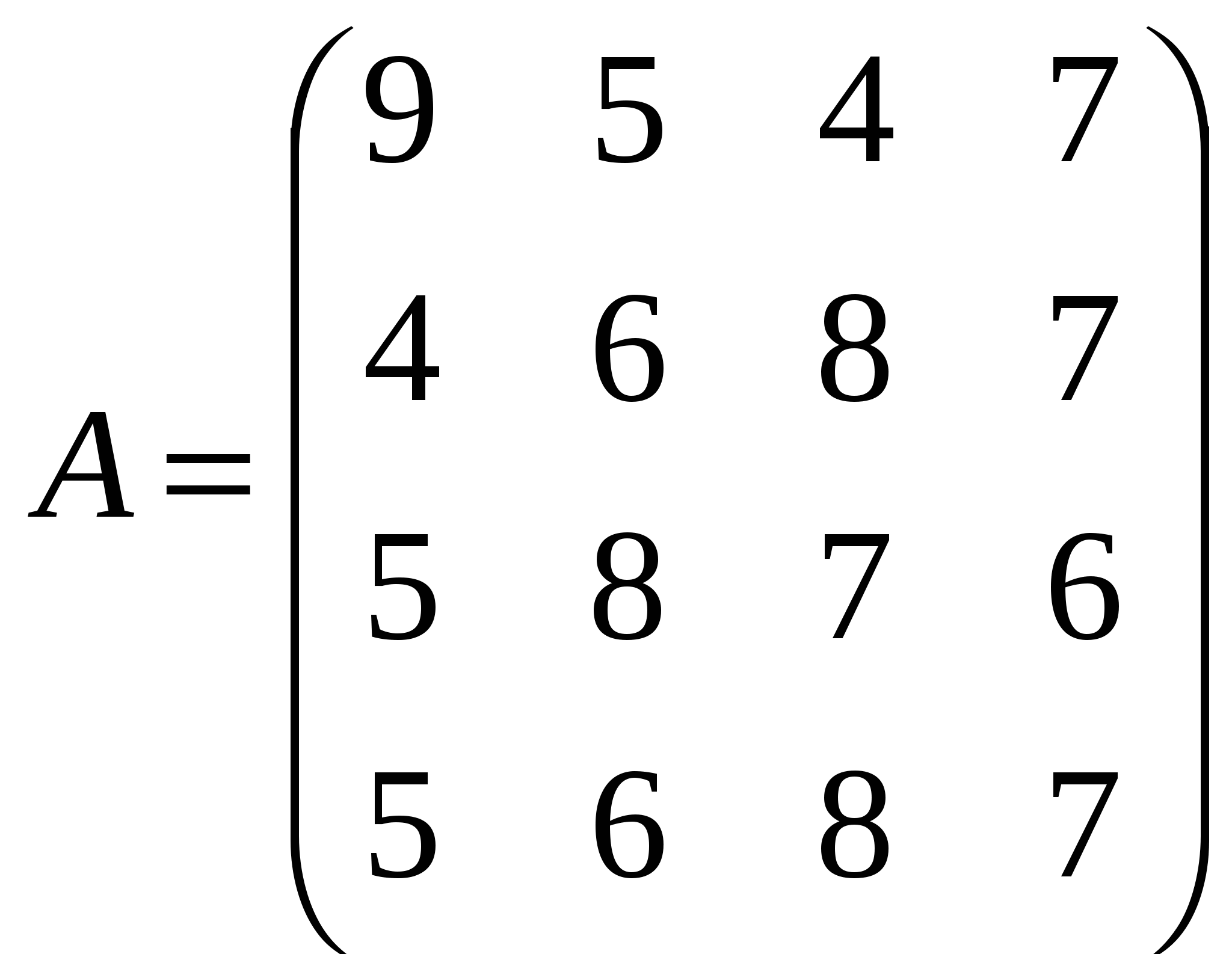 , , 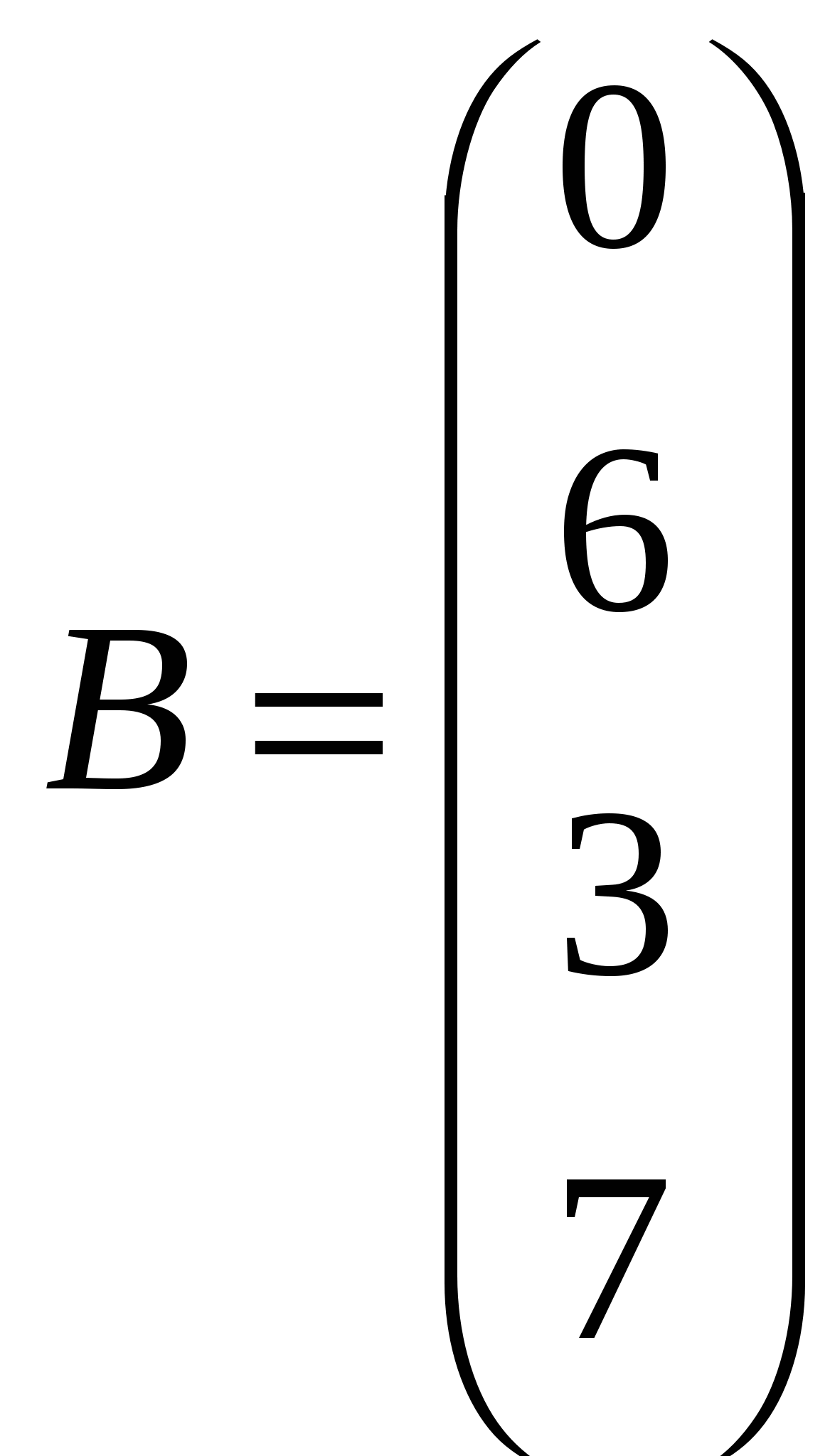 , , 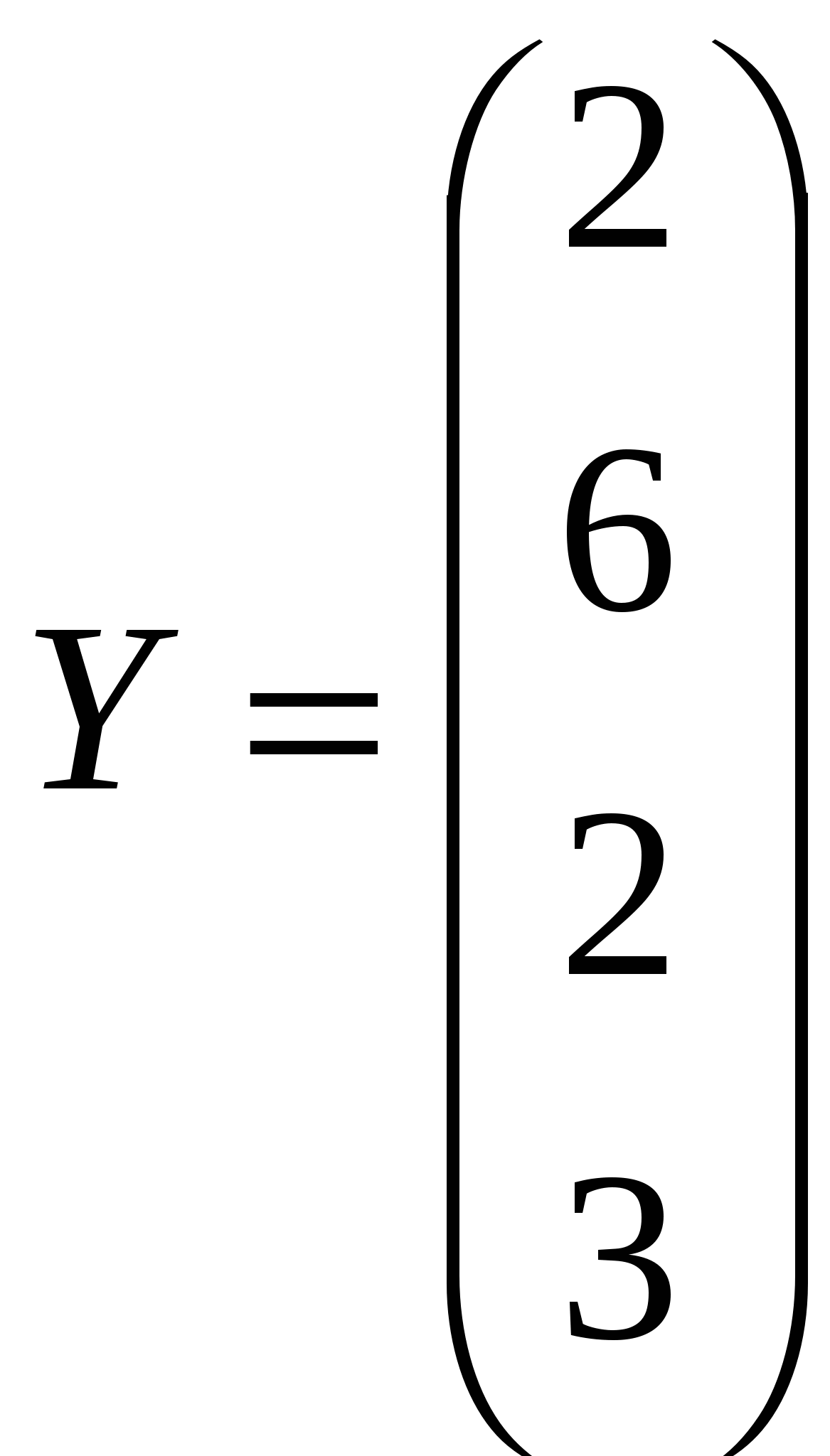
-
Вычислить:
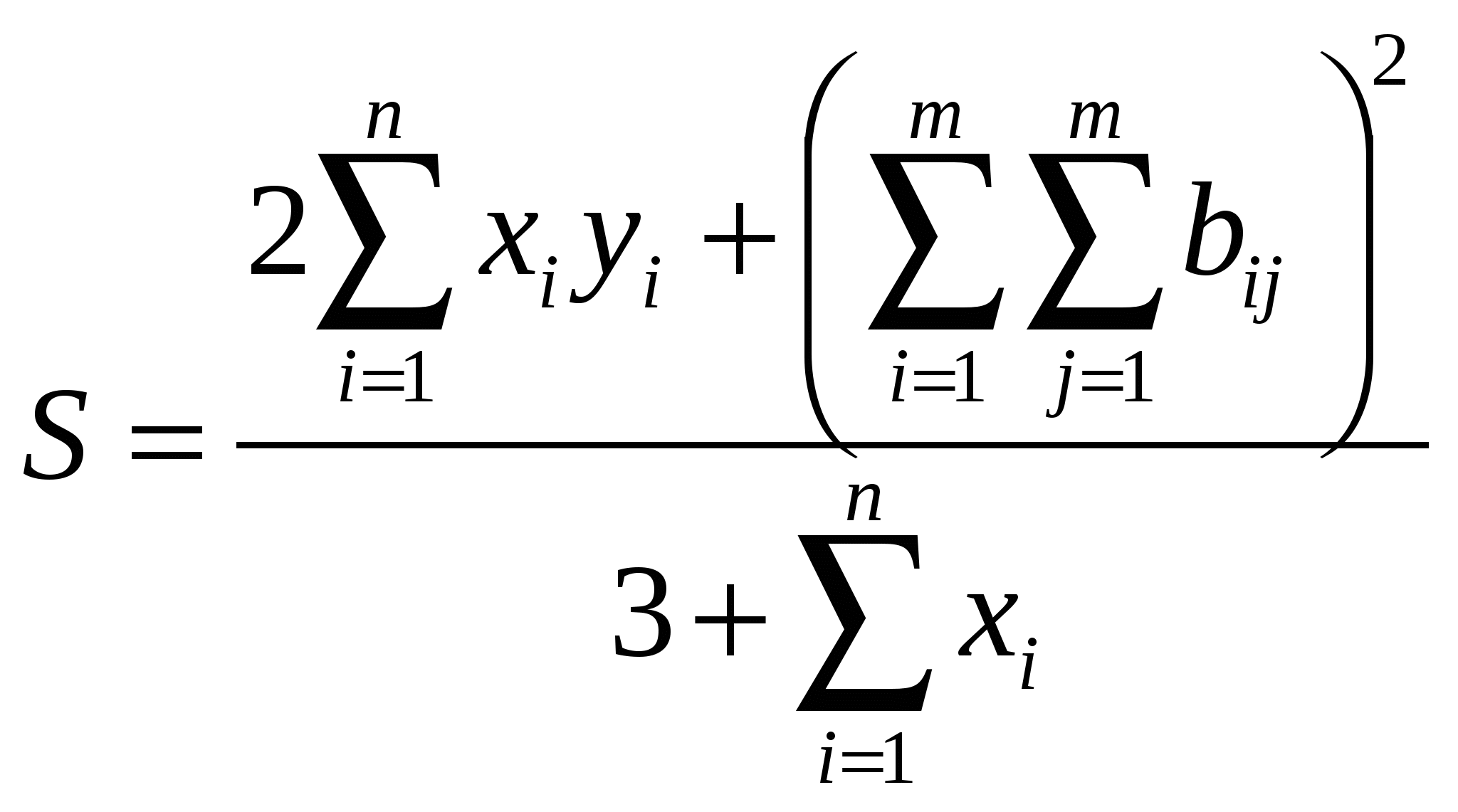 , ,
где x, y – векторы из n компонентов, b – матрица размера mxm, причем n=4, m=2 и
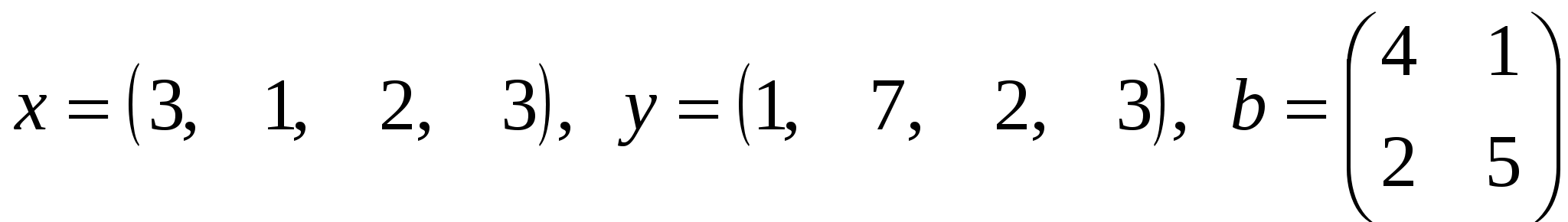 . .
Вариант 2
-
Решить системы линейных уравнений АХ=B, A2ATX=B вычислить значение квадратной формы Z=YТA3Y, где
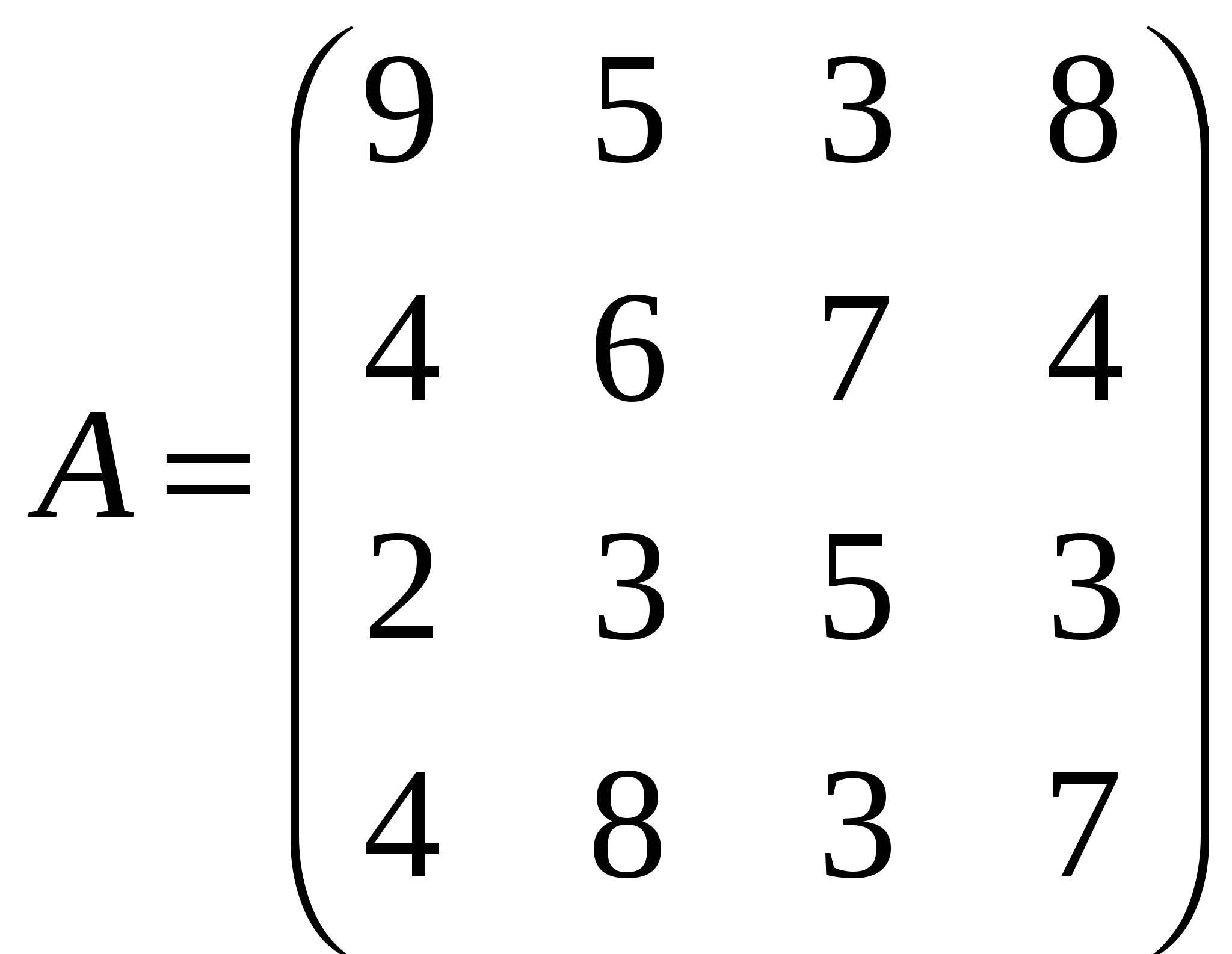 , ,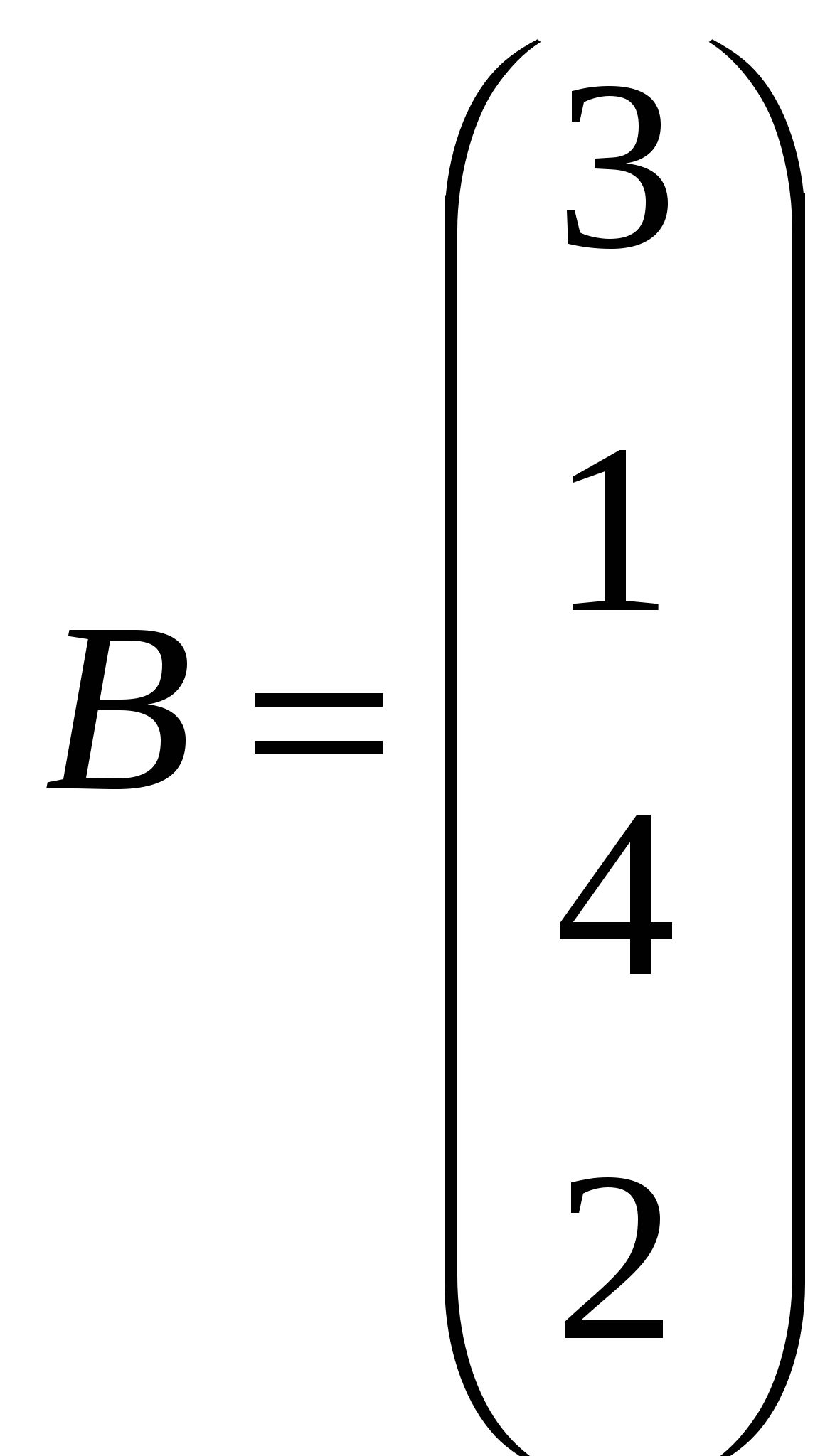 , , 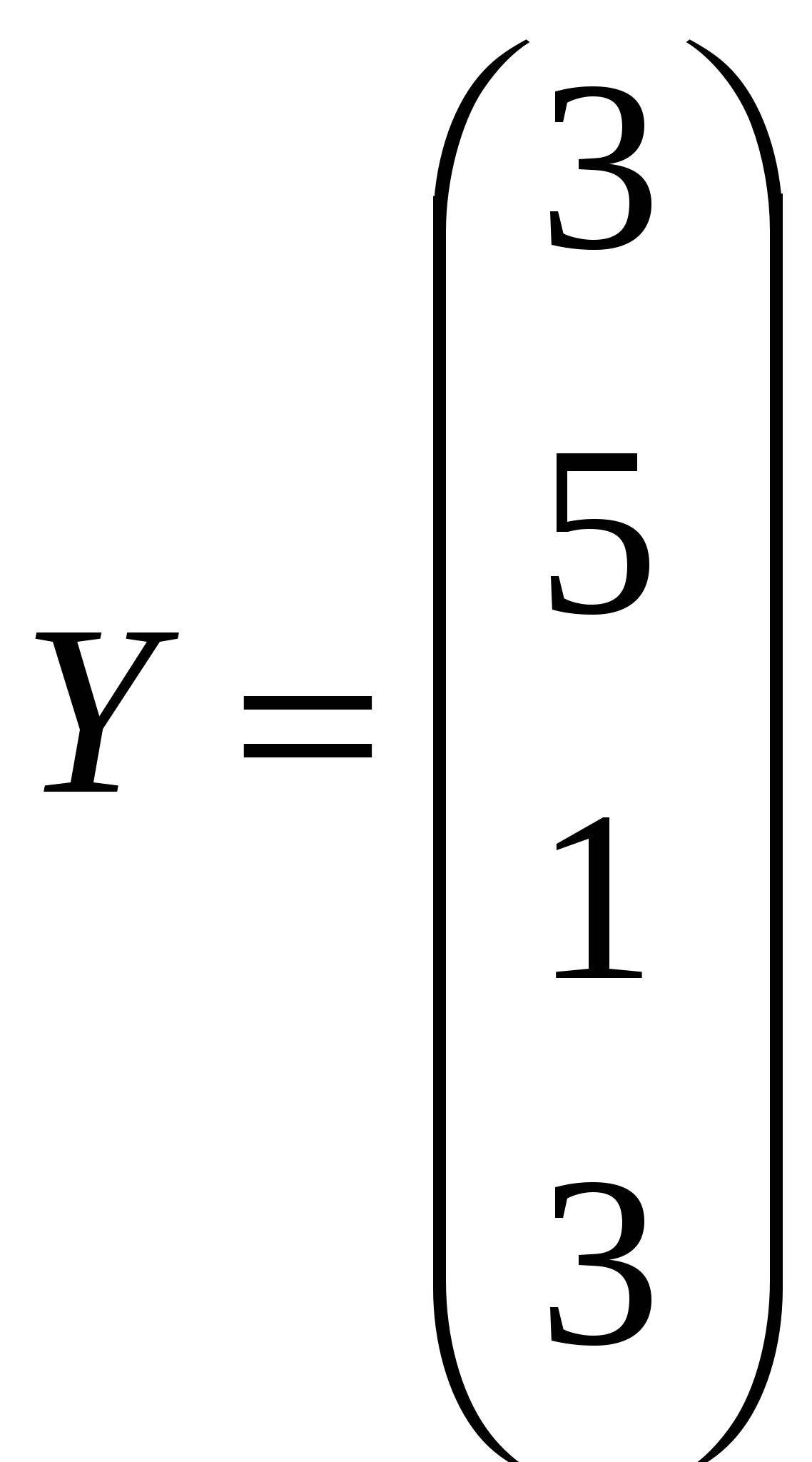
-
Вычислить
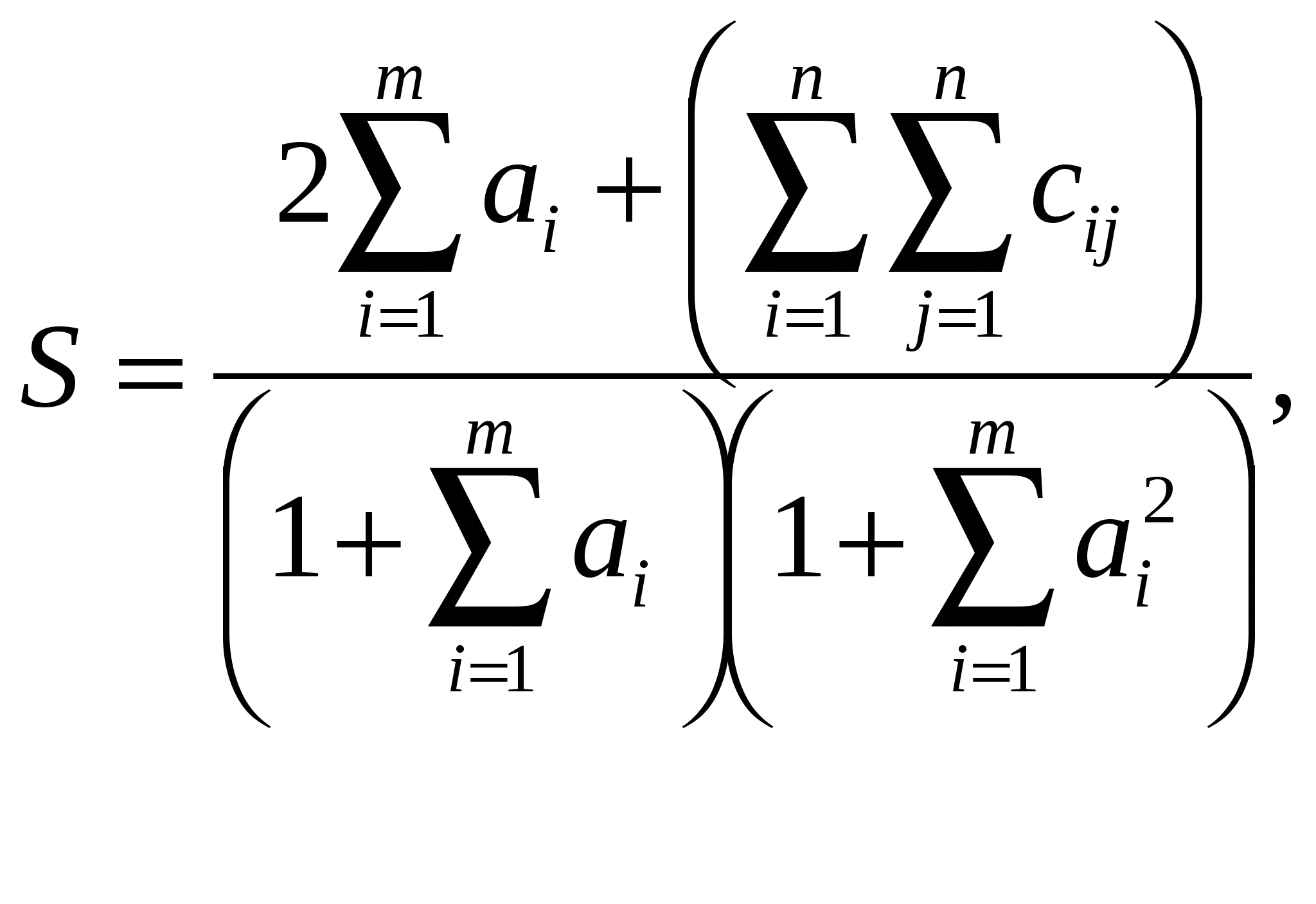
где a – вектор из m – компонентов, с – матрица размера nxn, причем n=3, m=4
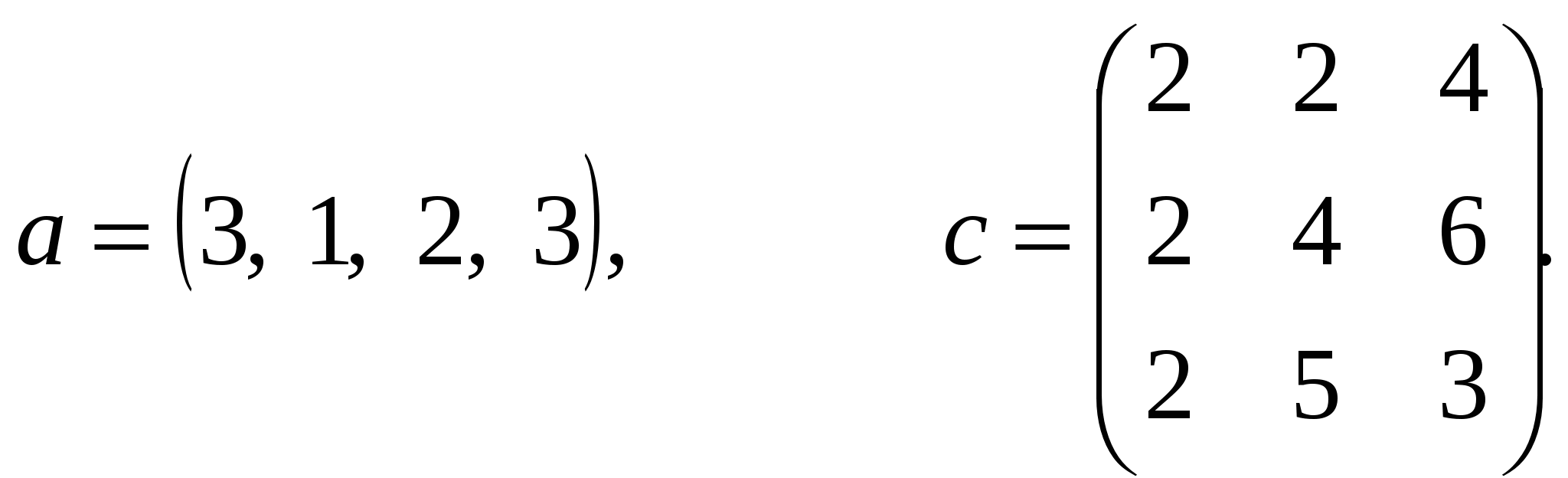
Вариант 3
-
Решить системы линейных уравнений AX=B, AАТАХ=B и вычислить значение квадратичной формы Z=YTATA3Y, где
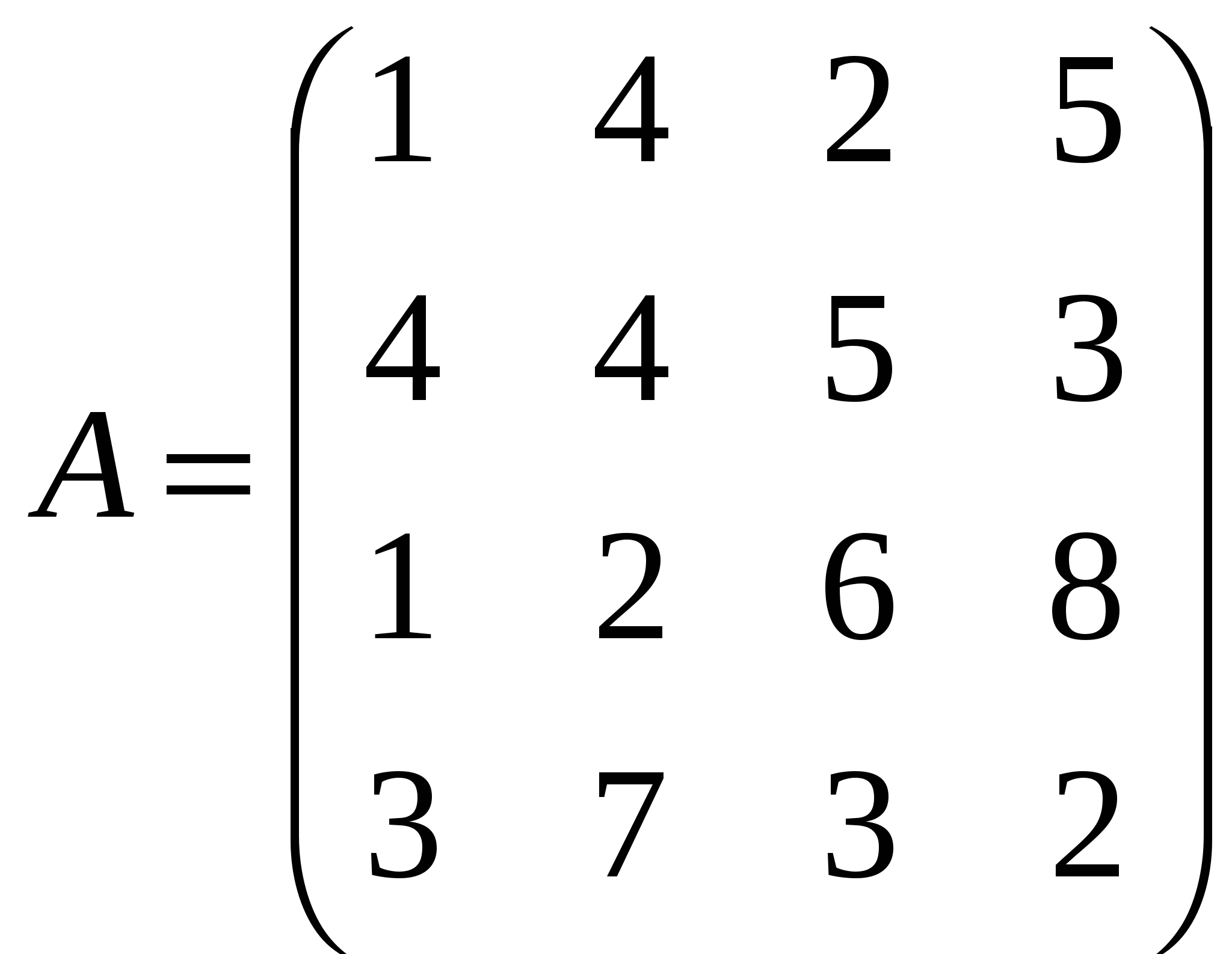 , , 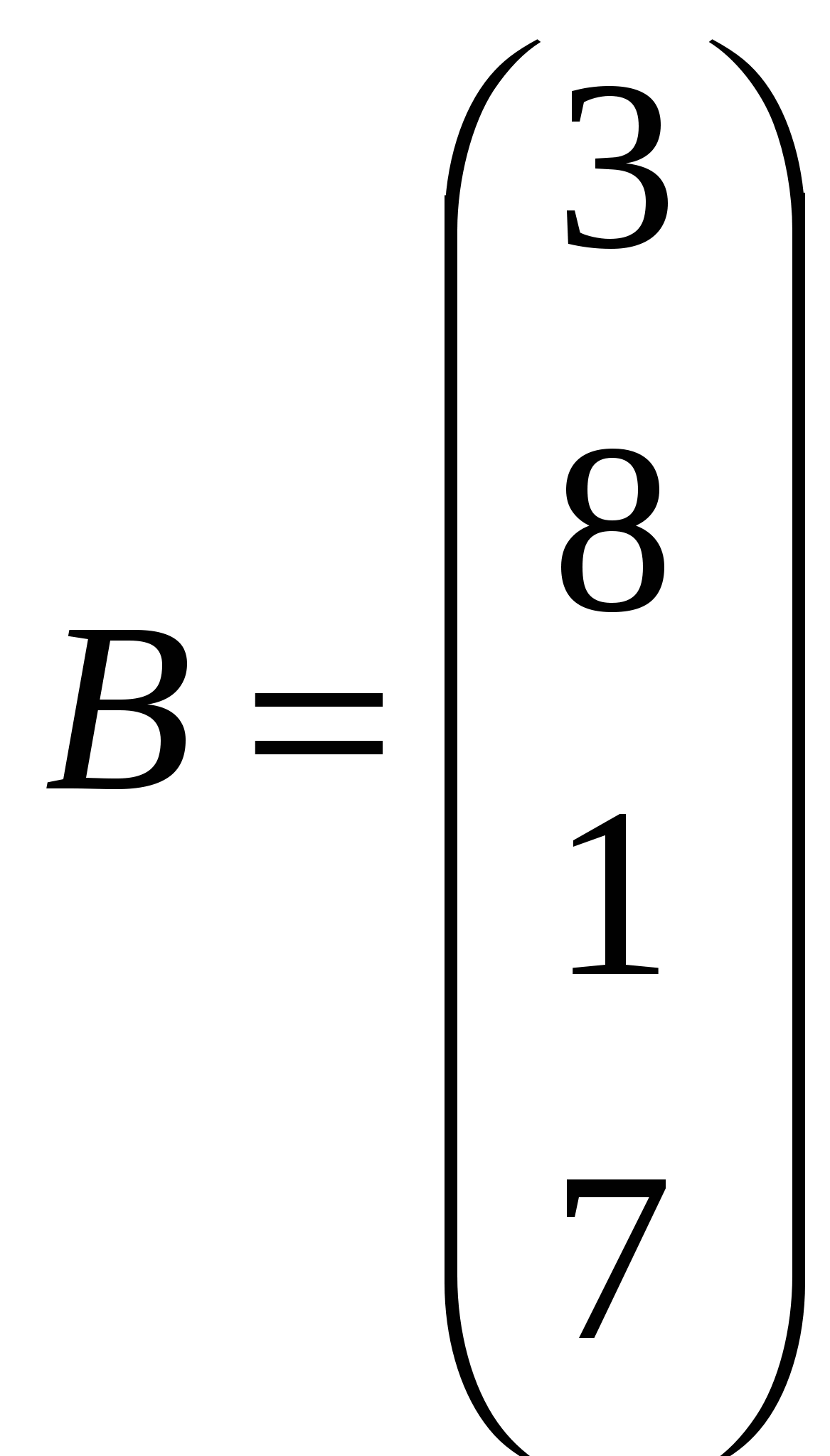 , , 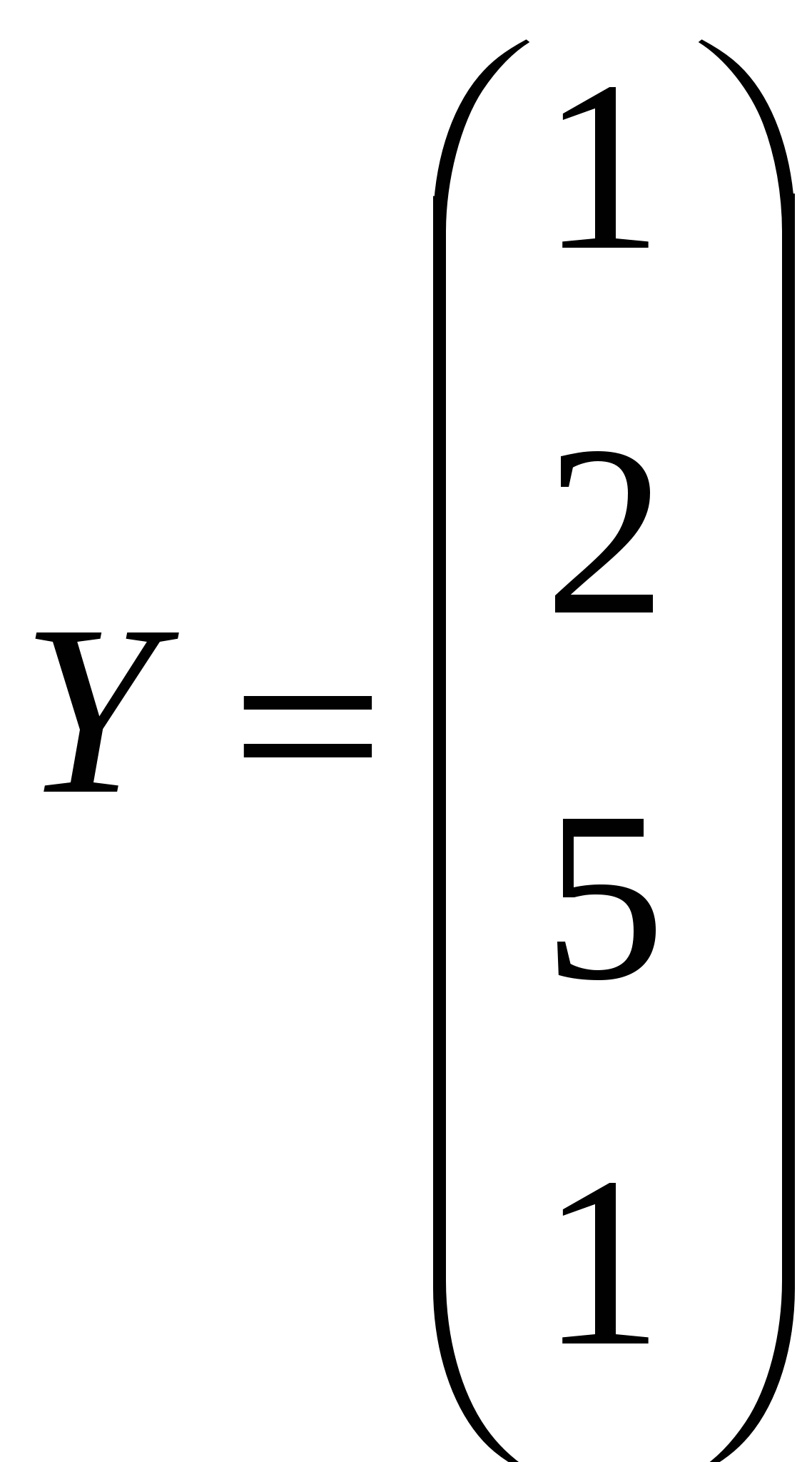 . .
-
Вычислить
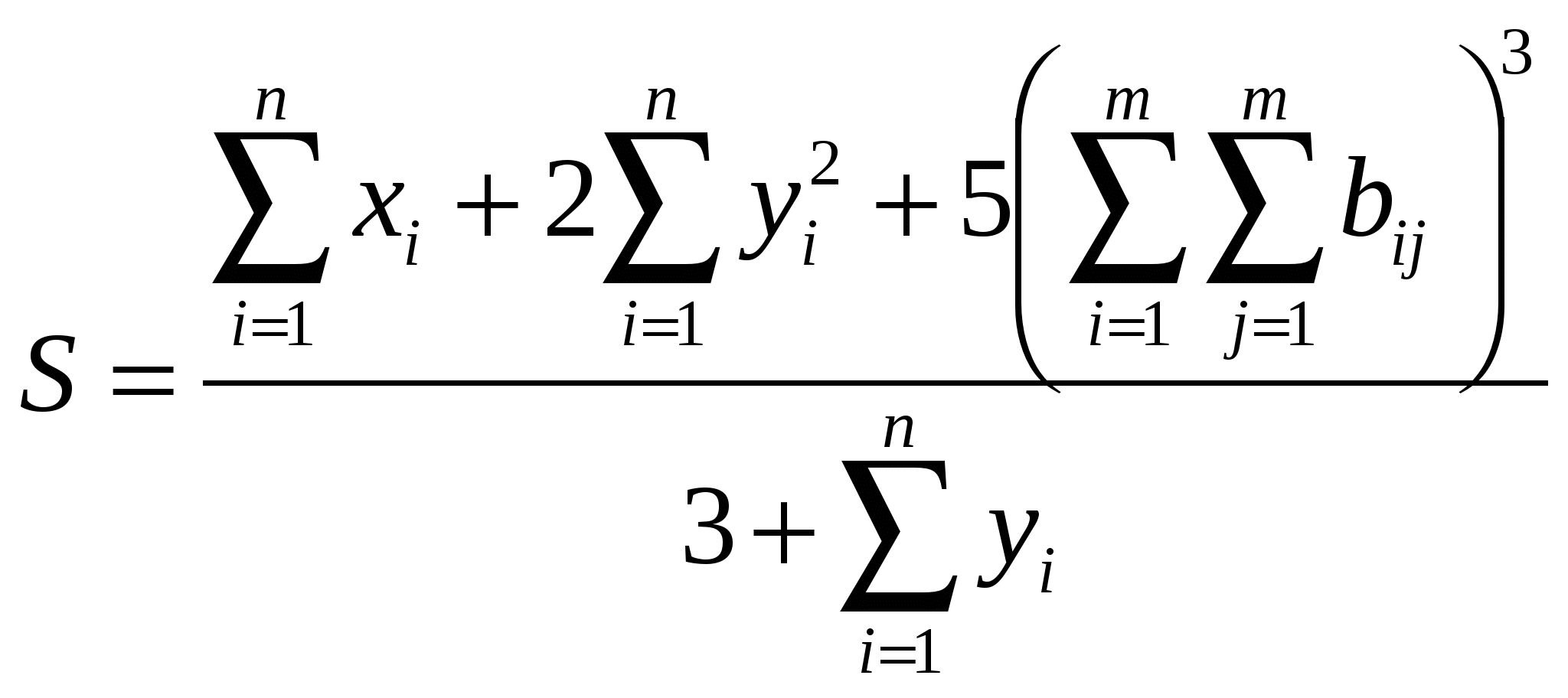 , ,
где x, y – векторы из n компонентов, b – матрица размерности mxm, причем n= 4, m = 2 и
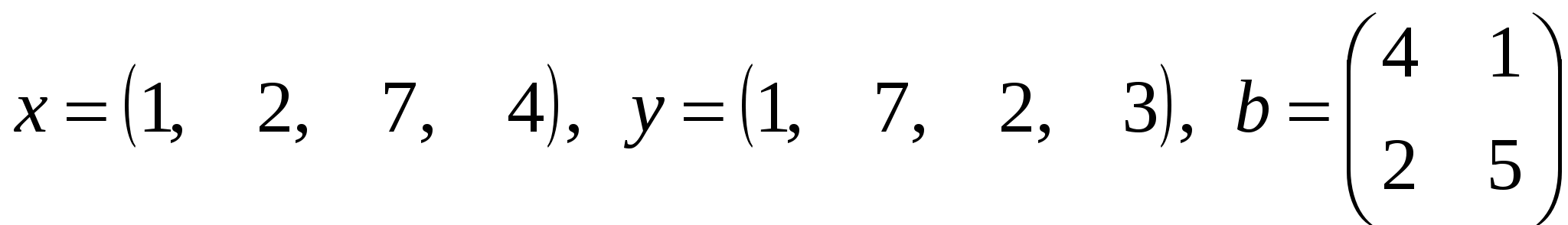
Вариант 4
-
Решить системы линейных уравнений AX=B, A2АТАХ=B и вычислить значение квадратичной формы Z=YTATAАTY, где
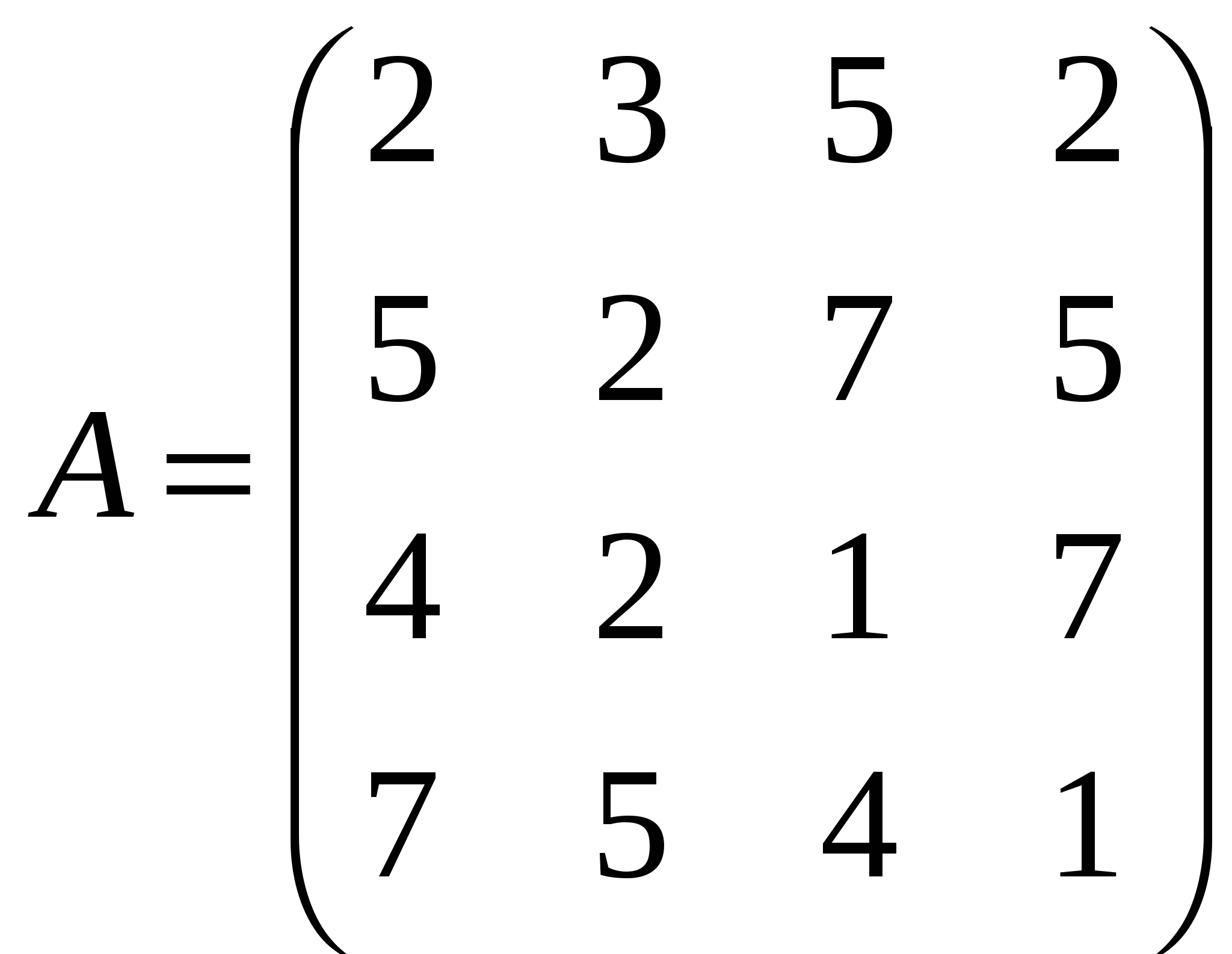 , , 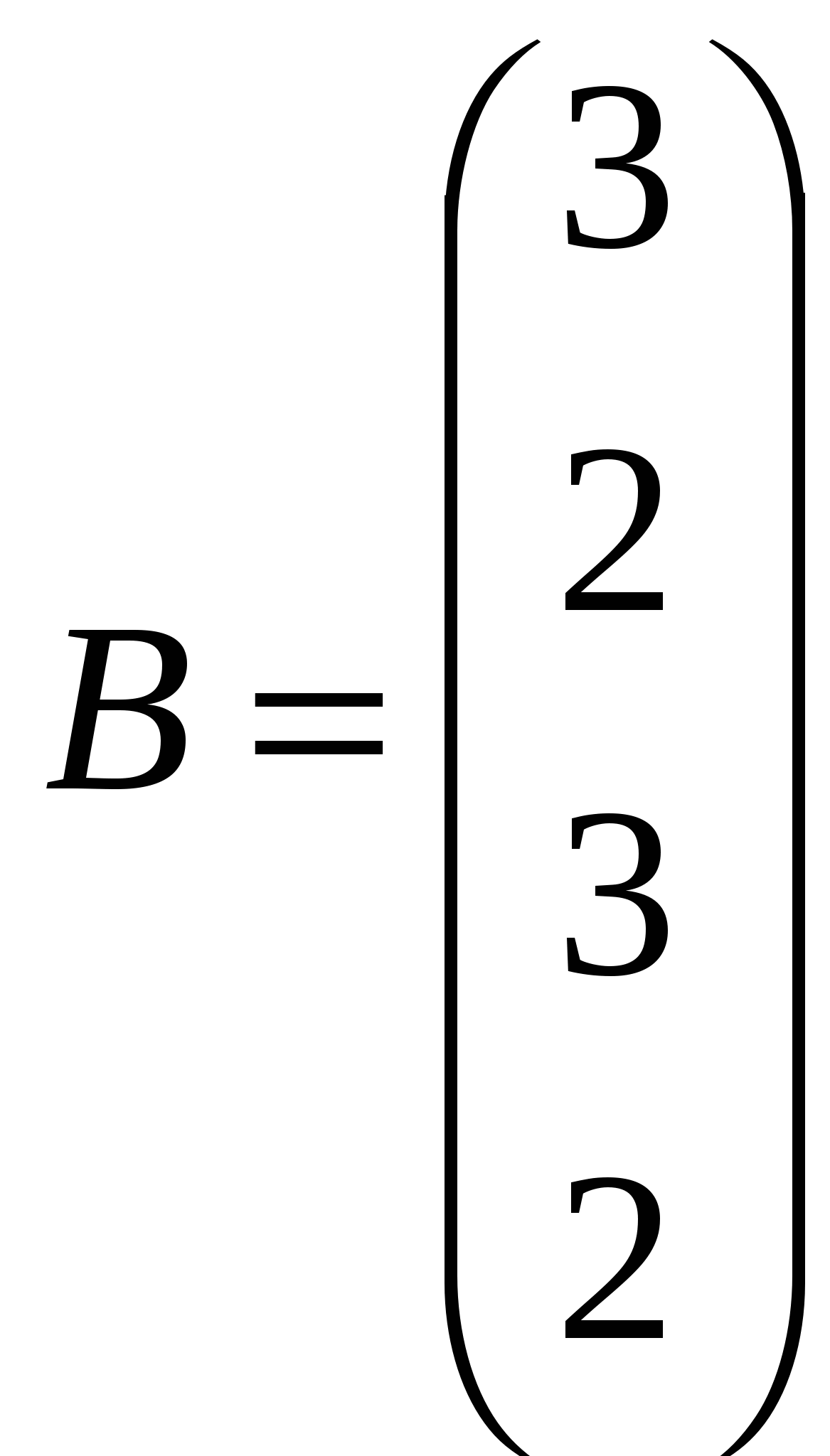 , , 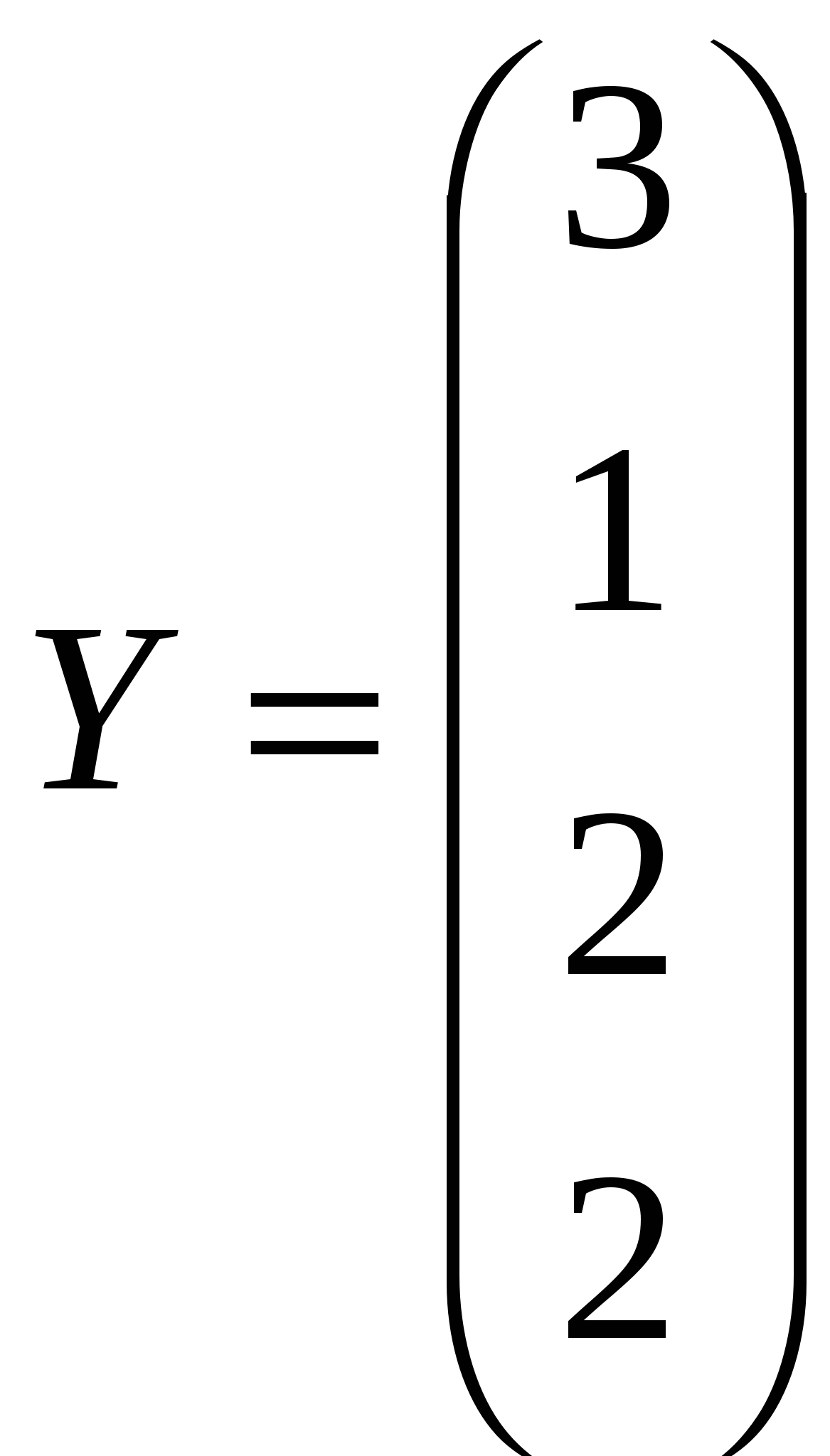 . .
-
Вычислить
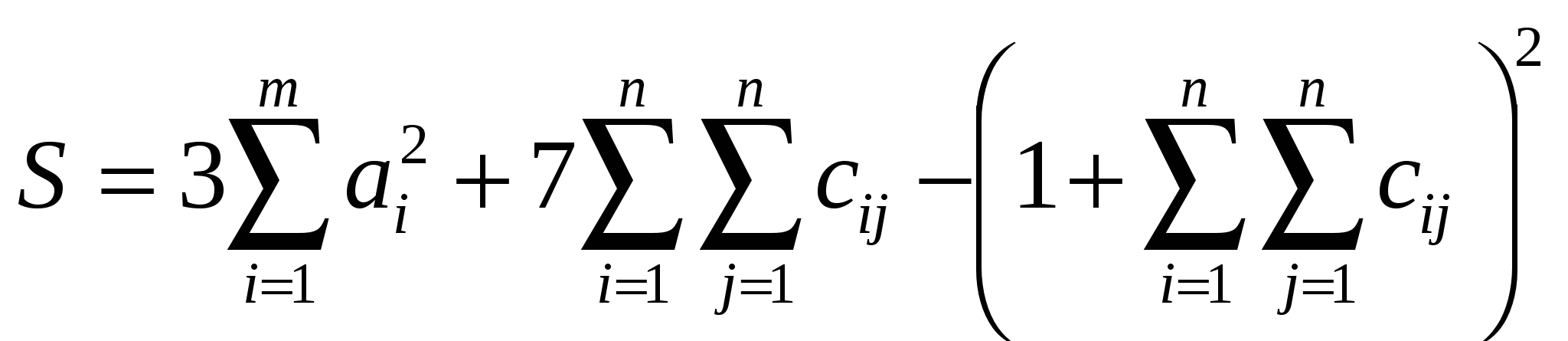 , ,
где a – векторы из m компонентов, c – матрица размера nxn, причем n= 3, m=4 и
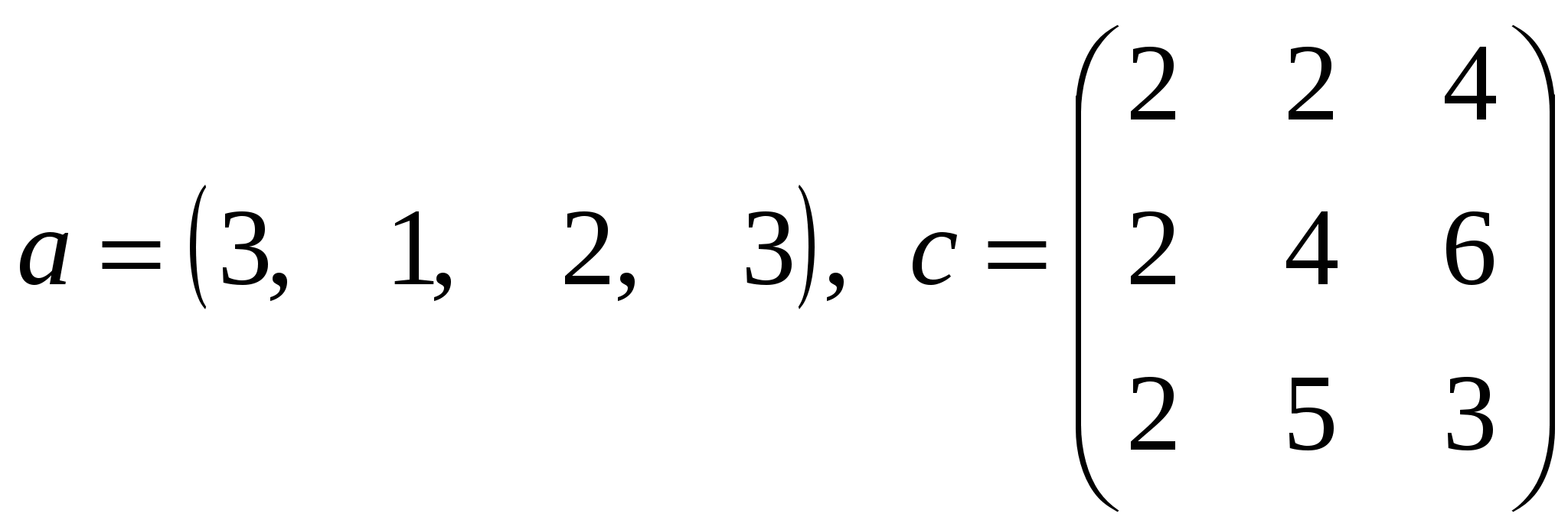 . .
Вариант 5
-
Решить системы линейных уравнений AX=B, AАТА2Х=B и вычислить значение квадратичной формы Z=YTA3ATY, где
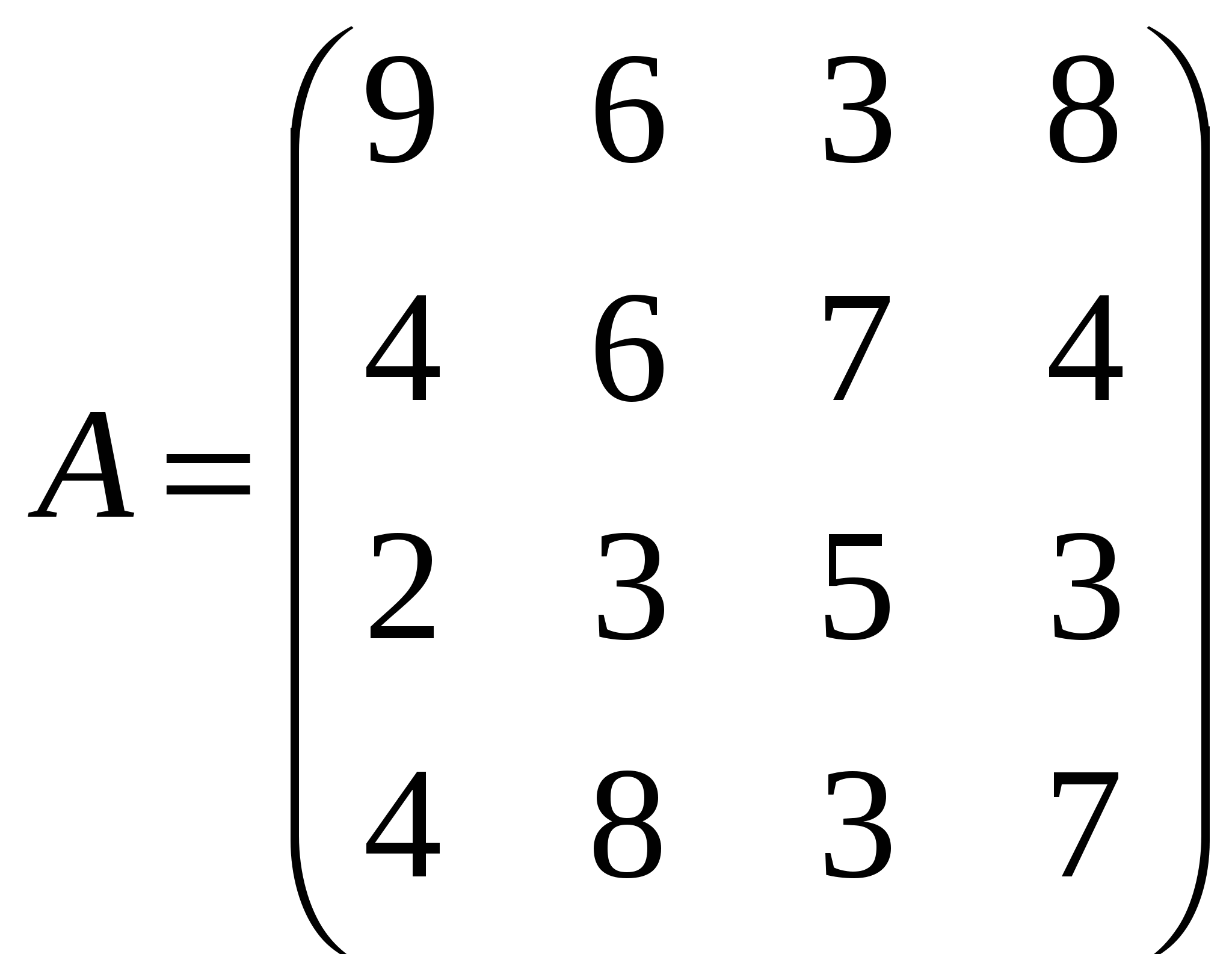 , , 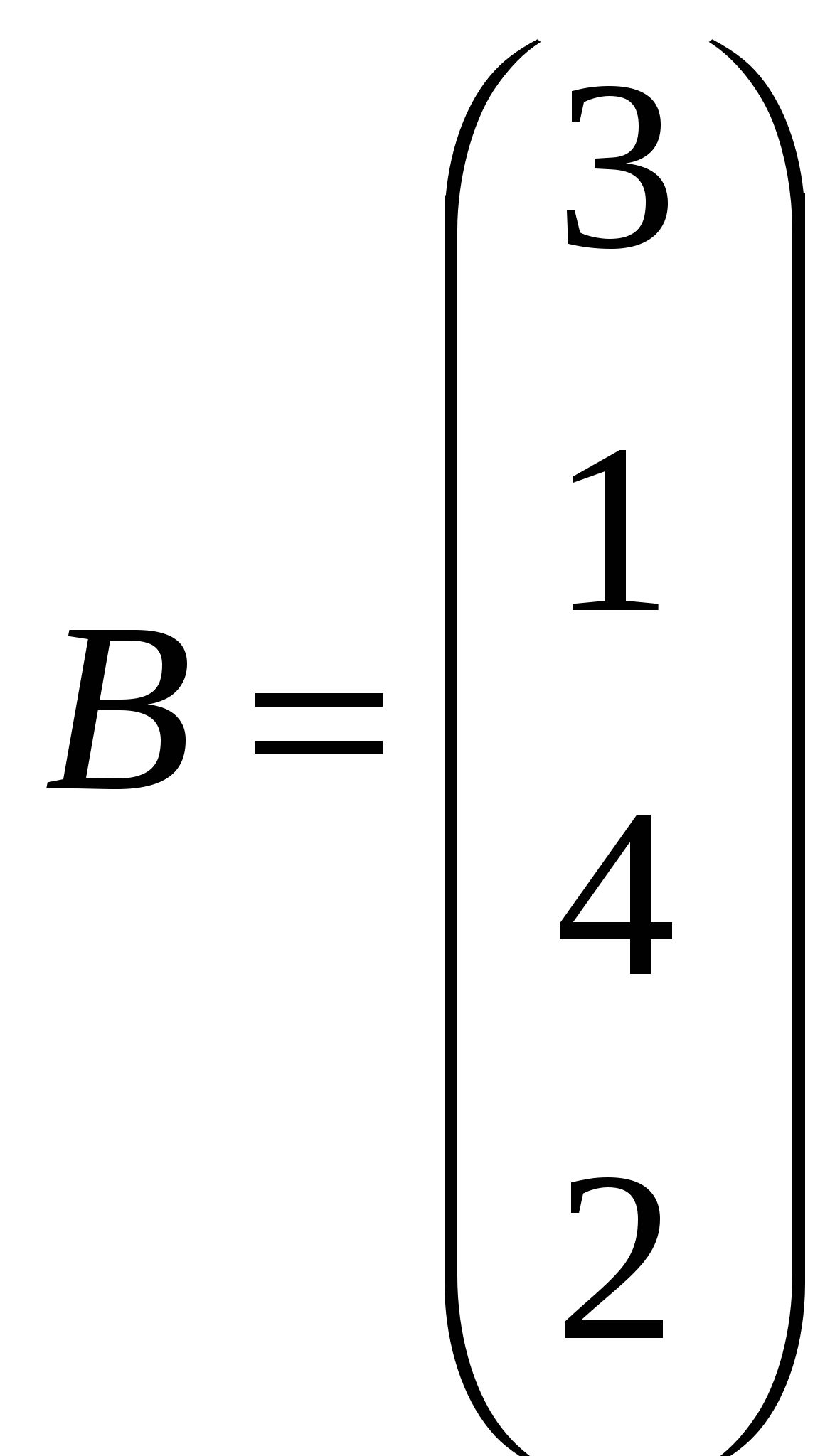 , , 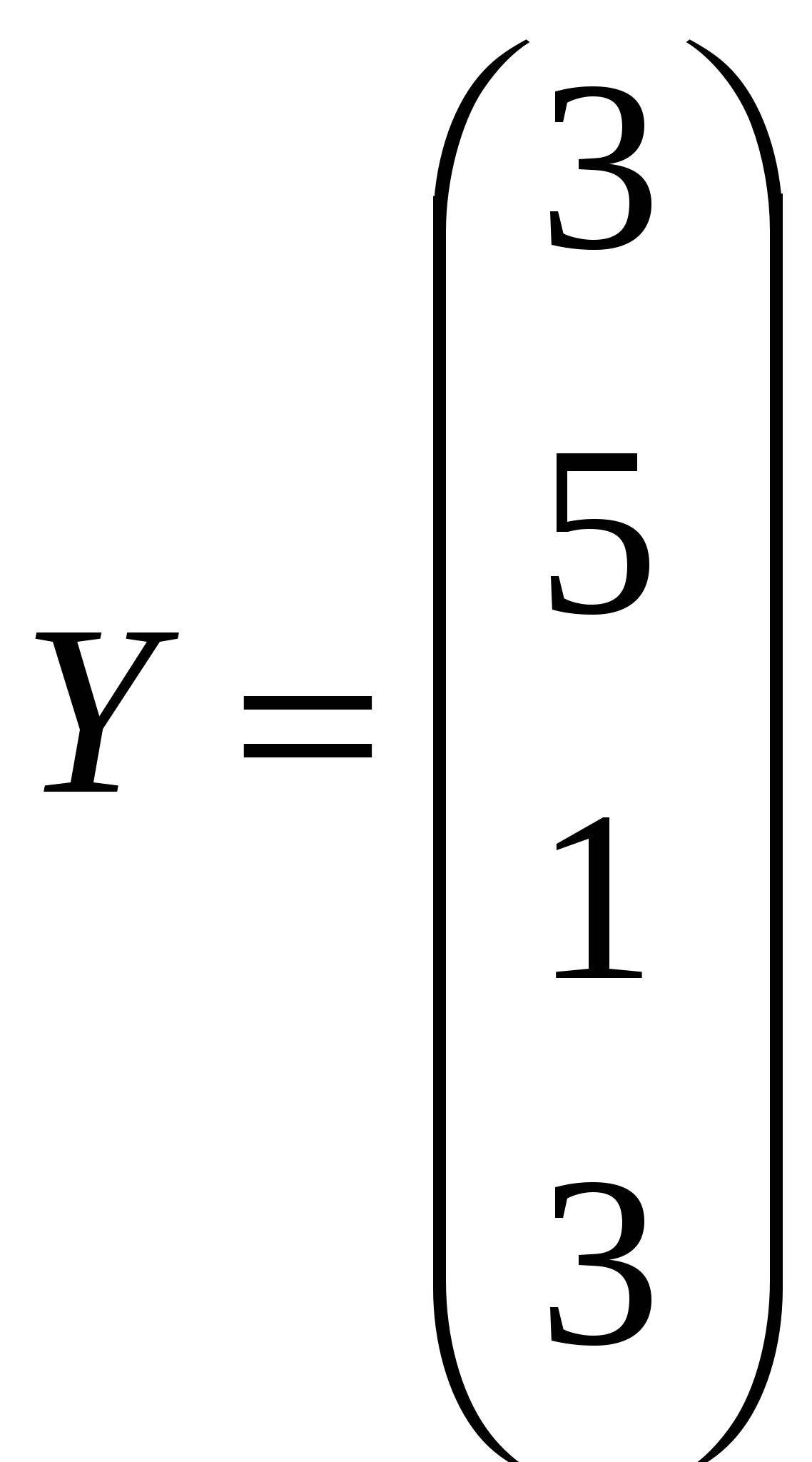 . .
-
Вычислить
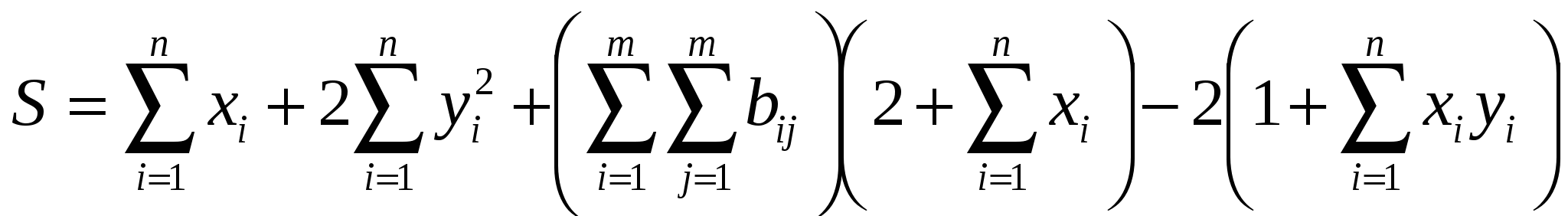 , ,
где x, y – векторы из n компонентов, b – матрица размера mxm, причем n = 4, m = 2 и
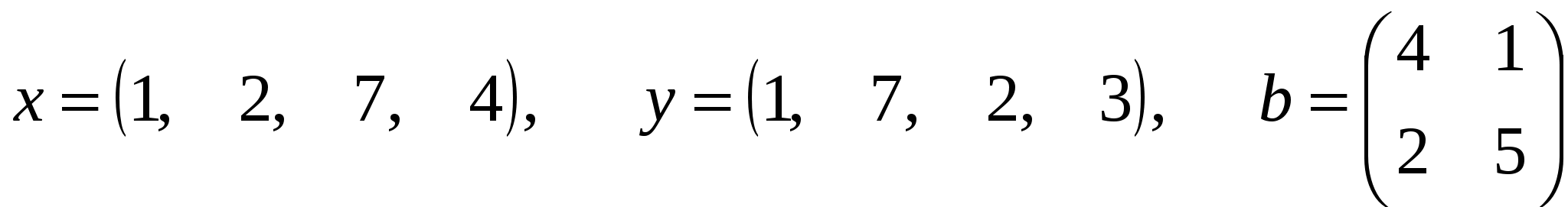 . .
Вариант 6
1.Решить системы линейных уравнений AX=B, A3ATX=B и вычислить значение квадратной формы Z=YTА2ATAY, где
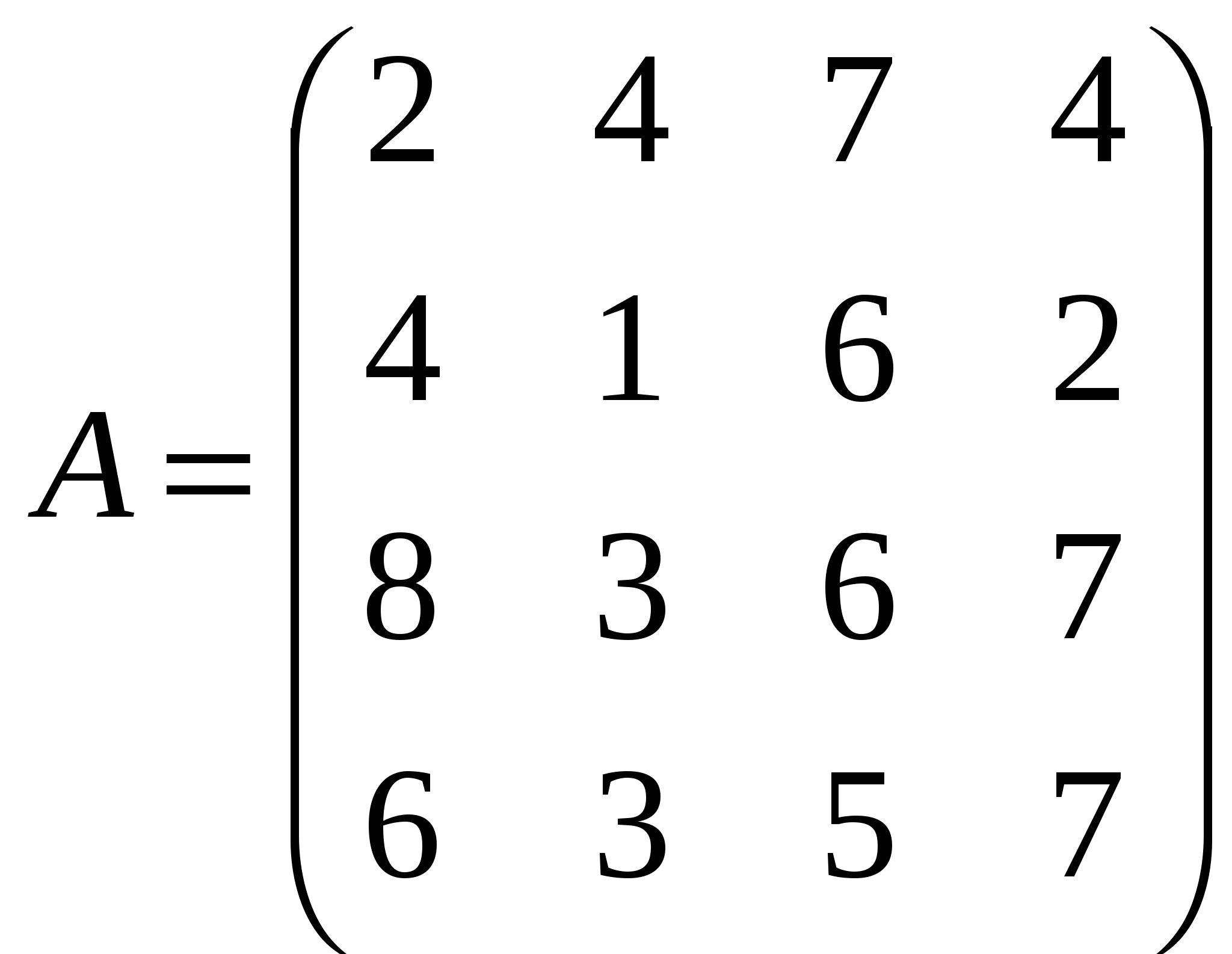 , ,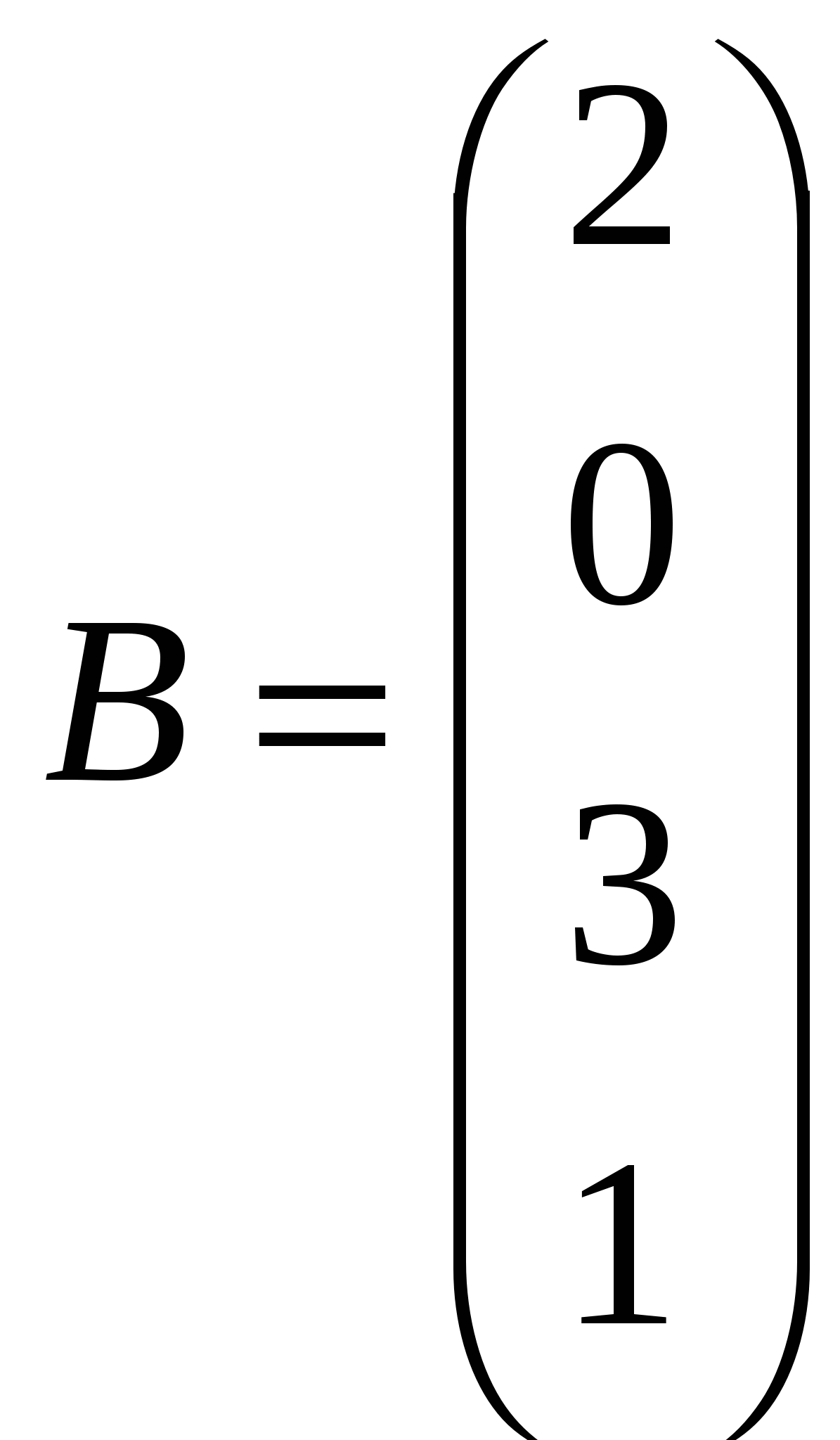 , , 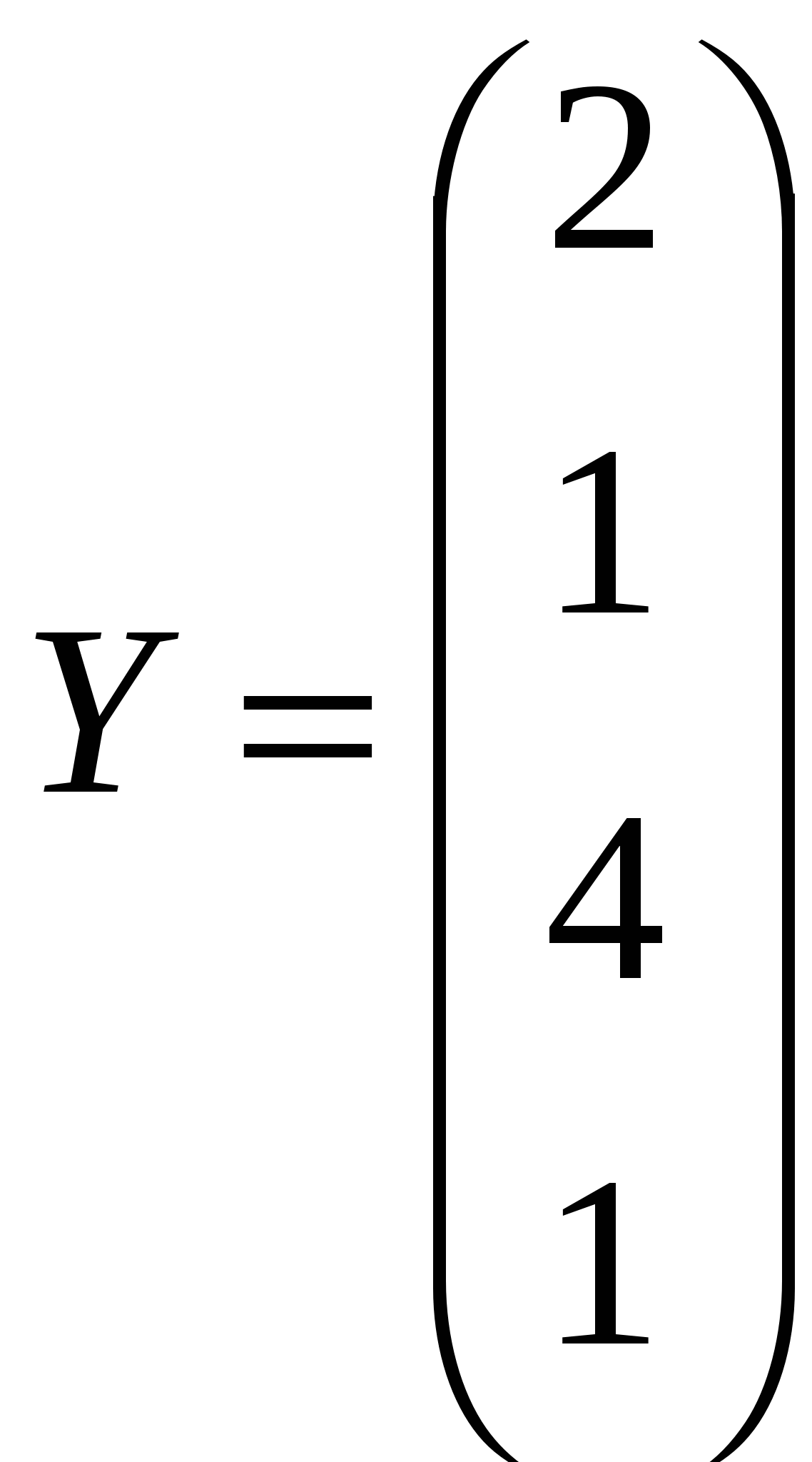
-
Вычислить
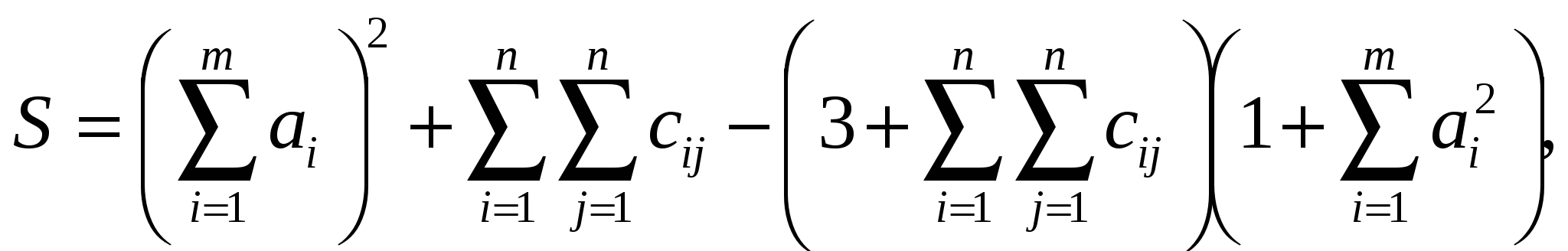
где a – вектор из m – компонентов, с – матрица размера nxn, причем n=3, m=4
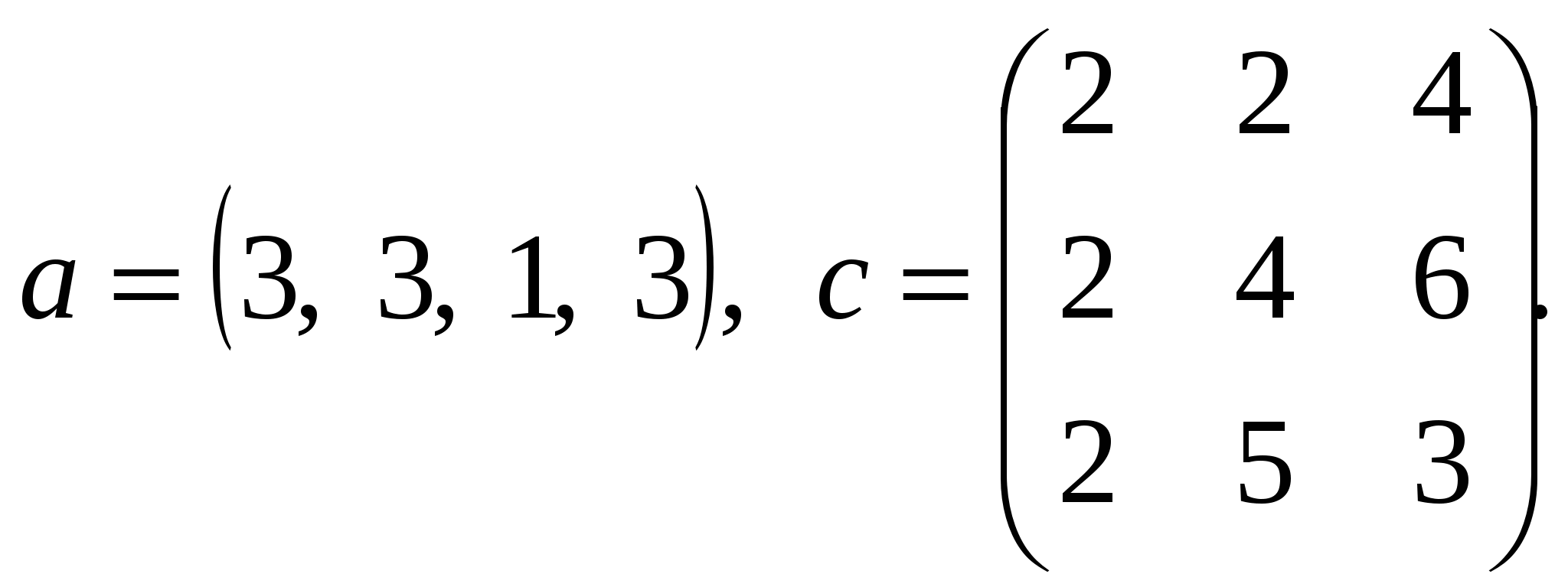
Вариант 7
-
Решить системы линейных уравнений AX=B, АТА3Х=B и вычислить значение квадратичной формы Z=YTAATA2Y, где
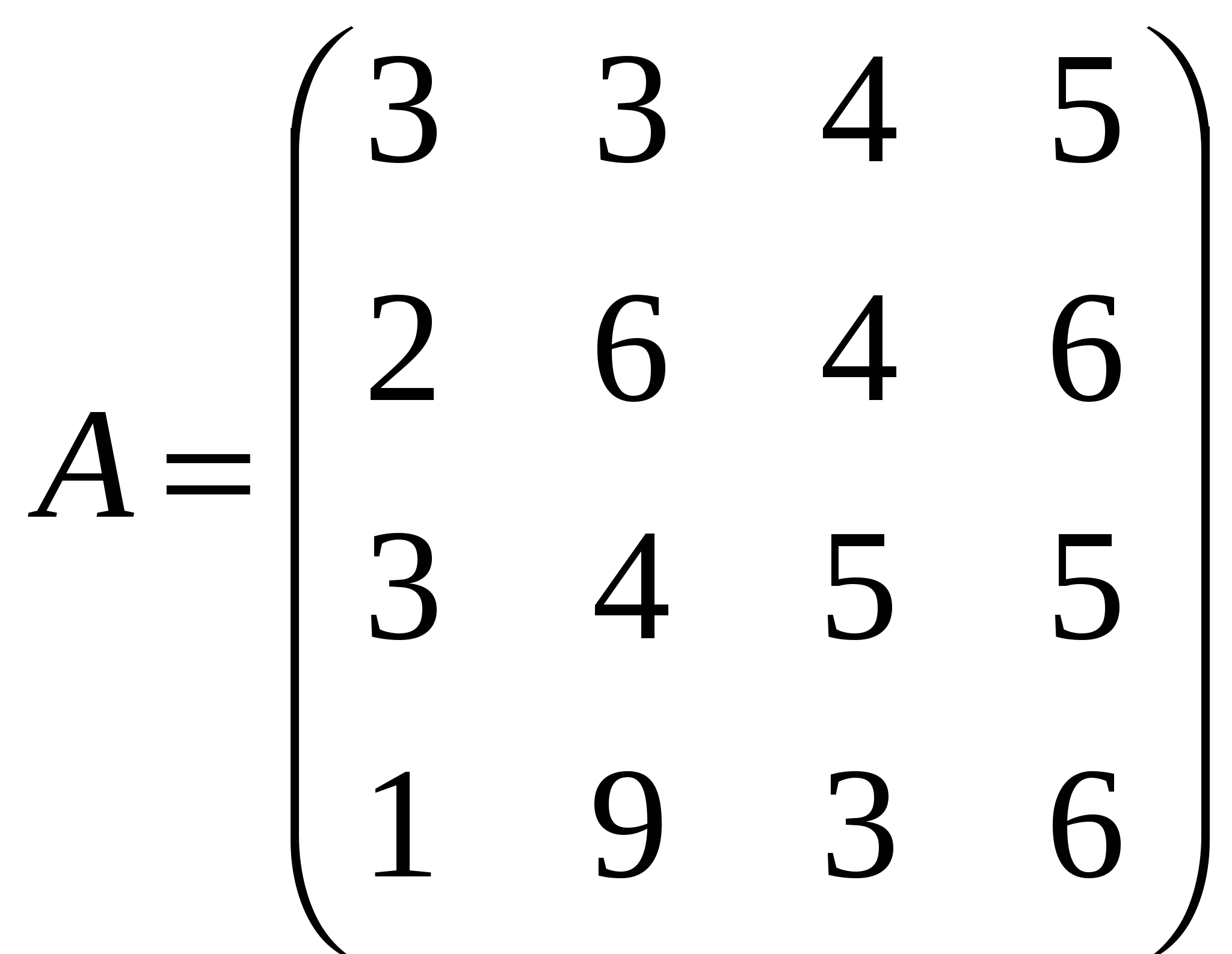 , , 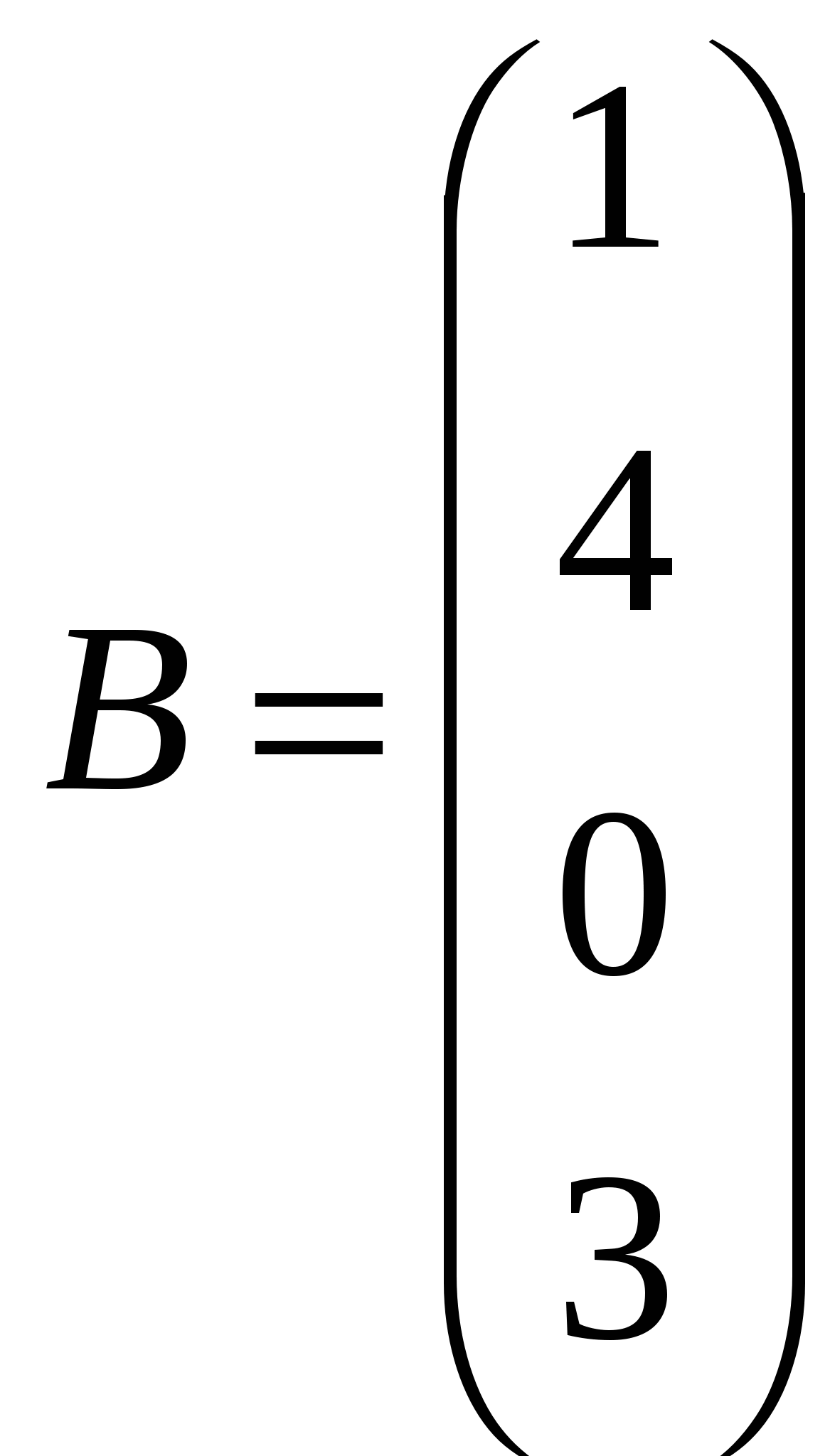 , , 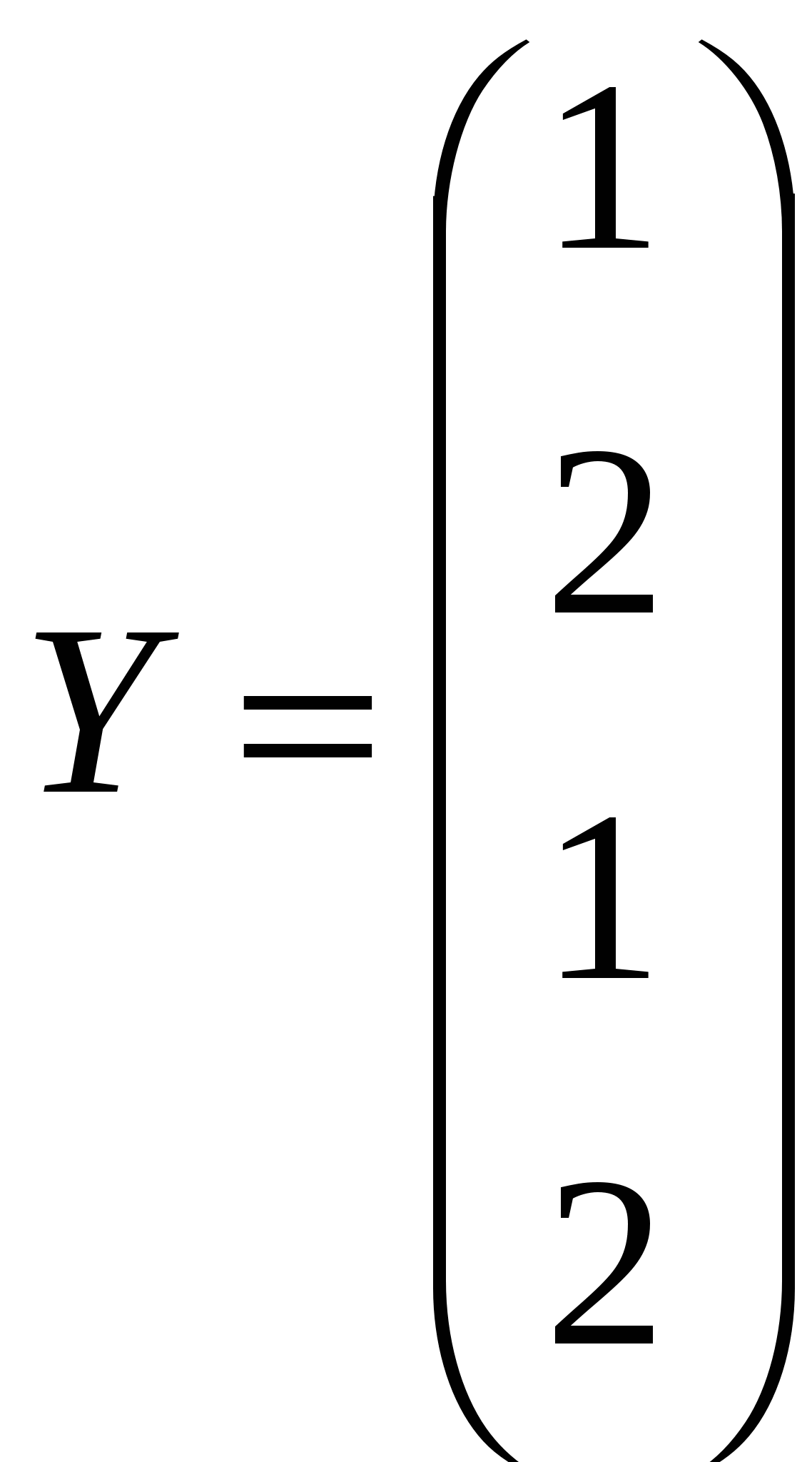 . .
-
Вычислить
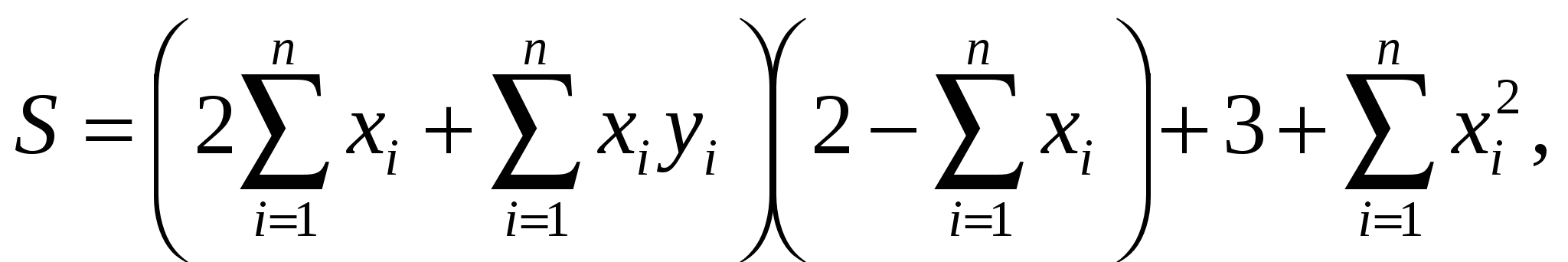
где x, y – векторы из n компонентов, причем n = 4 и
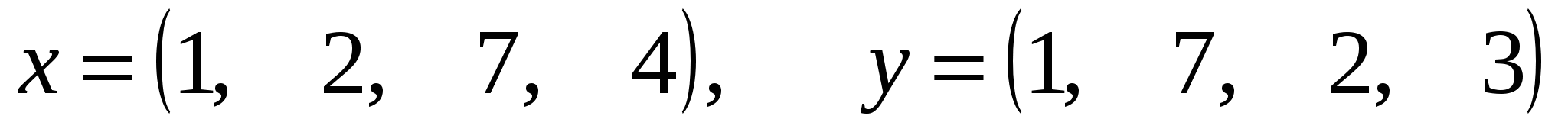 . .
Вариант 8
-
Решить системы линейных уравнений AX=B, AАТА2Х=B и вычислить значение квадратичной формы Z=YTA2ATAY, где
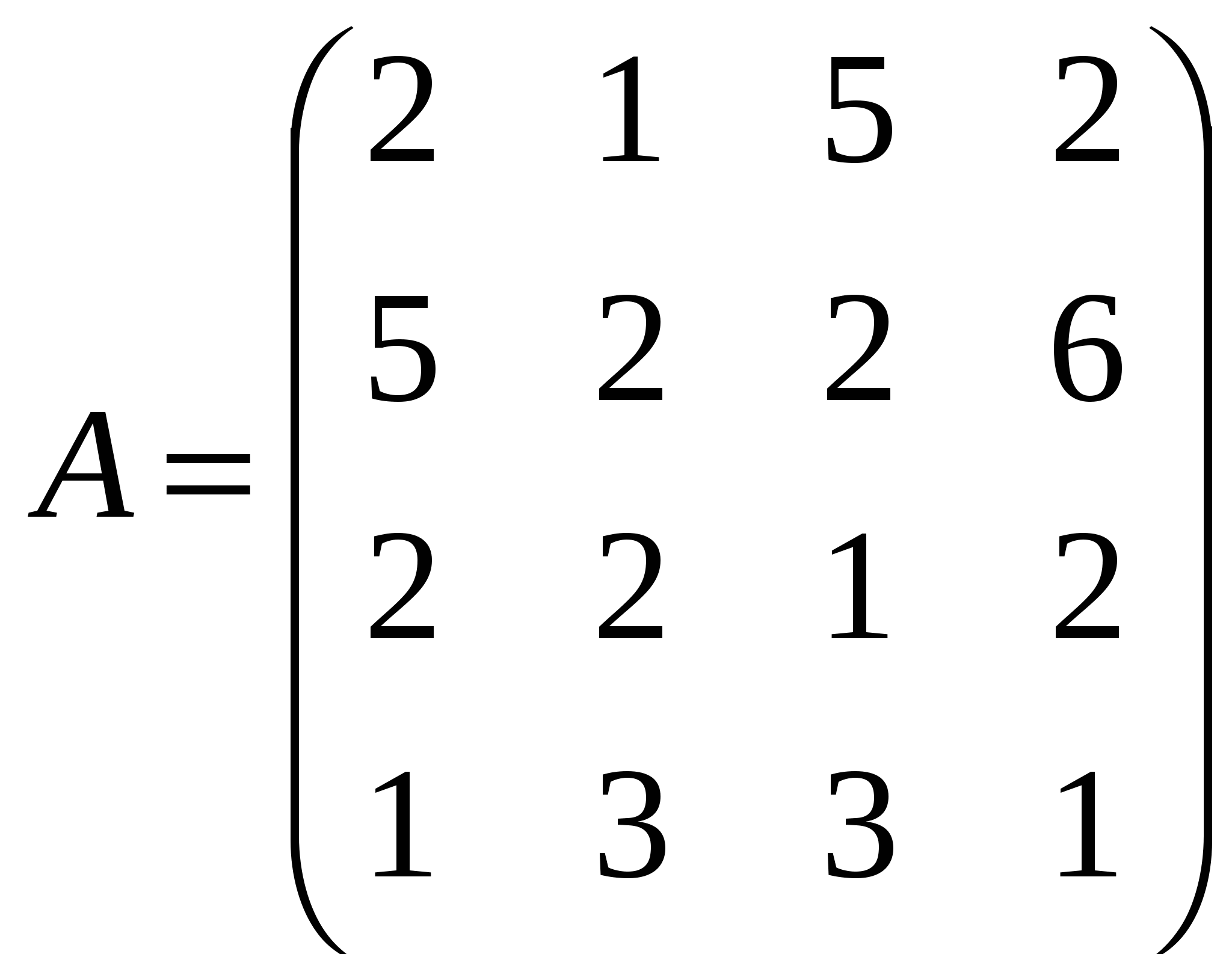 , , 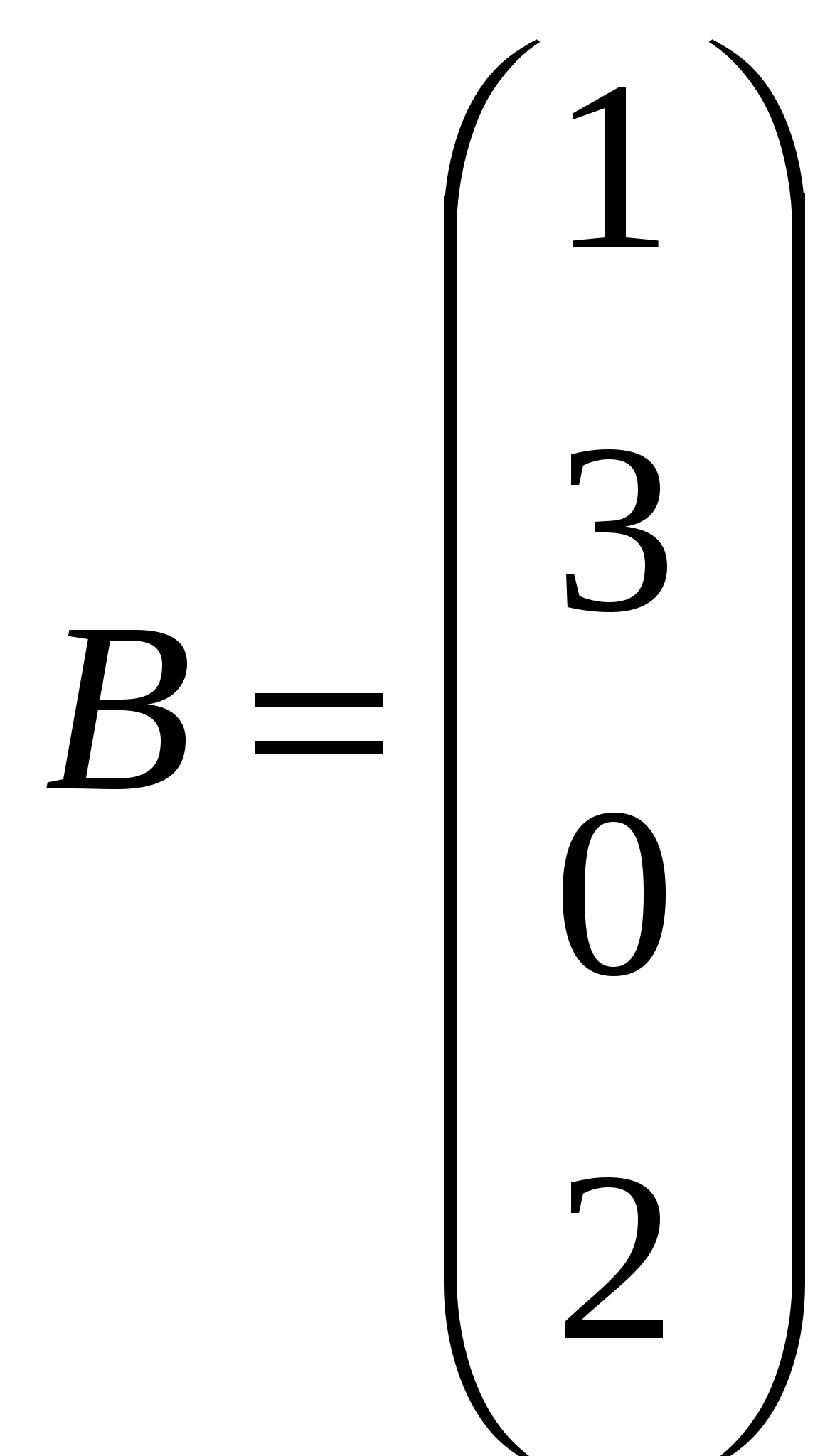 , , 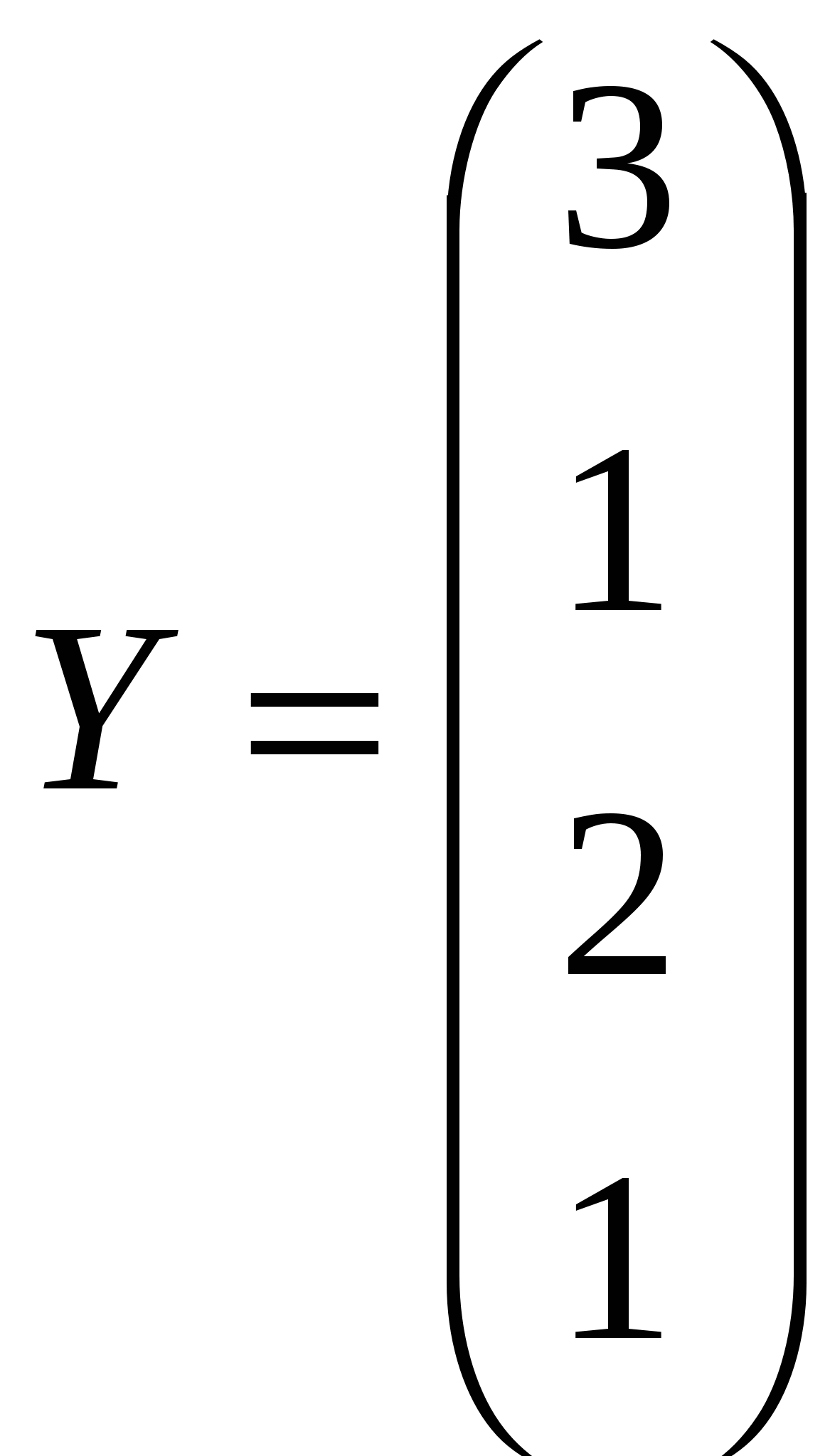 . .
-
Вычислить
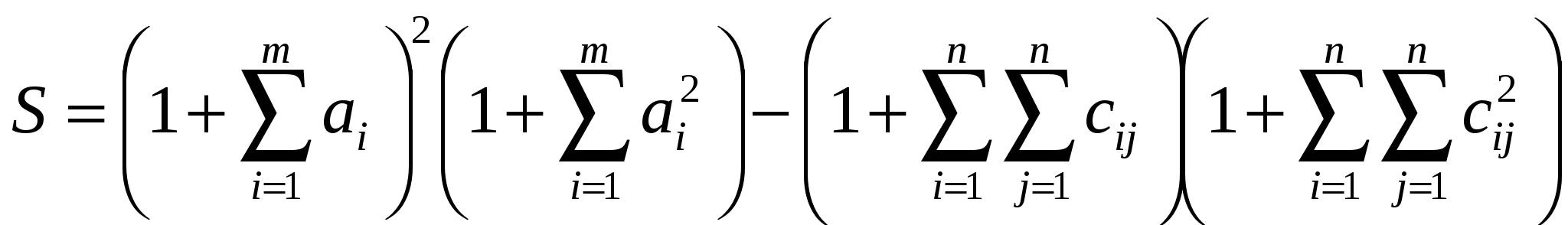 , ,
где a – вектор из m компонентов, c – матрица размера nxn причем n= 2, m= 4 и
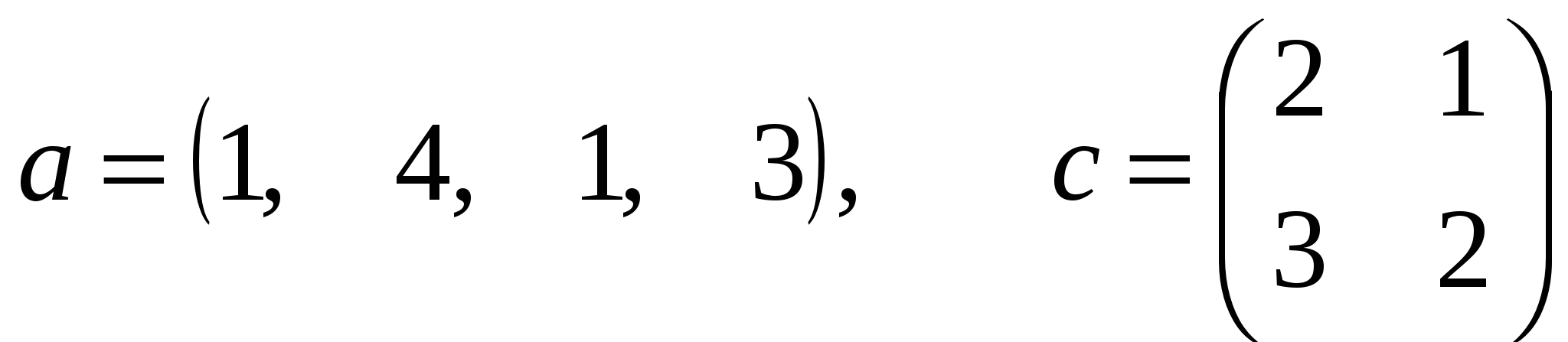 . .
Вариант 9
1. Решить системы линейных уравнений AX=B, ATAATX=B и вычислить значение квадратной формы Z=YTAATAATY, где
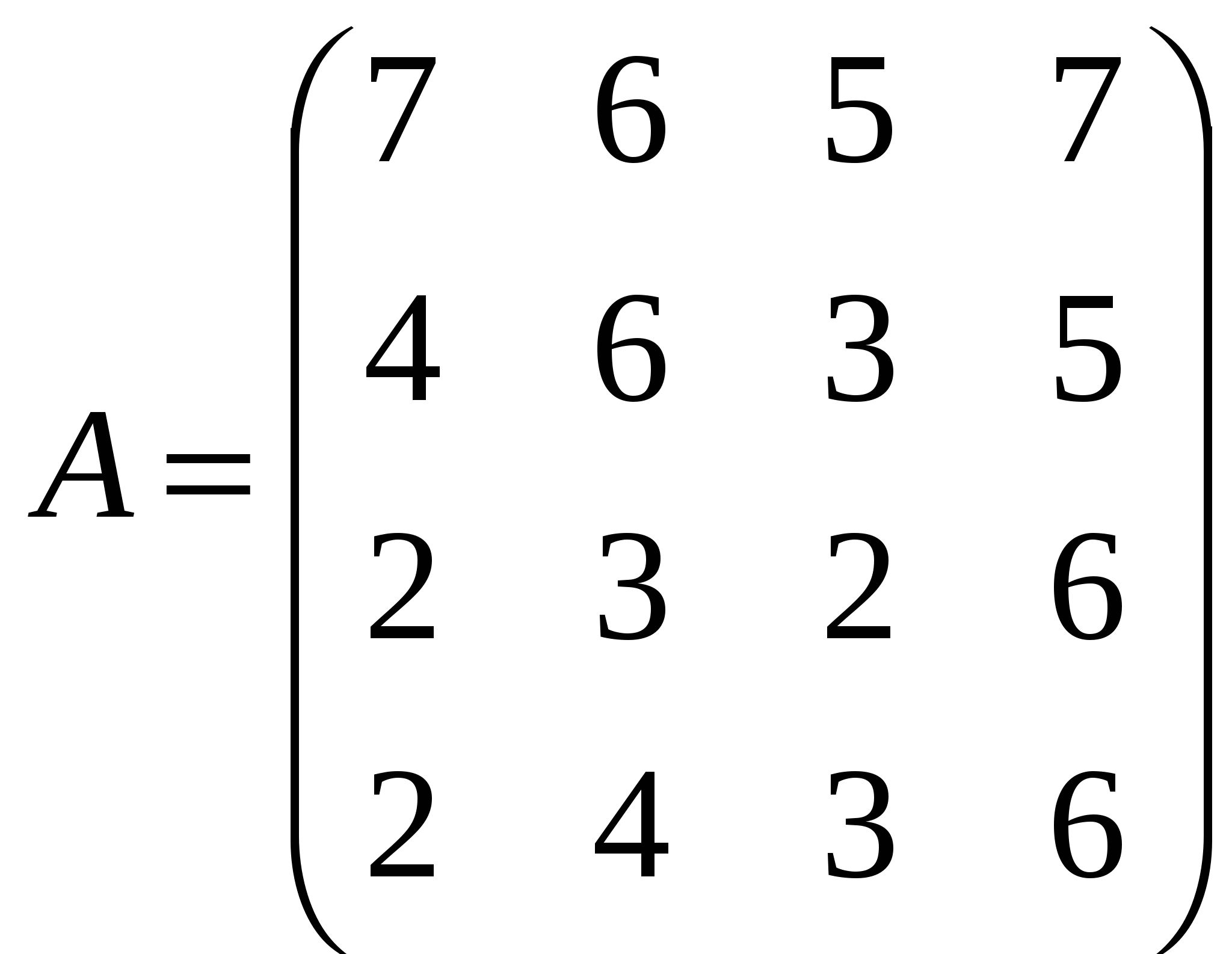 , , 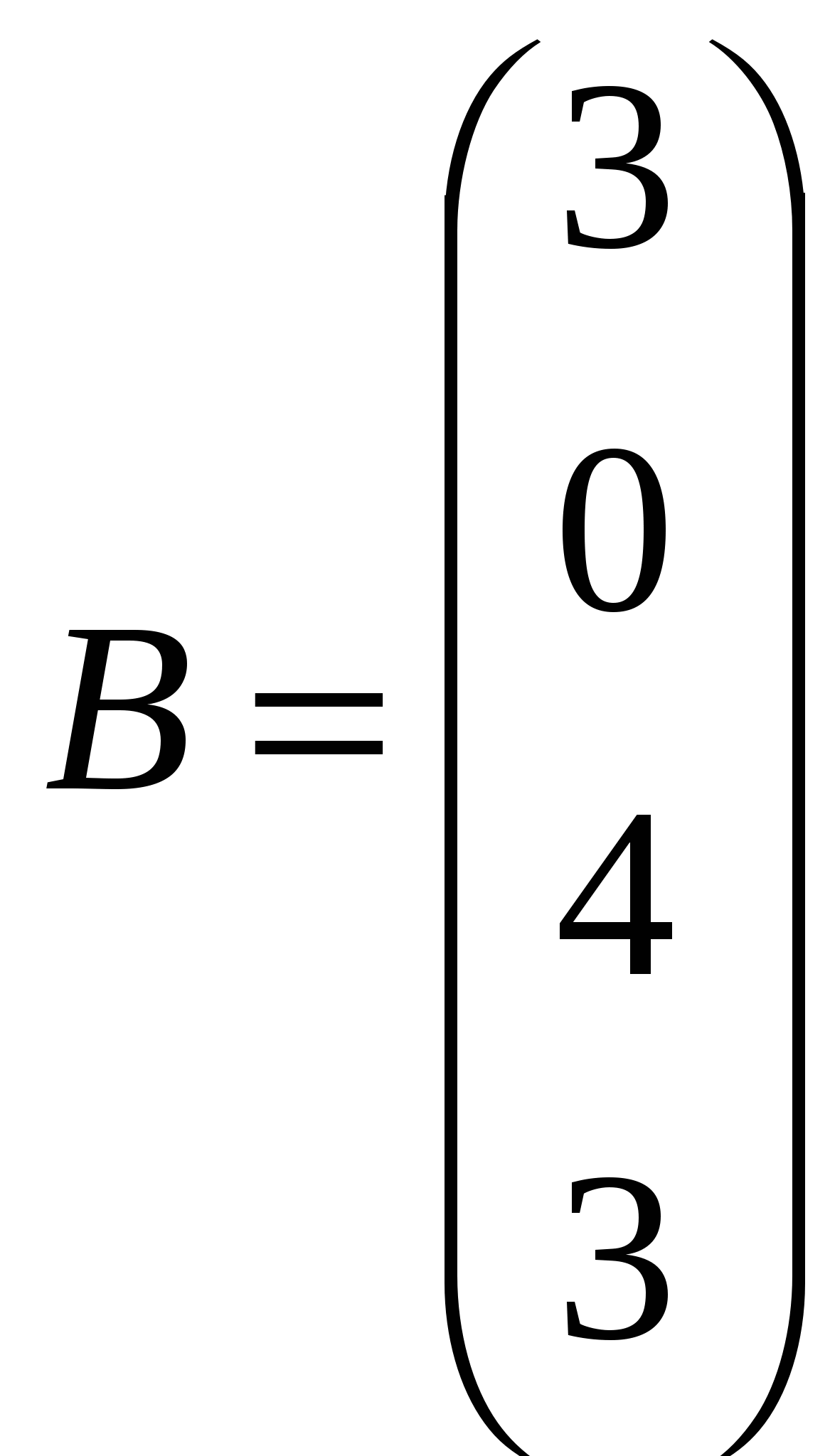 , , 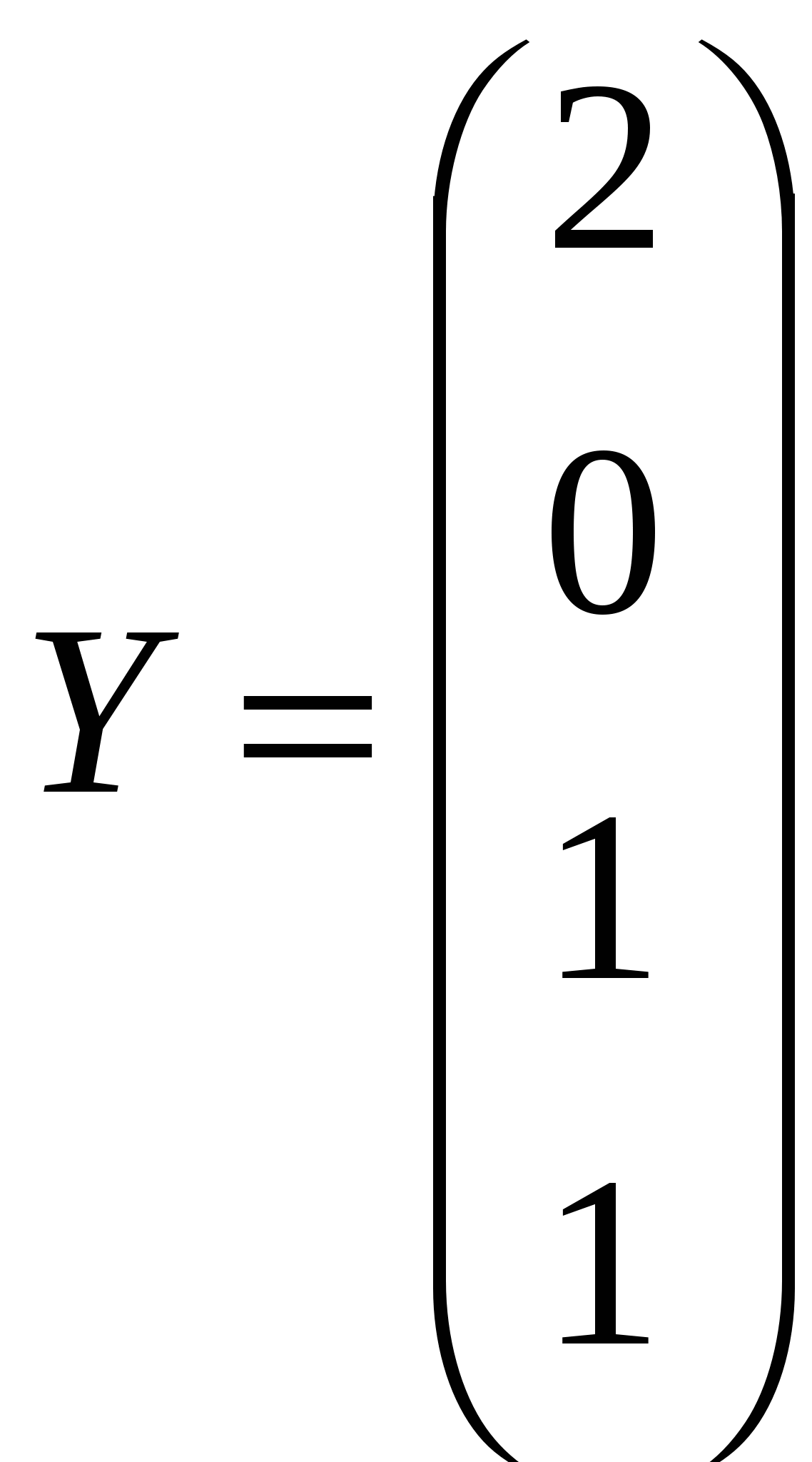
2. Вычислить
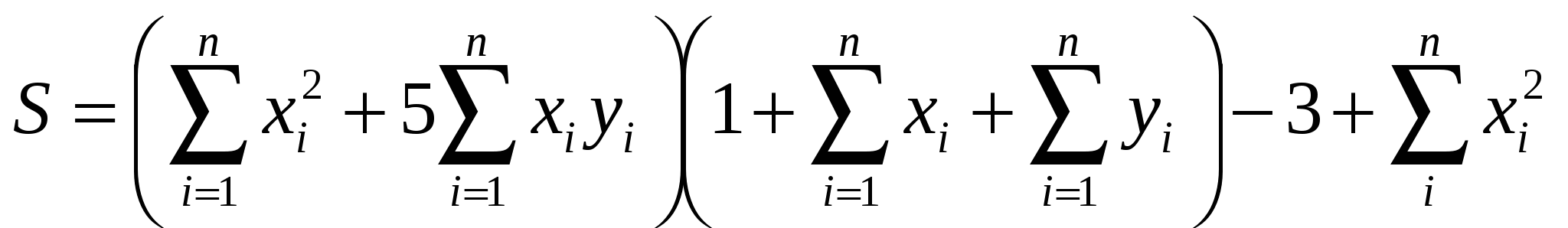
где x,y – векторы их n компонентов, причем n=4 и
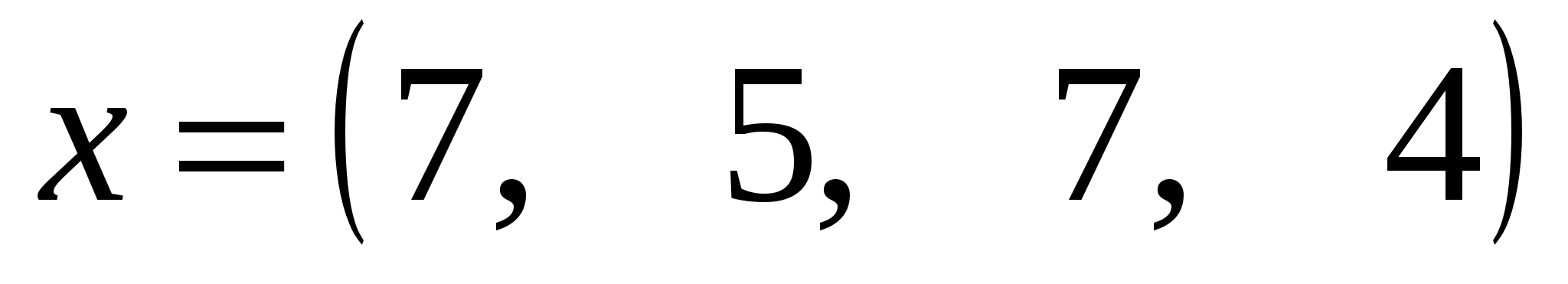 , , 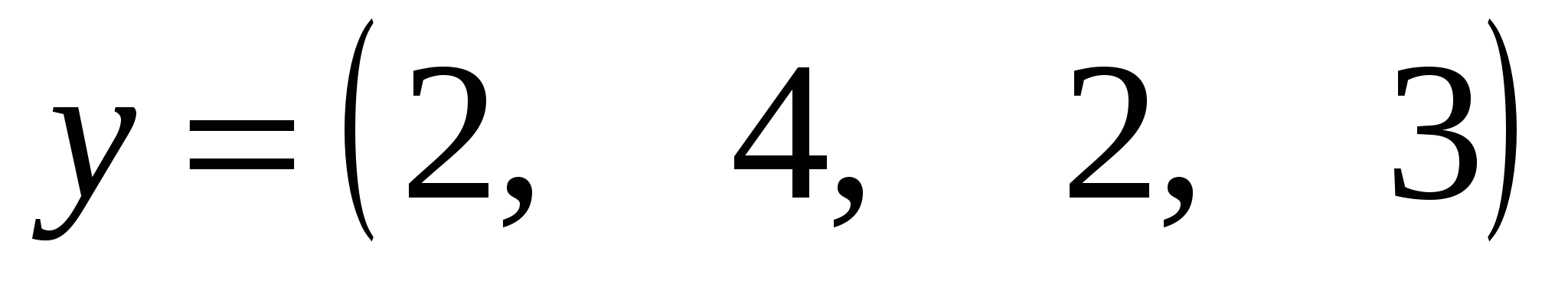 . .
Вариант 10
-
Решить системы линейных уравнений AX=B, А2АTAX=B и вычислить значение квадратичной формы Z=YTAATAATY, где
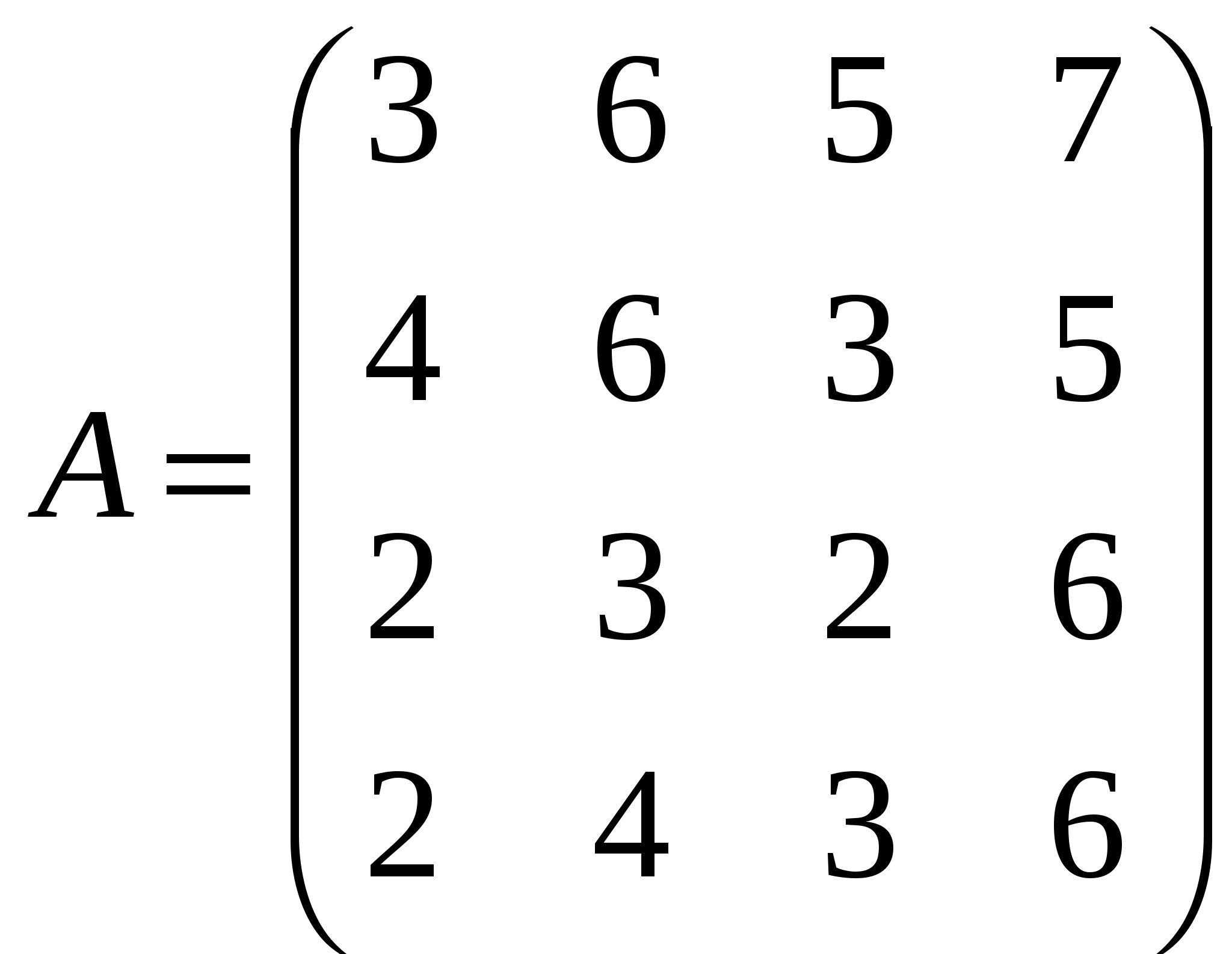 , , 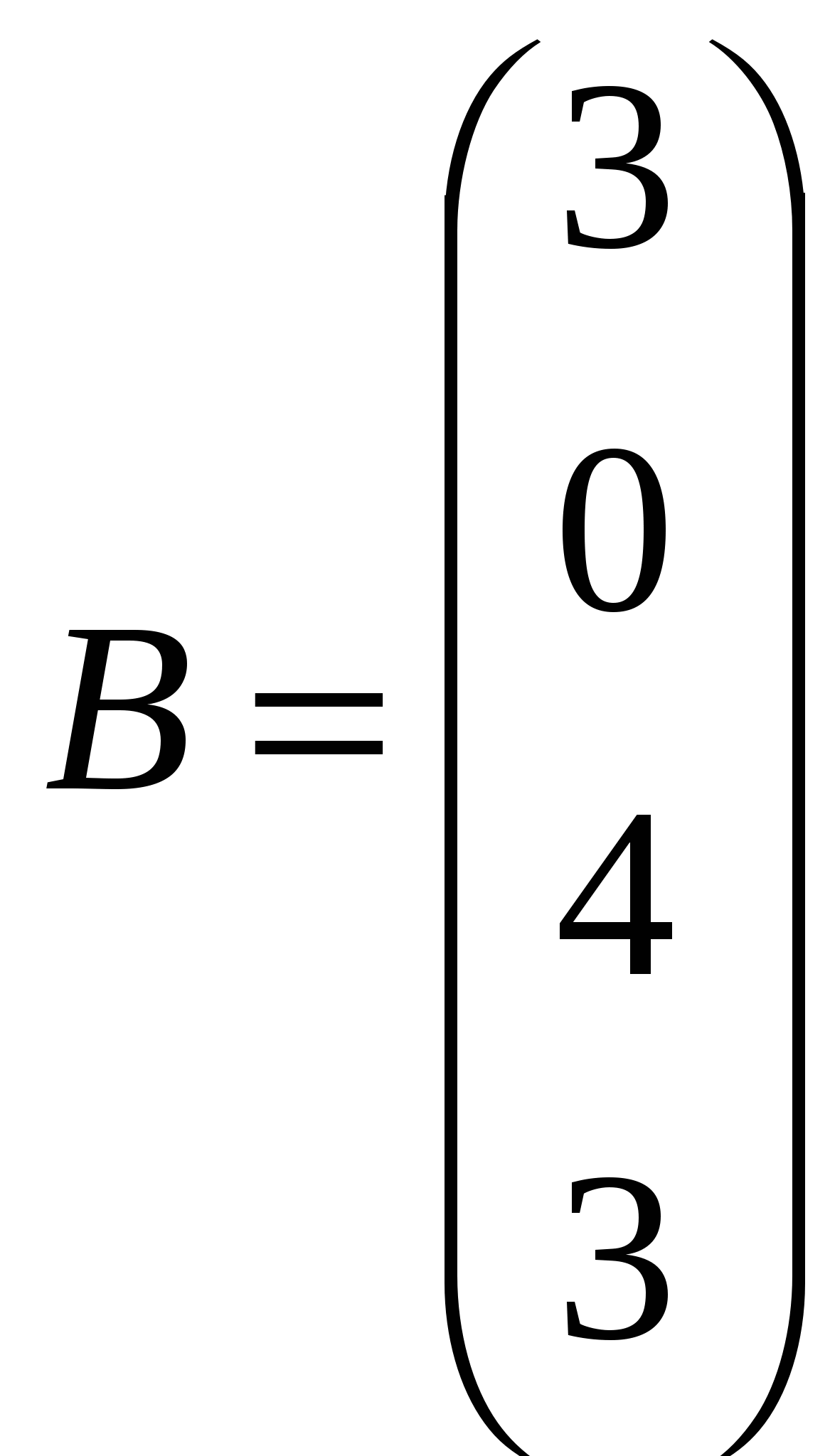 , , 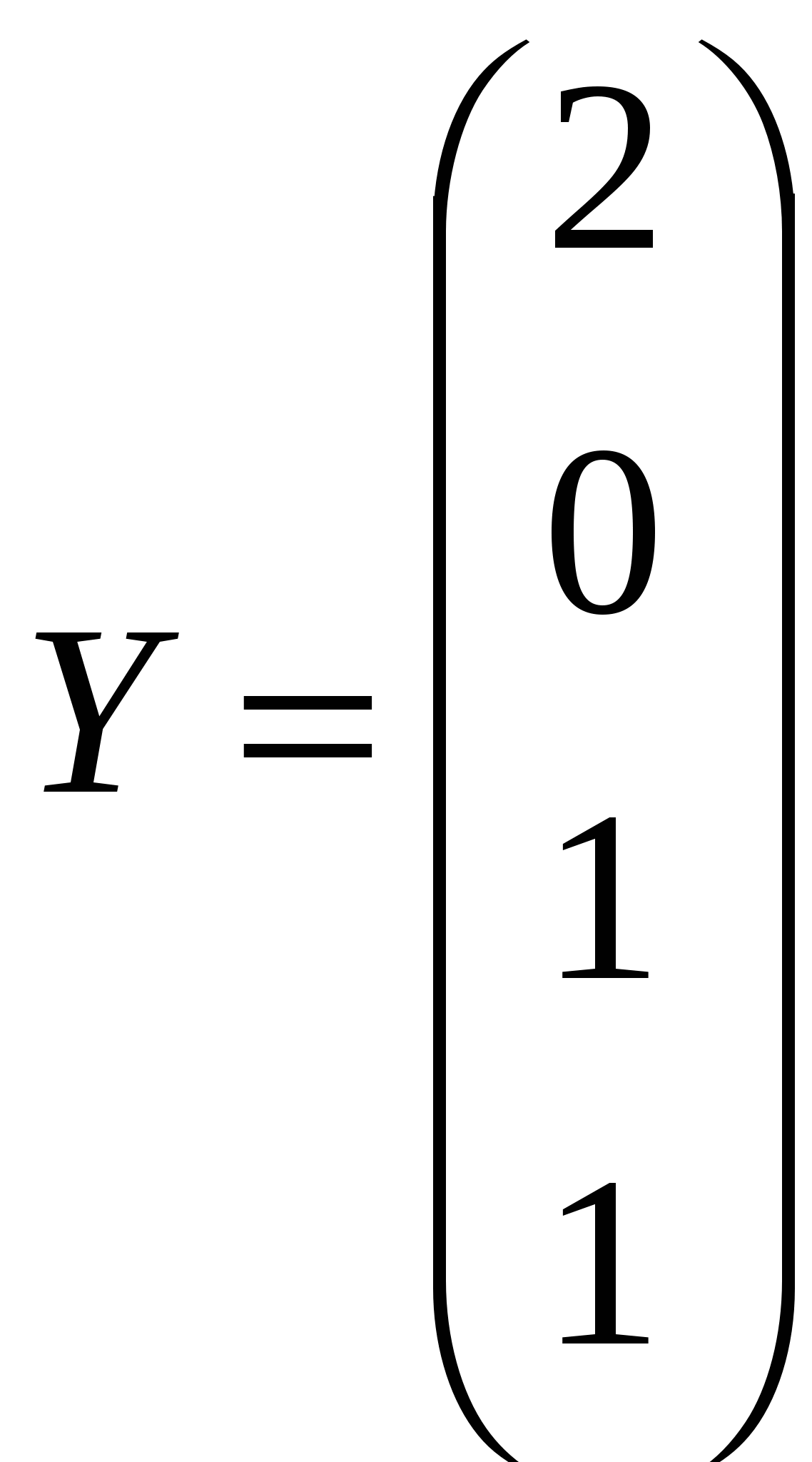 . .
-
Вычислить
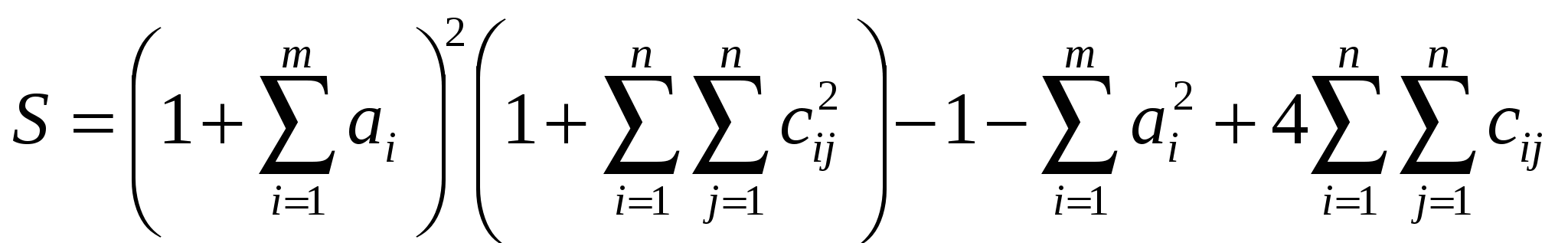 , ,
где a – вектор из m компонентов, c – матрица размера nxn причем n= 3, m= 4 и
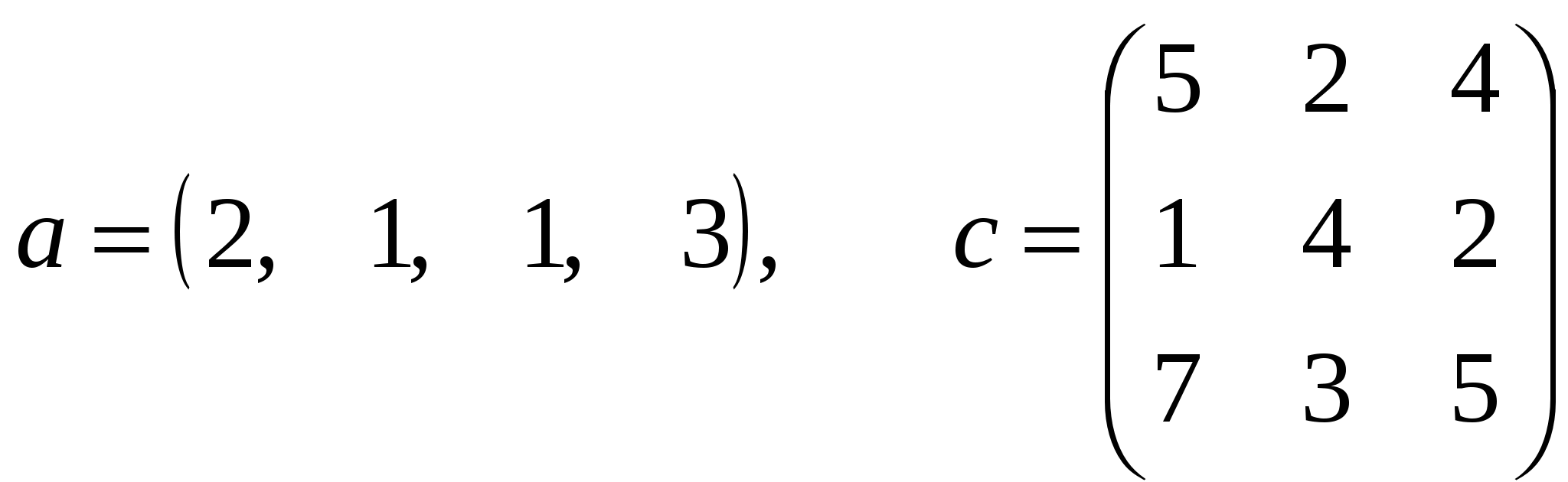 . .
II. Выполнить следующие задания экономического содержания 1-7, используя операции с матрицами в Microsoft Excel.
1. Частный предприниматель приобрел 250 единиц товара I вида и 600 единиц товара II вида; другой частный предприниматель — 200 единиц товара I вида и 700 единиц товара II вида. После удачно проведенной рекламной кампании товара I вида первый предприниматель сделал следующие закупки: I вида — 350 единиц, II вида — 550 единиц; второй предприниматель соответственно 350 и 600 единиц. Запишите матрицы: а) А1 и А2 всех закупок первым и вторым предпринимателем соответственно; б) общих закупок двумя предпринимателями сначала до, а затем после рекламной кампании.
2. Ниже приведены данные о продажах фирмы, владеющей несколькими магазинами. В строках матриц указаны суммы, вырученные на протяжении различных сезонов (весна, лето, осень, зима), а в столбцах — доходы от продажи различных видов товаров (телевизоры, музыкальные центры, видеокамеры):

(магазин 1) (магазин 2) (магазин 3)
Покажите, что в каждый сезон магазины 1 и 3 вместе взятые продали больше каждого вида товаров, чем магазин 2. Найдите матрицу общей продажи всех трех магазинов.
3. Данные о доходах (тыс. ден. ед.) холдинговой компании по трем регионам трех компаний за 2001 и 2003 гг. представлены в матрицах А и В.
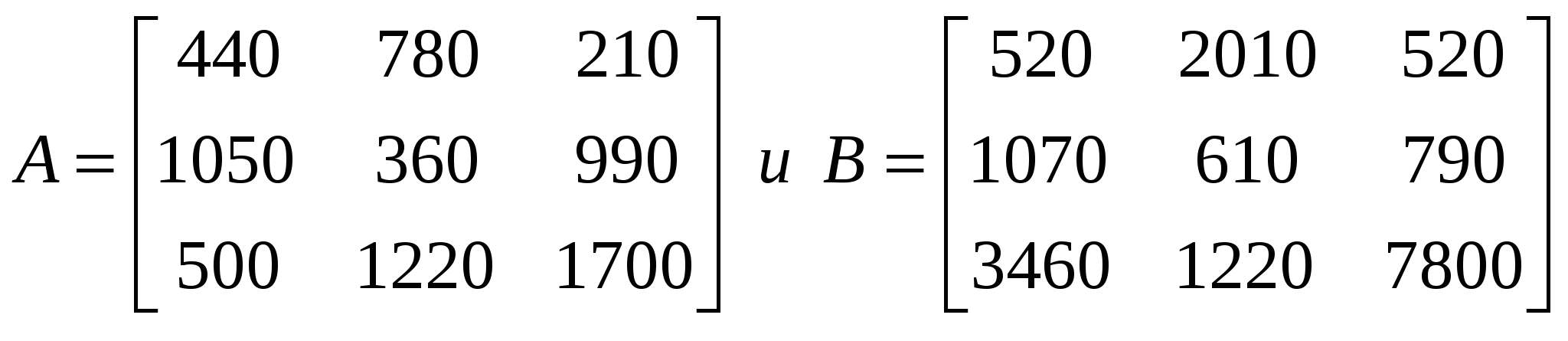
По строкам группируются данные о доходах трех компаний, по столбцам — по регионам продаж. Рассчитайте матрицу приростов доходов за период с 2001 по 2003 г. и матрицу, характеризующую средние размеры приростов доходов компании холдинга за год.
4. Тарифы (ден. ед.) перевозки единицы некоторого товара с трех фабрик четырем базам определяются матрицей
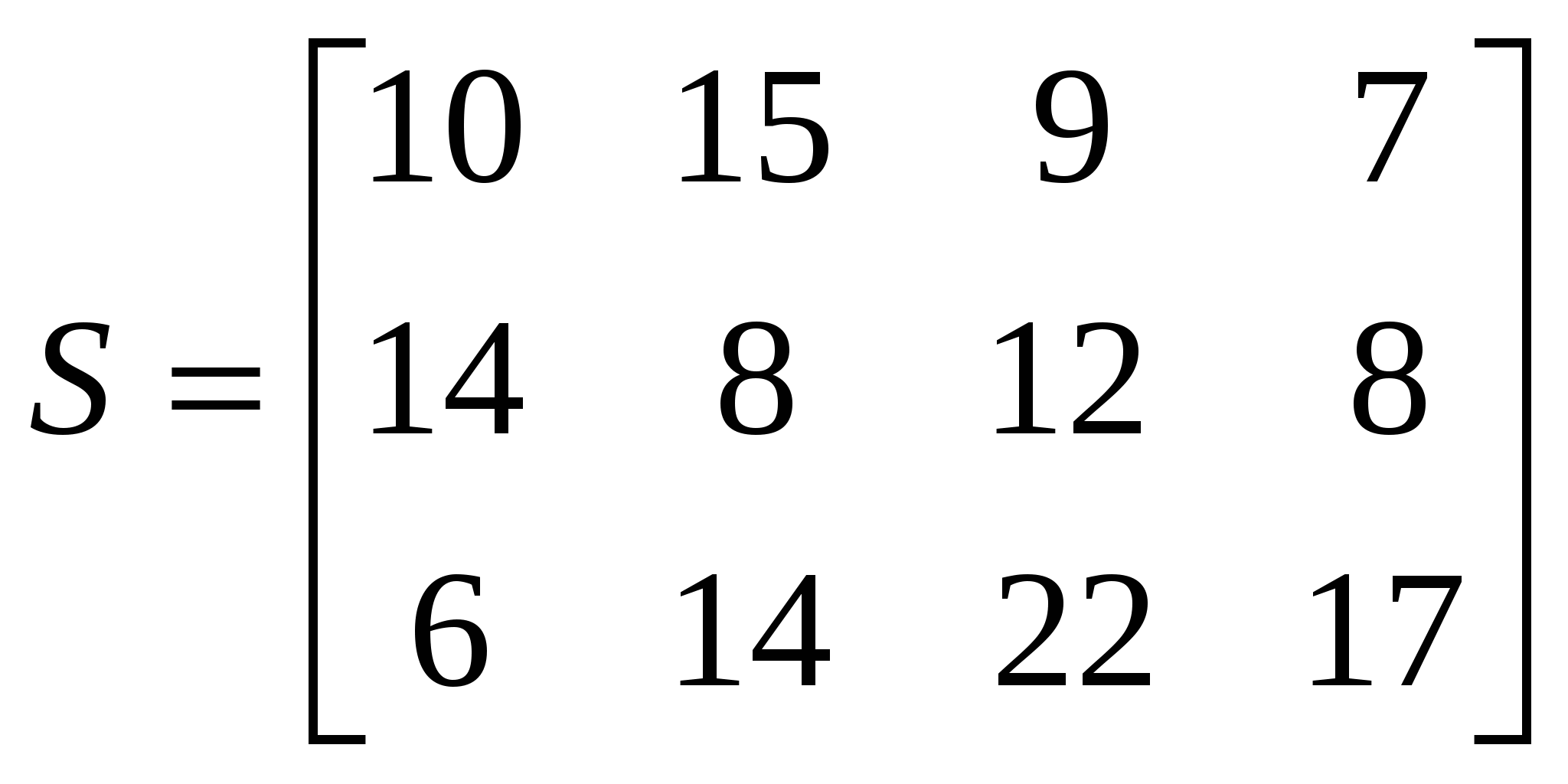
Себестоимость единицы товара на первой фабрике — 40 ден. ед., на второй — 38 ден. ед. и на третьей — 41 ден. ед. Запишите матрицу Р издержек производства размером 3x4, элементы которой группируются по строкам и столбцам так же, как и в S. Определите матрицу К совокупных издержек на производство и транспортировку товара.
5. Предприятие производит продукцию двух видов и использует сырье двух типов. Нормы затрат сырья на единицу продукции каждого вида заданы матрицей:
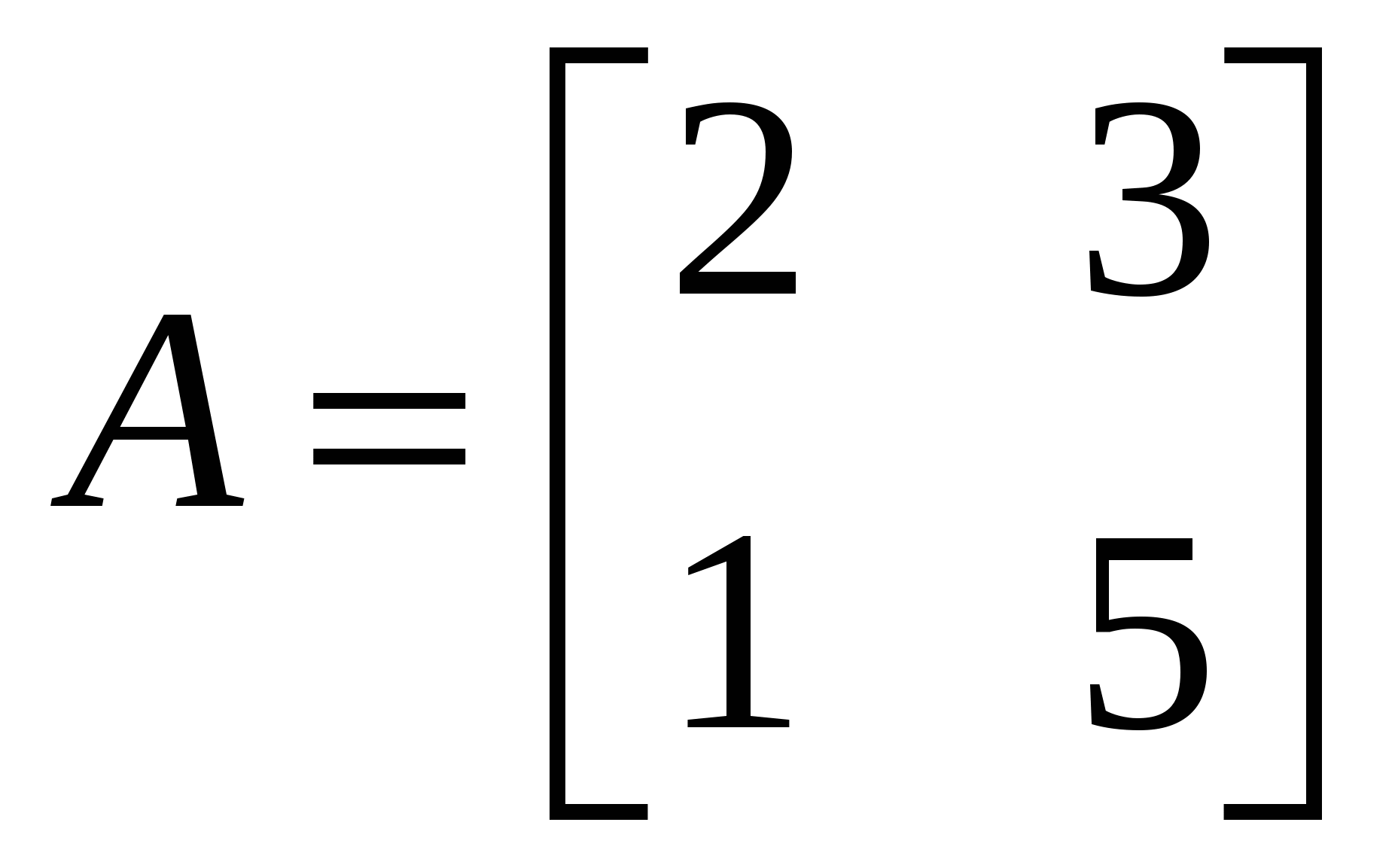 , ,
у которой по строкам указано количество (у. е.) сырья, расходуемого на производство единицы продукции I и II вида. Стоимость (ден. ед.) единицы сырья каждого типа задана матрицей В = [70 30]. Каковы общие затраты предприятия на производство 100 у.е. продукции I вида и 150 у.е. II вида?
6. Предприятие производит продукцию трех видов и использует сырье двух типов. Нормы затрат сырья (у. е.) на единицу продукции каждого вида заданы матрицей:
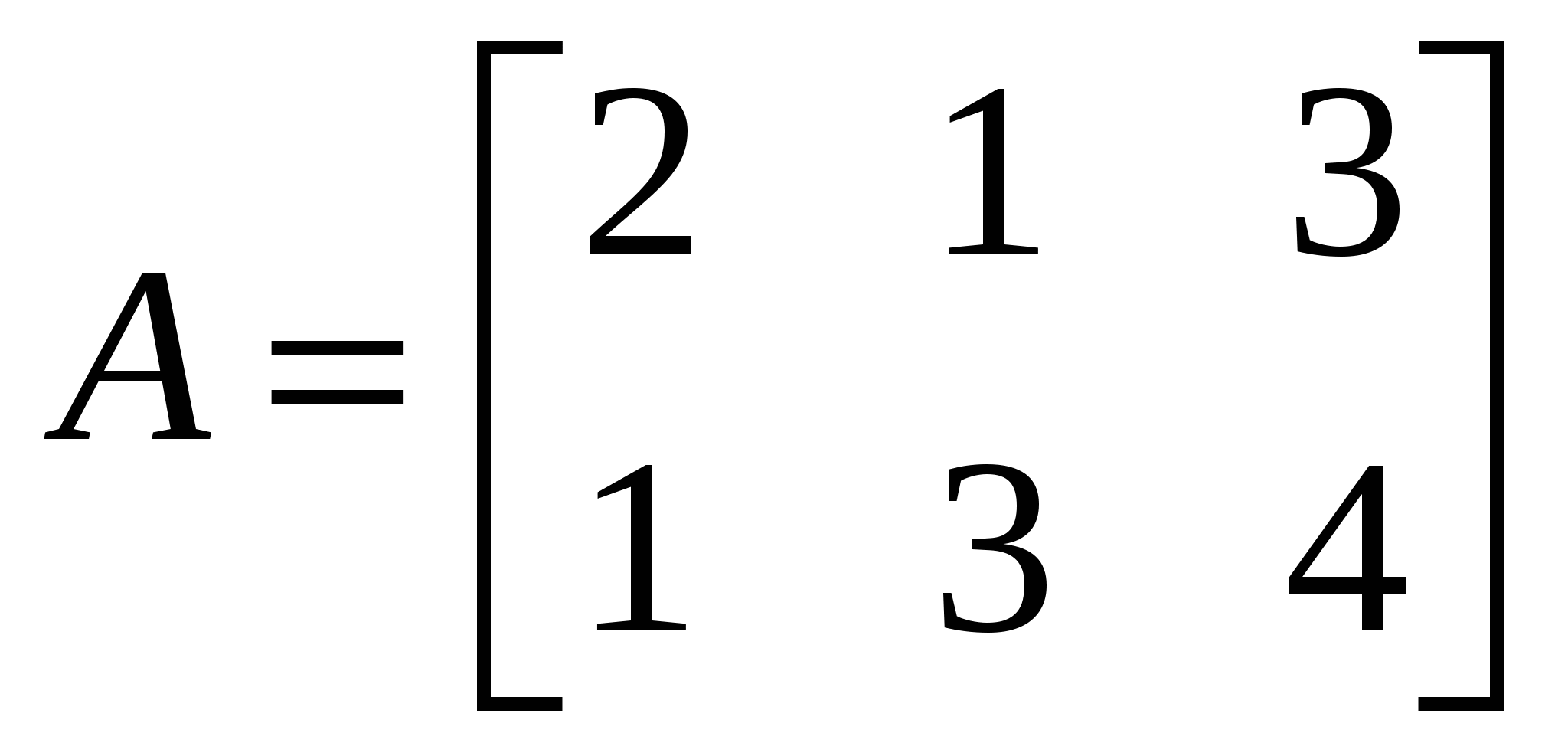
Стоимость (ден. ед.) единицы сырья каждого типа задана матрицей
В = [10 15]. Каковы общие затраты предприятия на производство 100 у.е. продукции I вида, 200 и 150 у.е. продукции II и III видов соответственно?
7. Предприятие выпускает 3 вида изделий, используя при этом сырье 3 типов. Нормы расхода сырья по видам изделий указаны в таблице.
Тип сырья
|
Норма расхода сырья на 1 изделие по видам
|
|
1
|
2
|
3
|
I
|
4
|
5
|
6
|
II
|
1
|
2
|
3
|
III
|
0
|
1
|
4
|
Требуется определить объем выпуска продукции каждого вида, если известно, что запас сырья I типа составляет 5500 единиц, II типа — 2050 единиц, III типа — 1400 единиц. Указанные запасы сырья должны быть использованы полностью.
III. Выполнить по вариантам следующие задания на решение систем уравнений.
Задания
-
Составить математическую модель в виде системы уравнений.
-
Решить ее средствами Microsoft Excel.
-
Вариант задания выбрать по номеру в списке.
Вариант 1
Расценки на проведение работ для каждого вида услуг приведены в таблице.
Вид работ
|
Нормативы по видам оборудования, ден.ед.
|
Полные затраты на услуги, ден.ед.
|
|
механическое
|
тепловое
|
энергетическое
|
|
Техническое
обслуживание
|
5
|
1
|
2
|
77
|
Транспортные услуги
|
4
|
3
|
6
|
132
|
Капитальный ремонт
|
12
|
23
|
18
|
536
|
Найдите расчетные объемы работ (у.е.), которые смогут окупить затраты на услуги.
Вариант 2
За 16 м материи 1-го сорта и 20 м материи 2-го сорта заплатили 62 ден. ед. Если бы материю покупали не в магазине, а на фабрике, производящей эту ткань, то за эту же покупку заплатили бы на 18 ден. ед. меньше, так как на фабрике цена материи 1-го сорта на 25 % меньше, чем в магазине, 2-го сорта — меньше на 33% . Сколько стоит 1 м ткани каждого сорта в магазине?
Вариант 3
Предприятие выпускает три вида продукции, используя сырье трех типов. Характеристики производства описаны в следующей таблице.
Тип сырья
|
Нормы расхода по видам изделий, у. е.
|
Запас сырья, у.е.
|
|
1
|
2
|
3
|
|
1
|
6
|
4
|
5
|
2400
|
2
|
4
|
3
|
1
|
1450
|
3
|
5
|
2
|
3
|
1550
|
Найдите объем выпуска продукции каждого вида при заданных запасах сырья.
Вариант 4
Предприятие выпускает три вида продукции, используя сырье трех типов. Характеристики производства описаны в следующей таблице.
Тип сырья
|
Нормы расхода по видам изделий, у. е.
|
Запас сырья, у.е.
|
|
1
|
2
|
3
|
|
1
|
8
|
12
|
16
|
1800
|
2
|
14
|
21
|
13
|
2700
|
3
|
9
|
11
|
19
|
2000
|
Найдите объем выпуска продукции каждого вида при заданных запасах сырья.
Вариант 5
Иванов, Петров и Сидоров купили продукты трех видов соответственно в количестве 2, 5 и 4 кг; 6, 2 и 3 кг; 1,4 и 7 кг. Иванов уплатил 27 ден. ед., Петров — 23,5 ден. ед. и Сидоров — 34 ден. ед. Определите цены этих продуктов.
Вариант 6
Бригада, которая состоит из пяти рабочих 4-го разряда, трех рабочих 5-го разряда и четырех рабочих 6-го разряда, за смену изготовляет продукцию в объеме 59 единиц. После того как двое рабочих 4-го разряда и один 6-го разряда были отправлены на уборку, объем изготовленной за смену продукции составил 45 единиц. Когда же из отпуска вернулись трое рабочих 5-го разряда и один 4-го разряда, а двое рабочих 6-го разряда ушли в отпуск, бригада за смену стала изготавливать 52 единицы продукции. Найдите производительности труда за смену рабочих 4-го, 5-го и 6-го разрядов.
Вариант 7
Иванов, желая увеличить свои сбережения, размещает денежные средства во вклады в трех банках, предлагающих разные условия, в том числе разные годовые проценты по вкладам.
В первом банке он разместил 1/3 сбережений размером 6000 ден. ед., во втором банке — 1/2, а оставшуюся часть — в третьем банке. К концу года сумма этих вкладов возросла до 7250 ден. ед. Если бы первоначально 1/6 сбережений была размещена в первом банке, 2/3 — во втором банке, а 1/6 — в третьем банке, то через год сумма вклада составила бы 7200 ден. ед. Если бы 1/2 сбережений была положена в первый банк, 1/6 — во второй банк, 1/3 — в третий банк, то сумма вкладов через год составила бы вновь 7250 ден. ед. Какой процент по вкладам был установлен каждым банком?
Вариант 8
Швейная фабрика в течение трех дней производила изделия трех видов. Объемы выпуска продукции за три дня и денежные затраты на производство за эти дни даны в следующей таблице.
День
|
Объем выпуска продукции, единиц
|
Затраты, тыс. ден. ед.
|
|
1-й вид
|
2-й вид
|
3-й вид
|
|
Первый
|
50
|
10
|
30
|
176
|
Второй
|
35
|
25
|
20
|
168
|
Третий
|
40
|
20
|
30
|
184
|
Найдите себестоимость единицы продукции каждого вида.
Вариант 9
Предприятие выпускает три вида продукции с использованием трех типов сырья. Характеристики производства содержатся в следующей таблице.
Тип сырья
|
Нормы расхода по видам продукции, у.е./изд.
|
Запасы сырья, у.е.
|
|
1-й вид
|
2-й вид
|
3-й вид
|
|
1
|
5
|
12
|
7
|
2350
|
2
|
10
|
6
|
8
|
2060
|
3
|
9
|
11
|
4
|
2270
|
Найдите объем выпуска продукции каждого вида при заданных запасах сырья.
Лабораторная работа №7. “Финансовый анализ
и построение отчетных ведомостей”
Задания
Выполнить задания 1-9 в соответствии с номером варианта (номер варианта выбирается по номеру студента в списке).
-
Вас просят дать в долг Р руб. и обещают вернуть Р1 руб. через год, Р2 руб. – через два года и т.д. Рn руб. – через n лет. При какой годовой процентной ставке эта сделка имеет смысл?
Вариант
|
n
|
Р
|
Р1
|
Р2
|
Р3
|
Р4
|
Р5
|
1
|
3
|
17 000
|
5000
|
7000
|
8000
|
|
|
2
|
4
|
20 000
|
6000
|
6000
|
9000
|
7000
|
|
3
|
5
|
22 000
|
5000
|
8000
|
8000
|
7000
|
5000
|
4
|
3
|
30 000
|
5000
|
10 000
|
18 000
|
|
|
5
|
4
|
35 000
|
5000
|
9000
|
10 000
|
18 000
|
|
6
|
5
|
21 000
|
4000
|
5000
|
8000
|
10 000
|
11 000
|
7
|
3
|
25 000
|
8000
|
9000
|
10 000
|
|
|
8
|
4
|
31 000
|
9000
|
10 000
|
10 000
|
15 000
|
|
9
|
5
|
32 000
|
8000
|
10 000
|
10 000
|
10 000
|
11 000
|
10
|
3
|
36 000
|
10 000
|
15 000
|
21 000
|
|
|
-
Вас просят дать в долг Р руб. и обещают возвращать по А руб. в течение n лет. При какой годовой процентной ставке эта сделка имеет смысл?
Вариант
|
n
|
Р
|
А
|
1
|
7
|
170 000
|
30 000
|
2
|
8
|
200 000
|
31 000
|
3
|
9
|
220 000
|
33 000
|
4
|
10
|
300 000
|
34 000
|
5
|
11
|
350 000
|
41 000
|
6
|
7
|
210 000
|
32 000
|
7
|
8
|
250 000
|
37 000
|
8
|
9
|
310 000
|
40 000
|
9
|
10
|
320 000
|
35 000
|
10
|
11
|
360 000
|
41 000
|
-
Вычислить ежегодные платежи на примере ссуды Р руб. под годовую ставку i% срок n лет.
Вариант
|
n
|
Р
|
i
|
1
|
7
|
170 000
|
5
|
2
|
8
|
200 000
|
6
|
3
|
9
|
220 000
|
7
|
4
|
10
|
300 000
|
8
|
5
|
11
|
350 000
|
9
|
6
|
7
|
210 000
|
10
|
7
|
8
|
250 000
|
11
|
8
|
9
|
310 000
|
12
|
9
|
10
|
320 000
|
13
|
10
|
11
|
360 000
|
14
|
-
Вы берете в долг Р руб. под годовую ставку i% и собираетесь выплачивать по А руб. в год. Сколько лет займут эти выплаты?
Вариант
|
P
|
A
|
i
|
1
|
170 000
|
31 000
|
3
|
2
|
200 000
|
32 000
|
4
|
3
|
220 000
|
33 000
|
5
|
4
|
300 000
|
34 000
|
6
|
5
|
370 000
|
41 000
|
7
|
6
|
210 000
|
32 000
|
8
|
7
|
260 000
|
37 000
|
9
|
8
|
310 000
|
40 000
|
10
|
9
|
320 000
|
35 000
|
4
|
10
|
360 000
|
41 000
|
5
|
-
Составить отчетную ведомость реализации товаров n магазинами с месяца А по месяц В, структура которой приведена ниже.
Вариант
|
А
|
В
|
n
|
1
|
май
|
декабрь
|
5
|
2
|
июнь
|
Январь
|
4
|
3
|
июль
|
октябрь
|
5
|
4
|
август
|
январь
|
6
|
5
|
сентябрь
|
декабрь
|
7
|
6
|
октябрь
|
март
|
8
|
7
|
ноябрь
|
март
|
9
|
8
|
декабрь
|
июль
|
10
|
9
|
январь
|
июль
|
6
|
10
|
февраль
|
август
|
5
|
Примерная структура отчетной ведомости
Выручка сети магазинов в млн. руб.
|
|
Магазин
|
Июнь
|
Июль
|
Август
|
Суммарная выручка
|
Место
|
Средняя выручка
|
Доля
|
Диапазон
|
Количество
|
1
|
324
|
435
|
534
|
1293
|
6
|
431,00
|
12%
|
1000
|
0
|
2
|
435
|
645
|
354
|
1434
|
5
|
478,00
|
13%
|
1500
|
2
|
3
|
532
|
623
|
451
|
1606
|
4
|
535,33
|
15%
|
2000
|
1
|
4
|
723
|
634
|
751
|
2108
|
2
|
702,67
|
20%
|
|
3
|
5
|
536
|
734
|
876
|
2146
|
1
|
715,33
|
20%
|
|
|
6
|
834
|
811
|
435
|
2080
|
3
|
693,33
|
19%
|
|
|
Итого:
|
3384
|
3882
|
3401
|
10667
|
|
|
|
|
|
-
Вы берете в долг Р руб. под годовую ставку i% и собираетесь отдавать по А руб. в год. Сколько лет займут выплаты?
Вариант
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
А
|
200
|
190
|
178
|
164
|
146
|
243
|
320
|
423
|
521
|
711
|
n
|
1000
|
1700
|
3100
|
5900
|
6190
|
6509
|
6860
|
7246
|
7670
|
8138
|
i%
|
2
|
3
|
4
|
2
|
2
|
3
|
4
|
5
|
6
|
7
|
-
Вы собираетесь вкладывать по А руб. в течение n лет при годовой ставке i%. Сколько денег будет на счету через n лет?
Вариант
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
А
|
200
|
190
|
178
|
164
|
146
|
243
|
320
|
423
|
521
|
711
|
n
|
10
|
11
|
12
|
13
|
14
|
8
|
9
|
10
|
11
|
12
|
i%
|
2
|
3
|
4
|
2
|
2
|
3
|
4
|
5
|
6
|
7
|
-
Определить процентную ставку для n годичного займа в Р руб. с ежегодной выплатой в А руб.
Вариант
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
А
|
200
|
190
|
178
|
164
|
146
|
243
|
320
|
423
|
521
|
711
|
Р
|
1000
|
1700
|
3100
|
5900
|
6190
|
6509
|
6860
|
7246
|
7670
|
8138
|
n
|
2
|
3
|
4
|
2
|
2
|
3
|
4
|
5
|
6
|
7
|
-
Составьте таблицу начисления премии по итогам работы сети n магазинов с месяца А по месяц В по следующему правилу:
-
если продукции продано не меньше чем на С руб., то комиссионные составляют i%;
-
за первое место дополнительно начисляется j1%, за второе место – j2% и т.д., за k-е место дополнительно начисляется jk%.
Вариант
|
С
|
i
|
j1
|
j2
|
j3
|
j4
|
n
|
A
|
B
|
1
|
23 000
|
1
|
3
|
1,5
|
|
|
7
|
Май
|
Июль
|
2
|
44 000
|
2
|
4
|
2
|
|
|
6
|
Июнь
|
Август
|
3
|
65 000
|
3
|
5
|
2,5
|
1,25
|
|
5
|
Июль
|
Ноябрь
|
4
|
86 000
|
4
|
6
|
3
|
1,5
|
0,75
|
6
|
Август
|
Февраль
|
5
|
107 000
|
5
|
7
|
3,5
|
1,75
|
0,88
|
7
|
Май
|
Декабрь
|
6
|
128 000
|
1
|
3
|
1,5
|
0,75
|
0,38
|
8
|
Октябрь
|
Январь
|
7
|
149 000
|
2
|
4
|
2
|
1
|
0,50
|
10
|
Ноябрь
|
Май
|
8
|
170 000
|
3
|
5
|
2,5
|
1,25
|
0,63
|
9
|
Декабрь
|
Май
|
9
|
191 000
|
4
|
6
|
3
|
1,5
|
|
5
|
Январь
|
Май
|
10
|
212 000
|
5
|
7
|
3,5
|
|
|
6
|
Февраль
|
Июнь
|
Лабораторная работа №8. “Анализ и распределение данных.
Подбор параметра”
Задания
-
Найти все корни уравнения, строя график функции и затем используя средство Подбор параметра.
Задание выполнить в соответствии с номером варианта (по списку студента в группе).
-
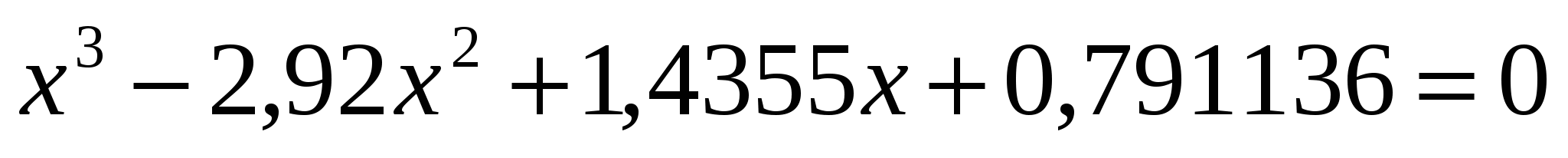 ; ;
-
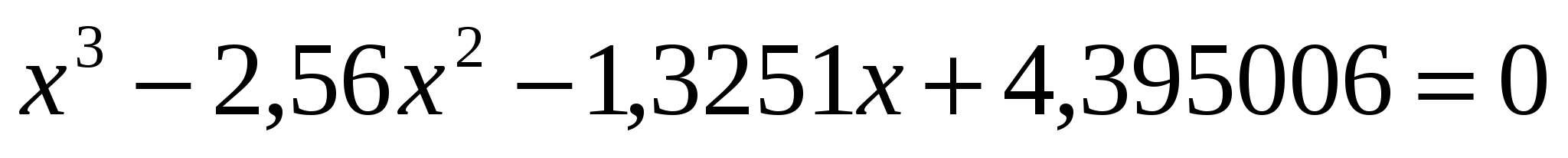 ; ;
-
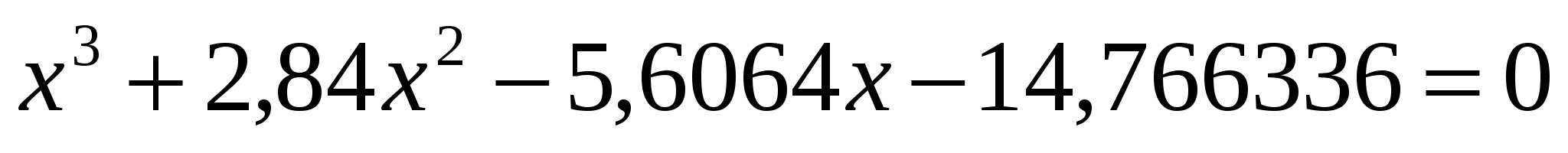 ; ;
-
x3 +1,41x2 – 5,4724x – 7,380384 = 0;
-
x3 +0,85x2 – 0,4317x + 0,043911 = 0;
-
x3 – 0,12x2 – 1,4775x + 0,191906 = 0;
-
x3 + 0,77x2 – 0,2513x + 0,016995 = 0;
-
 ; ;
-
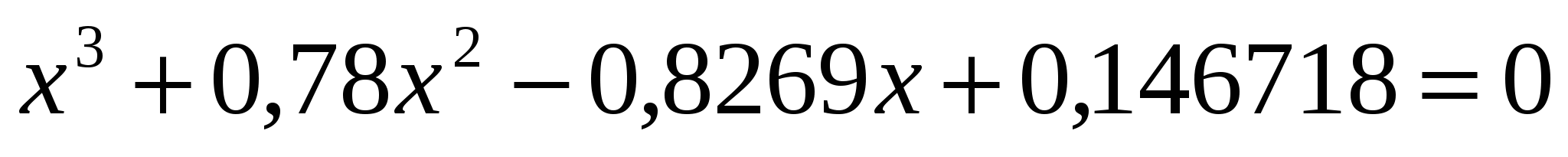 ; ;
-
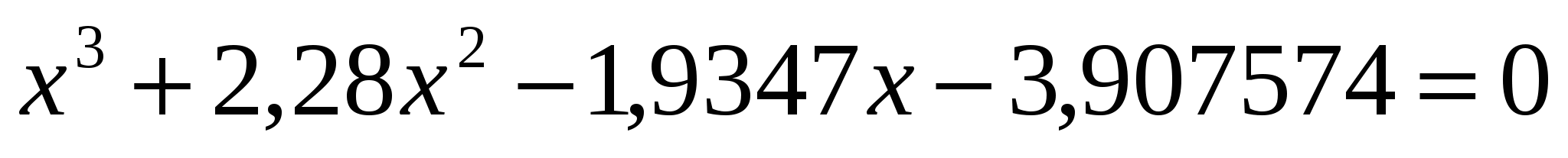 . .
II. Решение уравнений методом деления отрезка пополам
Задания
-
Преобразовать заданное уравнение к виду F(x) = 0.
-
Построить таблицу значений функции на заданном отрезке.
-
Построить график функции F(x).
-
Локализовать корни, т. е. найти интервалы, на которых корни уравнения существуют. Такими интервалами локализации корней могут служить промежутки, на концах которых функция имеет противоположные знаки.
-
Определить по графику первый из корней уравнения и первый отрезок локализации этого корня.
-
Методом половинного деления найти корень уравнения с точностью =0,001.
-
Повторить пункты 5 и 6 для следующих корней уравнения.
Вариант уравнения выбирается по номеру студента в списке.
Варианты уравнений
-
Найти корни нелинейного алгебраического уравнения
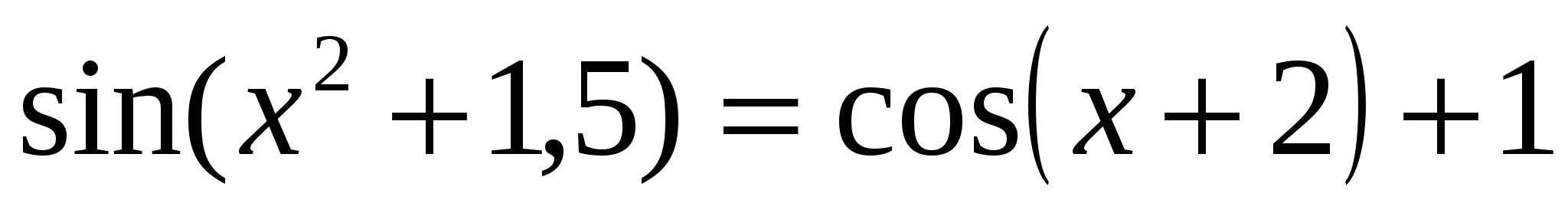
при 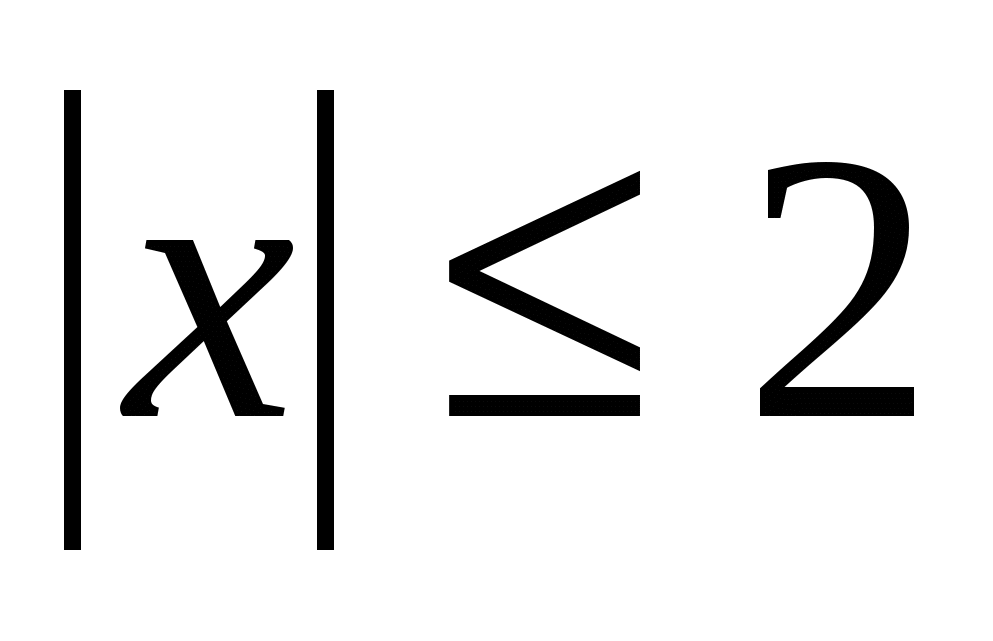 . .
-
Найти корни нелинейного алгебраического уравнения
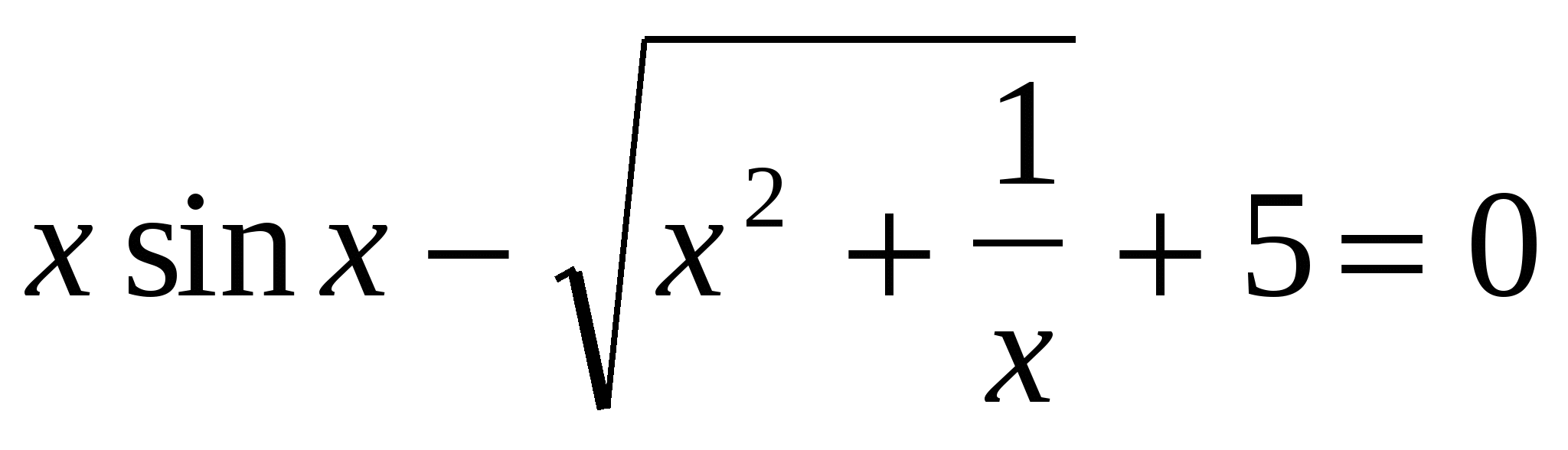
на отрезке 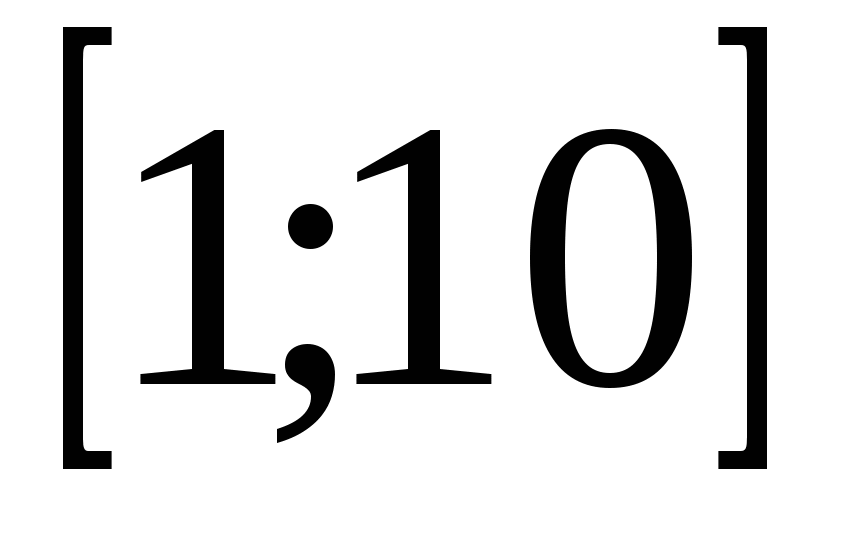 . .
-
Найти корни нелинейного алгебраического уравнения
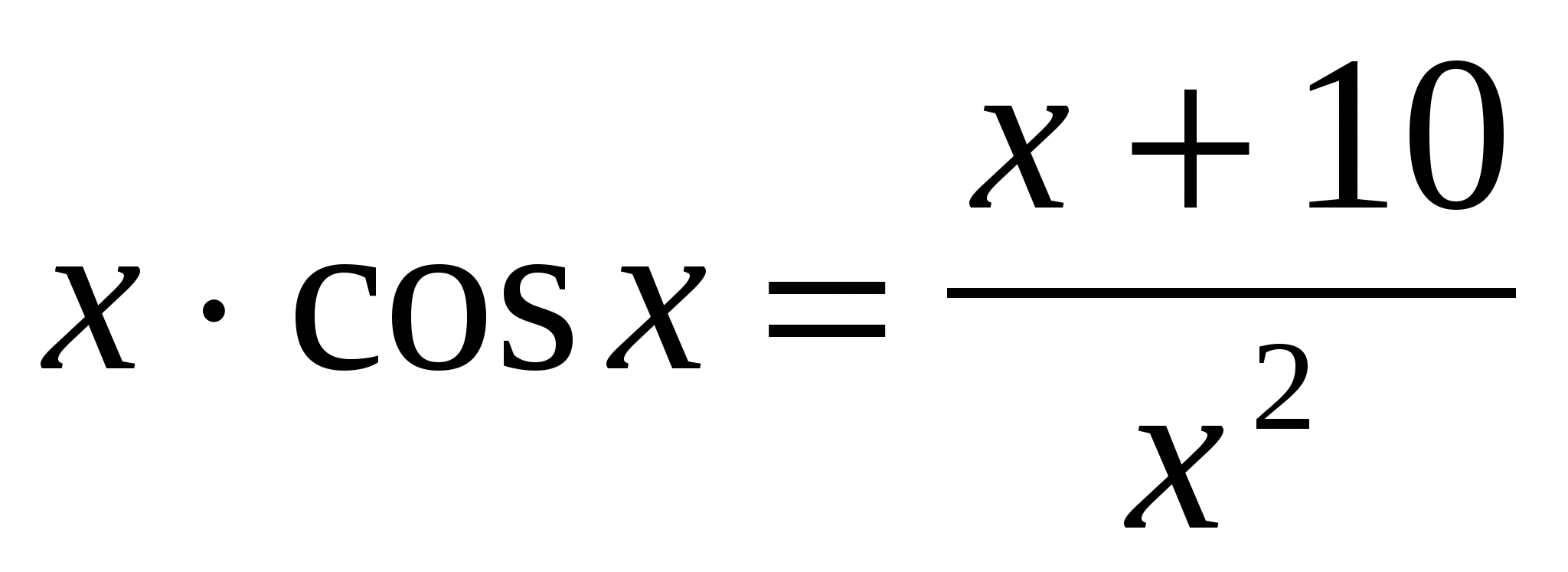 при при 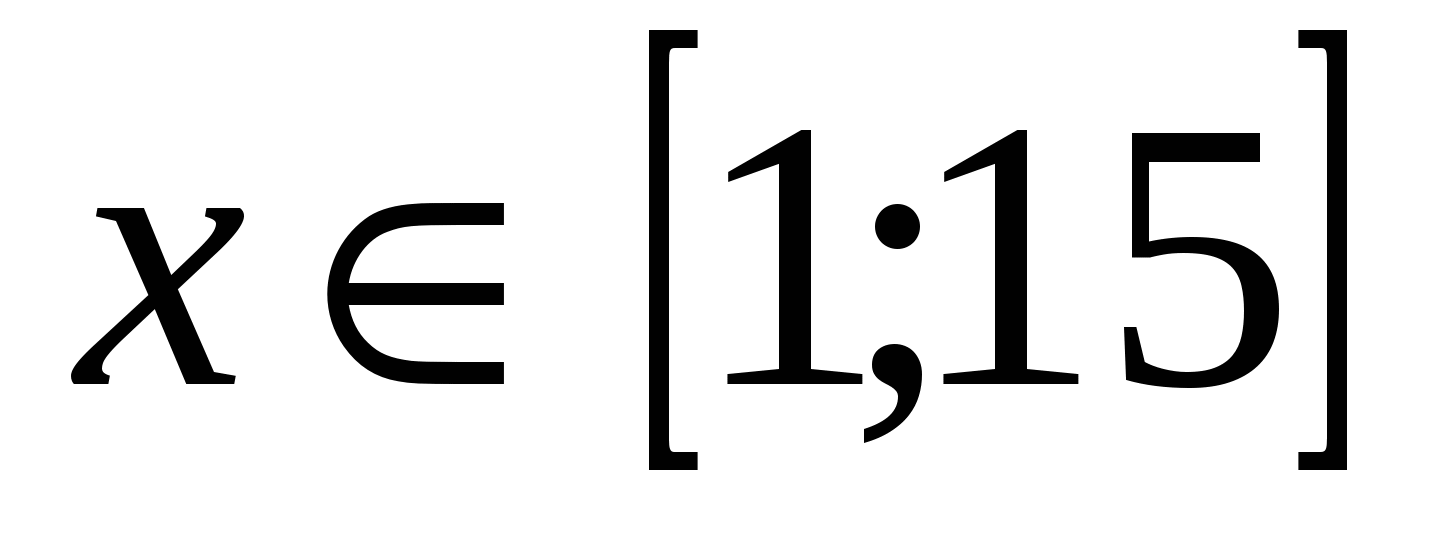 . .
-
Решить нелинейное уравнение
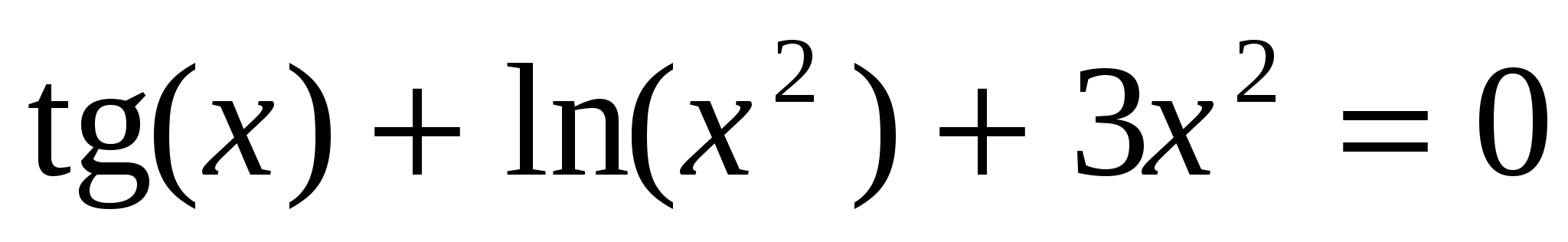
на отрезке 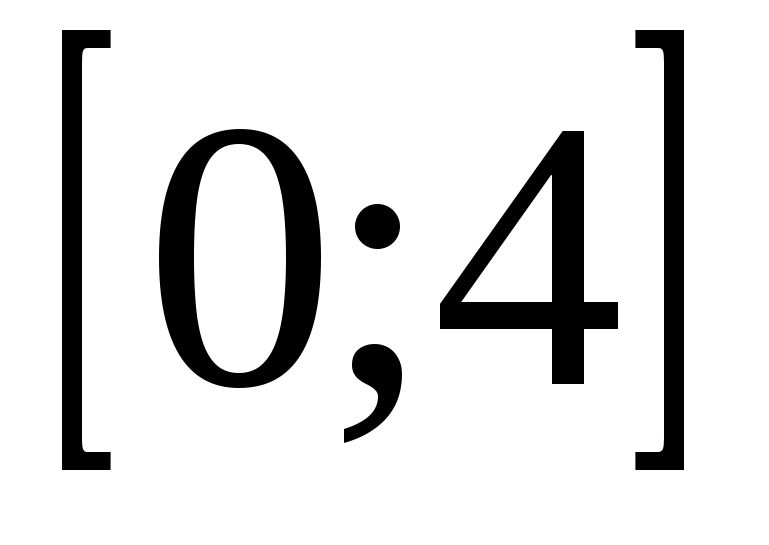 . .
-
Решить нелинейное уравнение
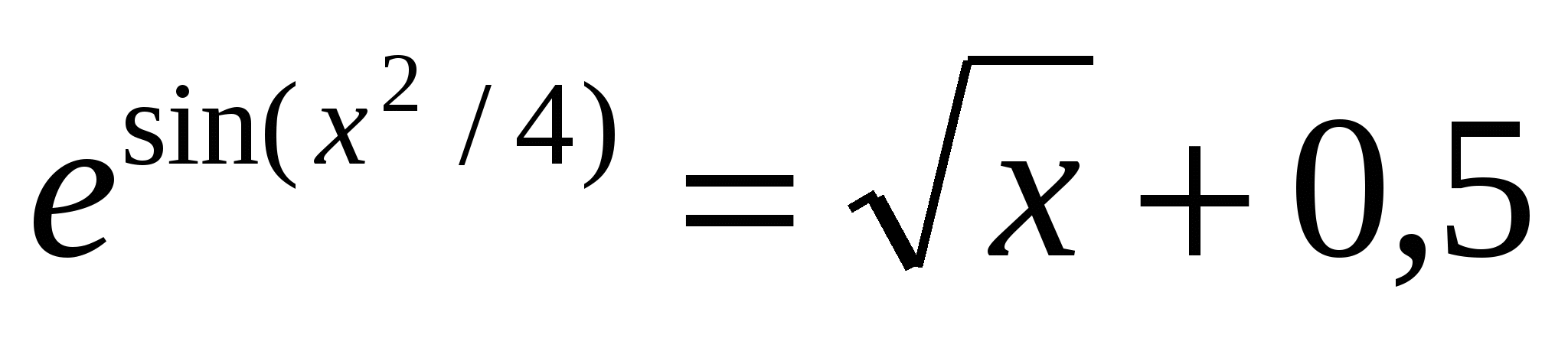
и найти его корни на отрезке 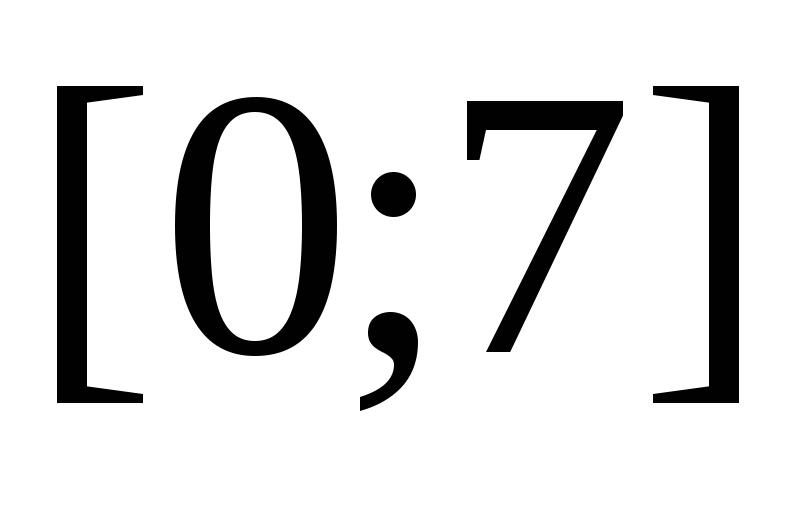 . .
-
Найти корни нелинейного алгебраического уравнения
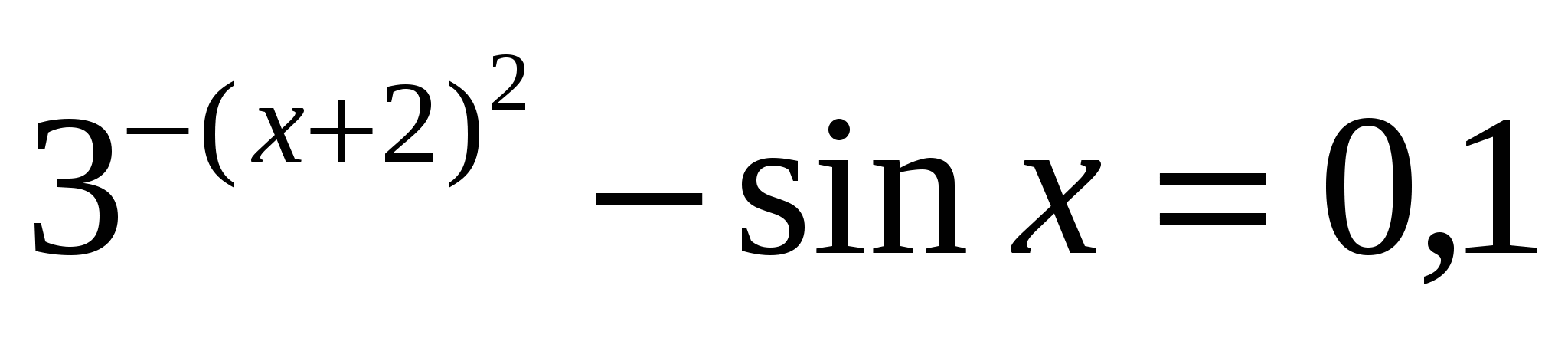
на отрезке 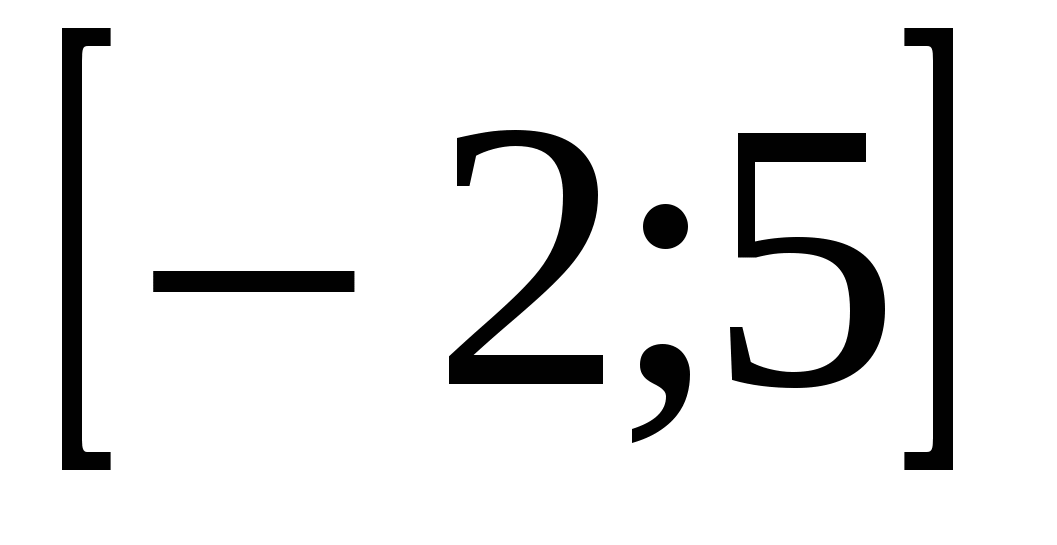 . .
-
Найти корни нелинейного уравнения
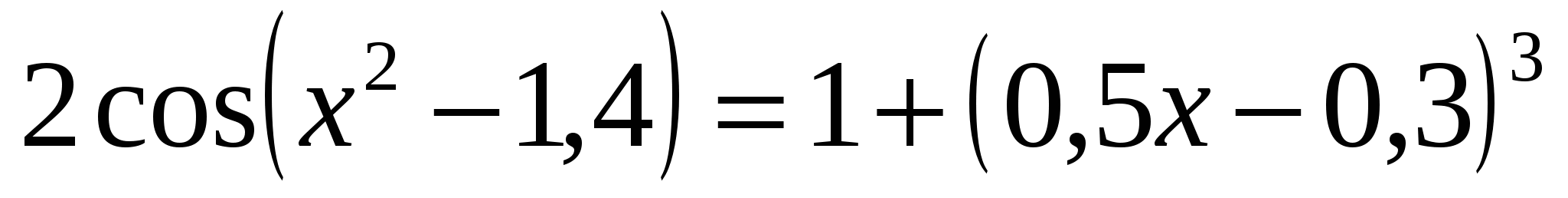
на отрезке 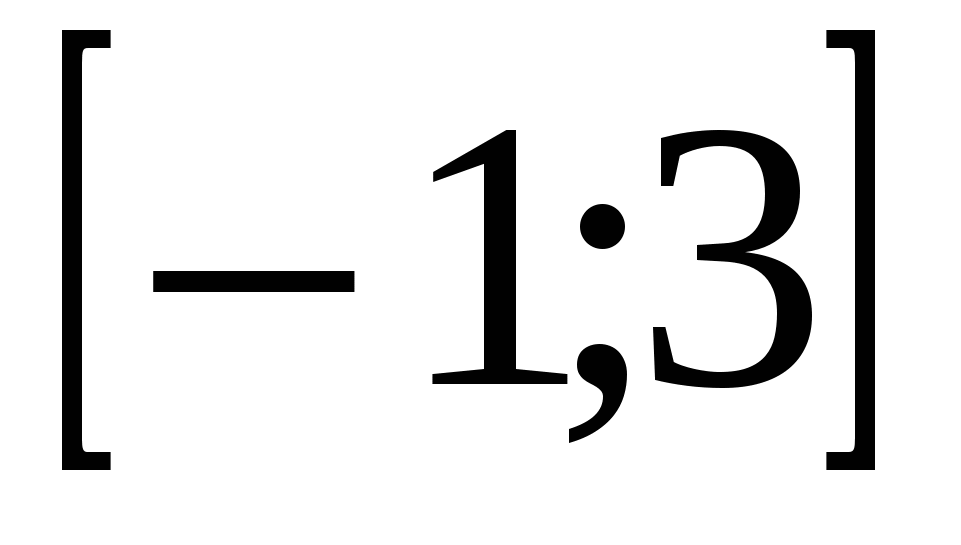 . .
-
Найти корни нелинейного алгебраического уравнения
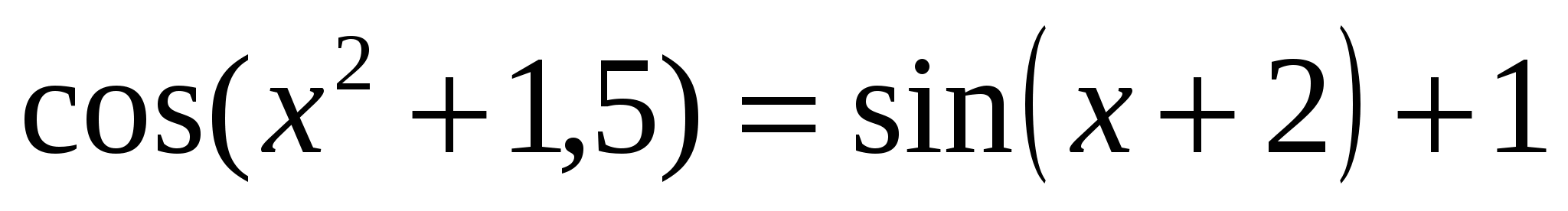
при 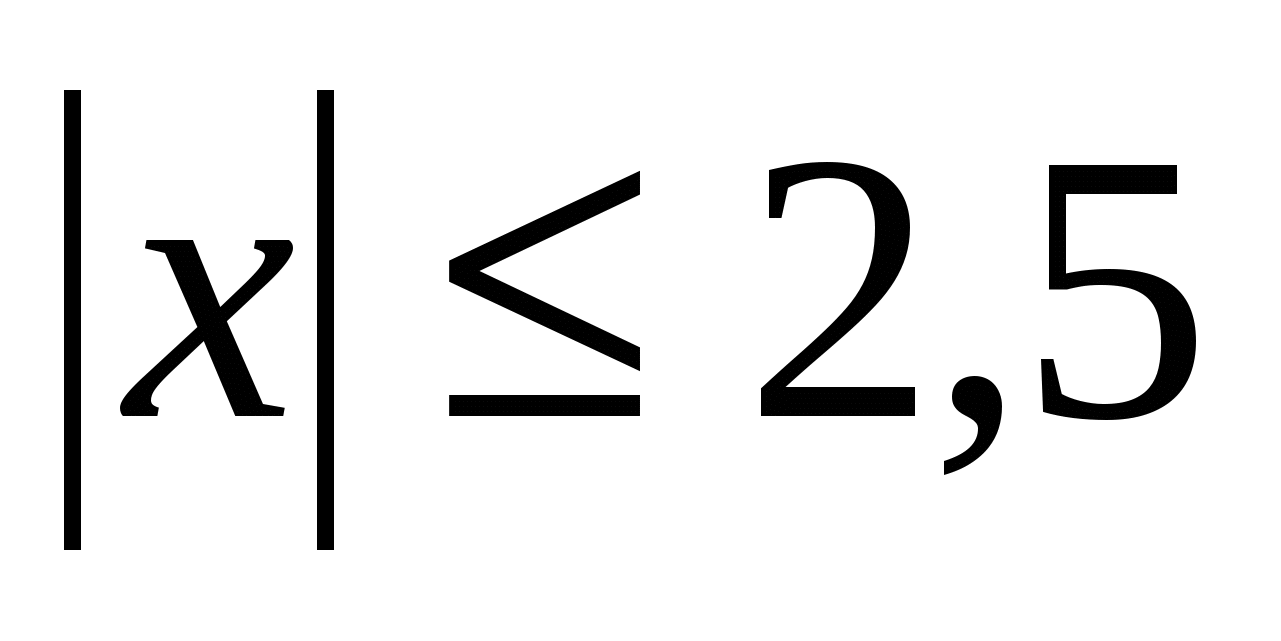 . .
III. Решить следующую задачу.
Требуется найти сумму кредита на постройку дома, который можно взять сроком на 30 лет. Годовая ставка составляет 6,5 %, а ежемесячные выплаты не должны превышать 200000 руб.
Указание. Для расчета выплат следует использовать функцию ППЛАТ (ПЛТ), а для нахождения суммы кредита – Подбор параметра.
IV. Решить следующую задачу.
Пусть имеется фирма, занимающаяся продажей компьютеров. Ее торговые агенты осуществили продажи компьютеров в 2007 и 2008 годах на следующие суммы:
|
2007
|
2008
|
Милова Жанна
|
22592 тыс. руб.
|
23051 тыс. руб.
|
Белкин Самсон
|
21383 тыс. руб.
|
21817 тыс. руб.
|
Сергеев Иван
|
26688 тыс. руб.
|
27240 тыс. руб.
|
Лампов Федор
|
29454 тыс. руб.
|
30052 тыс. руб.
|
Победин Георгий
|
28399 тыс. руб.
|
28976 тыс. руб.
|
Исходные данные для дальнейшего анализа можно представить следующей таблицей в Excel на рабочем листе "Продажа компьютеров":
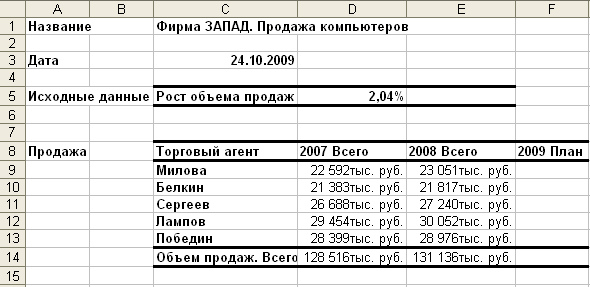
Таким образом, с 2007 по 2008 год объем продаж компьютеров вырос с 128526 тыс. руб. до 131136 тыс. руб., что в процентном выражении составляет 2,04 %.
-
Аналитический отдел фирмы в 2009 г. планирует достигнуть объема продаж в 140000 тыс. руб. Необходимо определить, каков должен быть процент относительного прироста объема продаж для получения такого результата.
Указание. Заполнить ячейки F9:F13, используя значения объемов продаж в 2008 г. и рост объема продаж, равный 2,04 %. В ячейке F14 подсчитать сумму значений, содержащихся в ячейках F9:F13. Далее с помощью команды Подбор параметра получить в ячейке F14 результат 140000, изменяя значение в ячейке D5.
-
Фирму заинтересовало, какой рост дохода можно ожидать при изменении процента прироста объемов продаж от 3 % до 10 %. Построить для этой цели таблицу подстановки данных.
Указание. Для решения задачи построить на листе "Продажа компьютеров" в ячейках С18:D26 следующую таблицу:
Рост объема продаж |
|
3 %
|
|
4 %
|
|
5 %
|
|
6 %
|
|
7 %
|
|
8 %
|
|
9 %
|
|
10 %
|
|
Скопировать формулу ячейки F14 в формулу ячейки D18. С помощью команды "Таблица подстановки" заполнить таблицу, подставляя значения в столбце С19:C26 в ячейку D5.
3) Полученные результаты отформатировать и сохранить в своей папке.
Лабораторная работа №9. “Шаблоны”
Задания
Создание собственных шаблонов
1. Создать свои шаблоны по предлагаемым образцам 1-4; защитить ячейки с формулами.
2. Сохранить их в своей папке как шаблоны.
3. Заполнить таблицы для вновь созданных шаблонов по предлагаемым образцам и сохранить результаты в файлах Excel.
Формулы для образцов
Образец 2.
Расчет осуществляется по следующим формулам:
формула1=(конец сеанса – начало сеанса)*24 (должен быть числовой формат!);
формула2=(Если (И (начало сеанса>=7/24; начало сеанса<22/24)); времясеанса*2,4; время сеанса*1,4);
формула3=сумма всех столбцов в этой категории (т.е. По данной оплате)
формула4=(число оплаты в $) умножить на (число = курс доллара). Здесь используется абсолютная адресация.
формула5=(количество килобайт) умножить на (Если(ячейка="По Беларуси");0,01;(Если(ячейка="По СНГ";0,02;0,04));
формула6=(абонентная плата)+(Итого за Internet)+(Итого за электронную почту)
Замечание. В образце 2 для ячейки F5 используется "денежный" формат в единицах "Английский $ (США)".
Образец 3.
Расчет осуществляется по следующей схеме:
ЕСЛИ (количество дней проката<31;то вычисления по формуле 3;
ЕСЛИ (И(количество дней проката>31;количество дней проката<61));
то вычисления по формуле 4; иначе вычисления по формуле 5))
Формула 1: =С4 – С3;
Формула 2: =D9+D10+D11;
Формула 3: =В9;
Формула 4: =В10*количество дней;
Формула 5: =B11*количество дней
Образец 1
|
Калькуляция
|
|
№
|
Наимено-
Вание
|
Обозначение
(имена ячеек)
|
Вычисления по формуле
(вводить, начиная с символа "=")
|
|
|
Объем работ
|
О
|
сюда ввести любое число, равное объему работ
|
|
|
|
X
|
формула для Х =О-(К+М)
|
|
1
|
Зарплата
|
ЗРП
|
формула для ЗРП =Х/1,71
|
|
2
|
Фонд занятости
|
ФЗ
|
формула для ФЗ =ЗРП*0,01
|
|
3
|
Фонд страхования
|
ФС
|
формула для ФС =ЗРП*0,35
|
|
4
|
Материалы
|
М
|
сюда ввести любое число меньше О
|
|
5
|
Командиров-ки
|
К
|
сюда ввести любое число меньше О
|
|
6
|
Накладные расходы
|
Р
|
формула для P =ЗРП*0,35
|
|
|
|
|
|
|
|
Итого
|
|
=(ЗРП+ФЗ+ФС+М+К+Р)
сумма должна быть равна О!
|
|
|
|
|
|
|
страница 1 страница 2 | страница 3 | страница 4
|