страница 1 ... страница 2 | страница 3 страница 4 страница 5 ... страница 10 | страница 11
1.3. Некоторые приложения вейвлет-анализа. Восстановление зашумленных сигналов
Пусть имеется n = 2J+1 наблюдений yi функции f(t) на отрезке [0,1], содержащих "белый" шум:
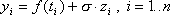
Для очистки сигнала от шума применяется последовательно:
-
прямое вейвлет-преобразование;
-
зануление незначимых коэффициентов преобразования с порогом, пропорциональным амплитуде шума;
-
обратное вейвлет-преобразование.
Ниже на Рис.2.18 приведены результаты подавления шума в модельном ступенчатом сигнале на основе вейвлет-преобразования, сплайн-методов и метода Фурье. Такие ступенчатые сигналы характерны, например, для геофизических задач акустического анализа слоистой среды.
Видно, что с использованием вейвлет-преобразования достигается более глубокое подавление шума при сохранении структуры сигнала.
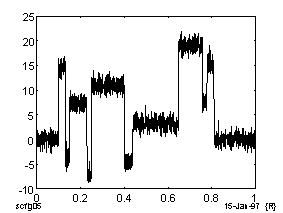
Зашумленный ступенчатый сигнал.
|

Сигнал, очищенный при помощи W-преобразования.
|

Сигнал, очищенный при помощи сплайн-сглаживания.
|

Сигнал, очищенный при помощи обрезания высоких гармоник Фурье.
|
Рис. 2.18. Восстановление ступенчатого сигнала.
Идея нелинейного (порогового) удаления шума состоит в том [9], что ортогональное вейвлет-преобразование "сжимает" сигнал до небольшого числа относительно больших коэффициентов. С другой стороны, "белый" шум в при любом ортогональном преобразовании сохраняет свою структуру и амплитуду. Поэтому пороговое обрезание коэффициентов вейвлет-преобразования не влияет на структуру сигнала, сильно понижая шум. вейвлет-преобразование близко к "идеальному" проектору, сохраняющему те и только те коэффициенты, для которых сигнал превышает шум.
На Рис. 2.19 приведен пример вейвлет-реконструкции реального ЯМР-сигнала из шума, при котором не наблюдается уширения пиков, характерного для традиционных линейных методов.
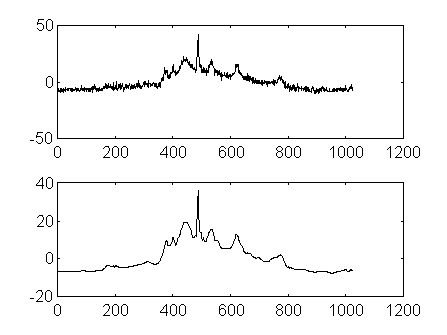
Рис. 2.19. Очистка шума в ЯМР сигнале.
Аналогично может быть восстановлен двумерный сигнал - изображение. На Рис 2.20 изображен портрет Ингрид Добечи (Ingrid Daubechies) - одной из основателей теории вейвлет-преобразования. Фрагмент образа был подвергнут зашумлению и восстановлен при помощи вейвлет-преобразования с койфлет-функцией, предложенной Добечи [10].
Рис. 2.20. Исходное, зашумленное и восстановленное изображение.
Восстановление из шума, а также описываемое в следующем пункте сжатие информации может использоваться для дальних телекоммуникаций с узкой полосой пропускания.
Сжатие информации
Рис. 2.21 иллюстрирует качество восстановления сигнала при "сжатии" его при помощи сохранения заданного количества коэффициентов при ортогональном преобразовании [9]. В качестве тестового выбран сейсмический сигнал. При сохранении 100 коэффициентов Фурье-преобразования и 100 коэффициентов вейвлет-преобразования, более высокое качество последнего проявляется даже при визуальной инспекции.
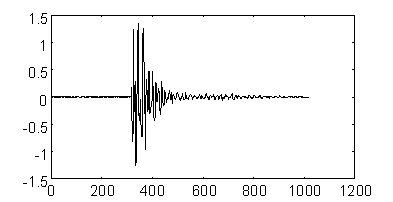
Исходный сейсмический сигнал.

Сигнал, восстановленный по 100 коэффициентам вейвлет -преобразования.
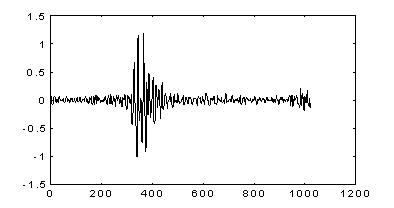
Сигнал, восстановленный по 100 коэффициентам Фурье-преобразования.
Рис. 2.21. Сжатие сейсмического сигнала.
В приведенном примере степень сжатия равна 10:1.
Приложения методов глубокой компрессии и качественного восстановления сигналов при помощи вейвлет-преобразований охватывают не только область телекоммуникаций, но и емких архивов видео и телеинформации.
На Рис.2.22 приведен пример использования глубокой компрессии информации для хранения в архиве. Сжатие информации достигает нескольких десятков раз, т.е. в базе данных хранится лишь 2-3 % от исходного объема данных.

Рис. 2.22. Реконструкция (справа) отпечатка пальца (слева) после сжатия с помощью вейвлет-преобразования со степенью 26:1. Данные получены из Лос-Аламосской лаборатории США (URL: ftp.c3.lanl.gov/pub/WSQ/print_data)
Сжатие информации используется не только для ее хранения или передачи по каналам связи, но и для решения задач анализа и распознавания. При этом значительно сокращается объем вычислений распознающей системы (например, нейронной сети), что ускоряет обработку. Это иллюстрировалось, в частности, и в разделе, посвященном прогнозу временных рядов.
Одним из важных приложений в этой области является анализ радиационных и нейтронных спектров при помощи вейвлет-преобразований, с целью контроля и учета делящихся материалов, их классификации (в частности, распознавания материалов, применяемых при разработке систем ядерных вооружений, среди образцов, используемых в энергетике, см., например, http://www.pnl.gov/statistics/research/testban.html).
Анализ электромагнитных явлений
Компактные волны представляются удобным и естественным инструментом для исследований электромагнитных явлений[11], поскольку уравнения Максвелла (как и вейвлеты) инвариантны относительно перемещений и изменений масштаба. При этом формализм вейвлет-преобразований позволяет сформулировать физические принципы волновых явлений и вопросы обработки сигналов на едином языке. В книге [11] построен универсальный вейвлет-базис для решений уравнений Максвелла в свободном пространстве.
В работе [12] вейвлет-представление было успешно применено для моделирования прохождения оптического импульса в нелинейной среде. При этом численно решалось нелинейное уравнение Шредингера для слабо меняющейся амплитуды электрического поля в волноводе:
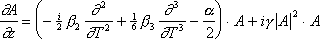
Данное уравнение учитывает групповую дисперсию, фазовую само-модуляцию и поглощение волны. Решения для распространения гауссового пакета, приведенные в [12], получены на основе метода расщепления линейного и нелинейного операторов в правой части, с разложением решения по вейвлет-базису Добечи.
Метод вейвлет-разложения сравнивался с традиционно используемым разложением Фурье, при этом, при одинаковой точности результатов, схема на основе вейвлет-разложения имеет вычислительную сложность O(N), в то время, как Фурье-схема - O(N log N).
Исследование явлений турбулентности
Исследование метеорологических и климатических процессов в последнее время особенно актуально. При этом возрастает как объем обрабатываемых данных, так и сложность моделируемых процессов [2,13].
В обзоре [2] описаны применения методов компактных волн к анализу климатических временных рядов. Исследованы долговременные (на масштабах (10-100 лет) аномалии температур Южного и Северного полушария.
В работе [13] методы компактных волн применены для анализа явлений атмосферной турбулентности, которая характеризуется локализованными событиями, происходящими на широком диапазоне масштабов. Вейвлет-преобразование является инструментом, напрямую нацеленным на описание таких явлений. В этой работе используется двумерный аналог G2-вейвлета (описанного во вводном разделе):
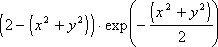
На Рис. 2.23 приведены изображения турбулентной струи (полученные в модельных экспериментах при помощи теневой фотографии) и результаты вейвлет-анализа для двух различных пространственных масштабов. Компактно волновое представление экспериментальных данных дает наглядную и количественно интерпретируемую картину явлений разных масштабов.
Рис. 2.23 Теневая фотография турбулентной струи (слева) и ее вейвлет-преобразование на двух различных пространственных масштабах.
Коэффициенты вейвлет-преобразований используются в [13] для построения статистических моделей турбулентности. Оригинальный подход к исследованию турбулентных течений методами вейвлет анализа предложен в новом совместном проекте ФИАН и ВНИИТФ для Международного научно-технического центра (http://www.istc.ru).
страница 1 ... страница 2 | страница 3 страница 4 страница 5 ... страница 10 | страница 11
|