страница 1 ... страница 2 | страница 3 | страница 4 страница 5 страница 6 ... страница 10 | страница 11
2. Алгоритм вейвлет-анализа акустических сигналов
В данной главе описаны основные этапы двух методов реализации алгоритма вейвлет-анализа, использованного в дальнейшем в программе вейвлет-анализа акустических сигналов.
2.1 Предварительная генерация данных.
Вейвлет-преобразование задаётся следующим выражением:

(3.1)
где
τ – временной сдвиг,
а – масштаб вейвлета.
Компьютер в конечном итоге работает с дискретными данными, поэтому запишем дискретную версию вейвлет-преобразования:
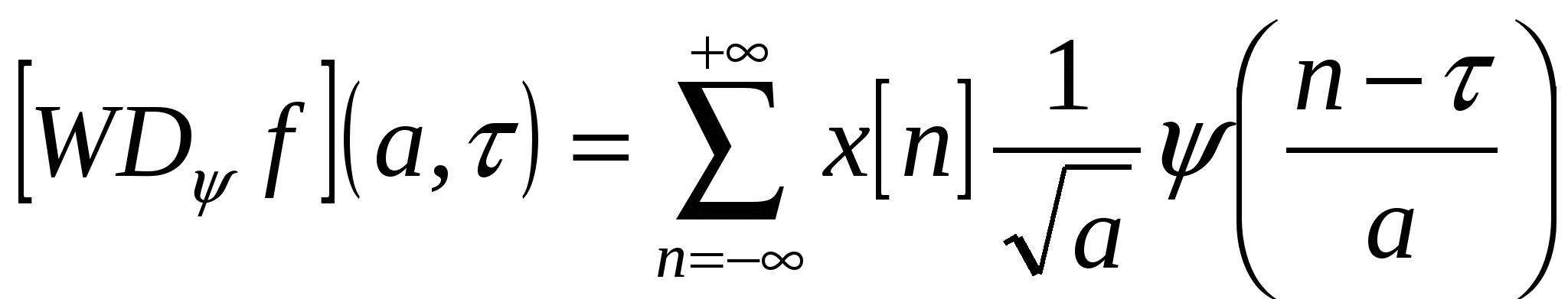
(3.2)
Прямая реализация алгоритма вейвлет-преобразования требует больших вычислительных затрат. Вместе с тем, затраты можно существенно сократить, если предварительно сгенерировать те данные, которые не изменяются в процессе вычислений. Надо заметить, что, в свою очередь, это может привести к значительному увеличению требуемой алгоритмом памяти.
В данном случае мы можем предварительно сгенерировать массив вейвлетов различного масштаба. Для этого необходимо выполнить несколько шагов:
-
Выбрать минимальный и максимальный масштаб вейвлетов, необходимый для анализа сигналов и, при необходимости, выбрать закон изменения масштаба.
-
Сгенерировать массив масштабов (scales) вейвлетов.
-
Для данных масштабов сгенерировать массивы вейвлетов.
Остановимся подробнее на каждом шаге.
Выбор минимального и максимального масштаба. При анализе различных групп сигналов часто возникает необходимость лишь в частичном анализе сигнала. Так, например, нас может интересовать лишь низкочастотная область сигнала (соответствующая вейвлетам с бóльшим масштабом) или, наоборот, лишь высокочастотная (соответствующая вейвлетам с меньшим масштабом). В таком случае нужно выбирать минимальный и максимальный масштабы вейвлета, соответственно, большими или меньшими.
Как правило, для большинства задач анализа сигналов наилучшим образом подходит логарифмический закон изменения масштаба, когда на каждую октаву приходится равное число вейвлетов с различными масштабами. Однако иногда может возникать ситуация, когда необходимо более тщательно «рассмотреть» одни участки спектра и более грубо – другие. В таком случае мы можем выбрать не логарифмический, а иной закон изменения масштаба, вплоть до задания его вручную.
Пример.
При логарифмическом законе изменения масштабов вейвлетов масштабы будут рассчитываться по следующей формуле:
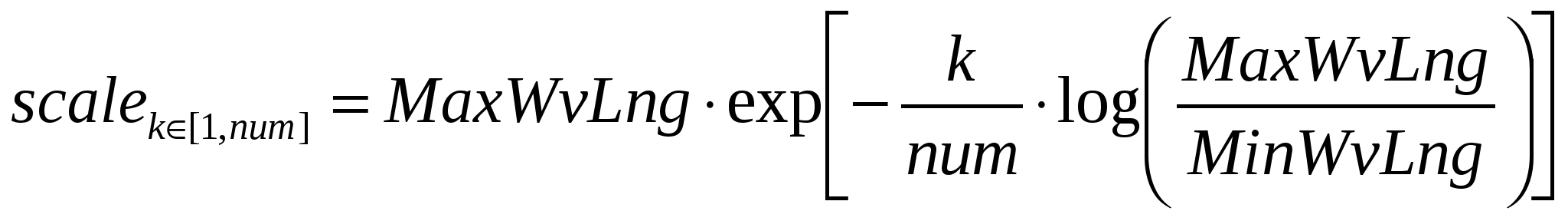
(3.3)
где
scalek – текущий масштаб (с порядковым номером k);
MaxWvLng – наибольший требуемый масштаб вейвлета;
MinWvLng – наименьший требуемый масштаб вейвлета;
num – общее число масштабов.
Генерация массива масштабов. На данном шаге этапа предварительной генерации данных формируется массив масштабов вейвлетов в соответствии с заданным на предыдущем шаге законом изменения масштаба.
Генерация массивов вейвлетов различных масштабов. На этом шаге генерации данных необходимо сформировать num массивов, каждый из которых будет содержать вейвлет заранее выбранного типа и соответствующего масштаба. При этом необходимо определить область вычисления вейвлета (и, фактически, длину массива) таким образом, чтобы отсечённая часть вейвлета была близкой к нулю и пренебрежение ею не вносило бы существенную ошибку в вычисления. Следует заметить, данная проблема присутствует не во всех случаях, так как некоторые типы вейвлетов (например, B-сплайновые вейвлеты) отличны от нуля лишь в некоторой ограниченной области. С другой стороны, для многих типов вейвлетов заранее известна так называемая эффективная область, за пределами которой значения вейвлет-функции можно считать равными нулю.
Графический вид массивов для различных масштабов и различных типов вейвлетов представлен на Рис. 3.1
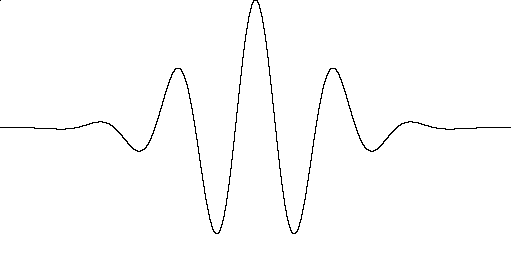 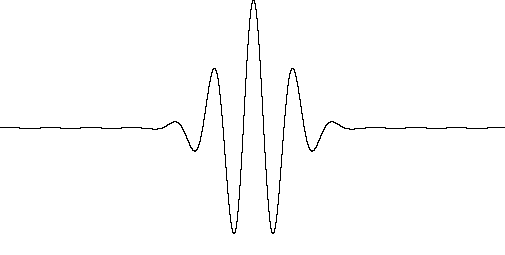
a б
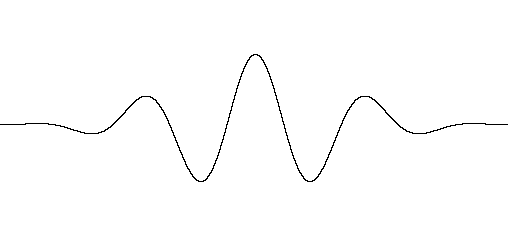 
в г
Рис. 3.2 Различные виды сгенерированных вейвлетов: а,б – Morlet, в,г – B-сплайновые.
страница 1 ... страница 2 | страница 3 | страница 4 страница 5 страница 6 ... страница 10 | страница 11
|