страница 1 ... страница 3 | страница 4 | страница 5 страница 6 страница 7 ... страница 10 | страница 11
2.2 Вычисление вейвлет-преобразования.
Следующим (и основным) шагом алгоритма вейвлет-анализа является непосредственно вычисление вейвлет-преобразования.
При реализации вейвлет-преобразования с использованием предварительно сгенерированных данных алгоритм преобразования в общем случае будет выглядеть следующим образом:
-
Произвести предварительную генерацию данных (массива масштабов и массивов вейвлетов).
-
Для каждого интересуемого момента времени подсчитать num-мерный вейвлет-вектор.
Вычислительная сложность и, соответственно, время работы алгоритма напрямую зависит от того, каким образом будет реализован подсчёт вейвлет-вектора. Были разработаны и реализованы 2 метода.
2.2.1 Прямой метод подсчёта вейвлет-вектора.
В данном случае каждую компоненту вейвлет-вектора необходимо вычислять, используя массив с вейвлетом соответствующего масштаба. Компоненты вычисляются по следующей формуле:
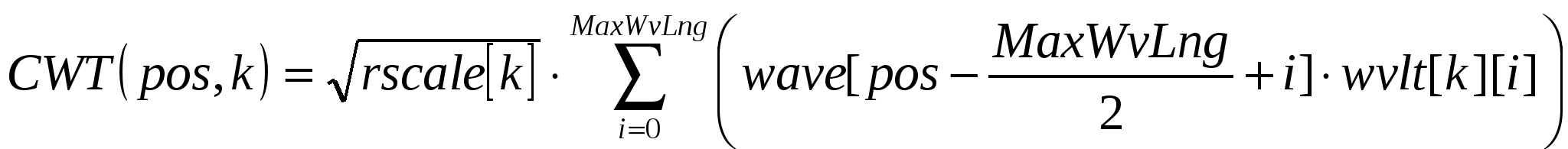
где
pos – текущая позиция (во времени);
k – номер вейвлета;
rscale[k] – число, обратно пропорциональное масштабу вейвлета;
wave[] – массив со значениями выборок анализируемого сигнала;
wvlt[k][i] – i-ая выборка k-ого вейвлета, масштаб которого обратно пропорционален значению rscale[k];
Прямой метод подсчёта вейвлет-вектора характеризуется большей точностью, но и, вместе с тем, относительно низким быстродействием. Кроме того, как уже было отмечено ранее, необходимость хранить num массивов с вейвлетами различного масштаба приводит к значительному увеличению объёма требуемой алгоритмом памяти.
В связи с этим была разработана модификация предыдущего метода, сочетающая в себе, с одной стороны, большее быстродействие, и, с другой стороны, меньший требуемый объём памяти.
2.2.2 Быстрый октавный метод подсчёта вейвлет-вектора.
Суть предложенного метода состоит в том, что ось масштабов делится на октавы, в пределах которых масштаб вейвлета меняется ровно в два раза; а в каждой октаве для вычисления части вейвлет-вектора, соответствующей этой октаве, используется один и тот же небольшой набор масштабированных вейвлетов (для всех октав). При этом вместо исходного анализируемого сигнала используется сигнал, сжатый по времени в соответствующее октаве число раз. После вычисления необходимо скорректировать получаемое значение с учётом того, что и вейвлет, и исходный сигнал сжаты по времени (следовательно, полученное значение будет отличаться от вычисленного обычным методом). Также следует учитывать, что при достаточно небольшом минимальном масштабе вейвлета целесообразно делить на октавы лишь часть оси масштабов с бóльшими масштабами, а оставшиеся компоненты вейвлет-вектора подсчитывать с помощью первого метода.
Проиллюстрируем сказанное следующими рисунками:
Р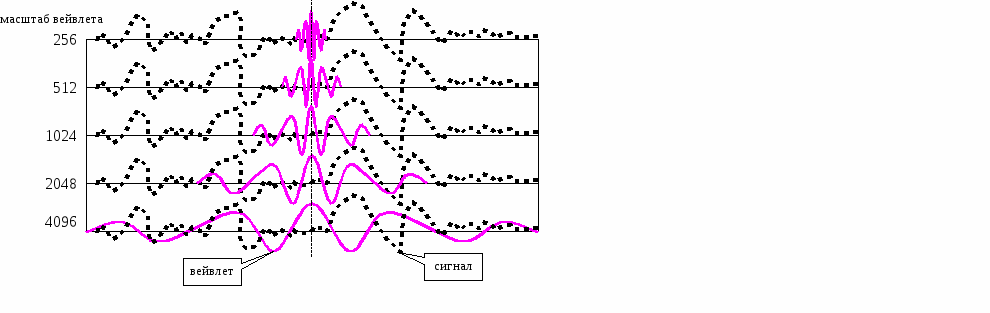
ис. 3.3 Условная схема вычисления вейвлет-компонент при использовании первого метода.
На рисунке 3.3 условно показана схема вычисления пяти компонент вейвлет-вектора, соответствующих вейвлет-масштабам 4096, 2048, 1024, 512 и 256. При вычислении каждой компоненты исходный сигнал (показан пунктирной линией) умножается на масштабированный вейвлет (показан сплошной линией) и считается интеграл (сумма) от полученного произведения.
Изменим схему вычислений следующим образом:
Р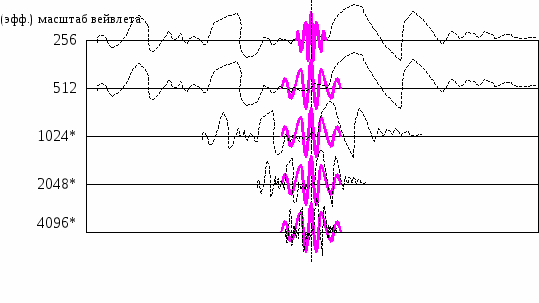
ис. 3.4 Условная схема вычисления компонент вейвлет-вектора при использовании октавного метода.
В этом случае для компонент, соответствующих вейвлет-масштабам 1024, 2048, 4096 производится масштабирование не вейвлета, а самого анализируемого сигнала. Звёздочки рядом с масштабами в этом случае указывают на то, что это не реальный масштаб (реальный масштаб вейвлета для всех трёх компонент равен 512), а эффективный – то есть при перемножении вейвлета на масштабированный сигнал мы в результате получим функцию того же вида, что и для трёх нижних случаев на рис. 3.3, но сжатую соответственно в 2, 4 и 8 раз. После интегрирования (суммирования) нам необходимо умножить получившиеся результаты соответственно на 2, 4 и 8 для того, чтобы получить значения компонентов вейвлет-вектора такие же, как и в первом методе.
При этом значительно сокращается объём требуемой памяти благодаря тому, что не нужно хранить в памяти вейвлеты всех масштабов – достаточно только хранить часть отмасштабированных вейвлетов, находящихся в одной октаве (для случая, показанного на рисунке 3.4 – вейвлеты с масштабами, изменяющимися от 512 до 256). Также нам потребуется сжатый с различными масштабами анализируемый сигнал.
Вообще говоря, так как сигнал в конечном итоге дискретный, то при его сжатии в 2, 4, 8 и т.д. раз нам необходимо предварительно накладывать на него фильтр нижних частот и только после этого производить процедуру прореживания и масштабирования. Следует отметить, что само наложение фильтра НЧ могло бы существенно замедлить общую процедуру обработки и анализа сигнала и свести на нет преимущества октавного метода. Однако, как выяснилось в ходе исследований, для подавляющего числа сигналов, в том числе речевых, использование вместо процедуры наложения НЧ-фильтра простейшей процедуры усреднения по времени приводило к тому, что результаты работы первого и второго метода были практически идентичными (по крайней мере, визуально). С учётом того, что октавный метод можно использовать как метод очень быстрой визуализации общей вейвлет-картины и выбора существенных временных интервалов для последующего более точного анализа с помощью первого метода, было принято решение оставить процедуру усреднения по времени в качестве процедуры предобработки при масштабировании анализируемого сигнала.
Таким образом, на этапе предварительной генерации данных (либо на этапе загрузки данных) появился дополнительный пункт – создание масштабированного сигнала.
Формирование сжатого по времени сигнала происходит согласно следующей формуле:

где
k – номер октавы или номер массива, содержащего сжатый в 2k раз сигнал;
pos – номер выборки в новом массиве, описывающем сжатый сигнал;
datalen – размер исходных данных (анализируемого сигнала);
wave – массив, описывающий исходный сигнал.
Noctaves – общее число октав. В общем случае это число не обязательно является целым; вычисляется по формуле

где
MaxWvLng – наибольший масштаб вейвлета;
MinWvLng – наименьший масштаб вейвлета.
Непосредственно алгоритм быстрого октавного метода вычисления одной вейвлет-компоненты будет выглядеть следующим образом:
1. Подсчитать текущую октаву:

где MaxOctave – номер октавы, вплоть до которой будет применяться быстрый октавный алгоритм;
k – номер текущей вейвлет-компоненты.
2. Определить номер использующегося вейвлета (согласно масштабам вейвлетов, сгенерированным по формуле (3.3))

3. Подсчитать значение компоненты вейвлет-вектора:

где
WvLng – длина массива, описывающего масштабированный вейвлет с номером k’.
Легко показать, что при этом максимальный масштаб вейвлета будет соответствовать нижней границе той октавы, которая выбрана в качестве последней, где используется алгоритм октавного вейвлет-преобазования. Таким образом, отпадает необходимость хранить вейвлеты с масштабом, большим этого максимального масштаба, что приводит не только к уменьшению требуемой памяти, но и к увеличению быстродействия вследствие того, что максимальный масштаб вейвлета уменьшился в 2MaxOctave раз. Более того, при реализации данного алгоритма эти два фактора могут привести к дополнительному «внеплановому» увеличению быстродействия благодаря тому, что все наиболее часто используемые при вычислении данные попадут в кэш первого или второго уровня центрального процессора.
Следует, однако, отметить, что, несмотря на то, что для большинства акустических сигналов данный метод приводит к несущественным отличиям от первого метода, для некоторых специфических типов сигнала происходит существенное искажение вейвлет-картины из-за отсутствия НЧ-фильтрации в процедуре предобработки перед сжатием сигнала.
страница 1 ... страница 3 | страница 4 | страница 5 страница 6 страница 7 ... страница 10 | страница 11
|