страница 1 страница 2 страница 3 | страница 4
Тема№5 Основные показатели надежности программного обеспечения
5.1. Основные понятия
Решение любой задачи, выполнение любой функции, возложенной на ЭВМ, работающей в сети или локально, возможно при взаимодействии ап- паратных и программных средств. Поэтому при анализе надежности вы- полнения ЭВМ заданных функций следует рассматривать единый ком- плекс аппаратных и программных средств.
По аналогии с терминами, принятыми для обозначения показателей надежности ТУ, под надежностью программного обеспечения (ПО) пони- мается свойство этого обеспечения выполнять заданные функции, сохра- няя свои характеристики в установленных пределах при определенных ус- ловиях эксплуатации.
Надежность ПО определяется его безотказностью и восстанавливаемостью. Безотказность ПО – это свойство сохранять работоспособность при использовании его для обработки информации в ИС. Безотказностью программного обеспечения оценивается вероятность его работы без отказов при определенных условиях внешней среды в течение заданно-
го периода наблюдения.
В приведенном определении под отказом ПО понимается недопус- тимое отклонение характеристик функционирования этого обеспечения от предъявляемых требований. Определенные условия внешней среды – это совокупность входных данных и состояние самой ИС. Заданный пери-
од наблюдения соответствует времени, необходимому для выполнения на
ЭВМ решаемой задачи.
Безотказность ПО может характеризоваться средним временем воз-
никновения отказов при функционировании программы. При этом предполагается, что аппаратные средства ЭВМ находятся в исправном состоянии.
С точки зрения надежности, принципиальное отличие ПО от аппаратных средств состоит в том, что программы не изнашиваются и их выход из строя из-за поломки невозможен. Следовательно, характеристики функ- ционирования ПО зависят только от его качества, предопределяемого про- цессом разработки. Это означает, что безотказность ПО определяется его корректностью и зависит от наличия в нем ошибок, внесенных на этапе его создания. Кроме того, проявление ошибок ПО связано еще и с тем, что в некоторые моменты времени на обработку могут поступать ранее не встречавшиеся совокупности данных, которые программа не в состоянии корректно обработать. Поэтому входные данные в определенной мере влияют на функционирование ПО.
В ряде случаев говорят об устойчивости функционирования ПО. Под этим термином понимается способность ПО ограничивать последствия собственных ошибок и неблагоприятных воздействий внешней среды или противостоять им. Устойчивость ПО обычно обеспечивается с помощью введения различных форм избыточности, позволяющих иметь дублирую- щие модули программ, альтернативные программы для одних и тех же за- дач, осуществлять контроль за процессом исполнения программ.
5.2. Основные причины отказов программного обеспечения
Основными причинами, вызывающими нарушения нормального функционирования ПО, являются:
- ошибки, скрытые в самой программе;
- искажение входной информации;
- неверные действия пользователя;
- неисправность аппаратных средств ИС, на которой реализуется вычис-
лительный процесс.
Ошибки, скрытые в программе. При разработке сложного ПО воз- можно возникновение ошибок, которые не всегда удается обнаружить и ликвидировать в процессе отладки. В силу этого в программах остается некоторое количество скрытых ошибок. Они являются причиной неверно-
го функционирования этих программ. Среди ошибок подобного рода мож-
но выделить следующие характерные группы.
Ошибки вычислений. Ошибки этой группы связаны с некорректной за- писью или программированием математических выражений, а также не- верное преобразование типов переменных. Вследствие этого получаются неправильные результаты.
Логические ошибки. Эта группа ошибок является причиной искажения алгоритма решения задачи. К ошибкам подобного рода можно отнести не- верную передачу управления, неверное задание диапазона изменения па- раметра цикла, неверное условие и другие ошибки.
Ошибки ввода-вывода. Эти ошибки связаны с неправильным управле- нием ввода-вывода, формированием выходных записей, определением размера записей и другими неправильно свершенными действиями.
Ошибки манипулирования данными. К числу таких ошибок относятся: неверное определение числа элементов данных; неверные начальные зна- чения, присвоенные данным; неверное указание длины операнда или име-
ни переменной и другие ошибки.
Ошибки совместимости связаны с отсутствием совместимости разра- батываемого или применяемого ПО с операционной системой или другими прикладными программами.
Ошибки сопряжений. группа этих ошибок вызывает неверное взаимо-
действие ПО с другими программами или подпрограммами, с системными программами, устройствами ЭВМ или входными данными.
Искажение входной информации. Указанная причина вызывает нару-
шение функционирования ПО, когда входные данные не попадают в до-
пустимую область значения переменных. В этом случае возникает несоот-
ветствие между исходной информацией и возможностями программы.
Неверные действия пользователя связаны с неправильной интерпре-
тацией сообщений, с неправильными действиями пользователя при работе
в диалоговом режиме. Часто эти ошибки являются следствием некачест-
венной программной документацией.
Неисправность аппаратных средств ИС. Эти неисправности оказы- вают определенное влияние на характеристики надежности ПО. Появление отказов или сбои в работе аппаратуры приводят к нарушению хода обра- ботки информации и, как следствие, могут искажать как исходные данные, так и саму программу.
Следствием появления ошибок в программе является ее отказ. По-
следствия отказов ПО можно разделить на:
- полное прекращение выполнения функций программы;
- кратковременное нарушение хода обработки информации в ИС.
Степень серьезности последствий отказов ПО оценивается соотноше- нием между временем восстановления программы после отказа и динами- ческими характеристиками объектов, использующих результаты работы этой программы.
Аварийное завершение работы прикладного ПО легко идентифициру-
ется, так как операционная система выдает сообщения, содержащие ава- рийный код. Характерными причинами появления аварийного завершения являются ошибки при выполнении макрокоманды, неверное использова- ние методов доступа, нарушение защиты памяти, нехватка ресурсов памя- ти, неверное использование макрокоманды, возникновение программных прерываний, для которых не указан обработчик, и другие причины.
5.3. Основные показатели надежности программного обеспечения
Если рассматривать отказавшее ПО без учета его восстановления, а также случайный характер отказов в программах, то основные показатели надежности в этом случае не отличаются от тех, которые были рассмотре- ны в п.п. 2.2. – 2.4. При этом характер изменения этих показателей во вре- мени будет зависеть от модели надежности ПО.
Таким образом, основными показателями надежности ПО являются:
- вероятность безотказной работы программы p(t) , представляющая со- бой вероятность того, что ошибки программы не проявятся в интервале времени (0, t ) ;
- вероятность отказа программы
до момента времени t ;
q(t ) или вероятность события отказа ПО
- интенсивность отказов программы
(t) ;
- средняя наработка программы на отказ T , являющаяся математическим ожиданием временного интервала между последовательными отказами. При определении характеристик надежности ПО учитывается тот факт, что возникающие при работе программ ошибки устраняются, коли- чество ошибок уменьшается и, следовательно, их интенсивность понижа- ется, а наработка на отказ программы увеличивается.
Тема№6 Аналитические модели надежности программного обеспечения
В связи с такими предположениями рассматривается несколько моделей надежности ПО: модель с дискретно-понижающей частотой появления ошибок, модель с дискретным увеличением наработки на отказ или ошибку ПО, экспоненциальная модель надежности ПО.
(t)
6.1. Модель с дискретно-понижающей частотой появления
ошибок ПО
В этой модели предполагается, что интенсивность отказов программы
является постоянной величиной до обнаружения возникшей ошибки
и, как следствие – отказа программы и ее устранения. После этого значе-
ние
(t ) уменьшается и интенсивность отказов снова становится констан-
той. В этой модели предполагается, что между (t) и числом оставшихся
в программе ошибок существует зависимость
( t) K ( M i) i ,
где M – неизвестное первоначальное число ошибок;
i – число обнаруженных ошибок, зависящее от времени t ;
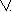 K K – некоторая константа.
Характер изменения интенсивности отказов для этой модели представлен на рисунке 4.
(t)
-
 t t
Рис. 4. Характер изменения интенсивности отказов программы от времени наработки при модели с дискретно-понижающей частотой появления ошибок
Плотность распределения времени обнаружения i -й ошибки t i
деляется соотношением
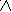 опре- опре-
f (ti ) i e
i t i .
Значения неизвестных параметров K и M могут быть оценены на основании последовательности наблюдения интервалов между моментами обнаружения ошибок.
На практике условия рассмотренной модели нередко не соблюдаются,
а именно:
- не всегда при устранении ошибки интенсивность отказов уменьшается
на одну и ту же величину K , так как разные ошибки имеют различное влияние на ход исполнения программы;
- довольно часто возникают ситуации, при которых устранение одних ошибок приводит к появлению новых;
- не всегда удается устранить причину ошибки и программу продолжают
использовать, так как при других исходных данных ошибка может себя
и не проявить.
6.2. Модель с дискретным увеличением времени наработки на отказ
Основным допущением в этой модели является предположение о том,
что отказы и ошибки программы в начале эксплуатации возникают часто. По мере отладки программы таких ошибок становится меньше, а время на- работки на отказ после ликвидации очередного отказа увеличивается
(рис.5).
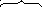 t (1) t (1)
t (2)
t (3)
t (m 1)
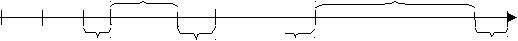 t t
t (1)
0 t1
t (2)
t (2)
t2
t (3)
t (3)
t (m 1)
  t (m 1) t (m 1)
t3
tm 1
t (m)
t m
tm
Рис. 5. Диаграмма интервалов времени наработки на отказ компьютерной программы
На диаграмме величины
t1, t2 , t3 ,K, tm 1, tm
– случайные моменты
времени возникновения первого, второго, третьего и так далее – m -го от-
казов. Величины
t (1) , t (2) , t (3) ,K, t (m 1) , t (m)
– случайные интервалы
времени между соседними отказами программы (обозначены под первым
рядом нижних скобок диаграммы). Интервалы
t (2) , t (3) , t (m 1) , t (m)
также являются случайными временными интервалами.
Пусть первая ошибка, проявившаяся в результате отказа программы,
произошла в случайный момент времени t1
и была устранена. Наработка
до первого отказа и возникшей ошибки равна интервалу времени t (1) . Вто-
рая ошибка возникла в момент времени
t2 . Наработка до второй ошибки
определяется интервалом t (2) . В соответствии с предположением, этот ин- тервал больше, чем t (1) , так как после перезапуска программа проработала время до первой ликвидированной ошибки, продолжила работу до новой,
второй ошибки. Следовательно, интервал t (2) можно представить в виде
t (2) t (1) t (2) ,
где t (2) – дополнение интервала t (1)
 до величины интервала t (2) . до величины интервала t (2) .
Обобщая эти рассуждения до любого i -го интервала ( i 1, m ), можно
записать
Случайные величины
t (i )
t (i) t (i 1) t (i ) .
являются независимыми, имеют математиче-
ское ожидание
M [t ] и дисперсию 2 t .
Случайное время возникновения ( i 1) ошибки ti
отсчитывается от
начального момента времени
t0 0 . Время, необходимое на ликвидацию
ошибки, в расчет не берется. В этом случае для всех случайных моментов времени возникновения ошибки и временных интервалов между соседни- ми ошибками можно записать:
t1 t (1) ;
t2 t1 t (2)
t (1) t (1) t 2 ;
t3 t2 t (3)
t (1) t (2) t (3)
t (1) t (1) t (2) t (1) t (2) t (3) ;
tm mt (1) (m 1)t ( 2) (m 2)t (3) L 2t (m 1) t (m) .
Учитывая, что от момента времени
t0 0
до начала момента
t1 не выяв-
лено ни одной ошибки программы и в силу того, что интервал t (1)
сравни-
тельно невелик, так как ошибки программы вначале ее эксплуатации про-
исходят довольно часто, можно представить интервал t (1) как t (1) . Тогда,
с учетом этой замены, выражение для tm
примет вид
tm
или
mt (1) (m 1)t ( 2) (m 2)t (3) L 2t (m 1) t (m) ,
m i
tm t ( j ) .
i 1 j 1
Рассмотрим выражение для t (i ) при i 1. Согласно ранее принятой замене
t (1)
на t (1) , получим
t (1)
t (0) t (1) t (1) .
Действительно, интервал t (0)
равен нулю, так как до начала эксплуатации
программы никаких ее отказов произойти не могло. Поэтому для любого
i m
при i 1 можно записать
t (m)
m
t (i ) .
i 1
Но t ( m)
– это наработка между (m 1)
и m – отказами. Тогда, для любых
m , средняя наработка между
му ожиданию интервала t (m) :
(m 1)
и m отказами равна математическо-
m
t
(m)
ср
M [t
(m) ]
M [ t
(i ) ] .
Но для любого i
Поэтому
i 1
M [t (i ) ] M [t ] .
m m
ср
t (m) M [ t (i ) ] M [t ] mM [t ] .
i 1
i 1
Отсюда видно, что с увеличением m увеличивается и средняя наработка между двумя отказами.
Рассмотрим среднюю наработку до возникновения m -го отказа. Она
равна математическому ожиданию от tm :
m i ( j ) m i
 m(m 1) m(m 1)
tm ср
M [tm ] M [ t
i 1 j 1
] M [t ]
i 1 j 1
M [t ].
2
Как и предыдущем случае, из полученного выражения видно, что средняя
наработка до отказа возрастает с увеличением числа отказов
Оценки M [t ] и 2 t
получаются по данным об отказах программы в
течение периода наблюдения tн :
mн

M [t] 1 t (i ) ;
mн i 1
2 1 ( 2
t
1)
(mн
(t
i 1
M [t] ,
где mн
– число отказов за интервал времени ( 0, tн ).
6.3. Экспоненциальная модель надежности ПО
Основным предположением этой модели является экспоненциальный характер изменения числа ошибок в программе во времени. Прогноз на- дежности программы производится на основании данных, получаемых во время ее тестирования.
Основными параметрами модели являются:
- – суммарное время функционирования от начала тестирования (с устра-
нением обнаруженных ошибок) до момента оценки надежности;
- M – число ошибок, имеющихся в программе перед началом тестирова-
ния;
- m( )
– конечное число исправленных ошибок;
- m0 ( ) – число оставшихся ошибок.
Предполагается, что число ошибок в программе в каждый момент вре-
мени имеет пуассоновское распределение, а временной интервал между двумя ошибками распределен по экспоненциальному закону. Параметр этого распределения изменяется после распределения очередной ошибки. Интенсивность отказов считается непрерывной функцией, пропорциональ- ной числу оставшихся ошибок. С учетом введенных параметров и предпо- ложений очевидно, что
а интенсивность ошибок
m0 ( ) M m( ) ,
( ) Cm0 ( ) ,
где C – коэффициент пропорциональности, учитывающий быстродейст-
вие ЭВМ и число команд в программе.
Пусть в процессе исправления ошибок новые ошибки не появляются. Следовательно, интенсивность исправления ошибок будет равна интен- сивности их обнаружения:
dm( )
( ) .
d
Совместное решение полученных выражений дает
dm( )
Cm( ) CM .
d
Решением этого уравнения является выражение
m( ) M [1 exp( C )] .
Будем характеризовать надежность программы после тестирования в течение времени средним временем наработки на отказ:
T 1 .
0 ( )
Следовательно,
T 1 exp(C ) .
0 CM
Введем величину
T0 т
– исходное значение среднего времени нара-
ботки на отказ перед тестированием, которое равно
1
T0 т
.
CM
Подставляя это значение в выражение T0 , получим
MT
0 0 m
T T exp( ) .
0 m
Из этого выражения видно, что среднее время наработки на отказ уве-
личивается по мере выявления и исправления ошибок.
Таким образом, аналитические модели надежности дают возможность исследовать закономерности проявления ошибок в программе и прогнози- ровать надежность при ее разработке и эксплуатации.
Вопросы для самоконтроля
1. Что понимается под термином «надежность программного обеспече-
ния» (ПО)?
2. Что понимается под терминами «безотказность ПО» и «отказ ПО»?
3. Основные причины отказов ПО.
4. В чем сущность модели с дискретно-понижающей частотой появления ошибок ПО?
5. В чем сущность экспоненциальной модели надежности ПО?
Тема№7 Элементы теории восстановления
7.1 Основные понятия и определения теории восстановления
К восстанавливаемым ТУ относятся такие, ремонт которых в слу- чае отказов или выработки ими предусмотренного срока эксплуатации производится в соответствии с заданной технологией и в необходимом объеме. После эксплуатация ТУ возобновляется до его предельного со- стояния или следующего ремонта.
Восстанавливаемые ТУ в общем случае представляют собой сложные системы, состоящие из высоконадежных элементов, отказы которых явля- ются независимыми. Для таких систем появление отказов на одном интер- вале наработки практически не влияет на вероятность появления какого- либо количества отказов на другом интервале, не пересекающемся с пер- вым. В этом случае отказы можно считать независимыми, а время нара- ботки между отказами распределенным по экспоненциальному закону.
Восстановление устройства после отказа производят путем замены
неисправного элемента или путем его ремонта. При этом в теории надеж- ности не учитывают время, необходимое на восстановление. Предполага- ется, что возникающие отказы ТУ устраняются мгновенно. Это – так назы- ваемая модель мгновенного восстановления работоспособности ТУ. При рассмотрении характеристик надежности восстанавливаемых ТУ считает- ся, что восстановление полностью возвращает устройству те же свойства, которыми оно обладало до отказа так, что его невозможно отличить от но- вого. При таком допущении продолжительность работы ТУ с момента его восстановления до очередного отказа не зависит от того, сколько раз оно отказывало в прошлом.
Одной из основных характеристик восстанавливаемых ТУ является
ремонтопригодность или восстанавливаемость. Определение термина
«ремонтопригодность» было дано в п. 3.1. Численной мерой восстанавли- ваемости является вероятность восстановления, под которой понимается вероятность того, что за определенный интервал времени и в заданных условиях ремонта неисправное ТУ будет восстановлено:
P(t рем )
p(tф t рем ) ,
где tф
– фактическое время восстановления;
t рем
– заданное время процесса восстановления.
В процессе эксплуатации сложные восстанавливаемые ТУ в любой
момент времени, принятый за начало отсчета времени эксплуатации, могут находиться в одном из двух состояний: исправном или неисправном. Ис- правное состояние восстанавливаемого ТУ в течение некоторого периода
рабочего времени ( t ) определяется следующими двумя необходимыми
условиями:
- наличием исправного состояния в любой данный момент вре-
мени t , принятый за начало отсчета;
- непоявления отказа в полуинтервале времени ( t ), исключая момент t .
В силу сказанного, количественная мера надежности определяется как эксплуатационная надежность, представляющая собой функцию эксплуа- тационной надежности или вероятность исправного состояния ТУ в тече-
ние интервала ( t ):
pЭ ( )
p0 (t ) p( ) .
Это выражение определяется произведением вероятности исправного
состояния
p0 (t )
в любой момент времени
t
и вероятности непоявле-
ния отказа ТУ
сам момент t .
p( )
в течение интервала от момента t до , исключая
Первый сомножитель равен
,
p (t ) N (t)
0 N
где N – некоторое постоянное количество восстанавливаемых ТУ, на-
ходящихся под наблюдением;
N (t)
– количество восстанавливаемых ТУ, находящихся к момен-
ту времени t в исправном состоянии.
Аналогично определяется и вероятность отказа в любой момент вре-
мени t :
(t)
N N (t ) n(t)
q .
0 N N
Очевидно, что
p0 (t ) q0 (t ) 1.
Если предположить, что t меняется от 0 до (а это корректное пред- положение, так как по принятому условию момент времени t принят за начало отсчета), то второй сомножитель эксплуатационной надежности
равен
p( )
t
p(t) e T
 e t . e t .
Последовательности событий, состоящие в возникновении отказов в
случайные моменты времени t1, t2 , t3 ,K, tn , образуют поток событий или поток отказов. Тогда, в качестве характеристик надежности восстанавли- ваемых ТУ можно принять характеристики потока отказов. Основными
характеристиками потока отказов являются средняя статистическая плотность вероятности отказов или параметр потока отказов и После- довательности событий, состоящие в возникновении отказов в случайные моменты времени t1, t2 , t3 ,K, tn , образуют поток событий или поток отка-
зов. Тогда, в качестве характеристик надежности восстанавливаемых ТУ
можно принять характеристики потока отказов. Основными характеристи-
ками потока отказов являются средняя статистическая плотность веро- ятности отказов и суммарная статистическая плотность вероятности отказов.
Средняя статистическая плотность вероятности отказов или па-
раметр потока отказов определяется как отношение количества отка-
завших ТУ
ni
в интервале времени
ti
к числу ТУ
N Э , находящихся в
эксплуатации, при условии, что все отказавшие ТУ мгновенно восстанав-
ливаются или заменяются исправными:
i
ni .
N Э ti
Суммарная статистическая плотность вероятности отказов вы-
ражается отношением полного числа отказов
тации t :
n(t )
по времени эксплуа-
n(t )
.
t
Одной из важных показателей в теории восстановления является
среднее время наработки между двумя отказами Tмо . Оно определяется как отношение времени наработки t ТУ к полному числу отказов ТУ, воз- никших в нем за это время
или
Tмо
t
,
n(t )
1
 Tмо . Tмо .
Известно, что для любого закона распределения времени безотказной
работы ТУ значение средней плотности вероятности отказов
(t )
Для восстанавливаемых устройств в установившемся режиме их работы при t имеет предел:
lim (t ) 1 const ,
t T
где – интенсивность отказов, а T – среднее время безотказной ра-
боты.
7.2. Коэффициенты отказов
Иногда, в качестве вспомогательного критерия надежности элементов восстанавливаемых ТУ применяются различные коэффициенты, в частно- сти – коэффициент отказов.
Коэффициент отказов представляет собой отношение числа отка-
зов однотипных элементов nэ к общему числу отказов в системе nс :
n
o
k Кnэ .
c
Величина этого коэффициента позволяет оценить степень влияния определенного типа элемента на надежность системы в целом. Однако он
не дает возможности определить, какой тип элементов системы менее на- дежен, а какой более надежен. Для этой цели может быть использован от- носительный коэффициент отказов
k Кnэ Nc ,
oo
n
N
c э
где
N э – количество элементов определенного типа в системе;
Nc – полное количество элементов всех типов в системе.
Эти коэффициенты могут быть выражены через другие показатели
надежности. Так, количество отказов в системе вследствие неисправных
элементов определенного типа в течение промежутка времени t
определить с помощью выражения
nэ N э эt ,
можно
где э – средняя плотность вероятности отказов элементов определенного типа. За это же время в системе произойдет всего отказов:
nc c t ,
где c
– суммарная плотность вероятности отказов в системе.
Подставим полученные значения в выражение коэффициента отказов
o
k КN э э t
Кэ .
c t
N э
с
При
предельное значение средней плотности вероятности эле-
ментов определенного типа будет равно
э э .
Следовательно,
o э
k N Кэ .
с
Аналогично можно найти зависимость относительного коэффициента от-
казов
koo от средней и суммарной плотности вероятности отказов:
k Кnэ Nc
К э N э Nc t
Кэ .
oo
В предельном случае
nc N э
с N
э t
Nc
с
будет получено значение
э э
k N
Кэ
oo c .
с
Таким образом, коэффициенты отказов могут быть выражены через интенсивность отказов и суммарную плотность вероятности отказов.
7.3. Комплексные показатели надежности
Процесс эксплуатации сложных восстанавливаемых ТУ не следует рассматривать как непрерывный процесс. Обычно функциональное ис- пользование их чередуется с простоем вследствие двух основных причин:
- бездействие исправных ТУ ввиду отсутствия необходимости их приме-
нения или наличия причин и условий, препятствующих их эксплуатации.
В результате образуется так называемый конъюнктурный простой;
- проведение мероприятий, связанных с профилактикой и текущим ремон-
том, в результате чего образуется вынужденный простой.
Поэтому текущее время эксплуатации ТУ складывается из следующих компонентов:
tэ t
tВП tКП ,
где t
– суммарное время наработки ТУ в течение определенного кален-
дарного времени эксплуатации tэ ;
t ВП
– суммарное время вынужденного простоя (по отказам и плано-
вым профилактикам и восстановлению после них) за этот же период экс-
плуатации;
t КП
– суммарное время конъюнктурного простоя за этот же период.
Здесь под конъюнктурным простоем понимается бездействие исправного
ТУ ввиду отсутствия необходимости применения.
Время вынужденного простоя t ВП
представляет собой сумму
t ВП
t ПЛ
t НПЛ ,
где
t ПЛ
– плановое время вынужденного простоя, которое образуется
вследствие проведения плановых профилактик. Эта величина вполне опре-
делена и практически пропорциональна времени эксплуатации;
t НПЛ - неплановое время вынужденного простоя из-за восстановле-
ния по отказам. Это величина случайная и определяется временем
t p ,
необходимым для восстановления по всем отказам за определенный ка-
лендарный период.
Одним из важнейших критериев надежности является готовность ТУ быть эксплуатируемым (или готовность к применению), которая вы- ражается коэффициентом эксплуатационной готовности:
t
K ЭГ
.
t t
ВП
Величина этого коэффициента зависит не только от надежности, но и
от эксплуатационного совершенства, характеризующего степень его (ТУ)
приспособленности к проведению профилактических работ.
Ввиду того, что плановое время вынужденного простоя не является случайной величиной и значение его отношения к наработке не зависит от количества возникающих отказов, то можно определить величину, выра- жающую собой вероятность того, что ТУ в любой момент времени мо- жет находиться в исправном состоянии. Это величина носит название ко- эффициента готовности и выражается как
t
K .
Г t
t p
На практике важен такой показатель, как степень использования ТУ
в эксплуатации за календарное время
коэффициент использования:
tэ . Определяется эта величина как
t
K ИС
.
tЭ
Коэффициент использования численно равен вероятности того, что в лю-
бой момент времени tЭ
ТУ выполняет свои предписанные функции.
В рассмотренном ранее коэффициенте готовности
Г
K t ,
t
t p
величины t
и tp
могут быть получены из выражений:
t p
n(t
)T p ,
t (t
)Tмо ,
где T p
– среднее время восстановления ТУ;
Tмо – среднее время наработки между двумя отказами.
Тогда, после подстановки этих значений в исходную формулу коэф-
фициента готовности, получим
Г
K К Tмо .
Tмо
Tp
При
t
предельное значение среднего времени наработки между дву-
мя отказами будет равно
lim Tмо T .
t
Подставляя это значение в выражение коэффициента готовности, получим
T
K Г .
T T
С учетом того, что
p
1
 Tмо , Tмо ,
последнее выражение можно записать в виде
1
K Г .
1 T p
Для сложных информационных систем понятие надежности в боль-
шей степени определяется по коэффициенту готовности
K Г , то есть по
вероятность того, что ИС в любой момент времени находится в исправном
состоянии. Для типичного современного сервера K Г
0,99. Это означает
примерно 3.5 суток простоя в год. За рубежом популярной является клас-
сификация ИС по уровню надежности (табл. 2).
Таблица 2
Коэффициент готовности
K Г
|
Максимальное время про-
стоя в год
|
Тип информационной системы
|
0,99
|
3,5 суток
|
Обычная
|
0,999
|
8,5 часов
|
Высокая надежность
|
0,9999
|
1 час
|
Отказоустойчивая
|
0,99999
|
5 минут
|
Безотказная
|
Необходимо отметить и другие качества и надежности функциониро-
вания ИС. Так, одним из важнейших комплексных показателей качества функционирования ИС функциональная полнота F , представляющая со-
бой отношение области автоматизированной обработки информации Qa
той системы, для которой была спроектирована ИС, к области обработки
информации Qи
для функционирования всей обслуживаемой системы:
F Qa .
Qи
Качественной характеристикой ИС являются показатели их надежно-
сти. Различают функциональную и адаптивную надежность.
Функциональная надежность представляет собой свойство ИС реали- зовать в определенной степени функции программно-технологического, технического и эргономического обеспечения.
Адаптивная надежность ИС состоит в возможности реализовывать свои функции в пределах установленных границ:
ад
K К Tис ,
T
ис Tвис
где Tис – средняя наработка на отказ ИС;
Tвис
– среднее время восстановления ИС.
Как видно из последнего выражения,
фициент готовности для ИС.
K ад
есть не что иное, как коэф-
Вопросы для самоконтроля
1. Какие ТУ называются восстанавливаемыми?
2. Определить основные характеристики надежности восстанавливае-
мых ТУ.
3. Что такое коэффициент отказов? Виды коэффициентов отказов.
4. Какие показатели надежности относятся к комплексным?
5. Что такое коэффициент готовности?
6. Аналитические выражения коэффициента готовности.
7. Что такое интенсивность восстановления?
8. Основные аналитические зависимости между показателями надеж-
ности восстанавливаемых ТУ.
9. Определить полную вероятность выполнения заданных функций.
10. Основные показатели надежности для восстанавливаемых информа-
ционных систем.
страница 1 страница 2 страница 3 | страница 4
|