страница 1 ... страница 2 | страница 3 страница 4
10.2. Экспериментальное определение характеристик надежности
Вероятностные элементы характеристик надежности ТУ могут быть получены на основании использования статистических данных по резуль- татам эксплуатации или путем проведения специальных испытаний. Осно- вой для экспериментального определения надежности ТУ в процессе экс- плуатации являются статистические данные об отказах. Для сбора сведе- ний об отказах применяются специальные формы учета, в которые входят такие показатели, как, например, наименование отказавшего элемента, время его работы до отказа, общее количество однотипных элементов, подвергшихся испытаниям.
Достоинством метода получения статистических сведений о фактиче-
ской надежности ТУ в процессе их эксплуатации являются реальные усло- вия и режимы работы, обеспечивающие возможность получения наиболее точной информации. К недостаткам этого метода можно отнести несвое- временное получение необходимой информации, в виду того, что характе- ристики надежности становятся известными только после накопления опыта эксплуатации.
Несмотря на достоинства способа получения информации путем про- ведения специальных испытаний, он не всегда является экономически це- лесообразным из-за необходимости проведения длительных и дорогостоя- щих экспериментов.
Применение ускоренных испытаний элементов и сложных ТУ, при ко- торых подвергающиеся испытаниям устройства работают в режиме повы- шенных нагрузок, позволяет в значительной степени сократить время про- ведения испытаний и отчасти сократить объем выборки для испытаний.
Для экспериментального определения статистических характеристик
надежности могут применяться несколько способов планирования испыта-
ний, что показано в таблице 3.
Таблица 3
Номер способа испыта- ний
|
Прове- дение замены элемен- тов
|
Фиксация моментов отказов
|
Цели испытаний
|
Результаты испы-
таний
|
1
|
Нет
|
Да
|
Испытания ведутся до отказа всех устройств
|
Суммарная нара-
ботка
|
2
|
Нет
|
Да
|
Число отказов при n N
|
Суммарная нара-
ботка
|
3
|
Нет
|
Нет
|
Длительность испытаний
|
Число отказов
|
4
|
Да
|
Да
|
Число отказов
|
Длительность ис-
пытаний
|
5
|
Да
|
Да
|
Длительность испытаний
|
Число отказов
|
Первые три способа характеризуются фиксированным начальным
объемом выборки без применения замены отказавших устройств. В случае проведения испытаний до отказа всех элементов выборочной совокупно- сти (способ первый) имеется возможность получить полное распределение времени появления отказов, однако при определении статистических ха- рактеристик надежности следует иметь в виду, что различные по своей природе отказы имеют различные законы распределения. Так, внезапные
отказы имеют экспоненциальное распределение, а отказы, появляющиеся в результате износа и старения – нормальное распределение. Кроме того,
средняя наработка на один внезапный отказ T имеет существенно боль-
вн
шее значение, чем средняя наработка на один постепенный отказ T . Оп-
пс
ределить статистическое значение величины T можно лишь на этапе
вн
нормальной эксплуатации. Статистическое значение величины T опре-
пс
деляется значительно позже, когда вероятность появления отказов в ре- зультате износа становится доминирующим фактором с точки зрения на- дежности и численно подавляет вероятность появления внезапных отказов
(рис. 22).
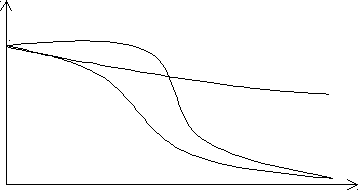 pи(t) pи(t)
pвн(t)
p(t)
p(t)=pвн(t)+ pи(t)
0 t
Рис. 22. Кривые вероятности безотказной работы: pвн(t) — при действии внезапных от- казов; pи (t) — при действии износовых отказов; p(t) — при одновременном действии внезапных и износовых отказов
Рассматриваемый способ позволяет определить интенсивность отка-
зов технических устройств и другие характеристики надежности.
При проведении испытаний до отказа лишь некоторого определенного количества элементов выборки (способ второй) имеется возможность зна- чительно сократить продолжительность испытаний и вместе с этим ис- ключить влияние износа и старения на надежность элементов. Однако, в этом случае, следует иметь в виду, что при этом достоверность оценки на-
дежности несколько понижается. При этом на испытание ставится также
N элементов, но испытания заканчиваются в момент, когда отказывают
ровно
n N
элементов.
Известно, что если N элементов подвергнуть испытаниям способом
«без замены», то n из них будут отказывать в моменты времени
t1, t2 ,K, tn , отсчитываемые от начала испытания. Сами испытания пре-
кратятся к моменту времени tn
наступления n -го отказа, так что
( N n)
элементов еще не откажут к концу испытания. Тогда оценка максимально-
го правдоподобия средней наработки на один отказ определяется выраже-
нием
n 1
ti ( N n 1) tn
T * i 1 ,
n
где числитель представляет собой суммарную наработку всех испытывае-
мых элементов.
Рассмотрим способ постоянного объема выборки на протяжении всех испытаний. Элементы, отказавшие в процессе испытаний или эксплуата- ции, немедленно заменяются новыми из той же генеральной совокупности. Следовательно, если n элементов отобраны для испытания, общее число
элементов, проходящих испытание, все время остается равным N . Если
испытания прекращаются по истечении времени t при наступлении n -о
отказа, то суммарная наработка для N элементов равна
N t , а оценка
средней наработки элементов на отказ в этом определяется как отношение
T * N t ,
n
где N – постоянное число однотипных элементов, проходящих испытание.
Этот вид испытаний не позволяет, за исключением экспоненциально-
го закона распределения, определить непосредственно по первичным ста-
тистическим данным вид закона распределения. Такой способ и приведен- ное выражение широко применяются при оценке надежности элементов в процессе эксплуатация, тем более что в этом случае имеют место главным образом внезапные отказы и в значительно меньшем количестве отказы, произошедшие в результате износа и старения.
Определение размера выборки при испытании на надежность. При
ограниченном объеме испытаний возрастает величина риска неправильно-
го решения в приемке или браковке ТУ, проверяемых на надежность.
Величина риска – это убыток, выраженный в стоимостных единицах. Чтобы увеличить информацию и тем самым уменьшить вероятность ошиб- ки, можно увеличить объем выборки или число и время испытаний, на ос- новании которых принимается решение. Однако испытания обладают сами
по себе большой стоимостью, причем пропорциональной величине выбор-
ки, числа и времени испытаний.
Для определения оптимального размера выборки
Nв следует задаться
предполагаемым значением математического ожидания интенсивности
отказов m
генеральной совокупности элементов. В качестве оценки m
может быть принята известная средняя интенсивность отказов аналогич-
ных элементов.
Тогда исходная формула для определения величины
представлена выражением
Nв может быть
где
mn – математическое ожидание количества отказов в выборке Nв за
время t .
Пусть определена вероятность того, что за время t произойдет не бо-
лее n отказов, то есть
p(nф n) , где
nф – фактическое количество отка-
зов, полученных при испытаниях выборки
Nв . Эта вероятность является
суммой вероятностей несовместных событий, представляющих собой со-
вокупность одновременно существующих не появлений отказов вообще или появления одного, двух или трех и так далее до появления n отказов включительно.
Такая вероятность несовместимых событий, согласно закону Пуассо-
на, определяется выражением
0 1 2 n
p(n
n) (t) t (t ) t (t ) t (t ) t
e e e L e
ф 0!
1! 2! n!
2 n
m n m n m n m
(1 L )e n ,
1! 2! n!
Подставляя сюда m n
из выражения математического ожидания интенсив-
ности отказов
получим
m :
m n Nв m t ,
j
p(nф
n)
n
j 0
н( Nв m t )
j!
e N в m t .
Вероятность того, что число отказов выборки будет не меньше
( n 1) , определяется следующим образом:
p(nф
n 1) 1 p(nф
n) 1
n
j 0
н( Nв m t) j
j!
e N
в m t .
Для определения размера выборки при заданных значениях m и t
следует исходить из наиболее приемлемого числа
nф и достаточной по ве-
личине вероятности
p(nф n) . Тогда по графику (рис. 23), составленно-
му на основания выражений для определения значений величин
p(nф n) и
mn , можно найти величину количества устройств выбороч-
ной совокупности
в
N mn .
m t
Пример 5.1. Необходимо провести испытание на надежность новых генераторов посто- янного тока. Согласно условиям, испытание производится в течение 100 часов. Пред- полагается, что в течение этого времени произошло более трех отказов с досто- верностью p(nф n)=0,95.Ориентировочное значение математического ожидания ин- тенсивности отказов выбираем из справочных таблиц для аналогичных генераторов по-
4
стоянного тока =3 10
. Математическое ожидание количества отказов находим по
графику рис. 23
формуле
nm 6 . Размер выборки генераторов для испытания определяем по
6
в 4
N =200 шт.
100310
ln nm
5
2
 1
0,5
0,2
0,1
0,0001 0,005 0,05 0,1 0,2 0,3 0,9 0,95 0,999 1
0,5
0,2
0,1
0,0001 0,005 0,05 0,1 0,2 0,3 0,9 0,95 0,999 ln p(nф n)
Рис.23. Вспомогательный график для определения размера выборки
при испытании на надежность
10.3. Ускоренные испытания на надежность
Ускоренные испытания ТУ на надежность проводятся в рабочем ре- жиме с повышенными нагрузками и представляют собой разновидность метода физического моделирования.
Для экспоненциального закона вероятность безотказной работы равна
 t t
p(t) e T .
Если безразмерные коэффициенты модели и реального процесса рав-
ны, то в этом случае метод физического моделирования для опыта приме-
ним. В данном случае
t у t
,
Tу T
где t у
и Tу
– временные характеристики надежности при ускоренных
испытаниях. Отсюда
у
t T t ,
Tу
где
T
k
Tу
– коэффициент подобия.
Аналогично можно написать
p(t)
p(t у ) .
Коэффициент подобия выражает собой величину соответствия време-
ни работы ТУ в условиях нормальной эксплуатации одному часу ускорен-
ных испытаний.
Для любых элементов ТУ вероятность безотказной работы является функцией комплексной нагрузки Z и времени работы t :
p ( Z , t ).
Комплексная нагрузка включает в себя различные частные
нагрузки, влияющие на величину интенсивности отказов, например, для информационных систем:
Z ( U , Q, t 0 , V ,K),
127
где U – качество электропитания информационной системы;
Q и t 0 – влажность и температура окружающей среды соответственно;
V – объем перерабатываемой информации и другие нагрузки.
Комплексная нагрузка может быть выражена в виде безразмерного коэффициента . Тогда выражение для вероятности безотказной работы можно записать в виде
p 1( , t )
и аналогично для ускоренных испытаний:
где у , t t у , p
p у .
p у 1( у , t у ) ,
Эти равенства и служат критерием соответствия параметров при ус-
коренных испытаниях и в реальных условиях эксплуатации.
Чем больше коэффициент подобия, тем больше сокращается срок проведения испытаний, однако надо учитывать, что при достаточно боль- ших значениях коэффициента подобия может быть нарушено соответствие
между вероятностями p и
p у .
Для экспоненциального закона распределения оценка среднего време-
ни безотказной работы при ускоренных испытаниях равно
Tу N t1у ,
где t1у – время появления первого отказа при ускоренных испытаниях;
N – количество однотипных ТУ или элементов, поставленных на ус- коренные испытания. Очевидно, что чем больше число N , тем достовер- нее станет величина Tу .
Из выражения коэффициента подобия k и среднего времени безот-
казной работы при ускоренных испытаниях Tу
мя безотказной работы для реальных условий:
определяется среднее вре-
T kTу
kN t1у .
Если определить некоторое заданное время работы испытуемого ТУ
как tз
и минимальное допустимое время безотказной работы Tmin для это-
го случая, то время ускоренных испытаний может быть определено из со-
отношения
t нtз у k
T min .
N k
Количество ТУ, необходимое для проведения ускоренных испытаний
на надежность с учетом желаемой точности эксперимента, может быть оценено на основании следующего выражения:
lg[1 Q(t у )]
N ,
lg p(t y )
так как статистическая вероятность отказа, полученная при ускоренных
испытаниях N ТУ, определяется по формуле
Q * ( t у ) 1 [ p * ( t у )] N ,
где
p * (t у )
– статистическая вероятность безотказной работы одного
испытываемого ТУ.
10.4. Метод статистического моделирования надежности
Метод статистического моделирования надежности основан на так на- зываемом методе Монте-Карло. Суть метода Монте-Карло состоит в ис- пользовании данных предыдущего опыта для оценки возможных ситуаций
в будущем. Принципиальная особенность метода состоит в том, что влия-
ние различных случайных факторов в процессе опыта учитывается не рас-
четным, а игровым способом. В качестве универсального механизма слу- чайного выбора используется совокупность случайных чисел, равномерно распределенных в интервале (0 – 1), которые вырабатываются датчиком случайных чисел. Случайные числа используются для получения дискрет- ного ряда случайных переменных, имитирующих результаты, которые можно было бы ожидать в соответствии с вероятностным распределением, полученным на основании предыдущего опыта.
Метод Монте-Карло можно проиллюстрировать на довольно простом примере. Пусть под наблюдением находится некоторое количество про- стых ТУ. Каждые 100 часов число отказов этих устройств соответствует распределению, приведенному в таблице 4.
Таблица 4
Число отказов
|
Вероятность
|
Кумулятивная вероятность
|
26
34
31
29
24
28
33
|
0,105
0,175
0,15
0,145
0,125
0,14
0,16
|
0,105
0,28
0,43
0,575
0,7
0,84
1,00
|
По этой таблице строим график распределения кумулятивной вероят-
ности (график закона распределения) случайной величины – число отказов
ТУ (рис. 24).
Пусть в дальнейшем необходимо получить предполагаемое число от- казов для шести аналогичных периодов времени. Для этого запускается ранее описанный датчик случайных чисел и фиксируются шесть первых полученных значений. Пусть это будут значения: 0,1; 0,22; 0,37; 0,17; 0,56;
0,87. Полученные случайные числа можно рассматривать как вероятности.
страница 1 ... страница 2 | страница 3 страница 4
|