страница 1 | страница 2 страница 3 страница 4
Тема№8 Структурные схемы надежности
Ранее говорилось о том, что ТУ подразделяются на элементы и систе- мы, причем система состоит из элементов. Элементы, составляющие сис- тему, могут быть соединены между собой различным образом. С точки зрения надежности, такие соединения представляют собой структуры, ка- ждая из которых имеет свой способ расчета. Такой расчет представляет собой расчет надежности. Сами структуры носят название структурных схем надежности. Структурные схемы надежности нельзя путать с прин- ципиальными, функциональными, структурными и другими схемами сис- тем, хотя в частных случаях они могут совпадать. Соединение элементов в структурных схемах надежности можно свести к четырем видам:
- последовательному,
- параллельному,
- смешанному,
- произвольному.
В качестве основных показателей надежности здесь используются ве-
роятность безотказной работы и вероятность отказа.
8.1. Структурные схемы надежности с последовательным соединением элементов
Последовательное соединение в структурной схеме надежности –
это такое соединение, при котором отказ хотя бы одного элемента при-
водит к отказу всей системы в целом (рис. 9).
1 2 n
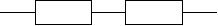  . . . . . .
Рис. 9. Структурная схема надежности с последовательным соединением элементов
Этот тип соединения в теории надежности еще называет основным со-
единением.
Если считать отказы элементов независимыми, то на основании тео- ремы умножения вероятностей, вероятность безотказной работы ТУ выра- жается следующим образом:
Pc (t )
n
p1 (t) p2 (t) ... pn (t) pi (t ) ,
i 1
где
pi (t ) – вероятность безотказной работы i -о элемента;
Pc (t ) – вероятность безотказной работы системы.
Если
p1(t)
то
p2 (2) ...
pn (t )
p(t ) ,
Pc (t ) p n (t) .
С учетом выражения вероятности безотказной работы через интенсив-
ность отказов можно записать
t n t t n
n
P (t ) П
i (t )dt
0
i (t )dt
i 1 0
i (t )dt
0 i 1 .
c e e e
i 1
Отсюда можно сделать заключение, что суммарная интенсивность от- казов n последовательно соединенных элементов находится как сумма ин- тенсивностей отдельных элементов.
n
(t ) i (t) ,
i 1
или, для случая равнонадежных элементов,
(t) n (t ) .
Для случая const
Имеем откуда
Pc (t) en i t i 1 , n
i .
i 1
 Из последнего выражения видно, что для обеспечения требуемой тех- ническими условиями вероятности безотказной работы ТУ при увеличении числа последовательно соединенных элементов необходимо снижать вели- чину интенсивности отказов каждого элемента или, что то же самое, при- нимать меры к увеличению их средней наработки на отказ.
Нередки случаи, когда система последовательно соединенных элемен-
тов состоит из k подсистем, а каждая j -я
( j 1, k )
подсистема состоит
из n j
равнонадежных элементов. В этом случае вероятность безотказной
работы системы будет определяться выражением
k n
Pc (t ) p j
j 1
(t )
,
где
n j – количество равнонадежных элементов j -о типа;
p(t) – вероят-
ность безотказной работы элемента j -й подсистемы.
Суммарная интенсивность отказов равна
k
(t )
n j (t) .
j 1
Анализ полученных выражений показывает:
- вероятность безотказной работы будет тем ниже, чем больше элементов в него входит;
- вероятность безотказной работы последовательного соединения будет
ниже, чем эта же вероятность у самого надежного элемента системы.
8.2. Структурные схемы надежности с параллельным соединением элементов
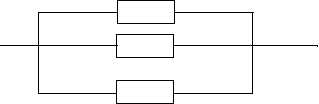
Параллельным соединением элементов в структурной схеме надеж-
ности называется такое соединение, при котором система отказывает только при отказе всех n элементов, образующих эту схему (рис. 10).
Согласно определению,
n n
Qc (t ) q1(t) q2 (t) ... qn (t ) qi (t) (1 pi (t )) .
i 1
i 1
Отсюда
n
Pc (t ) 1 Qc (t) 1 (1 pi (t)) .
i 1
 1
2
n
Рис. 10. Структурная схема надежности с параллельным соединением элементов
С учетом интенсивности отказов выражение примет вид
t
n i (t )dt
P (t ) 1 П (1 e 0 ) .
c i 1
Для случая равнонадежных элементов имеем
Pc (t ) 1 (1 e
t
(t ) dt
o
) n ,
а при const
последнее выражение примет вид
n
pc (t ) 1 (1 ei t ) .
i 1
Основные правила расчета надежности при последовательном и па-
раллельном соединениях элементов в структурной схеме надежности мож-
но формулировать следующим образом:
- определить количество элементов, составляющих структурную схему надежности;
- из справочных таблиц или статистики определить интенсивность отказов
i каждого элемента;
- на основании i
по формулам видов соединений в структурных схемах
надежности определяется ВБР.
8.3. Структурные схемы надежности со смешанным соединением элементов
Иногда в сложных устройствах структурные схемы надежности со-
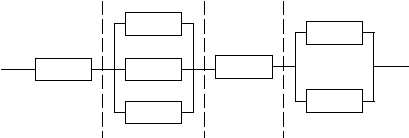 держат как последовательные, так и параллельные надежностные структу- ры. Речь идет о том, что в схеме надежности присутствуют и те и другие виды соединений, что и показано на рисунке 11.
I II III IV
Рис. 11. Пример структурной схемы надежности со смешанным соединением эле-
ментов
В этом случае для расчета надежности структурную схему разбивают
на последовательные или параллельные участки таким образом, чтобы ка-
ждый участок имел либо только последовательную, либо только парал-
лельную структурную схему. На каждом участке определяется вероятность безотказной работы в соответствии с теми формулами, которые соответст- вуют структурным схемам рассматриваемого участка. Таким образом, ис- ходная структурная схема надежности превращается в структуру с после- довательным или параллельным соединением элементов. Такая эквива- лентная последовательная структура показана на рисунке 12. Здесь, на
примере предыдущего рисунка 11,
PI , PII , PIII , PIV
– вероятности без-
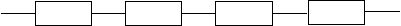 отказной работы соответственно первого, второго, третьего и четвертого последовательных участков, на которые структурная схема со смешанным соединением элементов предварительно была разбита.
PI PII PIII PIV
Рис. 12. Преобразованная структура со смешанным соединением элементов
Тогда вероятность безотказной работы системы в представленном примере будет равна
Pc (t) PI PII PIII PIV .
В общем случае, для системы с k последовательными участками, по- лученными в результате предварительных преобразований, выражение для вероятности безотказной работы будет иметь вид
k
Pc (t ) Pj (t) ,
j 1
где
Pj (t 0 – вероятность безотказной работы j -о участка.
8.4. Сложная произвольная структура
Когда невозможно при составлении структурных схем надежности применить последовательную, параллельную или смешанную схемы, то
приходится иметь дело с так называемой сложной произвольной структу- рой. Для такой структуры не существует общих методов расчета надеж- ности. Одной из наиболее часто встречающихся схем такой структуры яв- ляется мостиковая схема (рис. 13).
1 4
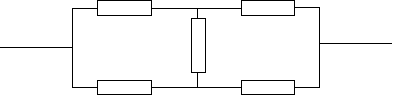 3 3
2 5
Рис. 13. Произвольная структурная «мостиковая» схема надежности
Расчет вероятности безотказной работы этой схемы можно осущест- вить методом прямого перебора всех состояний. В частности, мостиковая схема считается работоспособной при пяти вариантах отказов по одному элементу (отказавшие элементы: 1, или 2, или 3, или 4, или 5), при восьми вариантах отказов по два элемента (отказавшие группы элементов: 1 и 4, или 2 и 5, или 1 и 3, или 2 и 3, или 3 и 4, или 3 и 5, или 1 и 5, или 2 и 4), при двух вариантах отказа по трем элементам (отказавшие группы элементов: 1
и 3 и 4, или 2 и 3 и 5) или когда все 5 элементов работоспособны. Тогда, для случая равнонадежных элементов вероятность безотказной работы системы, структурная схема надежности которой представляет собой мос- тиковую схему, будет равна
pc (t )
p5 5 p 4q 8 p3q 2 2 p 2q3
где
p p(t )
p5 5 p 4 (1 p) 8 p3 (1 p)2 2 p 2 (1 p)3 ,
– вероятность безотказной работы одного элемента;
q q(t )
– вероятность отказа одного элемента.
В начале главы говорилось о том, что в большинстве случаев струк- турные схемы надежности не совпадают с принципиальными, функцио- нальными и структурными схемами ТУ. Наиболее ярко это утверждение можно продемонстрировать на примере электрических систем, показав, что принципиальная электрическая схема может не совпадать со структур- ной схемой надежности.
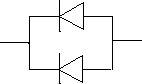
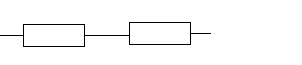
Известно, что основными отказами электрических систем являются отказы типа «обрыв» и «короткое замыкание». Пусть система состоит из двух диодов Д 1 и Д 2 , включенных параллельно (рис.14, а). Для отказа ти-
 Д 1 Д 1
  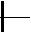 С 1 С 1 С 1 С 1
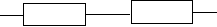 1 Д 2 2 1 Д 2 2
1
 2 «обрыв» 2 «обрыв»
1
1 2 «короткое
 2 замыка- 2 замыка-
ние»»
 б б
а
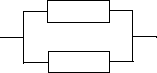
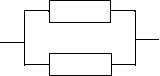
Рис. 14. Принципиальные электрические схемы и соответствующие им структур-
ные схемы надежности: а) - для диодов; б) - для конденсаторов
па «короткое замыкание» система выйдет из строя, когда откажет любой
из двух диодов. Поэтому структурная схема надежности для этого случая изображается в виде последовательного соединения элементов. В другом случае при отказе типа «обрыв» параллельная цепочка диодов откажет только в случае отказа двух диодов. Следовательно, структурная схема на- дежности будет представлять собой параллельное соединение элементов. На рисунке 14, б изображена последовательная цепочка конденсаторов С 1
и С 2 . При «коротком замыкании» эта схема выйдет из строя, если только
«пробьет» и С 1 и С 2 . В силу этого структурная схема надежности пред-
ставляется в виде параллельного соединения элементов. И, наконец, при
«обрыве» конденсаторная цепочка откажет, если откажет любой из двух конденсаторов. Это значит, что структурная схема надежности будет иметь последовательное соединение.
8.5. Расчет надежности по внезапным отказам
В связи с наличием двух типов отказов элементов (постепенные и внезапные отказы) различаются и два способа расчета надежности, соот- ветствующих двум типам отказов. При внезапных отказах применяют по- каскадный метод расчета надежности и (или) поэлементный метод. Рас- смотрим эти методы.
8.5.1. Покаскадный метод расчета надежности
Кроме расчета надежности по внезапным отказам этот подход дает приемлемую оценку безотказности на самых ранних этапах проектирова- ния ТУ. В качестве исходных данных используется число каскадов и при- надлежность их к той или иной группе. Считается, что все элементы кас- када образуют основное соединение элементов в смысле надежности. По- этому для расчета берутся формулы:
pв (t) e
t
(t )dt
0 ,
где
(t)
представляет собой суммарную интенсивность отказов по
где ni
k
(t) ni i (t) ,
i 1
 – количество однотипных элементов в i -м (i 1,n) каскаде; – количество однотипных элементов в i -м (i 1,n) каскаде;
k – количество каскадов.
Для оценки суммарной интенсивности используют выражение
* k 10 4 (1/час),
ka
где ka – коэффициент, учитывающий условия эксплуатации.
Для надежных элементов значение этого коэффициента лежат в диа-
пазоне от величины 1,2 до 1,4.
8.5.2. Поэлементный метод расчета надежности
Этот метод позволяет получить более точную оценку безотказности. Его также можно применять при проектировании ТУ, но на более поздних этапах. В качестве исходных данных берется общее число элементов, их тип и данные по эксплуатации аналогичного типа оборудования. Расчет производится по вышеприведенным формулам, но при определении вели- чины интенсивности отказов используются данные, полученные на преды- дущем этапе эксплуатации ТУ аналогичного типа. При этом
Пэа
nэа na ,
nna
где
эа , na
– суммарные интенсивности отказов эксплуатируемого аналога и проектируемой аппаратуры;
nэа , nna – количество элементов эксплуатируемой и проектируемой аппаратуры.
Отсюда
n
n
na
эа
na .
эа
Эти методы расчета (покаскадный и поэлементный) по интенсивно- стям отказов позволяют достаточно полно оценить безотказность проекти- руемой аппаратуры.
В качестве исходных данных используются:
- принципиальная схема;
- сведения о количестве групп и типов комплектующих элементов;
- сведения об интенсивностях отказов комплектующих элементов и узлов.
Порядок расчета следующий:
1. Согласно принципиальной схеме и спецификации, производят разбивку всех элементов на группы, имеющие приблизительно одинаковую интен-
сивность отказов. Подсчитывают число элементов в каждой группе
ni .
2. По справочным данным находят минимальную и максимальную интен-
сивности отказов i max , i min .
3. Определяют максимальную и минимальную интенсивности отказов по
группам:
ni i max,min .
k
4. Вычисляют общую интенсивность отказов (t) ni i .
i 1
5. Используя это выражение, определяют вероятность безотказной работы
и Tср
(расчет ведется по значения
i max и i min , а также по средним значениям интенсивностей отказов).
8.6. Расчет надежности по постепенным отказам
Основой для расчета являются данные о закономерностях изменения определяющих параметров исследуемого ТУ во времени, а также установ- ленные допуски на эти параметры.
Исследования поведения параметров многочисленных типов транс- портных ТУ показывают, что распределение времени безотказной работы при постепенных отказах соответствует нормальному закону. Это значит,
что для каждого параметра могут быть найдены значения Ti и i .
Вероятность безотказной работы по i -у параметру системы или эле-
мента определяется выражением
T t
i
i
Pпi (t) .
T
i
i
В этом случае вероятность безотказной работы по постепенным отказам всего ТУ, если считать отказы элементов независимыми, находится из вы- ражения
h
Pn (t ) Pni (t ) ,
i 1
где h – число определяющих параметров.
Вероятность безотказной работы сложного ТУ по внезапным и посте-
пенным отказам может быть найдена из выражения
k
t ni i h
P (t ) Рв pп (t) e i1 Pni (t).
i 1
Вопросы для самоконтроля
1. Что такое структурная схема надежности и чем она отличается от принципиальной схемы ТУ?
2. Что такое структурная схема надежности с последовательным со-
единением элементов?
3. Что такое структурная схема надежности с параллельным соедине-
нием элементов?
4. Надежность при структурной схеме с последовательным соединени-
ем элементов.
5. Надежность при структурной схеме с параллельным соединением элементов.
6. Что такое сложная произвольная структурная схема надежности?
7. Надежность при произвольной структурной схеме.
8. Основы расчета надежности при постепенных отказах.
9. Основы расчета надежности при внезапных отказах.
10. Вероятность безотказной работы сложного ТУ при внезапных и по-
степенных отказах.
Тема №9 Методы повышения надежности. Резервирование
Существуют следующие методы повышения надежности:
-
Резервирование;
-
Уменьшение интенсивности отказов элементов системы
-
Сокращение времени непрерывной работы
-
Уменьшение времени восстановления
-
Выбор рациональной периодичности и объема контроля системы
Резервирование – один из наиболее эффективных методов повышения надежности объектов. Резервирование – применение дополнительных средств и (или) возможностей с целью сохранения работоспособного состояния объекта при отказе одного или нескольких его элементов. Существуют разнообразные методы резервирования.
По виду резервирования методы подразделяются:
1) Структурное резервирование (аппаратурное) – предусматривает применение резервных элементов структуры объекта, то есть в минимально необходимый вариант объекта вводятся дополнительные элементы. Основной элемент – элемент структуры объекта, необходимый для выполнения объектом требуемых функций при отсутствии отказов его элементов. Резервный элемент – элемент объекта, предназначенный для выполнения функций основного элемента, в случае отказа последнего. Резервируемый элемент – основной элемент, на случай отказа которого, в объекте предусмотрен резервный элемент.
2) Временное резервирование- предполагается, что на выполнение объектом необходимой работы отводится время, заведомо больше минимально необходимого.
3) Информационное резервирование – резервирование с применением избыточности информации, то есть когда избыток информации позволяет компенсировать искажения передаваемой информации или устранять их.
4) Функциональное резервирование – резервирование, при котором данная функция может выполняться различными способами и техническими средствами.
5) Нагрузочное резервирование – резервирование с применением нагрузочных резервов. Заключается в обеспечении оптимальных запасов способности элементов выдерживать действующие на них нагрузки.
Перечисленные виды резервирования могут быть применены либо к системе в целом (общее резервирование), либо к отдельным элементам системы или к их группе (раздельное резервирование). Сочетание различных видов резервирования в одном и том же объекте называется смешанным.
По способу включения резервных элементов различают:
1) Постоянное резервирование – это резервирование без перестройки структуры объекта при возникновении отказа его элемента. Для него характерно отсутствие перерыва в работе, отсутствие необходимости специальных устройств, параллельное соединение элементов без переключающих устройств.
2) Динамическое резервирование – резервирование с перестройкой структуры объекта при возникновении отказа его элемента. Оно подразделяется на:
2.1) Резервирование замещением – когда функции основного элемента передаются резервному элементу только после отказа основного. Включение резерва замещением обладает преимуществами – не нарушает режима работы, сохраняет надежность резервных элементов (т.к. они находятся в нерабочем состоянии), позволяет использовать один резервный элемент на несколько основных. Недостаток – необходимость наличия переключающих устройств, применяется при общем резервировании.
2.2) Скользящее резервирование – резервирование замещением при котором группа основных элементов объекта резервируется одним или несколькими резервными элементами, каждый из которых может заменить любой отказавший основной элемент в данной группе.
2.3) Широко применяется мажоритарное резервирование – этот способ основан на применении дополнительного логического элемента, который позволяет вести сравнение сигналов, поступающих от элементов, выполняющих одну и ту же функцию. Если результаты совпадают, то они передаются на выход устройства.
Степень избыточности характеризуется кратностью резервирования. Кратность резерва – отношение числа резервных элементов объекта к числу резервируемых или основных элементов.
По кратности резервирования:
1) Резервирование с целой кратностью – когда один основной элемент резервируется одним или более резервными.
2) Резервирование с дробной кратностью – когда два и более однотипных элементов резервируются одним и более резервными элементами. Дублирование – резервирование кратность которого равна 1.
В зависимости от режима работы резерва различают:
1) Нагруженный резерв – резерв, который содержит один или несколько резервных элементов, находящихся в режиме основного элемента. 2) Облегченный резерв – резерв, который содержит один или несколько резервных элементов, находящихся в менее нагруженном режиме, чем основной. 3) Ненагруженный резерв – резерв, который содержит один или несколько резервных элементов, находящихся в ненагруженном режиме доя начала выполнения ими функций основного элемента.
По восстанавливаемости резерва:
Резервирование, при котором работоспособность любого одного или нескольких элементов в случае возникновения отказов подлежит восстановлению при эксплуатации, называется 1) резервированием с восстановлением, в противном случае 2) без восстановления.
Расчет надежности при общем и раздельном резервировании систем
Общее резервирование с постоянно включенным резервом допускает, что отказы элементов системы описываются простейшим потоком; резервируемые и резервные элементы равнонадежны.
ВБР системы и вероятность отказа системы без резервирования равны
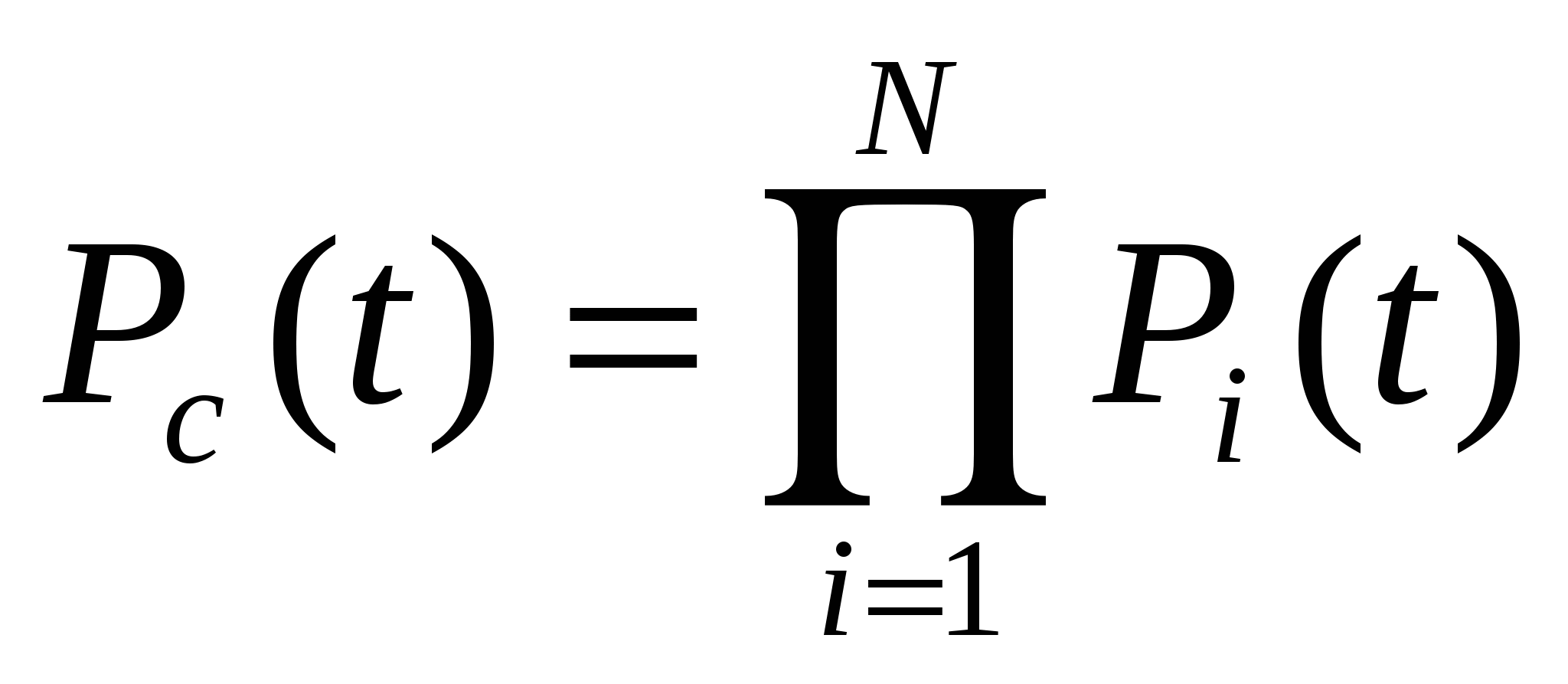 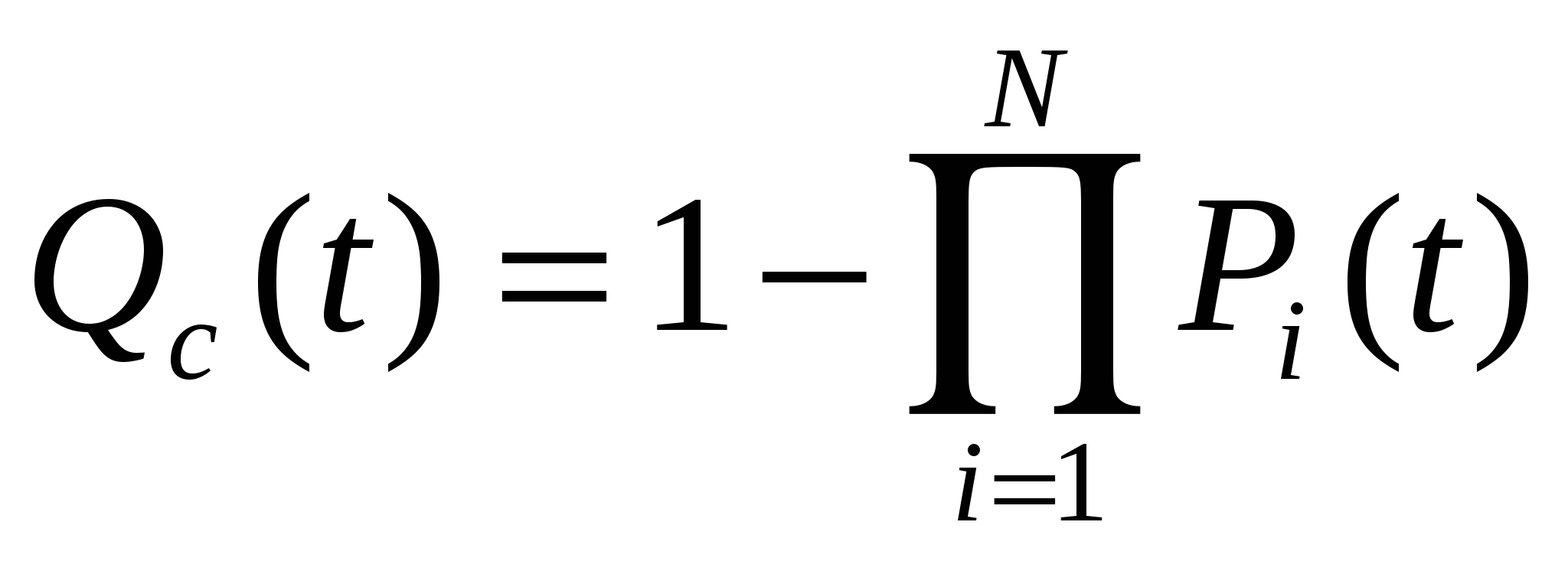 , где N-число основных элементов в системе
Вероятность отказа системы с общим резервированием
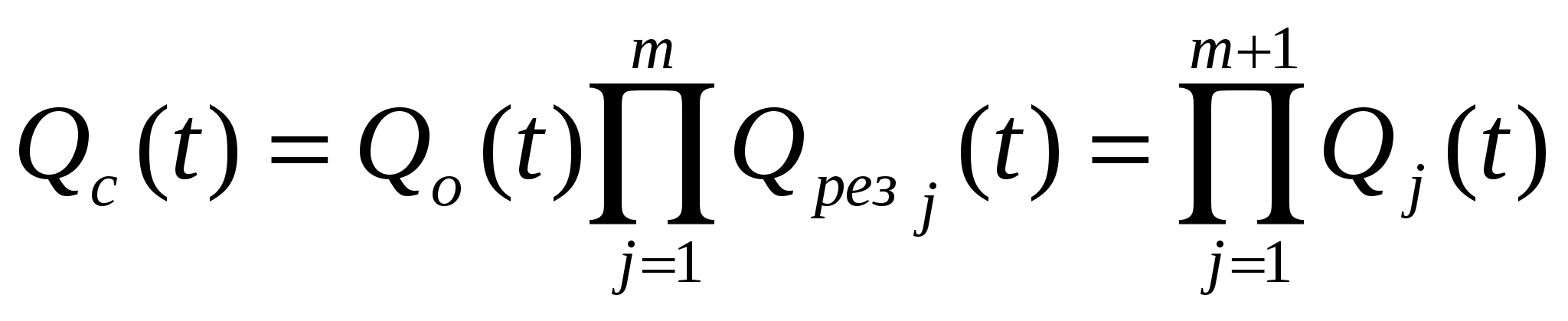 , где m-число резервных элементов в системе
В случае равенства вероятностей отказа основной и резервных систем
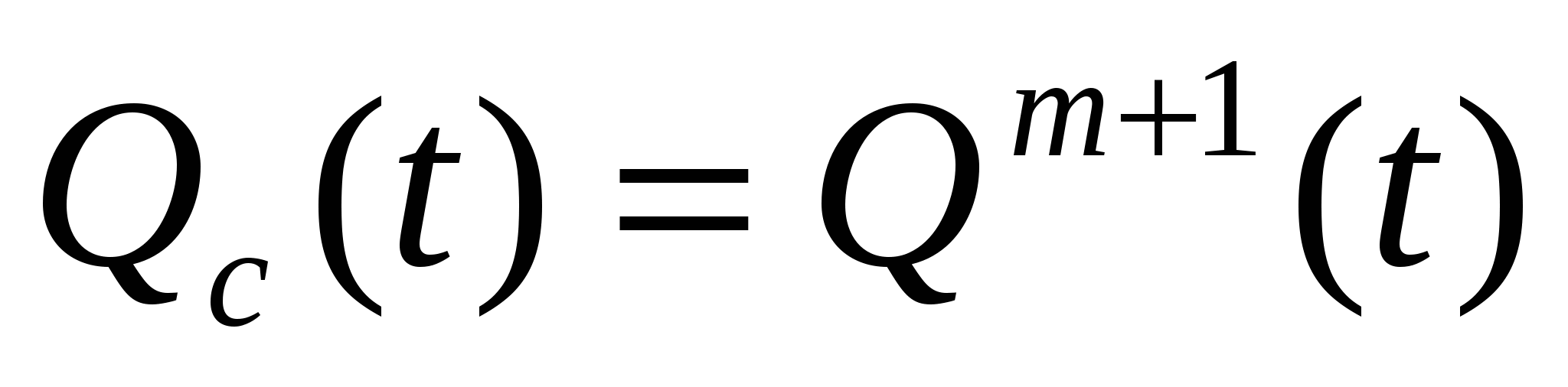 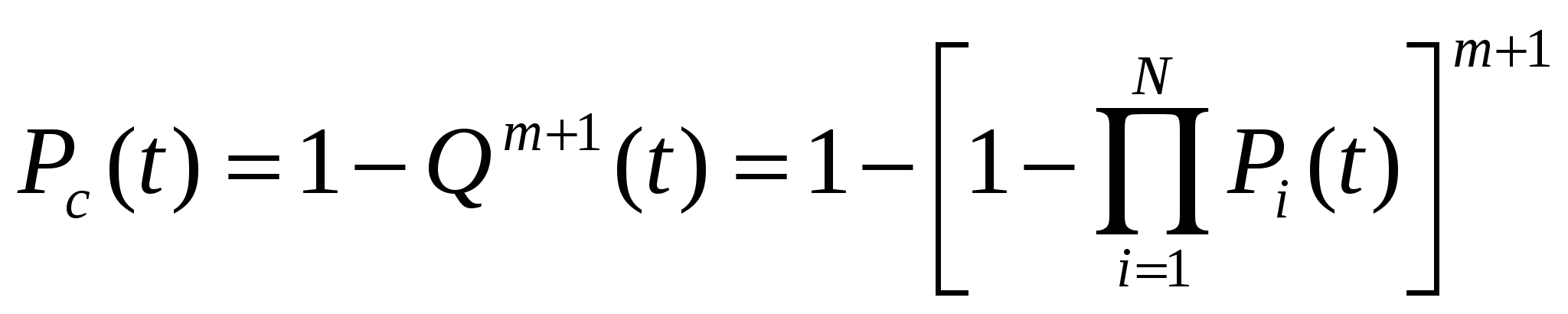
Для экспоненциального закона надежности 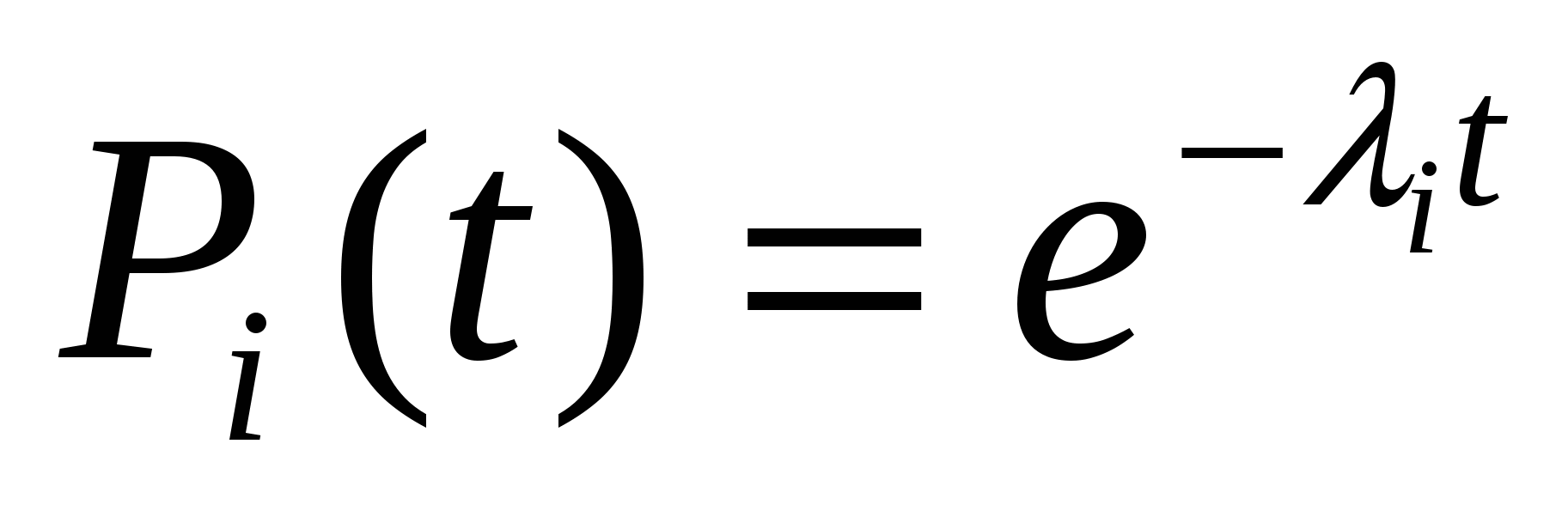
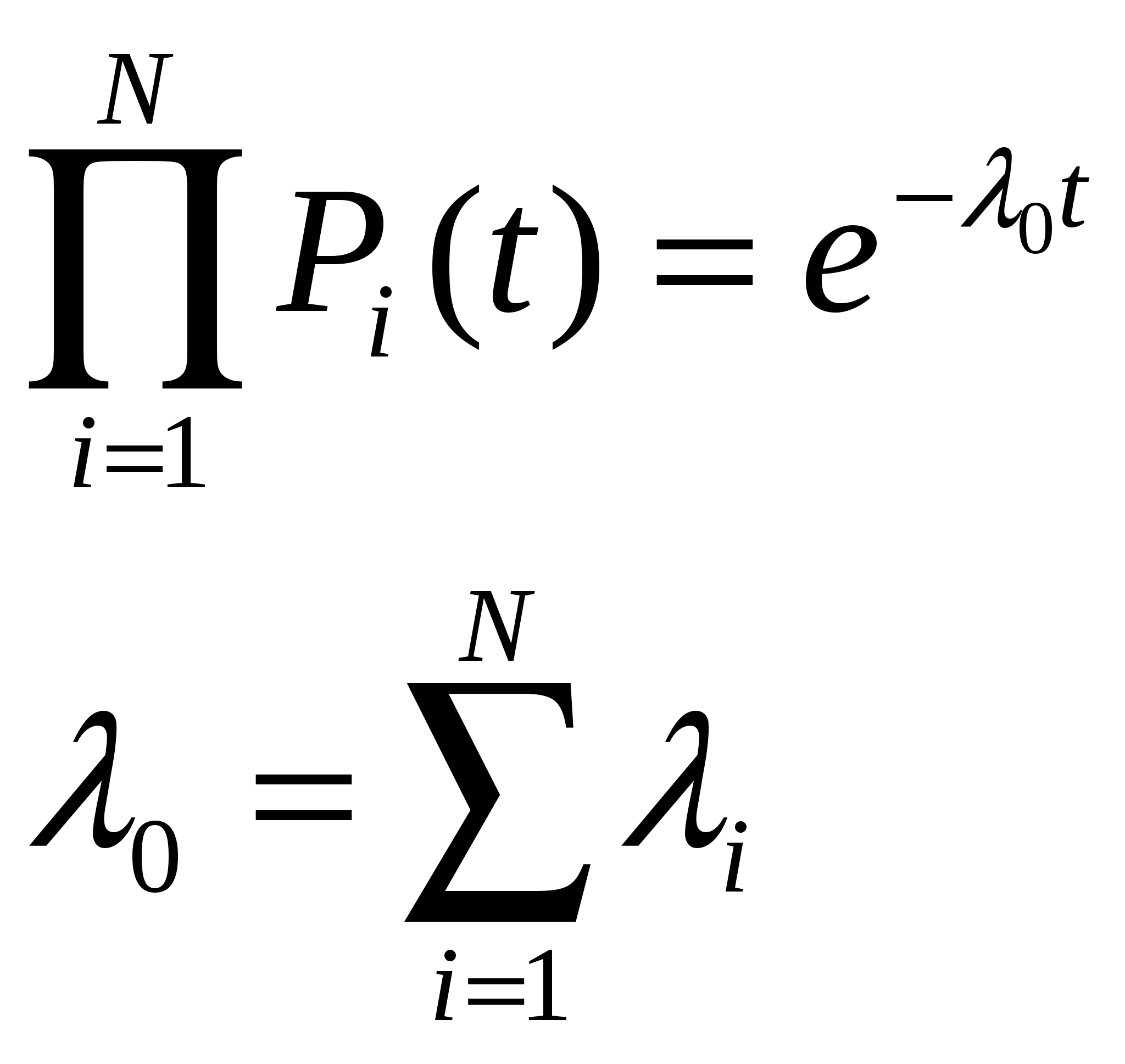
где I – интенсивность отказов любой из m+1систем
Средняя наработка до отказа
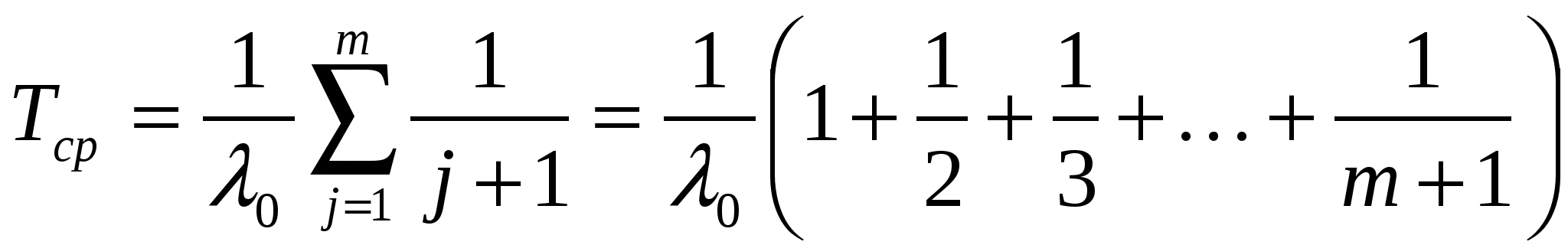
Плотность вероятности
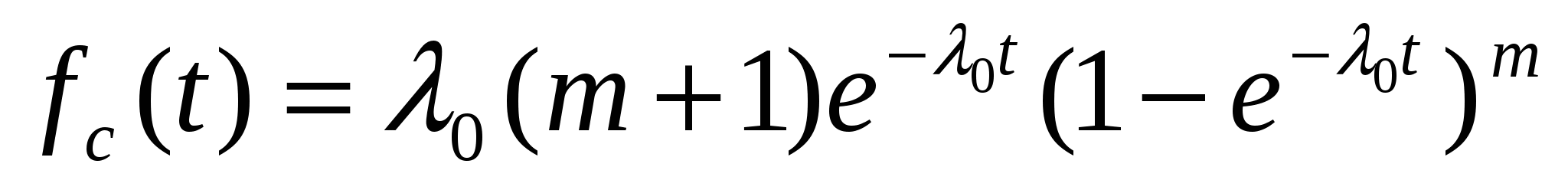
Интенсивность отказов
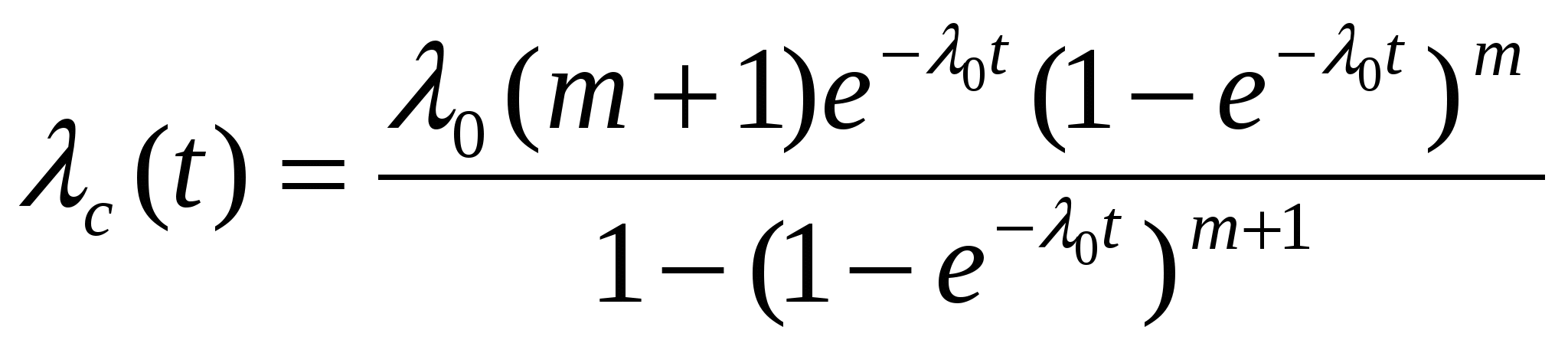
За критерий качества резервирования принимается эффективность резервирования – отношение количественной характеристики надежности резервированного устройства к той же количественной характеристике нерезервированного устройства или устройства с другим видом резервирования.
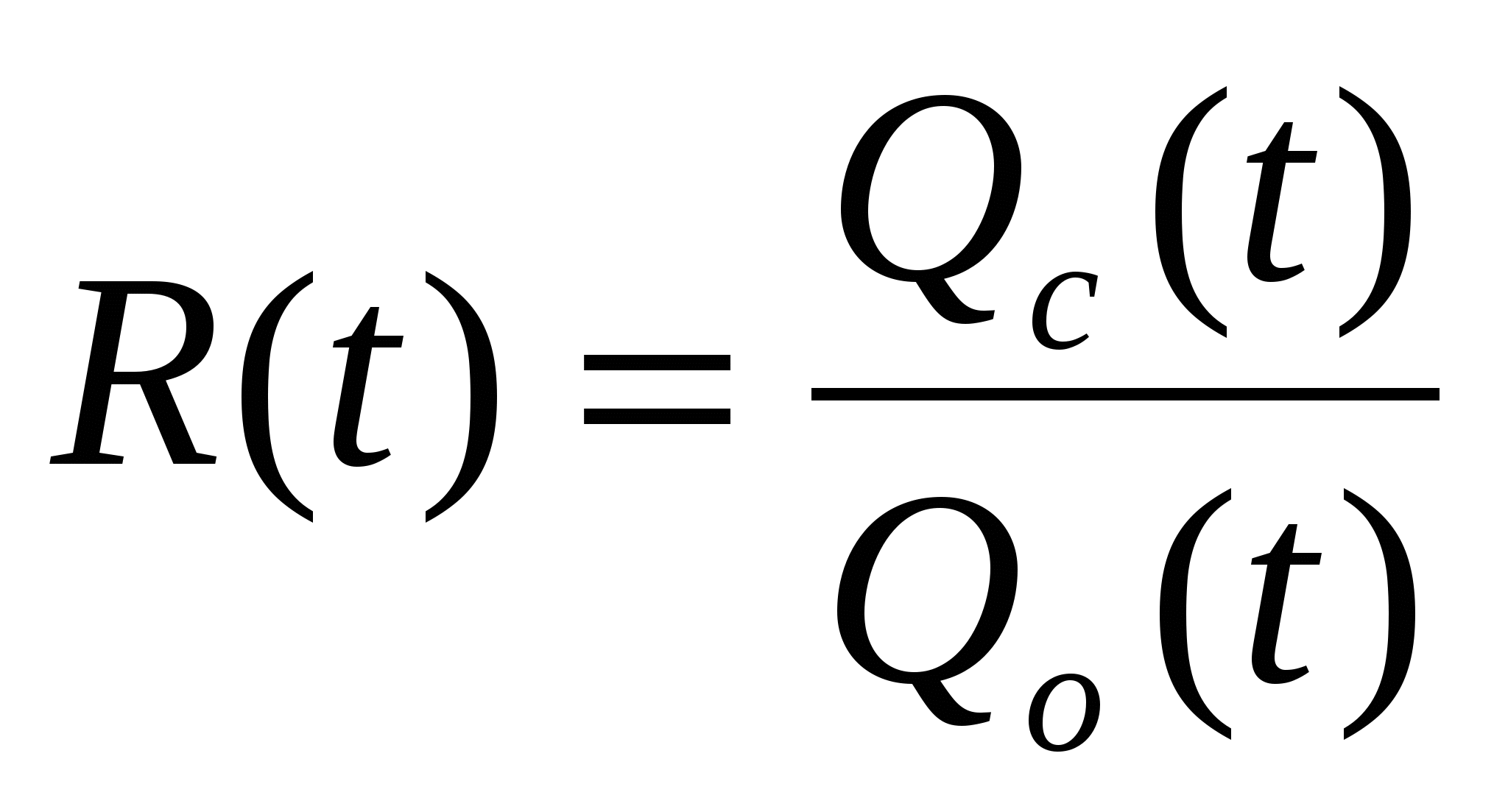 - эффективность резервирования в течение времени t по вероятности отказов
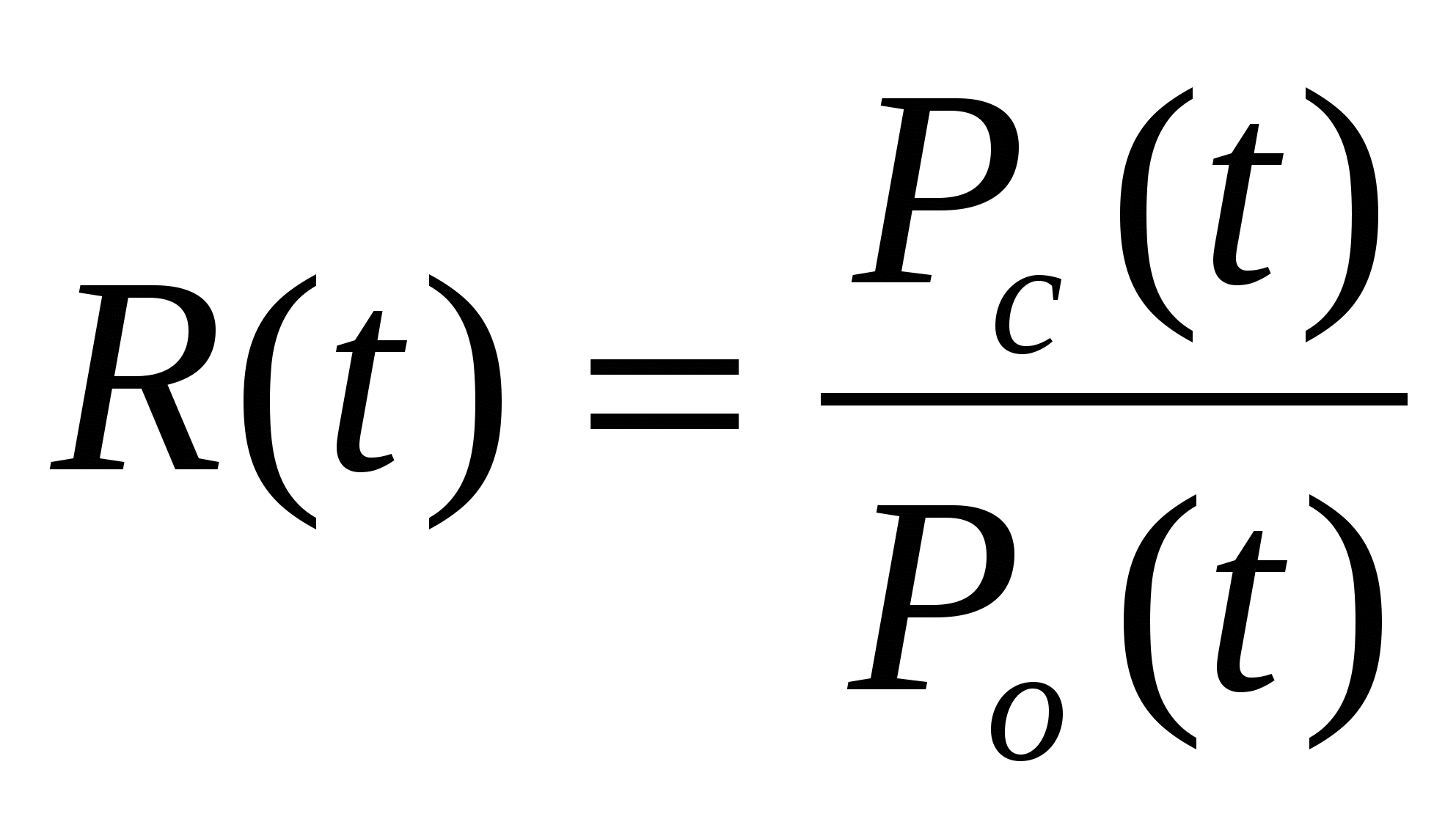 - эффективность резервирования в течение времени t по вероятности безотказной работы
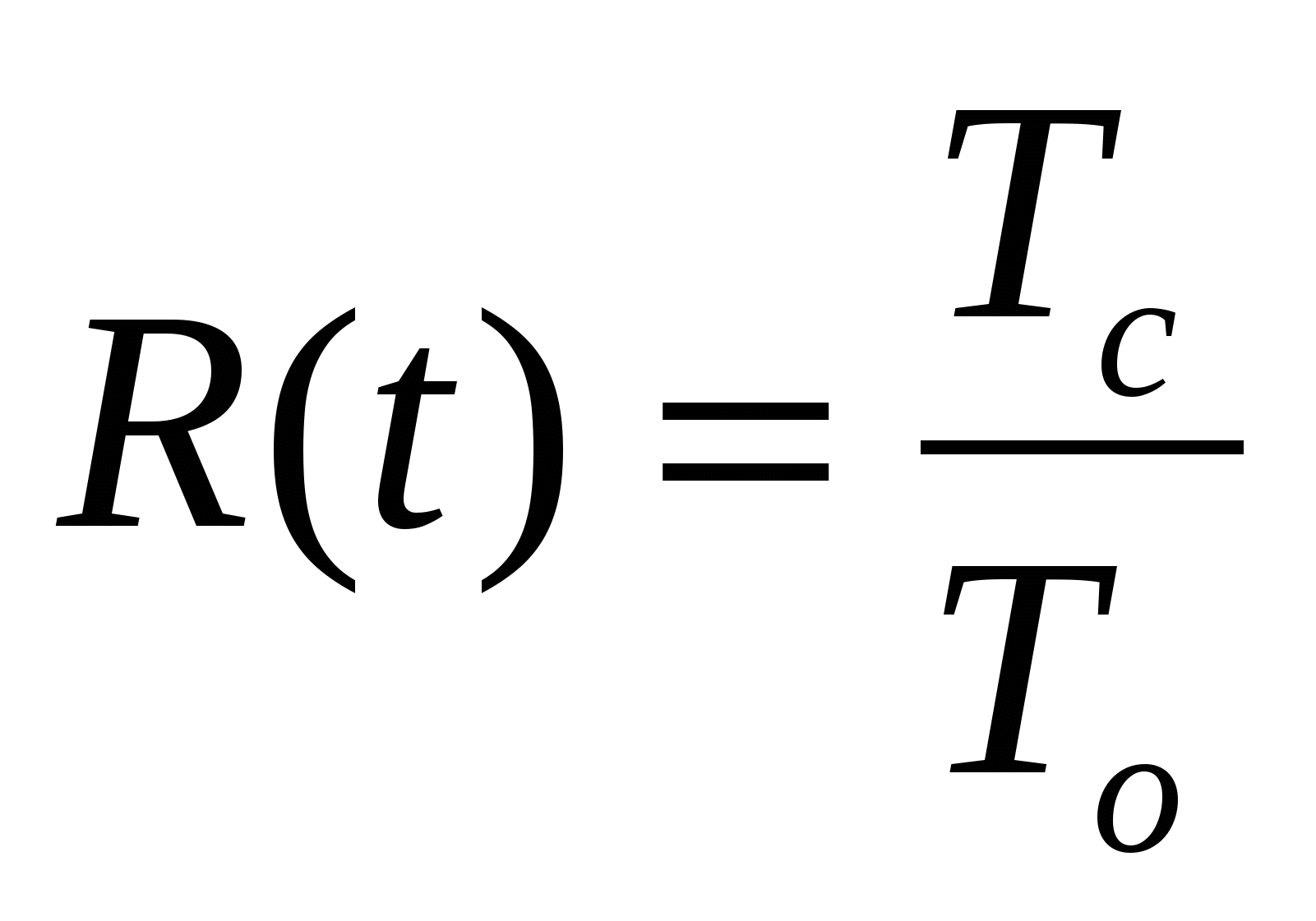 - эффективность резервирования по среднему времени безотказной работы
Общее резервирование с замещением
При наличии идеального переключателя все формулы общего резервирования с постоянно включенным резервом подходят и для данного способа резервирования. Но с учетом отказов переключателя:
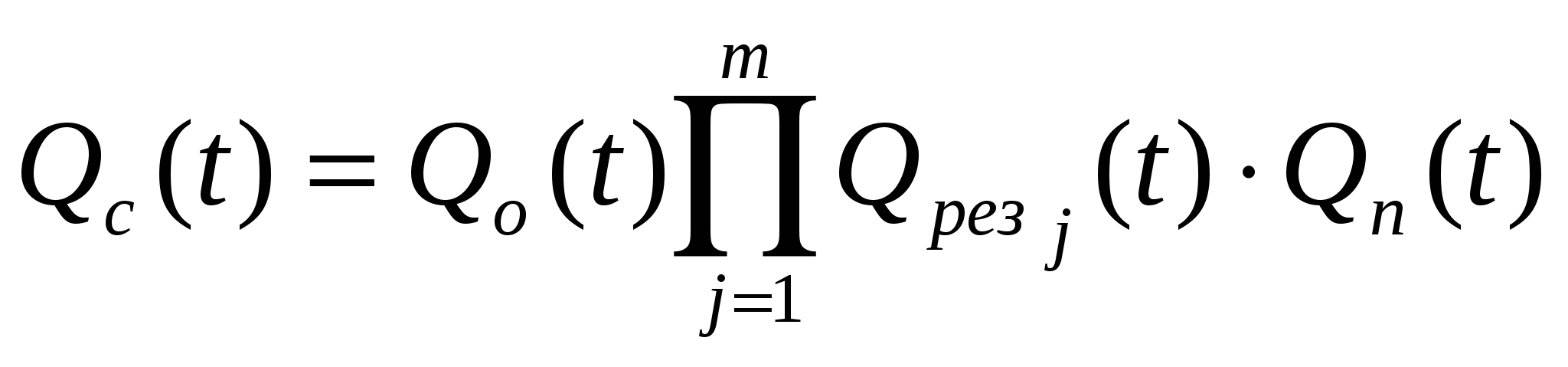 Раздельное резервирование с постоянно включенным резервом
Раздельное резервирование с постоянно включенным резервом
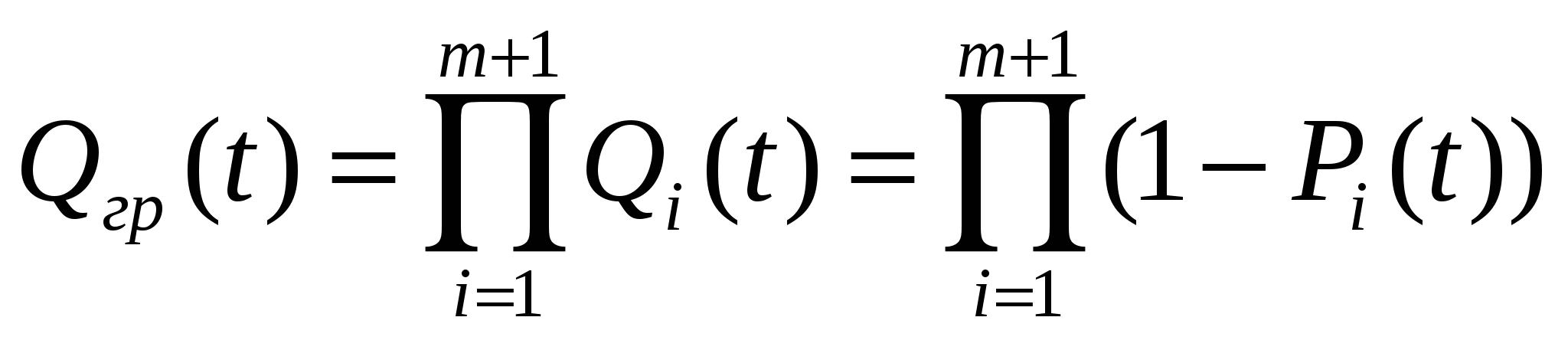 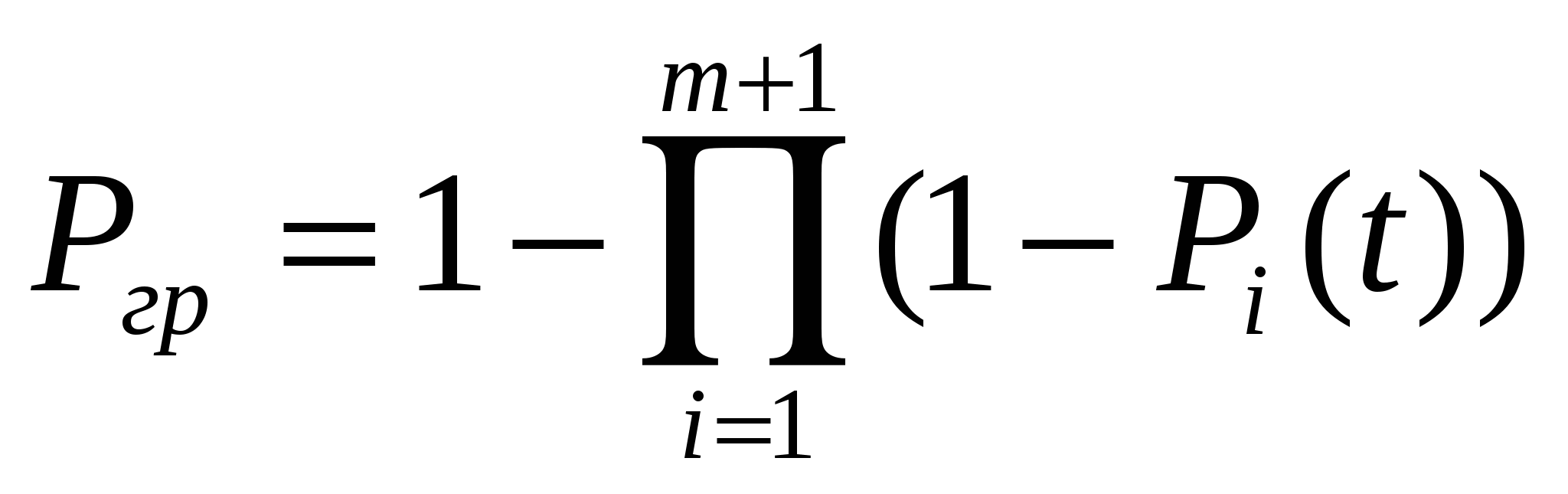
Так как обычно основные и резервные элементы равнонадежны, то
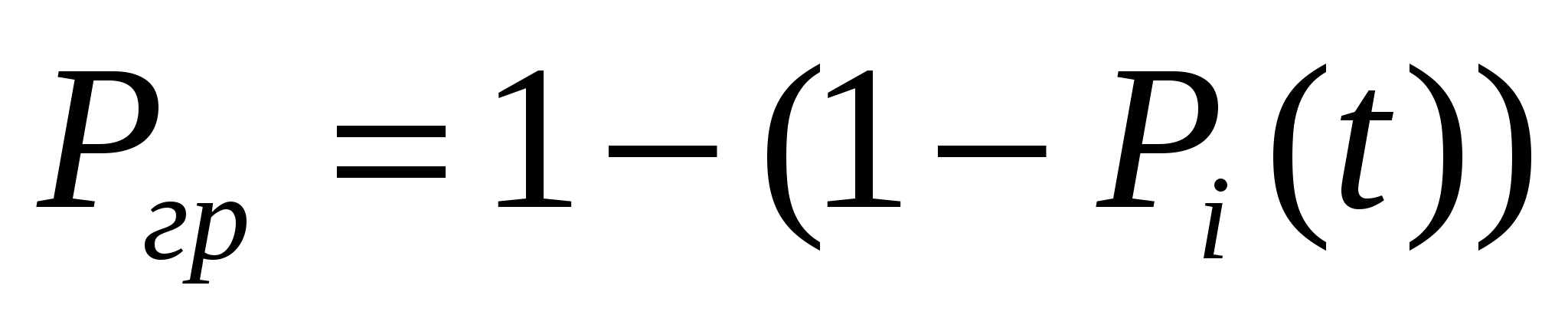
ВБР системы будет равна
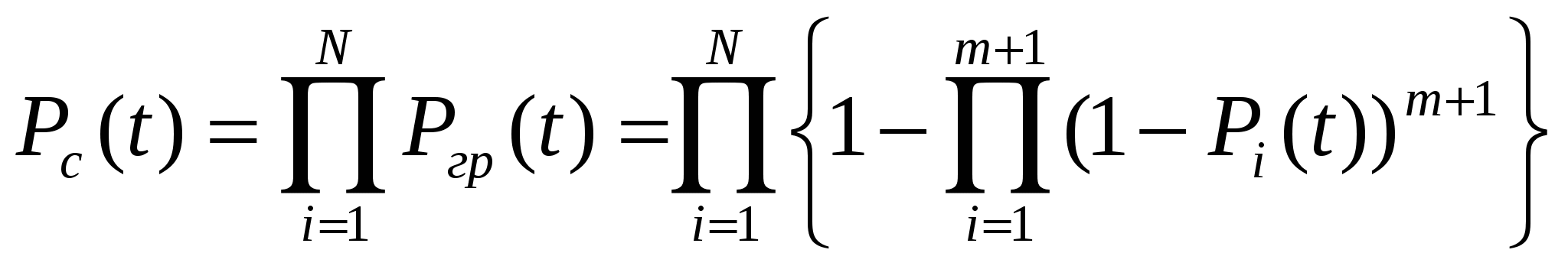
Если все элементы равнонадежны, то 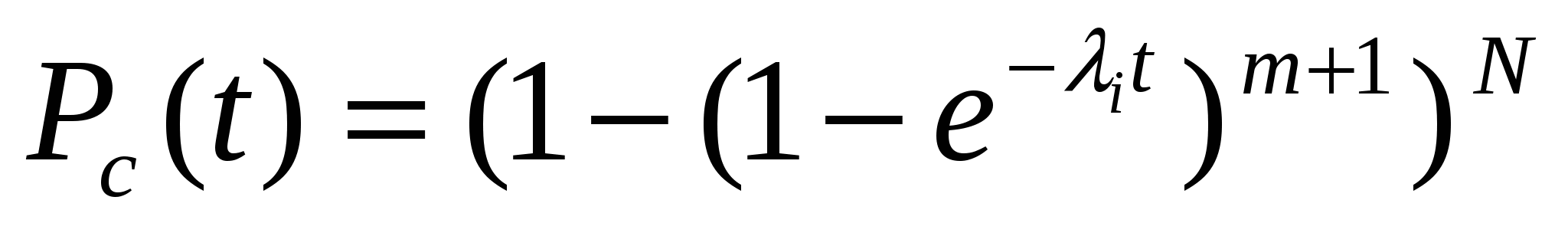
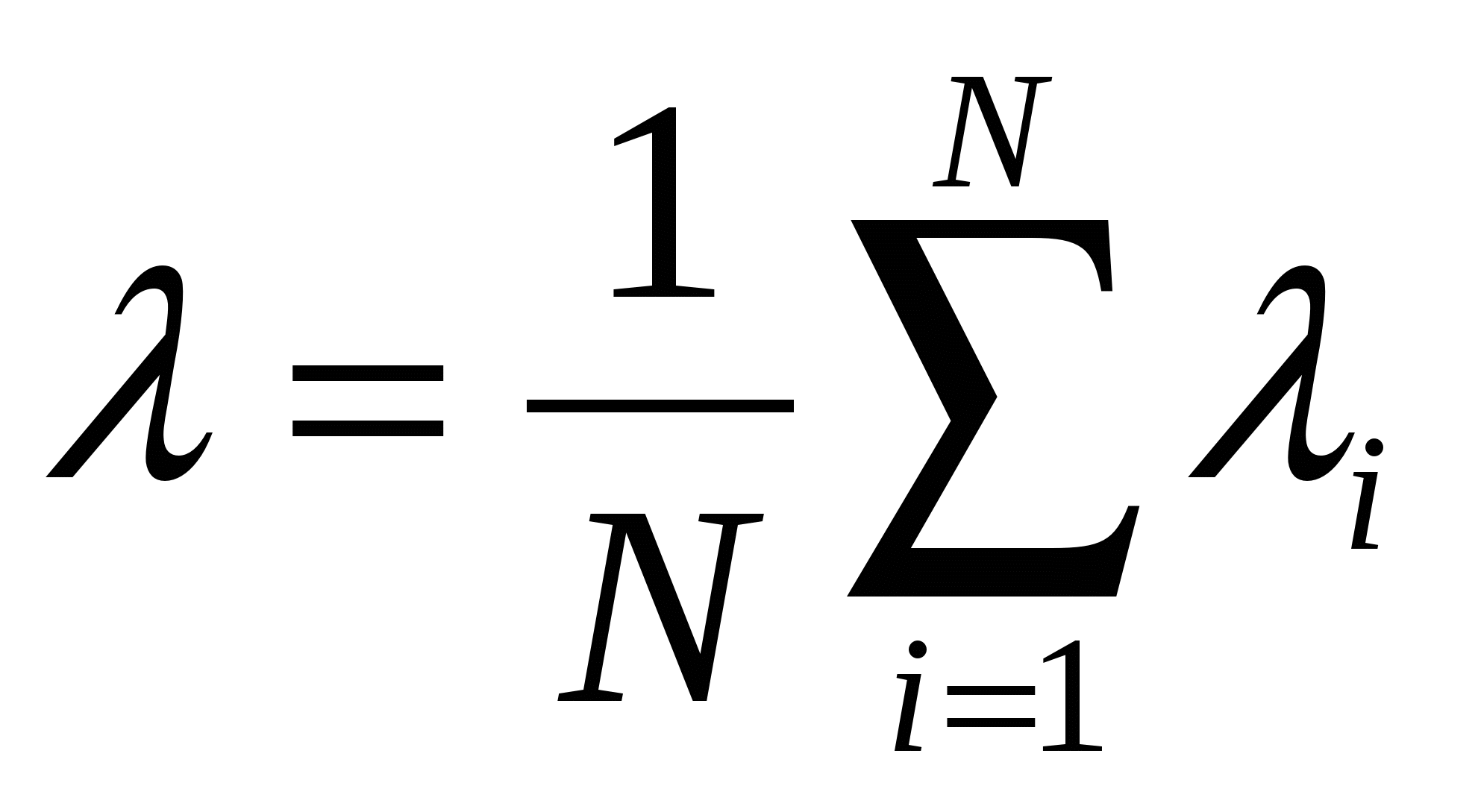
Выражения для вычисления Tср с, fс(t), с(t) имеют вид:
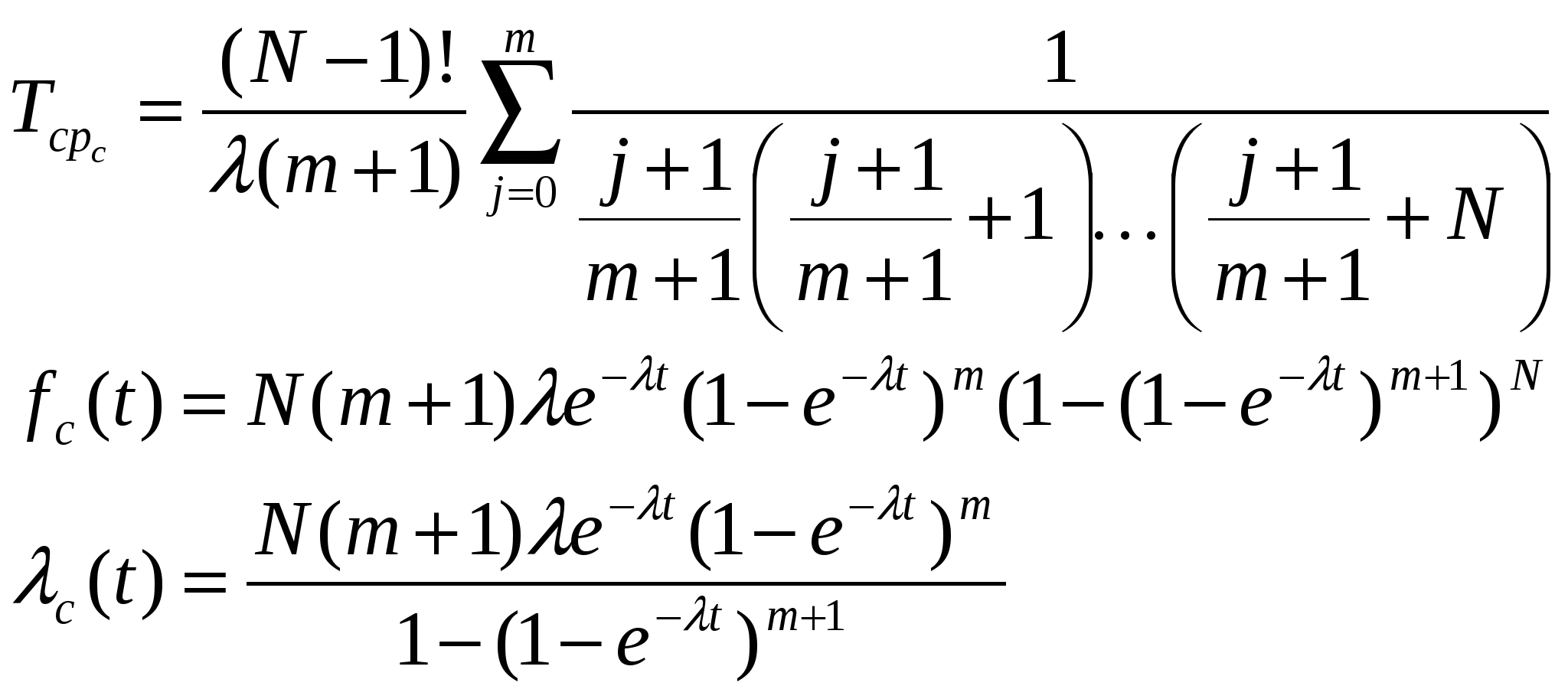 Тема №10 Испытание систем на надежность
10.1 Временные характеристики, применяющиеся при статистических исследованиях надежности
Тема №10 Испытание систем на надежность
10.1 Временные характеристики, применяющиеся при статистических исследованиях надежности
Определяющим параметром долговечности любого устройства явля-
ется наработка, под которой понимается продолжительность работы ТУ. Основной мерой, оценивающей продолжительность работы, принято счи- тать время в часах, то есть время, в течение которого ТУ выполняет свои рабочие функции. Время наработки нельзя смешивать со временем экс- плуатации, то есть календарным временем, в течение которого устройство находится в эксплуатации.
У некоторых ТУ мерой оценки продолжительности работы являются другие показатели, например, продолжительность работы электрических аккумуляторных батарей измеряется числом зарядно-разрядных циклов; продолжительность работы реле – числом включений и выключении; объ- ектов подвижного состава железнодорожного транспорта – количеством пройденных километров и так далее.
Тем не менее все основные характеристики надежности, являющиеся функциями времени наработки, должны быть использованы при решении задач надежности, когда определяющие параметры имеют другую размер- ность. В этом случае под символом t следует понимать любой вид нара-
ботки, а под T – математическое ожидание появления отказа, оцениваю-
щееся любой из возможных размерностей.
При оценке надежности ТУ или сложных систем в целом по характе- ристикам надежности составляющих этих систем, имеющих разную раз- мерность наработки, необходимо, чтобы количественные показатели опре- деляющих параметров были приведены к одинаковой размерности для всех элементов таких систем. Если для какого-нибудь элемента или уст- ройства, входящего в систему, размерность определяющих параметров на-дежности равна величине ar , а для системы в целом она равна A, то коэффициент приведения определяющих параметров элементов к размерности соответствующих параметров системы выразится в виде соотношения
A
r .
a
r
Тогда, чтобы привести характеристики наработки элементов, имею- щих размерность r , к размерности, например, времени, их следует умно- жить на коэффициент приведения:
T[час ] r Tr ;
t [час] r t r .
При проведении статистических испытаний на надежность и расчетов
в качестве определяющего параметра применяется случайная величина – суммарное время наработки ТУ, взятых под наблюдение в течение неко- торого времени эксплуатации этих устройств:
N
t ti ,
i 1
где ti – время наработки до отказа i-о ТУ.
Для непрерывно работающих невосстанавливаемых ТУ можно запи-
сать
t
n 1
ti ( N n 1) tn ,
i 1
где ti – время наработки i-о невосстанавливаемого ТУ;
tn – время, соответствующее n случаям отказа ТУ.
Практически для вычисления суммарного времени наработки весь ис-
пытательный период рабочего времени разбивается на разряд, соответст-
вующий равным отрезкам времени
t .
Если
ni
– число отказов в течение i -о отрезка рабочего времени, то
суммарное время наработки всех функционирующих в процессе эксплуа-
тации ТУ может быть выражено следующим образом:
t (( N n( t )) t 0,5 t n1 1,5 t n2 L ( k 0,5) t nk ,
где 0,5t;1,5t; K, (k 0,5)t
k – полное число разрядов.
Учитывая, что
– времена наработки отказавших ТУ;
k
и
получим
n(t) n1 n2 K nk
t t ,
k
n j
j 1
t t [ N 1
k
k
(k 0,5
j 1
j)n j ].
Для восстанавливаемых ТУ суммарное время наработки равно
N k
где ti j
t ti j ,
i 1 j 1
– время наработки j -о ТУ в течение i -о интервала испытательного
времени.
Одной из основных количественных характеристик долговечности яв-
ляется среднее время наработки.
Среднее время наработки ТУ измеряется математическим ожиданием суммарного времени их наработки от начала до заданного момента време-
ни эксплуатации.
Среднее статистическое время наработки в границах заданного времени эксплуатации есть отношение суммарного времени наработки од-
нотипных ТУ за весь период времени эксплуатации к общему этих уст-
ройств:
T * t .
N
На практике в качестве одного из основных критериев часто применя- ется среднее время наработки на один отказ. Эта величина оценивается отношением суммарного времени наработки однотипных ТУ за заданное время эксплуатации к числу отказавших за это же время устройств:
T
* t .
но n
страница 1 | страница 2 страница 3 страница 4
|