страница 1 ... страница 3 | страница 4 | страница 5 страница 6
Практическая работа № 16
Транспортная задача
Рассмотрим еще один пример, где используется средство поиска решений. Предположим, что фирма имеет четыре фабрики и пять центров распределения ее товаров. Фабрики фирмы располагаются в Денвере, Бостоне, Новом Орлеане и Далласе с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Лос-Анджелесе, Далласе, Сент-Луисе, Вашингтоне и Атланте с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в $0,75 в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен $2,5 в день. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице 4.
Таблица 4 - Транспортные расходы
|
|
1
|
2
|
3
|
4
|
5
|
|
|
Лос-Анджелес
|
Даллас
|
Сент-Луис
|
Вашингтон
|
Атланта
|
1
|
Денвер
|
1,5
|
2
|
1,75
|
2,25
|
2,25
|
2
|
Бостон
|
2,5
|
2
|
1,75
|
1
|
1,5
|
3
|
Новый Орлеан
|
2
|
1,5
|
1,5
|
1,75
|
1,75
|
4
|
Даллас
|
2
|
0,5
|
1,75
|
1,75
|
1,75
|
Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.
Поскольку данная модель сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребностей в ней), то в этой модели не надо учитывать издержки, связанные как со складированием, так и с недопоставками продукции. В противном случае в модель нужно было бы ввести:
-
в случае перепроизводства – фиктивный пункт распределения, стоимость перевозок единицы продукции в который полагается равной стоимости складирования, а объемы перевозок – объемам складирования излишков продукции;
-
в случае дефицита – фиктивную фабрику, стоимость перевозок единицы продукции с которой полагается равной стоимости штрафов за недопоставку продукции, а объемы перевозок – объемам недопоставок продукции в пункты распределения.
Для решения данной задачи построим ее математическую модель. Неизвестными в данной задаче являются объемы перевозок. Пусть 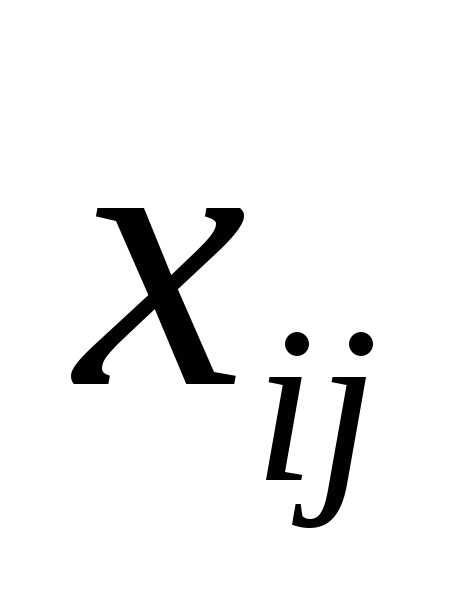 – объем перевозок с i-й фабрики в j-й центр распределения. Функция цели – это суммарные транспортные расходы, то есть – объем перевозок с i-й фабрики в j-й центр распределения. Функция цели – это суммарные транспортные расходы, то есть
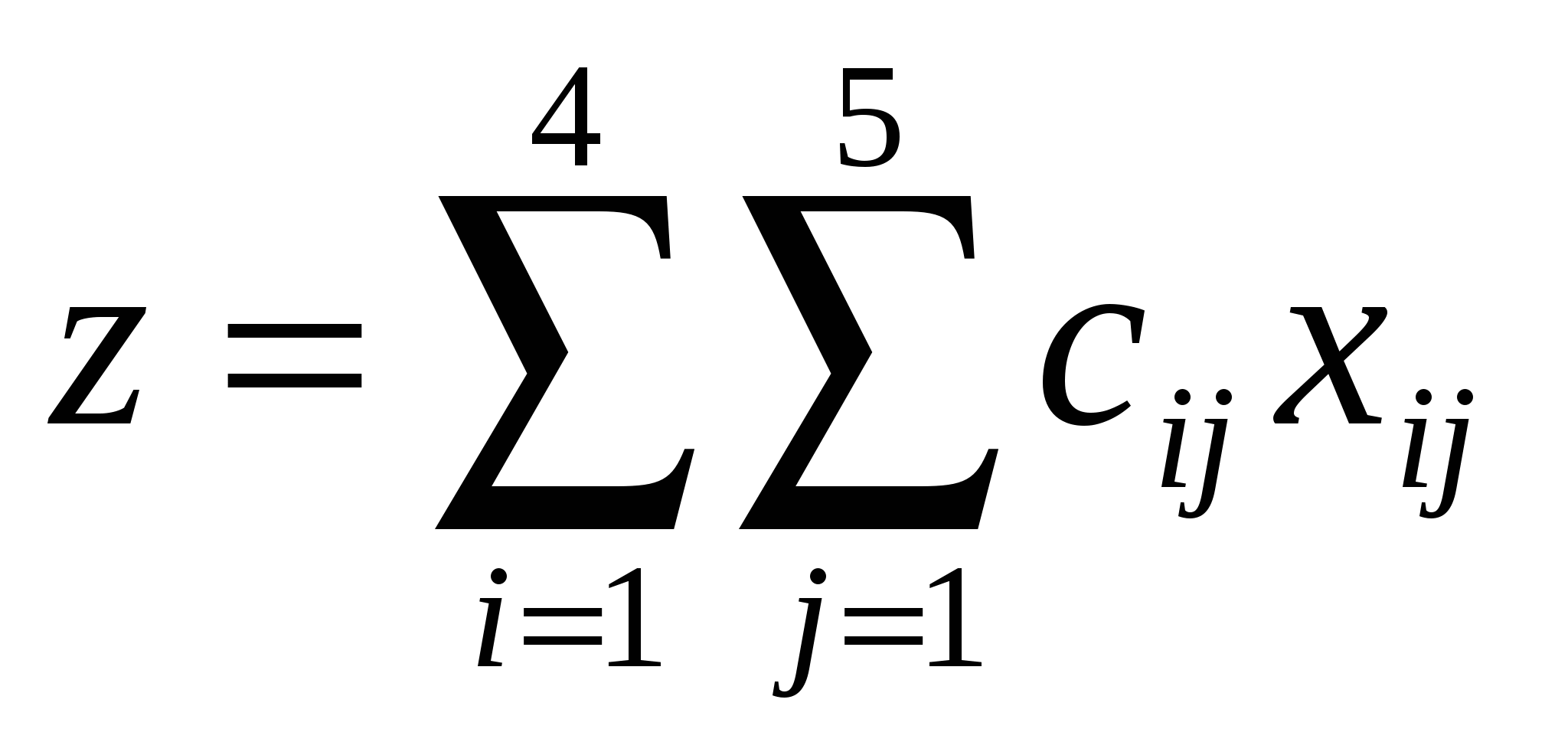 , ,
где  – стоимость перевозки единицы продукции с i-й фабрики в j-й центр распределения. – стоимость перевозки единицы продукции с i-й фабрики в j-й центр распределения.
Неизвестные в данной задаче должны удовлетворять следующим ограничениям:
-
объемы перевозок не могут быть отрицательными;
-
так как модель сбалансирована, то вся продукция должна быть вывезена с фабрик, а потребности всех центров распределения должны быть полностью удовлетворены.
В результате имеем следующую модель:
минимизировать:
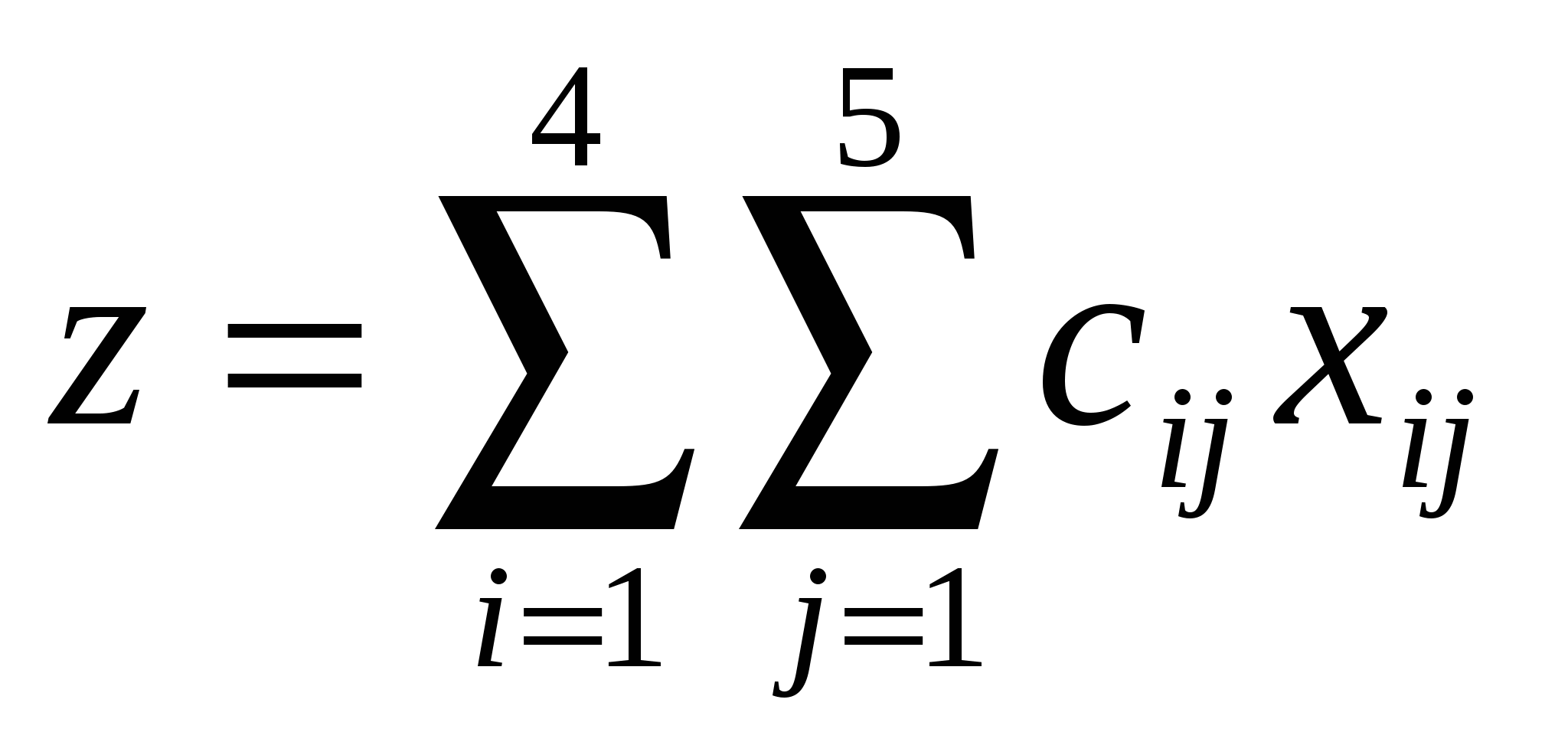
при ограничениях:
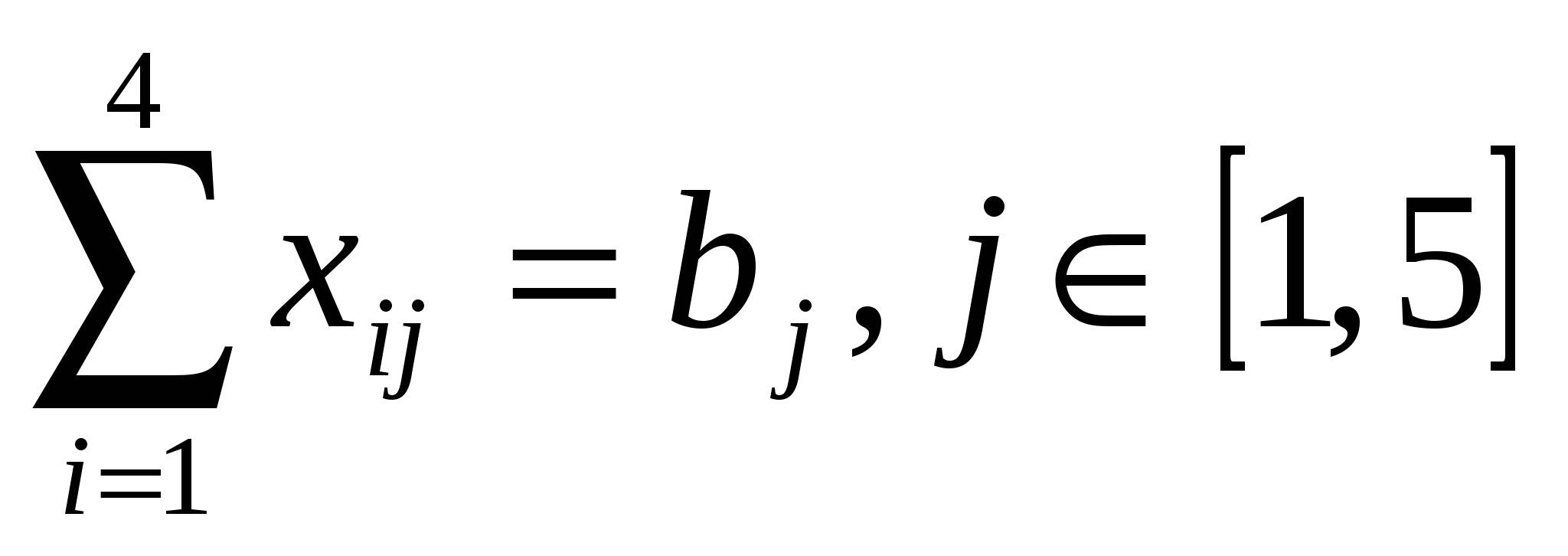 , ,
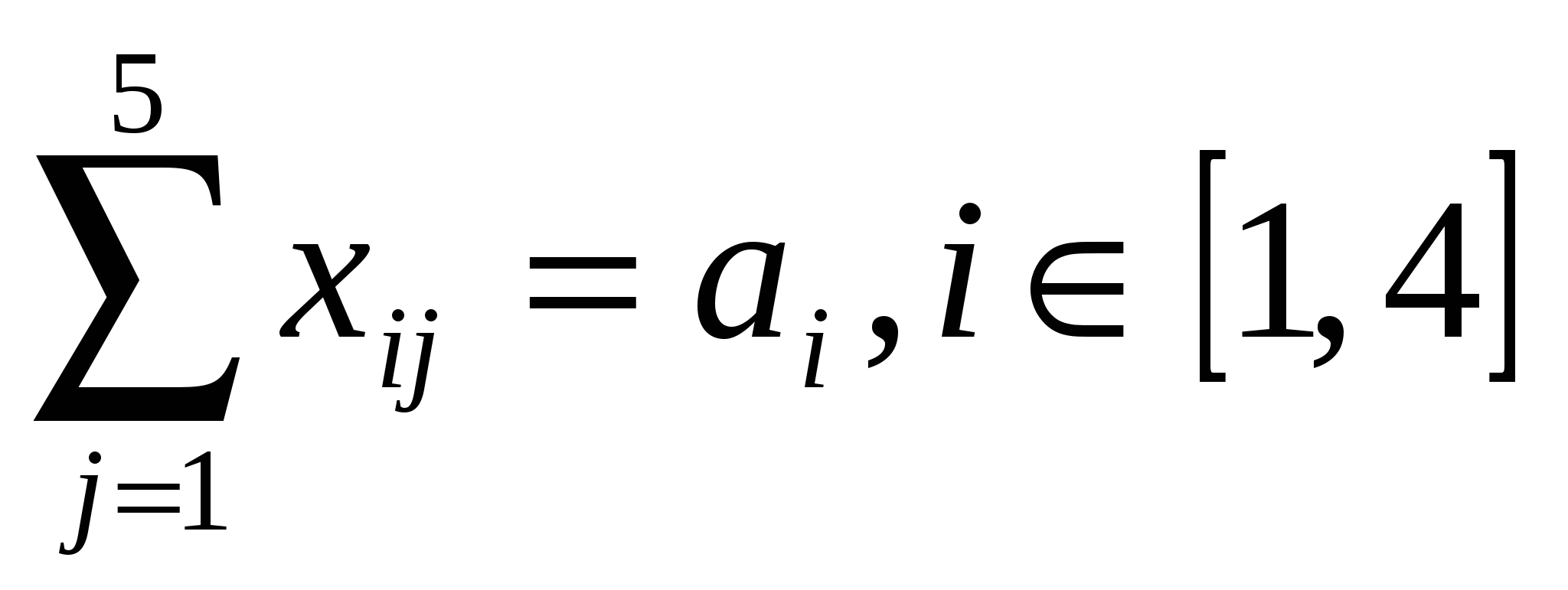 , ,
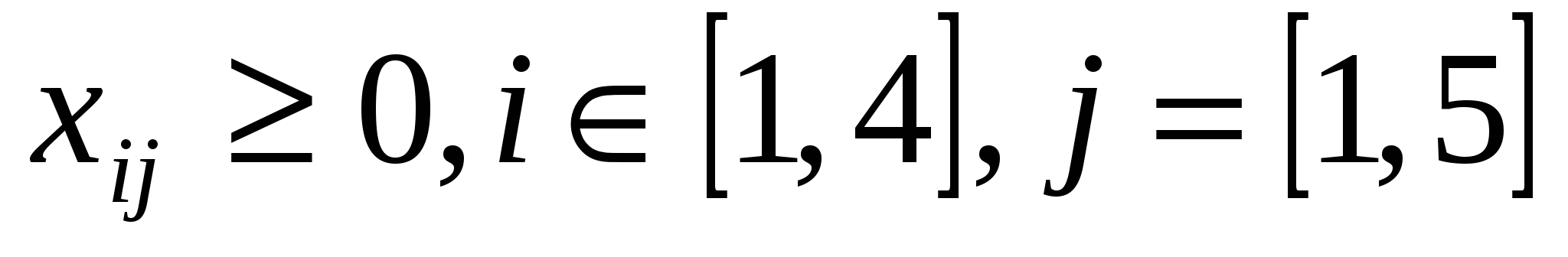 . .
где 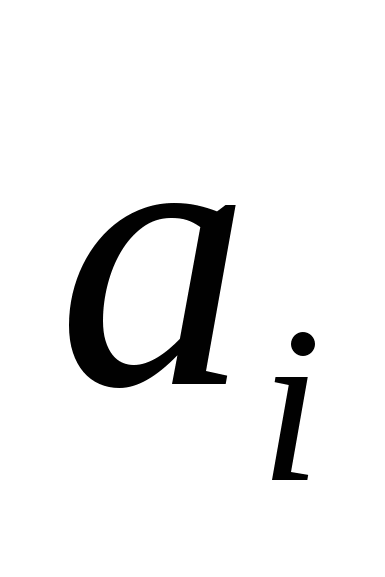 – объем производства на i-й фабрике, – объем производства на i-й фабрике, 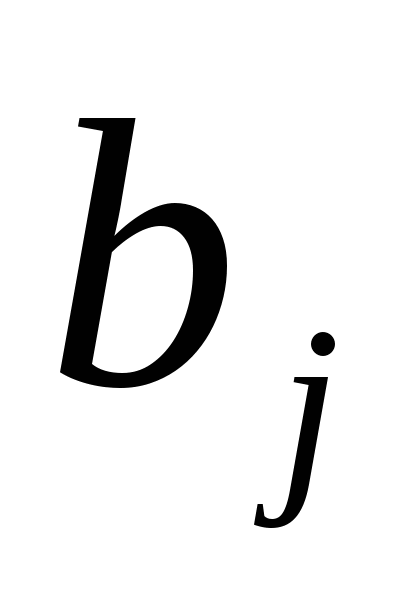 – спрос в j-м центре распределения. – спрос в j-м центре распределения.
Для решения этой задачи с помощью средства поиска решений введем данные, как показано на рисунке 7.
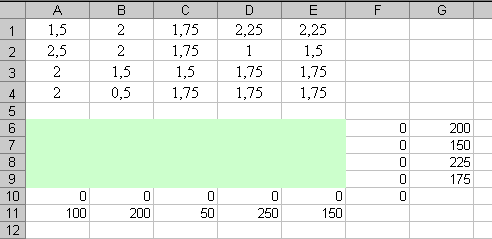
Рисунок 7 - Исходные данные транспортной задачи
В ячейки А1:Е4 введены стоимости перевозок. Ячейки А6:Е9 отведены под значения неизвестных (объемы перевозок). В ячейки G6:G9 введены объемы производства на фабриках, а в ячейки А11:Е11 введена потребность в продукции в пунктах распределения.
В ячейку F10 введена целевая функция
=СУММПРОИЗВ(А1:Е4;А6;Е9)
В ячейки А10:Е10 введены формулы
=СУММ(А6:А9),
=СУММ(Вб:В9),
=СУММ(С6:С9),
=СУММ(П6:09),
=СУММ(Е6:Е9),
определяющие объем продукции, ввозимой в центры распределения.
В ячейки F6:F9 введены формулы
=СУММ(А6:Е6),
=СУММ(А7:Е7),
=СУММ(А8:Е8),
=СУММ(А9:Е9),
вычисляющие объем продукции, вывозимой с фабрик.
Теперь выберем команду Сервис, Поиск решения и заполним открывшееся диалоговое окно Поиск решения, как показано на рисунке 8.
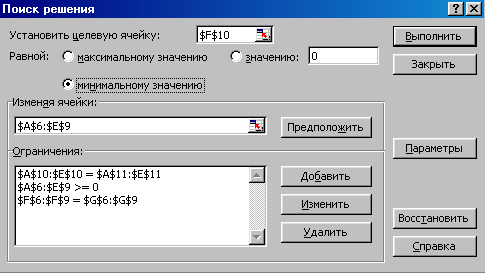
Рисунок 8 - Диалоговое окно Поиск решения для транспортной задачи
Не забудьте в диалоговом окне Параметры поиска решения установить флажок Линейная модель. После нажатия кнопки Выполнить средство поиска решений находит оптимальный план поставок продукции и соответствующие ему транспортные расходы, что показано на рисунке 9.
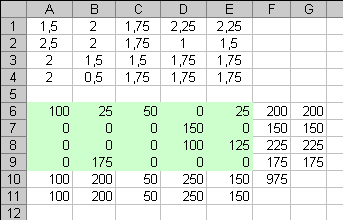
Рисунок 9 - Оптимальное решение транспортной задачи
Практическая работа № 17
Задача о назначениях
Рассмотрим пример решения задачи о назначениях. Четверо рабочих могут выполнять четыре вида работ. Стоимости  выполнения i-м рабочим j-й работы приведены в ячейках диапазона A1:D4 на рисунке 10. выполнения i-м рабочим j-й работы приведены в ячейках диапазона A1:D4 на рисунке 10.
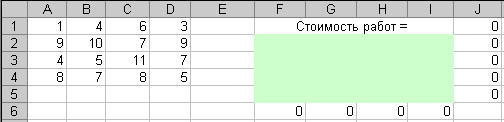
Рисунок 10 - Стоимости работ в задаче о назначениях
В этой таблице строки соответствуют рабочим, а столбцы – работам. Необходимо составить план выполнения работ так, чтобы все работы были выполнены, каждый рабочий был загружен только на одной работе, а суммарная стоимость выполнения всех работ была минимальной. Отметим, что данная задача является сбалансированной, то есть число работ совпадает с числом рабочих. Если задача не сбалансирована, то перед началом решения ее необходимо сбалансировать, введя недостающее число фиктивных строчек или столбцов с достаточно большими штрафными стоимостями работ.
Для решения данной задачи построим ее математическую модель. Пусть переменная 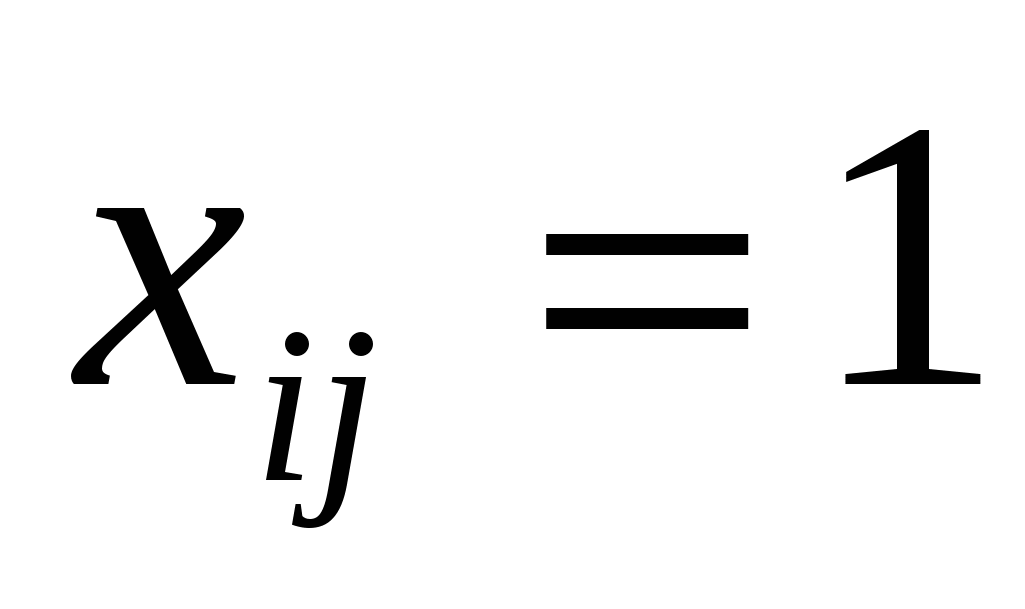 , если i-м рабочим выполняется j-я работа, и , если i-м рабочим выполняется j-я работа, и 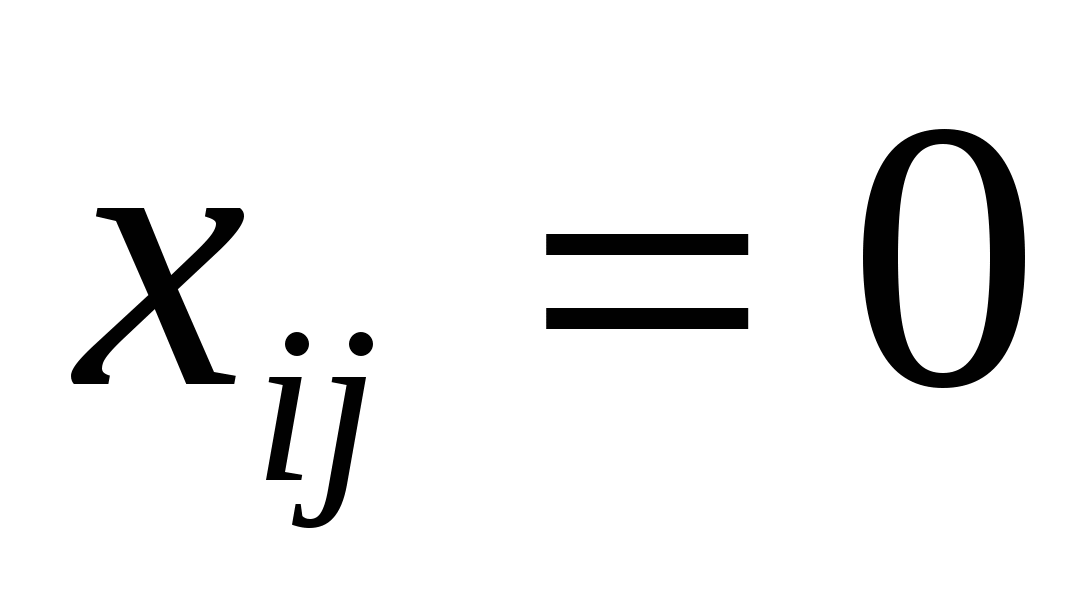 , если i-м рабочим не выполняется j-я работа. Тогда модель имеет следующий вид: , если i-м рабочим не выполняется j-я работа. Тогда модель имеет следующий вид:
минимизировать:
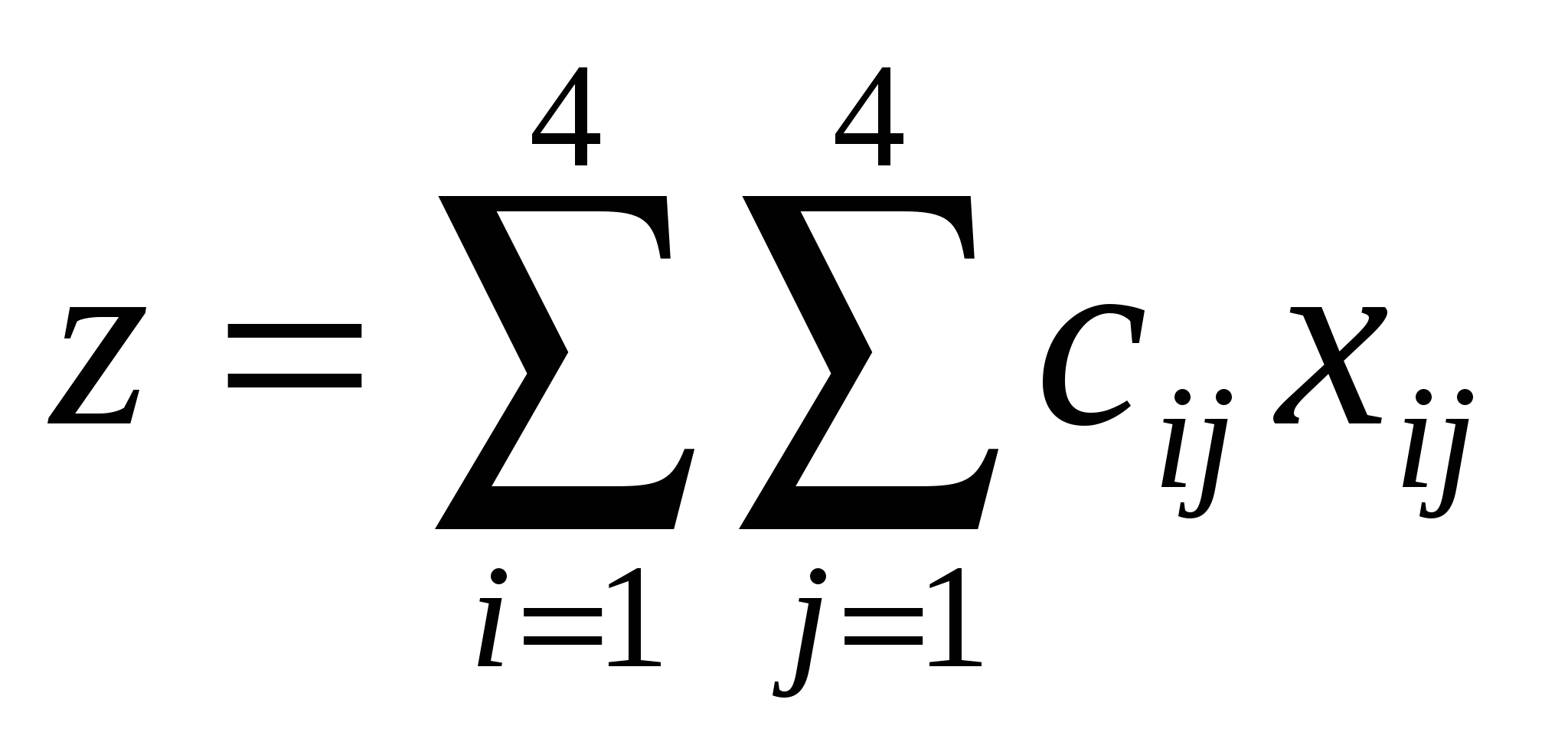 , ,
при ограничениях:
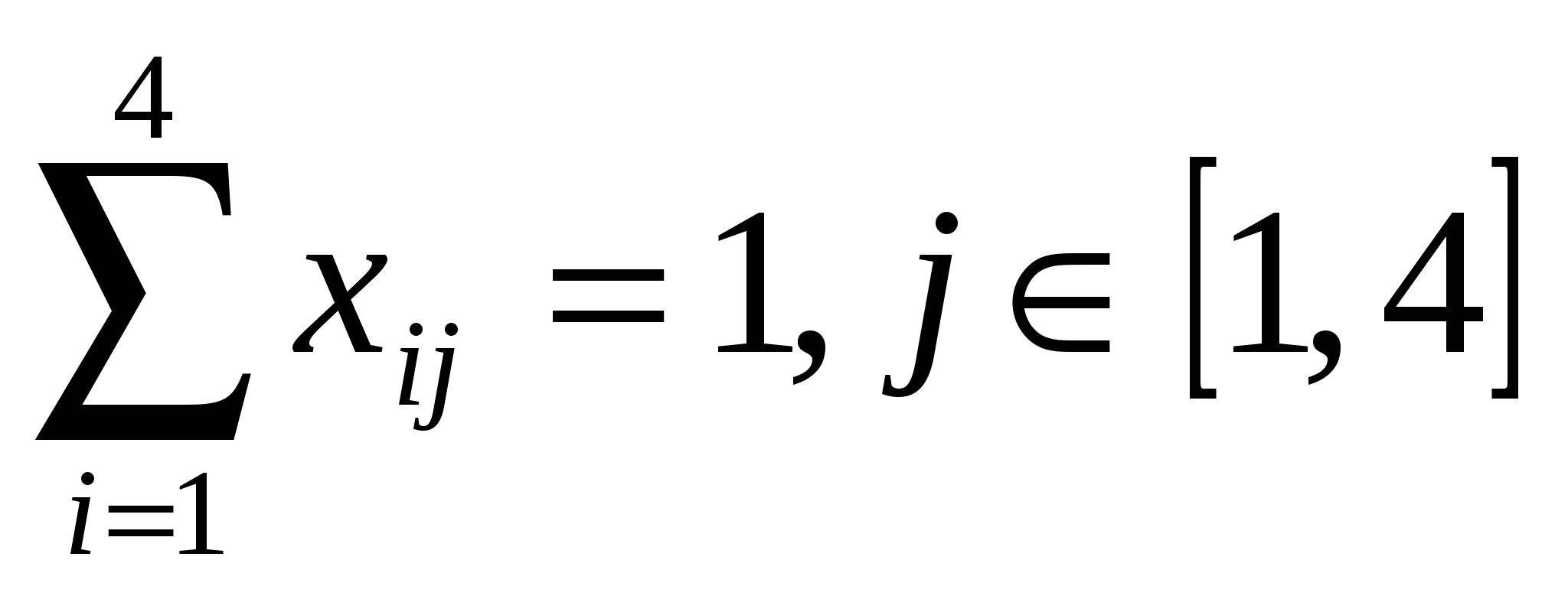 , ,
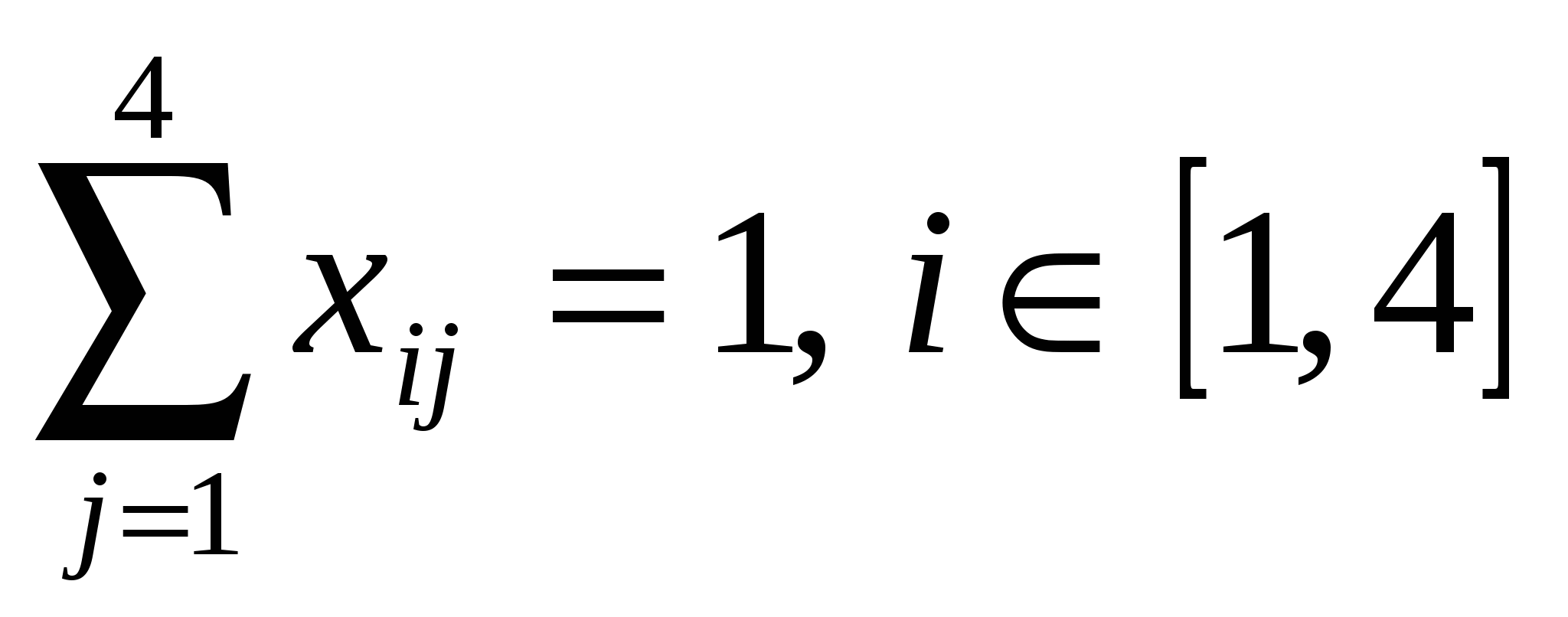 , ,
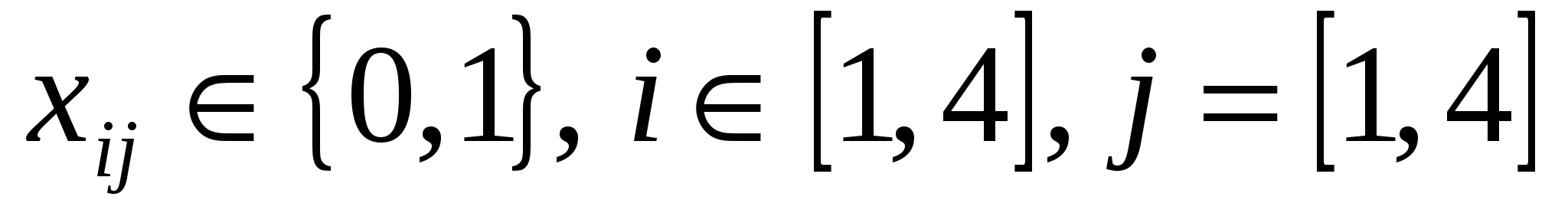 . .
Для решения этой задачи с помощью средства поиска решений отведем под неизвестные диапазон ячеек F2:I5. В ячейку J1 введем целевую функцию:
=СУММПРОИЗВ(F2:I5;A1:D4),
вычисляющую стоимость работ. Введем формулы, задающие левые части ограничений, как показано на рисунке 11.

Рисунок 11 - Левые части ограничений в задаче о назначениях
Затем выберем команду Сервис, Поиск решения и заполним открывшееся диалоговое окно Поиск решения, как показано на рисунке 12.
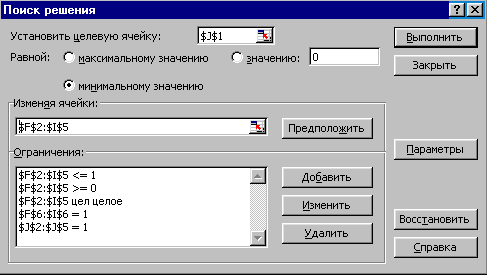
Рисунок 12 – Диалоговое окно Поиск решения задачи о назначениях
Не забудьте в диалоговом окне Параметры поиска решения установить флажок Линейная модель. После нажатия кнопки Выполнить средство поиска решений найдет оптимальное решение, которое приведено на рисунке 13.
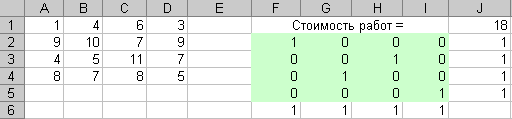
Рисунок 13 – Оптимальный план работ в задаче о назначениях
Практическая работа № 18
Использование механизмов линейного программирования в решении экономико-математических задач.
Задача 1. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн, соответственно. Расходы продуктов А и В на 1 т соответствующих красок приведены в таблице 1.
Таблица 1 - Исходные данные задачи о планировании производства красок
Исходный продукт
|
Расход исходных продуктов на тонну краски, т
|
Максимально возможный запас, т
|
краска Е
|
краска I
|
А
|
1
|
2
|
6
|
B
|
2
|
1
|
8
|
Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3000 руб. для краски Е и 2000 руб. для краски I. Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Методика выполнения практической части работы
Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса:
-
для определения каких величин строится модель (то есть каковы переменные модели)?
-
в чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?
-
каким ограничениям должны удовлетворять неизвестные?
В нашем случае фабрике необходимо спланировать объем производства красок так, чтобы максимизировать прибыль. Поэтому переменными являются: 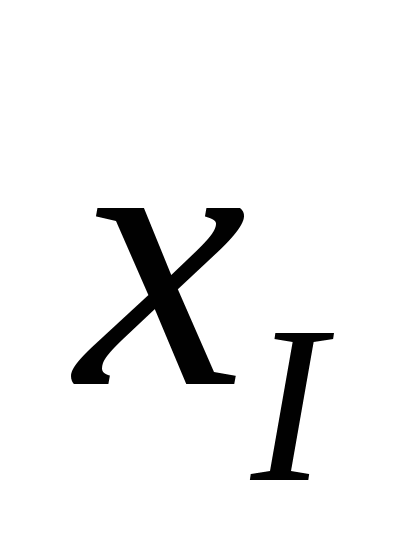 - суточный объем производства краски I и - суточный объем производства краски I и 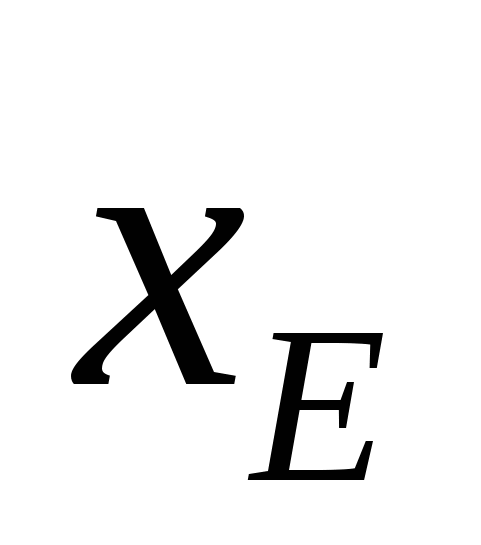 - суточный объем производства краски Е. - суточный объем производства краски Е.
Суммарная суточная прибыль от производства 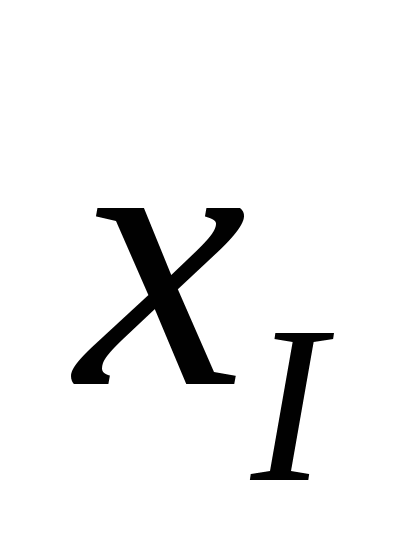 краски I и краски I и 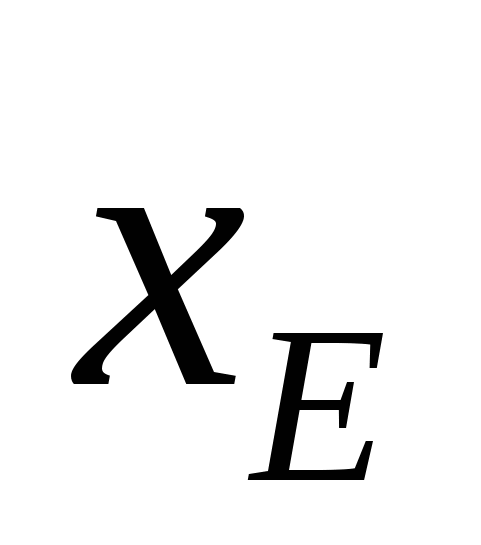 краски Е равна краски Е равна 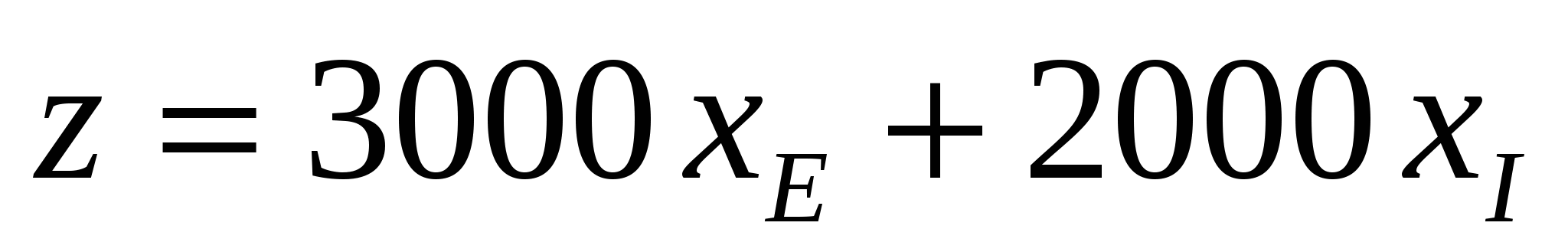 . Целью фабрики является определение среди всех допустимых значений . Целью фабрики является определение среди всех допустимых значений 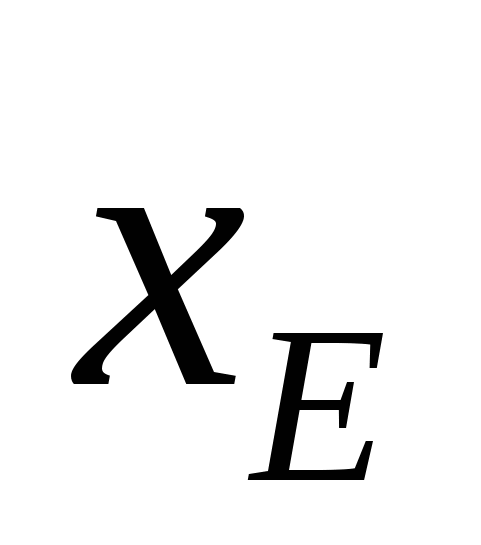 и и 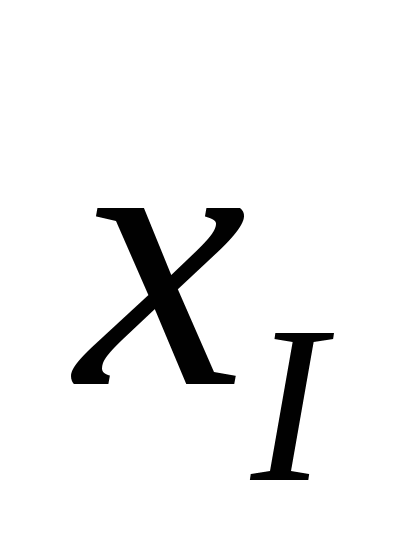 таких, которые максимизируют суммарную прибыль, т. е. целевую функцию таких, которые максимизируют суммарную прибыль, т. е. целевую функцию  . .
Перейдем к ограничениям, которые налагаются на 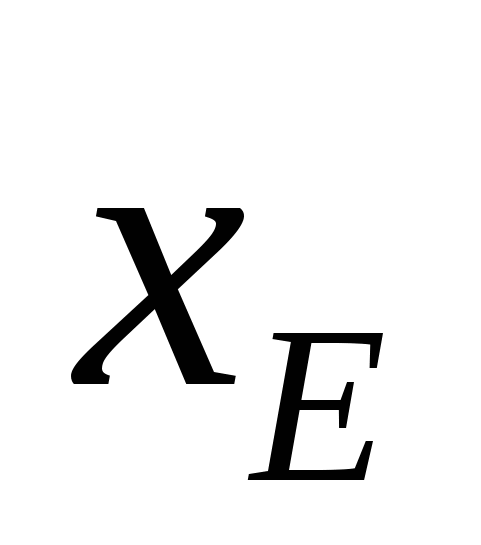 и и 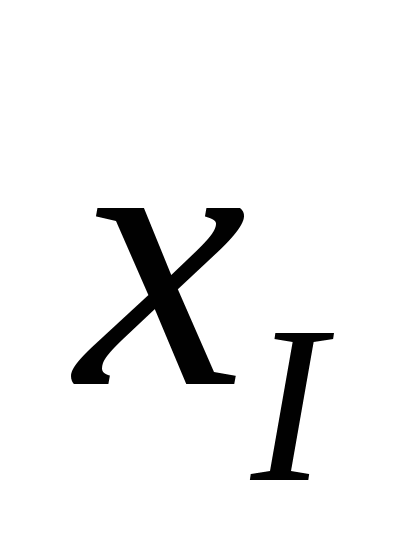 . Объем производства красок не может быть отрицательным, следовательно, . Объем производства красок не может быть отрицательным, следовательно, 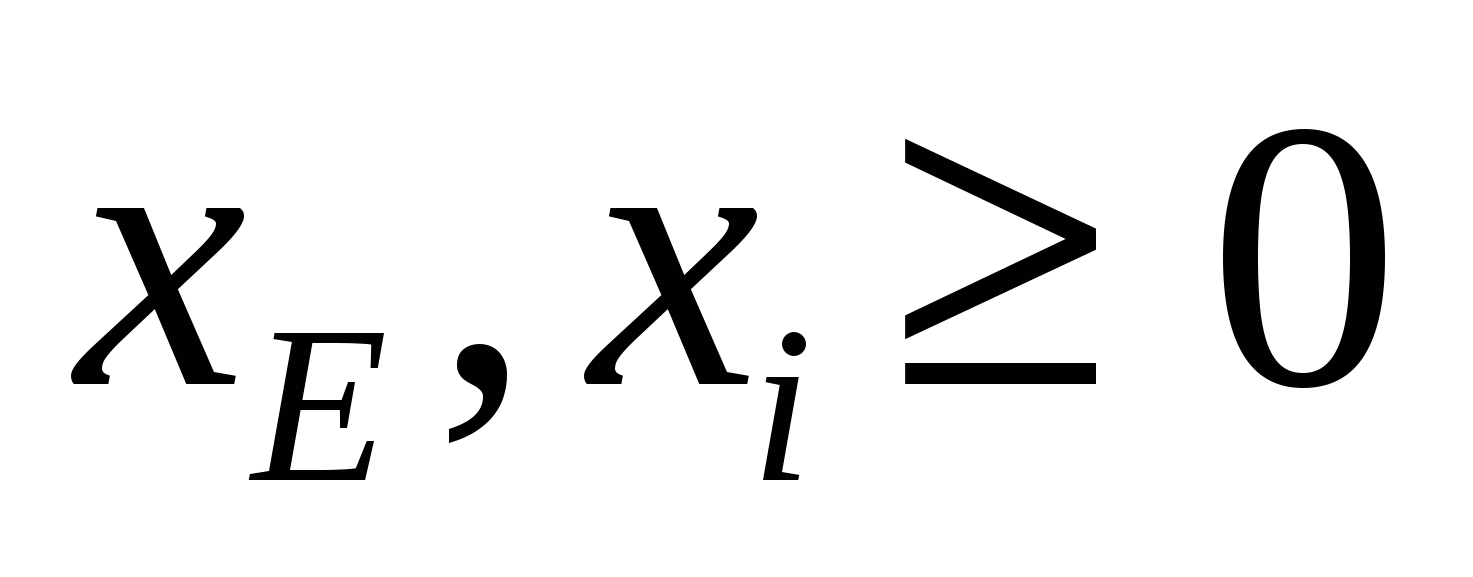 . .
Расход исходного продукта для производства обоих видов красок не может превосходить максимально возможный запас данного исходного продукта, следовательно:
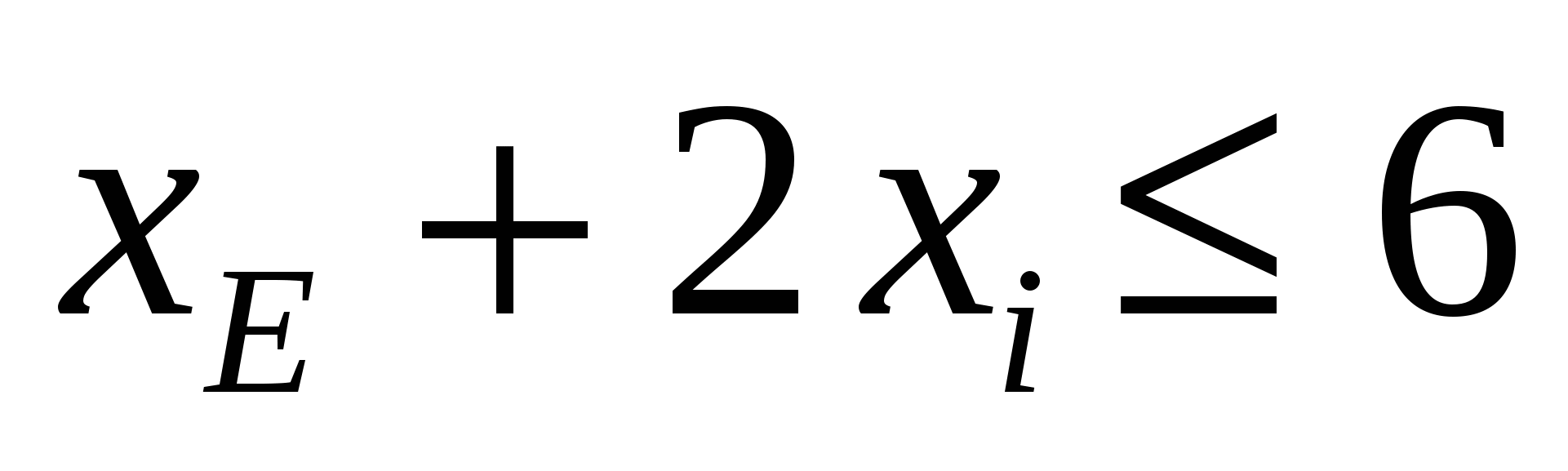 , ,
 . .
Кроме того, ограничения на величину спроса на краски таковы:
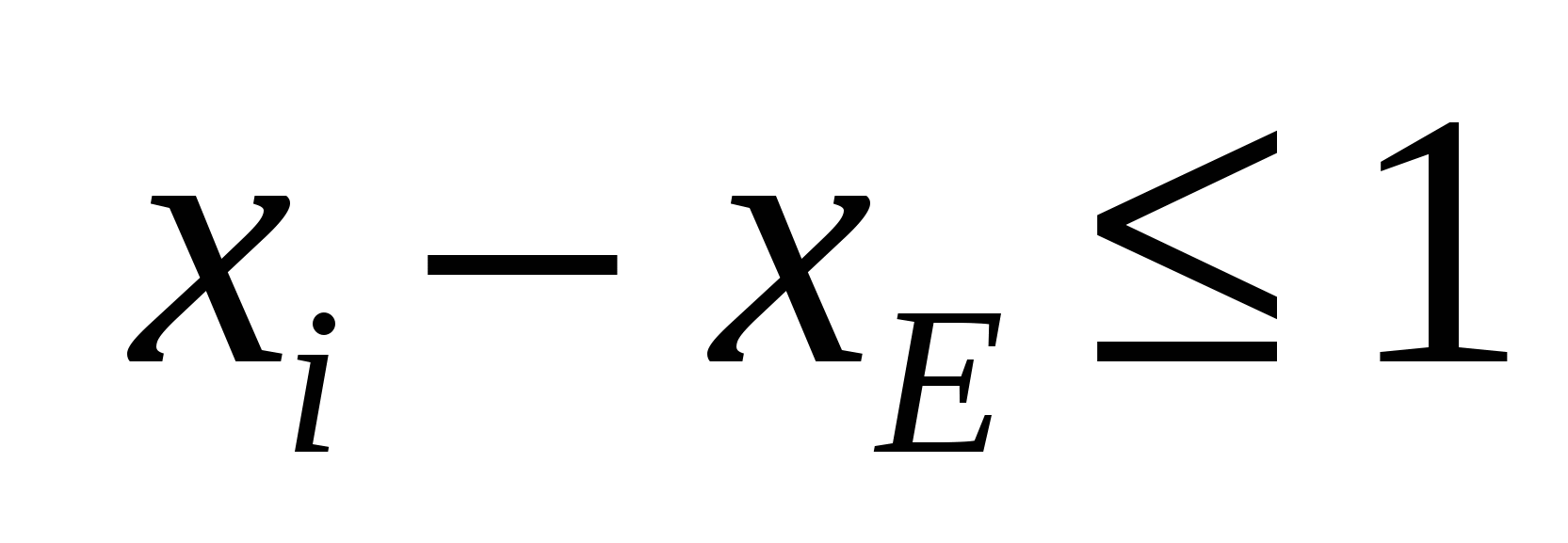 , ,
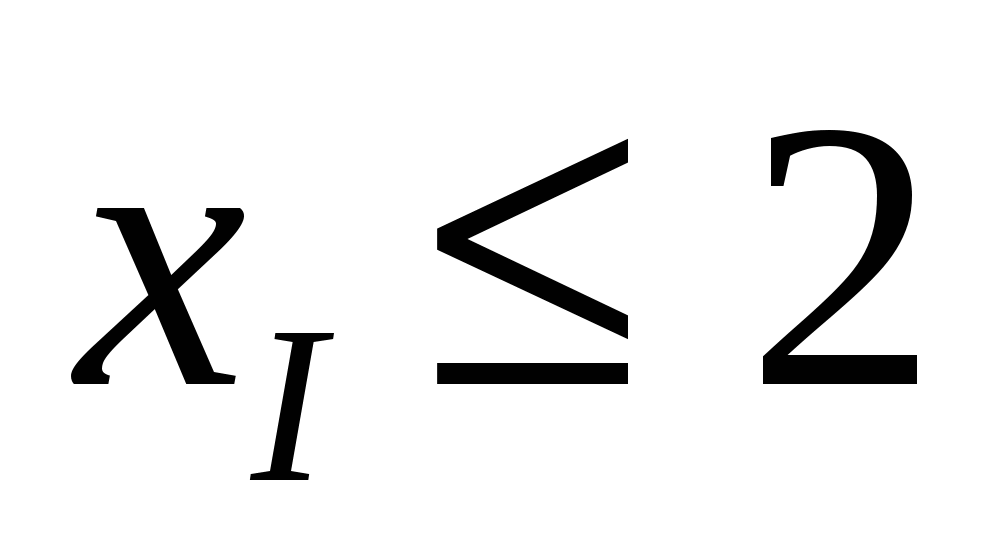 . .
Таким образом, математическая модель данной задачи имеет следующий вид: максимизировать 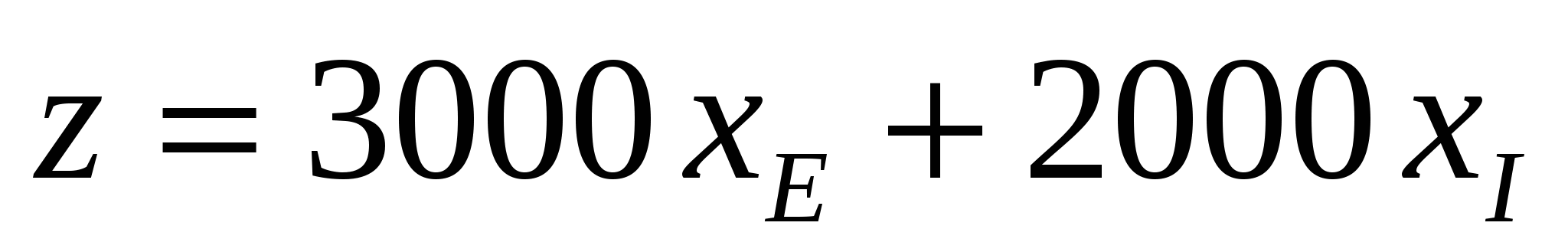
при следующих ограничениях:
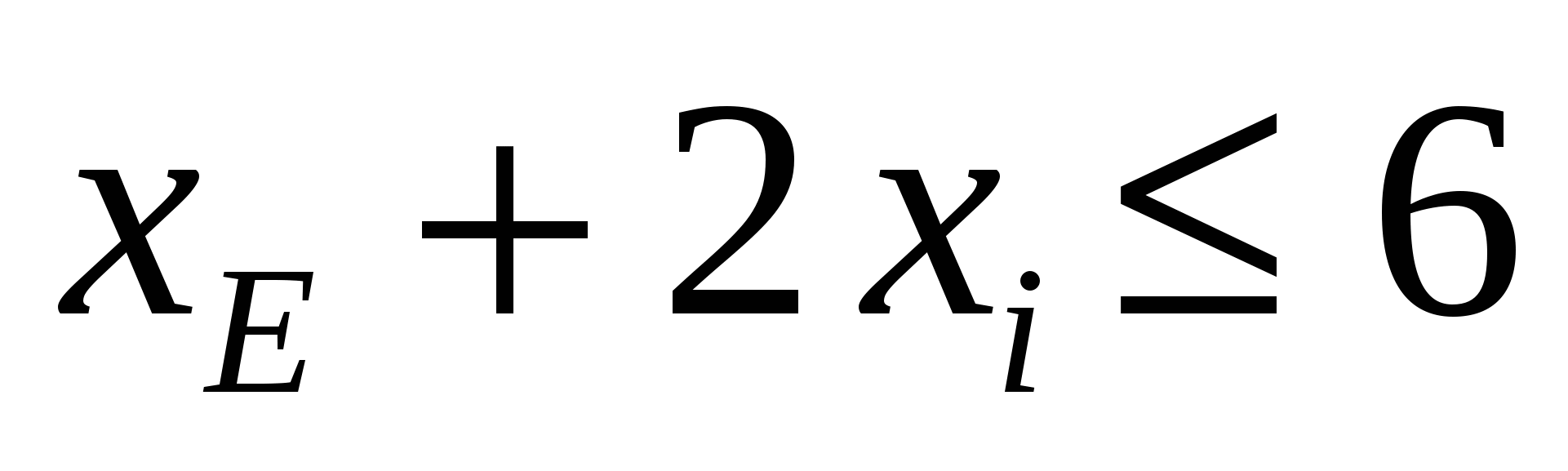 , ,
 , ,
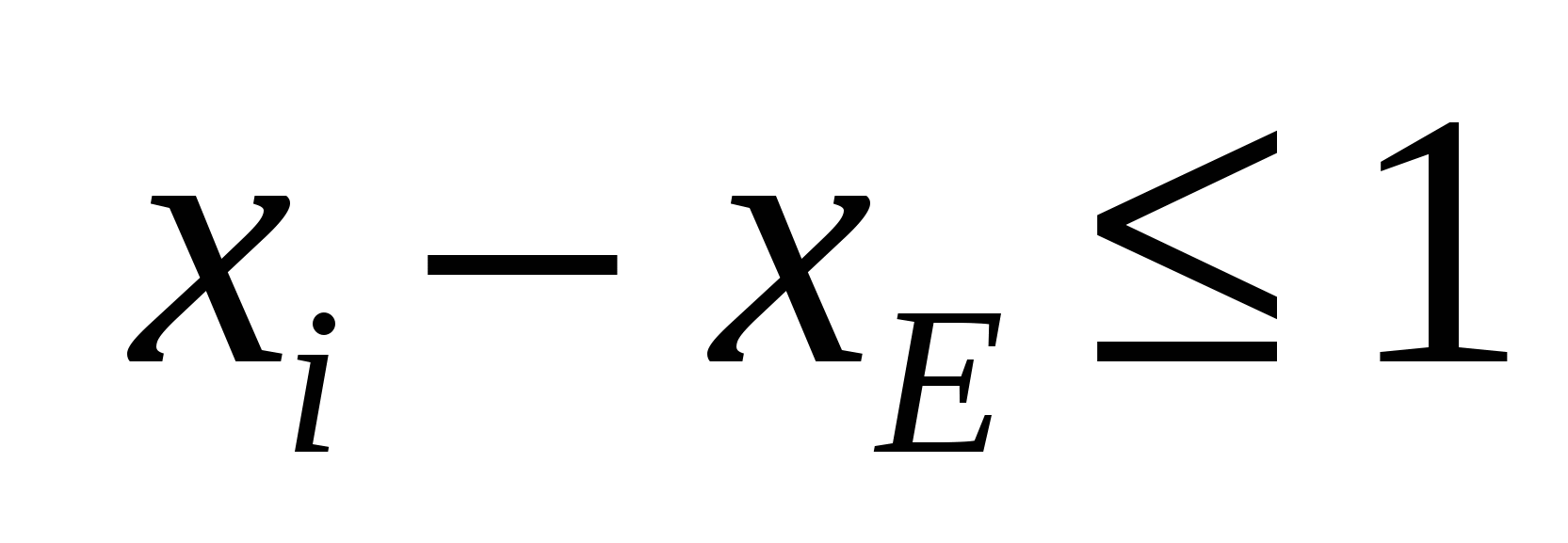 , ,
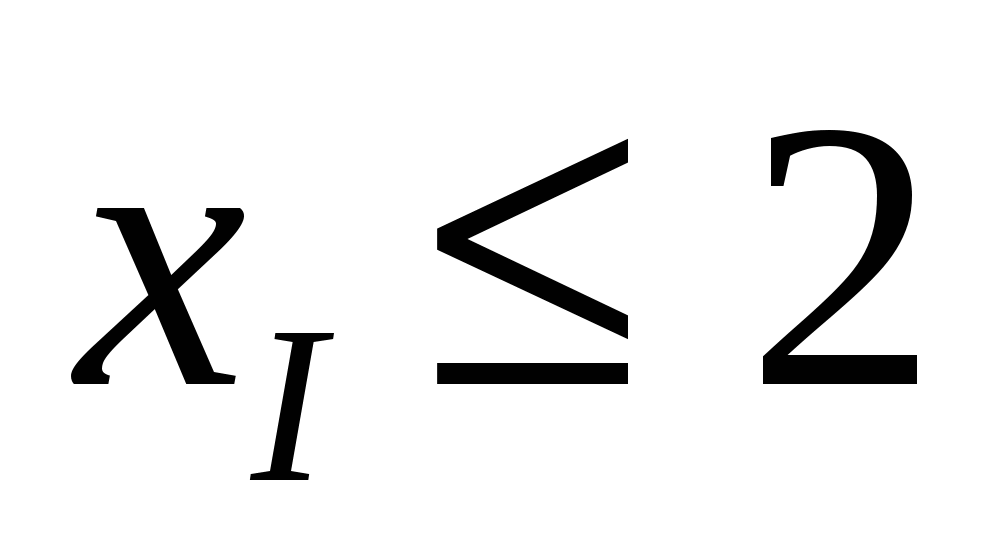 , ,
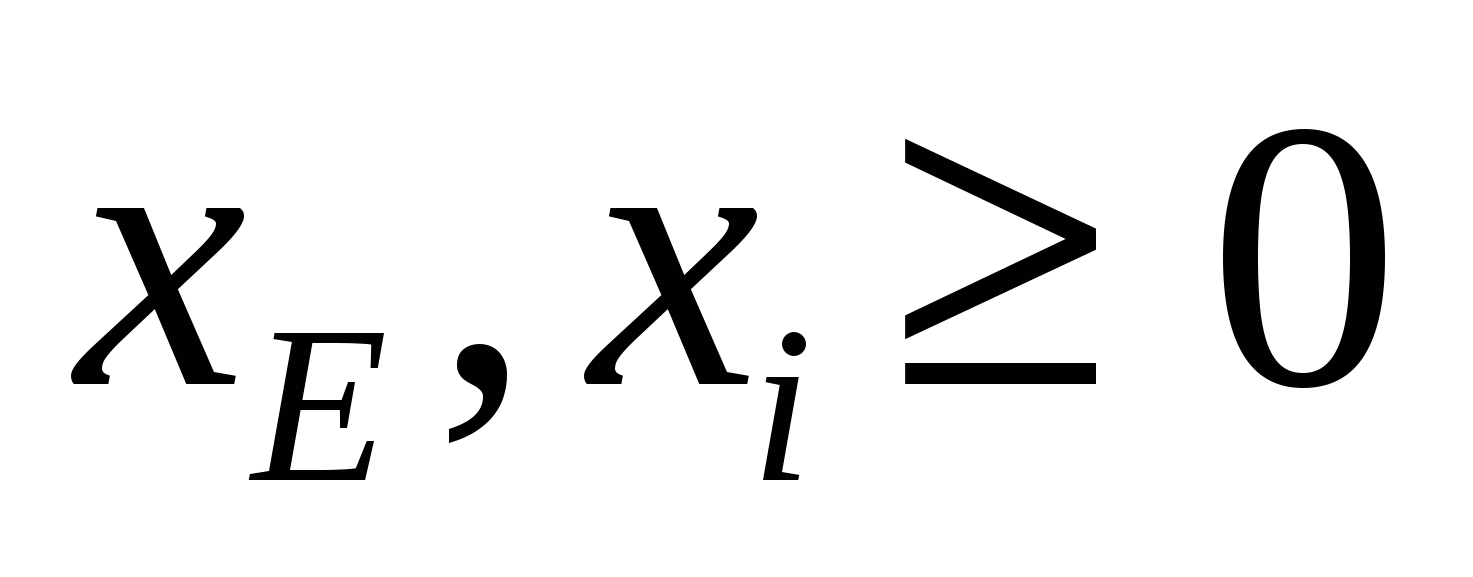 . .
Заметим, что данная модель является линейной, так как целевая функция и ограничения линейно зависят от переменных.
Решим данную задачу с помощью команды Сервис, Поиск решения. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис, Надстройки, Поиск решения.
Отведем ячейки A3 и ВЗ под значения переменных 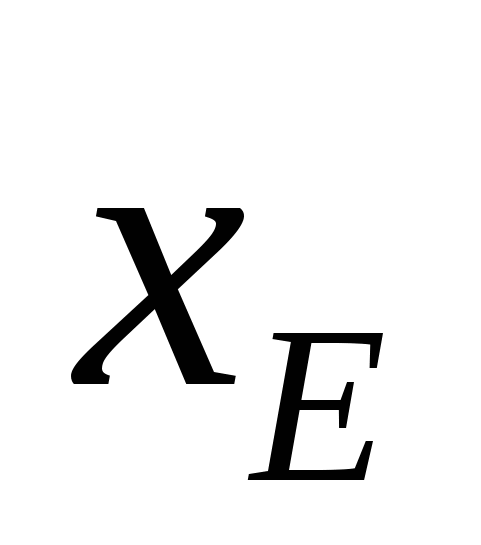 и и 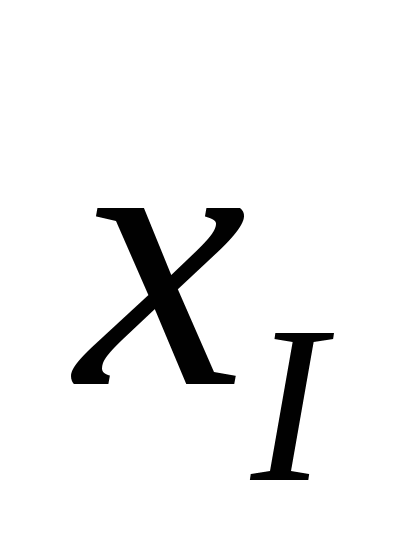 , как показано на рисунке 1. , как показано на рисунке 1.

Рисунок 1 - Диапазоны, отведенные под переменные, целевую функцию и ограничения
В ячейку С4 введем функцию цели
=3000*АЗ+2000*ВЗ.
В ячейки А7:А10 введем левые части ограничений:
=АЗ+2*ВЗ;
=2*АЗ+ВЗ;
=ВЗ-АЗ;
=ВЗ,
а в ячейки В7:В10 – правые части ограничений.
После этого выберем команду Сервис, Поиск решения и заполним открывшееся диалоговое окно Поиск решения, как показано на рисунке 2.
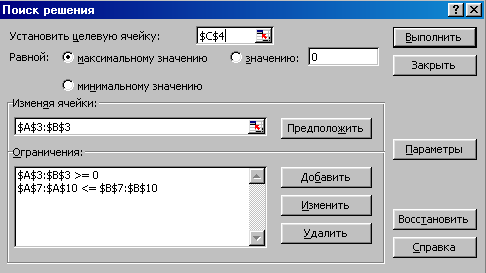
Рисунок 2 - Диалоговое окно Поиск решения задачи о планировании производства красок
После нажатия кнопки Выполнить открывается окно Результаты поиска решения, которое сообщает, что решение найдено.
Задача 2. Рассмотрим задачу: для получения сплавов А и В используются четыре металла I, II, III и IV, требования к содержанию которых в сплавах А и В приведены в таблице 2.
Таблица 2 - Требования к содержанию металлов в задаче определения состава сплавов
Сплав
|
Требования к содержанию металла
|
А
|
Не более 80% металла I
|
Не более 30% металла II
|
B
|
От 40 до 60% металла II
|
Не менее 30% металла III
|
Не более 70% металла IV
|
Характеристики и запасы руд, используемых для производства металлов I, II, III и IV, указаны в таблице 3.
Таблица 3 - Характеристики и запасы руд в задаче об определении состава сплавов
Руда
|
Максимальный запас, т
|
Состав, %
|
Цена, $/т
|
1
|
II
|
III
|
IV
|
Другие компоненты
|
1
|
1000
|
20
|
10
|
30
|
30
|
10
|
30
|
2
|
2000
|
10
|
20
|
30
|
30
|
10
|
40
|
3
|
3000
|
5
|
5
|
70
|
20
|
0
|
50
|
Пусть цена 1 т сплава А равна 200 долларов, а 1 т сплава В – 210 долларов. Необходимо максимизировать прибыль от продажи сплавов А и В.
Обозначим через 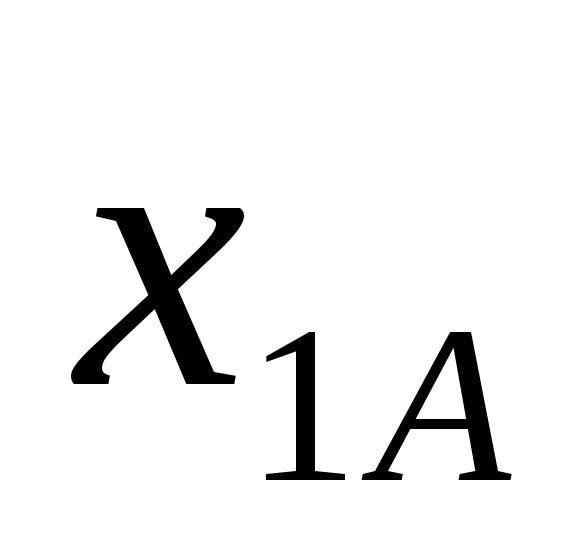 , , 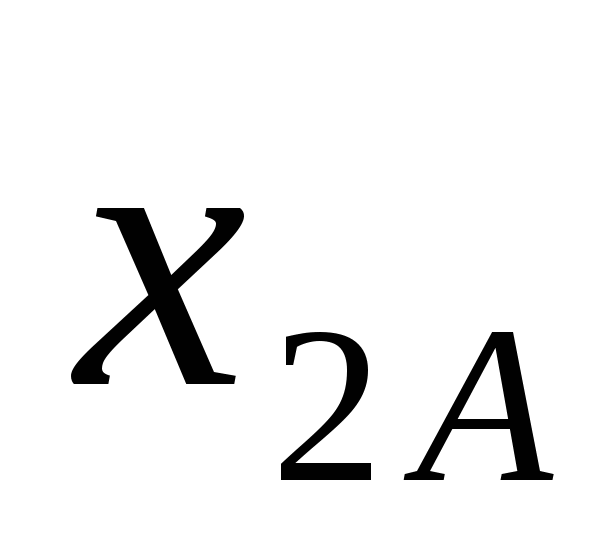 , , 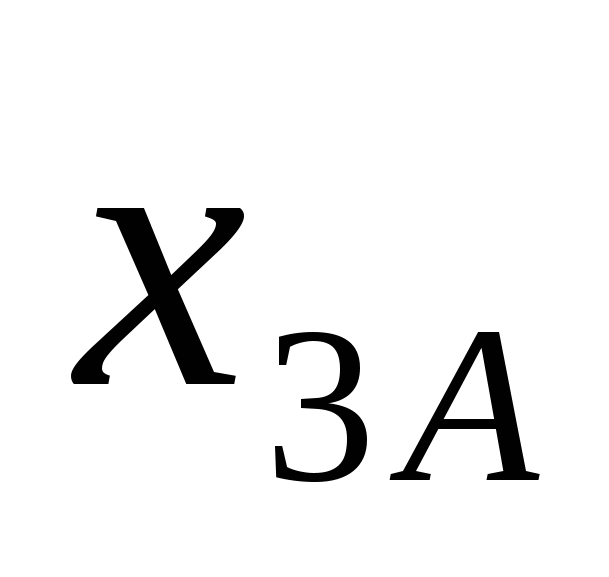 , , 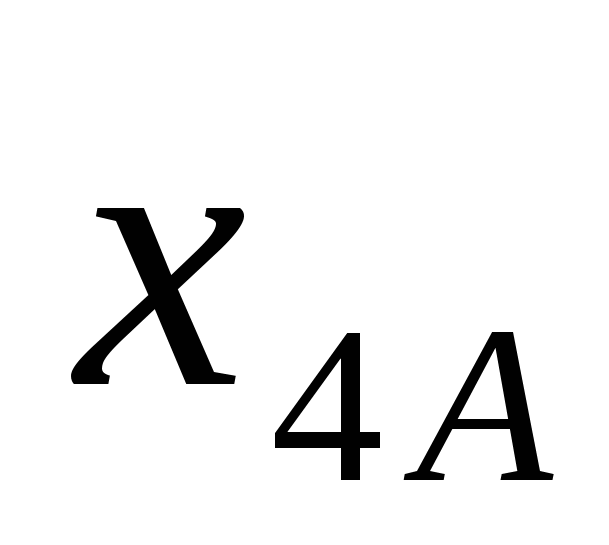 и и 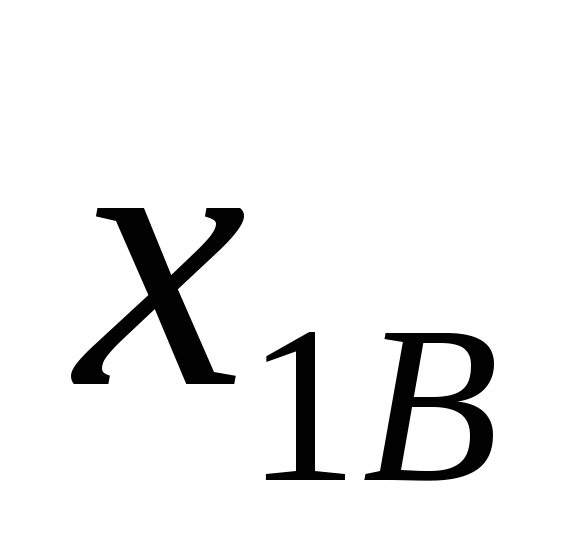 , , 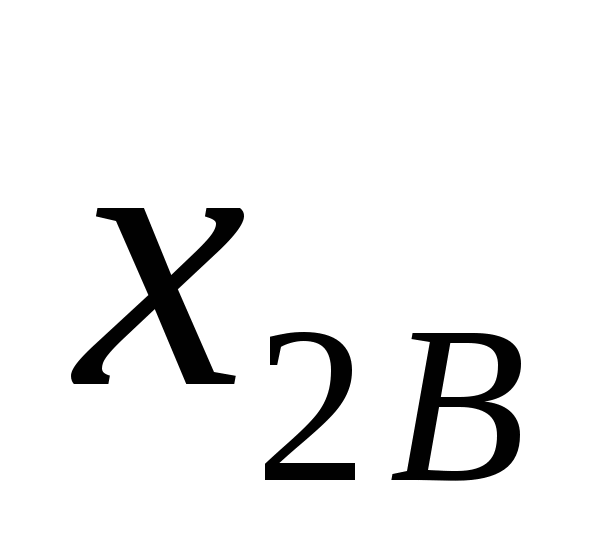 , ,  , , 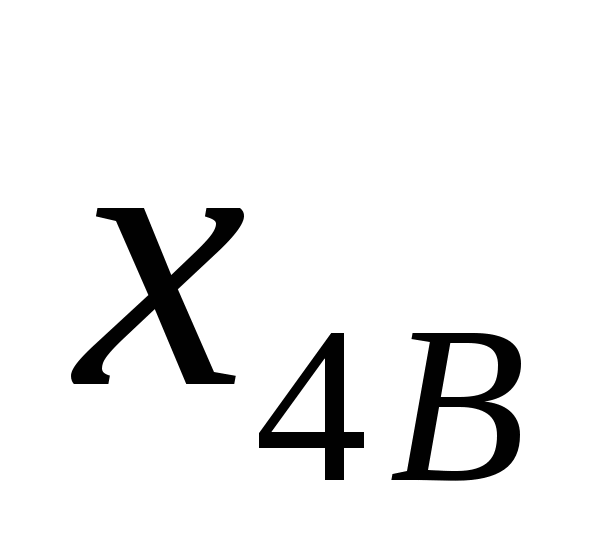 количество I, II, III и IV металлов, используемых для получения сплавов А и B, соответственно. Количество использованной количество I, II, III и IV металлов, используемых для получения сплавов А и B, соответственно. Количество использованной 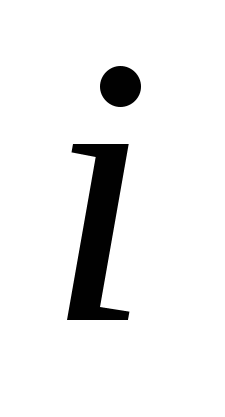 -й руды обозначим -й руды обозначим 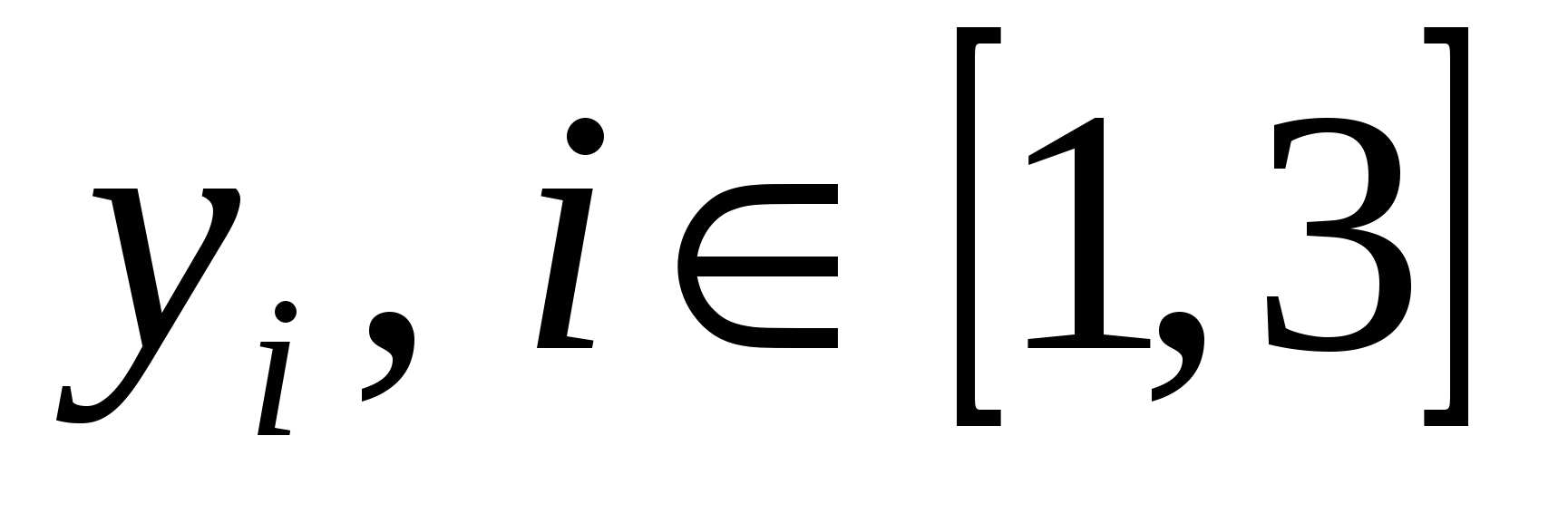 . .
Тогда математическая модель данной задачи имеет вид:
максимизировать:
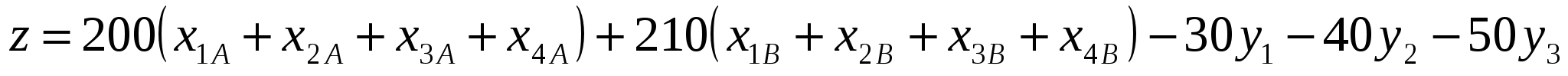
при ограничениях на состав сплавов (на основании данных из таблицы 2):
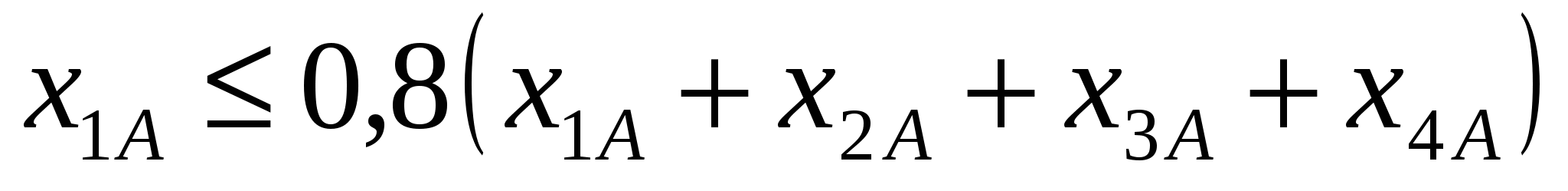 , ,
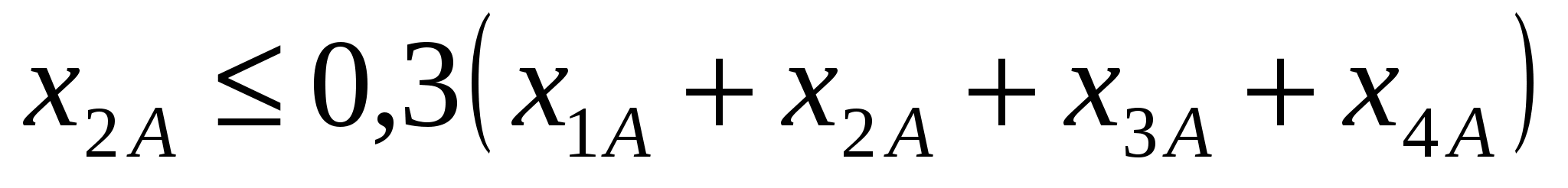 , ,
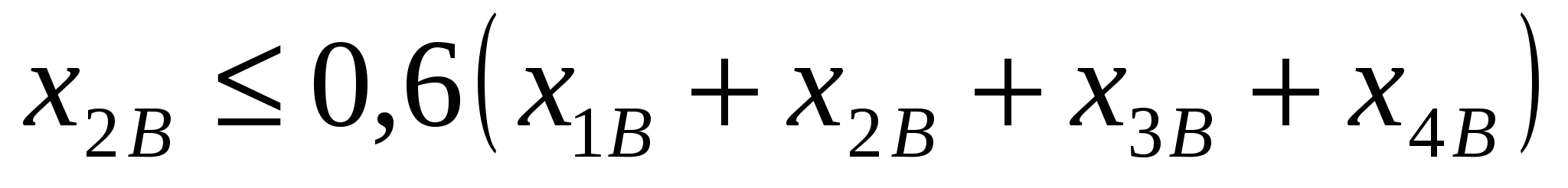 , ,
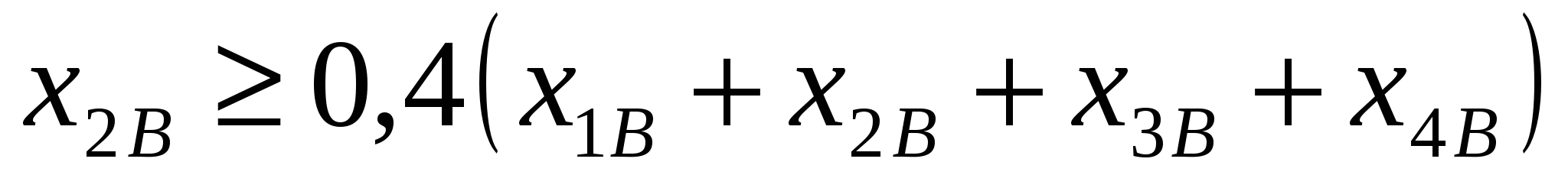 , ,
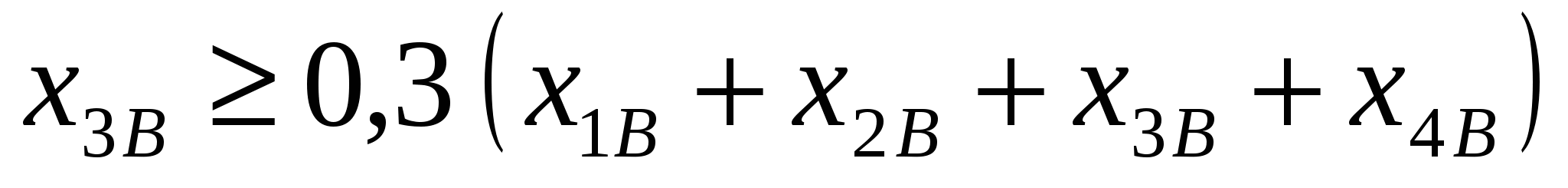 , ,
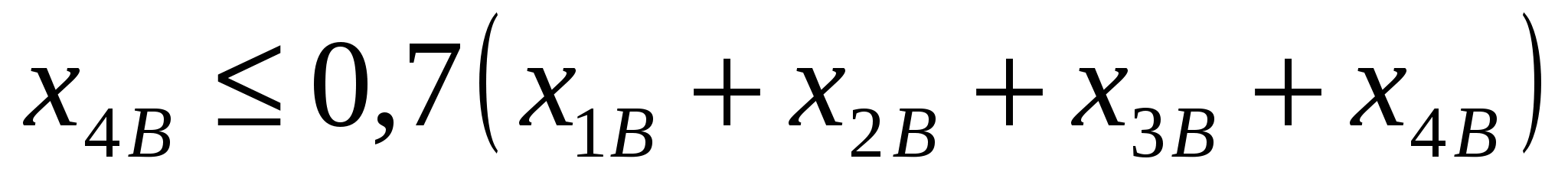 , ,
на характеристики и состав руды (на основании данных из таблицы 3):
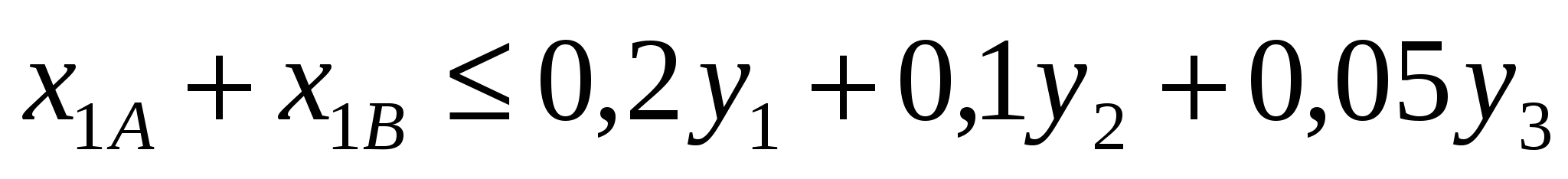 , ,
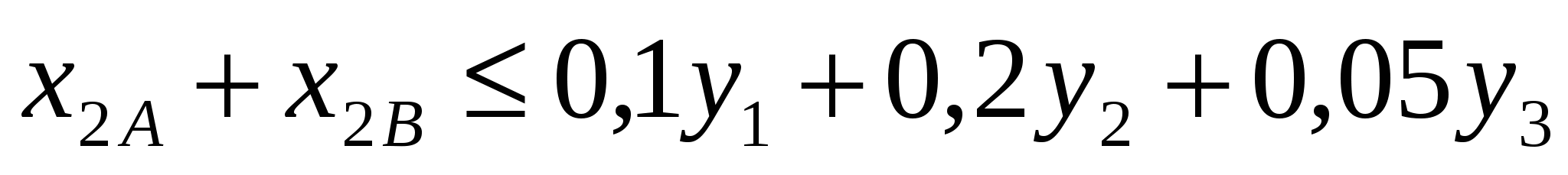 , ,
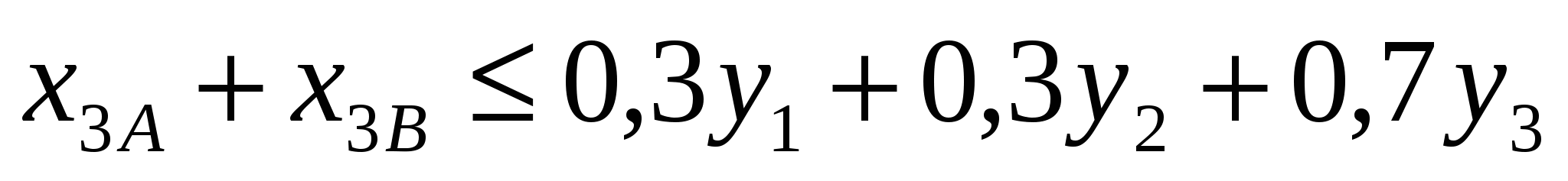 , ,
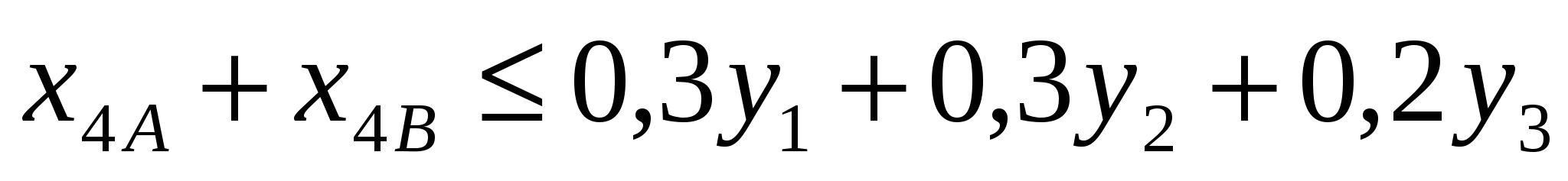 , ,
а также на диапазоны использования переменных:
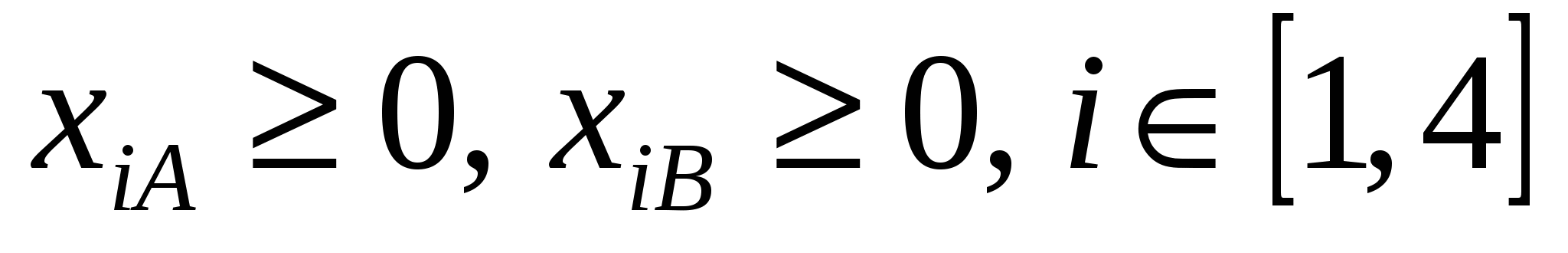 , ,
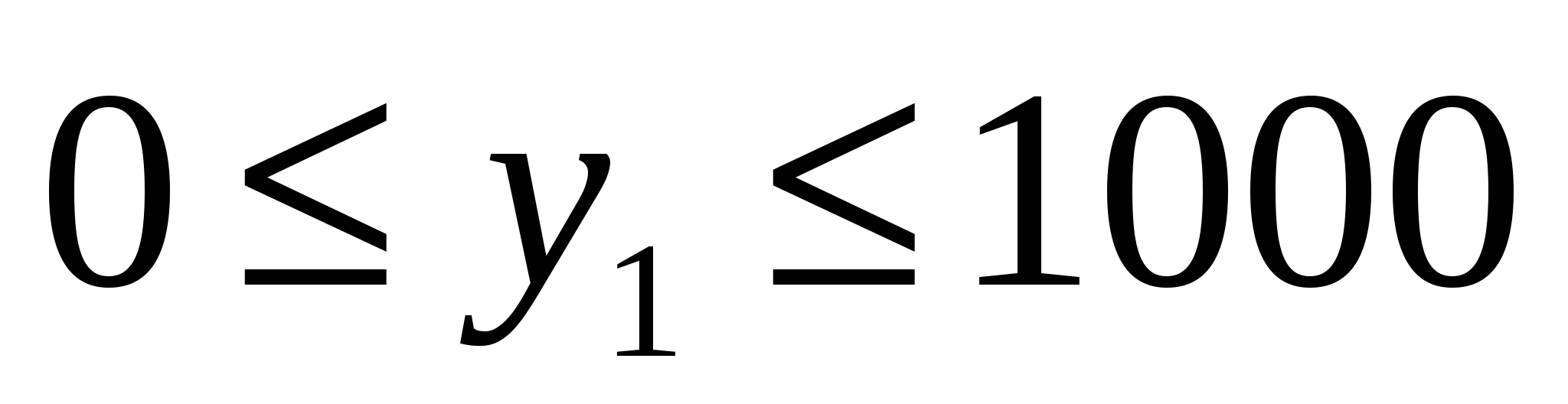 , ,
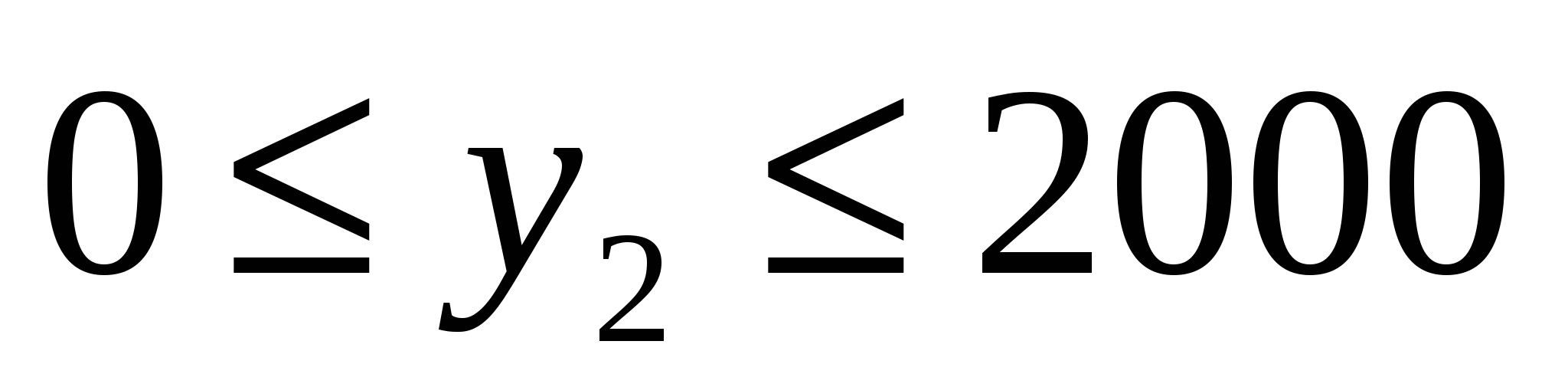 , ,
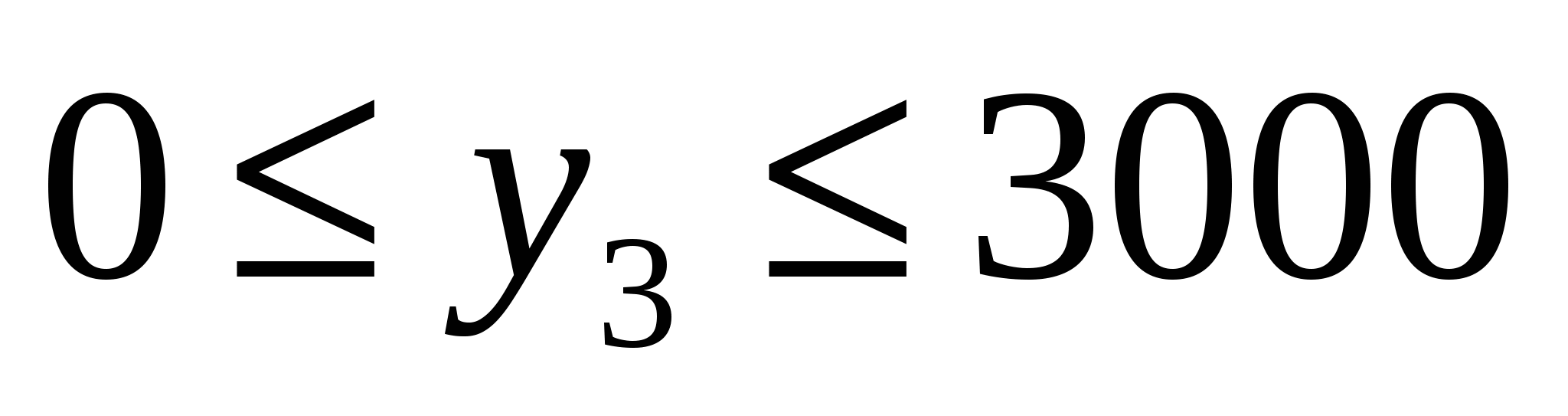 , ,
Отведем под переменные 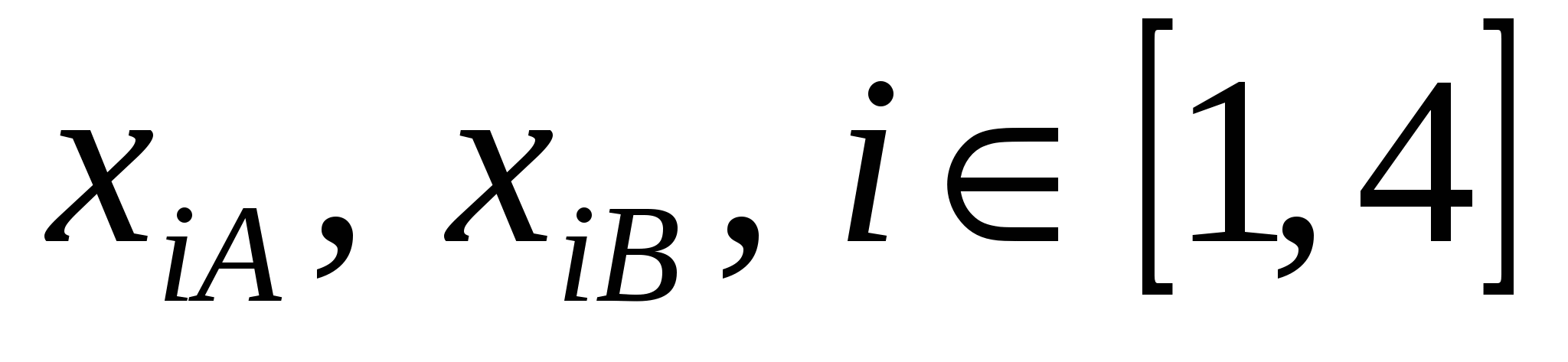 диапазон ячеек C3:D6, а под переменные диапазон ячеек C3:D6, а под переменные 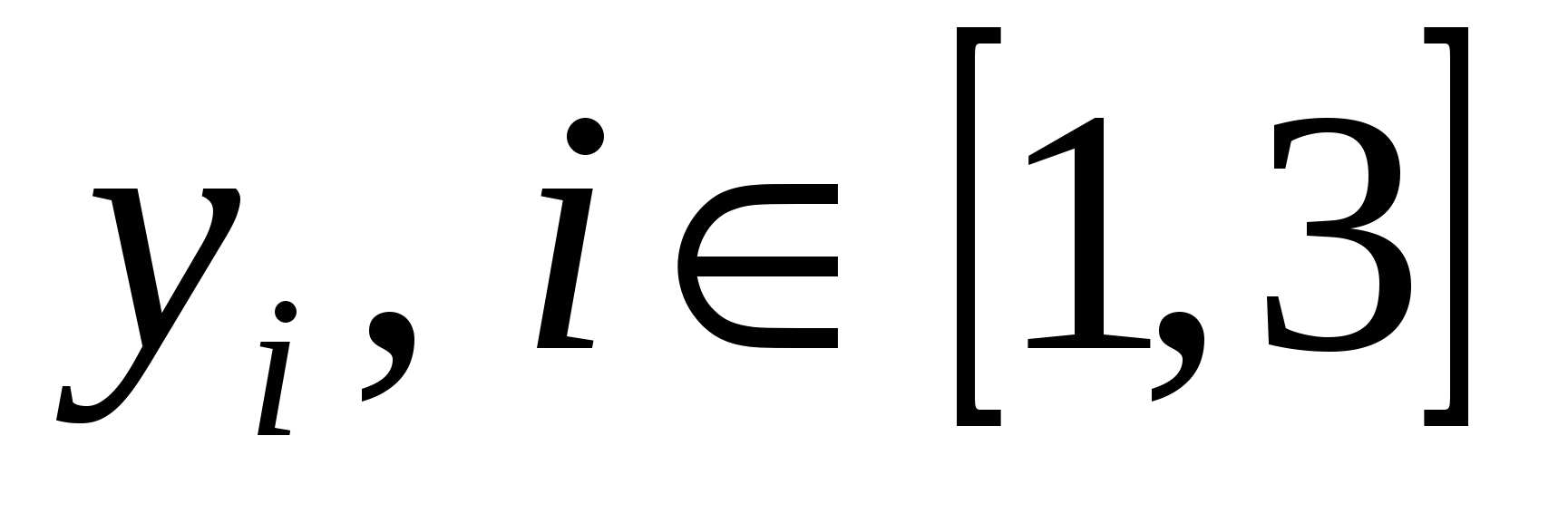 – диапазон ячеек F3:F5, как показано на рисунке 5. – диапазон ячеек F3:F5, как показано на рисунке 5.
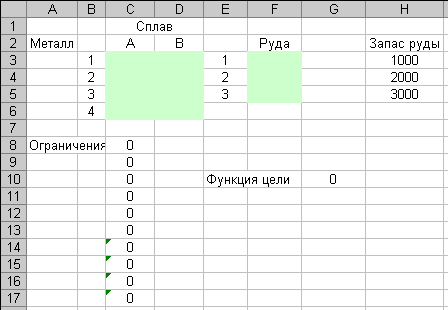
Рисунок 5 – Исходные данные к задаче определения состава сплавов
В ячейку G9 введем функцию цели
=200*СУММ(СЗ:С6)+210*СУММ(03:D6)-30*F3-40*F4-50*F5
В диапазон ячеек С8:С17 введем левые части ограничений, причем преобразуем их к виду, когда все переменные находятся слева, а все знаки неравенств – меньше или равно:
=СЗ-0.8*СУММ(СЗ:С6),
=С4-0.3*СУММ(СЗ:С6),
=04-0.6*СУММ(D3:D6),
=0.4*СУММ(03:06)-D4,
=0.3*СУММ(03:Об)-D5,
=D6-0.7*CYMM(D3:D6),
=СУММ(СЗ:03)-0.2*$F$3-0.1*$F$4-0.05*$F$5,
=СУММ(С4:04)-0.1*$F$3-0.2*$F$4-0.05*$F$5,
=СУММ(С5:05)-0.3*$F$3-0.3*$F$4-0.7*$F$5,
=СУММ(С6:06)-0.3*$F$3-0.3*$F$4-0.2*$F$5.
В диапазон ячеек НЗ:Н5 введем количество имеющихся запасов руд. Выберем команду Сервис, Поиск решения и заполним диалоговое окно Поиск решения, как показано на рисунке 6.
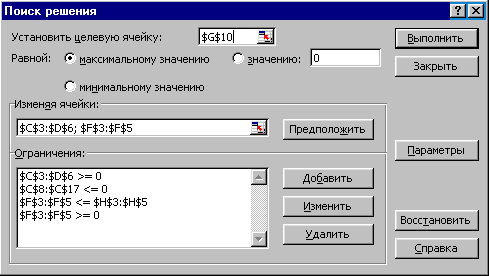
Рисунок 6 - Диалоговое окно Поиск решения в задаче определения состава сплавов
Практическая работа №19
Задачи для самостоятельного решения
Задача 1. Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй модели равна 30 и 20 долларов соответственно. Определить суточный объем производства первой и второй моделей.
Задача 2. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого их них на трех станках. Время использования этих станков для производства данных изделий ограничено 10-ю часами в сутки. Время обработки и прибыль от продажи одного изделия каждого вида приведены в таблице 1. Найти оптимальный объем производства изделий каждого вида.
Таблица 1 – Время обработки и прибыль от продажи одного изделия
Изделие
|
Время обработки одного изделия, мин
|
Удельная прибыль, долл.
|
Станок 1
|
Станок 2
|
Станок 3
|
1
|
10
|
6
|
8
|
2
|
2
|
5
|
20
|
15
|
3
|
Задача 3. Фирма имеет возможность рекламировать свою продукцию, используя местные радио и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены суммой 1000 долларов в месяц. Каждая минута радиорекламы обходится в 5 долларов, а каждая минута телерекламы – в 100 долларов. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем телевидение. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше, чем объем сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Задача 4. Фирма производит два вида продукции – А и В. Объем сбыта продукции А составляет не менее 60 % общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции А составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны 20 и 40 долларов, соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.
Задача 5. Фирма выпускает ковбойские шляпы двух фасонов (А и В). Трудоемкость изготовления шляпы фасона А вдвое выше трудоемкости изготовления шляпы фасона В. Если бы фирма выпускала только шляпы фасона А, суточный объем производства мог бы составить 500 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 150 до 200 штук. Прибыль от продажи шляпы фасона А равна 8 долларам, а фасона В = 5 долларам. Определить, какое количество шляп каждого фасона следует изготовить, чтобы максимизировать прибыль.
Задача 6. Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков приведено в таблице 2.
Таблица 2 – Время обработки одного изделия
Станок
|
Время обработки одного изделия, ч
|
Тип 1
|
Тип 2
|
Тип 3
|
Тип 4
|
1
|
2
|
3
|
4
|
2
|
2
|
3
|
2
|
1
|
2
|
Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в Машино-часах). Стоимость Машино-часа составляет 10 и 15 долларов для станков 1 и 2, соответственно. Допустимое время использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1, 2, 3 и 4 равны 65, 70, 55 45 долларов соответственно. Составить план производства, максимизирующий чистую прибыль.
Задача 7. Завод выпускает изделия трех моделей (I, II и III). Для их изготовления используются два вида ресурсов (А и В), запасы которых составляют 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели приведены в таблице 3.
Таблица 3 – Расходы ресурсов
Ресурс
|
Расход ресурсов на одно изделие данной модели
|
I
|
II
|
III
|
А
|
2
|
3
|
5
|
В
|
4
|
2
|
7
|
Трудоемкость изготовления изделия модели I вдвое больше, чем изделия модели II, и втрое больше, чем изделия модели III. Численность рабочих завода позволяет выпускать 1500 изделий модели I. Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I, II и III, соответственно. Однако соотношение выпуска изделий моделей I, II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I, II и IIIсоставляет 30, 20 и 50 долларов, соответственно. Определить выпуск изделий, максимизирующий прибыль.
Задача 8. Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. В таблице 4 приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для каждого из трех исходов. У игрока имеется 500 долларов, причем использовать их в игре можно только один раз. Точный исход игры заранее неизвестен. Учитывая эту неопределенность, нужно распределить деньги так, чтобы максимизировать минимальную отдачу от этой суммы.
Таблица 4 – Возможные выигрыши и проигрыши
Исход
|
Выигрыш или проигрыш на каждый доллар, вложенный в данный вариант
|
1
|
2
|
3
|
4
|
1
|
-3
|
4
|
-7
|
15
|
2
|
5
|
-3
|
9
|
4
|
3
|
3
|
-9
|
10
|
-10
|
Задача 9. Небольшая фирма выпускает два типа автомобильных деталей (А и В). Для этого она закупает литье, подвергаемое токарной обработке, сверловке и шлифовке. Данные, характеризующие производительность станочного парка фирмы, приведены в таблице 5.
Таблица 5 – Производительность станков
Станки
|
Деталь А, шт./ч
|
Деталь В, шт./ч
|
Токарный
|
25
|
40
|
Сверлильный
|
28
|
35
|
Шлифовальный
|
35
|
25
|
Каждая отливка, из которой изготавливают деталь А, стоит 2 доллара. Стоимость отливки для детали В – 3 доллара. Продажная цена деталей равна, соответственно, 5 и 6 долларов. Стоимость часа станочного времени составляет по трем типам используемых станков 20, 14 и 17,5 долларов, соответственно. Предполагая, что можно выпускать для продажи любую комбинацию деталей А и В, нужно найти план выпуска продукции, максимизирующий прибыль.
Задача 10. Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.
Для того, чтобы цыплята достигли к восьмой неделе необходимого веса, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. В таблице 6 приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.
Таблица 6 - Содержание (по весу) питательных веществ
Ингредиент
|
Содержание питательных веществ, фунт/фунт ингредиента
|
Стоимость, долларов/фунт
|
Кальций
|
Белок
|
Клетчатка
|
Известняк
|
0,38
|
-
|
-
|
0,04
|
Зерно
|
0,001
|
0,09
|
0,02
|
0,15
|
Соевые бобы
|
0,002
|
0,5
|
0,08
|
0,4
|
Смесь должна содержать:
-
не менее 0,8 %, но и не более 1,2 % кальция;
-
не менее 22 % белка;
-
не более 5 % клетчатки.
Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и ее питательности.
страница 1 ... страница 3 | страница 4 | страница 5 страница 6
|